Multi-UAV Task Allocation Based on Grid-Based Particle Swarm and Genetic Hybrid Algorithm

Abstract

To address the uneven distribution of the Pareto front and insufficient convergence in multi-UAV task allocation, this paper proposes GrEAPSO, an improved algorithm that hybridizes Particle Swarm Optimization (PSO) with Genetic Algorithm (GA). GrEAPSO balances exploitation and exploration through grid partitioning, adopts a dual-encoding scheme coupled with crossover and mutation to enhance population diversity, and employs a grid-based environmental selection mechanism to improve the uniformity of the Pareto set. After initialization, the algorithm iteratively performs a PSO-based local search, genetic crossover and mutation, and grid-based environmental selection. The offspring and parent populations are then merged, and the archive set is updated accordingly. Across three military UAV task-allocation scenarios (small, medium, and large), GrEAPSO is benchmarked against MOPSO, NSGA-II/III, MOEA/D-DE, RVEA, IBEA, MOMVO, and MaOGOA. All experiments use a population size of 100. Its reference point is undominated and dominates some competitors, with median gains of 55.78% in hypervolume and 8.11% in spacing. Finally, the sensitive analysis further indicates that dividing the objective space into 15–20 grids offers the best trade-off between search breadth and solution distribution.

1. Introduction

Unmanned Aerial Vehicles (UAVs) possess advantages such as flexible spatial maneuverability, small target volume, and relatively low cost [1]. Currently, UAVs have extensive applications and development prospects in both military and civilian fields. In military scenarios, they are often used for strikes against hostile units, whereas in civilian scenarios, they are commonly used in agricultural production and for collecting photographic information [2,3]. However, a single UAV has limitations in practical applications, necessitating the coordination of multiple UAVs to accomplish complex tasks.

Multi-UAV task allocation refers to determining the number and performance characteristics of UAVs, defining the task area, and assigning specific tasks within the area to individual or multiple UAVs. Under the constraints of the allocation scheme, the objective is to compare the proposed schemes and identify one that meets the required criteria. Multi-UAV task allocation often involves various constraints, such as UAV payload, time windows, and threat levels, as well as multiple evaluation metrics, such as task rewards, task duration, energy consumption, and task risk. These factors make the multi-UAV task allocation problem NP-hard, with computational complexity that increases exponentially [4].

Currently, significant progress has been made in the research on multi-UAV task allocation [5,6]. Reference [7] analyzes the development of existing UAV allocation models and algorithms, categorizes them into centralized and distributed approaches, and discusses their advantages and disadvantages. Reference [8] proposes a Differential Evolution Adaptive Elite Butterfly Optimization Algorithm that achieves remarkable improvements in task allocation efficiency, avoiding plan stagnation and accelerating convergence. Reference [9] improves the traditional Wolf Pack Algorithm by proposing a Multi-Discrete Wolf Pack Algorithm that combines hybrid variable encoding with path planning to accommodate the discreteness and uncertainty in UAV task allocation. Reference [10] introduces an adaptive step-size factor to the classical Cuckoo Search Algorithm to accelerate the solving speed in the early stages and incorporates simulated annealing to prevent the algorithm from falling into local optima.

Genetic Algorithms (GAs) are known for their strong global search capability, parallelism, and adaptability, and researchers have made various improvements to apply them to UAV task allocation problems. Reference [11] employs an improved NSGA-II algorithm that features enhanced non-dominated sorting and elite retention strategies to preserve superior individuals from the parent generation directly. Reference [12] combines an improved Genetic Algorithm with an enhanced Simulated Annealing Algorithm to create a hybrid genetic algorithm that enriches population diversity through two-round selection and annealing mechanisms.

Particle Swarm Optimization (PSO) algorithms are characterized by their ease of implementation, fast search speed, and robustness, and are often used to optimize UAV task allocation problems. Reference [13] develops an improved multi-objective PSO algorithm based on adaptive angle region division, utilizing a global attraction mechanism to converge the algorithm to the global non-dominated solution. Reference [14] proposes an improved PSO algorithm for cooperative task allocation among multiple UAVs, employing discrete encoding to represent particle positions. Reference [15] introduces an improved algorithm that combines PSO and GA, incorporating partial-matching crossover and double transposition mutation. Reference [16] integrates an adaptive perturbation strategy with the local search mechanism of simulated annealing, enabling the algorithm to escape local optima and find superior solutions. Reference [17] introduces an improved PSO algorithm based on local random search and variable neighborhood search, employing a novel encoding scheme to address “deadlock” issues.

To address the multi-objective optimization problem in multi-UAV task allocation, a grid-based multi-objective PSO algorithm is proposed. The key innovations are as follows:

• A grid partitioning strategy is introduced, refining solution screening via a grid-scoring mechanism to effectively balance local exploitation and global exploration.
• The algorithm integrates a Genetic Algorithm and Particle Swarm Optimization, leveraging PSO for rapid localization of advantageous regions in the early stages and using genetic crossover and mutation to enhance population diversity in later stages, thereby avoiding premature convergence.
• A dual-coding mechanism is designed to coordinate the transition between PSO and GA, enabling efficient encoding and decoding between particle and genetic representations.
• An adaptive parameter adjustment strategy is employed. In the PSO phase, an adaptive inertia weight facilitates rapid localization of target regions in the early stages and fine-grained search in the later stages. In the GA phase, adaptive crossover and mutation probabilities effectively regulate population diversity.
• A grid-based environmental selection mechanism is designed, prioritizing Pareto dominance relationships and grid scoring to ensure uniform population and solution distribution. This mechanism is also incorporated into the selection of PSO’s global best point, further enhancing algorithm convergence.

It should be emphasized that the present study focuses on military strike missions, where strike benefit and UAV survivability are the primary concerns.

Nevertheless, the proposed GrEAPSO framework is generic; by simply redefining the objective functions—e.g., minimizing energy consumption or flight duration—the same algorithm can be readily applied to civilian applications such as parcel delivery [18], precision agriculture, or disaster-area surveillance [19].

In the simulation experiments, a bi-objective UAV task allocation model is employed. Three experimental environments are designed to simulate small-scale, medium-scale, and large-scale task allocation scenarios. The proposed algorithm is compared with other mainstream algorithms through practical simulations, with performance evaluated using Pareto front, hypervolume, and spacing metrics. Sensitivity analysis is also conducted by varying the number of grid divisions to assess their impact on the algorithm. Experimental results demonstrate that the proposed algorithm outperforms others in terms of Pareto front quality, hypervolume, and spacing, with optimal results achieved for grid divisions between 15 and 20.

2. Multi-UAV Task Allocation Modeling

2.1. Problem Description

In the field of UAV task allocation, various models exist, each tailored to different application scenarios, resulting in significant diversity. This study considers a military application UAV task allocation model, focusing on two optimization objectives: the strike benefits of task points and the damage costs of UAVs. These objectives exhibit low correlation and are computationally independent, facilitating the discovery of more non-dominated solutions and broadening the Pareto front, making the model suitable for comparative studies across multiple algorithms. Similar research on this type of model can be found in [20,21,22].

To reduce problem complexity, the following assumptions are made:

• This model mainly considers the strike benefits and destruction costs of drones. For the convenience of modeling, constraints on energy consumption and time costs are not imposed.
• UAV task execution is treated as an independent event, and only damage costs and task benefits are evaluated.
• The sequence of task execution by UAVs is disregarded.
• Suppose there are N_U(N_U∈N⁺) UAVs on the battlefield, tasked with striking N_T(N_T∈N⁺) targets. $U=\{U_1,U_2,\dots ,U_{N_U}\}$ represents the set of UAVs, where $U_i$ represents the i-th UAV, $T=\{T_1,T_2,\dots ,T_{N_T}\}$ and $T_j$ represents the j-th task.

When a UAV attacks a target, UAV damage is likely, and the probability of damage varies depending on the UAV and the specific task it performs. Similarly, target points also have a probability of being destroyed. The success rate of a UAV executing a task also varies based on the specific UAV and the target it is assigned to.

2.2. Task Allocation Constraints

During UAV task execution, there are two common constraints: payload and maximum range. To prevent UAVs from repeatedly executing the same task, we require that different UAVs perform different tasks for the same target.

The aforementioned requirements imply that each UAV can strike a target point only once. If this constraint is not considered, it may lead to an uneven distribution of limited ammunition, causing an over-concentration on high-value targets. Therefore, the number of strikes on high-value targets must be restricted. In conclusion, UAV allocation needs to satisfy the following constraints.

• Ammunition Constraint for UAVs: The number of tasks assigned to each UAV must not exceed its ammunition capacity.

  $${\displaystyle \sum _{j=1}^{N_T}{x}_{ij}\le n_i,i\in I_{N_U}}$$

  (1)
• Target Task Number Constraint: The number of tasks for each target is limited.

  $${\displaystyle \sum _{i=1}^{N_U}{x}_{ij}\le m_j,j\in I_{N_T}}$$

  (2)
• UAV Attack Constraint: Each UAV can only attack the same target once.

  $$a_{ij}\le 1,i\in I_{N_U},j\in I_{N_T}$$

  (3)

  where $I_n=\{1,2,\dots ,n\}$, we define $n_i(i\in I_{N_U})$ as the ammunition capacity of UAV $U_i$, $m_j(j\in I_{N_T})$ as the maximum number of tasks for target point $T_j$, and $a_{ij}(i\in I_{N_U},j\in I_{N_T})$ as the number of tasks executed by UAV $U_i$ on target point $T_j$.

2.3. Objective Function Model

The optimal task allocation plan for UAVs often implies that the UAV collaborative operation system has achieved optimal performance. Performance measurement has diverse characteristics, so evaluating UAV task allocation results often involves multiple dimensions. It is difficult to directly determine whether one plan is better than another by simply comparing individual results. Therefore, a multi-objective combinatorial optimization problem is proposed for evaluating UAV task execution metrics.

Considering that both UAVs and target points have their own probabilities of being destroyed, and aligning with the practice of multi-objective optimization to minimize objective functions, the following two objective functions are proposed: minimize the number of undestroyed targets and minimize the operational cost of UAVs.

The two objectives quantify the expected loss in strike effectiveness and the expected operational cost, both from a probabilistic perspective. Objective 1 computes the expected total value of targets that remain undestroyed after all strikes. Objective 2 computes the expected total cost of UAVs that are destroyed during the same strikes.

• Minimize the value of targets not destroyed by UAVs:

  $$\min f_1(x)=V_{all}-{\displaystyle \sum _{i=1}^{N_U}{\displaystyle \sum _{j=1}^{N_T}{K}_{ij}{V}_{T_j}{x}_{ij}}}$$

  (4)
• Minimize the UAV damage cost:

  $$\min f_2(x)={\displaystyle \sum _{i=1}^{N_U}{\displaystyle \sum _{j=1}^{N_T}{P}_{ij}{W}_{U_i}{x}_{ij}}}$$

  (5)

  where $x_{ij}\in \{0,1\}$, $x_{ij}=1$ if and only if UAV $U_i$ strikes target $T_j$, $P_{ij}$ and $K_{ij}$ represent the probabilities of the UAV and the target point being destroyed during the strike process, respectively. $W_{U_i}$ represent the value of the UAV, $V_{T_j}$ represents the benefit of destroying the target, and $V_{all}$ represents the total value of the tasks. Equation (4) is measured in monetary units (same dimension as target value); a lower value indicates fewer high-value targets surviving, hence better strike effectiveness. Equation (5) is also measured in monetary units (same dimension as UAV cost); a lower value indicates fewer UAVs lost, hence lower operational risk.

Combine the constraint conditions and objective functions to form a multi-objective optimization model.

3. Task Allocation with Improved GrEAPSO Algorithm

3.1. Algorithm Description

The Particle Swarm Optimization (PSO) algorithm, proposed by Kennedy and Eberhart, is a swarm intelligence algorithm that simulates the social behavior of birds foraging. Multi-objective Particle Swarm Optimization (MOPSO) stores historically optimal solutions found by particles, retaining previously generated non-dominated solutions. By combining these historical non-dominated solutions, it uses a global attraction mechanism to converge the solutions toward the overall Pareto-optimal front [23].

On the other hand, Genetic Algorithms (GAs) are inspired by Darwin’s theory of evolution, simulating the process of biological inheritance and mutation to produce offspring. Multi-objective Genetic Algorithms (MOGAs) improve the quality of solutions in the population through processes such as selection, crossover, and mutation [24].

This section introduces the GrEAPSO algorithm, specifically designed to solve constrained multi-objective optimization problems. The algorithm employs an innovative two-layer solution update strategy, combining the crossover and mutation strategies of Genetic Algorithms with the position update mechanism of Particle Swarm Optimization. This integration enhances the balance between diversity and convergence. The two-layer update strategy leverages the efficient search capabilities of PSO in continuous spaces while incorporating the diversity-maintaining ability of GAs in combinatorial optimization problems, making it particularly suitable for hybrid-discrete optimization problems like UAV task allocation.

In each iteration, the algorithm first applies PSO for position updates, then generates new candidate solutions through genetic mutation operations, and finally determines the next generation of the population using an environment selection mechanism based on a grid strategy. This hybrid strategy allows the algorithm to escape local optima, explore the solution space more effectively, and address both optimization and constraint challenges.

3.2. Encoding, Decoding, and Initialization

For the multi-objective optimization problem proposed in the previous section, a dual encoding mechanism combining continuous and binary encodings is adopted. Continuous space encoding is suitable for updates in the Particle Swarm Optimization (PSO) algorithm, while binary encoding is well suited to crossover and mutation operations.

In continuous space encoding, each individual in the algorithm is represented by a three-dimensional array $position(U_i,T_j,k)$, where $k$ represents the individual’s index. Its range is $[-1,1]$, representing the tendency of UAV $U_i$ to strike target $T_j$ in the continuous space. The higher the value, the stronger the tendency to strike. Binary encoding $binary(U_i,T_j,k)$ takes values of 0 or 1 and directly represents the task allocation relationship between UAV $U_i$ and target $T_j$. A value of 1 indicates an assignment, while a value of 0 indicates no assignment.

The encoding mechanism maps binary encodings to spatial particle positions using a differentiated mapping method. Binary elements with a value of 1 are mapped to higher values in the continuous value space, while binary elements with a value of 0 are mapped to lower values in the continuous value space.

Random perturbations are introduced to prevent particle homogenization, adding randomness within their respective intervals and increasing the search space. This approach enhances diversity and improves the algorithm’s ability to explore the solution space. The implementation is as follows:

$$p(i)=\left\{\begin{array}{l}{\displaystyle \frac{(1+r)x_{\max }}{2}},b(i)=1\\ x_{\min }+{\displaystyle \frac{r·\left|x_{\min }\right|}{2}},b(i)=0\end{array}\right.$$

(6)

where $p(i)$ represents the i-th element of the continuous position matrix $b(i)$ represents the i-th element of the binary matrix, r denotes a random real number in the interval $[0,1]$, $x_{\max }$ and $x_{\min }$ are the lower and upper bounds of the position, respectively.

We use a banded mapping to maintain exploration while preserving a strong discrete signal: map 1 s to the upper band of the position interval and 0 s to the lower band, and inject small uniform noise within each band. This ensures “1 > 0” in the continuous domain (stabilizing PSO velocity updates and guidance) while the in-band noise prevents particle homogenization and enlarges the effective search space. For Scenarios 2 and 3, a stronger-signal variant is also available when harder boundaries are desired. The core principle is: the continuous→binary step uses structured selection rules to translate PSO updates into meaningful allocations; the binary→continuous step uses banded back-mapping with light perturbations to re-embed discrete assignments into a smooth domain, providing stable, exploitable guidance for the next PSO step while maintaining diversity and exploratory power.

The decoding mechanism focuses on the continuous-space particle positions in the algorithm. This mechanism determines how to translate particle swarm optimization (PSO) updates into meaningful task allocation decisions.

In this process:

• Extract the Number of UAVs and Tasks: The first step is to extract the number of UAVs and tasks from the problem definition.
• Max-Value-Based Allocation Strategy: For each task, the UAV with the highest value in the continuous space is selected for assignment.
• UAV Allocation Check and Global Validity Verification: Finally, a check is performed to verify the validity of UAV assignments and the overall effectiveness of the allocation globally.

To ensure that evaluation and archiving operate only on feasible solutions, GREAPSO centralizes structural feasibility in a decode → repair → evaluate pipeline. After decoding a particle into a binary UAV–task assignment matrix, the repair step (i) resolves column conflicts to enforce at most one UAV per task, (ii) truncates rows to impose per-UAV upper bounds on the number of assigned tasks, and (iii) guarantees at least one task per UAV by preferentially assigning unallocated tasks or transferring a task from UAVs with multiple assignments. These operations are executed in a fixed order and are designed not to invalidate previously satisfied constraints, thereby jointly enforcing column uniqueness, row upper bounds, and row lower bounds. Although decoding (e.g., argmax per task or probabilistic Top-k) may temporarily violate constraints, the repair deterministically eliminates such violations, ensuring every solution used for fitness computation and stored in the external archive is feasible.

3.3. Grid Scoring Theory and Embedding

To ensure the diversity of solutions, the solution space is evenly divided into grids. Environmental selection is performed based on the grid ranking of particles, the grid crowding degree ranking, and the distance ranking of the optimal point in the grid. This mechanism is introduced in the multi-objective multi-UAV task allocation problem, as described in [25].

Assuming the number of grids is predetermined, the grid division is based on the positions of the solutions. To achieve the corresponding grid division, the upper and lower bounds for each dimension must be determined first. The formulas for this process are as follows:

$$l_k={\min }_k(P)-[\max ({\max }_k(P)-{\min }_k(P),\epsilon )]/(2div)$$

(7)

$$u_k={\max }_k(P)+[\max ({\max }_k(P)-{\min }_k(P),\epsilon )]/(2div)$$

(8)

where k represents the corresponding dimension, ${\min }_k(p)$ and ${\max }_k(p)$ represent the minimum and maximum values of the population P in the k-th objective dimension, $div$ represents the number of grid divisions, $l_k$ and $u_k$ represent the grid lower and upper bounds of the population in the k-th objective dimension. $\epsilon$ is a very small positive number.

The grid width in the k-th objective dimension and the grid position of particle x are calculated as follows:

$$d_k=(u_k-l_k)/div$$

(9)

$$G_k(x)=floor(F_k(x)-l_k)$$

(10)

where $F_k(x)$ represents the objective value of particle x in the k-th objective dimension.

The grid difference between particles x and y in the population is calculated as follows:

$$G{D}_{(x,y)}={\displaystyle \sum _{k=1}^M|G_k(x)-G_k(y)|}$$

(11)

where M represents the number of dimensions, the grid difference of particles is influenced by the size of the dimensions. The larger M, the denser the grid division, and the greater the grid difference of the particles. Therefore, the grid mechanism is particularly suitable for solving high-dimensional objective functions

The solutions are comprehensively evaluated using the grid ranking $(GR)$, the grid crowding degree indicator $(GCD)$, and the grid coordinate point distance indicator $(GCPD)$ of particle x. The calculation formulas are given below:

$$G{R}_{(x)}={\displaystyle \sum _{k=1}^M{G}_k(x)}$$

(12)

$$GC{D}_{(x)}={\displaystyle \sum _{y\in N(x)}(M-G{D}_{(x,y)})}$$

(13)

$$GCP{D}_{(x)}=\sqrt{{\displaystyle \sum _{k=1}^M((F_k(x)-(l_k+G_k(x)\times d_k))/d_k{)}^2}}$$

(14)

where if $G{D}_{(x,y)}\le M$, then $y\in N(x)$.

During the environmental selection process, the population is selected according to the priority order of $GR, GCD, GCPD$. Traditional pairwise comparisons significantly increase the runtime of the algorithm, so normalized calculations are used for fast environmental selection. The normalization calculation for particles is as follows:

$$G{R}_{norm}={\displaystyle \frac{G{R}_{(x)}-G{R}_{\min }}{G{R}_{\max }-G{R}_{\min }+\epsilon }}$$

(15)

where $G{R}_{\max }$ and $G{R}_{\min }$ represent the maximum and minimum values of the current population particles in the grid indicator $GR$. $\epsilon$ is a very small positive number to prevent the denominator from being zero. The normalization formulas for $GCD$ and $GCPD$ are similar to that of $GR$

After obtaining the normalized indicators, a unified calculation is performed for the particles. The grid indicator is used to measure the particle’s grid performance, and its calculation is as follows:

$$Scor{e}_x=100\times G{R}_{norm(x)}+10\times GC{D}_{norm(x)}+GCP{D}_{norm(x)}$$

(16)

The normalized indicator values all fall within the range $[0,1]$. Therefore, the weighted indicator $Scor{e}_x$ effectively represents the grid indicator, where a lower value indicates a better-performing particle, which is given priority for selection.

3.4. Population Particle Update Mechanism

Using the Particle Swarm Optimization (PSO) algorithm, particles are updated by adjusting their positions and velocities. In PSO, each particle has two characteristics: velocity and position. The updated positions of the new generation of particles are primarily determined by the velocities and positions of the previous generation. The update equations are as follows:

$$V^{(t+1)}=\omega \cdot V^t+c_1\cdot r_1(P_{best}-X^t)+c_2\cdot r_2(G_{best}-X^t)$$

(17)

$$X^{(t+1)}=X^t+V^{(t+1)}$$

(18)

Among them, $V^t$ represents the velocity of the particle in the t-th generation population, and $X^t$ represents the position of the particle in the t-th generation population. $\omega$ is the inertia weight, which affects the overall update speed of the particle swarm. Generally, $\omega$ is within the range $\omega \in [0.4,0.8]$

$P_{best}$ and $G_{best}$ represent the individual best particle position and the global best particle position, respectively. The grid mechanism is used to evaluate the solutions in the archive set, prioritizing the selection of the solution with the best grid score as the global best. $r_1$ and $r_2$ are two random numbers in the range $[0,1]$.

In early iterations, we prefer a higher inertia weight to approach the Pareto front quickly. Conversely, at later stages of iteration, we prefer a lower inertia weight to thoroughly explore the solution space. This paper adopts a linearly decreasing inertia weight adjustment strategy:

$${\omega }^t={\omega }_{\max }-({\omega }_{\max }-{\omega }_{\min })\times {\displaystyle \frac{t}{T_{\max }}}$$

(19)

where ${\omega }^t$ represents the inertia weight of the t-th generation, ${\omega }_{\max }$ and ${\omega }_{\min }$ represent the upper and lower limits of the inertia weight, respectively, $T_{\max }$ represents the maximum number of iterations.

To limit the search space and prevent particles from flying out of the search region, the following constraints are applied to the particle’s velocity and position:

$$V_i^{t+1}=\max (\min (V_i^{t+1},V_{\max }),-V_{\max })$$

(20)

$$X_i^{t+1}=\max (\min (X_i^{t+1},X_{\max }),X_{\min })$$

(21)

Using a genetic algorithm to generate diverse solutions, similarly, to address the different requirements for crossover and mutation at the early and later stages of iterations, an adaptive crossover and mutation strategy is adopted

$$P_c^t=P_{c,\min }+(P_{c,\max }-P_{c,\min })\times (1-{\displaystyle \frac{t}{T_{\max }}})$$

(22)

$$P_m^t=P_{m,\min }+(P_{m,\max }-P_{m,\min })\times {(1-{\displaystyle \frac{t}{T_{\max }}})}^2$$

(23)

where $P_c^t$ and $P_m^t$ are the crossover rate and mutation rate of the t-th generation, $P_{c,\min }$ and $P_{c,\max }$ are the minimum and maximum values of the crossover rate, $P_{m,\min }$ and $P_{m,\max }$ are the minimum and maximum values of the mutation rate.

Three crossover strategies are used, and a crossover mode is randomly selected each time to enhance search diversity. A position-flipping mutation strategy is applied, in which the binary value at the mutation point is flipped.

• Uniform Crossover: For each position in the binary representation, a fixed probability is used to determine whether to exchange the values at the corresponding positions of the parents. The related formula is as follows:

  $$child1(i,j)=parent2(i,j)$$

  (24)

  $$child2(i,j)=parent1(i,j)$$

  (25)
• Row Crossover: Row crossover is performed at the level of drones, where the specific task sequences of two drones are exchanged. One or two-point crossover along the row (UAV) dimension. We swap contiguous blocks of whole rows between parents, effectively exchanging bundles of tasks assigned to subsets of UAVs. The formula is as follows:

  $$child1(i,j)=\left\{\begin{array}{l}parent2(i,j),i\in (p_1,p_2]\\ parent1(i,j),otherwise\end{array}\right.$$

  (26)

  $$child2(i,j)=\left\{\begin{array}{l}parent1(i,j),i\in (p_1,p_2]\\ parent2(i,j),otherwise\end{array}\right.$$

  (27)
• Column Crossover: The object of column crossover is a specific task, where the allocation status of a particular task between two parent solutions is exchanged. One- or two-point crossover along the column (task) dimension. We swap contiguous blocks of whole columns, effectively exchanging the multi-UAV assignment pattern for task subsets. The formula is as follows:

  $$child1(i,j)=\left\{\begin{array}{l}parent2(i,j),j\in (q_1,q_2]\\ parent1(i,j),otherwise\end{array}\right.$$

  (28)

  $$child2(i,j)=\left\{\begin{array}{l}parent1(i,j),j\in (q_1,q_2]\\ parent2(i,j),otherwise\end{array}\right.$$

  (29)

3.5. Environment Selection and Archive Set Update

Maintaining the diversity and convergence of the solution set is crucial in multi-objective optimization problems. A grid-based scoring mechanism is used to handle environmental selection and to update the archive set. Environmental selection and archive set updating are closely related. Environmental selection determines which solutions remain in the population to participate in updates, while archive-set updating decides which solutions are retained in the optimal solution set and serve as candidates. Both processes utilize the grid scoring mechanism, with environmental selection focusing on the evolutionary diversity of the population, and archive set updating ensuring the quality of the optimal solution set and the selection of the global optimal points.

During the environmental selection process of each generation, the population updated by the particle swarm is first merged with the offspring generated through crossover and mutation. The merged population is then subjected to non-dominated sorting to obtain multiple non-dominated levels. Starting from the first non-dominated level, individuals are added to the population until the population size is reached. If the remaining capacity is sufficient to include all individuals at the current level, all of them are added. Otherwise, individuals are added sequentially according to the grid scoring order until the population size is reached.

$$J_1(x_1)\le J_1(x_2),J_2(x_1)\le J_2(x_2)$$

(30)

where $x_1$ and $x_2$ represent the two particles to be compared, $J_1$ and $J_2$ are the two objective functions.

3.6. Overall Algorithm Process

Algorithm 1 shows the overall algorithm process.

Algorithm 1. GrEAPSO Algorithm Process

1. Initialize the population and archive set, calculate the objective function using Equations (4) and (5), and repair infeasible solutions.

2. for iter = 1:maxiter

3. Update the weights and crossover-mutation probabilities using Equations (19), (22) and (23).

4. if iter = 1:

5. Select $G_{best}$ according to the traditional particle swarm method.

6. end if

7. Update the particle swarm positions using Equations (17) and (18), and update the particles’ $P_{best}$

8. Decode and repair using Equation (6), calculate the fitness function after particle swarm operations using Equations (4) and (5), and record the results.

9. Perform crossover and mutation operations using Equations (24)–(29), repair and evaluate the solutions, calculate the offspring fitness function using Equations (4) and (5), and record the results.

10. Perform environmental selection, merge the populations, and partition the solution space grid using Equations (7) and (8).

11. Perform fast non-dominated sorting to populate the population, and use Equation (16) to score and filter the solutions on the contentious front.

12. Update the archive set and $G_{best}$

13.end for

14. Output the archive set as candidate solutions.

4. Simulation Analysis of Instances

The verification platform is a PC equipped with an Intel(R) Core(TM) i5-8250U processor and 8.00 GB of memory. All algorithms are executed on MATLAB R2023a, with the maximum number of iterations set to 100 for all algorithms.

4.1. Dual-Scenario Simulation

This section presents simulation experiments comprising three scenarios corresponding to small-, medium-, and large-scale UAV task allocation settings. The objective is to validate the feasibility and superiority of the proposed GrEAPSO algorithm within the current military application model.

The algorithm proposed in this paper is compared with the traditional multi-objective particle swarm optimization algorithm MOPSO [26], the NSGAII [27] algorithm, the NSGA-III algorithm [28], the MOEA/D-DE algorithm [29], the RVEA algorithm [30], the IBEA algorithm [31], the MOMVO algorithm [32] and the MaOGOA algorithm [33] by solving the problem separately and comparing the results. The algorithm’s detailed parameter settings are provided below.

Common settings: population size 100; 100 iterations $T_{\max }=100$; decision bounds [−5, 5]; for PSO-based methods, the maximum velocity is $v_{\max }=1.0$; archive size = 100 when applicable.

GREAPSO: PSO with linearly decreased inertia weight $\omega$ from 0.9 to 0.4, cognitive/social factors $c_1=c_2=1.5$; position bounds $[-5,5]$. A grid-based external archive (archive size 100, grid divisions 10) is used for leader selection. A GA-style diversity stage applies simulated binary crossover $P_c=0.9$ and polynomial mutation $P_m=0.1$ on binary assignments, followed by repair.

MOPSO: inertia weight $\omega$ linearly decreases from 0.9 to 0.4; $c_1=c_2=1.5$; position bounds [−5, 5], $v_{\max }=1.0$. Uses an external repository (archive size 100) with a grid density estimator (10 divisions per objective) for leader selection.

NSGA-II: tournament selection, simulated binary crossover with $P_c=0.9$ and polynomial mutation with $P_m=0.1$, fast non-dominated sorting and crowding distance for environmental selection. Representation is a binary assignment with problem-specific repair.

NSGA-III and RVEA: we employ simulated binary crossover $P_c=0.9$ and polynomial mutation $P_m=0.1$. NSGA-III uses Deb–Jain normalization and Das–Dennis reference vectors (H = 99 for two objectives). RVEA uses $\alpha =2$ and adapts reference vectors every $fr=0.2\times T_{\max }$.

MOEA/D-DE:Tchebycheff decomposition with neighborhood size $T=20$; $F=0.5$ $C_r=0.9$; the ideal point is updated online.

IBEA: ε-indicator with κ = 0.05 by default (2-objective HV-indicator is also supported but costlier).

MOMVO and MaOGOA: we follow the original MVO/GOA schedules: wormhole existence probability $WEP\in [0,2,1.0]$, traveling distance rate $TDR\in [0.01,1.0]$, and GOA contraction factor $c\in [1.0,4\ast {10}^{-5}]$, with GOA social function parameters $f=0.5$ and $L=1.5$.

4.1.1. Experiment 1

The random seed is fixed to $rng(42)$.The task scenario involves four UAVs $(N_U=4)$ and eight target points $(N_T=8)$. Each UAV carries two rounds of ammunition $(n_i=2)$, and each target point has only one task to be executed $(m_j=1)$. When a UAV strikes a target point, the probabilities of destruction for both the UAV $P_{ij}$ and the target point $K_{ij}$ are shown in

Table 1. Destruction Rate of UAVs and Target Points.

UAVS		Target Point $({\mathit{T}}_1-{\mathit{T}}_8)$ Destruction Rate
$U_1$	P	[0.16,0.65,0.14,0,16,0.44,0.14,0.35,0.25]
	K	[0.5,0.8,0.3,0.4,0.5,0.6,0.6,0.7]
$U_2$	P	[0.14,0.16,0.44,0.14,0.65,0.16,0.45,0.35]
	K	[0.8,0.4,0.4,0.8,0.7,0.6,0.8,0.6]
$U_3$	P	[0.44,0.14,0.16,0.16,0.14,0.65,0.35,0.18]
	K	[0.6,0.5,0.8,0.3,0.8,0.3,0.7,0.7]
$U_4$	P	[0.65,0.14,0.16,0.44,0.06,0.16,0.55,0.48]
	K	[0.6,0.4,0.2,0.3,0.3,0.6,0.5,0.6]

. The values of the UAVs and target points are listed in

Table 2. Value of UAVs and Target Points.

Target Point Number	${\mathit{T}}_1-{\mathit{T}}_8$
Value	[0.62,0.65,0.68,0.7,0.73,0.78,0.81,0.85]
UAV number	$U_1-U_4$
Value	[0.8,1.1,0.9,1.3]

.

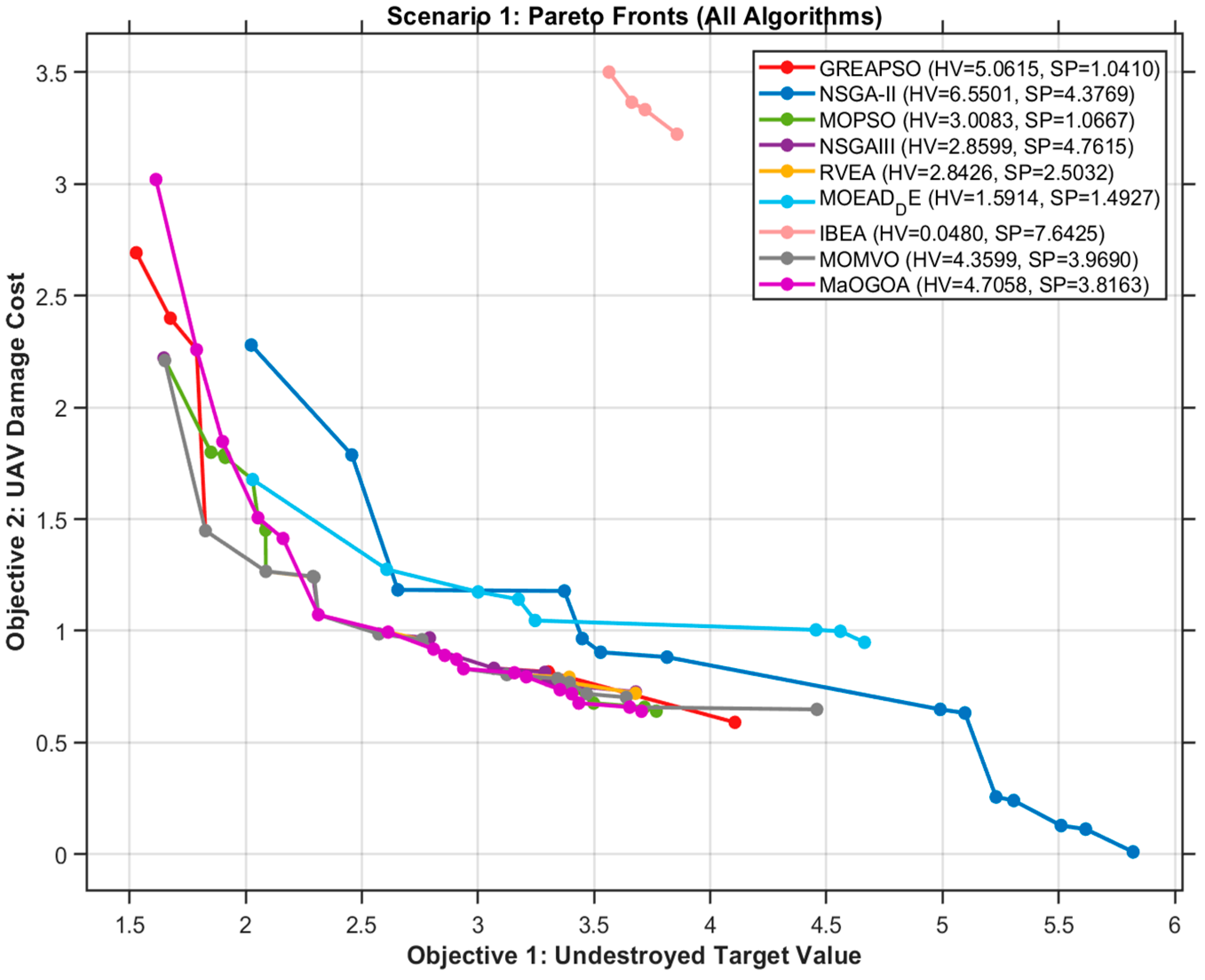
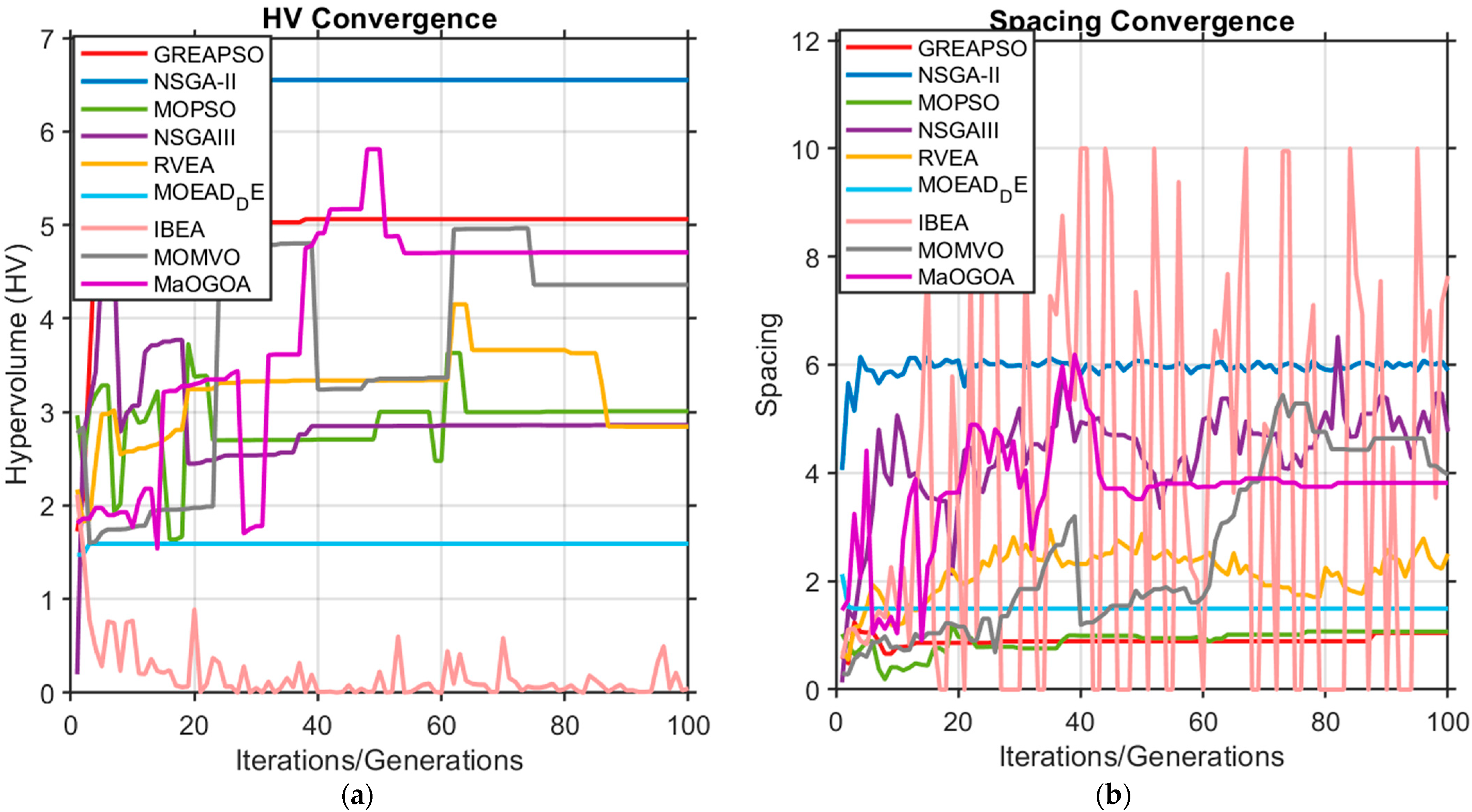
Figure 1, Figure 2 and Figure 3 present the simulation results for Scenario 1. Figure 1 shows the Pareto front distributions of each algorithm, with the legend reporting their final hypervolume and spacing metrics. It can be observed that GrEAPSO, MOMVO, MaOGOA, MOPSO, NSGA-III, and RVEA all produce well-formed Pareto fronts, with widely distributed front points and no clear dominance among them. In contrast, MOEA/D-DE, NSGA-II, and IBEA exhibit inferior Pareto fronts, with their points largely dominated by those of other algorithms; among these, MOEA/D-DE and NSGA-II still maintain reasonably good distributions, whereas IBEA performs worst in both solution quality and spread.

Figure 2 depicts the evolution of hypervolume and spacing with the number of iterations. The results indicate that GrEAPSO achieves the second-best hypervolume and the best spacing, with relatively smooth trajectories, demonstrating solid performance. Notably, IBEA’s spacing fluctuates markedly because it finds few non-dominated solutions, its archive degrades severely, and the Pareto front is sparsely populated, leading to pronounced oscillations—an observation consistent with Figure 1.

Figure 3 reports, for each algorithm, the front-point solution closest to the ideal point (0, 0). GrEAPSO’s solution dominates those of NSGA-II and IBEA and is not dominated by the solutions of the remaining algorithms.

4.1.2. Experiment 2

A medium-scale allocation model is used, with more task points and increased UAV ammunition capacity compared to Experiment 1. The random seed is fixed to $rng(42)$. The relevant information for the newly added points is shown in

Table 3. Information on Newly Added Target Points.

UAVS	New Point $({\mathit{T}}_9-{\mathit{T}}_{20})$ Corresponding Destruction Rate
$U_1$	P	[0.21,0.15,0.32,0.18,0.46,0.23,0.55,0.14,0.35,0.16,0.26,0.25]
	K	[0.7,0.6,0.5,0.6,0.4,0.6,0.4,0.3,0.3,0.8,0.3,0.7]
$U_2$	P	[0.3,0.24,0.51,0.44,0.44,0.3,0.42,0.15,0.16,0.18,0.08,0.48]
	K	[0.6,0.7,0.7,0.3,0.3,0.5,0.3,0.5,0.3,0.7,0.3,0.6]
$U_3$	P	[0.53,0.16,0.44,0.68,0.14,0.25,0.5,0.48,0.14,0.09,0.13,0.6]
	K	[0.7,0.4,0.6,0.5,0.3,0.5,0.4,0.6,0.3,0.8,0.4,0.8]
$U_4$	P	[0.63,0.3,0.42,0.08,0.5,0.18,0.48,0.15,0.16,0.2,0.15,0.6]
	K	[0.7,0.6,0.6,0.7,0.4,0.7,0.6,0.5,0.4,0.8,0.4,0.8]
		New Point $(T_9-T_{20})$
Value		[0.72,0.78,0.62,0.65,0.76,0.88,0.63,0.7,0.68,0.82,0.75,0.81]

.

Figure 4, Figure 5 and Figure 6 present the simulation results for Scenario 2. Figure 4 shows the Pareto front distributions for each algorithm, with the legend reporting their final hypervolume and spacing metrics. It can be observed that GrEAPSO, MOMVO, MaOGOA, MOPSO, NSGA-III, MOEA/D-DE, and RVEA all achieve well-formed Pareto fronts, with broadly distributed front points and no obvious dominance among them. In contrast, NSGA-II and IBEA exhibit inferior Pareto fronts, with their points generally dominated by those of other algorithms and lying far from the ideal point. While NSGA-II’s front distribution is still reasonably good, it contains many solutions with low task-assignment rates, which would typically be filtered out in practical military scenarios. IBEA performs worst in both the quality and spread of front solutions.

Figure 5 depicts the evolution of hypervolume and spacing over iterations. The results indicate that GrEAPSO attains the third-best hypervolume and the third-best spacing, with relatively smooth trajectories, demonstrating solid performance. Notably, IBEA and MOEA/D-DE exhibit pronounced fluctuations in spacing because they identify few non-dominated solutions, leading to severe archive degradation and an insufficiently populated Pareto front—an observation consistent with Figure 4.

Figure 6 reports, for each algorithm, the solution on its Pareto front that is closest to the ideal point (0, 0). GrEAPSO’s solution dominates those of NSGA-III, RVEA, MaOGOA, and IBEA, and is not dominated by the solutions of the remaining algorithms.

4.1.3. Experiment 3

Scenario 3 considers a large-scale UAV strike mission planning simulation as an extension of Scenarios 1 and 2. The parameters of the originally defined UAVs and targets remain unchanged, while additional UAVs and target points are randomly generated at scales consistent with Scenarios 1 and 2. The random seed is fixed to $rng(2025)$. The task scenario involves ten UAVs $(N_U=10)$ and fifty target points $(N_T=50)$. Each UAV carries four rounds of ammunition $(n_i=4)$, and each target point has only one task to be executed $(m_j=1)$.

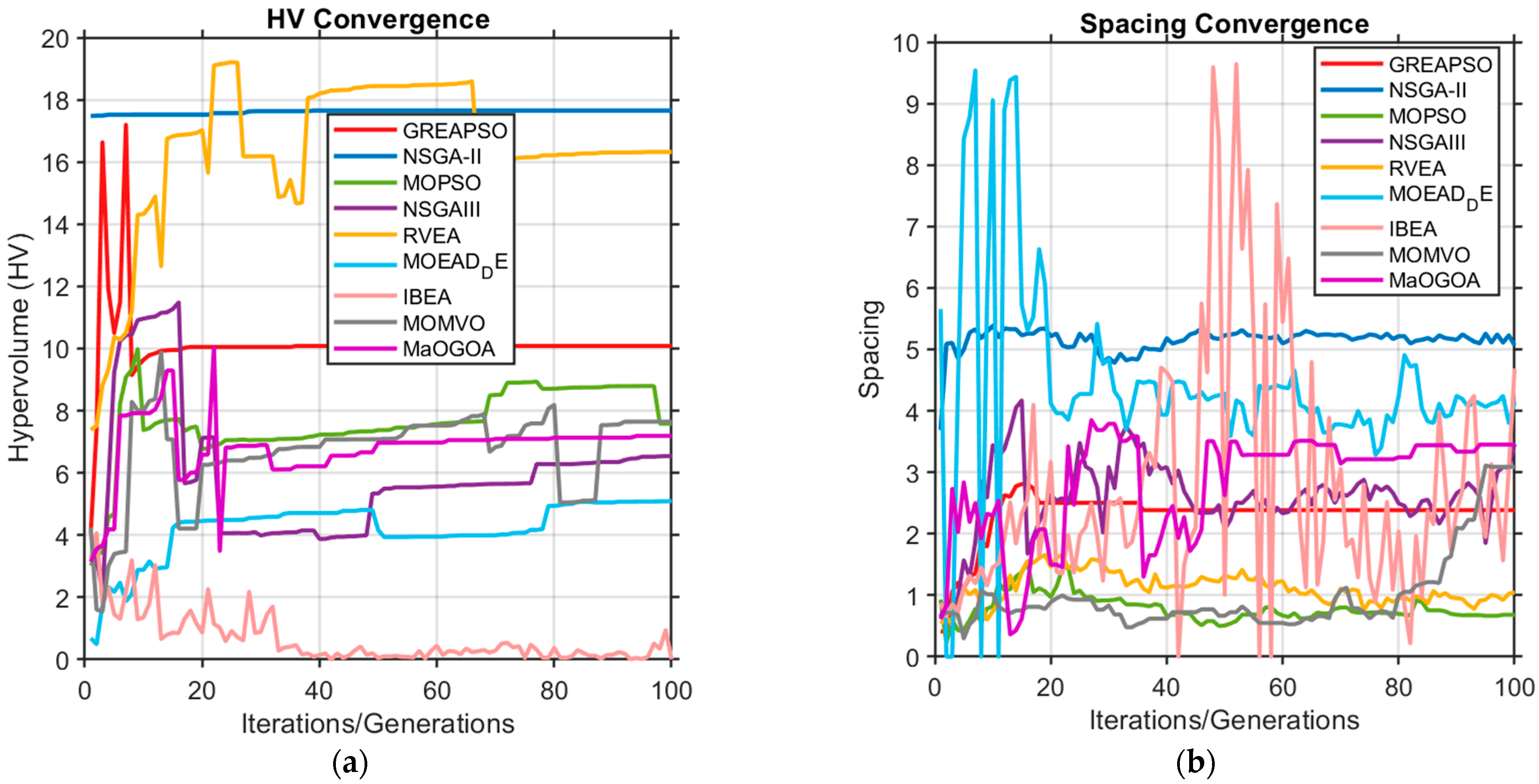
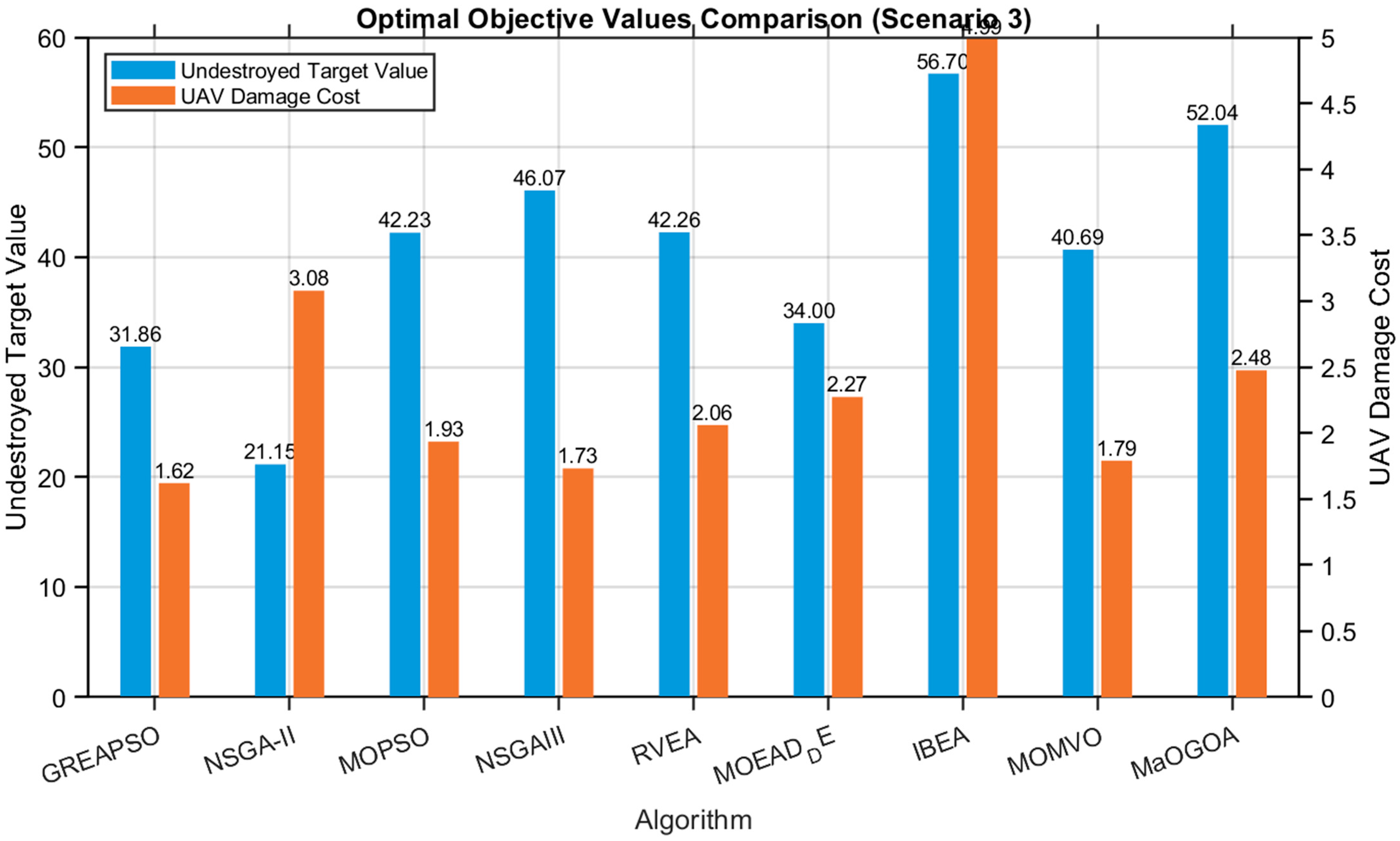
Figure 7, Figure 8 and Figure 9 present the simulation results for Scenario 2. Figure 7 shows the Pareto front distributions of each algorithm, with the legend reporting their final hypervolume and spacing metrics. It can be observed that GrEAPSO achieves the best Pareto front; MOMVO, MOPSO, NSGA-II, NSGA-III, MOEA/D-DE, and RVEA all obtain well-formed Pareto fronts with broadly distributed points and no obvious mutual dominance. In contrast, MaOGOA and IBEA exhibit inferior Pareto fronts, with their points generally dominated by other algorithms and lying far from the ideal point. Except for IBEA and MaOGOA, the other algorithms contain many solutions with low task-assignment rates, which would typically be filtered out in practical military scenarios. IBEA performs worst in both the quality and distribution of front solutions.

Figure 8 depicts the evolution of hypervolume and spacing over iterations. GrEAPSO ranks sixth in hypervolume and fourth in spacing, with overall smooth trajectories, though its hypervolume shows fluctuations in the early iterations. This indicates substantial early changes in the archive, yet overall, it demonstrates good performance. As in the previous two scenarios, IBEA’s spacing fluctuates severely because it finds few non-dominated solutions, its archive degrades markedly, and the Pareto front is sparsely populated, leading to pronounced oscillations—an observation consistent with Figure 7.

Figure 9 reports, for each algorithm, the solution on its Pareto front that is closest to the ideal point (0, 0). The results show that the GrEAPSO solution dominates all solutions except NSGA-II’s, and is not dominated by NSGA-II’s solution.

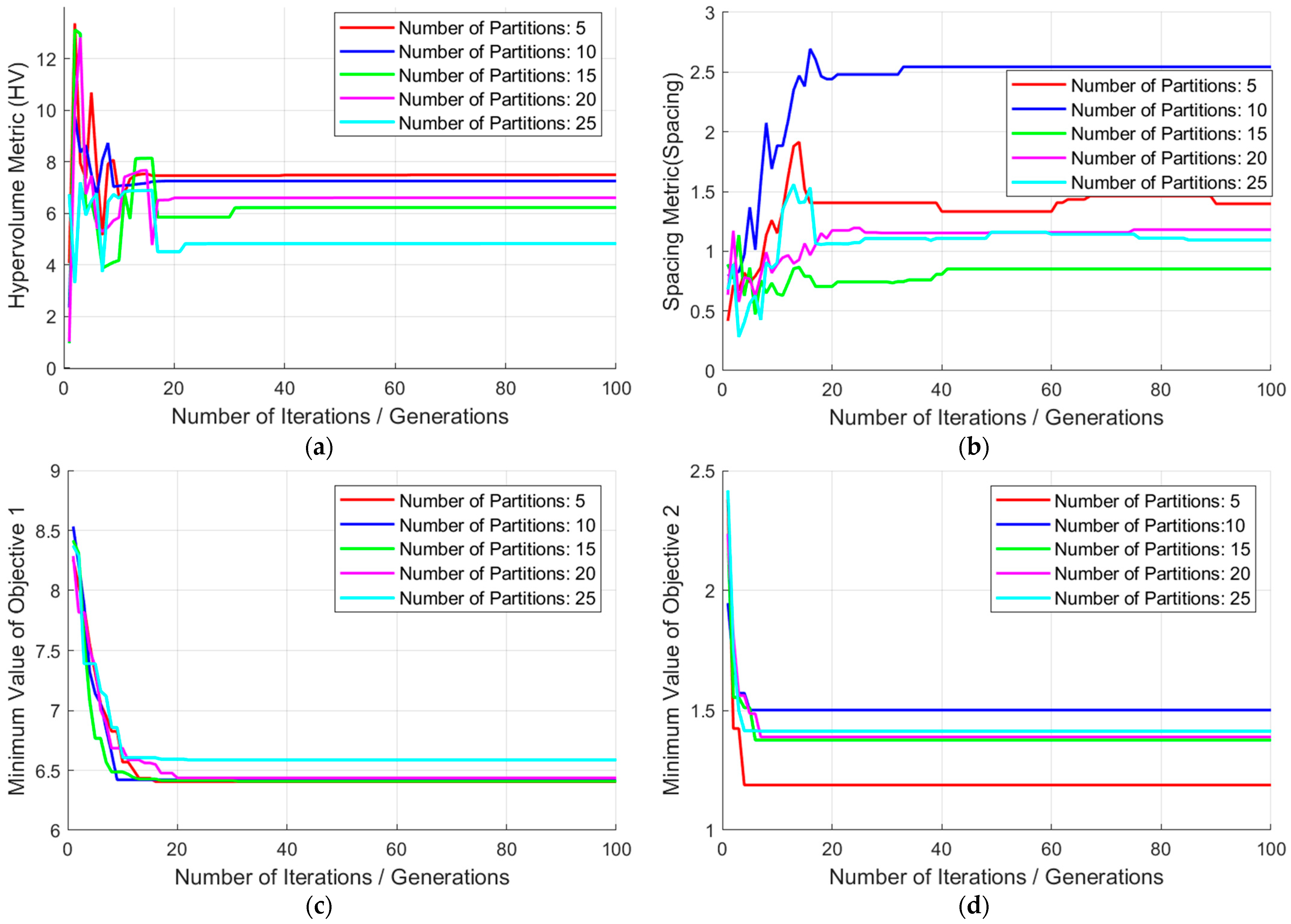
4.2. Sensitivity Analysis

Considering the impact of the number of grid partitions on the results, a sensitivity analysis was conducted in Scenario 2 by setting the number of grid partitions to 5, 10, 15, 20, and 25, respectively.

Table 4. Metrics under Different Division Quantities.

Number of Partitions/Each Object	Hypervolume	Spacing	Number of Non-Dominated Solutions
5	7.4923	1.3969	24
10	7.2540	2.5440	33
15	6.2220	0.8508	31
20	6.6020	1.1807	37
25	4.8293	1.0936	34

presents the relevant metrics under different grid partition numbers. Figure 10 shows the convergence performance for different partition quantities. It can be observed that the hypervolume decreases as the partition number increases, with the largest hypervolume occurring when the partition number is 5, indicating the largest search space. However, the number of solutions at this point is too small, which means the local optimization capability is insufficient. The spacing metric reaches its optimum when the partition number is 15, indicating the best solution distribution. The number of dominant solutions is relatively low with 5 partitions, higher with 20 partitions, and similar in other cases. Overall, a lower grid partition number provides excellent search space, but affects local optimization capability. Conversely, an excessively high partition number has a significant impact on the search space. Choosing 15 or 20 partitions can maintain good comprehensive search ability.

5. Conclusions

For the multi-UAV allocation problem, this paper considers task strike benefits, UAV costs, and UAV ammunition carrying capacity. By using dual encoding, the particle position attributes are converted into a task allocation matrix, enabling the synergy between the particle swarm optimization (PSO) algorithm and the genetic algorithm (GA). The proposed approach combines PSO and GA, introduces a grid mechanism to improve the global optimal selection step of PSO and the environmental selection step of GA, and optimizes the update of the archive set.

Through simulation experiments, the proposed algorithm was compared with two other existing intelligent algorithms. A sensitivity analysis was conducted to evaluate performance metrics across different grid partition sizes. The results show that the GrEAPSO algorithm proposed in this paper achieves the best Pareto front and superior hypervolume and spacing metrics. It achieves a wide, uniform distribution of Pareto solutions, optimizes population diversity and convergence, and yields satisfactory results that meet objectives and decision constraints. The choice of an appropriate grid partition number is critical; too few partitions result in insufficient local optimization, while too many partitions severely limit the search space.

There are still some issues in the current research. For Pareto front comparison, real fronts should be sought; in algorithm comparison, results should be compared with as many algorithms as possible; in sensitivity analysis, testing more partition numbers would make the results more convincing. In practical applications, UAV and target parameters often change. Applying the algorithm to UAV allocation problems under uncertain conditions will be a future research direction.