Global Well-Posedness and Stability of Nonlocal Damage-Structured Lineage Model with Feedback and Dedifferentiation

Abstract

A nonlocal transport–reaction system is proposed to model the coupled dynamics of stem and differentiated cell populations, structured by a continuous damage variable. The framework incorporates bidirectional transitions via differentiation and dedifferentiation, with nonlocal birth operators encoding damage redistribution upon division and Hill-type feedback regulation dependent on total populations. Global well-posedness of solutions in $C([0,\infty );L^1([0,\infty )\times L^1\left([0,\infty )\right))$ is established by combining the contraction mapping principle for local existence with a priori $L^1$ bounds for global existence, ensuring uniqueness and nonnegativity. Integration yields balance laws for total populations, reducing to a finite-dimensional autonomous ordinary differential equation (ODE) system under constant death rates. Linearization reveals a bifurcation threshold separating extinction, homeostasis, and unbounded growth. Under compensatory feedback, Dulac’s criterion precludes periodic orbits, and the Poincaré–Bendixson theorem confines bounded trajectories to equilibria or heteroclinics. Uniqueness implies global asymptotic stability. A scaling invariance for steady states under uniform feedback rescaling is identified. The analysis extends structured population theory to feedback-regulated compartments with nonlocal operators and reversible dedifferentiation, providing explicit stability criteria and linking an infinite-dimensional structured model to tractable low-dimensional reductions.

1. Introduction

Stem cells maintain tissue homeostasis by producing progenitors and terminally differentiated (TD) cells to keep a hierarchical differentiation structure within the stem cell lineage [1,2,3,4,5]. Certain feedback loops exist in lineages for tissue maintenance and robust response to environmental changes [6,7,8,9]. On the other hand, recent advances in cell biology demonstrate that differentiation is not strictly irreversible, and TD cells may revert to a stem-like stage through dedifferentiation [10,11,12,13,14]. This plasticity contributes to tissue regeneration but also underlies oncogenic transformations and therapeutic resistance [15,16,17,18,19]. Moreover, stem cell aging, driven by the progressive accumulation of cellular damage, disrupts homeostatic balance and elevates malignancy risks [20,21,22,23,24].

Motivated by these phenomena, a compact transport–reaction model for stem P and TD W cell densities structured by a continuous damage variable $x\ge 0$ is proposed. The model incorporates advective damage accumulation, nonlocal birth operators that redistribute damage at division, reversible dedifferentiation $W\to P$, and Hill-type feedback that modulate division and transition rates. The model reads

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\begin{array}{ccc}{\partial }_{t}P+v_P{\partial }_{x}P={\mathcal{B}}_P\left[P\right](t,x)-{\lambda }_{P}P(t,x)+{\lambda }_{R}W(t,x),\hfill & \hfill & x>0,t>0,\hfill \\ {\partial }_{t}W+v_W{\partial }_{x}W={\mathcal{B}}_W\left[P\right](t,x)-(\delta \left(x\right)+{\lambda }_R)W(t,x),\hfill & \hfill & x>0,t>0,\hfill \\ P(t,0)=W(t,0)=0,\hfill & \hfill & t\ge 0,\hfill \\ P(0,x)=P_0\left(x\right),W(0,x)=W_0\left(x\right),\hfill & \hfill & x>0.\hfill \end{array}\hfill \end{array}\right.\end{array}$$

(1)

Here, $v_P,v_W>0$ denote the rates of damage accumulation, ${\lambda }_P\ge 0$ is the proliferation rate of stem cells, ${\lambda }_R\ge 0$ the dedifferentiation rate, and $\delta \left(x\right)\ge 0$ the death rate of TD cells. The nonlocal birth operators ${\mathcal{B}}_P$ and ${\mathcal{B}}_W$ describe self-renewal and differentiation processes with redistribution of damage following cell division. The structure of Equation (1) combines transport along the damage axis with nonlocal division terms. This model builds on the foundational theory of transport equations and structured partial differential equations (PDEs) [25,26] and extends prior frameworks by introducing a damage variable linked to stem and TD compartments, dedifferentiation fluxes, and nonlinear feedback regulation [27,28,29,30].

Numerous mathematical models have been proposed to investigate the process of dedifferentiation, as highlighted by various studies [31]. These works examine their impact on tumor growth and treatment response [32], stochastic and evolutionary dynamics [33,34,35], mutation accumulation and cancer initiation [36], transient dynamics and tumor invasion [37,38,39,40], and therapy resistance [41]. Apart from dedifferentiation, the continuum model of stem cell aging [42] describes two damage- and cycle-structured hyperbolic PDEs with nonlocal division and Hill-type feedback. It assumes irreversible differentiation and is analyzed numerically without rigorous well-posedness or global stability results.

Unlike parabolic frameworks, our system is first-order hyperbolic and describes advective transport of the damage variable. The analysis establishes global well-posedness in $C([0,\infty );L^1\times L^1)$, derives balance laws, and obtains an exact reduction to a two-dimensional autonomous ODE under constant TD mortality. Analysis of the reduced system yields an explicit bifurcation threshold separating extinction, homeostasis, and unbounded growth, a global nonoscillation result (Dulac), and, under compensatory feedback, global asymptotic stability (Poincaré–Bendixson).

The paper is organized as follows. Section 2 establishes global well-posedness of solutions to the PDE system, including existence, uniqueness, and positivity. Section 3 derives the reduced ODE system for total populations. Section 4 and Section 5 provide, respectively, local and global stability analyses of equilibria. Section 6 presents numerical illustrations supporting analytical results. The concluding section discusses biological implications, model limitations, and future extensions.

2. PDE Model and Well-Posedness

The transport–reaction system is studied in $C([0,\infty );L^1\left([0,\infty )\right)\times L^1\left([0,\infty )\right))$. The analysis starts with the explicit partition operators and then develops the functional–analytic framework.

The construction of the nonlocal birth operators in Equation (1) is now outlined. Stem-cell division is modeled as a renewal process where the damage of a mother cell is partitioned between its daughters, inducing a nonlocal dependence on the damage variable. Let $P(t,x^{\prime })$ be the density of stem cells with damage $x^{\prime }$, dividing at rate ${\lambda }_P$. Each division follows one of three modes with probabilities $p_1,p_2,p_3$ (symmetric self-renewal, symmetric differentiation, and asymmetric division, respectively; $p_1+p_2+p_3=1$). Only stem cells divide, so the birth terms depend on P.

If a daughter inherits a fraction $\theta \in (0,1)$ of the mother’s damage, its damage satisfies $x=\theta x^{\prime }$. Let $K_{(·)}(x,x^{\prime })$ be the probability density that a daughter with damage x arises from a mother with damage $x^{\prime }$. Summing the daughter flux with damage level x from the mother cell with damage level $x^{\prime }$ over all possible mother cell damage levels $x^{\prime }$ yields the total daughter flux

$${\int }_0^{\infty }{\lambda }_P{p}_i{K}_{i,(·)}(x,x^{\prime })P(t,x^{\prime })d{x}^{\prime }.$$

Two stem daughters inherit damage fractions ${\alpha }_1,{\alpha }_2$ in symmetric self-renewal, two TD daughters inherit ${\beta }_1,{\beta }_2$ in symmetric differentiation, and the stem daughter inherits ${\gamma }_1$, with the TD daughter inheriting ${\gamma }_2$ in asymmetric division. The fractions satisfy

$${\alpha }_1+{\alpha }_2={\beta }_1+{\beta }_2={\gamma }_1+{\gamma }_2=1,min\{{\alpha }_i,{\beta }_i,{\gamma }_i\}>0,$$

and the delta kernels take the form [43]

$$\begin{array}{cc}\hfill K_{1,P}(x,x^{\prime })& =\delta (x-{\alpha }_1{x}^{\prime })+\delta (x-{\alpha }_2{x}^{\prime }),\hfill \\ \hfill K_{2,W}(x,x^{\prime })& =\delta (x-{\beta }_1{x}^{\prime })+\delta (x-{\beta }_2{x}^{\prime }),\hfill \\ \hfill K_{3,P}(x,x^{\prime })& =\delta (x-{\gamma }_1{x}^{\prime }),\hfill \\ \hfill K_{3,W}(x,x^{\prime })& =\delta (x-{\gamma }_2{x}^{\prime }).\hfill \end{array}$$

Incorporating three stem cell division modes with their probabilities and damage partition parameters, the birth operator is taken as

$$\begin{array}{cc}\hfill {\mathcal{B}}_P\left[P\right](t,x)& :={\int }_0^{\infty }{p}_1{\lambda }_P{K}_{1,P}(x,x^{\prime })P(t,x^{\prime })d{x}^{\prime }+{\int }_0^{\infty }{p}_3{\lambda }_P{K}_{3,P}(x,x^{\prime })P(t,x^{\prime })d{x}^{\prime },\hfill \\ \hfill {\mathcal{B}}_W\left[P\right](t,x)& :={\int }_0^{\infty }{p}_2{\lambda }_P{K}_{2,W}(x,x^{\prime })P(t,x^{\prime })d{x}^{\prime }+{\int }_0^{\infty }{p}_3{\lambda }_P{K}_{3,W}(x,x^{\prime })P(t,x^{\prime })d{x}^{\prime }.\hfill \end{array}$$

Substituting these kernels into the integral expressions above and using the scaling property of the Dirac delta,

$$\delta \left(\alpha x\right)={\displaystyle \frac{1}{\left|\alpha \right|}}\delta \left(x\right),\alpha \ne 0,$$

one obtains

$${\int }_0^{\infty }{p}_i{\lambda }_{P}K(x,x^{\prime })P(t,x^{\prime })d{x}^{\prime }={\int }_0^{\infty }{p}_i{\lambda }_P\delta (x-\alpha x^{\prime })P(t,x^{\prime })d{x}^{\prime }={\displaystyle \frac{p_i{\lambda }_P}{\alpha }}P(t,x/\alpha ).$$

Collecting all division modes yields the explicit nonlocal advection–reaction system

$$\left\{\begin{array}{c}\begin{array}{cc}{\partial }_{t}P+v_P{\partial }_{x}P={\displaystyle \frac{p_1{\lambda }_P}{{\alpha }_1}}P(t,x/{\alpha }_1)+{\displaystyle \frac{p_1{\lambda }_P}{{\alpha }_2}}P(t,x/{\alpha }_2)+{\displaystyle \frac{p_3{\lambda }_P}{{\gamma }_1}}P(t,x/{\gamma }_1)-{\lambda }_{P}P+{\lambda }_{R}W,\hfill & x>0,t>0,\hfill \\ {\partial }_{t}W+v_W{\partial }_{x}W={\displaystyle \frac{p_2{\lambda }_P}{{\beta }_1}}P(t,x/{\beta }_1)+{\displaystyle \frac{p_2{\lambda }_P}{{\beta }_2}}P(t,x/{\beta }_2)+{\displaystyle \frac{p_3{\lambda }_P}{{\gamma }_2}}P(t,x/{\gamma }_2)-(\delta \left(x\right)+{\lambda }_R)W,\hfill & x>0,t>0,\hfill \\ P(t,0)=W(t,0)=0,\hfill & t\ge 0,\hfill \\ P(0,x)=P_0\left(x\right),W(0,x)=W_0\left(x\right),\hfill & x>0.\hfill \end{array}\hfill \end{array}\right.$$

(2)

The initial data $P_0\left(x\right),W_0\left(x\right)$ are nonnegative and belong to $L^1\left([0,\infty )\right)$.

Feedback is encoded using Hill-type laws that depend on the totals

$$\overline{P}\left(t\right):={\int }_0^{\infty }P(t,x)dx,\overline{W}\left(t\right):={\int }_0^{\infty }W(t,x)dx.$$

The maps

$$\begin{array}{cc}\hfill p_1\left(t\right)& ={\displaystyle \frac{{\widehat{p}}_1}{1+{(k_1\overline{W}\left(t\right))}^{m_1}}},\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill p_2\left(t\right)& ={\displaystyle \frac{{\widehat{p}}_2}{1+{(k_2\overline{W}\left(t\right))}^{m_2}}},\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill {\lambda }_P\left(t\right)& ={\displaystyle \frac{{\widehat{\lambda }}_P}{1+{(k_3\overline{W}\left(t\right))}^{m_3}}},\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill {\lambda }_R\left(t\right)& ={\displaystyle \frac{{\widehat{\lambda }}_R}{1+{(k_4\overline{P}\left(t\right))}^{m_4}}},\hfill \end{array}$$

(6)

use baseline values ${\widehat{p}}_1$, ${\widehat{p}}_2$, ${\widehat{\lambda }}_P$, ${\widehat{\lambda }}_R$, strength $k_i>0$, and exponents $m_i\ge 1$. The renewal fraction f is introduced to represent the effective probability that a proliferating stem cell self-renews rather than differentiates at time t. Biologically, $f\left(t\right)\in [0,1]$ quantifies the balance between symmetric self-renewal $p_1$ and differentiation $p_2$, with $2f\left(t\right)-1=p_1\left(t\right)-p_2\left(t\right)$ measuring the net bias toward renewal. When $k_1=k_2$ and $m_1=m_2$, the renewal fraction satisfies

$$2f\left(t\right)-1=p_1\left(t\right)-p_2\left(t\right)={\displaystyle \frac{2\widehat{f}-1}{1+{(k_1\overline{W}\left(t\right))}^{m_1}}},\widehat{f}={\displaystyle \frac{1+{\widehat{p}}_1-{\widehat{p}}_2}{2}}.$$

(7)

The baseline value $\widehat{f}$ gives the renewal tendency in the absence of feedback $(\overline{W}=0)$.

2.1. Notation and Standing Assumptions

Write $\parallel ·\parallel$ for the $L^1\left([0,\infty )\right)$ norm and $L_{+}^1\left([0,\infty )\right)$ for the cone of almost-everywhere nonnegative functions. For $T>0$ define

$${\mathcal{X}}_T:= C\left([0,T];L^1\left([0,\infty )\right)\times L^1\left([0,\infty )\right)\right),{\parallel (P,W)\parallel }_{{\mathcal{X}}_T}:= \underset{0\le t\le T}{sup}\left(\parallel P(t,·)\parallel +\parallel W(t,·)\parallel \right).$$

and set ${\mathcal{X}}_{\infty }:= C([0,\infty );L^1\left([0,\infty )\right)\times L^1\left([0,\infty )\right))$ with the analogous norm. The following hypotheses are adopted.

(H1)

Fix $p_i(i=1,2)$, ${\lambda }_P$, ${\lambda }_R$ by Equations (3)–(6) with $k_i>0$ and $m_i\ge 1$ for $i=1,2,3,4$; the probabilities satisfy $p_1+p_2+p_3=1$; the fractions satisfy ${\alpha }_1+{\alpha }_2={\beta }_1+{\beta }_2={\gamma }_1+{\gamma }_2=1$ with $min\{{\alpha }_i,{\beta }_i,{\gamma }_i\}>0$; the death rate $\delta \left(x\right)$ is nondecreasing, bounded, and equals a positive constant in the constant death case.

(H2)

$P_0\left(x\right),W_0\left(x\right)\in L_{+}^1\left([0,\infty )\right)$.

Define the nonlocal birth operators compactly as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathcal{B}}_P\left[P\right](t,x):=& {\displaystyle \frac{p_1\left(t\right){\lambda }_P\left(t\right)}{{\alpha }_1}}P(t,x/{\alpha }_1)+{\displaystyle \frac{p_1\left(t\right){\lambda }_P\left(t\right)}{{\alpha }_2}}P(t,x/{\alpha }_2)+{\displaystyle \frac{p_3\left(t\right){\lambda }_P\left(t\right)}{{\gamma }_1}}P(t,x/{\gamma }_1),\hfill \\ \hfill {\mathcal{B}}_W\left[P\right](t,x):=& {\displaystyle \frac{p_2\left(t\right){\lambda }_P\left(t\right)}{{\beta }_1}}P(t,x/{\beta }_1)+{\displaystyle \frac{p_2\left(t\right){\lambda }_P\left(t\right)}{{\beta }_2}}P(t,x/{\beta }_2)+{\displaystyle \frac{p_3\left(t\right){\lambda }_P\left(t\right)}{{\gamma }_2}}P(t,x/{\gamma }_2).\hfill \end{array}\end{array}$$

(8)

Table 1 lists all notations in this work.

Table 1. Summary of main notation.

Symbol	Meaning
$\overline{P}\left(t\right)={\int }_0^{\infty }P(t,x)dx$	Total stem-cell population at time t
$\overline{W}\left(t\right)={\int }_0^{\infty }W(t,x)dx$	Total TD cell population at time t
$M\left(t\right)=\overline{P}\left(t\right)+\overline{W}\left(t\right)$	Total cell mass
$v_P,v_W$	Damage accumulation velocities in P and W compartments
${\mathcal{B}}_P,{\mathcal{B}}_W$	Nonlocal birth operators (damage partitioning at division)
${\lambda }_P$	Effective replication rate of P
${\lambda }_R$	Dedifferentiation rate from W to P (possibly state dependent)
${\alpha }_i,{\beta }_i,{\gamma }_i$	Partition fractions in stem cell divisions
$\delta \left(x\right)\ge 0$	Death rate of W (damage dependent, or constant $\delta$)
${\widehat{p}}_i,{\widehat{\lambda }}_P,{\widehat{\lambda }}_R$	Baseline (unregulated) probabilities and rates
$k_i>0$	Feedback strength parameters in Hill-type regulation
$m_i\ge 1$	Hill exponents governing feedback steepness
$\mathcal{S}=({\overline{P}}^{*},{\overline{W}}^{*})$	Equilibrium/steady state of the reduced ODE system

The nonlinear coefficients can be extended to globally Lipschitz functions.

Lemma 1.

(i)

Globally Lipschitz extensions of the coefficients: The nonlinearities $p_i$$(i=1,2,3)$, ${\lambda }_P$, and ${\lambda }_R$ on $[0,\infty )$ can be extended to globally Lipschitz functions ${\tilde{p}}_i,{\tilde{\lambda }}_p,{\tilde{\lambda }}_R$ on $\mathbb{R}$ with the Lipschitz bounds $L_1, L_2, L_1 + L_2, L_3, L_4$ for ${\tilde{p}}_1,{\tilde{p}}_2,{\tilde{p}}_3,{\tilde{\lambda }}_P,{\tilde{\lambda }}_R$, respectively, where $L_1, L_2, L_3, L_4 > 0$ are positive constants.

(ii)

$L^1$ boundedness of  ${\mathcal{B}}_P, {\mathcal{B}}_W$: Let ${\mathcal{B}}_P, {\mathcal{B}}_W$ be the nonlocal birth operators in (8). Then for all $t\ge 0$,

$${\int }_0^{\infty }\left({\mathcal{B}}_P\left[P\right]+{\mathcal{B}}_W\left[P\right]\right)(t,x)dx=2{\lambda }_P\left(\overline{W}\left(t\right)\right)\overline{P}\left(t\right),$$

so on ${\mathcal{X}}_T$ or ${\mathcal{X}}_{\infty }$, the birth operators are bounded with norm controlled by ${\lambda }_P$.

(iii)

Local existence: For any $R>0$ and initial data $(P_0,W_0)$ with $\parallel P_0\parallel + \parallel W_0\parallel \le R$, there exists $T=T\left(R\right)>0$ such that the transport system admits a unique local solution

$$\begin{array}{c}\hfill (P(t,·),W(t,·))\in {\mathcal{X}}_T,{\parallel (P,W)\parallel }_{{\mathcal{X}}_T}\le 2R.\end{array}$$

Proof. 

(i)

The nonlinearities $p_i(i=1,2,3)$, ${\lambda }_P$, and ${\lambda }_R$ on $[0,\infty )$ can be extended to globally Lipschitz functions on $\mathbb{R}$. Specifically, define the extensions:

$${\tilde{p}}_i\left(x\right):=p_i\left(x_{+}\right),{\tilde{\lambda }}_P\left(x\right):={\lambda }_P\left(x_{+}\right),{\tilde{\lambda }}_R\left(x\right):={\lambda }_R\left(x_{+}\right),$$

where $x_{+}=max\{x,0\}$. Since each of $p_1,p_2,{\lambda }_P,{\lambda }_R$ is $C^1$ and bounded on $[0,\infty )$, the following definition is introduced

$$\begin{array}{c}\hfill L_1:=\underset{x\ge 0}{sup}|p_1^{\prime }\left(x\right)|,L_2:=\underset{x\ge 0}{sup}|p_2^{\prime }\left(x\right)|,L_3:=\underset{x\ge 0}{sup}|{\lambda }_P^{\prime }\left(x\right)|,L_4:=\underset{x\ge 0}{sup}|{\lambda }_R^{\prime }\left(x\right)|.\end{array}$$

Define the truncation map $T:\mathbb{R}\to [0,\infty )$ by $T\left(x\right)=x_{+}$. Note that T is Lipschitz with constant 1. Then the extensions ${\tilde{p}}_1, {\tilde{p}}_2, {\tilde{\lambda }}_P, {\tilde{\lambda }}_R$ are globally Lipschitz on $\mathbb{R}$ with Lipschitz constant $L_1, L_2, L_3, L_4$, respectively. Finally, because $p_3=1-p_1-p_2$ on $[0,\infty )$, the corresponding extension ${\tilde{p}}_3$ has the Lipschitz constant $L_1+L_2$.

(ii)

This follows from applying the change of variable $y=x/\alpha$ in each term of the integral and using the properties of the delta kernels.

(iii)

Local existence is used in Step 5 of Theorem 1. It establishes the local existence of solutions under a mass bound on the initial data, and is proved in Step 1 of the same theorem.

           □

2.2. Existence, Uniqueness, Positivity, and $L^1$ Bounds

The preparatory lemmas above provide the analytic foundation: the nonlinear coefficients are globally Lipschitz after extension, and the local existence of solutions. With these tools, the global theory is established.

Theorem 1 (Global well-posedness in ${\mathcal{X}}_{\infty }$).

Assume (H1)–(H2). Then the PDE system admits a unique global solution

$$(P,W)\in C([0,\infty );L^1\left([0,\infty )\right)\times L^1\left([0,\infty )\right)).$$

The solution remains nonnegative for all $t\ge 0$ and satisfies the a priori mass bound

$$M\left(t\right)\le e^{2{\widehat{\lambda }}_{P}t}{M}_0,\forall t\ge 0$$

for $M\left(t\right)=\overline{P}\left(t\right)+\overline{W}\left(t\right)$, $M_0= \parallel P_0\parallel + \parallel W_0\parallel$. Moreover, the total populations $\overline{P}$ and $\overline{W}$ are absolutely continuous in t and obey the following balance laws for a.e. $t\ge 0$:

$$\left\{\begin{array}{c}\begin{array}{cc}{\displaystyle \frac{d\overline{P}}{dt}}=\left[p_1\left(\overline{W}\right)-p_2\left(\overline{W}\right)\right]{\lambda }_P\left(\overline{W}\right)\overline{P}+{\lambda }_R\left(\overline{P}\right)\overline{W},\hfill & t>0,\hfill \\ {\displaystyle {\displaystyle \frac{d\overline{W}}{dt}}=\left[1-p_1\left(\overline{W}\right)+p_2\left(\overline{W}\right)\right]{\lambda }_P\left(\overline{W}\right)\overline{P}-{\lambda }_R\left(\overline{P}\right)\overline{W}-{\int }_0^{\infty }\delta \left(x\right)W(t,x)dx,}\hfill & t>0,\hfill \\ \overline{P}\left(0\right)={\overline{P}}_0=\parallel P_0\parallel ,\overline{W}\left(0\right)={\overline{W}}_0=\parallel W_0\parallel .\hfill \end{array}\hfill \end{array}\right.$$

(9)

Proof. 

The proof is organized into steps:

(i)

Define the Picard map on ${\mathcal{X}}_T=C([0,T];L^1\times L^1)$ by a mild formulation along characteristics.

(ii)

Use Lipschitz feedback and change-of-variable formulas in the nonlocal births to show the map is a contraction for small T.

(iii)

Positivity is invariant by construction.

(iv)

Pass from mild to weak formulations and derive exact balance laws for total counts.

(v)

Obtain an a priori mass bound $M^{\prime }\left(t\right)\le aM\left(t\right)$; Grönwall ensures ${sup}_{t\in [0,T]}M\left(t\right)<\infty$.

(vi)

Iterate the local solution using the bound to cover all $t>0$.

To avoid confusion in notation, we emphasize that both $(P,W)$ and $(\overline{P},\overline{W})$ appear in the proof. Here, $P(t,x)$ and $W(t,x)$ denote the stem and TD cell density functions over the damage variable x, while $\overline{P}\left(t\right)={\int }_0^{\infty }P(t,x)dx$ and $\overline{W}\left(t\right)={\int }_0^{\infty }W(t,x)dx$ represent their corresponding total population counts.

• Step 1: Contraction. The proof begins by employing the Picard map $\Psi$, defined by the following formulas

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill P(t,x)& =exp(-{\Lambda }_P\left[W\right](0;t))P_0(x-v_{P}t){\mathbf{1}}_{x\ge v_{P}t}\hfill \\ \hfill & +{\int }_0^{t}exp(-{\Lambda }_P\left[W\right](s;t))\left({\mathcal{B}}_P\left[P\right]+{\lambda }_R\left(s\right)W\right)(s,X_P(s;t,x)){\mathbf{1}}_{x\ge v_P(t-s)}ds,\hfill \end{array}\end{array}$$

(10)

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill W(t,x)& =exp(-{\Lambda }_W\left[P\right](0;t,x))W_0(x-v_{W}t){\mathbf{1}}_{x\ge v_{W}t}\hfill \\ \hfill & +{\int }_0^{t}exp(-{\Lambda }_W\left[P\right](s;t,x)){\mathcal{B}}_W\left[P\right](s,X_W(s;t,x)){\mathbf{1}}_{x\ge v_W(t-s)}ds.\hfill \end{array}\end{array}$$

(11)

along the characteristic lines

$$\begin{array}{cc}\hfill X_P(s;t,x)& =x-v_P(t-s),\hfill \\ \hfill X_W(s;t,x)& =x-v_W(t-s),0\le s\le t.\hfill \end{array}$$

Here, ${\Lambda }_P\left[W\right](s;t)$ and ${\Lambda }_W\left[P\right](s;t,x)$ are defined as

$$\begin{array}{cc}\hfill {\Lambda }_P\left[W\right](s;t)& :={\int }_s^t{\lambda }_P\left(\overline{W}\left(\tau \right)\right)d\tau ,\hfill \\ \hfill {\Lambda }_W\left[P\right](s;t,x)& :={\int }_s^t\left(\delta \left(X_W(\tau ;t,x)\right)+{\lambda }_R\left(\overline{P}\left(\tau \right)\right)\right)d\tau .\hfill \end{array}$$

and involves the global Lipschitz extensions ${\tilde{p}}_i$, ${\tilde{\lambda }}_P$, ${\tilde{\lambda }}_R$ (notation simplified by dropping tildes, justified after Step 2).

To be precise, define

$$\Psi :(P,W)\in {\mathcal{X}}_T\mapsto (\tilde{P},\tilde{W})=S_0+F(P,W),$$

where

$$S_0(t,x)\left(\begin{array}{c}exp(-{\Lambda }_P\left[W\right](0;t))P_0(x-v_{P}t){\mathbf{1}}_{x\ge v_{P}t}\\ exp(-{\Lambda }_W\left[P\right](0;t,x))W_0(x-v_{W}t){\mathbf{1}}_{x\ge v_{W}t}\end{array}\right),$$

and F represents the birth and reaction terms in (10) and (11) with nonlinearities evaluated at $(P,W)$.

For two pairs $(P_j,W_j)\in {\mathcal{X}}_T,j=1,2$, their images under $\Psi$ are denoted by $({\tilde{P}}_i,{\tilde{W}}_i)$. Introduce

$$\begin{array}{c}\hfill \begin{array}{cc}{p}_i^j\left(t\right):=p_i\left({\overline{W}}_j\left(t\right)\right),\hfill & p_3^j\left(t\right)=1-p_1^j\left(t\right)-p_2^j\left(t\right),\hfill \\ {\lambda }_P^j\left(t\right):={\lambda }_P\left({\overline{W}}_j\left(t\right)\right),\hfill & {\lambda }_R^j\left(t\right):={\lambda }_R\left({\overline{P}}_j\left(t\right)\right).\hfill \end{array}\end{array}$$

to ease notation. Also define

$$\begin{array}{cc}\hfill {\Lambda }_P^j(s;t)& :={\int }_s^t{\lambda }_P^j\left(\tau \right)d\tau ,\hfill \\ \hfill {\Lambda }_W^j(s;t,x)& :={\int }_s^t\left(\delta \left(X_W(\tau ;t,x)\right)+{\lambda }_R^j\left(\tau \right)\right)d\tau .\hfill \end{array}$$

For each $j=1,2$, corresponding to the two candidate solutions $(P_j,W_j)$, define the nonlocal birth operators as ${\mathcal{B}}_P^j\left[P_j\right]$ and ${\mathcal{B}}_W^j\left[P_j\right]$ using the coefficients $p_i^j\left(t\right)$ and ${\lambda }_P^j\left(t\right)$ evaluated at ${\overline{W}}_j\left(t\right)$:

$$\begin{array}{cc}\hfill & {\mathcal{B}}_P^j\left[P_j\right](t,x):={\displaystyle \frac{p_1^j\left(t\right){\lambda }_P^j\left(t\right)}{{\alpha }_1}}{P}_j(t,x/{\alpha }_1)+{\displaystyle \frac{p_1^j\left(t\right){\lambda }_P^j\left(t\right)}{{\alpha }_2}}{P}_j(t,x/{\alpha }_2)+{\displaystyle \frac{p_3^j\left(t\right){\lambda }_P^j\left(t\right)}{{\gamma }_1}}{P}_j(t,x/{\gamma }_1),\hfill \\ \hfill & {\mathcal{B}}_W^j\left[P_j\right](t,x):={\displaystyle \frac{p_2^j\left(t\right){\lambda }_P^j\left(t\right)}{{\beta }_1}}{P}_j(t,x/{\beta }_1)+{\displaystyle \frac{p_2^j\left(t\right){\lambda }_P^j\left(t\right)}{{\beta }_2}}{P}_j(t,x/{\beta }_2)+{\displaystyle \frac{p_3^j\left(t\right){\lambda }_P^j\left(t\right)}{{\gamma }_2}}{P}_j(t,x/{\gamma }_2).\hfill \end{array}$$

Write

$$\begin{array}{cc}\hfill & F(P_1,W_1)-F(P_2,W_2)=(F_1(P_1,W_1;P_2,W_2),F_2(P_1,W_1;P_2,W_2))\hfill \end{array}$$

with

$$\begin{array}{cc}\hfill & F_1(P_1,W_1;P_2,W_2)\hfill \\ \hfill =& \underset{A_1}{\underbrace{exp(-{\Lambda }_P^1(0;t))P_0(x-v_{P}t){\mathbf{1}}_{x\ge v_{P}t}-exp(-{\Lambda }_P^2(0;t))P_0(x-v_{P}t){\mathbf{1}}_{x\ge v_{P}t}}}\hfill \\ \hfill +& \underset{A_2}{\underbrace{{\int }_0^t\left[exp(-{\Lambda }_P^1(s;t)){\mathcal{B}}_P^1\left[P_1\right](s,X_P(s;t,x))-exp(-{\Lambda }_P^2(s;t)){\mathcal{B}}_P^2\left[P_2\right](s,X_P(s;t,x))\right]{\mathbf{1}}_{x\ge v_P(t-s)}ds}}\hfill \\ \hfill +& \underset{A_3}{\underbrace{{\int }_0^t\left[exp(-{\Lambda }_P^1(s;t)){\lambda }_R^1\left(s\right)W_1(s,X_P(s;t,x))-exp(-{\Lambda }_P^2(s;t)){\lambda }_R^2\left(s\right)W_2(s,X_P(s;t,x))\right]{\mathbf{1}}_{x\ge v_{P}t}ds}},\hfill \end{array}$$

$$\begin{array}{cc}\hfill & F_2(P_1,W_1;P_2,W_2)\hfill \\ \hfill =& \underset{B_1}{\underbrace{\left[exp(-{\Lambda }_W^1(0;t,x))-exp(-{\Lambda }_W^2(0;t,x))\right]W_0(x-v_{W}t){\mathbf{1}}_{x\ge v_{W}t}}}\hfill \\ \hfill +& \underset{B_2}{\underbrace{{\int }_0^t\left[exp(-{\Lambda }_W^1(s;t,x)){\mathcal{B}}_W^1\left[P_1\right](s,X_W(s;t,x))-exp(-{\Lambda }_W^2(s;t,x)){\mathcal{B}}_W^2\left[P_2\right](s,X_W(s;t,x))\right]{\mathbf{1}}_{x\ge v_W(t-s)}ds}}.\hfill \end{array}$$

Each $A_i,B_i$ is next estimated in the $L^1$-norm, uniformly for $t\in [0,T]$. The strategy is standard: expand differences, use the mean value theorem, and apply the Lipschitz bounds from Lemma 1 and the following integral identities, such as

$$\begin{array}{cc}\hfill {\int }_0^{\infty }{P}_0(x-v_{P}t){\mathbf{1}}_{x\ge v_{P}t}dx& =\parallel P_0\parallel ,\hfill \\ \hfill {\int }_0^{\infty }{\displaystyle \frac{1}{\alpha }}P(s,X_P(s;t,x)/\alpha ){\mathbf{1}}_{x\ge v_P(t-s)}dx& =\parallel P(s,·)\parallel ,\hfill \end{array}$$

where the second identity follows from the change of variable $y=X_P(s;t,x)/{\alpha }_1$:

$$\begin{array}{cc}\hfill {\int }_0^{\infty }{\displaystyle \frac{1}{\alpha }}{P}_1(s,X_P(s;t,x)/{\alpha }_1){\mathbf{1}}_{x\ge v_P(t-s)}dx& ={\int }_{\frac{-v_P(t-s)}{{\alpha }_1}}^{\infty }{P}_1(s,y){\mathbf{1}}_{y\ge 0}dy\hfill \\ \hfill & ={\int }_0^{\infty }{P}_1(s,y)dy=\parallel P_1(s,·)\parallel .\hfill \end{array}$$

First, the $L^1$-norm of $A_1$ on $[0,T]$ is estimated:

$$\begin{array}{cc}\hfill \parallel A_1\parallel & ={\int }_0^{\infty }{P}_0(x-v_{P}t){\mathbf{1}}_{x\ge v_{P}t}|exp(-{\Lambda }_P^1(0;t))-exp(-{\Lambda }_P^2(0;t))|dx\hfill \\ \hfill & \le {\int }_0^{\infty }{P}_0(x-v_{P}t){\mathbf{1}}_{x\ge v_{P}t}{\int }_0^t|{\lambda }_P^1\left(s\right)-{\lambda }_P^2\left(s\right)|dsdx\hfill \\ \hfill & \le L_3{\int }_0^t|{\overline{P}}_1\left(s\right)-{\overline{P}}_2\left(s\right)|{\int }_0^{\infty }{P}_0(x-v_{P}t){\mathbf{1}}_{x\ge v_{P}t}dxds.\hfill \end{array}$$

Taking the sup over $t\in [0,T]$ gives

$$\underset{t\in [0,T]}{sup}\parallel A_1\parallel \le L_3\parallel P_0\parallel T\underset{t\in [0,T]}{sup}\parallel P_1(t,·)-P_2(t,·)\parallel \le L_3\parallel P_0\parallel T\parallel (P_1,W_1)-(P_2,W_2){\parallel }_{{\mathcal{X}}_T}.$$

Here, the following fact is used:   

$$\begin{array}{c}\hfill |{\overline{P}}_1\left(s\right)-{\overline{P}}_2\left(s\right)|\le {\int }_0^{\infty }|P_1(s,x)-P_2(s,x)|dx=\parallel P_1(s,·)-P_2(s,·)\parallel .\end{array}$$

The analysis now proceeds for $A_2$. Decompose $A_2$ as

$$\begin{array}{cc}\hfill A_2& =\underset{A_{2,1}}{\underbrace{{\int }_0^t\left[exp(-{\Lambda }_P^1(s;t))-exp(-{\Lambda }_P^2(s;t))\right]{\mathcal{B}}_P^1\left[P_1\right](s,X_P(s;t,x)){\mathbf{1}}_{x\ge v_P(t-s)}ds}}\hfill \\ \hfill & +\underset{A_{2,2}}{\underbrace{{\int }_0^{t}exp(-{\Lambda }_P^2(s;t))\left[{\mathcal{B}}_P^1\left[P_1\right](s,X_P(s;t,x))-{\mathcal{B}}_P^2\left[P_2\right](s,X_P(s;t,x))\right]{\mathbf{1}}_{x\ge v_P(t-s)}ds}}\hfill \end{array}$$

The term $A_{2,1}$ admits the following decomposition:

$$\begin{array}{cc}\hfill A_{2,1}& =\underset{A_{2,1,1}}{\underbrace{{\int }_0^t\left[exp(-{\Lambda }_P^1(s;t))-exp(-{\Lambda }_P^2(s;t))\right]{\displaystyle \frac{p_1^1\left(s\right){\lambda }_P^1\left(s\right)}{{\alpha }_1}}{P}_1(s,X_P(s;t,x)/{\alpha }_1){\mathbf{1}}_{x\ge v_P(t-s)}ds}}\hfill \\ \hfill & +\underset{A_{2,1,2}}{\underbrace{{\int }_0^t\left[exp(-{\Lambda }_P^1(s;t))-exp(-{\Lambda }_P^2(s;t))\right]{\displaystyle \frac{p_1^1\left(s\right){\lambda }_P^1\left(s\right)}{{\alpha }_2}}{P}_1(s,X_P(s;t,x)/{\alpha }_2){\mathbf{1}}_{x\ge v_P(t-s)}ds}}\hfill \\ \hfill & +\underset{A_{2,1,3}}{\underbrace{{\int }_0^t\left[exp(-{\Lambda }_P^1(s;t))-exp(-{\Lambda }_P^2(s;t))\right]{\displaystyle \frac{p_3^1\left(s\right){\lambda }_P^1\left(s\right)}{{\gamma }_1}}{P}_1(s,X_P(s;t,x)/{\gamma }_1){\mathbf{1}}_{x\ge v_P(t-s)}ds}}\hfill \end{array}$$

The term $A_{2,1,1}$ is estimated:

$$\begin{array}{cc}\hfill \parallel A_{2,1,1}(t,·)\parallel & \le {\int }_0^t{\int }_0^{\infty }|exp(-{\Lambda }_P^1(s;t))-exp(-{\Lambda }_P^2(s;t))|\hfill \\ \hfill & \times {\displaystyle \frac{{\widehat{p}}_1{\widehat{\lambda }}_P}{{\alpha }_1}}\left|P_1(s,X_P(s;t,x)/{\alpha }_1)\right|{\mathbf{1}}_{x\ge v_P(t-s)}dxds\hfill \\ \hfill & \le L_3{\widehat{p}}_1{\widehat{\lambda }}_P{\int }_0^t{\int }_s^t\parallel W_1(\tau ,·)-W_2(\tau ,·)\parallel d\tau ·\parallel P_1(s,·)\parallel ds.\hfill \end{array}$$

Taking the supremum over $t\in [0,T]$ gives

$$\begin{array}{cc}\hfill \underset{t\in [0,T]}{sup}\parallel A_{2,1,1}(t,·)\parallel & \le {\widehat{p}}_1{\widehat{\lambda }}_P{L}_3\parallel (P_1,W_1){\parallel }_{{\mathcal{X}}_T}{\parallel (P_1,W_1)-(P_2,W_2)\parallel }_{{\mathcal{X}}_T}{\int }_0^T(T-s)ds\hfill \\ \hfill & \le \frac{1}{2}{\widehat{p}}_1{\widehat{\lambda }}_P{L}_3{T}^2\parallel (P_1,W_1){\parallel }_{{\mathcal{X}}_T}{\parallel (P_1,W_1)-(P_2,W_2)\parallel }_{{\mathcal{X}}_T}.\hfill \end{array}$$

By the same argument as for $A_{2,1,1}$ (collapsing the mean-value/inner-integral steps), one obtains symmetric bounds for the other two terms. Combining these three estimates gives the compact bound

$$\underset{t\in [0,T]}{sup}\parallel A_{2,1}(t,·)\parallel \le \frac{1}{2}(2{\widehat{p}}_1+1){\widehat{\lambda }}_P{L}_3{T}^2\parallel (P_1,W_1){\parallel }_{{\mathcal{X}}_T}{\parallel (P_1,W_1)-(P_2,W_2)\parallel }_{{\mathcal{X}}_T}.$$

Similar procedures yields the bounds for $A_{2,2}$:

$$\begin{array}{cc}\hfill \underset{t\in [0,T]}{sup}\parallel A_{2,2}(t,·)\parallel & \le ((3L_1+L_2){\widehat{\lambda }}_P\parallel (P_1,W_1){\parallel }_{{\mathcal{X}}_T}+(2{\widehat{p}}_1+1)L_3{\widehat{p}}_1{\parallel (P_1,W_1)\parallel }_{{\mathcal{X}}_T}\hfill \\ \hfill & +(2{\widehat{p}}_1+1){\widehat{\lambda }}_P)T{\parallel (P_1,W_1)-(P_2,W_2)\parallel }_{{\mathcal{X}}_T}.\hfill \end{array}$$

The sup-norm of $A_2$ is given by

$$\begin{array}{cc}\hfill \underset{t\in [0,T]}{sup}\parallel A_2(t,·)\parallel & \le [\frac{1}{2}(2{\widehat{p}}_1+1){\widehat{\lambda }}_P{L}_3{T}^2{\parallel (P_1,W_1)\parallel }_{{\mathcal{X}}_T}\hfill \\ \hfill & +T\left((3L_1+L_2){\widehat{\lambda }}_P+(2{\widehat{p}}_1+1)L_3{\widehat{p}}_1\right){\parallel (P_1,W_1)\parallel }_{{\mathcal{X}}_T}\hfill \\ \hfill & +(2{\widehat{p}}_1+1){\widehat{\lambda }}_{P}T]{\parallel (P_1,W_1)-(P_2,W_2)\parallel }_{{\mathcal{X}}_T}.\hfill \end{array}$$

Similar procedures yield the bounds for $A_3$, $B_1$, and $B_2$. Therefore, combining the estimate for $A_i,B_i$, it follows that for $(P_1,W_1),(P_2,W_2)\in {\mathcal{X}}_T$,

$$\parallel \Psi (P_1,W_1)-\Psi (P_2,W_2){\parallel }_{{\mathcal{X}}_T}\le C((P_i,W_i),T){\parallel (P_1,W_1)-(P_2,W_2)\parallel }_{{\mathcal{X}}_T}.$$

(12)

Let $M_0= \parallel P_0\parallel +\parallel W_0\parallel$. On the closed ball $\overline{\mathbb{B}}(0,2M_0)\subset {\mathcal{X}}_T$ of radius $2M_0$, the constant C in Equation (12) can be written as $C(M_0,T)$. Choosing $T_0>0$ to be sufficiently small such that $C(M_0,T)<1$ for all $T\in [0,T_0]$, then the Picard map $\Psi$ is a strict contraction on $\overline{\mathbb{B}}(0,2M_0)$. By the Banach fixed point theorem, there exists a unique solution on ${\mathcal{X}}_{T_0}$.

• Step 2: Positivity. The solution is shown to remain nonnegative for all $t\in [0,T_0]$. The analysis is conducted in the ordered space

$$X=L^1\left([0,\infty )\right)\times L^1\left([0,\infty )\right)$$

with its natural cone $X_{+}=L_{+}^1\left([0,\infty )\right)\times L_{+}^1\left([0,\infty )\right)$. The iteration is initiated from $(P^{\left(0\right)},W^{\left(0\right)})=(0,0)$. Assume $(P^{\left(n\right)},W^{\left(n\right)})\ge 0$. Iterate $(P^{(n+1)},W^{(n+1)})$ as

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill P^{(n+1)}(t,x)& =exp(-{\Lambda }_P\left[W^{\left(n\right)}\right](0;t))P_0(x-v_{P}t){\mathbf{1}}_{x\ge v_{P}t}\hfill \\ \hfill & +{\int }_0^{t}exp(-{\Lambda }_P\left[W^{\left(n\right)}\right](s;t))\left({\mathcal{B}}_P\left[P^{\left(n\right)}\right]+{\lambda }_R\left(s\right)W^{\left(n\right)}\right)(s,X_P(s;t,x)){\mathbf{1}}_{x\ge v_P(t-s)}ds,\hfill \end{array}\end{array}$$

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill W^{(n+1)}(t,x)& =exp(-{\Lambda }_W\left[P^{\left(n\right)}\right](0;t,x))W_0(x-v_{W}t){\mathbf{1}}_{x\ge v_{W}t}\hfill \\ \hfill & +{\int }_0^{t}exp(-{\Lambda }_W\left[P^{\left(n\right)}\right](s;t,x)){\mathcal{B}}_W\left[P^{\left(n\right)}\right](s,X_W(s;t,x)){\mathbf{1}}_{x\ge v_W(t-s)}ds.\hfill \end{array}\end{array}$$

Since the nonlinearities $p_i$, ${\lambda }_P$, and ${\lambda }_R$ are nonnegative, and initial data $P_0\ge 0,W_0\ge 0$, all terms on the right-hand sides in $(P^{(n+1)},W^{(n+1)})=\Psi (P^{\left(n\right)},W^{\left(n\right)})$ are nonnegative whenever $(P^{\left(n\right)},W^{\left(n\right)})\ge 0$. This proves by induction that $(P^{\left(n\right)},W^{\left(n\right)})\ge 0$ for all n. Banach fixed point theorem implies that ${\left\{(P^{\left(n\right)},W^{\left(n\right)})\right\}}_n$ converges to the unique solution $(P,W)$ in ${\mathcal{X}}_{T_0}$. Convergence in ${\mathcal{X}}_{T_0}$ means

$$\begin{array}{cc}\hfill P^{\left(n\right)}(t,·)& \to P(t,·)\mathrm{in}{L}^1\left([0,\infty )\right),\hfill \\ \hfill W^{\left(n\right)}(t,·)& \to W(t,·)\mathrm{in}{L}^1\left([0,\infty )\right),\hfill \end{array}$$

uniformly in $t\in [0,T_0]$. Since the cone $X_{+}$ is closed in X, the limit also satisfies

$$\begin{array}{c}\hfill (P,W)(t,·)\in L_{+}^1\left([0,\infty )\right)\times L_{+}^1\left([0,\infty )\right)\forall t\in [0,T_0].\end{array}$$

Because $(P,W)$ remains nonnegative during the iteration, the arguments $(\overline{P},\overline{W})$ of the nonlinearities $p_i,{\lambda }_P,{\lambda }_R$ remains in $[0,\infty )$. Consequently, the extended Lipschitz versions ${\tilde{p}}_i, {\tilde{\lambda }}_P, {\tilde{\lambda }}_R$ introduced in Lemma 1 coincide with the original coefficients along the solution trajectory:   

$$\begin{array}{c}\hfill {\tilde{p}}_i\left(\overline{W}\left(t\right)\right)=p_i\left(\overline{W}\left(t\right)\right),{\tilde{\lambda }}_P\left(\overline{W}\left(t\right)\right)={\lambda }_P\left(\overline{W}\left(t\right)\right),{\tilde{\lambda }}_R\left(\overline{P}\left(t\right)\right)={\lambda }_R\left(\overline{P}\left(t\right)\right).\end{array}$$

Therefore, the fixed point constructed in Step 1 is a genuine solution of the original PDE system, not merely of the extended one.

• Step 3: Weak formulations. Repeating the same arguments in Step 1 for the Picard map defined by the following formulas

$$\begin{array}{cc}\hfill P(t,x)& =P_0(x-v_{P}t){\mathbf{1}}_{x\ge v_{P}t}+{\int }_0^t{\mathcal{B}}_P\left[P\right]\left(\tau ,X_P(\tau ;t,x)\right){\mathbf{1}}_{x\ge v_P(t-\tau )}d\tau \hfill \\ \hfill & +{\int }_0^{\infty }\left\{-{\lambda }_P\left(\tau \right)P\left(\tau ,X_P(\tau ;t,x)\right)+{\lambda }_R\left(\tau \right)W\left(\tau ,X_P(\tau ;t,x)\right)\right\}{\mathbf{1}}_{x\ge v_P(t-\tau )}d\tau ,\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill W(t,x)& =W_0(x-v_{W}t){\mathbf{1}}_{x\ge v_{W}t}+{\int }_0^t{\mathcal{B}}_W\left[P\right]\left(\tau ,X_W(\tau ;t,x)\right){\mathbf{1}}_{x\ge v_W(t-\tau )}d\tau \hfill \\ \hfill & +{\int }_0^{\infty }\left\{-\delta \left(X_W(\tau ;t,x)\right)W\left(\tau ,X_W(\tau ;t,x)\right)-{\lambda }_R\left(\tau \right)W\left(\tau ,X_W(\tau ;t,x)\right)\right\}{\mathbf{1}}_{x\ge v_W(t-\tau )}d\tau .\hfill \end{array}$$

(14)

also yield a unique local solution. Uniqueness implies that the local solutions given by (10) and (11) and by (13) and (14) coincide. The weak formulation is verified for the local solution by employing (13) and (14). Specifically, let $T>0$, for $\xi \in C_c^{\infty }((0,T)\times (0,\infty ))$, the weak formulation holds:

$$\begin{array}{cc}\hfill & {\int }_0^T{\int }_0^{\infty }P({\partial }_t\xi +v_P{\partial }_x\xi )dxdt+{\int }_0^T{\int }_0^{\infty }{g}_P\xi dxdt=0,\hfill \\ \hfill & {\int }_0^T{\int }_0^{\infty }W({\partial }_t\xi +v_W{\partial }_x\xi )dxdt+{\int }_0^T{\int }_0^{\infty }{g}_W\xi dxdt=0,\hfill \end{array}$$

where

$$\begin{array}{c}\hfill g_P(t,x):={\mathcal{B}}_P\left[P\right](t,x)-{\lambda }_P\left(t\right)P(t,x)+{\lambda }_R\left(t\right)W(t,x),\\ \hfill g_W(t,x):={\mathcal{B}}_W\left[P\right](t,x)-\delta \left(x\right)W(t,x)-{\lambda }_R\left(t\right)W(t,x).\end{array}$$

The analysis focuses on P, and the argument for W is analogous. P is written as the sum of two parts:

$$P=P^{\left(0\right)}+P^{\left(g\right)},P^{\left(0\right)}(t,x)=P_0(x-v_{P}t){\mathbf{1}}_{x\ge v_{P}t},P^{\left(g\right)}(t,x)={\int }_0^t{g}_P(\tau ,X_P(\tau ;t,x)){\mathbf{1}}_{x\ge v_P(t-\tau )}d\tau .$$

For the transport part $P^{\left(0\right)}$, setting $y=x-v_{P}t$ yields

$$\begin{array}{cc}\hfill I_0:=& {\int }_0^T{\int }_0^{\infty }{P}^{\left(0\right)}({\partial }_t\xi +v_P{\partial }_x\xi )dxdt={\int }_0^{\infty }{\int }_0^T{P}_0\left(y\right)({\partial }_t\xi +{\partial }_x\xi )(t,y+v_{P}t)dtdy\hfill \\ \hfill =& {\int }_0^{\infty }{P}_0\left(y\right){\int }_0^T{\displaystyle \frac{d}{dt}}\xi (t,y+v_{P}t)dtdy={\int }_0^{\infty }{P}_0\left(y\right)\left[\xi (T,y+v_{P}T)-\xi (0,y)\right]dy=0\hfill \end{array}$$

since $\xi$ has compact support. Next, the source term $P^{\left(g\right)}$ is used to compute

$$\begin{array}{cc}\hfill I_g& :={\int }_0^T{\int }_0^{\infty }{P}^{\left(g\right)}({\partial }_t\xi +v_P{\partial }_x\xi )dxdt\hfill \\ \hfill & ={\int }_0^{\infty }{\int }_0^T\left[{\int }_0^t{g}_P(\tau ,X_P(\tau ;t,x))d\tau \right]({\partial }_t\xi +v_P{\partial }_x\xi )dtdx.\hfill \end{array}$$

Changing variables and using Fubini’s theorem:

$$\begin{array}{cc}\hfill I_g& ={\int }_0^T{\int }_0^{\infty }{g}_P(\tau ,y)\left[{\int }_{t=\tau }^T{\displaystyle \frac{d}{dt}}\xi (t,y+v_P(t-\tau ))dt\right]dyd\tau \hfill \\ \hfill & ={\int }_0^T{\int }_0^{\infty }{g}_P(\tau ,y)\left[\xi (T,y+v_P(T-\tau ))-\xi (\tau ,y)\right]dyd\tau \hfill \\ \hfill & =-{\int }_0^T{\int }_0^{\infty }{g}_P(t,x)\xi (t,x)dxdt.\hfill \end{array}$$

Thus, the weak formulation for P is obtained.

• Step 4: Balance law. The functions $\overline{P}$ and $\overline{W}$ are absolutely continuous and satisfy exact balance laws.

Let ${\psi }_R$ be a smooth cutoff with $0\le {\psi }_R\le 1$, ${\psi }_R\left(x\right)\equiv 1$ for $x\in [0,R]$, $\mathrm{supp}{\psi }_R\in [0,R+1]$, $|{\psi }_R^{\prime }|\le C$, where C is independent of R. Define

$$F_R\left(t\right):={\int }_0^{\infty }P(t,x){\psi }_R\left(x\right)dx.$$

Testing the weak formulation with $\phi \left(t\right){\psi }_R\left(x\right)$ for $\phi \in C_c^{\infty }\left((0,\infty )\right)$ gives

$$\begin{array}{c}\hfill {\int }_0^T{\int }_0^{\infty }P({\phi }^{\prime }{\psi }_R+v_P\phi {\psi }_R^{\prime })dxdt+{\int }_0^T{\int }_0^{\infty }({\mathcal{B}}_P\left[P\right]-{\lambda }_{P}P+{\lambda }_R\overline{W})\phi {\psi }_{R}dxdt=0.\end{array}$$

By Fubini,

$$\begin{array}{cc}\hfill -& {\int }_0^T{\phi }^{\prime }\left(t\right)F_R\left(t\right)dt\hfill \\ \hfill ={\int }_0^T\phi \left(t\right)& \underset{=:L\left(t\right)}{\underbrace{\left\{v_P{\int }_0^{\infty }P(t,x){\psi }_R^{\prime }\left(x\right)dx+{\int }_0^{\infty }({\mathcal{B}}_P\left[P\right]-{\lambda }_P\overline{P}+{\lambda }_R\overline{W})(t,x){\psi }_R\left(x\right)dx\right\}}}dt.\hfill \end{array}$$

Since $(P,W)\in {\mathcal{X}}_T$, $L\in L^1\left([0,T]\right)$. Hence, $F_R$ is absolutely continuous on $[0,T]$ with, for a.e. t,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & F_R^{\prime }\left(t\right)=L\left(t\right)\hfill \\ \hfill =v_P& {\int }_0^{\infty }P(t,x){\psi }_R^{\prime }\left(x\right)dx+{\int }_0^{\infty }({\mathcal{B}}_P\left[P\right]-{\lambda }_{P}P+{\lambda }_{R}W)(t,x){\psi }_R\left(x\right)dx.\hfill \end{array}\end{array}$$

(15)

Integrating over $[0,t]$ yields

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & {\int }_0^{\infty }P(t,x){\psi }_R\left(x\right)dx-{\int }_0^{\infty }{P}_0\left(x\right){\psi }_R\left(x\right)dx\hfill \\ \hfill =& {\int }_0^t\left\{v_P{\int }_0^{\infty }P(\tau ,x){\psi }_R^{\prime }\left(x\right)dx+{\int }_0^{\infty }({\mathcal{B}}_P\left[P\right]-{\lambda }_{P}P+{\lambda }_{R}W)(\tau ,x){\psi }_R\left(x\right)dx\right\}d\tau .\hfill \end{array}\end{array}$$

(16)

The limit is passed to each term. Since $0\le {\psi }_R\le 1$ and $P\in L^1$, dominated convergence theorem gives

$$\begin{array}{cc}\hfill \underset{R\to \infty }{lim}{\int }_0^{\infty }P(t,x){\psi }_R\left(x\right)dx& ={\int }_0^{\infty }P(t,x)dx=\overline{P}\left(t\right),\hfill \\ \hfill \underset{R\to \infty }{lim}{\int }_0^{\infty }{P}_0\left(x\right){\psi }_R\left(x\right)dx& ={\int }_0^{\infty }{P}_0\left(x\right)dx=\overline{P}\left(0\right).\hfill \end{array}$$

Because ${\psi }_R^{\prime }$ is supported in the annulus $[R,R+1]$ and $\parallel P(\tau ,·)\parallel$ is uniformly bounded on $[0,T]$, $\int P{\psi }_R^{\prime }dx\to 0$ uniformly in $\tau$, so the first term on the right-hand side of Equation (16) vanishes as $R\to \infty$. For the source term, define

$$\begin{array}{c}\hfill H_R:=({\mathcal{B}}_P\left[P\right]-{\lambda }_{P}P+{\lambda }_{R}W){\psi }_R.\end{array}$$

Pointwise, $H_R\to {\mathcal{B}}_P\left[P\right]-{\lambda }_{P}P+{\lambda }_{R}W$, and

$$|H_R| \le B_P\left[P\right]+{\lambda }_{P}P+{\lambda }_{R}W$$

$${\int }_0^{\infty }(B_P\left[P\right]+{\lambda }_{P}P+{\lambda }_{R}W)(\tau ,x)dx\le [(2p_1\left(\tau \right)+p_3\left(\tau \right)+1){\lambda }_P+{\lambda }_R]M\left(\tau \right),$$

with $M\left(\tau \right)=\parallel P(\tau ,·)\parallel +\parallel W(\tau ,·)\parallel$ uniformly bounded in $\tau$. Hence dominated convergence (in x and $\tau$) gives

$$\underset{R\to \infty }{lim}{\int }_0^t{\int }_0^{\infty }{H}_R(\tau ,x)dxd\tau ={\int }_0^t{\int }_0^{\infty }({\mathcal{B}}_P\left[P\right]-{\lambda }_{P}P+{\lambda }_{R}W)(\tau ,x)dxd\tau .$$

Collecting limits in Equation (16) gives the identity

$$\begin{array}{c}\hfill \overline{P}\left(t\right)=\overline{P}\left(0\right)+{\int }_0^{t}G\left(\tau \right)d\tau ,G\left(\tau \right):={\int }_0^{\infty }({\mathcal{B}}_P\left[P\right]-{\lambda }_{P}P+{\lambda }_{R}W)(\tau ,x)dx.\end{array}$$

Since $G\in L^1(0,T)$, $\overline{P}$ is absolutely continuous with derivative $G\left(t\right)$ a.e., i.e.,

$$\begin{array}{c}\hfill {\displaystyle \frac{d}{dt}}\overline{P}\left(t\right)={\int }_0^{\infty }({\mathcal{B}}_P\left[P\right]-{\lambda }_{P}P+{\lambda }_{R}W)(t,x)dx=(p_1\left(t\right)-p_2\left(t\right)){\lambda }_P\left(t\right)\overline{P}\left(t\right)+{\lambda }_R\left(t\right)\overline{W}\left(t\right).\end{array}$$

Repeating the argument for W gives

$$\begin{array}{c}\hfill {\displaystyle \frac{d}{dt}}\overline{W}\left(t\right)=(1-p_1\left(t\right)+p_2\left(t\right)){\lambda }_P\left(t\right)\overline{P}\left(t\right)-{\lambda }_R\left(t\right)\overline{W}\left(t\right)-{\int }_0^{\infty }\delta \left(x\right)W(t,x)dx.\end{array}$$

Adding both equations provides

$$\begin{array}{c}\hfill {\displaystyle \frac{dM}{dt}}={\int }_0^{\infty }({\mathcal{B}}_P\left[P\right]+{\mathcal{B}}_W\left[P\right]-{\lambda }_{P}P-\delta W)dx\le 2{\widehat{\lambda }}_{P}M,\end{array}$$

so $M\left(t\right)\le exp\left(2{\widehat{\lambda }}_{P}t\right)M_0$ by Grönwall.

• Step 5: Global existence. From Step 4, the local solution $(P,W)\in {\mathcal{X}}_{T_0}$ satisfies

  $$M\left(T_0\right)=\parallel P(T_0,·)\parallel +\parallel W(T_0,·)\parallel \le e^{2{\widehat{\lambda }}_P{T}_0}{M}_0<\infty ,$$

  so no blow-up occurs at $t=T_0$.

By induction on n, assume that $(P,W)$ is defined on $[0,T_n]$. The same bound implies $M\left(T_n\right)\le exp\left(2{\widehat{\lambda }}_P{T}_n\right)M_0<\infty$, so Lemma 1 applies at $t=T_n$ with data $(P(T_n,·),W(T_n,·))$, delivering a unique extension to $[T_n,T_{n+1}]$ with

$$M\left(t\right)\le e^{2{\widehat{\lambda }}_{P}t}{M}_0,t\in [T_n,T_{n+1}].$$

Iterating gives a strictly increasing sequence $\left\{T_n\right\}$ and a solution on $[0,T^{*})$, $T^{*}={sup}_n{T}_n$.

If $T^{*}<\infty$, then for any $t_0<T^{*}$, the a priori bound ensures a bounded mass at $t_0$. By choosing $t_0$ sufficiently close to $T^{*}$, Lemma 1 then yields an extension beyond $T^{*}$, a contradiction.

Hence $T^{*}=\infty$ and the solution is global.    □

The following schematic summary in Figure 1 provides an overview of the global well-posedness proof.

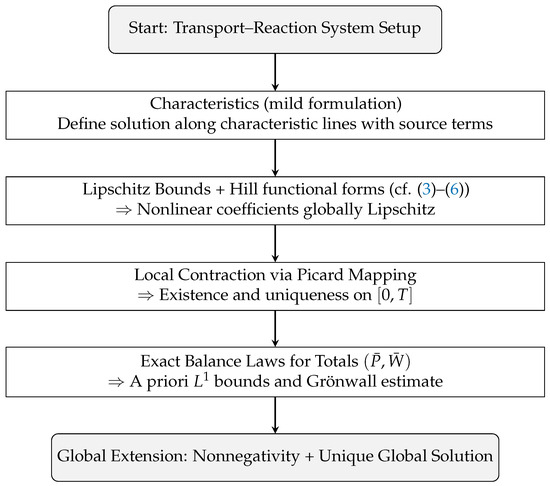
Figure 1. Method at a glance. Mild formulation → local contraction → exact balance laws → global extension.

Our global well-posedness result is established in $L^1$ space. Additional results in the weighted $L^1$ space are also included, yielding the following estimate:

Theorem 2 (Weighted $L^1$ estimate).

Define

$$M_1\left(t\right):={\int }_0^{\infty }x(P(t,x)+W(t,x))dx.$$

Under (H1)–(H2) and assume sufficient decay for $P,W$, i.e., for every $t\ge 0$,

$$x\left(P\right(t,x)+W(t,x\left)\right)<\infty \mathrm{as}x\to \infty ,$$

the solution $(P,W)$ of (2) satisfies the following weighted $L^1$ estimate:

$$M_1\left(t\right)\le max\{v_P,v_W\}M\left(t\right),\forall t\ge 0.$$

Therefore,

$$M_1\left(t\right)\le M_1\left(0\right)+{\displaystyle \frac{max\{v_P,v_W\}{M}_0}{2{\widehat{\lambda }}_P}}\left(e^{2{\widehat{\lambda }}_{P}t}-1\right),$$

and the weighted $L^1$ norm has at most exponential growth.

Proof. 

Multiplying the equations for P and W by x and integrating over $x\in [0,\infty )$ yields   

$$\begin{array}{cc}\hfill & {\displaystyle \frac{d}{dt}}{\int }_0^{\infty }xPdx+v_P\left(xP(t,x)\right){|}_0^{\infty }-v_P{\int }_0^{\infty }Pdx\hfill \\ \hfill =& \left(p_1{\lambda }_P{\alpha }_1+p_1{\lambda }_P{\alpha }_2+p_3{\lambda }_P{\gamma }_1-{\lambda }_P\right){\int }_0^{\infty }xPdx+{\lambda }_R{\int }_0^{\infty }xWdx,\hfill \\ \hfill & {\displaystyle \frac{d}{dt}}{\int }_0^{\infty }xWdx+v_W\left(xW(t,x)\right){|}_0^{\infty }-v_W{\int }_0^{\infty }Wdx\hfill \\ \hfill =& \left(p_2{\lambda }_P{\beta }_1+p_2{\lambda }_P{\beta }_2+p_3{\lambda }_P{\gamma }_2\right){\int }_0^{\infty }xPdx-{\int }_0^{\infty }\delta \left(x\right)xWdx-{\lambda }_R{\int }_0^{\infty }xWdx\hfill \end{array}$$

Adding the two equations yields

$${\displaystyle \frac{d}{dt}}{M}_1\left(t\right)=-v_P\left(xP(t,x)\right){|}_0^{\infty }-v_W\left(xW(t,x)\right){|}_0^{\infty }+v_P{\int }_0^{\infty }Pdx+v_W{\int }_0^{\infty }Wdx-{\int }_0^{\infty }\delta \left(x\right)xWdx.$$

The positivity of $P,W$ and $x\left(P\right(t,x)+W(t,x\left)\right)<\infty$ as $x\to \infty$ yields

$$\begin{array}{c}\hfill {\partial }_t{M}_1\left(t\right)\le max\{v_P,v_W\}M\left(t\right).\end{array}$$

Using the $L^1$ norm estimate $M\left(t\right)\le e^{2{\widehat{\lambda }}_{P}t}{M}_0$ for $t\ge 0$, the stated estimate for $M_1$ is easily obtained.    □

Theorems 1 and 2 show that under the $L^1$ or weighted $L^1$ spaces, P and W do not become unbounded. The $L^{\infty }$ estimate is a natural extension and is left for future work. The resulting balance laws in Theorem 1 for the totals $\overline{P}\left(t\right)$ and $\overline{W}\left(t\right)$ lay the foundation for the reduced system analyzed in the next section.

3. Exact Reduction to ODE

The balance laws derived from the PDE model project the dynamics of the system onto the total populations $\overline{P}$ and $\overline{W}$. However, the mortality term ${\int }_0^{\infty }\delta \left(x\right)W(t,x)dx$ depends on the full spatial profile of W and prevents a closed ODE in general. Under the constant death assumption $\delta \left(x\right)=\delta >0$, however, the mortality term simplifies to $\delta \overline{W}$, allowing for an exact reduction to an autonomous two-dimensional system. The autonomous system is presented, and several results are collected (with their proof in Theorem 5):

Theorem 3 (Planar reduction and global nonoscillation under compensatory feedback).

Assume $\delta \left(x\right)\equiv \delta >0$. Then the totals $\overline{P},\overline{W}$ obey the closed planar system

$$\left\{\begin{array}{c}\begin{array}{cc}{\displaystyle \frac{d\overline{P}}{dt}}=\left[p_1\left(\overline{W}\right)-p_2\left(\overline{W}\right)\right]{\lambda }_P\left(\overline{W}\right)\overline{P}+{\lambda }_R\left(\overline{P}\right)\overline{W},\hfill & t>0,\hfill \\ {\displaystyle \frac{d\overline{W}}{dt}}=\left[1-p_1\left(\overline{W}\right)+p_2\left(\overline{W}\right)\right]{\lambda }_P\left(\overline{W}\right)\overline{P}-({\lambda }_R\left(\overline{P}\right)+\delta )\overline{W},\hfill & t>0,\hfill \\ \overline{P}\left(0\right)={\overline{P}}_0=\parallel P_0\parallel ,\overline{W}\left(0\right)={\overline{W}}_0=\parallel W_0\parallel .\hfill \end{array}\hfill \end{array}\right.$$

(17)

obtained by integrating (1) and using $\int \delta W(t,x)dx=\delta \overline{W}\left(t\right)$. Suppose further that

(i)

$p_1, p_2, {\lambda }_P:{\mathbb{R}}_{\ge 0}\to {\mathbb{R}}_{\ge 0}$ are $C^1$ and nonincreasing in $\overline{W}$; ${\lambda }_R:{\mathbb{R}}_{\ge 0}\to {\mathbb{R}}_{\ge 0}$ is $C^1$ and nonincreasing in $\overline{P}$ (Hill-type laws (3)–(6) satisfy this), and $0\le p_1+p_2\le 1$.

(ii)

(Compensatory feedback) self-renewal decays more slowly than differentiation:

$$\begin{array}{c}\hfill p_1\left(\overline{W}\right)<p_2\left(\overline{W}\right),{\displaystyle \frac{d{p}_2\left(\overline{W}\right)}{d\overline{W}}}<{\displaystyle \frac{d{p}_1\left(\overline{W}\right)}{d\overline{W}}},\forall \overline{W}\ge 0.\end{array}$$

(18)

Equivalently, $p\left(\overline{W}\right):=p_1\left(\overline{W}\right)-p_2\left(\overline{W}\right)$ satisfies $p\left(\overline{W}\right)<0$ and $p^{\prime }\left(\overline{W}\right)>0$.

Then

(i)

(17) admits a unique global positive solution $(\overline{P},\overline{W})$ that is absolutely continuous in t.

(ii)

The positive quadrant $\{\overline{P}\ge 0,\overline{W}\ge 0\}$ is forward-invariant for the flow of the system.

(iii)

The system admits no nontrivial periodic orbits in $\{\overline{P}>0,\overline{W}>0\}$ (Dulac nonoscillation). Consequently, every bounded trajectory has an ω-limit set consisting only of equilibria and heteroclinic connections.

(iv)

If, in addition, the equilibrium is unique and all solutions are bounded, the unique equilibrium is globally asymptotically stable.

Our PDE model (1) employed the constant damage accumulation speed $v_P,v_W$. A natural extension is the nonlinear accumulation and repair mechanism. The damage-dependent drift is decomposed into “accumulation” and “repair” components:

$$v_P\left(x\right)=a_P\left(x\right)-r_P\left(x\right),v_W\left(x\right)=a_W\left(x\right)-r_W\left(x\right),$$

where $a_{·}\ge 0$ models damage accumulation and $r_{·}\ge 0$ models active repair. The boundary condition $v_{·}\left(0\right)=0$ is imposed to ensure consistency of the no-flux boundary at $x=0$ when repair dominates at low damage. Then for any drift $v_{·}\left(x\right)$ with $v_{·}\left(0\right)=0$ and sufficient decay so that the boundary flux at $x\to \infty$ vanishes, integrating (2) over x eliminates the transport term:

$${\int }_0^{\infty }{\partial }_x\left(v_{P}P\right)dx={\left[v_{P}P\right]}_0^{\infty }=0,{\int }_0^{\infty }{\partial }_x\left(v_{W}W\right)dx={\left[v_{W}W\right]}_0^{\infty }=0.$$

Consequently, the population-level ODEs for the totals remain the same as (17) under constant death rate $\delta$. In summary, the nonlinear accumulation and repair mechanisms will impact the damage distribution in the stem and TD compartments, but yield the same total population dynamics under no-flux assumptions.

After closure, each term is interpreted in biological terms:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\displaystyle \frac{d\overline{P}}{dt}}& =\underset{\mathrm{forward}\mathrm{self}-\mathrm{renewal}}{\underbrace{p\left(\overline{W}\right){\lambda }_P\left(\overline{W}\right)\overline{P}}}+\underset{\mathrm{reverse}\left(\mathrm{dedifferentiation}\right)}{\underbrace{{\lambda }_R\left(\overline{P}\right)\overline{W}}},\hfill \\ \hfill {\displaystyle \frac{d\overline{W}}{dt}}& =\underset{\mathrm{forward}\mathrm{differentiation}}{\underbrace{(1-p\left(\overline{W}\right)){\lambda }_P\left(\overline{W}\right)\overline{P}}}-\underset{\mathrm{loss}}{\underbrace{\delta \overline{W}}}-\underset{\mathrm{reverse}\mathrm{sink}}{\underbrace{{\lambda }_R\left(\overline{P}\right)\overline{W}}}.\hfill \end{array}\end{array}$$

(19)

Dedifferentiation simultaneously augments $\dot{\overline{P}}$ and damps $\dot{\overline{W}}$.

This finite-dimensional reduction (17) captures self-renewal, differentiation, dedifferentiation, and constant mortality at the population level. The feedback laws in Equations (3)–(6) produce nonlinear dependence on totals while preserving exact closure. Section 4 and Section 5 analyze equilibria and prove local and global stability by linearization, Dulac criterion, and the Poincaré–Bendixson theorem.

4. Local Stability and Bifurcation Threshold

With the ODE reduction in Equation (9), the linearized dynamics near equilibria are analyzed under constant $\delta$ and constant ${\lambda }_R$. In this section, uniform feedback on $p_1, p_2$ is assumed: $k_1=k_2$ and $m_1=m_2$. It then follows that

$$p_1\left(t\right)-p_2\left(t\right)={\displaystyle \frac{{\widehat{p}}_1-{\widehat{p}}_2}{1+{\left(k_1\overline{W}\right)}^{m_1}}}.$$

(20)

Let a nontrivial steady state $\mathcal{S}=({\overline{P}}^{*},{\overline{W}}^{*})$ exist with stationary damage distributions $P^{*}\left(x\right)$ and $W^{*}\left(x\right)$. Setting ${\displaystyle \frac{d\overline{P}}{dt}}={\displaystyle \frac{d\overline{W}}{dt}}=0$ in Equation (17) gives   

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill 0& =\left[p_1\left({\overline{W}}^{*}\right)-p_2\left({\overline{W}}^{*}\right)\right]{\lambda }_P\left({\overline{W}}^{*}\right){\overline{P}}^{*}+{\lambda }_R{\overline{W}}^{*},\hfill \\ \hfill 0& =\left[1-p_1\left({\overline{W}}^{*}\right)+p_2\left({\overline{W}}^{*}\right)\right]{\lambda }_P\left({\overline{W}}^{*}\right){\overline{P}}^{*}-{\lambda }_R{\overline{W}}^{*}-D^{*},\hfill \end{array}\end{array}$$

(21)

where $D^{*}={\int }_0^{\infty }\delta \left(x\right)W^{*}\left(x\right)dx$. Define the W-weighted mean death rate

$${⟨\delta ⟩}_{W^{*}}:={\displaystyle \frac{D^{*}}{{\overline{W}}^{*}}}.$$

(22)

Eliminating $\overline{P}$ from (21) yields the compact balance relation

$$(p_2\left({\overline{W}}^{*}\right)-p_1\left({\overline{W}}^{*}\right)){⟨\delta ⟩}_{W^{*}}={\lambda }_R.$$

In the constant-death case ($⟨\delta ⟩=\delta$),

$$(p_2\left({\overline{W}}^{*}\right)-p_1\left({\overline{W}}^{*}\right))\delta ={\lambda }_R.$$

(23)

Here $p_1\left({\overline{W}}^{*}\right)-p_2\left({\overline{W}}^{*}\right)<0$, so the left-hand side is positive. This ensures consistency with the positivity of the dedifferentiation rate ${\lambda }_R\left({\overline{P}}^{*}\right)>0$ on the right-hand side. Summing the two steady equations in (21) yields the population ratio

$$\begin{array}{c}\hfill {\lambda }_P\left({\overline{W}}^{*}\right){\overline{P}}^{*}=D^{*}={⟨\delta ⟩}_{W^{*}}{\overline{W}}^{*},⟹{\displaystyle \frac{{\overline{P}}^{*}}{{\overline{W}}^{*}}}={\displaystyle \frac{{⟨\delta ⟩}_{W^{*}}}{{\lambda }_P\left({\overline{W}}^{*}\right)}},\end{array}$$

(24)

so the equilibrium ratio depends only on replication and death rates at the fixed point (not on ${\lambda }_R$ directly). Assuming feedback laws in Equations (3)–(5). The steady state is given by

$$\begin{array}{cc}\hfill {\overline{P}}^{*}& ={\displaystyle \frac{{⟨\delta ⟩}_{W^{*}}{\widehat{W}}^{*}}{{\lambda }_P\left({\overline{W}}^{*}\right)}},\hfill \\ \hfill {\overline{W}}^{*}& =k_1^{-1}{\left({\displaystyle \frac{({\widehat{p}}_2-{\widehat{p}}_1){⟨\delta ⟩}_{W^{*}}-{\lambda }_R}{{\lambda }_R}}\right)}^{1/m_1}.\hfill \end{array}$$

(25)

The closed ODE (constant-$\delta$ reduction) is now linearized about $\mathcal{S}=({\overline{P}}^{*},{\overline{W}}^{*})$. Write $p\left(\overline{W}\right):=p_1\left(\overline{W}\right)-p_2\left(\overline{W}\right)$ and omit explicit $\left({\overline{W}}^{*}\right)$ evaluation where clear. The reduced dynamics are

$${\displaystyle \frac{d\overline{P}}{dt}}=\underset{=:f_P}{\underbrace{p\left(\overline{W}\right){\lambda }_P\left(\overline{W}\right)\overline{P}+{\lambda }_R\overline{W}}},{\displaystyle \frac{d\overline{W}}{dt}}=\underset{=:f_W}{\underbrace{(1-p\left(\overline{W}\right)){\lambda }_P\left(\overline{W}\right)\overline{P}-({\lambda }_R+\delta )\overline{W}}}.$$

The Jacobian $\mathcal{J}\left(\mathcal{S}\right)$ evaluated at $\mathcal{S}$ has entries

$$\begin{array}{cccc}\hfill a_{11}& ={\partial }_{\overline{P}}{f}_P=p{\lambda }_P,\hfill & \hfill a_{12}& ={\partial }_{\overline{W}}{f}_P=\overline{P}{\displaystyle \frac{d}{d\overline{W}}}\left(p{\lambda }_P\right)+{\lambda }_R,\hfill \\ \hfill a_{21}& ={\partial }_{\overline{P}}{f}_W=(1-p){\lambda }_P,\hfill & \hfill a_{22}& ={\partial }_{\overline{W}}{f}_W=\overline{P}{\displaystyle \frac{d}{d\overline{W}}}\left((1-p){\lambda }_P\right)-({\lambda }_R+\delta ).\hfill \end{array}$$

all evaluated at $({\overline{P}}^{*},{\overline{W}}^{*})$. A straightforward algebraic expansion with (23) yields identities

$$\begin{array}{cc}\hfill \mathrm{tr}\mathcal{J}\left(\mathcal{S}\right)& =a_{11}+a_{22}=p\left({\overline{W}}^{*}\right){\lambda }_P\left({\overline{W}}^{*}\right)-{\overline{P}}^{*}{p}^{\prime }\left({\overline{W}}^{*}\right){\lambda }_P\left({\overline{W}}^{*}\right)+{\overline{P}}^{*}(1-p\left({\overline{W}}^{*}\right)){\lambda }_P^{\prime }\left(\overline{W}\right)-({\lambda }_R+\delta )\hfill \\ \hfill det\mathcal{J}\left(\mathcal{S}\right)& =a_{11}{a}_{22}-a_{12}{a}_{21}=-{\lambda }_P\left({\overline{W}}^{*}\right)\left({\lambda }_R+p\left({\overline{W}}^{*}\right)\delta \right)-{\overline{P}}^{*}{\lambda }_P{\left({\overline{W}}^{*}\right)}^2{p}^{\prime }\left({\overline{W}}^{*}\right)\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill & =-{\overline{P}}^{*}{\lambda }_P{\left({\overline{W}}^{*}\right)}^2{p}^{\prime }\left({\overline{W}}^{*}\right).\hfill \end{array}$$

(27)

Without feedback, the Jacobian at equilibrium satisfies

$$tr\mathcal{J}\left(\mathcal{S}\right)=p{\lambda }_P-({\lambda }_R+\delta )=-{\displaystyle \frac{{\lambda }_P{\lambda }_R}{\delta }}-({\lambda }_R+\delta )<0,det\mathcal{J}\left(\mathcal{S}\right)=0.$$

Hence, the eigenvalues are

$${\lambda }_1=0,{\lambda }_2=-{\displaystyle \frac{{\lambda }_P{\lambda }_R}{\delta }}-({\lambda }_R+\delta )<0,$$

confirming that the system has one neutral and one strictly stable direction in the non-feedback case. The zero determinant ensures that $\mathcal{J}\left(\mathcal{S}\right)$ is singular; therefore, there is a continuum of equilibria, unique up to a scalar factor. With feedback, (23) yields $p\left({\overline{W}}^{*}\right)<0$. (20) ensures ${\widehat{p}}_1-{\widehat{p}}_2<0$. Then, taking differentiation of p gives $p^{\prime }\left({\overline{W}}^{*}\right)>0$, and the determinant is negative, and the equilibrium is a saddle (one unstable, one stable direction). The following result summarizes how dedifferentiation introduces a neutral direction in the absence of feedback, and how feedback then selects and reveals a saddle structure.

Theorem 4 (Local saddle revealed  by feedback when dedifferentiation is present).

Assume that $\delta \left(x\right)\equiv \delta >0$ is constant. In the absence of feedback on $p_1, p_2, {\lambda }_P,{\lambda }_R$, a nontrivial equilibrium exists only when

$$(p_2-p_1)\delta ={\lambda }_R,i.e.{(p_1-p_2)}_{\mathrm{crit}}=-{\displaystyle \frac{{\widehat{\lambda }}_R}{\delta }}.$$

At this threshold, the Jacobian satisfies $det\mathcal{J}=0$ and possesses one zero and one negative eigenvalue; hence, the equilibrium is non-hyperbolic and belongs to a continuous family of steady states.

When Hill-type feedback on $p_1, p_2, {\lambda }_P, {\lambda }_R$ is introduced, this degeneracy is lifted and the equilibrium becomes a saddle point.

The above analysis establishes the local bifurcation structure: dedifferentiation creates a degenerate (non-hyperbolic) continuum of equilibria in the no-feedback limit, and feedback lifts this degeneracy and reveals a saddle. The non-hyperbolic vs, saddle structure is merely a local result under the concrete feedback on $p_1, p_2, {\lambda }_P$ with constant ${\lambda }_R$ and $\delta$ in this section. For the general feedback on $p_1, p_2, {\lambda }_P, {\lambda }_R$, some additional assumptions could yield globally asymptotic stability, in contrast to the local and unstable saddle classification.

If the death rate increases with damage, ${\delta }^{\prime }\left(x\right)>0$, highly damaged cells are removed more efficiently, shifting the stationary damage distribution toward lower x. This reduces the mean death rate ${⟨\delta ⟩}_{W^{*}}$, hence ${\overline{W}}^{*}$ decreases by (25). Since ${\lambda }_P$ is a decreasing function of $\overline{W}$, an increasing $\delta$ function renders the decline of the stem population ${\overline{P}}^{*}$ and ratio ${\overline{P}}^{*}/{\overline{W}}^{*}$ by (24). Biologically, an increasing $\delta \left(x\right)$ promotes a lineage biased toward more differentiated cells and a more fragile stem-cell pool, consistent with age-related decline in regenerative capacity.

The global behavior of the reduced system is next considered to determine whether these local stability properties extend to the entire positive quadrant.

5. Global Stability Analysis

Extending the local results, the global dynamics of the reduced system  (9) are classified under the constant death rate $\delta \left(x\right)\equiv \delta >0$. The positive quadrant is forward-invariant because the PDE solutions remain nonnegative (Theorem 1). It is assumed that the feedback maps $p_1, p_2, {\lambda }_P, {\lambda }_R$ are continuous, monotone decreasing, and vanish at infinity: for all $\overline{P},\overline{W}\ge 0$,

$$\begin{array}{c}\hfill \begin{array}{cccc}{p}_1^{\prime }\left(\overline{W}\right)<0,\hfill & p_2^{\prime }\left(\overline{W}\right)<0,\hfill & {\lambda }_P^{\prime }\left(\overline{W}\right)<0,\hfill & {\lambda }_R^{\prime }\left(\overline{P}\right)<0,\hfill \\ \underset{\overline{W}\to \infty }{lim}{p}_1\left(\overline{W}\right)=0,\hfill & \underset{\overline{W}\to \infty }{lim}{p}_2\left(\overline{W}\right)=0,\hfill & \underset{\overline{W}\to \infty }{lim}{\lambda }_P\left(\overline{W}\right)=0,\hfill & \underset{\overline{P}\to \infty }{lim}{\lambda }_R\left(\overline{P}\right)=0.\hfill \end{array}\end{array}$$

The compensatory feedback condition (18) is imposed. Biologically, the compensatory feedback condition (18) expresses a stabilizing regulatory mechanism that maintains homeostasis in the lineage. The inequalities $p_1\left(\overline{W}\right)<p_2\left(\overline{W}\right)$ and $p_1^{\prime }\left(\overline{W}\right)>p_2^{\prime }\left(\overline{W}\right)$ together mean that as the total TD population $\overline{W}$ increases, the system responds by reducing the differentiation bias and relatively sustaining self-renewal. In other words, differentiation weakens more rapidly than self-renewal under strong feedback, providing a compensatory effect that prevents excessive depletion of stem cells when $\overline{W}$ is large.

The global asymptotic behavior under compensatory feedback is now presented. For notational clarity, the shorthand already used in Section 4 is introduced:

$$p\left(\overline{W}\right):=p_1\left(\overline{W}\right)-p_2\left(\overline{W}\right),$$

which measures the net self-renewal bias. Negative p corresponds to dominance of difference, while positive p indicates dominance of self-renewal. This notation simplifies the divergence computation and subsequent algebraic expressions.

Theorem 5 (Global asymptotic behavior under compensatory feedback).

Assume the ODE reduction (Equation (17)) holds, with constant δ. Assume the compensatory feedback condition (18). Moreover, the system admits only finite number of equilibria. Then the ω-limit set of any bounded solution $\Phi \left(t\right)=(\overline{P}\left(t\right),\overline{W}\left(t\right))$ is either a single equilibrium point, or a finite set of equilibria $\{{\mathbf{q}}_1,\dots ,{\mathbf{q}}_m\}$ connected by heteroclinic orbits.

If, in addition, the equilibrium $\mathcal{S}=({\overline{P}}^{*},{\overline{W}}^{*})$ is unique, the following dichotomy holds:

(i)

Convergence: If $\Phi \left(t\right)$ is bounded, then $\Phi \left(t\right)\to \mathcal{S}$ as $t\to \infty$, and

$$\begin{array}{cc}\hfill & \underset{t\to \infty }{lim}\left((p_2\left(\overline{W}\left(t\right)\right)-p_1\left(\overline{W}\left(t\right)\right))\delta -{\lambda }_R\left(\overline{P}\left(t\right)\right)\right)\hfill \\ \hfill =& \underset{t\to \infty }{lim}\left(-p\left(\overline{W}\left(t\right)\right)\delta -{\lambda }_R\left(\overline{P}\left(t\right)\right)\right)=0\hfill \end{array}$$

If, moreover, every solution of (9) is bounded, then $\mathcal{S}$ is globally asymptotically stable.

(ii)

Divergence: Conversely, if the balance relation fails asymptotically, then $\Phi \left(t\right)$ cannot remain bounded. More precisely, $\underset{t\to \infty }{lim\; sup}\parallel \Phi \left(t\right)\parallel \to \infty$ as $t\to \infty$, if

$$\underset{t\to \infty }{lim\; sup}|-p\left(\overline{W}\left(t\right)\right)\delta -{\lambda }_R\left(\overline{P}\left(t\right)\right)|>0.$$

Proof. 

Step 1: Negative divergence and Dulac.

Let

$$\mathbf{G}(\overline{P},\overline{W})=(G_1,G_2),$$

with

$$G_1=p\left(\overline{W}\right){\lambda }_P\left(\overline{W}\right)\overline{P}+{\lambda }_R\left(\overline{P}\right)\overline{W},G_2=(1-p\left(\overline{W}\right)){\lambda }_P\left(\overline{W}\right)\overline{P}-(\delta +{\lambda }_R\left(\overline{P}\right))\overline{W}.$$

Then,

$$\nabla ·\mathbf{G}={\displaystyle \frac{\partial G_1}{\partial \overline{P}}}+{\displaystyle \frac{\partial G_2}{\partial \overline{W}}}.$$

A straightforward calculation gives

$$\nabla ·\mathbf{G}=p\left(\overline{W}\right){\lambda }_P\left(\overline{W}\right)+{\lambda }_R^{\prime }\left(\overline{P}\right)\overline{W}-p^{\prime }\left(\overline{W}\right){\lambda }_P\left(\overline{W}\right)\overline{P}+(1-p\left(\overline{W}\right)){\lambda }_P^{\prime }\left(\overline{W}\right)\overline{P}-(\delta +{\lambda }_R\left(\overline{P}\right)).$$

Under compensatory feedback, $\nabla ·\mathbf{G}<0$ on $\Omega$. Hence, Dulac’s criterion precludes periodic orbits.

• Step 2: No homoclinic orbits. Assume $\Gamma$ is a homoclinic orbit with limit point $\mathbf{q}$, and E is the interior of $\Gamma \cup \left\{\mathbf{q}\right\}$. Green’s theorem yields

  $$\begin{array}{c}\hfill \underset{E}{\int \int }\nabla ·\mathbf{G}d\overline{P}d\overline{W}={\oint }_{\Gamma \cup \left\{\mathbf{q}\right\}}(G_{1}d\overline{W}-G_{2}d\overline{P})={\int }_{-\infty }^{\infty }(G_1{G}_2-G_2{G}_1)dt=0.\end{array}$$

  This contradicts $\nabla ·\mathbf{G}<0$.

• Step 3: Classification of $\omega$-limit sets. With periodic and homoclinic orbits ruled out and only finitely many equilibria assumed, the Poincaré–Bendixson theorem implies that the $\omega$-limit set of any bounded trajectory is either a single equilibrium or a finite set of equilibria connected by a countable family of heteroclinic orbits, as stated.

• Step 4: Uniqueness ⇒ convergence of bounded trajectories. If the equilibrium $\mathcal{S}=({\overline{P}}^{*},{\overline{W}}^{*})$ is unique, any bounded trajectory’s $\omega$-limit set lies in $\left\{\mathcal{S}\right\}$. Hence, $\Phi \left(t\right)\to \mathcal{S}$. At equilibria

  $$\begin{array}{c}\hfill -p\left(\overline{W}\left(t\right)\right)\delta -{\lambda }_R\left(\overline{P}\left(t\right)\right)=0.\end{array}$$

Continuity of $p_1, p_2, {\lambda }_R$ along $\Phi \left(t\right)$ thus gives

$$\begin{array}{c}\hfill \underset{t\to \infty }{lim}\left(-p\left(\overline{W}\left(t\right)\right)\delta -{\lambda }_R\left(\overline{P}\left(t\right)\right)\right)=0.\end{array}$$

If, moreover, every trajectory is bounded, then all trajectories converge to $\mathcal{S}$, i.e., $\mathcal{S}$ is globally asymptotically stable. The divergence result follows easily.    □

For standard references, see [44] for Dulac’s criterion and the (generalized) Poincaré–Bendixson theorem and [45] for monotone dynamical systems.

Theorem 6 (Global stability under uniqueness).

Assume $\delta >0$, compensatory feedback, and that at least one of $(p_1-p_2)\left(\overline{W}\right)$ and ${\lambda }_R\left(\overline{P}\right)$ depends nontrivially on its argument. Then $G_1$ and $G_2$ share no nontrivial common factor [44], and the equilibrium $\mathcal{S}$ is unique. Then the ω–limit set of any bounded trajectory $\Phi \left(t\right)=(\overline{P}\left(t\right),\overline{W}\left(t\right))$ in the positive quadrant reduces to $\mathcal{S}$. In particular, if all solutions are bounded, $\mathcal{S}$ is globally asymptotically stable.

Proof. 

For the concrete vector field

$$\begin{array}{c}\hfill G_1=p{\lambda }_P\overline{P}+{\lambda }_R\overline{W},G_2=(1-p){\lambda }_P\overline{P}-(\delta +{\lambda }_R)\overline{W},\end{array}$$

a necessary condition for $G_1$ and $G_2$ to have a nontrivial common factor is that the determinant of their coefficient matrix A vanishes identically. A direct computation shows that $\det A\equiv 0$ is equivalent to

$$\begin{array}{c}\hfill -p\left(\overline{W}\right)\delta ={\lambda }_R\left(\overline{P}\right),\forall (\overline{P},\overline{W})\in \Omega .\end{array}$$

If at least one side depends nontrivially on its argument, the equality cannot hold for all $(\overline{P},\overline{W})$.

The following relations hold at any equilibrium $\mathcal{S}=({\overline{P}}^{*},{\overline{W}}^{*})$:   

$$\begin{array}{cc}\hfill & -p\left({\overline{W}}^{*}\right)\delta ={\lambda }_R\left({\overline{P}}^{*}\right),\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill & {\displaystyle \frac{{\overline{P}}^{*}}{{\overline{W}}^{*}}}={\displaystyle \frac{\delta }{{\lambda }_P\left({\overline{W}}^{*}\right)}},\hfill \end{array}$$

(29)

Then

(1)

If both p and ${\lambda }_R$ vary with their arguments, then (28) holds for only one pair $({\overline{P}}^{*},{\overline{W}}^{*})$.

(2)

If only p is non-constant, (28) fixes a unique ${\overline{W}}^{*}$, and ${\overline{P}}^{*}/{\overline{W}}^{*}=\delta /{\lambda }_P\left({\overline{W}}^{*}\right)$ gives a unique ${\overline{P}}^{*}$.

(3)

If only ${\lambda }_R$ is non-constant, (28) fixes a unique ${\overline{P}}^{*}$, and the ratio law ${\overline{P}}^{*}{\lambda }_P\left({\overline{W}}^{*}\right)=\delta {\overline{W}}^{*}$—whose left-hand side decreases and right-hand side increases in $\overline{W}$—yields a unique ${\overline{W}}^{*}$.

Therefore, the equilibrium is unique. Dulac’s criterion and the generalized Poincaré-Bendixson theorem apply.    □

A scaling invariance result for steady states under uniform rescaling of feedback strengths is now quantified.

Proposition 1 (Scaling law of the steady state).

Assume the Hill type laws (3)–(6). Fix all parameters except $k_1, k_2, k_3, k_4$. If $k_i$ are rescaled by a common factor $A>0$, then the rescaled system admits the steady state $({\overline{P}}^{*}/A,{\overline{W}}^{*}/A)$.

Proof. 

The rescaling gives $p_j^{\prime }(\overline{W}/A)=p_j\left(\overline{W}\right)(j=1,2)$, ${\lambda }_P^{\prime }(\overline{W}/A)={\lambda }_P\left(\overline{W}\right)$, ${\lambda }_R^{\prime }(\overline{P}/A)={\lambda }_R\left(\overline{P}\right)$. Substituting $({\overline{P}}^{\prime },{\overline{W}}^{\prime })=({\overline{P}}^{*}/A,{\overline{W}}^{*}/A)$ into Equation (21) recovers the steady-state relations (up to a factor of $1/A$), so $({\overline{P}}^{\prime },{\overline{W}}^{\prime })$ is again an equilibrium. Assuming Hill-type laws ensures p and ${\lambda }_R$ depend nontrivially on their arguments, and Theorem 6 guarantees the uniqueness of the equilibrium. Then this uniqueness implies that the scaling of $k_i$ inversely shifts the steady state.    □

Proposition 1 provides a practical control strategy: first adjust the ratio ${\displaystyle \frac{{\overline{W}}^{*}}{{\overline{P}}^{*}}}$ by tuning ${\displaystyle \frac{{\lambda }_P}{\delta }}$, then the absolute sizes $({\overline{P}}^{*},{\overline{W}}^{*})$ by rescaling all $k_i$.

The mathematical operation of rescaling feedback strength in our reduced model has concrete biological counterparts. In tissues, the effective strength of a feedback loop can be modulated by changing the abundance or availability of receptors at the niche interface. For example, receptor degradation directly attenuate niche signaling: as shown in a Drosophila germline niche, “the Tkv receptor is internalized into hub cells from the MT-nanotube surface and subsequently degraded in the hub cell lysosomes”, and perturbation of this process “resulted in an overabundance of Tkv protein in GSCs and hyperactivation of a downstream signal, suggesting that the MT-nanotubes also serve a second purpose to dampen the niche signaling” [46].

The local and global stability guarantees lend themselves to empirical verification through targeted simulations.

6. Numerical Results

This section corroborates the analytical results with simulations of the reduced ODE under a constant death rate. Consider

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\begin{array}{cc}{\displaystyle \frac{d\overline{P}\left(t\right)}{dt}}=(2f\left(t\right)-1){\widehat{\lambda }}_P\overline{P}\left(t\right)+{\widehat{\lambda }}_R\overline{W}\left(t\right),\hfill & t>0,\hfill \\ {\displaystyle \frac{d\overline{W}\left(t\right)}{dt}}=(2-2f\left(t\right)){\widehat{\lambda }}_P\overline{P}\left(t\right)-({\widehat{\lambda }}_R+\delta )\overline{W}\left(t\right),\hfill & t>0,\hfill \\ \overline{P}\left(0\right)={\overline{P}}_0,\overline{W}\left(0\right)={\overline{W}}_0,\hfill \end{array}\hfill \end{array}\right.\end{array}$$

(30)

which coincides with Equation (17) since $2f\left(t\right)-1=p_1\left(t\right)-p_2\left(t\right)={\displaystyle \frac{2\widehat{f}-1}{1+{\left(k_1\overline{W}\right)}^{m_1}}}$ (Equation (7)). The simulations confirm the bifurcation threshold $\tilde{f}=0.25$ implied by $(1-2\widehat{f})\delta ={\widehat{\lambda }}_R$ and reproduces the predicted scaling behavior.

To ensure consistency between the PDE and its finite-dimensional reduction, the full damage-structured PDE system is first solved, and the computed solution is then integrated over the damage variable to obtain the corresponding total-population trajectories in the ODE reduction. The damage domain $x\in [0,\tilde{A}]$ is discretized uniformly as $x_i=i\Delta x$ for $i=0,1,\dots ,N$, and the transport terms are approximated using conservative upwind finite-volume fluxes to preserve nonnegativity and total mass. Temporal evolution is advanced using an explicit scheme subject to a Courant–Friedrichs–Lewy (CFL) condition,

$$\Delta t\le C{\displaystyle \frac{\Delta x}{max\{v_P,v_W\}}},0<C<1.$$

The total populations at discrete times $t^n=n\Delta t$ are evaluated by numerical quadrature,

$${\overline{P}}^n=\sum _{i=1}^N{P}_i^n\Delta x,{\overline{W}}^n=\sum _{i=1}^N{W}_i^n\Delta x,P_i^n\approx P(t^n,x_i),W_i^n\approx W(t^n,x_i).$$

For phase portraits of the reduced ODE system, the governing equations are directly integrated using the adaptive Runge–Kutta method implemented in ode45 (MATLAB R2025b). All simulations are verified to respect the CFL condition, ensuring numerical stability.

Figure 2 illustrates three regimes as $\widehat{f}$ crosses the analytical threshold $\tilde{f}$. For $\widehat{f}>\tilde{f}$, both populations grow exponentially. For $\widehat{f}=\tilde{f}$, trajectories approach a steady state. For $\widehat{f}<\tilde{f}$, both populations decay to extinction. Figure 3 shows the threshold condition $(1-2\widehat{f})\delta ={\widehat{\lambda }}_R$ in the $({\widehat{\lambda }}_R,\widehat{f})$ plane for several $\delta$, which separates growth, steady state, and extinction. Figure 4 presents phase portraits with nullclines, the saddle equilibrium, and its stable and unstable manifolds, in agreement with the local analysis. Figure 5 verifies the scaling law under Hill feedback and shows that uniform rescaling of feedback strengths rescales the steady state while preserving the population ratio.

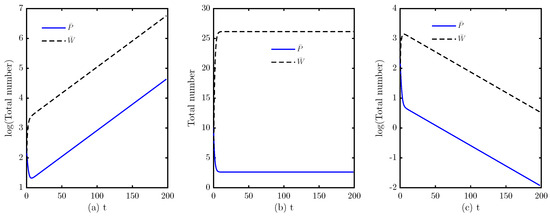
Figure 2. Bifurcation dynamics in the stem and terminally differentiated (TD) system as $\widehat{f}$ crosses the threshold $\tilde{f}=0.25$ with ${\widehat{\lambda }}_P=1$, ${\widehat{\lambda }}_R=0.05$, $\delta =0.1$, and $\overline{P}\left(0\right)=\overline{W}\left(0\right)=4$. (a) $\widehat{f}>\tilde{f}$ and both populations grow exponentially, (b) $\widehat{f}=\tilde{f}$ and the system stabilizes to a steady state, (c) $\widehat{f}<\tilde{f}$ and populations decay exponentially towards extinction. Numerical fits confirm exponential growth or decay. A step size of $\Delta t=0.025$ and $\Delta x=0.01$ is used, with domain boundary $\tilde{A}=4$. Other parameter values are ${\widehat{p}}_1=\tilde{f}$, ${\widehat{p}}_2=1-\tilde{f}$, $p_3=0$, $v_P=v_W=0.05$, ${\alpha }_1={\alpha }_2=0.5$, ${\beta }_1={\beta }_2=0.5$, ${\gamma }_1=1/3$, ${\gamma }_2=2/3$, $k_1=k_2=k_3=k_4=0$, $m_1=m_2=m_3=m_4=2$.

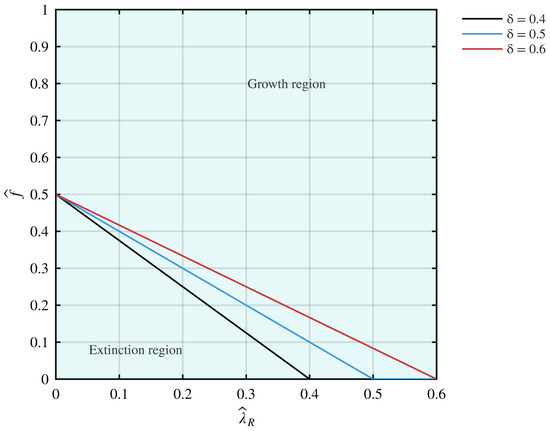
Figure 3. Bifurcation diagram in the $({\widehat{\lambda }}_R,\widehat{f})$ plane for $\delta =0.4$ (black), $\delta =0.5$ (blue), and $\delta =0.6$ (red). The curve $(1-2\widehat{f})\delta ={\widehat{\lambda }}_R$ separates exponential growth (above), extinction (below), and marginal equilibrium (on the line). The diagram quantifies how $\widehat{f}$ and ${\widehat{\lambda }}_R$ control transitions among three regimes.

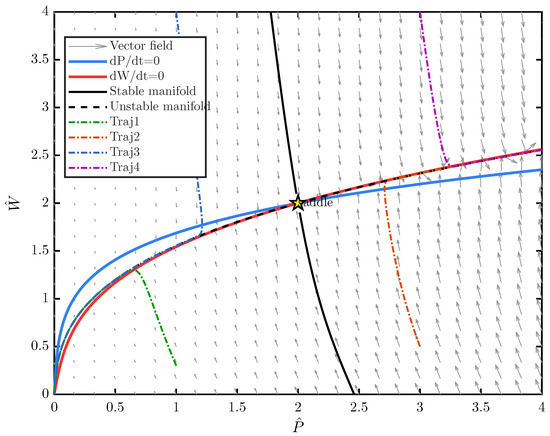
Figure 4. Phase portrait with nullclines, saddle equilibrium, and manifolds. The vector field appears in grey. The blue nullcline solves $d\overline{P}/dt=0$ and the red nullcline solves $d\overline{W}/dt=0$. Their intersection marks the saddle equilibrium. The stable manifold (solid black line) forms the separatrix between bounded and unbounded trajectories, and the unstable manifold (dashed black line) repels trajectories from the equilibrium. Representative trajectories are shown as dashed colored lines. Parameters: ${\widehat{\lambda }}_P=1$, ${\widehat{\lambda }}_R=0.02$, $\delta =0.2$, $\widehat{f}=0.25$, ${\widehat{p}}_1=0.25$, ${\widehat{p}}_2=0.75$, $p_3=0$, $k_1=k_2=k_3=1$, $k_4=0$, $m_1=m_2=m_3=m_4=2$. The initial values for the four trajectories are $({\overline{P}}_0,{\overline{W}}_0)=(1,0.3)$ for $i=1$, $(3,0.5)$ for $i=2$, $(1,4)$ for $i=3$, and $(3,4)$ for $i=4$. The Runge-Kutta method, implemented via the ode45 solver in Matlab, is used to solve (30), so parameters $v_P$, $v_W$, ${\alpha }_i$, ${\beta }_i$, ${\gamma }_i$ are not involved. The equilibrium $({\overline{P}}^{*},{\overline{W}}^{*})=(2,2)$ satisfies $(1-2f\left({\overline{P}}^{*}\right))\delta ={\lambda }_R\left({\overline{W}}^{*}\right)$.

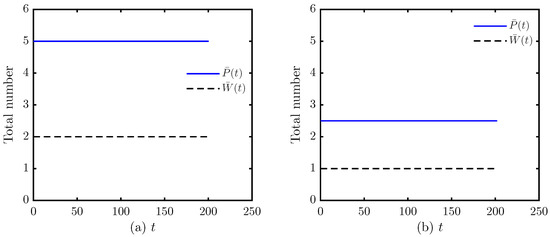
Figure 5. Numerical validation of the scaling law for Hill feedback. Trajectories of $\overline{P}\left(t\right)$ (solid) and $\overline{W}\left(t\right)$ (dashed) are shown. Rescaling the feedback parameters by a factor A rescales the steady state by $1/A$ while preserving ${\overline{P}}^{*}/{\overline{W}}^{*}=\delta /{\lambda }_P\left({\overline{W}}^{*}\right)$. (a) For $A=1$ with $k_1=k_2=k_3=1$, the system converges to $\mathcal{S}=(5,2)$; (b) for $A=2$ with $k_1=k_2=k_3=2$, the system converges to ${\mathcal{S}}^{\prime }=(2.5,1)=\mathcal{S}/2$. Parameters: $$\begin{gathered} ({\widehat{\lambda }}_P,{\widehat{\lambda }}_R,\widehat{\delta },\widehat{f},{\widehat{p}}_1,{\widehat{p}}_2,p_3,v_P,v_W,{\alpha }_1,{\alpha }_2,{\beta }_1,{\beta }_2,{\gamma }_1,{\gamma }_2,m_1,m_2,m_3,m_4,\Delta t,\Delta x,\tilde{A})= \\ (0.4,0.02,0.2,0.25,0.25,0.75,0,0.05,0.05,0.5,0.5,0.5,0.5,1/3,2/3,2,2,2,2,0.025,0.005,2) \end{gathered}$$.

The computations align with the theory. The algebraic threshold $(1-2\widehat{f})\delta ={\widehat{\lambda }}_R$ organizes the regimes, the phase portrait matches the local classification, and the uniform rescaling of feedback strengths produces the predicted steady state scaling without altering the steady population ratio. These illustrations underscore the model’s predictive power, as synthesized in the conclusion.

7. Conclusions

A damage-structured transport–reaction model is introduced, coupling stem (P) and differentiated (W) cells with reversible dedifferentiation, nonlocal birth operators (damage partitioning at division), and Hill-type feedback. Main results: (i) global well-posedness in $C([0,\infty );L^1\times L^1)$ (existence, uniqueness, positivity and an a priori mass bound); (ii) exact reduction to a two-dimensional autonomous ODE when mortality is constant, via explicit balance laws; (iii) characterization of equilibria and a bifurcation threshold separating extinction, homeostasis, and unbounded growth; (iv) global nonoscillation and, under compensatory feedback, global asymptotic stability (Dulac’s criterion + Poincaré–Bendixson). Key innovations: inclusion of reversible dedifferentiation between compartments, nonlocal damage redistribution at division, and a novel steady-state scaling invariance under uniform rescaling of feedback strengths. Limitations and outlook: the ODE closure requires constant death rates; extensions to damage-dependent mortality, stochastic partitioning, variable transport speeds, demographic noise [47], or hybrid PDE–agent-based models [48] are natural next steps.

Short, testable analytical criteria and the reduction to a tractable ODE make the framework directly applicable to simulations and experimental validation.