Analysis of a Markovian Queueing Model with an Alternating Server and Queue-Length-Based Threshold Control
Abstract
1. Introduction
2. Literature Review
3. Analysis of the Model
3.1. Model Description
3.2. Mathematical Formulation
3.2.1. Joint Queue Length Distribution at Departure Epochs
3.2.2. Queue Length Distribution at an Arbitrary Time
3.2.3. Performance Measures
- Loss probability of buffer :
- Mean queue length of buffer :
- Mean waiting time in buffer , obtained by applying Little’s Law:
4. Numerical Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Takagi, H. Analysis of Polling Systems; MIT Press: Cambridge, MA, USA, 1986. [Google Scholar]
- Boon, M.A.; van der Mei, R.D.; Winands, E.M. Applications of polling systems. Surv. Oper. Res. Manag. Sci. 2011, 16, 67–82. [Google Scholar] [CrossRef]
- Borst, S.; Boxma, O. Polling: Past, present, and perspective. Top 2018, 26, 335–369. [Google Scholar] [CrossRef]
- Vishnevsky, V.; Semenova, O. Polling systems and their application to telecommunication networks. Mathematics 2021, 9, 117. [Google Scholar] [CrossRef]
- Nimisha, M.; Manoharan, M.; Krishnamoorthy, A. Polling Models: A Short Survey and Some New Results. Queueing Model. Serv. Manag. 2024, 7, 25–42. [Google Scholar]
- Bruneel, H. Analysis of a threshold-based priority queue. Queueing Syst. 2025, 109, 8. [Google Scholar] [CrossRef]
- Lin, W.; Wang, J.Z.; Liang, C.; Qi, D. A threshold-based dynamic resource allocation scheme for cloud computing. Procedia Eng. 2011, 23, 695–703. [Google Scholar] [CrossRef]
- Klimenok, V.; Dudin, A.; Dudina, O.; Kochetkova, I. Queuing system with two types of customers and dynamic change of a priority. Mathematics 2020, 8, 824. [Google Scholar] [CrossRef]
- Avrachenkov, K.; Perel, E.; Yechiali, U. Finite-buffer polling systems with threshold-based switching policy. Top 2016, 24, 541–571. [Google Scholar] [CrossRef]
- Boxma, O.; Perry, D.; Ravid, R.; Yechiali, U. A Polling Model with Threshold Switching. 2024. Preprint. Available online: https://www.eurandom.tue.nl/pre-prints-new/ (accessed on 7 March 2025).
- Jolles, A.; Perel, E.; Yechiali, U. Alternating server with non-zero switch-over times and opposite-queue threshold-based switching policy. Perform. Eval. 2018, 126, 22–38. [Google Scholar] [CrossRef]
- Borst, S.C.; Boxma, O.J.; Levy, H. The use of service limits for efficient operation of multistation single-medium communication systems. IEEE/ACM Trans. Netw. 1995, 3, 602–612. [Google Scholar] [CrossRef]
- Vishnevsky, V.M.; Semenova, O.V.; Bui, D. Investigation of the Stochastic Polling System and Its Applications to Broadband Wireless Networks. Autom. Remote Control 2021, 82, 1607–1613. [Google Scholar] [CrossRef]
- Winands, E.; Adan, I.J.B.F.; Van Houtum, G.; Down, D. A state-dependent polling model with k-limited service. Probab. Eng. Informational Sci. 2009, 23, 385–408. [Google Scholar] [CrossRef]
- Iliadis, I.; Jordan, L.; Lantz, M.; Sarafijanovic, S. Performance evaluation of tape library systems. Perform. Eval. 2022, 157, 102312. [Google Scholar] [CrossRef]
- Boon, M.A.; Adan, I.J.; Winands, E.M.; Down, D.G. Delays at signalized intersections with exhaustive traffic control. Probab. Eng. Informational Sci. 2012, 26, 337–373. [Google Scholar] [CrossRef]
- Uncu, N. Load balancing in polling systems under different policies via simulation optimization. Int. J. Simul. Model. 2022, 21. [Google Scholar] [CrossRef]
- Wu, Z.; Liu, R.; Pan, E. Server Routing-Scheduling Problem in Distributed Queueing System with Time-Varying Demand and Queue Length Control. Transp. Sci. 2023, 57, 1209–1230. [Google Scholar] [CrossRef]
- Dudin, A.; Dudina, O. Analysis of Polling Queueing System with Two Buffers and Varying Service. In Proceedings of the Distributed Computer and Communication Networks: 27th International Conference, DCCN 2024, Moscow, Russia, 23–27 September 2024; Revised Selected Papers. Springer Nature: Berlin/Heidelberg, Germany, 2024; p. 129. [Google Scholar]
- Dudin, A.; Sinyugina, Y. Analysis of the Polling System with Two Markovian Arrival Flows, Finite Buffers, Gated Service and Phase-Type Distribution of Service and Switching Times. In Proceedings of the International Conference on Information Technologies and Mathematical Modelling, Tomsk, Russia, 1–5 December 2021; Springer: Berlin/Heidelberg, Germany, 2021; pp. 1–15. [Google Scholar]
- Shausan, A.; Vuorinen, A. Thirty-six years of contributions to queueing systems: A content analysis, topic modeling, and graph-based exploration of research published in the QUESTA journal. Queueing Syst. 2023, 104, 3–18. [Google Scholar] [CrossRef]
- Dudin, A.; Dudin, S.; Manzo, R.; Rarità, L. Queueing system with batch arrival of heterogeneous orders, flexible limited processor sharing and dynamical change of priorities. AIMS Math. 2024, 9, 12144–12169. [Google Scholar] [CrossRef]
- Takács, L. Two queues attended by a single server. Oper. Res. 1968, 16, 639–650. [Google Scholar] [CrossRef]
- Eisenberg, M. Two queues with alternating service. SIAM J. Appl. Math. 1979, 36, 287–303. [Google Scholar] [CrossRef]
- Boon, M.; Winands, E. Heavy-traffic analysis of k-limited polling systems. Probab. Eng. Informational Sci. 2014, 28, 451–471. [Google Scholar] [CrossRef]
- Ozawa, T. Alternating service queues with mixed exhaustive and K-limited services. Perform. Eval. 1990, 11, 165–175. [Google Scholar] [CrossRef]
- Perel, E.; Yechiali, U. Two-queue polling systems with switching policy based on the queue that is not being served. Stoch. Model. 2017, 33, 430–450. [Google Scholar] [CrossRef]
- Choi, D.I.; Kim, T.S.; Lee, S. Analysis of a queueing system with a general service scheduling function, with applications to telecommunication network traffic control. Eur. J. Oper. Res. 2007, 178, 463–471. [Google Scholar] [CrossRef]
- Lee, T.T. M/G/1/N queue with vacation time and exhaustive service discipline. Oper. Res. 1984, 32, 774–784. [Google Scholar] [CrossRef]


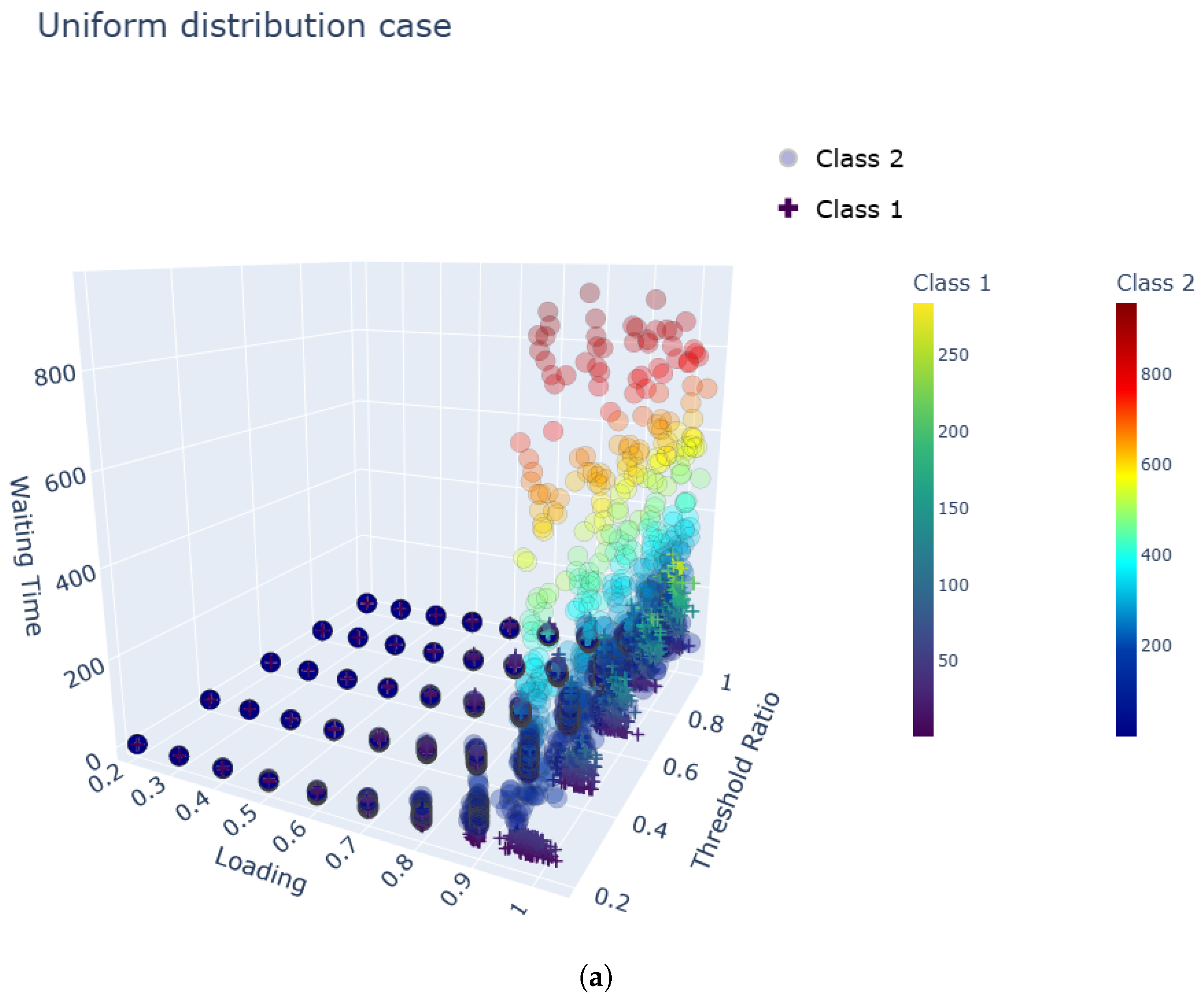

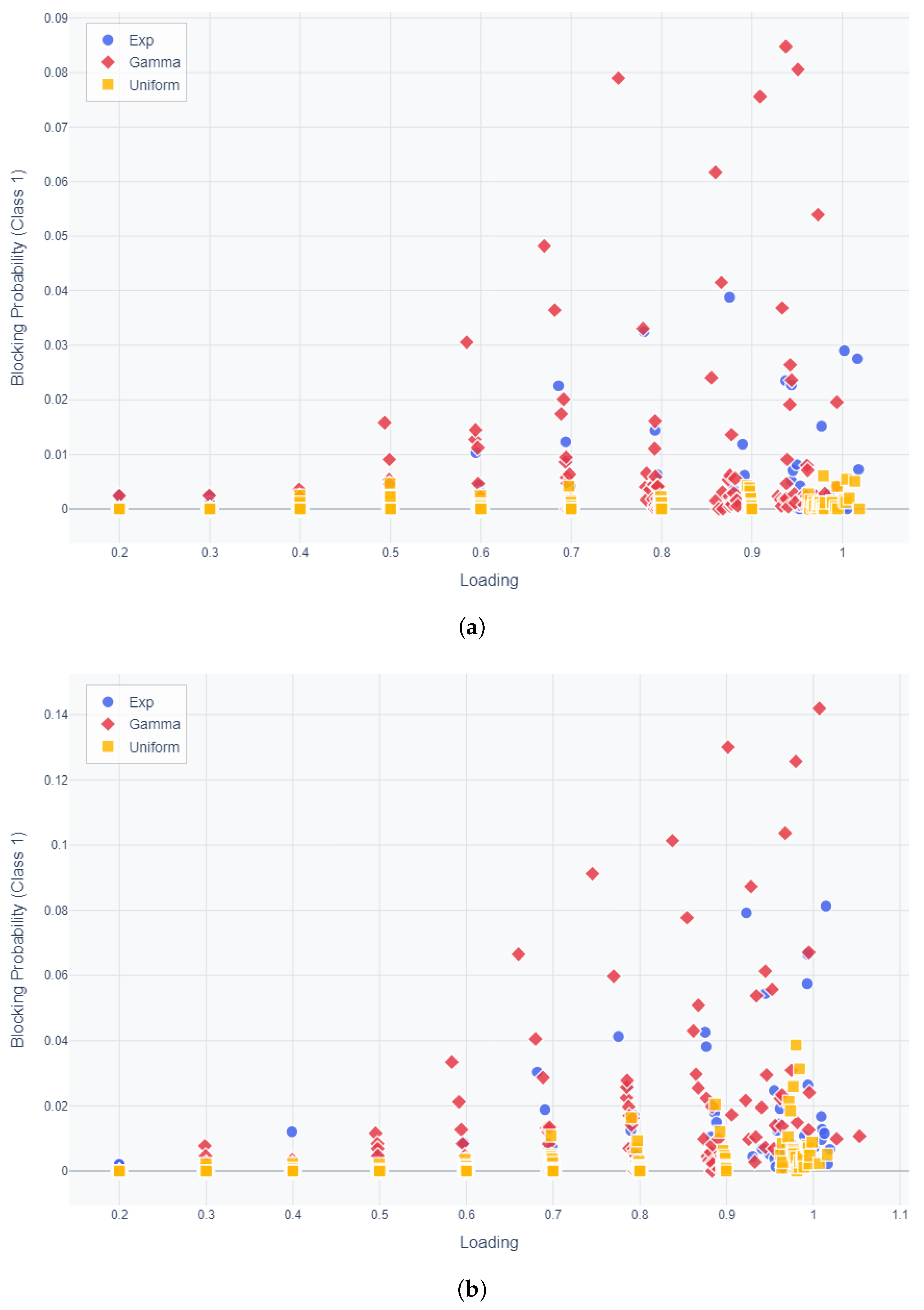
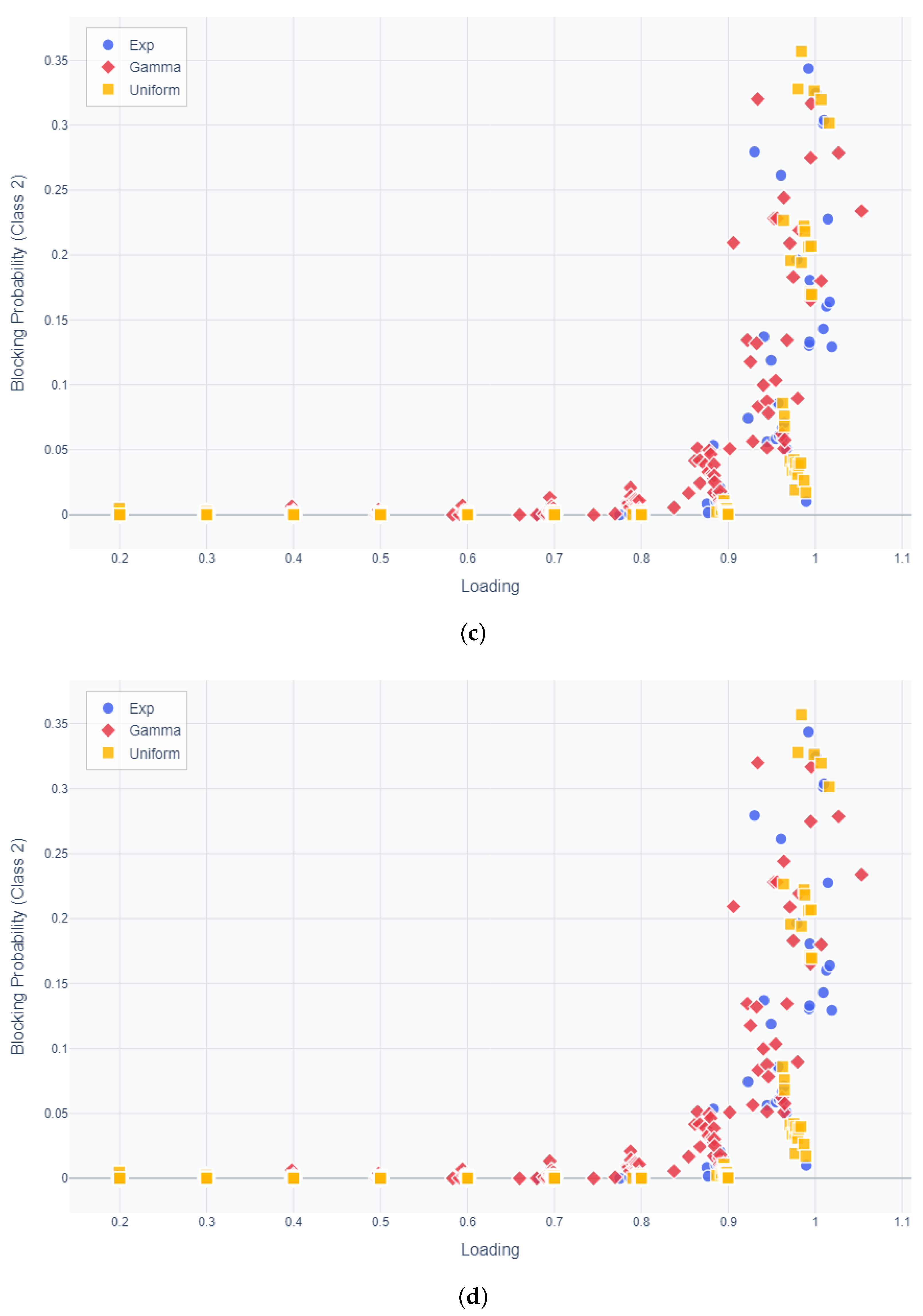
| Category | Description |
|---|---|
| Service Time Distributions | All service time distributions have a mean of 10 but differ in CV: Uniform(5, 15) with CV = 0.3; Exponential distribution with rate = 0.1 (CV = 1.0); Gamma distribution with a shape parameter of 0.44 and a scale parameter of 22.52 (CV = 1.4). |
| Arrival Rate per Class | Arrival rates for each class range from 0.01 to 0.06. |
| Class 1 Buffer Size | Buffer sizes range from 5 to 25 in increments of 5. The threshold is set as a proportion of the buffer size, with ratios ranging from 0.2 to 1.0. For example, if the buffer size is 5 and the ratio is 0.2, the threshold is 1. |
| Class 2 Buffer Size | Buffer sizes range from 10 to 40 in increments of 10. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, D.I.; Lim, D.-E. Analysis of a Markovian Queueing Model with an Alternating Server and Queue-Length-Based Threshold Control. Mathematics 2025, 13, 3555. https://doi.org/10.3390/math13213555
Choi DI, Lim D-E. Analysis of a Markovian Queueing Model with an Alternating Server and Queue-Length-Based Threshold Control. Mathematics. 2025; 13(21):3555. https://doi.org/10.3390/math13213555
Chicago/Turabian StyleChoi, Doo Il, and Dae-Eun Lim. 2025. "Analysis of a Markovian Queueing Model with an Alternating Server and Queue-Length-Based Threshold Control" Mathematics 13, no. 21: 3555. https://doi.org/10.3390/math13213555
APA StyleChoi, D. I., & Lim, D.-E. (2025). Analysis of a Markovian Queueing Model with an Alternating Server and Queue-Length-Based Threshold Control. Mathematics, 13(21), 3555. https://doi.org/10.3390/math13213555






