Data-Driven Optimal Treatment Combination Regimes for Multiple Stressors Controlling for Multiple Adverse Effects
Abstract
1. Introduction
2. Background
Dose Optimization
3. Methodology
3.1. Posterior Sampling with MCMC
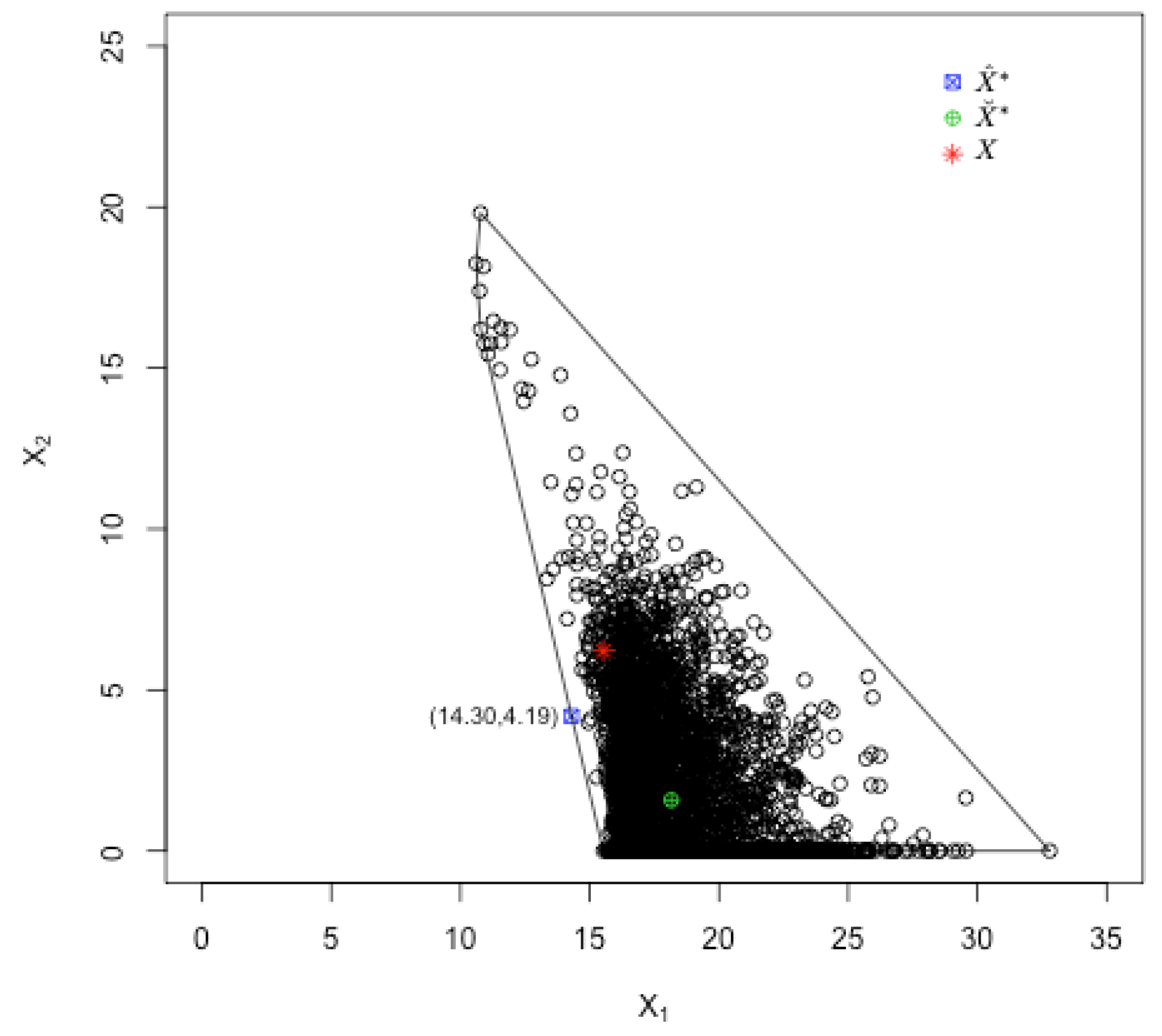
3.2. PEOF: Positive Effect-Oriented Filtration
- Step 1: For each , let
- Step 2: For a pre-determined threshold , where , find
- Step 3: Construct the convex hull, , of . Find
3.3. NEOF: Negative Effect-Oriented Filtration
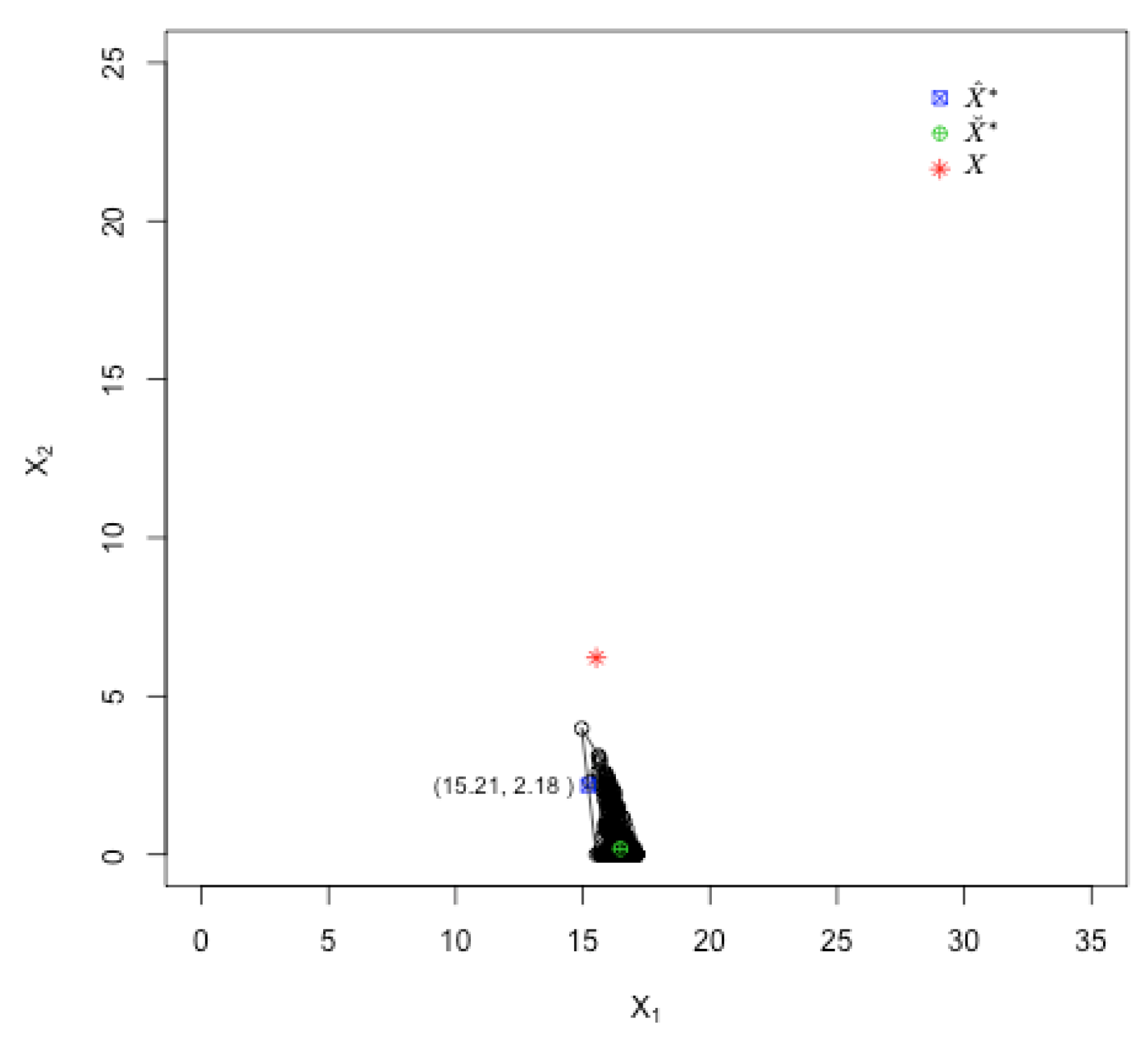
3.4. BOF: Balance-Oriented Filtration
3.5. Mean-Based Estimation
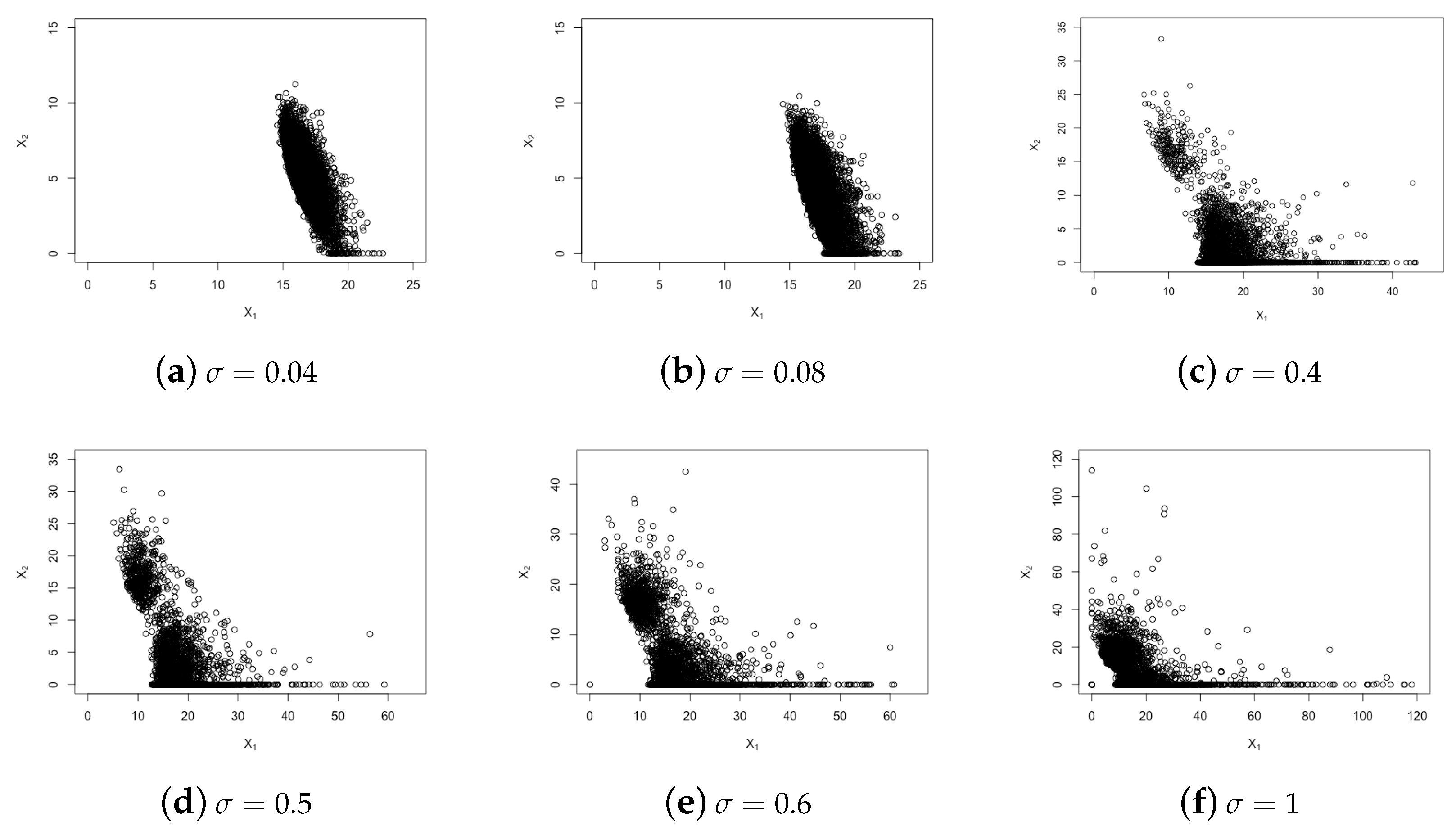
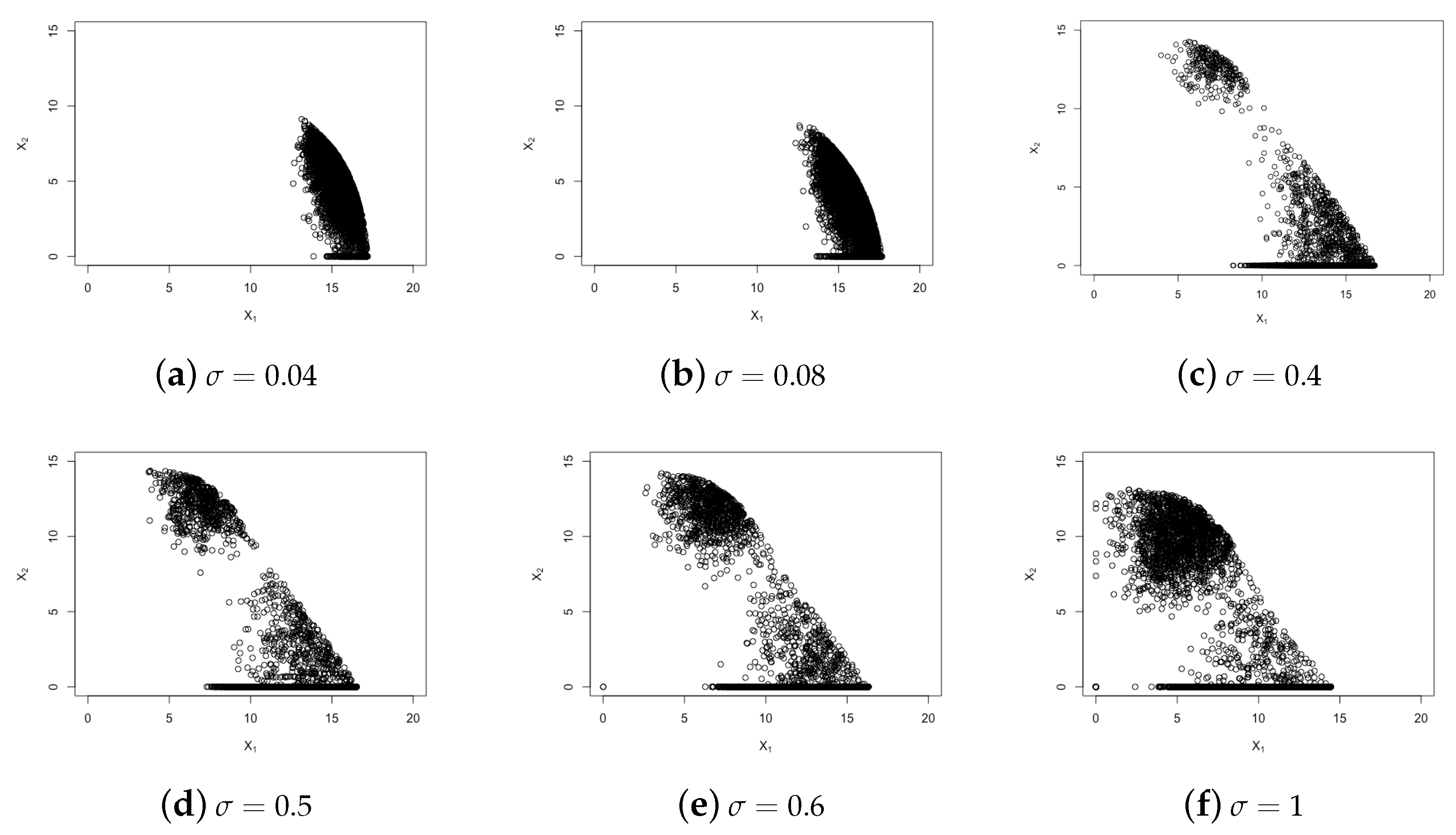
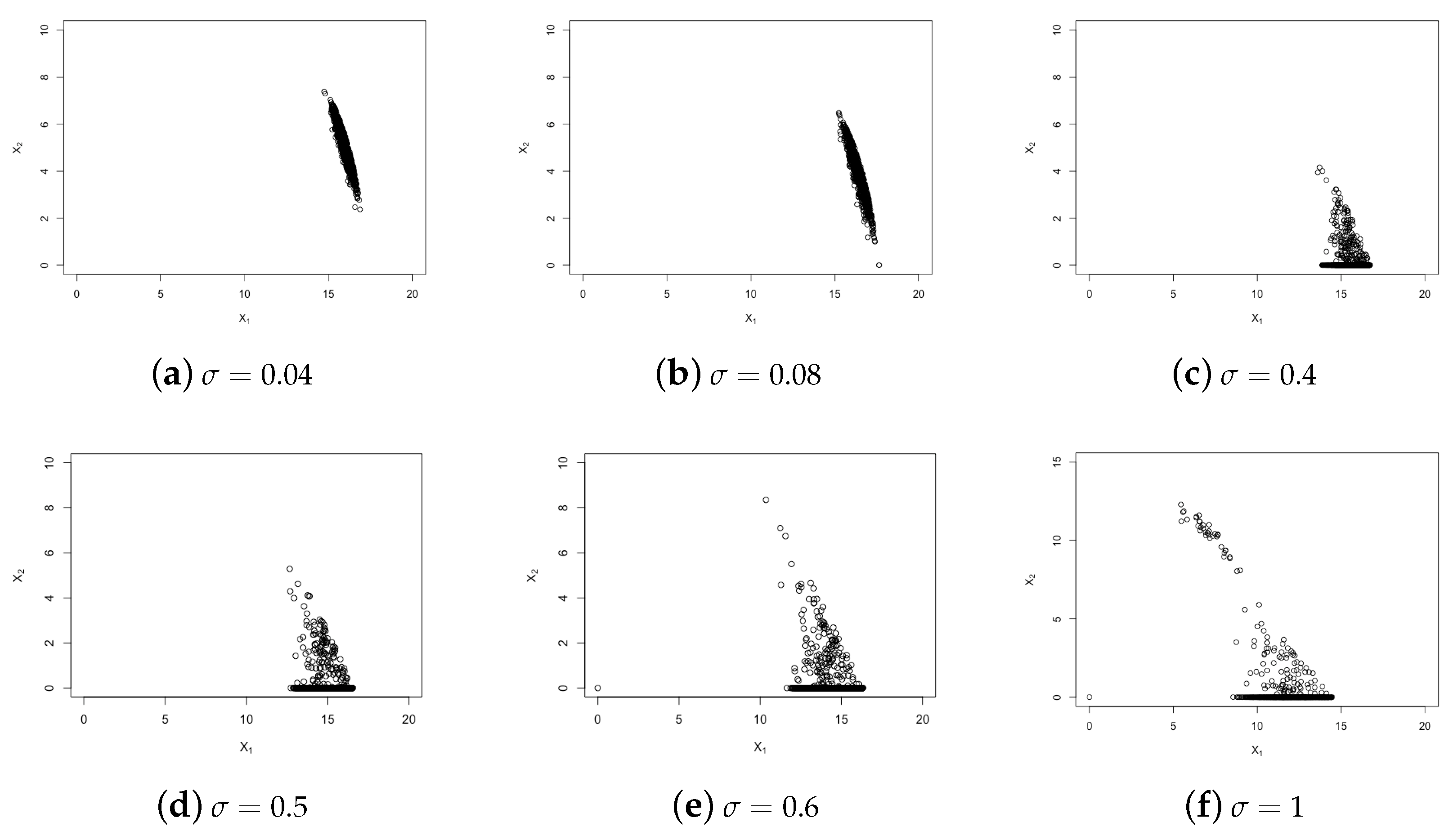
4. Numerical Experiments
4.1. True Model Formulation
4.2. Test Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Merigan, T.C. Treatment of AIDS with combinations of antiretroviral agents. Am. J. Med. 1991, 90, S8–S17. [Google Scholar] [CrossRef]
- Weiss, A.; Ding, X.; van Beijnum, J.R.; Wong, I.; Wong, T.J.; Berndsen, R.H.; Dormond, O.; Dallinga, M.; Shen, L.; Schlingemann, R.O.; et al. Rapid optimization of drug combinations for the optimal angiostatic treatment of cancer. Angiogenesis 2015, 18, 233–244. [Google Scholar] [CrossRef]
- Sarhan, E.; Walker, M.; Selai, C. Evidence for Efficacy of Combination of Antiepileptic Drugs in Treatment of Epilepsy. J. Neurol. Res. 2016, 5, 269–276. [Google Scholar] [CrossRef]
- Kabir, M.T.; Uddin, M.S.; Mamun, A.A.; Jeandet, P.; Aleya, L.; Mansouri, R.A.; Ashraf, G.M.; Mathew, B.; Bin-Jumah, M.N.; Abdel-Daim, M.M. Combination Drug Therapy for the Management of Alzheimer’s Disease. Int. J. Mol. Sci. 2020, 21, 3272. [Google Scholar] [CrossRef]
- Zimmermann, G.R.; Lehár, J.; Keith, C.T. Multi-target therapeutics: When the whole is greater than the sum of the parts. Drug Discov. Today 2007, 12, 34–42. [Google Scholar] [CrossRef]
- Lehár, J.; Krueger, A.S.; Avery, W.; Heilbut, A.M.; Johansen, L.M.; Price, E.R.; Rickles, R.J.; Short, G.F., 3rd; Staunton, J.E.; Jin, X.; et al. Synergistic drug combinations tend to improve therapeutically relevant selectivity. Nat. Biotechnol. 2009, 27, 659–666. [Google Scholar] [CrossRef] [PubMed]
- Chou, T.C. Theoretical basis, experimental design, and computerized simulation of synergism and antagonism in drug combination studies. Pharmacol. Rev. 2006, 58, 621–681. [Google Scholar] [CrossRef] [PubMed]
- Greco, W.R.; Bravo, G.; Parsons, J.C. The search for synergy: A critical review from a response surface perspective. Pharmacol. Rev. 1995, 47, 331–385. [Google Scholar] [CrossRef]
- Geary, N. Understanding synergy. Am. J. Physiol.-Endocrinol. Metab. 2013, 304, E237–E253. [Google Scholar] [CrossRef] [PubMed]
- Nowak-Sliwinska, P.; Weiss, A.; Ding, X.; Dyson, P.J.; van den Bergh, H.; Griffioen, A.W.; Ho, C.M. Optimization of drug combinations using Feedback System Control. Nat. Protoc. 2016, 11, 302–315. [Google Scholar] [CrossRef]
- Derendorf, H.; Hochhaus, G. (Eds.) Handbook of Pharmacokinetic/Pharmacodynamic Correlation, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2019; pp. 67–72. [Google Scholar]
- Das, P.; Delost, M.D.; Qureshi, M.H.; Smith, D.T.; Njardarson, J.T. A Survey of the Structures of US FDA Approved Combination Drugs. J. Med. Chem. 2019, 62, 4265–4311. [Google Scholar] [CrossRef] [PubMed]
- Korn, E.L.; Moscow, J.A.; Freidlin, B. Dose optimization during drug development: Whether and when to optimize. JNCI J. Natl. Cancer Inst. 2022, 115, 492–497. [Google Scholar] [CrossRef]
- Pan, Y.; Ren, H.; Lan, L.; Li, Y.; Huang, T. Review of Predicting Synergistic Drug Combinations. Life 2023, 13, 1878. [Google Scholar] [CrossRef] [PubMed]
- Cheng, F.; Kovács, I.A.; Barabási, A.L. Network-based prediction of drug combinations. Nat. Commun. 2019, 10, 1197. [Google Scholar] [CrossRef]
- Zhou, W.; Wang, Y.; Lu, A.; Zhang, G. Machine learning approaches for synergistic drug discovery. Trends Pharmacol. Sci. 2020, 41, 482–494. [Google Scholar] [CrossRef]
- Berry, D.A. Adaptive clinical trials: The promise and the caution. J. Clin. Oncol. 2011, 29, 606–609. [Google Scholar] [CrossRef] [PubMed]
- Thall, P.F.; Wathen, J.K.; Bekele, B.N. Hierarchical Bayesian approaches to adaptive dosing in clinical trials. Stat. Med. 2014, 33, 2425–2443. [Google Scholar] [CrossRef]
- Parmigiani, G.; Inoue, L. Decision Theory: Principles and Approaches; Wiley Series in Probability and Statistics; Wiley: Hoboken, NJ, USA, 2009; pp. 35–41. [Google Scholar] [CrossRef]
- Mager, D.E.; Jusko, W.J. Development of translational pharmacokinetic-pharmacodynamic models. Clin. Pharmacol. Ther. 2008, 83, 909–912. [Google Scholar] [CrossRef]
- Derendorf, H.; Hochhaus, G. Handbook of Pharmacokinetic/Pharmacodynamic Correlation; CRC Press: Boca Raton, FL, USA, 1995; pp. 45–52. [Google Scholar] [CrossRef]
- Korn, E.L.; Freidlin, B. Adaptive clinical trials: Advantages and disadvantages of various adaptive design elements. J. Natl. Cancer Inst. 2017, 109, djx013. [Google Scholar] [CrossRef]
- Walter, E.; Pronzato, L. Identification of Parametric Models; Communications and Control Engineering; Springer: Berlin/Heidelberg, Germany, 1997; pp. 55–70. [Google Scholar] [CrossRef]
- van der Vaart, A.W. Asymptotic Statistics; Cambridge Series in Statistical and Probabilistic Mathematics; Cambridge University Press: Cambridge, UK, 1998; pp. 15–25. [Google Scholar] [CrossRef]
- Ben-Tal, A.; Nemirovski, A. Robust optimization–methodology and applications. Math. Program. 2002, 92, 453–480. [Google Scholar] [CrossRef]
- Bertsimas, D.; Brown, D.B.; Caramanis, C. Theory and applications of robust optimization. SIAM Rev. 2011, 53, 464–501. [Google Scholar] [CrossRef]
- Delage, E.; Ye, Y. Distributionally robust optimization under moment uncertainty with application to data-driven problems. Oper. Res. 2010, 58, 595–612. [Google Scholar] [CrossRef]
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Dunson, D.B.; Vehtari, A.; Rubin, D.B. Bayesian Data Analysis, 3rd ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2013; pp. 3–5. [Google Scholar] [CrossRef]
- Spiegelhalter, D.J.; Abrams, K.R.; Myles, J.P. Bayesian Approaches to Clinical Trials and Health-Care Evaluation; Statistics in Practice; Wiley: Hoboken, NJ, USA, 2004; pp. 45–52. [Google Scholar] [CrossRef]
- Ibrahim, J.G.; Chen, M.H.; Sinha, D. Bayesian Survival Analysis; Springer Series in Statistics; Springer: Berlin/Heidelberg, Germany, 2014; pp. 25–32. [Google Scholar] [CrossRef]
- Robert, C.P.; Casella, G. Monte Carlo Statistical Methods, 2nd ed.; Springer Texts in Statistics; Springer: Berlin/Heidelberg, Germany, 2004; pp. 145–160. [Google Scholar] [CrossRef]
- Annis, J.; Miller, B.J.; Palmeri, T.J. Bayesian inference with Stan: A tutorial on adding custom distributions. Behav. Res. Methods 2017, 49, 863–886. [Google Scholar] [CrossRef]
- Brooks, S.; Gelman, A.; Jones, G.; Meng, X.L. Handbook of Markov Chain Monte Carlo; Chapman & Hall/CRC Handbooks of Modern Statistical Methods; Chapman & Hall/CRC: Boca Raton, FL, USA, 2011; pp. 45–60. [Google Scholar] [CrossRef]
- Farhat, N.J.; Boone, E.L.; Edwards, D.J. A new method for determining the benchmark dose tolerable region and endpoint probabilities for toxicology experiments. J. Appl. Stat. 2020, 47, 775–803. [Google Scholar] [CrossRef] [PubMed]
- Neuenschwander, B.; Branson, M.; Gsponer, T. Critical aspects of the Bayesian approach to phase I cancer trials. Stat. Med. 2008, 27, 2420–2439. [Google Scholar] [CrossRef] [PubMed]
- Ben-Tal, A.; Nemirovski, A. Robust convex optimization. Math. Oper. Res. 1998, 23, 769–805. [Google Scholar] [CrossRef]
- Bertsimas, D.; Sim, M. The price of robustness. Oper. Res. 2004, 52, 35–53. [Google Scholar] [CrossRef]
- Shapiro, A.; Dentcheva, D.; Ruszczyński, A. Lectures on Stochastic Programming: Modeling and Theory, 2nd ed.; SIAM: Bangkok, Thailand, 2014; pp. 55–60. [Google Scholar] [CrossRef]
- Lunn, D.J.; Thomas, A.; Best, N.; Spiegelhalter, D. WinBUGS—A Bayesian Modelling Framework: Concepts, Structure, and Extensibility. Stat. Comput. 2000, 10, 325–337. [Google Scholar] [CrossRef]
- Plummer, M. JAGS: A Program for Analysis of Bayesian Graphical Models using Gibbs Sampling. In Proceedings of the 3rd International Workshop on Distributed Statistical Computing (DSC 2003), Vienna, Austria, 20–22 March 2003; Hornik, K., Leisch, F., Zeileis, A., Eds.; pp. 1–16. Available online: https://www.r-project.org/conferences/DSC-2003/Proceedings/Plummer.pdf (accessed on 20 October 2025).
- Thomas, A.; O’Hara, B.; Ligges, U.; Sturtz, S. Making BUGS open. R News 2006, 6, 12–17. [Google Scholar]
- Hoffman, M.D.; Gelman, A. The No-U-Turn sampler: Adaptively setting path lengths in Hamiltonian Monte Carlo. J. Mach. Learn. Res. 2014, 15, 1593–1623. [Google Scholar]
- Ben-Tal, A.; El Ghaoui, L.; Nemirovski, A. Robust Optimization; Princeton Series in Applied Mathematics; Princeton University Press: Princeton, NJ, USA, 2009; pp. 95–150. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004; pp. 27–29. [Google Scholar] [CrossRef]
- Preparata, F.P.; Shamos, M.I. Computational Geometry: An Introduction; Springer: New York, NY, USA, 1985; pp. 95–128. [Google Scholar] [CrossRef]
- Rockafellar, R.T.; Uryasev, S. Optimization of Conditional Value-at-Risk. J. Risk 2000, 2, 21–42. [Google Scholar] [CrossRef]
- Miettinen, K. Nonlinear Multiobjective Optimization; International Series in Operations Research & Management Science; Springer: Berlin/Heidelberg, Germany, 1999; Volume 12, pp. 109–113. [Google Scholar] [CrossRef]
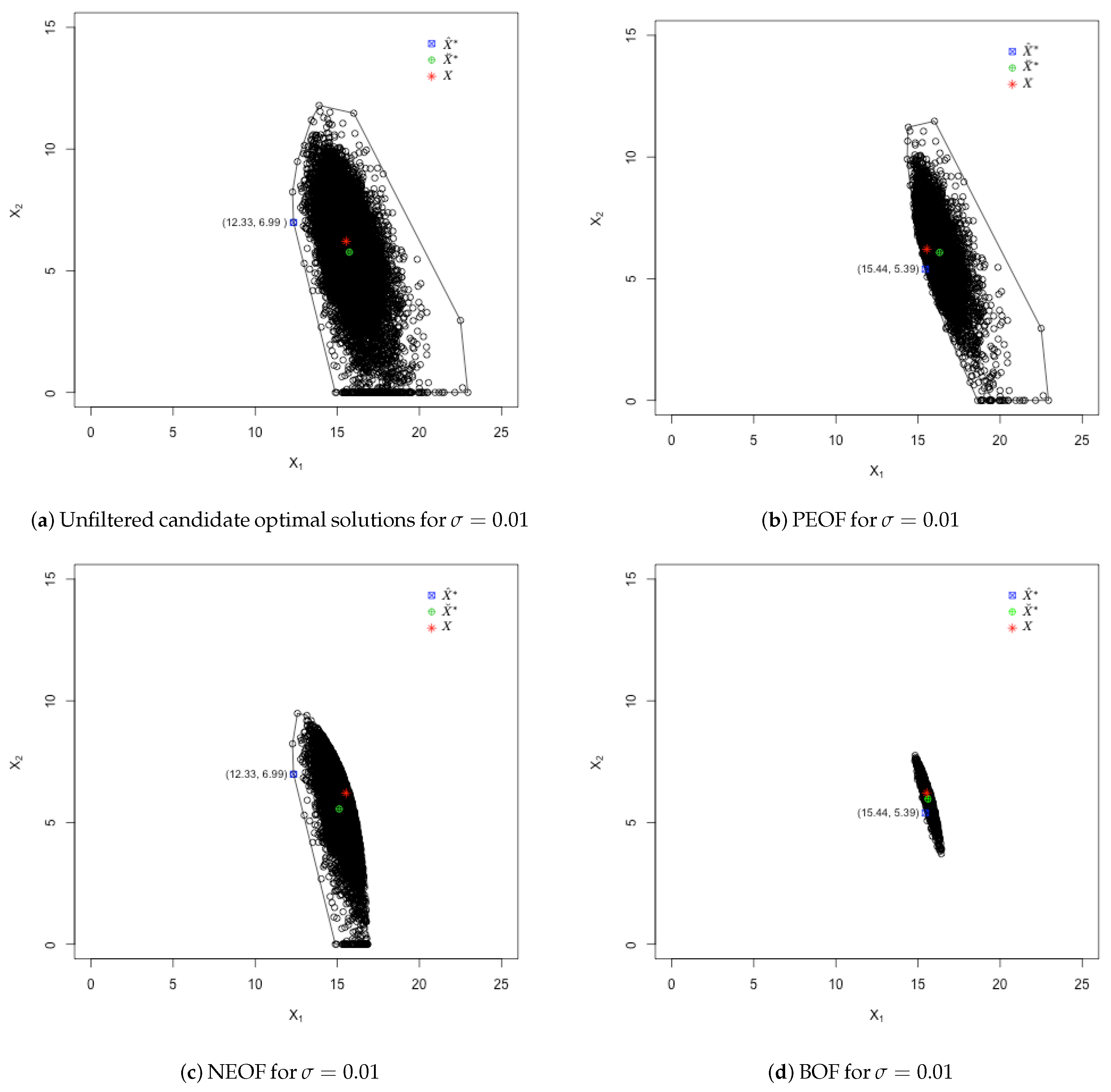




| Unfiltered | (12.33, 6.99) | (15.73, 5.77) | 87.97 | 105.93 | Y | N |
| PEOF | (15.44, 5.39) | (16.31, 6.08) | 103.44 | 110.03 | Y | N |
| NEOF | (12.33, 6.99) | (15.11, 5.56) | 87.97 | 101.78 | Y | N |
| BOF | (15.44, 5.39) | (15.61, 5.97) | 103.44 | 105.61 | Y | N |
| Unfiltered | (11.80, 3.36) | (16.55, 3.40) | 77.50 | 106.13 | Y | N |
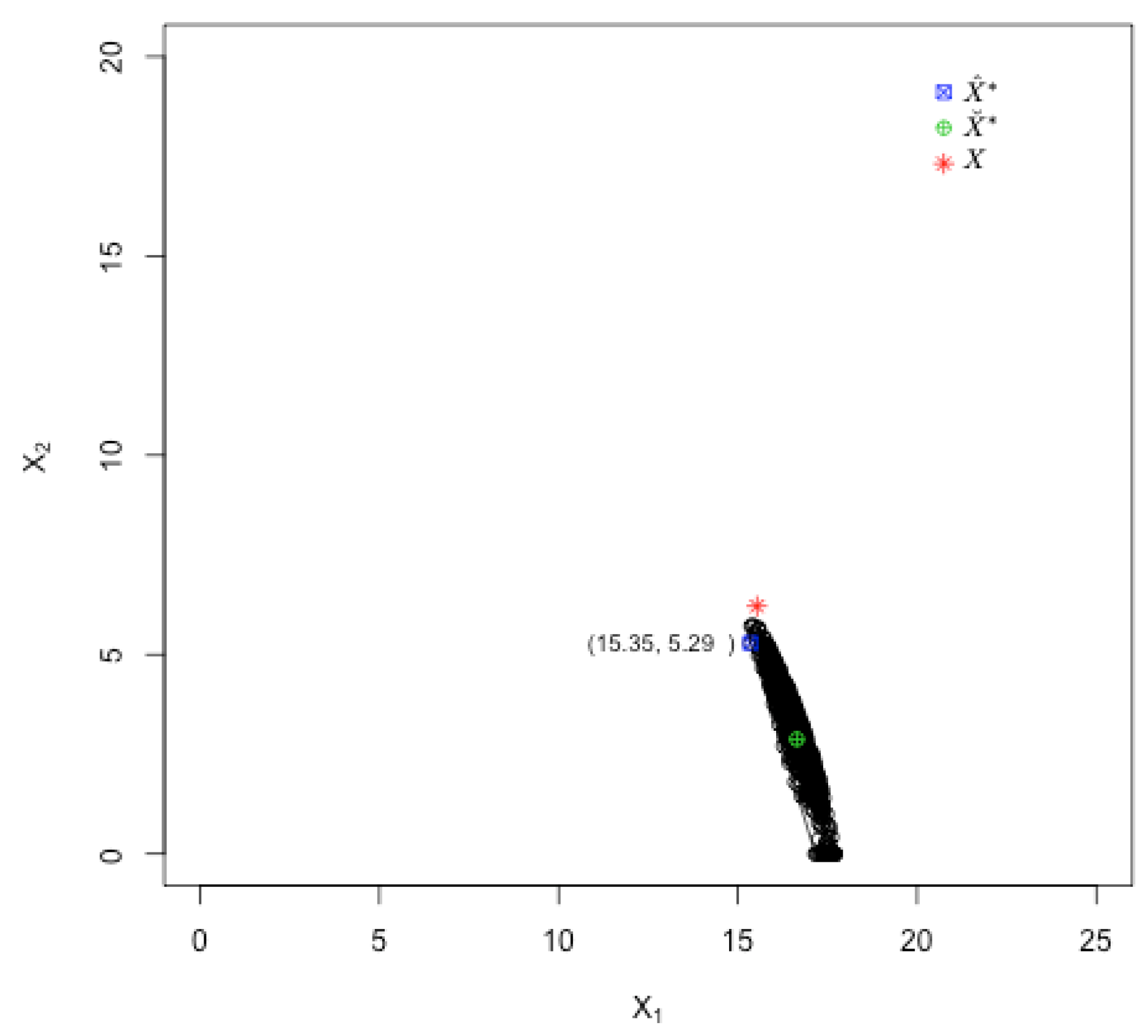
| PEOF | (15.35, 5.27) | (17.63, 3.41) | 102.67 | 112.60 | Y | N |
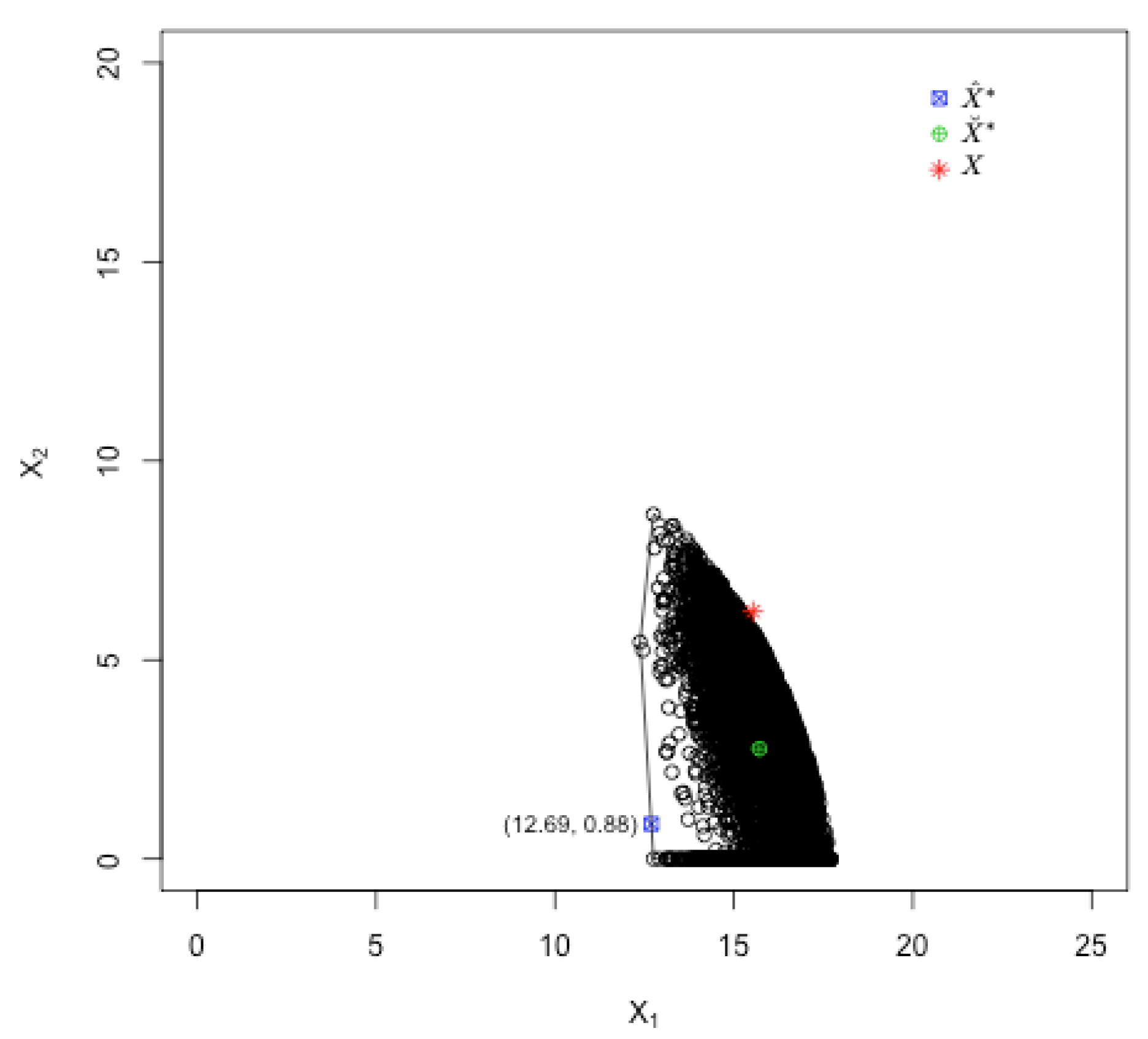
| NEOF | (12.69, 0.88) | (15.71, 2.77) | 77.92 | 99.82 | Y | N |
| BOF | (15.35, 5.29) | (16.65, 2.88) | 102.67 | 105.63 | Y | N |
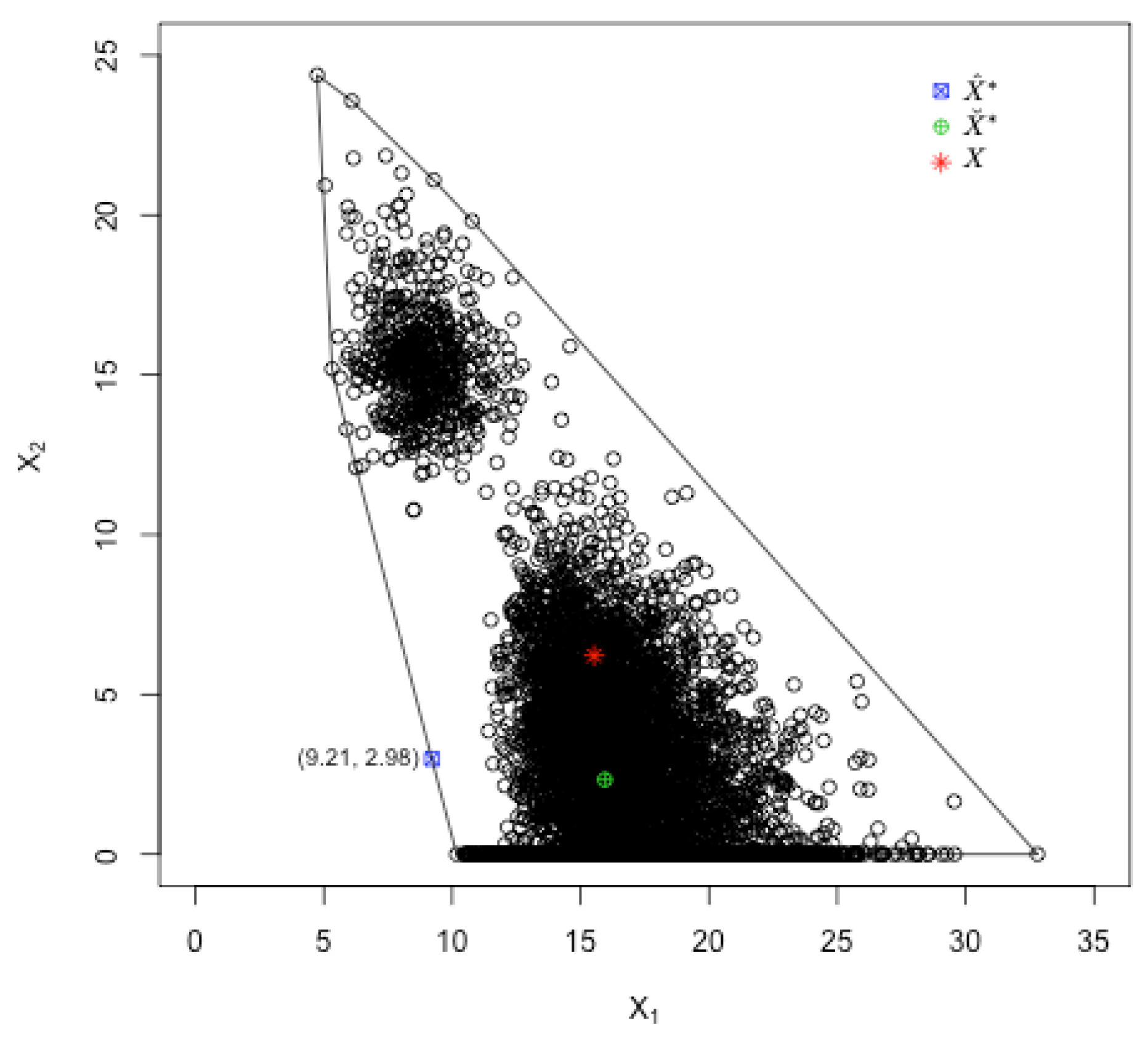
| Unfiltered | (9.21, 2.98) | (15.94, 2.33) | 61.21 | 100.32 | Y | N |
| PEOF | (14.30, 4.19) | (18.15, 1.58) | 94.17 | 112.08 | Y | N |
| NEOF | (9.21, 2.98) | (14.74, 0.72) | 61.21 | 89.90 | Y | Y |
| BOF | (15.21, 2.18) | (16.48, 0.18) | 95.64 | 99.24 | Y | N |
| 0.02 | (13.20, 3.80) | 86.80 | (15.17, 6.00) | 103.02 | (13.20, 3.80) | 86.80 | (15.17, 6.00) | 103.02 |
| 0.03 | (13.41, 3.28) | 87.00 | (15.35, 5.74) | 103.60 | (13.41, 3.28) | 87.00 | (15.35, 5.74) | 103.60 |
| 0.04 | (12.82, 3.67) | 84.27 | (15.22, 5.77) | 102.85 | (13.01, 3.36) | 84.75 | (15.22, 5.77) | 102.85 |
| 0.05 | (13.63, 2.33) | 86.47 | (15.31, 5.77) | 103.40 | (13.63, 2.33) | 86.47 | (15.31, 5.77) | 103.40 |
| 0.06 | (11.96, 3.48) | 78.71 | (15.49, 5.29) | 103.51 | (12.59, 2.18) | 79.92 | (15.49, 5.29) | 103.51 |
| 0.07 | (12.51, 3.19) | 81.44 | (15.19, 6.17) | 103.48 | (12.98, 2.09) | 82.09 | (15.19, 6.17) | 103.48 |
| 0.08 | (12.22, 4.20) | 81.73 | (15.33, 5.35) | 102.70 | (12.99, 1.98) | 81.92 | (15.33, 5.35) | 102.70 |
| 0.09 | (11.82, 3.76) | 78.43 | (15.50, 4.74) | 102.47 | (12.68, 2.06) | 80.20 | (15.50, 4.74) | 102.47 |
| 0.20 | (10.11, 3.37) | 67.40 | (14.79, 4.55) | 97.84 | (11.24, 0.00) | 67.44 | (15.28, 2.96) | 97.60 |
| 0.30 | (8.48, 3.24) | 57.34 | (13.44, 4.53) | 89.71 | (8.52, 3.19) | 57.51 | (14.86, 1.29) | 91.72 |
| 0.40 | (7.50, 2.39) | 49.78 | (12.46, 4.18) | 83.12 | (7.50, 2.39) | 49.78 | (13.80, 0.90) | 84.62 |
| 0.50 | (6.64, 2.11) | 44.03 | (11.41, 3.87) | 76.21 | (6.64, 2.11) | 44.03 | (12.72, 0.17) | 76.67 |
| 0.02 | (15.81, 5.53) | 105.94 | (16.41, 5.86) | 110.16 | (15.15, 5.35) | 101.63 | (15.69, 5.73) | 105.57 |
| 0.03 | (15.96, 5.19) | 106.13 | (16.61, 5.45) | 110.55 | (15.29, 4.96) | 101.68 | (15.85, 5.33) | 105.76 |
| 0.04 | (16.01, 4.97) | 106.02 | (16.68, 5.27) | 110.61 | (15.34, 4.69) | 101.41 | (15.93, 5.07) | 105.73 |
| 0.05 | (16.17, 4.70) | 106.44 | (16.90, 4.93) | 111.25 | (15.48, 4.39) | 101.66 | (16.08, 4.79) | 106.09 |
| 0.06 | (16.28, 4.35) | 106.38 | (17.06, 4.55) | 111.48 | (15.55, 4.00) | 101.28 | (16.18, 4.44) | 105.96 |
| 0.07 | (16.33, 4.10) | 106.17 | (17.18, 4.26) | 111.57 | (15.58, 3.66) | 100.84 | (16.27, 4.11) | 105.83 |
| 0.08 | (16.42, 3.95) | 106.40 | (17.31, 4.07) | 112.03 | (15.65, 3.50) | 100.88 | (16.39, 3.85) | 106.06 |
| 0.09 | (16.49, 3.63) | 106.21 | (17.50, 3.66) | 112.35 | (15.68, 3.09) | 100.26 | (16.54, 3.32) | 105.86 |
| 0.20 | (16.44, 2.20) | 103.02 | (18.29, 1.80) | 113.36 | (15.25, 0.93) | 93.35 | (16.92, 0.34) | 102.20 |
| 0.30 | (15.54, 2.69) | 98.64 | (18.18, 1.52) | 112.12 | (14.32, 0.63) | 87.17 | (16.14, 0.16) | 97.18 |
| 0.40 | (14.58, 3.75) | 94.98 | (17.84, 1.88) | 110.77 | (13.35, 1.06) | 82.24 | (15.52, 0.13) | 93.39 |
| 0.50 | (13.72, 4.84) | 91.97 | (17.38, 2.56) | 109.41 | (12.38, 1.70) | 77.71 | (14.92, 0.12) | 89.74 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shrestha, K.; Boone, E.L.; Ghanam, R. Data-Driven Optimal Treatment Combination Regimes for Multiple Stressors Controlling for Multiple Adverse Effects. Mathematics 2025, 13, 3542. https://doi.org/10.3390/math13213542
Shrestha K, Boone EL, Ghanam R. Data-Driven Optimal Treatment Combination Regimes for Multiple Stressors Controlling for Multiple Adverse Effects. Mathematics. 2025; 13(21):3542. https://doi.org/10.3390/math13213542
Chicago/Turabian StyleShrestha, Kiran, Edward L. Boone, and Ryad Ghanam. 2025. "Data-Driven Optimal Treatment Combination Regimes for Multiple Stressors Controlling for Multiple Adverse Effects" Mathematics 13, no. 21: 3542. https://doi.org/10.3390/math13213542
APA StyleShrestha, K., Boone, E. L., & Ghanam, R. (2025). Data-Driven Optimal Treatment Combination Regimes for Multiple Stressors Controlling for Multiple Adverse Effects. Mathematics, 13(21), 3542. https://doi.org/10.3390/math13213542







