Abstract
Counting data play a critical role in various real-life applications across different scientific fields. This study handles the classical and Bayesian estimation of the one-parameter discrete linear exponential distribution under randomly right-censored data. Maximum likelihood estimators, both point and interval, are derived for the unknown parameter. In addition, Bayesian estimators are gained using informative and non-informative priors, assessed under three distinct loss functions: squared error loss, linear exponential loss, and generalized entropy loss. An algorithm for generating randomly right-censored data from the proposed model is also developed. To evaluate the efficiency of the estimators, considerable simulation studies are conducted, revealing that the maximum likelihood and the Bayesian approach under the generalized entropy loss function with a positive weight consistently outperform other methods across all sample sizes, achieving the lowest root mean squared errors. Finally, the discrete linear exponential distribution demonstrates strong applicability in modeling discrete count lifetime data in physical and medical sciences, outperforming related alternative distributions.
Keywords:
linear exponential distribution; random right-censored; maximum likelihood estimation; Bayesian estimation; lifetime count data MSC:
65H10; 65Z05; 60-08; 60E05; 62E10; 62F15; 62F25; 62N01; 62N05; 62P35; 65C05; 65H10; 65K05
1. Introduction
Lifetime distributions play a crucial role in analyzing and modeling data across a wide range of applied fields, including economics, engineering, finance, and the medical and biological sciences. In practice, data collection is frequently constrained by time or budget limitations, often resulting in incomplete datasets. Such incomplete datasets are commonly referred to as censored data. Various censoring schemes are available in the literature to examine these data sets, such as left, right, type I, type II, random, and hybrid censoring schemes. One of the most important censoring techniques in the literature is random censoring. Random right-censored data occur when the precise event time is unknown, as a subject is yet to test the desired event at the end of the study or drops out of the study before the event occurs, and this decision to drop out is not influenced by the event itself. This incomplete information forms a time interval, rather than a specific point, where the event’s occurrence is “censored” at the right side [1]. Randomly censored lifetime data are commonly used in multiple applications such as medical science, biology, reliability studies, etc.
The literature on censoring has been largely developed in a continuous setting. Classical contributions include the Kaplan–Meier estimator proposed by [2], kernel-based approaches for censored data introduced by [3], and prediction methods under random censoring by [4], with further developments addressing complex schemes such as twice-censored data by [5,6]. These works highlight the theoretical depth of continuous censoring methods. Many real-world datasets are inherently discrete, which limits the direct application of continuous methods. There remains a need to develop novel discrete distributions that can effectively model censored data and accommodate diverse types of lifetime discrete data. In this regard, several studies have made notable contributions. For instance, refs. [7,8,9,10,11,12,13] introduced multi-parameter discrete models, whereas refs. [14,15,16] proposed one-parameter models for discrete lifetime data. The challenge of random censoring in discrete settings has also been addressed, notably by [17,18,19,20], who developed methodological frameworks for practical implementation.
One of the recently proposed discrete lifetime models is the Discrete Linear Exponential (DLE) distribution [16], which provides the flexibility to fit over-dispersed, positively skewed, and increasing failure data. The probability mass function (PMF) of DLE distribution is given by:
The corresponding CDF is given by:
While the original work by [16] examined the fundamental properties and estimation of the DLE distribution under complete data, the current study extends this model to the case of randomly right-censored data, which frequently occurs in medical and reliability studies. New inferential procedures are developed for parameter estimation using both maximum likelihood (ML) and Bayesian methods under various loss functions. Furthermore, an algorithm for generating randomly right-censored samples from the DLE model is proposed, and extensive simulation experiments are conducted to evaluate the performance of the estimators. Finally, an analysis of real data is carried out to validate and illustrate the practical applicability of the proposed methods.
2. Maximum Likelihood Estimations
The ML method is one of the most widely used classical estimation techniques. In this Section, both point and interval estimation methods under randomly right-censored data are considered.
2.1. Point Estimation
The ML estimation of the parameter is derived for the DLE distribution under random right-censored sample. In this case, each observation contributes to the likelihood function through a random sample of size nm defined as:
where denotes the observed lifetime, is the probability mass function, is the survival function and is a censoring indicator, taking the value if the lifetime is observed and if it is censored , see [1]. Then, for the DLE distribution under random right-censoring, the likelihood function of is given by:
The corresponding log-likelihood function is:
The nonlinear likelihood equation corresponding to the parameter is derived by differentiating Equation (4) with respect to , as shown below:
The detailed derivation of Equation (5) can be found in Appendix A. Now, the ML estimator of parameters can be found by equating Equation (5) to zero. However, due to the complexity of this likelihood equation, deriving a closed-form solution for the ML estimator of is challenging. Consequently, numerical methods, such as the Newton–Raphson iteration technique, are employed to approximate the ML estimate of . An R program has been developed to solve the ML equations numerically.
2.2. Interval Estimation
The ML estimation of the unknown parameter does not have a closed-form solution; therefore, the exact sampling distribution of the ML estimator cannot be derived. As a result, it is not feasible to construct an exact confidence interval for . Instead, an asymptotic confidence interval (ACI) for is developed based on the asymptotic distribution of its ML estimator. It is well known that the ML estimator of is consistent asymptotically and follows a normal distribution such that , where is the expected Fisher information defined as:
In many practical situations, it is difficult to obtain an explicit form of this expectation. Therefore, following [21], the observed Fisher information is employed instead. The observed Fisher information is given by:
with replaced by its estimate , where the second-order partial derivative of the log-likelihood (LL) function can be expressed as:
The ACI for the parameter is given by:
where is the upper quantile of the standard normal distribution, and , where .
3. Bayesian Estimation
In this section, Bayesian estimation procedures are developed for the parameter of the DLE distribution under randomly right-censored samples. The analysis is conducted using several loss functions, including the squared error loss function (SELF), the linear exponential (LINEX) loss function, and the general entropy loss function (GELF). Corresponding Bayesian credible intervals are also constructed. The estimators are derived under two cases of prior distributions: informative and non-informative priors.
- case I
- Assume the parameter flowing Gamma priors with shape parameter and rate parameter 1. The Gamma prior is employed due to its flexibility and capacity to encapsulate a wide range of prior beliefs, making it a suitable choice for Bayesian analysis. The hyperparameter of the Gamma prior was selected in such a way that the Gamma prior mean (shape/rate) was the same as the original mean (parameter value); see [22,23,24]. The corresponding prior density function of is given by:where is a positive parameter. The posterior density function of given the data is expressed as follows:
- case II
- In the case of a non-informative prior, little or no prior information is available about the unknown parameter. For , an improper non-informative prior is adopted, which can be expressed in the form of a uniform density over its parameter space, with probability density function given by:The uniform prior was preferred for its simplicity and computational stability. The posterior density function of can be expressed as follows:
For the two prior cases described above, the Bayes estimator of is derived under three different loss functions, as detailed in the following subsections.
3.1. Bayesian Estimator Under SELF
The SELF is one of the most commonly used symmetric loss functions and is defined as:
Under this criterion, the Bayesian estimator corresponds to the posterior mean and can be expressed, for both prior cases, as:
For the gamma prior, the estimator takes the following integral form:
For the non-informative prior, it is represented as:
3.2. Bayesian Estimator Under LINEX Loss Function
The LINEX loss function proposed by [25] allows for asymmetric penalization of overestimation and underestimation and is defined as:
where a shape parameter determines both the direction and the degree of asymmetry. The Bayesian estimator of under this function is expresed as:
For the two prior assumptions, the estimators can be formulated as follows:
3.3. Bayesian Estimation Under GELF
The GELF introduced by [26] is an asymmetric loss function which can be given as:
where q controls the asymmetry. The corresponding Bayesian estimator is
For the two prior structures, the estimators can be formulated as follows:
The Bayesian credible interval for is constructed using the following formula:
where and denote the lower and upper bounds of the credible interval, respectively, and is the posterior density of .
The Bayesian estimation of the parameter with different loss functions does not provide straightforward formulas, as shown in Equations (9) and (11). Therefore, advanced Bayesian Markov Chain Monte Carlo (MCMC) techniques are employed to approximate these estimators by generating samples from the posterior distributions. It’s important to note that the full conditional posterior density functions of in Equations (9) and (11) do not match up with any common distributions. This leads to the use of the Metropolis-Hastings algorithm to generate MCMC samples. Graphs of these posterior distributions are included to highlight their similarity to the normal distribution (see Figure 1). This similarity supports the application of the Metropolis–Hastings method with normal proposal distributions. The main steps of the Metropolis–Hastings procedure are summarized as follows:
- 1
- Set the initial values
- 2
- Generate from a normal distribution centered at the current estimate as
- 3
- The acceptance probability is computed as
- 4
- The chain is iterated M times to obtain posterior samples, .
For more details, see [16].
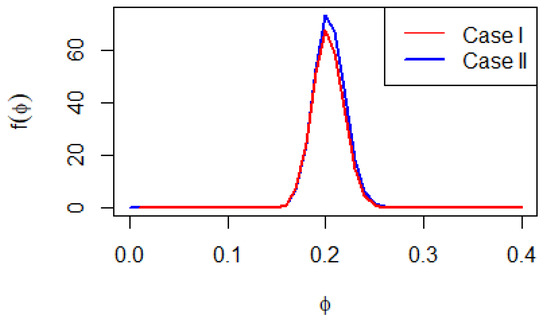
Figure 1.
Posterior density for two cases.
4. Simulation
Simulation studies offer a powerful tool for assessing the performance of statistical estimators under controlled conditions, particularly when analytical solutions are difficult to obtain or unavailable. In this study, a Monte Carlo simulation is conducted to assess the performance of the proposed estimation methods for the parameter of the DLE distribution under random right-censoring. The main objectives are:
- *
- To evaluate the accuracy and precision of parameter estimates for the DLE distribution based on random right-censored samples.
- *
- To compare the performance of the ML and Bayesian approaches under different loss functions.
- *
- To investigate the impact of sample size and prior assumptions on the performance of the estimation methods.
A total of random right-censored samples are generated from the DLE distribution for various sample sizes . The simulations are conducted under four true parameter values: For each generated dataset, parameter estimation is performed using both ML and Bayesian approaches. Bayesian estimation is implemented under both symmetric and asymmetric loss functions, including SELF, LINEX, and GELF, with weights . Two prior specifications are considered: a gamma prior (informative) and a uniform prior (non-informative). The random right-censored samples are generated using the following algorithm:
- 1.
- Fix the value of the parameter .
- 2.
- Obtain from DLE distribution; i = 1,…, n.
- 3.
- Draw n random pseudo from uniform distribution i.e., This distribution controls the censorship mechanism.
- 4.
- Construct the observed data as follows:Consequently, the pairs form the random right-censored dataset.
For more details on this algorithm, see [27]. For each configuration, both the ML and Bayesian estimates are obtained, along with their associated asymptotic confidence intervals (ACI) or credible intervals, computed at a 95% confidence level. For the Bayesian approach, posterior inference is carried out using the Metropolis–Hastings algorithm with a chain of 12,000 samples, discarding the first 2000 as burn-in. The effectiveness of the proposed point estimation methods is assessed using two key measures: the bias and the root mean squared error (RMSE), defined respectively as , and The performance of the interval estimation procedures is evaluated by considering the average lengths of the confidence intervals for ML estimates and the credible intervals for Bayesian estimates. All computational procedures were implemented in the R 4.5.1 software.
Table 1 and Table 2 summarize the simulation outcomes, and Figure 2 provides a heat-map representation of RMSE values across different scenarios. Several important findings emerge:
- As the sample size increases, the RMSE of both ML and Bayesian estimators declines, reflecting enhanced accuracy and convergence toward unbiasedness.
- An increase in sample size leads to a reduction in the RMSE for both ML and Bayesian estimators, confirming their improved precision and asymptotic unbiased behavior.
- The Bayesian estimators with informative priors generally outperform those with non-informative priors.
- Bayesian estimates under asymmetric loss functions with a positive weight yield smaller RMSE values and shorter credible intervals compared to those with a negative weight.
- Among the Bayesian methods, GELF with positive weight consistently yields the smallest RMSE and the shortest interval lengths.
- The ML estimator and the Bayesian estimator under GELF with positive weight show superior and consistent performance across all sample sizes.
Figure 2 further confirms these findings. Overall, the results demonstrate that both ML and Bayesian estimation, when combined with informative priors and asymmetric loss functions with positive weights, substantially enhance estimation efficiency in the presence of censoring.
Figure 2 presents heat maps illustrating the RMSE results for two cases: Case 1 corresponds to the Gamma prior, and Case 2 corresponds to the Uniform prior. Here, “P” denotes a positive weight and “N” denotes a negative weight. In the heat maps, darker colors indicate higher RMSE values, while lighter colors indicate lower RMSE values.

Table 1.
The ML and Bayesian estimates (SELF, LINEX, and GELF) of using Case I: Gamma prior under random right-censored samples.
Table 1.
The ML and Bayesian estimates (SELF, LINEX, and GELF) of using Case I: Gamma prior under random right-censored samples.
| n | ML | Bayesian Estimation | |||||
|---|---|---|---|---|---|---|---|
| SELF | LINEX | GELF | |||||
| c = −1.5 | c = 1.5 | q = −1.5 | q=1.5 | ||||
| Estimate Bias MSE Length | Estimate Bias MSE Length | Estimate Bias MSE Length | Estimate Bias MSE Length | Estimate Bias MSE Length | Estimate Bias MSE Length | ||
| 0.01 | 20 | ||||||
| 100 | |||||||
| 500 | |||||||
| 1000 | |||||||
| 0.1 | 20 | ||||||
| 100 | |||||||
| 500 | |||||||
| 1000 | |||||||
| 0.5 | 20 | ||||||
| 100 | |||||||
| 500 | |||||||
| 1000 | |||||||
| 1 | 20 | ||||||
| 100 | |||||||
| 500 | |||||||
| 1000 | |||||||

Table 2.
The ML and Bayesian estimates (SELF, LINEX, and GELF) of using Case II: Uniform prior under random right-censored samples.
Table 2.
The ML and Bayesian estimates (SELF, LINEX, and GELF) of using Case II: Uniform prior under random right-censored samples.
| n | ML | Bayesian Estimation | |||||
|---|---|---|---|---|---|---|---|
| SELF | LINEX | GELF | |||||
| c = −1.5 | c = 1.5 | q = −1.5 | q=1.5 | ||||
| Estimate Bias MSE Length | Estimate Bias MSE Length | Estimate Bias MSE Length | Estimate Bias MSE Length | Estimate Bias MSE Length | Estimate Bias MSE Length | ||
| 0.01 | 20 | ||||||
| 100 | |||||||
| 500 | |||||||
| 1000 | |||||||
| 0.1 | 20 | ||||||
| 100 | |||||||
| 500 | |||||||
| 1000 | |||||||
| 0.5 | 20 | ||||||
| 100 | |||||||
| 500 | |||||||
| 1000 | |||||||
| 1 | 20 | ||||||
| 100 | |||||||
| 500 | |||||||
| 1000 | |||||||
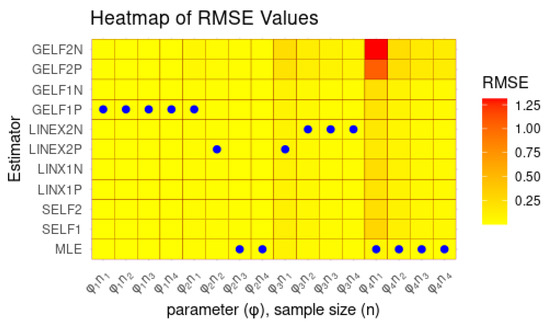
Figure 2.
Heat-map of RMSE under random right-censored samples for ML estimation and Bayesian estimations at different values for parameter and different sample sizes .
5. Applications in Random Right-Censored Data
5.1. Real Data Analysis for Comparing Competing Discrete Models
In this subsection, three real datasets are analyzed to illustrate the applicability of the proposed distribution to censored data. Model performance is assessed using the maximum log-likelihood (-LL) and several goodness-of-fit criteria, including the Kolmogorov–Smirnov (KS) test with its corresponding p-value, as well as the Akaike information criterion (AIC) and Bayesian information criterion (BIC) to compare the DLE distribution against other competing one-parameter discrete distributions, as listed in Table 3.

Table 3.
Competing models for the DLE distribution.
5.1.1. Dataset I
A sample of the failure time of 20 epoxy insulation samples at the voltage level of 57.5 Kv. The failure times, in minutes, are 510, 1000*, 252, 408, 528, 690, 900*, 714, 348, 546, 174, 696, 294, 234, 288, 444, 390, 168, 558, and 288 (see [1]). Here, the censoring times are indicated with asterisks *. Table 4 presents the ML estimates along with their standard errors for the parameter of the DLE distribution and other competing models. Additionally, the corresponding goodness-of-fit criteria are provided.

Table 4.
ML Estimates, log-likelihood (-LL) and associated goodness-of-fit criteria for Dataset I.
From Table 4, the DLE distribution provided a satisfactory fit, with AIC = 254.761 and a non-significant K–S test (p = 0.784), indicating good agreement with the observed data. Although the Discrete Rayleigh distribution achieved slightly lower AIC and BIC values, the DLE distribution demonstrated comparable performance, confirming its suitability and flexibility for modeling the data. The results presented in Figure 3 further support the findings of Table 4.
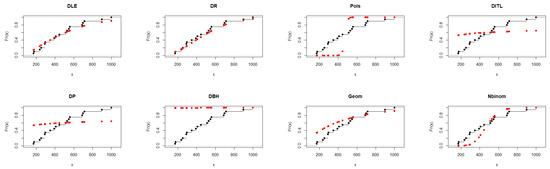
Figure 3.
Fitted CDFs (red) compared with empirical CDFs (black) for Dataset I.
5.1.2. Dataset II
The dataset below reports the remission times, in weeks, for a group of 30 leukemia patients who received similar treatment (see [1]): 1, 1, 2, 4, 4, 6, 6, 6, 7, 8, 9, 9, 10, 12, 13, 14, 18, 19, 24, 26, 29, 31*, 42, 45*, 50*, 57, 60, 71*, 85*, and 91. Here, the censoring times are indicated with asterisks *. Table 5 presents the ML estimates and their standard errors for the parameter of the DLE distribution, alongside estimates for other competing models. The corresponding goodness-of-fit criteria are also provided.

Table 5.
ML Estimates, log-likelihood (-LL) and associated goodness-of-fit criteria for Dataset II.
Regarding Table 5, the DLE distribution achieved an adequate fit with AIC = 237.817 and a K–S p-value = 0.042, indicating reasonable agreement with the observed data. Although the geometric distribution showed slightly lower AIC and BIC values, the DLE distribution provided comparable performance and better flexibility in capturing the data pattern, supporting its applicability as an alternative discrete distribution. Figure 4 further illustrates and supports the findings presented in Table 5.
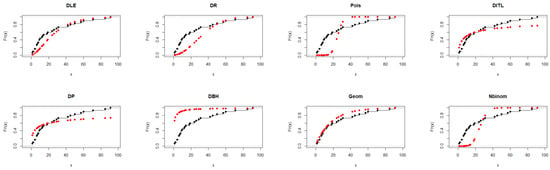
Figure 4.
Fitted CDFs (red) compared with empirical CDFs (black) for Dataset II.
5.1.3. Dataset III
The following data represent the survival times (in months) of individuals with Hodgkin’s disease who were treated with nitrogen mustards and had received extensive prior therapy (see [1]): 1, 2, 3, 4, 4, 6, 7, 9, 9, 14*, 16, 18*, 26*, 30*, 41*. Here, the censoring times are indicated with asterisks *. Table 6 presents the ML estimates along with their standard errors for the parameter of the DLE distribution, as well as for other competing models. The corresponding goodness-of-fit criteria are also provided.

Table 6.
ML Estimates, log-likelihood (-LL) and associated goodness-of-fit criteria for Dataset III.
As shown in Table 6, the DLE distribution achieved a good overall fit to the data, with AIC = 86.358 and a non-significant K–S test (p = 0.276). This result indicates that the DLE distribution adequately represents the observed distribution. Although the Geometric and DITL distributions exhibited marginally smaller AIC values, the DLE distribution provided a competitive and more flexible fit, supporting its effectiveness as a suitable alternative among the considered discrete models. The results presented in Figure 5 further support the findings of Table 6.
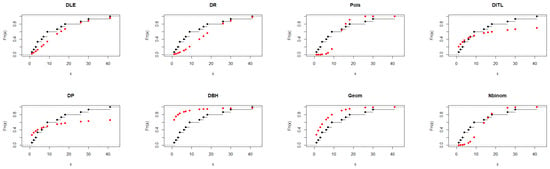
Figure 5.
Fitted CDFs (red) compared with empirical CDFs (black) for Dataset III.
5.2. Real Data Analysis for Assessing Classical and Bayesian Estimation Techniques
In this subsection, the random right-censored datasets described in the previous subsections are analyzed to compare classical and Bayesian estimation methods. Model performance is assessed using the AIC, BIC, and the Kolmogorov–Smirnov (K–S) test along with its corresponding p-value, allowing a comprehensive evaluation of the estimation approaches.
5.2.1. Dataset I
The estimators obtained using classical and Bayesian methods, along with the AIC, BIC, and Kolmogorov–Smirnov (K–S) test with its p-value for Dataset I, are presented in Table 7.

Table 7.
Classical and Bayesian estimators and corresponding goodness-of-fit criteria for Dataset I.
Table 7 shows that the parameter estimate is consistent across all methods at 0.004. The AIC and BIC values are very close, with the lowest values obtained under the ML and N-GELF estimators, indicating comparable performance. The results of the K-S test confirm a good fit for all methods, with the P-GELF estimator for case II achieving the best fit (lowest statistic 0.143 and highest p-value 0.805). Overall, both classical and Bayesian approaches perform similarly, with P-GELF showing a slight advantage.
5.2.2. Dataset II
The classical and Bayesian estimators, together with AIC, BIC, KS statistics, and p-values for Dataset II, are summarized in Table 8.

Table 8.
Classical and Bayesian estimators and corresponding goodness-of-fit criteria for Dataset II.
As Table 8 shows that the parameter estimate for dataset II is stable across methods. The AIC and BIC values are nearly identical for all estimators, with ML and N-GELF producing the lowest values (AIC = 237.817, BIC = 239.218), indicating similar model performance. The best fit within Dataset II is obtained under N-GELF for Case II.
5.2.3. Dataset III
For Dataset III, Table 9 presents the estimates obtained using both classical and Bayesian methods, along with the corresponding AIC, BIC, and KS test statistics, including their p-values.

Table 9.
Classical and Bayesian estimators and corresponding goodness-of-fit criteria for Dataset III.
According to Table 9, the parameter estimate for dataset III varies slightly between 0.113 and 0.127 across methods. The AIC and BIC values remain very close, with the lowest values obtained under ML and N-GELF (AIC = 86.358, BIC = 87.066), suggesting comparable performance. Among the Bayesian estimators, the N-GELF method in Case II achieved the best fit.
The Geweke diagnostic test [35] was applied to evaluate the convergence of the MCMC chains. This diagnostic compares the means of the initial and final segments of each Markov chain; convergence is achieved when the difference between these means is approximately zero, with Z-scores falling within ±1.96 at the 95% confidence level. As reported in Table 10, the calculated Z-scores for all three chains under the gamma prior are close to zero, indicating satisfactory convergence. Convergence was also assessed by trace plots, autocorrelation plots (ACF), and posterior density plots for the three datasets (Figure 6, Figure 7 and Figure 8). The ACF indicates that the posterior samples are almost independent. Trace plots confirm the chains behave stably across iterations. These diagnostics confirm appropriate convergence and a sufficient burn-in period.

Table 10.
Geweke diagnostic Z-scores of MCMC result for datasets.

Figure 6.
MCMC diagnostic plots for Dataset I: trace, ACF, and histogram of sampled values.

Figure 7.
MCMC diagnostic plots for Dataset II: trace, ACF, and histogram of sampled values.

Figure 8.
MCMC diagnostic plots for Dataset III: trace, ACF, and histogram of sampled values.
6. Conclusions
In this study, we extend the DLE distribution originally introduced by [16] to the case of randomly right-censored data. The focus is on developing inferential procedures and evaluating the distribution’s performance under incomplete lifetime observations. The model parameter is estimated using classical ML and Bayesian approaches under SELF, LINEX, and GELF loss functions, with both informative and non-informative priors. Since closed-form posterior distributions are not available, MCMC techniques are employed for sampling. Extensive simulation studies are performed to evaluate the performance of classical and Bayesian methods across various parameter values and sample sizes. The results indicate that both the ML estimator and the Bayesian estimator under GELF with a positive weight () consistently achieve the lowest RMSE. The practical utility of the extended DLE distribution is further demonstrated using real-world physical and medical lifetime datasets. Statistical measures, including AIC, BIC, and the Kolmogorov–Smirnov test, confirm the superior fit of the proposed distribution compared to other discrete alternatives. Overall, this work offers a significant extension of the DLE distribution to censored data scenarios, thereby enhancing its flexibility and applicability in reliability and medical analyses. Future work may extend this study by exploring other censoring techniques and incorporating regression models.
Author Contributions
Conceptualization, A.F.; Methodology, K.A.-H.; Software, H.B. and K.A.-H.; Formal analysis, K.A.-H. and A.F.; Investigation, K.A.-H.; Resources, K.A.-H.; Data curation, K.A.-H.; Writing—original draft, K.A.-H.; Writing—review & editing, H.B. and A.F.; Visualization, H.B.; Supervision, H.B. and A.F.; Project administration, A.F.; Funding acquisition, H.B. All authors have read and agreed to the published version of the manuscript.
Funding
This project was funded by the Deanship Scientific Research (DSR), King Abdulaziz University, Jeddah, under Grant No. IPP: 1616-247-2025. The authors acknowledge the DSR for the technical and financial support.
Data Availability Statement
The data presented in this study are openly available in [1].
Acknowledgments
The authors sincerely thank King Abdulaziz University for their kind support.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. The Derivative of log-Likelihood
References
- Lawless, J.F. Statistical Models and Methods for Lifetime Data; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Kaplan, E.L.; Meier, P. Nonparametric estimation from incomplete observations. J. Am. Stat. Assoc. 1958, 53, 457–481. [Google Scholar] [CrossRef]
- Giné, E.; Guillou, A. On consistency of kernel density estimators for randomly censored data: Rates holding uniformly over adaptive intervals. In Proceedings of the Annales de l’IHP Probabilités et Statistiques, Paris, France, 18–20 June 2001; Volume 37, pp. 503–522. [Google Scholar]
- Kohler, M.; Máthé, K.; Pintér, M. Prediction from randomly right censored data. J. Multivar. Anal. 2002, 80, 73–100. [Google Scholar] [CrossRef]
- Khardani, S. Relative error prediction for twice censored data. Math. Methods Stat. 2019, 28, 291–306. [Google Scholar] [CrossRef]
- Khardani, S.; Lemdani, M.; Saïd, E.O. Some asymptotic properties for a smooth kernel estimator of the conditional mode under random censorship. J. Korean Stat. Soc. 2010, 39, 455–469. [Google Scholar] [CrossRef]
- El-Morshedy, M.; Eliwa, M.; Nagy, H. A new two-parameter exponentiated discrete Lindley distribution: Properties, estimation and applications. J. Appl. Stat. 2020, 47, 354–375. [Google Scholar] [CrossRef]
- Eliwa, M.S.; Altun, E.; El-Dawoody, M.; El-Morshedy, M. A new three-parameter discrete distribution with associated INAR (1) process and applications. IEEE Access 2020, 8, 91150–91162. [Google Scholar] [CrossRef]
- ul Haq, M.A.; Babar, A.; Hashmi, S.; Alghamdi, A.S.; Afify, A.Z. The discrete type-II half-logistic exponential distribution with applications to COVID-19 data. Pak. J. Stat. Oper. Res. 2021, 17, 921–932. [Google Scholar] [CrossRef]
- Eliwa, M.; Altun, E.; Alhussain, Z.A.; Ahmed, E.A.; Salah, M.M.; Ahmed, H.H.; El-Morshedy, M. A new one-parameter lifetime distribution and its regression model with applications. PLoS ONE 2021, 16, e0246969. [Google Scholar] [CrossRef] [PubMed]
- Alghamdi, A.S.; Ahsan-ul Haq, M.; Babar, A.; Aljohani, H.M.; Afify, A.Z.; Cell, Q.E. The discrete power-Ailamujia distribution: Properties, inference, and applications. AIMS Math. 2022, 7, 8344–8360. [Google Scholar] [CrossRef]
- Eldeeb, A.S.; Ahsan-ul Haq, M.; Eliwa, M.S.; Cell, Q.E. A discrete Ramos-Louzada distribution for asymmetric and over-dispersed data with leptokurtic-shaped: Properties and various estimation techniques with inference. AIMS Math. 2022, 7, 1726–1741. [Google Scholar] [CrossRef]
- Almetwally, E.M.; Abdo, D.A.; Hafez, E.; Jawa, T.M.; Sayed-Ahmed, N.; Almongy, H.M. The new discrete distribution with application to COVID-19 Data. Results Phys. 2022, 32, 104987. [Google Scholar] [CrossRef] [PubMed]
- Afify, A.Z.; Ahsan-ul Haq, M.; Aljohani, H.M.; Alghamdi, A.S.; Babar, A.; Gómez, H.W. A new one-parameter discrete exponential distribution: Properties, inference, and applications to COVID-19 data. J. King Saud Univ.-Sci. 2022, 34, 102199. [Google Scholar] [CrossRef]
- Shamlan, D.; Baaqeel, H.; Fayomi, A. A Discrete Odd Lindley Half-Logistic Distribution with Applications. J. Phys. Conf. Ser. 2024, 2701, 012034. [Google Scholar] [CrossRef]
- Al-Harbi, K.; Fayomi, A.; Baaqeel, H.; Alsuraihi, A. A Novel Discrete Linear-Exponential Distribution for Modeling Physical and Medical Data. Symmetry 2024, 16, 1123. [Google Scholar] [CrossRef]
- Krishna, H.; Goel, N. Maximum likelihood and Bayes estimation in randomly censored geometric distribution. J. Probab. Stat. 2017, 2017. [Google Scholar] [CrossRef]
- Achcar, J.A.; Martinez, E.Z.; de Freitas, B.C.L.; de Oliveira Peres, M.V. Classical and Bayesian inference approaches for the exponentiated discrete Weibull model with censored data and a cure fraction. Pak. J. Stat. Oper. Res. 2021, 17, 467–481. [Google Scholar] [CrossRef]
- Pandey, A.; Singh, R.P.; Tyagi, A. An Inferential Study of Discrete Burr-Hatke Exponential Distribution under Complete and Censored Data. Reliab. Theory Appl. 2022, 17, 109–122. [Google Scholar]
- Tyagi, A.; Singh, B.; Agiwal, V.; Nayal, A.S. Analysing Random Censored Data from Discrete Teissier Model. Reliab. Theory Appl. 2023, 18, 403–411. [Google Scholar]
- Cohen, A.C. Maximum likelihood estimation in the Weibull distribution based on complete and on censored samples. Technometrics 1965, 7, 579–588. [Google Scholar] [CrossRef]
- Basu, S.; Singh, S.K.; Singh, U. Estimation of inverse Lindley distribution using product of spacings function for hybrid censored data. Methodol. Comput. Appl. Probab. 2019, 21, 1377–1394. [Google Scholar] [CrossRef]
- Kurdi, T.; Nassar, M.; Alam, F.M.A. Bayesian Estimation Using Product of Spacing for Modified Kies Exponential Progressively Censored Data. Axioms 2023, 12, 917. [Google Scholar] [CrossRef]
- Alkhairy, I. Classical and Bayesian inference for the discrete Poisson Ramos-Louzada distribution with application to COVID-19 data. Math. Biosci. Eng. 2023, 20, 14061–14080. [Google Scholar] [CrossRef]
- Varian, H.R. A Bayesian approach to real estate assessment. In Studies in Bayesian Econometrics and Statistics in Honor of Leonard J. Savage; Fienberg, S.E., Zellner, A., Eds.; North-Holland Publishing Company: Amsterdam, The Netherlands, 1975; pp. 195–208. [Google Scholar]
- Calabria, R.; Pulcini, G. An engineering approach to Bayes estimation for the Weibull distribution. Microelectron. Reliab. 1994, 34, 789–802. [Google Scholar] [CrossRef]
- Ramos, P.L.; Guzman, D.C.; Mota, A.L.; Rodrigues, F.A.; Louzada, F. Sampling with censored data: A practical guide. arXiv 2020, arXiv:2011.08417. [Google Scholar] [CrossRef]
- Roy, D. Discrete rayleigh distribution. IEEE Trans. Reliab. 2004, 53, 255–260. [Google Scholar] [CrossRef]
- Poisson, S.D. Recherches sur la Probabilité des Jugements en Matière Criminelle et en Matière Civile: Précédées des Règles GénéRALES du Calcul des Probabilités; Bachelier: Oslo, Norway, 1837; pp. 206–207. [Google Scholar]
- Krishna, H.; Pundir, P.S. Discrete Burr and discrete Pareto distributions. Stat. Methodol. 2009, 6, 177–188. [Google Scholar] [CrossRef]
- El-Morshedy, M.; Eliwa, M.S.; Altun, E. Discrete Burr-Hatke distribution with properties, estimation methods and regression model. IEEE Access 2020, 8, 74359–74370. [Google Scholar] [CrossRef]
- Eldeeb, A.S.; Ahsan-Ul-Haq, M.; Babar, A. A discrete analog of inverted Topp-Leone distribution: Properties, estimation and applications. Int. J. Anal. Appl. 2021, 19, 695–708. [Google Scholar]
- de Laplace, P.S. Théorie Analytique des Probabilités; Courcier: Paris, France, 1820; Volume 7. [Google Scholar]
- de Montmort, P.R.; Bernoulli, J.; Bernoulli, N. Essai d’Analyse sur les Jeux de Hazards; Seconde Édition Revue & augmentée de Plusieurs Lettres; Chez Claude Jombert: Paris, France, 1714. [Google Scholar]
- Geweke, J. Evaluating the accuracy of sampling-based approaches to the calculation of posterior moments. Bayesian Stat. 1992, 4, 169–193. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).