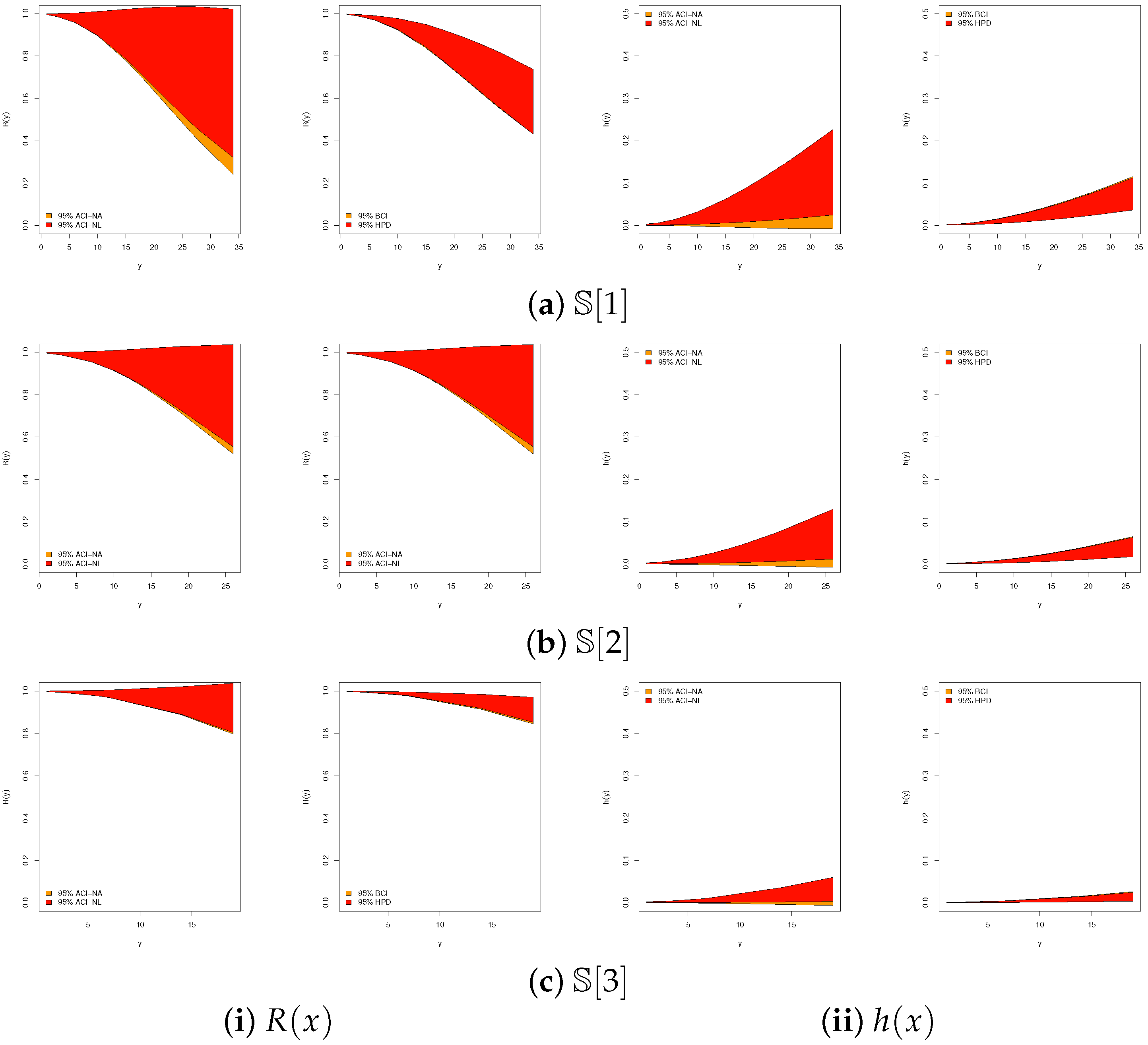1. Introduction
Recently, Saaidia et al. [
1] introduced the ZLindley (ZL) distribution, a new one-parameter model designed to enhance the flexibility of Lindley-type families. The proposed distribution extends the modeling capacity of existing alternatives, demonstrating superior performance in terms of goodness-of-fit when compared with several well-established models, including the Zeghdoudi, XLindley, New XLindley, Xgamma, and the classical Lindley distributions. In their study, the authors derived key statistical properties of the ZL distribution, such as its probability density and cumulative distribution functions, measures of central tendency and dispersion, and reliability characteristics. Furthermore, estimation procedures for the model parameters were explored, with particular emphasis on classical inference approaches. The distribution was also evaluated empirically through real data applications, illustrating its potential as a flexible and competitive alternative for modeling lifetime and reliability data.
Unlike the Weibull and Gamma lifetime models, which are restricted to monotone hazard rate shapes (increasing or decreasing) and hence fail to accommodate data exhibiting non-monotonic or bathtub-shaped hazard structures, the classical Lindley-type families also show limitations in modeling high-variance or heavy-tailed reliability data, often leading to biased tail-area estimates and underestimation of extreme lifetimes. In contrast, the proposed ZLindley distribution exhibits enhanced flexibility through its parameter-induced shape control. It allows for both increasing and near-constant hazard rate patterns and improved representation of over-dispersed datasets. This flexibility leads to more efficient and accurate estimation of the reliability and hazard rate functions, particularly in heterogeneous systems such as biomedical survival studies and environmental lifetime processes. Empirically, the superiority of the proposed ZLindley model was confirmed through the two real data analyses: One for the leukemia survival dataset and the other for the River Styx flood. Both applications demonstrate a significantly better fit than the classical Lindley, Weibull, and Gamma models. Collectively, these results confirm that the ZLindley framework not only enhances shape adaptability and inferential efficiency but also offers superior empirical performance across diverse reliability environments.
Let
Y denote a non–negative continuous random variable representing a lifetime. If
, with
as the scale parameter, then its probability density function (PDF) and cumulative distribution function (CDF) are defined as
and
respectively, where
.
Estimating the reliability and hazard rate functions offers essential insights into a system’s survival characteristics, where the reliability function measures the probability of operating beyond a certain time, and the hazard rate function indicates the immediate risk of failure. These estimates are crucial in engineering, medical, and industrial fields, among others. However, the respective reliability function (RF) and hazard rate function (HRF) at time
, of the ZL lifespan model, are given by
and
It is worth mentioning that the ZL distribution’s PDF is unimodal, starting at a positive value, rising to a peak, and then decaying exponentially with the rate of decay increasing as grows, whereas its HRF is monotonically increasing with respect to y.
In reliability analysis and survival studies, a variety of censoring mechanisms have been suggested, which are typically organized into two major groups: Single-stage and multi-stage procedures. A single-stage censoring plan is characterized by the absence of withdrawals during the course of the test; the experiment proceeds uninterrupted until it concludes, either upon reaching a predetermined study duration or once a specified number of failures has been recorded. The traditional Type-I and Type-II censoring schemes fall within this category. On the other hand, multi-stage censoring frameworks introduce greater flexibility by permitting the removal of units at scheduled stages prior to the completion of the experiment. Well-established examples include progressive Type-I censoring and its Type-II counterpart (T2-PC), which have been studied extensively in the literature (see Balakrishnan and Cramer [
2]). On the other hand, to save more time and testing cost, the hybrid progressive Type-I censoring (T1-HPC) has been introduced by Kundu and Joarder [
3]. To enhance their flexibility, Ng et al. [
4] introduced the adaptive progressive Type-II censoring (T2-APC) scheme, from which the T2-PC plan can be obtained as a special case. This approach allows the experimenter to terminate the test earlier if the study time exceeds a pre-specified limit. According to Ng et al. [
4], the T2-APC performs well in statistical inference provided that the overall duration of the test is not a primary concern.
Nevertheless, when the test units are highly reliable, the procedure may lead to excessively long experiments, making it unsuitable in contexts where test duration is an important factor. To overcome this drawback, Yan et al. [
5] introduced the improved adaptive progressive Type-II censoring (T2IAPC) scheme. This design offers two notable advantages: It guarantees termination of the experiment within a specified time window, and it generalizes several multi-stage censoring strategies, including T2-PC and T2-APC plans. Formally, consider
n items placed on test with a pre-specified number of failures
r, a T2-PC
, and two thresholds
. When the
ith failure occurs at time
,
of the remaining items are randomly withdrawn from the test. Within this censoring framework, one of the following three distinct situations may occur:
Case 1: When , the test terminates at , yielding the standard T2-PC;
Case 2: When , the test ends at after modifying the T2-PC at by assigning , where denotes the number of failures observed before . Following the rth failure, all remaining units are removed. This corresponds to the T2-APC;
Case 3: When , the test stops at . The T2-PC is then adapted by setting , where is the number of failures observed before . At time , all remaining units are withdrawn, with their total given by .
Let
denote T2I-APC order statistics with size
collected from a continuous population characterized by PDF
and CDF
, then the corresponding joint likelihood function (JLF) for this sample can be defined as
where
for simplicity. All math notations presented in Equation (
5) are defined in
Table 1.
Several well-known censoring plans can be regarded as particular cases of the T2I-APC strategy, from Equation (
5), such as:
The T1-HPC (by Kundu and Joarder [
3]) when
;
The T2-APC (by Ng et al. [
4]) when
;
The T2-PC (by Balakrishnan and Cramer [
2]) when
;
The T2-C (by Bain and Engelhardt [
6]) when
,
for
, and
.
Within this setting, the lower threshold
plays the role of a warning point that signals the progress of the experiment, while the upper threshold
specifies the maximum admissible testing time. If
is reached before observing the required number of failures
m, the test must be stopped at
. This feature overcomes the drawback of the T2-APC plan of Ng et al. [
4], in which the total test length could become unreasonably long. The inclusion of the upper bound
guarantees that the test duration is always confined to a predetermined finite interval. Although the T2I-APC plan has proven to be effective in statistical inference, it has attracted relatively limited attention; see, for example, Nassar and Elshahhat [
7], Elshahhat and Nassar [
8], and Dutta and Kayal [
9], among others.
Reliability analysis is very important in medicine, engineering, and applied sciences because it helps us understand how long systems will last when we don’t know for sure. The newly proposed ZL distribution has demonstrated greater flexibility compared to classical Lindley-type families for modeling lifetime data; however, its implementation in practical situations frequently encounters the issue of censoring. Taking into account the T2I-APC scheme, which fixes these problems by making sure that experiments end in a set amount of time while still being able to draw conclusions quickly. Nonetheless, its utilization in contemporary flexible lifetime models, such as the ZL distribution, remains insufficiently investigated. This study addresses the gap by incorporating the ZL model through T2I-APC to create a more robust and applicable framework for survival analysis. The main objectives in this study are summarized in sixfold:
A comprehensive reliability analysis of the ZL model under the proposed censoring is introduced, enhancing both flexibility and practical relevance.
Both maximum likelihood (with asymptotic and log-transformed confidence intervals) and Bayesian methods (with credible and highest posterior density (HPD) intervals) are developed for the estimation of the model parameters, reliability function, and hazard function.
Efficient iterative schemes, including Newton–Raphson for likelihood estimation and a Metropolis–Hastings iterative algorithm for Bayesian inference, are tailored.
Extensive Monte Carlo simulations are conducted to compare the performance of different estimation approaches across varying censoring designs, thresholds, and sample sizes, identifying optimal conditions for practitioners.
The study demonstrates how different censoring strategies (left-, middle-, and right-censoring) influence the accuracy of estimating the scale parameter, hazard rate, and reliability function, offering practical guidelines for experimenters.
The methodology is validated using clinical data on leukemia patients and physical data from engineering contexts, confirming the versatility of the proposed model for heterogeneous reliability scenarios.
The structure of the paper is as follows:
Section 2 and
Section 3 develop the frequentist estimations, respectively.
Section 4 reports the Monte Carlo results and their interpretations, while
Section 5 demonstrates the applicability of the proposed approaches and techniques through two real data analyses. Concluding remarks and final observations are provided in
Section 6.
3. Bayesian Inference
In this section, we derive Bayesian point and credible estimates for the ZL parameters
,
, and
. The Bayesian approach requires explicit specification of prior information and a loss function, both of which strongly influence the resulting inference. Choosing an appropriate prior distribution for an unknown parameter, however, is often a challenging task. As highlighted by Gelman et al. [
12], there is no universally accepted rule for selecting priors in Bayesian analysis. Given that the parameter
of the ZL model is strictly positive, a gamma prior offers a convenient and widely adopted option. Accordingly, we assume
with prior density
From (
6) and (
11), the posterior PDF (say
) of
is
where its normalized term (say,
) is given by
It should be emphasized that the squared-error loss (SEL) function is adopted here, as it represents the most commonly employed symmetric loss criterion in Bayesian inference. Nevertheless, the proposed framework can be readily generalized to accommodate alternative loss functions without altering the overall estimation procedure. Given the posterior PDF (
12) and the JLF (
6), the Bayes estimator of
, denoted by
, against the SEL is given by
It noted, from (
13), that obtaining (closed-form) Bayes estimator of
,
, or
under the SEL function is not feasible. To address the analytical intractability of the Bayes estimates, we rely on the Markov chain Monte Carlo (MCMC) procedure to simulate samples from the posterior distribution in (
12). These simulated draws enable the computation of Bayesian point estimates together with Bayes credible interval (BCI) and HPD interval estimates for the parameters of interest. Since the posterior density of
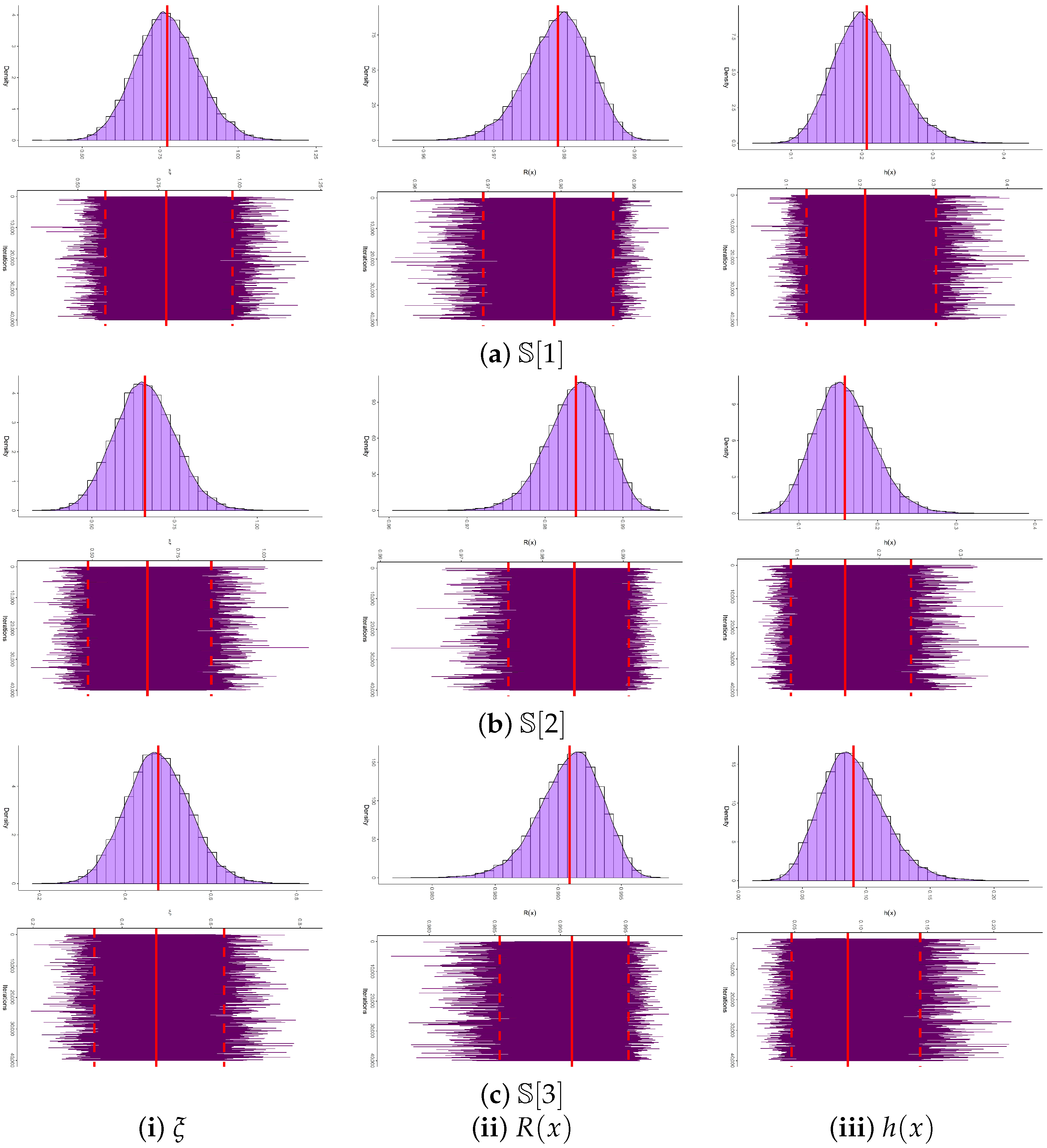
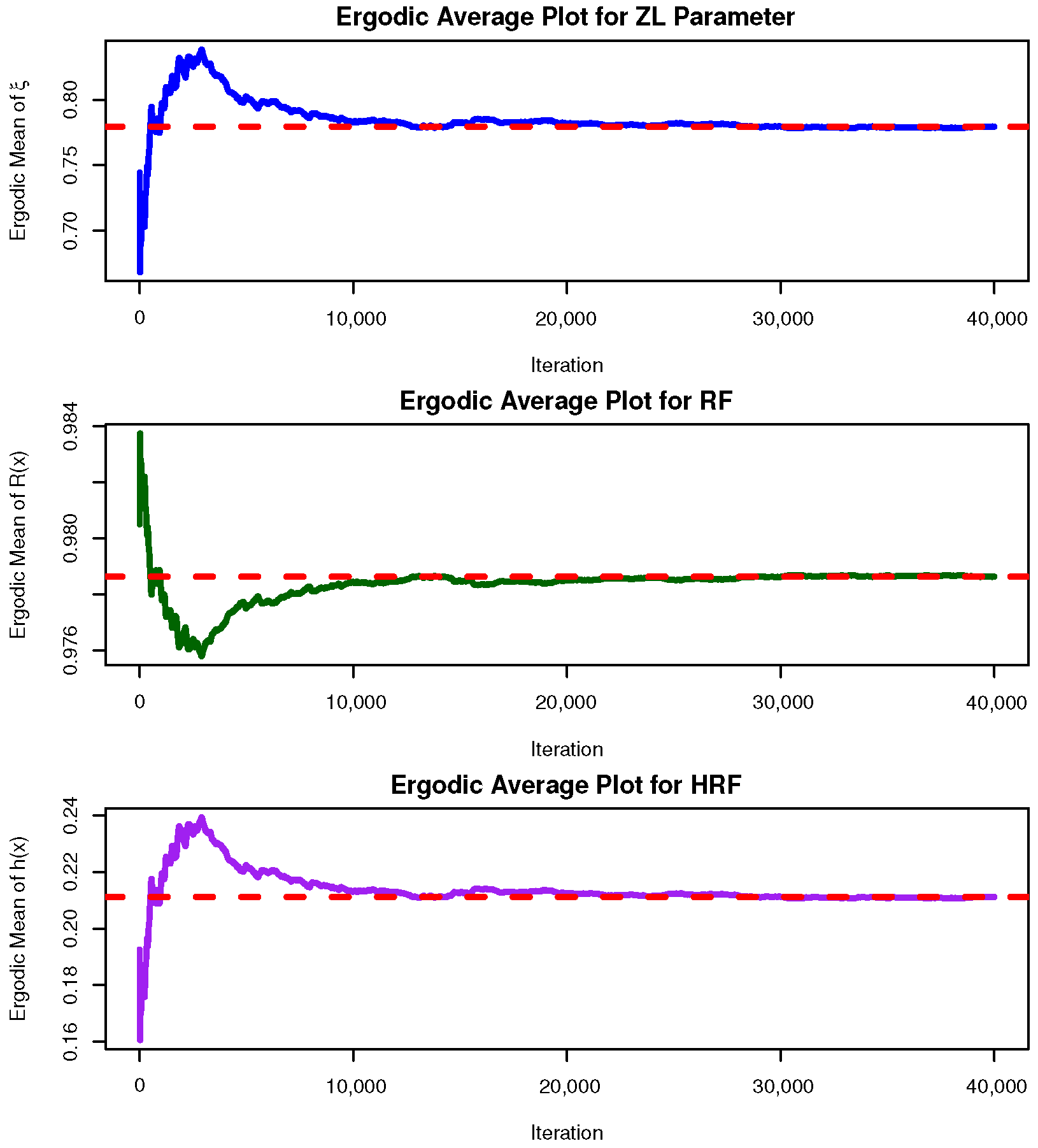
does not follow any known continuous law, yet resembles a normal distribution as illustrated in
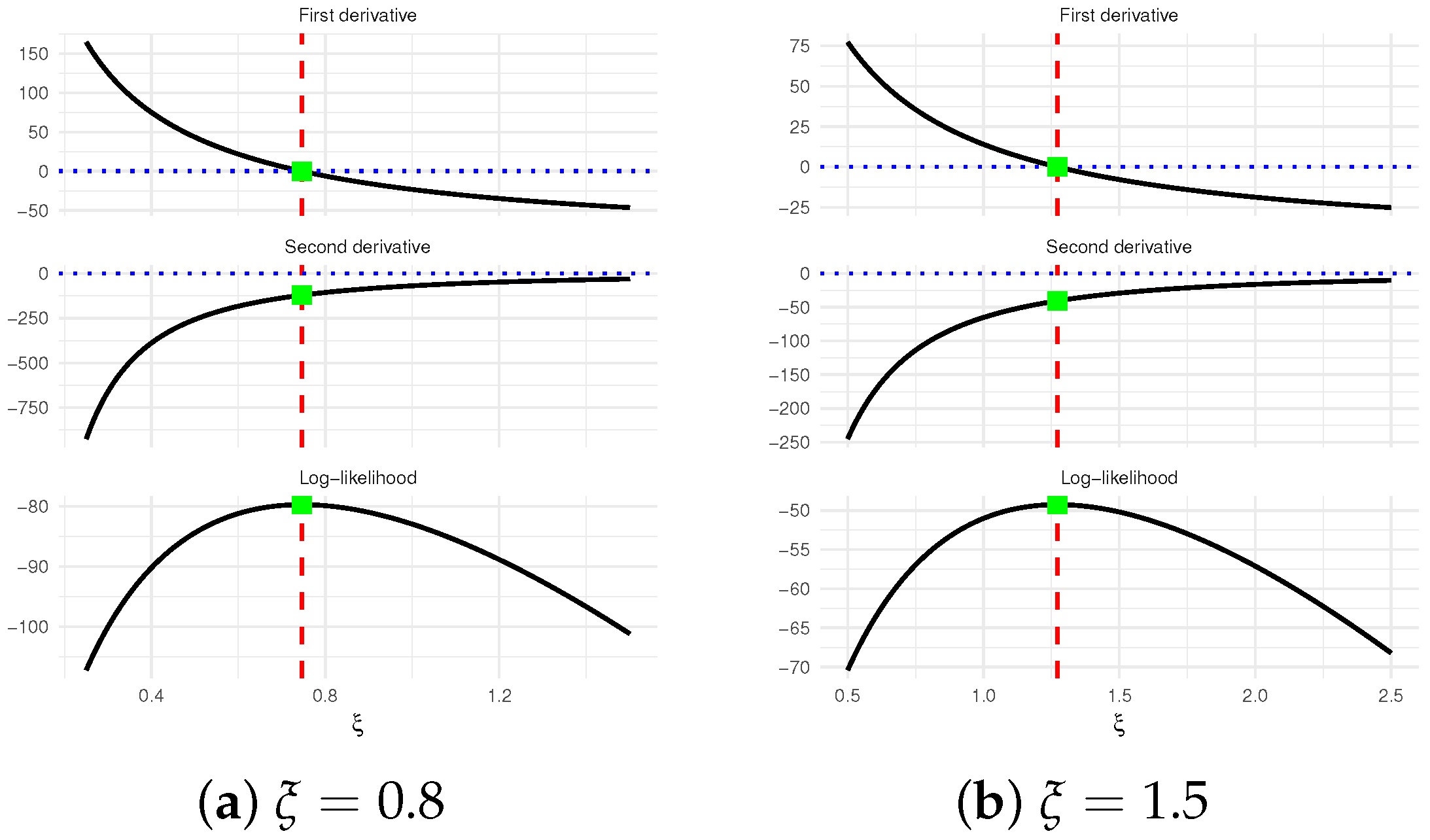
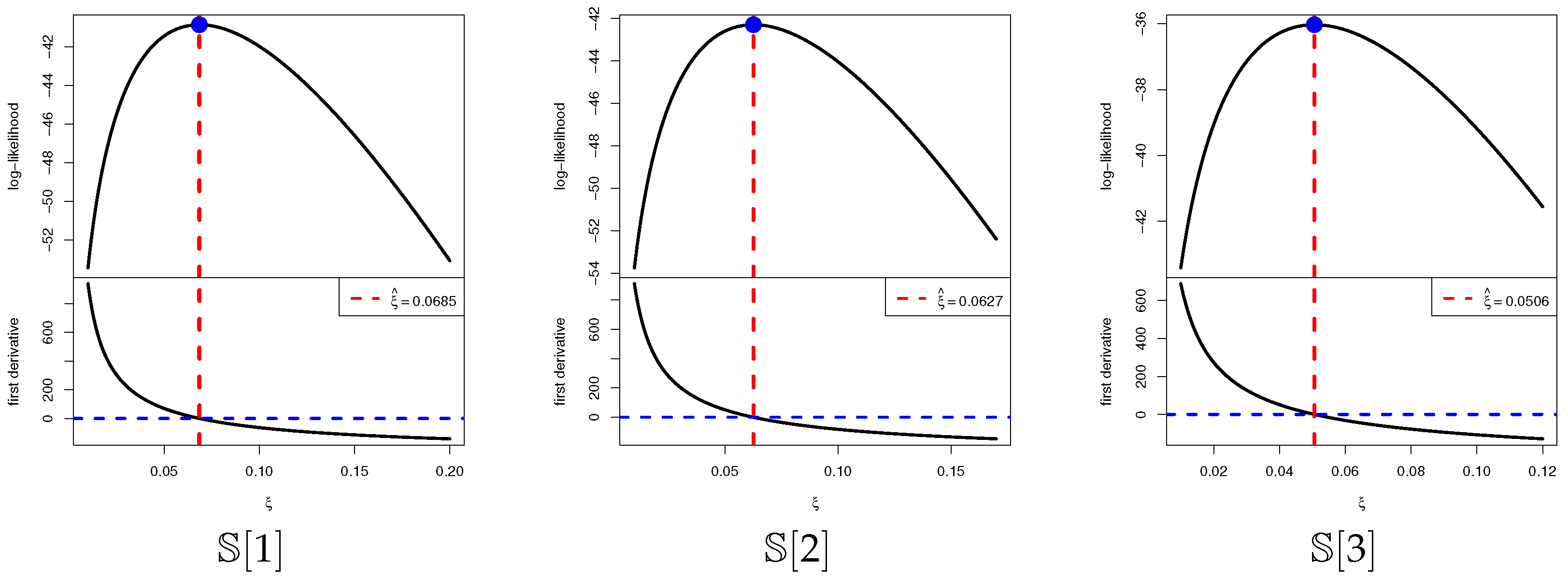
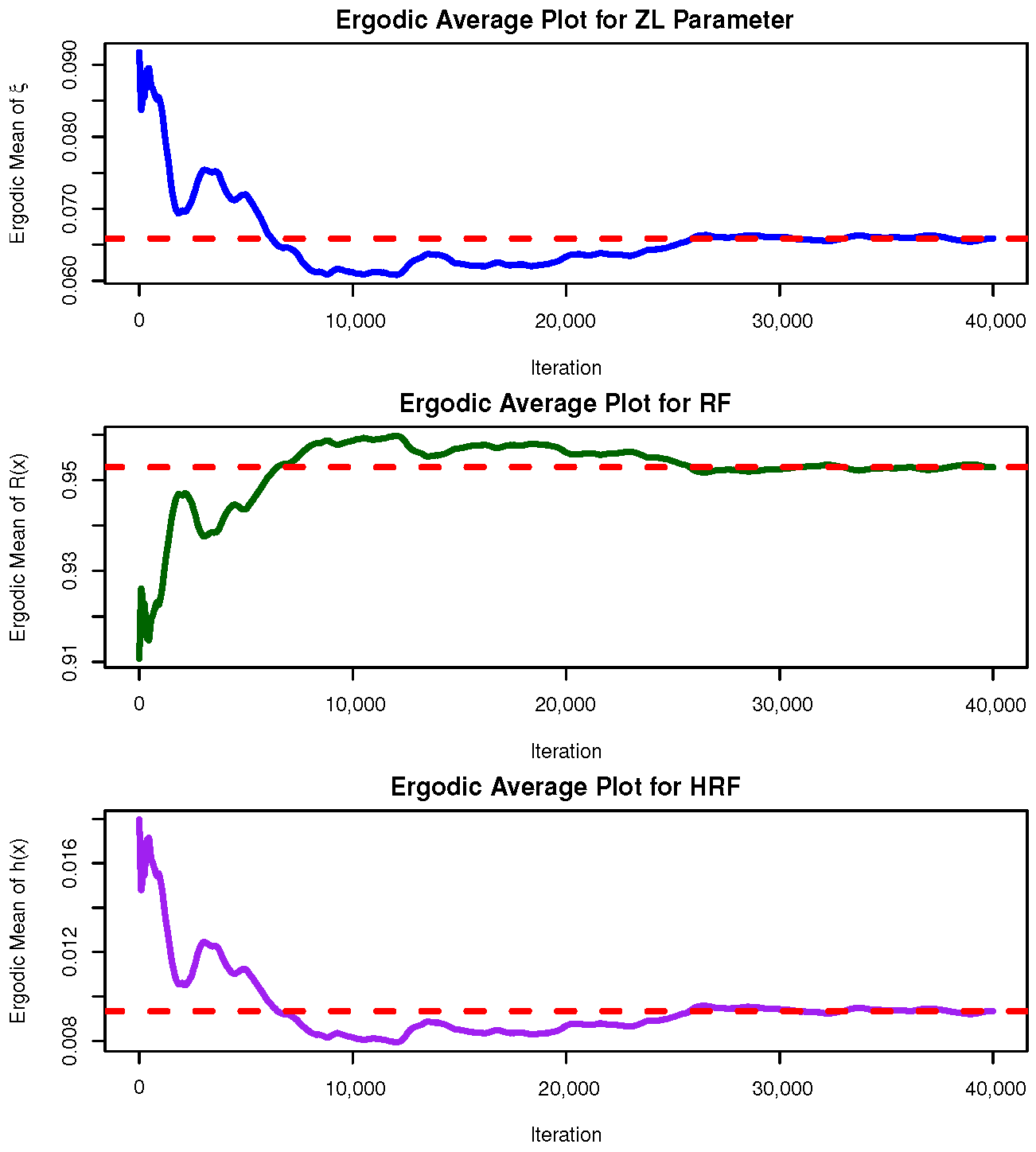
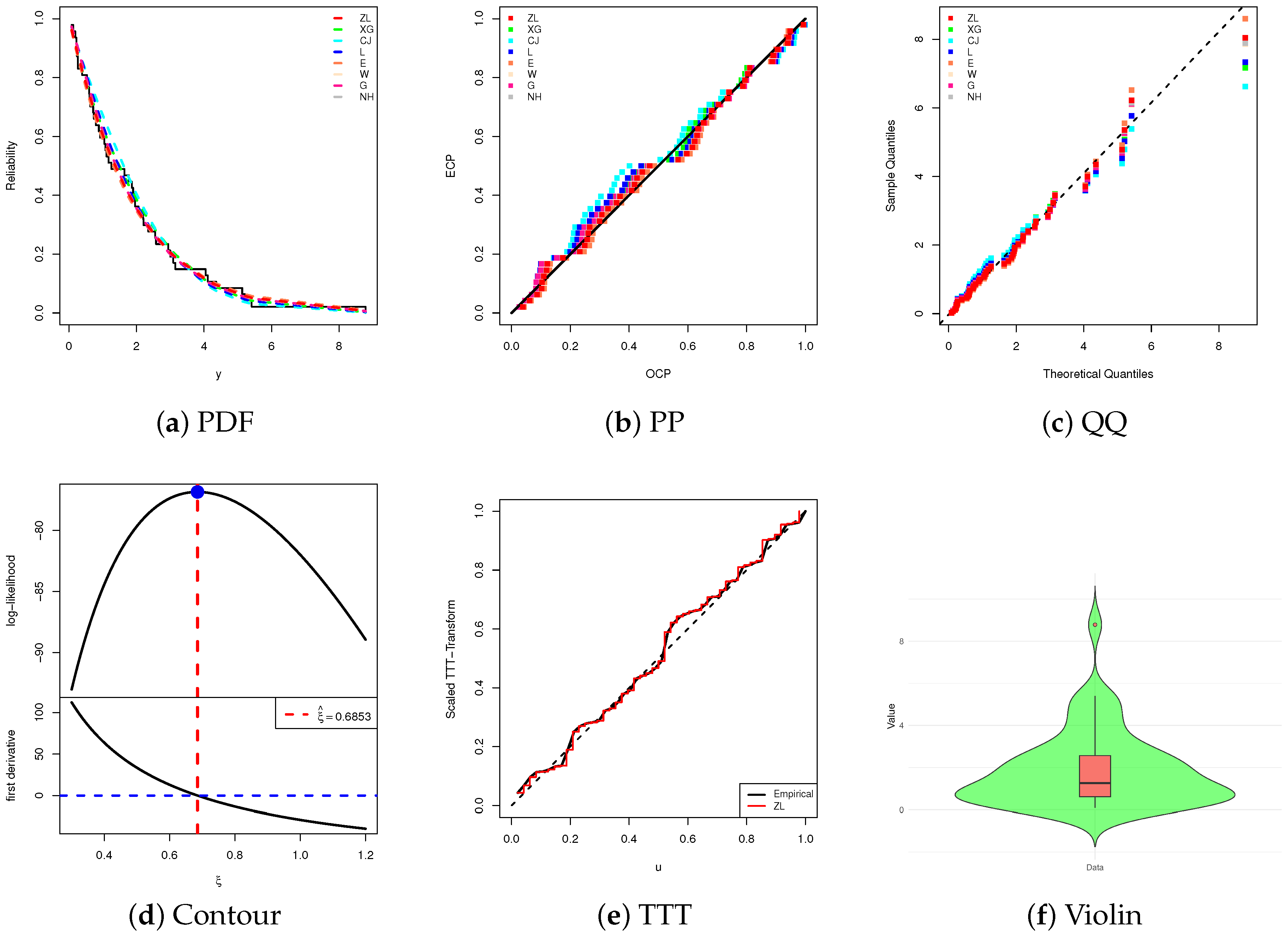
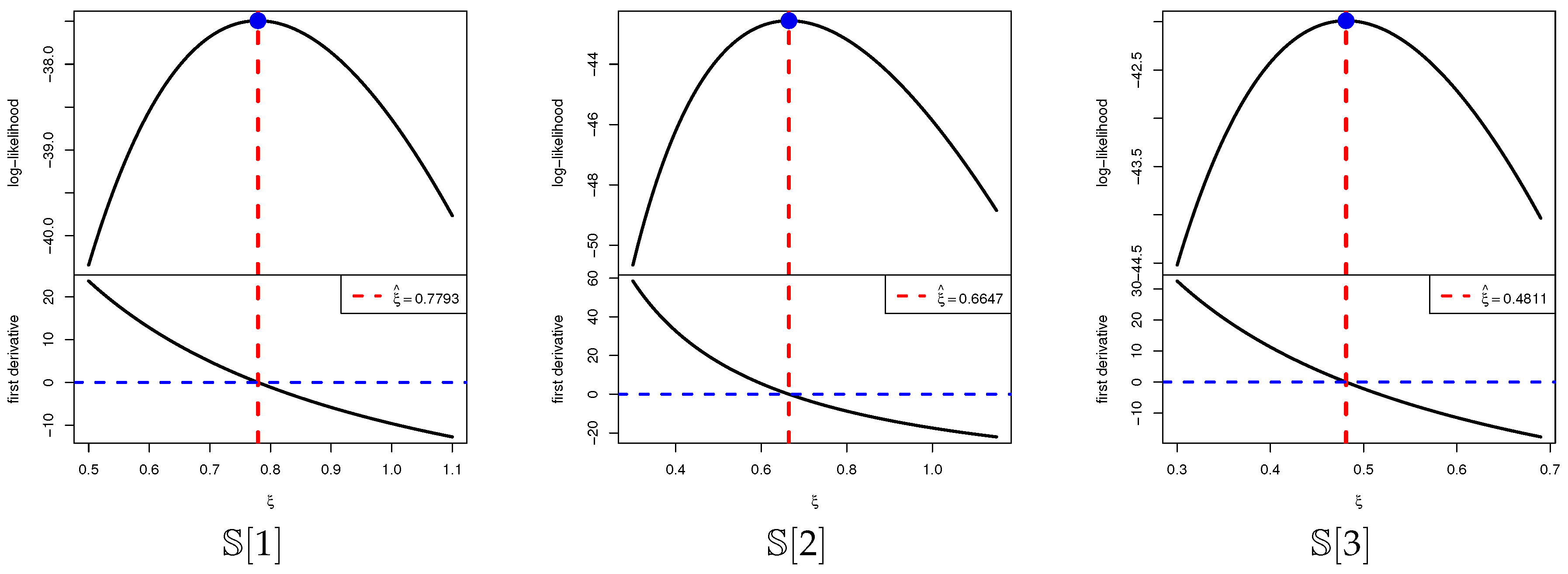
Figure 2, the Metropolis–Hastings (M-H) algorithm is adopted to update the posterior draws of
(see Algorithm 1). The resulting samples are then employed to evaluate Bayes estimates of
,
, and
as well as their corresponding uncertainty measures.
| Algorithm 1 The MCMC Steps for Sampling , , and |
- 1:
Input: Initial estimate , estimated variance , total iterations ð, burn-in , confidence level - 2:
Output: Posterior mean , BCI and HPD intervals of - 3:
Put - 4:
Put - 5:
while
do - 6:
Generate - 7:
Compute - 8:
Generate - 9:
if then - 10:
Put - 11:
else - 12:
Put - 13:
end if - 14:
Update and using in ( 3) and ( 4) - 15:
Increment - 16:
end while - 17:
Discard the first samples as burn-in - 18:
Define - 19:
Compute - 20:
Sort for in ascending order - 21:
Compute the BCI of as: - 22:
Compute the HPD interval of as:
where is the index that minimizes: - 23:
Redo Steps 19–22 for and
|
4. Monte Carlo Evaluations
To evaluate the accuracy and practical performance of the estimators of
,
, and
derived earlier, a series of Monte Carlo simulations were carried out. Using Algorithm 2, the T2I-APC procedure was replicated 1000 times for each of the parameter settings
and
, yielding estimates of all quantities of interest. At the fixed time point
, the corresponding reliability measures are obtained as
for
and
for
. Additional simulations were performed under varying conditions defined by the threshold parameters
, the total sample size
n, the effective sample size
r, and the censoring pattern
. In particular, we considered
,
, and
.
Table 2 summarizes, for each choice of
n, the corresponding values of
r along with their associated T2-PC schemes
. For ease of presentation, a notation such as
indicates that five units are withdrawn at each of the first two censoring stages.
| Algorithm 2 Simulation of T2I-APC Sample. |
- 1:
Input: Values of n, r, , and . - 2:
Set the true parameter value of the ZL() distribution. - 3:
Generate r independent random variables . - 4:
for to r do - 5:
Compute . - 6:
end for - 7:
for to r do - 8:
Compute . - 9:
end for - 10:
for to r do - 11:
Compute . - 12:
end for - 13:
Observe failures at time . - 14:
Remove observations for . - 15:
Set truncated sample size as . - 16:
Simulate order statistics from the truncated distribution with PDF - 17:
if
then - 18:
Case 1: Stop the test at . - 19:
else if
then - 20:
Case 2: Stop the test at . - 21:
else if
then - 22:
Case 3: Stop the test at . - 23:
end if
|
Once 1000 T2I-APC datasets are generated, the frequentist estimates along with their corresponding 95% asymptotic confidence intervals (ACI-NA and ACI-NL) for
,
, and
are obtained using the
maxLik package (Henningsen and Toomet [
13]) in the
R environment (version 4.2.2).
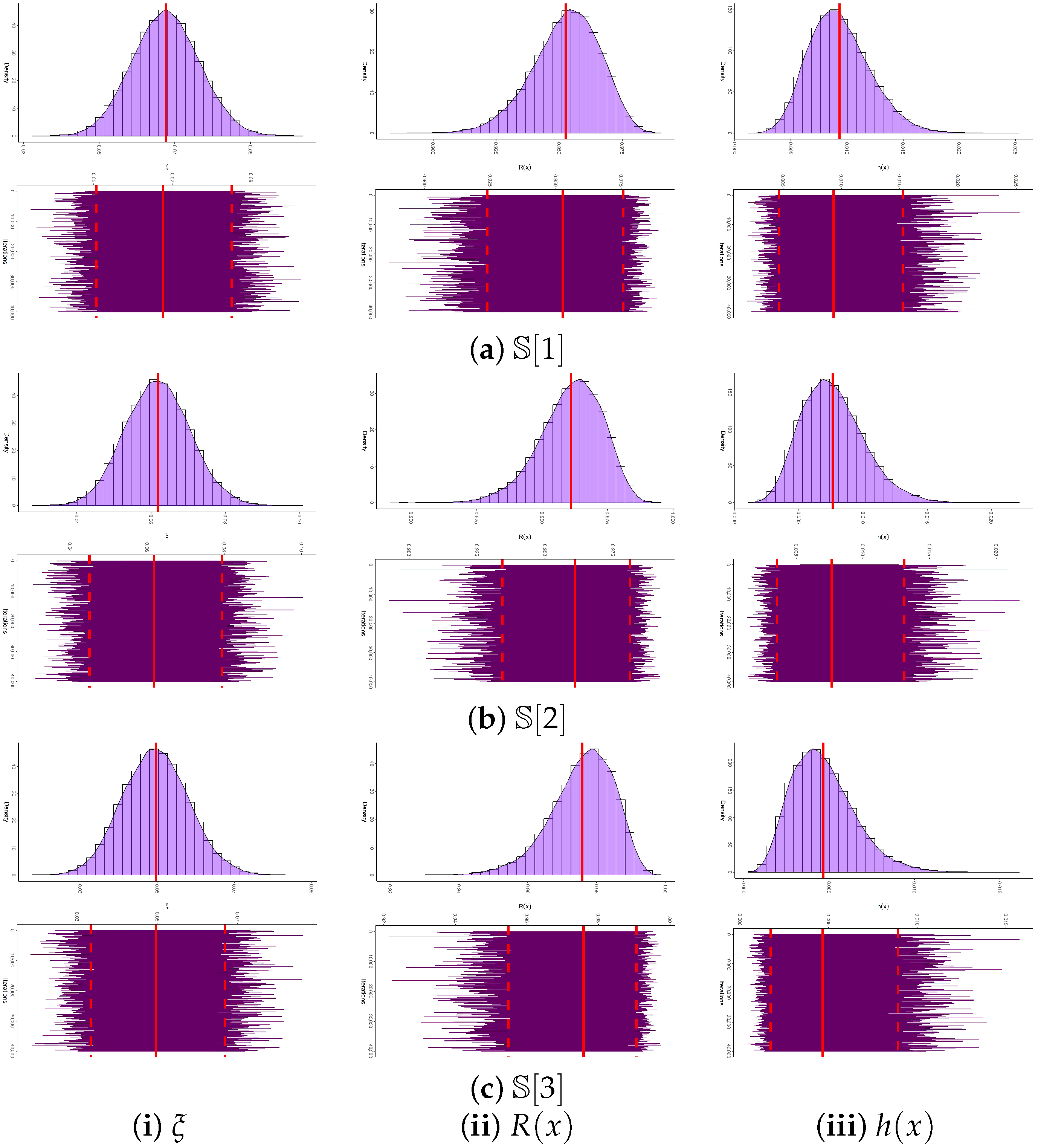
For the Bayesian analysis, we generate
MCMC samples, discarding the first
iterations as burn-in. The Bayesian posterior estimates, together with their 95% BCI/HPD intervals for
,
, and
, are computed using the coda package (Plummer et al. [
14]) in the same R environment.
To further assess the sensitivity of the proposed Bayesian estimation procedures, two distinct sets of hyperparameters
were examined. Following the prior elicitation strategy of Kundu [
15], the hyperparameters of the gamma prior distribution were specified as follows: Prior-A =
and Prior-B =
for
, and Prior-A =
and Prior-B =
for
. The hyperparameter values of
and
for the ZL parameter
were selected such that the resulting prior means corresponded to plausible values of
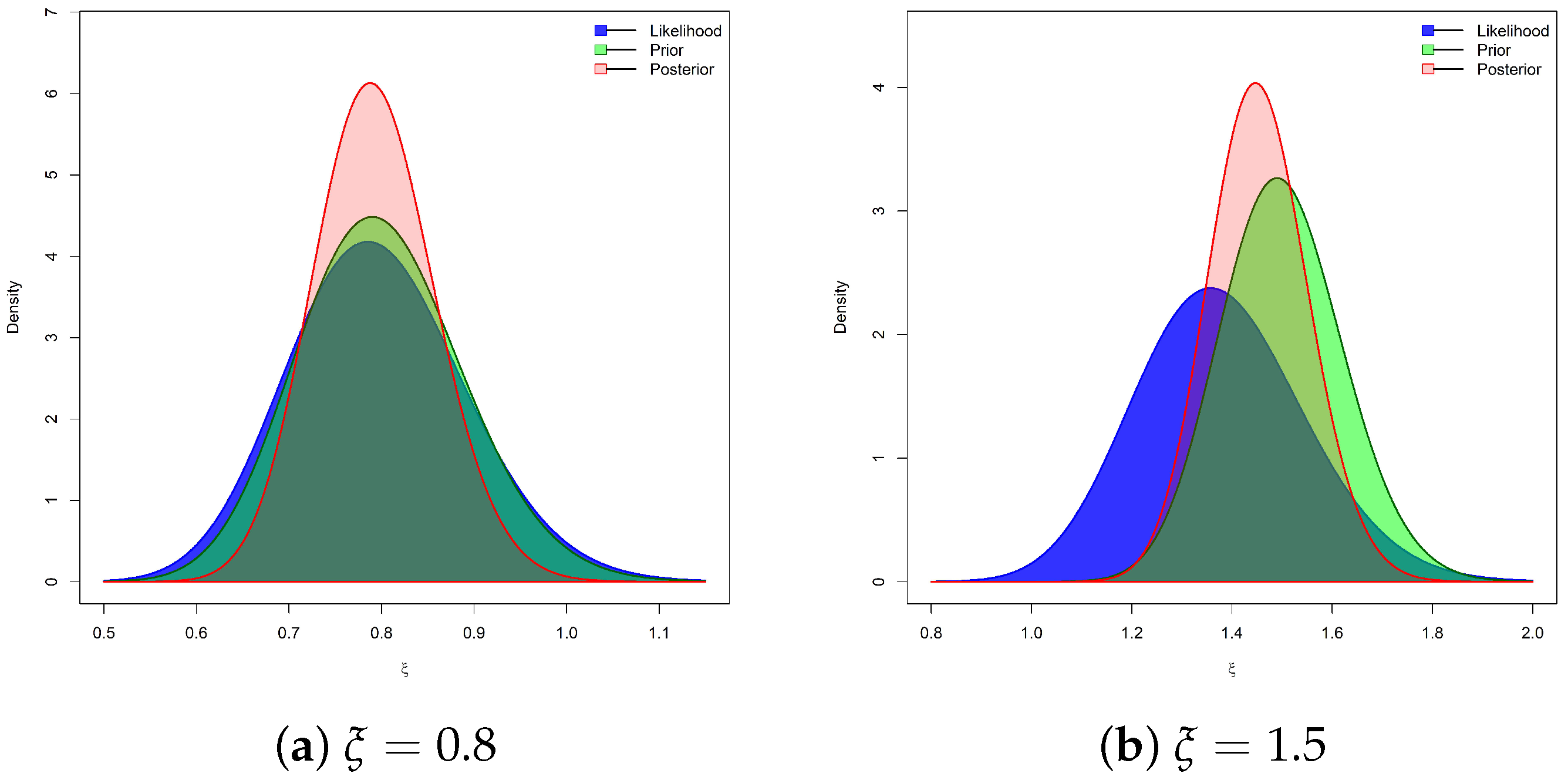
. Notably, Prior-A represents a diffuse prior with larger variance, reflecting minimal prior information, whereas Prior-B corresponds to a more concentrated prior informed by empirical knowledge of the ZLindley model’s scale range. Simulation evidence revealed that, although both priors produced consistent posterior means, Prior-B yielded smaller posterior variances, narrower HPD intervals, and improved coverage probabilities, highlighting the stabilizing influence of informative priors without introducing substantial bias.
To evaluate the performance of the ZL parameter estimators of , , and , we compute the following summary metrics:
Mean Point Estimate:
Root Mean Squared Error:
Average Relative Absolute Bias:
Average Interval Length:
Coverage Probability: where denotes the ith point estimate of and is the indicator function. The same precision metrics are also applied to the estimates of and .
Across all simulation scenarios, the estimation of , , and performs satisfactorily.
Estimation accuracy improves as either n (or r) increases, with similar gains achieved when the total number of removals decreases.
Higher threshold values () yield more precise parameter estimates. Specifically, the RMSEs, ARABs, and AILs decrease, while CPs increase.
As increases:
- -
RMSEs of , , and rise;
- -
ARABs of and decreased, whereas that of increased;
- -
AILs grow for all parameters, with corresponding CPs narrowed down.
Bayesian estimates obtained via MCMC, together with their credible intervals, exhibit greater robustness than frequentist counterparts due to the incorporation of informative priors.
For all tested values of , the Bayesian estimator under Prior-B consistently outperforms alternative approaches, benefiting from the smaller prior variance relative to Prior-A. A parallel advantage is observed when comparing Bayesian intervals (BCI and HPD) to asymptotic ones (ACI-NA and ACI-NL).
A comparative assessment of the proposed designs of
in
Table 2, for each set of
n and
r, reveals that:
- -
Estimates of achieve superior accuracy based on Ci (for ), i.e., right censored sampling;
- -
Estimates of achieve superior accuracy based on Bi (for ), i.e., middle censored sampling;
- -
Estimates of achieve superior accuracy based on Ai (for ), i.e., left censored sampling.
Regarding interval estimation strategies:
- -
ACI-NA outperforms ACI-NL for and , whereas ACI-NL is more suitable for ;
- -
HPD intervals are uniformly superior to BCIs;
- -
Overall, Bayesian interval estimators (BCI and HPD) dominate their asymptotic counterparts (ACI-NA and ACI-NL).
As a conclusion, for reliability practitioners, the ZL lifetime model is most effectively analyzed within a Bayesian framework, leveraging MCMC methods—particularly the Metropolis–Hastings algorithm.
6. Concluding Remarks
This study has advanced the reliability analysis of the ZLindley distribution by embedding it within the improved adaptive progressive Type-II censoring framework. Methodologically, both classical and Bayesian estimation procedures were developed for the model parameters, reliability, and hazard functions. Asymptotic and log-transformed confidence intervals, along with Bayesian credible and highest posterior density intervals, were derived to provide robust inferential tools. The incorporation of MCMC techniques, particularly the Metropolis–Hastings algorithm, ensured accurate Bayesian inference and highlighted the practical benefits of prior information. Through extensive Monte Carlo simulations, the proposed inferential methods were systematically evaluated. The findings confirmed that estimation accuracy improves with larger sample sizes, fewer removals, and higher censoring thresholds. Moreover, Bayesian estimators under informative priors consistently outperformed their frequentist counterparts, and HPD intervals dominated alternative interval estimators in terms of coverage and precision. Importantly, the comparative assessment of censoring schemes demonstrated that left, middle, and right censoring each provide superior accuracy depending on the parameter of interest, offering guidance for practitioners in reliability testing. The practical utility of the proposed methodology was demonstrated through two diverse real-life applications: Leukemia remission times and River Styx flood peaks. In both datasets, the ZLindley distribution outperformed a range of established lifetime models, as confirmed by goodness-of-fit measures, model selection criteria, and graphical diagnostics. These applications validate the model’s flexibility in accommodating both biomedical and environmental reliability data, thereby broadening its applicability in clinical and physical domains. The ZLindley model inherently exhibits a monotonically increasing hazard rate, a behavior commonly associated with ageing or wear-out mechanisms in reliability analysis. This property makes the model suitable for processes where the risk of failure intensifies over time, such as medical survival data under cumulative treatment exposure or environmental stress models like flood levels. However, in systems characterized by early-life failures or mixed failure mechanisms, more flexible distributions such as the exponentiated Weibull, generalized Lindley, or Kumaraswamy–Lindley may provide improved adaptability. Future work could extend the ZLindley framework by introducing an additional shape parameter to capture non-monotonic hazard patterns, thereby broadening its range of applicability. In summary, the contributions of this work are threefold: (i) the integration of the ZLindley distribution with an improved censoring design that ensures efficient and cost-effective testing, (ii) the development of a comprehensive inferential framework combining likelihood-based and Bayesian approaches, and (iii) the demonstration of practical superiority through simulation studies and real data analysis. Collectively, these findings underscore the potential of the ZLindley distribution, under improved adaptive censoring, as a powerful model for modern reliability and survival analysis. Future research may explore its extension to competing risks, accelerated life testing, and regression-based reliability modeling.