Bayesian Network Applications in Decision Support Systems

Abstract

Decision support systems are designed to provide decision makers with a view of the present and the future under alternative scenarios. A decision support system is different from a dashboard application representing current conditions and trends using a set of indicators and descriptive statistics. This paper focuses on decision support systems implementing Bayesian networks, with three case studies presenting applications in different areas. The first case study is about the integration of mobility data available from Google with hospitalization data related to COVID-19. This data from the pandemic era provides an impact assessment of non-pharmaceutical interventions such as the closure of airports. A second case study is from a website usability assessment with data from web surfing characteristics. A third application is a conflict resolution politography application where economic, demographic, and other types of data are analyzed to create a data-driven narrative for decision makers and researchers. These three different examples show how Bayesian networks are used in different contexts to support decision support systems. The paper is about decision support systems and Bayesian networks, with examples of implementation. It begins with an introduction to general decision support systems, then case studies, and concludes with a section describing future research pathways.

1. Introduction to Decision Support Systems

Decision support systems combine data with visualization methods and analytics to support decision making. A related platform is known as a situation room or war room, which is a dedicated space designed to enable teams to collaborate in order to solve complex problems and make critical decisions. Such rooms are often set up during emergencies and crisis management events. Decision support systems are also used more routinely than situation rooms. Examples of the application of such systems include industrial processes, customer service centers, and health care systems.

Keen [1], Sprague [2], and Bonczek et al. [3] consider decision support systems as data-driven systems for use by managers. This covers a range of definitions determined by strategies for development, usage, and implementation. The development and operation of a decision support system can involve a management information system (MIS) manager, who manages the process of developing and installing it; an information or data science specialist, who builds it; and/or system designers, who create and assemble the technology on which these systems are based.

Decision support systems integrate data from different sources and decision-making models. For a modern approach to model-based system engineering (MBSE), see Hanke et al. [4]. Decision support systems are systems with system engineering principles being applied to them. Here, we consider decision support systems as data-driven systems delivering a current view and providing the ability to evaluate the impact of alternative scenarios. This combination of data and analytic capabilities aims to support decision makers and researchers in the formulation of policies and decisions.

The next three sections cover case studies that include (i) the management of the COVID-19 pandemic, (ii) the operation of a website through usability indicators, and (iii) studies of conflict resolution situations for designing policies and strategies. In all three case studies, the decision support system provides a rendering of current conditions and of “what-if” evaluations that enable the assessment of alternative scenarios. Implementations of such decision support systems typically start with a prototype followed by adaptations to users’ changing demands. A management approach that implements this is called agile development. This consists of short cycles of development driven by the delivery of specific functionalities called “sprints” and evaluations at the end of each cycle called “scrums”, like in rugby. For more on agile development, see Kenett et al. [5]. Here, we focus on the functionality of decision support systems with a special emphasis on applications of Bayesian networks.

This paper does not introduce Bayesian network theory, but shows examples of their application. References that include details on Bayesian networks are Pearl [6], Kenett [7,8,9], Pearl and Mackenzie [10], Zhang and Kim [11], and Scutari and Denis [12]. The next three sections are self-contained case studies of decision support system applications. We start with a decision support system used in managing pandemic outbreaks.

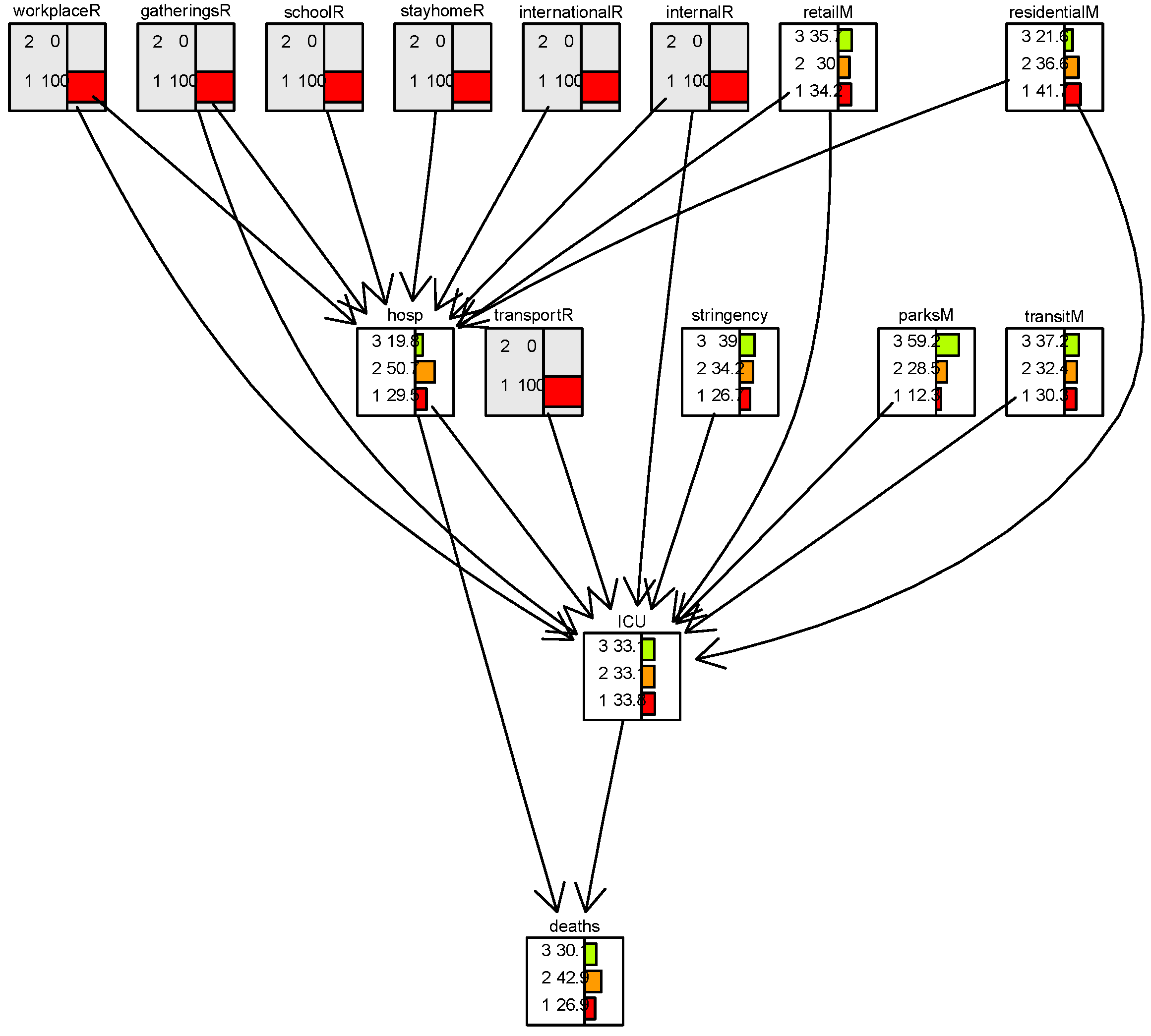
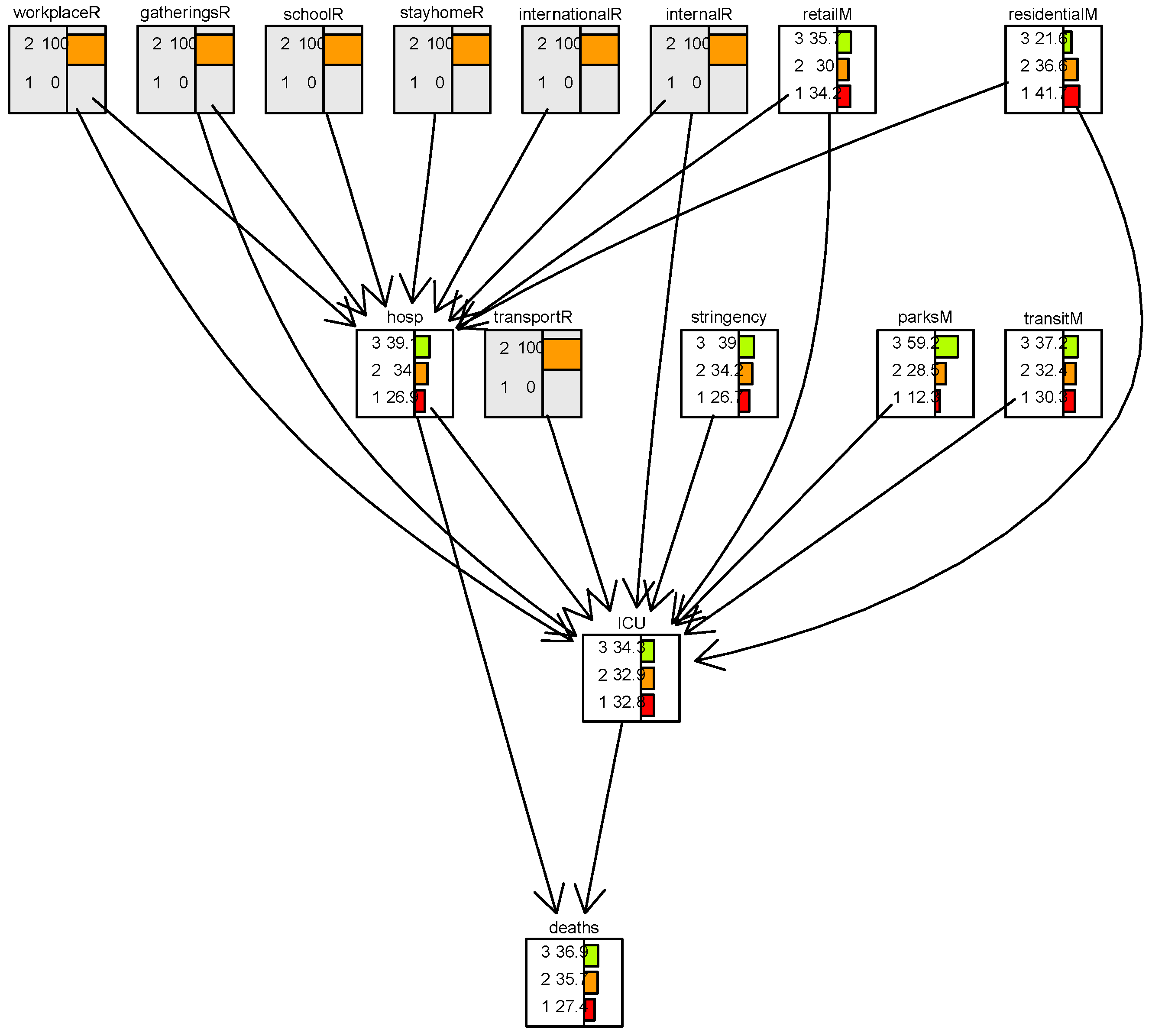
2. The COVID-19 Case Study

The COVID-19 pandemic had far-reaching consequences on global, national, and local scales. Managing the pandemic was based on national policies that included movement restrictions (such as lockdowns) and massive testing to detect outbreaks. An important factor in handling pandemic effects is population behavior and public cooperation with health authorities’ instructions. Adherence to Ministry of Health instructions—e.g., wearing face masks, maintaining physical distance, and washing hands—is affected by psycho-social aspects such as trust in policy makers, fear and anxiety, and the quality of risk communication.

With the ongoing waves of the pandemic around the world, efforts to model population behavior were instigated to shed light on social processes that impact compliance with such instructions, as well as to reveal social patterns and trends over time. The decision support system described below was part of this effort, which included an integration of health-related data from hospitals with population mobility data captured by Google mobility indicators.

COVID-19 pandemic management policies were based on national and local lockdowns including the closure of air traffic hubs, education institutions, and economic sectors. Citizens were called to adhere to protection measures, such as maintaining physical distance, practicing hygiene measures, and using face masks. Government-applied policies of lockdowns and re-openings were decided according to the perceived “acceptable loss”. Such decisions were based on identifying a balance between running the economy and minimizing economic and social damage versus the need to save lives. As expected, the easing of lockdowns frequently led to increases in morbidity. At the same time, lockdowns and quarantines caused severe damage in terms of social and economic considerations with increased rates of domestic violence, unemployment, depression, and non-normative behavior (alcohol drinking and drugs), among others. The decision support system presented in Kenett et al. [13] was designed to answer specific questions by an assessment of the impact of lockdowns on hospital admissions and COVID-19-related deaths.

Research has shown that citizens’ compliance with stay-at-home policies is predicted by perceived risks and trust in science, scientists, the authorities (Bargain and Aminjonov [14]), and social capital (Borgonovi and Andrieu [15]). Restricted mobility directives (such as the closure of airports, shopping malls, sport events, and education institutions) were found to effectively prevent outbreaks and reduce the number of deaths. Furthermore, research found that citizens voluntarily decreased their mobility even without official instructions to stay at home (Yilmazkuday [16]). This theoretical understanding needed to be quantified in specific areas with the modeling of relevant data.

The pandemic management decision support system presented in Kenett et al. [13] was designed and implemented by integrating hospital data from ministries of health in Israel and Italy with Google mobility data that was available during the pandemic (https://www.google.com/covid19/mobility/, accessed on 20 October 2024).

To set up the decision support system, a database of health and mobility data was organized for each country with appropriate time lags. The data-driven learning of Bayesian network structures is possible with various algorithms (He et al. [17]). Here, a Hill-climbing algorithm was applied to the data in order to derive a Bayesian network structure accounting for whitelists and blacklists.

The learning algorithm was applied to the number of hospitalized COVID patients, the number of COVID-19 related deaths, and mobility data in various setups such as workplaces, shopping centers, and public transportation utilities. A structural equation model of the learned network was used to test the significance of links between variables. Structural equation models, also called path analysis, are often used in social sciences to represent links between observed and latent variables. As a next step, a Bayesian network of statistically significant effects was constructed. Through conditioning on this Bayesian network, one can assess alternative scenarios corresponding to non-pharmaceutical interventions (NPIs) such as restricting access to parks or airports. Figure 1 is a scenario from the COVID-19 study based on data from Israel when all of the NPI restrictions are set to state = 1 (close), and Figure 2 is a scenario from the COVID-19 study when all of the NPI restrictions are set to state = 2 (open). The figures are adapted from Kenett et al. [13]. The analysis shows the impact of non-pharmaceutical interventions in Israel on the number of patients admitted to hospital intensive care units (ICUs) and COVID-19-related deaths.

Figure 1 and Figure 2 show the distributions of discretized data representing mobility and COVID-19 health-related data. The discretization was carried out separately for Israel and Italy to reflect the different country-specific decision threshold guidelines. The arrows in the figures correspond to links between these discretized variables. Comparing Figure 1, with full restrictions, to Figure 2, with no restrictions, we see by how much the distribution of hosp and death changes. In particular, the percentage of level 3 (high number) increases in hosp from 19% to 39% and of death from 30% to 36%. The Bayesian network provides an analysis of scenarios with and without enforcing (or lifting) mobility restrictions, thus supporting decisions made by decision makers.

Kenett et al. [13] show how this combination of structural equation models and Bayesian networks sets up a decision support system for pandemic management. Conditioning on variables in this network enables a quantitative analysis of alternative scenarios. Figure 1 and Figure 2 are examples of a decision support system with interactive functionality. This case study also demonstrates the ability of Bayesian networks to integrate data from different sources and evaluate alternative scenarios. Bayesian networks also provide an effective visual rendering: see, for example, the bnlearn R application Scutari [18] or the GeNIe software (https://www.bayesfusion.com/genie/, accessed on 20 October 2024). The next case study is about a decision support system used in managing the usability of websites.

3. The Website Usability Case Study

This section presents a decision support system used in managing the usability of a website, the decision support system for user interface design (DSUID). For more details, see Harel et al. [19]. A DSUID includes an analytic method based on the integration of models for estimating and analyzing website visitors’ activities. It consists of a seven-layer model with a Bayesian network applied to clickstream data.

The goal of usability design diagnostics is to identify, for each website page, design deficiencies that hamper the user navigation experience. To understand the user experience, we need to know the user activity and the user expectations. The diagnosis of design deficiency involves measurements of the site navigation, statistical calculations and statistical decisions.

How can we tell whether website visitors encounter difficulties in exploring a particular page, and if so, what kind of difficulty do they experience? Website visitors are usually task-driven, but we do not know whether the visitors’ goals are related to a specific web page. We also usually cannot tell whether visitors know anything a priori about the site, if they believe that the site is relevant to their goals, or if they have visited it before. It may be that the visitors are simply exploring the site, or that they are following a procedure to accomplish a task. Yet, their behavior reflects their perceptions of the site content. Server logs provide time stamps for all hits, including those of page html text files, but also of image files and scripts used for the page display. The time stamps of the additional files enable us to estimate three important time intervals:

  i.

The time the visitors wait until the beginning of the file download. This is used as a measure of page responsiveness.

 ii.

The download time. This is used as a measure of page performance.

iii.

The time from download completion to the visitor’s request for the next page. This is a time stamp of when the visitor reads the page content, but also does other things, some of them unrelated to the page content.

The DSUID needs to decide, based on the statistics of these time intervals, whether the visitors feel comfortable during website navigation, for instance, if they feel that they waited too long for the page to download and how they feel about what they see on webpage screen.

We want to determine whether a time interval is acceptable by page visit, i.e., whether it is too short or too long. For example, consider an average page download time of 5 s. If the user expects the page to load quickly, site visitors may regard it as too lengthy in response to a search request. However, 5 s may be acceptable if the user’s goal is to learn or explore specific information. Same 5 s, different goal-driven experience.

Diagnostic-oriented time analysis observes the correlation between the page download time and page exits. If visitors are indifferent about the download time, then the page exit rate will be invariant with respect to the page download time. However, if the download time matters, then the page exit rate depends on this download time. When the page download time is acceptable, most visitors stay on the site, looking for additional information. When the download time is too long, more visitors abandon the site and go to other websites. The longer the download time, the higher the exit rate. In operating a DSUID, one distinguishes between three status conditions:

• Design—At this state, data is collected and analyzed. System architects and designers develop guidelines and operating procedures representing accumulated knowledge and experience on preventing operational failures. A prototype DSUID is then developed.
• Testing—the prototype DSUID is subjected to beta testing. This is repeated when new website versions are launched for evaluating the way they are actually being used.
• Tracking—ongoing DSUID tracking systems are required to handle changing operational patterns. Statistical process control (SPC) is employed to monitor the user experience by comparing actual results to expected results, acting on the gaps.

In setting up a DSUID, we identify several layers of data collection and data analytics:

• The first and lowest layer—user activity. This layer records significant user actions (involving screen changes or server-side processing).
• The second layer—page hit attributes. This layer consists of download time, processing time, and user response time.
• The third layer—transition analysis. The third-layer data are about transitions and repeated form submission (indicative of visitors’ difficulties in form filling).
• The fourth layer—user problem indicator identification. Indicators of possible navigational difficulty, including (a) predicted estimates for site exit by the time elapsed until the next user action (as no exit indication is recorded on the server log file), (b) backward navigation, and (c) transitions to main pages, interpreted as escaping the current sub task.
• The fifth layer—usage data. This consists of usage statistics, such as the following:
  • Average entry time;
  • Average download time;
  • Average time between repeated form submission;
  • Average time on website (indicating content related behavior);
  • Average time on a previous screen (indicating ease of link finding).
• The sixth layer—statistical decision. For each of the page attributes, DSUID compares the data over the exceptional page views to those over all page views. The null hypothesis is that (for each attribute) the statistics of both samples are the same. A simple two-tailed t test can be used to reject it, and therefore to conclude that certain page attributes are potentially problematic. A typical error level is set to 5%.
• The seventh and top layer—interpretation. For each of the page attributes, DSUID provides a list of possible reasons for the difference between the statistics over the exceptional navigation patterns and that over all of the page hits. Typically, the usability analyst decides which of the potential source of visitors’ difficulties is applicable to the particular deficiency.

Bayesian networks are used in the 4–7th layers of a DSUID system. Figure 3 and Figure 4, prepared with GeNIe 2.0, present Bayesian networks derived from the analysis of web log analyzers. The networks indicate associations between page size, text size, download time, reading time, seek time, reading time, back activations, and exits.

With low seek time (Figure 3), we see 49% of high (s4) and very high exit rates (s5). With high seek time (Figure 4), these numbers jump to 96% so that seek time affects the behavior of the users.

This case study introduces a seven-layer architecture used to design a decision support system aimed at tracking the usability of websites. The characteristics of DSUID can be generalized to other applications such as industrial process management where online data from sensors is used to manage processes. For a more general introduction and a state-of-the-art review of dashboards used in web usability, see Almasi et al. [20].

4. The Political Conflict Resolution Case Study

Politography refers to an analysis of how nations, states, or any political entities interact in relation to each other. In specific projects, it consists of a data-driven tool describing, measuring, and evaluating the level of control between political entities over particular territories or domains. This context is primarily empirical and analytic, aiming to inform political decision-making about current and project changes in loci of control. A more general perspective applies politography to regional conflicts and is classified as a conflict resolution or conflict management tool. Here, we consider politography as a decision support system.

Below, we describe the design and construction of a politography decision support system for policy makers related to intergroup conflict management, focused on the Israeli–Palestinian conflict. It provides a case study that can be generalized to other applications. The decision support system developed in this case study has over 9000 indicators pertaining to geographical areas labeled A, B, and C according to the Oslo Accords. These designated areas have distinct legal status specified in the 1993 Oslo Accords. A second level of the decision support system hierarchy consists of three domains that characterize levels of control in each one of the geographic areas: security, geo-spatial, and economic. In addition, the system contains contextual data from different sources such as political, diplomatic, social, and legal domains. For more details on this case study, see Arieli et al. [21].

In developing a politography decision support system, the main methodological challenges include the following:

(i)  

Integrating data from different sources and in different update timings and units;

(ii) 

Defining composite indicators that provide unified views;

(iii)

Tracking and modeling trends at various levels of the system hierarchy;

(iv)

Analyzing alternative scenarios for supporting decision makers.

The methodology applied in designing and implementing the politography decision support system involves four parts: (i) Map, (ii) Construct, (iii) Identify, and (iv) Analyze.

I.  

Map: Mapping categorizes factors into economic, security, and geo-spatial (demographic) domains. In this phase, experts determine indicators reflecting domains of control by geographical area. A methodology for supporting this part is the Goals–Question–Metrics (GQM) approach presented in Van Solingen et al. [22]. The GQM steps are to (1) generate a set of goals, (2) derive a set of questions relating to the goals, and (3) develop a set of metrics needed to answer the questions. Data can be viewed using dynamic graphs with the ability to zoom in on any individual indicator and by navigating the data hierarchy.

II. 

Construct: This stage involves developing an integrated database combining indicators from different domains, by year or by quarter. In this phase, research teams load data into a database and compute indices relative to a common annual baseline. The politography decision support system updates a configuration file with indicator names and identifies missing values and outliers. We determine data subsets for use in integration (by year or quarter) and conduct linkage analysis to obtain integrated data.

III.

Identify: Here, trends are identified in individual indicators and composite indicators and relative control levels are computed by year and by entity over one of the predetermined territories listed above. For trend analysis, we compute composite indicators by domain using the median. Bar charts, trend charts, and variable cluster analysis are used to identify the most representative cluster indicator. In addition, domains are combined to compute an overall trend with a composite indicator. The method applied to define composite indicators is to compute individual indicators relative to a base year and then using the yearly median across indicators. To derive the combined composite indicators for each indicator, Yi(x), we define a desirability function di(Yi), which assigns numbers between 0 and 1 to the values of Yi. The value di(Yi) = 0 represents an undesirable value of Yi and di(Yi) = 1 represents a desirable or ideal value. The individual desirabilities are then combined to an overall desirability index using the geometric mean of the individual desirabilities:

Overall Desirability Function = [(d₁(Y₁) x d₂(Y₂))x … d_k(Y_k))]^1/k

where k denotes the number of indicators. Notice that if any response Y_i is completely undesirable (d_i(Y_i) = 0), then the overall desirability is zero. To account for this “zero control,” we apply an additional step that mitigates such cases and the desirability function is used as a composite indicator based on individual indicators. The final composite indicators are plotted on a Y by X graph, with four triangular quadrants. Each triangle represents a different combination of Israeli and PA control levels. For more on desirability functions, see Derringer and Suich [23].

IV.

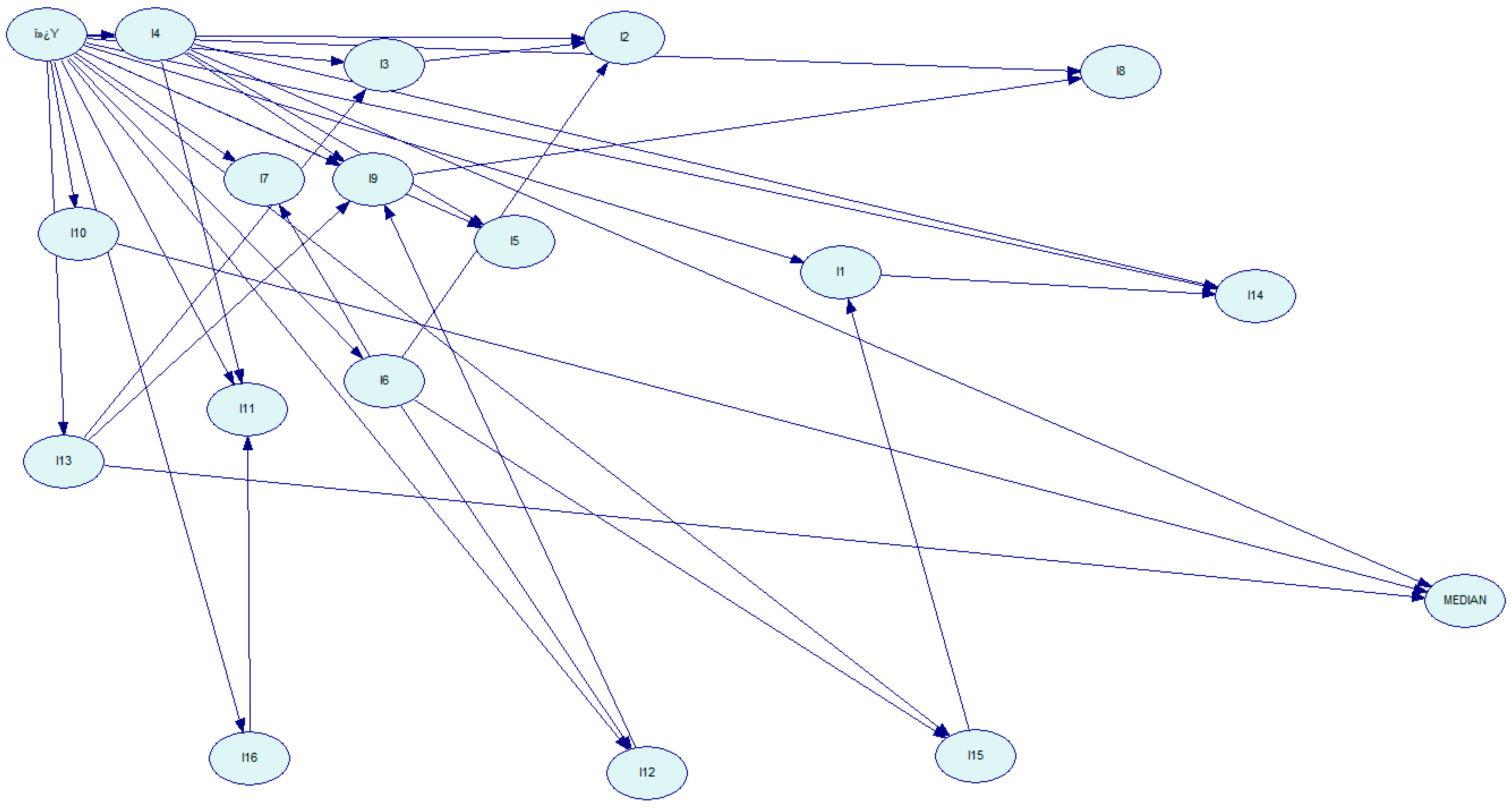
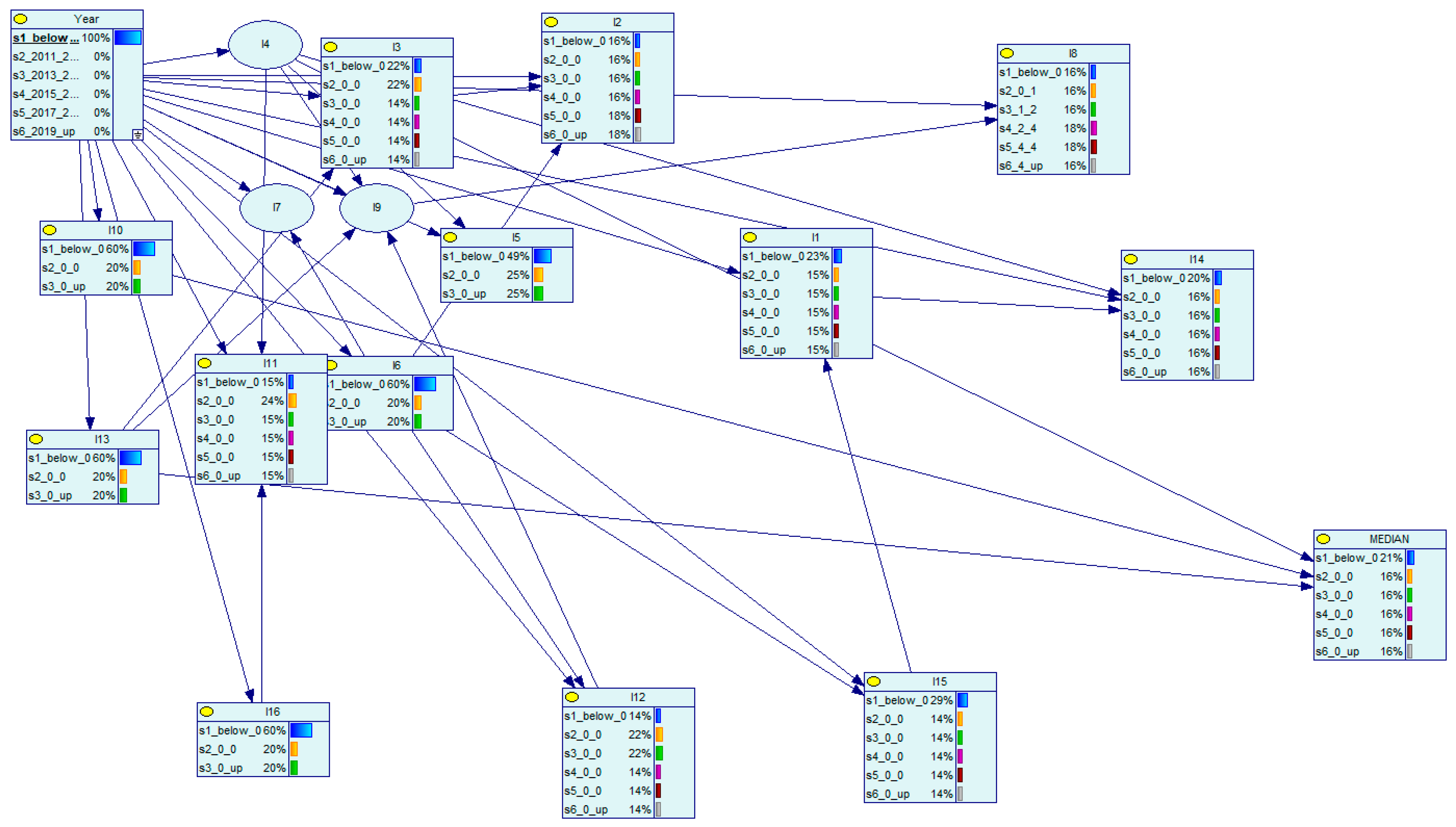
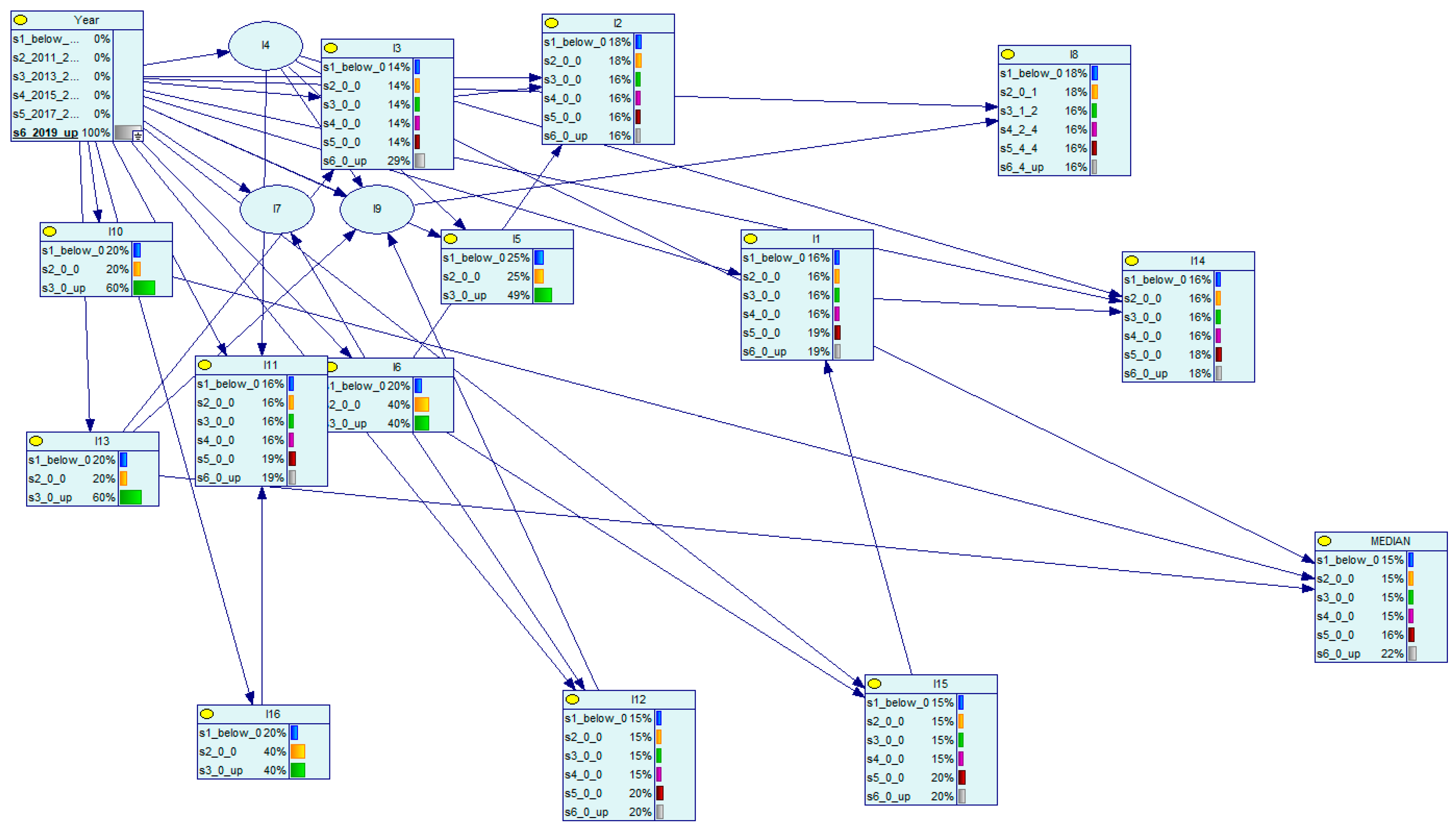
Analyze: Scenarios are analyzed by determining the list and contribution of indicators affecting target indicators. Here, we apply Bayesian network analysis in order to understand the links between indicators from the same or different domains, and how changes in the level of one indicator influence the other indicators. This provides the ability to run what-if scenarios to assist policymakers in making informed decisions that account for the consequences of policy decisions. Below, we demonstrate an application of Bayesian networks to a subset of 18 indicators labeled I1–I16 over 12 years (2010–2021). The data analyzed is calibrated to the year 2022 as the baseline. The last column, labeled MEDIAN, is the median of the row used as a composite indicator representing the specific year. We first discretized the data and the indicator data was classified into three groups of equal width.

From this data, we can derive a directed acyclic graph, as shown in Figure 5.

In Figure 6, we show the network, conditioned on the year 2010 and, in Figure 7, the data is conditioned on years above 2019. In Figure 6, we see that indicator I10 is, with a probability of 60%, in the lowest category and in Figure 7, 9 years later, this probability drops to 20%.

These model-driven estimates provide probabilistic statements to changes over time. This Bayesian network analysis provides the decision support system with an ability to consider future-looking alternative scenarios.

5. Discussion and Future Research Pathways

As mentioned in the Introduction, decision support systems use multivariate data to provide a status report in specific contexts. Bayesian networks can be used to link multiple variables and, by conditioning the network, evaluate the impact of specific decisions. The situation rooms and war rooms mentioned in the Introduction were initially designed to provide a reflection of reality such as a combat zone. Decision support systems with Bayesian networks take this a step further.

With modern sensor technology, powerful computing, advanced analytics, and flexible systems, we are seeing the ubiquitous development of digital twins that consist of digital assets in parallel to physical assets (see Kenett and Bortman [24]). Digital assets are designed and implemented to provide monitoring, diagnostic, prognostic, and prescriptive capabilities supporting the performance of systems. Digital twins have been implemented in a wide range of domains including health care, energy management, and social ecosystems (see Elkefi and Asan [25], and Yossef Ravid and Aharon-Gutman [26]).

The scope of Bayesian network applications has been extended to veterinary epidemiology, maternal health, and road safety. For papers that introduce methodological developments in additive Bayesian networks, see [27,28].

A more general perspective is to consider developments in analytics in the context of decision support systems. The exponential interest in artificial intelligence and data science has forced some rethinking on the role and integration of statistics and analytics, especially with big or massive datasets (see Ruggeri et al. [29]).

An additional direction with significant impact is the widespread interest in large language models (LLMs) and related prompt engineering methodologies. These LLM-generative pre-trained transformers can operate on data obtained from open media and publications or specific corpora of documents like Google notebookLM (https://notebooklm.google/, accessed on 20 October 2024) or deep research (https://openai.com/index/introducing-deep-research/, accessed on 20 October 2024). Properly integrating LLMs into decision support systems remains a challenge.

The paper covers three case studies where Bayesian networks were applied in the context of decision support systems. The case studies are from epidemiology, website engineering, and political science. They cover completely different domains and show different methodologies of design and implementation. A comprehensive approach to such initiatives is needed and requires future research covering both applied and theoretical developments. Such developments in decision support systems can impact the future of civic societies as envisaged over 120 years ago (Geddes [30]).