Leveraging Max-Pooling Aggregation and Enhanced Entity Embeddings for Few-Shot Knowledge Graph Completion

Abstract

Few-shot knowledge graph (KG) completion is challenged by the dynamic and long-tail nature of real-world KGs, where only a handful of relation-specific triples are available for each new relation. Existing methods often over-rely on neighbor information and use sequential LSTM aggregators that impose an inappropriate order bias on inherently unordered triples. To address these limitations, we propose a lightweight yet principled framework that (1) enhances entity representations by explicitly integrating intrinsic (self) features with attention-aggregated neighbor context, and (2) introduces a permutation-invariant max-pooling aggregator to replace the LSTM-based reference set encoder. This design faithfully respects the set-based nature of triples while preserving critical entity semantics. Extensive experiments on the standard few-shot KG completion benchmarks NELL-One and Wiki-One demonstrate that our method consistently outperforms strong baselines, including non-LSTM models such as MetaR, and delivers robust gains across multiple evaluation metrics. These results show that carefully tailored, task-aligned refinements can achieve significant improvements without increasing model complexity.

1. Introduction

With the development of Internet technology, various electronic devices have been rapidly popularized, resulting in a large amount of data. Extracting useful knowledge from vast amounts of data is extremely important and necessary. Knowledge graph just has this function, which can extract structured knowledge from massive texts and images. At present, many large-scale KGs in the real world have also been constructed, such as Freebase [1], DBpedia [2], NELL [3], YAGO [4], and Wikidata [5]. Because of its structural characteristics, KG is widely used in a variety of downstream applications, such as recommendation system [6,7], semantic search [8], information extraction [9], machine reading [10], affective cognition [11] and intelligent dialogue system [12].

The KGs [2] consist of a large number of facts, that is, the triplet composed of (head entity, relation, and tail entity) is called a fact. Although a KG contains a great number of facts, it is mostly constructed manually, so it is highly incomplete. For example, 71% of people in Freebase have no known place of birth, and 75 % have no known nationality [13]. Measures need to be taken to complete these missing information. The task of knowledge graph completion is to automatically fill in missing facts in the KG, so as to make the KG contain as many facts as possible, so as to improve the quality of the existing KG. A lot of research work has been carried out [14,15,16,17,18]. The previous work mainly focused on using a large number of facts to train models. However, recent research work shows that when studying the well-known large-scale KGs, a large number of relations in the KGs have long-tailed distribution [19] and only contain few triples. In other words, there is insufficient training samples for model training. For instance, about 10% of relations in Wikidata has no more than 10 triples [5]. In addition, most KGs of the real world are usually dynamic [20]. That is, events happen at every time, and the triples of these events may be added to the constructed KGs. Due to these newly added relations, there are fewer triples as training examples for large-scale sample training.

The existence of the above situations makes the previous large-scale completion models unable to play with good performance or no longer suitable, which promotes the emergence of few-shot knowledge graph completion methods. Xiong et al. [21] first researched on few-shot learning for KGs and proposed a GMatching model that only relies on entity embeddings and one-hop graph structures. The main purpose of this model is to learn a matching metric based on one-shot reference triplets to discover triples with more similar relations. Chen et al. [22] leveraged a model-agnostic meta-learning method (MAML) [23] for fast adaptation of policy network parameters or relation meta. This model utilizes relation meta and gradient meta modules to transfer relation-specific meta information, enabling the model to learn more important knowledge and learn faster. Zhang et al. [24] proposed a few-shot relation learning model, FSRL. This model adds the module of aggregating reference set information based on the LSTM method, which plays a certain role in the expression capabilities of the relation. Niu et al. [25] proposed a gated and attentive neighbor aggregator to capture the most valuable semantics of a few-shot relation. It also incorporated MAML with TransH [26] to conduct a few-shot knowledge graph completion (FKGC) module which can deal with complex relations. However, the above models ignored the information of the entity itself in the entity neighbor representation, or did not have a good aggregation reference set using a similar LSTM time series method.

However, two key challenges remain, as follows:

• Incomplete representation of entities: Prior models, such as FSRL and GMatching, focus mainly on neighborhood aggregation and tend to overlook the intrinsic semantic features of entities themselves, leading to biased representations in sparse settings.
• Inappropriate sequential bias: LSTM-based reference set aggregators assume an order over triples that are, by nature, unordered, introducing unnecessary inductive bias and potentially degrading generalization.

To solve the above problems, we propose a few-shot relation learning model with max-pooling aggregator and enhanced entity embeddings. The purpose of this model is to learn a matching function that can effectively infer the predicted entity pairs according to the given few-shot reference set entity pairs for each relation. Firstly, we propose a relation-aware heterogeneous neighbor encoder to learn entity embedding according to heterogeneous graph architecture, attention mechanisms, and entity own information. It can not only represent entities through neighbors with different relations, but also retain entity own information. Next, we use a max-pooling aggregator to aggregate the reference set entity pairs and enhance the expression capabilities of the relation. Compared with LSTM aggregator, this aggregator is more suitable for the characteristics of triplet disorder, and can give better play to the performance of this method. Finally, based on the aggregated embeddings of the reference set entity pairs, the matching network is used to discover similar reference set entity pairs.

In summary, the main contributions of this work are listed as follows:

• We propose a novel few-shot knowledge graph completion model that creatively designs the max-pooling aggregator module to improve the expression capabilities of relations from the few-shot triples, which is obviously different from the common-used LSTM aggregator module in [24];
• We propose an enhanced entity embedding module to enrich the head/tail entity embeddings according to the corresponding neighbor entities, and the learned entity embeddings still retain their own entity formation;
• We design a max-pooling aggregator module to aggregate the critical relation embeddings using the reference set, which significantly enhances the expression capabilities of relation and obtains satisfactory experimental performance.

The remainder of this paper is organized as follows. Section 2 introduces some related work. We describe problem formulation in Section 3. The methodlogy is introduced in Section 4. Section 5 presents the experimental results. Finally, we conclude this paper in Section 6.

2. Related Work

In this section, we introduce some related work on embedding models for relational learning and few-shot knowledge graph completion.

2.1. Embedding Models for Relational Learning

An embedding model is one of the important methods to solve the problem of knowledge graph completion. It maps the entities and relations in the knowledge graph to the continuous vector space through the embedding model, and learns the latent embedding of entities and relations in this space, so as to not only facilitate the calculation, but also retain the structural information in the knowledge graph.

In recent years, embedding models for relational learning have been widely studied and used to automatically complete the knowledge graph. For example, Nickels et al. [27] proposed the RESCAL model, which is one of the earliest models to build relations using tensor operations. This model considers the inherent structure of relational data and captures the binary relations between entities bilinearly. Bordes et al. [28] proposed a classical translation model TransE. This model treats the relation as a translation between the head entity and the tail entity. It hopes that the entity and relation meet the equation (head entity + relation ≈ tail entity), and measures rationality of triples by defining the scoring function based on distance difference by the translated relation. Zhen et al. [26] proposed TransH model. This model overcomes the limitations of TransE in dealing with complex relations. It maps the head and tail entities to the relation plane, and then uses the relation vector as the translation vector on the hyperplane of the relation to find the head and tail entities with specific relations. Lin et al. [29] proposed the TransR model on the basis of TransH. This model believes that if the semantic attributes of entities and relations are different, the embedding space of entities and relations should be different. That is, entities and relations should be embedded into different semantic spaces, and then the translation relations from head entity to tail entity are established based on the embedding space of relations. Ji et al. [30] proposed the TransD model, which overcomes the shortcomings of TransR by mapping the head entity and tail entity to the relation space with different matrixs. Yang et al. [31] proposed the DistMult model, which is a general network framework for multi-relational learning. This method can effectively extract logical rules by modeling the binary relations in the triples, and can learn the representation vectors of entities and relations from the bilinear method, and then use the learned semantic information to explore the latent logical rules. This method learns the vector representation of existing entities and relations, and then uses the representation vector to effectively infer whether the new triple is true. Trouillon et al. [32] proposed the ComplEx model, which is a method based on complex number representation. The ComplEx model performs representation learning in the complex space, and can effectively use bilinear abilities to represent asymmetric semantic relations. However, these embedding-based models usually require a large number of training samples. Due to the long-tail relations in the knowledge graph and the newly added relationships lacking sufficient training samples, these models are no longer suitable for these situations. In this paper, we propose a model that can solve these situations and achieve good results.

2.2. Multimodal Knowledge Graph Completion (MKGC)

MKGC [33] has attracted increasing attention due to the inherently multimodal nature of real-world knowledge. By integrating auxiliary information such as images and text, MKGC methods can effectively leverage inter-modal complementarity, thereby enhancing the representational capacity and reasoning performance of entities and relations. MKGC enhances structural knowledge by incorporating visual or textual information to assist in missing entity prediction tasks, thereby improving the accuracy of entity inference. Wang et al. [34] proposed an automated filtering mechanism designed to dynamically identify and attenuate unnecessary or redundant visual context information during model learning, thereby mitigating its potential negative impact on representation learning and reasoning outcomes. Chen et al. [35] introduced a hybrid Transformer architecture that unifies the input–output representation in the MKGC task, while enabling hierarchical fusion across coarse-grained and fine-grained levels. Zhao et al. [36] proposed an MKGC framework based on modality split representation learning and ensemble reasoning. The approach adopts relation embedding learning during training and modality independent inference during reasoning, thereby alleviating inter-modal interference and enabling dynamic modeling. Li et al. [37] further proposed a two stage cross-modal fusion mechanism, which achieves inter-modal complementarity while preserving modality-specific knowledge.

To enhance inductive reasoning over unseen entities in real world scenarios, some studies [38,39] attempt to learn embeddings for unseen entities by integrating structural neighbors from existing knowledge graphs. Subsequently, Chen et al. [40] constructed an open-book datastore that stores prompt-based instance representations and their corresponding relation labels as queryable key–value pairs, while Wang et al. [41] retrieved the k-nearest neighbor entity labels from the training set and incorporated their distribution into the model’s reasoning process to enhance entity recognition. Zhao et al. [33] leveraged a contrastive learning mechanism to model text–visual and text–text associations of query entity pairs within a unified representation space.

2.3. Few-Shot Knowledge Graph Completion

In previous research work, few-shot learning method is mainly used in the fields of computer vision [42] and imitation learning [43] fields. In recent years, this method has been extended to knowledge graph completion and some achievements have been made. The task of a few-shot knowledge graph has also gradually received more and more attention. Some models have been proposed, which are mainly divided into two categories:

(1) Metric-based approaches: Xiong et al. [21] first proposed the knowledge graph completion model GMatching based on few-shot learning. This model takes into account the long-tailed relations and the newly added relations. There are not many known triples that can be used for training, so they proposed a one-shot learning framework. A matching criterion is learned through the learned embedding and the entity’s one-hop graph neighbor framework. This matching criterion can discover more similar triples from the candidate set according to a given reference set triplet. Zhang et al. [24] extended the GMatching model and proposed the FSRL model. This model adds an information aggregator module of the reference set on the basis of the GMatching model. The information aggregator module enables the model to increase the expression capability of the relation on the original basis, and the application scenario has been expanded from the original one-shot learning to the few-shot learning scenario, and good results have been achieved.

(2) Meta-learner-based approaches: Meta learning aims to learn common experiences from different tasks, and then generalize these experiences to adapt to new tasks. Wang et al. [44] proposed a meta-learning framework, MeatR, which considers the few-shot learning problem of uncommon relationships and uncommon entities, and generates some additional triples by extracting key information from the text description, thereby solving the problem of insufficient training samples. Niu et al. [25] proposed a global and local framework to solve the problem of noisy neighbors and the inference of complex relations. The neighbor aggregator based on the gate and attention mechanisms is proposed, for the first time, to capture the valuable semantic information of few-shot relations, and, for the first time, MAML and TransH are combined to construct a few-shot knowledge graph completion model, which effectively solves the problem of inference of complex relations.

Although these methods have achieved certain results, there are still some problems in the above methods. They do not make full use of the entity’s own information or do not have a good aggregate reference set of information. The above problems are considered in our proposed model, and its effectiveness is proved by experiments.

3. Problem Formulation and Preliminaries

In this section, we, respectively, introduce the problem formulation, few-shot learning, and other necessary notations used in this paper.

A knowledge graph G is composed of a large number of triples (h, r, t), where h∈$ϵ$ represents the head entity, r∈R represents the connection relation, and t∈$ϵ$ represents the tail entity. Since the existing knowledge graphs are mostly constructed artificially, it is impossible to include all the relations and entities in the real world, so the knowledge graphs have incomplete characteristics. However, with the development of artificial intelligence technology, knowledge graphs have begun to be applied to various fields, playing an important auxiliary role. Therefore, how to use technical means to fill in missing triples in knowledge graph is extremely important. The completed knowledge graph can better play the auxiliary role. Therefore, the knowledge graph completion task has gradually gained attention and development. At present, most of knowledge graph completion tasks are mainly concentrated in the following two categories: (1) given head entity and relation in the triple (h, r, ?) to infer tail entity; (2) given head entity and tail entity in the triple (h, ?, t) to infer relation. This work mainly studies the former.

Definition 1 

(Background Knowledge Graph $G^{\prime }$). In the knowledge graph, we select the low-frequency relations with few triples from all relations as few-shot relations. At the same time, we take the triples of these low-frequency relations as the training set, testing set, and validation set, and the remaining high-frequency relation triples as the background knowledge graph $G^{\prime }$.

Definition 2 

(Few-Shot Knowledge Graph Completion). Given a relation r∈ R and its k-shot reference set triples, the purpose is to predict the missing tail entity t from the given candidate entities set C according to the constructed model. Specifically, all candidate set entities are scored and ranked for each new triplet with (h, r, $t_c$∈ C). Since the score of the true entity is higher than the score of the false candidate set entity, the confidence ranking of all the candidate set entities can be obtained. The top-ranked entities $t_c$ are the entities most likely to be established. Among them, the candidate set entities are constructed based on entity type constraint [45].

Next, we introduce the few-shot learning settings [46,47]. For the knowledge graph completion task in this paper, the purpose of few-shot learning is to enable the model to rank the triples composed of the candidate set entities as the tail entities according to the score function to calculate similarity scores when few-shot reference triples are given. Then, we predict the missing tail entity t from the given candidate entities set C. Following the standard few-shot learning settings, the dataset can be divided into meta-training set $T_{mtr}$, meta-validation set $T_{val}$, and meta-testing set $T_{mte}$. For each meta-training, meta-validation and meta-testing task, it corresponds to different relations in the knowledge graph G. For the meta-training set, each training task of relation r∈R has its own reference (training)/query (testing) entity pairs, denoted as $D_r$ = {$D_r^{ref}$, $D_r^{query}$}. Among them, $D_r^{ref}$ only contains few-shot entity pairs with relation r. The query set includes the head entity $h_i$, the ground-truth tail entities $t_i$, and the corresponding candidate set entities $t_c$∈C. According to the given few-shot reference set entity pairs and candidate set entities, the proposed model can calculate the score of the triple composed of each candidate entity based on the scoring function, and then rank them according to the scores to get the entities with high confidence.

After sufficient training in the meta-training stage, the obtained few-shot learning model can be used to predict the missing triples of each new relation task $r^{\prime }$∈$R^{\prime }$ in the meta-testing set. In the meta-testing stage, the relations $r^{\prime }$ do not appear in the meta training stage, that is, $R\cap R^{\prime }=⌀$. At this time, the model needs to have good generalization ability. Similar to the meta-training set, each relation $r^{\prime }$ in the meta test set also has its own reference set and query set.

In this paper, we define some notations, and the specific description meanings are shown in

Table 1. Notations.

Symbol	Description	Symbol	Description
h	A head entity	r	A relation of meta-training set
t	A tail entity	$ϵ$	A set of head/tail entities
R	A relation set of meta-training set	G	Knowledge graph
$G^{\prime }$	Background knowledge graph	C	A set of candidate entities
$T_{mtr}$	Meta-training set	$T_{val}$	Meta-validation set
$T_{mte}$	Meta-testing set	$D_r$	A training task of meta-training set
$D_r^{ref}$	A reference set of a task	$D_r^{query}$	A query set of a task
$t_c$	A candidate set entity	$r^{\prime }$	A relation of meta-testing set
$R^{\prime }$	A relation set of meta-testing set	${\mathbf{e}}_{h_{nei}}$	A head entity embedding with
$\sigma$	A activation function		neighbor information
${\mathbf{e}}_{r_i}$	The pre-trained embedding representations	${\mathbf{e}}_{t_i}$	The pre-trained embedding representations of
	the i-th neighbor relation $r_i$		the i-th neighbor tail entity $t_i$
$\alpha$	Attention value of each neighbor	$N_h$	The neighborhood of the head entity h
${\mathbf{U}}_1$	A learnable parameter	${\mathbf{W}}_{1-5}$	Learnable parameters
${\mathbf{b}}_{1-3}$	Learnable parameters	d	Pre-trained embedding dimension
k	The size of reference set	$Re{f}_k$	Reference set entity pairs with randomly
${\mathbf{R}}_k$	The embeddings of aggregated k-shot		sampled k-shot triples
	reference set entity pairs	$g_1$	Number of neurons in the first hidden
$g_2$	Number of neurons in the second hidden		layer
	layer	${\mathbf{Q}}_r$	A batch of query triples
ℏ	Hidden state of LSTM cell	c	Cell state of LSTM cell
$\gamma$	A margin distance	$scor{e}^{-}$	The similarity score of the negative query
$scor{e}^{+}$	The similarity scores of the positive query		set
	set	$\left|Q\right|$	The number of query set triples
$ran{k}_i$	The score sorting of the i-th query set triple	$\mathbb{I}(·)$	The indicator function
$\mathrm{MRR}$	The mean reciprocal rank of the correct	$\mathrm{Hits}$@n	The proportion of correct entities ranked
	entities		in the top n

.

4. The Proposed Model

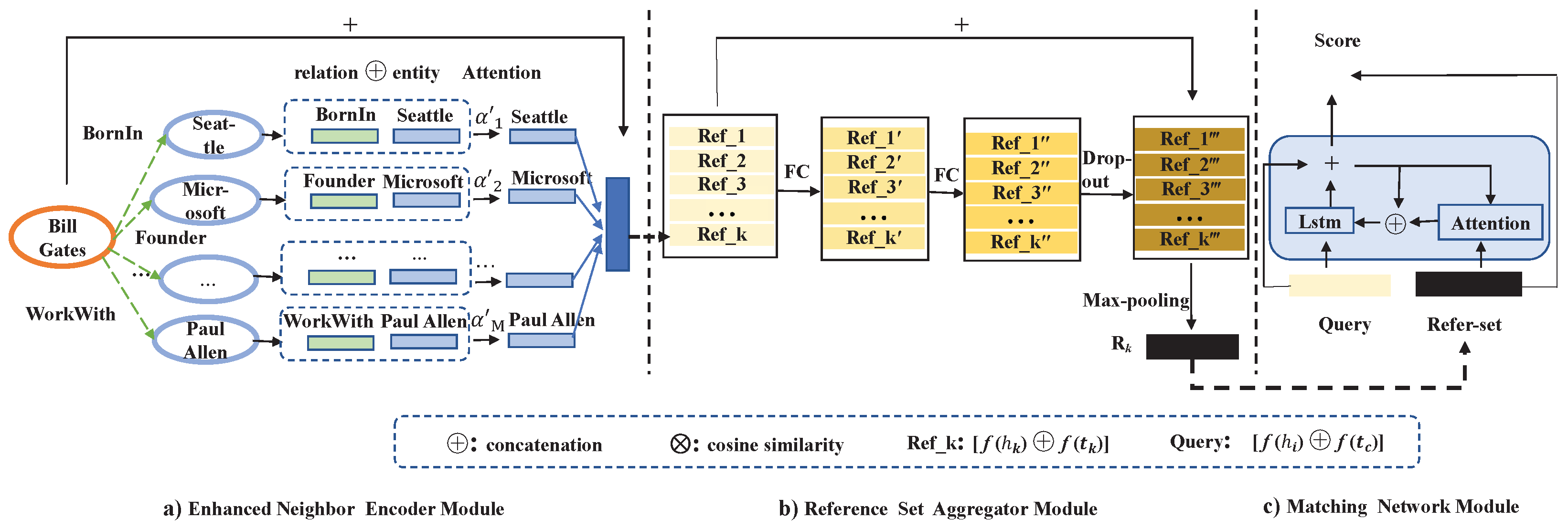
In this section, we introduce our model. An overview of our model is shown in Figure 1. The purpose of our model is to get the similarity between few-shot reference entity pairs and the query entity pairs by scoring function, so as to get a generalized metric function for the prediction of new relation triples. This model is mainly divided into three modules: (1) an encoder based on the entity neighbor information of the attention mechanism and combined with the entity’s own information; (2) the aggregator that learns the relation representation of the few-shot reference set based on the max-pooling method; (3) the matching processor that compares the query set with the aggregated reference set entities representation. More details of each module are listed as follows.

4.1. Enhanced Entity Encoder

The purpose of this module is to use the neighbor information connected to the entity in the knowledge graph and the entity’s own information to better represent the entity.

There have been some works [21,24,27,31] that use the relational information of entities in the knowledge graph to learn the entity embeddings information, but they mainly focus on the simple use of neighbor information. For example, Xiong et al. [21] proposed that the graph local structure uses the average feature representation of neighbors. However, it ignores that different neighbors may have different effects on their entity representation and the influence of the entity own information. Zhang et al. [24] proposed that the model FSRL considers the influence of the neighbors of different relations on the entity encoder, but it also ignores the entity’s own information.

In view of the above problems, we propose a relation-aware entity neighbor encoder. At the same time, this encoder incorporates the entity’s own information. The representation of entity information takes into account both its own information and the information of relational neighbors, so as to better represent the entity. The specific method is as follows.

Take the head entity h as an example. First, suppose that a head entity h is given. Then, the neighbor relation $r_i$∈$G^{\prime }$ and the tail entity $t_i$∈$G^{\prime }$ associated with this entity are found from the background knowledge graph $G^{\prime }$, and then these neighbor relations and tail entities are used to encode the head entity h. Here, the attention mechanism and the entity’s own information are used to construct this module, so as to obtain an enhanced representation of the head entity. The head entity enhanced embedding representation is composed of its neighbor entity information and its own entity information, and its formula can be expressed as follows:

$$f\left(h\right)=\sigma \left({\mathbf{W}}_2{\mathbf{e}}_h\right)+\sigma \left({\mathbf{W}}_3{\mathbf{e}}_{h_{nei}}\right)$$

(1)

where $\sigma$ denotes nonlinear activation function ($\mathrm{i}.\mathrm{e}.$, tanh). ${\mathbf{W}}_2$∈${\mathbb{R}}^{d\times d}$ and ${\mathbf{W}}_3$∈${\mathbb{R}}^{d\times d}$ are learnable parameters, and d is the pre-trained embedding dimension.

The head entity h neighbor embedding ${\mathbf{e}}_{h_{nei}}$ formulas used are listed as follows:

$${\mathbf{e}}_{h_{nei}}=\sigma (\sum _i^{N_h}\left({\alpha }_i{e}_{t_i}\right))$$

(2)

$${\alpha }_i=softmax\left(o_i\right)={\displaystyle \frac{exp\left(o_i\right)}{{\Sigma }_{(e_{r_i},e_{t_i})\in N_h}exp\left(o_i\right)}}$$

(3)

$$o_i={\mathbf{U}}_1^T({\mathbf{W}}_1({\mathbf{e}}_{r_i}\oplus {\mathbf{e}}_{t_i})+{\mathbf{b}}_1)$$

(4)

where $\sigma$ denotes nonlinear activation function ($\mathrm{i}.\mathrm{e}.$, tanh), ⊕ is concatenation operator, and ${\mathbf{e}}_{r_i}$ and ${\mathbf{e}}_{t_i}$ represent the pre-trained embedding representations of $r_i$ and $t_i$, respectively. $N_h$ denotes the neighborhood of the head entity h. ${\mathbf{U}}_1$∈${\mathbb{R}}^{d\times 1}$ and ${\mathbf{W}}_1$∈${\mathbb{R}}^{d\times 2d}$ are learnable parameters, and d is the pre-trained embedding dimension.

4.2. Reference Set Aggregator

The main purpose of this module is to construct the interaction of few-shot samples in the reference set, so that only few-shot reference set samples can maximize the expression capability of the relation, so as to better discover more similar triples in the matching network.

The existing model GMatching [21] cannot interact with few-shot samples in the reference set, which limits model capability. The FSRL [24] model uses LSTM network to interact with few-shot samples in the reference set, but this method cannot interact well because there is no time series relation in the triples of the knowledge graph.

In view of the disorder between triples, this paper adopts the aggregation method of max-pooling [48]. k-shot reference set triples $R_k$ of each relation r will be randomly sampled, and head entity $h_k$ and tail entity $t_k$ of the triples will be encoded by the entity coder module, and $f\left(h_k\right)$ and $f\left(t_k\right)$ will be obtained. Then, we get the representation of each reference set triplet entity pair, Ref($h_k$,$t_k$) = [$f\left(h_k\right)$⊕$f\left(t_k\right)$]. Because there are very few triples, in order to make only a few-shot reference set triples play the greatest role as much as possible, let these triples interact and mine latent common information, so as to better assist in finding more similar triples in the subsequent matching process. The aggregate representation of all reference set entity pairs in the reference set can be expressed by the following formula $f_k$:

$$f_k\left(R_k\right)=A{G}_{(h_k,t_k)\in R_k}Ref(h_k,t_k)$$

(5)

where $AG$ is an aggregation function. This paper adopts the max-pooling operation function.

As shown in Figure 1b, this paper first uses the fully connected layer and dropout layer to process the entity pairs of the reference set, and finally uses the max-pooling layer to fuse k-shot reference set entity pairs. By applying the max-pooling operator to k-shot reference set entity pairs, this module effectively captures the latent information representation of the relation between reference set entities, so as to obtain a rich representation of the relation. The formulas can be expressed as follows:

$$Re{f}_{\_k}^{″}=\sigma ({\mathbf{W}}_{\mathbf{5}}\sigma ({\mathbf{W}}_{\mathbf{4}}Re{f}_{\_k}+{\mathbf{b}}_{\mathbf{2}})+{\mathbf{b}}_{\mathbf{3}})$$

(6)

We use the residual network method to fuse the original information of the reference set:

$$Re{f}_{\_k}^{‴}=Drop\left(Re{f}_{\_k}^{″}\right)+Re{f}_{\_k}$$

(7)

$$A{G}_{(h_k,t_k)\in R_k}=\mathbf{max}\_\mathbf{pool}\left\{Re{f}_{\_k}^{‴}\right\}$$

(8)

where $\sigma$ is a nonlinear activation function, $Drop$ is a dropout layer, and $Re{f}_{\_k}$ is the i-th reference set entity pair. ${\mathbf{W}}_4$∈${\mathbb{R}}^{g_1\times 2d}$, ${\mathbf{W}}_5$∈${\mathbb{R}}^{g_2\times g_1}$, ${\mathbf{b}}_2$∈${\mathbb{R}}^{g_1\times 1}$, and ${\mathbf{b}}_3$∈${\mathbb{R}}^{g_2\times 1}$ are learnable parameters, and $g_1$ and $g_2$ are the number of neurons in the hidden layer of the first layer and the second layer, respectively.

4.3. Matching Network

The purpose of this module is to match the query set and the aggregated reference set information according to the matching network, and get the ranking scores of each candidate set entity $t_c$∈C.

Before matching the query set with the reference set, we first use the enhanced entity encoder module f to enhance the representation of the entities in the reference set entity pairs ($h_k$,$t_k$) and the query set entity pairs ($h_i$, $t_c$). We can get two of the enhanced entity embeddings $Ref$($h_k$,$t_k$) = [$f\left(h_k\right)$⊕$f\left(t_k\right)$] and $\mathbf{Q}$($h_i$, $t_c$) = [$f\left(h_i\right)$⊕$f\left(t_c\right)$], respectively. Then, the reference set entity embedding is fed into the reference set aggregator module for information aggregation, and the aggregated embedding vector $f_k$(${\mathbf{R}}_k$) is obtained. In order to measure the semantic similarity between the two vectors, although a simple cosine function can also be used, it cannot achieve a good performance. Therefore, this paper leverages a LSTM-based multi-step matching module [33,49]. After multi-step matching, the score function formula of query set entity pair and reference set entity pair is listed as follows:

$$score={\hslash }_t\otimes f_k\left({\mathbf{R}}_k\right)$$

(9)

where the score is the similarity score between the query set pair and the reference set pair after LSTM multi-step processing. For each relation r, we can compare the aggregated reference set pair $f_k$(${\mathbf{R}}_k$) with each query set entity pair ($h_i$, $t_c$∈C), and sort all the scores, so as to select the candidate set entities with top scores.

The t-th process step formulas are listed as follows:

$${\hslash }_t^{\prime },c_t=Matc{h}_{LSTM}(\mathbf{Q},[{\hslash }_{t-1}\oplus s,c_{t-1}])$$

(10)

$${\hslash }_t={\hslash }_t^{\prime }+\mathbf{Q}$$

(11)

$$atten=softmax({\hslash }_t\otimes f_k\left({\mathbf{R}}_k\right))$$

(12)

$$s=atten\otimes f_k\left({\mathbf{R}}_k\right)$$

(13)

where $Matc{h}_{LSTM}(x,[\hslash ,c])$ is a standard LSTM cell, x is input data, ℏ is hidden state, and c is cell state. ⊕ is concatenation operator and ⊗ is cosine similarity operator.

4.4. Loss and Model Training

In the meta-training set, for each few-shot relation r, we randomly sample k samples as the reference set $Re{f}_k$ and the other samples as the positive query set ${\mathbf{Q}}_r$. At the same time, we construct a negative query set ${\mathbf{Q}}_r^{-}$ of the same size by randomly replacing the tail entity of the positive query set. For example, a positive sample triplet ($h_i$, r, $t_i$) ∈G, whose corresponding negative triplet is ($h_i$, r, $t_i^{-}$) ∉G. Finally, we adopt a hinge loss function to optimize our model, and the loss formula L is as follows:

$$L=\sum _{(h_i,t_i)\in {\mathbf{Q}}_r}\sum _{(h_i,t_i^{-})\in {\mathbf{Q}}_r^{-}}max[0,\gamma +scor{e}^{-}-scor{e}^{+}]$$

(14)

where $\gamma$ is margin distance, and $scor{e}^{-}$ and $scor{e}^{+}$ are the similarity scores of the positive query set ${\mathbf{Q}}_r^{+}$ and the negative query set ${\mathbf{Q}}_r^{-}$ compared with the aggregated reference set information $f_k\left({\mathbf{R}}_k\right)$, respectively. The detailed training procedure of our model is shown in Algorithm 1:

Algorithm 1: Model Training

1: Input: Meta-training task set $T_{mtr}$        Pre-trained KG embeddings        Initial model parameters   2: while not done do   3:     Shuffle tasks in $T_{mtr}$   4:     for $T_r$ in $T_{mtr}$ do   5:         Sample k-shot triples from $T_r$ as reference set $Re{f}_k$   6:         Sample a batch of query triples ${\mathbf{Q}}_r$   7:         Replace the tail entity of the query set to construct a negative sample set ${\mathbf{Q}}_r^{-}$   8:         Use the enhanced entity encoder module to encode the entity of $Re{f}_k$, ${\mathbf{Q}}_r$ and ${\mathbf{Q}}_r^{-}$ by Equations (1)–(4)   9:         Use the reference set aggregator module to aggregate reference set information by Equations (6)–(18) 10:         Calculate the matching scores entity pairs in ${\mathbf{Q}}_r$ and ${\mathbf{Q}}_r^{-}$ by Equations (9)–(13) 11:         Calculate the batch loss in ${\mathbf{Q}}_r$ by Equation (14) 12:         Update model parameters by Adam optimizer 13:    end for 14: end while

5. Experiments

In this section, we introduce the datasets, experimental settings and do a lot of experiments to prove the effectiveness of our model, including overall results of different models, the prediction performance of each relation, ablation study, and impact of few-shot size.

5.1. Datasets

As shown in

Table 2. Dataset statistics information about ICEWS14, ICEWS05-15, Wikidata12k, and YAGO11k.

Datasets	#Ent.	#R.	#Triples	#Tasks
NELL-One	$\mathrm{68,545}$	358	$\mathrm{181,109}$	67
Wiki-One	$\mathrm{4,838,244}$	822	$\mathrm{5,859,240}$	183

#Ent. denotes the number of all entities, #R. represents the number of all relations, #Triples denotes the number of all relational triples, and #Tasks represents the number of relations selected as few-shot tasks.

, this paper uses two public datasets for experiments. The two datasets are NELL-One and Wiki-One, respectively (https://github.com/chuxuzhang/AAAI2020_FSRL, accessed on 8 October 2025). NELL-One and Wiki-One are constructed by selecting some long-tailed relations based on NELL [3] and Wikidata [5], respectively. The relations between the two datasets are greater than 50 but less than 500, which are mainly used for few-shot tasks. There are 67 and 183 tasks in the NELL-One and Wiki-One, respectively. In NELL-One and Wiki-One data, the task relations of training/validation/testing set are 51/5/11 and 133/16/34, respectively.

5.2. Evaluation Metrics

We adopt common knowledge graph completion evaluation metrics MRR and Hits@n to evaluate our model and other baselines. MRR is the mean reciprocal rank of the correct entities, and Hits@n is the proportion of correct entities ranked in the top n. The larger the value of MRR and Hits@n, the better the effect of triples completion. In this paper, the values of n are 1, 5, and 10, respectively. The calculation formulas are listed as follows:

$$MRR={\displaystyle \frac{1}{\left|Q\right|}}\sum _{i=1}^{\left|Q\right|}{\displaystyle \frac{1}{ran{k}_i}}$$

(15)

$$Hits@n={\displaystyle \frac{1}{\left|Q\right|}}\sum _{i=1}^{\left|Q\right|}\mathbb{I}(ran{k}_i\le n)$$

(16)

where $\left|Q\right|$ is the number of query set triples and $ran{k}_i$ is the score sorting of the i-th query set triple. $\mathbb{I}(·)$ indicates the indicator function. If the condition is true, it is 1; otherwise, it is 0.

5.3. Baselines

From the existing papers, the traditional knowledge representation learning models have worse results in few-shot knowledge graph completion, and there is a gap in the completion results compared with the few-shot knowledge graph completion model. Therefore, we adopt some existing knowledge graph completion models as the baselines.

We utilize several well-known few-shot knowledge graph completion methods of GMatching (https://github.com/xwhan/One-shot-Relational-Learning, accessed on 8 October 2025), MetaR (https://github.com/AnselCmy/MetaR, accessed on 8 October 2025), and FSRL as comparison methods. For these models, we use the same pre-trained embeddings generated by ComplEx to train these models. For GMatching, we not only use max-pooling and mean-pooling methods to aggregate the information of few-shot reference sets to obtain the representation of reference sets, but we also consider taking the maximum of similarity scores between a query and all k-shot reference sets as the final ranking score of this query. Its parameters are set to be consistent with our method. For MetaR and FSRL, we retain the parameter settings provided in their papers.

5.4. Implementation Details

In this paper, we adopt the entity and relation embeddings in a background knowledge graph pre-trained by ComplEx on the two datasets. At the same time, it also has the input for GMatching, FSRL, and MetaR models. The embedding dimension is set to 100 for NELL-One and 50 for Wiki-One, respectively. In enhanced entity encoder, the maximum size of neighbors is set to 30 for the two datasets. In reference set aggregator, we select k = 3 as the reference triples. The number of neurons for first/second fully connected layer are set to 400/250 for NELL-One and 350/200 for Wiki-One. In the matching network, there are two recurrent steps. We adopt the Adam optimizer [50] to optimize model parameters. The initial learning rates is set to 0.0001 for NELL-One and 0.001 for Wiki-One. The batch size is 128 and the margin is fixed to 5.0. All the programs were implemented in Python 3.12.0 and all the experiments were conducted on GeForce RTX 3090.

5.5. Experimental Results and Analysis

Overall Results of Different Models

Paragraph. The simulation results of different models are presented in

Table 3. The experimental results on NELL-One and Wiki-One.

NELL-One
Models	MRR	Hits@10	Hits@5	Hits@1
Gmatching (MaxP)	$0.256$	$0.417$	$0.335$	$0.175$
Gmatching (MeanP)	$0.262$	$0.438$	$0.336$	$0.176$
Gmatching (Max)	$0.260$	$0.448$	$0.351$	$0.174$
FSRL	$0.329$	$0.508$	$0.422$	$0.233$
MetaR	$0.209$	$0.388$	$0.303$	$0.113$
Ours (MeanP)	$0.295$	0480	$0.384$	$0.203$
Ours (MaxP)	$0.342$	$0.540$	$0.454$	$0.245$
Wiki-One
Models	MRR	Hits@10	Hits@5	Hits@1
Gmatching (MaxP)	$0.175$	$0.333$	$0.235$	$0.101$
Gmatching (MeanP)	$0.176$	$0.337$	$0.221$	$0.106$
Gmatching (Max)	$0.178$	$0.354$	$0.248$	$0.091$
FSRL	$0.205$	$0.381$	$0.306$	$0.109$
MetaR	$0.293$	$0.443$	$0.359$	$0.217$
Ours (MeanP)	$0.260$	$0.411$	$0.338$	$0.179$
Ours (MaxP)	$0.298$	$0.442$	$0.374$	$0.219$

.

5.6. Results on Two Datasets

The experimental results on two datasets are shown in Table 3. Bold numbers are the best results. From the results, we can conclude that

(1) The results of our model are better than other few-shot knowledge completion models. Compared with the best baseline model FSRL on NELL-One, our model is 3.95%, 6.30%, 7.58%, and 5.15% higher than FSRL model in the evaluation of MRR, Hits@10, Hits@5, and Hits@1 metrics, respectively. At the same time, compared with the best baseline model MetaR on Wiki-One, our model is 1.71%, 4.17%, and 0.09% higher than the FSRL model in the evaluation of MRR, Hits@5, and Hits@1 metrics, respectively. It demonstrates the effectiveness of our model. The results show that the combination of our enhanced entity coder module and reference set max-pooling aggregator has a certain effect on the completion of missing triples.

(2) For GMatching and FSRL models, we can obtain that the addition of the reference set aggregator can better learn the latent information between reference set triples, so as to better discover the missing triples. At the same time, by our different pooling experiments, we can also see that selecting the appropriate reference set aggregator gets better results.

5.6.1. The Results of Different Relations in NELL-One

In order to better understand the prediction performance of each relation, we select the relations in NELL-One with fewer relations as the research object. Here, we adopt the FSRL with better performance and our model to analyze the prediction of 11 relations in the test dataset. Because the size of the candidate set for most relations is too large, the maximum candidate set is 1000 in this paper. The evaluation results of each relation are shown in

Table 4. The results of FSRL and ours for each relation. (RId) on NELL-One.

Models	RId	MRR	Hits@10	Hits@5	Hits@1	RId	MRR	Hits@10	Hits@5	Hits@1
FSRL	1	$0.976$	$0.986$	$0.986$	$0.972$	7	$0.442$	$0.810$	$0.620$	$0.260$
Ours		$0.977$	$1.000$	$0.986$	$0.972$		$0.579$	$0.820$	$0.720$	$0.490$
FSRL	2	$0.361$	$0.463$	$0.429$	$0.303$	8	$0.355$	$0.635$	$0.467$	$0.226$
Ours		$0.366$	$0.514$	$0.417$	$0.309$		$0.394$	$0.657$	$0.526$	$0.270$
FSRL	3	$0.380$	$0.500$	$0.364$	$0.333$	9	$0.534$	$0.763$	$0.720$	$0.366$
Ours		$0.117$	$0.318$	$0.273$	$0.030$		$0.682$	$0.892$	$0.860$	$0.559$
FSRL	4	$0.056$	$0.114$	$0.086$	$0.021$	10	$0.107$	$0.213$	$0.136$	$0.050$
Ours		$0.075$	$0.114$	$0.093$	$0.043$		$0.201$	$0.393$	$0.302$	$0.107$
FSRL	5	$0.170$	$0.366$	$0.238$	$0.089$	11	$0.571$	$0.814$	$0.771$	$0.381$
Ours		$0.128$	$0.300$	$0.178$	$0.050$		$0.520$	$0.881$	$0.819$	$0.338$
FSRL	6	$0.415$	$0.626$	$0.544$	$0.306$
Ours		$0.422$	$0.633$	$0.544$	$0.306$

. Bold numbers are the best results. From the results, we can conclude that

(1) Our model has better results than FSRL in most cases. It demonstrates that our model has better robustness and generalization for most relations.

(2) It can also be seen from the results that the relation with fewer candidate set entities is easier to predict tail entities. For example, relation 1 has higher prediction metrics. At the same time, the relations with more candidate set entities to predict tail entities are difficult, and the prediction results are relatively worse, which needs to be improved.

5.6.2. Ablation Study

In order to study the contributions of different components, we conducted ablation experiments on two datasets, and the results are shown in

Table 5. The experimental results of the ablation study.

NELL-One
Models	MRR	Hits@10	Hits@5	Hits@1
Full model(MaxP)	$0.342$	$0.540$	$0.454$	$0.245$
Full model(LSTM)	$0.338$	$0.498$	$0.406$	$0.257$
-own infor(MaxP)	$0.340$	$0.502$	$0.421$	$0.256$
Wiki-One
Models	MRR	Hits@10	Hits@5	Hits@1
Full model(MaxP)	$0.298$	$0.442$	$0.374$	$0.219$
Full model(LSTM)	$0.277$	$0.421$	$0.355$	$0.196$
-own infor(MaxP)	$0.259$	$0.430$	$0.351$	$0.172$

. Bold numbers are the best results.

(1) Full model(LSTM): We mainly compare the functions of the LSTM aggregator and max-pooling aggregator. Here, we use the LSTM aggregator module in FSRL to replace the max-pooling aggregator. As we all know, there is no time series characteristic between triples in the general knowledge graph. According to this data characteristic, we use the max-pooling operation to aggregate the reference set triples. From the results of the two datasets, the effect of the max-pooling aggregator is better.

(2) -own infor(MaxP): In order to verify the effectiveness of the enhanced entity encoder module, we only use the information of entity neighbors to encode entities. We believe that the encoder information of an entity should be related not only to its neighbor information, but also to its own information. Therefore, we also integrate the entity’s own information to enhance entity representation. From the experimental results, the entity’s own information does play a role in enhanced representation.

5.6.3. Impact of Few-Shot Size

We adopt different few-shot sizes k to analyze the impact of the size of the reference set on the prediction results, and compare the better baseline model FSRL with our proposed model. The results of NELL-One dataset are shown in Figure 2:

(1) It can be seen from the results in Figure 2 that the results of our model are above the baseline model FSRL, which proves the effectiveness and robustness of our model.

(2) It can also be seen from the Figure 2 that the results do not always increase with the increase of k. We believe that there may be the following reasons: (i) Although the number of reference sets has increased, the added reference sets have little relevance to the current tail entity prediction. For example, when the triples of the reference set are the relationship between the capital and the country, it is difficult to predict the subordination between foods. (ii) In the entity encoder module, there is noise in the fusion of entity neighbors, which is useless for the current tail entity prediction. For example, there are few neighbor entities or the types are not rich enough to represent entities well.

6. Conclusions

In this paper, in order to enhance entity embedding and better aggregate entity pairs of reference sets, we propose a few-shot knowledge graph completion model with a max-pooling aggregator and enhanced entity embedding. In entity coder, the model not only considers the information of neighbor entities, but also integrates the information of entities. At the same time, the disorder of triples in the knowledge graph is considered in reference set aggregation, and a max-pooling reference set aggregator is proposed. Through a variety of different experiments, such as comparing with some existing few-shot knowledge graph completion models, changing the size of the reference set and ablation experiments, these experiments prove the effectiveness and robustness of our model. In addition, we also found some problems. For example, the performance does not necessarily increase with the increase in reference set size, which also points out the next research direction for us. In future work, we will focus on the encoder module and correlation selection of entity neighbors to explore the reasons and try to find solutions.