The DDMRP Replenishment Model: An Assessment by Simulation

Abstract

Demand-Driven Material Requirements Planning (DDMRP) has been proposed as a solution for managing uncertainty and variability in supply chains by combining decoupling, buffer management and demand-driven planning principles. A key element of DDMRP is its inventory replenishment model, which relies on dynamically adjusted inventory buffers rather than fixed stock levels. However, parameterization of these buffers often involves subjective choices, raising concerns about consistency and performance. This paper assesses the DDMRP replenishment model through discrete-event simulation of a multi-echelon, capacity-constrained production system. Two alternative formulations of the safety stock term in the red zone are compared: the original factor-based approach and a revised formula that incorporates measurable variability coefficients. While both safety stock formulations yield similar numerical results, the revised formula enhances transparency and reduces subjectivity. Assessing the impact of introducing a buffer for components in addition to a finished goods buffer further shows that the components buffer can reduce finished goods inventory requirements while maintaining service levels. These findings contribute to a better understanding of the DDMRP replenishment model, offering practical insights for parameter selection and supply chain design.

1. Introduction

Demand-Driven Material Requirements Planning (DDMRP) is an approach to production planning and control proposed by Ptak & Smith [1,2]. It was specifically developed for VUCA (Volatility, Uncertainty, Complexity, and Ambiguity) environments, addressing the shortcomings of traditional Material Requirements Planning (MRP) systems by integrating elements from Lean Production, Theory of Constraints (TOC), and traditional planning tools to create a demand-driven and decoupled supply chain model [2].

DDMRP has been shown to reduce replenishment lead times and improve customer order service levels, particularly in environments with high demand variability [3,4,5,6]. Nevertheless, the effectiveness of DDMRP is highly contingent on its correct parameterization. One of the core components of DDMRP is the replenishment model, which governs inventory management at strategically placed decoupling points. This model operates on the principle of buffer profiles that are dynamically adjusted based on actual demand signals, ensuring that inventory levels are neither excessively high nor dangerously low.

Inventory replenishment models have long relied on probabilistic approaches to manage demand variability and ensure service level targets. A common feature of these models is the calculation of safety stock using a safety factor derived from a desired service level, underpinned by assumptions about the statistical probability distribution of demand during the replenishment time. For a review, the reader is referred to e.g., [7,8,9]. The application of safety stock formulas based on incorrect demand distributions can, however, lead to miscalculations, resulting in either excessive inventory costs or inadequate service performance.

DDMRP eliminates the reliance on fixed safety factors associated with service levels and instead adopts a buffer-based methodology. This approach allows users to define buffer parameters within specified ranges. However, this may result in users subjectively selecting parameter values within the recommended ranges. This subjectivity can lead to inconsistencies in inventory performance, as pointed out by [10]. This paper, therefore, explores the theoretical foundations and practical implications of the DDMRP replenishment model, with particular attention paid to the buffer’s safety stocks. Specifically, it seeks to address the following research questions: RQ1: How does buffer positioning affect DDMRP service levels? RQ2: How does the safety stock calculation affect the DDMRP replenishment model?

The remainder of the paper is organized as follows. Section 2 reviews the DDMRP replenishment model and introduces the two approaches to determine safety stock levels from the literature. The production system considered and the simulation model used to assess the performance are presented in Section 3, before the simulation results are presented and discussed in Section 4. Finally, Section 5 puts forward conclusions and future research directions.

2. Background

2.1. Replenishment Policies

The concept of buffering in production systems has long been explored as a means of absorbing variability and promoting flow of materials [11]. Buffers act as decoupling points between production chain stages, allowing upstream and downstream processes to operate with greater autonomy. These buffers are not only a physical inventory but also represent a strategic approach to managing uncertainty in demand and supply. Within this context, replenishment policies play a crucial role in determining how and when these buffers are replenished to maintain operational stability.

The Reorder Point policy is one of the most well-established and widely used inventory replenishment policies in both academic and industrial practice [8,12]. Under this policy, a replenishment order is triggered when inventory falls to or below a predetermined threshold known as the reorder point [13]. This threshold is typically calculated based on expected demand during the replenishment lead time, often with an added safety stock component to account for variability. The primary advantage of the Reorder Point policy lies in its simplicity and ease of implementation. However, it assumes static or stable conditions [14], which are increasingly rare in today’s dynamic and uncertain supply chain environments. In situations with high demand volatility, frequent supply disruptions, or long and variable replenishment lead times, the Reorder Point policy may lead to suboptimal outcomes, such as stockouts or overstocking.

A closely related and slightly more flexible replenishment policy is the Min–Max model [15,16]. In this approach, inventory levels are managed within a defined range, consisting of a minimum threshold, similar to the Reorder Point, and a maximum target level. When inventory drops to or below the minimum, a replenishment order is placed to bring the stock up to the target level. While the Min–Max model retains the reactive nature of the Reorder Point policy, it introduces a controlled (i.e., variable) replenishment quantity, which improves demand responsiveness.

Despite its broader application, the Min–Max model still relies heavily on forecast-based planning and fixed parameter settings, which can render it ineffective in highly variable environments. Both Reorder Point and Min–Max struggle to adequately handle demand signal volatility, replenishment lead time uncertainty, and the bullwhip effect, particularly in multi-echelon manufacturing settings [17]. These limitations have prompted the development of more adaptive and demand-driven methodologies, such as DDMRP, which aim to overcome the rigidity of traditional replenishment models by incorporating dynamic buffer zones, real-time demand inputs, and flow-based priorities.

DDMRP aligns with the Min–Max model, where a reorder is initiated when inventory drops below a calculated “reorder zone,” and replenishment targets the top of the buffer. However, while Min–Max models typically rely on historical demand averages and static safety stock, DDMRP enhances this approach by incorporating real-time demand signals and dynamic buffer adjustments [2].

Recent research has continued to refine and expand DDMRP capabilities in complex manufacturing settings. Habbadi et al. [18] proposed a hybrid methodology that combines DDMRP with intelligent production control to enhance buffer positioning for smart manufacturing environments. Bayard et al. [19] examined DDMRP behavior through an applied case study and highlighted both its responsiveness and sensitivity to buffer parameterization. Complementary work by Dessevre and Benali [20] demonstrated that buffer positioning must be coordinated with dynamic capacity variations to preserve overall system flow. Furthermore, Favaretto et al. [21] provided a theoretical validation of the DDMRP reorder mechanism, reinforcing its stability and performance under variability.

Research also underscores that replenishment outcomes are significantly influenced by multi-echelon dynamics and capacity constraints. Maggiar et al. [22] examined a non-stationary, capacitated, multi-echelon distribution network and showed how upstream flow constraints alter optimal inventory placement and effective lead times. Thürer et al. (2020) [3] similarly demonstrated that buffering decisions must account for bottleneck behavior, since upstream protection can meaningfully reshape replenishment times and the distribution of inventory across the system. These insights strongly support this study’s focus on multi-echelon system evaluation and the assessment of a revised, more objective safety-stock formulation within DDMRP.

2.2. Demand-Driven MRP

DDMRP is structured around three core principles: Position, Protect, and Pull. These principles guide the strategic design and operational execution of supply chain processes within the DDMRP framework. To implement these principles effectively, DDMRP follows a structured methodology composed of five sequential and interdependent phases, as outlined by Ptak and Smith [2]:

• Strategic Inventory Positioning: This phase involves identifying the most effective locations within the supply chain to place inventory buffers. These positions are selected based on decoupling points, lead time compression opportunities, and points of high variability or strategic importance. The goal is to ensure that materials are available where and when they are needed to support flow and responsiveness.
• Buffer Profile and Level Determination: Once strategic positions are established, this phase defines the size and structure of the inventory buffers. It involves determining buffer zones based on factors such as average demand, replenishment lead time, and variability. The objective is to adapt each buffer to its specific context, ensuring it effectively absorbs variability while avoiding overstocking.
• Dynamic Buffer Adjustment: Recognizing that demand patterns, replenishment lead times, and operating conditions are not static, DDMRP continuously adjusts buffer levels. These adjustments can be made periodically or in response to significant changes in the operating environment, allowing the system to maintain optimal inventory levels.
• Demand-Driven Planning: This phase replaces traditional forecast-driven planning with a pull-based approach that uses actual demand signals to trigger replenishment. It focuses on net flow position (NFP) calculations, taking into account on-hand inventory, open replenishment orders, and qualified demand to determine when and how much to replenish.
• Visible and Collaborative Execution: The final phase emphasizes real-time visibility into buffer status and supply chain performance, enabling proactive management of exceptions and priorities.

By dynamically evaluating the NFP against the buffer zones, DDMRP provides a visual and intuitive framework for decision-making. The buffer status not only facilitates prioritization of production and procurement but also supports responsive manufacturing execution, aligned with real-time consumption patterns and business needs.

Inventory buffers in DDMRP are strategically segmented into three distinct zones (green, yellow, and red), each serving a unique and essential function in inventory management:

• Green Zone (GZ): This zone, which represents the upper portion of the buffer, primarily governs the generation and frequency of replenishment orders. When the inventory level reaches this zone, it signals that there is sufficient stock, and thus no immediate replenishment is necessary.
• Yellow Zone (YZ): This zone, which represents the middle of the buffer, is intended to cover average demand during the replenishment lead time. When the NFP drops to this zone, a replenishment order is generated.
• Red Zone (RZ): This zone, which occupies the lowest part of the buffer, incorporates the safety stock and serves as a critical protection layer against variability in supply and demand. When NFP drops into this zone, it signals an elevated risk of stockouts, triggering high-priority replenishment orders.

Our study is focused specifically on RZ. According to Ptak and Smith [2], the RZ is expressed as the sum of the red zone base, defined as the demand (d) during the replenishment lead time (L) multiplied by a lead time factor (F_L), and the red zone safety, defined by the red zone base multiplied by a variability factor (F_V), as follows:

RZ = (d × L) × F_L + (d × L × F_L) × F_V

(1)

The lead time factor and the variability factor in DDMRP can be assigned based on the guidelines provided by Ptak and Smith [2] (see

Table 1. Guidelines for lead time and variability factors.

Lead Time	Lead Time Factor	Example
Long	0.20–0.40	26+ days
Medium	0.41–0.60	11–25 days
Short	0.61–1	1–10 days
Variability	Variability Factor
High	0.61–1
Medium	0.41–0.60
Low	0.20–0.40

).

These guidelines allow users to select parameter values subjectively within recommended ranges. However, this subjectivity can lead to inconsistencies in inventory performance, as highlighted by Lee and Reem [10]. To address this issue and eliminate the subjectivity in determining the safety stock, these authors introduced a revised RZ formula for DDMRP replenishment, using coefficients of variation in demand CV_d and lead time, CV_L, as follows:

$$\mathrm{RZ} = \left[\mathrm{d}\times (1.02\sqrt{L}+1.15)\right]\times \left[1+\sqrt{{{CV}_d^2+CV}_L^2\times L}\right]$$

(2)

This revised formula ties the safety buffer explicitly to measurable variability in demand and lead time, not arbitrary factors. However, Lee and Reem did not test the proposed formula in the context of a multi-echelon capacity-constrained production environment. This study compares these two formulas by comprehensively investigating the replenishment performance of DDMRP in this context, to answer RQ2.

3. Method

Discrete-event simulation is used as a research method to evaluate and compare the performance of the two red zone formulas from Section 2.2. It has become widely adopted for evaluating inventory control policies and buffer configurations in manufacturing systems [23] because it allows for the modeling of complex dynamics, including stochastic demand, setup times, rework, and bottleneck behavior, as present in our study.

Section 3.1 describes the production system considered, while Section 3.2 describes the experimental setup and simulation conditions.

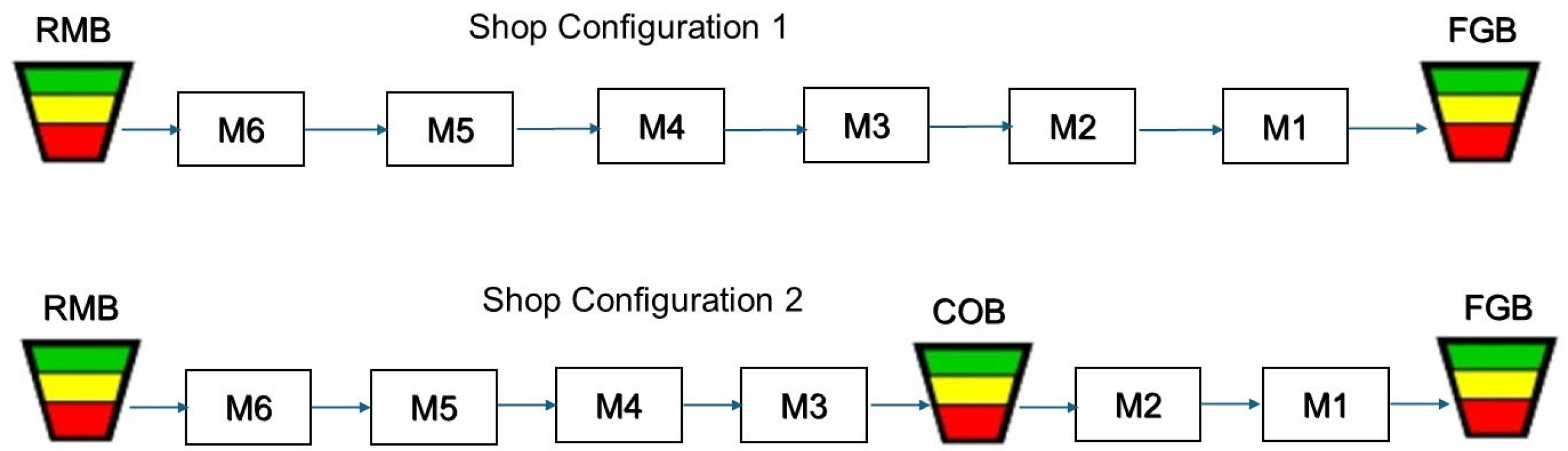
3.1. Production System

The production system considered is based on [24]. It involves a line with 6 stations, M6 to M1, where ten different types of finished products, A1 to A10, are produced (Figure 1). To answer our first RQ1, two shop configurations with different buffer positioning are tested, as illustrated in Figure 1. Shop configuration 1 includes a Finished Goods Buffer (FGB) and a Raw Materials Buffer (RMB), while shop configuration 2 introduces an additional Components Buffer (COB) positioned after M3, the bottleneck station.

For example, product A1 at station M1 is assembled from two units of B1, while B1 is assembled at station M2 from 3 units of C1, and while C1 is assembled at station M4 from 1 unit of D1, etc., as shown in

Table 2. Product characteristics.

Station M1	Station M2	Station M3	Station M4	Station M5	Station M6
A1	B1 (2)	C1 (3)	D1	E1	F1
A2	B2 (2)	C1 (2)	D1	E1	F1
A3	B3 (2)	C1	D1	E1	F1
A4	B4 (2)	C2 (2)	D2	E2	F2
A5	B5 (2)	C2	D2	E2	F2
A6	B1	C1 (3)	D1	E1	F1
A7	B2	C1 (2)	D1	E1	F1
A8	B3	C1	D1	E1	F1
A9	B4	C2 (2)	D2	E2	F2
A10	B5	C2	D2	E2	F2

. Material flow is sequential: M1 is supplied by M2, M2 by M3, and so forth, with M6 receiving inputs directly from the Raw Materials Buffer (RMB), which is assumed to have unlimited immediate availability.

Supplier uncertainty at the raw materials buffers was abstracted to avoid introducing additional interactions that limit the understanding of the main effects. Processing and setup times are stochastic for all stations and summarized in

Table 3. Production system characteristics.

Characteristics	Value
Shop	Assembly line with 6 stations
Stations capacity	Fixed
Rework	5% of products require rework
Stations availability	100% (no failures)
Movement time between station	2″
Demand Interarrival time	Random.Exponential (52′)
Processing time at M1	Random.Exponential (25′)
Processing time at M2	Random.Exponential (18′)
Processing time at M3	Random.Exponential (13′)
Processing time at M4	Random.Exponential (9′)
Processing time at M5 and M6	Random.Exponential (5′)
Setup time at M1 and M2	Random.Exponential (5′)
Setup time at M3	Random.Exponential (10′)
Setup time at M4	Random.Exponential (9′)
Setup time at M5 and M6	Random.Exponential (5′)

. Setup times were assumed to occur at every operation. The system assumes no machine failures, while each product has a 5% probability of requiring rework at any station, with rework duration equal to the standard processing time. To capture high demand variability, we assumed that demand follows an exponential distribution, which reflects the propensity for frequent small orders interspersed with occasional large spikes. Demand occurs randomly following an exponential distribution, with equal probability for each final product. The average interval between demand arrivals is 68 m, which results in about 94% utilization at the bottleneck station (M3), when combined with processing times, setup times, and rework. All this also results in stochastic replenishment lead times.

Dispatching at all stations is based on the FCFS (First-Come-First-Served) rule.

3.2. Experimental Setup and Performance Measures

Three experimental factors were considered in the study (see

Table 4. Experimental factors and levels.

Buffer	Experimental Factor	Levels
FGB	GZ	1 and 4 units
	YZ	2 units
	RZ	1 to 8 units
COB	GZ	C1 (4 units)
		C2 (2 units)
	YZ	1 unit
	RZ	C1 (5, 9, 13, 17, 21, 25, 29 and 33) units
		C2 (2, 4, 6, 8, 10, 12, 14 and 16) units
	Shop Configuration	1 and 2

): (i) the GZ of the FGB was tested at two levels (1 and 4 units); (ii) the RZ of the FGB was tested at eight levels (from 1 to 8 units), and the RZ of the COB tested at 8 levels, as indicated in Table 3, and (iii) the shop configuration was tested at two levels (shop 1 and shop 2). This results in a full factorial design with 128 experiments.

Each experiment consists of 100 simulation runs, each one of duration 26,000 h, of which 6000 h were used for the warm-up period. Six performance measures were recorded: the service level at the FGB and at the COB, the replenishment time at the FGB and at the COB, and the quantity in stock at the FGB and at the COB.

4. Results

We first present the results for shop configuration 1 in Section 4.1, followed by the results for shop configuration 2 in Section 4.2. A performance analysis is presented in Section 4.3, before a discussion of results is provided in Section 4.4.

4.1. Results for Shop Configuration 1

For shop configuration 1, the finished goods buffer (FGB) is managed through the DDMRP replenishment policy. This buffer is supplied from the beginning of the production line, meaning that all components required to assemble the ten finished products, A1 to A10, must be produced and assembled from raw materials. It is assumed that raw materials are always available in the Raw Materials Buffer (RMB); therefore, the RMB is not subject to a replenishment policy.

Figure 2 depicts the results for the finished goods buffer in terms of service level and replenishment time of finished goods, respectively, versus the buffer size in units. Each mark along the performance curves represents a different TOY (i.e., RZ + YZ) value, ranging from 3 units (leftmost mark) to 10 units (rightmost mark), while each curve in the figures corresponds to a different GZ value, with two values tested, i.e., 1 and 4 units.

The following can be observed from the results:

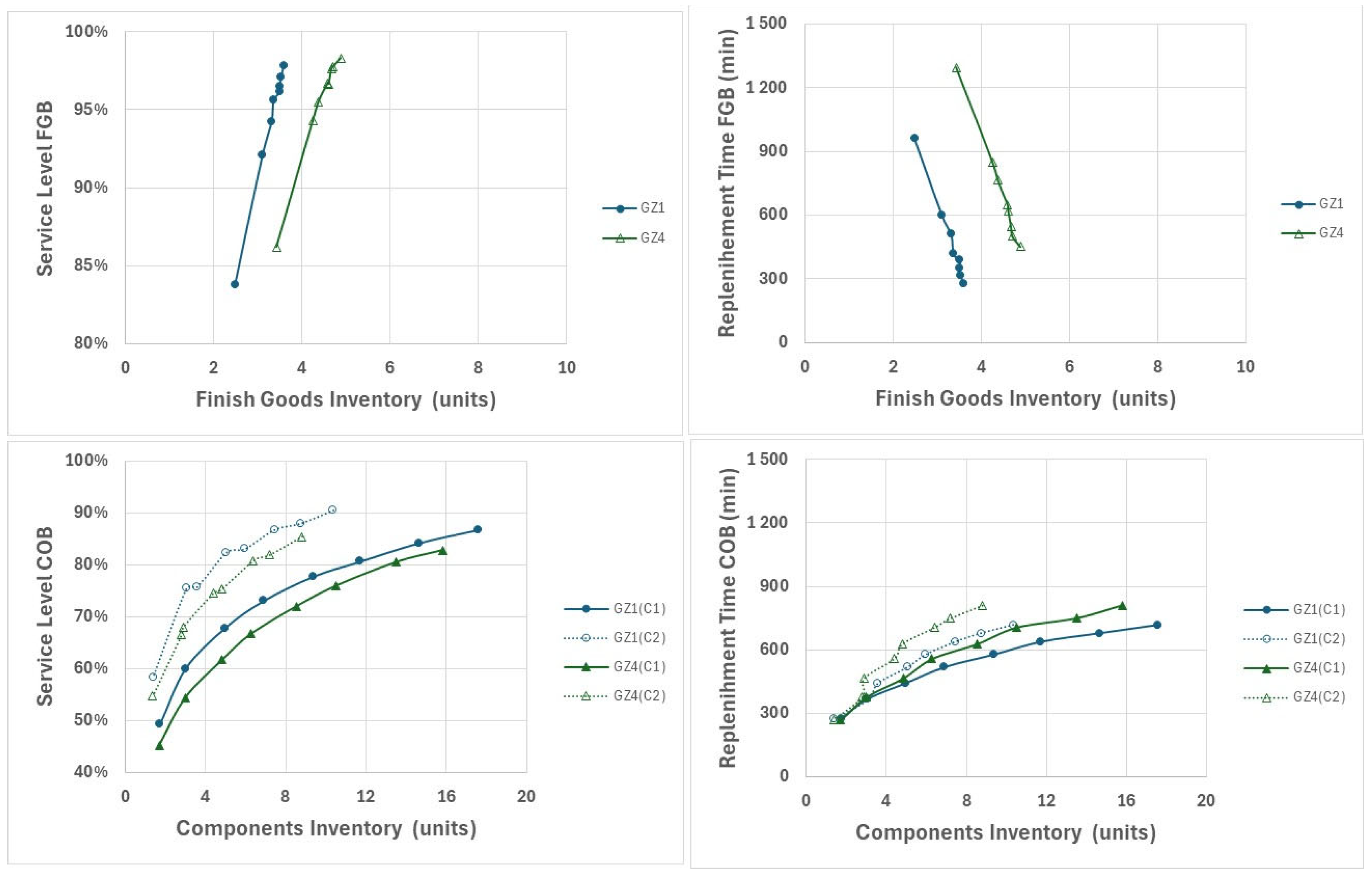
• Decreasing the TOY (i.e., the reorder point) results in a lower service level. TOY also impacts replenishment times, which becomes slightly lower for lower values of this parameter. This will be explored further below in our performance analysis.
• Increasing the GZ from 1 to 4 units results in longer replenishment times. The Green Zone determines the reorder quantity and frequency: increasing its size raises the reorder quantity and reduces the number of replenishment cycles. However, larger reorder quantities can create peaks in workload within the production system, leading to congestion and longer replenishment times. These delays can, in turn, deteriorate overall service performance. Shorter replenishment times, contrary to longer ones, tend to improve the service level as they enable faster replenishment of the finished goods buffer.

4.2. Results for Shop Configuration 2

For Shop Configuration 2, two buffers are managed by the DDMRP replenishment policy: the FGB and the components buffer (COB). The FGB is supplied by the COB, which, in turn, is supplied by the RMB. Results are presented in Figure 3. The results were obtained by keeping the TOY of finished products at its minimum value (3 units) while varying the TOY of the components at COB. There is consequently a separate curve for each of the two components. For component C1, TOY ranges from 6 units (leftmost point) to 34 units (rightmost point). For component C2, whose average consumption in product assembly is about half that of C1, the TOY ranges from 3 to 17 units.

The following can be observed from the results:

• A reduction in the TOY values for the components buffer leads to a decline in service level at this buffer, due to lower component availability—an effect also observed in shop configuration 1 for the finished goods buffer.
• Increasing the GZ of the FGB from 1 to 4 units results in longer replenishment times for both components and finished products due to congestion effects. This increase in replenishment times, as expected, significantly impacts the service level.

For the results in Figure 4, the TOY values for components C1 and C2 were kept at their maximum levels, 34 and 17 units, respectively, providing both the best customer service and lowest finished good inventory replenishment times, while the TOY for finished products was varied.

The following can be observed from the results:

• Lower TOY values in the FGB lead to lower service levels, as expected. However, this effect is less pronounced than in shop configuration 1 since the availability of components in the COB helps reduce replenishment times for finished products. Because the reorder point (i.e., TOY) for components is held constant, the service level of the component buffer remains largely unaffected.
• Once again, increasing the Green Zone values for finished products results in longer replenishment times for both finished products and components. This can adversely affect service levels, particularly in the component buffer, where congestion effects are more pronounced. Nevertheless, as expected, for both GZ levels, the replenishment times are considerably reduced due to the existence of the components buffer.

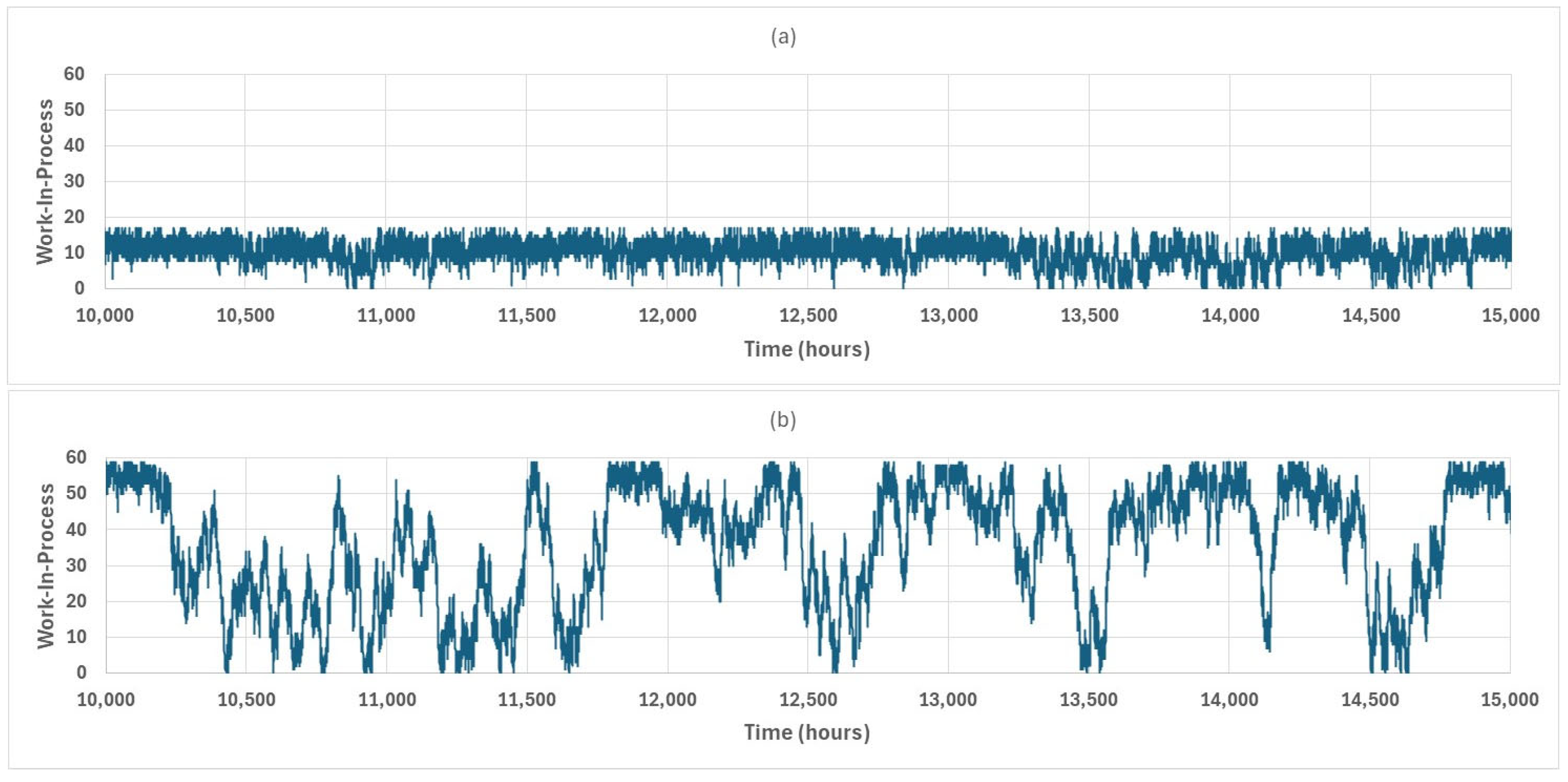
4.3. Performance Analysis

In the FGB of shop configuration 2, when TOY values of the FGB are held constant, while varying TOY values of the COB, the service level of FGB could be expected to remain unchanged, but this is not the case. This happens because the service level at the FGB is strongly impacted by the service level at the COB. This is corroborated by the impact that TOY has on the replenishment times of components C1 and C2 (Figure 3). Lower TOY values at COB reduce component availability, delaying final product replenishment and thereby increasing throughput times. That is, less availability of components at the COB leads to less availability of finished products at FGB.

The TOY of the components buffer at shop configuration 2 also affects the components’ replenishment times, i.e., the time the components take to arrive at COB (Figure 3). Lower TOY values are associated with shorter replenishment times. Raising the TOY raises the target stock level that replenishment orders must reach. This strengthens buffer protection at the expense of longer and more variable replenishment times due to increased system load, as illustrated in Figure 5. This figure depicts the work-in-process for the replenishment of COB with component C1 using a GZ of 4 units and C2 of 2 units. The same occurs at shop configuration 1, where the TOY of the FGB also impacts replenishment times (Figure 2).

4.4. Discussion of Results

In general, by positioning buffers at stages characterized by high variability or long lead times, the system can decouple production processes, isolate disturbances and reduce delivery times. Therefore, in our study buffer positioning was analyzed: RQ1—“How does buffer positioning affect DDMRP service levels?”. Findings indicate that an additional buffer can substantially reduce the replenishment time of the finished goods buffer, thereby potentially enhancing its service level to customers. However, this gain in responsiveness is offset by the need to hold additional inventory in the form of components. The introduction of a component buffer makes it possible to reach service levels similar to those achieved using only the FGB. For instance, a 98% service level at the FGB can be obtained while reducing finished goods inventory from 5 units, as shown in Figure 2, to about 3.5 units per product type when the component buffer (COB) is added—a reduction of roughly 30% (see Figure 3). However, this requires maintaining component inventories of at least 17 units for component C1 and 10 units for component C2, as shown in Figure 3. Thus, a trade-off arises between finished goods and component inventories to realize a desired customer service level. Component buffers are particularly valuable when holding finished goods is costly (e.g., when products are bulky, perishable, or have short life cycles), when postponing product differentiation provides an advantage (e.g., reducing the risk of producing the wrong product mix), or when components are shared across multiple products (i.e., a component buffer can serve several finished goods, improving responsiveness and reducing total safety stock).

With respect to RQ2—“How does the safety stock calculation impact the DDMRP replenishment model?”—we examined the effect of different formulations of the safety stock term by comparing Formulas (1) and (2) in the context of DDMRP replenishment performance. Our analysis is restricted to the Finished Goods Buffer (FGB) at Shops 1 and 2.

Table 5. Calculated values of RZ.

Shop Configuration	Formula (1)			Formula (2)
	FL	FV	RZ	CVD	CVL	RZ
1	0.2	0.65	1	1	0.8	2
	0.3	0.65	1
	0.4	0.65	2
	0.2	0.80	1
	0.3	0.80	1
	0.4	0.80	2
	0.2	0.95	1
	0.3	0.95	1
	0.4	0.95	2
2	0.2	0.65	1	1	1.5	1
	0.3	0.65	1
	0.4	0.65	1
	0.2	0.80	1
	0.3	0.80	1
	0.4	0.80	1
	0.2	0.95	1
	0.3	0.95	1
	0.4	0.95	1

reports the resulting Red Zone (RZ) values under both formulations. For Shop 1, we assumed a relatively long replenishment time at the FGB, combined with high demand variability. In this setting, both the Lead time Factor (F_L) and the Variability Factor (F_V) were fixed at different levels within the ranges specified in Table 4. In the case of Formula (2), the coefficients of variation obtained from the simulation model were CV_D = 1, CV_L = 0.8 for shop 1 and CV_L = 1.5 for shop 2. The comparison shows that the calculated safety stock (reflected in the RZ) is broadly similar across both formulas. However, an important distinction emerges: Formula (2) directly incorporates measurable variability coefficients, enabling the user to compute safety stock based on objective, data-driven parameters. In contrast, Formula (1) relies on subjective definitions of adjustment factors, which can introduce inconsistency or bias. Thus, while both approaches yield comparable numerical results under certain conditions, Formula (2) offers greater transparency, reproducibility, and adaptability to different operational contexts.

DDMRP is increasingly applied in industrial environments characterized by volatile demand, variable replenishment lead times, and multi-echelon product structures. Typical contexts include automotive and industrial equipment manufacturing, electronics and high-tech assembly. These sectors combine high service-level requirements with variability that challenge traditional MRP or Reorder-point policies. The revised safety buffer formulation of DDMRP is particularly well aligned with these conditions, as it links inventory protection directly to observed variability, rather than subjective parameter selection. From a practical feasibility perspective, most organizations that have adopted DDMRP already possess the digital infrastructure required to support dynamic buffer sizing, including data acquisition from shop-floor execution systems and planning platforms.

User acceptability also represents an important determinant of successful adoption. Operational teams benefit from greater transparency because the revised formulation eliminates ambiguity around factor selection and directly links inventory protection to measurable system behavior. This supports more consistent decision-making and clearer managerial justification of safety stock policies.

Overall, these practical considerations indicate that the revised DDMRP replenishment model is well positioned for industrial implementation in data-rich, variability-laden environments where both service performance and inventory efficiency are critical.

5. Conclusions

This study examined the performance of the DDMRP replenishment model through a simulation-based assessment of a multi-echelon, capacity-constrained production system. Two main aspects were investigated: (i) the role of buffer positioning and (ii) the impact of alternative safety stock formulations on replenishment performance. Regarding buffer positioning, results demonstrate that introducing a component buffer can enhance responsiveness at the finished goods level by reducing replenishment throughput times. This improvement, however, comes at the cost of higher component inventories, underscoring the trade-off between finished goods stockholding and upstream buffer investments. Such trade-offs highlight the importance of carefully selecting buffer locations according to cost structures and product differentiation strategies. Concerning safety stock formulation, the comparison between the factor-based red zone definition and the revised, variability-driven formula shows broadly similar outcomes in terms of calculated inventory levels. Nevertheless, the revised formula provides greater transparency and objectivity by directly incorporating measurable demand and lead time variability coefficients, thereby reducing subjectivity in parameter selection. This characteristic makes it more suitable for practical application in complex, data-rich production environments.

Overall, the findings suggest that DDMRP can be an effective replenishment approach in volatile environments, but its performance depends strongly on the configuration of buffers and the method used to calculate safety stock. Future research should extend this work by testing the revised safety stock formula across a broader set of production settings, incorporating stochastic supply disruptions and machine failures, and exploring its integration with advanced analytics for automated parameter tuning. Further investigation into the sensitivity of system performance under varying demand patterns and coefficients of variability represents an additional important direction for future work.