Prime Graphs with Almost True Twin Vertices

Abstract

A graph G consists of a possibly infinite set $V\left(G\right)$ of vertices with a collection $E\left(G\right)$ of unordered pairs of distinct vertices, called the set of edges of G. Such a graph is denoted by $\left(V\right(G),E(G\left)\right)$. Two distinct vertices u and v of a graph G are adjacent if $\{u,v\}\in E\left(G\right)$. Let G be a graph. A subset M of $V\left(G\right)$ is a module of G if every vertex outside M is adjacent to all or none of the vertices in M. The graph G is prime if it has at least four vertices, and its only modules are ∅, the single-vertex sets, and $V\left(G\right)$. Given two adjacent vertices u and v of G, v is a negative almost true twin of u in G if there is a vertex $x_v$ in $V\left(G\right)\setminus \left\{u\right\}$ non-adjacent to u such that the pair $\{u,v\}$ is a module of the graph $(V\left(G\right),E\left(G\right)\cup \left\{\{u,x_v\}\right\})$. In this paper, we study graphs with a negative almost true twin for a given vertex, and we give some applications. Firstly, we characterize these graphs by a special decomposition, and we specify the prime graphs among them. Secondly, we give three applications, giving methods for extending graphs to prime graphs. Finally, we study the prime induced subgraphs of the prime graphs with at least two negative almost true twins for a given vertex.

1. Introduction

All graphs in this paper are simple and undirected. Thus a graph G consists of a possibly infinite set $V\left(G\right)$ of vertices with a collection $E\left(G\right)$ of unordered pairs of distinct vertices, called the set of edges of G. Such a graph is denoted by $\left(V\right(G),E(G\left)\right)$. For example, given a set V, the graph $K_V:=(V,\{\{u,v\}:u\ne vs.\in V\})$ is called the complete graph on V, whereas the graph $(V,\varnothing )$ is called the empty graph on V.

Let $G:=(V,E)$ be a graph. Two distinct vertices u and v of G are adjacent if $\{u,v\}\in E$. An edge $\{u,v\}$ of G is denoted by $uv$. Given a vertex u, a neighbor of u is a vertex adjacent to u; the neighborhood of u, denoted by $N_G\left(u\right)$, is the set of all neighbors of u; and the vertex subset $V\setminus (N_G\left(u\right)\cup \left\{u\right\})$ is denoted by ${\overline{N}}_G\left(u\right)$. A dominating vertex (respectively, an isolated vertex) of the graph G is a vertex u such that $N_G\left(u\right)=V\setminus \left\{u\right\}$ (respectively, $N_G\left(u\right)=\varnothing$). Given two non-adjacent vertices u and v of G, the graph $(V,E\cup \{uv\left\}\right)$ is denoted by $G+uv$. Each vertex subset X is associated with the subgraph $G\left[X\right]:=(X,E\cap \{xy,x\ne y\in X\left\}\right)$ of G induced by X. Given a vertex subset X, the subgraph $G[V\setminus X]$ is denoted by $G-X$. Given a vertex x, the subgraph $G-\left\{x\right\}$ is also denoted by $G-x$. The cardinality of a (possibly infinite) set X is denoted by $\left|X\right|$.

A clique in G is a vertex subset X such that the subgraph $G\left[X\right]$ is the complete graph on X. An isomorphism from the graph G onto a graph $G^{\prime }=(V^{\prime },E^{\prime })$ is a bijection f from V onto $V^{\prime }$ such that for all $x,y\in V$, $xy\in E$ if and only if $f\left(x\right)f\left(y\right)\in E^{\prime }$. Two graphs are isomorphic if there exists an isomorphism from one onto the other.

Let x be a vertex and let Y be a subset of $V\setminus \left\{x\right\}$. The vertex x is complete (respectively, anti-complete) to Y if x is adjacent (respectively, is non-adjacent) to all vertices in Y. The vertex subset Y is uniform with respect to the vertex x if x is complete or anti-complete to Y; otherwise, x splits Y (or x is a splitter of Y).

Two disjoint vertex subsets X and Y are complete (respectively, anti-complete) to each other if the vertices x and y are adjacent (respectively, non-adjacent) for any $x\in X$ and $y\in Y$.

Given a graph G, a vertex subset M is a module [1] (interval [2] or autonomous [3]) of G if M is uniform with respect to any vertex outside it. The trivial modules of G are the empty set ∅, the vertex set $V\left(G\right)$, and the singletons $\left(\right\{x\},x\in V(G\left)\right)$. A module of a graph G distinct from $V\left(G\right)$ is a proper module of G. A graph is indecomposable if all its modules are trivial; otherwise, it is decomposable. Clearly, all graphs with at most two vertices are indecomposable, and all 3-vertex graphs are decomposable. Indecomposable graphs with at least four vertices are called prime graphs.

As usual, a partition of a set V is any collection of pairwise disjoint nonempty subsets of V covering V, i.e., of which the union is V. Notice that we consider ∅ as the unique partition of ∅.

A modular partition of a graph G is any partition of its vertex set into modules. According to the fifth assertion of Proposition 3 below, to any such modular partition $\mathcal{M}$, there corresponds a (quotient) graph $G/\mathcal{M}$ on the set of classes of $\mathcal{M}$: for any two distinct classes X and Y, $XY$ is an edge of $G/\mathcal{M}$ if and only if there is an $x\in X$ and a $y\in Y$ such that $xy$ is an edge of G (in which case $xy$ is an edge of G for any $x\in X$ and $y\in Y$).

Given two distinct vertices u and v of a graph G, the vertex v is a true twin (respectively, false twin) of u in G if it is adjacent (respectively, non-adjacent) to u and the pair $\{u,v\}$ is a module of G. Thus v is a true twin (respectively, false twin) of u if and only if $N_G\left(v\right)\cup \left\{v\right\}=N_G\left(u\right)\cup \left\{u\right\}$ (respectively, $N_G\left(v\right)=N_G\left(u\right)$).

In this paper, given a vertex u of a graph G, we introduce the following notion of the negative almost true twin vertex of u.

Consider a graph $G:=(V,E)$ and two distinct vertices $u\mathrm{and}v$ of G.

In a graph G, a vertex v is a negative almost true twin of u if the following two conditions hold: v is adjacent to u, and there exists at least one vertex $x_v$ not adjacent to u for which v and u are true twins in the graph $G+u{x}_v$. Notice that a negative almost true twin of u in G is neither a true twin nor a false twin of u in G. We denote $at{t}^{-}(G,u)$ as the set of negative almost true twins of u in G.

Consider $v\in at{t}^{-}(G,u)$. Clearly, the non-neighbor $x_v$ of u such that v is a true twin of u in the graph $G+u{x}_v$ is the unique splitter of the pair $\{u,v\}$ in G, and hence such a vertex is unique and is denoted by $Sp\left(\right\{u,v\left\}\right)$. The set $\{Sp\left(\{u,v\}\right):v\in at{t}^{-}(G,u)\}$ is denoted by $Spt{t}^{-}(G,u)$.

Example 1.

Consider the graph G illustrated in Figure 1. In this graph, the vertex a (respectively, b) is adjacent to u, while the vertex $a^{\prime }$ (respectively, $b^{\prime }$) is non-adjacent to u but adjacent to a (respectively, b). Furthermore, the pair $\{u,a\}$ (respectively, $\{u,b\}$) forms a module in $G+u{a}^{\prime }$ (respectively, $G+u{b}^{\prime }$), which means the vertex a (respectively, b) is a true twin of u in this augmented graph. Consequently, in G, the vertex a (respectively, b) is a negative almost true twin of u, and $a^{\prime }$ (respectively, $b^{\prime }$) is the unique splitter of the pair $\{u,a\}$ (respectively, $\{u,b\}$). However, the vertex c is adjacent to u, but the pair $\{u,c\}$ has two splitters in G, namely, $c^{\prime }$ and $d^{\prime }$. Therefore, c is not a negative almost true twin of u in G. Since, by definition, a negative almost true twin of u must be adjacent to u and $N_G\left(u\right)=\{a,b,c\}$, it follows that $at{t}^{-}(G,u)=\{a,b\}$ and $Spt{t}^{-}(G,u)=\{a^{\prime },b^{\prime }\}$.

The following observation is immediately deduced from the definitions.

Observation 1.

Given a graph $G:=(V,E)$ having a negative almost true twin of a vertex u, $at{t}^{-}(G,u)$ is a nonempty subset of $N_G\left(u\right)$, and $Spt{t}^{-}(G,u)$ is a nonempty subset of ${\overline{N}}_G\left(u\right)$.

In this paper, we study graphs with a negative almost true twin for a given vertex, and we give some applications. First, we characterize these graphs by a special decomposition. Second, we specify the prime graphs among these graphs. Third, we give three applications of our study. By these applications, we give particular methods for extending graphs to prime graphs. Fourth, we study the prime induced subgraphs of the prime graphs with at least two negative almost true twins for a given vertex. Finally, we introduce the negatively critical prime u-true twin graphs, and we obtain, as a consequence of our previous results a characterization of these graphs and a study of their prime subgraphs.

The subject of prime graphs is attractive. In particular, their importance is illustrated by the decomposition theorems obtained by T. Gallai for finite binary relations [3,4] and by B. Courcelle and C. Delhommé for the infinite binary relations [5] (see Section 3). Over the last twenty years, this topic has attracted the attention of several researchers. See [6,7,8,9,10,11].

2. Presentation of Results

To begin, given a vertex u of a graph G, we introduce the following notion of the u-characteristic triple of G; such a triplet leads to a special decomposition of G.

Definition 1.

Given a graph G and a vertex u, we call a u-characteristic triple of G any triple $(X,S,s)$, where X is a nonempty subset of $N_G\left(u\right)$, S is a nonempty subset of ${\overline{N}}_G\left(u\right)$, s is a surjective function from X to S, and by considering the subgraph $H:=G-(X\cup \{u\left\}\right)$ and the vertex subsets $\overline{X}:=N_G\left(u\right)\setminus X$ and $\overline{S}:={\overline{N}}_G\left(u\right)\setminus S$, the following three assertions hold.

(A₁) 

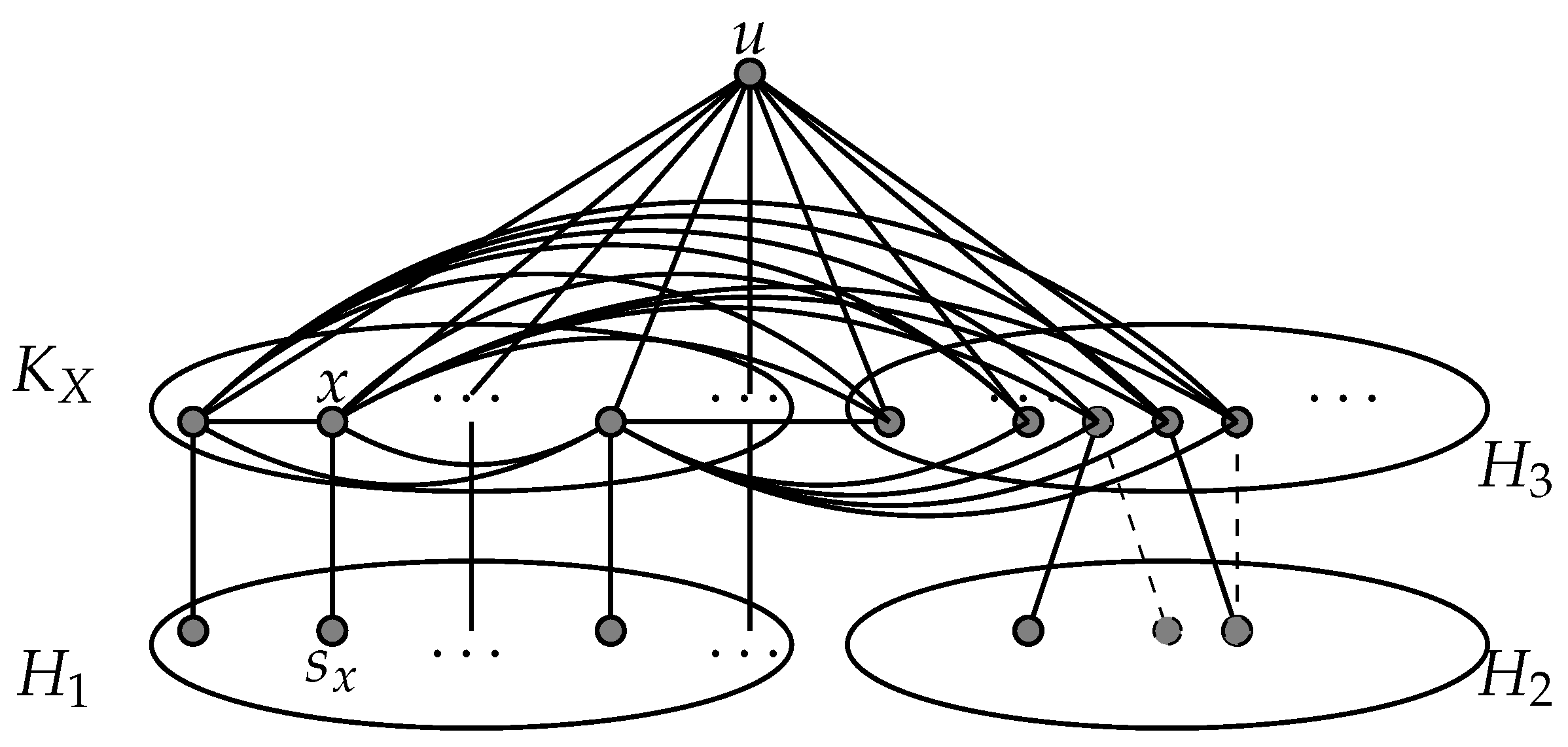
X is a clique in G, and $s\left(x\right)$ is the unique neighbor of x in S, for each vertex x in X.

(A₂) 

The two vertex subsets X and $\overline{X}$ are complete to each other, while X and $\overline{S}$ are anti-complete to each other.

(A₃) 

For each dominating vertex t of the subgraph $H\left[\overline{X}\right]$, $|N_H\left(t\right)\cap (S\cup \overline{S})|\ne 1$.

From the examples below, we see that there is no uniqueness of the triplet $(X,S,s)$ satisfying $\left(A_1\right)$ and $\left(A_2\right)$. On the other hand, as we will see in Theorem 1, we will have uniqueness of the triplet $(X,S,s)$ satisfying $\left(A_1\right),\left(A_2\right)$, and $\left(A_3\right)$.

Example 2.

(a) 

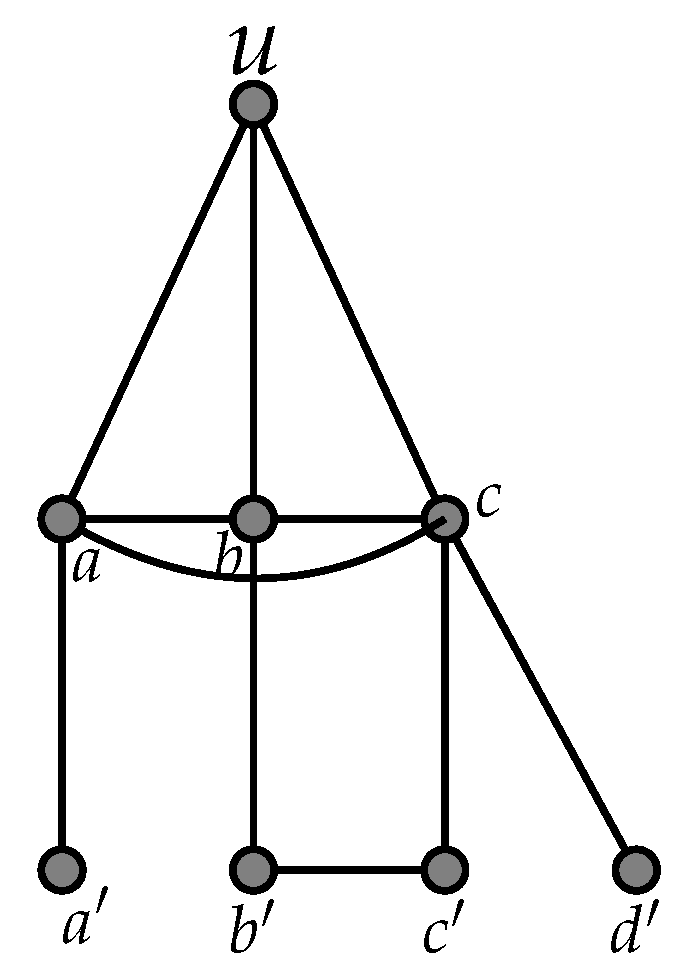
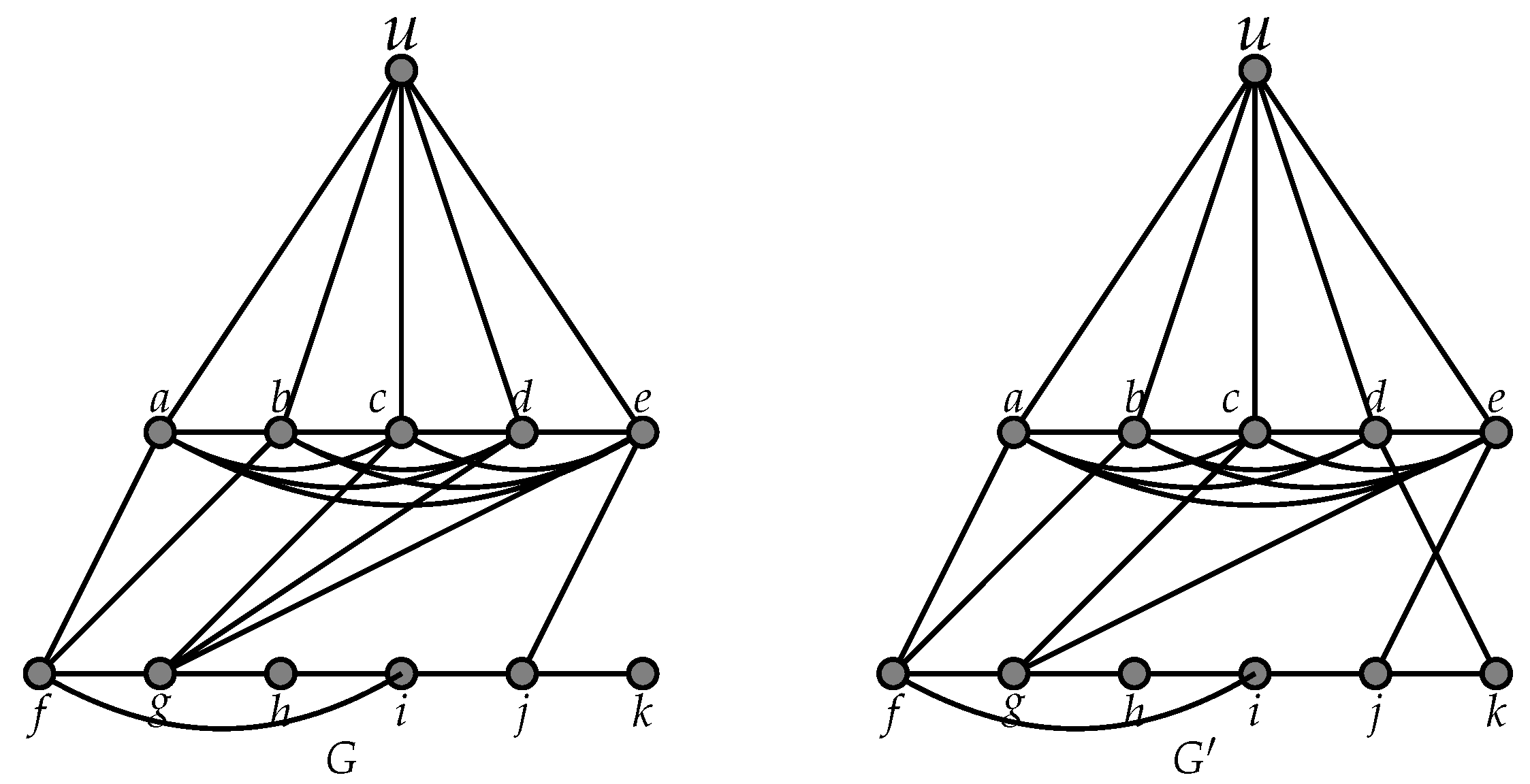
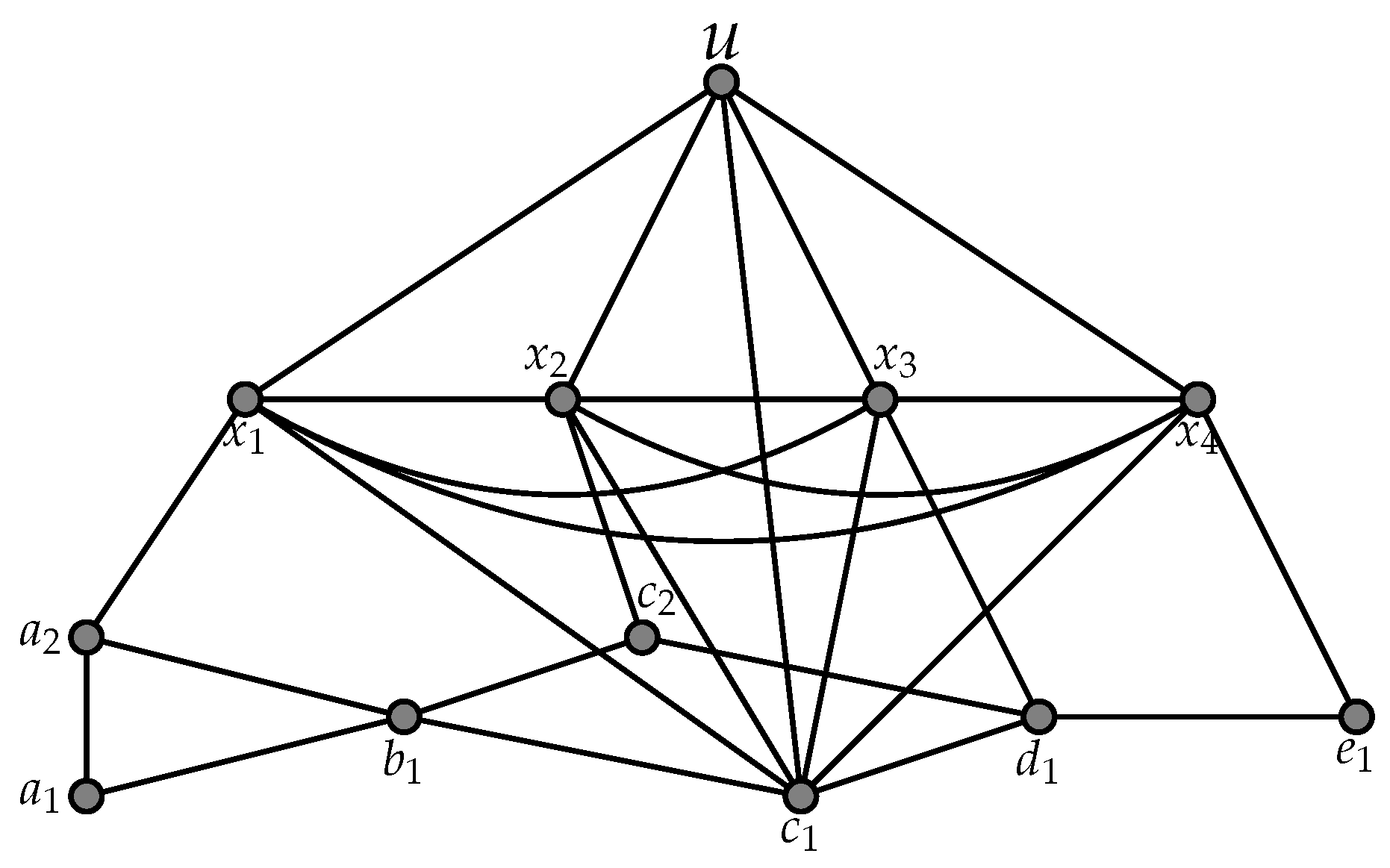
Consider the graph G illustrated in Figure 2. Let $X_1:=\{a,b,c\}$, $S_1:=\{f,g\}$, $\overline{X_1}:=N_G\left(u\right)\setminus X_1$, and $\overline{S_1}:={\overline{N}}_G\left(u\right)\setminus S_1$, and consider the subgraph $H_1:=G-(X_1\cup \left\{u\right\})$. Thus $\overline{X_1}=\{d,e\}$, $\overline{S_1}=\{h,i,j,k\}$. Let $s_1$ be the surjection from $X_1$ to $S_1$ defined by $s_1\left(a\right)=s_1\left(b\right)=f$ and $s_1\left(c\right)=g$. The triple $(X_1,S_1,s_1)$ satisfies assertions $\left(A_1\right)$ and $\left(A_2\right)$ but does not satisfy Assertion $\left(A_3\right)$ (because d is a dominating vertex in $H_1\left[\overline{X_1}\right]$, and $N_{H_1}\left(d\right)\cap (S_1\cup {\overline{S}}_1)=\left\{g\right\}$, and hence $N_{H_1}\left(d\right)\cap (S_1\cup {\overline{S}}_1)$ is a singleton of $S_1$). Now, consider the vertex subsets $X_2:=\{a,b,c,d\}$, $S_2:=\{f,g\}$, $\overline{X_2}:=N_G\left(u\right)\setminus X_2$, and $\overline{S_2}:={\overline{N}}_G\left(u\right)\setminus S_2$, and consider the subgraph $H_2:=G-(X_2\cup \left\{u\right\})$. Thus $\overline{X_2}=\left\{e\right\}$, $\overline{S_2}=\{h,i,j,k\}$. Let $s_2$ be the surjection from $X_2$ to $S_2$ defined by $s_2\left(a\right)=s_2\left(b\right)=f$ and $s_2\left(c\right)=s_2\left(d\right)=g$. The triple $(X_2,S_2,s_2)$ satisfies assertions $\left(A_1\right)$, $\left(A_2\right)$, and $\left(A_3\right)$. Notice that $X_2=at{t}^{-}(G,u)$ and $S_2=Spt{t}^{-}(G,u)$.

(b) 

Consider the graph $G^{\prime }$ illustrated in Figure 2. Let $X_1:=\{a,b,c\}$, $S_1:=\{f,g\}$, $\overline{X_1}:=N_{G^{\prime }}\left(u\right)\setminus X_1$, and $\overline{S_1}:={\overline{N}}_{G^{\prime }}\left(u\right)\setminus S_1$, and consider the subgraph $H_1:=G^{\prime }-(X_1\cup \left\{u\right\})$. Thus $\overline{X_1}=\{d,e\}$, $\overline{S_1}=\{h,i,j,k\}$. Let $s_1$ be the surjection from $X_1$ to $S_1$ defined by $s_1\left(a\right)=s_1\left(b\right)=f$ and $s_1\left(c\right)=g$. The triple $(X_1,S_1,s_1)$ satisfies assertions $\left(A_1\right)$ and $\left(A_2\right)$ but does not satisfy Assertion $\left(A_3\right)$ (because d is a dominating vertex in $H_1\left[\overline{X_1}\right]$, and $N_{H_1}\left(d\right)\cap (S_1\cup {\overline{S}}_1)=\left\{k\right\}$, and hence $N_{H_1}\left(d\right)\cap (S_1\cup {\overline{S}}_1)$ is a singleton of $\overline{S_1}$). Now, consider the vertex subsets $X_2:=\{a,b,c,d\}$, $S_2:=\{f,g,k\}$, $\overline{X_2}:=N_{G^{\prime }}\left(u\right)\setminus X_2$, and $\overline{S_2}:={\overline{N}}_{G^{\prime }}\left(u\right)\setminus S_2$, and consider the subgraph $H_2:=G^{\prime }-(X_2\cup \left\{u\right\})$. Thus $\overline{X_2}=\left\{e\right\}$, $\overline{S_2}=\{h,i,j\}$. Let $s_2$ be the surjection from $X_2$ to $S_2$ defined by $s_2\left(a\right)=s_2\left(b\right)=f$, $s_2\left(c\right)=g$, and $s_2\left(d\right)=k$. The triple $(X_2,S_2,s_2)$ satisfies assertions $\left(A_1\right)$, $\left(A_2\right)$, and $\left(A_3\right)$. Notice that $X_2=at{t}^{-}(G^{\prime },u)$ and $S_2=Spt{t}^{-}(G^{\prime },u)$.

Our first result, which is quite elementary, is the following characterization of graphs with a negative almost true twin for a given vertex.

Theorem 1.

A vertex u of a graph G has a negative almost true twin in G if and only if G admits a u-characteristic triple. Furthermore, if it exists, the u-characteristic triple is unique. In this case, the unique u-characteristic triple of G is $(at{t}^{-}(G,u),Spt{t}^{-}(G,u),s)$, where s is the function from $at{t}^{-}(G,u)$ to $Spt{t}^{-}(G,u)$, defined by $s:x\mapsto Sp\left(\right\{u,x\left\}\right)$.

Notice that the uniqueness of the u-characteristic triple, when it exists, is established in Lemma 5.

Notice that given a graph G having a negative almost true twin of some vertex u, we may have $Sp\left(\{u,v_1\}\right)=Sp\left(\{u,v_2\}\right)$ for some distinct vertices $v_1$ and $v_2$ in $at{t}^{-}(G,u)$. For instance, for each integer $n\ge 4$, in the graph $H:=K_{\{1,\dots ,n\}}-1n$, obtained from the complete graph on the set $\{1,\dots ,n\}$ by deleting the edge $1n$, we have $at{t}^{-}(H,1)=\{2,\dots ,n-1\}$ and $Spt{t}^{-}(H,1)=\left\{n\right\}$.

Our second result is the following characterization of prime graphs with a negative almost true twin for a given vertex.

Theorem 2.

Let G be a graph with at least four vertices, u be a vertex having a negative almost true twin in G, and $(at{t}^{-}(G,u),Spt{t}^{-}(G,u),s)$ be the u-characteristic triple of G. Consider the vertex subsets $X:=at{t}^{-}(G,u),\overline{X}:=N_G\left(u\right)\setminus X,S:=Spt{t}^{-}(G,u),and\overline{S}:={\overline{N}}_G\left(u\right)\setminus S$.

The graph G is prime if and only if the following two assertions hold.

1.

$|{\overline{N}}_G\left(u\right)|\ge 2$ and the function s is bijective.

2.

The subgraph $H:=G-(X\cup \{u\left\}\right)$ satisfies the following four conditions.

(a) 

The graph H has no dominating vertex in $\overline{X}$ and has no isolated vertex in $\overline{S}$.

(b) 

For each dominating vertex t of the subgraph $H\left[\overline{X}\right]$, t has at least two neighbors in $S\cup \overline{S}$.

(c) 

The graph H has no module M with $\left|M\right|\ge 2$ such that $M\subseteq \overline{S}$ or $M\subseteq \overline{X}$.

(d) 

The vertex set of the graph H has no 3-element partition $\{Z,Z^{-},Z^{+}\}$ with $\varnothing \ne Z^{-}\subseteq \overline{S}$ and $\varnothing \ne Z^{+}\subseteq \overline{X}$ such that Z and $Z^{-}$ are anti-complete to each other, while Z and $Z^{+}$ are complete to each other.

Observation 2.

(a) 

If Condition $\left(a\right)$ is not satisfied, then either the graph H has a dominating vertex t in $\overline{X}$ or an isolated vertex t in $\overline{S}$. As seen in the proof of Claim 3 of the proof of this theorem, $V\setminus \left\{t\right\}$ will be a non-trivial module of G.

(b) 

If Condition $\left(b\right)$ is not satisfied, then there is a dominating vertex t of the subgraph $H\left[\overline{X}\right]$ such that $|N_H\left(t\right)\cap (S\cup \overline{S})|\le 1$. As seen in the proof of Claim 4 of the proof of this theorem, $\{u,t\}$ will be a non-trivial module of G.

(c) 

If Condition $\left(c\right)$ is not satisfied, then the graph H has a non-trivial module M with $\left|M\right|\ge 2$ such that $M\subseteq \overline{S}$ or $M\subseteq \overline{X}$. As seen in the proof of Claim 5 of the proof of this theorem, M will be a non-trivial module of G.

(d) 

If Condition $\left(d\right)$ is not satisfied, then there is a 3-element partition $\{Z,Z^{-},Z^{+}\}$ of the graph H with $\varnothing \ne Z^{-}\subseteq \overline{S}$ and $\varnothing \ne Z^{+}\subseteq \overline{X}$ such that Z and $Z^{-}$ are anti-complete to each other, while Z and $Z^{+}$ are complete to each other. As seen in the proof of Claim 6 of the proof of this theorem, $V\setminus (Z^{-}\cup Z^{+})$ will be a non-trivial module of G.

After having given the notions and results which are needed in our proofs in Section 3, we prove Theorem 1 in Section 4 and Theorem 2 in Section 5.

In Section 6, we give three applications of Theorems 1 and 2. By these applications, we give particular methods for extending graphs to prime graphs.

Our first application is the following result by which we prove in particular that for any graph H with at least two vertices, there is a prime graph G, the vertex set of which is the disjoint union of $V\left(H\right)$ and a set Y such that Y is a clique in G, and H is an induced subgraph of G.

Proposition 1.

Given two (possibly infinite) equipotent disjoint sets S and X with at least two elements, a graph H on the set S, the complete graph $K_X$ on the set X, and a bijection $s:x\mapsto s_x$ from X onto S, consider the graph G with $V\left(G\right)=S\cup X\cup \left\{u\right\}$, where $u\notin S\cup X$ such that $N_G\left(u\right)=X$ and $E(G-u)=E\left(H\right)\cup E\left(K_X\right)\cup \{x{s}_x:x\in X\}$.

Then the graph G is prime and admits $(X,S,s)$ as the u-characteristic triple (Figure 3).

Example 3.

In this example, we present a graph that illustrates Proposition 1. Let G be the graph illustrated in Figure 4, named the Taurus. By denoting $X:=\{x_1,x_2\}$, $S:=\{s_1,s_2\}$ and s as the bijection from X to S defined by $s\left(x_1\right)=s_1$ and $s\left(x_2\right)=s_2$, the graph G verifies Proposition 1, and hence it is prime and admits $(X,S,s)$ as u-characteristic triple.

Our second application is the following result by which we prove in particular that given a graph $H_1$ with at least one vertex and two prime graphs $H_2$ and $H_3$ such that the vertex sets $V\left(H_1\right),V\left(H_2\right)$, and $V\left(H_3\right)$ are pairwise disjoint, there are many prime graphs G, the vertex set of which is the disjoint union of $V\left(H_1\right)\cup V\left(H_2\right)\cup V\left(H_3\right)$ and a set Y, where Y is a clique in G and each of the graphs $H_1,H_2$, and $H_3$ is an induced subgraph of G.

Proposition 2.

Let S and X be two (possibly infinite) equipotent disjoint nonempty sets, a graph $H_1$ on the set S, the complete graph $K_X$ on the set X, a bijection $s:x\mapsto s_x$ from X onto S, and two prime graphs $H_2$ and $H_3$ such that the sets $V\left(H_2\right),V\left(H_3\right),S$, and X are pairwise disjoint.

Consider a graph G with $V\left(G\right)=S\cup X\cup V\left(H_2\right)\cup V\left(H_3\right)\cup \left\{u\right\}$, where $u\notin S\cup X\cup V\left(H_2\right)\cup V\left(H_3\right)$ such that $N_G\left(u\right)=X\cup V\left(H_3\right)$ and $N_G\left(x\right)=(X\setminus \left\{x\right\})\cup V\left(H_3\right)\cup \{u,s_x\}$ for each $x\in X$.

Assume that there is a vertex in S having a neighbor in $V\left(H_2\right)$ or a non-neighbor in $V\left(H_3\right)$, and for each $i\in \{2,3\}$, there is a vertex in $V\left(H_j\right)$ having a neighbor and a non-neighbor in $V\left(H_i\right)$, where $\left\{j\right\}=\{2,3\}\setminus \left\{i\right\}$.

Then the graph G is prime and admits $(X,S,s)$ as a u-characteristic triple (Figure 5).

Example 4.

In this example, we present a graph that illustrates Proposition 2. Let G be the graph illustrated in Figure 6. We begin by denoting $X:=\{x_1,x_2\}$, $S:=\{s_1,s_2\}$, and s as bijection from X to S defined by $s\left(x_1\right)=s_1$ and $s\left(x_2\right)=s_2$. By denoting the graph $H_2:=G\left[\{s_3,s_4,s_5,s_6,s_7\}\right]$ and the graph $H_3:=G\left[\{x_3,x_4,x_5,x_6\}\right]$, we see that $H_3$ is a path of length greater than 3, and $H_2$ is a 5-cycle, then $H_2$ and $H_3$ are prime graphs. Thus the graph G verifies Proposition 2, and hence it is prime and admits $(X,S,s)$ as u-characteristic triple.

Our third application is the following result by which we prove in particular that for any possibly infinite graph H having a modular partition of which the corresponding quotient is prime, there are many prime graphs G, the vertex set of which is the disjoint union of $V\left(H\right)$ and a set Y such that Y is a clique in G, and H is an induced subgraph of G.

Theorem 3.

Consider a graph H having a modular partition $\mathcal{Q}$ of which the corresponding quotient is prime and two disjoint subsets ${\mathcal{A}}_1$ and ${\mathcal{A}}_2$ of $\mathcal{Q}$ such that $|\mathcal{Q}\setminus ({\mathcal{A}}_1\cup {\mathcal{A}}_2\left)\right|\ge 2$, and let T be a vertex subset of the graph H such that $|T\cap M|=1$ for each member M of $\mathcal{Q}$.

Then there are two disjoint subsets $Y_1$ and $Y_2$ of T with $|Y_1| = |{\mathcal{A}}_1\left|and\right|Y_2| = |{\mathcal{A}}_2|$ such that by considering the complete graph $K_X$ on a set X which is disjoint from $V\left(H\right)$ and equipotent to $V\left(H\right)\setminus (Y_1\cup Y_2)$ and a bijection $s:x\mapsto s_x$ from X onto $V\left(H\right)\setminus (Y_1\cup Y_2)$, the graph G with vertex set $X\cup V\left(H\right)\cup \left\{u\right\}$, where $u\notin V\left(H\right)\cup X$, such that $N_G\left(u\right)=X\cup Y_2$ and $E(G-u)=E\left(H\right)\cup E\left(K_X\right)\cup \{x{s}_x:x\in X\}\cup \{xy:x\in Xandy\in Y_2\}$, is prime and admits $(X,V\left(H\right)\setminus (Y_1\cup Y_2),s)$ as the u-characteristic triple (Figure 7).

Example 5.

In this example, we present a graph that illustrates Theorem 3. Let G be the graph illustrated in Figure 8. We begin by denoting the graph $H:=G\left[\{a_1,a_2,b_1,c_1,c_2,d_1,e_1\}\right]$. By denoting $X:=\{x_1,x_2,x_3,x_4\}$, $Y_1=\{a_1,b_1\}$, $Y_2=\left\{c_1\right\}$, $S:=V\left(H\right)\setminus (Y_1\cup Y_2)=\{a_2,c_2,d_1,e_1\}$ and s as the bijection from X to S defined by $s\left(x_1\right)=a_2$, $s\left(x_2\right)=c_2$, $s\left(x_3\right)=d_1$ and $s\left(x_4\right)=e_1$, we see that the graph G verifies Theorem 3, and hence it is prime and admits $(X,S,s)$ as a u-characteristic triple.

Observation 3.

Let $n\ge 4$ be an integer, and let $P_n$ be the usual n-vertex path; we name the vertices $v_1,v_2,\dots ,v_n$ in order. For the vertex $v_1$, we see that $at{t}^{-}(P_n,v_1)=\left\{v_2\right\}$ and $Spt{t}^{-}(P_n,v_1)=\left\{v_3\right\}$. Let s be the surjection from $at{t}^{-}(P_n,v_1)$ to $Spt{t}^{-}(P_n,v_1)$ defined by $s\left(v_2\right)=v_3$. By denoting $X:=\left\{v_2\right\}$, $S:=\left\{v_3\right\}$, $\overline{X}:=N_{P_n}\left(v_1\right)\setminus X$, and $\overline{S}:={\overline{N}}_{P_n}\left(v_1\right)\setminus S$, it is clear that $P_n$ is a prime graph with $(X,S,s)$ as the $v_1$—characteristic triple, with $\left|X\right|=1$, $\overline{X}=\varnothing$, and $\overline{S}\ne \varnothing$, and hence Theorem 2 is satisfied. However, the fact that $\overline{S}\ne \varnothing$ (respectively, $\overline{X}=\varnothing$, $\left|X\right|<2$) implies that this graph $P_n$ is not obtainable via Proposition 1 (respectively, Proposition 2 and Theorem 3).

In Section 7, we study the prime subgraphs of prime graphs with a negative almost true twin for a given vertex. Finally, in Section 8, after introducing the negatively critical prime u-true twin graphs, we obtain, as a consequence of our previous results, a characterization of these graphs and a study of their prime subgraphs.

3. Preliminaries

In this section, we recall some notions and results which are needed in our proofs.

The following proposition lists some basic properties of the modules of a graph.

Proposition 3

([12]). Let G be a graph.

1.

Given a vertex subset W of G, if M is a module of G, then $M\cap W$ is a module of $G\left[W\right]$.

2.

If M and N are modules of G, then $M\cap N$ is a module of G.

3.

If M and N are modules of G such that $M\cap N\ne \varnothing$, then $M\cup N$ is a module of G.

4.

If M and N are modules of G such that $M\setminus N\ne \varnothing$, then $N\setminus M$ is a module of G.

5.

If M and N are disjoint modules of G, then $MandN$ are either complete to each other or anti-complete to each other.

6.

If M is a module of G and N is a module of the subgraph $G\left[M\right]$, then N is a module of G.

It is well known that if a finite graph G is $P_4$-free, then G or its complement is disconnected. It follows that every finite prime graph has $P_4$ as an induced subgraph. Recall that $P_4$ denotes a 4-vertex path, and it is easy to verify that, up to isomorphism, $P_4$ is the unique 4-vertex prime graph. In [11], P. Ille proved that an infinite graph G is prime if and only if for each finite vertex subset A of G there is a finite vertex subset X including A such that $G\left[X\right]$ is prime. Thus, every (possibly infinite) prime graph has $P_4$ as an induced subgraph. The following theorem of A. Ehrenfeucht and G. Rozenberg permits the construction of larger, prime induced subgraphs.

Theorem 4

([13]). Let X be a vertex subset of a prime graph G such that $G\left[X\right]$ is prime. If G has at least two vertices outside X, then it has two distinct vertices x and y outside X such that $G[X\cup \{x,y\left\}\right]$ is prime.

Notice that this result was proved only for finite prime graphs in [13] and was proved for possibly infinite prime graphs in [11].

To prove its above compacity result, P. Ille obtained the following.

Theorem 5

([11]). Let X be a vertex subset of a prime graph G such that $G\left[X\right]$ is prime. If the vertex subset $V\left(G\right)\setminus X$ is infinite, then for each vertex v in $V\left(G\right)\setminus X$, there is a finite subset F of $V\left(G\right)\setminus X$ containing v such that the subgraph $G[X\cup F]$ is prime.

Using Theorem 5, P. Ille obtained the following corollary.

Corollary 1

([11]). Given an infinite prime graph G, for each infinite vertex subset X, there is a vertex subset Y including X such that $\left|Y\right|=\left|X\right|$, and the subgraph $G\left[Y\right]$ is prime.

To prove Theorem 3, we also need the following notions.

A module M of a graph G is strong if it is comparable with every module that it meets: for any module N of G, if $M\cap N\ne \varnothing$, then $M\subseteq N$ or $N\subseteq M$.

The following definition is a special case of Definition $2.1$ in [14].

Definition 2.

We say that a graph is robust if its maximal proper strong modules form a partition of its vertex set or if that vertex set is a singleton. For a robust graph with at least two vertices, we call its maximal proper strong modules the modular components, and we call the canonical partition the partition that they form. For a graph with at most one vertex, we call the canonical partition the unique partition of its vertex set. The frame of a robust graph is its quotient by its canonical partition.

In the sequel, the canonical partition of a robust graph G is denoted by $\mathcal{P}\left(G\right)$.

The two assertions of the following result of B. Courcelle and C. Delhommé are derived, respectively, from Corollaries 4.2 and 4.4 of [5]. (Cf. [15,16] for posets and graphs and [3,4] for finite binary relations.)

Theorem 6

([5]).

1.

A graph G is robust as soon as it has a maximal proper strong module.

2.

The frame of a robust graph G is either prime or a complete graph or an empty graph.

Notice that, by the first assertion of Theorem 6, every finite graph is robust.

Now, we recall two results on robust graphs.

The following lemma is a special case of Lemma 2.3 obtained by Boudabbous and Delhommé in [17].

Lemma 1

([17]). Consider a graph G admitting a modular partition $\mathcal{M}$ of which the corresponding quotient is prime. Then the graph G is robust, and $\mathcal{M}$ is its canonical partition. The members of $\mathcal{M}$ are the maximal proper modules, and every proper module is included in such a member.

We shall also need the following lemma, which is an immediate consequence of Lemma 1.

Lemma 2.

Given a robust graph G admitting a prime frame, the following assertions hold.

1.

Given a vertex subset A, if A does not include any element of $\mathcal{M}$, then the subgraph $G-A$ is robust, $\mathcal{P}(G-A)=\{X\setminus A:X\in \mathcal{P}(G\left)\right\}$, and $G-A$ has a prime frame which is isomorphic to the frame of G.

2.

G has no modular partition in exactly two modules.

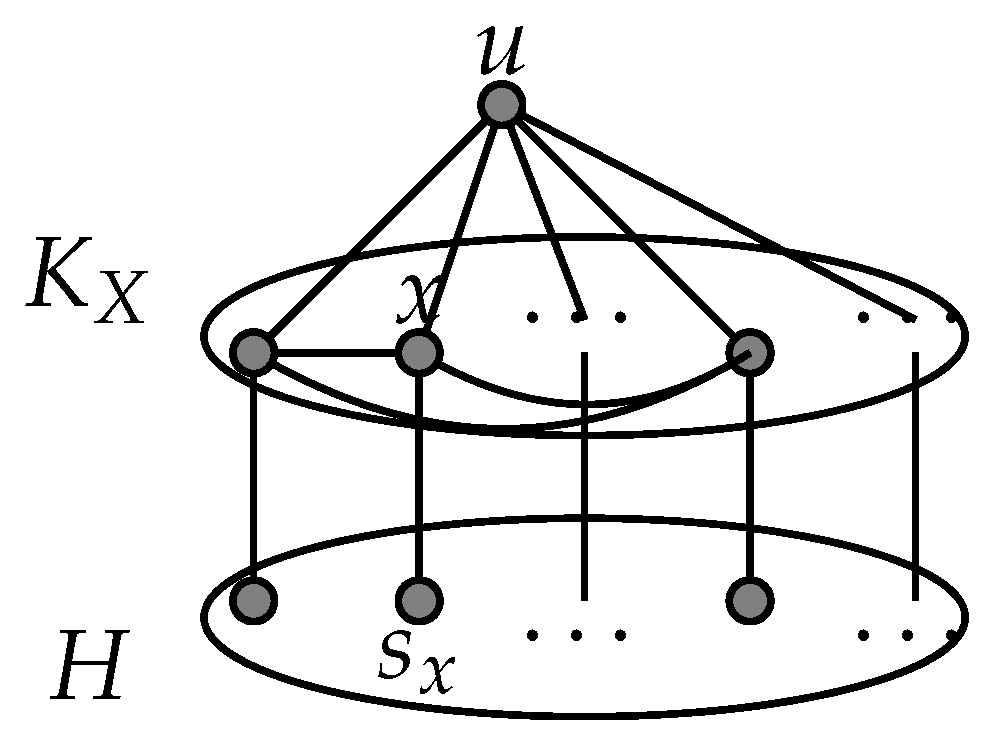
4. A Special Decomposition of Graphs with a Negative Almost True Twin for a Given Vertex

This section is reserved for the proof of Theorem 1.

First, we obtain the following lemma, which provides a constructive definition of the sets $at{t}^{-}(G,u)$ and $Spt{t}^{-}(G,u)$. Its first assertion characterizes the elements of $at{t}^{-}(G,u)$ based on adjacency to the vertex u, while the second constructs $Spt{t}^{-}(G,u)$ explicitly from $at{t}^{-}(G,u)$. This lemma is crucial for the proofs of Lemmas 4 and 5.

Lemma 3.

Given a vertex u of a graph G, the following two assertions hold.

1.

$at{t}^{-}(G,u)=\{x\in N_G\left(u\right):\exists v\in {\overline{N}}_G\left(u\right)such that{N}_G\left(x\right)\cup \left\{x\right\}=N_G\left(u\right)\cup \{u,v\}\}$.

2.

$Spt{t}^{-}(G,u)=\{v\in {\overline{N}}_G\left(u\right):\exists x\in at{t}^{-}(G,u)such thatvx\in E\left(G\right)\}$.

Proof. 

Consider a vertex u of a graph G.

1.

Consider a neighbor x of u in G.

Clearly, $x\in at{t}^{-}(G,u)$ iff there is a non-neighbor v of u such that the pair $\{u,x\}$ is a module of the graph $G+uv$. It follows that $x\in at{t}^{-}(G,u)$ iff there is a non-neighbor v of u such that $N_{G+uv}\left(x\right)\cup \left\{x\right\}=N_{G+uv}\left(u\right)\cup \left\{u\right\}$.

Note that, given a non-neighbor v of u, $N_{G+uv}\left(u\right)=N_G\left(u\right)\cup \left\{v\right\}$ and $N_{G+uv}\left(x\right)=N_G\left(x\right)$. Therefore, $x\in at{t}^{-}(G,u)$ iff there is a non-neighbor v of u such that $N_G\left(x\right)\cup \left\{x\right\}=N_G\left(u\right)\cup \{u,v\}$.

It follows that $at{t}^{-}(G,u)=\{x\in N_G\left(u\right):\exists v\in {\overline{N}}_G\left(u\right)\mathrm{such} \mathrm{that}{N}_G\left(x\right)\cup \left\{x\right\}=N_G\left(u\right)\cup \{u,v\}\}$.

2.

Recall that $Spt{t}^{-}(G,u)=\{Sp\left(\{u,x\}\right):x\in at{t}^{-}(G,u)\}$, and consider a vertex v of G. Clearly, $v\in Spt{t}^{-}(G,u)$ iff v is a non-neighbor of u, and there is a vertex x in $at{t}^{-}(G,u)$ such that v is the unique splitter of the pair $\{u,x\}$ in G. It follows that $v\in Spt{t}^{-}(G,u)$ iff $v\in {\overline{N}}_G\left(u\right)$, and there is a vertex x in $at{t}^{-}(G,u)$ such that $vx\in E\left(G\right)$. Therefore, $Spt{t}^{-}(G,u)=\{v\in {\overline{N}}_G\left(u\right):\exists x\in at{t}^{-}(G,u)\mathrm{such} \mathrm{that}vx\in E\left(G\right)\}$.

□

Second, we obtain the following two lemmas from which Theorem 1 can be immediately deduced.

Lemma 4.

Let G be a graph, u be a vertex having a negative almost true twin, and s be the function from $at{t}^{-}(G,u)$ to $Spt{t}^{-}(G,u)$, defined by $s:x\mapsto Sp\left(\right\{u,x\left\}\right)$.

Then $(at{t}^{-}(G,u),Spt{t}^{-}(G,u),s)$ is a u-characteristic triple of G.

Proof. 

First notice that by Observation 1, $at{t}^{-}(G,u)$ is a nonempty subset of $N_G\left(u\right)$ and $Spt{t}^{-}(G,u)$ is a nonempty subset of ${\overline{N}}_G\left(u\right)$, and by the definition of $Spt{t}^{-}(G,u)$, the function s is surjective.

Second, consider the subgraph $H:=G-(at{t}^{-}(G,u)\cup \left\{u\right\})$ and the vertex subsets $\overline{at{t}^{-}(G,u)}:=N_G\left(u\right)\setminus at{t}^{-}(G,u)$ and $\overline{Spt{t}^{-}(G,u)}:={\overline{N}}_G\left(u\right)\setminus Spt{t}^{-}(G,u)$.

To prove that $(at{t}^{-}(G,u),Spt{t}^{-}(G,u),s)$ is a u-characteristic triple of G, we will prove that this triple satisfies the three assertions $\left(A_1\right),\left(A_2\right)$, and $\left(A_3\right)$ of Definition 1.

• The fact that $at{t}^{-}(G,u)$ is a clique in G is an immediate consequence of the first assertion of Lemma 3. The fact that the vertex $s\left(x\right)=Sp\left(\right\{u,x\left\}\right)$ is the unique neighbor of x in $Spt{t}^{-}(G,u)$ is an immediate consequence of Lemma 3. Thus Assertion $A_1$ is satisfied.
• Consider three vertices $v,t$, and w with $v\in at{t}^{-}(G,u),t\in \overline{at{t}^{-}(G,u)}$, and $w\in \overline{Spt{t}^{-}(G,u)}$.
  It follows from Lemma 3 that v is adjacent to t and is non-adjacent to w.
  It follows that the vertex subsets $at{t}^{-}(G,u)$ and $\overline{at{t}^{-}(G,u)}$ are complete to each other, while $at{t}^{-}(G,u)$ and $\overline{Spt{t}^{-}(G,u)}$ are anti-complete to each other. Thus Assertion $A_2$ is satisfied.
• If t is a dominating vertex of the subgraph $H\left[\overline{at{t}^{-}(G,u)}\right]$, then by Assertion $A_2$, t is complete to the vertex subset $N_G\left(u\right)\setminus \left\{t\right\}$, and hence by Lemma 3, the fact that $t\notin at{t}^{-}(G,u)$ implies that $|N_H\left(t\right)\cap {\overline{N}}_G\left(u\right)|\ne 1$. Thus Assertion $A_3$ is satisfied.

□

Lemma 5.

Consider a graph G and a vertex u of G. If $(X,S,s)$ is a u-characteristic triple of G, then the vertex u has a negative almost true twin in G, $X=at{t}^{-}(G,u),S=Spt{t}^{-}(G,u))$, and $s\left(x\right)=Sp\left(\right\{u,x\left\}\right),foreachx\in X$.

Proof. 

Assume that $(X,S,s)$ is a u-characteristic triple of G. Thus X is a nonempty subset of $N_G\left(u\right)$, S is a nonempty subset of ${\overline{N}}_G\left(u\right)$, s is a surjective function from X to S, and by considering the subgraph $H:=G-(X\cup \{u\left\}\right)$ and the vertex subsets $\overline{X}:=N_G\left(u\right)\setminus X$ and $\overline{S}:={\overline{N}}_G\left(u\right)\setminus S$, the three assertions $\left(A_1\right),\left(A_2\right)$, and $\left(A_3\right)$ of Definition 1 are satisfied.

Claim 1. The vertex u has a negative almost true twin in G, $X\subseteq at{t}^{-}(G,u)$, and $S\subseteq Spt{t}^{-}(G,u)$.

Indeed, notice that the vertex u has a negative almost true twin in G iff the vertex subset $at{t}^{-}(G,u)$ is nonempty. Thus since the vertex subset X is nonempty, it suffices to prove that $X\subseteq at{t}^{-}(G,u)$, and $S\subseteq Spt{t}^{-}(G,u)$. Since, in addition, the function s is surjective, it suffices to prove that $x\in at{t}^{-}(G,u)$ and $s\left(x\right)\in Spt{t}^{-}(G,u)$ for each $x\in X$. Consider a vertex x in X. By assertions $\left(A_1\right)$ and $\left(A_2\right)$, it is easy to see that $x\in N_G\left(u\right),s\left(x\right)\in {\overline{N}}_G\left(u\right)$, and $N_G\left(x\right)\cup \left\{x\right\}=N_G\left(u\right)\cup \{u,s\left(x\right)\}$. Thus by Lemma 3, $x\in at{t}^{-}(G,u)$ and $s\left(x\right)\in Spt{t}^{-}(G,u)$.

Claim 2. $at{t}^{-}(G,u)=X$.

Indeed, by definition, $at{t}^{-}(G,u)\subseteq N_G\left(u\right)$. Thus by Claim 1, it suffices to prove that $at{t}^{-}(G,u)\cap \overline{X}=\varnothing$. To do so, consider a vertex t in $\overline{X}$, and let us prove that $t\notin at{t}^{-}(G,u)$.

First, assume that t is a dominating vertex of the subgraph $H\left[\overline{X}\right]$. By Assertion $\left(A_3\right)$, $|N_H\left(t\right)\cap (S\cup \overline{S})|=|N_H\left(t\right)\cap {\overline{N}}_G\left(u\right)|\ne 1$, and hence the first assertion of Lemma 3 implies that $t\notin at{t}^{-}(G,u)$.

Second, assume that t is not a dominating vertex of $H\left[\overline{X}\right]$. Thus there is a non-neighbor w of t in $\overline{X}$. Clearly, $w\in N_G\left(u\right)\setminus (N_G\left(t\right)\cup \left\{t\right\})$, which implies that $N_G\left(t\right)\cup \left\{t\right\}\ne N_G\left(u\right)\cup \{u,v\}$ for each vertex v in ${\overline{N}}_G\left(u\right)$. Therefore by the first assertion of Lemma 3, $t\notin at{t}^{-}(G,u)$.

Claim 3. $Spt{t}^{-}(G,u)=S$.

Indeed, by definition, $Spt{t}^{-}(G,u)\subseteq {\overline{N}}_G\left(u\right)$. Thus by Claim 1, it suffices to prove that $Spt{t}^{-}(G,u)\cap \overline{S}=\varnothing$. To do so, consider a vertex t in $\overline{S}$, and let us prove that $t\notin Spt{t}^{-}(G,u)$.

By Assertion $\left(A_2\right)$, the vertex t is anti-complete to the vertex subset X, and hence it is anti-complete to $at{t}^{-}(G,u)$ by Claim 2. Therefore the second assertion of Lemma 3 implies that $t\notin Spt{t}^{-}(G,u)$.

Claim 4. $s\left(x\right)=Sp\left(\right\{u,x\left\}\right),foreachx\in X$.

Indeed, let $x\in X$. By Claim 2, $x\in at{t}^{-}(G,u)$. Thus $Sp\left(\right\{u,x\left\}\right)$ is the unique splitter of the pair $\{u,x\}$ in G. The fact that $s\left(x\right)$ is adjacent to x and non-adjacent to u implies that $s\left(x\right)$ is a splitter of the pair $\{u,x\}$ in G. It follows that $s\left(x\right)=Sp\left(\right\{u,x\left\}\right)$. □

5. A Characterization of Prime Graphs with a Negative Almost True Twin for a Given Vertex

This section is reserved for the proof of Theorem 2.

For a graph G containing a vertex u with a negative almost true twin, Theorem 2 uses the u-characteristic triple of G to provide necessary and sufficient conditions for G to be prime.

Proof. 

Let $G:=(V,E)$ be a graph with at least four vertices, u be a vertex such that $at{t}^{-}(G,u)$ is nonempty, and $(at{t}^{-}(G,u),Spt{t}^{-}(G,u),s)$ be the u-characteristic triple of G.

Consider the vertex subsets $X:=at{t}^{-}(G,u),\overline{X}:=N_G\left(u\right)\setminus X$, $S:=Spt{t}^{-}(G,u),\mathrm{and}\overline{S}:={\overline{N}}_G\left(u\right)\setminus S$, and the subgraph $H:=G-(\left\{u\right\}\cup at{t}^{-}(G,u))$. Thus the triple $(X,S,s)$ satisfies the three assertions $A_1,A_2,$ and $A_3$ of Definition 1. By Theorem 1, s is the surjective function $s:x\mapsto s_x:=Sp\left(\{u,x\}\right)$ from X to S, and by Assertion $A_1$ of Definition 1, the vertex $s_x$ is the unique neighbor of x in S for each vertex x in X.

First, assume that the graph G is prime. We prove the necessity of the two conditions of Theorem 2 by the following six claims.

Claim 1. The function s is bijective.

Indeed, we have only to prove that the function s is injective. To the contrary, suppose that there are two distinct vertices $v_1\mathrm{and}{v}_2$ in $at{t}^{-}(G,u)$ such that $s_{v_1}=s_{v_2}$, and let $w:=s_{v_1}=s_{v_2}$. Thus w is a non-neighbor of u in G, and each of the pairs $\{u,v_1\}$ and $\{u,v_2\}$ is a module of the graph $G+uw$, and hence $w\notin \{u,v_1,v_2\}$, and by the third assertion of Proposition 3, $\{u,v_1,v_2\}$ is a module of the graph $G+uw$. To obtain a contradiction, we will prove that the pair $\{v_1,v_2\}$ is a module of the prime graph G. First, notice the fact that $\{u,v_1,v_2\}$ is a module of the graph $G+uw$ implies that, in the graph G, the pair $\{v_1,v_2\}$ is uniform with respect to any vertex outside $\{u,v_1,v_2,w\}$. Second, in the graph G, the vertex w is non-adjacent to u and is adjacent to both $v_1$ and $v_2$, and hence the pair $\{v_1,v_2\}$ is also uniform with respect to w. Finally, the vertex u is complete to the pair $\{v_1,v_2\}$ in G. Therefore, the pair $\{v_1,v_2\}$ is a module of G.

Claim 2. $|{\overline{N}}_G\left(u\right)|\ge 2$.

Indeed, to the contrary, suppose that $|{\overline{N}}_G\left(u\right)|\le 1$. Thus the fact that S is a nonempty subset of ${\overline{N}}_G\left(u\right)$ implies that $|{\overline{N}}_G\left(u\right)|=1$ and $S={\overline{N}}_G\left(u\right)$. Since the function s is bijective, it follows that there is a neighbor v of u such that $X=\left\{v\right\}$ and $S={\overline{N}}_G\left(u\right)=\left\{s_v\right\}$. Therefore, the fact that X and $\overline{X}$ are complete to each other implies that the vertex v is a dominating vertex of G, and hence $V\setminus \left\{v\right\}$ is a non-trivial module of G, contradicting the fact that the graph G is prime.

Claim 3. The graph H has no dominating vertex in $\overline{X}$ and has no isolated vertex in $\overline{S}$.

Indeed, to the contrary, suppose that the graph H has a dominating vertex (respectively, an isolated vertex) t in $\overline{X}$ (respectively, in $\overline{S}$). Assertion $A_2$ of Definition 1 implies that in the graph G, the vertex t is complete (respectively, is anti-complete) to $\left\{u\right\}\cup X$. It follows that t is complete (respectively, is anti-complete) to $V\setminus \left\{t\right\}$, and hence $V\setminus \left\{t\right\}$ is a non-trivial module of the graph G, contradicting the fact that the graph G is prime.

Claim 4. For each dominating vertex t of the subgraph $H\left[\overline{X}\right]$, t has at least two neighbors in $S\cup \overline{S}$.

Indeed, to the contrary, suppose that the subgraph $H\left[\overline{X}\right]$ has a dominating vertex t such that t has at most one neighbor in $S\cup \overline{S}$. Since by Assertion $A_3$ of Definition 1, $|N_H\left(t\right)\cap (S\cup \overline{S})|\ne 1$, it follows that $|N_H\left(t\right)\cap (S\cup \overline{S})|=0$. Thus in the graph G, on the one hand, t is anti-complete to $S\cup \overline{S}$, and on the other hand, Assertion $A_2$ of Definition 1 implies that the vertex t is complete to $(N_G\left(u\right)\cup \left\{u\right\})\setminus \left\{t\right\}$. If follows that $N_G\left(t\right)\cup \left\{t\right\}=N_G\left(u\right)\cup \left\{u\right\}$, which implies that the vertex t is a true twin of u in G, and hence the pair $\{u,t\}$ is a module of G, contradicting the fact that the graph G is prime.

Claim 5. The graph H has no module M with $\left|M\right|\ge 2$ such that $M\subseteq \overline{X}$ or $M\subseteq \overline{S}$.

Indeed, to the contrary, suppose that the graph H has a module M with $\left|M\right|\ge 2$ such that $M\subseteq \overline{X}$ or $M\subseteq \overline{S}$. Given a vertex t of G in $\left\{u\right\}\cup X$, Assertion $A_2$ of Definition 1 implies that in the graph G, the vertex t is anti-complete to M when $M\subseteq \overline{S}$ and is complete to M when $M\subseteq \overline{X}$. Thus, in the graph G, the vertex subset M is uniform with respect to any vertex in $\left\{u\right\}\cup X$. Since, in addition, M is a module of the subgraph $H=G-\left(\right\{u\}\cup X)$, it follows that M is a non-trivial module of G, contradicting the fact that the graph G is prime.

Claim 6. The vertex set of the graph H has no 3-element partition $\{Z,Z^{-},Z^{+}\}$ with $\varnothing \ne Z^{-}\subseteq \overline{S}$ and $\varnothing \ne Z^{+}\subseteq \overline{X}$ such that Z and $Z^{-}$ are anti-complete to each other, while Z and $Z^{+}$ are complete to each other.

Indeed, to the contrary, suppose that the vertex set of the graph H has a 3-element partition $\{Z,Z^{-},Z^{+}\}$ with $\varnothing \ne Z^{-}\subseteq \overline{S}$ and $\varnothing \ne Z^{+}\subseteq \overline{X}$ such that Z and $Z^{-}$ are anti-complete to each other, while Z and $Z^{+}$ are complete to each other. Assertion $A_2$ of Definition 1 implies that in the graph G, the vertex subsets $Z^{-}$ and $\left\{u\right\}\cup X$ are anti-complete to each other, while the vertex subsets $Z^{+}$ and $\left\{u\right\}\cup X$ are complete to each other. Since $V=V\left(H\right)\cup \left(\right\{u\}\cup X)$, it follows that, in the graph G, $Z^{-}$ and $V\setminus (Z^{-}\cup Z^{+})$ are anti-complete to each other, while $Z^{+}$ and $V\setminus (Z^{-}\cup Z^{+})$ are complete to each other. Thus $V\setminus (Z^{-}\cup Z^{+})$ is a non-trivial module of the graph G, contradicting the fact that the graph G is prime.

Second, assume that the two assertions of Theorem 2 are satisfied. Thus the function $s:x\mapsto s_x=Sp\left(\{u,x\}\right)$ is a bijection from X onto S such that for each vertex x in X, the vertex $s_x$ is the unique neighbor of x in S. It follows that each vertex w in S has a unique neighbor in X, namely, the vertex x in X such that $w=s_x$.

We prove that the graph G is prime by the following four claims.

Claim 7. For any vertices $t\in \overline{X}$ and $w\in V\setminus \left\{t\right\}$, the pair $\{t,w\}$ is not a module of G.

Indeed, consider a vertex t in $\overline{X}$.

First, let us prove that $\{t,u\}$ is not a module of G. To the contrary, suppose that $\{t,u\}$ is a module of G. Thus t is a true twin of u in G, and hence $N_G\left(t\right)\cup \left\{t\right\}=N_G\left(u\right)\cup \left\{u\right\}=X\cup \overline{X}\cup \left\{u\right\}$. It follows that t is a dominating vertex of the subgraph $H\left[\overline{X}\right]$ such that t has no neighbor in $S\cup \overline{S}$, contradicting Condition $\left(b\right)$ of the second assertion of Theorem 2.

Second, given a vertex w in $\overline{N_G}\left(u\right)=S\cup \overline{S}$, the fact that u is adjacent to t in G implies that u is a splitter of the pair $\{w,t\}$ in G, and hence $\{w,t\}$ is not a module of G.

Third, given a vertex w in $\overline{X}\setminus \left\{t\right\}$, the pair $\{w,t\}$ is not a module of G because otherwise, $\{w,t\}$ will be a 2-element module of the subgraph H included in $\overline{X}$, which contradicts Condition $\left(c\right)$ of the second assertion of Theorem 2.

Finally, to the contrary, suppose that there is $w\in X$ such that the pair $\{w,t\}$ is a module of G, and consider the unique neighbor $s_w$ of w in S. By Assertion $A_2$ of Definition 1, w is adjacent to t, and hence w is a true twin of t in the graph G. Thus $N_G\left(t\right)\cup \left\{t\right\}=N_G\left(w\right)\cup \left\{w\right\}$. Since $w\in X=at{t}^{-}(G,u)$, Lemma 3 implies that $N_G\left(w\right)\cup \left\{w\right\}=N_G\left(u\right)\cup \{u,s_w\}$. It follows that t is a dominating vertex of the subgraph $H\left[\overline{X}\right]$ such that $N_H\left(t\right)\cap (S\cup \overline{S})=\left\{s_w\right\}$, contradicting Assertion $A_3$ of Definition 1.

Claim 8. The graph G has no non-trivial module M such that $u\notin M$.

Indeed, to the contrary, suppose that G has a non-trivial module M such that $u\notin M$. Thus, the vertex subset M is uniform with respect to the vertex u, and hence either $M\subseteq {\overline{N}}_G\left(u\right)=S\cup \overline{S}$ or $M\subseteq N_G\left(u\right)=X\cup \overline{X}$. Thus Condition $\left(c\right)$ of the second assertion of Theorem 2 implies that either M is a subset of $S\cup \overline{S}$ with $M\cap S\ne \varnothing$ or M is a subset of $X\cup \overline{X}$ with $M\cap X\ne \varnothing$ because otherwise, M would be a module with at least two vertices of the subgraph H such that $M\subseteq \overline{S}$ or $M\subseteq \overline{X}$.

To begin, assume that M is a subset of $S\cup \overline{S}$ with $M\cap S\ne \varnothing$ and let w be a vertex in $M\cap S$. Consider the vertex x in X such that $w=s_x$. Thus w is the unique neighbor of x in S. The fact that ($x\notin M,w\in M,\mathrm{and}x$ is adjacent to w) implies that x is complete to the vertex subset M. It follows that $M\cap S=\left\{w\right\}$. By Assertion $A_2$ of Definition 1, the vertex x is anti-complete to the vertex subset $\overline{S}$, and hence $M\subseteq S$. Therefore $M=\left\{w\right\}$, which contradicts the fact that M is a non-trivial module of G.

Now, assume that M is a subset of $X\cup \overline{X}$ with $M\cap X\ne \varnothing$, and let x be a vertex in $M\cap X$. Consider the vertex $s_x$, which is the unique neighbor of x in S and for which x is the unique neighbor in X. Clearly, the fact that $s_x\notin M$ and $x\in M$ implies that $s_x$ is complete to the vertex subset M. It follows that $M\cap X=\left\{x\right\}$. By the first assertion of Proposition 3, $M\cap V\left(H\right)$ is a module of the graph H, and hence the fact that $M\cap V\left(H\right)=M\cap \overline{X}=M\setminus \left\{x\right\}$ implies that $M\setminus \left\{x\right\}$ is a nonempty module of the subgraph H included in $\overline{X}$. Thus Condition $\left(c\right)$ of the second assertion of Theorem 2 implies that $M\setminus \left\{x\right\}$ is a singleton $\left\{t\right\}$ of $\overline{X}$. Therefore $M=\{t,x\}$ with $t\in \overline{X}$ and $x\in X$, which contradicts Claim 7.

Claim 9. The graph G has no non-trivial module M such that $u\in M$ and $M\cap X\ne \varnothing$.

Indeed, to the contrary, suppose that G has a non-trivial module M such that $u\in M$ and $M\cap X\ne \varnothing$.

Given a vertex x in $M\cap X$, the fact that the vertex $s_x$ is a splitter of $\{u,x\}$ in G implies that $s_x\in M$. On the other hand, given $x\in M\cap X$ and $y\in X\setminus \left\{x\right\}$, y is adjacent to x and non-adjacent to $s_x$, and hence the fact that $\{x,s_x\}\subseteq M$ implies that $y\in M$. It follows that $X\cup S\subseteq M$, and hence $X\cup S\cup \left\{u\right\}\subseteq M$. Since the vertex u is anti-complete to $\overline{S}$, while it is complete to $\overline{X}$, $\overline{S}\setminus M$ and M are anti-complete to each other, while $\overline{X}\setminus M$ and M are complete to each other. Consider the three vertex subsets $Z,Z^{-}$, and $Z^{+}$ of the subgraph H defined by $Z:=S\cup (M\cap (\overline{S}\cup \overline{X}))=M\setminus (X\cup \left\{u\right\}),Z^{-}:=\overline{S}\setminus M$, and $Z^{+}:=\overline{X}\setminus M$.

Clearly, in the subgraph H, Z and $Z^{-}$ are anti-complete to each other, while Z and $Z^{+}$ are complete to each other. Since $V\left(H\right)$ is the disjoint union $Z\cup Z^{-}\cup Z^{+}$, Condition $\left(d\right)$ of the second assertion of Theorem 2 implies that at least one of the sets $Z^{-}$ and $Z^{+}$ is empty. Thus, the fact that M is a non-trivial module of G implies that exactly one of the sets $Z^{-}$ and $Z^{+}$ is empty. In the sequel, we assume that $Z^{-}$ (respectively, $Z^{+}$) is empty. Clearly, in the graph H, $Z^{+}$ and $V\left(H\right)\setminus Z^{+}$ (respectively, $Z^{-}$ and $V\left(H\right)\setminus Z^{-}$) are complete to each other (respectively, anti-complete to each other), and hence $Z^{+}$ (respectively, $Z^{-}$) is a nonempty module of the graph H included in $\overline{X}$ (respectively, in $\overline{S}$). Therefore Condition $\left(c\right)$ of the second assertion of Theorem 2 implies that there is a vertex t in $\overline{X}$ (respectively, in $\overline{S}$) such that $Z^{+}=\left\{t\right\}$ (respectively, $Z^{-}=\left\{t\right\}$). It follows that the vertex t is a dominating vertex in $\overline{X}$ (respectively, an isolated vertex in $\overline{S}$) of the graph H, contradicting Condition $\left(a\right)$ of the second assertion of Theorem 2.

Claim 10. The graph G has no non-trivial module M such that $u\in M$ and $M\cap X=\varnothing$.

Indeed, to the contrary, suppose that G has a non-trivial module M such that $u\in M$ and $M\cap X=\varnothing$. Since $u\in M$ and u is complete to the vertex subset X, it follows that X and M are complete to each other. By Assertion $A_2$ of Definition 1, X and $\overline{S}$ are anti-complete to each other. Therefore, $M\cap \overline{S}=\varnothing$, and hence $u\in M\subseteq \left\{u\right\}\cup S\cup \overline{X}$, and the fact that u is anti-complete to $\overline{S}$ implies that $\overline{S}$ and M are anti-complete to each other.

At the beginning, assume that $M\cap S=\varnothing$. Thus $\left\{u\right\}\subseteq M\subseteq \left\{u\right\}\cup \overline{X}$ and $M\cap \overline{X}\ne \varnothing$. By the first assertion of Proposition 3, $M\cap V\left(H\right)$ is a module of the graph H, and hence the fact that $M\cap V\left(H\right)=M\cap \overline{X}=M\setminus \left\{u\right\}$ implies that $M\setminus \left\{u\right\}$ is a nonempty module of the graph H included in $\overline{X}$. Therefore Condition $\left(c\right)$ of the second assertion of Theorem 2 implies that $M\setminus \left\{u\right\}$ is a singleton $\left\{t\right\}$ of $\overline{X}$. Thus $M=\{t,u\}$ with $t\in \overline{X}$, which contradicts Claim 7.

Now, assume that $M\cap S\ne \varnothing$. In this case, the fact that X and M are complete to each other implies that X and $M\cap S$ are complete to each other. Since each vertex in $M\cap S$ has a unique neighbor in X, it follows that X is a singleton $\left\{x\right\}$, and hence $S=M\cap S=\left\{s_x\right\}$. Thus the fact that u is complete to $\overline{X}\setminus M$ implies that M and $\overline{X}\setminus M$ are complete to each other. Consider the three vertex subsets $Z,Z^{-}$, and $Z^{+}$ of the subgraph H defined by $Z:=S\cup (M\cap \overline{X}),Z^{-}:=\overline{S}$, and $Z^{+}:=\overline{X}\setminus M$. Clearly, in the graph H, Z and $Z^{-}$ are anti-complete to each other, while Z and $Z^{+}$ are complete to each other. Since $V\left(H\right)$ is the disjoint union $Z\cup Z^{-}\cup Z^{+}$, Condition $\left(d\right)$ of the second assertion of Theorem 2 implies that at least one of the sets $Z^{-}$ and $Z^{+}$ is empty. The first assertion of Theorem 2 implies that $|{\overline{N}}_G\left(u\right)|=|S\cup \overline{S}|\ge 2$. It follows that $\overline{S}$ is nonempty, and hence $Z^{-}$ is nonempty. It follows that $Z^{+}=\varnothing$, and hence $M=\{u,s_x\}\cup \overline{X}=\left\{u\right\}\cup S\cup \overline{X}$. Thus $\{\overline{S},S\cup \overline{X}\}$ is a partition of $V\left(H\right)$ such that $\overline{S}$ and $S\cup \overline{X}$ are anti-complete to each other, and hence $\overline{S}$ is a nonempty module of the graph H. Thus Condition $\left(c\right)$ of the second assertion of Theorem 2 implies that $\overline{S}$ is a singleton $\left\{v\right\}$. It follows that v is an isolated vertex in $\overline{S}$ of the graph H, contradicting Condition $\left(a\right)$ of the second assertion of Theorem 2. □

6. Applications: Methods for Extending Graphs to Prime Graphs

Decomposable graphs possess a rich hierarchical structure as they can be fragmented into proper modules, at least one of which is non-singleton, which facilitates their analysis and the development of algorithms. In contrast, prime graphs admit no such decomposition, making them the fundamental building blocks of modular decomposition theory.

Our three applications are motivated by the need to master this challenging class. To this end, we introduce a systematic construction method that transforms various initial graphs, such as arbitrary graphs, those decomposable into prime components, or those with a prime quotient, into a prime graph by adjoining a clique under specific constraints. The result is a new prime graph but one for which we already possess a “recipe” for its construction. Therefore, we can use our knowledge of the original graph’s structure to understand the complex structure of the new prime graph.

6.1. Proof of Proposition 1

Given two (possibly infinite) equipotent disjoint sets S and X with at least two elements, a graph H on the set S, the complete graph $K_X$ on the set X, and a bijection $s:x\mapsto s_x$ from X onto S, consider the graph G with $V\left(G\right)=S\cup X\cup \left\{u\right\}$, where $u\notin S\cup X$ such that $N_G\left(u\right)=X$ and $E(G-u)=E\left(H\right)\cup E\left(K_X\right)\cup \{x{s}_x:x\in X\}$.

Clearly, $N_G\left(u\right)=X,{\overline{N}}_G\left(u\right)=S$, X is a clique in G, and $\overline{X}=\overline{S}=\varnothing$, where $\overline{X}:=N_G\left(u\right)\setminus X$ and $\overline{S}:={\overline{N}}_G\left(u\right)\setminus S$. Moreover, for each vertex x in X, the vertex $s_x$ is the unique neighbor (in G) of x in S. Thus Assertion $A_1$ of Definition 1 is satisfied, and the two other assertions of Definition 1 are trivially satisfied because $\overline{X}=\overline{S}=\varnothing$. Thus $(X,S,s)$ is a u-characteristic triple of G, and hence Theorem 1 implies that $(at{t}^{-}(G,u),Spt{t}^{-}(G,u))=(X,S)$. On the other hand, since the function s is bijective and $|{\overline{N}}_G\left(u\right)|=|X|\ge 2$, the first assertion of Theorem 2 is satisfied. Therefore since its second assertion is trivially satisfied because $\overline{X}=\overline{S}=\varnothing$, Theorem 2 implies that the graph G is prime. □

6.2. Proof of Proposition 2

Let S and X be two (possibly infinite) equipotent disjoint nonempty sets, a graph $H_1$ on the set S, the complete graph $K_X$ on the set X, a bijection $s:x\mapsto s_x$ from X onto S, and two prime graphs $H_2$ and $H_3$ such that the sets $V\left(H_2\right),V\left(H_3\right),S$, and X are pairwise disjoint. Consider a graph G with $V\left(G\right)=S\cup X\cup V\left(H_2\right)\cup V\left(H_3\right)\cup \left\{u\right\}$, where $u\notin S\cup X\cup V\left(H_2\right)\cup V\left(H_3\right)$ such that $N_G\left(u\right)=X\cup V\left(H_3\right)$ and $N_G\left(x\right)=(X\setminus \left\{x\right\})\cup V\left(H_3\right)\cup \{u,s_x\}$ for each $x\in X$.

Assume that there is a vertex in S having a neighbor in $V\left(H_2\right)$ or a non-neighbor in $V\left(H_3\right)$, and for each $i\in \{2,3\}$, there is a vertex in $V\left(H_j\right)$ having a neighbor and a non-neighbor in $V\left(H_i\right)$, where $\left\{j\right\}=\{2,3\}\setminus \left\{i\right\}$.

Let $\overline{X}:=N_G\left(u\right)\setminus X$ and $\overline{S}:={\overline{N}}_G\left(u\right)\setminus S$, and consider the subgraph $H:=G-(X\cup \{u\left\}\right)$. Thus $\overline{X}=V\left(H_3\right)$ and $\overline{S}=V\left(H_2\right)$. Clearly, the fact that $N_G\left(x\right)=(X\setminus \left\{x\right\})\cup V\left(H_3\right)\cup \{u,s_x\}$ for each $x\in X$ implies that Assertion $A_1$ and Assertion $A_2$ of Definition 1 are satisfied. Moreover, the subgraph $H\left[\overline{X}\right]$ has no dominating vertex because $H\left[\overline{X}\right]=H_3$, and hence it is prime. Thus Assertion $A_3$ of Definition 1 is trivially satisfied. Therefore $(X,S,s)$ is a u-characteristic triple of G, and hence Theorem 1 implies that $(at{t}^{-}(G,u),Spt{t}^{-}(G,u))=(X,S)$. On the other hand, since the function s is bijective and $|{\overline{N}}_G\left(u\right)|=|S\cup V\left(H_2\right)|\ge 2$, the first assertion of Theorem 2 is satisfied.

Finally, to conclude that the graph G is prime, we will prove that the four conditions $\left(a\right),\left(b\right),\left(c\right),$ and $\left(d\right)$ of the second assertion of Theorem 2 are satisfied.

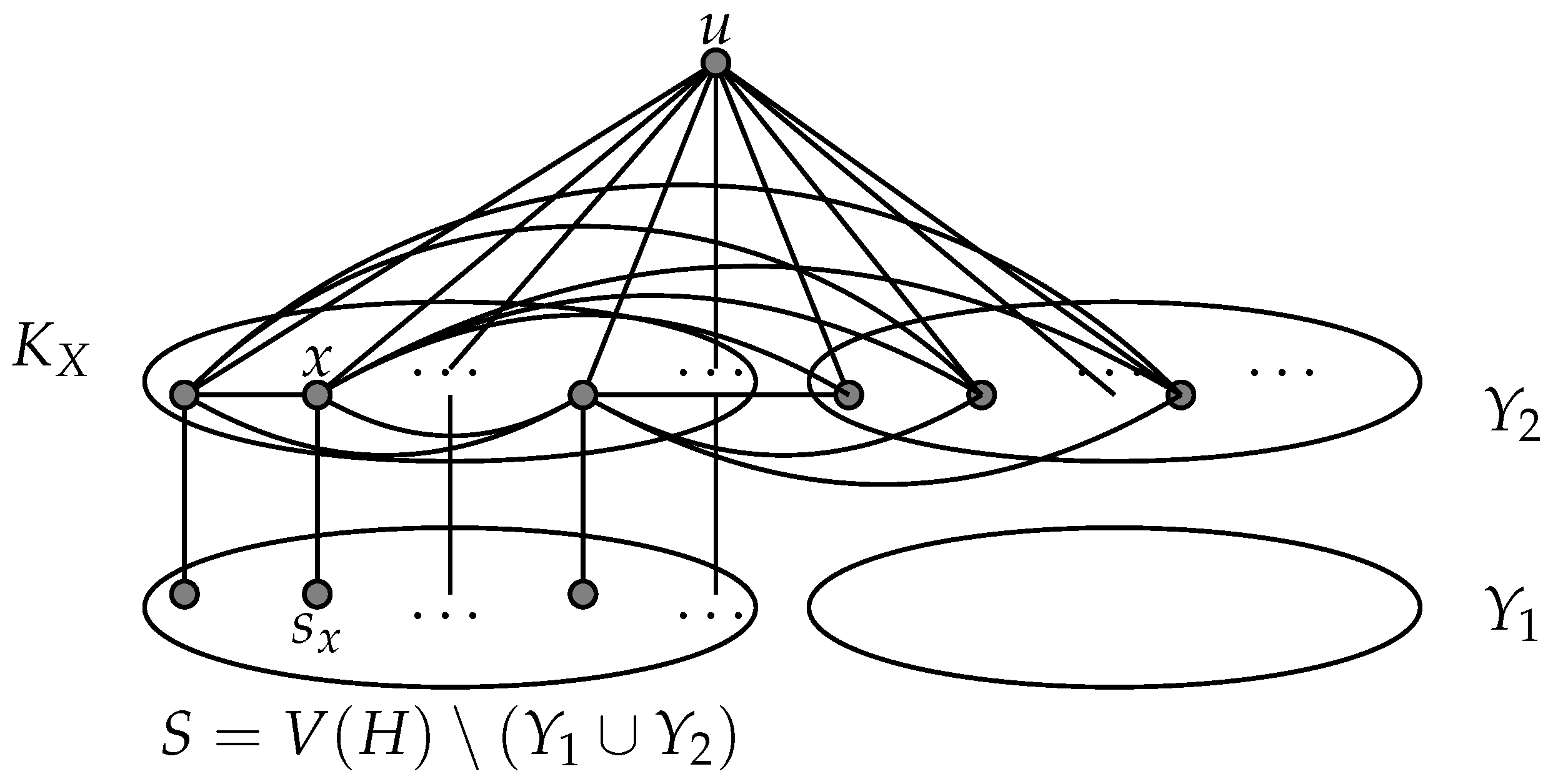
• Firstly, we will prove that conditions $\left(a\right)$ and $\left(b\right)$ are satisfied. Clearly, $H\left[\overline{X}\right]=H_3$ and $H\left[\overline{S}\right]=H_2$, and hence the subgraphs $H\left[\overline{X}\right]$ and $H\left[\overline{S}\right]$ are prime. It follows that the subgraph $H\left[\overline{X}\right]$ has no dominating vertex and the subgraph $H\left[\overline{S}\right]$ has no isolated vertex, which implies that the graph H has no dominating vertex in $\overline{X}$ and has no isolated vertex in $\overline{S}$, and hence Condition $\left(a\right)$ is satisfied. Moreover, Condition $\left(b\right)$ is trivially satisfied because the prime graph $H\left[\overline{X}\right]$ has no dominating vertex.
• Secondly, we will prove that Condition $\left(c\right)$ is satisfied. To the contrary, suppose that Condition $\left(c\right)$ is not satisfied, and consider a module M of the graph H with $\left|M\right|\ge 2$ such that $M\subseteq \overline{S}$ (respectively, $M\subseteq \overline{X}$). Since $M\cap V\left(H_2\right)=M\cap \overline{S}=M$ (respectively, $M\cap V\left(H_3\right)=M\cap \overline{X}=M$), the first assertion of Proposition 3 implies that M is a module with at least two elements of the prime graph $H_2$ (respectively, $H_3$), and hence $M=V\left(H_2\right)=\overline{S}$ (respectively, $M=V\left(H_3\right)=\overline{X}$), contradicting the fact that there is a vertex in $V\left(H_3\right)$ having a neighbor and a non-neighbor in $V\left(H_2\right)$ (respectively, the fact that there is a vertex in $V\left(H_2\right)$ having a neighbor and a non-neighbor in $V\left(H_3\right)$).
• Finally, we will prove that Condition $\left(d\right)$ is satisfied. To the contrary, suppose that Condition $\left(d\right)$ is not satisfied, and consider a 3-element partition $\{Z,Z^{-},Z^{+}\}$ of $V\left(H\right)=S\cup \overline{S}\cup \overline{X}$ with $\varnothing \ne Z^{-}\subseteq \overline{S}$ and $\varnothing \ne Z^{+}\subseteq \overline{X}$ such that Z and $Z^{-}$ are anti-complete to each other, while Z and $Z^{+}$ are complete to each other. Clearly, in the graph $H_2$ (respectively, $H_3$), the vertex subsets $Z^{-}andV\left(H_2\right)\setminus Z^{-}$ (respectively, $Z^{+}$ and $V\left(H_3\right)\setminus Z^{+}$) are anti-complete (respectively, complete) to each other. Thus, $Z^{-}$ and $V\left(H_2\right)\setminus Z^{-}$ (respectively, $Z^{+}$ and $V\left(H_3\right)\setminus Z^{+}$) are two disjoint modules of the prime graph $H_2$ (respectively, $H_3$) such that $V\left(H_2\right)=Z^{-}\cup (V\left(H_2\right)\setminus Z^{-})$ (respectively, $V\left(H_3\right)=Z^{+}\cup (V\left(H_3\right)\setminus Z^{+})$). Therefore, since the set $Z^{-}$ (respectively, $Z^{+}$) is nonempty, the second assertion of Lemma 2 implies that $Z^{-}=V\left(H_2\right)$ and $Z^{+}=V\left(H_3\right)$, which implies that $Z=S$. It follows that in the graph H, the vertex subsets S and $V\left(H_2\right)$ are anti-complete to each other, while the vertex subsets S and $V\left(H_3\right)$ are complete to each other, contradicting the fact that there is a vertex in S having a neighbor in $V\left(H_2\right)$ or a non-neighbor in $V\left(H_3\right)$.

□

6.3. Proof of Theorem 3

According to Theorem 6 and Lemma 1, Theorem 3 is an immediate consequence of the following result.

Theorem 7.

Consider a robust graph H having a prime frame and two disjoint subsets ${\mathcal{A}}_1$ and ${\mathcal{A}}_2$ of the canonical partition $\mathcal{P}\left(H\right)$ of H such that $|\mathcal{P}\left(H\right)\setminus ({\mathcal{A}}_1\cup {\mathcal{A}}_2)|\ge 2$, and let T be a vertex subset of the graph H such that $|T\cap M|=1$ for each modular component M of H.

Then there are two disjoint subsets $Y_1$ and $Y_2$ of T with $|Y_1| = |{\mathcal{A}}_1\left|and\right|Y_2| = |{\mathcal{A}}_2|$ such that by considering the complete graph $K_X$ on a set X which is disjoint from $V\left(H\right)$ and equipotent to $V\left(H\right)\setminus (Y_1\cup Y_2)$ and a bijection $s:x\mapsto s_x$ from X onto $V\left(H\right)\setminus (Y_1\cup Y_2)$, the graph G with vertex set $X\cup V\left(H\right)\cup \left\{u\right\}$, where $u\notin V\left(H\right)\cup X$, such that $N_G\left(u\right)=X\cup Y_2$, and $E(G-u)=E\left(H\right)\cup E\left(K_X\right)\cup \{x{s}_x:x\in X\}\cup \{xy:x\in Xandy\in Y_2\}$ is prime and admits $(X,V\left(H\right)\setminus (Y_1\cup Y_2),s)$ as the u-characteristic triple.

Proof. 

Consider a robust graph H having a prime frame and two disjoint subsets ${\mathcal{A}}_1$ and ${\mathcal{A}}_2$ of the canonical partition $\mathcal{P}\left(H\right)$ of H such that $|\mathcal{P}\left(H\right)\setminus ({\mathcal{A}}_1\cup {\mathcal{A}}_2)|\ge 2$, and let T be a vertex subset of the graph H such that $|T\cap M|=1$ for each modular component M of H. Thus by the first assertion of Lemma 2, the subgraph $H\left[T\right]$ is a prime graph isomorphic to the frame of H. Clearly, by Proposition 1, we may assume that the union ${\mathcal{A}}_1\cup {\mathcal{A}}_2$ is nonempty.

First, notice that since the graph H has a prime frame, Lemma 1 implies that the elements of the canonical partition $\mathcal{P}\left(H\right)$ of H are the maximal proper modules of H. Thus the following claim is immediate.

Claim 1. There is no proper module of H that meets at least two modular components of H.

Second, we obtain the following claim.

Claim 2. Given an integer k with $2\le k\le \left|T\right|-2$, there is a k-element subset Z of the vertex subset T such that the subgraph $H\left[Z\right]$ has no dominating vertex.

Indeed, we will proceed by induction on k.

If $k=2$, we can consider a pair Z of two nonadjacent vertices of the prime subgraph $H\left[T\right]$.

For the inductive step, assume that there a is k-element subset $Z_1$ of the vertex subset T such that the subgraph $H\left[Z_1\right]$ has no dominating vertex, where $2\le k\le \left|T\right|-3$. Clearly, $Z_1$ is a proper subset of the set T with $|Z_1|\ge 2$. Since the subgraph $H\left[T\right]$ is prime, $Z_1$ is not a module of $H\left[T\right]$, and hence there is $v\in T\setminus Z_1$ such that in the graph $H\left[T\right]$, v has a neighbor and a non-neighbor in $Z_1$. Consider $Z:=Z_1\cup \left\{v\right\}$. Clearly, Z is a $(k+1)$-element subset of the vertex subset T such that the subgraph $H\left[Z\right]$ has no dominating vertex.

Third, we obtain the following claim.

Claim 3. There are two disjoint subsets $Y_1$ $Y_2$ of the vertex subset T with

$$|Y_1|=|{\mathcal{A}}_1|,|Y_2|=|{\mathcal{A}}_2|,\mathrm{and}|T\setminus (Y_1\cup Y_2)|\ge 2$$

such that for each dominating vertex t of the subgraph $H\left[Y_2\right]$, t has in the graph H at least two neighbors in $V\left(H\right)\setminus Y_2$.

Indeed, according to the cardinality of the set ${\mathcal{A}}_2$, we will distinguish the following four cases.

• If $|{\mathcal{A}}_2|=0$.
  In this case, we can consider $Y_2:=\varnothing$ and $Y_1$ any subset of T such that $|Y_1| = |{\mathcal{A}}_1|$ and $|T\setminus Y_1| \ge 2$. Notice that such a subset $Y_1$ exists since $\left|\mathcal{P}\right(H\left)\right|=\left|T\right|$ and $|\mathcal{P}\left(H\right)\setminus {\mathcal{A}}_1|\ge 2$. Clearly, since $Y_2=\varnothing$, the required condition is trivially satisfied.
• If $|{\mathcal{A}}_2| =1$.
  In this case, let $Y_2:=\left\{v\right\}$, where v is a vertex in T having at least two neighbors in the subgraph $H\left[T\right]$. Notice that such a vertex v exists since the prime graph $H\left[T\right]$ has $P_4$ as an induced subgraph. Now consider a subset $Y_1$ of $T\setminus \left\{v\right\}$ such that $|Y_1| = |{\mathcal{A}}_1|$ and $|T\setminus (\left\{v\right\}\cup Y_1\left)\right| \ge 2$. Notice that such a subset $Y_1$ exists since $\left|\mathcal{P}\right(H\left)\right|=\left|T\right|$ and $|\mathcal{P}\left(H\right)\setminus ({\mathcal{A}}_1\cup {\mathcal{A}}_2)| \ge 2$. Clearly, the unique vertex v of the subgraph $H\left[Y_2\right]$ has in the graph H at least two neighbors in $V\left(H\right)\setminus Y_2$ since it has at least two neighbors in the subgraph $H\left[T\right]$.
• If the set ${\mathcal{A}}_2$ is finite with $|{\mathcal{A}}_2| \ge 2$.
  By Claim 2, we can consider a subset $Y_2$ of the vertex subset T with $|Y_2| = |{\mathcal{A}}_2|$ such that the subgraph $H\left[Y_2\right]$ has no dominating vertex. Since $\left|\mathcal{P}\right(H\left)\right|=\left|T\right|$ and $|\mathcal{P}\left(H\right)\setminus ({\mathcal{A}}_1\cup {\mathcal{A}}_2)|\ge 2$, there is a subset $Y_1$ of $T\setminus Y_2$ such that $|Y_1|=|{\mathcal{A}}_1|$ and $|T\setminus (Y_1\cup Y_2\left)\right|\ge 2$. Since $H\left[Y_2\right]$ has no dominating vertex, the required condition is trivially satisfied.
• If the set ${\mathcal{A}}_2$ is infinite.
  Let ${\displaystyle Y_1:=T\cap \left(\bigcup _{M\in {\mathcal{A}}_1}M\right)}$ and ${\displaystyle Y_3:=T\cap \left(\bigcup _{M\in {\mathcal{A}}_2}M\right)}$. Clearly, $Y_1$ and $Y_3$ are two disjoint subsets of T with

  $$|Y_1| = |{\mathcal{A}}_1|,|Y_3| = |{\mathcal{A}}_2|,\mathrm{and}|T\setminus (Y_1\cup Y_3)|\ge 2.$$

First, if the subgraph $H\left[Y_3\right]$ has no dominating vertex, then by considering $Y_2:=Y_3$, it is clear that $Y_1$ and $Y_2$ are two disjoint subsets of T with

$$|Y_1| = |{\mathcal{A}}_1|,|Y_2| = |{\mathcal{A}}_2|,\mathrm{and}|T\setminus (Y_1\cup Y_2)|\ge 2$$

and the required condition is trivially satisfied. Second, assume that the subgraph $H\left[Y_3\right]$ has a unique dominating vertex v. Clearly, the subgraph $H[Y_3\setminus \left\{v\right\}]$ does not admit a dominating vertex because if it did, that vertex would be a dominating vertex of $H\left[Y_3\right]$ other than v. Thus by considering $Y_2:=Y_3\setminus \left\{v\right\}$, since the set $Y_3$ is infinite, it is clear that $Y_1$ and $Y_2$ are two disjoint subsets of T with

$$|Y_1| = |{\mathcal{A}}_1|,|Y_2| = |{\mathcal{A}}_2|,\mathrm{and}|T\setminus (Y_1\cup Y_2)|\ge 2$$

and the required condition is trivially satisfied. Finally, if the subgraph $H\left[Y_3\right]$ has at least two dominating vertices, then by considering $Y_2:=Y_3\setminus \{x,y\}$, where x and y are two distinct dominating vertices of $H\left[Y_3\right]$, since the set $Y_3$ is infinite, it is clear that $Y_1$ and $Y_2$ are two disjoint subsets of T with

$$|Y_1| = |{\mathcal{A}}_1|,|Y_2| = |{\mathcal{A}}_2|,\mathrm{and}|T\setminus (Y_1\cup Y_2)|\ge 2$$

and for each dominating vertex t (in fact for each vertex t) of the subgraph $H\left[Y_2\right]$, t has in the graph H at least two neighbors in $V\left(H\right)\setminus Y_2$, namely, x and y.

Fourth, we obtain the following claim where $Y_1$ and $Y_2$ are the two disjoint subsets of T obtained in Claim 3.

Claim 4. The following two assertions hold.

$\left(i\right)$ The graph H has no module M with $\left|M\right|\ge 2$ such that $M\subseteq Y_1$ or $M\subseteq Y_2$.

$\left(ii\right)$ The vertex set of the graph H has no 3-element partition $\{Z,Z^{-},Z^{+}\}$ with $\varnothing \ne Z^{-}\subseteq Y_1$ and $\varnothing \ne Z^{+}\subseteq Y_2$ such that Z and $Z^{-}$ are anti-complete to each other, while Z and $Z^{+}$ are complete to each other.

Indeed,

$\left(i\right)$ By the definition of the set T, each proper subset of T having at least two elements meets at least two modular components of H. Therefore, by Claim 1, the graph H has no module M with $\left|M\right|\ge 2$ such that $M\subseteq Y_1$ or $M\subseteq Y_2$.

$\left(ii\right)$ To the contrary, suppose that $V\left(H\right)$ has a 3-element partition $\{Z,Z^{-},Z^{+}\}$ with $\varnothing \ne Z^{-}\subseteq Y_1$ and $\varnothing \ne Z^{+}\subseteq Y_2$ such that Z and $Z^{-}$ are anti-complete to each other, while Z and $Z^{+}$ are complete to each other. Thus Z is a non-trivial module of H. The fact that $|T\setminus (Y_1\cup Y_2\left)\right|\ge 2$ implies that Z meets at least two modular components of H, contradicting Claim 1.

Finally, consider the two disjoint subsets $Y_1$ and $Y_2$ of T obtained in Claim 3, the complete graph $K_X$ on a set X which is disjoint from $V\left(H\right)$ and equipotent to $V\left(H\right)\setminus (Y_1\cup Y_2)$ and a bijection $s:x\mapsto s_x$ from X onto $V\left(H\right)\setminus (Y_1\cup Y_2)$, and let G be the graph with vertex set $X\cup V\left(H\right)\cup \left\{u\right\}$, where $u\notin V\left(H\right)\cup X$, such that $N_G\left(u\right)=X\cup Y_2$ and $E(G-u)=E\left(H\right)\cup E\left(K_X\right)\cup \{x{s}_x:x\in X\}\cup \{xy:x\in Xandy\in Y_2\}$.

We will use Theorems 1 and 2 to prove that the graph G is prime and admits $(X,V\left(H\right)\setminus (Y_1\cup Y_2),s)$ as the u-characteristic triple.

To do so, notice that $G-(X\cup \{u\left\}\right)=H$, and let $\overline{X}:=N_G\left(u\right)\setminus X,S:=V\left(H\right)\setminus (Y_1\cup Y_2)$, and $\overline{S}:={\overline{N}}_G\left(u\right)\setminus S$. Thus $\overline{X}=Y_2$ and $\overline{S}=Y_1$. Clearly, X is a clique in G, and for each vertex x in X, the vertex $s_x$ is the unique neighbor (in G) of x in S, and hence Assertion $A_1$ of Definition 1 is satisfied. Clearly, the definition of the graph G implies that Assertion $A_2$ of Definition 1 is satisfied. Moreover, by Claim 3, each dominating vertex t of the subgraph $H\left[\overline{X}\right]$ has in the graph H at least two neighbors in $V\left(H\right)\setminus Y_2=S\cup \overline{S}$, and hence Assertion $A_3$ of Definition 1 is satisfied. Therefore $(X,V\left(H\right)\setminus (Y_1\cup Y_2),s)$ is a u-characteristic triple of G, and hence Theorem 1 implies that $(at{t}^{-}(G,u),Spt{t}^{-}(G,u))=(X,V\left(H\right)\setminus (Y_1\cup Y_2))$. On the other hand, since the function s is bijective and $|{\overline{N}}_G\left(u\right)|=|V\left(H\right)\setminus Y_2|\ge |T\setminus (Y_1\cup Y_2)|\ge 2$, the first assertion of Theorem 2 is satisfied. To conclude that the graph G is prime, we will justify that the four conditions $\left(a\right),\left(b\right),\left(c\right),$ and $\left(d\right)$ of the second assertion of Theorem 2 are satisfied. Since the graph G has a prime frame, the second assertion of Lemma 2 implies that H has no modular partition in exactly two modules, and hence H has neither a dominating vertex nor an isolated vertex. Thus Condition $\left(a\right)$ is satisfied. Condition $\left(b\right)$ is satisfied by Claim 3 since $V\left(H\right)\setminus Y_2=S\cup \overline{S}$, and conditions $\left(c\right)$ and $\left(d\right)$ are satisfied by Claim 4. □

□

7. Prime Subgraphs of Prime Graphs with at Least Two Negative Almost True Twins for a Given Vertex

In this section, we consider a prime graph G containing a vertex u that has at least two negative almost true twins and its u-characteristic triple $(X,S,s)$. Firstly, in Lemma 6, we study the u-characteristic triples of the prime subgraphs $G\left[Y\right]$ of G, where Y is a vertex subset satisfying $Y\cap (X\cup S\cup \left\{u\right\})=X_1\cup s\left(X_1\right)\cup \left\{u\right\}$ for some subset $X_1$ of X with at least two elements. Note that $X_1\subseteq at{t}^{-}(G\left[Y\right],u)$. We introduce the notions of restriction and proper extension of the triple $(X,S,s)$. Secondly, in Proposition 4, we begin by proving that the subgraph $G[X_1\cup s\left(X_1\right)\cup \left\{u\right\}]$ for some subset $X_1$ of X with at least two elements is prime, and its u-characteristic triple is the restriction of $(X,S,s)$ to $X_1$. Thus the subgraph $G[X\cup S\cup \{u\left\}\right]$ is prime and admits $(X,S,s)$ as the u-characteristic triple. Then, we prove the existence of prime subgraphs $G\left[Y\right]$ of G, where Y includes $X\cup S\cup \left\{u\right\}$ under different conditions on the cardinality of Y; the u-characteristic triple of $G\left[Y\right]$ is either $(X,S,s)$ or a proper extension of it.

First, consider the following definition.

Definition 3.

Let G be a prime graph, u be a vertex having a negative almost true twin in G, and $(X,S,s)$ be the u-characteristic triple of G. Consider the vertex subsets $X:=at{t}^{-}(G,u),\overline{X}:=N_G\left(u\right)\setminus X,S:=Spt{t}^{-}(G,u),and\overline{S}:={\overline{N}}_G\left(u\right)\setminus S$.

Let $X_1$ be a nonempty subset of X.

1.

The restriction of the triple $(X,S,s)$ to $X_1$ is the triple $(X_1,s\left(X_1\right),s_1)$, where $s_1$ is the bijection from $X_1$ onto $s\left(X_1\right)$ which associates $s\left(x\right)$ with each element x of $X_1$.

2.

A proper extension of the triple $(X_1,s\left(X_1\right),s_1)$ is any triple

$(X_1\cup A,s\left(X_1\right)\cup f\left(A\right),g)$, where A is a nonempty subset of $\overline{X}$, f is an injective function from A to $\overline{S}$, and g is the bijection from $X_1\cup A$ onto $s\left(X_1\right)\cup f\left(A\right)$ which associates $s\left(x\right)$ with each $x\in X_1$ and $f\left(x\right)$ with each $x\in A$.

Second, we obtain the following lemma.

Lemma 6.

Let G be a prime graph, u be a vertex having at least two negative almost true twins in G, and $(at{t}^{-}(G,u),Spt{t}^{-}(G,u),s)$ be the u-characteristic triple of G. Consider the vertex subsets $X:=at{t}^{-}(G,u),\overline{X}:=N_G\left(u\right)\setminus X,$ $S:=Spt{t}^{-}(G,u),$ and $\overline{S}:={\overline{N}}_G\left(u\right)\setminus S$.

Given a vertex subset $X_1$ included in X with $|X_1|\ge 2$ and a vertex subset Y such that $Y\cap (X\cup S\cup \left\{u\right\})=X_1\cup s\left(X_1\right)\cup \left\{u\right\}$ and the subgraph $G\left[Y\right]$ is prime, the following assertions hold.

1.

If $Y\cap \overline{X}=\varnothing orY\cap \overline{S}=\varnothing$, then $G\left[Y\right]$ has the restriction of the triple $(X,S,s)$ to $X_1$ as the u-characteristic triple.

2.

If $Y\cap \overline{X}\ne \varnothing andY\cap \overline{S}\ne \varnothing$, then $G\left[Y\right]$ has either the restriction of the triple $(X,S,s)$ to $X_1$ or a proper extension of this restriction as the u-characteristic triple.

Proof. 

Consider a vertex subset $X_1$ included in X with $|X_1|\ge 2$ and a vertex subset Y such that $Y\cap (X\cup S\cup \left\{u\right\})=X_1\cup s\left(X_1\right)\cup \left\{u\right\}$ and the subgraph $G\left[Y\right]$ is prime. Recall that by Theorem 2, the function s is bijective, and let $(X_1,s\left(X_1\right),s_1)$ be the restriction of the triple $(X,S,s)$ to $X_1$. Clearly, the fact that $(X,S,s)$ is the u-characteristic triple of the graph G implies that, in the graph $G\left[Y\right]$, $X_1$ is a clique, and $s\left(x\right)$ is the unique neighbor of x in $S\left(X_1\right)$ for each vertex x in $X_1$. Thus, for the graph $G\left[Y\right]$, the triple $(X_1,s\left(X_1\right),s_1)$ satisfies Assertion $A_1$ of Definition 1.

1.

Assume that $Y\cap \overline{X}=\varnothing$ or $Y\cap \overline{S}=\varnothing$. Let us prove that $(X_1,s\left(X_1\right),s_1)$ is a u-characteristic triple of the graph $G\left[Y\right]$.

First, assume that $Y\cap \overline{X}=\varnothing$. Thus ${\overline{N}}_{G\left[Y\right]}\left(u\right)\setminus s\left(X_1\right)=\overline{S}\cap Y$, and hence the fact that $(X,S,s)$ is the u-characteristic triple of the graph G implies that, in the graph $G\left[Y\right]$, the two vertex subsets $X_1$ and ${\overline{N}}_{G\left[Y\right]}\left(u\right)\setminus s\left(X_1\right)$ are anti-complete to each other. Since, in addition, $N_{G\left[Y\right]}\left(u\right)\setminus X_1=\varnothing$, it follows that, for the graph $G\left[Y\right]$, the triple $(X_1,s\left(X_1\right),s_1)$ satisfies assertions $A_2$ and $A_3$ of Definition 1. Therefore $(X_1,s\left(X_1\right),s_1)$ is a u-characteristic triple of the graph $G\left[Y\right]$.

Second, assume that $Y\cap \overline{S}=\varnothing$. Thus $N_{G\left[Y\right]}\left(u\right)\setminus X_1=\overline{X}\cap Y$, and hence the fact that $(X,S,s)$ is the u-characteristic triple of the graph G implies that, in the graph $G\left[Y\right]$, the two vertex subsets $X_1$ and $N_{G\left[Y\right]}\left(u\right)\setminus X_1$ are complete to each other. Since, in addition, ${\overline{N}}_{G\left[Y\right]}\left(u\right)\setminus s\left(X_1\right)=\varnothing$ for the graph $G\left[Y\right]$, the triple $(X_1,s\left(X_1\right),s_1)$ satisfies Assertion $A_2$ of Definition 1. To the contrary, suppose that, for the graph $G\left[Y\right]$, this triple does not satisfy Assertion $A_3$ of Definition 1. Thus there is a dominating vertex t of the subgraph $G[N_{G\left[Y\right]}\left(u\right)\setminus X_1]$ having a unique neighbor w in $s\left(X_1\right)$. Clearly, $N_{G\left[Y\right]}\left(t\right)\cup \left\{t\right\}=N_{G\left[Y\right]}\left(s^{-1}\left(w\right)\right)\cup \left\{s^{-1}\left(w\right)\right\}$, and hence $\{s^{-1}\left(w\right),t\}$ is a module of the subgraph $G\left[Y\right]$, contradicting the fact that $G\left[Y\right]$ is a prime graph. Therefore $(X_1,s\left(X_1\right),s_1)$ is a u-characteristic triple of the graph $G\left[Y\right]$.

2.

Assume that $Y\cap \overline{X}\ne \varnothing$ and $Y\cap \overline{S}\ne \varnothing$, and let A be the set of dominating vertices of $G[Y\cap \overline{X}]$ having a unique neighbor in $s\left(X_1\right)\cup (\overline{S}\cap Y)$.

Clearly, the fact that $(X,S,s)$ is the u-characteristic triple of the graph G implies that, in the graph $G\left[Y\right]$, the two vertex subsets $X_1$ and $Y\cap \overline{X}$ are complete to each other, while $X_1$ and $Y\cap \overline{S}$ are anti-complete to each other. It follows that if the set A is empty, then, for the graph $G\left[Y\right]$, the triple $(X_1,s\left(X_1\right),s_1)$ satisfies assertions $A_2$ and $A_3$ of Definition 1, and hence the triple $(X_1,s\left(X_1\right),s_1)$ is a u-characteristic triple of the graph $G\left[Y\right]$. Therefore, in the sequel we may assume that the set A is nonempty. For each $t\in A$, let $f\left(t\right)$ be the unique neighbor of t in $s\left(X_1\right)\cup (\overline{S}\cap Y)$.

First, let us prove the following two claims.

Claim 1. For each $t\in A$, $f\left(t\right)\in \overline{S}\cap Y$.

Indeed, to the contrary, suppose that there is $t\in A$ such that $f\left(t\right)\in s\left(X_1\right)$, and let $x:=s^{-1}\left(f\left(t\right)\right)$. Clearly, $N_{G\left[Y\right]}\left(t\right)\cup \left\{t\right\}=N_{G\left[Y\right]}\left(x\right)\cup \left\{x\right\}$, and hence $\{x,t\}$ is a module of the subgraph $G\left[Y\right]$, contradicting the fact that $G\left[Y\right]$ is a prime graph.

Claim 2. The function f is an injection from A to $\overline{S}\cap Y$.

Indeed, to the contrary, suppose that there are two distinct elements t and $t^{\prime }$ of A such that $f\left(t\right)=f\left(t^{\prime }\right)$. Clearly, $N_{G\left[Y\right]}\left(t\right)\cup \left\{t\right\}=N_{G\left[Y\right]}\left(t^{\prime }\right)\cup \left\{t^{\prime }\right\}$, and hence $\{t,t^{\prime }\}$ is a module of the subgraph $G\left[Y\right]$, contradicting the fact that $G\left[Y\right]$ is a prime graph.

Second, consider the bijection g from $X_1\cup A$ onto $s\left(X_1\right)\cup f\left(A\right)$ which associates $s\left(x\right)$ with each $x\in X_1$ and $f\left(x\right)$ with each $x\in A$, and let us prove that the proper extension $(X_1\cup A,s\left(X_1\right)\cup f\left(A\right),g)$ of the triple $(X_1,s\left(X_1\right),s_1)$ is a u-characteristic triple of the graph $G\left[Y\right]$. Clearly, in the graph $G\left[Y\right]$, $X_1\cup A$ is a clique, and $g\left(x\right)$ is the unique neighbor of x in $s\left(X_1\right)\cup f\left(A\right)$ for each vertex x in $X_1\cup A$. Moreover, the two vertex subsets $X_1\cup A$ and $(Y\cap \overline{X})\setminus A$ are complete to each other, while $X_1\cup A$ and $(Y\cap \overline{S})\setminus f\left(A\right)$ are anti-complete to each other. On the other hand, clearly each dominating vertex of the subgraph $G[(Y\cap \overline{X})\setminus A]$ is a dominating vertex of the subgraph $G[Y\cap \overline{X}]$. Thus from the definition of A it follows that there is no dominating vertex of the subgraph $G[(Y\cap \overline{X})\setminus A]$ having a unique neighbor in $s\left(X_1\right)\cup (\overline{S}\cap Y)$. Therefore, for the graph $G\left[Y\right]$, the triple $(X_1\cup A,s\left(X_1\right)\cup f\left(A\right),g)$ satisfies assertions $A_1,A_2$, and $A_3$ of Definition 1, and hence it is a u-characteristic triple of the graph $G\left[Y\right]$.

In this lemma, we consider a prime graph G containing a vertex u that has at least two negative almost true twins and its u-characteristic triple $(at{t}^{-}(G,u),Spt{t}^{-}(G,u),s)$. We study the u-characteristic triples of the prime subgraphs $G\left[Y\right]$ of G, where Y is a vertex subset satisfying $Y\cap (at{t}^{-}(G,u)\cup Spt{t}^{-}(G,u)\cup \left\{u\right\})=X_1\cup s\left(X_1\right)\cup \left\{u\right\}$ for some subset $X_1$ of $at{t}^{-}(G,u)$ with at least two elements. Note that $X_1\subseteq at{t}^{-}(G\left[Y\right],u)$.

Finally, we obtain the following proposition, which enables our study of the prime induced subgraphs of the prime graphs having at least two negative almost true twins for some vertex u. □

Proposition 4.

Let G be a prime graph, u be a vertex having at least two negative almost true twins in G, and $(at{t}^{-}(G,u),Spt{t}^{-}(G,u),s)$ be the u-characteristic triple of G. Consider the vertex subsets $X:=at{t}^{-}(G,u),\overline{X}:=N_G\left(u\right)\setminus X,$ $S:=Spt{t}^{-}(G,u),and\overline{S}:={\overline{N}}_G\left(u\right)\setminus S$.

The following assertions hold.

1.

For each vertex subset $X_1$ included in X with $|X_1|\ge 2$, the subgraph

$G_1:=G[X_1\cup s\left(X_1\right)\cup \left\{u\right\}]$ is prime, and its u-characteristic triple is the restriction of the triple $(X,S,s)$ to $X_1$.

2.

For each positive integer k with $2k\le |\overline{X}\cup \overline{S}|$, there is a $2k$-element subset A of $\overline{X}\cup \overline{S}$ such that the subgraph $G[X\cup S\cup \{u\}\cup A]$ is prime and has either $(X,S,s)$ or a proper extension of $(X,S,s)$ as the u-characteristic triple.

3.

If the vertex subset $\overline{X}\cup \overline{S}$ is infinite, then for each vertex v in $\overline{X}\cup \overline{S}$, there is a finite subset F of $\overline{X}\cup \overline{S}$ containing v such that the subgraph $G[X\cup S\cup \{u\}\cup F]$ is prime and has either $(X,S,s)$ or a proper extension of $(X,S,s)$ as the u-characteristic triple.

4.

If the graph G is infinite, then for each infinite vertex subset Y including $X\cup S\cup \left\{u\right\}$, there is a vertex subset Z including Y such that $\left|Z\right|=\left|Y\right|$, and the subgraph $G\left[Z\right]$ is prime and has either $(X,S,s)$ or a proper extension of $(X,S,s)$ as the u-characteristic triple.

Proof. 

Let G be a prime graph, u be a vertex having at least two negative almost true twins in G, and $(at{t}^{-}(G,u),Spt{t}^{-}(G,u),s)$ be the u-characteristic triple of G. Consider the vertex subsets $X:=at{t}^{-}(G,u),\overline{X}:=N_G\left(u\right)\setminus X,S:=Spt{t}^{-}(G,u)$, and $\overline{S}:={\overline{N}}_G\left(u\right)\setminus S$.

1.

Consider the subgraph $G_1:=G[X_1\cup s\left(X_1\right)\cup \left\{u\right\}]$, where $X_1$ is a vertex subset included in X with $|X_1|\ge 2$, and let $(X_1,s\left(X_1\right),s_1)$ be the restriction of the triple $(X,S,s)$ to $X_1$. Since $(X,S,s)$ is the u-characteristic triple of the graph G, X is a clique of G, and for each vertex x in X, $s\left(x\right)$ is the unique neighbor of x in S. Moreover, since the graph G is prime, the function s is bijective by Theorem 2. It follows that the function $s_1$ is a bijection from $X_1$ onto $s\left(X_1\right)$ such that $N_{G_1}\left(u\right)=X_1$ and $E(G_1-u)=E\left(G\left[s\left(X_1\right)\right]\right)\cup E\left(K_{X_1}\right)\cup \{x{s}_1\left(x\right):x\in X_1\}$, where $K_{X_1}$ is the complete graph on $X_1$. Thus by Proposition 1, the subgraph $G_1$ is prime and admits $(X_1,s\left(X_1\right),s_1)$ as the u-characteristic triple.

2.

Let k be a positive integer k such that $2k\le |\overline{X}\cup \overline{S}|$. By the first assertion, the subgraph $G[X\cup S\cup \{u\left\}\right]$ is prime. Thus by k consecutive applications of Theorem 4, we obtain a $2k$-element subset A of $\overline{X}\cup \overline{S}$ such that the subgraph $G[X\cup S\cup \{u\}\cup A]$ is prime. If $A\subseteq \overline{X}$ or $A\subseteq \overline{S}$, then by the first assertion of Lemma 6, the subgraph $G[X\cup S\cup \{u\}\cup A]$ has $(X,S,s)$ as the u-characteristic triple. Otherwise, the second assertion of Lemma 6 implies that this subgraph has either $(X,S,s)$ or a proper extension of $(X,S,s)$ as the u-characteristic triple.

3.

Notice that by the first assertion, the subgraph $G[X\cup S\cup \{u\left\}\right]$ is prime. Assume that the vertex subset $\overline{X}\cup \overline{S}$ is infinite, and consider a vertex v in $\overline{X}\cup \overline{S}$. By Theorem 5, there is a finite subset F of $\overline{X}\cup \overline{S}$ containing v such that the subgraph $G[X\cup S\cup \{u\}\cup F]$ is prime. If $F\subseteq \overline{X}$ or $F\subseteq \overline{S}$, then by the first assertion of Lemma 6, the subgraph $G[X\cup S\cup \{u\}\cup F]$ has $(X,S,s)$ as the u-characteristic triple. Otherwise, the second assertion of Lemma 6 implies that this subgraph has either $(X,S,s)$ or a proper extension of $(X,S,s)$ as the u-characteristic triple.

4.

Assume that the graph G is infinite, and consider an infinite vertex subset Y including $X\cup S\cup \left\{u\right\}$. By Corollary 1, there is a vertex subset Z including Y such that $\left|Z\right|=\left|Y\right|$, and the subgraph $G\left[Z\right]$ is prime. If $Z\cap \overline{X}=\varnothing$ or $Z\cap \overline{S}=\varnothing$, then by the first assertion of Lemma 6, the subgraph $G\left[Z\right]$ has $(X,S,s)$ as the u-characteristic triple. Otherwise, the second assertion of Lemma 6 implies that this subgraph has either $(X,S,s)$ or a proper extension of $(X,S,s)$ as the u-characteristic triple.

□

In this proposition, we consider a prime graph G containing a vertex u that has at least two negative almost true twins and its u-characteristic triple $(X,S,s)$. By the first assertion, we prove that for each subset $X_1$ of X with $|X_1|\ge 2$, the subgraph $G[X_1\cup s\left(X_1\right)\cup \left\{u\right\}]$ is prime, and its u-characteristic triple is the restriction of $(X,S,s)$ to $X_1$. It follows that the subgraph $G[X\cup S\cup \{u\left\}\right]$ is prime and admits $(X,S,s)$ as the u-characteristic triple. By the three other assertions, we prove the existence of prime subgraphs $G\left[Y\right]$ of G, where Y includes $X\cup S\cup \left\{u\right\}$ under different conditions on the cardinality of Y; the u-characteristic triple of $G\left[Y\right]$ is either $(X,S,s)$ or a proper extension of it.

8. Negatively Critical Prime $\mathbf{u}$-True Twin Graphs

Since a prime graph has no pair of true twin vertices, we consider the following definition.

Definition 4.

Given a graph G and a vertex u, G is called a negatively critical prime u-true twin if G is prime and every non-neighbor x of u is the unique splitter of a pair $\{u,u_x\}$, where $u_x$ is a neighbor of u.

Notice that in Definition 4, given a non-neighbor x of u, the vertex $u_x$ is a negative almost true twin of u in G. Therefore given a vertex u of a prime graph G, the graph G is a negatively critical prime u-true twin if and only if ${\overline{N}}_G\left(u\right)=Spt{t}^{-}(G,u)$.

Consequently, in a negatively critical prime u-true twin graph G, adding any edge incident to u yields a decomposable graph that admits a pair of true twins containing u. This establishes G as a critical graph: while it is prime and therefore contains no true twin of u, it exists precisely at the threshold of losing this property. The addition of just one edge incident to u creates a true twin of u, which breaks the graph’s primeness and demonstrates its extremal nature, which is the primary motivation for introducing this class of graphs.

The following characterization of negatively critical prime u-true twin graphs is an immediate consequence of Theorems 1 and 2.

Proposition 5.

Given a graph G with at least four vertices and a vertex u of G, the graph G is a negatively critical prime u-true twin if and only if $|{\overline{N}}_G\left(u\right)|\ge 2$ and there is a clique X of G included in $N_G\left(u\right)$ such that by denoting $\overline{X}:=N_G\left(u\right)\setminus X$, the following assertions hold.

1.

There is a bijection $s:x\mapsto s_x$ from X onto ${\overline{N}}_G\left(u\right)$ such that for each vertex x in X, the vertex $s_x$ is the unique neighbor of x in ${\overline{N}}_G\left(u\right)$.

2.

The two vertex subsets X and $\overline{X}$ are complete to each other.

3.

The subgraph $H:=G-(X\cup \left\{u\right\})=G[{\overline{N}}_G\left(u\right)\cup \overline{X}]$ satisfies the following two conditions.

(a) 

If the subgraph $H\left[\overline{X}\right]$ has a dominating vertex, then $|{\overline{N}}_G\left(u\right)|\ge 3$, and each dominating vertex of $H\left[\overline{X}\right]$ is adjacent to at least two vertices in ${\overline{N}}_G\left(u\right)$ but not to all of them.

(b) 

The subgraph H has no module M with $\left|M\right|\ge 2$ such that $M\subseteq \overline{X}$.

Proof. 

Let G be a graph with at least 4 vertices and a vertex u of G.

Firstly, we begin by proving the necessity. We assume that the graph G is a negatively critical prime u-true twin. By Definition 4, the graph G is prime, and hence ${\overline{N}}_G\left(u\right)\ne \varnothing$ and for each $x\in {\overline{N}}_G\left(u\right)$, there is a negative almost true twin $u_x$ in G of u. Thus $at{t}^{-}(G,u)\ne \varnothing$, and hence by Theorem 1, G admits $(at{t}^{-}(G,u),Spt{t}^{-}(G,u),s)$ as the u-characteristic triple where s is the function from $at{t}^{-}(G,u)$ to $Spt{t}^{-}(G,u)$, defined by $s:x\mapsto Sp\left(\right\{u,x\left\}\right)$. Consider the vertex subsets $X:=at{t}^{-}(G,u),\overline{X}:=N_G\left(u\right)\setminus X$, and $S:=Spt{t}^{-}(G,u)$. Recall that ${\overline{N}}_G\left(u\right)=S$ because G is a negatively critical prime u-true twin. By Theorem 2, $|{\overline{N}}_G\left(u\right)|\ge 2$, X is a clique of G included in $N_G\left(u\right)$, and s is a bijection from X onto ${\overline{N}}_G\left(u\right)$. Thus the first assertion of Proposition 5 is satisfied. Moreover the second assertion is satisfied by Definition 1. Now we will prove that the third assertion of Proposition 5 is satisfied. Consider the subgraph $H:=G-(X\cup \{u\left\}\right)$. Theorem 2 implies that the subgraph H has no module M with $\left|M\right|\ge 2$ such that $M\subseteq \overline{X}$, which is Condition (b) of Assertion 3. If t is a dominating vertex in $H\left[\overline{X}\right]$, then by conditions (a) and (b) of Assertion 2 of Theorem 2, t is adjacent to at least two vertices in ${\overline{N}}_G\left(u\right)$, and t is not a dominating vertex in H, which implies that $|{\overline{N}}_G\left(u\right)|\ge 3$, and each dominating vertex of $H\left[\overline{X}\right]$ is not adjacent to all vertices in ${\overline{N}}_G\left(u\right)$. Thus, Condition (a) of Assertion 3 is satisfied.

Secondly, we prove the sufficiency. Assume that $|{\overline{N}}_G\left(u\right)|\ge 2$ and there is a clique X of G included in $N_G\left(u\right)$ such that by denoting $\overline{X}:=N_G\left(u\right)\setminus X$; the assertions (1), (2), and (3) of Proposition 5 are verified. Since X is a clique, the two vertex subsets X and $\overline{X}$ are complete to each other, and s is a bijection from X onto ${\overline{N}}_G\left(u\right)$ such that for each vertex x in X, the vertex $s_x$ is the unique neighbor of x in ${\overline{N}}_G\left(u\right)$. Thus, in the graph G, the triple $(X,{\overline{N}}_G\left(u\right),s)$ satisfies assertions $\left(A_1\right)$ and $\left(A_2\right)$ of Definition 1. Moreover, clearly, Condition (b) of Assertion 3 of Proposition 5 implies that Assertion $\left(A_3\right)$ of Definition 1 is satisfied. Therefore, $(X,{\overline{N}}_G\left(u\right),s)$ is a u-characteristic triple of G. By Theorem 1, $X=at{t}^{-}(G,u)$ and ${\overline{N}}_G\left(u\right)=Spt{t}^{-}(G,u)$, and hence, in particular, vertex u has a negative almost true twin. Consider the subsets $S:=Spt{t}^{-}(G,u)$ and $\overline{S}:={\overline{N}}_G\left(u\right)\setminus S$. Thus $S={\overline{N}}_G\left(u\right)$ and $\overline{S}=\varnothing$. Clearly, our assumption in this sufficiency proof implies that the two conditions of Theorem 2 are satisfied, and hence the graph G is prime. Therefore, the fact that ${\overline{N}}_G\left(u\right)=Spt{t}^{-}(G,u)$ implies that the graph G is a negatively critical prime u-true twin. □

The following corollary is an immediate consequence of Lemma 6 of Section 7.

Corollary 2.

Let G be a graph and u be a vertex. Assume that G is a negatively critical prime u-true twin, and let $(X,{\overline{N}}_G\left(u\right),s)$ be its u-characteristic triple.

Given a vertex subset $X_1$ included in X with $|X_1|\ge 2$ and a vertex subset Y such that $Y\cap (X\cup s\left(X\right)\cup \left\{u\right\})=X_1\cup s\left(X_1\right)\cup \left\{u\right\}$, if the subgraph $G\left[Y\right]$ is prime, then it is a negatively critical prime u-true twin and its u-characteristic triple is the restriction of the triple $(X,S,s)$ to $X_1$.

By the following result, which is an immediate consequence of Corollary 2 and Proposition 4, we study the prime induced subgraphs of the negatively critical prime u-true twin graphs.

Proposition 6.

Let G be a graph and u be a vertex. Assume that G is a negatively critical prime u-true twin, and let $(X,{\overline{N}}_G\left(u\right),s)$ be its u-characteristic triple.

The following assertions hold.

1.

For each vertex subset $X_1$ included in X with $|X_1|\ge 2$, the subgraph

$G_1:=G[X_1\cup s\left(X_1\right)\cup \left\{u\right\}]$ is a negatively critical prime u-true twin, and its

u-characteristic triple is the restriction of the triple $(X,S,s)$ to $X_1$.

2.

For each positive integer k with $2k\le |N_G\left(u\right)\setminus X|$, there is a $2k$-element subset A of $N_G\left(u\right)\setminus X$ such that the subgraph $G[X\cup {\overline{N}}_G\left(u\right)\cup \left\{u\right\}\cup A]$ is a negatively critical prime u-true twin and admits the same u-characteristic triple as G.

3.

If the vertex subset $N_G\left(u\right)\setminus X$ is infinite, then for each vertex v in $N_G\left(u\right)\setminus X$, there is a finite subset F of $N_G\left(u\right)\setminus X$ containing v such that the subgraph

$G[X\cup {\overline{N}}_G\left(u\right)\cup \left\{u\right\}\cup F]$ is a negatively critical prime u-true twin and admits the same u-characteristic triple as G.

4.

If the graph G is infinite, then for each infinite vertex subset Y including $X\cup {\overline{N}}_G\left(u\right)\cup \left\{u\right\}$, there is a vertex subset Z including Y such that $\left|Z\right|=\left|Y\right|$ and the subgraph $G\left[Z\right]$ is a negatively critical prime u-true twin and admits the same u-characteristic triple as G.

9. Conclusions and Future Work

In conclusion, this study has established the fundamental properties of graphs possessing a negative almost true twin for a given vertex. We characterized these graphs through a special decomposition and precisely identified the prime graphs within this family. This characterization enabled several practical applications, including methods for constructing new prime graphs. Furthermore, we advanced the structural analysis by investigating the prime induced subgraphs of a prime graph that contain a given vertex u and at least two other vertices that are negative almost true twins of u in the original graph. Finally, we introduced the class of negatively critical prime u-true twin graphs for a given vertex u and provided a characterization stemming directly from our core results.

As a direction for future work, we propose to investigate the validity of Ulam’s Reconstruction Conjecture [18] for the class of graphs possessing a negative almost true twin for a given vertex. Ulam’s Conjecture, one of the most famous open problems in graph theory, states that if two graphs G and $G^{\prime }$ have at least three vertices and their vertex-deleted subgraphs are isomorphic for every corresponding vertex (i.e., $G-v$ is isomorphic to $G^{\prime }-v$ for all $v\in V\left(G\right)$), then G and $G^{\prime }$ are isomorphic.

As another research direction, we propose to investigate how the notion of a negative almost true twin can be suitably extended to more complex structures such as digraphs and 2-structures.