Toward Trustworthy On-Device AI: A Quantization-Robust Parameterized Hybrid Neural Filtering Framework

Abstract

Recent advances in deep learning have led to a proliferation of AI services for the general public. Consequently, constructing trustworthy AI systems that operate on personal devices has become a crucial challenge. While on-device processing is critical for privacy-preserving and latency-sensitive applications, conventional deep learning approaches often suffer from instability under quantization and high computational costs. Toward a trustworthy and efficient on-device solution for image processing, we present a hybrid neural filtering framework that combines the representational power of lightweight neural networks with the stability of classical filters. In our framework, the neural network predicts a low-dimensional parameter map that guides the filter’s behavior, effectively decoupling parameter estimation from the final image synthesis. This design enables a truly trustworthy AI system by operating entirely on-device, which eliminates the reliance on servers and significantly reduces computational cost. To ensure quantization robustness, we introduce a basis-decomposed parameterization, a design mathematically proven to bound reconstruction errors. Our network predicts a set of basis maps that are combined via fixed coefficients to form the final guidance. This architecture is intrinsically robust to quantization and supports runtime-adaptive precision without retraining. Experiments on depth map super-resolution validate our approach. Our framework demonstrates exceptional quantization robustness, exhibiting no performance degradation under 8-bit quantization, whereas a baseline suffers a significant 1.56 dB drop. Furthermore, our model’s significantly lower Mean Squared Error highlights its superior stability, providing a practical and mathematically grounded pathway toward trustworthy on-device AI.

1. Introduction

Recent advances in deep learning have led to significant progress in image processing and computer vision tasks such as image restoration, enhancement, recognition, and segmentation, enabling applications in mobile photography, medical imaging, and autonomous driving [1,2,3]. With the growing demand for private and real-time inference, there is an increasing need to deploy AI systems directly on edge devices, including smartphones and wearable devices. This trend has shifted the research focus from solely maximizing accuracy to ensuring the development of trustworthy AI systems [4,5,6,7]. Although on-device processing inherently enhances privacy, a truly trustworthy system must also guarantee robustness and reliability. The full scope of Trustworthy AI includes critical aspects like fairness and uncertainty. However, for on-device applications, operational stability under hardware constraints is paramount. This work therefore focuses on robustness and reliability as the foundational pillars of trustworthiness in this context. These properties are particularly challenging to maintain under the limited computational power of on-device environments. Designing AI systems that satisfy these constraints is therefore essential, not only for practical deployment but also as a well-posed engineering problem under quantifiable resource limitations.

Conventional strategies [8,9,10] for image enhancement on the edge device can be broadly categorized into two approaches. The first approach adopts end-to-end neural network models, which can produce high-quality outputs but often incur computational and memory costs that exceed the limits of resource-constrained devices. Techniques such as quantization and pruning can help alleviate this issue. However, they often lead to noticeable performance degradation. This reliance on server-side processing to compensate for the quality loss can undermine the core principles of on-device trustworthiness. The second approach includes classical, hand-crafted filters such as the Gaussian Filter, Guided Filter [11], Bilateral Filter [12], and more advanced quasi-linear variants like Anisotropic Diffusion, Domain Transform, and Rolling Guidance Filtering [13,14]. These methods are computationally efficient and mathematically interpretable, but typically require per-image parameter tuning, which limits their reliability in practical applications. Hybrid approaches [15,16] that combine neural and classical filtering aim to alleviate this limitation. However, they often depend on deep architectures or suffer performance degradation under low-bit quantization. Therefore, achieving a well-balanced AI solution that satisfies performance, efficiency, and trustworthiness under on-device constraints remains an open challenge.

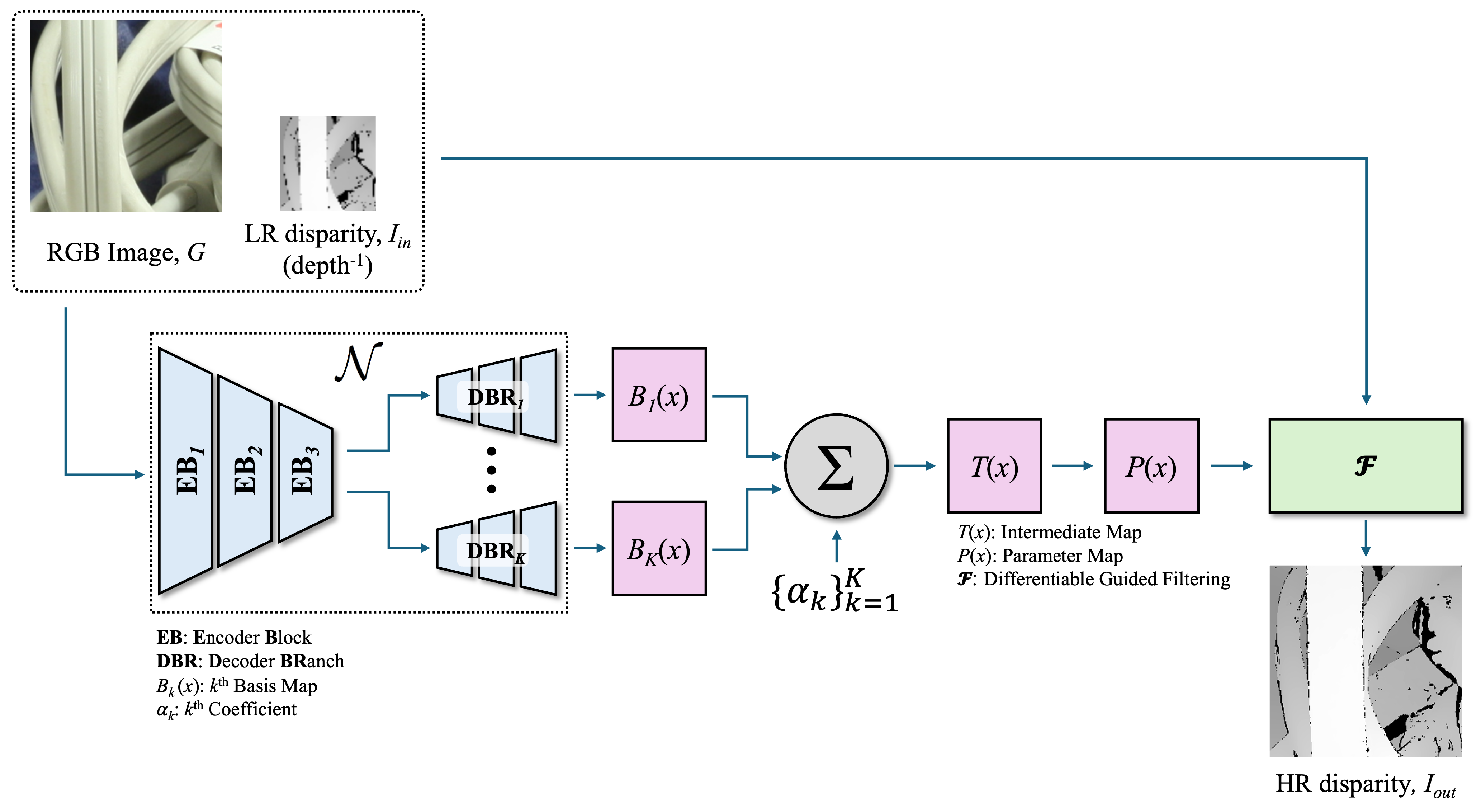
To address this challenge, we propose a parameterized hybrid neural filtering framework. The core idea is to decouple parameter estimation from signal reconstruction: a lightweight neural network predicts a compact parameter map, which then guides a classical filter to synthesize the final image. This design significantly reduces computational costs by limiting the neural network’s task to representation learning, rather than full image-to-image transformation. Crucially, this hybrid structure enhances robustness. By delegating the precision-sensitive synthesis stage to the mathematically stable classical filter, the framework is inherently more resilient to quantization errors.

We further amplify this robustness by introducing a basis-decomposed parameterization. The network predicts multiple low-precision basis maps that are combined via fixed coefficients, a design mathematically proven to bound reconstruction errors. This approach, interpretable as a form of low-rank factorization, provides an intrinsically quantization-friendly structure and enables runtime-adaptive precision, making our framework not only efficient but also inherently trustworthy.

In summary, this work makes four key contributions. First, we propose a hybrid framework that integrates the representational power of neural networks with the stability and interpretability of classical image filters, enabling efficient and reliable on-device image enhancement. Second, we introduce a basis-decomposed parameterization, interpretable as a form of multi-resolution basis expansion or low-rank factorization. This design inherently improves robustness under aggressive quantization and supports runtime-adjustable precision, enabling flexible trade-offs between quality and efficiency. Third, we experimentally demonstrate that our mathematically grounded approach achieves competitive performance while maintaining a lightweight profile suitable for on-device deployment. Lastly, by fully eliminating reliance on server-side computation, our method offers a practical foundation for building trustworthy AI systems that are robust, privacy-preserving, and deployable in real-world cases.

The remainder of this paper is organized as follows. Section 2 reviews related work. Section 3 presents the proposed hybrid framework and basis-decomposed parameterization. Section 4 describes the experimental setup and results. Section 5 discusses about limitations and outlines possible directions for future research.

2. Related Work

In this section, we review prior work across four relevant areas: (1) classical linear image filtering, (2) lightweight neural networks, (3) quantization for on-device inference, and (4) basis expansion (or low-rank parameterization) These domains respectively contribute to mathematical interpretability and differentiability, computational efficiency on edge devices, compact model design for on-device deployment, and structured representations for parameter efficiency and robustness. Each of these components is closely related to our proposed framework. In the following subsections, we summarize representative methods and highlight how our work builds upon and differs from existing approaches in each category.

2.1. Classical Linear Image Filtering

Classical edge-preserving filters, such as the Guided Filter [11] and Bilateral Filter [12], are valued for their mathematical interpretability and predictable behavior. A key property is their differentiability; many can be formulated such that their weights are differentiable with respect to external parameters, allowing them to be integrated into neural networks for end-to-end training. A representative example is the Guided Filter [11], which assumes a local linear model between a guidance image G and the output $\widehat{I}$ in each local window ${\omega }_k$:

$$\widehat{I}\left(x\right)=a_{k}G\left(x\right)+b_k,\forall x\in {\omega }_k$$

(1)

The coefficients $(a_k,b_k)$ are determined by minimizing a regularized least-squares cost function within the window:

$$(a_k,b_k)=arg\underset{a_k,b_k}{min}\sum _{x\in {\omega }_k}\left({(a_{k}G\left(x\right)+b_k-I\left(x\right))}^2+ϵa_k^2\right),$$

(2)

where $ϵ$ is a regularization parameter. This optimization problem has a closed-form solution for the coefficients based on the local mean and variance of the guidance and input images. This formulation is both interpretable and differentiable, making it a natural candidate for hybrid neural–classical frameworks.

In our framework, we adopt the Joint Guided Filter as a case study for the filtering module due to its efficiency, edge-preserving property, and differentiable nature. However, we emphasize that our method is not limited to any specific filter. The design generalizes to other differentiable filtering operators, such as Bilateral Filters, Domain Transform, and even anisotropic diffusion, so long as the filtering operation can be parameterized and differentiated through. By leveraging classical filters for the image synthesis stage and using neural networks solely for parameter prediction, our framework maintains the transparency and efficiency of classical methods while improving adaptability through learned representations. This design also improves robustness to quantization, as the precision-sensitive task of image synthesis is handled by the mathematically stable classical filter.

2.2. Lightweight Neural Networks

The need for compact and efficient models on resource-constrained devices has driven significant research into lightweight neural architectures for on-device AI. Representative examples includeMobileNet v1 and v2 [8,17], ShuffleNet v1 and v2 [9,18], and EfficientNet v1 [10], which leverage design principles such as depthwise separable convolutions, channel shuffling, or neural architecture search to significantly reduce computational cost and the number of parameters. These models demonstrate that with careful architectural design, a favorable trade-off between accuracy and efficiency is achievable. For instance, depthwise separable convolution decomposes standard convolutions into depthwise and pointwise operations, reducing complexity from $O(K^2·C_{\mathrm{in}}$$· C_{\mathrm{out}})$ to $O(K^2·C_{\mathrm{in}}+C_{\mathrm{in}}·C_{\mathrm{out}})$, where K is the kernel size and $C_{\mathrm{in}},C_{\mathrm{out}}$ are the input and output channels, respectively.

Recent task-specific lightweight networks [19,20,21], such as U-Net variants and transformers, often trade expressive capacity for efficiency to enable real-time applications. Despite these innovations, end-to-end neural solutions might still impose non-trivial memory and compute demands, especially when deployed on lower-end devices or operated under aggressive quantization.

To address these limitations, our framework takes a hybrid design approach: it leverages a compact neural network solely for estimating a low-dimensional parameter map, delegating the more compute-intensive image synthesis to a classical filter. This design not only reduces the computational cost compared to end-to-end neural network approaches but also enables fully trustworthy AI system by eliminating server-side assistance.

2.3. Distinction from End-to-End Hybrid Filtering

Several works have explored hybrid neural–classical filtering, with the Fast End-to-End Trainable Guided Filter (GFN) [16] being a prominent example. While both GFN and our framework leverage the Guided Filter, our objectives and technical approaches are fundamentally different, making them orthogonal contributions to the field. The primary goal of GFN, as its name suggests, is to create a fast and fully differentiable filtering layer that can be integrated into larger end-to-end networks for high-performance tasks like joint upsampling. It focuses on optimizing the speed and memory efficiency of the filtering operation itself, particularly in full-precision (FP32) environments.

In contrast, our framework is explicitly designed to solve the problem of quantization robustness for on-device AI. Our core innovation lies not in the filtering operation but in the parameter prediction stage. We achieve robustness by (1) decoupling parameter estimation from the final, precision-sensitive image synthesis, and (2) introducing a basis-decomposed parameterization that is mathematically proven (Proposition 1) to bound reconstruction errors under quantization. This focus on stability in low-bit environments, which is a critical challenge for trustworthiness, is a problem not explicitly addressed by GFN. Therefore, while GFN provides a powerful tool for fast filtering, our framework offers a novel solution for ensuring the reliability of such systems on resource-constrained hardware.

2.4. Quantization for On-Device Inference

Quantization is a standard technique for deploying neural networks on edge devices by reducing model size and accelerating inference [22,23]. However, unlike tasks such as classification, image processing is highly sensitive to the visual quality degradation caused by low-bit precision [24,25]. Existing mitigation strategies like quantization-aware training (QAT) [26,27] often introduce significant training complexity and data dependencies. Other model compression strategies such as pruning and knowledge distillation have also been explored to reduce model size and inference cost [28]. Nevertheless, these approaches primarily focus on parameter sparsity or teacher–student training schemes, and are less effective in addressing the quantization-induced instability that motivates our work.

To overcome these limitations, we adopt a fundamentally different strategy: we decouple the learning and synthesis stages. A lightweight neural network predicts a compact parameter map, which can be more robustly quantized, while the final image synthesis is performed by a classical filter operating in the floating-point domain. This structure prevents quantization artifacts from propagating into the output image and inherently improves system reliability. Furthermore, we introduce a basis-decomposed parameterization in which the guidance map is reconstructed as a weighted combination of multiple low-precision sub-maps. This design not only enhances robustness against quantization error but also allows dynamic precision adjustment at runtime, thereby supporting flexible trade-offs between performance and efficiency.

2.5. Basis Expansion and Low-Rank Parameterization

To improve parameter efficiency and quantization robustness, some recent works [29,30] have adopted structured representations like basis expansion or low-rank parameterization. These techniques reduce the parameter of model redundancy by expressing high-dimensional signals with a more compact set of basis functions or low-rank components.

In basis expansion, a target signal can be expressed as a weighted combination of K basis elements:

$$P\left(x\right)=\sum _{k=1}^K{\alpha }_k·B_k\left(x\right),$$

(3)

where $P\left(x\right)$ denotes the final parameter map at spatial location x, ${\left\{B_k\left(x\right)\right\}}_{k=1}^K$ are basis functions, and $\left\{{\alpha }_k\right\}$ are their corresponding weights. This formulation allows the learning problem to focus on predicting a compact set of coefficients ${\alpha }_k$ rather than entire dense parameters.

Low-rank parameterization similarly constrains model weights or intermediate representations to lie in a lower-dimensional subspace. A common approach is matrix factorization, where a weight matrix $W\in {\mathbb{R}}^{m\times n}$ is approximated as

$$W\approx U·V,U\in {\mathbb{R}}^{m\times r},V\in {\mathbb{R}}^{r\times n},\mathrm{with}r\ll min(m,n),$$

(4)

reducing the number of parameters and operations from $O\left(mn\right)$ to $O\left(r\right(m+n\left)\right)$. Such decompositions are widely used for compressing large models in vision transformers and convolutional networks.

Mathematically, basis expansion can be interpreted as a form of low-rank approximation in the functional domain. If we consider the parameter map $P\left(x\right)$ as a vector in a high-dimensional space, our formulation restricts this vector to lie within a low-dimensional subspace spanned by the K basis functions $\left\{B_k\left(x\right)\right\}$. Specifically, by representing the map as $P\left(x\right)={\sum }_{k=1}^K{\alpha }_k{B}_k\left(x\right)$, we are effectively performing a rank-K approximation of the signal.

While this structural constraint is powerful for general model compression, our framework leverages it in a unique manner. Instead of compressing an entire network, we strategically apply this basis-decomposed parameterization only to the guidance map that controls the classical filter. This targeted approach is what yields the key advantages for on-device deployment: it ensures the neural component remains compact and quantization robust, while also enabling the runtime-adaptive precision that is crucial for building flexible and trustworthy on-device AI systems.

3. Proposed Method

In this section, we present our quantization-robust parameterized hybrid neural filtering framework, that is designed to address the challenges of trustworthy on-device AI. Our method is built upon two core assumptions, which we will explain in the following subsections. First, we introduce the overall hybrid filtering framework, which decouples parameter estimation from image synthesis to enhance efficiency and interpretability. Second, we describe our basis-decomposed parameterization, a novel strategy to provide inherent robustness against quantization and enable runtime-adaptive precision. To demonstrate the effectiveness of the proposed approach, we choose RGB-guided depth map super-resolution as a representative task since it is a well-studied problem [31,32,33] using linear filtering, the Guided Filter [11], and has practical applications in mobile environments, such as Bokeh effect generation and 3D reconstruction. However, the proposed framework is general and applicable to any task that can be formulated with any differentiable filtering.

3.1. Overall Framework: A Hybrid Neural Filtering Approach

Our proposed method is built upon a hybrid neural filtering framework that decouples the complex task of image synthesis from the data-driven task of parameter estimation. As illustrated in Figure 1, the proposed approach represents distinct responsibilities to a lightweight neural network and a classical, mathematically defined filter. The overall process can be formulated as

$$I_{out}=\mathcal{F}(I_{in},G,P\left(x\right)),$$

(5)

where $I_{in}$ is the input image to be processed (e.g., a low-resolution depth map), G is a guidance image (e.g., a high-resolution RGB image), and $\mathcal{F}$ represents a classical differentiable filter. The behavior of this filter is controlled by a spatially varying parameter map $P\left(x\right)$, which is predicted and post-processed by a lightweight neural network $\mathcal{N}$:

$$P\left(x\right)=\mathcal{N}(I_{in},G;\theta ),$$

(6)

where $\theta$ denotes the learnable weights of the network.

For the differentiable filter $\mathcal{F}$ using the Guided Filter, the Guided Filter assumes a local linear model between the guidance image G and the output $I_{out}$ within a local window ${\omega }_k$:

$$I_{out}\left(i\right)=a_{k}G\left(i\right)+b_k,\forall i\in {\omega }_k,$$

(7)

where $(a_k,b_k)$ are the linear coefficients assumed to be constant in the window ${\omega }_k$. These coefficients have a closed-form solution derived from minimizing a regularized least-squares objective:

$$\begin{array}{cc}\hfill a_k& ={\displaystyle \frac{\frac{1}{|{\omega }_k|}{\sum }_{i\in {\omega }_k}G\left(i\right)I_{in}\left(i\right)-{\mu }_k{\overline{I}}_{in,k}}{{\sigma }_k^2+{ϵ}_k}}\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill b_k& ={\overline{I}}_{in,k}-a_k{\mu }_k,\hfill \end{array}$$

(9)

where ${\mu }_k$ and ${\sigma }_k^2$ are the mean and variance of the guidance image G in ${\omega }_k$, and ${\overline{I}}_{in,k}$ is the mean of the input image $I_{in}$ in the same window. Crucially, our framework introduces adaptability by allowing the neural network to control the regularization parameter ${ϵ}_k$, which dictates the degree of edge-preserving smoothing. We achieve this by defining ${ϵ}_k$ as a function of the predicted parameter map $P\left(x\right)$. Specifically, the network-predicted map $P\left(x\right)$ serves as a spatially varying regularization map, and ${ϵ}_k$ is computed as the average value of $P\left(x\right)$ within the window ${\omega }_k$. This allows the network to learn to apply strong smoothing ($\mathrm{high}{ϵ}_k$) in textured or flat regions while preserving sharp edges ($\mathrm{low}{ϵ}_k$) where needed, guided by the content of both the input and guidance images.

3.2. Quantization Robustness via Basis-Decomposed Parameterization

A primary challenge in on-device deployment is that the output of a neural network is sensitive to quantization. It is important to distinguish our proposed solution, basis decomposition, from traditional model compression techniques. Rather than being a method to reduce model size post hoc, our basis decomposition is an architectural design choice made a priori to ensure the network is inherently robust to the subsequent bit-precision reduction of quantization. To achieve this, we introduce a novel parameterization where, instead of predicting a single high-precision parameter map directly, our framework predicts a set of K basis maps. These maps are then combined using pre-defined, fixed coefficients to form the final parameter map as formulated below:

$$P\left(x\right)=\sum _{k=1}^K{\alpha }_k·B_k\left(x\right),$$

(10)

where ${\left\{B_k\left(x\right)\right\}}_{k=1}^K$ are the basis maps predicted by a neural network $\mathcal{N}$, and ${\left\{{\alpha }_k\right\}}_{k=1}^K$ is a set of fixed scalar coefficients.

3.2.1. Network Architecture for Basis Prediction

The core of our parameter estimation stage is the lightweight neural network, $\mathcal{N}$, which is designed for efficient on-device inference. As illustrated in Figure 1, our network $\mathcal{N}$ adopts a one-encoder, multi-decoder architecture. A single, shared encoder, designed with residual convolutional blocks, takes the concatenated input image $I_{in}$ and guidance image G to extract a compact feature representation. This shared representation is then fed into K parallel, lightweight decoders. Each decoder, ${\mathrm{Decoder}}_k$, is specialized to predict a single corresponding basis map, $B_k\left(x\right)$. This design allows the network to learn a disentangled representation for each basis component while maintaining high computational efficiency by sharing the feature extraction backbone.

3.2.2. Parameter Map Composition

The K basis maps predicted by the network are combined to form the final, spatially varying regularization map $P\left(x\right)$ for the Guided Filter. This composition involves two key steps. First, the basis maps are combined via a weighted summation using a set of fixed coefficients $\left\{{\alpha }_k\right\}$, which are structured as a geometric progression to create a hierarchical representation:

$${\alpha }_k={\beta }^{-(k-1)},\mathrm{for}k=1,\dots ,K,$$

(11)

where $\beta$ is the base of the progression (e.g., $\beta =2$ in our experiments). This choice is inspired by the principle of positional notation used in number systems. Our framework adapts this concept to the functional domain: the fixed coefficients $\left\{{\alpha }_k\right\}$ act as pre-defined place-value weights, and the neural network learns to predict the corresponding maps $\left\{B_k\left(x\right)\right\}$. This formulation transforms the unstructured task of regressing a single, continuous-valued map into a more constrained problem of predicting a set of basis maps that function like bit-planes. This structured approach provides a more stable learning target and encourages a coarse-to-fine representation, as the first few basis maps naturally learn to capture the most critical, large-scale information. The weighted sum is then normalized to produce an intermediate map $T\left(x\right)\in [0,1]$:

$$T\left(x\right)={\displaystyle \frac{{\sum }_{k=1}^K{\alpha }_k{B}_k\left(x\right)}{{\sum }_{k=1}^K{\alpha }_k}}.$$

(12)

Second, to address the non-linear sensitivity of the Guided Filter’s regularization parameter $ϵ$, we map the intermediate linear map $T\left(x\right)$ to the final parameter map $P\left(x\right)$ using a log-uniform transformation:

$$P\left(x\right)={ϵ}_{min}{\left({\displaystyle \frac{{ϵ}_{max}}{{ϵ}_{min}}}\right)}^{T\left(x\right)},$$

(13)

where $[{ϵ}_{min},{ϵ}_{max}]$ defines the target range for the regularization parameter (e.g., $[{10}^{-6},{10}^{-2}]$).

3.2.3. Analysis of Quantization Effects

For on-device deployment, the neural network $\mathcal{N}$ is quantized, which results in the prediction of quantized basis maps, ${\widehat{B}}_k\left(x\right)$. The final parameter map is then reconstructed at runtime following the same composition process. First, an intermediate quantized map $\widehat{T}\left(x\right)$ is formed:

$$\widehat{T}\left(x\right)={\displaystyle \frac{{\sum }_{k=1}^K{\alpha }_k{\widehat{B}}_k\left(x\right)}{{\sum }_{k=1}^K{\alpha }_k}}.$$

(14)

This is then transformed to the final quantized parameter map:

$$\widehat{P}\left(x\right)={ϵ}_{min}{\left({\displaystyle \frac{{ϵ}_{max}}{{ϵ}_{min}}}\right)}^{\widehat{T}\left(x\right)}.$$

(15)

The resulting quantization error in the parameter map domain is $\mathrm{\Delta }P\left(x\right)=P\left(x\right)-\widehat{P}\left(x\right)$. This formulation allows us to bound the error as stated in the following proposition.

Proposition 1 (Bounded reconstruction error).

The ${\mathit{\ell }}_2$ norm of the parameter map error, ${\parallel \mathrm{\Delta }P\parallel }_2$, is bounded by a scaled, weighted sum of the quantization errors of the individual basis maps:

$${\parallel \mathrm{\Delta }P\parallel }_2\le C·\sum _{k=1}^K{\alpha }_k·{\parallel B_k-{\widehat{B}}_k\parallel }_2,$$

(16)

where C is a constant determined by the range $[{ϵ}_{min},{ϵ}_{max}]$.

Proof. 

Let $f\left(t\right)={ϵ}_{min}{({ϵ}_{max}/{ϵ}_{min})}^t$. The error is $\mathrm{\Delta }P\left(x\right)=f\left(T\left(x\right)\right)-f(\widehat{T}\left(x\right))$. The function $f\left(t\right)$ is differentiable and its derivative is bounded over the domain $t\in [0,1]$. By the Mean Value Theorem, there exists a function $T_c\left(x\right)$ with values between $T\left(x\right)$ and $\widehat{T}\left(x\right)$ such that $\mathrm{\Delta }P\left(x\right)=f^{\prime }(T_c\left(x\right))(T\left(x\right)-\widehat{T}\left(x\right))$. Let $L={sup}_{t\in [0,1]}\left|f^{\prime }\left(t\right)\right|$ be the Lipschitz constant of f. Then, $\left|\mathrm{\Delta }P\left(x\right)\right|\le L|T\left(x\right)-\widehat{T}\left(x\right)|$. Integrating over the spatial domain and applying the triangle inequality yields the following derivation:

$$\begin{array}{cc}\hfill {\parallel \mathrm{\Delta }P\parallel }_2& \le L·\parallel T-\widehat{T}{\parallel }_2\hfill \\ & =L·{∥{\displaystyle \frac{{\sum }_{k=1}^K{\alpha }_k(B_k-{\widehat{B}}_k)}{{\sum }_{k=1}^K{\alpha }_k}}∥}_2\hfill \\ & \le {\displaystyle \frac{L}{{\sum }_{k=1}^K{\alpha }_k}}\sum _{k=1}^K{\parallel {\alpha }_k(B_k-{\widehat{B}}_k)\parallel }_2\hfill \\ & ={\displaystyle \frac{L}{{\sum }_{k=1}^K{\alpha }_k}}\sum _{k=1}^K|{\alpha }_k|·\parallel B_k-{\widehat{B}}_k{\parallel }_2.\hfill \end{array}$$

Letting $C=L/\left({\sum }_{k=1}^K{\alpha }_k\right)$, the proposition holds. □

This proposition reveals a crucial insight: the total reconstruction error is controlled by the fixed, pre-defined coefficients $|{\alpha }_k|$. This mathematical foundation provides two significant benefits for trustworthy on-device AI. First, it enhances quantization robustness. The network can learn to distribute information across the basis maps according to the importance dictated by the magnitude of their corresponding ${\alpha }_k$. As shown by Proposition 1, this structure actively suppresses the impact of quantization errors from the less significant basis maps on the final output. Second, as illustrated in Figure 2, this structure enables runtime-adaptive precision. By reconstructing the map using only a subset of the first $K^{\prime }<K$ basis maps, a faster, lower-fidelity approximation can be obtained without any need for retraining.

4. Experiments

In this section, we conduct a series of experiments to evaluate the effectiveness of the proposed framework. We first describe the experimental setup, including datasets, loss functions, and implementation details. We then present quantitative and qualitative comparisons against conventional methods on the task of RGB-guided depth map super-resolution.

4.1. Datasets Setup

For training the proposed framework, Middlebury stereo datasets [34,35,36,37,38] were used. These datasets are widely adopted for disparity-related tasks (disparity being the inverse of depth), providing high-quality RGB–disparity pairs captured under controlled indoor conditions. The data includes a variety of scenes with diverse textures, lighting conditions, and geometric structures, making them suitable for evaluating the performance of stereo estimation and disparity refinement.

Unlike RGB images, disparity (or depth) maps often contain large textureless regions, which can make the task of disparity super-resolution artificially easy. To mitigate this and ensure our model is trained on challenging examples, we employ a stratified sampling strategy based on depth variation. Specifically, we first generate a pool of 30,000 random $256\times 256$ patches from all available RGB–disparity pairs in the Middlebury Stereo collection. For each patch, we compute the standard deviation of its disparity values and cluster the patches into three groups: high, medium, and low variance.

To construct our dataset, we adopt a different sampling strategy for training versus validation and testing. The training set is created by randomly sampling exclusively from the high- and medium-variance groups, forcing the model to learn from more complex and structured regions. In contrast, the validation and test sets are sampled randomly from all three clusters to ensure that our evaluation reflects a realistic distribution of scenes, including simpler, textureless areas. For each selected patch, the original cropped disparity map is used as the ground truth ($D_{HR}$). The corresponding low-resolution input ($D_{LR}$) is generated by applying bicubic downsampling to the ground truth, followed by bicubic upsampling back to the original $256\times 256$ resolution. The entire set of patches is divided into training (70%), validation (15%), and testing (15%) sets.

4.2. Loss Functions

The proposed hybrid framework is trained end-to-end by optimizing a composite loss function designed to enforce reconstruction fidelity, structural similarity, and perceptual quality. The total loss $\mathcal{L}$ is a weighted sum of multiple components:

$$\mathcal{L}\left(\theta \right)={\lambda }_{rec}{\mathcal{L}}_{rec}+{\lambda }_{grad}{\mathcal{L}}_{grad}+{\lambda }_{lap}{\mathcal{L}}_{lap},$$

(17)

where ${\lambda }_{rec}$, ${\lambda }_{grad}$, and ${\lambda }_{lap}$ are weighting hyperparameters for each loss term.

4.2.1. Reconstruction Loss

For the primary data fidelity term, we employ the Charbonnier loss, a smooth variant of the L1 loss that is less sensitive to outliers:

$${\mathcal{L}}_{rec}={\displaystyle \frac{1}{N}}\sum _{i=1}^N\sqrt{\parallel I_{out}^{\left(i\right)}-I_{gt}^{\left(i\right)}{\parallel }_2^2+{ϵ}^2}.$$

(18)

4.2.2. Structural and Perceptual Losses

To better preserve fine details and sharp edges, we incorporate a gradient consistency loss, ${\mathcal{L}}_{grad}$, and a high-frequency loss, ${\mathcal{L}}_{lap}$. These are defined as

$$\begin{array}{cc}\hfill {\mathcal{L}}_{grad}& =\parallel \nabla I_{out}-\nabla I_{gt}{\parallel }_1,\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill {\mathcal{L}}_{lap}& =\parallel \mathrm{\Delta }{I}_{out}-\mathrm{\Delta }{I}_{gt}{\parallel }_1,\hfill \end{array}$$

(20)

where ∇ and $\mathrm{\Delta }$ denote the Sobel gradient magnitude and Laplacian operators, respectively.

4.3. Implementation Details

Our proposed framework is implemented in PyTorch 2.8.0 and trained on the Middlebury dataset as described above. The detailed architecture of our network is summarized in

Table 1. Detailed parameter distribution of our proposed network, $\mathcal{N}$. The network consists of a shared encoder, a shared upsampling path in the decoder, and four parallel, lightweight decoder branches for predicting the $B_k\left(x\right)$.

Our Network, $\mathcal{N}$
Component	Sub-Modules	Parameters
Encoder Path	Encoder Block 1 (16 channels)	9872
	Encoder Block 2 (32 channels)	41,632
	Encoder Block 3 (64 channels)	166,208
	Subtotal	217,712
Decoder Path	Shared Skip-Connection Blocks	2608
	Decoder Branch 1 ($B_1$)	138,145
	Decoder Branch 2 ($B_2$)	138,145
	Decoder Branch 3 ($B_3$)	138,145
	Decoder Branch 4 ($B_4$)	138,145
	Subtotal	555,188
Total Trainable Parameters		772,900
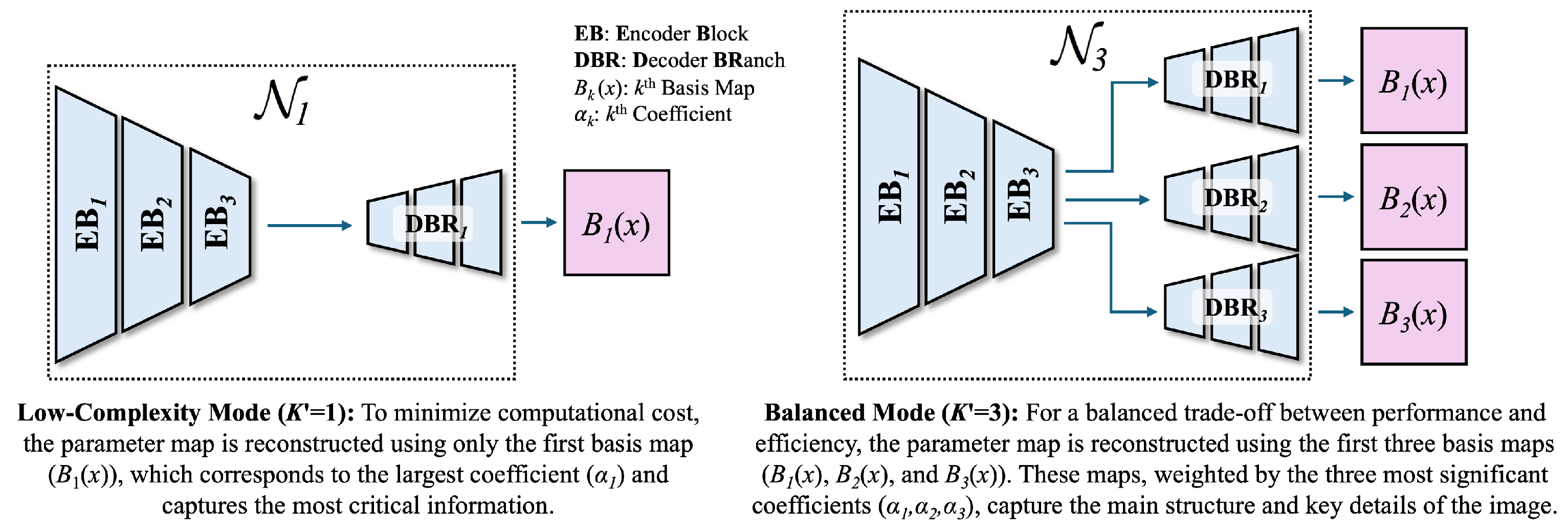
Total mult-adds (G)		10.26

. To maximize parameter efficiency, we employ a shared-encoder and parallel-decoder structure. The shared encoder is designed to be relatively deep to extract a rich feature representation that is common to all parallel decoder branches. Conversely, each of the four parallel decoders is intentionally designed to be lightweight. For our main experiments, the number of decoders, K, is empirically set to 4, as this provides the best trade-off between performance and complexity on our validation set. Furthermore, to enhance generalization and reduce the number of parameters, the upsampling convolution operations within the decoder path are also shared across all branches. This design provides an additional advantage for runtime flexibility; when operating on highly resource-constrained devices, a subset of the decoders can be activated, further reducing the total number of active parameters.

The network predicts a total of $K=4$ basis maps, which is adjustable. A $\beta$ for ${\alpha }_k$ is set to 2. The model is trained for 500 epochs using the Adam optimizer with an initial learning rate of ${10}^{-4}$, which is decayed according to a cosine annealing schedule. The loss weighting parameters are set to ${\lambda }_{rec}=1.0$, ${\lambda }_{grad}=0.5$, and ${\lambda }_{lap}=0.5$. Due to the inherent robustness of our parameterized approach, which results in a negligible performance gap between FP32 and INT8 precision, our model is trained natively in an 8-bit environment to reflect realistic on-device conditions. All experiments are conducted on a single NVIDIA RTX 5090 GPU.

As a baseline for comparison, we utilize a standard U-Net that achieves comparable performance to our proposed framework in a vanilla end-to-end setting. This network consists of a conventional single-encoder, single-decoder architecture. The detailed parameter distribution is presented in

Table 2. Parameter distribution of the baseline U-Net.

Baseline, BaseNet
Component	Sub-Modules	Parameters
Encoder	Encoder Block 1 (32 channels)	19,680
	Encoder Block 2 (64 channels)	92,352
	Encoder Block 3 (128 channels)	369,024
	Subtotal	481,056
Decoder	Decoder Block 1 (128→64 ch)	426,304
	Decoder Block 2 (64→32 ch)	106,656
	Final Blocks (32→1 ch)	29,121
	Subtotal	562,081
Total Trainable Parameters		1,043,137
Total mult-adds (G)		12.53

.

4.4. Ablation Study on Runtime-Adaptive Precision

To validate the flexibility of our framework, we first evaluate its performance by varying the number of active decoder branches (K) from 1 to 4. This corresponds to adjusting the number of basis maps used for reconstruction at runtime. The results are summarized in

Table 3. Quantitative comparison of performance and complexity on the Middlebury dataset. The best results are highlighted in bold and the second-best results are underlined.

Method	# Decoders (K)	Parameters	MACs (G)	PSNR (dB)	MSE
BaseNet	N/A	1.04 M	12.53	27.40	0.013941
Ours, $\mathcal{N}$	1	0.43 M	8.40	27.17	0.004979
Ours, $\mathcal{N}$	2	0.52 M	9.02	27.18	0.004968
Ours, $\mathcal{N}$	3	0.62 M	9.64	27.20	0.004950
Ours, $\mathcal{N}$	4	0.77 M	10.26	27.22	0.004928

.

The results clearly demonstrate the effectiveness of our runtime-adaptive precision mechanism. As the number of active decoders (K) increases from 1 to 4, the PSNR shows a corresponding monotonic improvement from 27.17 dB to 27.22 dB, at a modest and predictable increase in parameters and computational cost. This confirms that a single trained model can be flexibly deployed to meet different performance and efficiency requirements, a key feature for on-device applications.

4.5. Stability Analysis: Hybrid vs. End-to-End Approach

A more crucial insight is revealed by comparing the stability of our hybrid approach against the end-to-end BaseNet, using the PSNR and MSE metrics from Table 3. While the BaseNet achieves the highest PSNR (27.40 dB), its MSE (0.013941) is approximately 2.8 times higher than that of our full model (0.004928).

Since PSNR reflects average perceptual quality while MSE is highly sensitive to large, localized errors (outliers), this discrepancy suggests that the BaseNet, despite its high average performance, is prone to producing significant errors in challenging regions. In contrast, our framework’s consistently low MSE across all configurations indicates superior stability and reliability. This ability to avoid catastrophic failures is a cornerstone of a Trustworthy AI system, making our hybrid approach a more robust and predictable solution for practical on-device applications.

4.6. Ablation Study on Architectural Efficiency

To investigate the generality of our framework and address the feedback on mobile-optimized networks, we conducted an additional ablation study. We replaced the standard convolutions in our backbone architecture with depthwise separable convolutions (DSC) [8], a key technique used in efficient architectures like MobileNet.

DSC factorizes a standard convolution into a depthwise and a pointwise operation, which can significantly reduce parameters and computational cost. The results of this modification, which we term ${\mathcal{N}}^{\prime }$, are presented in

Table 4. Actual parameter distribution of the network after applying depthwise separable convolutions. The table compares the new lightweight model (${\mathcal{N}}^{\prime }$) against the original standard model ($\mathcal{N}$).

Standard Conv ($\mathcal{N}$) vs. Depthwise Separable Conv (${\mathcal{N}}^{\prime }$)
Component	Sub-Modules	Parameters	Reduction
Encoder Path	Encoder Block 1 (16 ch)	1848	−81.3%
	Encoder Block 2 (32 ch)	6208	−85.1%
	Encoder Block 3 (64 ch)	21,632	−87.0%
	Subtotal	29,688	−86.4%
Decoder Path	Shared Skip-Connection Blocks	2800	+7.4%
	Decoder Branches (4×)	70,532	−87.2%
	(17,633 per branch)
	Subtotal	73,332	−86.8%
Total Trainable Parameters		103,020	−86.7%
Total mult-adds (G)		1.71 G	−83.3%

. This experiment demonstrates that our proposed hybrid parameterization is not tied to a specific backbone architecture and can be flexibly combined with other efficiency-enhancing techniques for further optimization.

To examine the real-world feasibility of our proposed efficiency, the optimized $\mathcal{N}’$ model was deployed on a mobile AP processor (Qualcomm Snapdragon 865).

Table 5. On-device inference latency and memory footprint measured on Qualcomm Snapdragon 865.

Precision	Activations (MB)	Params (MB)	Estimated Peak (MB)	Latency (ms)
FP32	28.1	0.41	39.8	35.2
INT8	8.4	0.10	14.3	14.8

presents the measured average inference latency and peak memory footprint, obtained under the same experimental conditions as the PC-based experiments.

4.7. Analysis of Quantization Robustness

A core claim of our work is that the proposed framework is inherently robust to quantized inference. To verify this, we compare the performance of our models ($\mathcal{N}$ and the DSC-variant ${\mathcal{N}}^{\prime }$) against the BaseNet under post-training quantization. We quantize all models from full precision (FP32) to 8-bit integers (INT8) and measure the performance degradation (ΔPSNR). To evaluate generalizability, the experiments are conducted on both the Middlebury and, the more challenging, real-world NYU Depth V2 datasets.

The results, presented in

Table 6. Performance Quantitative comparison for 8-bit inference. The best results are highlighted in bold and the second-best results are underlined.

Middlebury Datasets				NYU Depth V2 Datasets
Method	Precision	PSNR	ΔPSNR	Method	Precision	PSNR	ΔPSNR
BaseNet	FP32	27.4031	1.5603	BaseNet	FP32	31.6097	0.8100
	INT8	25.8428			INT8	30.7997
$\mathcal{N}$ ($\mathit{K}=4$)	FP32	27.2245	0.0044	$\mathcal{N}$ ($\mathit{K}=4$)	FP32	32.1278	0.1439
	INT8	27.2201			INT8	31.9839
${\mathcal{N}}^{\prime }$ ($\mathit{K}=4$)	FP32	26.1132	0.0836	${\mathcal{N}}^{\prime }$ ($\mathit{K}=4$)	FP32	31.4593	0.1305
	INT8	26.0296			INT8	31.3288

, strongly validate our approach. On the Middlebury dataset, the standard BaseNet suffers a severe performance drop of 1.5603 dB after quantization, highlighting the well-known sensitivity of end-to-end models. In stark contrast, our proposed model, $\mathcal{N}$, exhibits a negligible degradation of only 0.0044 dB. This provides powerful empirical evidence for the effectiveness of our basis-decomposed parameterization. Furthermore, our DSC-variant, ${\mathcal{N}}^{\prime }$, also shows a minimal drop of just 0.0836 dB, confirming that the robustness stems from our framework’s architecture, not a specific convolutional backbone.

The experiments on the NYU Depth V2 dataset further confirm these findings. While the performance degradation is slightly higher across all models on this real-world dataset, the relative trend holds. The performance of BaseNet drops by a significant 0.81 dB, whereas our models, $\mathcal{N}$ and ${\mathcal{N}}^{\prime }$, degrade by only 0.14 dB and 0.13 dB, respectively. These results demonstrate that our framework’s superior quantization robustness is not limited to a single dataset but generalizes effectively, making it a reliable solution for practical on-device deployment.

4.8. Qualitative Analysis

To visually validate the stability and quantization robustness of our framework, we provide qualitative comparisons in Figure 3 and Figure 4.

Figure 3 compares final outputs on challenging cases. The end-to-end BaseNet fails to preserve sharp boundaries and often introduces blurry artifacts as shown by its bright and spatially widespread error map. In contrast, our approach reconstructs fine details with fewer localized errors, demonstrating much cleaner and more stable results. This supports the higher MSE performance in Table 3, showing that our approach achieves more stable results.

Figure 4 illustrates the effect of 8-bit quantization. Our approach produces nearly identical outputs before and after quantization (${\mathcal{N}}_{\mathrm{FP}32}$ vs. ${\mathcal{N}}_{\mathrm{INT}8}$), yielding an almost black quantization error map that confirms its robustness. In contrast, BaseNet exhibits visible degradation and large structured errors, indicating that our hybrid, parameter-decoupled design ensures stable performance under quantization.

4.9. Application to Other Tasks: Matting Mask Refinement

To verify the generalizability of our framework, we conduct an additional experiment on image matting mask refinement. Using the MODNet dataset [39], we task our model with refining a low-quality alpha matte, using the corresponding RGB image as guidance. The network, using the same efficient ${\mathcal{N}}^{\prime }$ architecture, predicts the optimal epsilon map for the Guided Filter. As shown in the qualitative results in Figure 5, our framework successfully estimates the context-aware filter parameters to produce a high-quality alpha matte with fine details. This experiment confirms that our proposed parameterization scheme is not limited to depth super-resolution but can be effectively applied to other image processing tasks.

5. Discussion

The experimental results demonstrate the effectiveness of the proposed framework. In this section, we discuss the broader implications of our findings, acknowledge the limitations of our current approach, and suggest potential directions for future research.

5.1. Implications for Trustworthy AI

Our framework’s contributions to Trustworthy AI extend beyond the core achievement of quantization robustness, offering inherent advantages in system stability and explainability. Unlike monolithic end-to-end networks, which often function as black boxes, the behavior of our hybrid model can be partially interpreted by visualizing the parameter map $P\left(x\right)$ predicted by the neural network. This map provides clear insight into the model’s decision-making process, showing which regions are designated for detail preservation (low ${ϵ}_k$) versus those requiring smoothing (high ${ϵ}_k$). This degree of transparency is a significant step toward building more interpretable and, therefore, trustworthy AI systems.

Furthermore, this explainability is complemented by the superior stability demonstrated in our experiments. The consistently low Mean Squared Error (MSE) of our framework, in contrast to the baseline’s high score, indicates an ability to avoid the large, localized errors and catastrophic failures common in end-to-end models. This reliability, especially under the hardware constraints of on-device environments, is a cornerstone of a trustworthy system. By successfully combining exceptional quantization robustness, predictable stability, and inherent explainability, our work provides a practical and mathematically grounded foundation for developing the next generation of trustworthy on-device AI applications.

5.2. Limitations and Scope

While our framework demonstrates significant advantages, we acknowledge several limitations and areas for further investigation. A primary challenge lies in the training process due to the indirect nature of the supervision signal. The network predicts a parameter map whose values have a non-linear effect on the final output, and the long backpropagation path from the final image loss can lead to instability. To mitigate this, we employed key strategies, including a composite loss function with structural regularizers (${\mathcal{L}}_{grad}$, ${\mathcal{L}}_{lap}$) and a robust cosine annealing learning rate scheduler, which proved sufficient to ensure stable convergence.

From a theoretical standpoint, our mathematical analysis is centered on the deterministic error bound provided in Proposition 1. We acknowledge that this analysis could be extended. For instance, deriving tighter error bounds by considering the statistical properties of the basis maps, or developing a probabilistic analysis of the quantization error distribution, could provide deeper insights and further strengthen the framework’s theoretical foundations.

At the application level, our framework is subject to the inherent limitations of RGB-guided methods, most notably the potential for texture copying artifacts. This issue arises when a geometrically flat region in the depth map corresponds to a high-frequency texture in the RGB guidance image, causing the model to misinterpret texture edges as depth discontinuities. While less critical for applications like synthetic bokeh, such artifacts can be detrimental to tasks requiring high geometric fidelity, like 3D reconstruction, and this remains an open challenge in the field.

Finally, the scope of our method is intentionally focused on lightweight, efficient performance in resource-constrained environments. Its advantages in parameter efficiency and quantization robustness are most pronounced on mobile and embedded systems. Consequently, in high-resource settings with ample computational capacity, the relative benefits of our design may diminish when compared to large-scale, full-precision models.

5.3. Future Directions

Our framework establishes a solid foundation and opens up several exciting avenues for future research. A promising direction is to address the inherent limitation of texture copying by integrating attention mechanisms. This could enable the model to dynamically modulate the influence of the guidance image, for instance by down-weighting the RGB guide in texture-rich but geometrically flat regions. The framework could be further enhanced through more advanced adaptive basis learning. For instance, the coefficients $\left\{{\alpha }_k\right\}$, which are currently fixed as a geometric progression, could be learned during training or even predicted dynamically by the network for each input. Exploring constraints such as basis orthogonality during learning could also enforce a more disentangled and efficient representation. Another avenue could involve learning a set of universal, fixed basis functions from the entire dataset, allowing the network to predict only a compact set of spatially varying coefficients. This could lead to a more powerful and compact representation.

Theoretically, extending our analysis beyond the current deterministic error bound is an important next step. Developing a probabilistic analysis of the quantization error distribution could provide deeper insights and stronger guarantees for the framework’s robustness. Furthermore, to broaden the scope of trustworthiness, the framework could be extended to quantify uncertainty, perhaps by applying techniques like Monte Carlo Dropout to the basis map prediction, which would significantly enhance system reliability in critical applications. Additionally, future work could investigate other facets of trustworthiness, such as fairness, by analyzing the model’s performance across diverse demographic or environmental conditions.

Finally, to demonstrate the true on-device viability and generalizability of our approach, future work must involve broader experimental validation. This includes applying the framework to a wider range of image processing tasks, such as denoising or dehazing, and complementing these experiments with the detailed profiling of latency and energy consumption on actual mobile hardware. We believe these future explorations will build upon our work to further advance the development of reliable and resource-efficient on-device AI.

6. Conclusions

In this work, we proposed a novel parameterized hybrid neural filtering framework designed to address the critical challenges of building trustworthy and efficient AI systems for on-device image processing. Our core contributions are twofold. First, by decoupling parameter estimation from image synthesis, our framework significantly enhances parameter efficiency and stability compared to standard end-to-end models. Second, we introduced a basis-decomposed parameterization, a mathematically grounded approach that provides exceptional robustness against quantization, a mandatory step for on-device deployment. Our experimental results on RGB-guided depth map super-resolution demonstrated that this design not only prevents performance degradation under 8-bit quantization but also enables runtime-adaptive precision, allowing a single model to flexibly adapt to diverse computational constraints. By providing a practical and theoretically sound solution, this work lays a solid foundation for the future development of reliable and resource-efficient AI applications.