Two-Layered Reward Reinforcement Learning in Humanoid Robot Motion Tracking

Abstract

In reinforcement learning (RL), reward function design is critical to the learning efficiency and final performance of agents. However, in complex tasks such as humanoid motion tracking, traditional static weighted reward functions struggle to adapt to shifting learning priorities across training stages, and designing a suitable shaping reward is problematic. To address these challenges, this paper proposes a two-layered reward reinforcement learning framework. The framework decomposes the reward into two layers: an upper-level goal reward that measures task completion, and a lower-level optimizing reward that includes auxiliary objectives such as stability, energy consumption, and motion smoothness. The key innovation lies in the online optimization of the lower-level reward weights via an online meta-heuristic optimization algorithm. This online adaptivity enables goal-conditioned reward shaping, allowing the reward structure to evolve autonomously without requiring expert demonstrations, thereby improving learning robustness and interpretability. The framework is tested on a gymnastic motion tracking problem for the Unitree G1 humanoid robot in the Isaac Gym simulation environment. The experimental results show that, compared to a static reward baseline, the proposed framework achieves 7.58% and 10.30% improvements in upper-body and lower-body link tracking accuracy, respectively. The resulting motions also exhibit better synchronization and reduced latency. The simulation results demonstrate the effectiveness of the framework in promoting efficient exploration, accelerating convergence, and enhancing motion imitation quality.

1. Introduction

Reinforcement learning (RL) is a branch of machine learning where an agent learns optimal behavior or policy through trial-and-error interactions with outer environments [1]. The agent receives scalar rewards as feedback and aims to maximize the cumulative reward over time. RL is particularly powerful for sequential decision-making tasks, such as robotic control [2], game playing [3], robotic manipulation [4], and humanoid robots [5].

Deep Reinforcement Learning (DRL) integrates deep neural networks with RL, enabling agents to handle high-dimensional sensory inputs (e.g., images, sensor data) and continuous action spaces [6]. DRL algorithms, such as Deep Deterministic Policy Gradient (DDPG) [7] and Proximal Policy Optimization (PPO) [8], have achieved remarkable success in various domains. They allow systems to adapt dynamically to changing conditions, optimize long-term performance, and learn end-to-end control policies without precise mathematical models.

Despite their power, DRL methods still face challenges in sample efficiency and training stability, particularly when rewards are delayed or sparse [9]. In reinforcement learning, the reward function is a critical component from environments that defines the agent’s objective by providing scalar feedback signals in response to its actions. It essentially tells the agent what goals to achieve by assigning positive or negative rewards for specific states or behaviors during interactions. However, a poorly designed or inherently sparse reward function can lead to significant learning difficulties.

When rewards are only provided upon task completion, the agent receives little-to-no guidance during the majority of its interactions, making exploration inefficient and the learning procedure extremely slow. In robotics such as humanoid robots, reinforcement learning can train controllers or agents to find optimal solutions for complex tasks by enabling the robot to interact repeatedly with the environment [10]. The reward function is an important aspect that guides humanoid robots to find the desired solution successfully. However, a sparse reward in tasks like motion tracking makes the training procedure inefficient.

Reinforcement learning always faces the trade-off between the ease of designing reward functions and the ease of learning from rewards, and reward shaping provides a solution [11]. Reward shaping entails modifying the reward function of a problem to expedite the training speed and efficiency of reinforcement learning algorithms [12].

The primary goal of reward shaping is to modify the agent’s learning environment by introducing supplementary reward signals [13]. This allows the agent to receive more frequent and informative feedback during its interactions, facilitating faster and more effective strategy adjustments to achieve the intended learning objectives.

Reward shaping is broadly categorized into two main types: curiosity-driven exploration, which motivates agents to explore novel states by providing intrinsic rewards for encountering unfamiliar or unpredictable situations [14]; and potential-based reward shaping (PBRS), which guides the agent by adding a reward signal derived from the difference in a potential function between consecutive states, thereby shaping the learning process without altering the optimal policy [15].

Reward shaping in reinforcement learning is a widely studied and active research area. To provide denser feedback, Ref. [16] introduces a shaped reward function based on potential functions to address the sparse reward problem in DQN for UAV emergency communication. By incorporating a shaping reward derived from the difference in potential between consecutive states, the method provides dense intermediate feedback to guide the agent’s exploration. This approach accelerates training convergence and improves overall performance while theoretically preserving the optimal policy of the original MDP. In [17], authors propose Rank2Reward, a novel reward shaping method that learns well-shaped reward functions directly from passive video demonstrations. The key innovation is to leverage the logit output of a video-discriminator as a ranking-based potential function. By incorporating these, the method provides dense, directional feedback that guides policy exploration towards more expert-like states, enabling effective reinforcement learning without requiring expensive state-action annotations. For robotic manipulation, Ref. [18] presents a framework for robotic hand manipulation that combines reward shaping with domain randomization to achieve efficient sim-to-real transfer. The key contribution lies in designing a dense, multi-component shaped reward function to accelerate RL training in simulation. Meanwhile, Ref. [19] proposes a novel safety-oriented reward shaping framework inspired by barrier functions (BFs). The key contribution is introducing a shaping reward term derived from the barrier function condition, which provides dense feedback to guide the agent towards safe states without requiring value function estimation. This method enhances training efficiency and reduces actuation effort while inherently promoting safety, as demonstrated in both simulation and real-world deployment on a quadruped robot.

While reward shaping (RS) is a powerful technique for guiding agent learning by providing additional rewards, designing such effective shaping functions remains a significant challenge. Constructing appropriate shaping rewards that reliably accelerate learning without altering the optimal policy requires deep domain knowledge and careful tuning—a challenge analogous to the difficulty of designing control Lyapunov functions (CLFs) in control theory [20], where both aim to ensure system convergence through carefully crafted functions. In [21], the authors propose a Lyapunov-based reward shaping strategy that incorporates physics-informed stability guarantees into reinforcement learning by using the negative change in a Lyapunov function as a shaping reward, ensuring stable and optimal control of robot manipulators. However, the construction of such a Lyapunov function lacks a systematic approach. Ref. [22] proposes a state-space segmentation-based potential function for potential-based reward shaping, where constant potential values are assigned to segmented regions of the state space, enabling systematic and efficient guidance for reinforcement learning agents. However, this potential function is designed offline and relies on predefined state-space segmentation, making it unable to adapt promptly to dynamic or changing environments. As a result, the agent may struggle to generalize across varying conditions or respond effectively to unforeseen disturbances.

In [23], the authors introduce adaptiveness into shaping rewards. They propose the EGCARL method, featuring a Dynamic Context-Aware Reward Weighting (DCARW) mechanism that dynamically adjusts reward weights based on real-time traffic conditions, combined with a Generative Adversarial Imitation Learning (GAIL) mechanism for expert-guided reward generation, enabling adaptive and efficient autonomous driving.

Therefore, there is a need for an online reward shaping method that can dynamically adjust the shaping signal in real time, enabling the agent to interact more effectively and explore more efficiently in diverse and evolving environments. In [23], the authors introduce adaptiveness into reward shaping by proposing the EGCARL method, which features a Dynamic Context-Aware Reward Weighting (DCARW) mechanism that adjusts reward weights in real time according to traffic conditions, enabling adaptive and efficient autonomous driving. However, this approach still relies on expert experience for effective reward generation.

In summary, there is a clear need for a reward shaping framework that is both adaptive and independent of expert supervision. Ideally, such a reward function should be dynamic rather than static, capable of adjusting itself in real time according to the environment, thereby providing timely and relevant guidance for efficient exploration and policy learning. Moreover, it should not rely on expert demonstrations; instead, the adaptiveness should emerge from an online optimization process that autonomously refines the shaping signal during learning. This would enable robust and generalizable learning across diverse and changing environments, paving the way for more autonomous and scalable reinforcement learning in real-world applications.

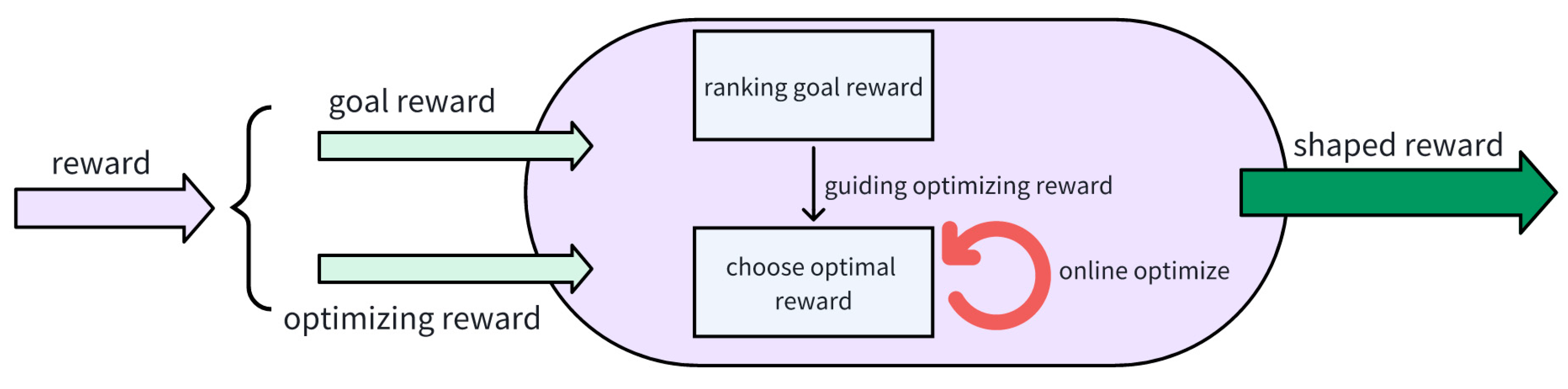
Thus, we introduce a novel reward framework, named two-layered reward, as illustrated in Figure 1. The overall reward function consists of two components: (1) the goal reward, which reflects the primary task objective, such as reproducing a desired motion trajectory in a humanoid robot; and (2) the optimizing reward, which incorporates secondary criteria like stability (e.g., preventing falls), smoothness, energy efficiency, and safety considerations. The goal reward forms the first layer of the framework and is used to evaluate task-level performance. The outcome of this evaluation is then fed into the second layer, where the optimizing reward is adjusted online through a meta-heuristic optimization process. This adaptation is performed without relying on expert demonstrations, enabling fully autonomous tuning of the shaping signal during learning. We implement this online optimization using meta-heuristic algorithms such as the Grey Wolf Optimizer (GWO) [24] and Optimal Stochastic Process Optimizer (OSPO) [25], allowing the agent to dynamically balance primary objectives with auxiliary constraints in response to environmental changes. This approach not only enhances learning efficiency and policy performance but also ensures robustness and adaptability in complex, dynamic tasks, addressing key limitations of existing reward shaping methods.

The proposed two-layered reward framework differs from existing approaches, such as hierarchical curricula [26], potential-based reward shaping (PBRS) [27], and meta-gradient reward learning [28], in both mechanism and objective. Hierarchical curricula rely on manually designed training stages with predefined difficulty progression. While effective, they require expert knowledge to specify transition conditions and lack adaptability to varying learning dynamics. In contrast, our method automatically adjusts the influence of auxiliary objectives based on real-time performance, eliminating the need for hand-crafted schedules. PBRS modifies rewards using a potential function to preserve the optimal policy, but this imposes strict mathematical constraints that limit the types of auxiliary objectives that can be incorporated. Our approach treats the lower-layer reward as a general optimization target, enabling flexible integration of domain-specific criteria without theoretical restrictions. Meta-gradient methods learn reward weights via gradient estimation, yet they suffer from high variance and instability, especially when trained on noisy or suboptimal trajectories. In contrast, our method employs a population-based meta-heuristic optimizer that updates reward weights using only high-performing rollouts. In summary, while prior methods require manual scheduling, impose theoretical constraints, or depend on unstable gradient estimates, our framework enables online, stable, and goal-conditioned reward shaping, autonomously balancing task completion with behavioral quality through performance-constrained adaptation.

2. Problem Statement

2.1. Reinforcement Learning

Reinforcement learning problems are commonly formulated using the Markov Decision Process (MDP) framework. Within the policy gradient framework introduced by [29], an MDP is defined as a tuple $M$ consisting of five fundamental elements:

$$M=(S,A,R,P,\gamma )$$

(1)

where $S,A,R,P$, and $\gamma$ represent the set of all possible states, the set of all possible actions, the immediate reward signal received from environment, the probability distribution of the transition dynamics, and the discount factor, respectively.

The agent’s policy is mathematically represented by $\pi$, which defines a mapping from the state space $S$ to the action space $A$, specifying the probability distribution over actions given a particular state. It can be expressed as follows:

$${\pi }_{\theta }\left(s\right)=P\left(a\right|s,\theta )$$

(2)

where $\theta$ denotes the learnable parameters of the deep neural network used to represent the policy.

At each time step $t$ during one episode, the agent observes the current state $s_t$ from the environment, selects an action $a_t\in A$ according to its policy ${\pi }_{\theta }\left(s_t\right)$, and then executes it to interact with the environment. This action induces a transition to a new state $s_{t+1}$ governed by the environment dynamics $P\left(s_{t+1}\right|s_t,a_t,\theta )$, and the agent receives an immediate reward $r_t=R\left(s_t,a_t\right)\in \mathbb{R}$. The agent’s objective is to learn an optimal policy ${\pi }_{\theta }$ that maximizes the expected cumulative reward over time by selecting optimal actions based on the observed states, which is shown as follows:

$$J_{\theta }\left({\pi }_{\theta }\right)={\mathbb{E}}_{{\pi }_{\theta }}\left[\sum _{t=0}^{\infty }{\gamma }^t{r}_t\right]$$

(3)

where $\mathbb{E}$ denotes the expectation.

2.2. Motion Tracking in Humaniod Robots

The motion-tracking problem in humanoid robots is formulated as a goal-conditioned reinforcement learning (RL) task, where the policy ${\pi }_{\theta }$ is trained to track the given robot movement trajectories such as Cristiano Ronaldo’s signature celebration jump [30].

Following [31], the state $s_t$ consists of the robot’s proprioceptive information $s_t^p$ and a time phase variable $\varphi \in \left[\mathrm{0,1}\right]$, where $\varphi =0$ indicates the beginning of the motion trajectory and $\varphi =1$ its end. The proprioception $s_t^p$ is defined as follows:

$$s_t^p\triangleq \left[q_{t-4:t},{\dot{q}}_{t-4:t},{\omega }_{t-4:t}^{root},g_{t-4:t},a_{t-4:t}\right]$$

(4)

Equation (4) includes five-step history of joint positions $q_t\in {\mathbb{R}}^{23}$, joint velocity ${\dot{q}}_t\in {\mathbb{R}}^{23}$, root angular velocity ${\omega }_t^{root}\in {\mathbb{R}}^3$, root projected gravity $g_t\in {\mathbb{R}}^3$, and robot action $a_t\in {\mathbb{R}}^{23}$. The action $a_t\in {\mathbb{R}}^{23}$ represents the target joint positions, which are then sent to a PD controller to actuate the robot’s degree of freedom. The dimension of these values is determined by the configuration of the humanoid robot, and in this work, we use the Unitree G1, as illustrated in Figure 2.

The reward function $r_t$ is defined as $R(s_t^p,s_t^g)$, a function of the agent’s proprioceptive state $s_t^p$ and the goal state $s_t^g=\varphi$, and this reward $r_t$ is used to guide policy optimization. The policy of the agent is optimized by Proximal Policy Optimization (PPO), with the objective of maximizing the cumulative discounted reward (return), expressed as:

$${\mathbb{E}}_{{\pi }_{\theta }}\left[\sum _{t=0}^T{\gamma }^t{r}_t\right],$$

where $T$ is the length of the episode.

2.3. Reward Function in Motion Tracking

The traditional reward function for motion tracking in humanoid robots usually consists of three components:

(1)

Penalty terms $r_{P,i}$: These terms penalize violations of joint position, velocity, and torque limits, as well as early episode termination.

(2)

Regularization terms $r_{R,j}$: These terms encourage energy efficiency (low torques), smooth actions (low action rate), and foot stability (orientation and slip prevention).

(3)

Task terms $r_{T,k}$: These terms incentivize accurate tracking of the reference motion across multiple aspects, including body position, orientation, angular and linear velocity, and joint positions and velocities.

These components are combined with appropriate weights to guide the policy toward effective task execution while maintaining stability and efficiency and are formulated as follows:

$$r_t=\sum _{i=0}^{N_P}{w}_{P,i}{r}_{P,i}+\sum _{j=0}^{N_R}{w}_{R,j}{r}_{R,j}+\sum _{k=0}^{N_T}{w}_{T,k}{r}_{T,k}$$

(5)

where $w_{P,i},w_{R,j}$, and $w_{T,k}$ denote the weights for the penalty term $r_{P,i},$ regularization term $r_{R,j}$, and task reward term $r_{T,k}$, respectively. $N_P$, $N_R$, and $N_T$ represent the number of penalty, regularization, and task reward terms, respectively.

2.4. Proximal Policy Optimization Formulation

PPO improves upon standard policy gradient methods by performing multiple minibatch updates on sampled data, enhancing sample efficiency and training stability. To prevent excessively large policy updates, PPO-Clip employs a clipping mechanism that limits the ratio between the new and old policy probabilities within a fixed threshold. This constraint stabilizes learning and avoids performance collapse. PPO optimizes the policy by maximizing the following surrogate objective:

$$L\left(\theta \right)={\mathbb{E}}_t\left[\min \left({\displaystyle \frac{{\pi }_{\theta }\left(a_t|s_t\right)}{{{\pi }_{\theta }}_{old}\left(a_t|s_t\right)}}\right){\widehat{A}}_t,clip\left({\displaystyle \frac{{\pi }_{\theta }\left(a_t|s_t\right)}{{{\pi }_{\theta }}_{old}\left(a_t|s_t\right)}},1-ϵ,1+ϵ\right){\widehat{A}}_t\right]$$

(6)

where $\theta$ denotes the learnable parameters of the policy network ${\pi }_{\theta }$, $t$ is the time step in the motion trajectory, and ${\displaystyle \frac{{\pi }_{\theta }\left(a_t|s_t\right)}{{{\pi }_{\theta }}_{old}\left(a_t|s_t\right)}}$ is the probability ratio between the new policy ${\pi }_{\theta }$ and the old policy ${{\pi }_{\theta }}_{old}$ for taking action $a_t$ in the state $s_t$. ${{\pi }_{\theta }}_{old}$ is the policy before the current update and remains fixed during the optimization epoch. ${\widehat{A}}_t$ represents the estimated advantage function at time step $t$, which quantifies how much better action $a_t$ is compared to the expected return under the current policy, typically computed using Generalized Advantage Estimation (GAE). $ϵ$ denotes the clipping hyperparameter which prevents large policy updates and ensures stable training. ${\mathbb{E}}_t$ represents the expectation over all time steps in the sampled trajectories.

The reward function $r_t$, defined in Equation (5) as a weighted sum of task, regularization, and penalty terms, serves as the immediate feedback signal that drives the learning process. During training, these rewards $r_t$ are collected from environment interactions and used to compute the advantage estimates ${\widehat{A}}_t$ via GAE, and it can be expressed as:

$${\widehat{A}}_t=\sum _{l=0}^{T-t}{\left(\gamma \lambda \right)}^l{\delta }_{t+l}$$

(7)

where ${\delta }_{t+l}=r_{t+l}+\gamma V\left(s_{t+l+1}\right)-V\left(s_{t+l}\right)$ is the TD residual, $V\left(s_t\right)$ is the value function estimating the expected future return, $\gamma \in \left[\mathrm{0,1}\right]$ is the discount factor, and $\lambda \in \left[\mathrm{0,1}\right]$ is the GAE smoothing parameter.

The advantage function thus encapsulates how much better or worse a given action is relative to the average action the current policy would take based on the cumulative rewards defined by $r_t$. In turn, ${\widehat{A}}_t$ directly shapes the policy update in the PPO defined by Equation (6): actions that yield higher returns are encouraged, while those with lower returns are discouraged. Therefore, maximizing the surrogate objective $L\left(\theta \right)$ effectively aligns the policy with the goals encoded in the reward function $r_t$, guiding it toward high-performance, stable, and efficient behaviors.

3. Two-Layered Reward Reinforcement Learning

3.1. Motivations for Two-Layered Reward

In reinforcement learning (RL), the reward function design plays an important role in shaping the learning efficiency and final performance of the agent. Traditional reward shaping methods typically employ a static, fixed-weight linear combination of multiple sub-rewards, such as Equation (5). However, such an approach has inherent limitations: the weights remain constant throughout the training procedure, and it cannot adapt to the evolving needs across different learning stages or respond to dynamically changing environmental conditions.

For instance, in the humanoid robot motion tracking tasks considered in this paper, the priorities of learning objectives gradually shift during training. Specifically, in the early stages, the primary goal is to maintain balance and avoid falling, making energy efficiency or precise trajectory tracking secondary. As training progresses and basic stability is achieved, the focus shifts toward accurately following the reference motion trajectory. Only in the later stages, once stable tracking has been established, should optimization emphasize secondary objectives such as energy conservation, motion smoothness, and joint effort minimization. A static reward function with fixed weights cannot effectively capture these evolving priorities, often leading to suboptimal learning dynamics and slowing down the initial training phase, as the critical but challenging objective of simply avoiding falls may be overshadowed by other goals such as precise trajectory tracking.

Moreover, real-world environments are inherently dynamic and uncertain. If the reward function can adapt online based on the current state and task progress, it can guide the agent toward more meaningful exploration, thereby accelerating convergence and improving policy robustness.

To address these challenges, we propose a two-layered reward structure that decomposes the overall reward into two distinct components:

(1)

Upper-layer reward (goal reward $r_{P,i}$): This represents the core task objective and is static and fixed, such as the tracking error between the robot’s body pose and the reference motion. It directly reflects task completion and serves as the fundamental driving force for policy learning.

(2)

Lower-layer reward (optimizing reward $r_{R,j}$ and $r_{T,k}$): This consists of auxiliary, manually designed sub-rewards, such as penalties on action magnitude, joint velocity, or orientation deviation, which encourage desirable behaviors beyond basic task execution. These sub-rewards are not essential for task success but act as “polishing” terms that refine the policy quality.

Crucially, the lower-layer reward is not merely a matter of weight adjustment; rather, it constitutes a “priority-driven optimization process.” The upper-layer reward establishes a performance threshold, and the optimization of the lower-layer reward is activated only when this primary goal is sufficiently achieved.

This hierarchical design enables “goal-conditioned” reward shaping: the lower-layer reward is dynamically optimized based on the achievement of the primary task objective. It allows the agent to first master fundamental skills before progressively refining secondary objectives, leading to more structured and interpretable exploration.

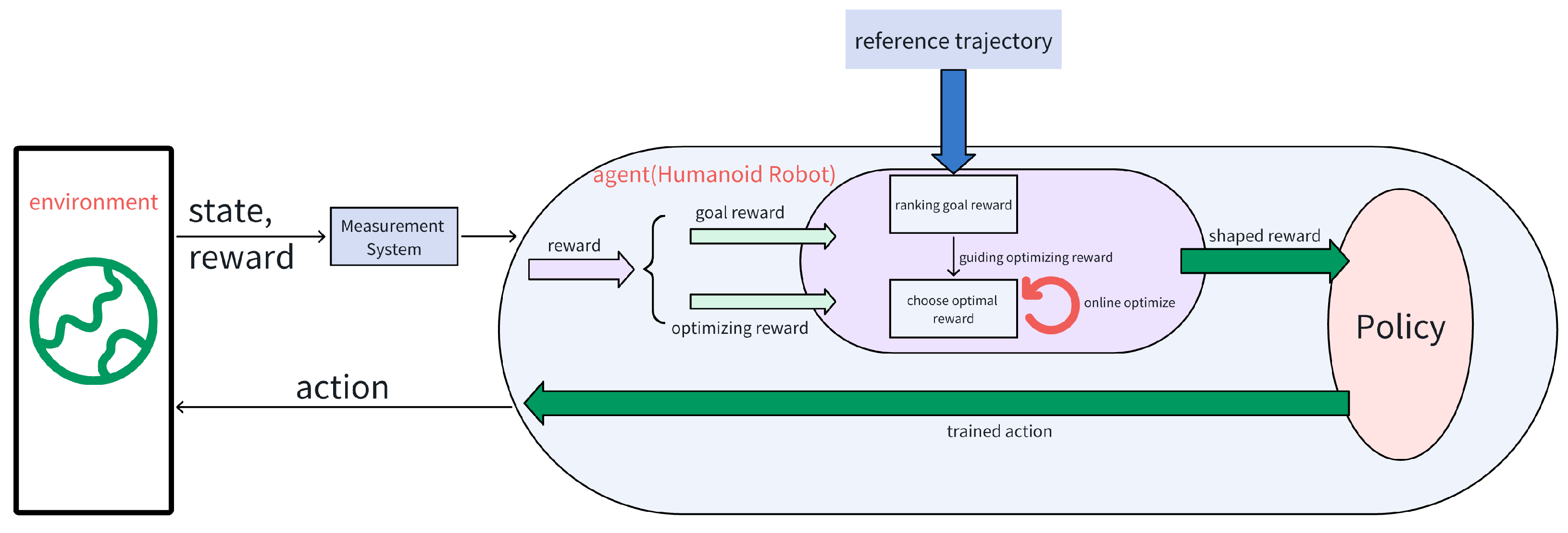
3.2. Two-Layered Reward Reinforcement Learning Framework

The two-layered reward reinforcement learning framework is depicted in Figure 3. This framework is designed to address the limitations of traditional fixed-weight reward shaping in complex control tasks. It decomposes the raw reward signal $r_t$ obtained from the environment into two distinct components: (1) the upper-layer goal reward $r_g$; and (2) the lower-layer optimizing reward $r_o$. Thereby, it establishes an adaptive, goal-conditioned reward shaping mechanism that enables explainable and meaningful exploration.

As illustrated in Figure 3, the agent interacts with the outer environment, receiving state observations $s_t$ and a composite reward $r_t$. This reward $r_t$ consists of two parts:

(1)

Upper-layer “goal reward” $r_g$: This component represents the core task objective and corresponds to the task-specific tracking error $r_T$, such as the deviation between the robot’s body pose and the reference motion trajectory. It serves as a fixed, static metric of task completion and forms the primary criterion for evaluating policy performance. In this work,

$$r_g=\sum _{k=0}^{N_T}{w}_{T,k}{r}_{T,k} .$$

where $r_{T,k}$ denotes individual tracking-related reward terms, $w_{T,k}$ are their weights, and $N_T$ is the number of tracking objectives.

(2)

Lower-layer “optimizing reward” $r_o$: This component consists of auxiliary, manually designed sub-rewards that encourage desirable behaviors beyond basic task execution, such as motion smoothness, energy efficiency, and dynamic stability. Specifically, in this work,

$$r_o=\sum _{i=0}^{N_P}{w}_{P,i}{r}_{P,i}+\sum _{j=0}^{N_R}{w}_{R,j}{r}_{R,j} ,$$

where $r_{P,i}$ denotes penalty terms (e.g., on joint torques or posture deviations), $r_{R,j}$ represents regularization terms (e.g., on action magnitude or velocity), and $w_{P,i},w_{R,j}$ are tunable weighting coefficients. These components act as “polishing” rewards that refine policy quality once the primary task objective is sufficiently achieved.

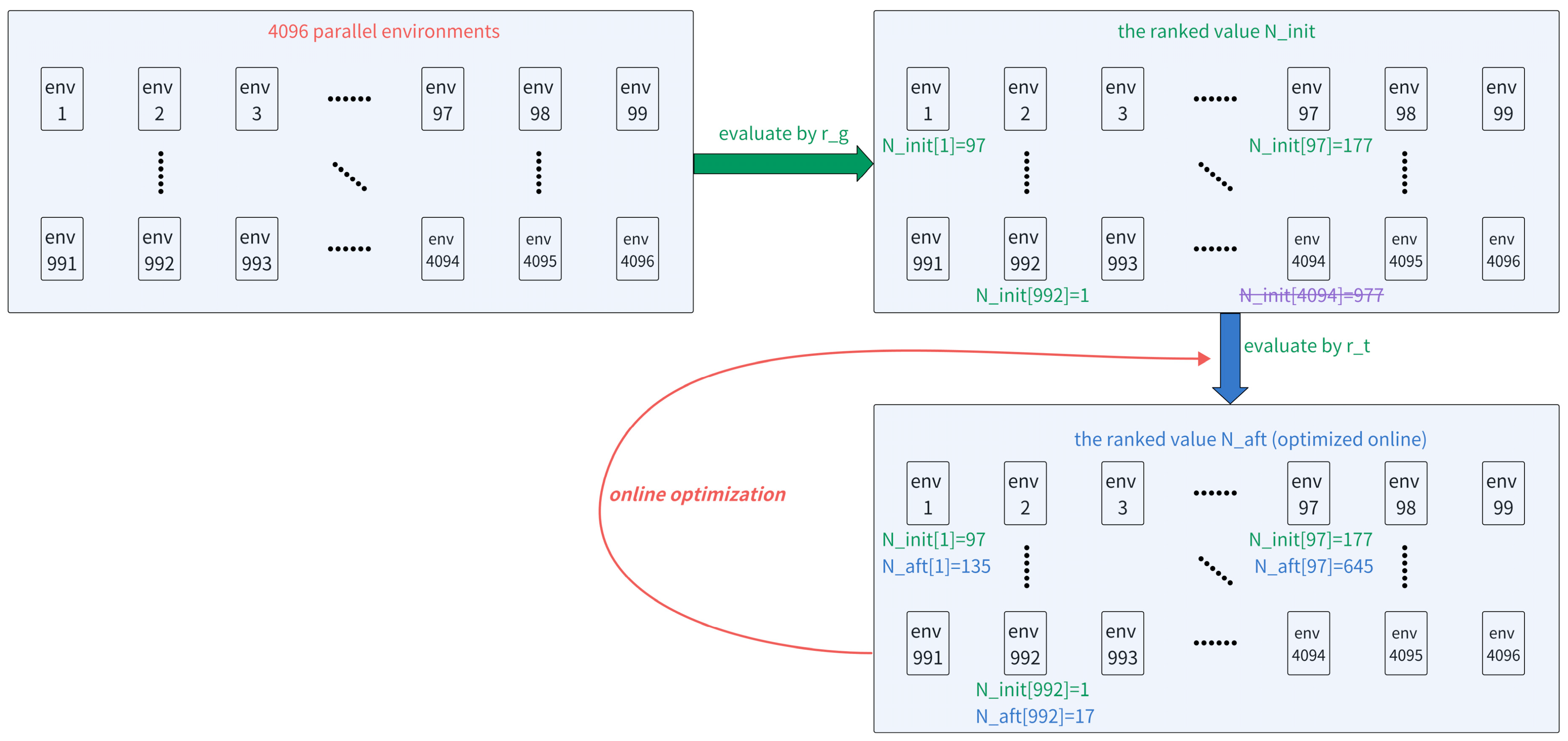
As illustrated in Figure 4, during training, we employ a parallel simulation setup with a large number of environments (e.g., 4096 independent rollouts). First, all episodes are evaluated and ranked based on the upper-layer goal reward $r_g$. The top 10% of episodes—those with the highest $r_g$ values, corresponding to the best task completion performance—are selected as the candidate set. For example, with 4096 environments, the top 409 episodes are selected for further evaluation.

Each of these selected episodes is assigned an initial rank $N_{\mathrm{ini}}\in [1, 409]$, which reflects its relative performance based solely on $r_g$. Specifically, $N_{\mathrm{ini}}=1$ denotes the episode with the highest $r_g$, while $N_{\mathrm{ini}}=409$ corresponds to the lowest-ranked episode within the top 10%. For instance, $N_{\mathrm{ini}}\left[{\mathrm{env}}_{992}\right]=1$ indicates that the 992nd environment (among the 4096 total) achieved the best task performance and thus holds the top rank in the candidate set.

Next, within this filtered set of 409 episodes, the full composite reward $r_t=r_g+r_o$ is computed for each episode, and the episodes are re-ranked based on this total reward. This re-ranking yields a new global rank $N_{\mathrm{aft}}\in [1, 4096]$, which reflects the episode’s position across all environments (not just the top 10%), meaning $N_{\mathrm{aft}}$ can indeed exceed 409.

To evaluate the effectiveness of the current optimizing reward $r_o$, we compute a rank deviation penalty that quantifies how much an episode’s relative standing degrades when $r_o$ is included. Specifically, if an episode falls outside the top 10% (i.e., $N_{\mathrm{aft}}>409$) despite having been selected based on high $r_g$, it suggests that $r_o$ may be encouraging behaviors that do not align with overall task performance.

We define the following objective function to capture this effect:

$$J_w=\sum _{i=1}^{409}{\left({\displaystyle \frac{N_{\mathrm{ini},i}-N_{\mathrm{aft},i}}{100}}\right)}^2\cdot \mathbb{I}(N_{\mathrm{aft},i}>409)$$

(8)

where $N_{\mathrm{ini},i}$ is the initial rank of the $i$-th episode within the top 10% based on $r_g$, $N_{\mathrm{aft},i}$ is its final global rank based on $r_t=r_g+r_o$, and $\mathbb{I}(\cdot )$ is the indicator function, equal to 1 if $N_{\mathrm{aft},i}>409$ and 0 otherwise.

This penalty term $\mathbb{I}(\cdot )$ is applied only when an episode drops out of the top 10% after incorporating $r_o$, indicating a misalignment between the optimizing reward and task success. Episodes that remain within the top 10% (i.e., $N_{\mathrm{aft}}\le 409$) receive no penalty, thereby encouraging exploration guided by $r_o$ as long as it does not compromise the primary task objective. In this way, the framework ensures that improvements in auxiliary objectives contribute meaningfully to overall performance, promoting structured and goal-consistent exploration.

The value of $J_w$ depends on the weighting parameters $w_{P,i}$ and $w_{R,j}$ used in the lower-layer reward: $r_o=\sum _{i=0}^{N_P}{w}_{P,i}{r}_{P,i}+\sum _{j=0}^{N_R}{w}_{R,j}{r}_{R,j}$. To ensure that the shaping reward improves policy quality without compromising task completion, we perform online optimization of these weights to minimize $J_w$. This optimization is carried out using a meta-heuristic algorithm. Specifically, the Grey Wolf Optimizer (GWO) is employed in this work. The optimization problem is formulated as:

$$J_w^{\ast }=\underset{w_{P,i},w_{R,j}}{\mathrm{m}\mathrm{i}\mathrm{n}}{J}_w(w_{P,i},w_{R,j})$$

(9)

$$w_{P,i}^{\ast },w_{R,j}^{\ast }=\underset{w_{P,i},w_{R,j}}{\mathrm{a}\mathrm{r}\mathrm{g}min}{J}_w(w_{P,i},w_{R,j})$$

(10)

where $J_w^{\ast }$ denotes the minimized value of the penalty objective, and $w_{P,i}^{\ast },w_{R,j}^{\ast }$ represent the optimal weight parameters that yield the best alignment between the optimizing reward $r_o$ and the primary task goal. By solving this problem during training, the framework adaptively tunes the auxiliary reward weights in a goal-conditioned manner, ensuring that exploration is both effective and task-consistent.

This process enables goal-conditioned reward shaping: the optimization of auxiliary rewards is explicitly conditioned on the agent first achieving a sufficient level of task proficiency, as measured by the upper-layer reward $r_g$. As a result, exploration guided by $r_o$ is not arbitrary but is restricted to policies that already satisfy the fundamental task objective, ensuring that refinement is built upon a foundation of task success.

Importantly, this framework effectively mitigates the issue of spurious rewards. For example, a policy that remains completely static may achieve a high $r_o$ (e.g., due to minimal action magnitude or joint velocity penalties), but it would fail to track the reference motion, resulting in a low $r_g$. Such a policy would not be included in the top 10% of episodes and therefore would have a worse $J_w$ value. This mechanism inherently filters out degenerate or misleading solutions that exploit auxiliary rewards without contributing to actual task performance.

Finally, the optimal shaping reward $r_t^{\ast }=r_g+r_o$, computed using the tuned weights $w_{P,i}^{\ast }$ and $w_{R,j}^{\ast }$, is fed into the policy optimization algorithm—Proximal Policy Optimization (PPO), in this work—to update the agent’s policy network. This establishes a closed-loop training pipeline: task performance filters candidate policies, auxiliary rewards are optimized based on goal rewards, and the resulting shaped reward guides policy improvement. The complete procedure is summarized in the pseudo-code provided in Algorithm 1.

Algorithm 1. The Pseudo Code of Two-Layered Reward Optimization via GWO

Input: $E=\{{\tau }_1,{\tau }_2,\dots ,{\tau }_{4096}\}$: Set of environment trajectories $r_g\left(\tau \right)$: Upper-layer goal reward $r_o(\tau ;\mathbf{w})={\sum }_{i=1}^{N_P}{w}_{P,i}{r}_{P,i}\left(\tau \right)+{\sum }_{j=1}^{N_R}{w}_{R,j}{r}_{R,j}\left(\tau \right)$: Lower-layer shaping reward ${\mathbf{w}}_{\mathrm{m}\mathrm{i}\mathrm{n}},{\mathbf{w}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$: Search bounds for weights $\mathrm{GWO}\_\mathrm{params}$: Population size, max iterations, etc.

Output: Optimal weight vector ${\mathbf{w}}^{\ast }=[w_{P,i}^{\ast },w_{R,j}^{\ast }]$ Begin: [initialize]

1: For each trajectory ${\tau }_k\in E$, $k\in \{1,2,\dots ,4096\}$: 2:         Compute $r_g^{\left(k\right)}=r_g\left({\tau }_k\right)$  3: Sort all episodes in descending order of $r_g^{\left(k\right)}$  4: Select top 10% (i.e., top 409) as candidate set $E_{\mathrm{top}}$  5: Assign initial rank $N_{\mathrm{ini}}\left[{\tau }_k\right]\in [1,409]$ to each ${\tau }_k\in E_{\mathrm{top}}$, where $N_{\mathrm{ini}}\left[{\tau }_k\right]=1$ indicates the best $r_g$ [GWO optimization] 6: Initialize population of wolves ${\mathbf{w}}_n=\left[{\mathit{w}}_{\mathit{P},\mathit{i}},{\mathit{w}}_{\mathit{R},\mathit{j}}\right], n=0,1,\dots N_{pop}$, randomly within $[{\mathbf{w}}_{\mathrm{m}\mathrm{i}\mathrm{n}},{\mathbf{w}}_{\mathrm{m}\mathrm{a}\mathrm{x}}]$  7: Assign initial values to GWO’s controlling parameters 8: while (maximum iterations not reached or convergence not achieved) do 9:         For each wolf ${\mathbf{w}}_n$: 10:             Compute composite reward $r_t^{\left(k\right)}=r_g^{\left(k\right)}+r_o({\tau }_k;{\mathbf{w}}_n)$ for all $k$  13:             Rank all 4096 episodes by $r_t^{\left(k\right)}$→ obtain global rank $N_{\mathrm{aft}}\left[{\tau }_k\right]$  14:             Compute objective value:                                     $J_w({\mathbf{w}}_n)={\displaystyle \sum _{{\tau }_k\in E_{\mathrm{top}}}}{\left({\displaystyle \frac{N_{\mathrm{ini}}\left[{\tau }_k\right]-N_{\mathrm{aft}}\left[{\tau }_k\right]}{100}}\right)}^2\cdot \mathbb{I}(N_{\mathrm{aft}}[{\tau }_k]>409)$ 15:         Evaluate and rank wolves by $J_w\left({\mathbf{w}}_n\right)$  16:         Update the best three solutions: ${\mathbf{w}}_{\alpha },{\mathbf{w}}_{\beta },{\mathbf{w}}_{\delta }$  17:         Update controlling parameters based on iteration 18:         for each wolf ${\mathbf{w}}_n$ do 19:             Update position using GWO update rule 20:         end for 21: end while 22: return ${\mathbf{w}}_{\alpha }$ (best solution) [Return and Apply Optimal Reward] 23: let ${\mathbf{w}}^{\ast }={\mathbf{w}}_{\alpha }$, compute final shaping rewards for all environments using ${\mathrm{w}}_{\mathrm{P},\mathrm{i}}^{\ast },{\mathrm{w}}_{\mathrm{R},\mathrm{j}}^{\ast }$:                             $r_t^{\ast }({\tau }_k)=r_g({\tau }_k)+{\displaystyle \sum _{i=1}^{N_P}}{w}_{P,i}^{\ast }{r}_{P,i}\left({\tau }_k\right)+{\displaystyle \sum _{j=1}^{N_R}}{w}_{R,j}^{\ast }{r}_{R,j}\left({\tau }_k\right),\forall k=1,\dots ,4096$

24: Pass $r_t^{\ast }$ to PPO for policy gradient computation and agent update End Algorithm.

In summary, the proposed two-layered reward framework enhances the adaptability and expressiveness of reward design in reinforcement learning. By decoupling task completion from performance refinement and enforcing priority-based optimization, it promotes structured exploration and ensures stable learning, particularly beneficial for high-dimensional, dynamic humanoid control tasks.

4. Results and Discussion

4.1. Application to Unitree G1 Motion Tracking

To validate the effectiveness of the proposed two-layered reward reinforcement learning framework, we evaluate its performance in a high-fidelity simulation using the Unitree G1 humanoid robot within the Isaac Gym environment.

The objective is to enable the robot to accurately track a diverse set of human-generated motion trajectories—such as walking, running, jumping, and kicking—while maintaining dynamic stability and energy efficiency.

In this work, we focus on enabling the Unitree G1 humanoid robot to imitate a user-defined gymnastic motion sequence, recorded by the author and referred to here as the “gym-motion” for brevity, as illustrated in Figure 5. The top sub-figure shows keyframes from the original human motion capture video, while the bottom sub-figure presents the corresponding motion retargeted onto the Unitree G1 robot. The sequence consists of a series of coordinated movements: starting from a neutral stance, the subject steps to the right (1), shifts weight with arms swinging outward (2), extends both arms sideways at shoulder height (3), steps leftward (4), transitions into a forward-facing pose with hands raised overhead (5–6), then returns to the right side with arms lowered (7–8), completing the motion cycle.

This gym-motion involves dynamic lateral movement, upper-body coordination, and precise timing between limb and body actions, making it a challenging-yet-representative task for evaluating the robot’s ability to replicate agile and dexterous human-like behaviors.

Successfully reproducing such a complex and fluid motion in simulation serves as a rigorous test of the proposed two-layered reward framework’s ability to learn and generalize high-dexterity locomotion skills under physical constraints.

The simulation is configured with 4096 parallel environments, enabling large-scale training with high sample efficiency. Each environment runs at a control frequency of 50 Hz, with a simulation timestep of 0.005 s (i.e., four physical steps per control step). The robot is actuated via PD controllers on all 23 actuated joints. Joint position and velocity limits are enforced based on the real robot’s specifications.

The observation space includes the robot’s base pose (position and orientation in world frame), base linear and angular velocities, joint positions and velocities, last action, and the reference motion state (projected 3D joint positions and velocities at the current phase). The action space consists of target joint positions (PD setpoints) relative to the current configuration.

We employ the two-layered reward structure introduced in Section 3:

(1)

The upper-layer goal reward $r_g$ measures task completion accuracy and is defined as:

$$r_g=\sum _{k=0}^4{w}_{T,k}{r}_{T,k},$$

(11)

$$s.t. r_{T,1}=r_{\mathrm{b}\mathrm{o}\mathrm{d}\mathrm{y}\_\mathrm{p}\mathrm{o}\mathrm{s}}=\exp \left(-{\displaystyle \frac{1}{{\sigma }_{T,1}}}\cdot {\displaystyle \frac{1}{N_{body}\cdot 3}}\sum _i\parallel \Delta p_i{\parallel }^2\right)$$

$$r_{T,2}=r_{\mathrm{body}\_\mathrm{rot}}=\mathrm{e}\mathrm{x}\mathrm{p}(-{\displaystyle \frac{1}{N_{body}}}\sum _i({\theta }_i{)}^2/{\sigma }_{T,2})$$

$$r_{T,3}=r_{\mathrm{body}\_\mathrm{vel}}=\mathrm{e}\mathrm{x}\mathrm{p}(-{\displaystyle \frac{1}{N_{body}}}\sum _i\parallel \Delta {\mathrm{v}}_i{\parallel }^2/{\sigma }_{T,3})$$

$$r_{T,4}=r_{\mathrm{body}\_\mathrm{ang}\_\mathrm{vel}}=\mathrm{e}\mathrm{x}\mathrm{p}(-{\displaystyle \frac{1}{N_{body}}}\sum _i\parallel \Delta {\omega }_i{\parallel }^2/{\sigma }_{T,4})$$

where the component rewards are defined as follows:

(a)

Body position tracking:

$$r_{\mathrm{b}\mathrm{o}\mathrm{d}\mathrm{y}\_\mathrm{p}\mathrm{o}\mathrm{s}}=\exp \left(-{\displaystyle \frac{1}{{\sigma }_{T,1}}}\cdot {\displaystyle \frac{1}{N_{body}\cdot 3}}\sum _i\parallel \Delta p_i{\parallel }^2\right)$$

where $\Delta {\mathrm{p}}_i={\mathrm{p}}_i^{\mathrm{sim}}-{\mathrm{p}}_i^{\mathrm{ref}}\in {\mathbb{R}}^3$ denotes the global position error of the $i$-th body link, ${\mathrm{p}}_i^{\mathrm{sim}}$ is the simulated position and ${\mathrm{p}}_i^{\mathrm{ref}}$ is the reference position, $N_{\mathrm{body}}$ is the number of tracked body links, and ${\sigma }_{T,1}$ is the temperature coefficient that controls the sensitivity to position errors.

(b)

Body orientation (rotation) tracking:

$$r_{\mathrm{body}\_\mathrm{rot}}=\mathrm{e}\mathrm{x}\mathrm{p}(-{\displaystyle \frac{1}{N_{body}}}\sum _i({\theta }_i{)}^2/{\sigma }_{T,2})$$

Here, ${\theta }_i=\parallel \mathrm{l}\mathrm{o}\mathrm{g}({\mathrm{q}}_i^{\mathrm{ref}}\otimes ({\mathrm{q}}_i^{\mathrm{sim}}{)}^{-1})\parallel$ is the rotation angle (in radians) between the reference and simulated orientations, represented as quaternions. This measures the angular discrepancy for each body link.

(c)

Body linear velocity tracking:

$$r_{\mathrm{body}\_\mathrm{vel}}=\mathrm{e}\mathrm{x}\mathrm{p}(-{\displaystyle \frac{1}{N_{body}}}\sum _i\parallel \Delta {\mathrm{v}}_i{\parallel }^2/{\sigma }_{T,3})$$

Here, $\Delta {\mathrm{v}}_i={\mathrm{v}}_i^{\mathrm{sim}}-{\mathrm{v}}_i^{\mathrm{ref}}$ is the linear velocity error between the simulated and reference values of the $i$-th body link.

(d)

Body angular velocity tracking:

$$r_{\mathrm{body}\_\mathrm{ang}\_\mathrm{vel}}=\mathrm{e}\mathrm{x}\mathrm{p}(-{\displaystyle \frac{1}{N_{body}}}\sum _i\parallel \Delta {\omega }_i{\parallel }^2/{\sigma }_{T,4})$$

Here, $\Delta {\mathit{\omega }}_i={\mathit{\omega }}_i^{\mathrm{sim}}-{\mathit{\omega }}_i^{\mathrm{ref}}$ is the angular velocity error.

The weights $w_k$ balance the relative importance of each tracking component, and ${\sigma }_{T,1},{\sigma }_{T,2},{\sigma }_{T,3},{\sigma }_{T,4}$ are temperature coefficients that modulate the sharpness of the exponential penalty.

Here, $w_k$ is a static value and is determined in advance.

(2)

The lower-layer optimizing reward $r_o$ promotes desirable behaviors such as stability, energy efficiency, and safety and is composed of:

$$r_o=\sum _{i=0}^{N_P}{w}_{P,i}{r}_{P,i}+\sum _{j=0}^{N_R}{w}_{R,j}{r}_{R,j},$$

where $r_{P,i}$ and $r_{R,j}$ denote the individual penalty and regularization reward terms, respectively, designed to penalize undesirable behaviors and encourage smooth, natural motions. The weights $w_{P,i}$ and $w_{R,j}$ are automatically adjusted online during training using the Grey Wolf Optimizer (GWO), allowing the system to dynamically balance competing objectives. These reward weights $w_{P,i}$ and $w_{R,j}$ are constrained within $\left[\mathrm{0,1}\right]$ to prevent unbounded growth and ensure stable reward shaping. Detailed definitions of $r_{P,i}$ and $r_{R,j}$ are provided in

Table 1. Detailed definitions of $r_{P,i}$ and $r_{R,j}$.

${\mathit{r}}_{\mathit{P},\mathit{i}}$	${\mathit{r}}_{\mathit{R},\mathit{j}}$
$r_{\mathrm{dof}\_\mathrm{pos}\_\mathrm{limits}}={\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N}\left[max{\left(0,{\displaystyle \frac{q_i-q_{max,i}}{\Delta q_i^{+}}}\right)}^2+max{\left(0,{\displaystyle \frac{q_{min,i}-q_i}{\Delta q_i^{-}}}\right)}^2\right]$	$r_{\mathrm{lin}\_\mathrm{vel}\_\mathrm{z}}=\parallel {\mathbf{v}}_{\mathrm{base}}^z{\parallel }^2$
$q_i$: Current position of the $i$-th joint. $q_{\mathrm{m}\mathrm{i}\mathrm{n},i}$: Lower limit (minimum allowable value) of the $i$-th joint position. $q_{\mathrm{m}\mathrm{a}\mathrm{x},i}$: Upper limit (maximum allowable value) of the $i$-th joint position. $\Delta q_i^{+}$: Safety margin below the upper limit, defined as $\Delta q_i^{+}=ϵ\cdot (q_{\mathrm{m}\mathrm{a}\mathrm{x},i}-q_{\mathrm{nominal},i})$, where $ϵ$ is a small coefficient and $q_{\mathrm{nominal},i}$ is the nominal operating point (often the midpoint). $\Delta q_i^{-}$: Safety margin above the lower limit, defined as $\Delta q_i^{-}=ϵ\cdot (q_{\mathrm{nominal},i}-q_{\mathrm{m}\mathrm{i}\mathrm{n},i})$. $N$: Total number of degrees of freedom (DoFs) or joints being penalized.	$v_{\mathrm{base}}^z$: The linear velocity of the robot’s base (typically the torso link) along the vertical (z) axis, expressed in the world frame. $\parallel v_{\mathrm{base}}^z\parallel$: Absolute value of the vertical velocity. $\parallel v_{\mathrm{base}}^z{\parallel }^2$: Squared magnitude of the vertical velocity.
$r_{\mathrm{d}\mathrm{o}\mathrm{f}\_\mathrm{v}\mathrm{e}\mathrm{l}\_\mathrm{l}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{t}\mathrm{s}}={\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N}max{\left(0,{\displaystyle \frac{\mid {\dot{q}}_i\mid -{\dot{q}}_{max,i}}{\Delta {\dot{q}}_i}}\right)}^2$	$r_{\mathrm{ang}\_\mathrm{vel}\_\mathrm{xy}}=\parallel {\mathit{\omega }}_{\mathrm{base}}^{xy}{\parallel }^2$
${\dot{q}}_i$: Current velocity of the $i$-th joint. $\mid {\dot{q}}_i\mid$: Absolute value of the joint velocity. ${\dot{q}}_{\mathrm{m}\mathrm{a}\mathrm{x},i}$: Maximum allowable velocity of the $i$-th joint (symmetric limits are assumed: ${\dot{q}}_{\mathrm{m}\mathrm{i}\mathrm{n},i}=-{\dot{q}}_{\mathrm{m}\mathrm{a}\mathrm{x},i}$). $\Delta {\dot{q}}_i$: Safety margin for velocity, defined as $\Delta {\dot{q}}_i=ϵ\cdot {\dot{q}}_{\mathrm{m}\mathrm{a}\mathrm{x},i}$, where $ϵ$ is a small coefficient. $N$: Total number of joints.	${\omega }_{\mathrm{base}}^{xy}$: The angular velocity of the robot’s base projected onto the horizontal plane (x and y axes), usually expressed in the base’s local frame or the world frame. $\parallel {\omega }_{\mathrm{base}}^{xy}\parallel$: Euclidean norm of the roll and pitch angular velocities. $\parallel {\omega }_{\mathrm{base}}^{xy}{\parallel }^2$: Squared norm of the horizontal angular velocity.
$r_{\mathrm{torque}}={\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N}\mathrm{m}\mathrm{a}\mathrm{x}{\left(0,{\displaystyle \frac{\mid {\tau }_i\mid -{\tau }_{max,i}}{\Delta {\tau }_i}}\right)}^2$	$r_{\mathrm{base}\_\mathrm{height}}=(h_{\mathrm{base}}-h_{\mathrm{des}}{)}^2$
${\tau }_i$: Actual torque applied to the $i$-th joint (output from the controller). $\mid {\tau }_i\mid$: Absolute value of the joint torque. ${\tau }_{\mathrm{m}\mathrm{a}\mathrm{x},i}$: Maximum allowable torque for the $i$-th joint (symmetric limits assumed: ${\tau }_{\mathrm{m}\mathrm{i}\mathrm{n},i}=-{\tau }_{\mathrm{m}\mathrm{a}\mathrm{x},i}$). $\Delta {\tau }_i$: Safety margin for torque, defined as $\Delta {\tau }_i=ϵ\cdot {\tau }_{\mathrm{m}\mathrm{a}\mathrm{x},i}$, with $ϵ$ typically set to 0.1. $N$: Total number of actuated joints.	$h_{\mathrm{base}}$: The current height of the robot’s base (e.g., z-coordinate of the pelvis or torso link) in the world frame. $h_{\mathrm{des}}$: The desired (target) base height, typically determined from the reference motion or a gait-specific setting (e.g., crouching vs. standing). $(h_{\mathrm{base}}-h_{\mathrm{des}}{)}^2$: Squared difference between actual and desired base height.

.

The specific values of the coefficients in reward functions are the same as those defined in [30]; readers are referred to that work for further details.

Training is performed using the Proximal Policy Optimization (PPO) algorithm. The policy is trained for 2500 iterations with a mini-batch size of 4096, a learning rate of $1\times {10}^{-3}$, and a GAE discount factor $\gamma =0.99$. Unless otherwise specified, all other PPO hyperparameters and the physical parameters of the Unitree robot are set according to [30]. The parameters of the Grey Wolf Optimizer (GWO) are adopted from [32]. For the baseline method, a static reward function is used with all weight coefficients set to 1. All experiments are carried out on a machine powered by an NVIDIA GeForce RTX 4070 Ti GPU.

4.2. Simulation Results

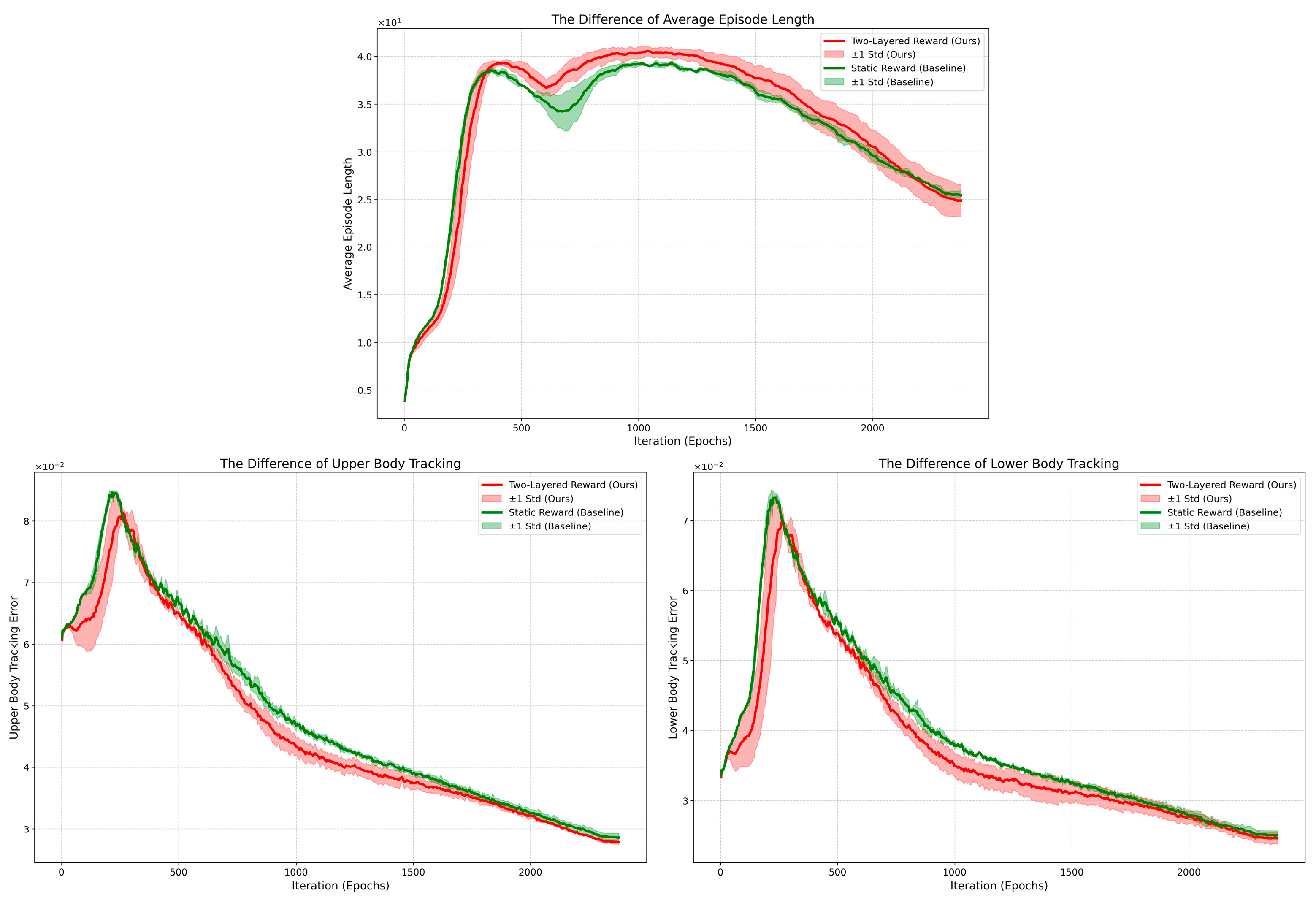
We first examine the average episode length over training epochs, as shown in Figure 6, which reflects the robot’s ability to maintain balance and complete motion sequences without falling. The red curve represents the proposed two-layered reward framework, while the green dashed curve corresponds to a baseline method using a static reward.

Initially, the static reward method achieves a higher average episode length, reaching approximately 180 steps earlier than our approach. This is because the static reward prioritizes survival and stability, encouraging conservative behaviors such as standing still or minimal movement, which reduces the risk of termination due to falls. In contrast, the upper-layer reward in our framework incentivizes the robot to actively track the desired gym-motion trajectory, even at the cost of increased instability during early learning stages. As a result, it exhibits more exploratory behavior and experiences higher failure rates initially.

However, as training progresses beyond 500 epochs, the two-layered reward strategy surpasses the static reward in both maximum episode length and overall robustness. It consistently maintains an average episode length above 200 steps for over 1000 epochs, indicating that the agent has successfully learned a stable and dynamic locomotion policy capable of executing complex motions.

The result shown in Figure 6 demonstrates that the two-layered reward framework promotes valuable exploration in the early training stage by prioritizing motion tracking in the reward design, enabling more effective imitation behavior to emerge during the mid-training phase and ultimately achieving superior overall tracking performance.

Figure 7 presents the body tracking errors for both the upper and lower body links over training epochs, illustrating the performance of the two reward frameworks in imitating the target gym-motion.

As shown in Figure 7, both the upper-body and lower-body tracking errors exhibit similar trends across the two methods: initially, the static reward approach achieves lower tracking error, particularly during the early stages of training. This is because the static reward emphasizes stability and penalizes large deviations from the current state, leading to conservative behavior.

In contrast, the two-layered reward framework, by elevating the priority of motion tracking through its upper-layer objective, actively encourages the agent to explore movements that align with the reference trajectory. As a result, the initial tracking error is higher due to increased exploratory actions and imperfect coordination. However, as training progresses beyond 500 epochs, the two-layered reward consistently outperforms the static reward, achieving significantly lower tracking errors in both the upper and lower body segments. This improvement reflects the agent’s growing ability to learn complex, coordinated motions while maintaining balance.

The overall trends in Figure 7 align well with the episode length trend shown in Figure 6, further validating the effectiveness of our framework. While the two-layered reward sacrifices short-term stability for long-term imitation fidelity, it ultimately enables more accurate and dynamic reproduction of the human gymnastic motion, demonstrating its superiority in learning high-dexterity behaviors.

Figure 8 quantifies the relative performance gain of the two-layered reward framework over the static baseline. Although early training exhibits high variance due to active exploration, the method surpasses the baseline after 500 epochs and maintains a consistent advantage. The average relative improvements reach 7.58% for upper-body and 10.30% for lower-body tracking, confirming that our approach effectively enhances tracking ability across both body segments.

Figure 9, Figure 10, Figure 11 and Figure 12 illustrate the evolution of motion tracking performance for both the proposed two-layered reward framework and the static reward baseline across key training stages at 100, 500, 1000, and 2200 epochs. These snapshots provide a qualitative comparison of how each method learns to imitate the target gym-motion over time.

Figure 9 depicts the motion tracking performance at 100 epochs. The two-layered reward agent attempts dynamic movements despite early falls, reflecting its prioritization of motion imitation over conservative stability. This behavior is consistent with the higher exploration levels observed in Figure 6, Figure 7 and Figure 8.

As shown in Figure 10, both agents have learned to maintain an upright posture by 500 epochs. By 1000 epochs, as illustrated in Figure 11, the static reward agent exhibits motion lag and tends to perform movements in place, while the two-layered reward agent achieves timely and accurate tracking with small delay, demonstrating superior motion imitation capability.

As reported in Figure 12, when it comes to 2200 epochs, the two-layered reward agent achieves highly accurate and synchronized motion tracking with minimal delay. In contrast, the static reward agent still exhibits slight motion lag, indicating a slower response to dynamic movements. This demonstrates the effectiveness and superiority of the proposed two-layered reward framework in humanoid robot motion imitation.

4.3. Discussion

The simulation results in the last sub-section demonstrate that the proposed two-layered reward framework outperforms the static reward baseline in human motion imitation on the Unitree G1 robot. Quantitatively, it achieves average improvements of 7.58% and 10.3% in upper-body and lower-body tracking performance, respectively.

To enhance the credibility of our results, we conducted a statistical significance analysis by evaluating the proposed method and baseline framework under five independent random seeds. The simulation results, shown in Figure 13, depict the mean performance as solid lines, and the shaded regions represent ±1 standard deviation across runs. The results demonstrate that our method consistently outperforms the static reward baseline throughout training. In terms of average performance, the proposed two-layered reward framework achieves a 4.25% improvement in upper-body tracking accuracy (the p-value $p = 1.72\times {10}^{-9}<0.05$) and a 4.98% improvement in lower-body tracking accuracy (the p-value $p = 6.00\times {10}^{-13}<0.05$), with both results statistically significant. This confirms the robustness and effectiveness of our two-layered reward framework.

Figure 14 shows the evolution of reward weights during training, with weight₀ to weight₅ corresponding to $r_{\mathrm{base}\_\mathrm{height}}$, $r_{\mathrm{ang}\_\mathrm{vel}\_\mathrm{xy}}$, $r_{\mathrm{lin}\_\mathrm{vel}\_\mathrm{z}}$, $r_{\mathrm{dof}\_\mathrm{pos}\_\mathrm{limits}}$, $r_{\mathrm{dof}\_\mathrm{vel}\_\mathrm{limits}}$, and $r_{\mathrm{action}\_\mathrm{smoothness}}$, respectively. The weights for $r_{\mathrm{ang}\_\mathrm{vel}\_\mathrm{xy}}$, $r_{\mathrm{lin}\_\mathrm{vel}\_\mathrm{z}}$, $r_{\mathrm{dof}\_\mathrm{pos}\_\mathrm{limits}}$, and $r_{\mathrm{dof}\_\mathrm{vel}\_\mathrm{limits}}$ converge to around 0.9, indicating their high importance. Notably, $r_{\mathrm{dof}\_\mathrm{pos}\_\mathrm{limits}}$ achieves a high final weight ($\approx 0.92$) with the highest mean value with 0.676, suggesting it is the most critical for the current motion tracking.

The key advantage stems from the hierarchical reward design: by prioritizing motion imitation in the upper layer, the framework explicitly encourages the agent to learn the target motion trajectory before optimizing for secondary objectives such as stability or energy efficiency. This structured learning paradigm leads to more meaningful exploration—sacrificing short-term success rates during early training for faster convergence in motion tracking.

Indeed, the initial phase exhibits higher failure rates due to aggressive exploration driven by the imitation objective. However, this trade-off proves beneficial, as the two-layered approach consistently surpasses the baseline by the middle of training procedure, indicating accelerated learning and superior long-term performance. The improved sample efficiency suggests that the framework effectively guides the policy search toward task-relevant behaviors.

The proposed two-layered reinforcement learning framework shares a conceptual synergy with recent advances in learning-augmented planning, such as Diffusion Tree (DiTree) [33], which combines the global completeness of sampling-based planners (SBPs) with the efficiency of diffusion policies as informed samplers. While DiTree focuses on kinodynamic motion planning in geometrically complex environments, our work addresses a complementary challenge: adaptive policy learning under dynamic task constraints in continuous control. Looking forward, an exciting direction is to integrate these paradigms and use a two-layered reward agent as the local policy within a DiTree-style planner, where the learned reward adaptation mechanism could dynamically reshape trajectory preferences based on terrain, task goals, or energy constraints. Such a hybrid architecture would combine global safety guarantees from SBPs with local behavioral adaptability, paving the way toward truly autonomous humanoid navigation in unstructured environments.

Nonetheless, there of course exist several limitations. First, the evaluated gym-motion is relatively simple and short in duration. For more complex or temporally extended motions, the initial performance instability may persist longer, potentially increasing training cost. Further research is needed to analyze and mitigate the negative impact of prolonged exploration phases, possibly through curriculum strategies.

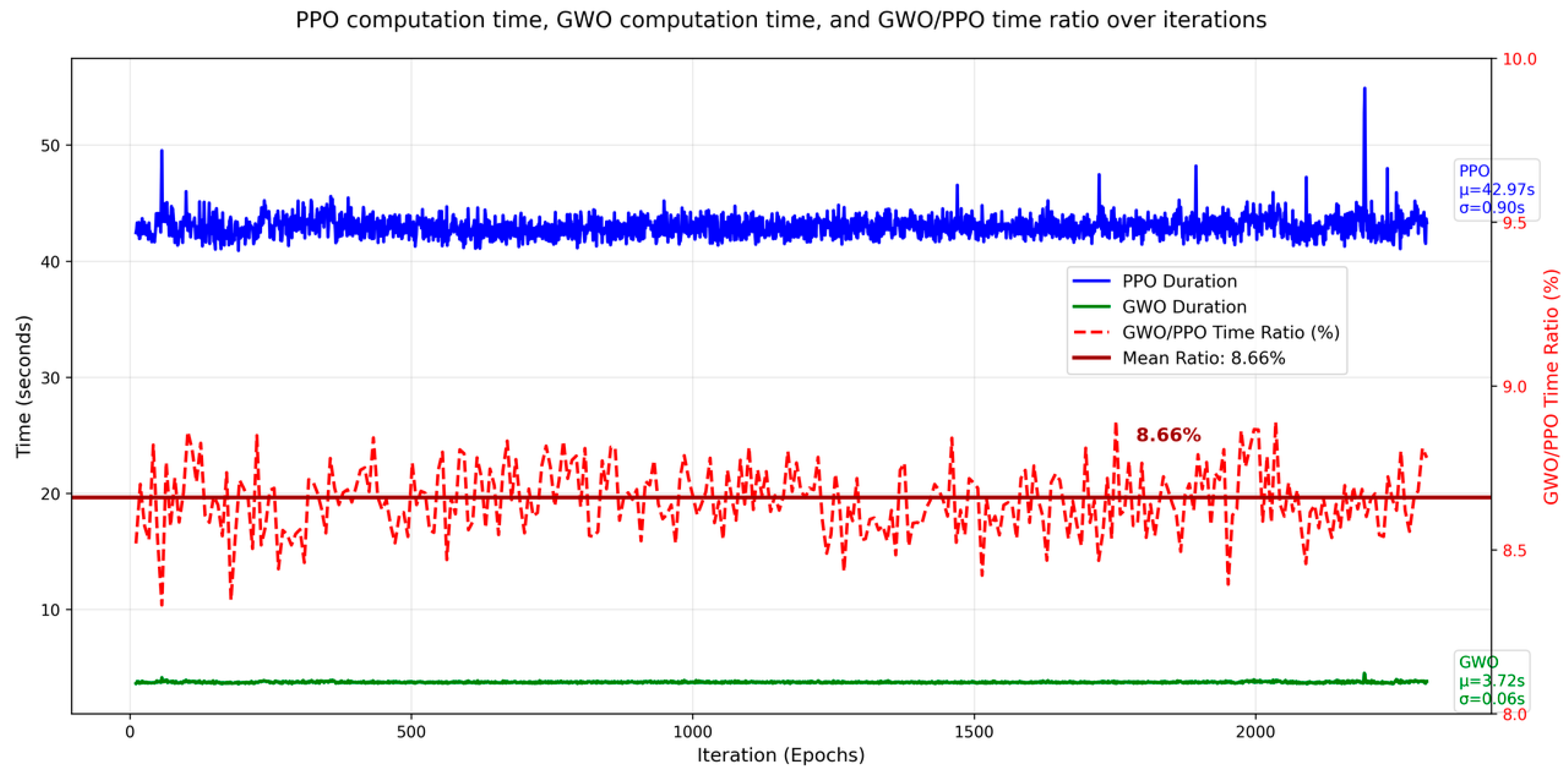
Second, while the two-layered structure enhances learning effectiveness, online optimization of reward weights introduces additional computational overhead. As depicted in Figure 15, the average wall-clock time overhead of the GWO algorithm computation per PPO iteration is 3.72 ± 0.06 s. In comparison, each PPO update takes approximately 43 s on the same hardware. Thus, the additional overhead is less than 10%, which we consider acceptable for the observed performance gains. While the current implementation employs the Grey Wolf Optimizer (GWO) due to its simplicity and effectiveness in low-to-moderate dimensional spaces (≤25 dimensions), we acknowledge that traditional meta-heuristic algorithms may encounter scalability challenges when applied to significantly higher-dimensional reward weight spaces. In high-dimensional settings, the search space grows exponentially, increasing the risk of slow convergence and premature optimization. To address this limitation, our framework can be extended with advanced dimensionality-aware techniques such as the Effective Dimension Extraction Mechanism (EDEM) [34]. EDEM is a novel mechanism designed to enhance meta-heuristic optimization in complex, high-dimensional problems by identifying and focusing search efforts on the most influential dimensions. Future work should investigate faster meta-heuristic algorithms other than GWO that are better suited to real-time reinforcement learning pipelines.

Thirdly, the 10% performance threshold is empirically motivated by preliminary training observations. While a higher threshold could yield marginally better results, it would also increase computational overhead. Therefore, we adopt 10% as a practical trade-off between performance improvement and computational efficiency. A more rigorous analysis of this threshold’s impact is left for our future work.

Finally, although validation is currently limited to the Isaac Gym simulation environment, the results sufficiently demonstrate the algorithmic advantages of the proposed framework. Deployment on the physical Unitree G1 robot involves sim-to-real transfer challenges, which are unrelated to the core contribution of this work. In follow-up studies, we may aim to develop a pipeline that bridges video-based motion capture to real-world humanoid robot execution based on the proposed two-layered reward framework.

5. Conclusions

A two-layered reward reinforcement learning framework for humanoid robot motion tracking is proposed in this work, which decomposes the whole reward into an upper-layer goal reward for task accuracy and a lower-layer optimizing reward for secondary objectives like stability and energy efficiency. The weights of the optimizing reward are dynamically optimized via an online meta-heuristic algorithm (GWO in this work), conditioned on upper-layer performance.

This hierarchical reward structure promotes effective exploration by prioritizing task completion early in training, leading to faster convergence and more dynamic motion learning compared to static reward designs. It also reduces reward hacking and improves training stability by aligning secondary optimization with primary task success.

Evaluated on the Unitree G1 robot performing a dynamic gymnastic motion in the Isaac Gym environment, the proposed method achieves 7.58% higher upper-body and 10.3% higher lower-body tracking accuracy than a static reward baseline, with better synchronization and reduced delay.

Our future research will test this framework on more complex motion tracking tasks and on diverse robot platforms other than Unitree G1. Real-world deployment on Unitree G1 will also be conducted to assess the practical effectiveness of the two-layered reward framework.