Spectral Collocation Method for Solving Nonlinear Riesz Distributed-Order Fractional Differential Equations
Abstract
1. Introduction
2. Related Work and Problem Statement
3. Preliminaries and Theories
4. Proposed Spectral Collocation Method
4.1. One-Dimensional Formulation
4.2. Two-Dimensional Extension
4.3. Reduction to Time-Ordinary Systems
5. Numerical Experiments and Discussion
5.1. One-Dimensional Test Problem
5.2. Two-Dimensional Test Problem
5.3. Computational Complexity Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DOFDEs | Distributed order fractional differential equations |
| FDEs | Fractional differential equations |
| FPDEs | Fractional partial differential equations |
| RDFDEs | Reisz distributed order fractional differential equations |
| RJPs | Romanovski–Jacobi polynomials |
| R-LFD | Riemann–Liouville fractional derivative |
| SL-G-L | Shifted Legendre–Gauss–Lobatto |
References
- Sarwar, N.; Asjad, M.I.; Sitthiwirattham, T.; Patanarapeelert, N.; Muhammad, T. A Prabhakar fractional approach for the convection flow of Casson fluid across an oscillating surface based on the generalized Fourier law. Symmetry 2021, 11, 2039. [Google Scholar] [CrossRef]
- Ionescu, C.; Lopes, A.; Copot, D.; Machado, J.A.T.; Bates, J.H.T. The role of fractional calculus in modeling biological phenomena: A review. Commun. Nonlinear Sci. Numer. Simul. 2017, 51, 141–159. [Google Scholar] [CrossRef]
- Raghavendran, P.; Gunasekar, T.; Balasundaram, H.; Santra, S.S.; Majumder, D.; Baleanu, D. Solving fractional integro-differential equations by Aboodh transform. J. Math. Comput. Sci. 2024, 32, 229–240. [Google Scholar] [CrossRef]
- Rihan, F.A. Fractional-order delay differential equations with predator-prey systems. In Delay Differential Equations and Applications to Biology; Springer: Berlin/Heidelberg, Germany, 2021; pp. 211–232. [Google Scholar]
- Alkandari, M.; Loutchko, D.; Luchko, Y. Anomalous Diffusion Models Involving Regularized General Fractional Derivatives with Sonin Kernels. Alex. Eng. J. 2025, 9, 363. [Google Scholar] [CrossRef]
- Caputo, M. Mean fractional-order-derivatives differential equations and filters. Ann. Dell’Universita Di Ferrara 1995, 41, 73–84. [Google Scholar] [CrossRef]
- Carrillo, J.A.; Fronzoni, S.; Süli, E. Finite element scheme for the fractional porous medium equation with fractional pressure. Numer. Math. 2025, 157, 1537–1614. [Google Scholar] [CrossRef]
- Ferrás, L.L. Fractional Derivatives: The ultimate operator for modelling complex viscoelastic materials? Fract. Calc. Appl. Anal. 2025. [Google Scholar] [CrossRef]
- Chechkin, A.V.; Gorenflo, R.; Sokolov, I.M. Retarding subdiffusion and accelerating superdiffusion governed by distributed-order fractional diffusion equations. Phys. Rev. E 2002, 66, 046129. [Google Scholar] [CrossRef]
- Caputo, M. Diffusion with space memory modelled with distributed order space fractional differential equations. Ann. Geophys. 2003, 46, 223–234. [Google Scholar] [CrossRef]
- Jian, H.-Y.; Huang, T.-Z.; Gu, X.-M.; Zhao, X.-L.; Zhao, Y.-L. Fast second-order implicit difference schemes for time distributed-order and Riesz space fractional diffusion-wave equations. Comput. Math. Appl. 2021, 94, 136–154. [Google Scholar] [CrossRef]
- Gao, Y.; Yin, D.; Zhao, B. A variable-order fractional constitutive model to characterize the rate-dependent mechanical behavior of soft materials. Fractal Fract. 2022, 6, 590. [Google Scholar] [CrossRef]
- Wang, Y.; Cai, M. Finite difference schemes for time-space fractional diffusion equations in one-and two-dimensions. Commun. Appl. Math. Comput. 2023, 5, 1674–1696. [Google Scholar] [CrossRef]
- Khan, M.A.; Alias, N.; Khan, I.; Salama, F.M.; Eldin, S.M. A new implicit high-order iterative scheme for the numerical simulation of the two-dimensional time fractional cable equation. Sci. Rep. 2023, 13, 1549. [Google Scholar] [CrossRef]
- Fei, M.; Huang, C. Galerkin–Legendre spectral method for the distributed-order time fractional fourth-order partial differential equation. Int. J. Comput. Math. 2020, 97, 1183–1196. [Google Scholar] [CrossRef]
- Luo, M.; Qiu, W.; Nikan, O.; Avazzadeh, Z. Second-order accurate, robust and efficient ADI Galerkin technique for the three-dimensional nonlocal heat model arising in viscoelasticity. Appl. Math. Comput. 2023, 440, 127655. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Gusu, D.M.; Mohammed, P.O.; Wedajo, G.; Nonlaopon, K.; Hamed, Y.S. Solutions of general fractional-order differential equations by using the spectral Tau method. Fractal Fract. 2021, 6, 7. [Google Scholar] [CrossRef]
- Hadhoud, A.R.; Srivastava, H.M.; Rageh, A.A.M. Non-polynomial B-spline and shifted Jacobi spectral collocation techniques to solve time-fractional nonlinear coupled Burgers’ equations numerically. Adv. Differ. Equ. 2021, 2021, 439. [Google Scholar] [CrossRef]
- Amin, A.Z.; Abdelkawy, M.A.; Solouma, E.; Al-Dayel, I. A spectral collocation method for solving the non-linear distributed-order fractional Bagley–Torvik differential equation. Fractal Fract. 2023, 7, 780. [Google Scholar] [CrossRef]
- Ahmed, H.; Abd-Elhameed, W. Spectral Solutions of Specific Singular Differential Equations Using A Unified Spectral Galerkin-Collocation Algorithm. J. Nonlinear Math. Phys. 2024, 31, 42. [Google Scholar] [CrossRef]
- Lachin, A.; Abdelkawy, M.A.; Sathasivam, S. An efficient collocation method based on Legendre and Romanovski polynomials for solving Riesz distributed fractional differential equations. Alex. Eng. J. 2025, 129, 312–328. [Google Scholar] [CrossRef]
- Shen, J.; Tang, T.; Wang, L.-L. Spectral Methods: Algorithms, Analysis and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011; Volume 41. [Google Scholar]
- Abdelkawy, M.A.; Alyami, S.A. Legendre-Chebyshev spectral collocation method for two-dimensional nonlinear reaction-diffusion equation with Riesz space-fractional. Chaos Solitons Fractals 2021, 151, 111279. [Google Scholar] [CrossRef]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley–Blackwell: Hoboken, NJ, USA, 1993. [Google Scholar]
- Huang, X.; Fang, Z.-W.; Sun, H.-W.; Zhang, C.-H. A circulant preconditioner for the Riesz distributed-order space-fractional diffusion equations. Linear Multilinear Algebra 2022, 70, 3081–3096. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, Y.; Xu, Y. Implicit Runge–Kutta and spectral Galerkin methods for Riesz space fractional/distributed-order diffusion equation. Comput. Appl. Math. 2020, 39, 47. [Google Scholar] [CrossRef]
- Izadi, M.; Veeresha, P.; Adel, W. The fractional-order marriage–divorce mathematical model: Numerical investigations and dynamical analysis. Eur. Phys. J. Plus 2024, 139, 205. [Google Scholar] [CrossRef]
- Nazari, J.; Heydari, M.H.; Hosseininia, M. Romanovski–Jacobi polynomials for the numerical solution of multi-dimensional multi-order time fractional telegraph equations. Results Phys. 2023, 53, 106937. [Google Scholar] [CrossRef]
- Abdelkawy, M.A.; Menaem, A.A.; Matoog, R.T.; Tedjani, A.H. Romanovski–Jacobi spectral collocation schemes for distributed order differential problems. Alex. Eng. J. 2024, 101, 98–107. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, F.; Jiang, X.; Zeng, F.; Turner, I. A Crank–Nicolson ADI Galerkin–Legendre spectral method for the two-dimensional Riesz space distributed-order advection–diffusion equation. Comput. Math. Appl. 2018, 76, 2460–2476. [Google Scholar] [CrossRef]
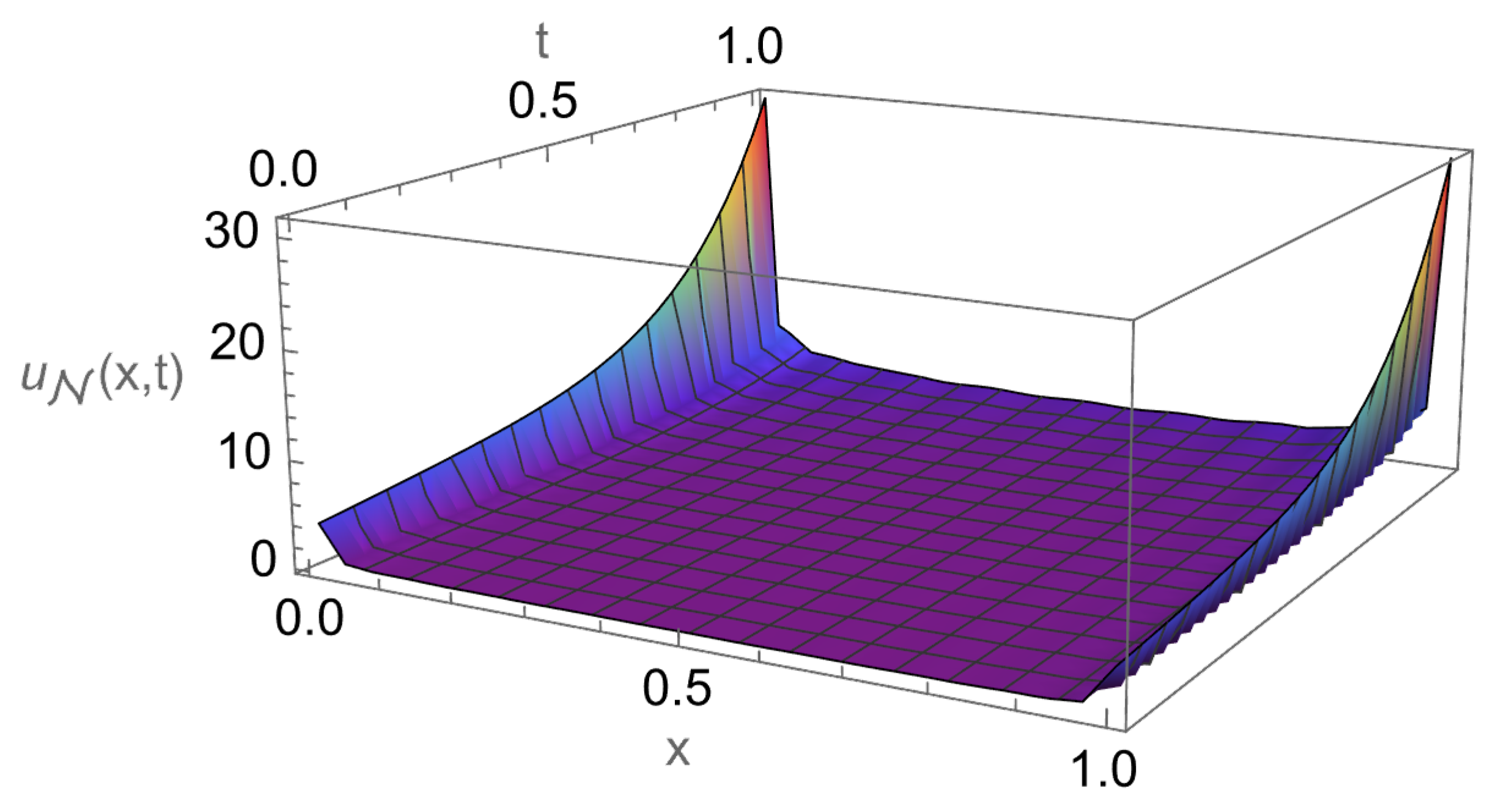
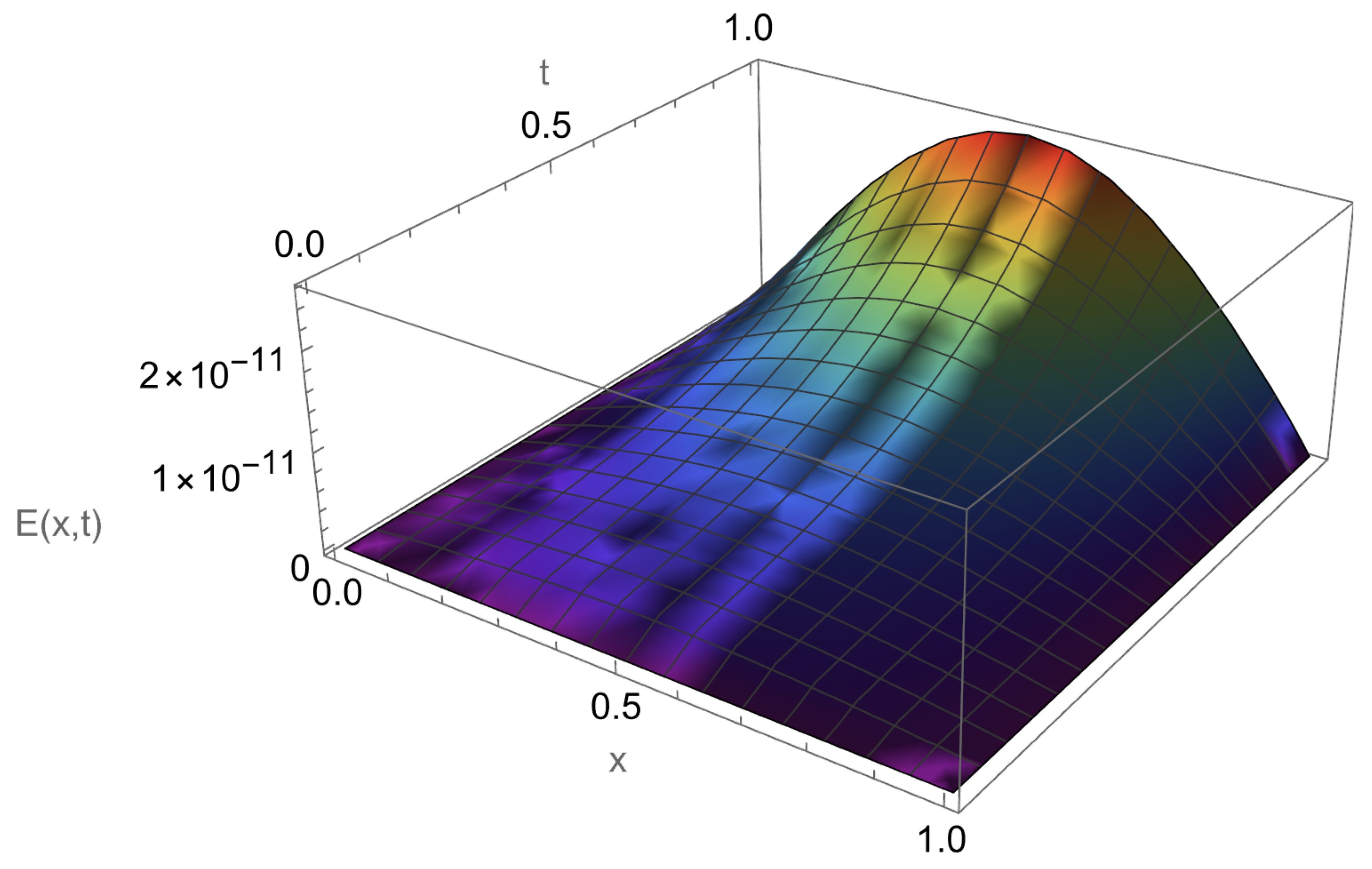

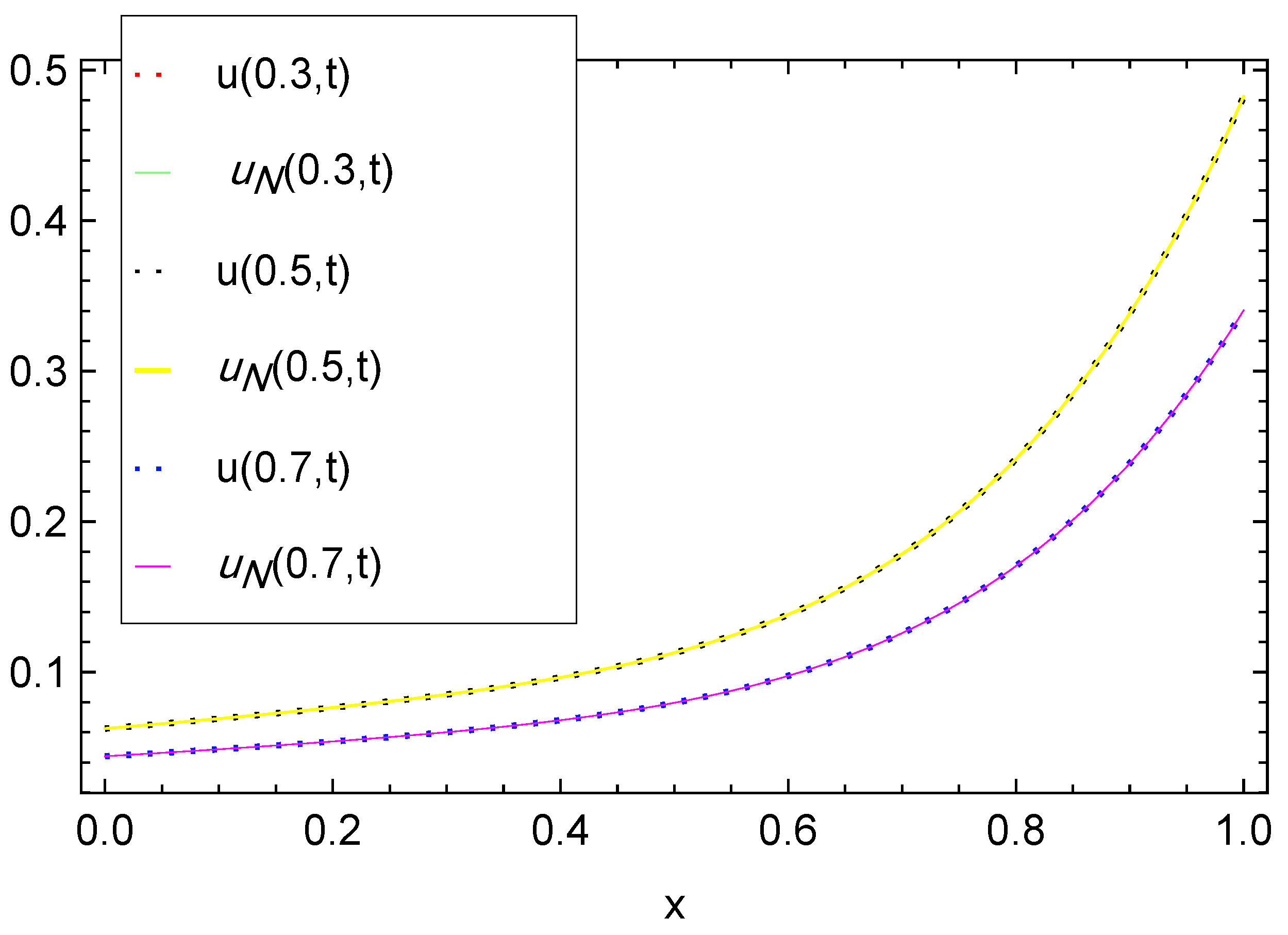
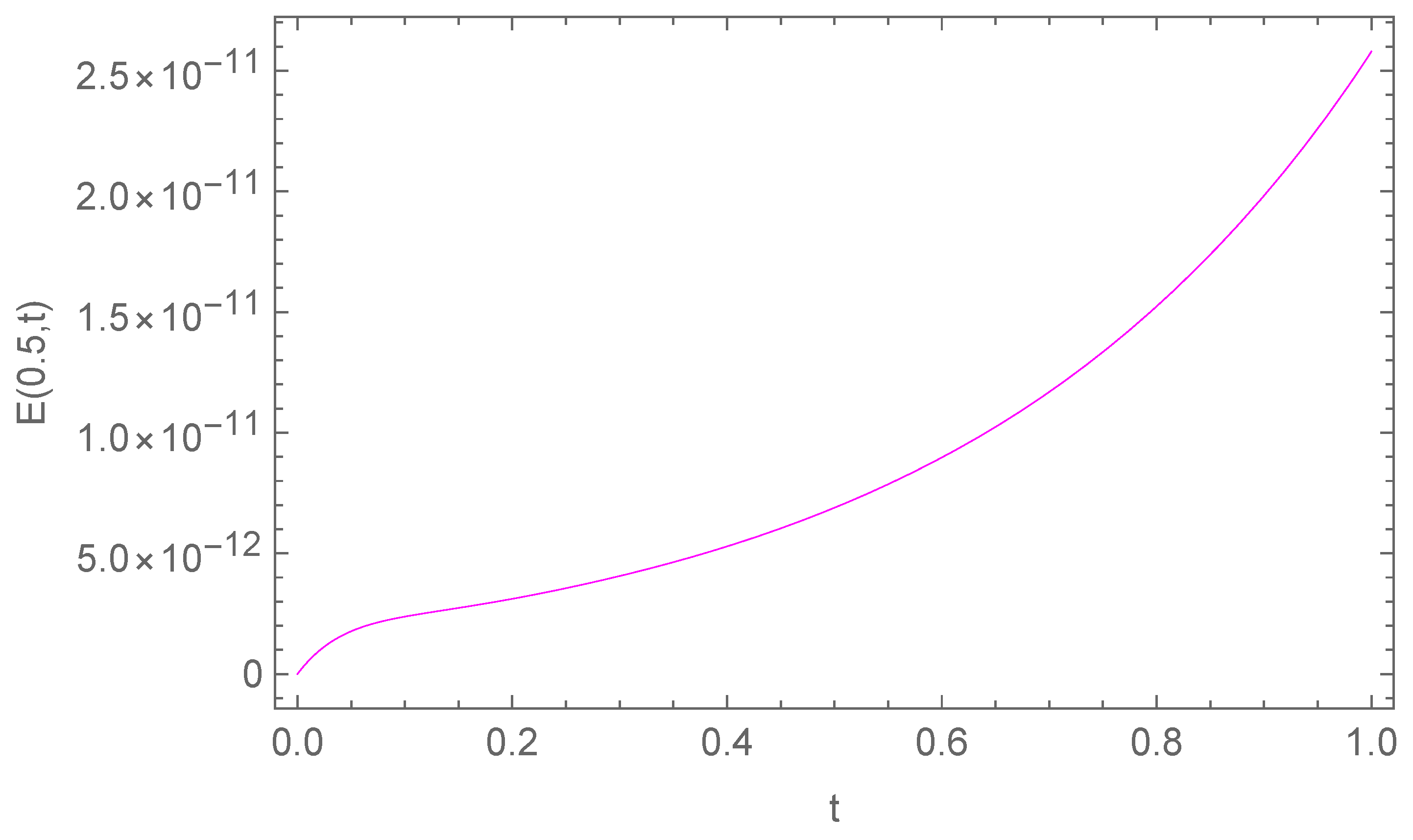
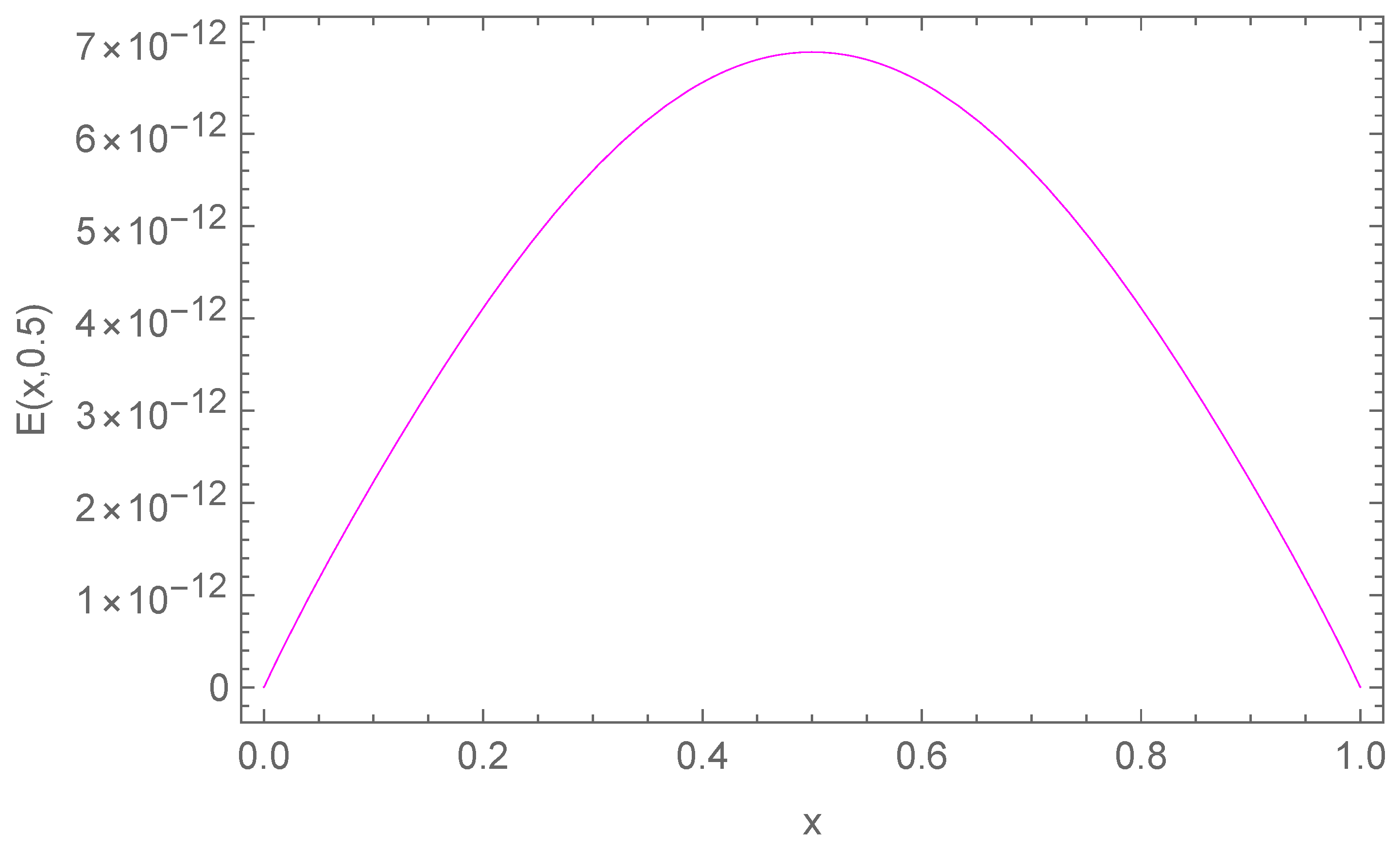
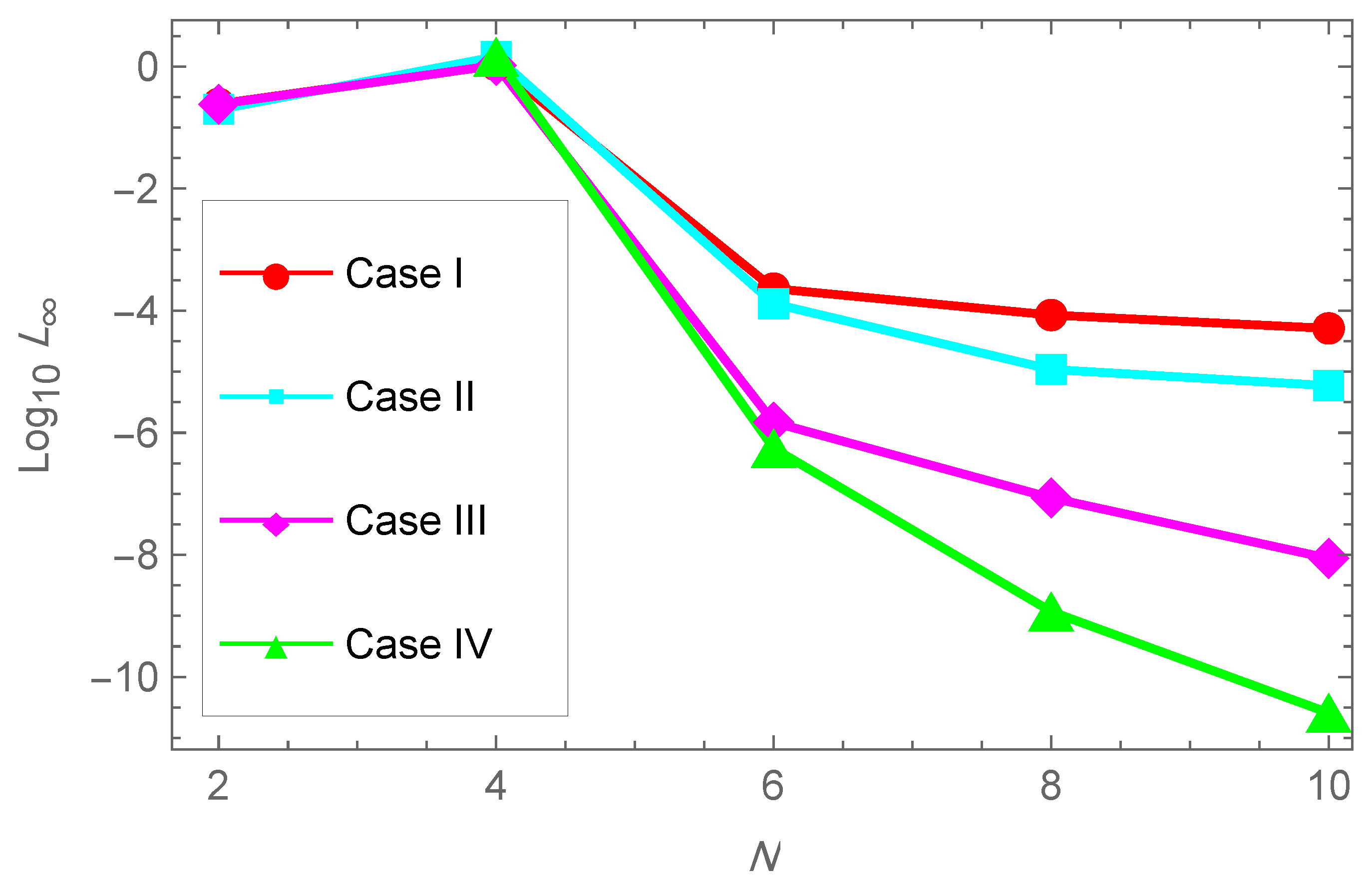


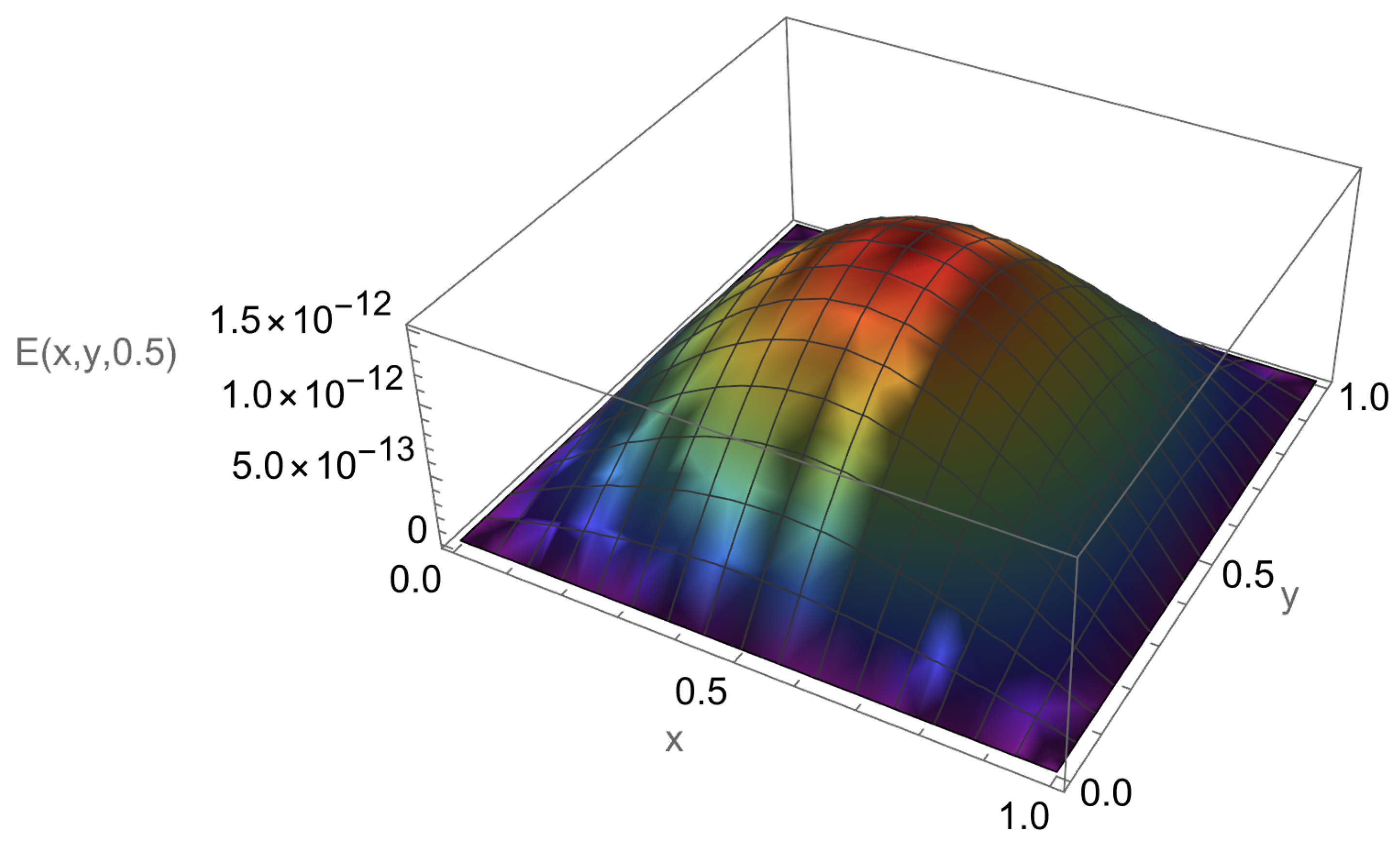
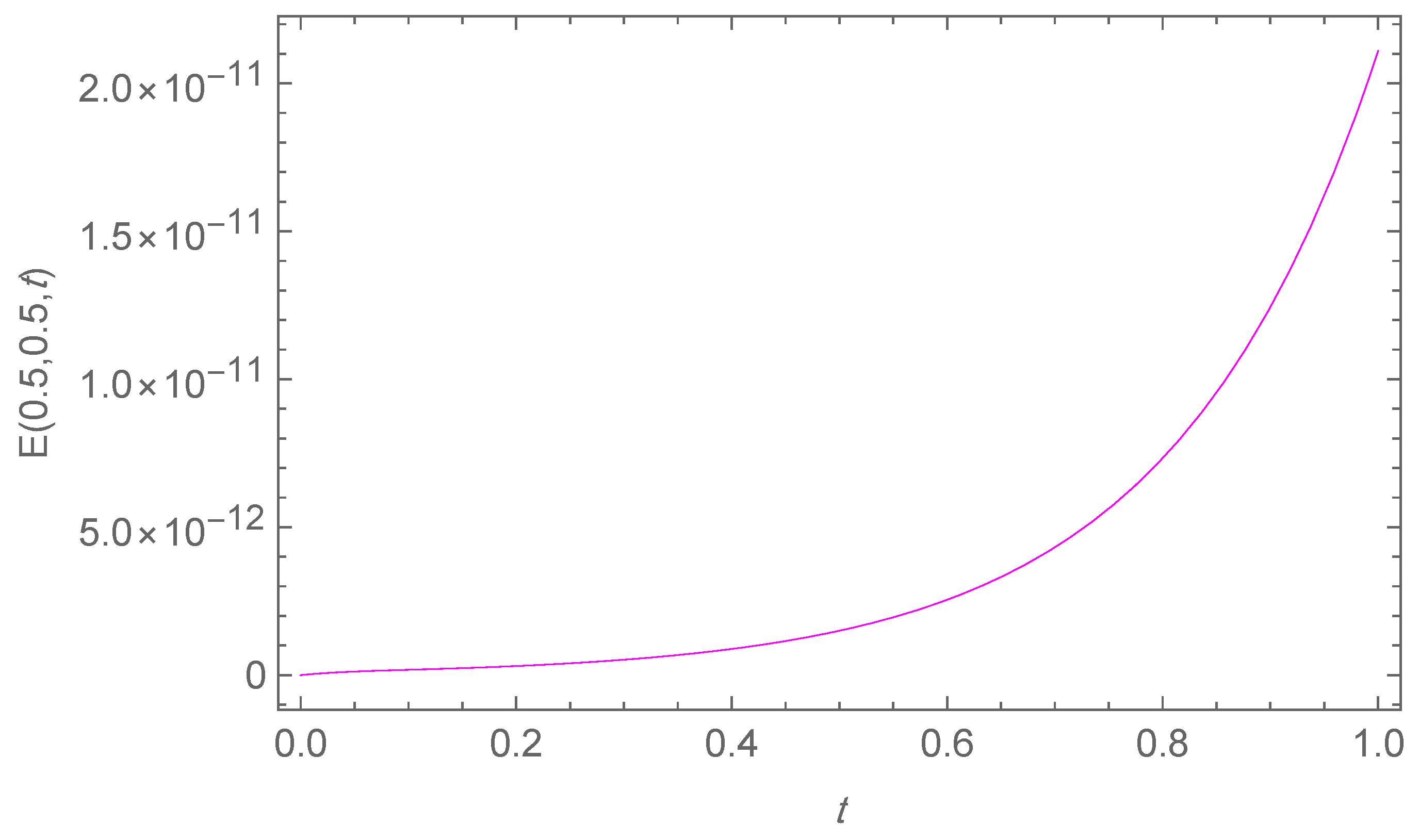
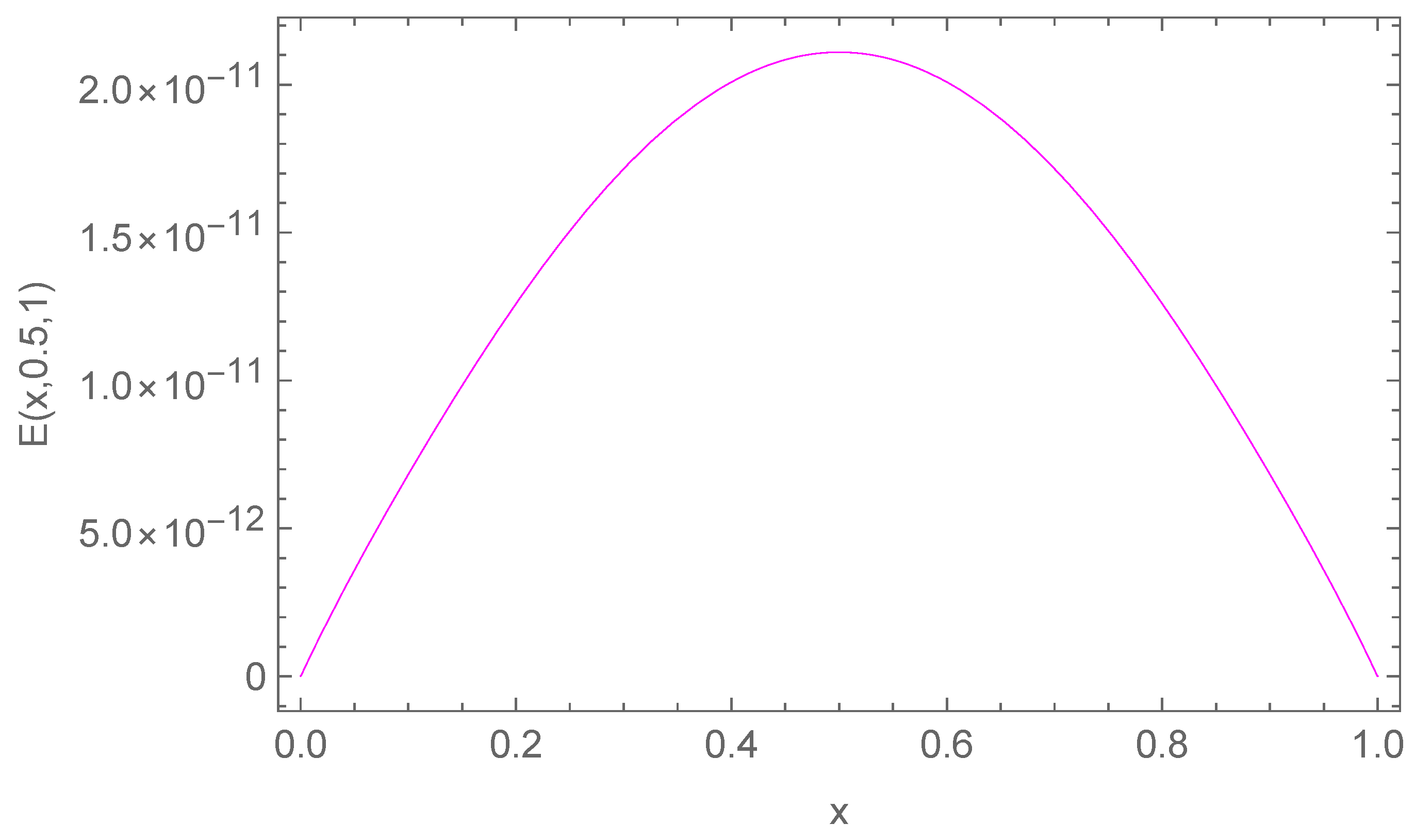
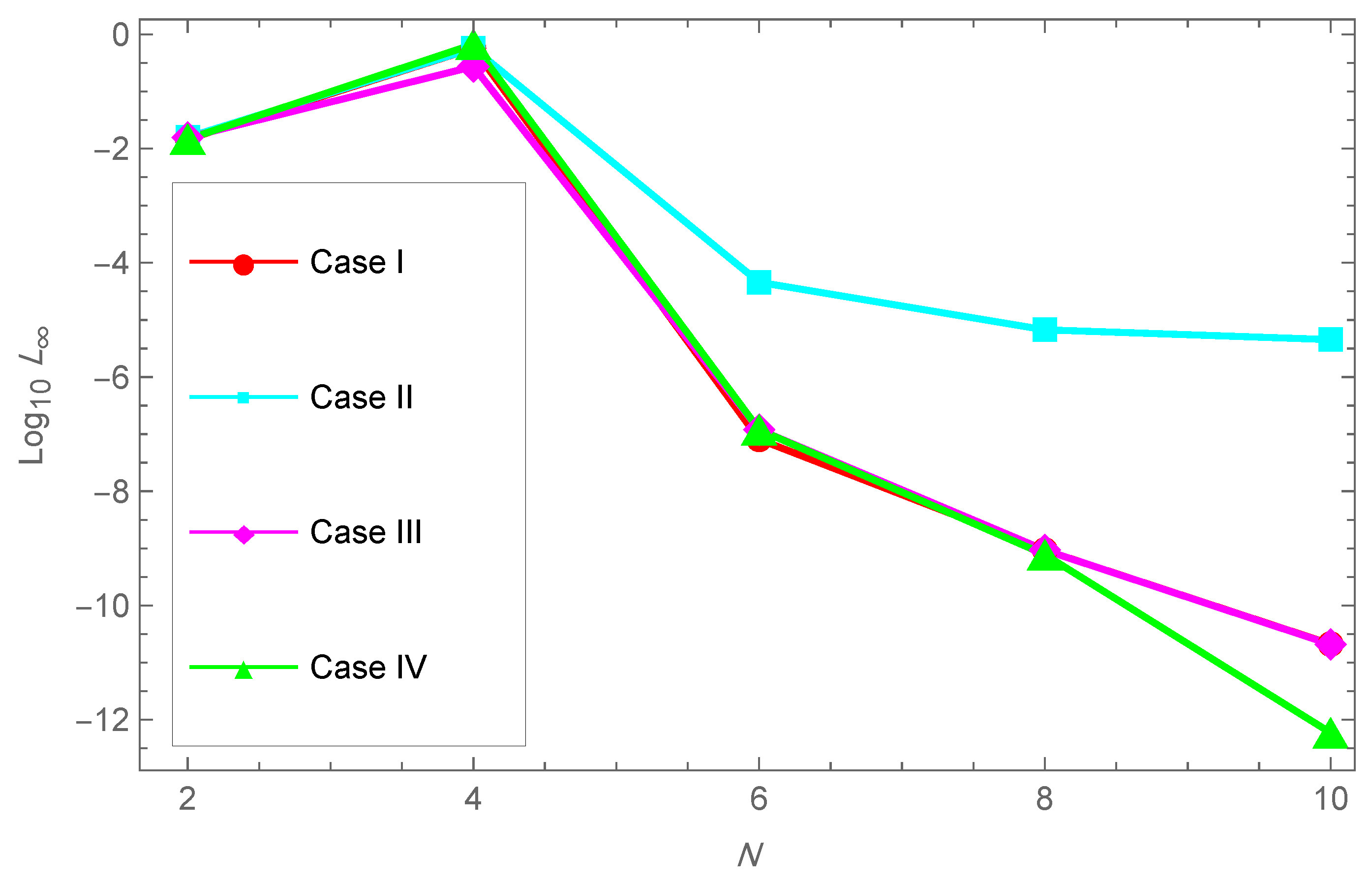
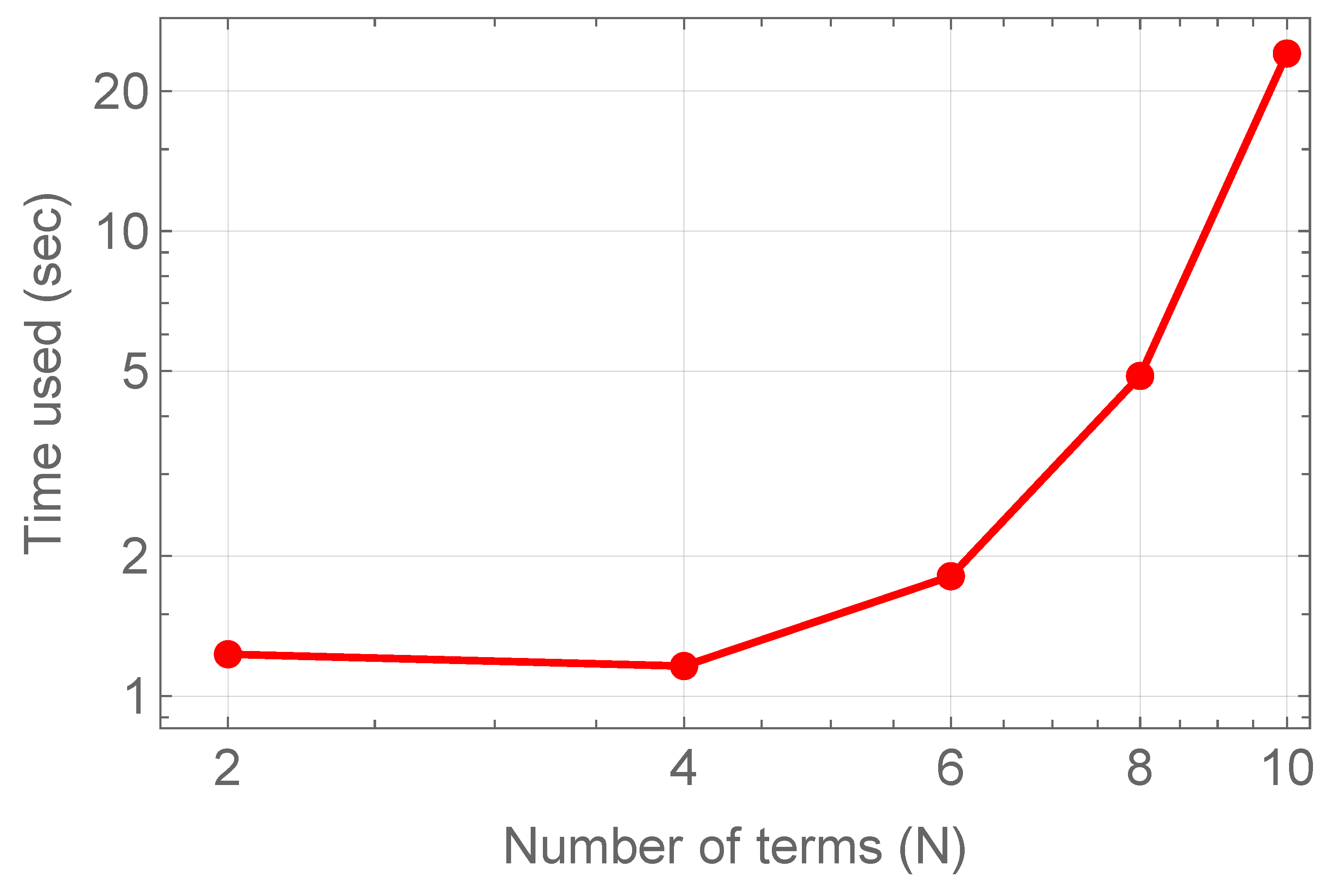

| N | Average CPU | ||||
|---|---|---|---|---|---|
| Time (s) | |||||
| 2 | 0.2436 | 0.1980 | 0.2407 | 0.1963 | 1.23 |
| 4 | 1.4525 | 1.0485 | 1.4395 | 1.16 | |
| 5 | 1.50 | ||||
| 6 | 1.81 | ||||
| 8 | 4.88 | ||||
| 10 | 24.095 | ||||
| Romanovski Legendre Collocation Method | CN-ADI-GSM [30] | ||||
|---|---|---|---|---|---|
| , , | |||||
| (4, 4) | 0.5696 | 0.5709 | 0.6696 | ||
| (5, 5) | 8 | ||||
| (6, 6) | 16 | ||||
| (8, 8) | 32 | ||||
| (10, 10) | 64 | ||||
| , | ||
|---|---|---|
| Error | Time Used (s) | |
| (2, 2) | ||
| (4, 4) | ||
| (5, 5) | 44.50 | |
| (6, 6) | 232.30 | |
| (8, 8) | 1810.41 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lachin, A.; Abdelkawy, M.A.; Sathasivam, S. Spectral Collocation Method for Solving Nonlinear Riesz Distributed-Order Fractional Differential Equations. Mathematics 2025, 13, 3425. https://doi.org/10.3390/math13213425
Lachin A, Abdelkawy MA, Sathasivam S. Spectral Collocation Method for Solving Nonlinear Riesz Distributed-Order Fractional Differential Equations. Mathematics. 2025; 13(21):3425. https://doi.org/10.3390/math13213425
Chicago/Turabian StyleLachin, Ammar, Mohammed A. Abdelkawy, and Saratha Sathasivam. 2025. "Spectral Collocation Method for Solving Nonlinear Riesz Distributed-Order Fractional Differential Equations" Mathematics 13, no. 21: 3425. https://doi.org/10.3390/math13213425
APA StyleLachin, A., Abdelkawy, M. A., & Sathasivam, S. (2025). Spectral Collocation Method for Solving Nonlinear Riesz Distributed-Order Fractional Differential Equations. Mathematics, 13(21), 3425. https://doi.org/10.3390/math13213425





