Conics and Transformations Defined by the Parallelians of a Triangle

Abstract

For any point P in the Euclidean plane of a triangle $\Delta$, the six parallelians of P lie on a single conic, which shall be called the parallelian conic of P with respect to $\Delta$. We provide a synthetic and an analytic proof of this fact. Then, we studied the shape of this particular conic, depending on the choice of the pivot point P. This led to the finding that the only circular parallelian conic is the first Lemoine circle. Points on the Steiner inellipse produce parabolae, and those on a certain central line yield equilateral hyperbolae. The hexagon built by the parallelians has an inconic $\mathcal{I}$ and the tangents of $\mathcal{P}$ at the parallelians define some triangles and hexagons with several circum- and inconics. Certain pairings of conics, together with in- and circumscribed polygons, give rise to different kinds of porisms. Further, the inconics and circumconics of the triangles and hexagons span exponential pencils of conics in which any pair of subsequent conics defines a new conic as the polar image of the inconic with regard to the circumconic. This allows us to construct chains of nested porisms. The trilinear representations of the centers of the appearing conics, as well as the perspectors of some deduced triangles, depending on the indeterminate coordinates of P, define some algebraic transformations that establish algebraic relations between well- and lesser-known triangle centers. We completed our studies by compiling a list of possible porisms between any pair of conics. Further, we describe the possible loci of pivot points so that the mentioned conics allow for porisms of polygons with arbitrary numbers of vertices.

1. Introduction

The parallelians of a point P in the Euclidean plane of a triangle $\Delta$ are the projections of P onto the sides of $\Delta$ by means of the three lines parallel to $\Delta$’s sides. The parallelians form a hexagon, the parallelian hexagon, with three of its sides coinciding with the sides of $\Delta$. It is more or less well-known (see [1,2,3]) that these six points lie on a single conic (provided an admissible choice of P), the parallelian conic of P with respect to $\Delta$, which is denoted by $\mathcal{P}$ in the following. A synthetic proof of this fact is given, together with an analytic proof, in this section. We do not claim that this proof is new, but it could not be found anywhere in the literature.

The shape of the parallelian conic $\mathcal{P}$, depending on various pivot points P, is one of the topics of Section 2. Further in Section 2, we show that the tangents of $\mathcal{P}$ at the parallelians form a hexagon whose vertices lie on a single conic $\mathcal{T}$, the tangent parallelian conic. Thus, the parallelian conic $\mathcal{P}$ gives rise to a hexagonal porism interscribed between the pair of conics $(\mathcal{T},\mathcal{P})$. Further, there exists a triangle porism around $\mathcal{P}$, as we can find two separate tangent triangles of $\mathcal{P}$ whose six vertices also lie on a single conic $\mathcal{D}$, which gives rise to a second hexagonal porism.

Section 3 is dedicated to the construction of further porisms. Naturally, these porisms allow for the construction of chains of porisms by means of polar conics, which belong to an exponential pencil of conics spanned by any two (subsequent) conics in the chain. Finally, in Section 4.2, we establish algebraic relations between the pivot point P and the centers of some conics mentioned in Section 2 and Section 3. Further, some of the triangles deduced from the parallelians constitute perspective pairs, and the corresponding perspectors also allow for the definition and construction of an algebraic relation between them and P. We added some tables showing the thus-established relations between some triangle centers.

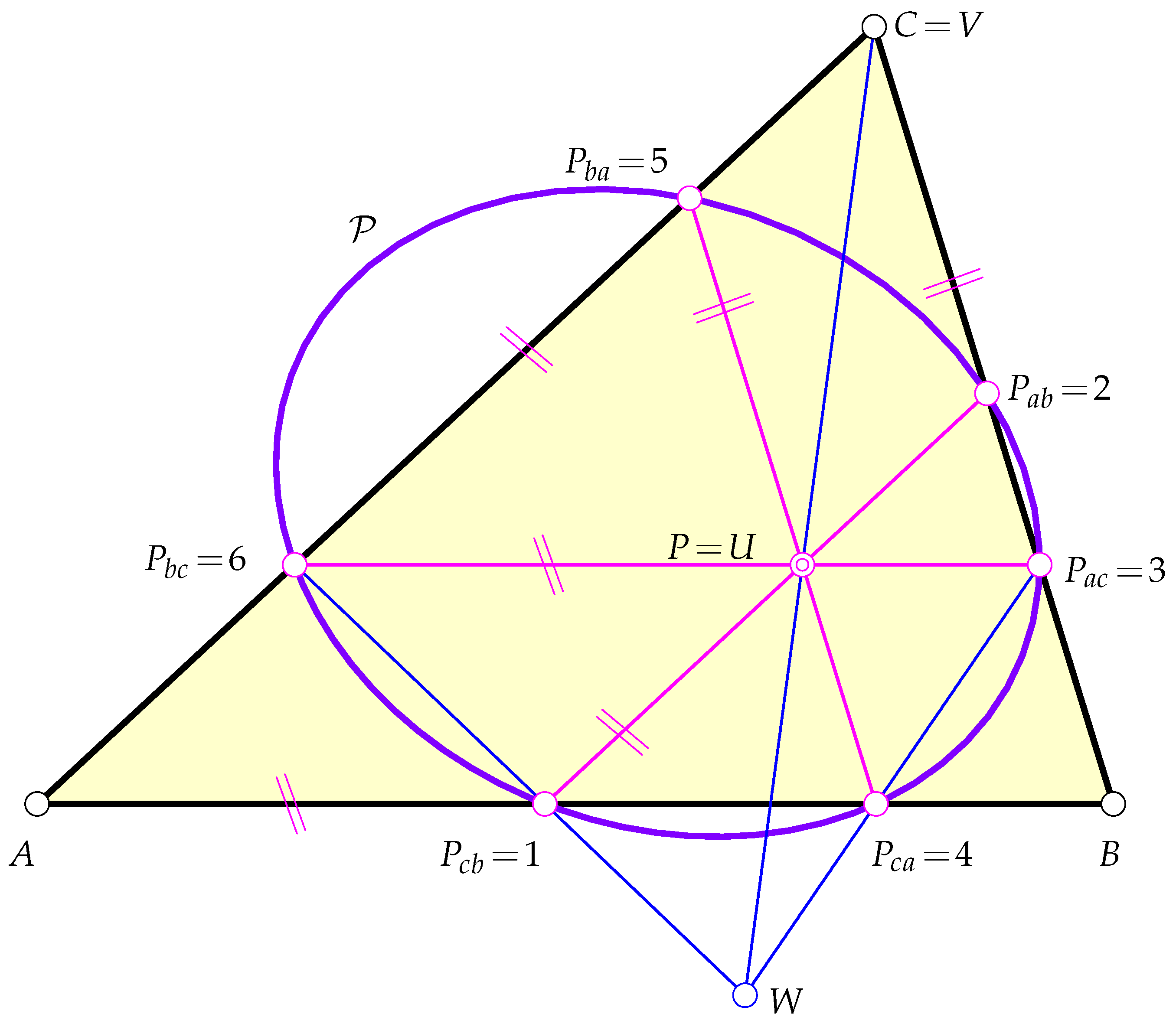
2. The Parallelian Conic and Inconic

2.1. The Shape of the Parallelian Conic

In what follows, we used homogeneous trilinear coordinates in the plane of the base triangle $\Delta =ABC$. Hence, the vertices of $\Delta$ are described by the homogeneous trilinear coordinates $A=1:0:0$, $B=0:1:0$, and $C=0:0:1$, and the unit point equals the incenter $X_1=1:1:1$. Here, and in the following, we used C. Kimberling’s notation for triangle centers (cf. [3,4]). In this particular projective extension of the Euclidean plane, the ideal line (line at infinity) $\omega$ can be described by the equation $ax+by+cz=0$, or simply by its homogeneous trilinear coordinates $a:b:c$. Note that $a=\overline{BC}$, $b=\overline{CA}$, and $c=\overline{AB}$ are the lengths of $\Delta$’s sides.

Let $P=\xi :\eta :\zeta$ be a point in the plane of the triangle $\Delta$ that is not on any side of $\Delta$, i.e., $\xi \eta \zeta \ne 0$. Then, the three lines parallel to $\Delta$’s sides and through P

$$\begin{array}{c}[P_{bc},P_{ac}]\Vert [A,B],[P_{ca},P_{ba}]\Vert [B,C],[P_{ab},P_{cb}]\Vert [C,A],\end{array}$$

meet the side lines in six points with the trilinear coordinates

$$\begin{array}{ccccc}{P}_{ab}& =& 0:a\xi +b\eta :b\zeta ,P_{ac}& =& 0:c\eta :c\zeta +a\xi ,\\ P_{ba}& =& c\xi :0:c\zeta +b\eta ,P_{bc}& =& a\xi +b\eta :0:a\zeta ,\\ P_{ca}& =& b\xi :c\zeta +b\eta :0,P_{cb}& =& c\zeta +a\xi :a\eta :0,\end{array}$$

which are called parallelians. It is well-known (cf. [3] (p. 104)) that the chords $P_{ab}{P}_{cb}$, $P_{bc}{P}_{ac}$, and $P_{ba}{P}_{ca}$ are of equal length if $P=X_{192}$ (congruent parallelians point).

Although the following result appears in some internet sources, we provide a proof that gives some geometric insight:

Theorem 1.

The points $P_{ab}$, …, $P_{cb}$ lie on a single conic $\mathcal{P}$, provided that P is neither chosen on a side line of Δ nor on the Steiner circumellipse nor on the ideal line.

Proof. 

In order to show that the above given points are conconic, we relabeled them according to $1:=P_{cb}$, $2:=P_{ab}$, $3:=P_{ac}$, $4:=P_{ca}$, $5:=P_{ba}$, and $6:=P_{bc}$ (see Figure 1). If these six points were conconic, then, according to Pascal’s theorem (see [5] (p. 220)), the three points $U:=[1,2]\cap [4,5]$, $V:=[2,3]\cap [5,6]$, and $W:=[3,4]\cap [6,1]$ are collinear.

By assumption, $U=P$ and $V=C$. We only have to show that $W=[3,4]\cap [6,1]$ is located on $[U,V]=[C,P]$. Since $[A,B] \Vert [3,6]$, the triangles $\Delta (=ABC)$ and $P_{bc}{P}_{ac}C=63C$ are similar. Further, since $[C,A] \Vert [1,2]$ and $[B,C]=[2,3] \Vert [4,5]$, the triangle $P_{cb}{P}_{ca}P=14P$ and $\Delta$ are similar. Further, for $[6,3] \Vert [1,4]$, $[3,C] \Vert [4,P]$, and $[C,6] \Vert [P,1]$, the latter triangles are part of a special Desargues configuration in which the perspector serves as the center of similarity. Consequently, the three lines $[6,1]$, $[3,4]$, and $[C,P]$ are concurrent.

In order to verify the exceptions made in Theorem 1, we computed the homogeneous trilinear equation of the conic $\mathcal{P}$ on the points $P_{ab}$, …, and $P_{cb}$. This yielded

$$\mathcal{P}:\sum _{\mathrm{cyclic}}a\eta \zeta (b\eta +c\zeta )x^2-\xi \left(a\xi (a\xi +b\eta +c\zeta )+2bc\eta \zeta \right)yz=0,$$

(1)

where ${\displaystyle \sum _{\mathrm{cyclic}}}$ means that the argument function in the sum undergoes cyclic replacement $a\to b\to c\to a$, $\xi \to \eta \zeta \to \xi$, and $x\to y\to z\to x$ twice and the three functions are summed up.

The conic $\mathcal{P}$ is regular if, and only if,

$$\xi \eta \zeta (\underset{{\displaystyle =:\sigma }}{\underbrace{ac\zeta \xi +bc\zeta \eta +ab\xi \eta }}){(\underset{{\displaystyle =:\tau }}{\underbrace{a\xi +b\eta +c\zeta }})}^4\ne 0.$$

(2)

The first three linear factors describe the side lines of $\Delta$, the second factor is an equation of Steiner’s circumellipse, and the third factor is an equation of the ideal line. Hence, $\mathcal{P}$ is regular if, and only if, P is not chosen on any of the components of Cycle (2), especially on the Steiner circumellipse. □

We shall call $\mathcal{P}$ the parallelian conic of P with respect to $\Delta$.

We can also describe the affine appearance of $\mathcal{P}$:

Theorem 2.

The conic $\mathcal{P}$ is a parabola if, and only if, P is chosen on the Steiner inellipse.

Proof. 

$\mathcal{P}$ is a parabola if it touches the ideal line $\omega$. We can eliminate from $\omega$’s and $\mathcal{P}$’s equation one variable, for example, z (the choice does not matter), which results (besides constant non-zero factors) in

$${\tau }^2\left(a\eta x^2+(a\xi +b\eta -c\zeta )xy+b\xi y^2\right).$$

The first factor is also constant and, since P may not be chosen on $\omega$, it is not equal to zero. Therefore, ${\tau }^2$ can be canceled. The second factor is a full square if the trilinears of P satisfy

$$\sum _{\mathrm{cyclic}}:a^2{\xi }^2-2bc\eta \zeta =0.$$

(3)

The latter is an equation of the Steiner inellipse.

On the other hand, if $\mathcal{P}$ is a parabola and touches the ideal line at some point Q, we may, without loss of generality, assume that $Q=cu:cv:-au-bv$ (with $u:v\ne 0:0$). Since Q has to lie on $\mathcal{P}$, the coordinates of P are then subject to

$${\tau }^2\left(a\eta u^2+(a\xi +b\eta -c\zeta )uv+b\xi v^2\right)=0,$$

where the first factor can be canceled, since the choice of $P\in \omega$ does not lead to a regular conic.

The contact of $\omega =a:b:c$ and $\mathcal{C}$ causes the linear dependency of $\mathrm{grad}\mathcal{P}\left(Q\right)$ and $[a,b,c]$, i.e.,

$$\begin{array}{ccc}-c\zeta u+a\xi u+b\eta u+2b\xi v& =& 0,\\ -c\zeta v+2a\eta u+a\xi v+b\eta v& =& 0,\\ ac\zeta u-bc\zeta v-a^2\xi u+ab\eta u-ab\xi v+b^2\eta v& =& 0.\end{array}$$

The system of the three latter equations is solved by $\xi :\eta :\zeta =ac{u}^2:bc{v}^2,{(au+bv)}^2$ which is a parametrization of the Steiner inellipse (3). □

Further, we can show the following:

Theorem 3.

Among the parallelian conics $\mathcal{P}$, there is only one circle. It is the first Lemoine circle.

Proof. 

The conic $\mathcal{P}$ is a circle if, and only if, it passes through the absolute points I and $J=\overline{I}$ of Euclidean geometry (also called absolute circle points, cf. [5] (p. 253)) with the trilinear coordinates

$$I=c(-bccosA+2\mathrm{i}F):b{c}^2:abccosA-2a\mathrm{i}F-b^{2}c,J=\overline{I},$$

where F denotes the area of the base triangle $\Delta$ and

$$cosA={\displaystyle \frac{b^2+c^2-a^2}{2bc}},cosB={\displaystyle \frac{c^2+a^2-b^2}{2ca}},cosC={\displaystyle \frac{a^2+b^2-c^2}{2ab}},$$

(4)

are the cosines of $\Delta$’s interior angles. By inserting the coordinates of these two points into $\mathcal{P}$’s equation, we obtain the following system of two linear and homogeneous conditions on $P=\xi :\eta :\zeta$ that define the pivot P such that $\mathcal{P}$ becomes a circle:

$$\begin{array}{c}({(b^2-c^2)}^2-a^2(b^2+c^2))\xi +ab(a^2-b^2+c^2)\eta +ac(a^2+b^2-c^2)\zeta =0,\\ (-b^2+c^2)\xi +ab\eta -ac\zeta =0.\end{array}$$

The latter system of linear equations has the unique solution $\xi :\eta :\zeta =a:b:c=X_6$. Hence, the equation of $\mathcal{P}$ simplifies to

$$\mathcal{L}:\sum _{\mathrm{cyclic}}abc(b^2+c^2)x^2-a\left(a^2(a^2+b^2+c^2)+2b^2{c}^2\right)yz=0,$$

which is centered at $X_{182}=a\left(a^2(a^2-b^2-c^2)-2b^2{c}^2\right)::$ (the midpoint of the Brocard diameter). Here, and in the following, $f(a,b,c)::$ means that the complete triple of trilinear coordinate functions of a point or a line (the center of the central line) is obtained by cyclically replacing a, b, c and $\xi$, $\eta$, $\zeta$, and in equations, x, y, and z.

Further, we find that $X_{1662}$, $X_{1663}$ (the first and second intersections of the Brocard axis $[X_3,X_6]$ with the first Lemoine circle) also lie on $\mathcal{L}$. This makes clear that $\mathcal{L}$ is the first Lemoine circle. □

The first Lemoine circle is sometimes referred to as the triplicate-ratio circle (cf. [3,6]), since its intersections with $\Delta$’s sides subdivide the edges of $\Delta$ into three segments whose lengths form the ratios $a^2:b^2:c^2$ (proper ordering provided).

Figure 2 (left) shows some parabolae as the conics on the parallelians of some points on the Steiner inellipse i. The right-hand side shows the two components of the envelope of the parabolae.

The parallelian conic $\mathcal{P}$ can also be an equilateral hyperbola:

Theorem 4.

1. 

The parallelian conic $\mathcal{P}$ is an equilateral hyperbola if, and only if, the pivot point P is chosen on the central line ${\mathcal{L}}_{647,690}=[X_{647},X_{690}]$.

2. 

The equilateral hyperbola becomes the repeated ideal line if $P=X_{690}$.

3. 

The centers of the equilateral hyperbolae gather on a triangle cubic.

Proof. 

• A conic is an equilateral hyperbola if, and only if, its ideal points correspond to orthogonal directions. The intersections of $\mathcal{P}$ and $\omega$ are given by

  $$\begin{array}{c}{A}_1=2bc\xi :c\left(c\zeta -a\xi -b\eta +\sqrt{\delta -2\sigma }\right):-b\left(c\zeta +a\xi -b\eta +\sqrt{\delta -2\sigma }\right),\\ A_2=2bc\xi :c\left(c\zeta -a\xi -b\eta -\sqrt{\delta -2\sigma }\right):-b\left(c\zeta +a\xi -b\eta -\sqrt{\delta -2\sigma }\right),\end{array}$$

  (5)

  where $\delta :=a^2{\xi }^2+b^2{\eta }^2+c^2{\zeta }^2$ and $\sigma$ as defined in (2). The asymptotes of $\mathcal{P}$ are the lines $a_1=[C_{\mathcal{P}},A_1]$ and $a_2=[C_{\mathcal{P}},A_2]$, with $C_{\mathcal{P}}$ being the center of $\mathcal{P}$ (i.e., the pole of the ideal line with regard to $\mathcal{P}$). According to [3] (p. 22), the lines $a_1$ and $a_2$ are orthogonal if, and only if, ${{\mathbf{a}}_1}^{\perp }\mathbf{G}{\mathbf{a}}_2=0$ with

  $$\mathbf{G}=\left(\begin{array}{ccc}1& -cosC& -cosB\\ -cosC& 1& -cosA\\ -cosB& -cosA& 1\end{array}\right)$$

  where ${\mathbf{a}}_1$, ${\mathbf{a}}_2$ are non-trivial multiples of either of the homogeneous triples given in (5). Note that, for $cosA$, $cosB$, and $cosC$, we set the rational expressions from (4). This yielded the following linear form:

  $$\sum _{\mathrm{cyclic}}a(a^4-b^4+4b^2{c}^2-c^4)x=0,$$

  where $\xi$, $\eta$, and $\zeta$ are replaced with x, y, and z. The latter form is the homogeneous trilinear equation of the line joining $X_{647}$ and $X_{690}$. (This line further contains the triangle centers $X_{47526}$, $X_{50551}$, and $X_{62568}$).
  On the other hand, if we choose a point on ${\mathcal{L}}_{647,690}$ for a pivot point and determine the parallelian conic, we find that $\mathcal{P}$ becomes an equilateral hyperbola.
• The second statement can be shown by inserting the trilinears of $X_{690}=bc(b^2-c^2)(2a^2-b^2-c^2)::$ into (1), or it follows from Theorem 1, since $P\in \omega$.
• Inserting a parametrization of ${\mathcal{L}}_{647,690}$ with $X_{647}=a(b^2-c^2)(-a^2+b^2+c^2)::$ into the trilinear representation of the centers of $\mathcal{P}$ yields a parametrization of a cubic curve, and an implicitization shows that the cubic is a triangle cubic (i.e., it has a cyclically symmetric trilinear equation).

□

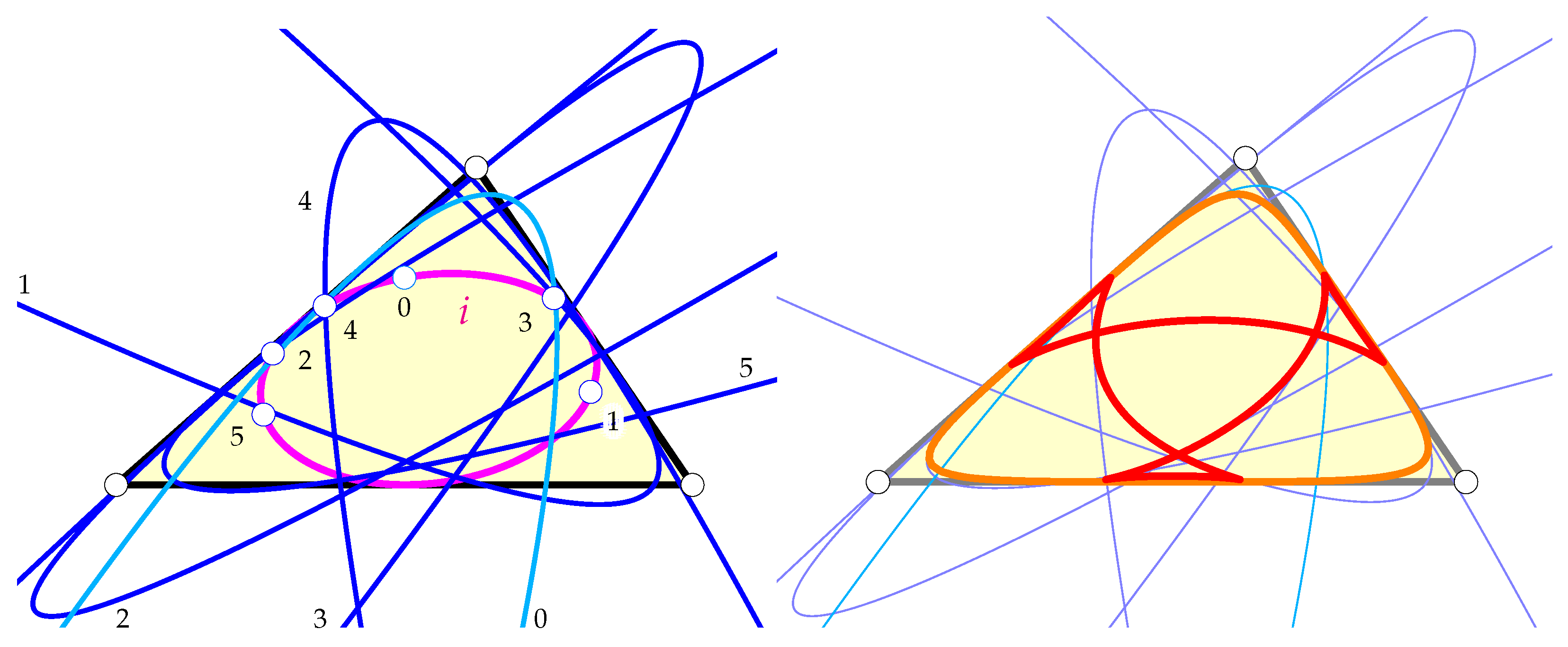
2.2. Inconic of the Parallelian Hexagon

The polygon $P_{ab}\dots P_{cb}$ has an inscribed conic $\mathcal{I}$ with the trilinear equation

$$\mathcal{I}:\sum _{\mathrm{cyclic}}{a}^2{(b\eta +c\zeta )}^2{x}^2-2bc(c\zeta +a\xi )(a\xi +b\eta )yz=0$$

(6)

which is regular, provided that P is not chosen on the cycle

$$\underset{=:\psi }{\underbrace{(c\zeta +b\eta )(c\zeta +a\xi )(a\xi +b\eta )}}=0,$$

(7)

i.e., the side lines of the anticomplementary triangle ${\Delta }_a$ of $\Delta$. Further, the conic $\mathcal{I}$ is never a parabola (since the pivot P cannot be chosen on the ideal line and on the sides of ${\Delta }_a$). The conic $\mathcal{I}$ shall be called the parallelian inconic with respect to $\Delta$.

The center $C_{\mathcal{I}}$ of $\mathcal{I}$ allows for the trilinear representation

$$C_{\mathcal{I}}=bc(2a\xi +b\eta +c\zeta )::$$

(8)

and is a triangle center if the pivot P is a center. The mapping $\pi :P\mapsto C_{\mathcal{I}}$ is linear, i.e., a collineation. Since $X_2=bc::$ is a fixed point of $\pi$ and $\omega$ is an axis (not just a fixed line), $\pi$ is a central similarity. All lines through $X_2$ are fixed lines, which is especially true for the Euler line. Further, $\pi$ sends $X_4$ to $X_5$ (orthocenter ↦ nine-point center). This yields the similarity factor as the characteristic cross-ratio f of $\pi$ (cf. [5] (p. 238)), which is constant and equal to ${\displaystyle \frac{1}{4}}$ (and thus, independent of $\Delta$ and P).

As a consequence of the existence of the parallelian conics $\mathcal{P}$ and the parallelian inconics $\mathcal{I}$, we can state the following:

Theorem 5.

1. 

The pair $(\mathcal{P},\mathcal{I})$ of conics allows for a porism of hexagons.

2. 

The pair $(\mathcal{P},\mathcal{I})$ spans an exponential pencil of conics in which any pair of subsequent conics allows for a hexagonal porism.

Proof. 

• The existence of a single hexagon interscribed between $\mathcal{P}$ and $\mathcal{I}$ guarantees the existence of the poristic family (cf. [5,7]). Here, one interscribed hexagon is already known: $P_{cb}{P}_{ca}{P}_{ac}{P}_{ab}{P}_{ba}{P}_{bc}$.
• This is clear from the definition of exponential pencils (cf. [8]).

□

Similar to Theorem 3, we can show the following:

Theorem 6.

The parallelian inconic is a circle if the pivot point P equals $X_{145}$ (the anticomplement of the Nagel point) or one of the following three points:

$$\begin{array}{c}{L}_1=-bc(3a+b+c):\phantom{-}ca(3b+a-c):\phantom{-}ab(3c+a-b),\\ L_2=\phantom{-}bc(3a+b-c):-ca(3b+a+c):\phantom{-}ab(3c-a+b),\\ L_3=\phantom{-}bc(3a-b+c):\phantom{-}ca(3b-a+c):-ab(3c+a+b).\end{array}$$

The circular parallelian inconics are the incircle if $P=X_{145}$ and the three excircles if P coincides with one of the points $L_i$.

Proof. 

$\mathcal{I}$ is a circle if it passes through the absolute points of Euclidean geometry. We proceeded in the same way as in the proof of Theorem 3 and obtained a system of two quadratic equations in $\xi :\eta :\zeta$ (equations of conics), which was solved precisely by $X_{145}=bc(3a+b+c)::$ and the three above-given points.

The last part of the theorem is shown by simply inserting the trilinears of $X_{145}$ and $L_i$ into Equation (6) of $\mathcal{I}$. □

3. Tangent Triangles and Hexagons

The tangents of $\mathcal{P}$ at the parallelians form a hexagon $H_1=P_A{T}_C{P}_B{T}_A{P}_C{T}_B$, where

$$\begin{array}{c}{P}_A:=t_{P_{ab}}\cap t_{P_{ac}},P_B:=t_{P_{ba}}\cap t_{P_{bc}},P_C:=t_{P_{ca}}\cap t_{P_{cb}},\\ T_A:=t_{P_{bc}}\cap t_{P_{cb}},T_B:=t_{P_{ca}}\cap t_{P_{ac}},T_C:=t_{P_{ab}}\cap t_{P_{ba}}.\end{array}$$

(9)

These six points can be arranged in two triples forming two triangles ${\Delta }_P:=P_A{P}_B{P}_C$ and ${\Delta }_T:=T_A{T}_B{T}_C$, which are perspective to $\Delta$ with the respective perspectors $P_P$ and $P_T$. The perspectors have the following trilinear representations:

$$\begin{array}{c}{P}_P=\xi (2ab\xi \eta +2bc\eta \zeta +ca\zeta \xi )(ab\xi \eta +2bc\eta \zeta +2ca\zeta \xi )::,\\ P_T=a{\xi }^2:b{\eta }^2:c{\zeta }^2.\end{array}$$

(10)

The respective perspectrices are

$$\begin{array}{c}{p}_P=\eta \zeta (2ac\zeta \xi +bc\eta \zeta +ab\xi \eta +b^2{\eta }^2)(2ab\xi \eta +c^2{\zeta }^2+ca\zeta \xi +bc\eta \zeta )::,\\ p_T=a:b:c.\end{array}$$

Note that the latter perspectrix equals the ideal line. Since the perspector of $\Delta$ and ${\Delta }_T$ is a proper point, these triangles are related in a central similarity. The similarity factor equals

$$s=2\sigma {\omega }^{-2}$$

and depends on the pivot point P. Again, we see that points on the Steiner circumellipse and on the ideal line are to be excluded, since the coordinates of the first annihilate the numerator while the coordinates of the latter annihilate the denominator of s, which leads in both cases to singular affine mappings.

Figure 3 shows the two triangles tangent to $\mathcal{P}$ and the respective perspectors relating ${\Delta }_P$ and ${\Delta }_T$ to $\Delta$.

Finally, we note that the triangles ${\Delta }_P$ and ${\Delta }_T$ are perspective with respect to the point P while the corresponding trilaterals are perspective to the line

$$\eta \zeta (b\eta +c\zeta ):\zeta \xi (c\zeta +a\xi ):\xi \eta (a\xi +b\eta ).$$

(11)

We can show that all six vertices (9) of $H_1$ lie on a single conic $\mathcal{T}$ with the trilinear equation

$$\begin{array}{c}\mathcal{T}:{\displaystyle \sum _{\mathrm{cyclic}}}abc{\eta }^2{\zeta }^2(b\eta +c\zeta )(3a\xi +b\eta +c\zeta )x^2=\\ ={\displaystyle \sum _{\mathrm{cyclic}}}a{\xi }^2\left(4b^2{c}^2{\eta }^2{\zeta }^2+{\displaystyle \sum _{\mathrm{cyclic}}}\left(a^{3}b{\xi }^3\eta +c{a}^3\zeta {\xi }^3+2a^2{b}^2{\xi }^2{\eta }^2+6a^{2}bc{\xi }^2\eta \zeta \right)\right)yz\end{array}$$

The conic $\mathcal{T}$ is regular if, and only if,

$${\left(\xi \eta \zeta \right)}^2\psi {\sigma }^2{\tau }^5\ne 0,$$

i.e., as long as P is not chosen (i) on any side of $\Delta$, (ii) on any side of ${\Delta }_a$ (cf. (7)), (iii) on the ideal line, or (iv) on the Steiner circumellipse.

Since there exists the hexagon $H_1$ interscribed between $\mathcal{T}$ and $\mathcal{P}$, and further, since there exists the hexagon $H_2:=P_{cb}{P}_{ca}{P}_{ac}{P}_{ab}{P}_{ba}{P}_{bc}$ interscribed between $\mathcal{P}$ and $\mathcal{I}$, we can state the following:

Theorem 7.

1. 

Each of the pairs of conics $(\mathcal{T},\mathcal{P})$ and $(\mathcal{P},\mathcal{I})$ allows for a poristic family of interscribed hexagons.

2. 

Both pairs of conics span the same exponential pencil of conics, and therefore, they define the same one-parameter family of nested hexagonal porisms.

Proof. 

• The first part of the theorem is clear, simply because of the existence of interscribed hexagons.
• In order to verify that the coefficient matrices $\mathbf{T}$, $\mathbf{P}$, and $\mathbf{I}$ of the respective conics satisfy $\mathbf{T}=\lambda \mathbf{P}{\mathbf{I}}^{-1}\mathbf{P}$ (which is the representation of the coefficient matrix of the conic following $\mathcal{I}$ and $\mathcal{P}$ in the (discrete) exponential pencil), one can extract the coefficient matrices from the equations. The scalar $\lambda$ depends on a, b, and c (i.e., the triangle) and the pivot point P solely and turns out to be $\lambda ={\displaystyle \frac{\tau }{4abc\psi }}$. On the other hand, by construction, $\mathcal{T}$ is the polar image of $\mathcal{I}$ with respect to $\mathcal{P}$, which is expressed algebraically by this matrix equation.

Figure 4 shows the three conics mentioned in Theorem 7 together with the hexagons of chords and tangents. □

The tangents of $\mathcal{P}$ give rise to further polygons circumscribed to the parallelian conic $\mathcal{P}$, illustrated in Figure 5. The intersections

$$\begin{array}{c}{U}_1:=t_{P_{ba}}\cap t_{P_{ac}},U_2:=t_{P_{ac}}\cap t_{P_{cb}},U_3:=t_{P_{cb}}\cap t_{P_{ab}},\\ V_1:=t_{P_{ca}}\cap t_{P_{ab}},V_2:=t_{P_{ca}}\cap t_{P_{bc}},V_3:=t_{P_{bc}}\cap t_{P_{ab}}\end{array}$$

are the vertices of two triangles ${\Delta }_U=U_1{U}_2{U}_3$ and ${\Delta }_V=V_1{V}_2{V}_3$ tangent to $\mathcal{P}$. We note that ${\Delta }_U$ and ${\Delta }_V$ are part of a Desargues figure that is completed by the perspector P and the perspectrix (11), which is also the perspectrix of ${\Delta }_P$ and ${\Delta }_T$. Since P serves as the perspector in some of the pairs of triangles, we see a collection of nested Desargues figures here, which are more special than the ones described in [9].

Now, we can prove the following:

Theorem 8.

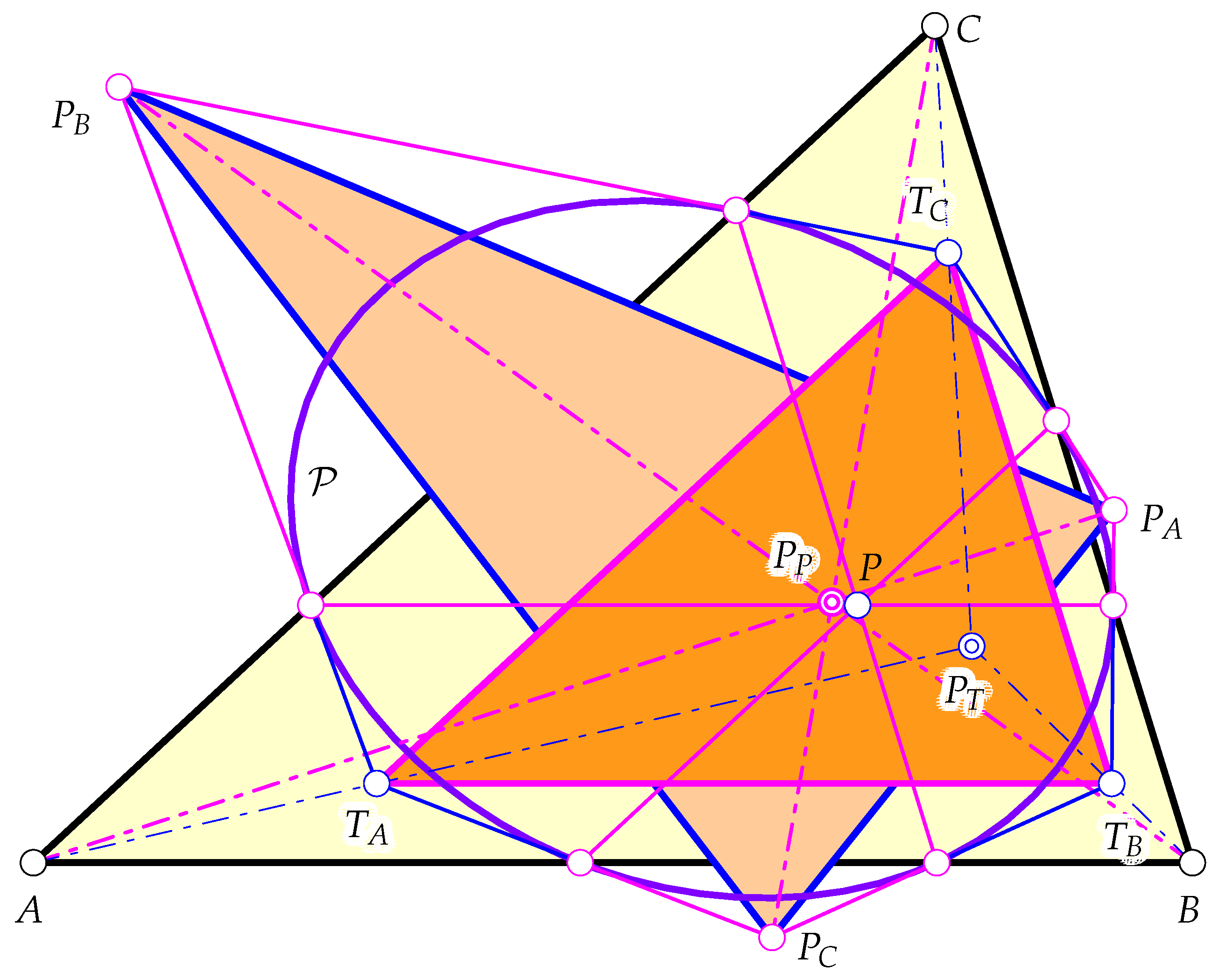
1. 

The vertices of ${\Delta }_U$ and ${\Delta }_V$ are located on a single conic $\mathcal{D}$ and the pair $(\mathcal{D},\mathcal{P})$ of conics allows for a triangle porism.

2. 

The pair $(\mathcal{D},\mathcal{P})$ allows for a hexagonal porism.

3. 

The pair $(\mathcal{D},\mathcal{P})$ spans an exponential pencil of conics, and thus, they define a one-parameter family of nested hexagonal porisms.

Proof. 

• The vertices of ${\Delta }_U$ and ${\Delta }_V$ are

  $$\begin{array}{c}{U}_1=-a{\xi }^2:b{\eta }^2:\zeta (2b\eta +c\zeta ),U_2=a{\xi }^2:\eta (2a\xi +b\eta ):-c{\zeta }^2,U_3=\xi (a\xi +2c\zeta ):-b{\eta }^2:c{\zeta }^2,\\ V_1=-a{\xi }^2:\eta (b\eta +2c\zeta ):c{\zeta }^2,V_2=\xi (a\xi +2b\eta ):b{\eta }^2:-c{\zeta }^2,V_3=a{\xi }^2:-b{\eta }^2:\zeta (c\zeta +2a\xi ),\end{array}$$

  and the conic $\mathcal{D}$ on these six points has the trilinear equation

  $$\begin{array}{c}\mathcal{D}:{\displaystyle \sum _{\mathrm{cyclic}}}{a}^{2}bc\xi {\eta }^2{\zeta }^2(b\eta +c\zeta )x^2=\\ ={\displaystyle \sum _{\mathrm{cyclic}}}\left(a{\xi }^2\left({\displaystyle \sum _{\mathrm{cyclic}}}4a^{2}bc{\xi }^2\eta \zeta +bc\eta \zeta {(b\eta +c\zeta )}^2\right)-2b^2{c}^2{\eta }^2{\zeta }^2\right)yz.\end{array}$$
  The existence of at least one triangle tangent to $\mathcal{P}$ (either ${\Delta }_U$ or ${\Delta }_V$) and inscribed into $\mathcal{D}$ is sufficient for the existence of a triangle porism.
• The second part of the theorem is shown with the Cayley criterion for pairs of conics as given in [5] (p. 432).
• The last part of the proof can be deduced in the same way as the proof of Theorem 7.

□

Using the Cayley criterion for porisms [5] (p. 432), we can show that the pair $(\mathcal{P},\mathcal{D})$ allows for a poristic family of quadrangles if, and only if, the pivot point P is chosen either on the Steiner circumellipse or on the triangle cubic

$${\mathcal{K}}_4:2abcxyz+\sum _{\mathrm{cyclic}}{a}^2{x}^2(bx+cz)=0$$

which houses the triangle centers $X_i$ with the Kimberling indices

$$\begin{array}{c}i=\{4169,4859,30720,47790,56081,64480,\\ 64481,64487,64488,64608,64609,64744\}.\end{array}$$

The cubic ${\mathcal{K}}_4$ does not show up in B. Gibert’s list [10].

Concerning the hexagon $H_3:=U_1{V}_2{U}_3{V}_1{U}_2{V}_3$ built by the vertices of ${\Delta }_U$ and ${\Delta }_V$, we can show the following:

Theorem 9.

1. 

The hexagon $H_3$ is tangent to a circumconic $\mathcal{J}$ of Δ.

2. 

The pair of conics $(\mathcal{D},\mathcal{J})$ allows for a porism of hexagons.

3. 

The pairs of conics $(\mathcal{J},\mathcal{I})$ allows for a porism of triangles.

4. 

The pairs of conics from 2. and 3. define chains of nested triangle and hexagon porisms.

Proof. 

• It is easily verified that the sides of the hexagon $H_2$ touch the conic given by the equation

  $$\mathcal{J}:\sum _{\mathrm{cyclic}}a{\xi }^{2}yz=0.$$

  (12)
  It is obvious that $\mathcal{J}$ passes through the vertices of $\Delta$.
• This is clear, since $H_2$ is a hexagon interscribed between the respective conics.
• Since $\mathcal{J}$ is circumscribed to $\Delta$ and $\mathcal{I}$ is inscribed into $\Delta$, there exists a (smooth) one-parameter family of such triangles.
• We use the arguments from the proof of Theorem 7.

□

The pair $(\mathcal{J},\mathcal{I})$ allows for a quadrangle porism if P is chosen on the side lines of the anticomplementary triangle ${\Delta }_a$ of $\Delta$. The same holds true for heptagons and octagons. Poristic families of pentagons will never occur between $\mathcal{J}$ and $\mathcal{I}$ (since P cannot be chosen on the side lines of $\Delta$). The existence of a poristic family of hexagons is guaranteed, since the star-shaped hexagon $U_1{U}_2{U}_3{V}_1{V}_2{V}_3$ (the union of ${\Delta }_U$ and ${\Delta }_V$) is an interscribed (degenerate) hexagon.

4. Some Algebraic Transformations

In the previous sections, five conics were discovered: the parallelian conic $\mathcal{P}$, the parallelian inconic $\mathcal{I}$, the parallelian tangent conic $\mathcal{T}$, the conic $\mathcal{D}$ on the triangle vertices, and the circumconic (of $\Delta$) $\mathcal{J}$, which is the inconic of $H_3$. Any two of them have the point P for a common pole and the line $p=\eta \zeta (b\eta +c\zeta )::$ for a common polar line. Surprisingly, not all triples of conics built from these five are contained in the same pencil. This is only the case for $\mathcal{D}$, $\mathcal{P}$, and $\mathcal{J}$, since the coefficient matrices $\mathbf{D}$, $\mathbf{P}$, $\mathbf{J}$ of the respective equations fulfill $\mathbf{D}-abc\xi \eta \zeta \mathbf{P}=\sigma {\tau }^2\mathbf{J}$.

We also met a collection of perspectors joining triangles in Desargues configurations. In any case, these perspectors depend on the pivot point P (and, of course, on the base triangle $\Delta$). The same holds true for the centers of all conics we have found so far. The dependencies are algebraic, and since we used homogeneous (trilinear) coordinates, the coordinate representations are polynomial in the coordinates $\xi$, $\eta$, $\zeta$ of P. In this section, we tried to study the action of the thus-induced algebraic transformations, starting with the perspectors and then changing to the centers. In this way, we will be able to establish relations between well- and lesser-known triangle centers from the inflationarily growing Encyclopedia of Triangle Centers [4]. Recently, algebraic transformations of higher degrees other than Cremona transformations (as explained in [5]) were the subject of study in [11].

4.1. Perspectors of Triangles

The perspectors $P_P$ and $P_T$ given in (10) join the base triangle $\Delta$ with the triangles ${\Delta }_P$ and ${\Delta }_T$. The homogeneous trilinear coordinates of the perspector $P_P$ are

$$\begin{array}{c}{P}_P=\xi (2ab\xi \eta +2bc\eta \zeta +ca\zeta \xi )(ab\xi \eta +2bc\eta \zeta +2ca\zeta \xi )::,\\ P_T=a{\xi }^2:b{\eta }^2:c{\zeta }^2.\end{array}$$

The mapping $P\mapsto P_P$ is quintic and not a Cremona transformation. It is undefined for points on $\Delta$’s sides. However, it maps the triangle centers $X_i$ to $X_j$ according to the list given in

Table 1. Triangle centers related by the mapping $P\mapsto P_P$.

i	1	2	3	4	6	7	98	190	523
j	10013	2	64842	8801	10014	57826	4590	1016	36955

.

Unfortunately, the monoidal quadratic mapping $P\mapsto P_T$ is also not invertible and the side lines of $\Delta$ form the exceptional set of the mapping. Nevertheless, it relates some triangle centers $X_i$ and $X_j$, as listed in

Table 2. Triangle centers related by the quintic mapping $P\mapsto P_T$.

i	1	2	3	4	5	6	7	8	9
j	6	2	577	393	36412	32	279	346	220
i	10	13	14	19	20	21	22–29	30	31
j	594	11080	11085	2207	36413	7054	36414–36421	3163	1501
i	32	36	37	38	39	42	43	44	49
j	9233	52059	1500	8041	59994	7109	53145	1017	14585
i	55	56	57	63	69	74	75	76	81
j	14827	52410	1407	394	3926	40353	76	1502	593

.

4.2. Centers of Conics

The centers $C_{\mathcal{P}}$ of the parallelian conics $\mathcal{P}$ given by (1) are

$$C_{\mathcal{P}}=\xi (a^2{\xi }^2-ca\zeta \xi -2bc\eta \zeta -ab\xi \eta )::$$

(13)

Obviously, the mapping $P\mapsto C_{\mathcal{P}}$ is a cubic transformation that is not defined on the sides of $\Delta$. The ideal line $\omega$ is mapped onto $X_2$. It sends the following triangle centers $X_i$ to centers $X_j$ with Kimberling indices i and j, as listed in

Table 3. Some triangle centers as pivots of the parallelian conic yield some other triangle centers as centers of the respective parallelian conic.

i	1	2	3	4	5	6	7	8	9	10
j	1001	2	182	10002	10003	182	10004	10005	1001	3842
i	11	13	14	20	25	36	38	54	55	68
j	10006	10217	10218	47381	42820	3842	10007	42834	42828	10008

:

The centers $C_{\mathcal{I}}$ of the parallelian inconics $\mathcal{I}$ are given in (8), and the mapping $P\mapsto C_{\mathcal{I}}$ is already described in Section 2.2. However, this mapping relates the triangle centers $X_i$ and $X_j$, as listed in

Table 4. Triangle centers $X_j$ as centers of parallelian inconics with pivot points $X_i$.

i	1	2	3	4	5	6	7	8
j	1125	2	140	5	3628	3589	142	59612
i	9	10	11–18	19	20	21	22	23
j	6666	3634	6667–6674	40530	3	6675	6676	468
i	24	25	26	27	28	29	30	31
j	16238	6677	10020	6678	52259	52260	30	6679
i	32	33–35		36	37	38–40	41	42–44
j	6680	58402–58404		6681	4698	6682–6684	31248	6685–6687
i	45	46	47	48	49	50	51	52
j	31285	58405	?	58406	58407	?	6688	5462
i	53	54–58		59	60	61	62	63
j	58408	6689–6693		40531	?	6694	6695	5745
i	64	65	66	67	68	69	70	71
j	6696	3812	6697	6698	5449	141	58409	58410
i	72	73	74	75	76	77	78–81
j	5044	58411	6699	3739	3934	58412	6700–6703
i	82	83–86		87	88–90		91	92
j	5044	6704–6707		?	58413–58415		?	6708
i	93	94	95	96	97	98	99	100
j	?	58416	6709	?	58417	6036	620	3035

.

The centers $C_{\mathcal{J}}$ of the conics $\mathcal{J}$ in (12) are given by the trilinear representation

$$C_{\mathcal{J}}=a{\xi }^2(a^2{\xi }^2-b^2{\eta }^2-c^2{\zeta }^2)::$$

which yields a quartic mapping $P\mapsto C_{\mathcal{J}}$ that is not birational. The ideal line is mapped onto itself pointwise. Nevertheless, a few triangle centers $X_i$ serving as pivot points P seem to be related to some other known triangle centers $X_j$ (as centers of the respective conics $\mathcal{J}$) by this mapping, as can be seen in

Table 5. Triangle centers $X_j$ occurring as centers of conics $\mathcal{J}$ corresponding to pivots $P=X_i$.

i	1	2	3	4	5	6	7	8
j	3	2	1147	6523	6663	206	17113	6552
i	9	10	11	19	31	32	37	39
j	6600	4075	64440	15259	40368	40369	40607	52042
i	57	63	65	69	75
j	6609	6503	15267	6338	6374

.

The mapping $P\mapsto C_{\mathcal{J}}$ fixes all points on the ideal line.

5. Conclusions and Future Work

The fact that the six parallelians lie on a single conic seems to be known, though proofs of this fact are not to be found in the literature or in online sources. To the best of our knowledge, it was not previously known that the hexagon built by the parallelians has an inconic. Therefore, it was surprising to see that a poristic family of hexagons interscribed between the parallelian conic $\mathcal{P}$ and the parallelian inconic $\mathcal{I}$ exists in any case. It is imperative to ask for projective generalizations, i.e., replace the ideal line with some proper line and repeat the construction. However, this is a subject for a future paper.

In this paper, we did not only find a single (chain of) hexagon porism(s). Since the tangent hexagon of $\mathcal{P}$ can also be used to define two triangles ${\Delta }_U$ and ${\Delta }_V$, not only tangent to $\mathcal{P}$, but also with vertices on a further conic $\mathcal{D}$, there exists a second and independent (chain of) triangle porism(s). Moreover, a certain hexagon defined by the triangle vertices has an inconic $\mathcal{J}$. Here, we observed some kind of bifurcation in the net of porisms. The hexagon porisms between the pair of conics $(\mathcal{T},\mathcal{P})$ and the pair of conics $(\mathcal{J},\mathcal{P})$ do not depend on each other and do not belong to the same chain of porisms.

The construction of porisms from the parallelian conics works well if the ideal line is replaced with any other line that is not incident with any vertex of $\Delta$. At the moment, it is not clear whether a suitable choice of the ideal line allows for universal porisms, i.e., such porisms that allow for rational (and then polynomial) parametrizations. These porisms would then be well-defined in projective (and affine) planes of various orders and characteristics (cf. [12]). The search for universal porisms among the parallelian porisms will be postponed to a future article.

Finally, we would like to address another open problem. We have not discussed whether it is possible to choose the pivot point such that the porisms in question can become porisms of n-gons other than triangles and hexagons. The loci of pivot points can be derived from the Cayley criterion and result in algebraic curves of degrees three and six. A discussion of these loci and the resulting porisms is by no means straightforward, since these cubics and sextics are elliptic.