Transient Waves in Linear Dispersive Media with Dissipation: An Approach Based on the Steepest Descent Path
Abstract
1. Introduction
2. The Klein–Gordon Equation with Dissipation
- If ,
- If ,where denotes the Heaviside theta function, and and are the Bessel and modified Bessel function of first order, respectively ([6], Chaps. 49&52).
- If ,
- If ,where now and are the Bessel and modified Bessel function of zeroth order, respectively. In particular case of the telegraph equation, i.e., , we get , and the corresponding response was found by Lee–Kanter for the Maxwell model of linear viscoelasticity [7].
3. The Determination of the Steepest Descent Path
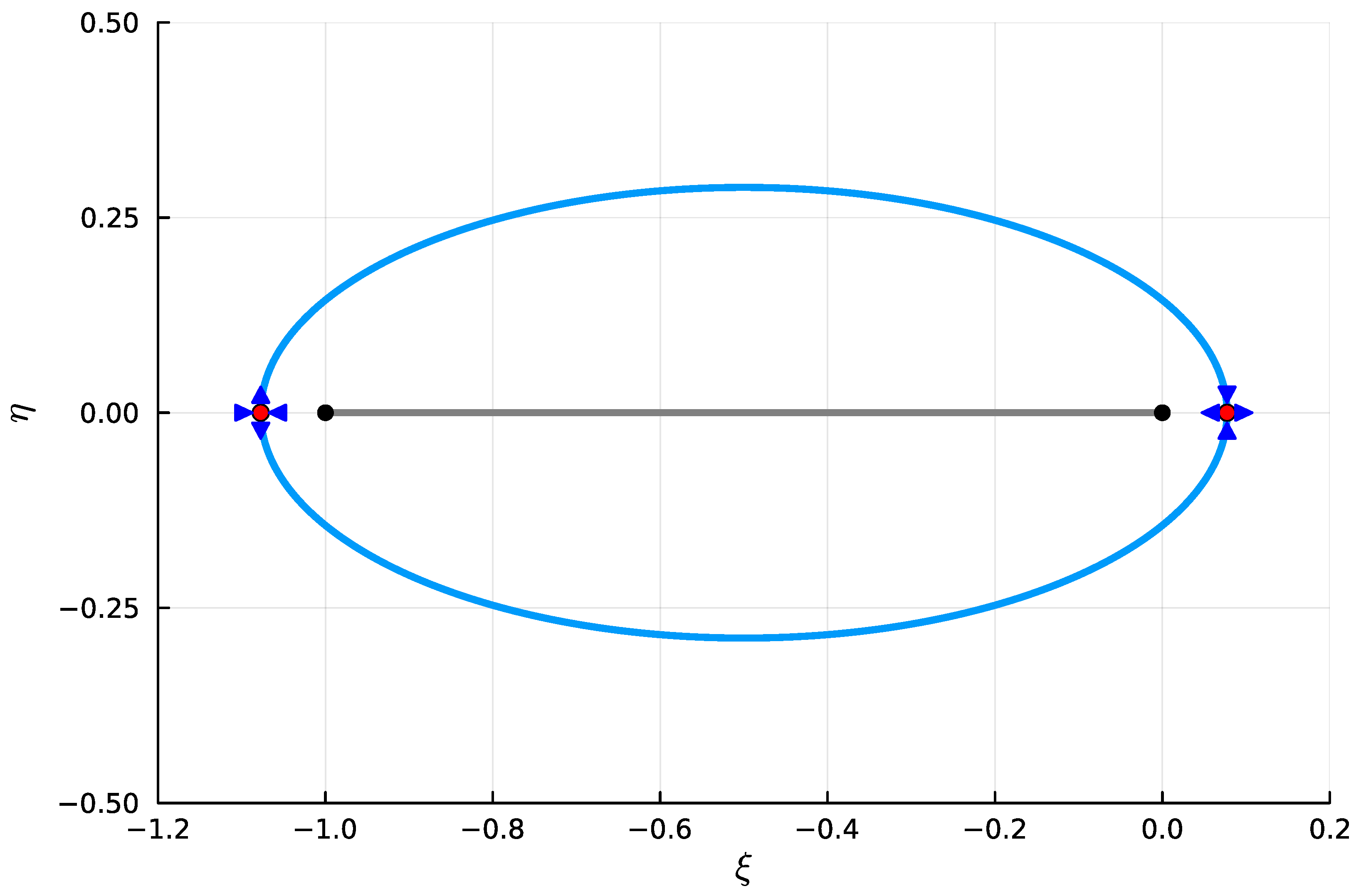
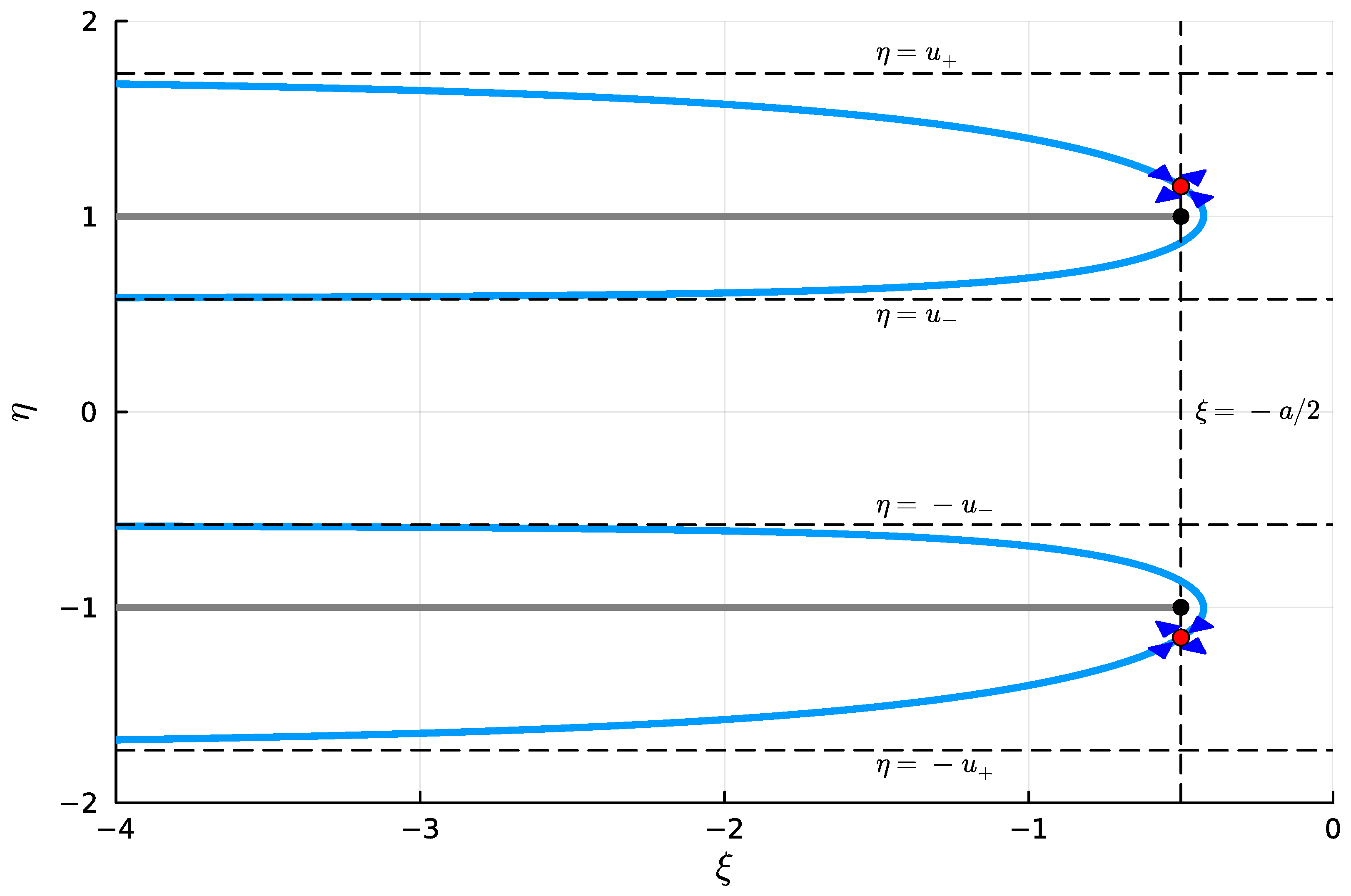
3.1. Case
3.2. Case
4. Numerical Evaluation of
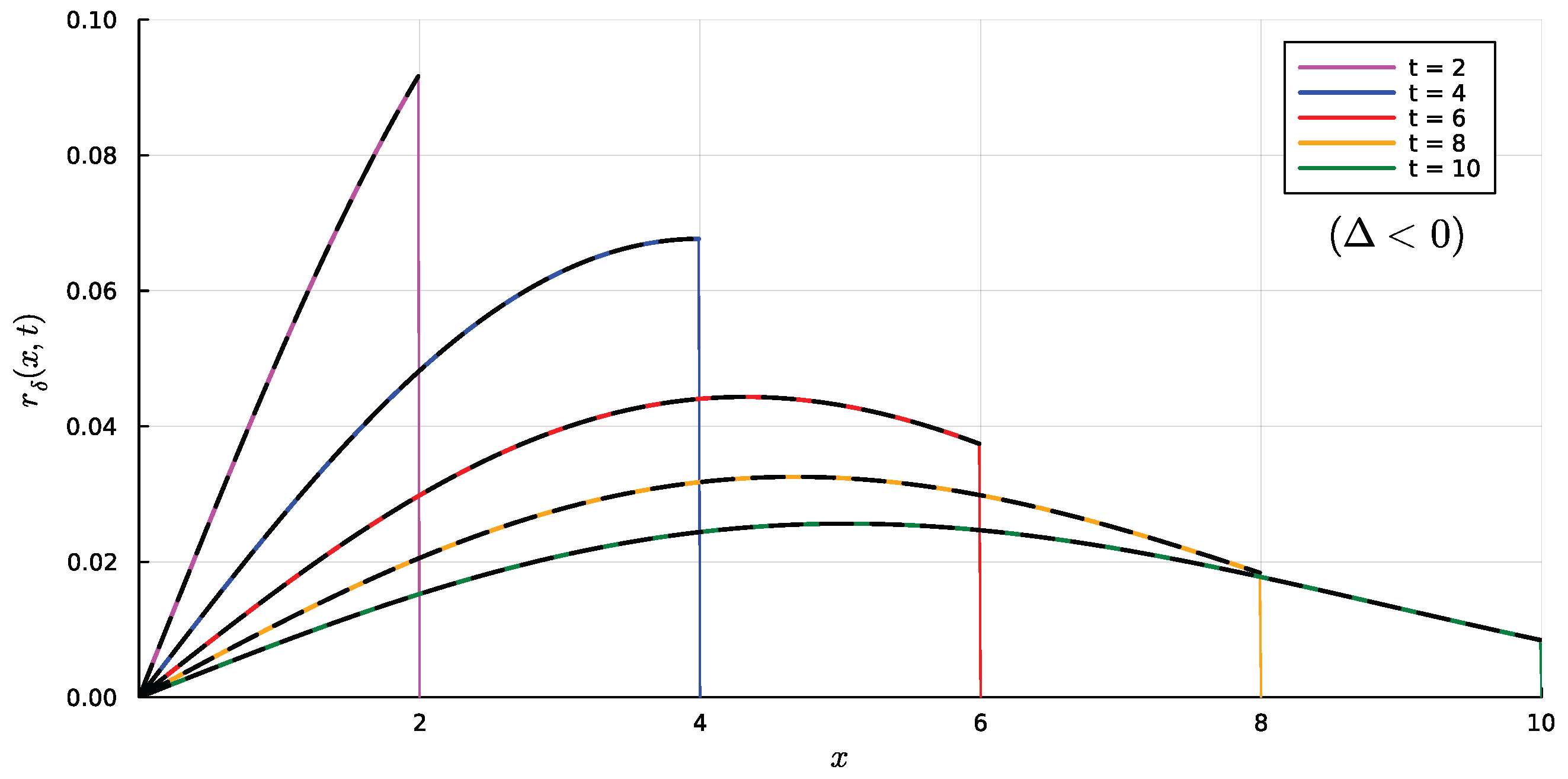
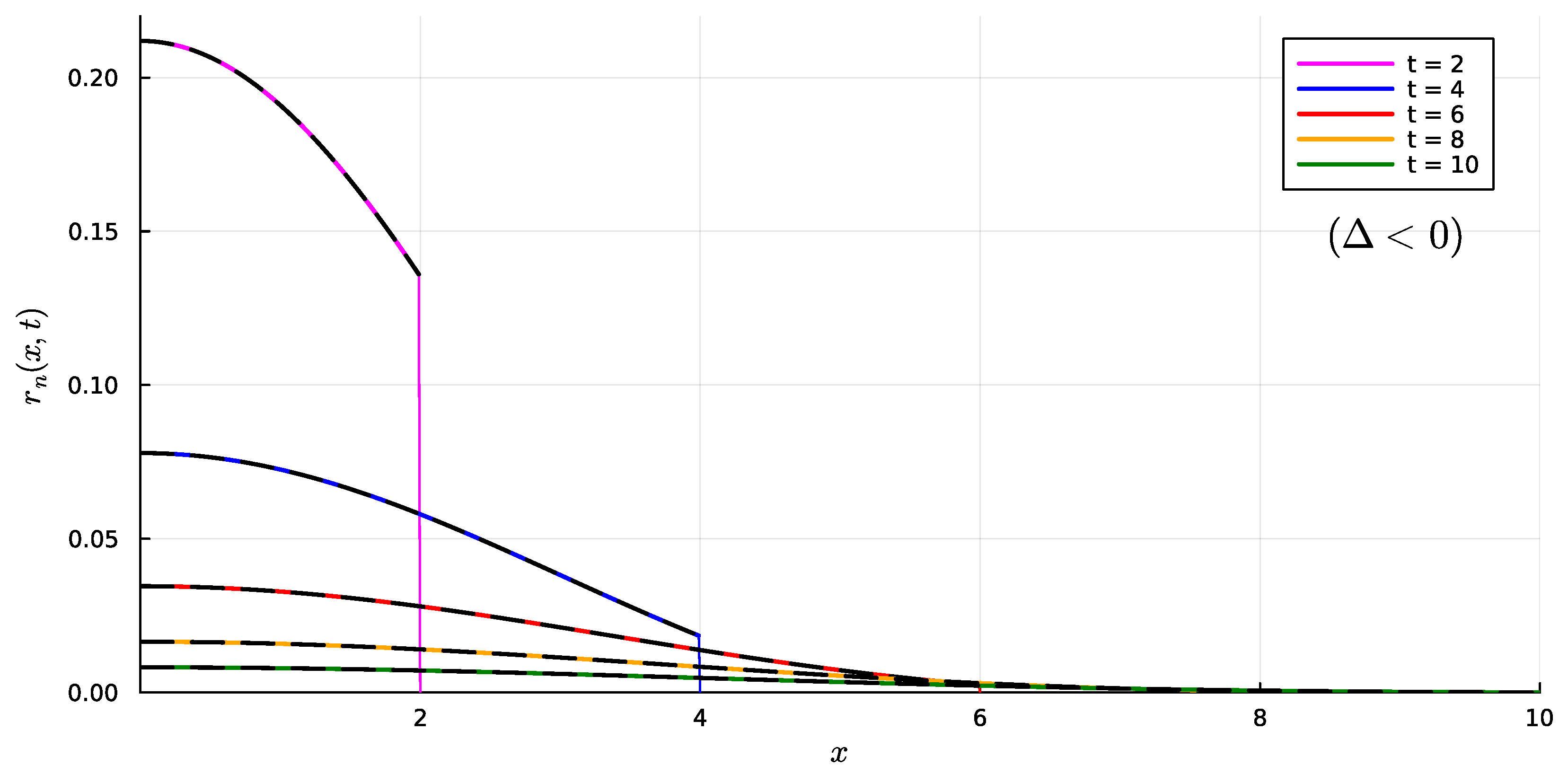
4.1. Case
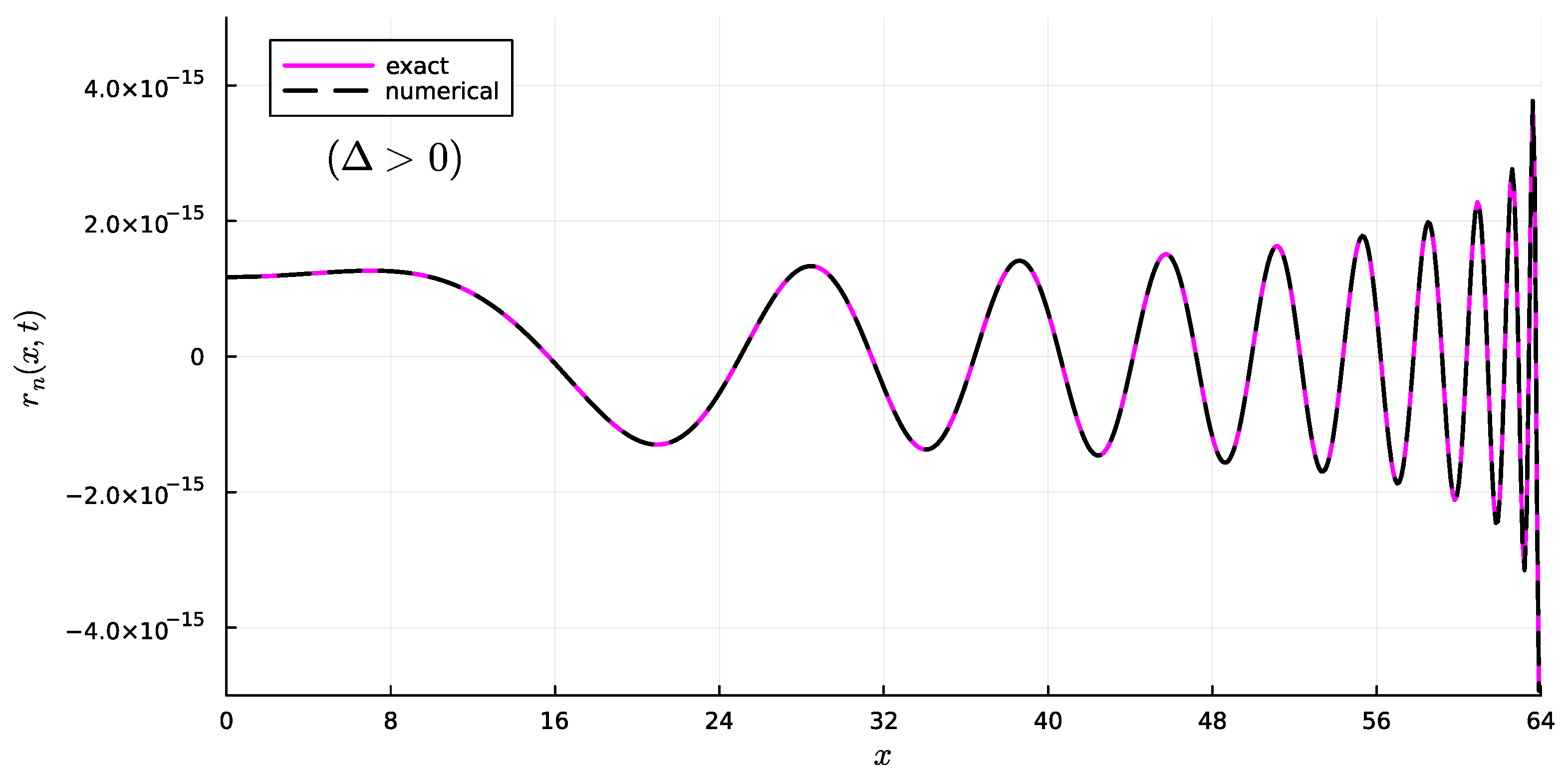
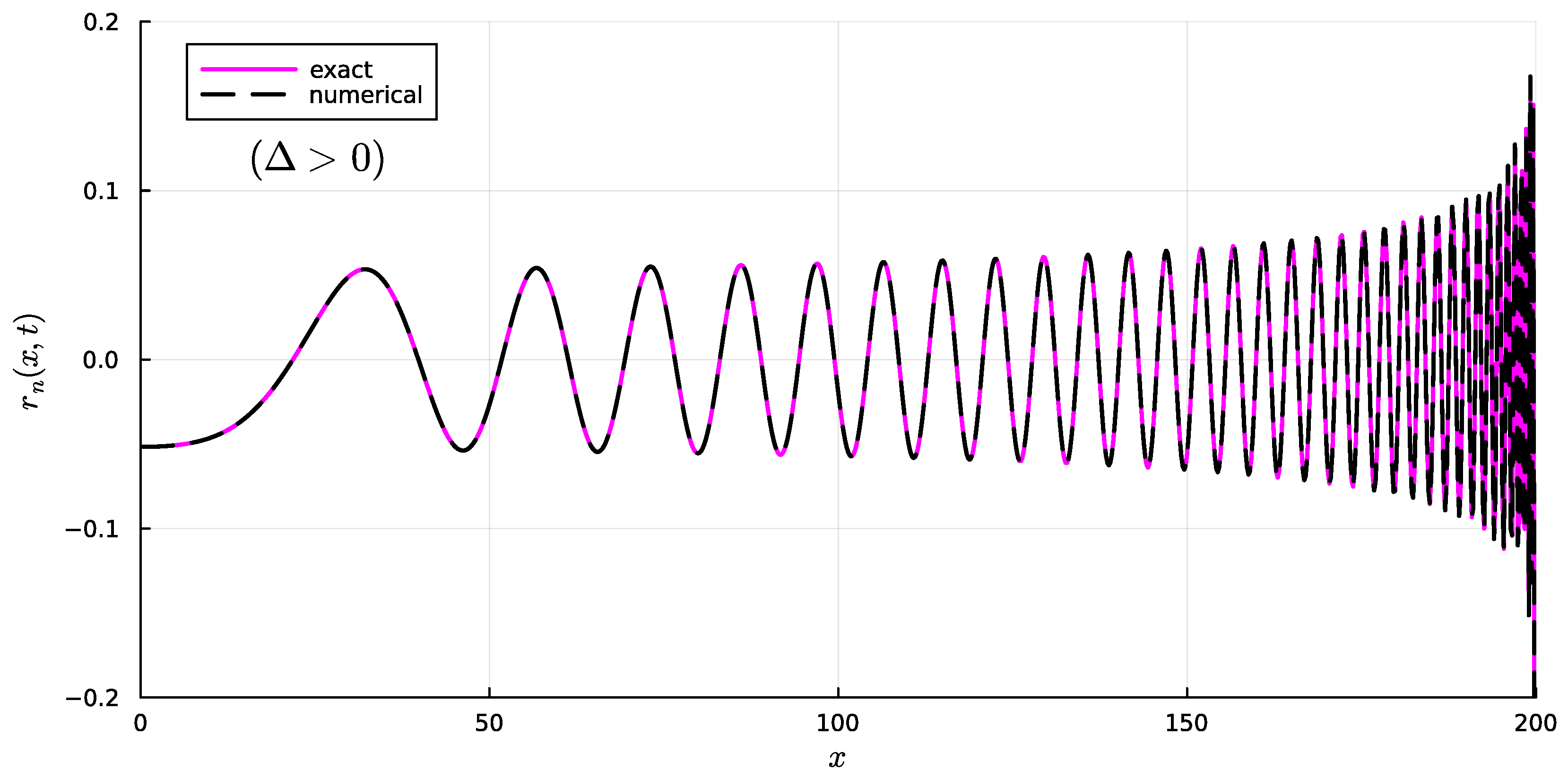
4.2. Case
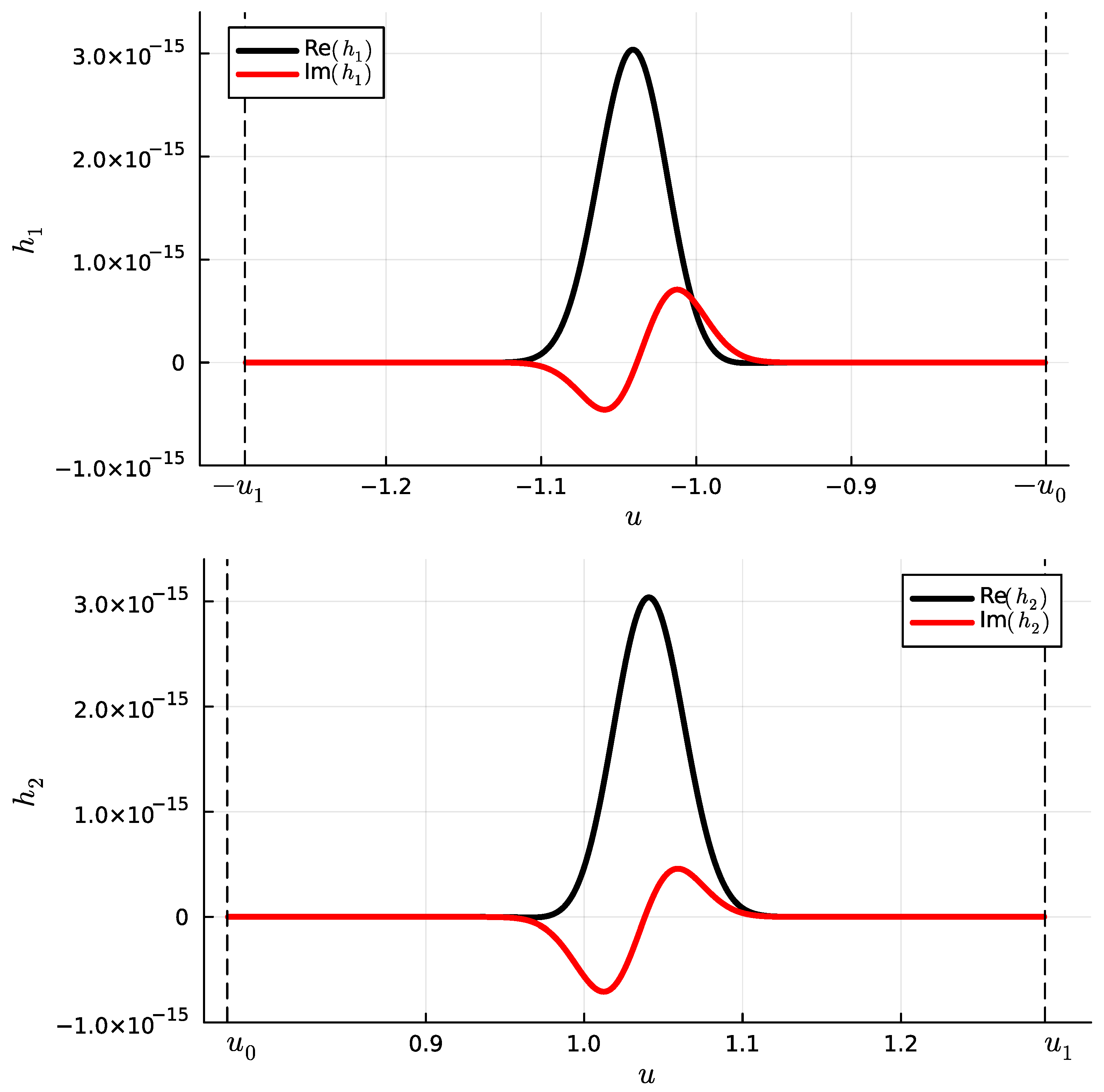
4.3. Useful Property of the Integrals for
5. Numerical Evaluation of
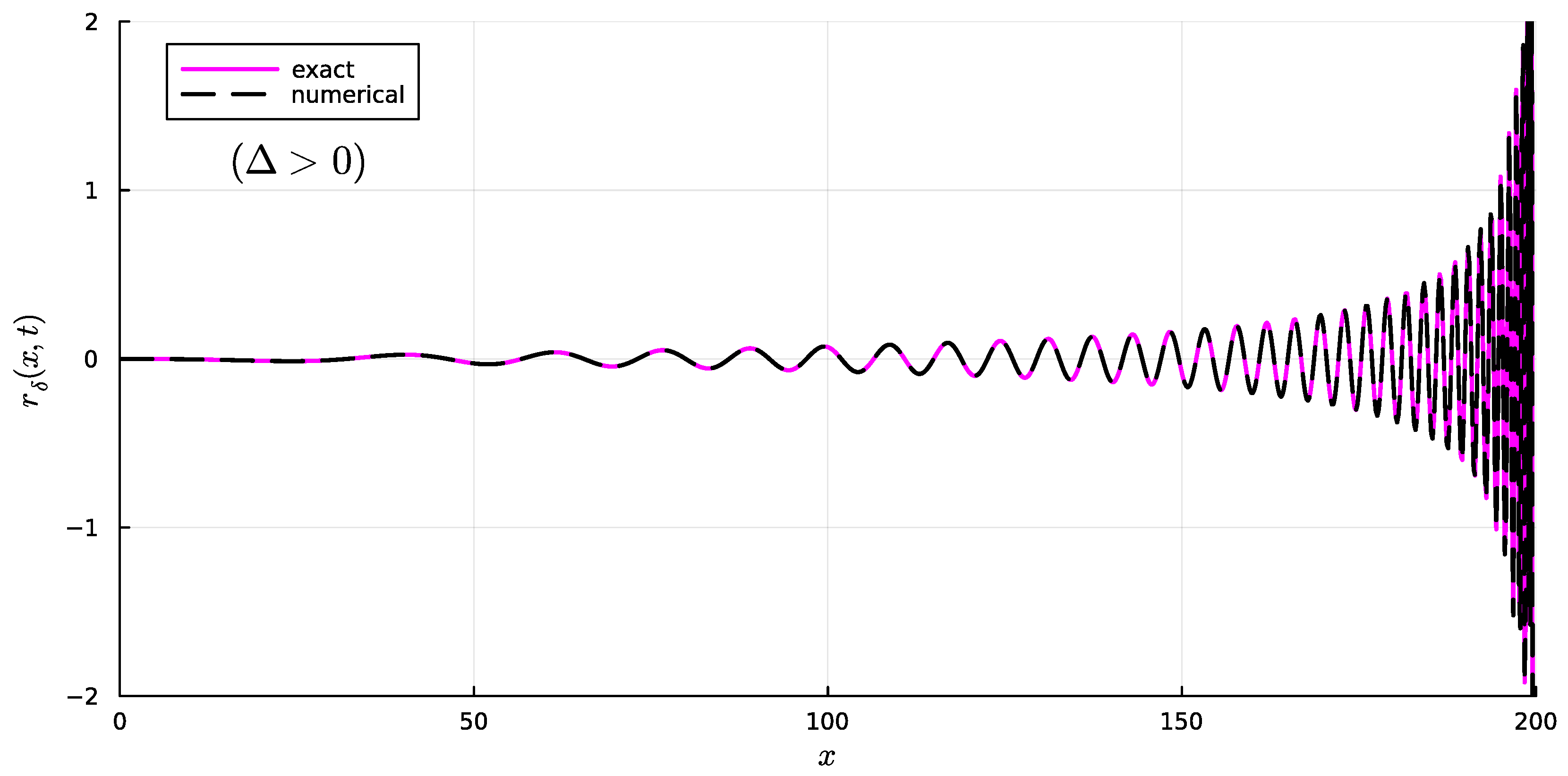
5.1. Case
5.2. Case
5.3. Useful Property of the Integrals for
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity: An Introduction to Mathematical Models, 2nd ed.; World Scientific: Singapore, 2022; [1st edition 2010]. [Google Scholar]
- Brillouin, L. Wave Propagation and Group Velocity; Academic Press: New York, NY, USA, 1960. [Google Scholar]
- Mainardi, F.; Vitali, G. Applications of the Method of Steepest Descents in Wave-Propagation Problems. In Asymptotic and Computational Analysis; Wong, R., Ed.; Marcel Dekker Inc.: New York, NY, USA, 1990; pp. 639–651. [Google Scholar]
- Mainardi, F. Signal velocity for transient waves in linear dissipative media. Wave Motion 1983, 5, 33–41. [Google Scholar] [CrossRef]
- Ghizzetti, A.; Ossicini, A. Trasformate di Laplace e Calcolo Simbolico; Unione Tipografico-Editrice Torinese: Turin, Italy, 1971. [Google Scholar]
- Oldham, K.B.; Myland, J.; Spanier, J. An Atlas of Functions: With Equator, the Atlas Function Calculator; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Lee, E.; Kanter, I. Wave propagation in finite rods of viscoelastic material. J. Appl. Phys. 1953, 24, 1115–1122. [Google Scholar] [CrossRef]
- Talbot, A. The accurate numerical inversion of Laplace transforms. Ima J. Appl. Math. 1979, 23, 97–120. [Google Scholar] [CrossRef]
- Weideman, J. Optimizing Talbot’s contours for the inversion of the Laplace transform. Siam J. Numer. Anal. 2006, 44, 2342–2362. [Google Scholar] [CrossRef]
- Weideman, J.; Trefethen, L. Parabolic and hyperbolic contours for computing the Bromwich integral. Math. Comput. 2007, 76, 1341–1356. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mainardi, F.; Mentrelli, A.; González-Santander, J.L. Transient Waves in Linear Dispersive Media with Dissipation: An Approach Based on the Steepest Descent Path. Mathematics 2025, 13, 3418. https://doi.org/10.3390/math13213418
Mainardi F, Mentrelli A, González-Santander JL. Transient Waves in Linear Dispersive Media with Dissipation: An Approach Based on the Steepest Descent Path. Mathematics. 2025; 13(21):3418. https://doi.org/10.3390/math13213418
Chicago/Turabian StyleMainardi, Francesco, Andrea Mentrelli, and Juan Luis González-Santander. 2025. "Transient Waves in Linear Dispersive Media with Dissipation: An Approach Based on the Steepest Descent Path" Mathematics 13, no. 21: 3418. https://doi.org/10.3390/math13213418
APA StyleMainardi, F., Mentrelli, A., & González-Santander, J. L. (2025). Transient Waves in Linear Dispersive Media with Dissipation: An Approach Based on the Steepest Descent Path. Mathematics, 13(21), 3418. https://doi.org/10.3390/math13213418






