Multiparty Quantum Private Comparison Protocol Using n-Particle GHZ State

Abstract

Multiparty quantum private comparison (MQPC) aims to determine the equality relationship of inputs from multiple participants while maintaining the confidentiality of these inputs. Current MQPC protocols primarily focus on utilizing d-level quantum states, which limits feasible implementation. To address this issue, we introduce an MQPC protocol that utilizes n-particle Greenberger–Horne–Zeilinger (GHZ) state to enable private comparison while preserving the secrecy of individual inputs. A semi-honest third party (TP), adhering to protocol specifications but potentially curious about private data, generates and distributes GHZ state qubits to all participants. Each party encodes their secret input through rotation operations on their allocated qubits and returns the modified state to the TP, which then performs single-particle quantum measurements to derive the outcomes without accessing the raw inputs. The protocol’s sequence distribution method yields a high qubit efficiency of 1/n, outperforming many existing MQPC protocols. Security analysis confirms resilience against external adversaries employing quantum attack strategies and collusion attempts among participants. Simulations using IBM Qiskit validate the feasibility of the protocol, which relies on GHZ state preparation, single-qubit operations, and single-particle quantum measurements.

1. Introduction

Quantum cryptography has garnered significant interest since the introduction of Bennett and Brassard’s seminal BB84 protocol, which established a framework for information-theoretic security in 1984 [1]. Subsequent advancements have spurred the development of quantum-enhanced cryptographic protocols aimed at countering emerging threats posed by quantum computing. These protocols include quantum key distribution [2,3,4,5], quantum secure direct communication [6,7,8,9], quantum key agreement [10,11,12], and quantum private set intersection [13,14,15,16], all designed to withstand attacks from quantum-enabled adversaries.

Secure multiparty computation (MPC) is a cryptographic paradigm that guarantees the privacy of individual inputs when multiple parties jointly compute a function, even in the presence of mutual distrust [17]. Formally, MPC allows n participants, $P_1,P_2,\dots ,P_n$, each holding a private input $x_i$, to collaboratively compute $y=f\left(x_1,x_2,\dots ,x_n\right)$ while ensuring that no participant learns more about the others’ inputs than what y reveals. However, classical MPC relies on computational complexity assumptions, rendering it vulnerable to quantum algorithms capable of undermining these foundations. This vulnerability has prompted the development of quantum MPC (QMPC) [18], which utilizes quantum mechanical principles to provide robustness against quantum attacks.

Private comparison, a crucial subset of MPC, originated from Yao’s millionaires’ problem [19], where two parties determine wealth superiority without revealing exact values. Boudot [20] later extended this concept to the socialist millionaires’ problem, enabling equality checks between two inputs. However, as demonstrated by Lo [21], secure two-party equality testing is inherently impossible without additional assumptions, necessitating a third party (TP) to facilitate secure privacy-preserving computations.

Traditional private comparison protocols, like classical MPC, rely on computational hardness assumptions that are vulnerable to quantum computing threats. Consequently, recent research has shifted towards quantum private comparison (QPC), which does not depend on computational complexity. Instead, QPC protocols leverage quantum principles, including the no-cloning theorem and the uncertainty principle, to achieve provable security, even in the presence of quantum adversaries. By utilizing the properties of quantum mechanics, QPC ensures unconditional security while facilitating collaborative computations.

The seminal QPC protocol [22] was developed to compare the equality of two secret integers using quantum technologies like Bell states and decoy photons, with security guaranteed by quantum mechanics principles. Following this, several two-party QPC protocols have been proposed, employing different quantum states (e.g., single photons [23,24,25,26], Bell states [27,28,29], multi-qubit states [30,31,32,33], and d-level quantum states [34,35,36,37]) as quantum resource media. The primary limitation of applying a two-party QPC protocol to a multi-party scenario is the combinatorial explosion in the number of required executions (between $n-1\sim {\displaystyle \frac{n(n-1)}{2}}$), leading to increased quantum resource consumption and reduced qubit efficiency.

The development of MQPC protocols has been driven by the goal of higher qubit efficiency. For instance, Chang et al. [38] proposed a protocol based on the entanglement of n-particle GHZ states, where participants use bitwise XOR operations to encrypt their inputs. This design allows any two participants to perform a comparison in one execution. Nevertheless, a fundamental drawback of this approach is its inability to conduct a genuine multi-party comparison, as it is restricted to pairwise analysis. Liu et al. [39] introduced a genuine MQPC protocol utilizing local unitary operations on d-dimensional states, which preserves input privacy without ciphertext encoding and avoids entanglement swapping. This catalyzed two main research strands in MQPC: entanglement-swapping-based and unitary-operation-based approaches (including quantum Fourier transform and phase/shift operations). Following the latter approach, Wang et al. [40] developed protocols using d-level entangled states with quantum Fourier transforms and phase shifts. Ji and Ye [41] developed an MQPC protocol that used entanglement swapping of d-level cat states and d-level Bell states for input encoding. Ye and Hu [42] proposed a protocol using d-level two-particle Bell entangled states to simplify implementation compared to higher-dimensional states. However, current MQPC protocols are constrained by their reliance on the manipulation of high-dimensional quantum states and d-level maximal entanglement, which are notoriously difficult to realize with current technology. Therefore, developing a practical MQPC protocol remains a significant challenge in the quantum field, necessitating continued research and innovation.

To address this limitation, this paper proposes a practical MQPC protocol based on more accessible n-particle GHZ states, which allows for secure multi-party private comparison without compromising input privacy. The main contributions of this work are as follows.

(1)

To achieve private comparison, the protocol employs a semi-honest TP that adheres to protocol specifications but may be curious about private data. The TP generates and distributes GHZ state qubits to all participants. Each party encodes their secret input through rotation operations on their allocated qubits and returns the modified state to the TP, which then performs single-particle quantum measurements to derive the outcomes without accessing the raw inputs.

(2)

To improve qubit efficiency, our scheme utilizes a distributed photon transmission mode, achieving a qubit efficiency of 1/n, which surpasses many existing MQPC protocols.

(3)

To ensure that the secret integers of the participants remain undisclosed to external eavesdroppers and curious participants, the protocol employs decoy-state and quantum key distribution technologies to prevent any leakage of private information.

(4)

To demonstrate the feasibility of the proposed protocol, we conduct a simulation experiment using IBM Qiskit, as the protocol utilizes more accessible quantum technologies, including n-particle GHZ state, rotation operations, and single-particle quantum measurements.

The remainder of this paper is structured as follows. Section 2 introduces n-particle GHZ state and rotation operations. Section 3 outlines the steps of the proposed protocol. Section 4 presents the simulation experiment. Security analysis is discussed in Section 5, and further discussion is provided in Section 6. Finally, we summarize our work in Section 7.

2. Preliminaries

2.1. n-Particle GHZ State

The n-particle GHZ state [43] is a maximally entangled state in which all n particles are entangled with one another. It is mathematically represented as

$$\left|GH{Z}_n\right.〉={\displaystyle \frac{1}{\sqrt{2}}}\left({\left|0\right.〉}^{\otimes n}+{\left|1\right.〉}^{\otimes n}\right)$$

(1)

where ${\left|0\right.⟩}^{\otimes n}$ is the tensor product of n qubits, all in the basis state $\left|0\right.⟩$. This can be expressed as

$${\left|0\right.〉}^{\otimes n}=\left|0\right.〉\otimes \left|0\right.〉\otimes \dots \otimes \left|0\right.〉=\left|00\dots 0\right.〉(\mathrm{with}n\mathrm{zeros})$$

(2)

Similarly, ${\left|1\right.⟩}^{\otimes n}$ is the tensor product of n qubits, all in the basis state $\left|1\right.⟩$, given by

$${\left|1\right.〉}^{\otimes n}=\left|1\right.〉\otimes \left|1\right.〉\otimes \dots \otimes \left|1\right.〉=\left|11\dots 1\right.〉(\mathrm{with}n\mathrm{ones})$$

(3)

Measuring the state of one particle instantaneously determines the states of all other particles. For instance, if the first particle is measured to be $\left|0\right.⟩$, then all particles collapse to $\left|00\dots 0\right.⟩$. Conversely, if the first particle is measured to be $\left|1\right.⟩$, they collapse to $\left|11\dots 1\right.⟩$.

Specifically, when $n=2$, the n-particle GHZ state is equivalent to a Bell state (e.g., $\left|\phi \right.⟩={\displaystyle \frac{1}{\sqrt{2}}}\left(\left|00\right.⟩+\left|11\right.⟩\right)$). When $n=3$, the n-particle GHZ state is a standard GHZ state (e.g., $\left|GHZ\right.⟩={\displaystyle \frac{1}{\sqrt{2}}}\left(\left|000\right.⟩+\left|111\right.⟩\right)$).

2.2. Rotation Operation

Rotation operation [44] for a qubit is expressed as

$$R_y\left(\theta \right)=e^{-i{\displaystyle \frac{\theta }{2}}Y}=\cos \left({\displaystyle \frac{\theta }{2}}\right)I-i\sin \left({\displaystyle \frac{\theta }{2}}\right)Y=\left(\begin{array}{cc}\cos {\displaystyle \frac{\theta }{2}}& -\sin {\displaystyle \frac{\theta }{2}}\\ \sin {\displaystyle \frac{\theta }{2}}& \cos {\displaystyle \frac{\theta }{2}}\end{array}\right)$$

(4)

where I denotes the identity matrix, Y denotes the Pauli-Y matrix, and $\theta$ denotes the rotation angle.

By applying $R_y\left(\theta \right)$ to a quantum state $\left|\psi \right.⟩$, the original state is encrypted. This process can be regarded as an encryption process, which can be mathematically represented as

$$\left|{\psi }^{\prime }\right.〉=R_y\left(\theta \right)\left|\psi \right.〉$$

(5)

where $\left|{\psi }^{\prime }\right.⟩$ is the transformed state after the rotation and $\theta$ is chosen from the range $\left.[0,2\pi \right)$.

The original quantum state is retrieved by applying the inverse rotation. This process can be regarded as a decryption process, which can be mathematically represented as

$$\left|\psi \right.〉=R_y\left(-\theta \right)\left|{\psi }^{\prime }\right.〉$$

(6)

Without knowledge of $\theta$, the original quantum state cannot be decrypted.

3. Description of the Proposed Protocol

3.1. Detailed Steps of the Protocol

Suppose that n participants $P_i\left(i=1,2,\cdots ,n\right)$ desire to compare the equality of their private inputs $M_i$ while ensuring the privacy of their data. The protocol engages a semi-honest TP that adheres to the protocol rules but cannot collude with any participant. Each participant encodes their input $M_i$ in binary format, ensuring uniform length L by padding with zeros if necessary. Specifically, each participant’s inputs $M_i$ in $F_2^L$ is represented in binary as $M_i=\left(m_i^{L-1},m_i^{L-2},\dots ,m_i^0\right)$. All quantum channels are assumed to be lossless and noiseless. The detailed steps of the proposed protocol are as follows.

Step 1. The n participants $P_i\left(i=1,2,\cdots ,n\right)$ perform a multiparty quantum key agreement [45] to establish a shared secret key $K=\left(k^{L-1},k^{L-2},\dots ,k^0\right)$, where each bit $k^j\in \left\{0,1\right\}$.

Step 2. The TP prepares L n-particle GHZ states, and divides these states into n quantum sequences, $S_1,S_2,\dots ,S_n$, which are generated by all the first, the second, $\cdots$, the L-th particles of these GHZ states. To detect the presence of eavesdroppers during the quantum communication process, the TP generates enough decoy photons from the states $\left\{\left|0\right.⟩,\left|1\right.⟩,\left|+\right.⟩,\left|-\right.⟩\right\}$ (where $\left|+\right.⟩={\displaystyle \frac{1}{\sqrt{2}}}\left(\left|0\right.⟩+\left|1\right.⟩\right)$ and $\left|-\right.⟩={\displaystyle \frac{1}{\sqrt{2}}}\left(\left|0\right.⟩-\left|1\right.⟩\right)$) to form decoy-state sequences $D_1,D_2,\dots ,D_n$ and randomly mixes the decoy-state sequences with the n quantum sequences, $S_1,S_2,\dots ,S_n$, to produce n new quantum sequences, ${S^{\prime }}_1,{S^{\prime }}_2,\dots ,{S^{\prime }}_n$. The TP records the positions of the bases of all decoy-state sequences and sends the quantum sequences, ${S^{\prime }}_1,{S^{\prime }}_2,\dots ,{S^{\prime }}_n$, to the n participants $P_1,P_2,\dots ,P_n$ via the quantum channels, respectively.

Step 3. Upon receiving the quantum sequences, the n participants $P_1,P_2,\dots ,P_n$ send acknowledgments back to TP who announces the positions and bases of the decoy-state sequences to all participants. Each participant extracts their respective decoy-state sequences $D_1,D_2,\dots ,D_n$ from the received quantum sequences ${S^{\prime }}_1,{S^{\prime }}_2,\dots ,{S^{\prime }}_n$, performs the corresponding measurements on the decoy-state sequences, and sends the results back to the TP who verifies the measurement results to assess the security of the quantum channels. TP checks the error rate of the measurements. If the error rate exceeds a predetermined threshold τ (ranging from 2% to 8.9% depending on channel conditions [46]), TP will abort the communication. If it is acceptable, the protocol proceeds to the next step.

Step 4. Each participant $P_i$ discard the decoy-state sequence $D_i\left(i=1,2,\cdots ,n\right)$, and obtain the quantum sequences $S_i$. Then, each participant $P_i$ performs the following operations:

(1)

Perform the rotation operation $R_y\left(\left(m_i^j\oplus k^j\right)\pi \right)$ on each j-th qubit in $S_i$ to produce a new sequence, denoted as $R{S}_i$.

(2)

Generate a secret key ${SK}_i=\left({sk}_i^{L-1},{sk}_i^{L-2},\dots ,{sk}_i^0\right)$, where $s{k}_i^j\in \left.[0,2\pi \right)$ for $j=0,1,\dots ,L-1$.

(3)

Perform the rotation operation $R_y\left({sk}_i^j\right)$ on $R{S}_i$ to get an encrypted quantum sequence, denoted as $E{S}_i$.

(4)

Prepare $\delta$ decoy photons chosen from the states $\left\{\left|0\right.⟩,\left|1\right.⟩,\left|+\right.⟩,\left|-\right.⟩\right\}$ randomly.

(5)

Insert these decoy photons into $E{S}_i$ at randomly positions to generate a modified quantum sequence, denoted as $E{S^{\prime }}_i$.

(6)

Send $E{S^{\prime }}_i$ to the TP via a quantum channel.

Step 5. Upon receiving $E{S^{\prime }}_i$, the TP sends an acknowledgment message to each participant $P_i$ and then performs the eavesdropping detection in the same manner as Step 3. If the quantum channel is not secure, the protocol is restarted. Otherwise, each participant $P_i$ sends the secret key ${SK}_i$ to the TP who then performs the following operations to obtain the comparison result.

(1)

Discard the $\delta$ decoy photons in $E{S^{\prime }}_i$ to recover $E{S}_i$.

(2)

Perform the rotation operation $R_y\left(-{sk}_i^j\right)$ on $E{S}_i$ to obtain the decrypted quantum sequence $R{S}_i$.

(3)

Conduct the $\left\{\left|0\right.⟩,\left|1\right.⟩\right\}$ basis measurement on $R{S}_i$ to obtain the results.

(4)

If all j-th qubit in $R{S}_i$ are identical, confirm that each participant’s inputs $M_i$ are equal; otherwise, they are different.

(5)

Announce the results to each participant $P_i$.

3.2. Correctness

In this section, we provide a formal proof connecting GHZ states and the $R_y$ rotation operation to show the correctness of our protocol.

Lemma 1.

Consider an n-particle system initialized in the n-particle GHZ state $\left|GH{Z}_n\right.⟩={\displaystyle \frac{1}{\sqrt{2}}}\left({\left|0\right.⟩}^{\otimes n}+{\left|1\right.⟩}^{\otimes n}\right)$. Each participant $P_i$ applies a rotation operation $R_y\left({\theta }_i\right)$ to i-th qubit of the n-particle GHZ state, this state becomes:

$${\left|GH{Z}_n\right.〉}^{\prime }={\displaystyle \frac{1}{\sqrt{2}}}\left({\otimes }_{i=1}^n{R}_y\left({\theta }_i\right)\left|0\right.〉+{\otimes }_{i=1}^n{R}_y\left({\theta }_i\right)\left|1\right.〉\right)$$

(7)

If all qubits are measured in the computational basis ($\left\{\left|0\right.⟩,\left|1\right.⟩\right\}$basis), the measurement results are identical.

Proof. 

The rotation operation $R_y\left(\theta \right)$ on the computational basis states $\left|0\right.⟩\mathrm{a}\mathrm{n}\mathrm{d}\left|1\right.⟩$ can be written as:

$$R_y\left(\theta \right)\left|0\right.〉==\left(\begin{array}{cc}\cos {\displaystyle \frac{\theta }{2}}& -\sin {\displaystyle \frac{\theta }{2}}\\ \sin {\displaystyle \frac{\theta }{2}}& \cos {\displaystyle \frac{\theta }{2}}\end{array}\right)\left(\begin{array}{c}1\\ 0\end{array}\right)=\left(\begin{array}{c}\cos {\displaystyle \frac{\theta }{2}}\\ \sin {\displaystyle \frac{\theta }{2}}\end{array}\right)=\cos {\displaystyle \frac{\theta }{2}}\left|0\right.〉+\sin {\displaystyle \frac{\theta }{2}}\left|1\right.〉$$

(8)

$$R_y\left(\theta \right)\left|1\right.〉==\left(\begin{array}{cc}\cos {\displaystyle \frac{\theta }{2}}& -\sin {\displaystyle \frac{\theta }{2}}\\ \sin {\displaystyle \frac{\theta }{2}}& \cos {\displaystyle \frac{\theta }{2}}\end{array}\right)\left(\begin{array}{c}0\\ 1\end{array}\right)=\left(\begin{array}{c}-\sin {\displaystyle \frac{\theta }{2}}\\ \cos {\displaystyle \frac{\theta }{2}}\end{array}\right)=-\sin {\displaystyle \frac{\theta }{2}}\left|0\right.〉+\cos {\displaystyle \frac{\theta }{2}}\left|1\right.〉$$

(9)

Appling the rotation operation $R_y\left({\theta }_i\right)$ to i-th qubit of the n-particle GHZ state, we have

$$\begin{array}{ll}{\left|GH{Z}_n\right.〉}^{\prime }& ={\displaystyle \frac{1}{\sqrt{2}}}\left({\otimes }_{i=1}^n{R}_y\left({\theta }_i\right)\left|0\right.〉+{\otimes }_{i=1}^n{R}_y\left({\theta }_i\right)\left|1\right.〉\right)\\ & ={\displaystyle \frac{1}{\sqrt{2}}}\left({\otimes }_{i=1}^n\left(\cos {\displaystyle \frac{{\theta }_i}{2}}\left|0\right.〉+\sin {\displaystyle \frac{{\theta }_i}{2}}\left|1\right.〉\right)+{\otimes }_{i=1}^n\left(-\sin {\displaystyle \frac{{\theta }_i}{2}}\left|0\right.〉+\cos {\displaystyle \frac{{\theta }_i}{2}}\left|1\right.〉\right)\right)\end{array}$$

(10)

If all ${\theta }_i=0$, the mesurement results using the computational basis ($\left\{\left|0\right.⟩,\left|1\right.⟩\right\}$) for each j-th qubit yield either ${\left|0\right.⟩}^{\otimes n}$ or ${\left|1\right.⟩}^{\otimes n}$ due to the entanglement of the n-particle GHZ states.

Similarly, if all ${\theta }_i=\pi$, the mesurement results also yield ${\left|0\right.⟩}^{\otimes n}$ or ${\left|1\right.⟩}^{\otimes n}$ for the same reason.

However, if not all ${\theta }_i$ are equal to $0$ or $\pi$, the measurement results will indicate both quantum states $\left|0\right.⟩$ and $\left|1\right.⟩$. □

Therefore, we can deduce that if the measurement results for each $j$-th qubit are either ${\left|0\right.⟩}^{\otimes n}$ or ${\left|1\right.⟩}^{\otimes n}$, then all ${\theta }_i$ must be identical.

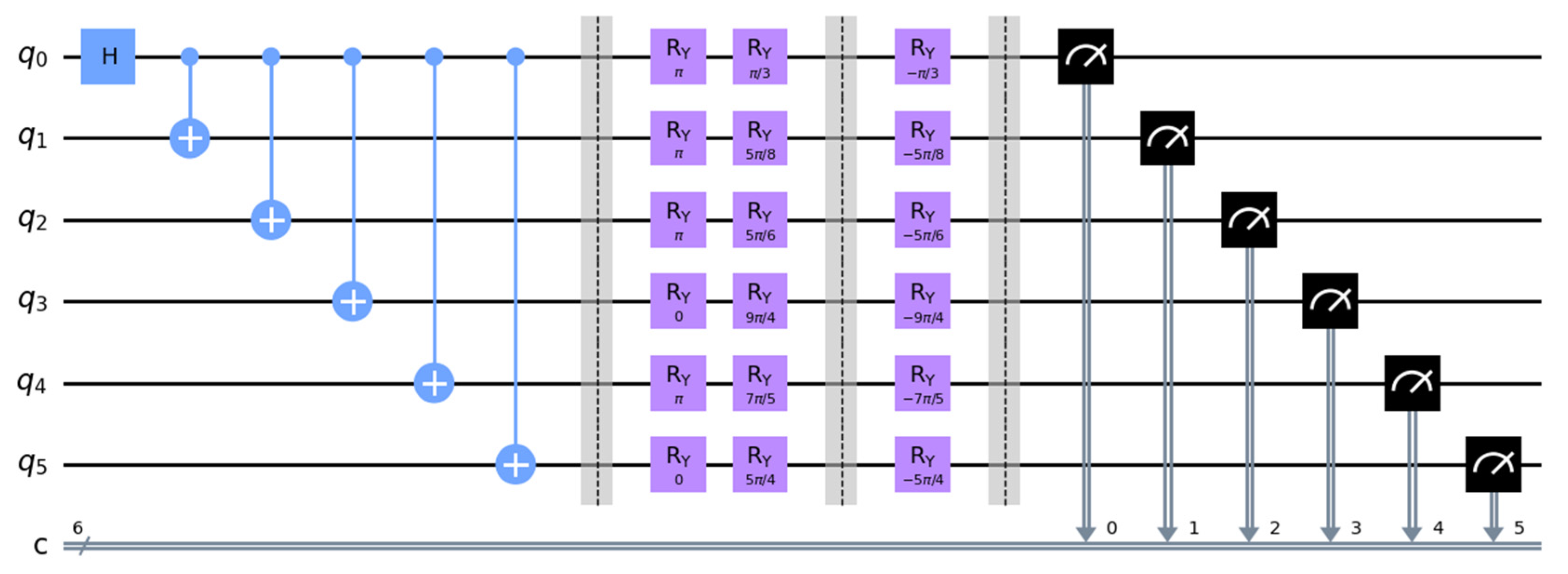
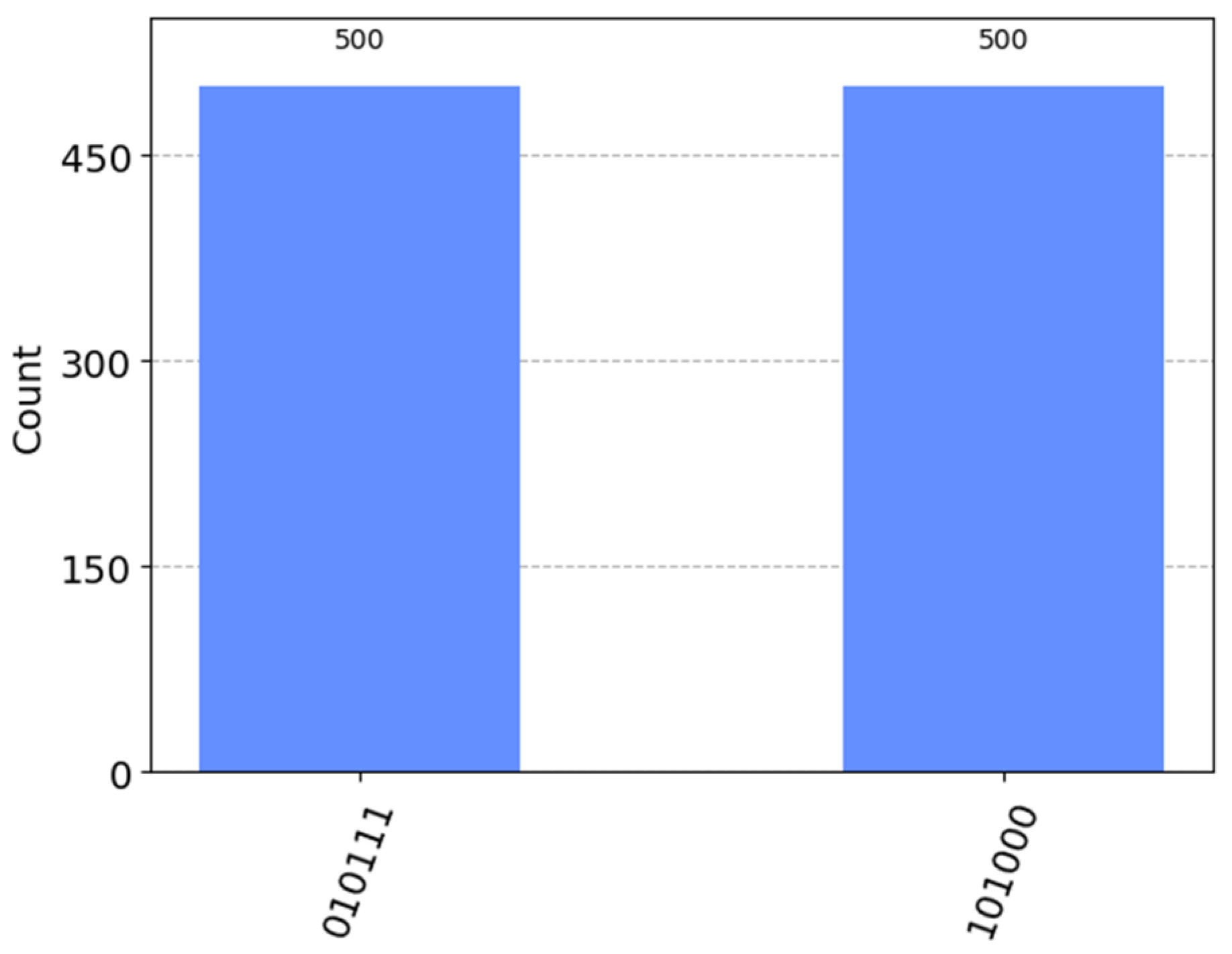
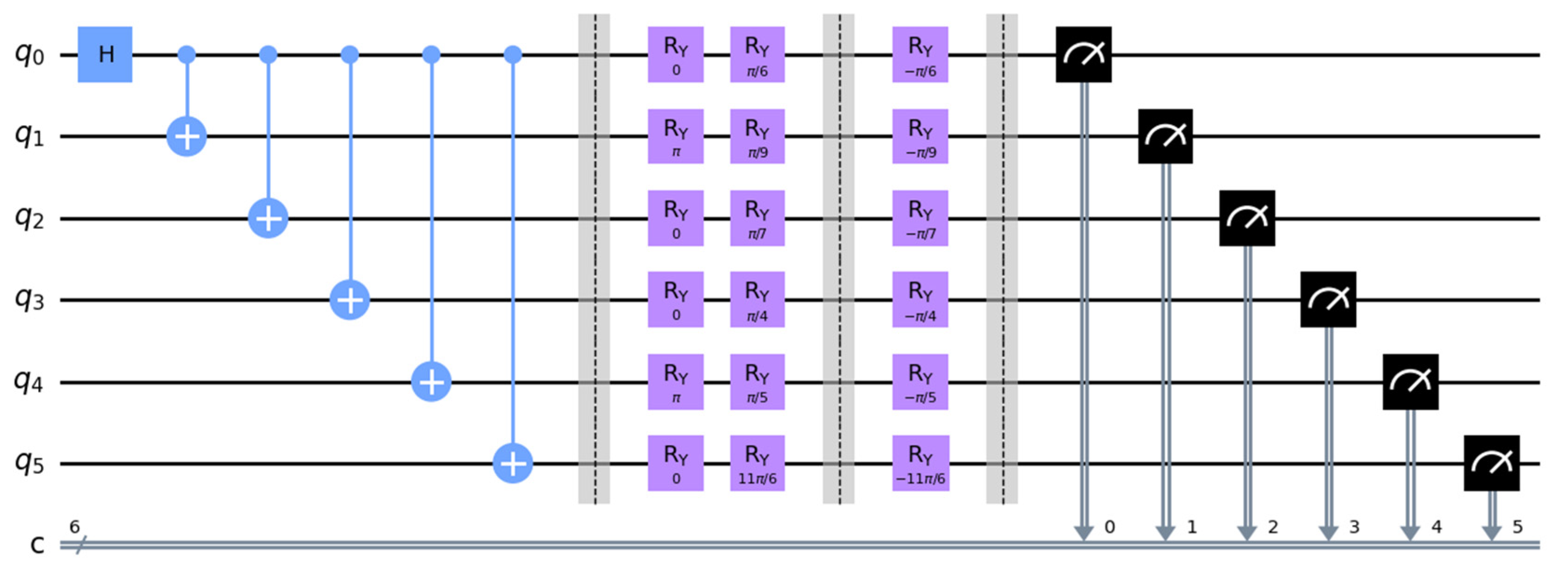
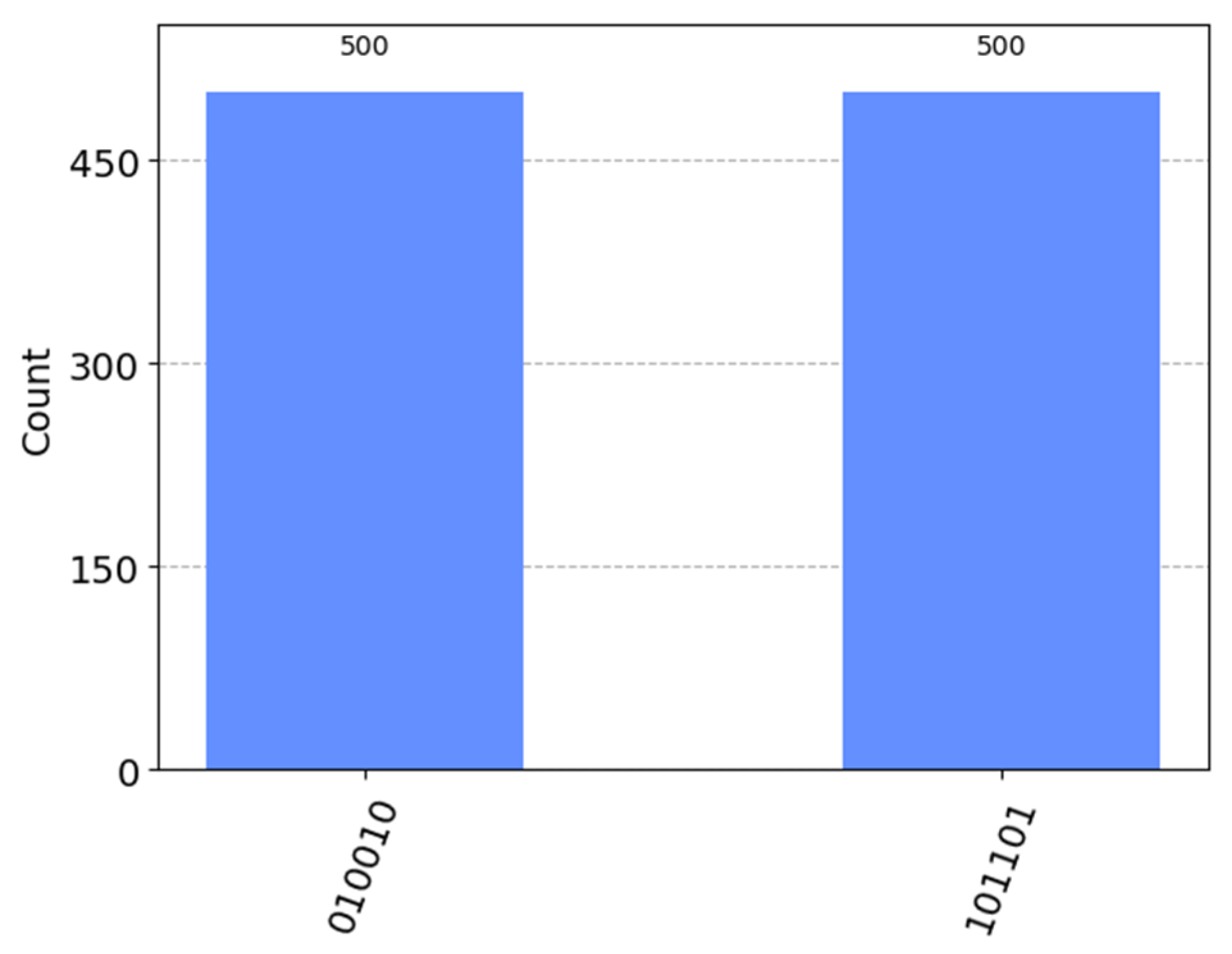
4. Simulation Experiment

We conduct a simulation experiment using IBM Qiskit (version 0.44.1) on Python (version 3.11.4) running on Windows. It is important to note that the following experiments are conducted 1000 times.

Considering a scenario with six participants $\left\{P_1,P_2,\cdots ,P_6\right\}$, the private inputs for each participant are as follows:

• $M_1=3$
• $M_2=1$
• $M_3=3$
• $M_4=2$
• $M_5=1$
• $M_6=2$

We set the uniform length $L=2$, with the binary representations of these private inputs in $F_2^2$ as:

• $M_1=\left(m_1^1,m_1^0\right)=11$
• $M_2=\left(m_2^1,m_2^0\right)=01$
• $M_3=\left(m_3^1,m_3^0\right)=11$
• $M_4=\left(m_4^1,m_4^0\right)=10$
• $M_5=\left(m_5^1,m_5^0\right)=01$
• $M_6=\left(m_6^1,m_6^0\right)=10$.

We assume that the shared secret key among the six participants is $K=\left(k^1,k^0\right)=\left(1,0\right)$. The secret key generated by each participant is as follows:

• ${SK}_1=\left({sk}_1^1,{sk}_1^0\right)=\left({\displaystyle \frac{\pi }{6}},{\displaystyle \frac{\pi }{3}}\right)$
• ${SK}_2=\left({sk}_2^1,{sk}_2^0\right)=\left({\displaystyle \frac{\pi }{9}},{\displaystyle \frac{5\pi }{8}}\right)$
• ${SK}_3=\left({sk}_3^1,{sk}_3^0\right)=\left({\displaystyle \frac{\pi }{7}},{\displaystyle \frac{5\pi }{6}}\right)$
• ${SK}_4=\left({sk}_4^1,{sk}_4^0\right)=\left({\displaystyle \frac{\pi }{4}},{\displaystyle \frac{4\pi }{9}}\right)$
• ${SK}_5=\left({sk}_5^1,{sk}_5^0\right)=\left({\displaystyle \frac{\pi }{5}},{\displaystyle \frac{7\pi }{5}}\right)$
• ${SK}_6=\left({sk}_6^1,{sk}_6^0\right)=\left({\displaystyle \frac{11\pi }{6}},{\displaystyle \frac{5\pi }{4}}\right)$.

According to the proposed protocol, the TP should prepare two 6-particle GHZ states. To evaluate the equality of the 0-th position of the private inputs, the rotation operations performed on one 6-particle GHZ state by the six participants are

• $\left\{R_y\left(\pi \right),R_y\left({\displaystyle \frac{\pi }{3}}\right)\right\}$
• $\left\{R_y\left(\pi \right),R_y\left({\displaystyle \frac{5\pi }{8}}\right)\right\}$
• $\left\{R_y\left(\pi \right),R_y\left({\displaystyle \frac{5\pi }{6}}\right)\right\}$
• $\left\{R_y\left(0\right),R_y\left({\displaystyle \frac{4\pi }{9}}\right)\right\}$
• $\left\{R_y\left(\pi \right),R_y\left({\displaystyle \frac{7\pi }{5}}\right)\right\}$
• $\left\{R_y\left(0\right),R_y\left({\displaystyle \frac{5\pi }{4}}\right)\right\}$

The rotation operations performed on each particle of the received states by the TP are $\left\{R_y\left(-{\displaystyle \frac{\pi }{3}}\right)\right\}$, $\left\{R_y\left(-{\displaystyle \frac{5\pi }{8}}\right)\right\}$, $\left\{R_y\left(-{\displaystyle \frac{5\pi }{6}}\right)\right\}$, $\left\{R_y\left(-{\displaystyle \frac{4\pi }{9}}\right)\right\}$, $\left\{R_y\left(-{\displaystyle \frac{7\pi }{5}}\right)\right\}$ and $\left\{R_y\left(-{\displaystyle \frac{5\pi }{4}}\right)\right\}$. The corresponding quantum circuit to evaluate the equality of the 0-th position of the private inputs is shown in Figure 1, and its measurement results are presented in Figure 2.

According to Figure 2, the measurement results corresponding to q [0]–q [5] are either $\left|1\right.⟩\left|1\right.⟩\left|1\right.⟩\left|0\right.⟩\left|1\right.⟩\left|0\right.⟩$ or $\left|0\right.⟩\left|0\right.⟩\left|0\right.⟩\left|1\right.⟩\left|0\right.⟩\left|1\right.⟩$. We can further deduce that each qubit of the measurement results is different, indicating that the 0-th positions of the private inputs are also different.

To evaluate the equality of the 1-th position of the private inputs, the rotation operations performed on two 6-particle GHZ state by the six participants are

• $\left\{R_y\left(0\right),R_y\left({\displaystyle \frac{\pi }{6}}\right)\right\}$
• $\left\{R_y\left(\pi \right),R_y\left({\displaystyle \frac{\pi }{9}}\right)\right\}$
• $\left\{R_y\left(0\right),R_y\left({\displaystyle \frac{\pi }{7}}\right)\right\}$
• $\left\{R_y\left(0\right),R_y\left({\displaystyle \frac{\pi }{4}}\right)\right\}$
• $\left\{R_y\left(\pi \right),R_y\left({\displaystyle \frac{\pi }{5}}\right)\right\}$
• $\left\{R_y\left(0\right),R_y\left({\displaystyle \frac{11\pi }{6}}\right)\right\}$

The rotation operations performed on each particle of the received states by the TP are $\left\{R_y\left(-{\displaystyle \frac{\pi }{6}}\right)\right\}$, $\left\{R_y\left(-{\displaystyle \frac{\pi }{9}}\right)\right\}$, $\left\{R_y\left(-{\displaystyle \frac{\pi }{7}}\right)\right\}$, $\left\{R_y\left(-{\displaystyle \frac{\pi }{4}}\right)\right\}$, $\left\{R_y\left(-{\displaystyle \frac{\pi }{5}}\right)\right\}$ and $\left\{R_y\left(-{\displaystyle \frac{11\pi }{6}}\right)\right\}$. The corresponding quantum circuit to evaluate the equality of the 1-th position of the private inputs is depicted in Figure 3, and Figure 4 presents its measurement results.

According to Figure 4, the measurement results corresponding to q [0]–q [5] are either $\left|0\right.⟩\left|1\right.⟩\left|0\right.⟩\left|0\right.⟩\left|1\right.⟩\left|0\right.⟩$ or $\left|1\right.⟩\left|0\right.⟩\left|1\right.⟩\left|1\right.⟩\left|0\right.⟩\left|1\right.⟩$. We can further deduce that each qubit of the measurement results is different, indicating that the 1-th positions of the private inputs are also different.

Following the descriptions of the proposed protocol, if the measurement results of all j-th qubits are identical, it confirms that each participant’s inputs are equal; otherwise, they are different. According to Figure 2 and Figure 4, we can confirm that the measurement results of both the 0-th and 1-th qubits are different. Therefore, each participant’s inputs are not equal.

5. Security Analysis

In a quantum cryptographic protocol, two types of quantum attacks must be considered: outsider attacks and participant attacks. Outsider attacks involve an eavesdropper, referred to as Eve, who attempts to obtain the private inputs of the participants through quantum attacks. In contrast, participant attacks occur when the TP or any participant attempts to deduce the private inputs of others by utilizing the immediate measurement results. In this section, we will demonstrate that our protocol is resistant to both types of attacks.

5.1. Outsider Attacks

In this protocol, external attacker Eve, may attempt to intercept and extract private inputs using strategies like intercept-resend [47], entangle-measure [48], and quantum Trojan horse attacks [49].

Intercept-resend attack. In this scenario, Eve intercepts the quantum sequences and uses forged sequence to replace the original sequence before forwarding them to the intended recipients. This could potentially allow her to deduce the private inputs through the measurement outcomes. However, the presence of decoy photons is specifically designed to detect such eavesdropping attempts. The legitimate parties can expose the eavesdropping by comparing a subset of the decoy photon measurement results. For example, if an initially prepared decoy photon is in the state $\left|+\right.⟩$, Eve’s eavesdropping attempt is successful if she selects the $\left\{\left|+\right.⟩,\left|-\right.⟩\right\}$ basis as the measurement basis. Conversely, her eavesdropping attempt has a success probability of 50% if she chooses the $\left\{\left|0\right.⟩,\left|1\right.⟩\right\}$ basis. Since the selection of either basis occurs with a probability of 50%, the total success probability per decoy photon is ${\displaystyle \frac{1}{2}}\times 1+{\displaystyle \frac{1}{2}}\times {\displaystyle \frac{1}{2}}={\displaystyle \frac{3}{4}}$. For $\delta$ decoy photons, the probability of detection is $1-{\left({\displaystyle \frac{3}{4}}\right)}^{\delta }$, making eavesdropping detectable with near certainty.

Entangle-measurement attack. In this type of attack, Eve intercepts the quantum sequences sent from the participants to the TP. She employs a unitary operation U to entangle the intercepted particles (including decoy photons $\left\{\left|0\right.⟩,\left|1\right.⟩,\left|+\right.⟩,\left|-\right.⟩\right\}$) with an ancillary quantum state $\left|\epsilon \right.⟩$. After entangling the intercepted particles, Eve measures the combined system. The measurement outcomes can provide her with information about the quantum states, which may correspond to the private inputs of the participants. The general form of the unitary operation can be expressed as:

$$U\left|0\right.〉\left|\epsilon \right.〉=a_{00}\left|0\right.〉\left|{\epsilon }_{00}\right.〉+a_{01}\left|1\right.〉\left|{\epsilon }_{01}\right.〉$$

(11)

$$U\left|1\right.〉\left|\epsilon \right.〉=a_{10}\left|0\right.〉\left|{\epsilon }_{10}\right.〉+a_{11}\left|1\right.〉\left|{\epsilon }_{11}\right.〉$$

(12)

$$\begin{array}{ll}U\left|+\right.〉\left|\epsilon \right.〉& ={\displaystyle \frac{1}{2}}\left|+\right.〉\left(a_{00}\left|{\epsilon }_{00}\right.〉+a_{01}\left|{\epsilon }_{01}\right.〉+a_{10}\left|{\epsilon }_{10}\right.〉+a_{11}\left|{\epsilon }_{11}\right.〉\right)\\ & +{\displaystyle \frac{1}{2}}\left|-\right.〉\left(a_{00}\left|{\epsilon }_{00}\right.〉-a_{01}\left|{\epsilon }_{01}\right.〉+a_{10}\left|{\epsilon }_{10}\right.〉-a_{11}\left|{\epsilon }_{11}\right.〉\right)\end{array}$$

(13)

$$\begin{array}{ll}U\left|-\right.〉\left|\epsilon \right.〉& ={\displaystyle \frac{1}{2}}\left|+\right.〉\left(a_{00}\left|{\epsilon }_{00}\right.〉+a_{01}\left|{\epsilon }_{01}\right.〉-a_{10}\left|{\epsilon }_{10}\right.〉-a_{11}\left|{\epsilon }_{11}\right.〉\right)\\ & +{\displaystyle \frac{1}{2}}\left|-\right.〉\left(a_{00}\left|{\epsilon }_{00}\right.〉-a_{01}\left|{\epsilon }_{01}\right.〉-a_{10}\left|{\epsilon }_{10}\right.〉+a_{11}\left|{\epsilon }_{11}\right.〉\right)\end{array}$$

(14)

where $\left|{\epsilon }_{00}\right.⟩,\left|{\epsilon }_{01}\right.⟩,\left|{\epsilon }_{10}\right.⟩$ and $\left|{\epsilon }_{11}\right.⟩$ represent the basis states of the ancillary state and they satisfy the following condition.

$${\displaystyle \sum _{\alpha ,\beta \in \left\{0,1\right\}}〈{\epsilon }_{\alpha ,\beta }|{\epsilon }_{\alpha ,\beta }〉}=1$$

(15)

For Eve to successfully carry out this attack without detection, certain conditions must be met regarding the parameters of the entangled states and the ancillary state. The conditions can be expressed mathematically as:

$$\left\{\begin{array}{l}{a}_{00}=a_{11}=1\\ a_{01}=a_{10}=0\\ a_{00}\left|{\epsilon }_{00}\right.〉-a_{01}\left|{\epsilon }_{01}\right.〉+a_{10}\left|{\epsilon }_{10}\right.〉-a_{11}\left|{\epsilon }_{11}\right.〉=0\\ a_{00}\left|{\epsilon }_{00}\right.〉+a_{01}\left|{\epsilon }_{01}\right.〉-a_{10}\left|{\epsilon }_{10}\right.〉-a_{11}\left|{\epsilon }_{11}\right.〉=0\end{array}\right.$$

(16)

From the conditions in Equation (12), we can deduce that $\left|{\epsilon }_{00}\right.⟩=\left|{\epsilon }_{11}\right.⟩$. Substituting $\left|{\epsilon }_{00}\right.⟩=\left|{\epsilon }_{11}\right.⟩$ into Equations (7)–(10), we have

$$U\left|0\right.〉\left|\epsilon \right.〉=\left|0\right.〉\left|{\epsilon }_{00}\right.〉=\left|0\right.〉\left|{\epsilon }_{11}\right.〉$$

(17)

$$U\left|1\right.〉\left|\epsilon \right.〉=\left|1\right.〉\left|{\epsilon }_{11}\right.〉=\left|1\right.〉\left|{\epsilon }_{00}\right.〉$$

(18)

$$U\left|+\right.〉\left|\epsilon \right.〉=\left|+\right.〉\left|{\epsilon }_{00}\right.〉=\left|+\right.〉\left|{\epsilon }_{11}\right.〉$$

(19)

$$U\left|-\right.〉\left|\epsilon \right.〉=\left|-\right.〉\left|{\epsilon }_{00}\right.〉=\left|-\right.〉\left|{\epsilon }_{11}\right.〉$$

(20)

From Equations (13)–(16), it can be concluded that the system composed of the particles $\left\{\left|0\right.⟩,\left|1\right.⟩,\left|+\right.⟩,\left|-\right.⟩\right\}$ and the ancillary quantum state is separable; that is, they are in a product state. This configuration ensures that such an attack would be unsuccessful.

Quantum Trojan horse attacks. Eve may also employ quantum Trojan horse attacks, such as delay-photon or invisible photon attacks, which target the transmission of quantum sequences. To mitigate these risks, the protocol recommends implementing protective measures, such as a wavelength quantum filter and photon number splitters [50].

In summary, the proposed protocol effectively secures the private inputs of the participants against various external attack strategies.

5.2. Participant Attacks

The participating entities, including the TP and any participants, may attempt to deduce the private inputs of others using the immediate results.

TP’s attacks. In our protocol, the TP is responsible for preparing n-particle GHZ states and performing quantum measurements to obtain comparison results. However, it cannot deduce the private inputs of the participants because it lacks knowledge of the secret key K. For instance, while the TP can measure the initial states (e.g., ${\left|0\right.⟩}^{\otimes n}$) and detect the collective rotation operations applied by the participants, it cannot interpret these rotations. The rotation angles encode the private inputs using the secret key K, which the TP does not possess. Therefore, the TP’s attempts to extract private information are ineffective.

The dishonest participants’ attacks. Consider a dishonest participant $P_i$ who aims to obtain the private inputs of other participants. Although $P_i$ knows the secret non-zero binary key K and the initial quantum sequences received by each participant, she cannot achieve their objective due to a lack of knowledge about the secret key generated by each participant. For example, if $P_i$ performs an intercept-resend attack, she may filter out the decoy photons after their positions are revealed. However, this action itself will introduce errors that reveal her eavesdropping. Even if $P_i$ manages to obtain the encoded quantum sequence, they still cannot deduce the private inputs of other participants, as the encoded quantum sequence is encrypted with the secret key SK. Similarly, if n − 1 participants collude to deduce the private inputs of others, they will also fail due to their lack of knowledge about the secret key generated by each participant. Therefore, attacks by dishonest participants cannot succeed.

6. Discussion

The qubit efficiency [41] is a key metric for evaluating the utilization of qubits in a quantum cryptographic protocol. It is defined as:

$${\eta }_e={\displaystyle \frac{{\eta }_c}{{\eta }_t}}$$

(21)

where ${\eta }_c$ denotes the length of the binary representations of the private input, and ${\eta }_t$ denotes is the total number of qubits consumed, excluding those used for eavesdropping detection. Since the decoy photon used for the eavesdropping detection can be viewed as an independent procedure in quantum cryptographic protocol. According to the protocol settings, the length of the binary representations of the private input $M_i$ is L, leading to ${\eta }_c=L$. The TP prepares L n-particle GHZ states as quantum resources, resulting in ${\eta }_t=nL$. According to the Equation (17), we have ${\eta }_e={\eta }_c/{\eta }_t=L/nL=1/n$.

Table 1. A comparison with other existing MQPC protocols.

Protocol	Quantum Resource	The Need for Entanglement Swapping	The Need for Unitary Operations	Measurement Manner for TP	Measurement Manner for Users	Qubit Efficiency
Liu et al. [39]	d-level basis state	No	Yes	d-level single-particle measurement	No	$1/n$
Wang et al. [40]	d-level n-particle entangled state and d-level two-particle entangled state	No	No	d-level single-particle measurement	d-level single-particle measurement	$1/3n$
Ji and Ye [41]	d-level n + 1-particle cat state and d-level two-particle Bell state	Yes	Yes	d-level n + 1-particle cat state measurement	d-level two-particle Bell state measurement	$1/(3n$ + 1)
Ye and Hu [42]	d-level two-particle Bell entangled state	Yes	Yes	d-level two-particle Bell entangled state	d-level two-particle Bell entangled state	$1/(2n$ + 2)
Ours	n-particle GHZ state	No	Yes	Z-basis	No	$1/n$

compares our protocol with other MQPC protocols.

As provided in Table 1, the proposed protocol demonstrates improvements in several key performance areas compared to existing solutions:

(1)

Unlike the protocols outlined in Refs. [39,40,41,42], which necessitate the creation of complex d-level states, our approach streamlines these requirements. It avoids the need for complicated quantum state preparations by utilizing n-particle GHZ states as quantum resources. This design increases practicality, facilitating implementation with existing quantum technologies, particularly through the straightforward preparation of n-particle GHZ states.

(2)

The existing MQPC protocols require sophisticated quantum technologies, such as quantum entanglement swapping of d-level states [41,42] and tailored unitary operations for d-level states [39]. In contrast, our approach uses rotation operations on n-particle GHZ states, which can be easily realized with current quantum technologies.

(3)

Our protocol focuses on measurements involving Z-basis instead of d-level quantum states, making it more compatible with existing technological capabilities.

Although the qubit efficiency of our protocol is similar to that of Ref. [39], it holds a distinct advantage in terms of experimental feasibility. This is due to its use of more readily implementable quantum technologies, especially regarding the nature of the quantum resources, the complexity of the unitary operations, and the simplicity of the measurement methods.

7. Conclusions

A novel MQPC protocol is introduced in this paper. The protocol utilizes n-particle GHZ states to facilitate the private comparison of inputs among multiple participants without revealing any individual’s private data. The protocol is designed to operate with a semi-honest TP which generates and distributes GHZ state qubits, allowing each participant to encode their secret inputs through rotation operations before returning the modified states to the TP, which then performs single-particle quantum measurements to derive outcomes without accessing the raw inputs. To enhance efficiency, the protocol employs a distributed photon transmission mode, achieving a qubit efficiency of $1/n$, which is superior to many existing MQPC protocols. Furthermore, to safeguard participants’ secret integers from external eavesdroppers and inquisitive participants, the protocol utilizes decoy-state and quantum key distribution technologies, effectively preventing any leakage of private information. Finally, the practicality of the proposed protocol is validated through an IBM Qiskit simulation, underscoring its implementation viability using readily available quantum resources, including n-particle GHZ states, rotation operations, and single-particle quantum measurements. In the future, we aim to develop a practical and efficient MQPC protocol that can assess size relations among multiple participants. Additionally, we will work on improving its robustness against noise in various environments and on developing semi-quantum private comparison protocols.