Abstract
The specificity and complexity of space networks render the traditional key management mechanism no longer applicable. The certificate-less-based distributed spatial network key management scheme proposed in this paper combines the characteristics of space networks, solving the problems regarding the difficulty of implementing centralized key management in space networks and the excessive overhead required for maintaining public key certificates by constructing a distributed key generation center and establishing strategies such as private key updates, master key component updates, and session key negotiation. This method also avoids the key escrow problem inherent in existing identity-based key management schemes. This scheme provides the DPKG construction method for space networks; designs the update strategy for the DPKG node’s master key sharing, providing a specific update algorithm; introduces the batch private key update mechanism; and uses the mapping function to evenly distribute the node’s update requests throughout the update time period, avoiding the problem of overly concentrated update requests. After analysis and simulation verification, it was proven that the scheme can meet the necessary security requirements, offering good stability and scalability.
MSC:
94A62
1. Introduction
In the context of the global commercialization of 5G [1], traditional ground networks are facing exponential growth in terms of throughput, user access, and high-speed information transmission. However, due to their limited coverage and network capacity, an increasing number of communication tasks and sharp resource conflicts have made it more difficult to arrange tasks properly, which has led researchers to pay extensive attention to space information networks [2,3,4]. The connotation of space information networks changes with the development of space communication technology, and these networks have now evolved into integrated comprehensive information networks consisting of satellite networks, adjacent space networks, and related ground facilities [5]. In terms of functionality, the structure of space information networks mainly includes space-based information acquisition systems, space information links, and ground support and control systems, as shown in Figure 1. Among these, the space-based information acquisition system mainly consists of communication satellites, reconnaissance satellites, navigation satellites, near-space spacecraft, and some high-altitude reconnaissance aircraft and early warning aircraft, which form the dynamic node set of the space information network. The various information nodes are connected by relay systems and network devices to form space information links, connecting different levels of aircraft and ground systems in the space information network that perform different tasks. The ground support and control system consist of ground measurement and control systems, information processing systems, command and control systems, and other ground facilities. The ground control center is the only static node in the space information network, and it plays an important role in maintaining the normal operation of the network [6]. Space information networks are based on traditional ground networks, supplemented by air-based networks and space-based networks, and they provide information security infrastructure for various applications in wide-area space [7]. By integrating various resources, they promote the rapid development of applications such as the Internet of things and the Internet of vehicles. Space information networks are also seen as the most promising development direction for future 6G networks [8].
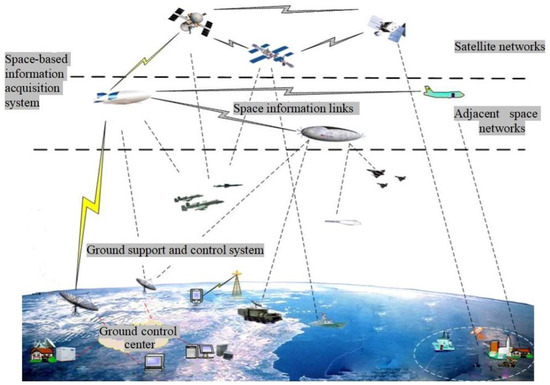
Figure 1.
Space information network structure.
The high openness of space networks and the dynamic nature of network topology mean that the security concerns are extremely critical [9,10,11]. To build a secure space information network environment, it is necessary to provide security services such as confidentiality, authentication, availability, integrity, and non-repudiation, and providing nearly all of these security services requires a sound key management strategy. Therefore, conducting research on space information network key management and designing key management schemes suitable for the characteristics of space information networks is of vital importance, providing significance for the secure application of space information networks [12,13,14].
The PKI/CA-based key management model used in traditional networks is no longer applicable to space networks, as mainly manifested in the dynamic nature of network topology that can easily lead to centralized key management single-point failure; the high error rate of long-distance wireless channels makes it costly for nodes to update and maintain public key certificates [15]. In 1984, Shamir proposed a new public key cryptosystem at the CRYPTO 1984 conference held in North America [16]. In the new system, the user’s public key can be any bit string related to the user’s identity, and the user’s private key is generated by a trusted private key generation center PKG (private key generator). Therefore, this system is also called identity-based public key cryptography (IBC). Identity-based public key cryptography realizes the automatic binding of user public keys and identity information, and the system no longer needs to maintain a user public key directory, saving the overhead cost of issuing and storing user certificates, thereby simplifying the key management process inherent in traditional public key systems. In 2001, Boneh and Franklin proposed the first practical and efficient identity-based encryption mechanism using bilinear pairings (BF-IBE) [17]. In the literature [18,19,20,21], to solve similar problems in ad hoc networks, some key management schemes based on identity-based public key cryptography and distributed key management mechanisms have been proposed, providing references for research on space network key management. Luo [22] proposed an identity-based distributed key management scheme to resolve the problems of centralized key management and over-consumption in regards to certificate maintenance in space networks. However, these schemes still exhibit key escrow issues.
Certificate-less cryptography is a new type of public key cryptography proposed by Al-Riyami and Paterson at the 2003 ASIACRYPT conference [23]. Similar to identity-based cryptography, it does not require the use of certificates to associate users and public keys. Although it also relies on a private key generation center PKG with a master key to participate in the generation of users’ private keys, the PKG only generates partial private keys corresponding to the user’s identity. The final user’s private key is composed of partial private keys and a randomly chosen secret value. Therefore, the PKG does not have full control over the user’s private key, and there is no key escrow problem. In the same year that Al-Riyami proposed the certificate-less public key cryptography model, Chen et al. also proposed an identity-based signature scheme that does not require a trusted PKG [24]. Afterwards, Gorantla et al. proposed a more efficient certificate-less signature scheme based on Al-Riyami’s work [25]. Al-Riyami [26] proposed a certificate-less public key encryption scheme (CL-PKE), which is guaranteed by the difficulty of solving the computational Diffie–Hellman problem (CDHP), and Baek [27] provided security proofs under the random oracle model. The literature [28,29] also proposed two-party key agreement schemes, but these cannot resist attacks in which the keys are leaked and or when a temporary private key leaks. Liu [30] proposed a certificate-less key agreement protocol, which only performs the one-way authentication of nodes and does not achieve the mutual authentication of two-party nodes. Although it saves some computational overhead, it increases security risks. Chen [31] proposed an efficient authentication protocol that only requires hash and XOR operations to reduce user computational overhead, but it cannot resist man-in-the-middle attacks. To avoid key escrow, certificate-less public key cryptography (CL-PKC) has been introduced into anonymous communication authentication in the Internet of vehicles [32,33,34]. However, these schemes either do not give the specific construction method of the distributed private key center (DPKG), or the construction method given does not match the reality of space networks; secondly, these schemes assign DPKG nodes with long-term validity of their master key shares and lack the updating mechanism, which allows attackers to reconstruct the master key if the value of the master key shares they have accumulated reaches the threshold value; in addition, these schemes lack an efficient node private key update strategy, which can cause network congestion when a large number of nodes apply for updates at the same time.
To address the above issues, the research motivation for this paper includes the following three main aspects:
- (1)
- Designing a DPKG construction strategy that is practically compatible with space networks;
- (2)
- Designing an update mechanism for DPKG node master key shares;
- (3)
- Designing a node private key phased update strategy to avoid the network congestion problem generated by centralized updates.
The certificate-less distributed key management scheme proposed in this paper for space networks uses threshold secret sharing mechanisms to reasonably distribute the functions of the PKG to multiple service nodes in the space information network to avoid the problem of PKG paralysis due to single-point failure and also solves the difficulties in maintaining certificates and key escrow.
The specific contributions of this paper include the following:
- (1)
- The concept of a secure field of view is proposed, and the construction method of the DPKG of space networks is given;
- (2)
- The problem of updating the master key shares of DPKG nodes is solved by introducing a 0-constant term polynomial of the same order as the master key share polynomial, and a specific update algorithm is designed;
- (3)
- A batchwise private key update mechanism is employed. The mapping function is used to distribute the update requests of the nodes evenly throughout the update time period, avoiding the problem of the over-concentration of update requests.
The content and arrangement of this paper are as follows: Section 2 introduces the preparatory knowledge. Section 3 describes the proposed certificate-less distributed key management scheme. Section 4 provides a detailed proof and analysis of the correctness and security of the scheme. Section 5 includes the simulation, verification and comparison. Finally, the paper concludes with a summary of the entire document.
2. Preparatory Knowledge
The threshold secret sharing mechanism is a secret information segmentation storage scheme proposed by Shamir in 1979. It is the main method used in the field of cryptography to solve the problem of the excessive concentration of security permissions, the dispersion of risks, and the tolerance of intrusion. An elliptic curve cryptosystem (ECC) is a system based on the elliptic curve over a finite field point group public key cryptography system. Compared with the traditional RSA public key cryptosystem, the elliptic curve public key system is able to use a shorter key length to achieve the same security strength; bilinear pair technology can realize the flexible transformation of input variable coefficients, and it is often used in cryptography to construct many protocols or schemes that are difficult to realize using other mathematical tools.
2.1. Threshold Secret Sharing Mechanism
Shamir’s threshold secret sharing mechanism generates secret shares through polynomials and reconstructs secrets using the Lagrange interpolation algorithm:
Parameter selection is achieved as follows: is the field of integers of order , is the number of secrets to be shared, is a secret share member collection with participants, randomly generating a degree secret-sharing polynomial on , as follows:
where is the random number on , and are kept secret, and the other parameters are disclosed to the public.
To achieve secret sharing, Select secret shares to generate the number , calculate and securely transmit the secret share for member , and publicize .
To achieve secret reconstruction, the polynomial can be reconstructed by the Lagrange interpolation theorem for any participants who want to recover the secret , as follows:
Obviously,
Call the interpolation factor, then
Since the time of f(x) is t − 1, then less than t participants cannot reconstruct the polynomial, and the secret d is not recovered.
2.2. Security Basis for Elliptic Curve Cryptosystems
Elliptic curve cryptosystems are based on the construction of elliptic curve point groups over finite fields. On a finite field , denote the set of points of the elliptic curve as (including the infinity points). Construct the cyclic addition group on under the defined rules of addition and multiplication operations, where is the generating element of . All elements on are generated by multiplication by , i.e., .
The security of elliptic curve cryptosystems relies on the following mathematical puzzle for elliptic curve point groups:
- (a)
- The elliptic curve discrete logarithm problem (ECDLP) is used as follows: is the group defining the group over ; if , compute the smallest nonnegative integer such that .
- (b)
- The elliptic curve computational Diffie–Hellman problem (ECCDH) is used as follows: is the group defining the group over ; if , compute without mastering .
- (c)
- The elliptic curve decisional Diffie-Hellman problem (ECDDH) is used as follows: is the group defining the group over ; if , without mastering distinguish between and .
2.3. Bilinear Pairings
Bilinear pairs are also called bilinear maps. Bilinear pairs based on elliptic curves are defined as follows:
Definition 1.
Let be a large prime, be an additive group on , and be a generator; is a multiplicative group on , where is the identity of . Bilinear pairs satisfy the following conditions:
- (a)
- Bilinear: For any and , we have: or holds.
- (b)
- Non-degenerative: .
- (c)
- Computability: for any , there exists an efficient algorithm to compute .
2.4. Adversary Model
In certificate-less public key cryptosystems (CL-PKC), the adversary model mainly considers the following situations:
Adversary I: This type of adversary can replace the public key of a user and obtain the system master key but cannot obtain the secret value of the user.
Adversary II: This type of adversary cannot obtain the system master key but can obtain the secret value of the user and can replace the public key of the user.
3. Certificate-Less Distributed Key Management Scheme
In the space network, the ground control center is the only static node in the network; other space communication platforms (including various types of satellites and proximity space vehicles, etc.) constitute a collection of dynamic nodes. All dynamic nodes need to go through the ground control center to access the network. With the different spatial locations of the dynamic nodes, the communication quality and security of the wireless links between them and the ground centers exhibit large differences. For example, when nodes are far away from the ground center, the link BER is higher, and the communication delay is longer; when nodes roam into non-friendly space regions, the threats of interference and eavesdropping on the link are also higher. For ease of description, we refer to the area of space that is relatively close to the ground center, displays good communication links, and exhibits a low security threat as the ground center’s security field of view. In dynamic nodes, the trajectories of satellite nodes are periodic and predictable. They are more evenly distributed in the space region, and some of the satellite nodes periodically operate within the security field of view of the ground center, as shown in the Figure 2. Based on these characteristics of the space network, the design ideas presented in this paper are described as follows:
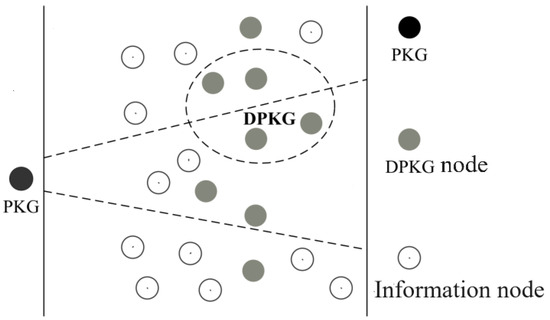
Figure 2.
Network model.
- (1)
- A centralized private key generation center PKG with the system master key is set up at the ground control center. The PKG generates the distribution of the initial portion of the private key for the node when it enters the network via the ground center.
- (2)
- A number of satellite nodes that can appear at least once in the PKG’s secure field of view within a specified time interval is selected to form distributed private key generation center distributed private key generators (DPKGs). A master key component is assigned to the DPKGs node by the PKG using the threshold secret sharing mechanism when it enters the network via the ground center. Threshold individual DPKGs nodes are federated to provide private key update service to the network nodes.
- (3)
- During the network operation phase, the PKG is responsible for providing the master key component update service to the DPKGs nodes when they are operating within the security horizon of the ground center.
3.1. Initialization
Consider a spatial network containing nodes, with a set of nodes , with the number of network nodes dynamically variable as nodes join or leave. Let be the node identity space; node has a network-wide unique identification . The initialization process is as follows:
- (1)
- System parameter selection: The PKG chooses a finite field of upper order , a cyclic additive group generated by , and a cyclic multiplicative group with the same order , as well as the bilinear mapping . Define two secure hash functions: , and ; randomly select as the system master key and compute as the system public key.
- (2)
- DPKGs setup: The PKG selects satellite nodes to form the set of DPKGs nodes and generates the initial master key sharing polynomial
For any DPKGs node , the initial master key component is computed using the above equation, as follows:
The public master key component authentication parameters array is . Clearly, number of DPKGs nodes can jointly reconstruct and then recover the master key by computing .
- (3)
- In a spatial network with distributed key generation centers, a node updating its private key once needs to broadcast a request message to at least number of DPKGs nodes. Since the space network uses wireless channels as communication links, a large number of nodes requesting key updates too centrally will inevitably cause network congestion and will greatly increase the computational delay of the DPKGs nodes. To avoid this, a batch update strategy is introduced: define the security usage period of a node’s private key as , set a discrete set of time points , where is the number of batches, and construct a mapping function from to update :
For node , the first key update is requested at the system clock , and thereafter key updates are requested every time. As long as the mapping function can map all nodes uniformly to , the private key update requests of all nodes can be spread evenly throughout the update time period. In real networks, the node identification is usually a set of serial and continuous number, such as IP, MAC address, etc., so it is easy to construct a mapping function that satisfies the conditions.
After initialization is complete, the parameters disclosed by the system include:
3.2. Node Private Key Generation
Set a non-zero string related to the number of node updates . Take at the initial moment and before each update of the node. Generate an initial public-private key pair for the node using and the node identity. For node , the initial public-private key pair is generated as follows:
- ①
- PKG generates a partial private key for node , where denotes a string concatenation operation;
- ②
- Node picks a secret value that makes up its full private key, ;
3.3. Node Public Key Generation
While generating the private key, node computes and generates its public key, .
3.4. Node Public-Private Key Update
In a spatial network with distributed key generation centers, a node updating its private key once needs to broadcast a request message to at least number of DPKGs nodes. Since the space network uses wireless channels as communication links, a large number of nodes requesting key updates too centrally will inevitably cause network congestion and will greatly increase the computational delay of DPKGs nodes. To avoid this, a batch update strategy is introduced, as follows: define the security usage period of a node’s private key as ; set a discrete set of time points , where is the number of batches; and construct a mapping function from to update mapping function
For node , the first key update is requested at the system clock , and thereafter, key updates are requested every time. As long as the mapping function can map all nodes uniformly to , the private key update requests of all nodes can be spread evenly throughout the update time period. In real networks, the node identification is usually a set of serial and continuous numbers, such as the IP, the MAC address, etc., so it is easy to construct a mapping function that satisfies the conditions. Expose to all nodes.
At the system time , node needs to perform the following steps if it wants to request an update of its private key, :
Step 1: Node calculates the value associated with this update as follows (where denotes the time of the first update of node, and denote the number of completed updates):
Step 2: Node picks a random number ; computes , and , and broadcasts a private key update request message to at least DPKGs nodes
Step 3: The DPKGs node that receives the request message verifies whether the requesting node is a revoked node. If yes, the algorithm ends; otherwise it continues.
Step 4: Node takes from ’s public key and utilizes bilinear pairwise qualities to verify whether is valid. If it is not valid, the update of a private key for it if refused; if it is valid, a partial private key message for node , is computed, where is the primary key component of node .
Step 5: Node picks a random number , computes , and encrypts part of the private key information . Return the private key update answer message to :
Step 6: After node receives the update answer cipher message, it decrypts the message to get part of the private key information issued by :
Read the validation parameter of from the validation array to verify that are equal. If unequal, discard; if equal, save .
Step 7: After node receives verified partial private key messages, it reconstructs the partial private key by using Lagrange interpolation, as follows:
where is the interpolation coefficient, and is the set of verified DPKGs nodes.
Step 8: For node , the new private key is , and the public key is .
3.5. DPKGs Master Key Component Update
In order to prevent the master key from being leaked by an attacker who has accumulated threshold key components, the system needs to update the master key components of each DPKGs node periodically. The updating principle is as follows:
Let the current cycle system master key sharing polynomial be . The PKG randomly selects the polynomial with the number of times , as follow:
Generate the master key sharing polynomial in the next cycle, as follows: . Since , the new polynomial still satisfies ; the polynomial form is changed, but the master key remains the same. To shorten the update elapsed time, the PKG can calculate the master key component and the array of authentication parameters for the next cycle of each DPKGs node in advance.
The specific update steps are as follows:
Step 1: When the DPKGs node runs into the safe field of view of the PKG, pick the random number and compute and ; this sends an update request message to the PKG, as follows:
Step 2: After receiving the request message, PKG checks whether node is a revoked node or not. If yes, the algorithm ends. Otherwise, continue with Step 3.
Step 3: The PKG verifies whether holds using the bilinear pair property. If it does not hold, the algorithm ends; if it holds, the message is considered to come from a legitimate node , and the execution continues to Step 4.
Step 4: The PKG picks the random number and the master key component , pre-generated from the new shared polynomial, and computes , , and . Return an update answer message to node , as follows:
Step 5: PKG broadcasts to the whole network, where is the new authentication parameter array, and is the new master key component enable time.
Step 6: After node receives the update answer message, verify whether is valid; if not, discard the answer message; if it is valid, prove that the answer is from the PKG, accept the answer message, and obtain the new master key component by calculating and get the new master key component.
Step 7: When the system clock , each DPKGs node updates the master key component; all nodes update the authentication parameter array .
3.6. Session Key Negotiation
If node and node need to negotiate the session key at the time of the system time , where ’s full private key and public key , and ’s full private key and public key , the node and session key negotiation process is as follows:
Step 1: picks a random number , computes , and sends , to .
Step 2: picks a random number , computes , and sends , to .
Step 3: calculates .
Step 4: calculates , where , is obtained as follows (where denotes taking the integer part):
, are calculated in a similar way.
This can be proved using the bilinear pair property, as follows:
Thus, is the session key negotiated between point and node . The negotiation of the session key can be completed after one interaction.
4. Security Analysis
4.1. Master Key Security
In the scheme of this paper, the attacker can compute , , and from the public parameters:
If one uses to invert or to invert , both will require the solving of discrete logarithms over a finite field. Solving this problem is difficult. Therefore, the attacker cannot obtain the system master key through the public parameters.
Attackers can also attempt to reconstruct the master key by accumulatively obtaining the threshold number of master key components by means of spoofing interference or listening to the failures of the DPKGs nodes. However, the periodic master key component update mechanism provided by the scheme in this paper can greatly reduce the possibility of the success of this attack. For a single DPKGs node, let the probability that an attacker is able to obtain its master key component in an update cycle be . Obviously, the length of the update period of the master key component affects the size of . The shorter the update period, the smaller will be. Let be the number of DPKGs nodes and be the threshold value; then, the probability that no less than the threshold number of the master key components are in the possession of the attacker (i.e., the probability that the attacker can reconstruct the master key) is calculated as follows:
when , and , the variation of with is shown in Figure 3.
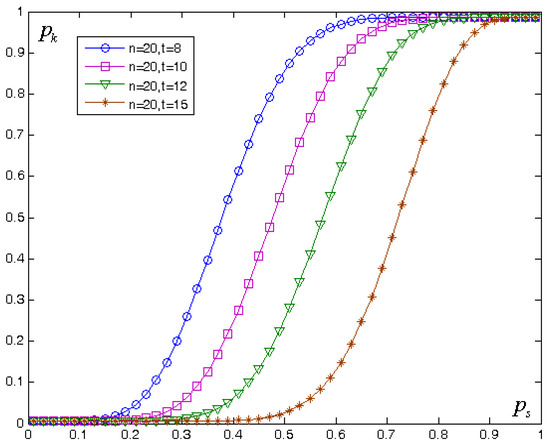
Figure 3.
Variation of pk with ps.
Properly setting the update period and the threshold value can make take a value that falls on the lower horizontal line on the left side of the graph, where the probability that the attacker can reconstruct the master key is close to 0.
4.2. Private and Master Key Component Update Security
During the private key update process, the DPKGs node utilizes the random number and in the request message to encrypt the new private key component and transmit it to the requesting node. The only messages an attacker can listen to are , , and . The inverse of from , is difficult. The attacker cannot decrypt because he cannot solve for .
The parameters and in the private key update request message provide the DPKGs node with the ability to authenticate itself to the requesting node . This is because
although the attacker can randomly select and forge . However, the forged cannot be verified by the DPKGs node because it cannot obtain part of the private key of the requesting node.
The authentication of the requesting node to the DPKGs node is realized by means of an authentication array, as follows:
The attacker, not having access to the master key component , similarly does not forge a false private key parameter that can be verified.
The same security mechanisms described above are provided during the master key component update process and will not be repeated here.
4.3. Session Key Negotiation Security
The session key negotiation mechanism security satisfies the following security properties.
- (1)
- Known session key security: During each negotiation of the session key, the interacting parties temporarily choose different random numbers to participate in generating the key for this session. If a session key between node and node is compromised, the attacker can only impersonate to communicate with or to communicate with in this session, but this will not affect the security of the other sessions between and ;
- (2)
- Perfect forward security: The long-term private key leakage of one of the parties in the scheme will not affect the confidentiality of the old session key. For an attacker who knows the private key of node , he is able to compute , but since he does not know with the private key of node , as well as , the attacker is not able to compute . For an attacker who knows the system’s master key , and can be computed, but without knowing and , the attacker cannot compute with . If the attacker knows the long-term private keys , of both parties, but cannot get any information about and , he cannot compute . Therefore, the negotiation mechanism provides perfect forward security.
- (3)
- Key disclosure plays security: For the known long-term private key of node attacker, although he can intercept by using and calculate by sending to , he cannot impersonate because he cannot calculate . For an attacker who knows the system master key s, although he can compute and , he is similarly unable to impersonate because he cannot compute .
- (4)
- Key control security: the session key is jointly generated by random numbers selected by each party; there is no question of one party controlling the result of generating the session key.
- (5)
- Unknown key sharing security: Even though the attacker obtains the private key of node or and can intercept the key negotiation parameters and , the attacker cannot obtain the information about and from node or and thus, cannot launch a man-in-the-middle attack.
4.4. Security Proof
In the scheme of this paper, the session key of A and B, , where are the public parameters, is the temporary session parameter provided by B, and is the secret parameter of A. If an attacker attempts to impersonate A and communicate with B, he needs to perform a round of communication interaction with A (exchange session parameters), and then output the correct and compute the correct session key. If the attacker is able to output the correct , we claim that his attack on this paper’s scheme is successful. From the previous section, , for Adversary I, who is able to make use of the master key in its possession, computationally obtains , but must guess ; Adversary II must guess the whole . In summary, for both types of adversary in this paper’s scheme to output the correct requires effort.
Theorem 1.
If an attacker is able to attack the scheme of this paper with a non-negligible advantage in polynomial time using a bounded number of random predicate queries (assuming public key queries and private key component queries and session key queries), then there exists an algorithm MB that can attack the scheme of this paper using the advantage of to solve the ECCDH problem, where is a natural constant, and is a system security parameter.
Proof.
MB first builds the scheme of this paper, publishes the public parameters , and securely stores Adversary I. MA is an attacker of the scheme of this paper (which can be that MB is the challenger of MA—either Adversary I or Adversary II—whose goal is to crack the authentication scheme of this paper by asking a bounded number of random questions). MB trains MA through a simulation process and tries to solve the ECCDH problem. □
MC defeats the ECCDH problem challenger for MB. Before the simulation starts, MC selects , computes , , and sends to MB. MB tries to solve the ECCDH problem by obtaining , without having .
In addition, MB needs to maintain an initially empty list for keeping track of the MA’s public key queries and private key components query; alternatively, , denotes the guess of the attack on the MA, and the MA will impersonate to negotiate for the key with other node members.
- Stage 1: Interrogation Stage
Public key query: MA asks MB for the public key of . For the th query, if , MB randomly selects , , he computes and adds to ; if he selects , he calculates , and adds to . After completing the above, MB returns to MA.
Private key component query: MA sends to MB, querying ’s private key component . If , MB uses to fetch from , calculates , updates the table entry of in to , and sends to MA; otherwise, the simulation is interrupted.
Session key interrogation: MA randomly selects , and sends to MB to ask as for the same information as the ’s session key . If , MB uses take out from , uses take out from , and randomly selects . He performs the calculation as follows: , sets , and returns it to MA; otherwise, the simulation is interrupted.
- Stage 2: Challenge Stage
MA randomly selects , counts , sends to MB, and tries to impersonate to negotiate the session key with . If , MB interrupts the simulation; otherwise, MB picks , selects , and sends to MA, which outputs as an attack result. MB verifies that holds. If it does not hold, the MA challenge fails; if it does, then , so , i.e., . At this point, the session key obtained by the MA through calculation is as follows:
MA’s challenge is successful. MB outputs to MC to successfully resolve the ECCDH problem.
In the above reduction process, the MB always replies to the MA’s query with a random value, i.e., the MA’s simulated view is co-distributed with the real attack, and thus the simulation process is complete. MB is able to solve the ECCDH problem, depending on the following three events:
: private key component query; no interruptions.
: The session key enquiry was not interrupted.
: when the MA initiates the challenge.
: MA challenge successful.
It is easy to observe the following: , , ; therefore, the advantages for MB to solve the ECCDH problem are as follows: Q.E.D.
In summary, these two types of adversary attacks on the scheme of this paper are difficult to complete.
5. Simulation Verification
A network environment is modeled using NS2 to simulate and analyze the scheme of this paper. The simulation scenarios are generated using setdest, a scenario generation tool provided by CMU, in which the nodes’ mobility model adopts the random point model, the link layer protocol adopts the Mac/802.11 protocol, the routing protocol adopts the AODV protocol, and the bandwidth of data transmission is 2 Mbps. Additional parameter settings are shown in Table 1 below:

Table 1.
Analog parameter settings.
Keeping the network size unchanged, the impact of node movement speed changes as the performance of the scheme is examined. During the network operation phase, the variation of node private key update delay and the average number of re-transmissions of update requests are shown in Figure 4 and Figure 5, respectively. It can be seen that in the low-speed case, the update delay is larger, and the number of re-transmissions is slightly higher, which is caused by the nodes not being able to find the threshold DPKGs node in time at low speed. With the increase in mobile speed, the delay is gradually stabilized, and the average delay is about 300 s, which shows that the scheme in this paper exhibits stability.
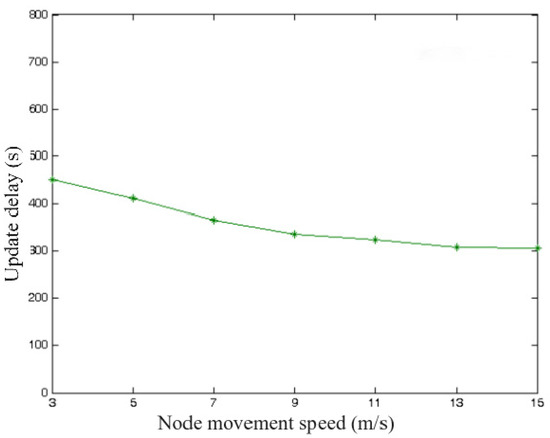
Figure 4.
Variation of node update delay.
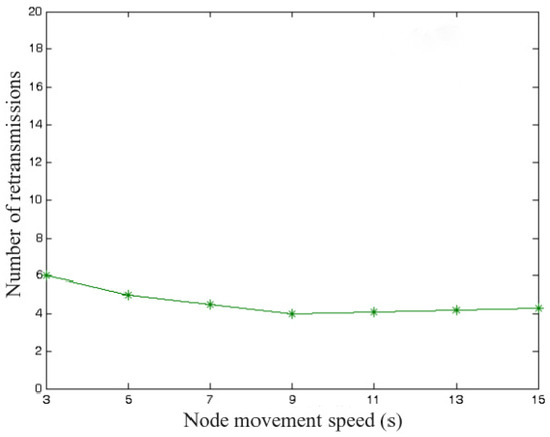
Figure 5.
Variation in the number of node re-transmissions.
The node private update success rate is shown in Figure 6, which indicates that the change of speed has little effect on the node private key update success rate, which is close to 100%. The variation of session key negotiation delay is shown in Figure 7, from which it can be seen that the key negotiation delay basically converges around 1.5 s. The above also shows the feasibility and stability of the scheme.
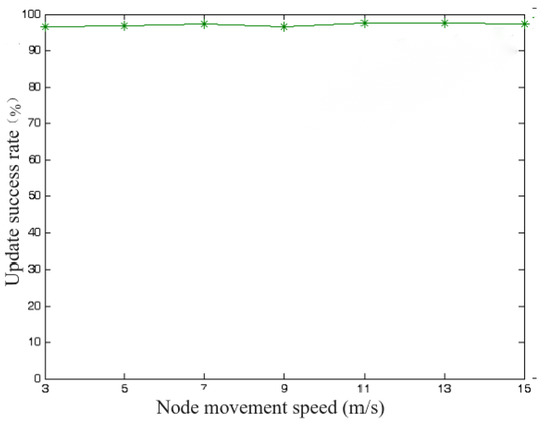
Figure 6.
Variation of node update success rate.
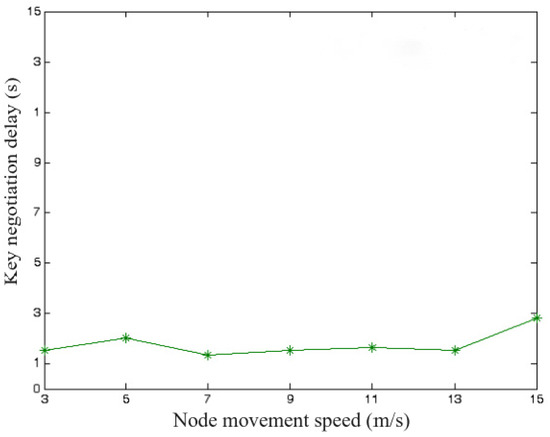
Figure 7.
Session key negotiation delay variation.
6. Conclusions
Because of the particularity and complexity of space networks, the key management schemes based on PKI/CA are no longer been applicable, and the identity-based cryptography used by existent schemes includes the inherent problem of key escrow. In order to resolve these problems, a certificate-less distributed key management scheme is proposed. On the basis of the properties of space networks, the method for constructing distributed private key generators is put forward. Using the identity-based cryptography proposed by Bonehg and Franklin, this scheme designs the methods of updating private keys, updating host-key shares, and negotiating session keys. Finally, the scheme is analyzed for security and simulated for correctness.
Author Contributions
C.L., writing—original draft preparation; L.S., writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the Key Science and Technology Program of Henan Province (No. 222102210224) and the Joint Fund Project of Science and Technology R&D Plan of Henan Province (No. 222103810044).
Data Availability Statement
The data used to support this research article are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Rinaldi, F.; Maattanen, H.-L.; Torsner, J.; Pizzi, S.; Andreev, S.; Iera, A.; Koucheryavy, Y.; Araniti, G. Non-terrestrial networks in 5G and beyond: A survey. IEEE Access 2020, 8, 165178–165200. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, D.; Song, N.; Sheng, M.; Li, J.; Liu, J. Concurrent reconfiguration of resource-oriented emergency TT and C mission planning for space information networks. J. Commun. Inf. Netw. 2021, 6, 142–152. [Google Scholar] [CrossRef]
- Li, J.; Wang, P.; Li, H.; Shi, K. Enhanced time-expanded graph for space information network modeling. Sci. China Inf. Sci. 2022, 65, 235–248. [Google Scholar] [CrossRef]
- Yu, Q.; Wang, J.; Shi, Y. Review of major research plan on “The Fundamental Theory and Key Technologies of The Space Information Networks”. Bull. Natl. Nat. Sci. Found. China 2023, 37, 831–839. [Google Scholar]
- Niu, Z.; Shen, X.S.; Zhang, Q.; Tang, Y. Space-air-ground integrated vehicular network for connected and automated vehicles: Challenges and solutions. Intell. Converg. Netw. 2020, 1, 142–169. [Google Scholar] [CrossRef]
- Bai, L.; De Cola, T.; Yu, Q.; Zhang, W. Space Information Networks. IEEE Wireless Commun. 2019, 26, 8–9. [Google Scholar] [CrossRef]
- Guo, H.; Zhou, X.; Liu, J.; Zhang, Y. Vehicular intelligence in 6G: Networking, communications, and computing. Veh. Commun. 2021, 33, 100399. [Google Scholar] [CrossRef]
- Yu, Q.; Wang, J.; Bai, L. Architecture and critical technologies of space information networks. J. Commun. Inf. Netw. 2016, 1, 1–9. [Google Scholar] [CrossRef]
- Li, G.D.; Zhao, Z.W.; Di, L. Research on survivability of spatial information network. In Proceedings of the 2022 2nd International Conference on Computer Science, Electronic Information Engineering and Intelligent Control Technology (CEI), Nanjing, China, 23–25 September 2022; pp. 171–175. [Google Scholar]
- Bhasin, K.; Hayden, J.L. Space Internet Architectures and Technologies for NASA Enterprises. Int. J. Satell. Commun. 2002, 20, 311–332. [Google Scholar] [CrossRef]
- Ji, S.; Sheng, M.; Zhou, D.; Bai, W.; Cao, Q.; Li, J. Flexible and Distributed Mobility Management for Integrated Terrestrial-Satellite Networks: Challenges, Architectures, and Approaches. IEEE Network 2021, 35, 73–81. [Google Scholar] [CrossRef]
- Yan, J.; Lu, Y.; Liu, Y.; Chen, L. Research on Beidou-based inter-domain identity authentication for mobile object. In Proceedings of the 2014 IEEE Workshop on Advanced Research and Technology in Industry Applications (WARTIA), Ottawa, ON, Canada, 29–30 September 2014; pp. 923–926. [Google Scholar]
- Wang, H.; Li, J.; Chengzhe, L.A.I. Identity Based Dynamic Key Management of Airborne Ad Hoc Network. J. Electron. Inf. Technol. 2018, 40, 1985–1991. [Google Scholar]
- Zhou, D.; Sheng, M.; Li, J.; Han, Z. Aerospace Integrated Networks Innovation for Empowering 6G: A Survey and Future Challenges. IEEE Commun. Surv. Tutor. 2023, 25, 975–1019. [Google Scholar] [CrossRef]
- Jiang, S.; Zhu, X.; Wang, L. An efficient anonymous batch authentication scheme based on HMAC for VANETs. IEEE Trans. Intell. Transp. Syst. 2016, 17, 2193–2204. [Google Scholar] [CrossRef]
- Shamir, A. Identity Based Cryptosystems and Signature Schemes. In Advances in Cryptology—CRYPTO 1984; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1984; Volume 196, pp. 47–53. [Google Scholar]
- Boneh, D.; Franklin, M. Identity-based encryption forms the Weil pairing. In Advances in Cryptology CRYPTO 2001; Lecture Notes in Computer Science 2139; Kilian, J., Ed.; Springer: Berlin/Heidelberg, Germany, 2001; pp. 213–229. [Google Scholar]
- Saxena, N.; Tsudik, G.; Yi, J.H. Identity-based Access Control for Ad Hoc Groups. In Information Security and Cryptology—ICISC 2004; Springer: Berlin/Heidelberg, Germany, 2004; pp. 362–379. [Google Scholar]
- Deng, H.; Mukherjee, A.; Agrawal, D. Threshold and Identity-based Key Management and Authentication for Wireless Ad Hoc Networks. In Proceedings of the International Conference on Information Technology: Coding and Computing, 2004, Las Vegas, NV, USA, 5–7 April 2004; pp. 107–111. [Google Scholar]
- Bao, Q.; Hou, M.; Choo, K.K.R. A one-pass identity-based authentication and key agreement protocol for wireless roaming. In Proceedings of the the Sixth International Conference on Information Science and Technology, Dalian, China, 6–8 May 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 443–447. [Google Scholar]
- Huo, S.W.; Luo, C.Y.; Xin, H.Z. Identity-Based Inter-domain Authentication Scheme in Pervasive Computing Environments. In Intelligent Computing and Information Science—ICICIS 2011—Communications in Computer and Information Science; Chen, R., Ed.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 135, pp. 314–320. [Google Scholar] [CrossRef]
- Luo, C.-y.; Li, W.; Xing, H.-z.; Chu, X. Research on Identity-based Distributed Key Management in Space Network. J. Electron. Inf. Technol. 2010, 32, 183–188. [Google Scholar] [CrossRef]
- Al-Riyami, S.S.; Paterson, K.G. Certificateless Public Key Cryptography. In Advances in Cryptology ASIA CRYPT 2003; LNCS 2894; Springer: Berlin/Heidelberg, Germany, 2003; pp. 452–473. [Google Scholar]
- Chen, X.; Zhang, E.; Kim, K. A New ID-based Group Signature Scheme from Bilinear Pairings—WISA’03; Springer: Berlin/Heidelberg, Germany, 2003; pp. 585–592. [Google Scholar]
- Gorantla, M.C.; Saxena, A. An Eficient Certificateless Signature Scheme. In Computational Intelligence and Security; CIS 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 110–116. [Google Scholar]
- Al-Riyami, S.S.; Paterson, K.G. CBE from CL-PKE: A Generic Construction and Efficient Schemes. Public Key Cryptography PKC 2005. In Proceedings of the 8th International Workshop on Theory and Practicein Public Key Cryptography, Les Diablerets, Switzerland, 23–26 January 2005; pp. 398–415. [Google Scholar]
- Baek, J.; Safavi-Naini, R.; Susilo, W. Certificateless pubic key encryption without pairing. In Proceedings of the Information Security: 8th International Conference, Singapore, 20–23 September 2005; pp. 134–148. [Google Scholar]
- Wu, C.; Chen, Z. A New Efficient Certificateless Signcryption Scheme. In Proceedings of the 2008 International Symposium on Information Science and Engineering, Shanghai, China, 20–22 December 2008; pp. 661–664. [Google Scholar] [CrossRef]
- Yuan, Y.M.; Li, D.; Tian, L.W.; Zhu, H.S. Certificateless signature scheme without random oracles. In Advances in Information Security and Assurance—ISA 2009; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5576, pp. 31–40. [Google Scholar]
- Liu, T.; Wang, X.F.; Xiao, G.Z. Security Analysis and Improvement of a Strongly Secure Certificateless Key Agreement Protocol. Comput. Sci. 2012, 39, 73–75. [Google Scholar]
- Chen, T.H.; Lee, W.B.; Chen, H.B. A self-verification authentication mechanism for mobile satellite communication systems. Comput. Electr. Eng. 2009, 35, 41–48. [Google Scholar] [CrossRef]
- Ming, Y.; Cheng, H.L. Efficient certificateless conditional privacy preserving authentication scheme in VANETs. Mob. Inf. Syst. 2019, 2019, 1–19. [Google Scholar] [CrossRef]
- Li, C.; Zhang, X.; Wang, H.; Li, D. An Enhanced Secure Identity-Based Certificateless Public Key Authentication Scheme for Vehicular Sensor Networks. Sensors 2018, 18, 194. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.B.; Huang, W.H.; Feng, J.Y. Secure communication mechanism for VSN based on certificateless signcryption. J. Commun. 2021, 42, 128–136. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).