Counting Tree-like Multigraphs with a Given Number of Vertices and Multiple Edges
Abstract
1. Introduction
1.1. General Context
1.2. Motivation
1.3. Literature Review
1.4. Contributions
1.5. Organization
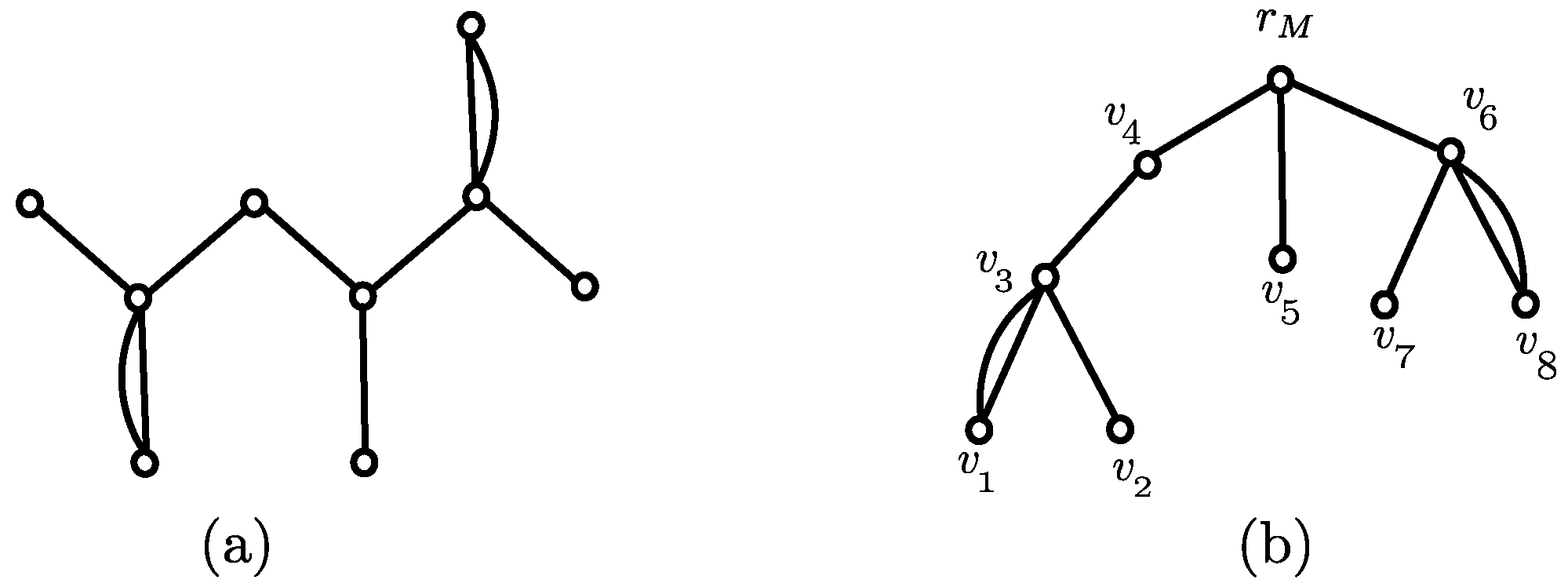
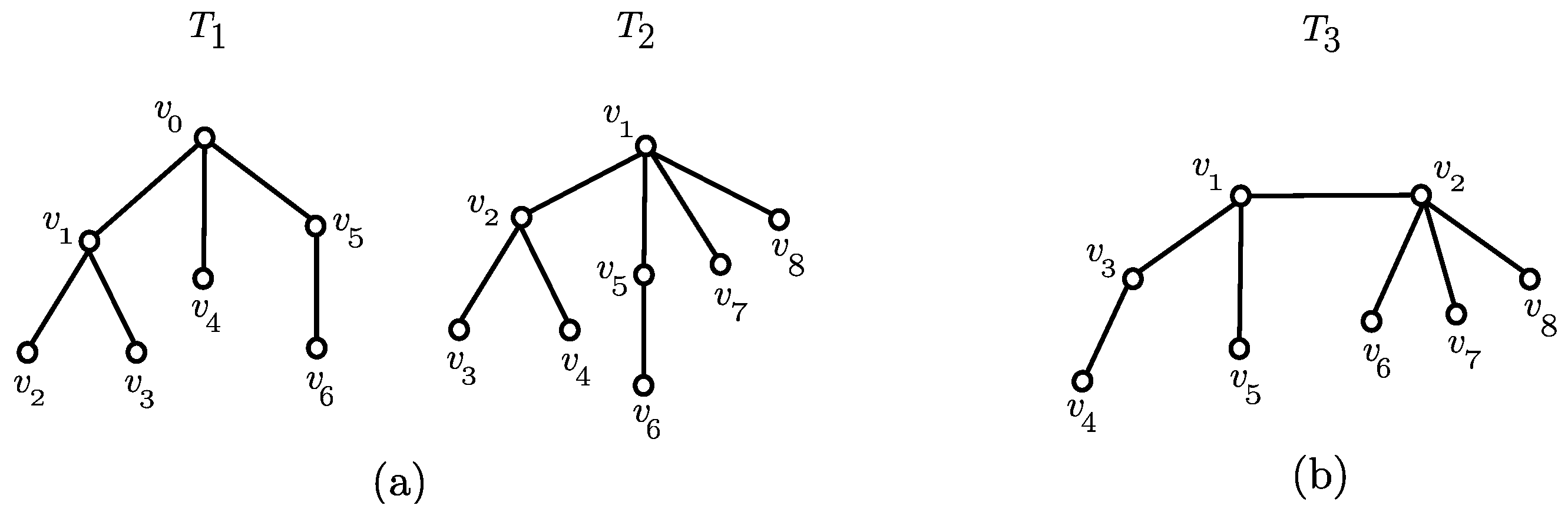
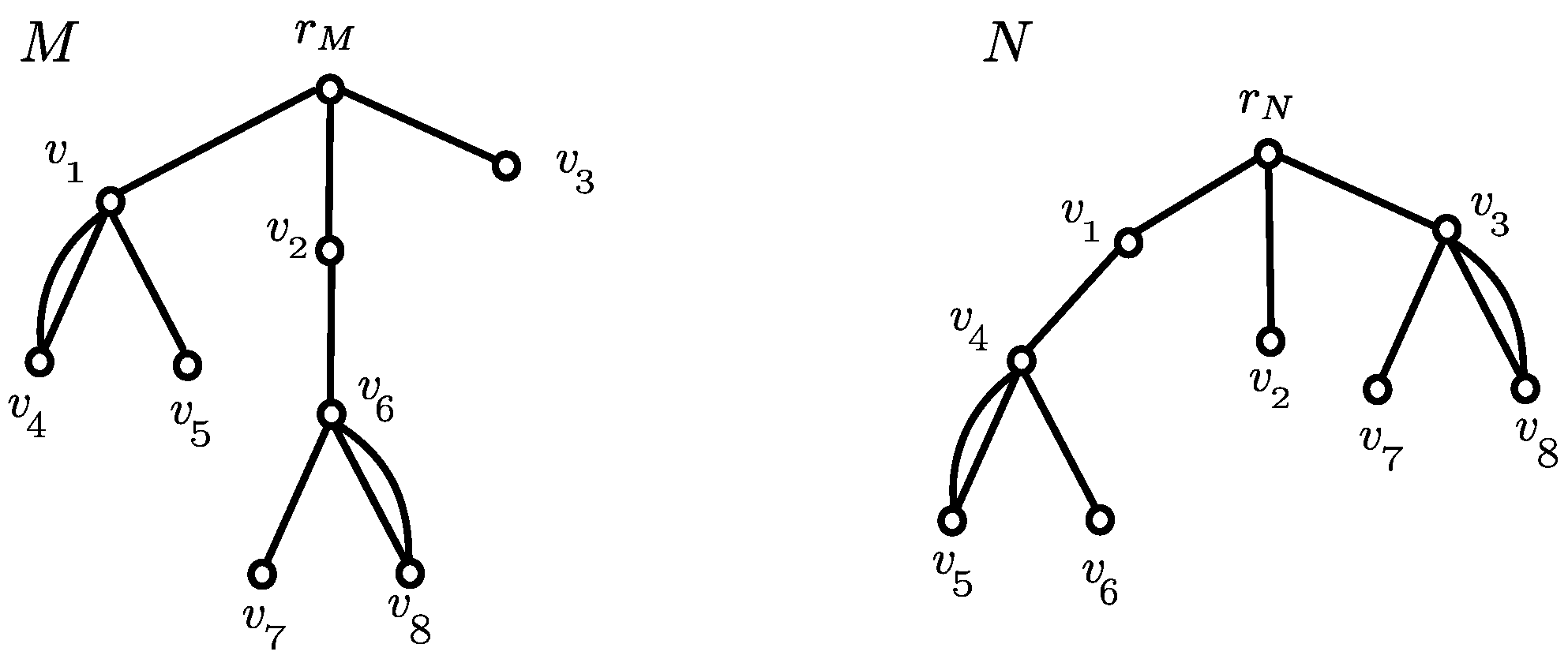
2. Preliminaries
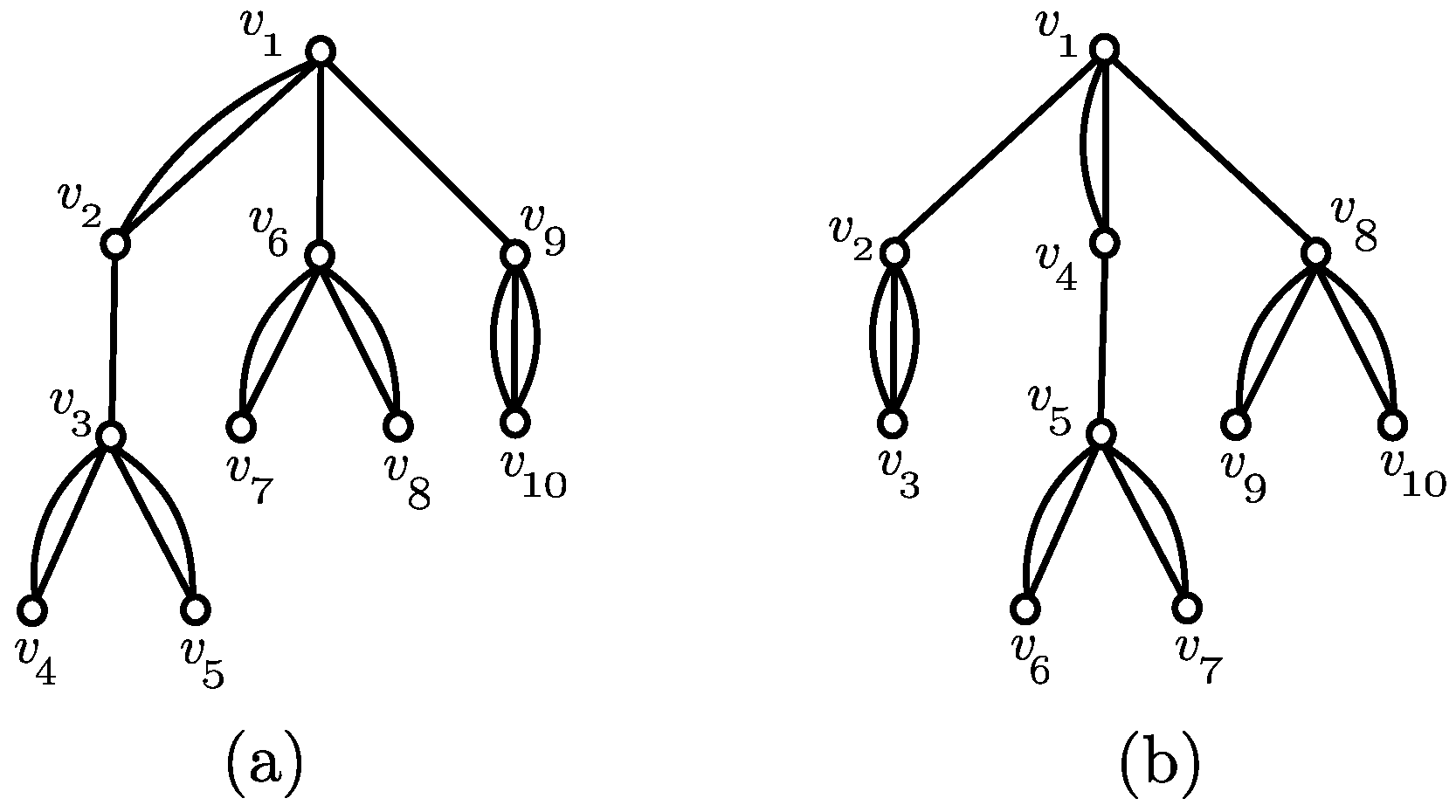
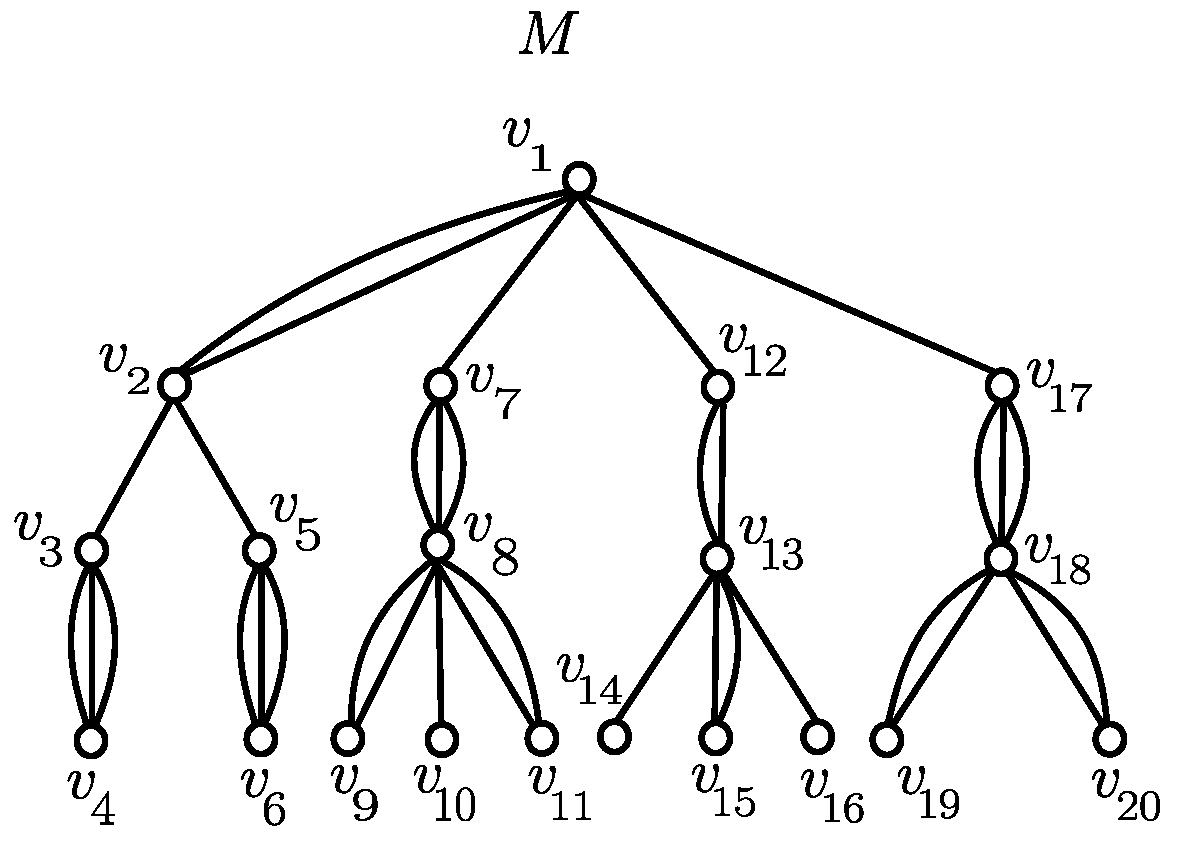
3. Proposed Method
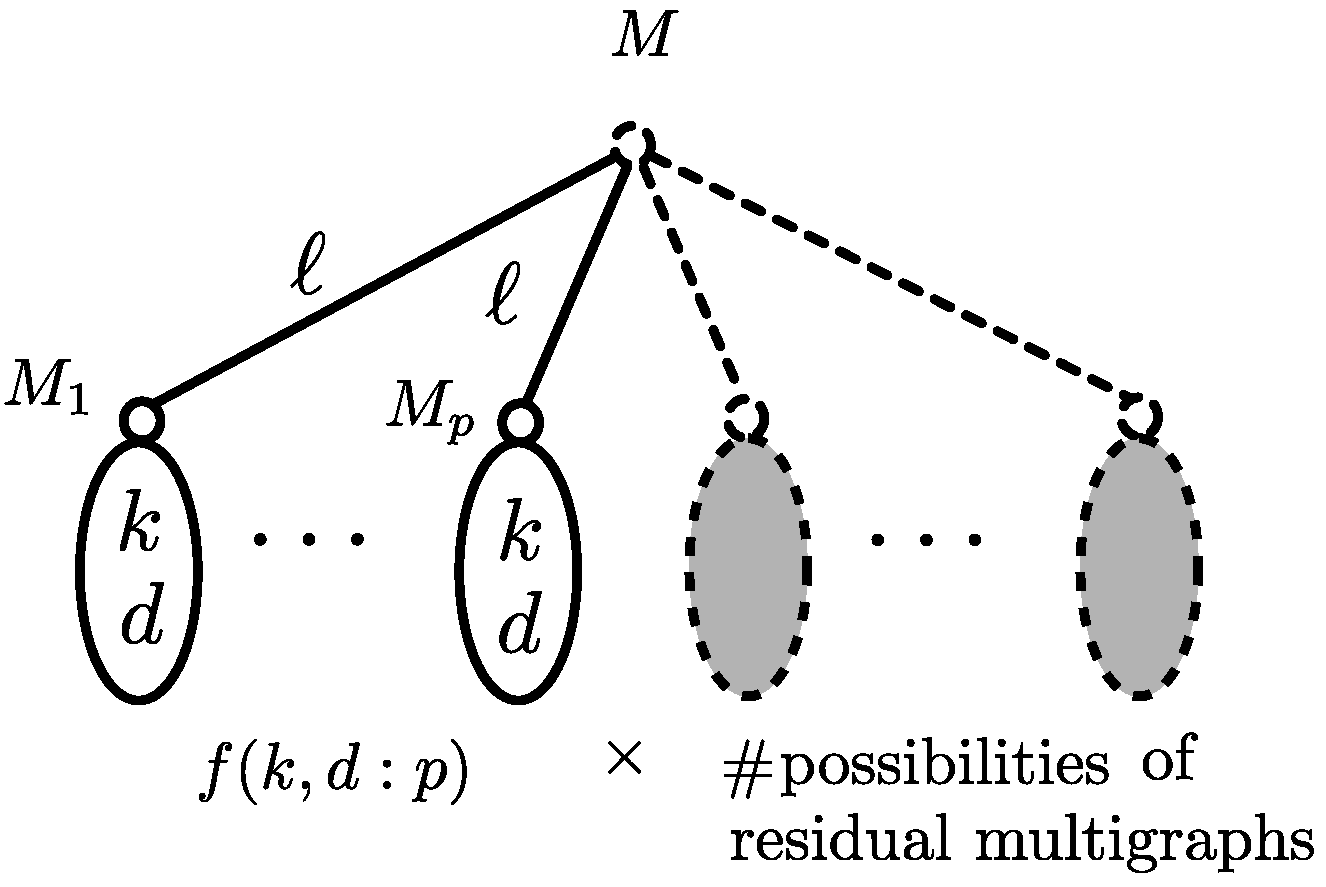
3.1. Canonical Representation
3.2. Subproblem
- (i)
- if ;
- (ii)
- if ;
- (iii)
- if ; and
- (iv)
- .
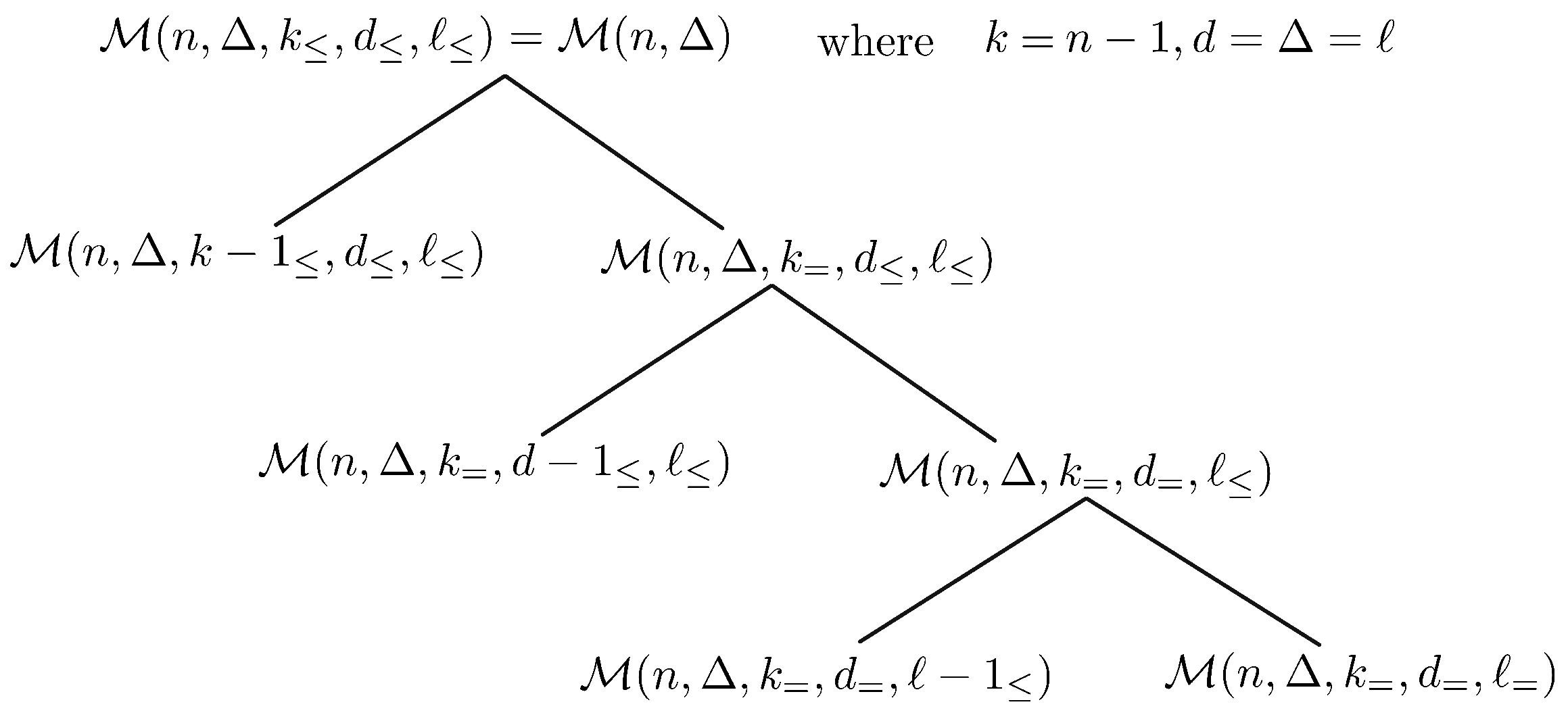
3.3. Recursive Relations
- (C1)
- , and .
- (C2)
- , and .
- (C3)
- , and .
- (C4)
- , and .
- (i)
- with when .
- (ii)
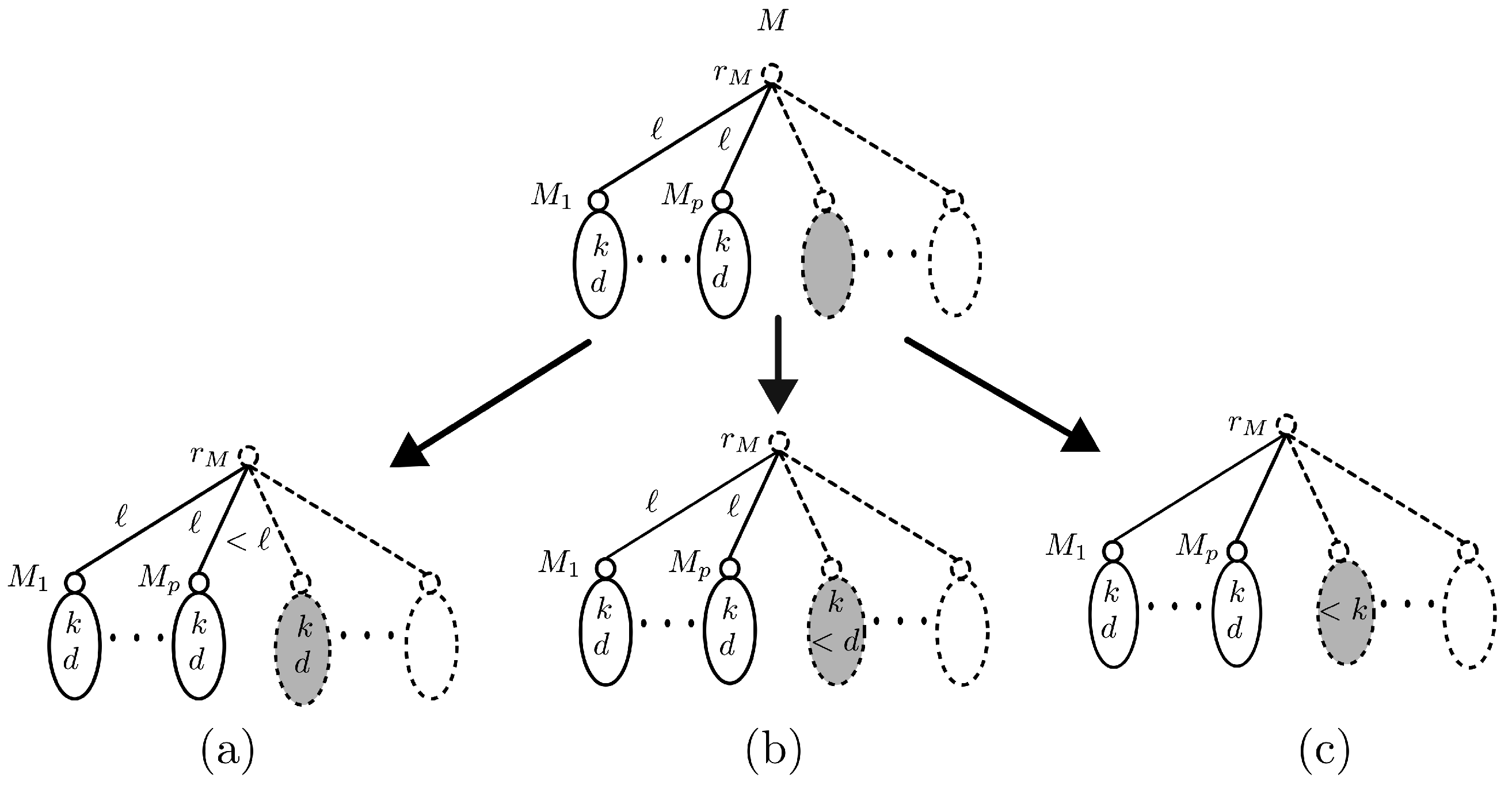
- The residual multigraph of M belongs to exactly one of the following families:;; or
- (i)
- Since , there is at least one vertex such that . It follows that . It further asserts that and . This concludes that with when .
- (ii)
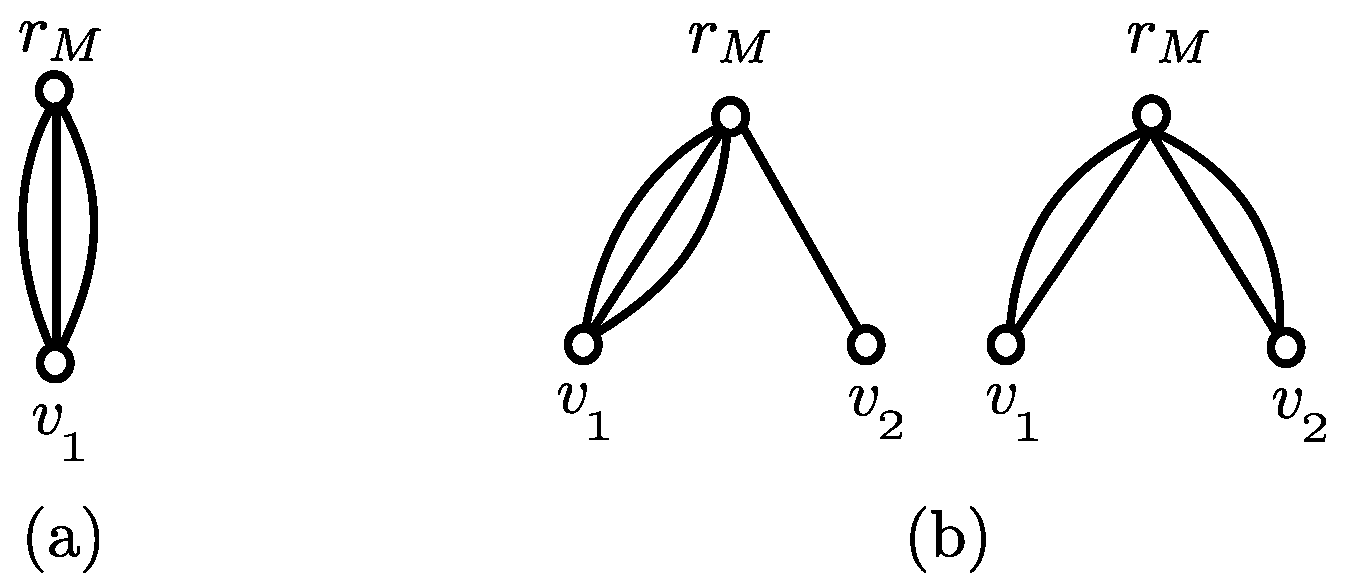
- Let R represent the residual multigraph of M. By definition of R, it holds that . Moreover, for each vertex the descendant subgraph satisfies exactly one of the Conditions (C2)–(C4). Now, if there exists a vertex such that satisfies Condition (C2) as illustrated in Figure 11a, then , and hence . For such that satisfies Condition (C3) as illustrated in Figure 11b, i.e., , and , then the residual multigraph . If satisfies Condition (C4) as illustrated in Figure 11c, i.e., , and , then by definition of R, it holds that .□
- (i)
- if and ;
- (ii)
- if and ;
- (iii)
- if and ;
- (iv)
- if and
- if and ; or
- if and ;
- if and
- (a)
- if and ;
- (b)
- if and ;
- (c)
- if and ;
- (d)
- if and
- (a)
- if and ;
- (b)
- if and ;
- (c)
- if and ;
- (d)
- if and
- (i)
- if and ;
- (ii)
- if and ;
- (iii)
- if and ;
- (iv)
- if and
- (i)
- if ;
- (ii)
- if ;
- (iii)
- if ;
- (iv)
- if ;
- (v)
- if ; and
- (vi)
- if
3.4. Initial Conditions
- (i)
- if “ and " and if “ and " or, “”;
- (ii)
- if and , and if ;
- (iii)
- if , and if ;
- (iv)
- if and ;
- (v)
- if ; and
- (vi)
- if “
- (i)
- A multigraph M with exists if and only if , , and . No such tree exists with a single vertex and multiple edges.
- (ii)
- It follows from Lemma 3(i) and (ii) that .
- (iii)
- Since for , the size of of the descendant subgraph must be at least 2 and ℓ must be in the range of
- (iv)
- There is only one descendant subgraph of size 1, so the only possibility for multiple edges to be on the edges , i.e., if In case , then there is no residual multigraph which can accommodate the remaining multiple edges.
- (v)
- The maximum number of multiple edges in the descendant subgraphs plus the tree-like multigraphs, i.e., must be less than or equal to Otherwise will exceed as both d and ℓ have the range from 0 to .
- (vi)
- The maximum size of the descendant subgraph can be
3.5. Proposed Algorithm
| Algorithm 1 An algorithm for counting based on DP |
|
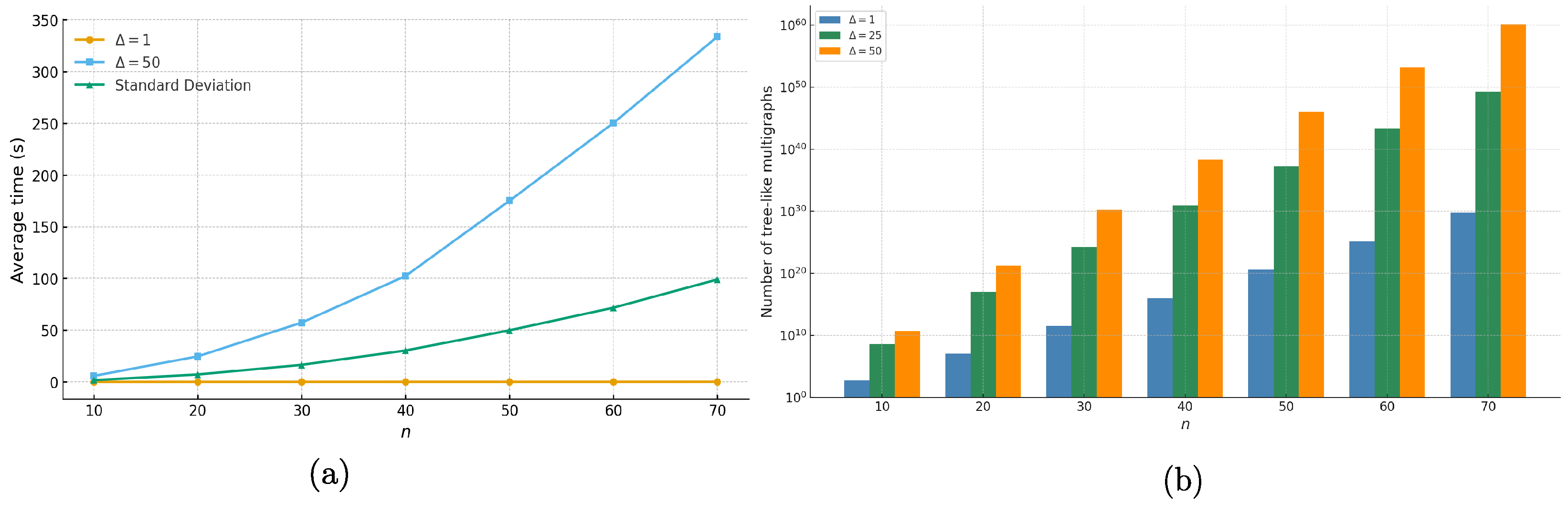
3.6. Experimental Results and Comparison
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DP | Dynamic Programming |
| CID | Compound identifier |
| RAM | Random Access Memory |
Notation
| Symbol | Description |
| n | Number of vertices |
| Number of multiple edges | |
| M | Rooted tree-like multigraph |
| Set of all mutually non-isomorphic rooted tree-like multigraphs with n vertices and multiple edges | |
| Number of non-isomorphic rooted tree-like multigraphs with n vertices and multiple edges | |
| Number of vertices in the descendent subgraphs | |
| Number of edges in the descendent subgraphs | |
| Number of edges between the roots of M and root of descendent subgraphs | |
| Maximum number of vertices in a descendant subgraph of M | |
| Maximum number of multiple edges in a descendant subgraph of M | |
| Maximum number of multiple edges between the root of M and roots of descendant subgraph | |
| Set of non-isomorphic rooted tree-like multigraphs with n vertices and maximum degree , where any descendant subgraph has at most k vertices, at most d multiple edges, and there are at most ℓ multiple edges between the root and roots of descendant subgraphs | |
| Subset of where | |
| Subset of where | |
| Subset where | |
| Number of combinations with repetition of x descendant subgraphs from the family |
References
- Blum, L.C.; Reymond, J.-L. 970 Million Druglike Small Molecules for Virtual Screening in the Chemical Universe Database GDB-13. J. Am. Chem. Soc. 2009, 131, 8732–8733. [Google Scholar] [CrossRef]
- Lim, J.; Hwang, S.-Y.; Moon, S.; Kim, S.; Kim, W.Y. Scaffold-Based Molecular Design with a Graph Generative Model. Chem. Sci. 2020, 11, 1153–1164. [Google Scholar] [CrossRef]
- Meringer, M.; Schymanski, E.L. Small Molecule Identification with MOLGEN and Mass Spectrometry. Metabolites 2013, 3, 440–462. [Google Scholar] [CrossRef]
- Fink, T.; Reymond, J.-L. Virtual Exploration of the Chemical Universe up to 11 Atoms of C, N, O, F: Assembly of 26.4 Million Structures (110.9 Million Stereoisomers) and Analysis for New Ring Systems, Stereochemistry, Physicochemical Properties, Compound Classes, and Drug Discovery. J. Chem. Inf. Model. 2007, 47, 342–353. [Google Scholar] [CrossRef]
- Faulon, J.-L.; Churchwell, C.J.; Visco, D.P. The Signature Molecular Descriptor. 2. Enumerating Molecules from Their Extended Valence Sequences. J. Chem. Inf. Comput. Sci. 2003, 43, 721–734. [Google Scholar] [CrossRef]
- Benecke, C.; Grund, R.; Hohberger, R.; Kerber, A.; Laue, R.; Wieland, T. MOLGEN+, a Generator of Connectivity Isomers and Stereoisomers for Molecular Structure Elucidation. Anal. Chim. Acta 1995, 314, 141–147. [Google Scholar] [CrossRef]
- Peironcely, J.E.; Rojas-Chertó, M.; Fichera, D.; Reijmers, T.; Coulier, L.; Faulon, J.-L.; Hankemeier, T. OMG: Open Molecule Generator. J. Cheminform. 2012, 4, 21. [Google Scholar] [CrossRef] [PubMed]
- Akutsu, T.; Nagamochi, H. Comparison and Enumeration of Chemical Graphs. Comput. Struct. Biotechnol. J. 2013, 5, e201302004. [Google Scholar] [CrossRef] [PubMed]
- Cayley, A. On the Analytical Forms Called Trees: With Application to the Theory of Chemical Combinations; Cambridge University Press: Cambridge, UK, 1875. [Google Scholar] [CrossRef]
- Tamura, Y.; Nishiyama, Y.; Wang, C.; Sun, Y.; Shurbevski, A.; Nagamochi, H.; Akutsu, T. Enumerating Chemical Graphs with Mono-block 2-Augmented Tree Structure from Given Upper and Lower Bounds on Path Frequencies. arXiv 2020, arXiv:2004.06367. [Google Scholar] [CrossRef]
- Zhang, F.; Zhu, J.; Chiewvanichakorn, R.; Shurbevski, A.; Nagamochi, H.; Akutsu, T. A New Approach to the Design of Acyclic Chemical Compounds Using Skeleton Trees and Integer Linear Programming. Appl. Intell. 2022, 52, 17058–17072. [Google Scholar] [CrossRef]
- Batool, M.; Azam, N.A.; Khan, M. A Unified Approach to Inferring Chemical Compounds with the Desired Aqueous Solubility. J. Cheminform. 2024, 16, 66. [Google Scholar] [CrossRef]
- Cao, P.-Y.; He, Y.; Cui, M.-Y.; Zhang, X.-M.; Zhang, Q.; Zhang, H.-Y. Group Graph: A Molecular Graph Representation with Enhanced Performance, Efficiency and Interpretability. J. Cheminform. 2024, 16, 133. [Google Scholar] [CrossRef]
- Pólya, G.; Read, R.C. Combinatorial Enumeration of Groups, Graphs, and Chemical Compounds; Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar] [CrossRef]
- Pólya, G. Kombinatorische Anzahlbestimmungen für Gruppen, Graphen und chemische Verbindungen. Acta Math. 1937, 68, 145–254. [Google Scholar] [CrossRef]
- McKay, B.D.; Piperno, A. Practical Graph Isomorphism, II. J. Symb. Comput. 2014, 60, 94–112. [Google Scholar] [CrossRef]
- Akutsu, T.; Fukagawa, D. Inferring a Chemical Structure from a Feature Vector Based on Frequency of Labeled Paths and Small Fragments. In Proceedings of the 5th Asia-Pacific Bioinformatics Conference, Hong Kong, 15–17 January 2007; pp. 165–174. [Google Scholar] [CrossRef]
- Fujiwara, H.; Wang, J.; Zhao, L.; Nagamochi, H.; Akutsu, T. Enumerating Tree-Like Chemical Graphs with Given Path Frequency. J. Chem. Inf. Model. 2008, 48, 1345–1357. [Google Scholar] [CrossRef]
- Nakano, S.; Uno, T. Efficient Generation of Rooted Trees. Natl. Inst. Inform. Tech. Rep. NII-2003 2003, 8, 4–63. [Google Scholar]
- Nakano, S.; Uno, T. Generating Colored Trees. In Graph-Theoretic Concepts in Computer Science, Proceedings of the 31st International Workshop, WG 2005, Metz, France, 23–25 June 2005; Revised Selected Papers; Springer: Berlin/Heidelberg, Germany, 2005; pp. 249–260. [Google Scholar] [CrossRef]
- Aringhieri, R.; Hansen, P.; Malucelli, F. Chemical Trees Enumeration Algorithms. Q. J. Belg. Fr. Ital. Oper. Res. Soc. 2003, 1, 67–83. [Google Scholar] [CrossRef]
- Ishida, Y.; Zhao, L.; Nagamochi, H.; Akutsu, T. Improved Algorithms for Enumerating Tree-Like Chemical Graphs with Given Path Frequency. Genome Inform. 2008, 21, 53–64. [Google Scholar] [CrossRef] [PubMed]
- Shimizu, M.; Nagamochi, H.; Akutsu, T. Enumerating Tree-Like Chemical Graphs with Given Upper and Lower Bounds on Path Frequencies. BMC Bioinform. 2011, 12, S3. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, M.; Nagamochi, H.; Akutsu, T. A 2-Phase Algorithm for Enumerating Tree-Like Chemical Graphs Satisfying Given Upper and Lower Bounds. IPSJ SIG Tech. Rep. 2012, 28, 1–8. [Google Scholar]
- Maudet, G.; Danoy, G. Search Strategy Generation for Branch and Bound Using Genetic Programming. arXiv 2024, arXiv:2412.09444. [Google Scholar] [CrossRef]
- Sciandra, L.; Esposito, R.; Grosso, A.C.; Sacerdote, L.; Zucca, C. Graph Convolutional Branch and Bound. arXiv 2024, arXiv:2406.03099. [Google Scholar] [CrossRef]
- Labassi, A.G.; Chételat, D.; Lodi, A. Learning to Compare Nodes in Branch and Bound with Graph Neural Networks. arXiv 2024, arXiv:2210.16934. [Google Scholar]
- Ye, X.; Li, R.-H.; Dai, Q.; Qin, H.; Wang, G. Efficient Biclique Counting in Large Bipartite Graphs. Proc. ACM Manag. Data 2023, 1, 78. [Google Scholar] [CrossRef]
- Akutsu, T.; Fukagawa, D. Inferring a Graph from Path Frequency. In Proceedings of the 16th Annual Symposium on Combinatorial Pattern Matching (CPM), Jeju Island, Republic of Korea, 19–22 June 2005; pp. 371–382. [Google Scholar] [CrossRef]
- Akutsu, T.; Fukagawa, D.; Jansson, J.; Sadakane, K. Inferring a Graph from Path Frequency. Discret. Appl. Math. 2012, 160, 1416–1428. [Google Scholar] [CrossRef]
- Rué, J.; Sau, I.; Thilikos, D.M. Dynamic Programming for Graphs on Surfaces. ACM Trans. Algorithms 2014, 10, 8. [Google Scholar] [CrossRef]
- Imada, T.; Ota, S.; Nagamochi, H.; Akutsu, T. Efficient Enumeration of Stereoisomers of Tree Structured Molecules Using Dynamic Programming. J. Math. Chem. 2011, 49, 910–970. [Google Scholar] [CrossRef]
- Imada, T.; Ota, S.; Nagamochi, H.; Akutsu, T. Efficient Enumeration of Stereoisomers of Outerplanar Chemical Graphs Using Dynamic Programming. J. Chem. Inf. Model. 2010, 50, 1667–1679. [Google Scholar] [CrossRef]
- Masui, R.; Shurbevski, A.; Nagamochi, H. Enumeration of Unlabeled Tree by Dynamic Programming; Technical Report; Kyoto University: Kyoto, Japan, 2009. [Google Scholar]
- He, F.; Hanai, A.; Nagamochi, H.; Akutsu, T. Enumerating Naphthalene Isomers of Tree-Like Chemical Graphs. In Proceedings of the 9th International Conference on Bioinformatics Models, Methods and Algorithms (BIOSTEC 2016), Rome, Italy, 21–23 February 2016; Volume 3: BIOINFORMATICS, pp. 258–265. [Google Scholar] [CrossRef]
- Azam, N.A.; Zhu, J.; Sun, Y.; Shi, Y.; Shurbevski, A.; Zhao, L.; Nagamochi, H.; Akutsu, T. A novel method for inference of acyclic chemical compounds with bounded branch-height based on artificial neural networks and integer programming. Algorithms Mol. Biol. 2021, 16, 18. [Google Scholar] [CrossRef] [PubMed]
- Azam, N.A.; Zhu, J.; Ido, R.; Nagamochi, H.; Akutsu, T. Experimental Results of a Dynamic Programming Algorithm for Generating Chemical Isomers Based on Frequency Vectors. In Proceedings of the Fourth International Workshop on Enumeration Problems and Applications (WEPA), Online, 7–10 December 2020; p. 15. [Google Scholar]
- Akutsu, T.; Nagamochi, H. A Novel Method for Inference of Chemical Compounds with Prescribed Topological Substructures Based on Integer Programming. arXiv 2020, arXiv:2010.09203. [Google Scholar] [CrossRef]
- Azam, N.A.; Shurbevski, A.; Nagamochi, H. An Efficient Algorithm to Count Tree-Like Graphs with a Given Number of Vertices and Self-Loops. Entropy 2020, 22, 923. [Google Scholar] [CrossRef]
- Azam, N.A.; Shurbevski, A.; Nagamochi, H. Enumeration of Tree-Like Graphs with a Given Cycle Rank Using Dynamic Programming. Entropy 2020, 22, 1295. [Google Scholar] [CrossRef]
- Ido, S.; Azam, N.A.; Akutsu, T. A Dynamic Programming Algorithm for Generating Chemical Isomers Based on Frequency Vectors. Sci. Rep. 2025, 15, 9576. [Google Scholar] [CrossRef]
- Maristany de las Casas, P.; Sedeño-Noda, A.; Borndörfer, R. New Dynamic Programming Algorithm for the Multiobjective Minimum Spanning Tree Problem. arXiv 2023, arXiv:2306.16203. [Google Scholar] [CrossRef]
- Yanhaona, M.N.; Nomaan, A.S.; Rahman, M.S. Efficiently Enumerating All Spanning Trees of a Plane 3-Tree. In Graph-Theoretic Concepts in Computer Science; Springer: Cham, Switzerland, 2023. [Google Scholar] [CrossRef]
- Haraguchi, K.; Nagamochi, H. A Polynomial-Delay Algorithm for Enumerating Connectors Under Various Connectivity Conditions. Leibniz Int. Proc. Inform. (LIPIcs) ISAAC 2019, 149, 3. [Google Scholar] [CrossRef]
- Tada, T.; Haraguchi, K. A Linear Delay Algorithm for Enumeration of 2-Edge/Vertex-Connected Induced Subgraphs. arXiv 2023, arXiv:2302.05526. [Google Scholar]
- Shota, K.; Haraguchi, K. A Linear Delay Algorithm of Enumerating Strongly-Connected Induced Subgraphs Based on SSD Set System. In Combinatorial Algorithms. IWOCA 2025; Fernau, H., Zhu, B., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2025; Volume 15885. [Google Scholar] [CrossRef]
- Sun, D.; Li, L.; Liu, K.; Wang, H.; Yang, Y. Enumeration of Subtrees of Planar Two-Tree Networks. Appl. Math. Comput. 2022, 434, 127404. [Google Scholar] [CrossRef]
- Qian, M.; Uehara, R. Constant Time Enumeration of Weighted Trees. Discret. Appl. Math. 2025, 375, 129–138. [Google Scholar] [CrossRef]
- Jordan, C. Sur les Assemblages de Lignes. J. Reine Angew. Math. 1869, 70, 185–190. [Google Scholar] [CrossRef]




| Reference | Method | Graph Type | Key Contribution |
|---|---|---|---|
| Pólya (1937) [15] | Combinatorics | General Graphs | Foundational combinatorial method and cycle indices |
| Akutsu and Fukagawa (2005) [29] | Dp | Trees, Planar | Polynomial time for bounded-degree trees; NP hard for planar graphs |
| Akutsu and Fukagawa (2007) [17] | Branch-and-Bound | Tree-Like Graphs | Enumeration from given frequency vector |
| Ishida et al. (2008) [22] | Branch-and-Bound | Chemical Graphs | Non-isomorphic tree-like chemical graph enumeration |
| Fujiwara et al. (2008) [18] | Branch-and-Bound | Chemical Graphs | Efficient performance for path frequency enumeration |
| Masui et al. (2009) [34] | DP | Rooted/Unrooted Trees | Ranking, unranking, and enumeration methods |
| Imada et al. (2010) [33] | DP | Outerplanar Graphs | Stereoisomer enumeration in chemical graphs |
| Imada et al. (2011) [32] | DP | Tree-Structured | Stereoisomer enumeration of molecules |
| Shimizu et al. (2011) [23] | Branch-and-Bound | Acyclic Chemical | Feature-vector-based enumeration methods |
| Akutsu et al. (2012) [30] | DP | Bounded Degree Trees | Tree-like graph enumeration with bounded degree |
| MacKay and Piperno (2014) [16] | Branch-and-Bound | General Graphs | Efficient graph isomorphism testing and enumeration |
| Rue et al. (2014) [31] | DP | Surface-Embedded | Surface cut decomposition for graphs |
| He et al. (2016) [35] | DP and Backtracking | Chemical Structures | Naphthalene-containing structure enumeration |
| Haraguchi and Nagamochi (2019) [44] | Polynomial Delay | Labeled Graphs | Enumeration of connectors and connected subgraphs |
| Azam et al. (2020) [39] | DP | Tree-like Multigraphs | Counting multigraphs with self-loops |
| Sun et al. (2022) [47] | Linear-Time Algorithm | Planar Networks | Subtree enumeration in planar two-tree networks |
| Maristany de las Casas et al. (2023) [42] | DP | General Graphs | Spanning tree problem approach |
| Tada and Haraguchi (2023) [45] | Partition-Based | Connected Subgraphs | Linear-delay enumeration of connected subgraphs |
| Yanhaona et al. (2023) [43] | Dp | Plane 3-Trees | Spanning tree enumeration |
| Ye et al. (2023) [28] | Structural Pruning | Bipartite Graphs | Biclique counting in large graphs |
| Maudet and Danoy (2024) [25] | Genetic Programming | General Graphs | Branching strategy improvement |
| Sciandra et al. (2024) [26] | Graph Convolutional | General Graphs | Structural information guided search |
| Labassi et al. (2024) [27] | GNN-Based | General Graphs | Adaptive node selection methods |
| Shota and Haraguchi (2025) [46] | SSD-Based | Strongly Connected | Linear-delay subgraph enumeration |
| Qian and Uehara (2025) [48] | Reverse Search Algorithm | Weighted Trees | Constant-time enumeration algorithm |
| Ido et al. (2025) [41] | DP | Chemical Graphs | Structure generation from frequency vectors |
| Time (s) | No. of Tree-like Multigraphs | Time (s) | No. of Tree-like Multigraphs | ||
|---|---|---|---|---|---|
| (80, 10) | 6.91 | (90, 10) | 8.80 | ||
| (80, 20) | 45.25 | (90, 20) | 56.26 | ||
| (80, 30) | 139.57 | (90, 30) | 179.61 | ||
| (80, 40) | 340.35 | (90, 40) | 411.81 | ||
| (80, 50) | 628.20 | (90, 50) | 805.91 | ||
| (90, 51) | Memory out | – | |||
| (100, 10) | 15.96 | (110, 10) | 12.16 | ||
| (100, 20) | 70.18 | (110, 20) | 83.09 | ||
| (100, 30) | 232.11 | (110, 30) | 280.37 | ||
| (100, 40) | 509.23 | (110, 39) | 601.18 | ||
| (100, 43) | 639.26 | (110, 40) | Memory out | – | |
| (100, 44) | Memory out | – | |||
| (120, 10) | 20.54 | (130, 10) | 18.79 | ||
| (120, 20) | 102.10 | (130, 20) | 120.05 | ||
| (120, 30) | 329.82 | (130, 30) | 379.62 | ||
| (120, 38) | 673.18 | (130, 36) | 653.50 | ||
| (120, 39) | Memory out | – | (130, 37) | Memory out | – |
| (140, 10) | 20.98 | (150, 10) | 23.20 | ||
| (140, 20) | 146.69 | (150, 20) | 155.67 | ||
| (140, 30) | 494.81 | (150, 30) | 506.93 | ||
| (140, 35) | 680.32 | (150, 34) | 722.01 | ||
| (140, 36) | Memory out | – | (150, 35) | Memory out | – |
| (160, 10) | 26.70 | (170, 10) | 30.10 | ||
| (160, 20) | 181.15 | (170, 20) | 199.35 | ||
| (160, 30) | 613.94 | (170, 30) | 637.20 | ||
| (160, 31) | 646.90 | (170, 31) | Memory out | ||
| (160, 32) | Memory out | – | |||
| (180, 10) | 43.43 | (190, 10) | 41.07 | ||
| (180, 20) | 223.74 | (190, 20) | 274.56 | ||
| (180, 28) | 610.58 | (190, 26) | 595.62 | ||
| (180, 29) | Memory out | – | (190, 27) | 687.59 | |
| (190, 28) | Memory out | – | |||
| (200, 10) | 47.08 | (200, 20) | 309.53 | ||
| (200, 25) | 546.71 | (200, 26) | 636.43 | ||
| (200, 27) | Memory out | – |
| Number of Multigraphs | Time (s) by Proposed Method | Time (s) by Nauty | |
|---|---|---|---|
| (5, 10) | 0.0127 | 0.0427 | |
| (5, 20) | 0.0834 | 0.0442 | |
| (5, 30) | 0.2577 | 0.0473 | |
| (5, 40) | 0.5830 | 0.0519 | |
| (5, 50) | 1.1472 | 0.0627 | |
| (6, 10) | 0.0208 | 0.0469 | |
| (6, 20) | 0.1338 | 0.0625 | |
| (6, 30) | 0.4087 | 0.1264 | |
| (6, 40) | 0.9271 | 0.2881 | |
| (6, 50) | 1.8167 | 0.6028 | |
| (7, 10) | 0.0291 | 0.0521 | |
| (7, 20) | 0.1891 | 0.2442 | |
| (7, 30) | 0.5882 | 1.2176 | |
| (7, 40) | 1.3371 | 4.4479 | |
| (7, 50) | 2.5024 | 12.5097 | |
| (8, 10) | 0.0402 | 0.1252 | |
| (8, 20) | 0.2566 | 1.9211 | |
| (8, 30) | 0.7887 | 16.0670 | |
| (8, 40) | 1.9782 | 78.7573 | |
| (8, 50) | 3.4009 | 294.2675 | |
| (9, 10) | 0.0507 | 0.7339 | |
| (9, 20) | 0.3711 | 17.5110 | |
| (9, 30) | 1.0394 | 205.9734 | |
| (9, 40) | 2.3700 | 1282.1714 | |
| (9, 50) | 5.8467 | Memory out | |
| (10, 10) | 0.0847 | 3.6110 | |
| (10, 20) | 0.4711 | 152.1980 | |
| (10, 30) | 1.3675 | Memory out | |
| (11, 10) | 0.0801 | 14.9310 | |
| (11, 20) | 0.5018 | 1293.4790 | |
| (11, 30) | 1.7742 | Memory out | |
| (12, 10) | 0.1095 | 85.5969 | |
| (12, 20) | 0.6919 | Memory out | |
| (13, 10) | 0.1144 | 573.7060 | |
| (13, 15) | 0.3242 | Memory out | |
| (14, 10) | 0.1319 | 4599.9461 | |
| (14, 11) | 0.1689 | Memory out |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ilyas, M.; Hayat, S.; Azam, N.A. Counting Tree-like Multigraphs with a Given Number of Vertices and Multiple Edges. Mathematics 2025, 13, 3405. https://doi.org/10.3390/math13213405
Ilyas M, Hayat S, Azam NA. Counting Tree-like Multigraphs with a Given Number of Vertices and Multiple Edges. Mathematics. 2025; 13(21):3405. https://doi.org/10.3390/math13213405
Chicago/Turabian StyleIlyas, Muhammad, Seemab Hayat, and Naveed Ahmed Azam. 2025. "Counting Tree-like Multigraphs with a Given Number of Vertices and Multiple Edges" Mathematics 13, no. 21: 3405. https://doi.org/10.3390/math13213405
APA StyleIlyas, M., Hayat, S., & Azam, N. A. (2025). Counting Tree-like Multigraphs with a Given Number of Vertices and Multiple Edges. Mathematics, 13(21), 3405. https://doi.org/10.3390/math13213405







