Asymptotic Analysis of the Bias–Variance Trade-Off in Subsampling Metropolis–Hastings
Abstract
1. Introduction
2. Asymptotic Optimization of the Approximate MH
2.1. Approximate MH Algorithm
| Algorithm 1: The Metropolis–Hastings Algorithm |
 |
2.2. Bias–Variance Trade-Off Analysis
- MSE Dominated by VarianceUnder the condition , the bias introduced by the estimated acceptance rate becomes negligible. Consequently, the algorithm’s efficiency is primarily constrained by the number of data passes, which emerges as the main computational bottleneck.
- MSE Dominated by Squared BiasThis case occurs when ample computational resources allow for a sufficiently large number of epochs, E, causing the variance term to become negligible. Under this condition, the MSE is dominated by the squared bias. Specifically, with the setting , the bias term itself is of order , and squaring it yields the final result, .
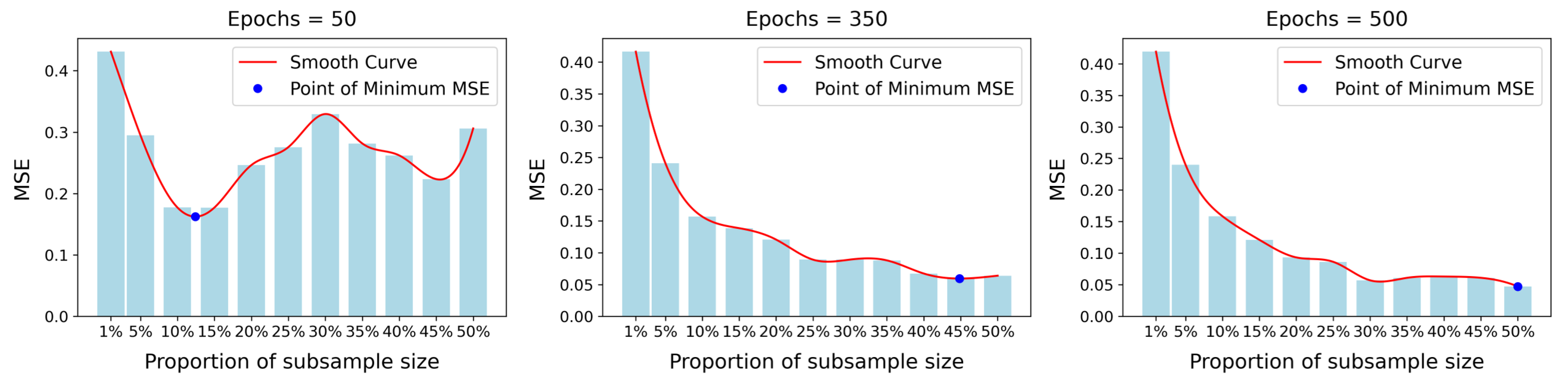
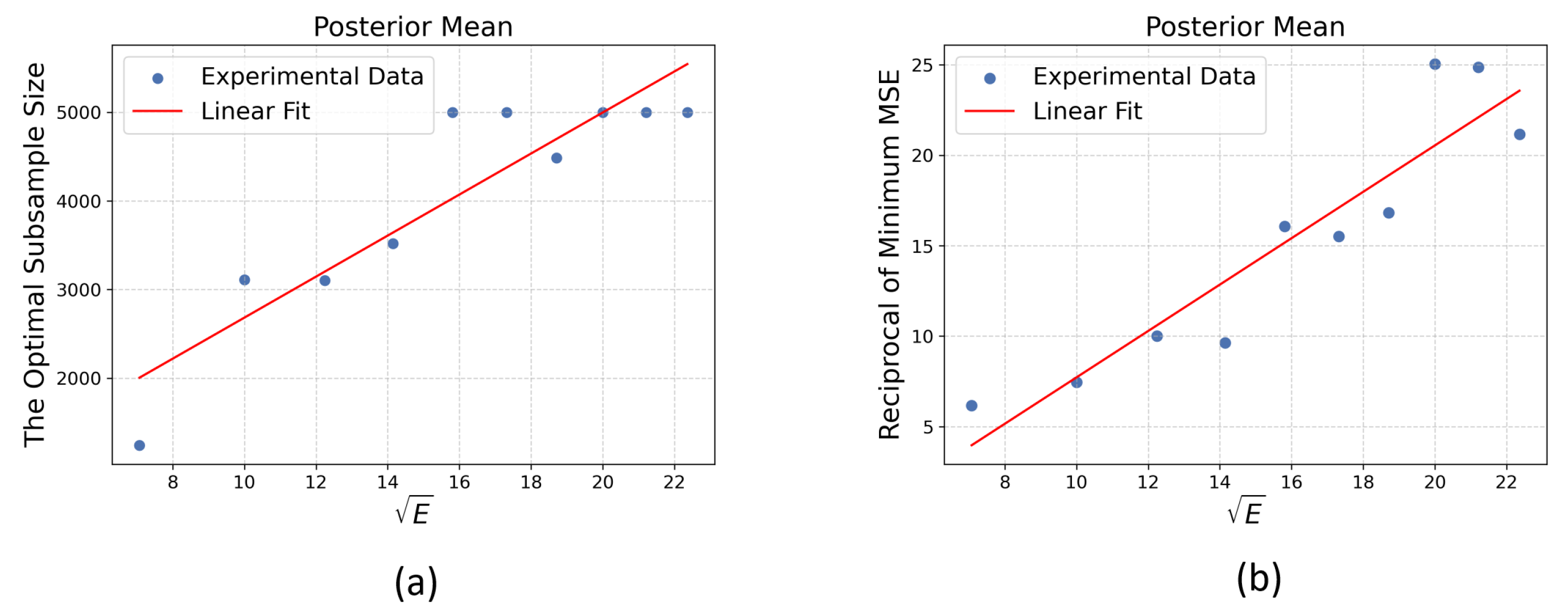
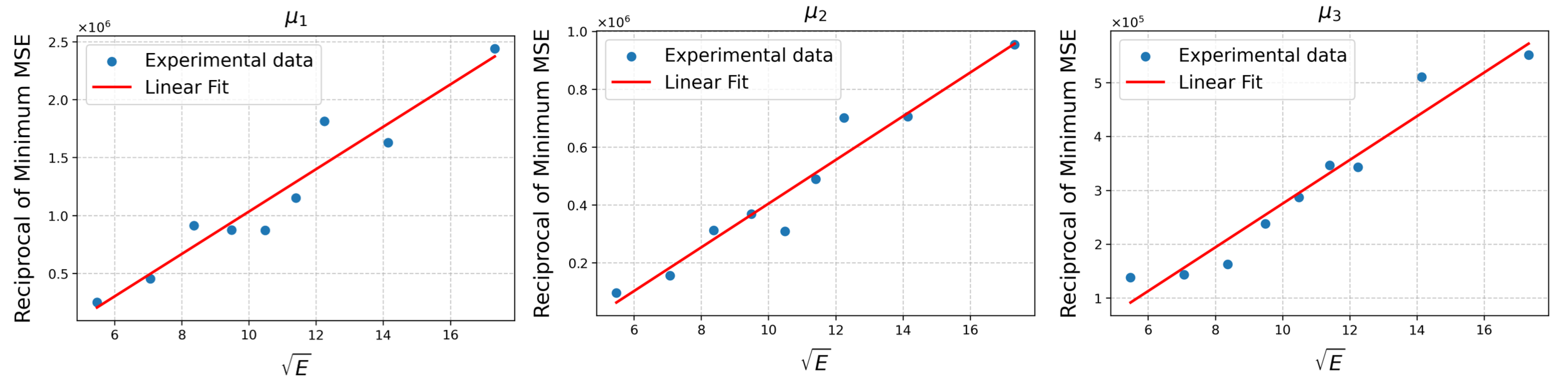
- MSE with Balanced Bias and Variance This scenario explores the optimal asymptotic trade-off, which dictates the best achievable convergence rate for the MSE. This optimum is found by balancing the two competing error sources. Specifically, we set leading-order terms—the squared bias, , and the variance, —to be of the same asymptotic order.Solving this balance yields the order of the optimal subsample size:Substituting this order for back into the MSE expression reveals that the minimal achievable MSE has an order of
2.3. Toy Example for Theoretical Validation
3. Asymptotic Comparison of Approximate and Exact MH
3.1. Asymptotic Analysis of Approximate MH
3.2. Enhancements via Control Variates
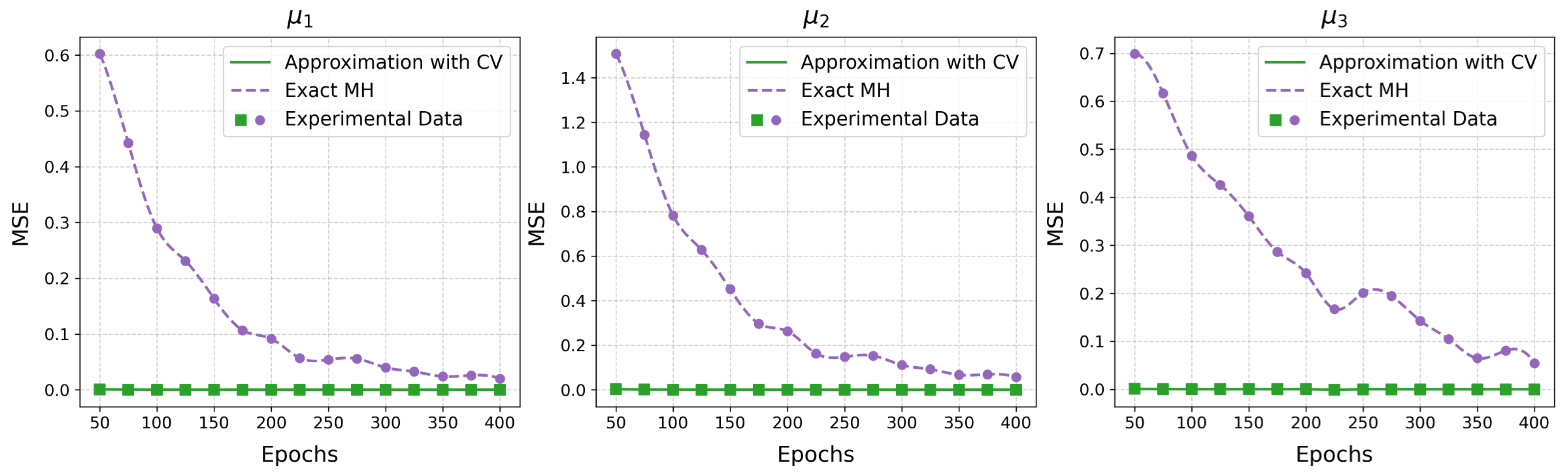
4. Numerical Experiments
4.1. AR(2) Model
4.2. Bayesian Logistic Regression
4.3. Softmax Classification
5. Conclusions and Future Work
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Proofs of Main Results
- If and , then .
- If and , then .
- If and , then for some .
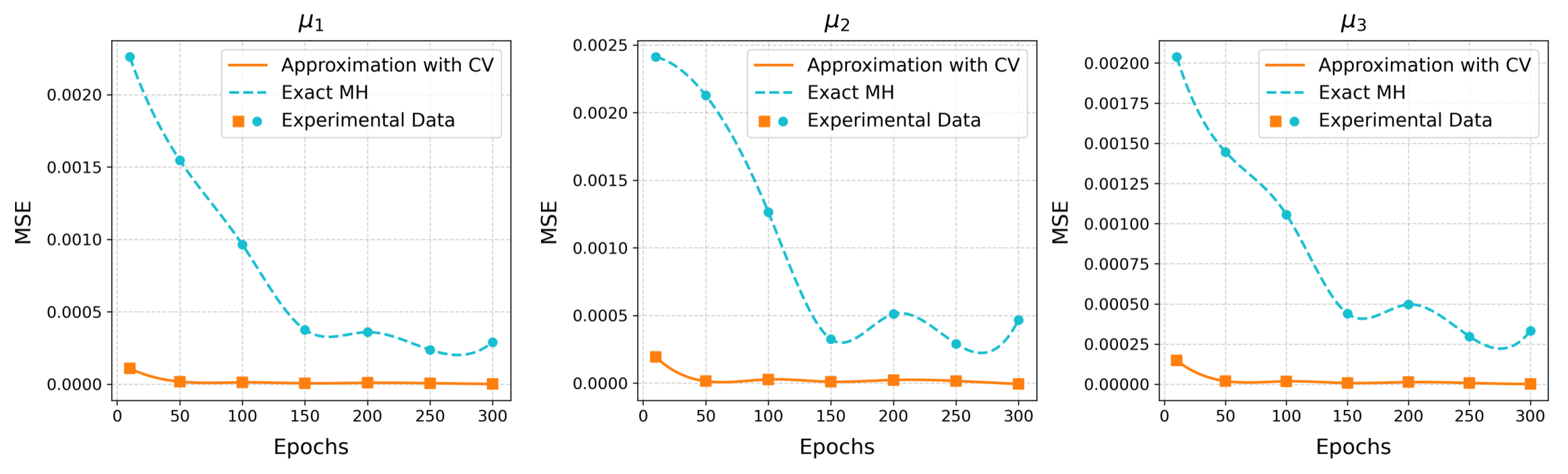
Appendix B. Additional Experiment and Model Code
Appendix B.1. Additional Experimental Results
Appendix B.2. Code Availability
| Listing A1. Python implementation for the Bayesian logistic regression model. |
 |
 |
 |
 |
References
- Bardenet, R.; Doucet, A.; Holmes, C. On Markov chain Monte Carlo methods for tall data. J. Mach. Learn. Res. 2017, 18, 1–43. [Google Scholar]
- Nemeth, C.; Fearnhead, P. Stochastic gradient markov chain monte carlo. J. Am. Stat. Assoc. 2021, 116, 433–450. [Google Scholar] [CrossRef]
- Neiswanger, W.; Wang, C.; Xing, E. Asymptotically exact, embarrassingly parallel MCMC. In Proceedings of the 30th Conference on Uncertainty in Artificial Intelligence (UAI’14), Quebec City, QC, Canada, 23–27 July 2014; pp. 623–632. [Google Scholar]
- Williamson, S.; Dubey, A.; Xing, E. Parallel Markov chain Monte Carlo for nonparametric mixture models. In Proceedings of the 30th International Conference on Machine Learning, PMLR, Atlanta, GA, USA, 16–21 June 2013; pp. 98–106. [Google Scholar]
- Angelino, E.; Kohler, E.; Waterland, A.; Seltzer, M.; Adams, R.P. Accelerating MCMC via parallel predictive prefetching. In Proceedings of the 30th Conference on Uncertainty in Artificial Intelligence (UAI’14), Quebec City, QC, Canada, 23–27 July 2014; pp. 22–31. [Google Scholar]
- Glatt-Holtz, N.E.; Holbrook, A.J.; Krometis, J.A.; Mondaini, C.F. Parallel MCMC algorithms: Theoretical foundations, algorithm design, case studies. Trans. Math. Its Appl. 2024, 8, tnae004. [Google Scholar] [CrossRef]
- Mesquita, D.; Blomstedt, P.; Kaski, S. Embarrassingly parallel MCMC using deep invertible transformations. In Proceedings of the 35th Uncertainty in Artificial Intelligence, PMLR, Tel Aviv, Israel, 22–25 July 2020; pp. 1244–1252. [Google Scholar]
- Wang, T.; Wang, G. Unbiased Multilevel Monte Carlo methods for intractable distributions: MLMC meets MCMC. J. Mach. Learn. Res. 2023, 24, 1–40. [Google Scholar]
- Vyner, C.; Nemeth, C.; Sherlock, C. SwISS: A scalable Markov chain Monte Carlo divide-and-conquer strategy. Stat 2023, 12, e523. [Google Scholar] [CrossRef]
- Maclaurin, D.; Adams, R.P. Firefly Monte Carlo: Exact MCMC with subsets of data. In Proceedings of the 30th Conference on Uncertainty in Artificial Intelligence (UAI’14), Quebec City, QC, Canada, 23–27 July 2014; pp. 543–552. [Google Scholar]
- Zhang, R.; Cooper, A.F.; De Sa, C.M. Asymptotically optimal exact minibatch metropolis-hastings. Adv. Neural Inf. Process. Syst. 2020, 33, 19500–19510. [Google Scholar]
- Putcha, S.; Nemeth, C.; Fearnhead, P. Preferential Subsampling for Stochastic Gradient Langevin Dynamics. In Proceedings of the 26th International Conference on Artificial Intelligence and Statistics, PMLR, Valencia, Spain, 25–27 April 2023; pp. 8837–8856. [Google Scholar]
- Wu, T.Y.; Rachel Wang, Y.; Wong, W.H. Mini-batch Metropolis–Hastings with reversible SGLD proposal. J. Am. Stat. Assoc. 2022, 117, 386–394. [Google Scholar] [CrossRef]
- Pollock, M.; Fearnhead, P.; Johansen, A.M.; Roberts, G.O. Quasi-stationary Monte Carlo and the ScaLE algorithm. J. R. Stat. Soc. Ser. B Stat. Methodol. 2020, 82, 1167–1221. [Google Scholar] [CrossRef]
- Lykkegaard, M.B.; Dodwell, T.J.; Fox, C.; Mingas, G.; Scheichl, R. Multilevel delayed acceptance MCMC. SIAM/ASA J. Uncertain. Quantif. 2023, 11, 1–30. [Google Scholar] [CrossRef]
- Maire, F.; Friel, N.; Alquier, P. Informed sub-sampling MCMC: Approximate Bayesian inference for large datasets. Stat. Comput. 2019, 29, 449–482. [Google Scholar] [CrossRef]
- Quiroz, M.; Kohn, R.; Villani, M.; Tran, M.N. Speeding up MCMC by efficient data subsampling. J. Am. Stat. Assoc. 2018, 114, 831–843. [Google Scholar] [CrossRef]
- Levi, E.; Craiu, R.V. Finding our way in the dark: Approximate MCMC for approximate Bayesian methods. Bayesian Anal. 2022, 17, 193–221. [Google Scholar] [CrossRef]
- Hermans, J.; Begy, V.; Louppe, G. Likelihood-free mcmc with amortized approximate ratio estimators. In Proceedings of the 37th International Conference on Machine Learning, PMLR, Virtual, 13–18 July 2020; pp. 4239–4248. [Google Scholar]
- Conrad, P.R.; Marzouk, Y.M.; Pillai, N.S.; Smith, A. Accelerating asymptotically exact MCMC for computationally intensive models via local approximations. J. Am. Stat. Assoc. 2016, 111, 1591–1607. [Google Scholar] [CrossRef]
- Sherlock, C.; Thiery, A.H.; Roberts, G.O.; Rosenthal, J.S. On the efficiency of pseudo-marginal random walk Metropolis algorithms. Ann. Stat. 2015, 43, 238–275. [Google Scholar] [CrossRef]
- Alquier, P.; Friel, N.; Everitt, R.; Boland, A. Noisy Monte Carlo: Convergence of Markov chains with approximate transition kernels. Stat. Comput. 2016, 26, 29–47. [Google Scholar] [CrossRef]
- Hu, G.; Wang, H. Most likely optimal subsampled Markov chain Monte Carlo. J. Syst. Sci. Complex. 2021, 34, 1121–1134. [Google Scholar] [CrossRef]
- Korattikara, A.; Chen, Y.; Welling, M. Austerity in MCMC land: Cutting the Metropolis-Hastings budget. In Proceedings of the 31st International Conference on Machine Learning, PMLR, Beijing, China, 21–26 June 2014; pp. 181–189. [Google Scholar]
- Bardenet, R.; Doucet, A.; Holmes, C. Towards scaling up Markov chain Monte Carlo: An adaptive subsampling approach. In Proceedings of the 31st International Conference on Machine Learning, PMLR, Beijing, China, 21–26 June 2014; pp. 405–413. [Google Scholar]
- Pitt, M.K.; dos Santos Silva, R.; Giordani, P.; Kohn, R. On some properties of Markov chain Monte Carlo simulation methods based on the particle filter. J. Econom. 2012, 171, 134–151. [Google Scholar] [CrossRef]
- Doucet, A.; Pitt, M.K.; Deligiannidis, G.; Kohn, R. Efficient implementation of Markov chain Monte Carlo when using an unbiased likelihood estimator. Biometrika 2015, 102, 295–313. [Google Scholar] [CrossRef]
- Jacob, P.E.; Thiery, A.H. On nonnegative unbiased estimators. Ann. Statist. 2015, 43, 769–784. [Google Scholar] [CrossRef]
- Johndrow, J.E.; Mattingly, J.C.; Mukherjee, S.; Dunson, D. Optimal approximating Markov chains for Bayesian inference. arXiv 2015, arXiv:1508.03387. [Google Scholar]
- Van der Vaart, A.W. Asymptotic Statistics; Cambridge University Press: Cambridge, UK, 2000; Volume 3. [Google Scholar]
- Roozbeh, M. Optimal ridge estimation in the restricted logistic semiparametric regression models using generalized cross-validation. J. Appl. Stat. 2025, 1–20. [Google Scholar] [CrossRef]
- Malinovsky, G.; Horváth, S.; Burlachenko, K.; Richtárik, P. Federated learning with regularized client participation. In Proceedings of the Workshop of Federated Learning and Analytics in Practice, Colocated with 40th International Conference on Machine Learning, Honolulu, HI, USA, 23–29 July 2023. [Google Scholar]
- Fishman, G.S. Monte Carlo: Concepts, Algorithms, and Applications; Springer: New York, NY, USA, 1996. [Google Scholar]
- Gelman, A.; Gilks, W.R.; Roberts, G.O. Weak convergence and optimal scaling of random walk Metropolis algorithms. Ann. Appl. Probab. 1997, 7, 110–120. [Google Scholar] [CrossRef]
- Roberts, G.O.; Rosenthal, J.S. Optimal scaling for various Metropolis-Hastings algorithms. Stat. Sci. 2001, 16, 351–367. [Google Scholar] [CrossRef]
- Chib, S.; Greenberg, E. Understanding the metropolis-hastings algorithm. Am. Stat. 1995, 49, 327–335. [Google Scholar] [CrossRef]
- Gelman, A.; Jakulin, A.; Pittau, M.G.; Su, Y.S. A weakly informative default prior distribution for logistic and other regression models. Ann. Appl. Stat. 2008, 2, 1360–1383. [Google Scholar] [CrossRef]
- Sen, D.; Sachs, M.; Lu, J.; Dunson, D.B. Efficient posterior sampling for high-dimensional imbalanced logistic regression. Biometrika 2020, 107, 1005–1012. [Google Scholar] [CrossRef]
- Bou-Rabee, N.; Marsden, M. Unadjusted Hamiltonian MCMC with stratified Monte Carlo time integration. Ann. Appl. Probab. 2025, 35, 360–392. [Google Scholar] [CrossRef]


| Epochs | 20 | 30 | 50 | 100 | 150 | 200 | 250 | 300 |
|---|---|---|---|---|---|---|---|---|
| Approximate | 90.49% | 90.67% | 91.53% | 92.27% | 92.04% | 92.39% | 92.29% | 93.14% |
| Vanilla | 89.65% | 89.88% | 89.69% | 90.14% | 90.12% | 90.31% | 90.53% | 90.59% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S. Asymptotic Analysis of the Bias–Variance Trade-Off in Subsampling Metropolis–Hastings. Mathematics 2025, 13, 3395. https://doi.org/10.3390/math13213395
Liu S. Asymptotic Analysis of the Bias–Variance Trade-Off in Subsampling Metropolis–Hastings. Mathematics. 2025; 13(21):3395. https://doi.org/10.3390/math13213395
Chicago/Turabian StyleLiu, Shuang. 2025. "Asymptotic Analysis of the Bias–Variance Trade-Off in Subsampling Metropolis–Hastings" Mathematics 13, no. 21: 3395. https://doi.org/10.3390/math13213395
APA StyleLiu, S. (2025). Asymptotic Analysis of the Bias–Variance Trade-Off in Subsampling Metropolis–Hastings. Mathematics, 13(21), 3395. https://doi.org/10.3390/math13213395




