A Robust Optimal Control Strategy for PMSM Based on VGPDO and Actor-Critic Neural Network Against Flux Weakening and Mismatched Load Torque
Abstract
1. Introduction
- •
- To mitigate flux linkage degradation in PMSM control systems during prolonged load operation, a VGPDO is proposed to simultaneously estimate torque and flux linkage disturbances, thereby enhancing system robustness.
- •
- To achieve optimality and robustness in PMSM speed regulation under varying load torque and flux linkage conditions, a robust optimal control strategy is proposed, which integrates feedforward-based VGPDO compensation with an actor-critic neural network-based optimal speed controller.
- •
- Comprehensive simulations are conducted to validate the effectiveness of the VGPDO and robust optimal control strategy.
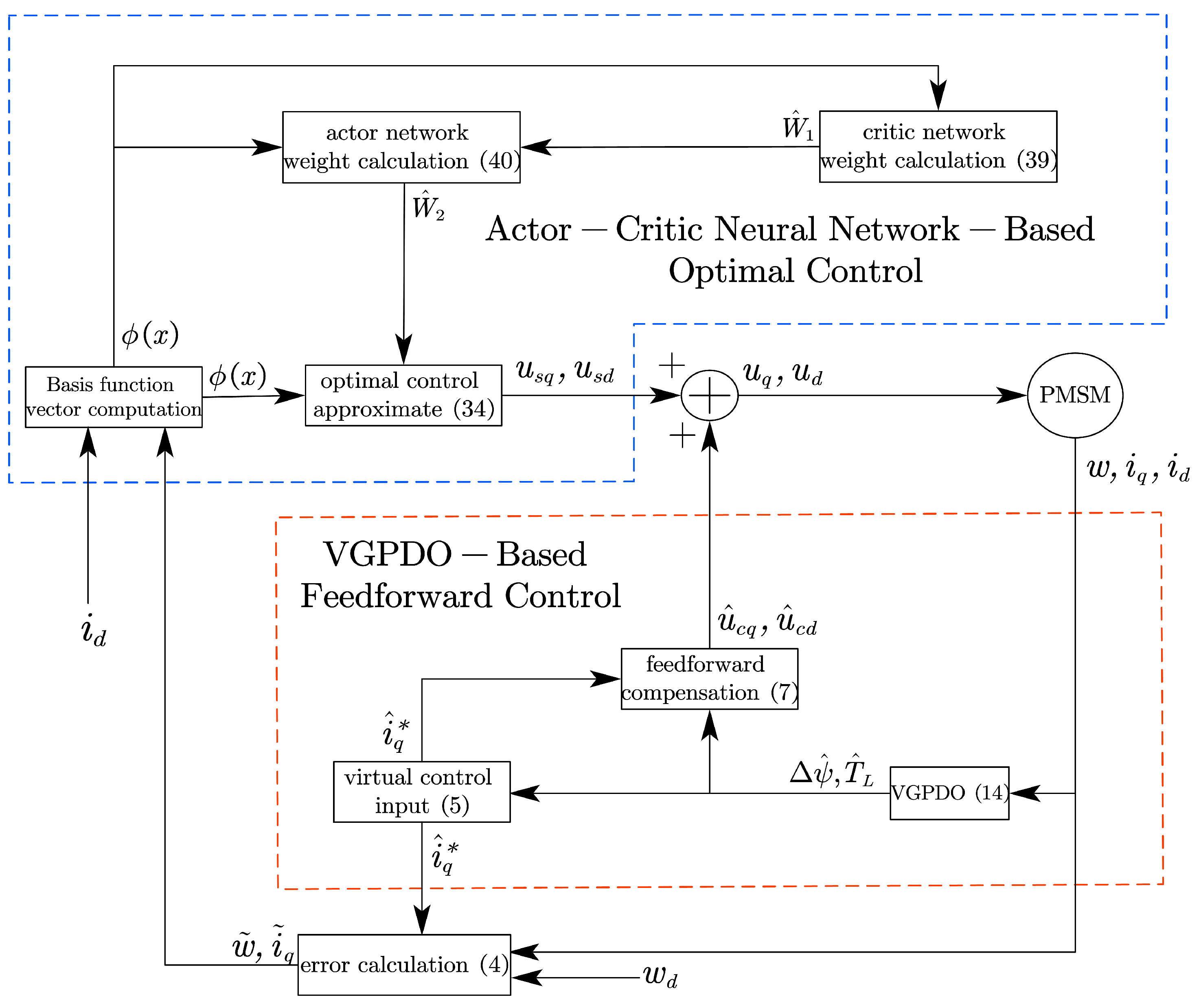
2. System Descriptions
3. Variable-Gain Proportional Disturbance Observer Design
- 1.
- The load torque of PMSM and its rate are bounded by: .
- 2.
- The flux linkage of PMSM variation rate is bounded by: .
- 3.
- The reference speed and its derivative for PMSM are bounded as follows: .
4. Actor-Critic Network-Based Optimal Controller Design
- 1.
- f(x) is Lipschitz, and g(x) is bounded by a constant:
- 2.
- The NN approximate error and its gradient are bounded by:
- 3.
- The NN basis functions and their gradients are bounded by:
5. Simulation Results
- The settling time of is defined as the earliest time such that for all , we have:
- The percentage deviation of is used to evaluate its tracking performance relative to and is computed as:where denotes the time instant at which the system state enters the steady-state regime, and is is computed as twice the value of .
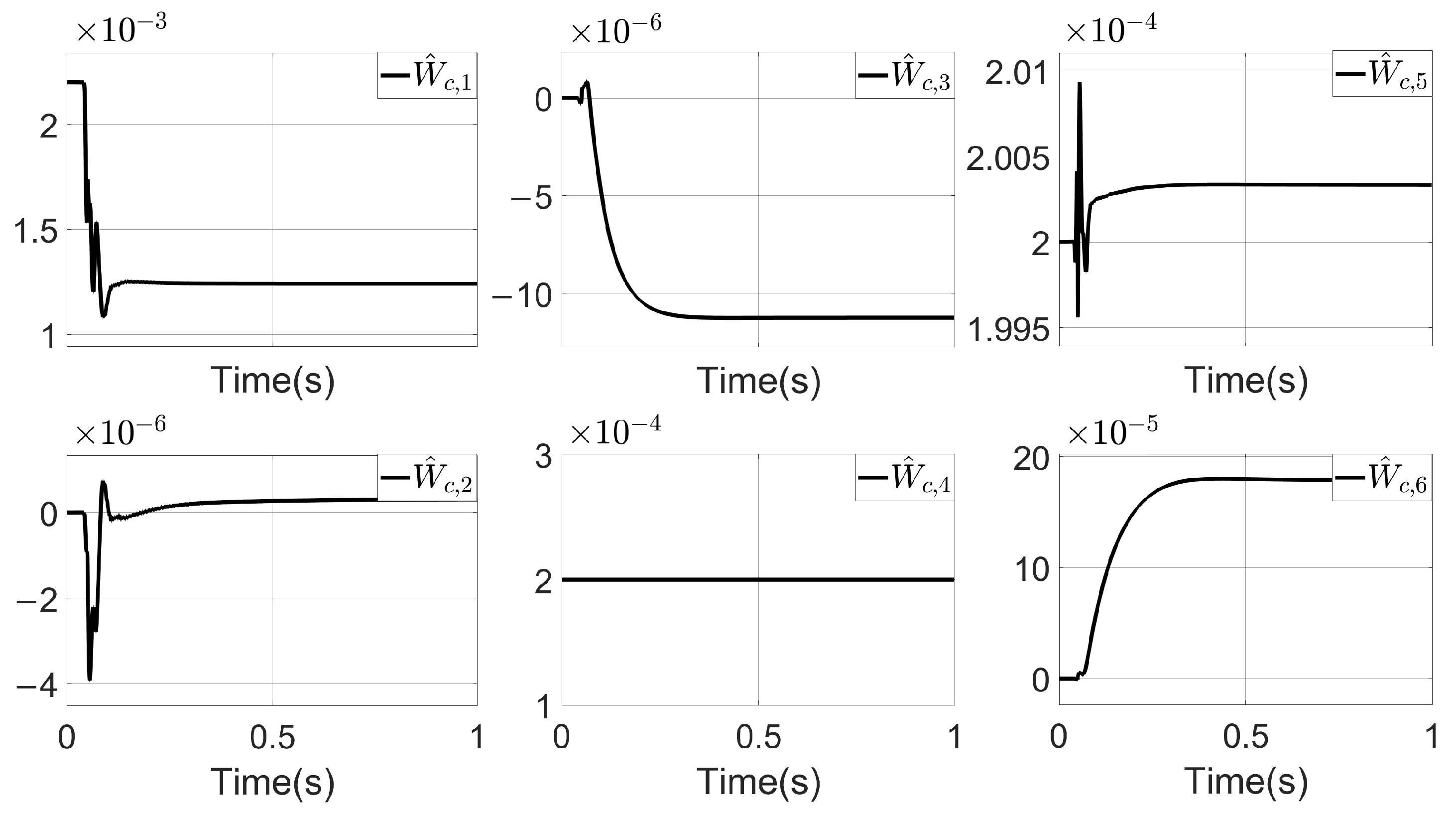
- The steady-state estimation error on is used to evaluate the approximation degree of to the actual cost function after has converged, and is calculated as:
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PMSM | Permanent magnet synchronous motor |
| UUB | Uniform ultimate boundedness |
| ADP | Adaptive dynamic programming |
| RL | Reinforcement learning |
| VGPDO | Variable-gain proportional disturbance observer |
| AC | actor-critic neural network |
Appendix A
Appendix A.1
Appendix A.2
References
- Wang, M.; Ren, X.; Chen, Q. Cascade Optimal Control for Tracking and Synchronization of a Multimotor Driving System. IEEE Trans. Control Syst. Technol. 2019, 27, 1376–1384. [Google Scholar] [CrossRef]
- Errouissi, R.; Al-Durra, A.; Muyeen, S.M. Experimental Validation of a Novel PI Speed Controller for AC Motor Drives with Improved Transient Performances. IEEE Trans. Control Syst. Technol. 2018, 26, 1414–1421. [Google Scholar] [CrossRef]
- Lee, H.; Lee, Y.; Shin, D.; Chung, C.C. H∞ control based on LPV for load torque compensation of PMSM. In Proceedings of the 2015 15th International Conference on Control, Automation and Systems (ICCAS), Busan, Republic of Korea, 13–16 October 2015; pp. 1013–1018. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, L.; Zhao, K.; Sun, L. Nonlinear Speed Control for PMSM System Using Sliding-Mode Control and Disturbance Compensation Techniques. IEEE Trans. Power Electron. 2013, 28, 1358–1365. [Google Scholar] [CrossRef]
- Repecho, V.; Biel, D.; Arias, A. Fixed Switching Period Discrete-Time Sliding Mode Current Control of a PMSM. IEEE Trans. Ind. Electron. 2018, 65, 2039–2048. [Google Scholar] [CrossRef]
- Linares-Flores, J.; García-Rodríguez, C.; Sira-Ramírez, H.; Ramírez-Cárdenas, O.D. Robust Backstepping Tracking Controller for Low-Speed PMSM Positioning System: Design, Analysis, and Implementation. IEEE Trans. Ind. Inform. 2015, 11, 1130–1141. [Google Scholar] [CrossRef]
- Yin, W.; Wu, X.; Rui, X. Adaptive Robust Backstepping Control of the Speed Regulating Differential Mechanism for Wind Turbines. IEEE Trans. Sustain. Energy 2019, 10, 1311–1318. [Google Scholar] [CrossRef]
- Li, S.; Zhou, M.; Yu, X. Design and Implementation of Terminal Sliding Mode Control Method for PMSM Speed Regulation System. IEEE Trans. Ind. Inform. 2013, 9, 1879–1891. [Google Scholar] [CrossRef]
- Preindl, M.; Bolognani, S. Model Predictive Direct Speed Control with Finite Control Set of PMSM Drive Systems. IEEE Trans. Power Electron. 2013, 28, 1007–1015. [Google Scholar] [CrossRef]
- Li, S.; Ding, L.; Gao, H.; Liu, Y.J.; Huang, L.; Deng, Z. ADP-Based Online Tracking Control of Partially Uncertain Time-Delayed Nonlinear System and Application to Wheeled Mobile Robots. IEEE Trans. Cybern. 2020, 50, 3182–3194. [Google Scholar] [CrossRef]
- Xue, S.; Zhao, N.; Zhang, W.; Luo, B.; Liu, D. A Hybrid Adaptive Dynamic Programming for Optimal Tracking Control of USVs. IEEE Trans. Neural Netw. Learn. Syst. 2025, 36, 9961–9969. [Google Scholar] [CrossRef] [PubMed]
- Yu, Y.; Ma, X.; Su, R.; Jet, T.K.; Viswanathan, V.; Gajanayake, C.J.; RamaKrishna, S.; Gupta, A.K. Application of integral reinforcement learning for optimal control of a high speed flux-switching permanent magnet machine. In Proceedings of the IECON 2016-42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; pp. 2702–2707. [Google Scholar] [CrossRef]
- Chen, G.; Wang, W.; Dong, J. Performance-Optimize Adaptive Robust Tracking Control for USV-UAV Heterogeneous Systems with Uncertainty. IEEE Trans. Veh. Technol. 2025, 74, 7251–7262. [Google Scholar] [CrossRef]
- Chen, G.; Dong, J. Approximate Optimal Adaptive Prescribed Performance Control for Uncertain Nonlinear Systems with Feature Information. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 2298–2308. [Google Scholar] [CrossRef]
- Jiang, Y.; Jiang, Z.P. Robust Adaptive Dynamic Programming with an Application to Power Systems. IEEE Trans. Neural Netw. Learn. Syst. 2013, 24, 1150–1156. [Google Scholar] [CrossRef]
- Heydari, A. Optimal Impulsive Control Using Adaptive Dynamic Programming and its Application in Spacecraft Rendezvous. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 4544–4552. [Google Scholar] [CrossRef]
- El-Sousy, F.F.M.; Amin, M.M.; Al-Durra, A. Adaptive Optimal Tracking Control Via Actor-Critic-Identifier Based Adaptive Dynamic Programming for Permanent-Magnet Synchronous Motor Drive System. IEEE Trans. Ind. Appl. 2021, 57, 6577–6591. [Google Scholar] [CrossRef]
- Lee, J.; You, S.; Kim, W.; Moon, J. Extended state observer-actor–critic architecture based output-feedback optimized backstepping control for permanent magnet synchronous motors. Expert Syst. Appl. 2025, 270, 126542. [Google Scholar] [CrossRef]
- Fan, Z.X.; Li, S.; Liu, R. ADP-Based Optimal Control for Systems with Mismatched Disturbances: A PMSM Application. IEEE Trans. Circuits Syst. II Express Briefs 2023, 70, 2057–2061. [Google Scholar] [CrossRef]
- Fan, Z.X.; Li, S.; Su, J. Adaptive Dynamic Programming for PMSM Control Under Safety, Robustness, and Optimality Constraints. IEEE Trans. Syst. Man Cybern. Syst. 2025, 55, 2724–2733. [Google Scholar] [CrossRef]
- Wang, Z.; Ye, H.; Wang, Y.; Shi, Y.; Liang, L. Optimal Output-Feedback Controller Design Using Adaptive Dynamic Programming: A Permanent Magnet Synchronous Motor Application. IEEE Trans. Circuits Syst. II Express Briefs 2025, 72, 208–212. [Google Scholar] [CrossRef]
- Vamvoudakis, K.G.; Lewis, F.L. Online actor–critic algorithm to solve the continuous-time infinite horizon optimal control problem. Automatica 2010, 46, 878–888. [Google Scholar] [CrossRef]
- Uddin, M.N.; Zou, H.; Azevedo, F. Online Loss-Minimization-Based Adaptive Flux Observer for Direct Torque and Flux Control of PMSM Drive. IEEE Trans. Ind. Appl. 2016, 52, 425–431. [Google Scholar] [CrossRef]
- Ye, S.; Yao, X. A Modified Flux Sliding-Mode Observer for the Sensorless Control of PMSMs with Online Stator Resistance and Inductance Estimation. IEEE Trans. Power Electron. 2020, 35, 8652–8662. [Google Scholar] [CrossRef]
- Podder, A.; Pandit, D. Study of Sensorless Field-Oriented Control of SPMSM Using Rotor Flux Observer & Disturbance Observer Based Discrete Sliding Mode Observer. In Proceedings of the 2021 IEEE 22nd Workshop on Control and Modelling of Power Electronics (COMPEL), Cartagena, Colombia, 2–5 November 2021; pp. 1–8. [Google Scholar] [CrossRef]
- Zhu, G.; Dessaint, L.A.; Akhrif, O.; Kaddouri, A. Speed tracking control of a permanent-magnet synchronous motor with state and load torque observer. IEEE Trans. Ind. Electron. 2000, 47, 346–355. [Google Scholar] [CrossRef]
- Apte, A.; Joshi, V.A.; Mehta, H.; Walambe, R. Disturbance-Observer-Based Sensorless Control of PMSM Using Integral State Feedback Controller. IEEE Trans. Power Electron. 2020, 35, 6082–6090. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Universal approximation of an unknown mapping and its derivatives using multilayer feedforward networks. Neural Netw. 1990, 3, 551–560. [Google Scholar] [CrossRef]
- Li, J.; Liu, H.; Zhang, Z.; Li, X.; Yang, X. Event-triggered adaptive NN tracking control with dynamic gain for a class of unknown nonlinear systems. Neurocomputing 2022, 467, 292–299. [Google Scholar] [CrossRef]
- Abu-Khalaf, M.; Lewis, F.L. Nearly optimal control laws for nonlinear systems with saturating actuators using a neural network HJB approach. Automatica 2005, 41, 779–791. [Google Scholar] [CrossRef]
- Modares, H.; Lewis, F.L. Optimal tracking control of nonlinear partially-unknown constrained-input systems using integral reinforcement learning. Automatica 2014, 50, 1780–1792. [Google Scholar] [CrossRef]
- Li, D.; Dong, J. Approximate Optimal Robust Tracking Control Based on State Error and Derivative Without Initial Admissible Input. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 1059–1069. [Google Scholar] [CrossRef]
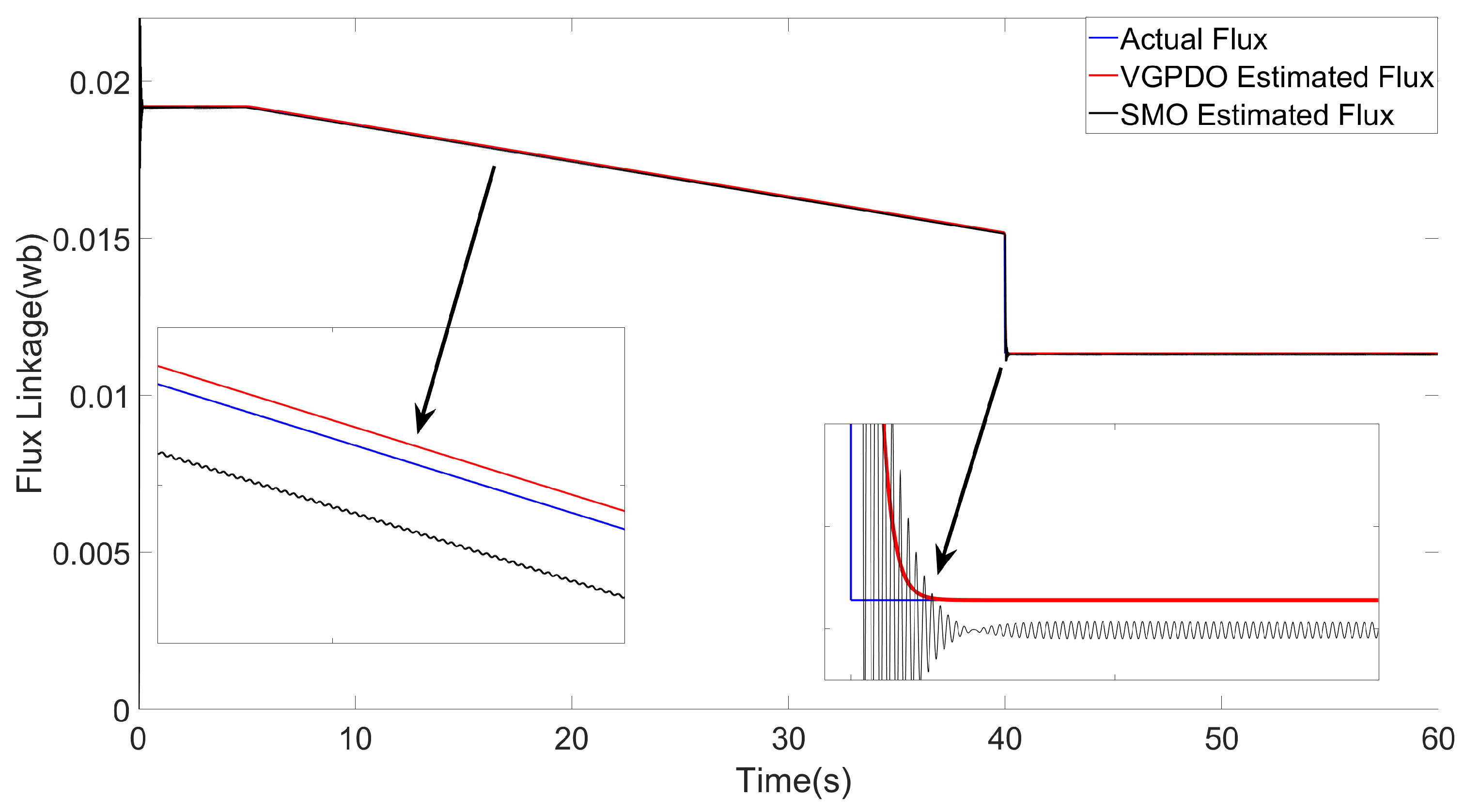
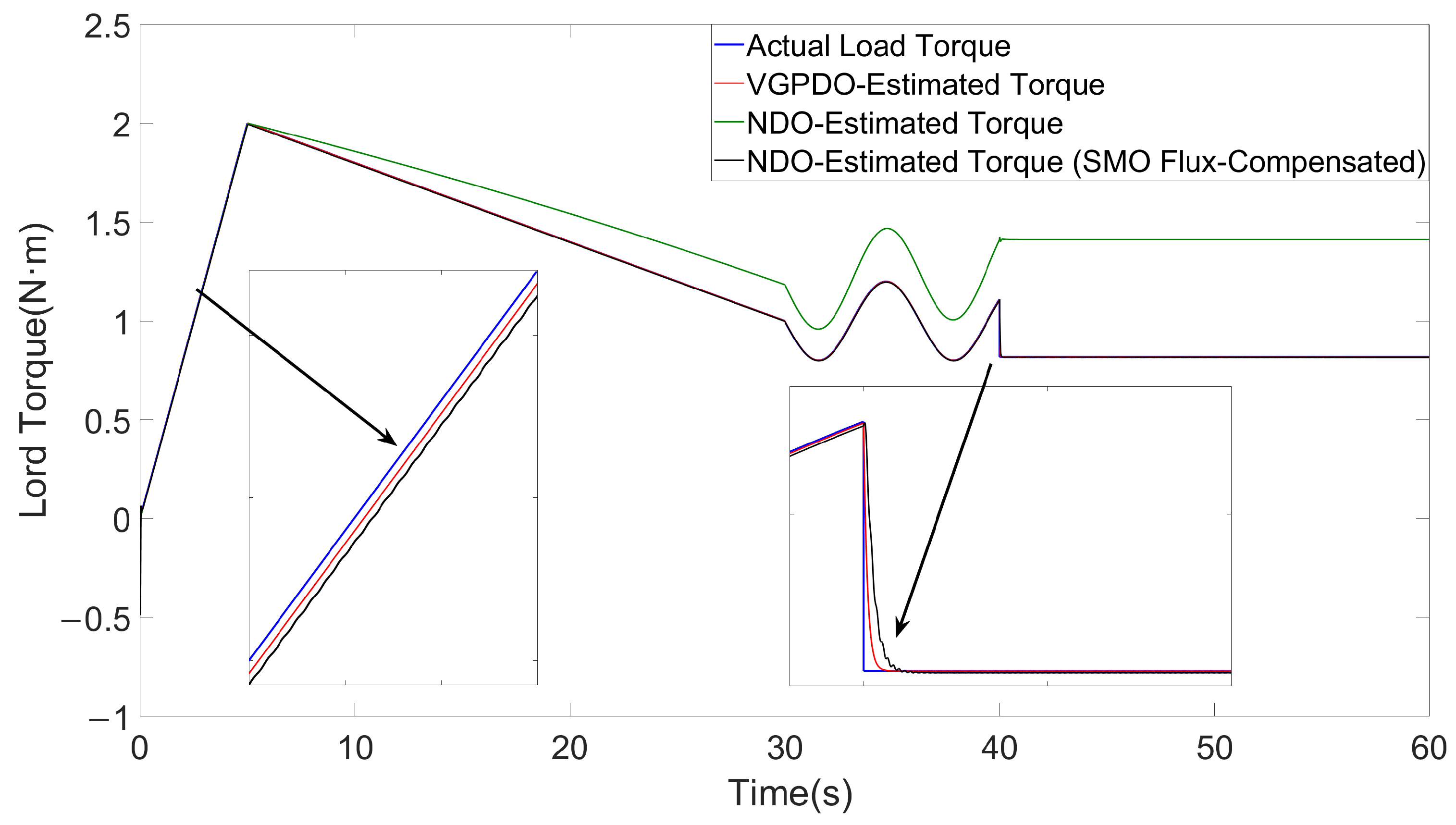
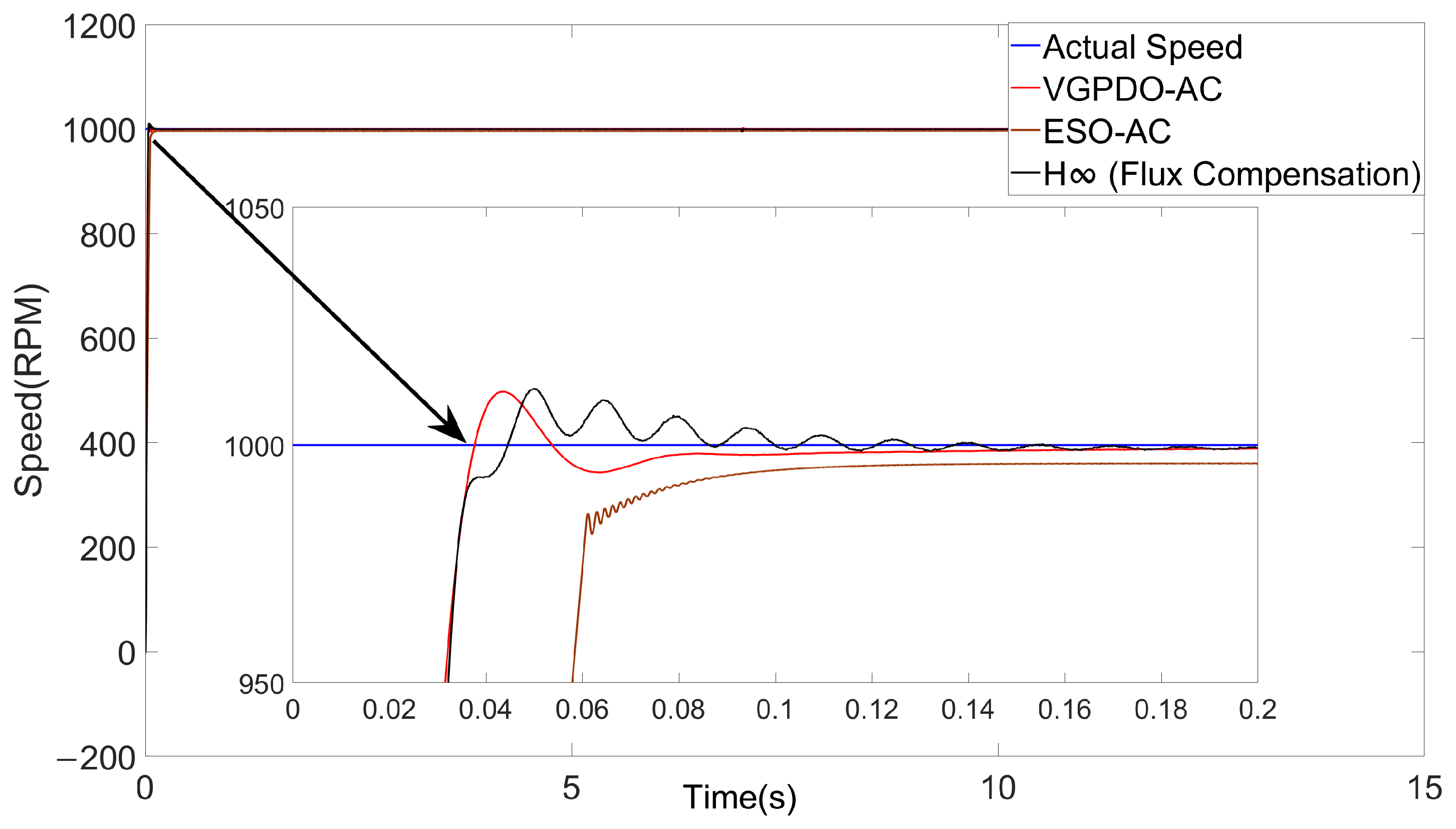


| Symbols | Values | Symbols | Values |
|---|---|---|---|
| 60 V | 4 | ||
| 12 A | 0.0192 Wb | ||
| J | |||
| B | L |
| Algorithm | Noise Variance () | Maximum Estimation Error (%) | RMSE | Maximum Setting Time (s) | CPU Usage (%) | |||
|---|---|---|---|---|---|---|---|---|
| Load Torque | Flux Linkage | Load Torque | Flux Linkage | |||||
| VGPDO | 0.3331 | 0.0755 | 2.961 × | 5.074 × | 0.0782 | 12.26 | ||
| 0.3964 | 0.1525 | 2.986 × | 5.083 × | 0.0801 | 13.98 | |||
| 0.6165 | 0.2469 | 3.271 × | 5.175 × | 0.0857 | 14.24 | |||
| 3.601 | 3.109 | 1.176 × | 1.263 × | N/A | 13.17 | |||
| NDOB-SMO | 0.7176 | 0.3496 | 1.148 × | 3.358 × | 0.1328 | 11.6 | ||
| 2.996 | 0.5022 | 1.251 × | 3.590 × | 0.1331 | 15.74 | |||
| 3.365 | 0.9817 | 1.955 × | 3.608 × | 0.1345 | 15.96 | |||
| 7.957 | 5.422 | 2.271 × | 4.244 × | N/A | 14.2 | |||
| Maximum Estimation Error (%) | RMSE | Maximum Setting Time (s) | CPU Usage (%) | ||||
|---|---|---|---|---|---|---|---|
| Load Torque | Flux Linkage | Load Torque | Flux Linkage | ||||
| 10 | 10 | 3.306 | 0.1265 | 1.520 × | 1.116 × | 0.3921 | 11.63 |
| 30 | 30 | 1.116 | 0.1183 | 6.470 × | 6.424 × | 0.1308 | 15.74 |
| 50 | 50 | 0.6842 | 0.1525 | 4.563 × | 4.987 × | 0.0801 | 15.96 |
| 100 | 100 | 0.3965 | 0.2206 | 2.986 × | 3.590 × | 0.0403 | 14.20 |
| 1000 | 1000 | 0.6471 | 0.8010 | 1.791 × | 2.782 × | N/A | 12.96 |
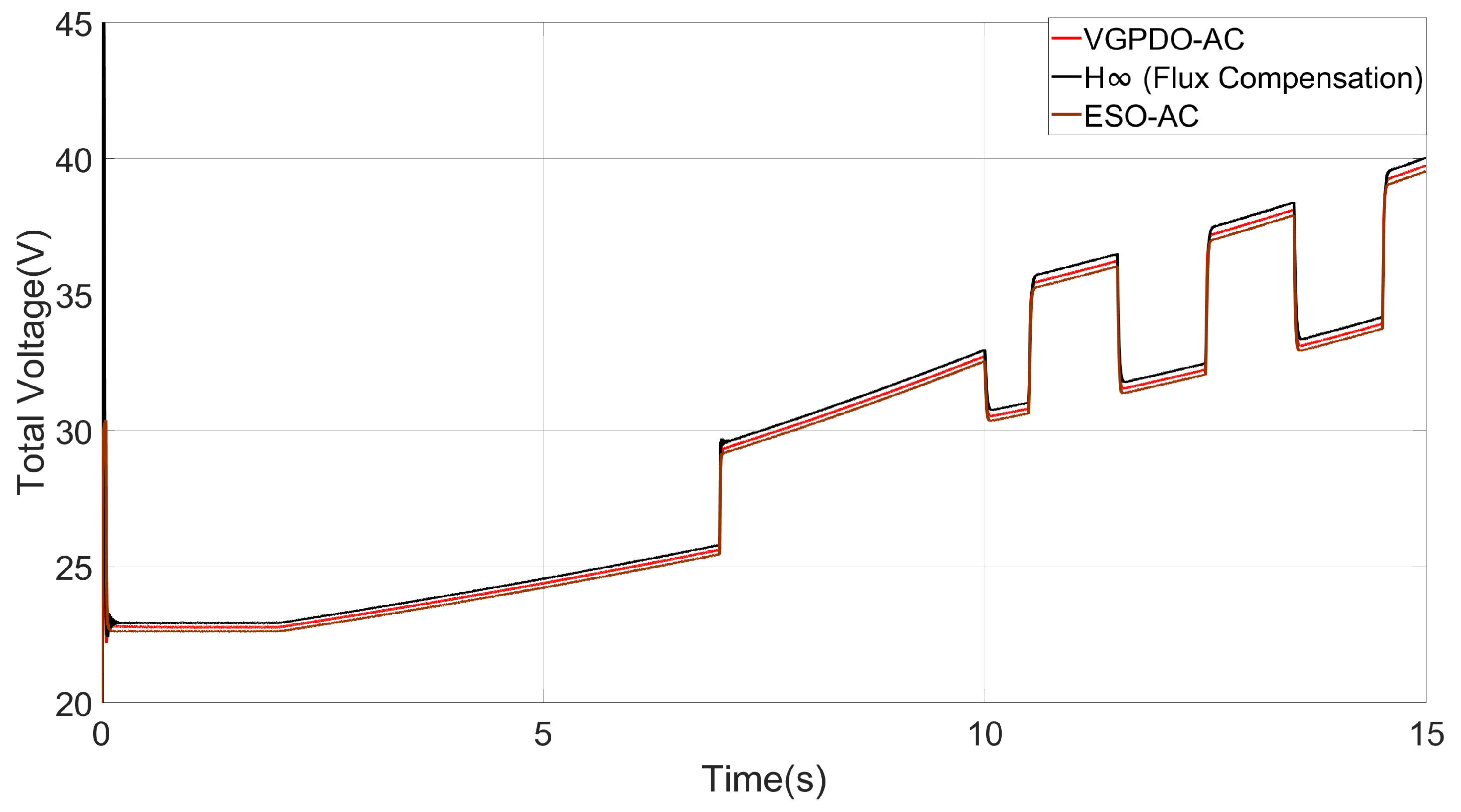
| Control Strategy | Steady-State Error (%) | RMSE | Energy Consumption (J) | Settling Time (s) |
|---|---|---|---|---|
| - Flux Compensation | 0.08331 | 32.8425 | 1.424 × | 0.0814 |
| ESO-AC | 0.39359 | 34.4345 | 1.387 × | 0.1044 |
| VGPDO-AC | 0.01217 | 27.3861 | 1.396 × | 0.0676 |
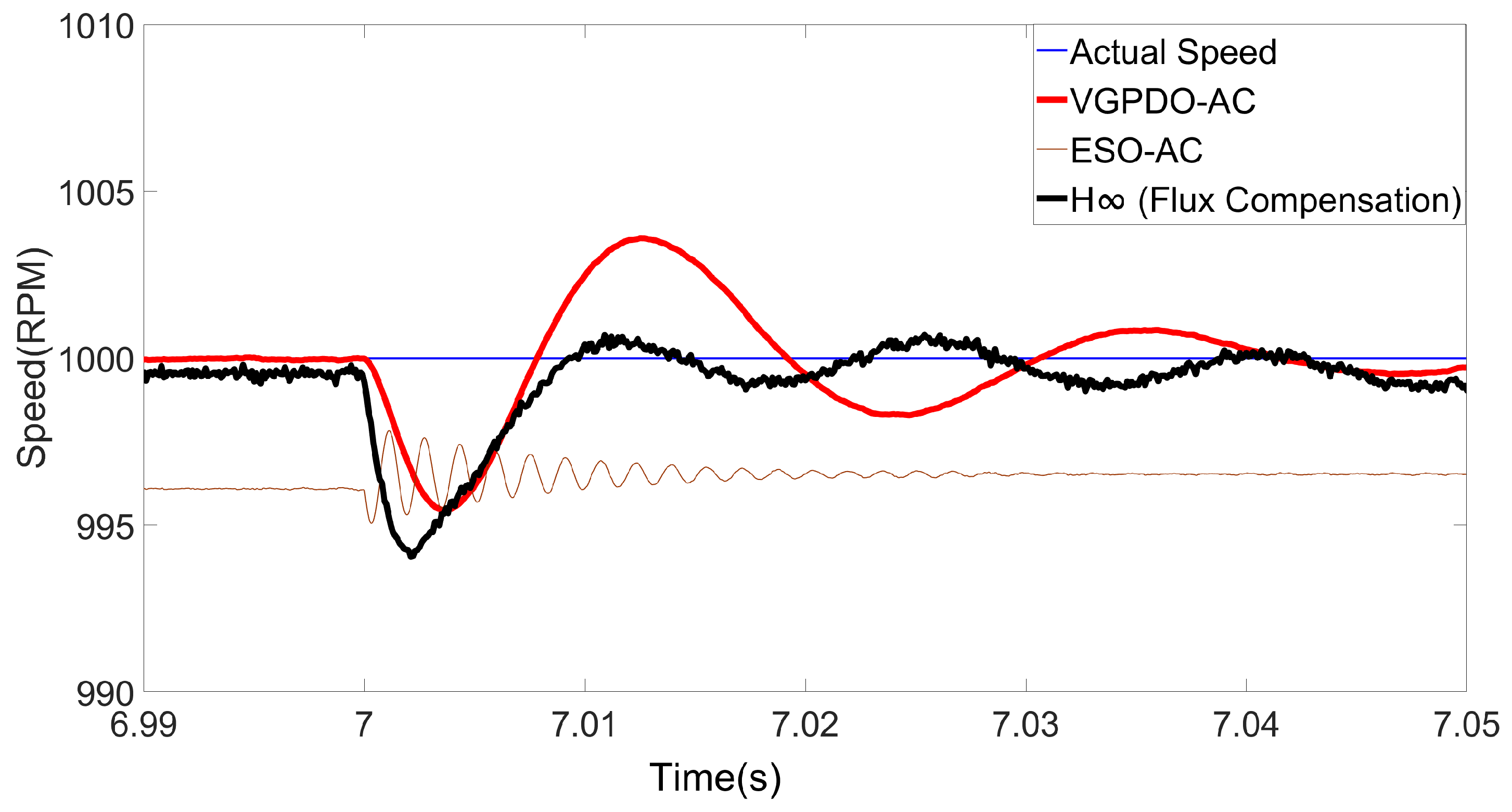
| Algorithm | Maximum Deviation (%) | RMSE |
|---|---|---|
| - Flux Compensation | 0.5957 | 0.6515 |
| ESO-AC | 0.495 | 3.4886 |
| VGPDO-AC | 0.4623 | 0.3582 |
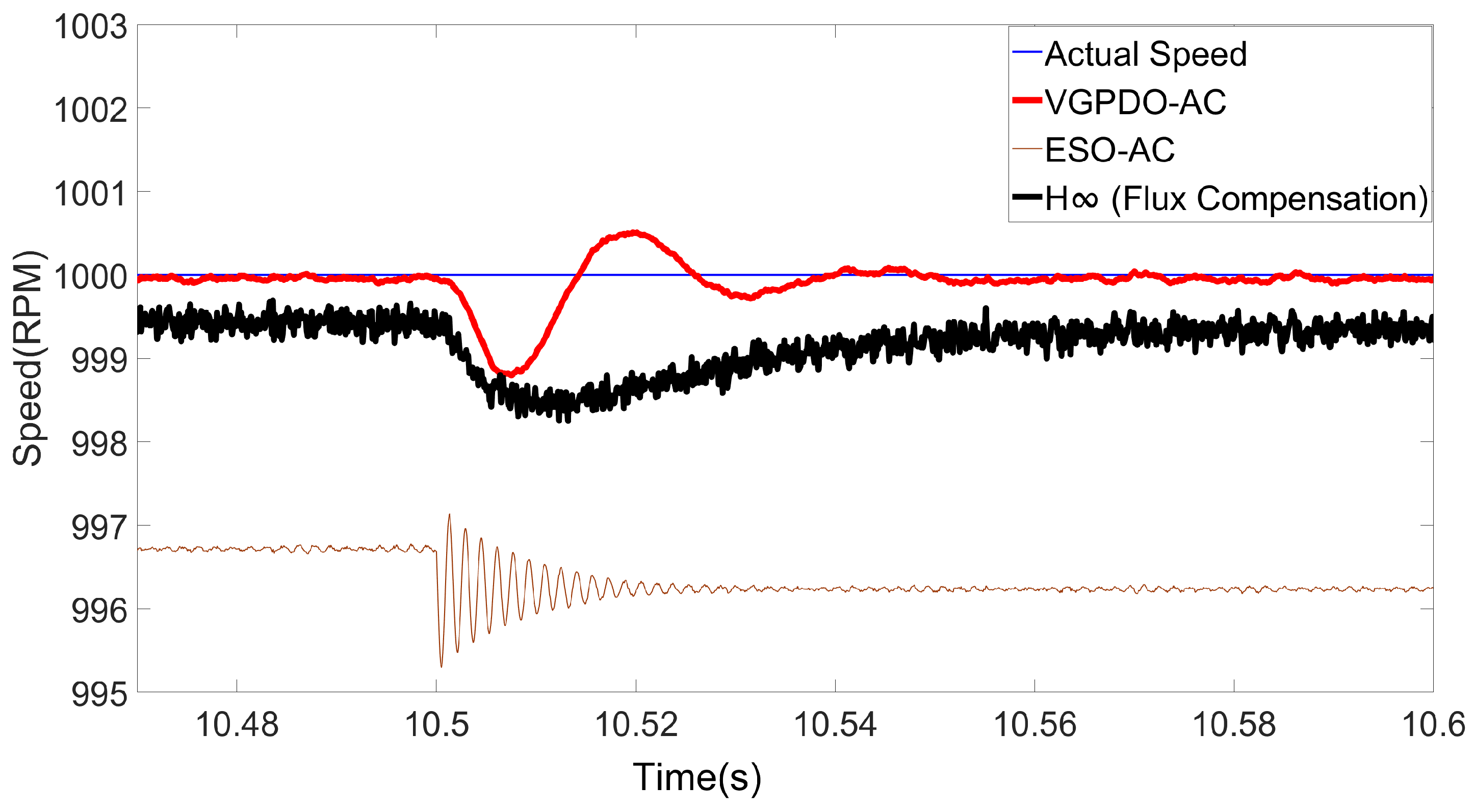
| Algorithm | Maximum Deviation (%) | RMSE |
|---|---|---|
| - Flux Compensation | 0.1747 | 0.6947 |
| ESO-AC | 0.3816 | 3.7403 |
| VGPDO-AC | 0.1156 | 0.1034 |
| Speed | ||||
|---|---|---|---|---|
| RMSE | Steady-State Error (%) | Settling Time (s) | ||
| 0.1 | 0.1 | 100.20 | 0.00972 | 0.1004 |
| 0.5 | 0.5 | 96.99 | 0.01058 | 0.0874 |
| 1 | 1 | 92.21 | 0.01217 | 0.0689 |
| 2 | 2 | 90.87 | 0.0226 | 0.0443 |
| Steady-State Estimation Error on (%) | CPU Usage (%) | ||||
|---|---|---|---|---|---|
| Percentage Deviation (%) | Settling Time (s) | ||||
| 0.1 | 0.1 | 0.5307 | 0.6329 | 1.684 | 60.329 |
| 0.5 | 0.5 | 0.3303 | 0.3048 | 1.653 | 59.484 |
| 1 | 1 | 0.1050 | 0.2066 | 1.640 | 56.649 |
| 2 | 2 | 0.0129 | 0.1609 | 1.807 | 52.418 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niu, Y.; Shi, H. A Robust Optimal Control Strategy for PMSM Based on VGPDO and Actor-Critic Neural Network Against Flux Weakening and Mismatched Load Torque. Mathematics 2025, 13, 3387. https://doi.org/10.3390/math13213387
Niu Y, Shi H. A Robust Optimal Control Strategy for PMSM Based on VGPDO and Actor-Critic Neural Network Against Flux Weakening and Mismatched Load Torque. Mathematics. 2025; 13(21):3387. https://doi.org/10.3390/math13213387
Chicago/Turabian StyleNiu, Yangyu, and Haibin Shi. 2025. "A Robust Optimal Control Strategy for PMSM Based on VGPDO and Actor-Critic Neural Network Against Flux Weakening and Mismatched Load Torque" Mathematics 13, no. 21: 3387. https://doi.org/10.3390/math13213387
APA StyleNiu, Y., & Shi, H. (2025). A Robust Optimal Control Strategy for PMSM Based on VGPDO and Actor-Critic Neural Network Against Flux Weakening and Mismatched Load Torque. Mathematics, 13(21), 3387. https://doi.org/10.3390/math13213387






