Abstract
This paper addresses the optimization of traffic signal timing at urban intersections by introducing a dynamic green ratio allocation framework based on cycle-based delay classification. Conventional methods such as the Webster delay model often fail to capture the asymmetric delay characteristics and the impact of fluctuating flows across multiple cycles. We propose a novel approach that classifies cycles into undersaturated and oversaturated states and develops dedicated optimization models for each type. For undersaturated cycles, a new delay function is derived to accurately capture the interaction between queue dissipation and green time allocation, enabling multi-period minimization of total vehicle delay. For oversaturated cycles, queue minimization at the end of each phase is adopted to accelerate congestion dissipation. The framework is validated through simulation and compared with existing methods, demonstrating superior performance in congestion clearance and delay minimization. The results show improved adaptability to changing traffic conditions and enhanced practicality for real-time signal control in smart transportation systems.
Keywords:
signal timing optimization; dynamic green ratio allocation; cycle-based delay classification; queue minimization; smart transportation systems MSC:
90C30
1. Introduction
With the continuous growth of the global economy and accelerating urbanization, urban traffic demand has shown a rapid upward trend. According to the United Nations’ World Urbanization Prospects report [1], the global urbanization rate exceeded as of 2018, and this figure is projected to surpass within the next three decades. Meanwhile, data from the International Road Federation (IRF) shows that the total length of the global road network has exceeded 64 million kilometers [2]. Urbanization brings not only increased population density but also significant spatio-temporal non-uniformity in traffic demand. Typically, traffic flow during peak hours can be three to five times that of off-peak periods [3]. This complex and variable traffic environment poses severe challenges to the operational efficiency, energy consumption, and emissions control of urban road networks.
As critical nodes in urban road networks, intersections’ capacity and signal timing efficiency directly impact the performance, energy consumption, and emission levels of the entire network [4]. An ideal signal timing plan must respond precisely to real-time, dynamic traffic demand. However, the non-uniform and stochastic traffic flows caused by short-term events and commuter peaks make achieving traffic equilibrium exceedingly challenging. Furthermore, Li [5] and Chow [6] have pointed out that frequent flow fluctuations can undermine the stability and efficiency of signal control. Traditional fixed-time control strategies (such as the Webster method), while performing well under stable traffic conditions, struggle to adapt to non-uniform flows. Their static parameters are difficult to adjust dynamically, leading to a disconnect between green time allocation and actual demand, which results in wasted resources or reduced operational efficiency [7].
Modern Intelligent Transportation Systems (ITSs), through the deployment of devices such as video detectors, radar sensors, and On-Board Units (OBUs), have enabled the possibility of real-time, data-driven control [8,9]. For instance, the SCOOT system dynamically adjusts signal cycles based on traffic data updated every second, with optimization objectives that include minimizing total delay and the number of stops [10]. However, despite the maturation of data acquisition technologies, determining how to leverage this vast amount of real-time data to design control algorithms that are both efficient and theoretically grounded remains a critical and unresolved scientific question.
To address this challenge, this paper proposes a model-driven framework for dynamic green time ratio optimization. By precisely classifying traffic states and applying tailored optimization strategies for each state, the framework aims to provide an interpretable, efficient, and real-time decision-making core for modern ITS platforms. The primary contribution of this research lies not only in enhancing the adaptability of signal control to dynamic traffic flows but also in providing new perspectives on signal optimization under congested conditions through rigorous theoretical analysis.
The main original contributions of this study are as follows:
- A multi-cycle dynamic green time ratio optimization framework is proposed. Based on multi-objective optimization and system-optimal principles, the framework is enabled, through the utilization of real-time sensor data, to respond effectively to non-uniform and stochastic traffic flows and to provide adaptive signal-timing strategies for complex traffic scenarios.
- A rigorous signal cycle classification method is established. This method systematically categorizes traffic states into undersaturated and oversaturated cycles based on key parameters such as cycle duration, traffic flow, and capacity. It is designed to serve as an efficient and reliable real-time decision analysis core within ITS platforms.
- A new delay function for undersaturated cycles is introduced. This function more accurately captures the delay dynamics caused by the interplay of initial queues and signal phases, correcting estimation biases of traditional models in specific scenarios.
- An optimization objective centered on residual queues for oversaturated cycles is proposed. It is theoretically demonstrated that the optimal strategy for rapid congestion dissipation involves maximizing the capacity of each phase and minimizing the residual queue at the end of the cycle, thereby providing a clear quantitative metric for congestion management.
- The framework is extended and applied to complex multi-phase intersection scenarios. The generality and effectiveness of the proposed method have been validated across various intersection geometries, demonstrating strong performance in minimizing total delay under undersaturated conditions and in mitigating congestion on critical approaches under oversaturated conditions.
2. Related Work
2.1. Classical Control Theory
Early traffic signal control theories laid an essential theoretical foundation for modern research. The principles of User Equilibrium (UE) and System Optimum (SO), established by Wardrop in 1952 [11], remain core guiding concepts in traffic planning and management today. Subsequently, Webster’s pioneering work proposed a classic method for calculating the optimal cycle length based on saturation and lost time, a model that has been widely adopted for its simplicity and effectiveness [12,13].
Building on this foundation, Miller proposed a method for optimizing traffic signal timing using dynamic programming, enabling real-time responses to fluctuations in traffic flow [14]. He also demonstrated how to minimize queuing delays by adjusting vehicle queues under conditions of traffic uncertainty. However, dynamic programming methods face the “curse of dimensionality” in high-dimensional state spaces, making them difficult to apply directly to multi-phase intersections. For example, Guo highlighted the complexity and convergence issues associated with traffic network computations [15]. Similarly, Zhou et al. optimized traffic light control strategies by designing green light sequences and determining green durations based on real-time traffic data, thereby increasing system throughput while reducing average vehicle waiting times and stops [16].
In engineering practice, the SCOOT system in the UK [10] and the SCATS system in Australia [17] are the most widely implemented urban traffic signal coordination control systems. They adjust signal parameters in real-time using sensors deployed across the road network and represent the tremendous success of classical control theory in practical applications [18]. However, these systems typically rely on predefined macroscopic traffic models, and their responsiveness and optimization precision still have room for improvement when dealing with instantaneous, sharp traffic surges at the intersection level. For example, when SCOOT handles coordinated optimization for adjacent intersections, it may achieve a local optimum at the expense of global network performance [19].
2.2. Data-Driven and Artificial Intelligence Methods
In recent years, Artificial Intelligence (AI) technologies, particularly Machine Learning (ML), have opened new avenues for signal control. Researchers have utilized algorithms like NSGA-II [20,21] and various Machine Learning models [22] to solve multi-objective optimization problems. For instance, NSGA-II uses Pareto front selection to strike a balance among multiple objectives (e.g., total delay, fairness, energy consumption), but it is often computationally expensive. With the advancement of deep learning, Reinforcement Learning (RL) has gained significant attention due to its strengths in sequential decision-making problems. For example, Arel et al. [23] proposed a control method based on Multi-Agent Reinforcement Learning (MARL).
More recently, Zhang et al. [24] proposed a MARL method for corridor-level traffic signal control, where agents collaborate to optimize the timing of consecutive intersections along an arterial road, also considering the issue of “fairness” (e.g., preventing vehicles in certain directions from queuing for extended periods). While such MARL methods have achieved excellent performance in simulation environments, they often operate as “black-box” models, lacking physical interpretability in their decision-making processes. Furthermore, existing research has predominantly focused on simple network structures (such as linear corridors), and their adaptability to complex intersections (e.g., four-phase or more) has not been fully validated.
Therefore, the method proposed in this paper aims to collect real-time traffic flow and queue length data from sensors within an ITS and translate this data into actionable, optimal signal timing strategies in real time. It is grounded in classical traffic flow theory and drives decision making through an explicit classification of traffic states, thereby providing clear physical interpretability while ensuring high efficiency.
3. Undersaturated Signal Cycle Intervals Under Uniform Traffic Flow at a Two-Phase Intersection
3.1. Classification of Undersaturated Signal Cycle Intervals
Consider the signal control at a two-phase intersection, as illustrated in Figure 1. This control scheme allocates the right-of-way to two mutually perpendicular directions, with only two one-way roads: west-to-east (road 1) and north-to-south (road 2).
Figure 1.
Two-phase intersection.
Since the duration of the amber phase is typically independent of both the signal cycle length and traffic conditions [25], it is considered part of the green phase for model simplification. This treatment effectively accounts for the start-up lost time and clearance lost time associated with vehicle acceleration and deceleration. Key parameters are defined as follows:
Cycle duration C: The time interval from the start of green for one road until it next receives green after all phases have been served.
Arrival flow : The flow rate of vehicles arriving at road i during cycle , assumed to follow a uniform arrival distribution within the cycle.
Green phase : The green phase duration for road i in cycle k.
Red phase : The red phase duration for road i in cycle k ().
Green time ratio : The proportion of cycle C allocated as green time for road i in cycle k (), satisfying .
Saturation capacity rate : The maximum rate at which vehicles can depart from the queue on road i during the green phase. In this study, it is treated as a constant parameter representing the inherent capacity of the road.
Initial queue : The number of vehicles remaining on road i at the end of its green phase in cycle k.
Residual queue : The number of vehicles on road i that failed to depart at the end of the green phase duration during cycle k.
Drawing on Gazis’s [26] necessary and sufficient conditions for undersaturation, intersection congestion is defined as follows:
An intersection is considered congested during cycle k if at least one road has a residual queue () at the end of its green phase. Conversely, it is uncongested if all queues are fully cleared () by the end of their respective green phases.
For the intersection in Figure 1, taking the start of the green phase for road 1 as the temporal origin of the 0-th cycle, this definition translates to
The intersection is uncongested in cycle k only if both (1) and (2) hold simultaneously. Otherwise, it is congested.
The congestion state of an intersection depends on the green time ratio , so each signal cycle is classified as either an “undersaturated cycle” or an “oversaturated cycle” according to whether congestion can be alleviated by adjusting the green time.
A signal cycle is classified as an undersaturated cycle if at least one feasible solution of simultaneously satisfies the system of Equations (1) and (2). Conversely, if the solution set of (1) and (2) is empty, the signal cycle is classified as an Oversaturated Cycle.
This classification differs from Webster’s degree of saturation, , which evaluates the saturation level for a given signal timing plan. By contrast, the proposed definition determines whether a feasible timing solution exists that is capable of clearing all queues.
For an undersaturated cycle k, there exists a feasible such that
where denotes the queue clearance time [27] for road i in cycle k.
If cycle is undersaturated, the initial queue for cycle k is given by
where represents the known initial queue at cycle 0.
To account for the potential cascading effects of green time settings on subsequent cycles, the propagation of congestion across consecutive cycles requires thorough analysis. Specifically, if every signal cycle k within the interval is classified as an undersaturated cycle, then this sequence is referred to as an undersaturated cycle interval. The objective is to minimize the total vehicle delay within this interval.
Theorem 1.
The cycle interval is undersaturated if the following conditions hold:
When and hold for each cycle , the following conditions must be satisfied:
Proof.
If or for any k, no feasible green time ratio exists that satisfies both (1) and (2), resulting in cycle k being classified as oversaturated.
For the boundary case where , the condition can be treated as through the introduction of an infinitesimal perturbation to .
Assuming and hold for cycle k, the undersaturated condition requires the existence of a satisfying the following inequalities derived from (3) and (4):
For , the initial queue is set to ; thus,
Therefore, for , the following expression is derived:
And for ,
□
3.2. Green Time Allocation for Undersaturated Cycle Intervals
Since its introduction by Webster, the delay function model has served as a fundamental tool for signalized intersection optimization owing to its theoretical simplicity and broad applicability [28]. The Webster delay function relies primarily on assumptions of random vehicle arrivals and uniform phase durations, effectively capturing the relationship between saturation degree and average vehicle delay. However, limitations have been identified: by treating the intersection as a single entity for aggregate analysis, the model fails to adequately characterize delay variations between distinct signal phases under multi-phase operations and uneven flow distributions. This is particularly evident in its inability to reflect the asymmetry of the delay–green time ratio relationship under practical traffic conditions [29,30].
In a typical two-phase intersection with significantly unequal cross-directional flows, the total delay function is generally not symmetric about . Consequently, equal green time allocation does not necessarily achieve optimal delay minimization.
The Webster delay function is expressed as
where the single-phase delay component is represented as
To address the symmetry limitation in Webster’s model, existing approaches such as the ROSCA method [31] incorporate flow- and green time ratio-based weighting into directional delay components, theoretically introducing asymmetry:
Empirical evidence has shown that, although the ROSCA method captures asymmetric variations, its delay predictions exhibit substantial discrepancies when compared with simulation results. To overcome this limitation, a novel intersection delay function is proposed, which more accurately models the effects of uneven traffic flows and signal phase configurations on the resulting delay distribution.
For road 2 in an undersaturated cycle k, when a vehicle arrives during the red interval , it encounters a queue of vehicles ahead and must wait for the residual red time . The expected waiting time during is given by
If a vehicle arrives during the queue dissipation interval , then there are vehicles queuing ahead, and the expected waiting time for arrivals during this interval is given by
If a vehicle arrives during the free-flow interval , the queue on road 2 has already cleared, and vehicles arriving in this interval do not need to wait, i.e., .
Summing up, for any vehicle on road 2 in the k-th cycle, the expected waiting time at the intersection is thus
Similarly for road 1, the expected waiting time at the intersection can be formulated as
with and satisfying (5) and (6).
To validate the effectiveness of the proposed delay model, a single intersection simulation scenario was configured according to the topology shown in Figure 1. The configuration represented a typical urban intersection with imbalanced traffic flows between a major and a minor road. Constant vehicle arrivals were assumed, with the major-road flow set to veh/min and the minor-road flow to veh/min. Both roads were assigned a saturation flow rate of veh/min, and the cycle duration was min.
In this scenario (Figure 2), delay predictions from the proposed model were compared against those of Webster’s formula and the ROSCA weighted method, using microscopic simulation delays from PTV VISSIM (PTV Group, Karlsruhe, Germany) as the reference. By varying the green time ratios of the major road, we recorded the average intersection delay calculated by each model.
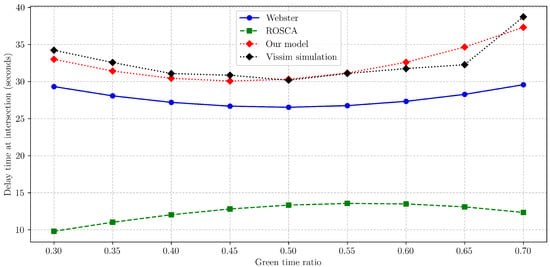
Figure 2.
Comparison of total delays under varying green time ratios.
The results can be summarized as follows:
- Webster’s model produces a delay curve that is strictly symmetric about , in line with its underlying assumptions. However, the shift in optimal green time ratio induced by flow imbalance () is not captured, yielding a significant deviation from the VISSIM reference.
- The ROSCA model successfully reflects the asymmetry of the delay curve. However, its predicted delay values are numerically distant from the simulation benchmark, showing a consistent underestimation.
- The proposed model outperforms both alternatives in two respects. First, the asymmetry of the delay curve is accurately represented. Second, the predicted delays closely match the VISSIM data, demonstrating improved accuracy and adaptability to imbalanced traffic flows.
In the multi-cycle signal control process, the green time ratio of cycle k affects the delays in subsequent cycles. Consequently, the total delay over multiple cycles needs to be considered for optimization. Considering a signal interval composed of consecutive undersaturated cycles, the optimization objective is to minimize the total system delay at the intersection over this interval. This problem can be formulated as follows:
To ensure the clearance of traffic arriving in each cycle effectively, the green time ratio is subject to the following constraint:
This constraint exhibits dynamic and coupled properties: its bounds are not fixed but are adjusted in real time according to the initial queue lengths and arrival flow rates in each cycle k, which significantly enhances the intersection’s adaptive control capability.
4. Oversaturated Signal Cycle Intervals Under Uniform Traffic Flow at Two-Phase Intersections
Delay time functions for traffic signal timing were developed by Chang [32] and Webster et al. using single-cycle vehicle queuing delays. However, under severe intersection congestion where vehicles require multiple signal cycles for passage clearance, traditional single-cycle delay models fail to accurately characterize actual queuing conditions. To address these limitations, this study proposes that single-cycle delay minimization is superseded by residual queue count minimization as the core evaluation metric for signal timing algorithms.
4.1. Classification of the Oversaturated Signal Cycle Interval
During an oversaturated cycle at an intersection, there must be at least one road with residual vehicles (congestion) at the end of its green phase. If exactly one road experiences congestion while other roads have cleared their queues before the end of their green phases, it indicates that the congested road has not fully utilized the “surplus green time” from other roads.
To ensure full phase utilization in oversaturated cycle k, if any road retains residual vehicles at green time termination, all other roads must likewise retain residual queues. Formally, the following conditions hold simultaneously:
For initial cycle , the initial queue is a known constant. If cycle is undersaturated, satisfies (5) and (6). If interval is oversaturated with full phase utilization, the initial queue satisfies
The case where Equations (25) and (26) are simultaneously satisfied constitutes a proper subset of the condition where Equations (1) and (2) are both unsatisfied. In other words, the scenario of “full phase utilization” represents merely a proper subset of the oversaturation condition.
In an oversaturated condition, the determination of the optimal green time ratio allocation within a single cycle becomes critical. One intuitive strategy maximizes total vehicle outflow, which might prioritize fully clearing the queue in one direction, whereas an alternative strategy fully utilizes the capacity of all congested phases, even if it means all directions have residual queues at the end of their green phases.
To theoretically determine which strategy is superior, we conduct a single-cycle, forward-looking comparative analysis. Our objective is to evaluate how different timing strategies applied in the current cycle, k, affect the initial state of the next cycle, .
An arbitrary oversaturated cycle, denoted as cycle k, is considered. The parameters , , and are treated as known initial conditions for this comparison, rather than as variables requiring recursive computation.
Strategy A: Full utilization of saturation capacity in each phase, such that and . The initial queue lengths for cycle are then given by
Queue clearance time for the initial queued vehicles , in cycle can be expressed as
Strategy B: Early clearance of the main road phase, such that and . Then, the queue clearance time for road 1 in cycle k, denoted as , satisfies
Accordingly, the initial queue lengths for cycle are given by
Queue clearance time for the initial queued vehicles and in cycle is expressed as
To compare and , their difference is taken. From Equation (30), it follows that
Strategy C: Early clearance of the minor road phase. The queue clearance time for road 2 in cycle k, denoted , satisfies
Queue clearance time for the initial queued vehicles and in cycle is expressed as
To compare and , their difference is taken. From Equation (34), it follows that
The results clearly show that and . Therefore, we can conclude that within any oversaturated cycle, a strategy that maximizes the utilization of all congested phases’ capacities (Strategy A) is more effective at reducing the total queue length carried over to the next cycle than strategies that allow some phases to clear early (Strategies B and C), thereby leading to faster congestion dissipation.
Theorem 2.
The cycle interval is oversaturated if for every subinterval and , the following condition holds:
Corollary 1.
If cycle interval is oversaturated but cycle is undersaturated, then constitutes the maximal oversaturated interval, requiring at least cycles for congestion dissipation.
4.2. Green Time Allocation for Oversaturated Signal Cycle Intervals
Since and are linearly and negatively correlated with , we formulate the signal control problem as an optimization problem to minimize the number of residual vehicles within each signal cycle over the oversaturated period . The objective function is defined as follows:
In this optimization problem, the decision variables are the sequence of green time ratios covering the next time steps, where . To ensure full utilization of the intersection’s signal phases, this optimization problem is subject to the following constraints:
The fundamental purpose of controlling oversaturated traffic flow is to restore the intersection to an undersaturated state. For the specific transitional phase defined as the ”longest oversaturated cycle interval” , the control objective is constructed as a composite function that simultaneously considers two aspects:
- (1)
- Efficient management of the cumulative queue within the oversaturated interval ;
- (2)
- Optimal operational efficiency in the first recovery cycle .
This control strategy aims to determine an optimal green time ratio sequence . During the oversaturated phase, the primary goal is to minimize the cumulative residual queue length. By adopting the sum of squares of the residual queue length, the strategy imposes a significant penalty on excessively long queues, thereby promoting balanced congestion among competing phases and preventing systematic failure of any single phase.
Meanwhile, this green time ratio decision sequence directly determines the initial queue lengths of the subsequent first undersaturated cycle . As the residual queue from the oversaturated cycle, its scale is a critical factor affecting the delay in cycle . Therefore, the optimization objective further includes minimizing the total delay in that cycle.
Hence, for the composite control problem over the cycle interval , the model applies the queue management objective in Equation (38) for the oversaturated interval , and the delay minimization objective in Equation (23) for the recovery cycle . This approach integrates two distinct control goals—queue dissipation and delay minimization—within a single, unified optimization framework.
To validate the proposed residual queue model, a comparative analysis was conducted with Chang’s delay model. The parameter settings are detailed in the “Data Availability Statement” section. Figure 3 illustrates the cumulative vehicle inflow–outflow trajectory under the proposed model, while Figure 4 shows the results from Chang’s model.
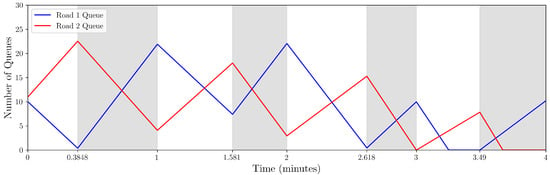
Figure 3.
Actual queue length (proposed residual queue model).
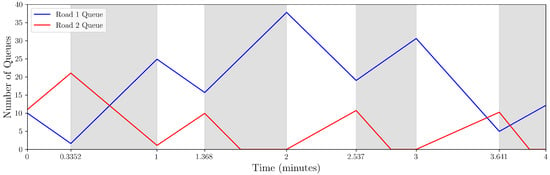
Figure 4.
Actual queue length (Chang’s delay model).
Two critical findings emerge:
Chang’s model exhibits underutilization of road 2’s saturation capacity during Cycles 1–2, preventing queue clearance on road 1 in Cycle 3.
The proposed residual queue model achieves complete congestion dissipation within fewer cycles, demonstrating superior queue clearance efficiency.
5. Green Light Timing for Undersaturated Cycles at Four-Phase Intersections
As shown in Figure 5, the most common type of intersection in urban traffic networks features four-phase control with two-way traffic flow. This type of intersection requires at least two straight-ahead signal controls and two left-turn signal controls, but does not have independent right-turn signal controls. Typically, either a dedicated right-turn lane is established, or the right-turn signal is integrated with the straight-ahead signal.
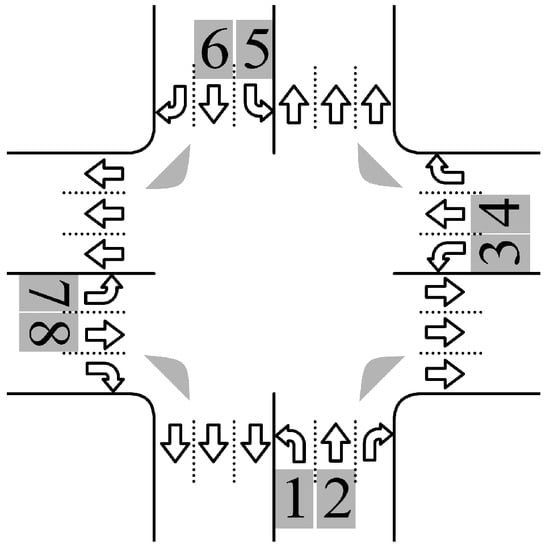
Figure 5.
A four-phase signalized intersection. Numbers indicate traffic movements, and arrows show the permitted movements for each phase.
For intersections with two-way traffic flow, opposing roads typically have the same signal phase. For example, roads from south to north and from north to south are controlled by the same straight-ahead signal. This means that when designing any phase control, the traffic conditions of the two corresponding roads must be considered.
Let represent the green signal duration for road . Let represent the red signal duration for road i.
where is the green time ratio for road i and road in the k-th signal cycle.
In a four-phase intersection, the green time ratios must satisfy the following equality constraint.
For a four-phase intersection, if a signal cycle k is defined as undersaturated, then there exists a feasible green time ratio allocation such that the queues on all roads can be completely cleared by the end of the cycle (i.e., ). This condition can be expressed as a set of linear inequalities:
At a four-phase intersection, opposite directions of traffic (road i and ) are typically served by the same signal phase, denoted as phase i. Consequently, the green time duration allocated to phase i must satisfy the clearance time requirements of both corresponding directions in that phase. This can be expressed as
When , the initial queue length for each road is a known constant . When , if the -th signal cycle is a undersaturated cycle, then the initial queue length for the k-th cycle satisfies
To ensure that the queues in both directions of phase i are fully cleared, the green time for phase i must be greater than or equal to the maximum clearance time between the two directions. This constraint is formulated as follows:
However, it is difficult to directly determine whether the inequality systems (42) or (45) have feasible solutions , as there are complex coupling relationships among the terms. To establish a more direct feasibility criterion, two core theoretical concepts are introduced: the “minimum initial queue” and the “minimum allowable green time.” These two parameters decouple the dependencies in the judgment process through a dual recursive structure.
The minimum initial queue is a theoretical value that characterizes the minimized queue accumulation effect from the previous cycle () to the current cycle (k). It is defined based on a core assumption that cycle is an undersaturated cycle, with the green light duration of each phase exactly equal to its “minimum allowable green light time”. Its meaning is the “initial queue“ strategy that has the least impact on cycle k under the condition that no congestion occurs in cycle .
Based on this assumption, the minimum initial queue at the beginning of cycle k can be recursively defined using parameters from cycle :
For the initial cycle , equals the known actual initial queue .
The minimum allowable green light time is the theoretically shortest green light duration required to clear the queue of phase i. Its calculation is also recursive, but this recursion occurs within cycle k.
Through these definitions, the dependency on the unknown green time ratios is transformed into a dependency on deterministic parameters which can be computed from historical data and current arrival rates.
Based on the above concepts, the following theorem provides a necessary and sufficient condition for identifying undersaturated cycles.
Theorem 3.
Under the condition that the saturation flow rates exceed the arrival flows for all roads (), a signal cycle k is feasible as an undersaturated cycle if and only if the sum of the minimum allowable green times across all phases does not exceed the total cycle length C.
Proof.
Sufficiency. Assume that the condition in Equation (48) holds. A green time ratio solution can be constructed as follows: for each phase , let . Based on the initial assumption, it follows that , which indicates that this is a valid allocation scheme satisfying the constraint in (41).
By substituting this scheme into Equation (43), it can be verified that when the initial queue is , the green time allocated to each phase, , is precisely equal to its required clearance time. Since a feasible green allocation scheme exists that can clear these idealized queues, the cycle is capable of operating in an undersaturated state. Thus, the condition is sufficient.
Necessity. Conversely, assume that cycle k is undersaturated. By definition, there exists a valid green split allocation that satisfies and is capable of clearing the actual initial queues on all approaches.
This implies that for each phase i, the allocated green time must be greater than or equal to the actual required clearance time, i.e., . Summing this inequality over all phases yields
The actual initial queue is inherently greater than or equal to the theoretical minimum initial queue . According to the clearance time equation, is a monotonically increasing function of the initial queue length . Therefore, the minimum allowable green time , which is calculated based on , serves as a lower bound for the actual clearance time . This relationship establishes the final inequality:
Hence, the condition is necessary. □
Therefore, when the k-th signal cycle is undersaturated, the green timing strategy can be optimized using a delay model. Specifically, analogous to the delay function for a two-phase intersection, the expected waiting time for vehicles on roads at a four-phase intersection under such conditions is given by
The expected waiting time of vehicles on roads is
The expected waiting time of vehicles on roads is
The expected waiting time of vehicles on roads is
where satisfies Equation (45) and satisfies Equation (44).
In a four-phase intersection, if the signal cycle interval is a undersaturated cycle interval, in order to minimize the total system delay at the entire intersection during this signal cycle interval, we have
subject to
6. Green Light Timing for Oversaturated Cycles at Four-Phase Intersections
Consider a four-phase intersection operating in an oversaturated cycle. This implies that preventing congestion on any given road is not achievable solely by adjusting the green timing strategy.
It has been demonstrated in Section 4.1 that to restore the intersection to an undersaturated state within the minimum number of signal cycles, each signal phase must be fully utilized. Specifically, for the two opposing roads (i and ) served by phase i, a residual queue must be present on at least one of these roads at the end of the green interval. This condition can be expressed as the following set of linear inequalities:
where is the number of residual vehicles on road i at the end of the green light time in the k-th cycle.
where, when , .
When the -th cycle is an oversaturated cycle, even if the signal phases of the -th cycle are fully utilized, there are still three possible congestion states for opposing roads: road i is congested while its opposing road is not congested, or both directions are congested simultaneously, or the opposing road is congested while the original road i is not congested. This means that when calculating the initial queue length for the k-th cycle, it is necessary to first determine whether roads were congested in the -th cycle.
For roads that were not congested in the -th cycle (), the initial queue length satisfies
For roads that were congested in the -th cycle (), the initial queue length satisfies
Theorem 3 provides the necessary and sufficient conditions for a signal cycle to be undersaturated. As a direct logical consequence, the contrapositive of the theorem provides the conditions for identifying a cycle as oversaturated.
Theorem 4.
A signal cycle k is identified as an oversaturated cycle if either of the following two conditions is met:
- There exists at least one road for which the arrival rate is greater than or equal to its saturation flow rate, i.e., .
- For all roads, the condition holds, but the sum of the minimum allowable green times for all phases exceeds the cycle length, i.e.,
Similarly, a corollary can be stated for a four-phase intersection. If there exists a period such that every cycle is oversaturated, while the subsequent cycle is undersaturated, then the period is defined as the longest oversaturated period.
The optimal green time ratios for the longest oversaturated period can be determined from the following optimization problem:
subject to
where satisfies Equation (57).
The implementation of the algorithms derived from the theorems and mathematical processes discussed herein is detailed in the Data Availability Statement.
7. Discussion
Although the proposed model has demonstrated its effectiveness on theoretical and simulation levels, several limitations need to be considered and addressed in future research and practical applications.
7.1. Limitations of the Current Study
- Ignoring induced demand: This study focuses on enhancing operational efficiency to manage existing traffic demand. However, as pointed out by Wiseman [33], improvements in traffic efficiency can generate an “induced demand” effect at the macroscopic level, where smoother traffic flows attract new travelers, potentially offsetting some of the optimization benefits in the long run. Our model does not incorporate this long-term traffic behavior feedback loop.
- Focus on isolated intersections: Our framework is currently designed primarily for the optimization of individual intersections. While crucial for a deep understanding of intersectional dynamics, this focus overlooks the interactions between adjacent intersections. Uncoordinated local optima may disrupt the “green wave” effect on arterial roads. This stands in contrast to the corridor-level coordinated control studied by Zhang et al. [24].
- Reliance on simulation and the reality gap: The validation of this research was conducted primarily through simulation. Although a simulated environment allows for variable control and the replication of diverse traffic conditions, a gap exists between simulation and the real world. Therefore, the model’s robustness in a real-data environment remains to be further validated.
- Simplified model assumptions: Our model is built upon several idealized assumptions, such as uniform vehicle arrivals within a cycle and a constant saturation flow rate. In reality, traffic arrivals can be platoon-based, and the saturation flow rate can be affected by factors like weather and the proportion of heavy vehicles. These factors may impact the accuracy of our traffic state classification and optimization results.
7.2. Future Work
Based on the limitations above, we have planned the following directions for future research:
- Real-world data validation and deployment: A primary objective is to test and calibrate our model using data from real-world intersections and to investigate the technical solutions for deploying the algorithm on actual ITS platforms.
- Extension to network-level coordinated control: We plan to extend the current single-point optimization framework into a network-level model. By leveraging multi-agent systems or distributed control theory, we can enable adjacent intersections to communicate and cooperate, aiming for a regional system optimum rather than just a local one.
- Considering multi-modal traffic and fairness: Future research will incorporate factors such as pedestrians and public transport into the optimization objectives to build a more comprehensive multi-modal traffic control model. Concurrently, we will explore how to strike a balance between efficiency and fairness (e.g., balancing waiting times between main and minor roads).
8. Summary
This study addresses the problem of signal timing optimization at urban intersections by proposing a dynamic green time ratio optimization method suitable for complex multi-cycle traffic scenarios, based on multi-objective optimization and system-optimal principles. Specifically, we analyzed the causes of congestion under different traffic conditions and classified signal cycles into undersaturated and oversaturated types based on parameters such as cycle length, traffic flow, and capacity, enabling precise adaptation to different traffic states.
For two-phase intersections, a new delay function for undersaturated cycles was introduced, which more accurately describes the delay differences between signal phases and the impact of initial queues on total delay. Considering the potential cascading effects of green time allocation on subsequent cycles, a multi-stage optimization model was established to minimize total delay during undersaturated periods. For oversaturated cycles, this study moves beyond the traditional Webster delay function, instead using the number of queued vehicles at the end of the green phase as the primary performance metric. The results show that by fully utilizing the saturation capacity of each phase and minimizing the number of vehicles retained per cycle, congestion can be dissipated more rapidly, and the optimal green time ratio can be identified.
Furthermore, the proposed framework was extended to complex four-phase intersections. During undersaturated cycles, total waiting time remains the objective, whereas during saturated cycles, minimizing the queue length of the most congested approach becomes the key target. Case studies have validated the effectiveness and adaptability of the method in improving overall traffic efficiency and real-time responsiveness.
The primary innovation of this research lies in providing a feasible path for real-time intelligent signal control that is both theoretically rigorous and practically operable, achieved through the explicit classification of signal cycles and the development of corresponding dynamic optimization models. This work takes a significant step toward bridging the gap between traditional analytical models and modern data-driven methods, offering theoretical support for building more efficient and transparent next-generation urban traffic management systems.
Author Contributions
Investigation, Z.G. and D.W.; methodology, Z.G.; software, Z.G.; validation, A.Y.K.; data curation, D.W.; writing—original draft preparation, Z.G.; writing—review and editing, A.Y.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the China Scholarship Council, grant number 202309010204.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data and algorithmic implementations presented in this study are openly available at https://github.com/GuoZhao1998/Dynamic-Signal-Timing-at-Urban-Intersections.git (accessed on 20 October 2025).
Conflicts of Interest
The authors declare no conflict of interest.
References
- United Nations, Department of Economic and Social Affairs, Population Division. World Urbanization Prospects: The 2018 Revision; ST/ESA/SER.A/420; United Nations: New York, NY, USA, 2019. [Google Scholar]
- International Road Federation. World Road Statistics 2022; International Road Federation: Geneva, Switzerland, 2022; Available online: https://datawarehouse.worldroadstatistics.org/ (accessed on 17 May 2025).
- Xing, H.; Chen, A.; Zhang, X. RL-GCN: Traffic Flow Prediction Based on Graph Convolution and Reinforcement Learning for Smart Cities. Displays 2023, 80, 102513. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, X.; Liang, H.; Liu, Y. A Review of the Self-Adaptive Traffic Signal Control System Based on Future Traffic Environment. J. Adv. Transp. 2018, 2018, 1096123. [Google Scholar] [CrossRef]
- Li, L.; Huang, W.; Chow, A.H.F.; Lo, H.K. Two-Stage Stochastic Program for Dynamic Coordinated Traffic Control under Demand Uncertainty. IEEE Trans. Intell. Transp. Syst. 2021, 23, 12966–12976. [Google Scholar] [CrossRef]
- Chow, A.H.F.; Sha, R.; Li, Y. Adaptive Control Strategies for Urban Network Traffic via a Decentralized Approach with User-Optimal Routing. IEEE Trans. Intell. Transp. Syst. 2019, 21, 1697–1704. [Google Scholar] [CrossRef]
- Ukkusuri, S.V.; Han, L.; Doan, K. Dynamic User Equilibrium with a Path Based Cell Transmission Model for General Traffic Networks. Transp. Res. Part B Methodol. 2012, 46, 1657–1684. [Google Scholar] [CrossRef]
- Azimjonov, J.; Özmen, A. A Real-Time Vehicle Detection and a Novel Vehicle Tracking Systems for Estimating and Monitoring Traffic Flow on Highways. Adv. Eng. Inform. 2021, 50, 101393. [Google Scholar] [CrossRef]
- Li, J.; Xu, Z.; Fu, L.; Xu, Z.; Fu, L.; Zhou, X.; Yu, H. Domain Adaptation from Daytime to Nighttime: A Situation-Sensitive Vehicle Detection and Traffic Flow Parameter Estimation Framework. Transp. Res. Part C 2021, 124, 102946. [Google Scholar] [CrossRef]
- Robertson, D.I.; Bretherton, R.D. Optimizing Networks of Traffic Signals in Real Time—The SCOOT Method. IEEE Trans. Veh. Technol. 1991, 40, 11–15. [Google Scholar] [CrossRef]
- Wardrop, J.G.; Whitehead, J.I. Correspondence. Some Theoretical Aspects of Road Traffic Research. Proc. Inst. Civ. Eng. 1952, 1, 767–768. [Google Scholar] [CrossRef]
- Yu, H.; Ma, R.; Zhang, H.M. Optimal Traffic Signal Control under Dynamic User Equilibrium and Link Constraints in a General Network. Transp. Res. Part B Methodol. 2018, 110, 302–325. [Google Scholar] [CrossRef]
- Krylatov, A.Y. Optimal Strategies for Traffic Flow Management on the Transportation Network of Parallel Links. Vestn. St. Petersburg Univ. Ser. 10 Appl. Math. Inform. Control Process. 2014, 2, 120–129. [Google Scholar]
- Miller, A.J. Settings for Fixed-Cycle Traffic Signals. J. Oper. Res. Soc. 1963, 14, 373–386. [Google Scholar] [CrossRef]
- Guo, Q.; Li, L.; Ban, X.J. Urban Traffic Signal Control with Connected and Automated Vehicles: A Survey. Transp. Res. Part C Emerg. Technol. 2019, 101, 313–334. [Google Scholar] [CrossRef]
- Zhou, B.; Cao, J.; Wu, H. Adaptive Traffic Light Control of Multiple Intersections in WSN-Based ITS. In Proceedings of the 2011 IEEE 73rd Vehicular Technology Conference (VTC Spring), Budapest, Hungary, 15–18 May 2011; IEEE: Piscataway, NJ, USA, 2011. [Google Scholar]
- Lowrie, P.R. The Sydney Coordinated Adaptive Traffic (SCAT) System—Principles, Methodology, Algorithm. In Proceedings of the Second International Conference on Road Traffic Signaling, 15–18 April 1986; IEE: London, UK, 1982. [Google Scholar]
- Eom, M.; Kim, B.-I. The Traffic Signal Control Problem for Intersections: A Review. Eur. Transp. Res. Rev. 2020, 12, 50. [Google Scholar] [CrossRef]
- McKenney, D.; White, T. Distributed and Adaptive Traffic Signal Control within a Realistic Traffic Simulation. Eng. Appl. Artif. Intell. 2013, 26, 574–583. [Google Scholar] [CrossRef]
- Shen, Z.; Wang, K.; Wang, F.-Y. GPU Based Non-Dominated Sorting Genetic Algorithm-II for Multi-Objective Traffic Light Signaling Optimization with Agent Based Modeling. In Proceedings of the 16th International IEEE Conference on Intelligent Transportation Systems (ITSC 2013), The Hague, The Netherlands, 6–9 October 2013; IEEE: Piscataway, NJ, USA, 2013. [Google Scholar] [CrossRef]
- Deb, K.; Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Araghi, S.; Khosravi, A.; Johnstone, M.; Creighton, D. Intelligent Traffic Light Control of Isolated Intersections Using Machine Learning Methods. In Proceedings of the 2013 IEEE International Conference on Systems, Man, and Cybernetics, Manchester, UK, 13–16 October 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 3621–3626. [Google Scholar] [CrossRef]
- Arel, I.; Liu, C.; Urbanik, T.; Kohls, A.G. Reinforcement Learning-Based Multi-Agent System for Network Traffic Signal Control. IET Intell. Transp. Syst. 2010, 4, 128–135. [Google Scholar] [CrossRef]
- Zhang, X.; Chan, L.S.; Nassir, N.; Sarvi, M. Towards Fair Lights: A Multi-Agent Masked Deep Reinforcement Learning for Efficient Corridor-Level Traffic Signal Control. Commun. Transp. Res. 2025, 5, 100203. [Google Scholar] [CrossRef]
- Traffic Management Science Research Institute, Ministry of Public Security. Design Manual for Planar Intersection Channelization of Urban Roads; China Machine Press: Beijing, China, 2021; pp. 10–39. ISBN 978-7-111-67789-5. [Google Scholar]
- Gazis, D.C. Optimum Control of a System of Oversaturated Intersections. Oper. Res. 1964, 12, 815–831. [Google Scholar] [CrossRef]
- Mohajerpoor, R.; Saberi, M.; Ramezani, M. Analytical Derivation of the Optimal Traffic Signal Timing: Minimizing Delay Variability and Spillback Probability for Undersaturated Intersections. Transp. Res. Part B Methodol. 2019, 119, 45–68. [Google Scholar] [CrossRef]
- Webster, F.V. Traffic Signal Settings; Technical Report No. 39; Road Research Laboratory: London, UK, 1958. [Google Scholar]
- Hall, R.W. Queueing Methods: For Services and Manufacturing; Prentice Hall: Englewood Cliffs, NJ, USA, 1991; ISBN 0137447566. [Google Scholar]
- Newell, C. Applications of Queueing Theory, 4th ed.; Springer Science & Business Media: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Rosca, M.A.; Rusca, A. Methods for Green Times Allocation in Under-Saturated Signalized Intersection. UPB Sci. Bull. Ser. D 2012, 74, 91–104. [Google Scholar]
- Chang, T.-H.; Lin, J.-T. Optimal Signal Timing for an Oversaturated Intersection. Transp. Res. Part B Methodol. 2000, 34, 471–491. [Google Scholar] [CrossRef]
- Wiseman, Y. Autonomous Vehicles Will Spur Moving Budget from Railroads to Roads. Int. J. Intell. Unmanned Syst. 2024, 12, 19–31. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).