A Chord Error-Priority Bilevel Interpolation Optimization Method for Complex Path Planning
Abstract
1. Introduction
2. Machining Path Modeling
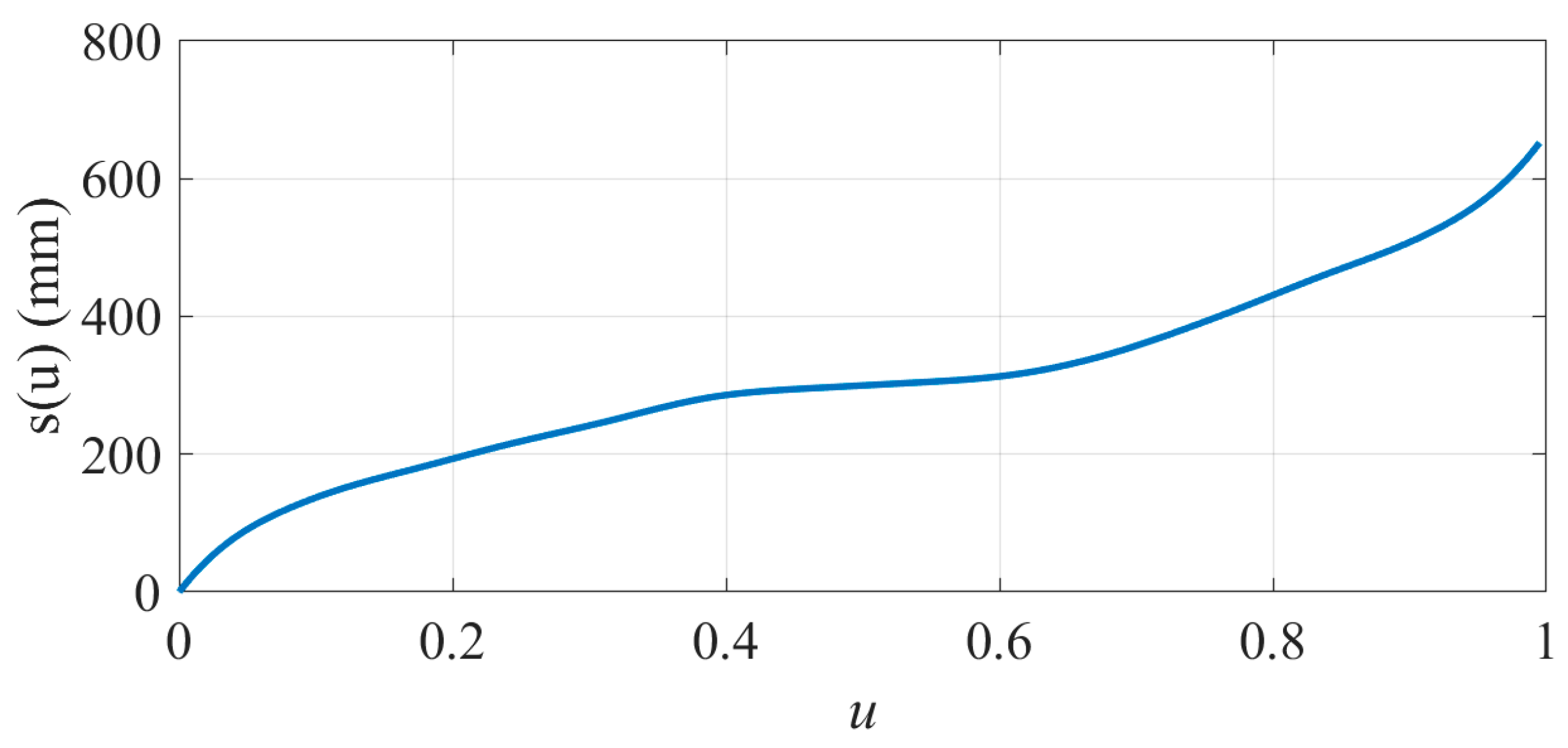
2.1. Arc Length Parameterization of Path
2.2. Path Curve Expansion Based on the Frenet–Serret Framework
2.3. Geometry-Driven Machining Constraints
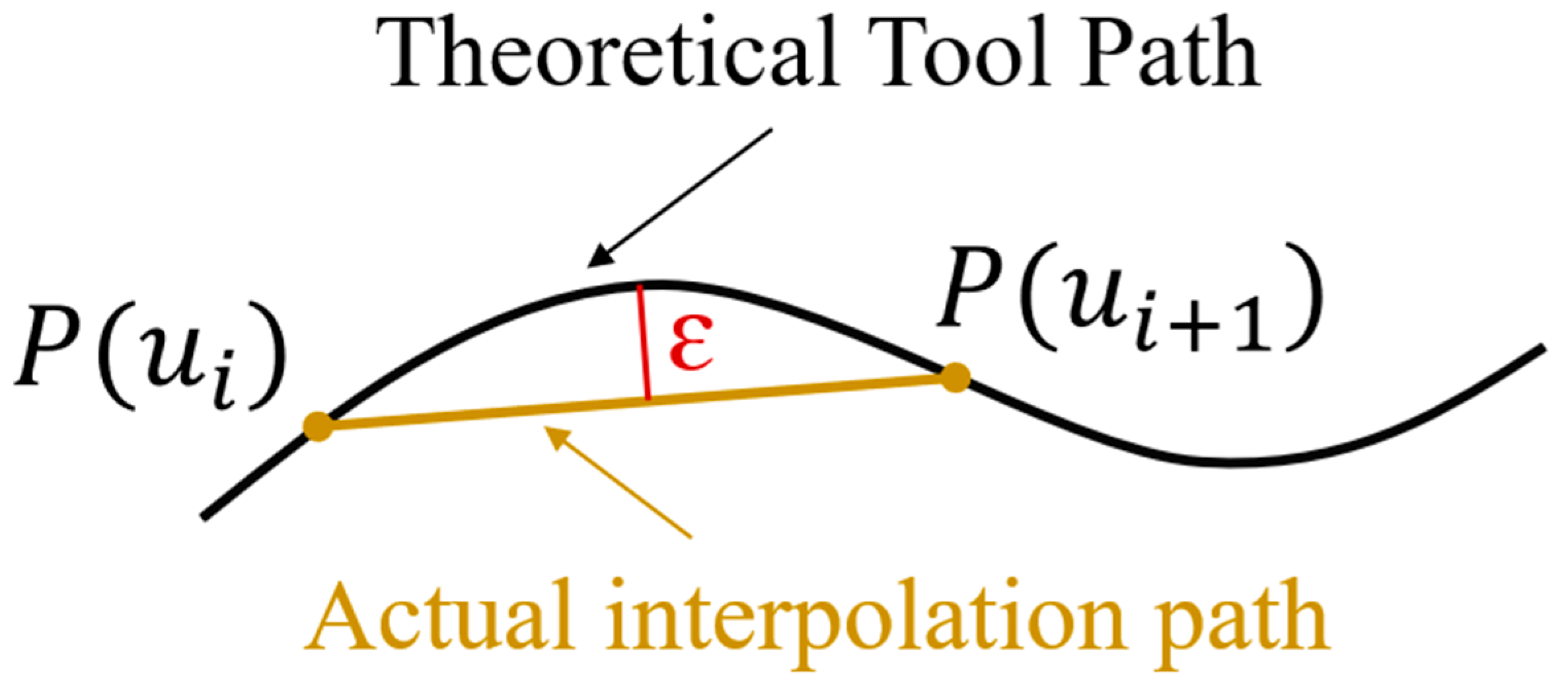
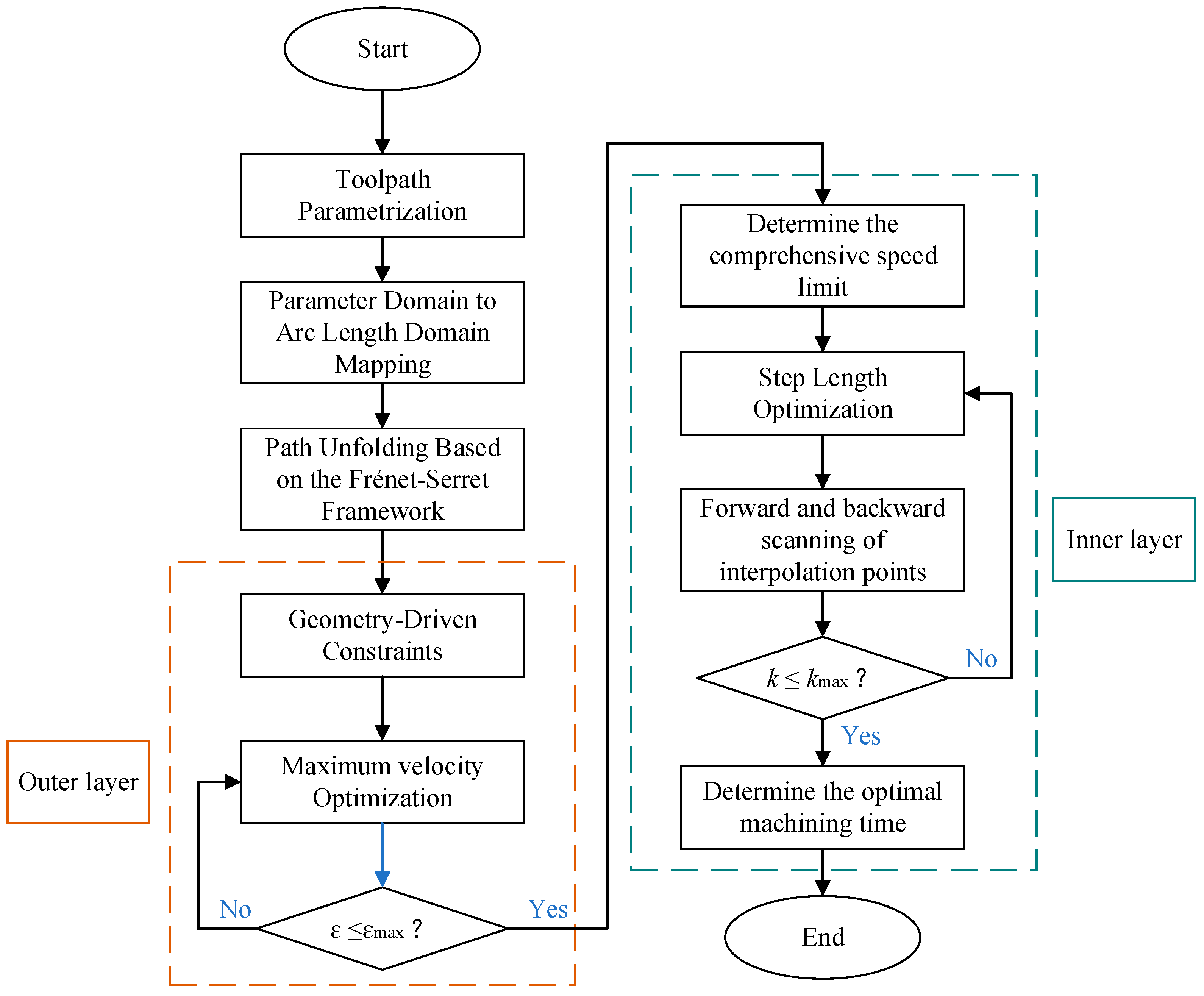
3. A Chord Error-Priority Bilevel Interpolation Optimization Method
3.1. Outer Layer—Global Velocity Optimization of Chord Error-Priority
3.2. Inner Layer—Interpolation Optimization Under Comprehensive Constraints
- Step 1: Initialize kinematic upper limits based on machine tool parameters.
- Step 2: Parametric machining paths based on the Frenet–Serret framework.
- Step 3: Calculate and set multi-kinematic constraints driven by geometry.
- Step 4: By determining the constraints of chordal error, the maximum feed rate is then calculated.
- Step 5: Based on comprehensive constraints, the feed rate and optimal step length are calculated using forward and backward scanning methods to determine the interpolation points.
4. Simulation Verification and Comparison
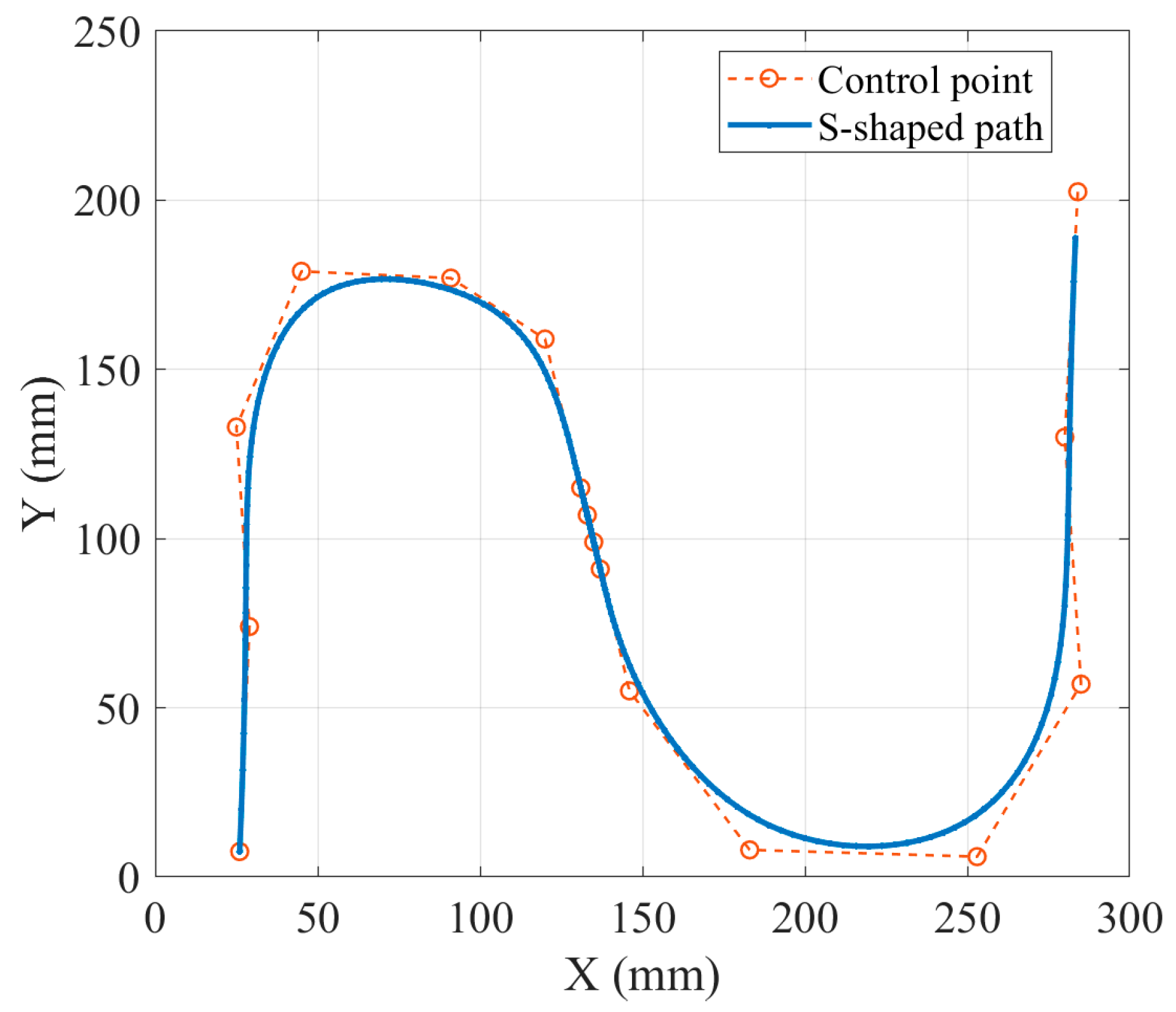
4.1. Machining Simulation Experiment for S-Shaped Path
4.2. Machining Simulation Experiment for Wave-Shaped Path
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CPBI | Chord error- priority bilevel interpolation optimization method |
| CNC | Computer numerical control |
| NURBS | Non-uniform rational B-spline |
| ICVP | Iteration control vector parametrization |
Appendix A
Derivation Process of Chord Error Inequality (Equation (22))
Appendix B
Appendix C
| Symbols | Meaning of the Symbol |
|---|---|
| Parametric curve equation | |
| Control point | |
| Basis function | |
| First derivative of the parameter curve with respect to u | |
| Second derivative of the parameter curve with respect to u | |
| Third derivative of the parameter curve with respect to u | |
| Arc length curve equation | |
| Tangent vector | |
| Principal normal vector | |
| Secondary normal vector | |
| Curvature | |
| Torsion | |
| The first derivative of curvature with respect to arc length | |
| The -th discrete arc length parameter | |
| The -th step velocity | |
| Single-step arc length | |
| Maximum Iterations for Bidirectional Scanning | |
| Chord error | |
| The maximum target chord error | |
| velocity | |
| The upper limit of velocity | |
| Tangential acceleration | |
| The upper limits of tangential acceleration | |
| Normal acceleration | |
| The upper limits of normal acceleration | |
| Jerk acceleration | |
| The first derivatives of velocity with respect to arc length | |
| the point-state velocity upper limit of the machining tools | |
| The upper limit of jerk acceleration | |
| The upper limit of velocity dominated by the chord error | |
| The comprehensive upper limit for velocity | |
| The step velocity variation parameter for adjacent tool positions | |
| Single-step arc length under distortion constraints | |
| Single-step arc length under chord error constraints | |
| Interpolation period | |
| Actual machining time | |
| The optimal velocity solution | |
| The smallest positive number to prevent the denominator from being 0 | |
| The total arc length of machining path | |
| Tangent component of the parameter curve | |
| Principal normal component of the parameter curve | |
| Secondary normal component of the parameter curve | |
| The vector from the start point to the midpoint of the chord | |
| Tangent component of | |
| Principal normal component of | |
| Secondary normal component of | |
| chord error vector |
References
- Hu, Y.; Jin, X.; Jiang, X.; Zheng, Z. Inverse kinematics model and trajectory generation of a dual-stage micro milling machine. J. Manuf. Process. 2024, 132, 425–450. [Google Scholar] [CrossRef]
- Xu, Y.; Zaman, M.; Zhou, F. Optimized dual NURBS curve interpolation for high-accuracy five-axis CNC path planning. Sci. Rep. 2025, 15, 25409. [Google Scholar] [CrossRef] [PubMed]
- Lu, Z.; Yang, X.; Zhao, J. Tool-path planning method for kinematics optimization of blade machining on five-axis machine tool. Int. J. Adv. Manuf. Technol. 2022, 121, 1253–1267. [Google Scholar] [CrossRef]
- Liao, Z.; Li, J.; Xie, H.; Wang, Q.; Zhou, X. Region-based toolpath generation for robotic milling of freeform surfaces with stiffness optimization. Robot. Comput. Integr. Manuf. 2020, 64, 101953. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, J.; Li, W.; Wang, Y.; Zhou, Y. Research on feedrate scheduling method for NURBS toolpath interpolation in high-speed CNC machining. Int. J. Adv. Manuf. Technol. 2025, 138, 3293–3313. [Google Scholar] [CrossRef]
- Zhong, W.; Luo, X.; Chang, W.; Cai, Y.; Ding, F.; Liu, H.; Sun, Y. Toolpath Interpolation and Smoothing for Computer Numerical Control Machining of Freeform Surfaces: A Review. Int. J. Autom. Comput. 2019, 17, 1–16. [Google Scholar] [CrossRef]
- Ma, H.; Shen, L.; Jiang, X.; Zou, Q.; Yuan, C. A survey of path planning and feedrate interpolation in computer numerical control. J. Graph. 2022, 43, 967–986. [Google Scholar] [CrossRef]
- Zhou, Y.; Jiang, Y.; Lu, C.; Huang, J.; Pei, J. A review of 5-axis milling techniques for centrifugal impellers: Tool-path generation and deformation control. J. Manuf. Process. 2024, 132, 160–186. [Google Scholar] [CrossRef]
- Zhou, X. An Adapted NURBS Interpolator with a Switched Optimized Method of Feed-Rate Scheduling. Machines 2024, 12, 186. [Google Scholar] [CrossRef]
- Zhang, G.; Gao, J.; Zhang, L.; Wang, X.; Luo, Y. Generalised NURBS interpolator with nonlinear feedrate scheduling and interpolation error compensation. Int. J. Mach. Tools Manuf. 2022, 183, 103956. [Google Scholar] [CrossRef]
- Jia, Z.; Song, D.; Ma, J.; Hu, G.; Su, W. A NURBS interpolator with constant speed at feedrate-sensitive regions under drive and contour-error constraints. Int. J. Mach. Tools Manuf. 2017, 116, 1–17. [Google Scholar] [CrossRef]
- Wang, L.; Liu, Q.; Sun, P.; Lv, S.; Yang, R.; Yang, Z. Dynamic look-ahead feedrate scheduling method based on sliding mode velocity control. Sci. Rep. 2024, 14, 15424. [Google Scholar] [CrossRef]
- Song, D.; Ma, J.; Zhong, Y.; Yao, J. Global smoothing of short line segment toolpaths by control-point-assigning-based geometric smoothing and FIR filtering-based motion smoothing. Mech. Syst. Signal Process. 2021, 160, 107908. [Google Scholar] [CrossRef]
- Sun, C.; Dominguez-Caballero, J.; Ward, R.; Ayvar-Soberanis, S.; Curtis, D. Machining cycle time prediction: Data-driven modelling of machine tool feedrate behavior with neural networks. Robot. Comput. Integr. Manuf. 2022, 75, 102293. [Google Scholar] [CrossRef]
- Ward, R.; Sun, C.; Dominguez-Caballero, J.; Ojo, S.; Ayvar-Soberanis, S.; Curtis, D.; Ozturk, E. Machining Digital Twin using real-time model-based simulations and lookahead function for closed loop machining control. Int. J. Adv. Manuf. Technol. 2021, 117, 3615–3629. [Google Scholar] [CrossRef]
- Sun, S.; Zhao, P.; Zhang, T.; Li, B.; Yu, D. Smoothing interpolation of five-axis tool path with less feedrate fluctuation and higher computation efficiency. J. Manuf. Process. 2024, 109, 669–693. [Google Scholar] [CrossRef]
- Yang, J.; Yin, X.; Sun, Y. PSO-Based Feedrate Optimization Algorithm for Five-Axis Machining with Constraint of Contour Error. Machines 2023, 11, 501. [Google Scholar] [CrossRef]
- Wang, Y.; Xie, Z.; Xie, F.; Liu, X. A symmetrical arrangement strategy based real-time toolpath planning method for a 5-DoF fully parallel machining robot. Int. J. Adv. Manuf. Technol. 2024, 134, 2299–2317. [Google Scholar] [CrossRef]
- Sencer, B.; Ishizaki, K.; Shamoto, E. High speed cornering strategy with confined contour error and vibration suppression for CNC machine tools. CIRP Ann. Manuf. Technol. 2015, 64, 369–372. [Google Scholar] [CrossRef]
- Sun, Y.; Zhao, Y.; Bao, Y.; Guo, D. A novel adaptive feedrate interpolation method for NURBS tool path with drive constraints. Int. J. Mach. Tools Manuf. 2014, 77, 74–81. [Google Scholar] [CrossRef]
- Sang, Y.; Yao, C.; Lv, Y.; He, G. An improved feedrate scheduling method for NURBS interpolation in five-axis machining. Precis. Eng. 2020, 64, 70–90. [Google Scholar] [CrossRef]
- Liu, X.; Yu, P.; Chen, H.; Peng, B.; Wang, Z.; Liang, F. Feedrate fluctuation minimization for NURBS tool path interpolation based on arc length compensation and iteration. Micromachines 2025, 16, 402. [Google Scholar] [CrossRef]
- Zhao, K.; Kang, Z.; Guo, X. Smooth Trajectory Generation for Predefined Path with Pseudo Spectral Method. IEEE Access 2020, 8, 158735–158744. [Google Scholar] [CrossRef]
- Wang, L.; Yang, R.; Lv, S.; Yang, Z.; Xin, S.; Liu, Y.; Liu, Q. Combined contour error control method for five-axis machine tools based on digital twin. Sci. Rep. 2025, 15, 17809. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Song, C.; Zhang, D.; Li, D.; Qu, S. Fast and Stable Iterative Algorithm for Searching Wheel-Rail Contact Point Based on Geometry Constraint Equations. J. Comput. Nonlinear Dyn. 2023, 18, 011004. [Google Scholar] [CrossRef]
- Ma, H.; Yuan, C.; Shen, L.; Gao, X. Optimal feedrate planning on a five-axis parametric tool path with global geometric and kinematic constraints. J. Comput. Des. Eng. 2022, 9, 2355–2374. [Google Scholar] [CrossRef]
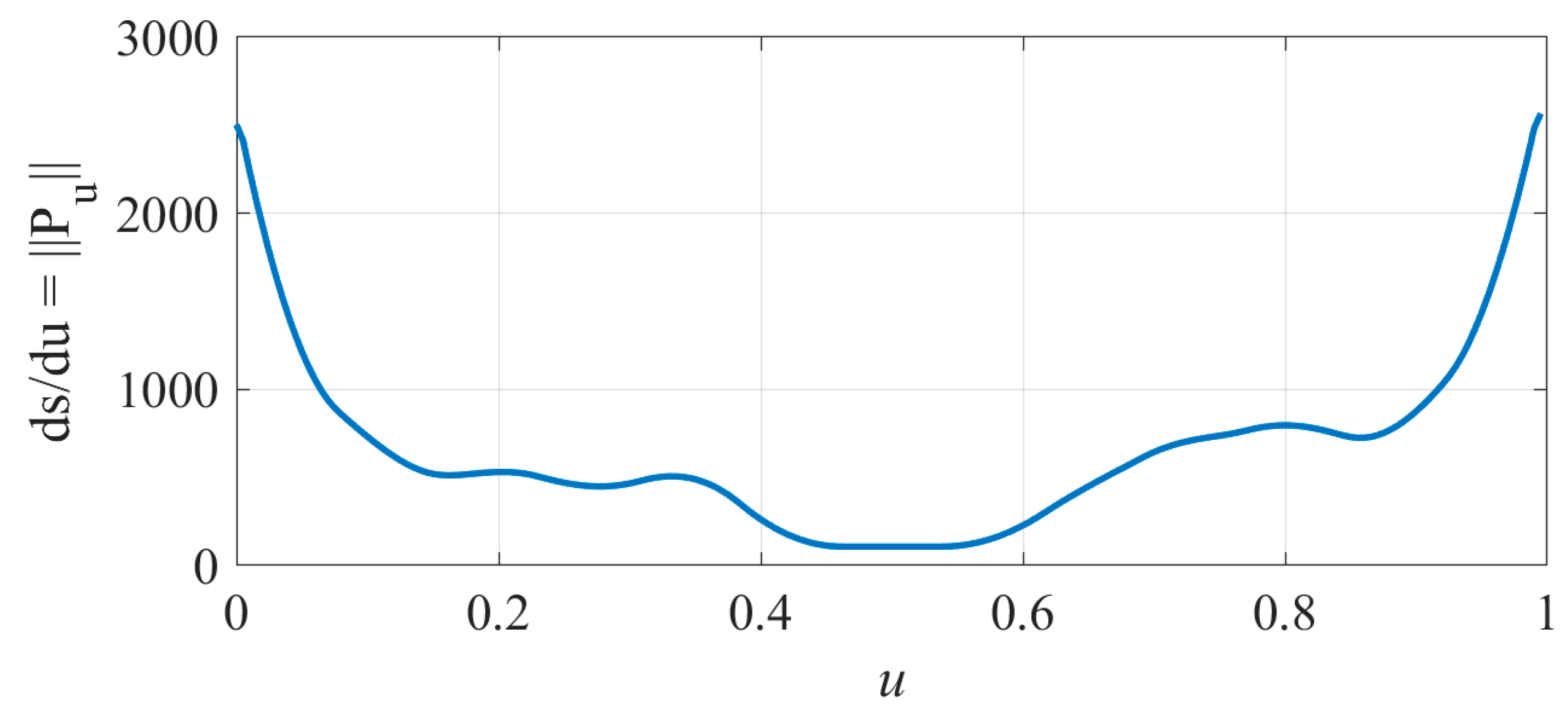
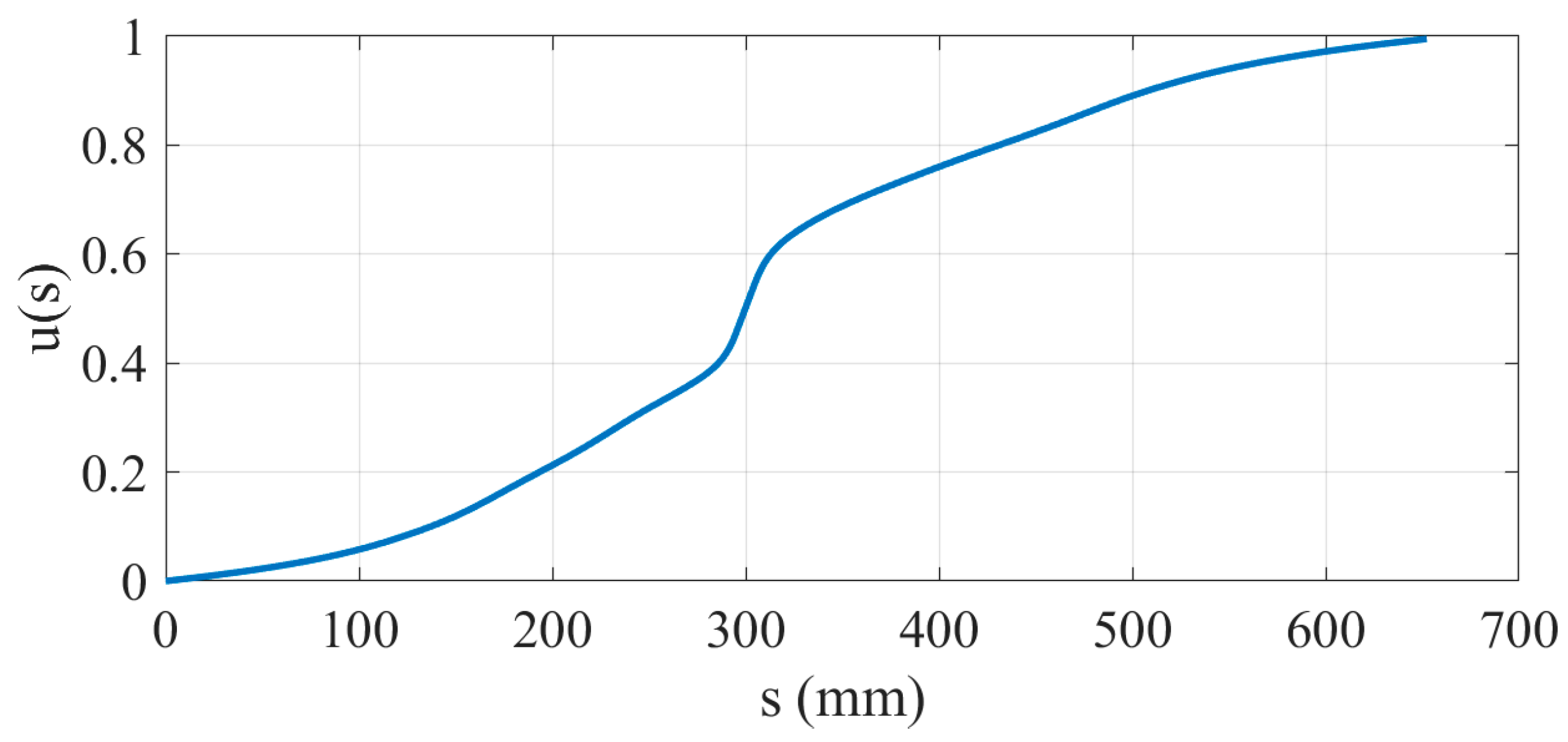
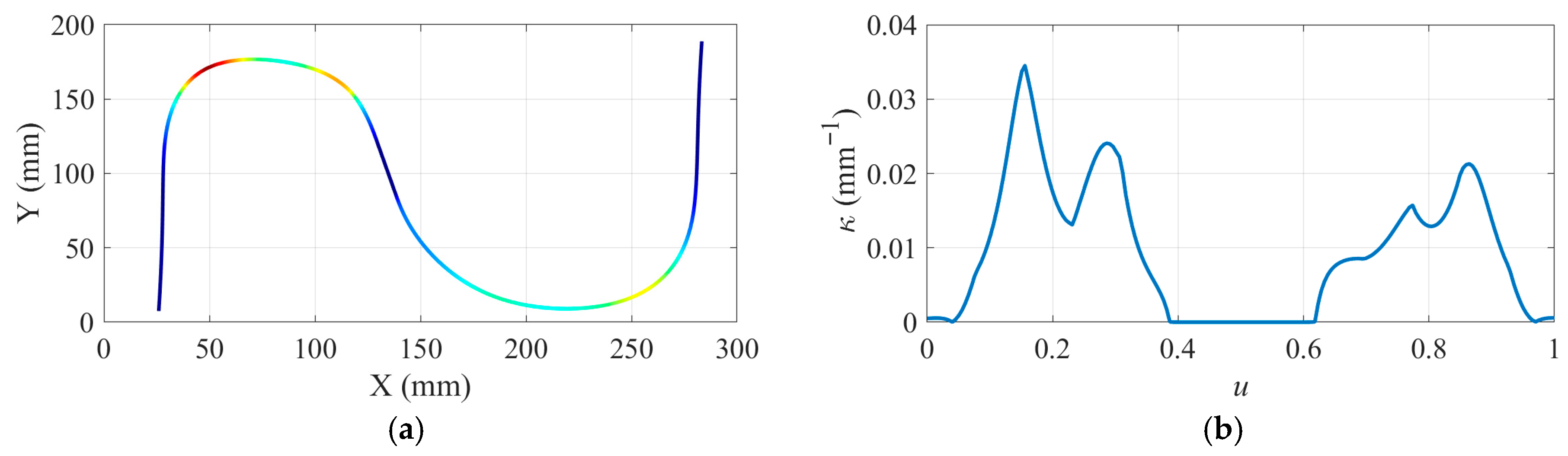
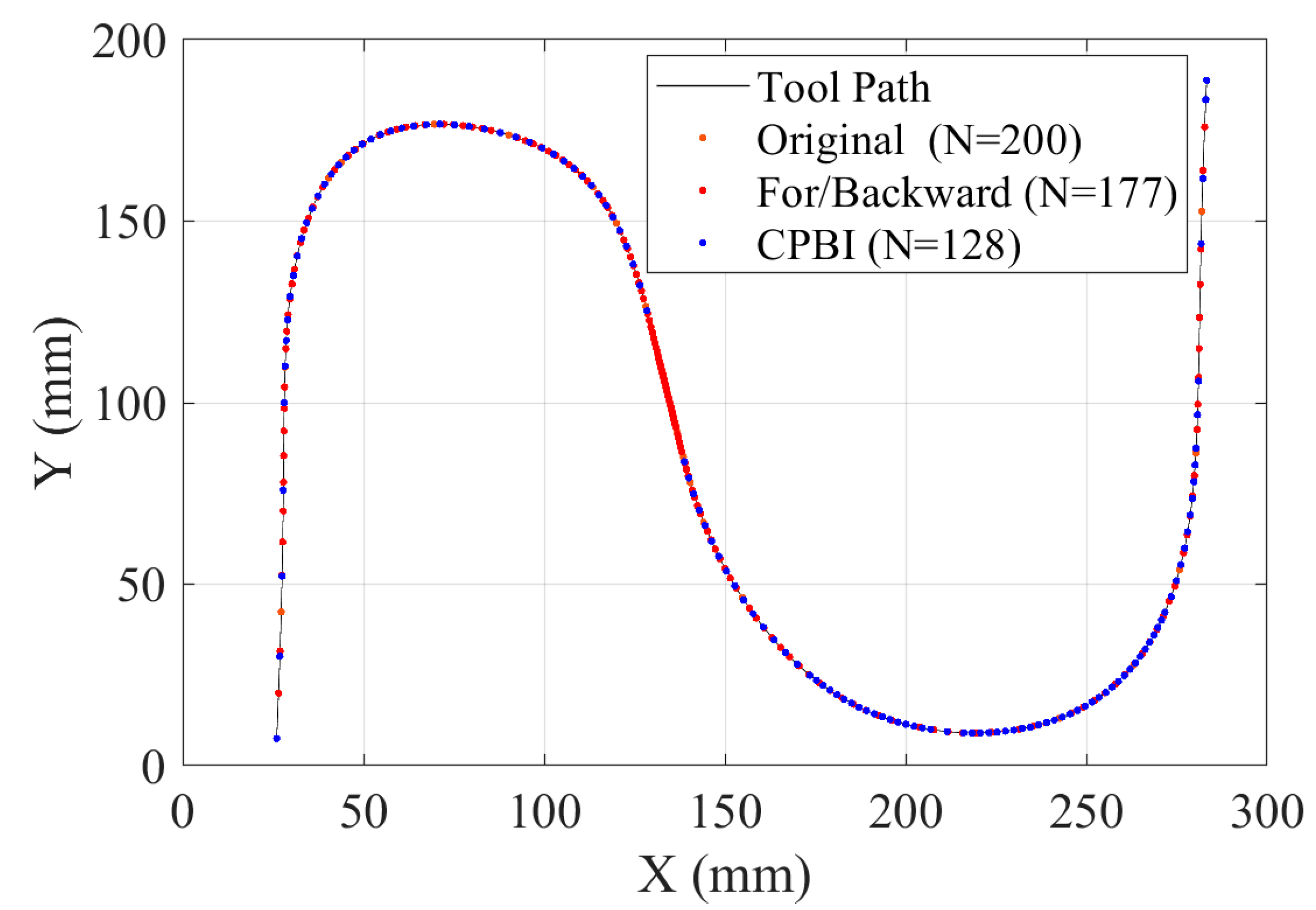
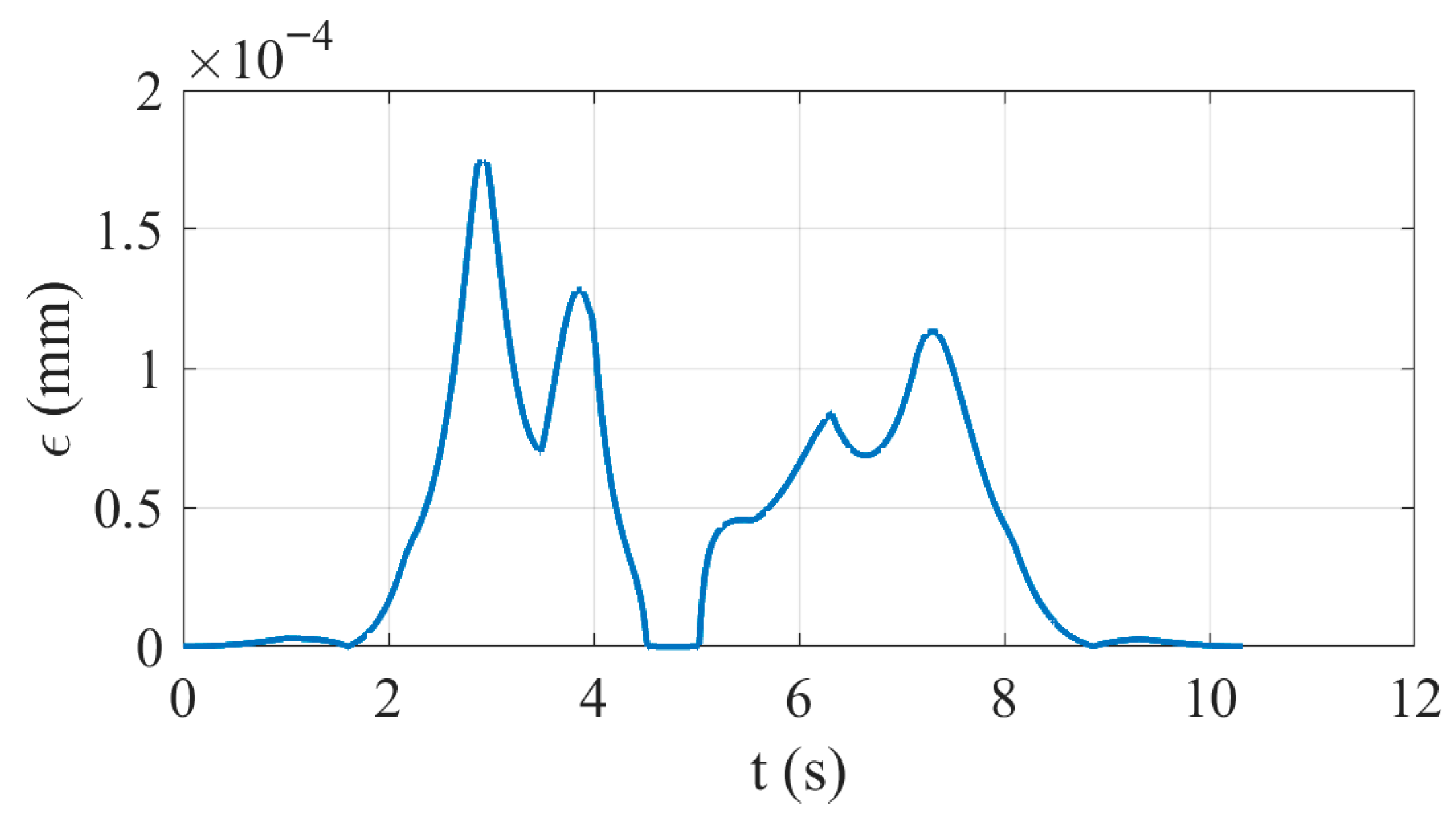
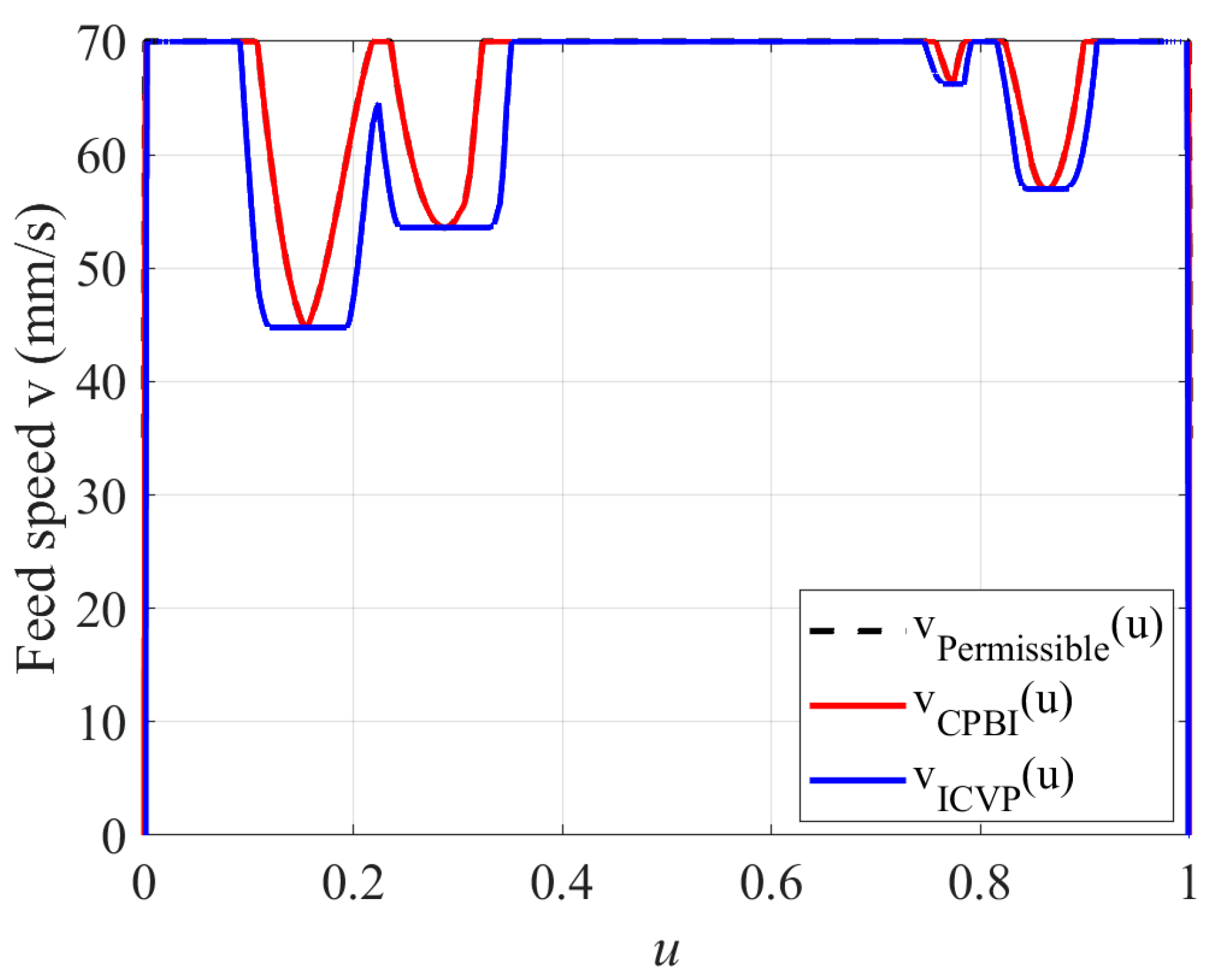
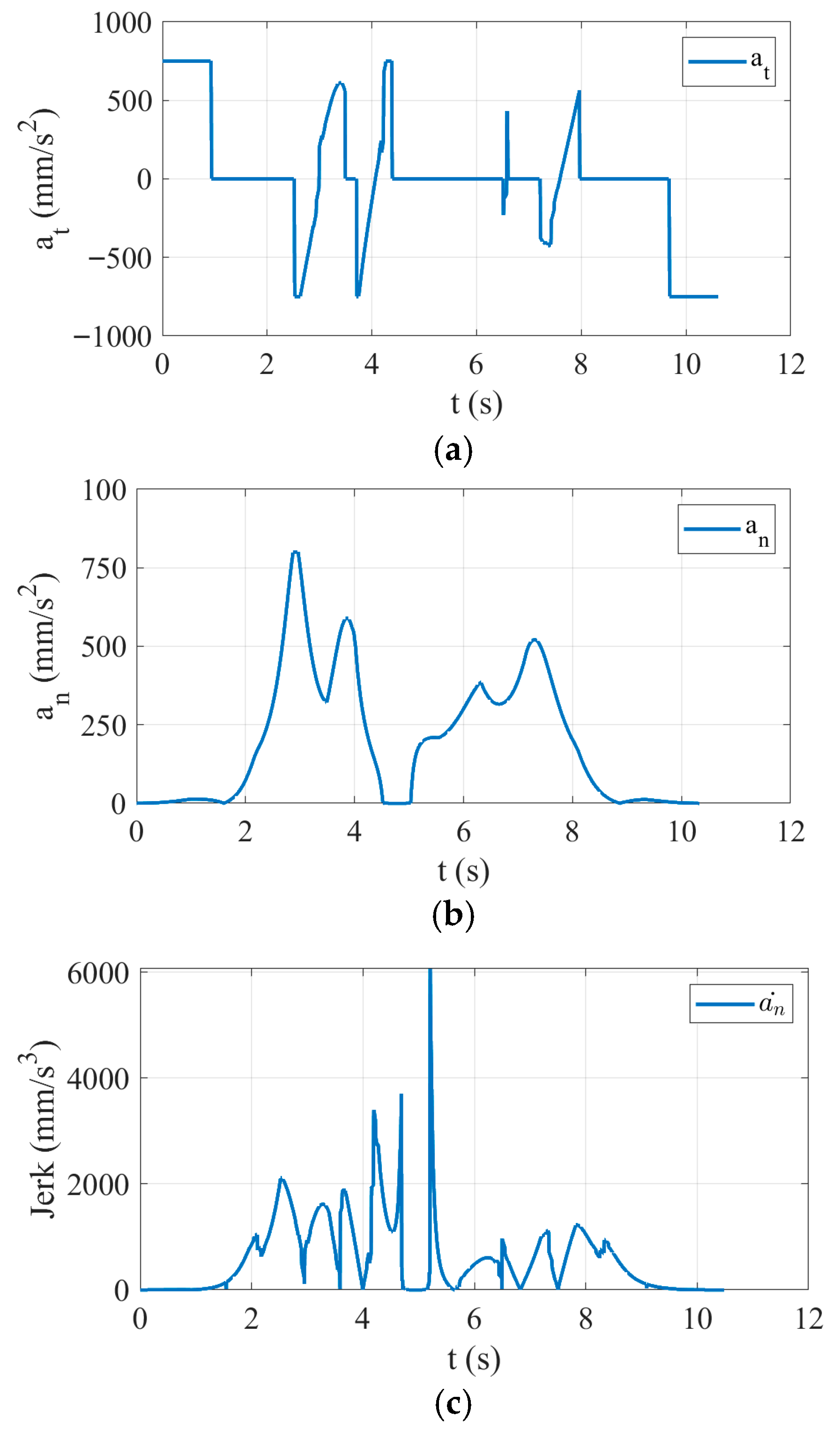
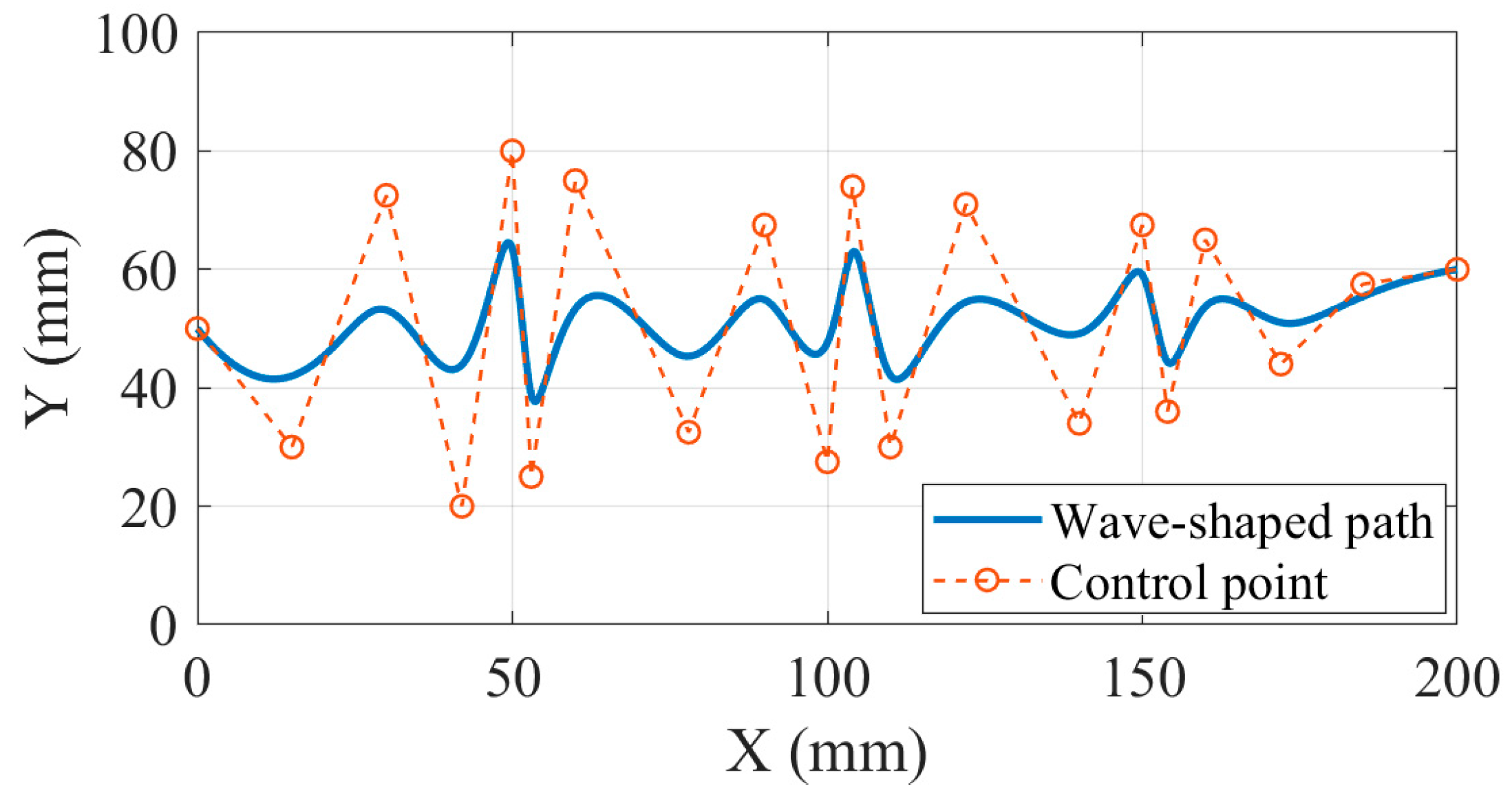
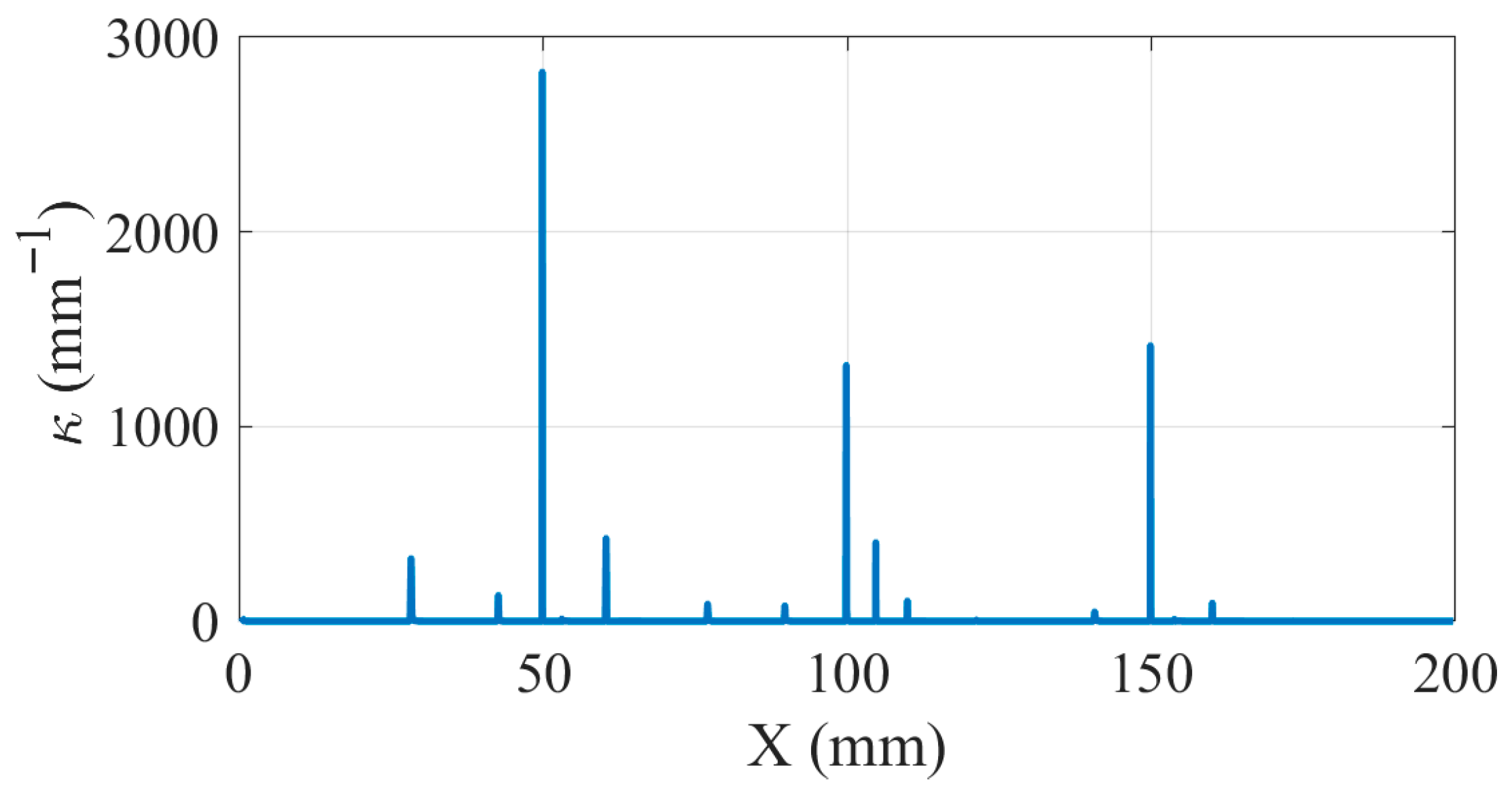
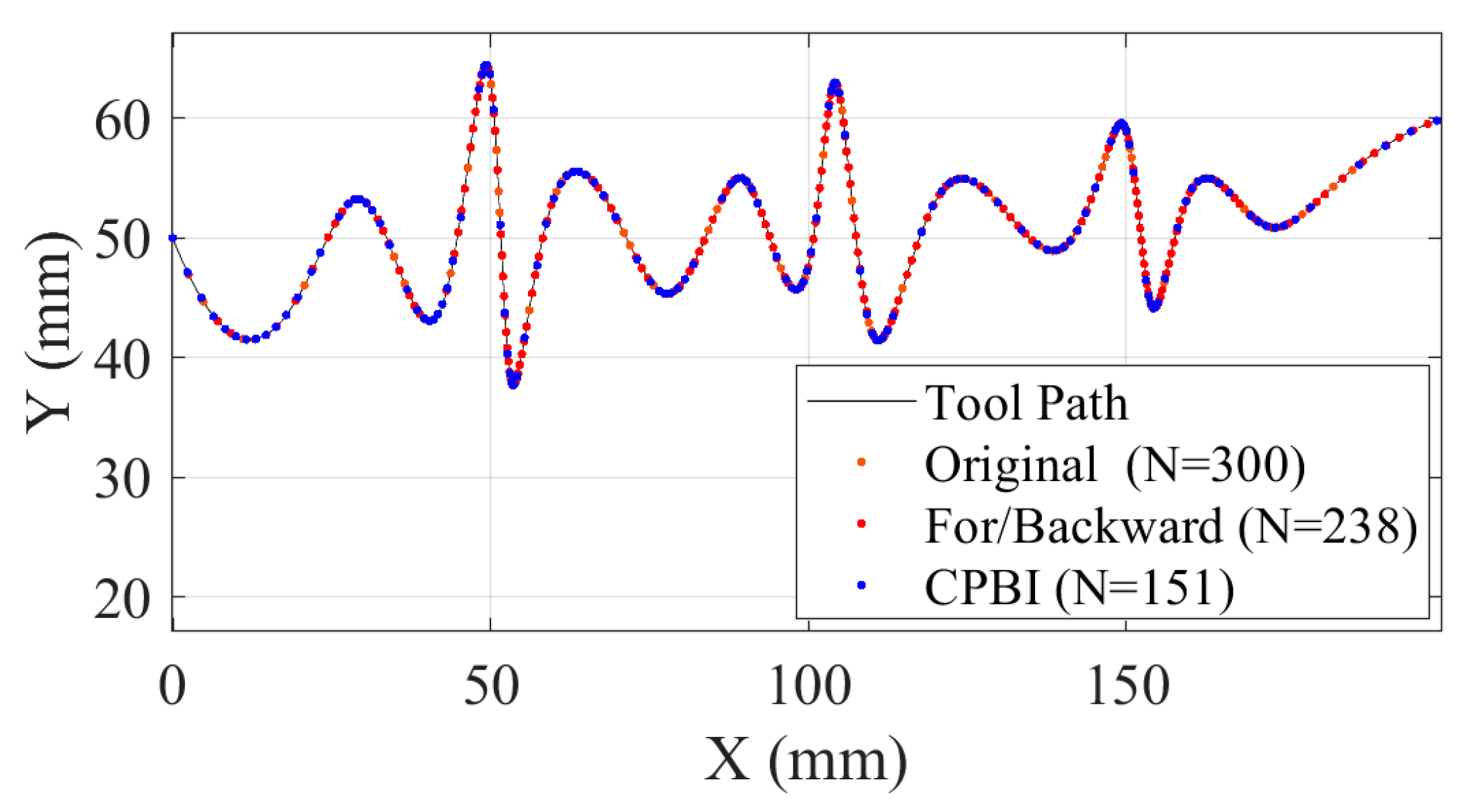
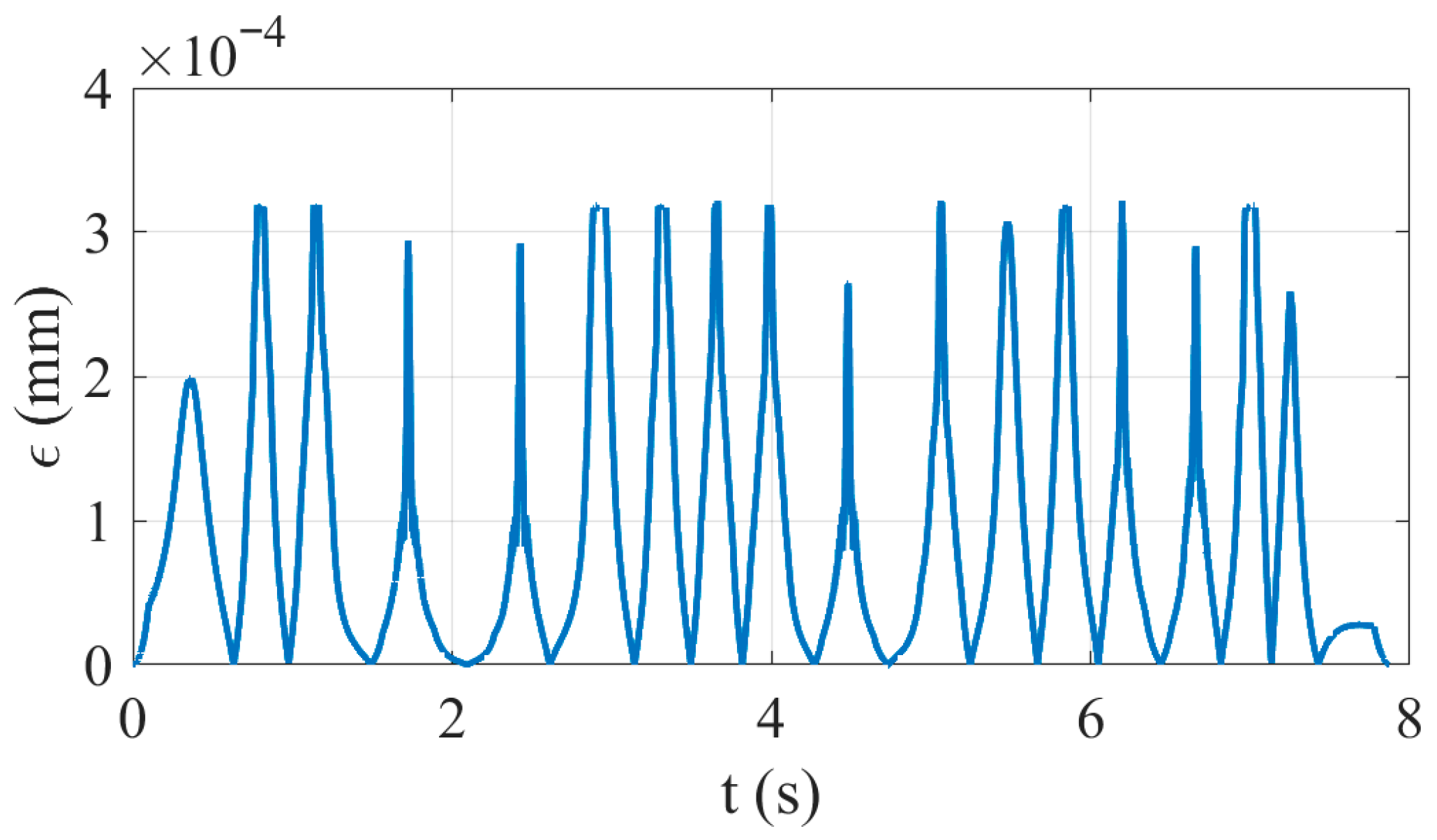
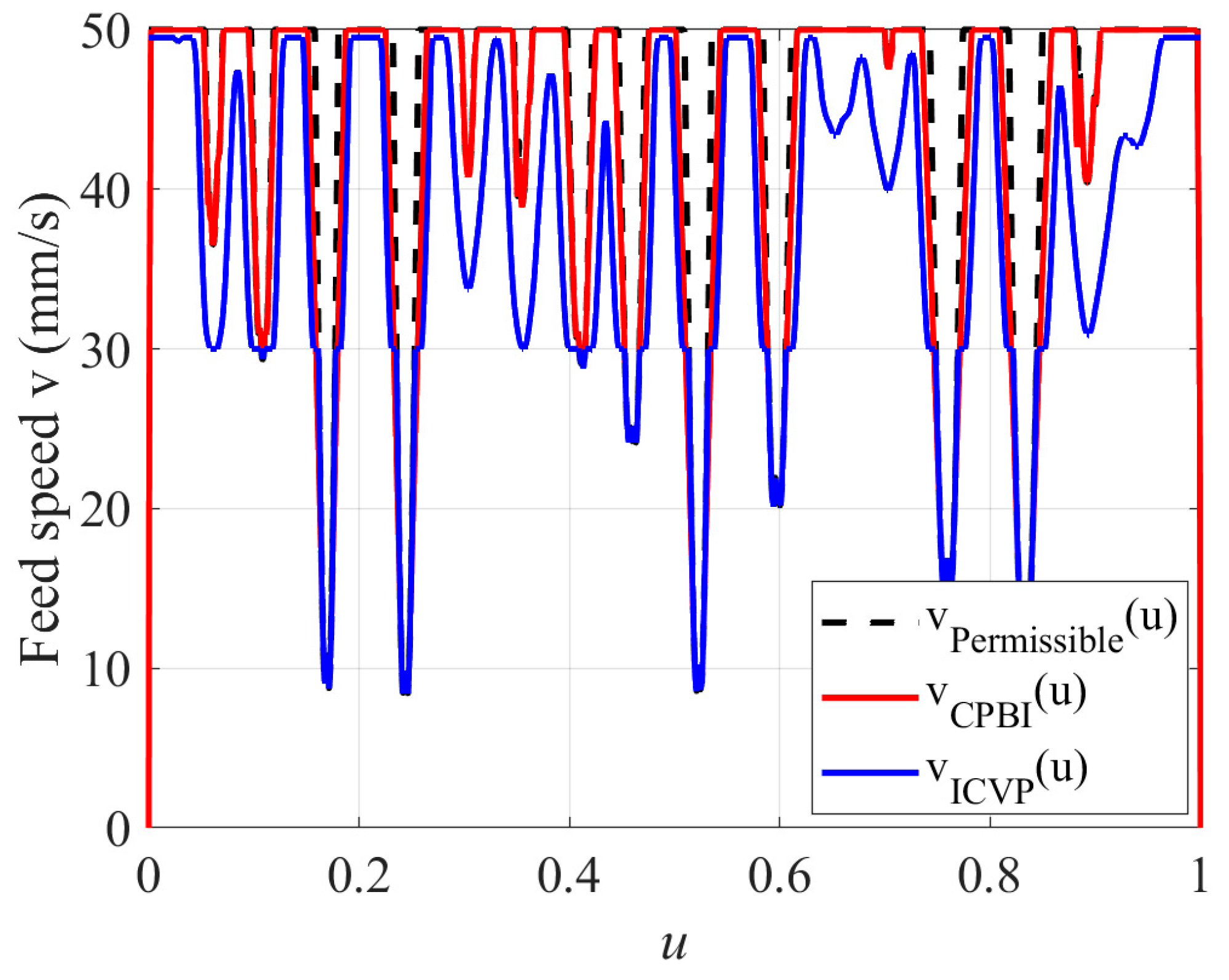

| Experimental Parameters | Value |
|---|---|
| 0.002 s | |
| 0.001 mm | |
| 70 mm/s | |
| 800 mm/s2 | |
| 750 mm/s2 | |
| 10,000 mm/s3 |
| Number of Interpolation Points | Maximum Chord Error | |
|---|---|---|
| 0.1 | 184 | 0.0001 mm |
| 0.15 | 128 | 0.00015 mm |
| 0.2 | 97 | 0.0006 mm |
| Experimental Parameters | Value |
|---|---|
| 0.002 s | |
| 0.001 mm | |
| 50 mm/s | |
| 500 mm/s2 | |
| 500 mm/s2 | |
| 10,000 mm/s3 |
| CPBI | ICVP | |
|---|---|---|
| Computational time | 3.47 s | 4.28 s |
| Number of interpolation points | 151 | 189 |
| Maximum chord error | 0.00035 mm | 0.0003 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, P.; Wang, L.; Wang, D.; Qi, J.; Ye, X. A Chord Error-Priority Bilevel Interpolation Optimization Method for Complex Path Planning. Mathematics 2025, 13, 3385. https://doi.org/10.3390/math13213385
Wei P, Wang L, Wang D, Qi J, Ye X. A Chord Error-Priority Bilevel Interpolation Optimization Method for Complex Path Planning. Mathematics. 2025; 13(21):3385. https://doi.org/10.3390/math13213385
Chicago/Turabian StyleWei, Pengxuan, Liping Wang, Dan Wang, Jun Qi, and Xiaolong Ye. 2025. "A Chord Error-Priority Bilevel Interpolation Optimization Method for Complex Path Planning" Mathematics 13, no. 21: 3385. https://doi.org/10.3390/math13213385
APA StyleWei, P., Wang, L., Wang, D., Qi, J., & Ye, X. (2025). A Chord Error-Priority Bilevel Interpolation Optimization Method for Complex Path Planning. Mathematics, 13(21), 3385. https://doi.org/10.3390/math13213385





