Environmental Disturbance Effects on Liquid Crystal Elastomer Photothermal-Oscillator Dynamics

Abstract

Self-oscillations convert ambient energy into continuous periodic motion through feedback mechanisms, but their response to external periodic disturbances is not yet fully understood. Through the combination of a photothermally-responsive liquid crystal elastomer fiber and a mass block within a linear light field, we consider a liquid crystal elastomer self-oscillator. Following theoretical modeling of the light-driven self-oscillator under external periodic forcing and numerical simulations, three distinct phase-locking regimes are identified: in-phase, anti-phase, and quadrature synchronizations. Mechanisms are elucidated through time-domain, frequency-domain, and phase-space analyses. Moreover, approximate analytical expressions for the steady-state amplitude–frequency and phase–frequency responses of the self-oscillator under periodic forcing are derived using the multi-scale method. The impact of periodic forcing on the self-oscillator and its response regulation via system parameters is examined. A close correspondence exists between numerical and analytical results. This work investigates the response characteristics of a liquid crystal elastomer self-oscillator under periodic forcing, advances fundamental insights into disturbance rejection in self-oscillators, and delivers practical guidance for their robust operation in complex oscillatory settings.

1. Introduction

Self-oscillation, an autonomously energy-sustained dynamic phenomenon, pervades both natural and engineering systems [1,2,3]. It can convert ambient energy into continuous periodic motion, circumventing the need for additional complex controllers or portable batteries [4,5]. Crucially, the inherent self-regulating nature and robustness [6,7] render self-oscillation highly attractive for deployment in soft robotics [8,9,10], energy-absorbing devices [11], biomimetic engineering [12], and mass transport devices [13,14].

The advent of stimuli-responsive materials has opened new pathways for engineering self-oscillators. Hydrogels [15,16,17,18], ionic gels [19,20,21], dielectric elastomers [22], and liquid crystal elastomers (LCEs) [23,24,25,26,27,28,29] are typical stimuli-responsive materials, exhibiting multifunctional actuation. Studies have confirmed multiple motion patterns, ranging from rolling [30], jumping [31,32], swing [33,34,35], swimming [36], bending [37,38], buckling [39,40], vibration [41,42,43], crawling [44], twisting [45,46,47], chaos [48,49], to synchronized motion in coupled self-oscillators [50,51]. Their defining attributes are manifested through several feedback mechanisms, such as self-shadowing [39,40], the coupling of large deformation and chemical reaction [19,20], and the interaction of liquid volatilization with membrane deformation [3].

LCEs have emerged as optimal materials for constructing self-oscillators. Through integrating anisotropic liquid crystal molecules and stretchable long chains, LCEs achieve functional convergence between rubber-like elasticity and liquid crystalline anisotropy [52,53,54]. Upon exposure to external stimuli, encompassing optical [55,56,57,58,59], thermal [60,61,62,63,64], magnetic [65], or electric [66,67,68,69] fields, mesogen reorientation triggers macroscopic shape morphing. In particular, optical excitation constitutes a prominent stimulus modality, owing to its eco-friendliness, contactless control, and programmability [70,71]. These benefits have driven the continuous refinement of the light-powered self-oscillators architected from LCEs, with the effectiveness validated in prior studies [72,73,74,75,76,77,78].

Previous studies have largely focused on the isolated self-oscillatory behavior. However, idealized models and laboratory performance often differ significantly from complex real-world applications. In practice settings, the self-oscillators inevitably encounter environmental perturbations [79,80], i.e., mechanical load fluctuations, or ambient vibrational noise. These typically manifest as persistent periodic or quasi-periodic forces acting directly on the oscillator or its supports. This interplay between intrinsic self-oscillation and external periodic forcing can give rise to rich nonlinear phenomena, including synchronization, quasi-periodicity, or even chaotic behavior. External periodic forcing can enhance oscillatory coherence in dynamical systems. A notable example is found in biomedical engineering, where cardiac pacemakers deliver precisely timed electrical impulses to synchronize and stabilize the heart’s intrinsic rhythms, thereby improving both regularity and robustness. Furthermore, such external periodic forcing can also reconfigure oscillatory patterns. In soft robotics, for instance, external acoustic signals are used to induce gait transitions, allowing for adaptive locomotion in response to varying operational demands. Conversely, unintended periodic disturbances may also degrade performance, leading to frequency drift, amplitude modulation, or phase instability. Thus, characterizing how external periodic forcing affects key attributes of the self-oscillator, such as frequency, amplitude, and phase, is fundamental for designing high-performance self-oscillators with enhanced reliability and environmental immunity.

At present, numerical approaches are commonly used to analyze self-oscillation, yet they are restricted by substantial resource consumption and prolonged computation time. However, extracting analytical solutions for the governing equations can deliver vital mathematical understanding. Frequently employed analytical approaches include the averaging method, the multi-scale method [81,82], the asymptotic method [83], the harmonic balance method [84,85], and the perturbation method [86,87]. Among these, the multi-scale method distinguishes itself through its superior accuracy, simplicity in operation, and broad applicability. In the current work, we model an LCE self-oscillator comprising a photothermally-responsive LCE fiber and a mass block within a linear light field. Building upon the photothermally-responsive LCE model, we formulate a theoretical model for the light-driven LCE self-oscillator under external periodic forcing. Combining the numerical simulation and multi-scale method, we systematically probe how external periodic forcing influences the core attributes of the LCE self-oscillator, i.e., amplitude, frequency, and phase. The response regulation of the LCE self-oscillator via system parameters is also investigated. This work may advance fundamental insights into the disturbance rejection of the LCE self-oscillators and deliver practical guidance for their robust operation in complex oscillatory settings.

The structure of this paper is as follows. Section 2 presents the theoretical model of a light-driven LCE self-oscillator under external periodic forcing, the governing equations incorporating the photothermally-responsive LCE model, and the dimensionless treatment of the equations. Section 3 explores the phase-locking regimes and the underlying mechanisms. In Section 4, we employ the multi-scale method to obtain the steady-state amplitude–frequency and phase–frequency responses of the LCE self-oscillator under periodic forcing. Section 5 utilizes numerical and analytical approaches to comparatively examine the effect of periodic forcing on the response of the LCE self-oscillator. Section 6 investigates how system parameters regulate the response of the LCE self-oscillator under periodic forcing. Finally, the conclusions are given in Section 7.

2. Theoretical Model and Formulation

In this section, we first develop the theoretical model for a light-driven LCE self-oscillator under external periodic forcing. Then, incorporating the photothermally-responsive LCE model, we derive the governing equation for the LCE self-oscillator under periodic forcing. Finally, the equation undergoes nondimensionalization, and its asymptotic expression is derived for analysis.

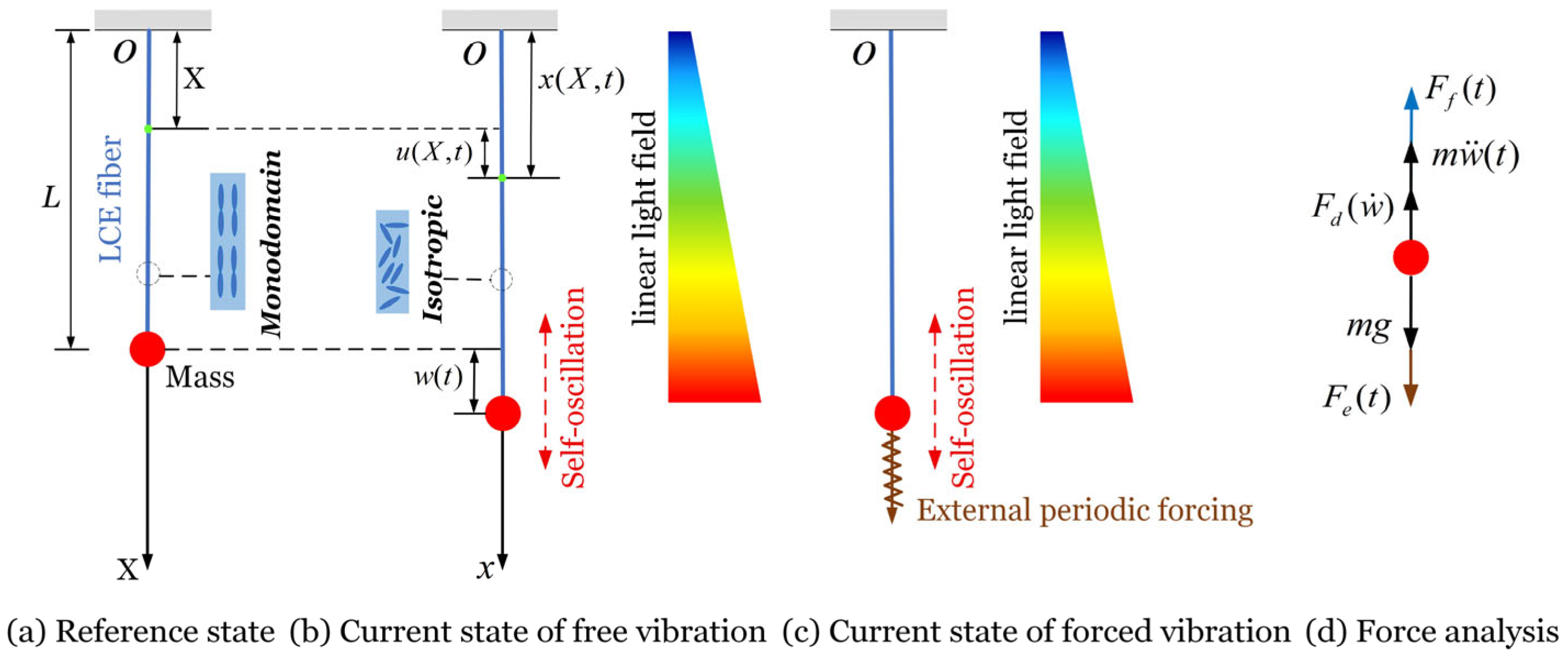
2.1. Theoretical Model and Dynamics

Figure 1 illustrates the theoretical model of a light-driven LCE self-oscillator under external periodic forcing. The LCE self-oscillator comprises a photothermally-responsive LCE fiber with an original length of $L$ and a mass block with a mass of $m$, as presented in Figure 1a. Attributed to the coupled effect of gravity and photothermally-driven contraction deformation of the LCE fiber, the system generates self-oscillations within a linear light field, as described in Figure 1b. Here, the mass block moves up and down, with its displacement being $w(t)$. Widely recognized, the LCE self-oscillator undergoes a periodic self-sustained vibration at its natural frequency [88,89]. After entering the steady state, an external periodic forcing $F_e(t)$ is applied to the LCE self-oscillator, as shown in Figure 1c. Given the force analysis in Figure 1d, the mass block experiences the tensile force $F_f(t)$ from the LCE fiber, the damping force $F_d(\dot{w})$, gravity $mg$, and external periodic forcing $F_e(t)$. Hence, the dynamic governing equation yields the following:

$$m\ddot{w}(t)+F_f(t)+F_d(\dot{w})-mg-F_e(t)=0,$$

(1)

where $\dot{w}(t)$ and $\ddot{w}(t)$ refer to the velocity and acceleration of the mass block, respectively; the damping force is $F_d(\dot{w})=({\beta }_1+{\beta }_2\left|\dot{w}\right|)\dot{w}$ with ${\beta }_1$ and ${\beta }_2$ being the first and second damping coefficients, respectively; $g$ is the gravitational acceleration; and the external periodic forcing can be described as $F_e(t)=F_e\cos \omega t$, with $F_e$ and $\omega$ being the forcing amplitude and angular frequency, respectively.

2.2. Tensile Force Incorporating LCE Model

Employing two coordinate systems allows for a better description of the self-oscillation and the tensile force $F_f(t)$ of the LCE fiber in the linear light field. As depicted in Figure 1a,b, the coordinate X denotes the position of an arbitrary point on the LCE fiber in the reference state, and $x(X,t)$ and $u(X,t)$ represent the instantaneous position and displacement of the point on the LCE fiber in the current state, respectively. Evidently, we have $x(X,t)=u(X,t)+X$.

Considering a linear elastic model with tension proportional to deformation, we derive the following:

$$F_f(t)=K_{f}L{\epsilon }_e(X,t)=K_{f}L\left[{\epsilon }_{tot}\left(X,t\right)-{\epsilon }_T\left(X,t\right)\right],$$

(2)

where $K_f$ denotes the elastic coefficient of the LCE fiber, and ${\epsilon }_e(X,t)$ represents the elastic strain calculated from the linear combination of total strain ${\epsilon }_{tot}(X,t)={\displaystyle \frac{\mathit{\partial }u(X,t)}{\mathit{\partial }X}}$ and photothermally-driven contraction strain ${\epsilon }_T(X,t)$. Notably, the elastic coefficient $K_f$ of the LCE fiber is temperature-dependent, typically decreasing initially with temperature before stabilizing within a certain range [90]. For model simplicity, however, $K_f$ is treated as constant.

Moreover, ${\epsilon }_T(X,t)$ originates from the temperature change within the linear light field, usually nonlinear with temperature. The core physics we aim to capture is the coupling between the photothermally-induced deformation and the resulting motion that triggers self-oscillation. The linear model for small deformations provides a physically sound and theoretically robust foundation. Hence, we assume that ${\epsilon }_T(X,t)$ changes linearly with temperature, i.e.,

$${\epsilon }_T(X,t)=\alpha T(X,t),$$

(3)

where $\alpha$ is the thermal expansion coefficient governing the contraction or expansion of the LCE fiber. A negative $\alpha <0$ denotes thermal contraction, while a positive $\alpha >0$ represents thermal expansion.

Substituting Equation (3) into Equation (2), and then integrating both sides simultaneously yields the following:

$$F_f(t)X=K_{f}L\left[u\left(X,t\right)-\alpha {\displaystyle {\int }_0^{x}T\left(X,t\right)dX}\right].$$

(4)

For simplicity, the tensile force within the LCE fiber is treated as spatially uniform, justified by the assumption of a quasi-static mechanical state; thus, the tensile force at $X=L$ is as follows:

$$F_f(t)=K_f\left[w(t)-\alpha {\displaystyle {\int }_0^{L}T\left(X,t\right)dX}\right].$$

(5)

Due to the non-uniform temperature distribution and its time variation in the LCE fiber, heat exchanges with the environment. To determine this temperature difference, we introduce two key assumptions: firstly, the radius of the thin fiber is much smaller than its length, justifying a uniform temperature profile across its cross-section; secondly, the surrounding temperature maintains a constant spatial gradient. Hence, the temperature distribution $T=T(X,t)$ in the LCE fiber becomes uniform, governed by the following:

$${\rho }_C{\displaystyle \frac{dT(X,t)}{dt }} = q_{\mathrm{ext}}(x) -K_{H}T(X,t),$$

(6)

where ${\rho }_c$ is the specific heat capacity, $q_{\mathrm{ext}}\left(\mathrm{x}\right) = bx+Q$ refers to the heat flux from the linear light field, with $b$ being the gradient of heat flux and $Q$ being the heat flux at $x=0$, $K_H$ is the heat transfer coefficient, and $\tau ={\displaystyle \frac{{\rho }_c}{K_H}}$ denotes the thermal characteristic time.

2.3. Nondimensionalization

The following dimensionless parameters are introduced: ${\overline{F}}_f=F_f/mg$, ${\overline{F}}_d=F_d/mg$, ${\overline{F}}_e=F_e/mg$, $\overline{t}=t/\sqrt{L/g}$, $\overline{u}=u/L$, $\overline{w}=w/L$, $\overline{X}=X/L$, $\overline{x}=x/L$, ${\overline{\beta }}_1={\beta }_1\sqrt{L/g}/m$, ${\overline{\beta }}_2={\beta }_{2}L/m$, $\overline{\tau }=\tau /\sqrt{L/g}$, $\overline{\omega }=\omega /\sqrt{L/g}$, ${\overline{K}}_f=K_{f}L/mg$, $\overline{\alpha }=\alpha T_L$, $\overline{T}=T/T_L$, ${\overline{q}}_{ext}=q_{ext}/K_H{T}_L$, $\overline{b}=bL/K_H{T}_L$, $\overline{Q}=Q/K_H{T}_L$ ($T_L$ is environmental temperature at $x=L$).

For $\tau <<1$, we can express the temperature distribution in the LCE fiber as $\overline{T}(\overline{X},\overline{t})={\overline{T}}^{(0)}(\overline{X},\overline{t})+\overline{\tau }{\overline{T}}^{(1)}(\overline{X},\overline{t})+O({\overline{\tau }}^2)$. According to the literature [88,91], an asymptotic expression for the temperature field can be written as follows:

$$\begin{array}{ll}\overline{T}(\overline{X},\overline{t})& ={\displaystyle \frac{\overline{b}\left[\overline{w}(\overline{t})+1\right]}{e^{\overline{\alpha }\overline{b}}-1}}(e^{\overline{\alpha }\overline{b}\overline{X}}-1)+\overline{Q}\\ & +\overline{\tau }{\displaystyle \frac{\overline{b}\overline{\dot{w}}(\overline{t})}{e^{\overline{\alpha }\overline{b}}-1}}\left[{\displaystyle \frac{(e^{\overline{\alpha }\overline{b}\overline{X}}-1)(\overline{\alpha }\overline{b}{e}^{\overline{\alpha }\overline{b}}-e^{\overline{\alpha }\overline{b}}+1)}{e^{\overline{\alpha }\overline{b}}-1}}-\overline{\alpha }\overline{b}\overline{X}{e}^{\overline{\alpha }\overline{b}\overline{X}}\right].\end{array}$$

(7)

Introduction of Equation (7) into Equation (5) yields the tensile force of the LCE fiber:

$${\overline{F}}_f(\overline{t})={\displaystyle \frac{{\overline{K}}_f\overline{\alpha }\overline{b}}{e^{\overline{\alpha }\overline{b}}-1}}\overline{w}(\overline{t})+{\overline{K}}_f\overline{\alpha }\overline{b}\overline{\tau }{\displaystyle \frac{1-e^{\overline{\alpha }\overline{b}}+\overline{\alpha }\overline{b}{e}^{\overline{\alpha }\overline{b}}}{{(e^{\overline{\alpha }\overline{b}}-1)}^2}}\overline{\dot{w}}(\overline{t})+{\overline{K}}_f\left({\displaystyle \frac{\overline{\alpha }\overline{b}}{e^{\overline{\alpha }\overline{b}}-1}}-1-\overline{\alpha }\overline{Q}\right).$$

(8)

Then, by substituting Equation (8) into Equation (1) and defining $\widehat{w}(\overline{t})=\overline{w}(\overline{t})+{\displaystyle \frac{e^{\overline{\alpha }\overline{b}}-1}{{\overline{K}}_f\overline{\alpha }\overline{b}}}\left[{\overline{K}}_f\left({\displaystyle \frac{\overline{\alpha }\overline{b}}{e^{\overline{\alpha }\overline{b}}-1}}-1-\overline{\alpha }\overline{Q}\right)-1\right]$, we obtain the following:

$$\begin{array}{l}\widehat{\ddot{w}}(\overline{t})+\left({\overline{K}}_f\overline{\alpha }\overline{b}\overline{\tau }{\displaystyle \frac{1-e^{\overline{\alpha }\overline{b}}+\overline{\alpha }\overline{b}{e}^{\overline{\alpha }\overline{b}}}{{(e^{\overline{\alpha }\overline{b}}-1)}^2}}+{\overline{\beta }}_1\right)\widehat{\dot{w}}(\overline{t})+{\overline{\beta }}_2\left|\widehat{\dot{w}}(\overline{t})\right|\widehat{\dot{w}}(\overline{t})\\ +{\displaystyle \frac{{\overline{K}}_f\overline{\alpha }\overline{b}}{e^{\overline{\alpha }\overline{b}}-1}}\widehat{w}(\overline{t})={\overline{F}}_e\cos \overline{\omega }\overline{t}.\end{array}$$

(9)

The differential equation in Equation (9) can be solved numerically using the classic fourth-order Runge–Kutta method within MATLAB_R2021b. Under the time step of 0.001 and initial conditions of $\overline{w}(0)=0$ and $\overline{\dot{w}}(0)=0$, the solution produces the time variation curves for the LCE self-oscillator.

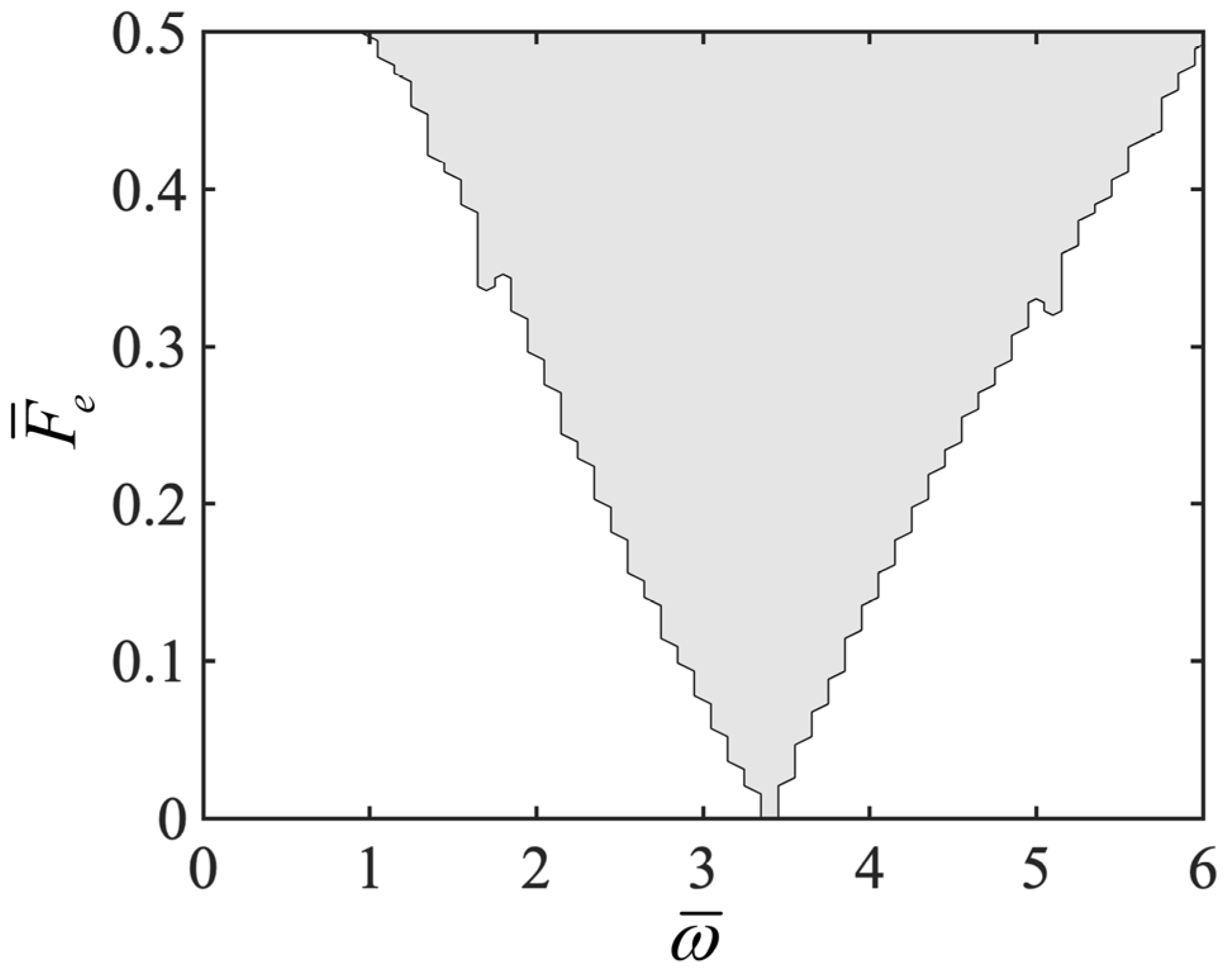
3. Phase-Locking Regimes and Mechanism

Numerical simulations reveal that the light-driven LCE self-oscillator under external periodic forcing could function in three phase-locking regimes, including in-phase synchronization, anti-phase synchronization, and quadrature synchronization. This section will explore the underlying mechanisms from the perspectives of the time domain, frequency domain, and phase space.

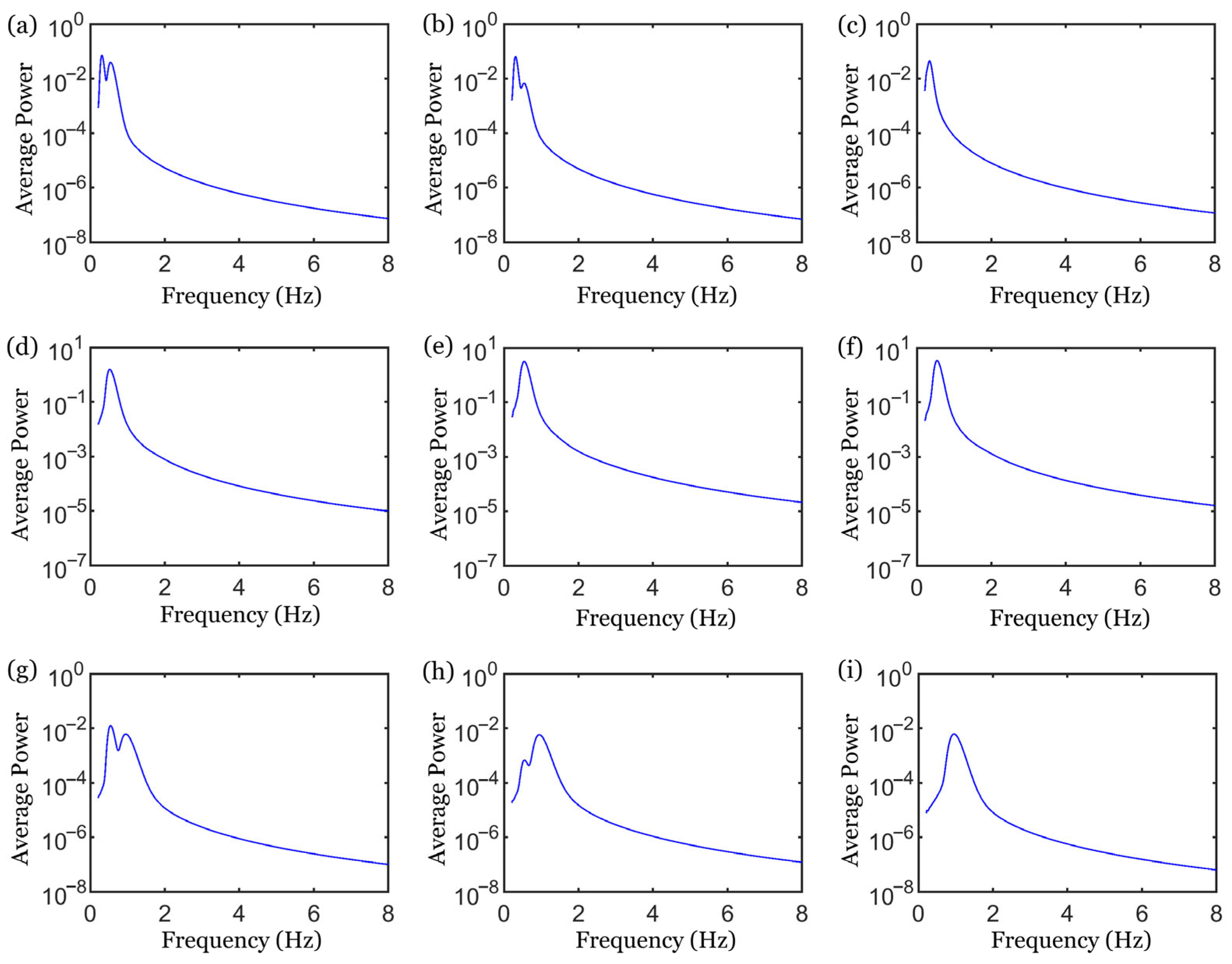
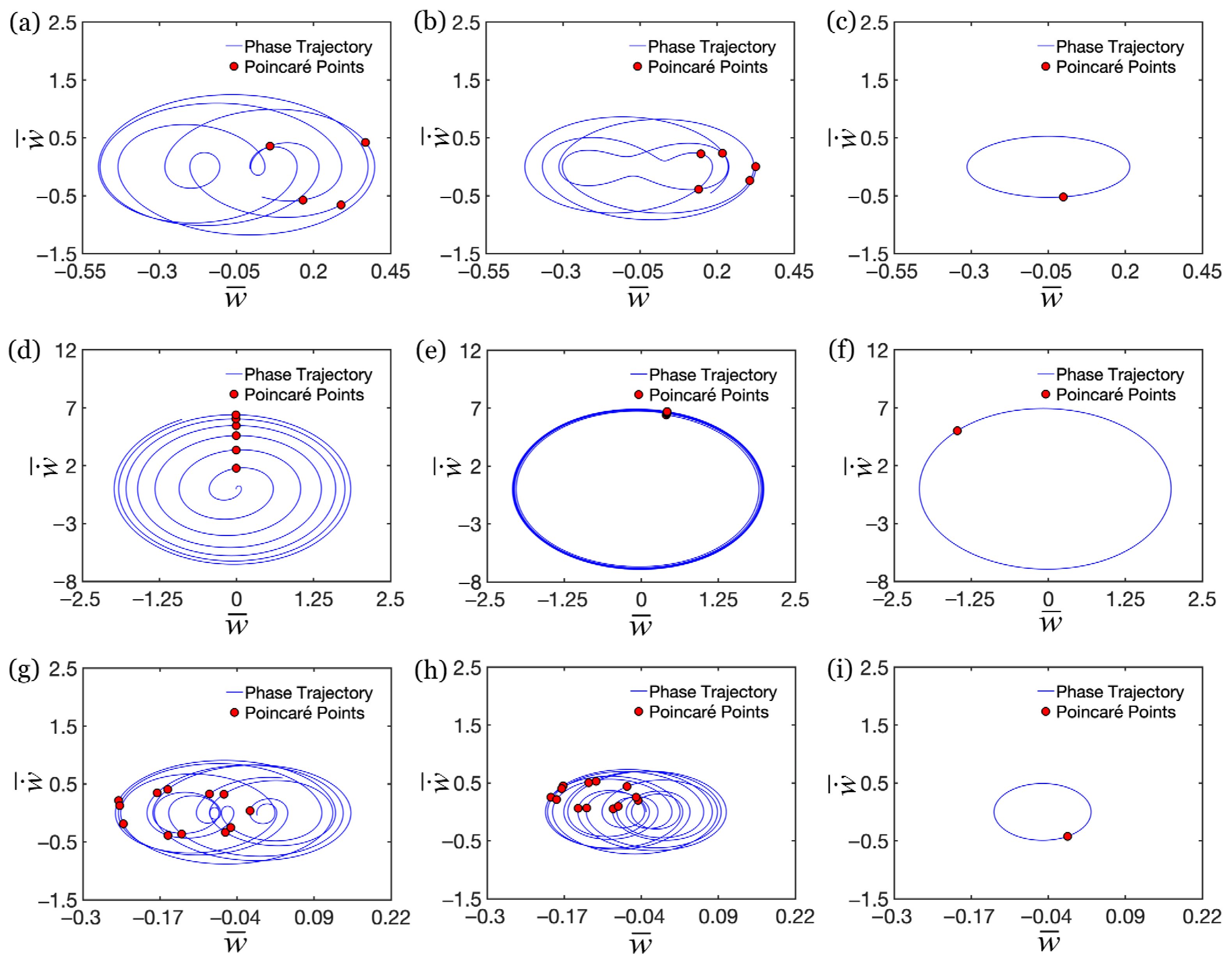
3.1. Phase-Locking Regimes

Guided by the available experiments [46,89,90,92],

Table 1. Material properties and geometric parameters.

Parameter	Definition	Value	Unit
$L$	Original length of LCE fiber	0.1	m
$K_f$	Elastic coefficient of LCE fiber	0~15	N/m
$m$	Mass of mass block	0.01	kg
$g$	Gravitational acceleration	9.8	m/s2
$\alpha$	Thermal expansion coefficient	−0.05~−0.01	1/°C
$b$	Gradient of heat flux	0~150	°C/m
$\tau$	Thermal characteristic time	0~0.2	s
${\beta }_1$	First damping coefficient	0~0.004	kg/s
${\beta }_2$	Second damping coefficient	0~0.02	kg/s

compiles representative material properties and geometric parameters, with corresponding dimensionless quantities systematically tabulated in

Table 2. Dimensionless parameters.

Parameter	$\overline{\alpha }$	${\overline{K}}_f$	$\overline{b}$	${\overline{\beta }}_1$	${\overline{\beta }}_2$	$\overline{\tau }$
Value	−0.5~−0.1	0~15	0~1.5	0~0.04	0~0.2	0~0.02

. These parameters are employed throughout the computational analysis.

It is well established that synchronization occurs when the frequency of the self-oscillator becomes entrained to the frequency of external periodic forcing, establishing a stable frequency–phase relationship. For consistency in the discussion, angular frequency will be used hereafter instead of frequency. It is noteworthy that $\overline{\omega }$ is the angular frequency of the external periodic forcing, ${\overline{\omega }}_0$ refers to the natural angular frequency of the LCE self-oscillator, and ${\overline{\omega }}_{response}$ denotes the angular frequency of the forced vibration in the LCE self-oscillator under periodic forcing.

Figure 2 presents the time variation curves of the light-driven LCE self-oscillator under external periodic forcing, demonstrating three distinct phase-locking regimes governed by forcing frequency $\overline{\omega }$, namely in-phase, anti-phase, and quadrature synchronizations. The other system parameters are ${\overline{K}}_f=10$, $\overline{\alpha }=-0.3$, $\overline{b}=1$, ${\overline{\beta }}_1=0.01$, ${\overline{\beta }}_2=0.05$, and $\overline{\tau }=0.01$. Notably, the natural frequency of the LCE self-oscillator is ${\overline{\omega }}_0=3.4$ for this given parameter set. The initial conditions of $\overline{w}(0)=0$ and $\overline{\dot{w}}(0)=0$ are set for the free vibration of the LCE self-oscillator. After entering its steady state, the external periodic forcing is applied with an initial phase difference of zero. For ${\overline{F}}_e=2$ and $\overline{\omega }=2$, in-phase synchronization occurs, as evidenced in Figure 2a. The LCE self-oscillator and the external periodic forcing reach their peaks simultaneously, i.e., the phase difference is locked to $\Delta \phi =0°$. Compared with the free vibration before the application of periodic forcing, the oscillatory amplitude of the forced vibration displays an increase. For ${\overline{F}}_e=2$ and $\overline{\omega }=3.4$, the quadrature synchronization emerges in Figure 2b. The LCE self-oscillator locks to the external periodic forcing at a phase difference of $\Delta \phi =90°$. The imposition of external forcing leads to a pronounced amplification in the oscillatory amplitude of the LCE self-oscillator. For ${\overline{F}}_e=2$ and $\overline{\omega }=6$, Figure 2c describes the anti-phase synchronization. Obviously, the vibration peak of the LCE self-oscillator is opposite to the peak of the forcing, i.e., the phase difference is locked to $\Delta \phi =180°$. The oscillatory amplitude after applying external forcing remains comparable to that observed prior to its application.

Moreover, the phase difference is explicitly visualized through the Lissajous figures in Figure 3, which correspond to the three cases in Figure 2. At phase difference of $\Delta \phi =0°$, the trajectory degenerates into a diagonal line with positive slope, as depicted in Figure 3a. The circular orbit in Figure 3b suggests a phase difference of $\Delta \phi =90°$. For the phase difference of $\Delta \phi =180°$, the trajectory collapses into an anti-diagonal line with a negative slope in Figure 3c.

3.2. Mechanism Analysis

The previous subsection discussed the three phase-locking regimes in the time domain. Next, we will examine their dynamical signatures across the frequency domain and phase space.

The time-frequency analyses based on the continuous wavelet transform corresponding to the three cases in Figure 2 are presented in Figure 4. For in-phase synchronization under ${\overline{F}}_e=2$ and $\overline{\omega }=2$, as shown in Figure 4a,b, the averaged wavelet power spectra in the transient stage features dual peaks located at ${\overline{\omega }}_{response}=3.4$ and ${\overline{\omega }}_{response}=2$. This bimodal distribution provides conclusive proof that the motion is initially driven by two incommensurate frequencies, with one being the natural frequency ${\overline{\omega }}_0=3.4$ of the LCE self-oscillator and the other being the forcing frequency $\overline{\omega }=2$. Whereas Figure 4c reveals a single spectral peak at ${\overline{\omega }}_{response}=2$ in the steady state, confirming complete frequency locking of the LCE self-oscillator to the forcing frequency $\overline{\omega }=2$. For quadrature synchronization at ${\overline{F}}_e=2$ and $\overline{\omega }=3.4$, only a single sharp peak is present at ${\overline{\omega }}_{response}=3.4$ in both transient and steady-state spectra, as depicted in Figure 4d–f. This spectral signature confirms strict 1:1 frequency locking where the forcing frequency precisely matches the natural frequency of the LCE self-oscillator, i.e., $\overline{\omega }={\overline{\omega }}_0=3.4$. Notably, a minor harmonic peak accompanies the steady-state spectrum as well. Analogous to in-phase synchronization, anti-phase synchronization under ${\overline{F}}_e=2$ and $\overline{\omega }=6$ in Figure 4g–i exhibits dual spectral peaks at ${\overline{\omega }}_{response}=3.4$ and ${\overline{\omega }}_{response}=6$ during the transient stage, followed by a single peak at ${\overline{\omega }}_{response}=6$ in the steady state. This spectral evolution demonstrates progressive frequency locking to the forcing frequency $\overline{\omega }=6$.

Following the analysis in the frequency domain, we now turn to the characterization in phase space. The phase trajectories and Poincaré points of the three cases in Figure 2 are plotted in Figure 5. For in-phase synchronization under ${\overline{F}}_e=2$ and $\overline{\omega }=2$, as depicted in Figure 5a, the transient phase trajectories wind irregularly on the phase space, forming non-closed curve clusters, while the Poincaré points exhibit a dispersed distribution. Then the evolving tendency toward attractors is demonstrated in Figure 5b. Upon reaching steady state, the trajectories in Figure 5c evolve into a smooth closed limit cycle, and the Poincaré points collapse into a single fixed point. This signifies that the LCE self-oscillator undergoes periodic motion at a single frequency, perfectly synchronized with the forcing frequency. The phase space evolution for quadrature synchronization at ${\overline{F}}_e=2$ and $\overline{\omega }=3.4$ is displayed in Figure 5d–f. During the transient stage, phase trajectories form clusters of non-closed curves with dramatically varying curvature radii, while Poincaré points appear as discrete point chains exhibiting rapid spacing decay. Upon rapidly evolving into the steady state, phase trajectories converge to a closed elliptical limit cycle and Poincaré points collapse to a single fixed point, indicating periodicity restoration where the system identically revisits its state after each forcing cycle. This confirms strict 1:1 frequency locking, where the forcing frequency equals the natural frequency of the LCE self-oscillator, i.e., $\overline{\omega }={\overline{\omega }}_0=3.4$. Similar to in-phase synchronization, anti-phase synchronization at ${\overline{F}}_e=2$ and $\overline{\omega }=6$ in Figure 5g–i also manifests an evolution of the phase trajectory from non-closed curves to a closed limit cycle, and of the Poincaré points from dispersion to a single fixed point.

In addition, Arnold tongue is plotted in Figure 6, which is the characteristic tongue-shaped region in parameter space that represents frequency-locking phenomena in nonlinear oscillators subjected to periodic forcing. Clearly observed in Figure 6, the frequency ${\overline{\omega }}_{response}$ of the LCE self-oscillator is locked to the forcing frequency $\overline{\omega }$ within the gray V-shaped tongue. The tongue tip is located at the frequency ratio of $\overline{\omega }/{\overline{\omega }}_0=1:1$. Moreover, stronger forcing widens the frequency-locking region. Specifically, as the forcing frequency approaches the natural frequency of the LCE self-oscillator, 1:1 frequency-locking occurs wherein the self-oscillator vibrates precisely at the forcing frequency. When the external forcing is sufficiently strong, it overcomes the intrinsic tendency of the self-oscillator to maintain its natural frequency, achieving full entrainment. The frequency-locking persists even for weak forcing amplitudes, provided the frequency detuning remains sufficiently small. Notably, different synchronization patterns emerge under varying parameters, which will be described in the subsequent parameter analysis.

4. Asymptotic Analysis Using Multi-Scale Method

This section will employ the multi-scale method [81,82] to derive the steady-state amplitude–frequency and phase–frequency responses of the LCE self-oscillator under external periodic forcing.

Through introducing $\epsilon ={\overline{K}}_f\overline{\alpha }\overline{b}\overline{\tau }{\displaystyle \frac{e^{\overline{\alpha }\overline{b}}-1-\overline{\alpha }\overline{b}{e}^{\overline{\alpha }\overline{b}}}{{(e^{\overline{\alpha }\overline{b}}-1)}^2}}-{\overline{\beta }}_1$, $c_1={\displaystyle \frac{{\overline{\beta }}_2{(e^{\overline{\alpha }\overline{b}}-1)}^2}{{\overline{K}}_f\overline{\alpha }\overline{b}\overline{\tau }(e^{\overline{\alpha }\overline{b}}-1-\overline{\alpha }\overline{b}{e}^{\overline{\alpha }\overline{b}})-{\overline{\beta }}_1{(e^{\overline{\alpha }\overline{b}}-1)}^2}}$, $c_2={\displaystyle \frac{{\overline{K}}_f\overline{\alpha }\overline{b}}{e^{\overline{\alpha }\overline{b}}-1}}$, Equation (9) can be expressed as

$$\widehat{\ddot{w}}(\overline{t})-\epsilon \left(\widehat{\dot{w}}(\overline{t})-c_1\left|\widehat{\dot{w}}(\overline{t})\right|\widehat{\dot{w}}(\overline{t})\right)+c_2\widehat{w}(\overline{t})={\overline{F}}_e\cos \overline{\omega }\overline{t}.$$

(10)

Let $x=\widehat{w}$, ${\omega }_0=\sqrt{c_2}$, ${\overline{F}}_e=\epsilon F_0$, and $\omega ={\omega }_0+\epsilon \sigma$ with $\sigma$ being the frequency detuning parameter, we have the following:

$$\ddot{x}-\epsilon (\dot{x}-c_1\left|\dot{x}\right|\dot{x})+{{\omega }_0}^{2}x=\epsilon F_0\cos ({\omega }_0+\epsilon \sigma )t.$$

(11)

We introduce time variables $T_n={\epsilon }^{n}t(n=0,1)$ representing different scales to discuss the approximate solutions. The solutions for Equation (11) can be expressed as the following:

$$x=x_0(T_0,T_1)+\epsilon x_1(T_0,T_1),$$

(12)

$$\dot{x}=D_0+\epsilon D_1,$$

(13)

$$\ddot{x}={D_0}^2+2\epsilon D_0{D}_1+O({\epsilon }^2).$$

(14)

where $D_n={\displaystyle \frac{\partial }{\partial T_n}}(n=0,1)$ denotes the symbol of a partial differential operator.

Let $f(x,\dot{x})=\dot{x}-c_1\left|\dot{x}\right|\dot{x}$. Substituting Equations (12)–(14) into Equation (11) and equating coefficients of like powers of $\epsilon$ gives the following system of linear partial differential equations:

$${D_0}^2{x}_0+{{\omega }_0}^2{x}_0=0,$$

(15)

$${D_0}^2{x}_1+{{\omega }_0}^2{x}_1=-2D_0{D}_1{x}_0+f\left(D_0{x}_0\right)+F_0\cos \left({\omega }_0{T}_0+\sigma T_1\right).$$

(16)

The solution to the zeroth-order approximation Equation (15) is expressed in complex-valued form as the following:

$$x_0=A(T_1)e^{i{\omega }_0{T}_0}+\overline{A}(T_1)e^{-i{\omega }_0{T}_0},$$

(17)

where $A$ is a complex-valued function to be determined, and $\overline{A}$ denotes its complex conjugate. $A$ is expressed in exponential form as

$$A(T_1)={\displaystyle \frac{1}{2}}a(T_1)e^{i\eta (T_1)},$$

(18)

where both $a(T_1)$ and $\eta (T_1)$ are real-valued functions of time.

Substituting Equation (17) into the right-hand side of the first-order approximation Equation (16) yields the following:

$${D_0}^2{x}_1+{{\omega }_0}^2{x}_1=-2i{\omega }_0{D}_{1}A{e}^{i{\omega }_0{T}_0}+2i{\omega }_0{D}_1\overline{A}{e}^{-i{\omega }_0{T}_0}+f\left(D_0{x}_0\right)+F_0\cos \left({\omega }_0{T}_0+\sigma T_1\right),$$

(19)

where $f(D_0{x}_0)$ is a periodic function of $T_0$, and it can be expanded as a Fourier series like $f(D_0{x}_0)={\displaystyle \sum _{n\to \infty }^{\infty }{f}_n(A,\overline{A})e^{in{\omega }_0{T}_0}}$ with $f_n(A,\overline{A})={\displaystyle \frac{{\omega }_0}{2\pi }}{\displaystyle {\int }_0^{2\pi /{\omega }_0}f\cdot e^{-in{\omega }_0{T}_0}}d{T}_0$.

Equation (19) can be rewritten as follows:

$$\begin{array}{l}{D_0}^2{x}_1+{{\omega }_0}^2{x}_1=-2i{\omega }_0{D}_{1}A{e}^{i{\omega }_0{T}_0}+2i{\omega }_0{D}_1\overline{A}{e}^{-i{\omega }_0{T}_0}+i{\omega }_{0}A{e}^{i{\omega }_0{T}_0}-i{\omega }_0\overline{A}{e}^{-i{\omega }_0{T}_0}\\ -c_{1}i{\displaystyle \frac{4a^2{{\omega }_0}^2}{3\pi }}{e}^{i({\omega }_0{T}_0+\eta )}+c_{1}i{\displaystyle \frac{4a^2{{\omega }_0}^2}{3\pi }}{e}^{-i({\omega }_0{T}_0+\eta )}+\dots +{\displaystyle \frac{F_0}{2}}{e}^{i({\omega }_0{T}_0+\sigma T_1)}+{\displaystyle \frac{F_0}{2}}{e}^{-i({\omega }_0{T}_0+\sigma T_1)}.\end{array}$$

(20)

To prevent the emergence of secular terms, the sum of the coefficients of $e^{i{\omega }_0{T}_0}$ should vanish. This requires that the function $A$ satisfies the following condition:

$$-2i{\omega }_0{D}_{1}A+i{\omega }_{0}A-i{\displaystyle \frac{8a{{\omega }_0}^2{c}_1}{3\pi }}A+{\displaystyle \frac{F_0}{2}}{e}^{i\sigma T_1}=0.$$

(21)

Through substituting Equation (18) into Equation (21), we obtain the following:

$$a^{\prime }+ia{\eta }^{\prime }={\displaystyle \frac{a}{2}}-{\displaystyle \frac{4a^2{\omega }_0{c}_1}{3\pi }}-i{\displaystyle \frac{F_0}{2{\omega }_0}}{e}^{i\psi },$$

(22)

where $\psi (T_1)=\sigma T_1-\eta (T_1)$ is the phase difference between the forcing and response.

Given $e^{i\psi }=\cos \psi +i\sin \psi$ and ${\eta }^{\prime }=\sigma -{\psi }^{\prime }$, separating the real and imaginary components of Equation (22) yields amplitude and phase equations:

$$a^{\prime }={\displaystyle \frac{a}{2}}-{\displaystyle \frac{4a^2{\omega }_0{c}_1}{3\pi }}+{\displaystyle \frac{F_0}{2{\omega }_0}}\sin \psi ,$$

(23)

$$a(\sigma -{\psi }^{\prime })=-{\displaystyle \frac{F_0}{2{\omega }_0}}\cos \psi .$$

(24)

$a^{\prime }=0$ and ${\psi }^{\prime }=0$ correspond to the steady-state amplitude $a$ and phase difference $\psi$, respectively:

$${\displaystyle \frac{4a^2{\omega }_0{c}_1}{3\pi }}-{\displaystyle \frac{a}{2}}={\displaystyle \frac{F_0}{2{\omega }_0}}\sin \psi ,$$

(25)

$$a\sigma =-{\displaystyle \frac{F_0}{2{\omega }_0}}\cos \psi .$$

(26)

Proceeding algebraically, we eliminate $\psi$ by squaring both sides of Equations (25) and (26) and adding the resulting expressions. Alternatively, dividing one equation by the other cancels $a$. Then, we have the following:

$${\left({\displaystyle \frac{4a^2{\omega }_0{c}_1}{3\pi }}-{\displaystyle \frac{a}{2}}\right)}^2+{\left(a\sigma \right)}^2={\left({\displaystyle \frac{F_0}{2{\omega }_0}}\right)}^2,$$

(27)

$$\tan \psi ={\displaystyle \frac{3\pi -8a{\omega }_0{c}_1}{6\pi \sigma }}.$$

(28)

To sum up, the steady-state amplitude–frequency and phase–frequency responses for $x$ are derivable from Equations (27) and (28).

Given $x=\widehat{w}$, the amplitude and phase difference for $\widehat{w}$ are ${\overline{A}}_{response}=a$ and $\Delta \phi =\psi$, respectively. Thus, by substituting $c_1={\displaystyle \frac{{\overline{\beta }}_2{(e^{\overline{\alpha }\overline{b}}-1)}^2}{{\overline{K}}_f\overline{\alpha }\overline{b}\overline{\tau }(e^{\overline{\alpha }\overline{b}}-1-\overline{\alpha }\overline{b}{e}^{\overline{\alpha }\overline{b}})-{\overline{\beta }}_1{(e^{\overline{\alpha }\overline{b}}-1)}^2}}$, ${\omega }_0=\sqrt{c_2}=\sqrt{{\displaystyle \frac{{\overline{K}}_f\overline{\alpha }\overline{b}}{e^{\overline{\alpha }\overline{b}}-1}}}$ and $\epsilon ={\overline{K}}_f\overline{\alpha }\overline{b}\overline{\tau }{\displaystyle \frac{e^{\overline{\alpha }\overline{b}}-1-\overline{\alpha }\overline{b}{e}^{\overline{\alpha }\overline{b}}}{{(e^{\overline{\alpha }\overline{b}}-1)}^2}}-{\overline{\beta }}_1$, the steady-state amplitude–frequency and phase–frequency responses for the LCE self-oscillator are derivable from Equations (29) and (30):

$${\left({\displaystyle \frac{4{\overline{A}}_{response}^2\sqrt{c_2}{c}_1}{3\pi }}-{\displaystyle \frac{{\overline{A}}_{response}}{2}}\right)}^2+{\left({\overline{A}}_{response}\sigma \right)}^2={\displaystyle \frac{{{\overline{F}}_e}^2}{4{\epsilon }^2{c}_2}},$$

(29)

$$\tan \Delta \phi ={\displaystyle \frac{3\pi -8{\overline{A}}_{response}\sqrt{c_2}{c}_1}{6\pi \sigma }},$$

(30)

where $\sigma ={\displaystyle \frac{\overline{\omega }-{\overline{\omega }}_0}{\epsilon }}$ refers to the frequency detuning parameter. Significantly, the case $\sigma =0$ corresponds to 1:1 frequency-locking, i.e., $\overline{\omega }={\overline{\omega }}_0$.

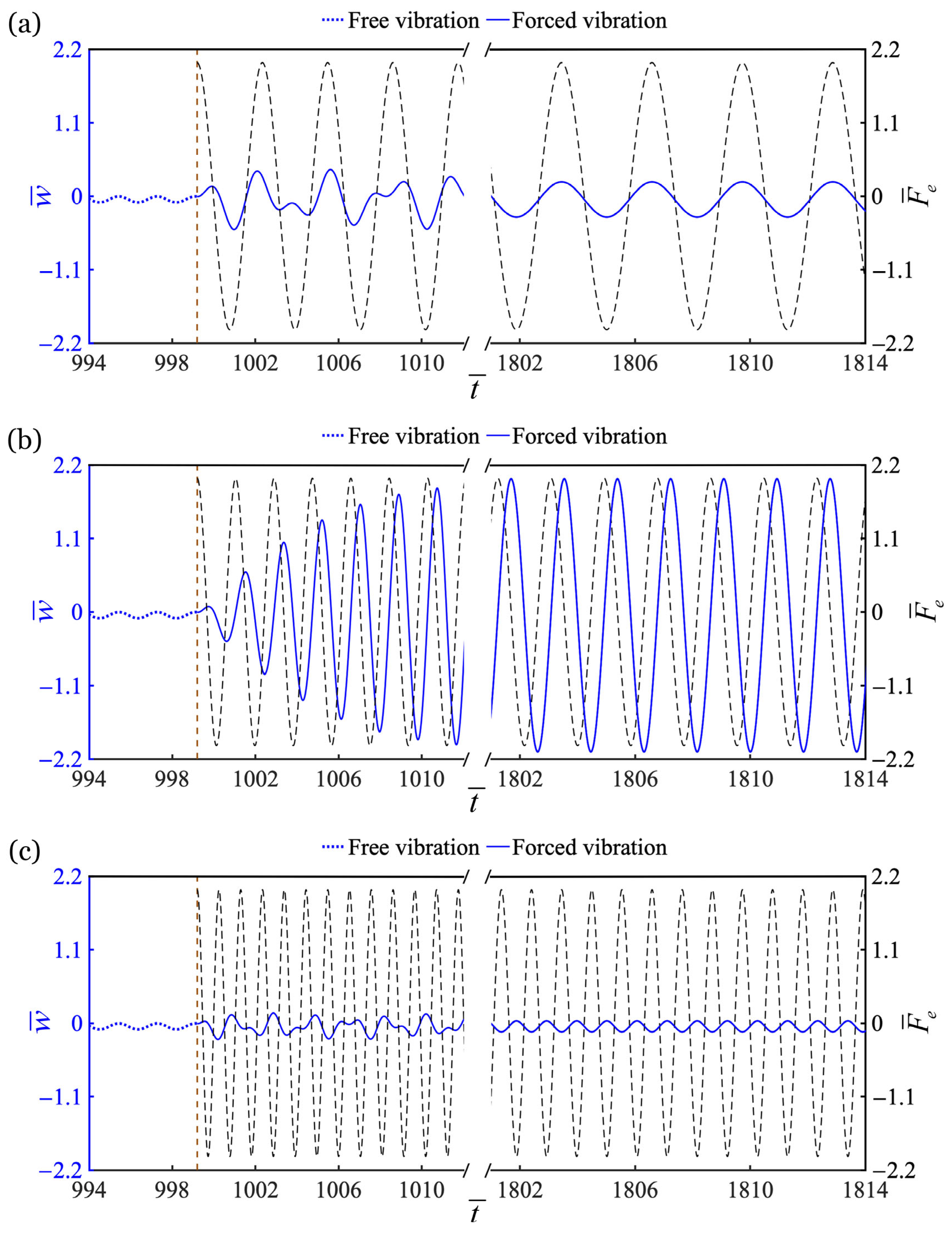
5. Response Characteristics of LCE Self-Oscillator Under Periodic Forcing

As mentioned above, variations in the amplitude and frequency of the external periodic forcing could alter the self-oscillatory response of the LCE self-oscillator. This section will employ numerical and analytical approaches to comparatively examine the response characteristics of the LCE self-oscillator under external periodic forcing.

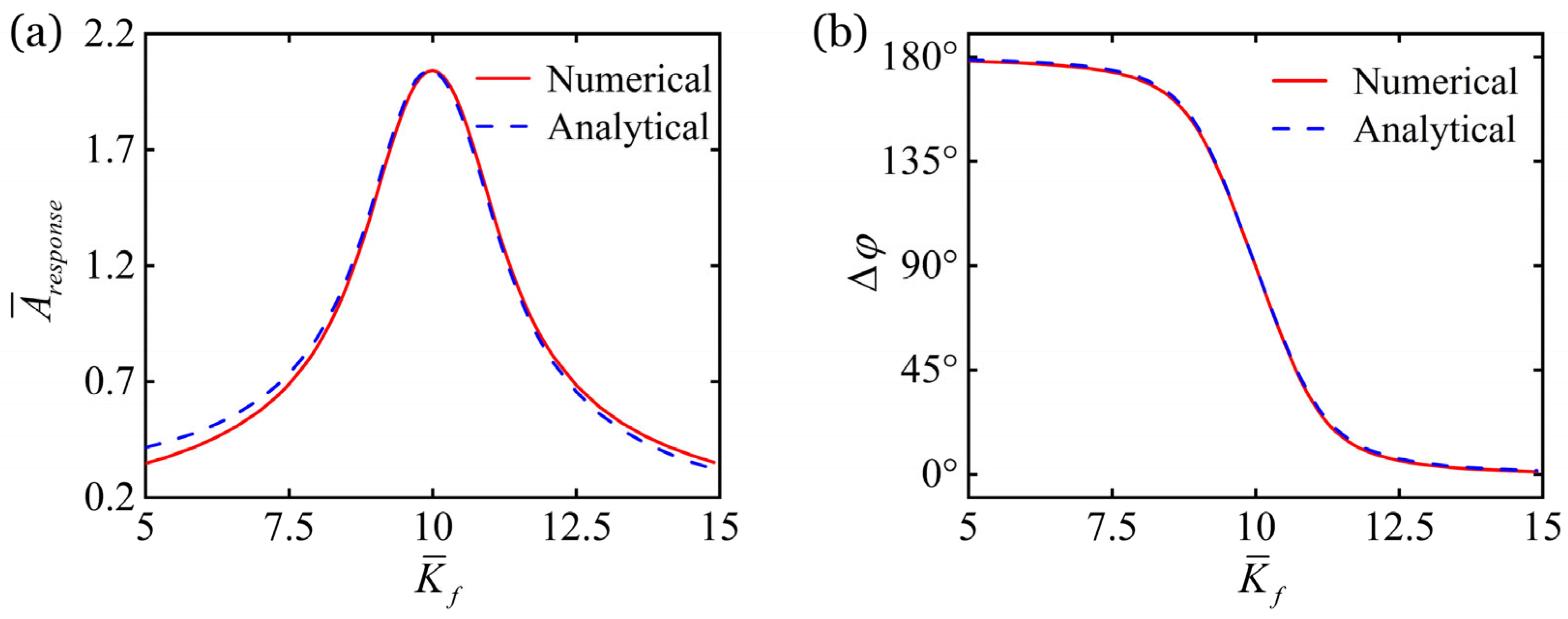
5.1. Effect of Forcing Frequency

Figure 7 describes how the forcing frequency $\overline{\omega }$ affects the self-oscillatory response of the LCE self-oscillator, with the other parameters being ${\overline{K}}_f=10$, $\overline{\alpha }=-0.3$, $\overline{b}=1$, ${\overline{\beta }}_1=0.01$, ${\overline{\beta }}_2=0.05$, $\overline{\tau }=0.01$ and ${\overline{F}}_e=2$. Figure 7a depicts the initial growth followed by decay in response amplitude with the increasing forcing frequency $\overline{\omega }$. Specifically, the response amplitude peaks when the forcing frequency equals the natural frequency, i.e., $\overline{\omega }={\overline{\omega }}_0=3.4$. As the forcing frequency $\overline{\omega }$ deviates from the natural frequency ${\overline{\omega }}_0$, whether higher or lower, the amplitude diminishes. If the forcing varies too rapidly, the system struggles to follow, requiring stronger forcing to maintain synchronization, which reduces the amplitude. Conversely, if the forcing varies too slowly, it cannot replenish the energy efficiently, also resulting in a decline of amplitude. Clearly observed in Figure 7b, the external forcing and self-oscillatory response maintain a consistent phase offset of $\Delta \phi =90°$ at $\overline{\omega }={\overline{\omega }}_0$. $\overline{\omega }<{\overline{\omega }}_0$ yields in-phase synchronization with $\Delta \phi =0°$, whereas $\overline{\omega }>{\overline{\omega }}_0$ exhibits anti-phase synchronization with $\Delta \phi =180°$. It is apparent that a close correspondence exists between numerical and analytical results. Furthermore, in future experimental validation, different types of synchronization phenomena can be accessed in an LCE self-oscillator with fixed parameters by adjusting the frequency of the external periodic forcing.

5.2. Effect of Forcing Amplitude

Figure 8 displays how the forcing amplitude ${\overline{F}}_e$ influences the self-oscillatory response of the LCE self-oscillator, where the other parameters are ${\overline{K}}_f=10$, $\overline{\alpha }=-0.3$, $\overline{b}=1$, ${\overline{\beta }}_1=0.01$, ${\overline{\beta }}_2=0.05$, $\overline{\tau }=0.01$ and $\overline{\omega }=3.4$. Figure 8a demonstrates a monotonic increase in the response amplitude with growing forcing amplitude ${\overline{F}}_e$. Given the specified parameters, the forcing frequency equals the natural frequency, i.e., $\overline{\omega }={\overline{\omega }}_0=3.4$, thus enabling 1:1 frequency-locking. A stronger external forcing propels the LCE self-oscillator more effectively, producing oscillations with greater amplitude. Correspondingly, quadrature synchronization is achieved for $\overline{\omega }={\overline{\omega }}_0$, and the phase difference remains invariant at $\Delta \phi =90°$ under changes in forcing amplitude, as plotted in Figure 8b. Likewise, excellent agreement is observed between numerical and analytical results. In future experimental demonstrations, for an LCE self-oscillator that has been phase-locked and synchronized with the external periodic forcing, its amplitude can be regulated by increasing the forcing amplitude.

In summary, the response characteristics described above can be effectively exploited to achieve active manipulation and optimized design of the LCE self-oscillators. External periodic forcing offers a non-contact means of control, enabling tailored manipulation of self-oscillatory behavior in terms of frequency, amplitude, and phase. Such deterministic responses facilitate programmable motion regimes. Furthermore, for practical applications in noisy and unpredictable environments, LCE self-oscillators can be engineered to exhibit enhanced robustness against perturbations—or even constructively harness stochastic disturbances to realize specific functional capabilities.

6. Response Regulation of LCE Self-Oscillator via System Parameters

Since variations in system parameters could influence the natural frequency of the LCE self-oscillator, a constant external periodic forcing combined with a shifted natural frequency may alter the self-oscillatory response. This section will employ numerical and analytical methods to comparatively examine how system parameters regulate the LCE self-oscillator under external periodic forcing. Notably, all parameter values used in the following parametric analysis fall within the self-oscillation regime.

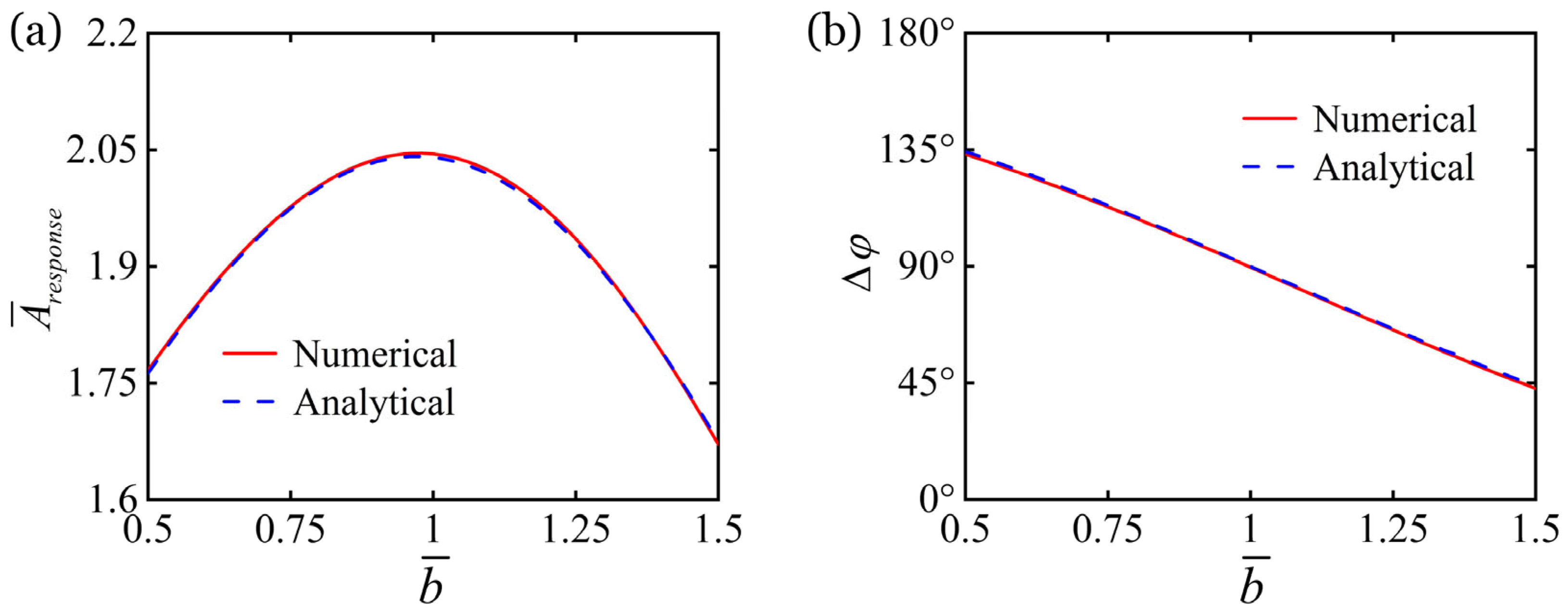
6.1. Regulation by Elastic Coefficient

As illustrated in Figure 9, the response regulation of the LCE self-oscillator under external periodic forcing by elastic coefficient ${\overline{K}}_f$ of LCE fiber is presented, where the other parameters are $\overline{\alpha }=-0.3$, $\overline{b}=1$, ${\overline{\beta }}_1=0.01$, ${\overline{\beta }}_2=0.05$, $\overline{\tau }=0.01$, ${\overline{F}}_e=2$, and $\overline{\omega }=3.4$. In self-oscillations, a rise in the elastic coefficient ${\overline{K}}_f$ generates a greater driving force from the LCE fiber, thereby enhancing the natural frequency ${\overline{\omega }}_0$. Consequently, Figure 9a depicts how the response amplitude initially grows and subsequently diminishes as the elastic coefficient ${\overline{K}}_f$ increases. The peak amplitude occurs at ${\overline{K}}_f=10$, where the natural frequency equals the forcing frequency, i.e., ${\overline{\omega }}_0=\overline{\omega }=3.4$. In addition, the variation of phase difference with the rising elastic coefficient ${\overline{K}}_f$ is clearly witnessed in Figure 9b. ${\overline{K}}_f<10$ corresponds to ${\overline{\omega }}_0<\overline{\omega }=3.4$, anti-phase synchronization with $\Delta \phi =180°$ occurs. ${\overline{K}}_f>10$ signifies ${\overline{\omega }}_0>\overline{\omega }=3.4$, in-phase synchronization with $\Delta \phi =0°$ emerges. Furthermore, close agreement between numerical and analytical results persists, exhibiting minor deviations exclusively at small values of ${\overline{K}}_f$. Notably, this finding provides a method to experimentally observe pronounced synchronization by tuning the elastic coefficient of the LCE fiber to shift its frequency.

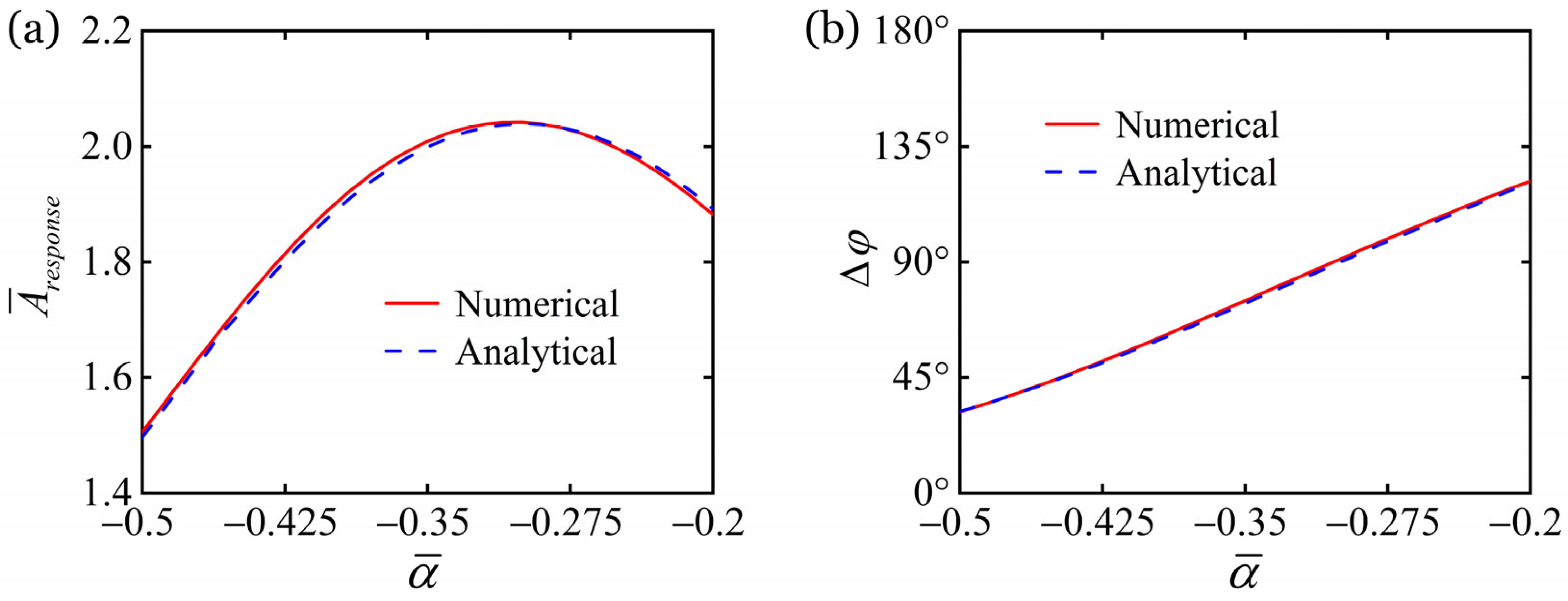
6.2. Regulation by Thermal Expansion Coefficient

The response regulation of the LCE self-oscillator under external periodic forcing by the thermal expansion coefficient $\overline{\alpha }$ is illustrated in Figure 10, with the other parameters being ${\overline{K}}_f=10$, $\overline{b}=1$, ${\overline{\beta }}_1=0.01$, ${\overline{\beta }}_2=0.05$, $\overline{\tau }=0.01$, ${\overline{F}}_e=2$ and $\overline{\omega }=3.4$. In self-oscillations, an elevation in the absolute value of the thermal expansion coefficient $\overline{\alpha }$ will raise the natural frequency ${\overline{\omega }}_0$. Thus, amplitude enhancement prior to progressive attenuation under increasing thermal expansion coefficient $\overline{\alpha }$ is captured in Figure 10a. The maximum amplitude is achieved at $\overline{\alpha }=-0.3$, where the natural frequency coincides with the forcing frequency, i.e., ${\overline{\omega }}_0=\overline{\omega }=3.4$. Moreover, the change in phase difference as the thermal expansion coefficient $\overline{\alpha }$ grows is distinctly shown in Figure 10b. $-0.5<\overline{\alpha }<-0.2$ corresponds to a slight variation in the natural frequency near ${\overline{\omega }}_0=3.4$, suggesting a close proximity to the quadrature synchronization with $\Delta \phi =90°$ at 1:1 frequency locking. Similarly, a strong consistency between numerical and analytical results persists.

6.3. Regulation by Gradient of Heat Flux

Figure 11 describes how gradient of heat flux $\overline{b}$ regulates the self-oscillatory response of the LCE self-oscillator under external periodic forcing, among which the other parameters are ${\overline{K}}_f=10$, $\overline{\alpha }=-0.3$, ${\overline{\beta }}_1=0.01$, ${\overline{\beta }}_2=0.05$, $\overline{\tau }=0.01$, ${\overline{F}}_e=2$ and $\overline{\omega }=3.4$. Since increasing the gradient of heat flux $\overline{b}$ leads to a gradual enhancement in the natural frequency ${\overline{\omega }}_0$ of the LCE self-oscillator, Figure 11a reveals that a larger gradient first amplifies and then suppresses the response amplitude. When $\overline{b}=1$, the natural frequency exactly matches the forcing frequency, namely ${\overline{\omega }}_0=\overline{\omega }=3.4$, thus resulting in maximum response amplitude. Furthermore, the progression of the phase difference with increasing gradient $\overline{b}$ is demonstrated in Figure 11b. For $0.5<\overline{b}<1.5$, the natural frequency exhibits minimal deviation around ${\overline{\omega }}_0=3.4$, placing the system near the quadrature synchronization with $\Delta \phi =90°$ of 1:1 frequency locking. Yet again, remarkable consistency is evident in numerical–analytical comparisons.

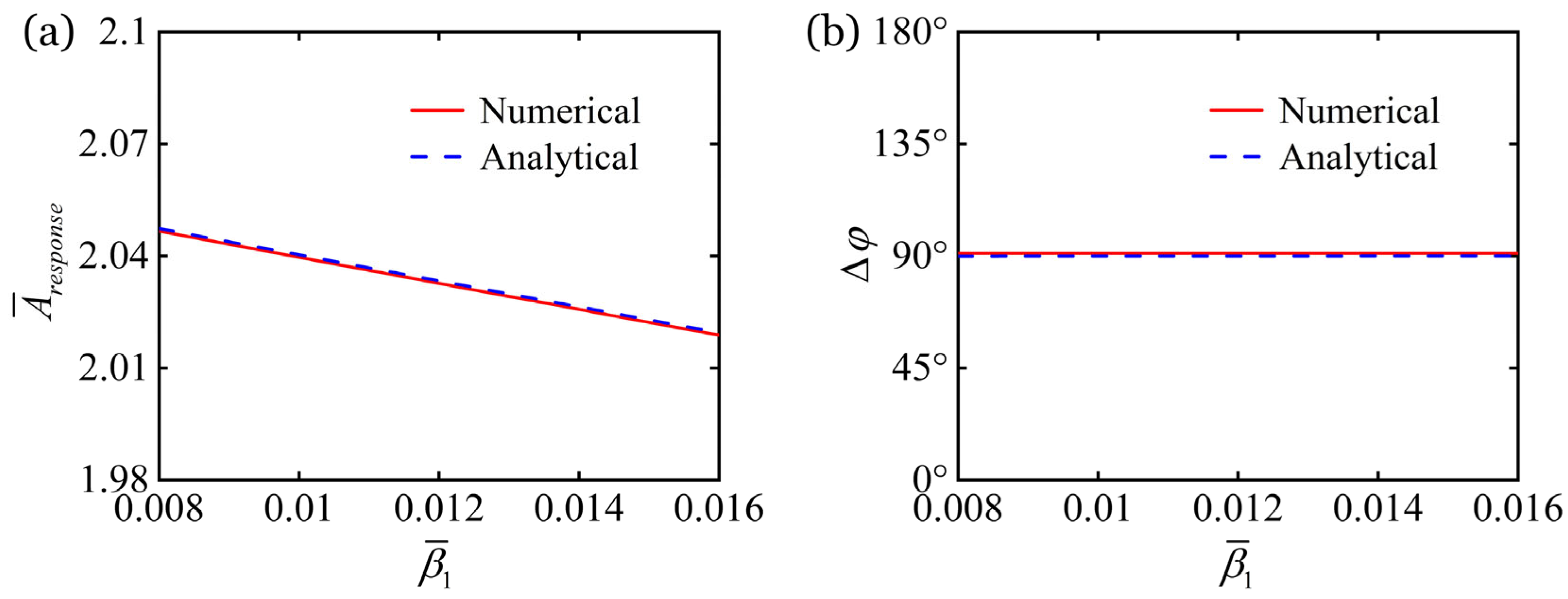
6.4. Regulation by First Damping Coefficient

As illustrated in Figure 12, the response regulation of the first damping coefficient ${\overline{\beta }}_1$ on the LCE self-oscillator under external periodic forcing is provided, with the other parameters being ${\overline{K}}_f=10$, $\overline{\alpha }=-0.3$, $\overline{b}=1$, ${\overline{\beta }}_2=0.05$, $\overline{\tau }=0.01$, ${\overline{F}}_e=2$ and $\overline{\omega }=3.4$. It is evident in Figure 12a that as damping rises, the consequent intensification of energy dissipation results in diminished response amplitude. However, changes in the first damping coefficient ${\overline{\beta }}_1$ exhibit no impact on the natural frequency, which remains constant at ${\overline{\omega }}_0=3.4$. Consequently, for ${\overline{\omega }}_0=\overline{\omega }=3.4$, the phase difference consistently maintains $\Delta \phi =90°$ regardless of changes in the first damping coefficient ${\overline{\beta }}_1$, as demonstrated in Figure 12b. Once again, close correspondence emerges between numerical and analytical results.

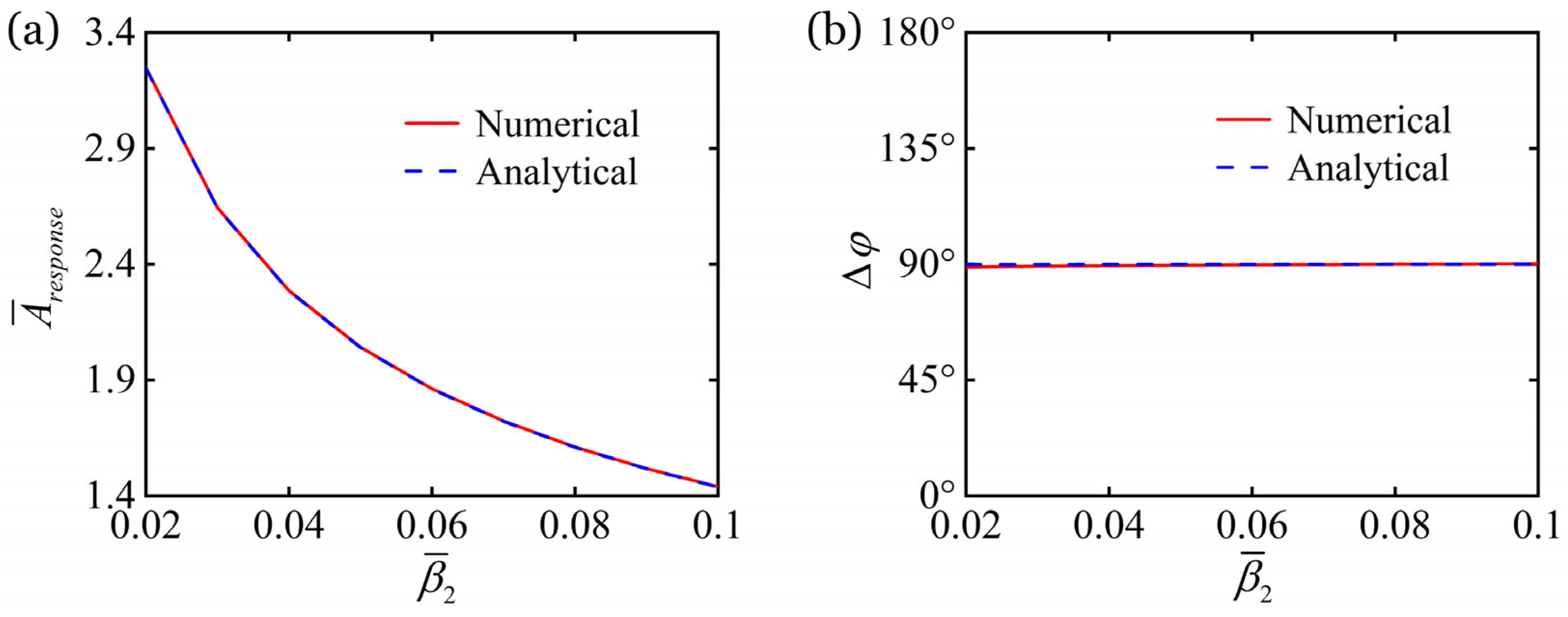
6.5. Regulation by Second Damping Coefficient

Figure 13 describes how the second damping coefficient ${\overline{\beta }}_2$ regulates the self-oscillatory response of the LCE self-oscillator under external periodic forcing, with the other parameters being ${\overline{K}}_f=10$, $\overline{\alpha }=-0.3$, $\overline{b}=1$, ${\overline{\beta }}_1=0.01$, $\overline{\tau }=0.01$, ${\overline{F}}_e=2$ and $\overline{\omega }=3.4$. In the LCE self-oscillator, elevated damping promotes greater energy dissipation, thereby decreasing the amplitude. Thus, Figure 13a visualizes the descending trend of response amplitude versus a higher damping coefficient ${\overline{\beta }}_2$. Similarly, the natural frequency is maintained at ${\overline{\omega }}_0=3.4$, independently of the second damping coefficient ${\overline{\beta }}_2$. Thus, for ${\overline{\omega }}_0=\overline{\omega }=3.4$, the phase difference remains unchanged at $\Delta \phi =90°$ despite variations in the second damping coefficient ${\overline{\beta }}_2$, as evidenced by Figure 13b. Likewise, strong alignment persists across numerical and analytical results.

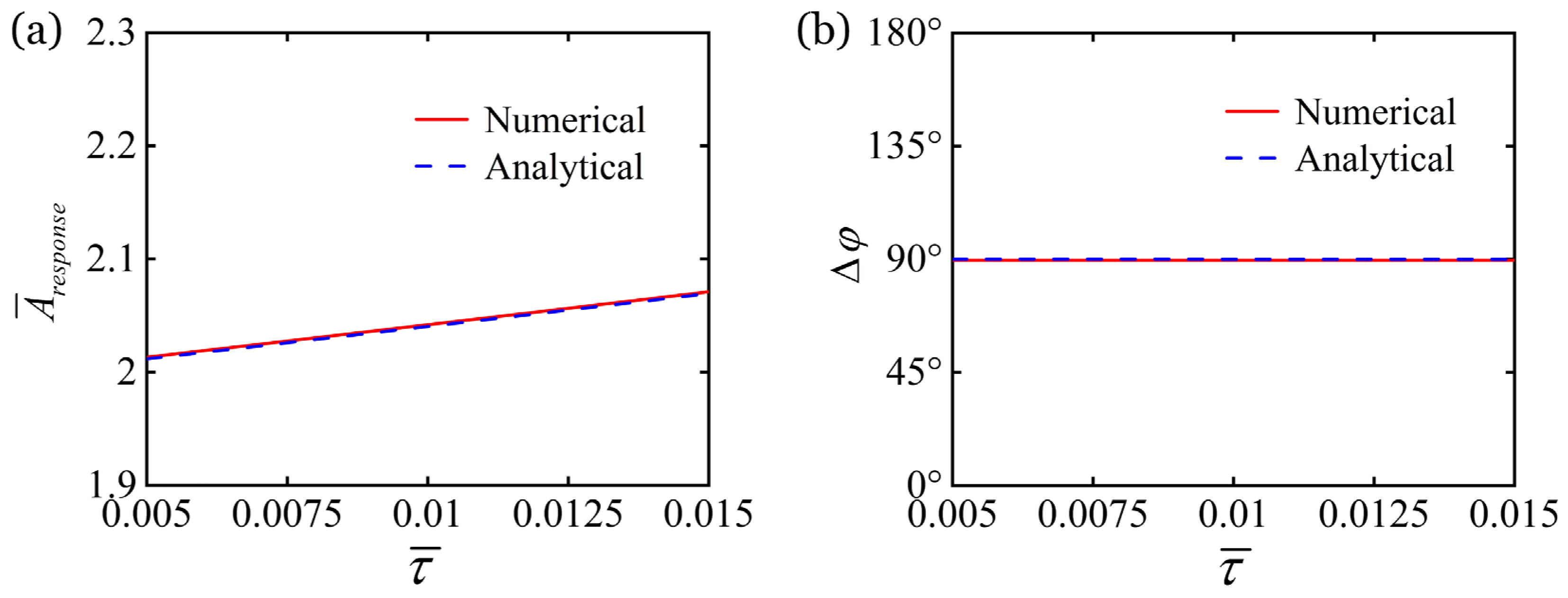
6.6. Regulation by Thermal Characteristic Time

The response regulation of the LCE self-oscillator under external periodic forcing by thermal characteristic time $\overline{\tau }$ is illustrated in Figure 14, where the other parameters are ${\overline{K}}_f=10$, $\overline{\alpha }=-0.3$, $\overline{b}=1$, ${\overline{\beta }}_1=0.01$, ${\overline{\beta }}_2=0.05$, ${\overline{F}}_e=2$ and $\overline{\omega }=3.4$. The growth in thermal characteristic time $\overline{\tau }$ augments photothermal conversion in the LCE fiber, directly amplifying the response amplitude of the LCE self-oscillator. Accordingly, the growth in response amplitude with increasing thermal characteristic time $\overline{\tau }$ is shown in Figure 14a. Since the natural frequency is unaffected by alterations to the thermal characteristic time $\overline{\tau }$, it remains fixed at ${\overline{\omega }}_0=3.4$. This invariance leads to a stable phase difference of $\Delta \phi =90°$ for ${\overline{\omega }}_0=\overline{\omega }=3.4$ under any modification of the thermal characteristic time $\overline{\tau }$, as displayed in Figure 14b. Yet again, numerical and analytical solutions exhibit exceptional concordance.

To sum up, the system parameters of LCE self-oscillators can be inversely designed according to the target operational environment to either efficiently harness ambient energy or robustly reject environmental disturbances. For LCE-based energy harvesters, the goal is to maximize the conversion of ambient mechanical vibrations into usable energy. This can be achieved by optimizing the oscillator parameters to promote synchronization with predominant environmental frequencies, thereby improving the energy capture efficiency. Conversely, for high-precision sensors utilizing LCE self-oscillators, it is essential to prevent the self-oscillatory frequency from being entrained or shifted by stray periodic signals. Targeted parameter design can avoid resonant interference bands, thus improving interference immunity.

7. Conclusions

Unlike previous studies on isolated LCE self-oscillators, we introduce external environmental disturbances into the system to investigate the synchronization behavior arising from the interplay between self-oscillation and external periodic forcing. To characterize the response of self-oscillation under external periodic forcing, an LCE self-oscillator is considered using a photothermally-responsive LCE fiber and a mass block within a linear light field. Building upon the photothermally-responsive LCE model, we develop a theoretical model for the light-driven LCE self-oscillator under external periodic forcing. Three distinct phase-locking regimes are identified: in-phase, anti-phase, and quadrature synchronizations. The underlying mechanisms are explored through time-domain, frequency-domain, and phase-space analyses. In addition, Arnold tongue is plotted to describe the frequency-locking region. The frequency of the LCE self-oscillator locks to the forcing frequency within the tongue, with the tongue tip located at the frequency ratio of $\overline{\omega }/{\overline{\omega }}_0=1:1$. And stronger forcing widens the frequency-locking region.

Utilizing the multi-scale method, we obtain the steady-state amplitude–frequency and phase–frequency responses of the LCE self-oscillator under external periodic forcing. The response amplitude displays an initial growth followed by decay with increasing forcing frequency $\overline{\omega }$, but a monotonic increase with growing forcing amplitude ${\overline{F}}_e$. For $\overline{\omega }={\overline{\omega }}_0$, 1:1 frequency-locking emerges, where the response amplitude peaks and a consistent phase offset of $\Delta \phi =90°$ is maintained. In-phase synchronization with $\Delta \phi =0°$ yields for $\overline{\omega }<{\overline{\omega }}_0$, whereas anti-phase synchronization with $\Delta \phi =180°$ occurs for $\overline{\omega }>{\overline{\omega }}_0$. Moreover, variations in the elastic coefficient ${\overline{K}}_f$ of LCE fiber, thermal expansion coefficient $\overline{\alpha }$, and gradient of heat flux $\overline{b}$ alter the natural frequency ${\overline{\omega }}_0$ of the LCE self-oscillator, thereby modifying its self-oscillatory response under periodic forcing. In contrast, the first and second damping coefficients ${\overline{\beta }}_1$, ${\overline{\beta }}_2$ and thermal characteristic time $\overline{\tau }$ exhibit no effect on the natural frequency ${\overline{\omega }}_0$, and therefore the phase difference consistently maintains at $\Delta \phi =90°$ for $\overline{\omega }={\overline{\omega }}_0$. Notably, a close correspondence exists between numerical and analytical results.

Nevertheless, this study still has several limitations. First, the theoretical framework incorporates certain simplifying assumptions, such as neglecting nonlinear constitutive behavior of the LCE material, which may affect the accuracy of model predictions under real-world conditions. Moving forward, we will explore adopting more generalized modeling approaches that account for nonlinear constitutive behavior. A second limitation lies in the representation of external disturbances as a purely periodic forcing, which offers only an approximate depiction of actual vibrational environments. In future work, we will employ more complex excitation patterns, such as random or multi-frequency excitation, to more accurately replicate real-world environments. Additionally, experimental validation will be conducted in the next research phase to further verify the numerical and analytical results. The self-oscillation frequency inherent to the LCE fiber system was found to be minimal, limiting clear observability. The current work provides theoretical support for improving experimental observability of synchronization. For instance, modifying system parameters, such as the elastic coefficient of the LCE fiber, can significantly alter the frequency.

This study establishes the feasibility of actively controlling and optimizing LCE self-oscillators through external periodic forcing. It provides a non-contact control strategy for precise manipulation of the self-oscillatory motion. Insights into phase-locking synchronization contribute to the design of LCE self-oscillators with enhanced robustness against environmental noise and unpredictable disturbances—even turning such interference into functional advantages. Moreover, this work lays a theoretical foundation for further explorations on collective phase-locking dynamics and group synchronization behaviors in coupled LCE self-oscillator networks.