Function-Theoretic and Probabilistic Approaches to the Problem of Recovering Functions from Korobov Classes in the Lebesgue Metric
Abstract
1. Introduction
2. Statement of the Problem
3. Necessary Definitions and Auxiliary Statements
4. Main Results and Their Proofs
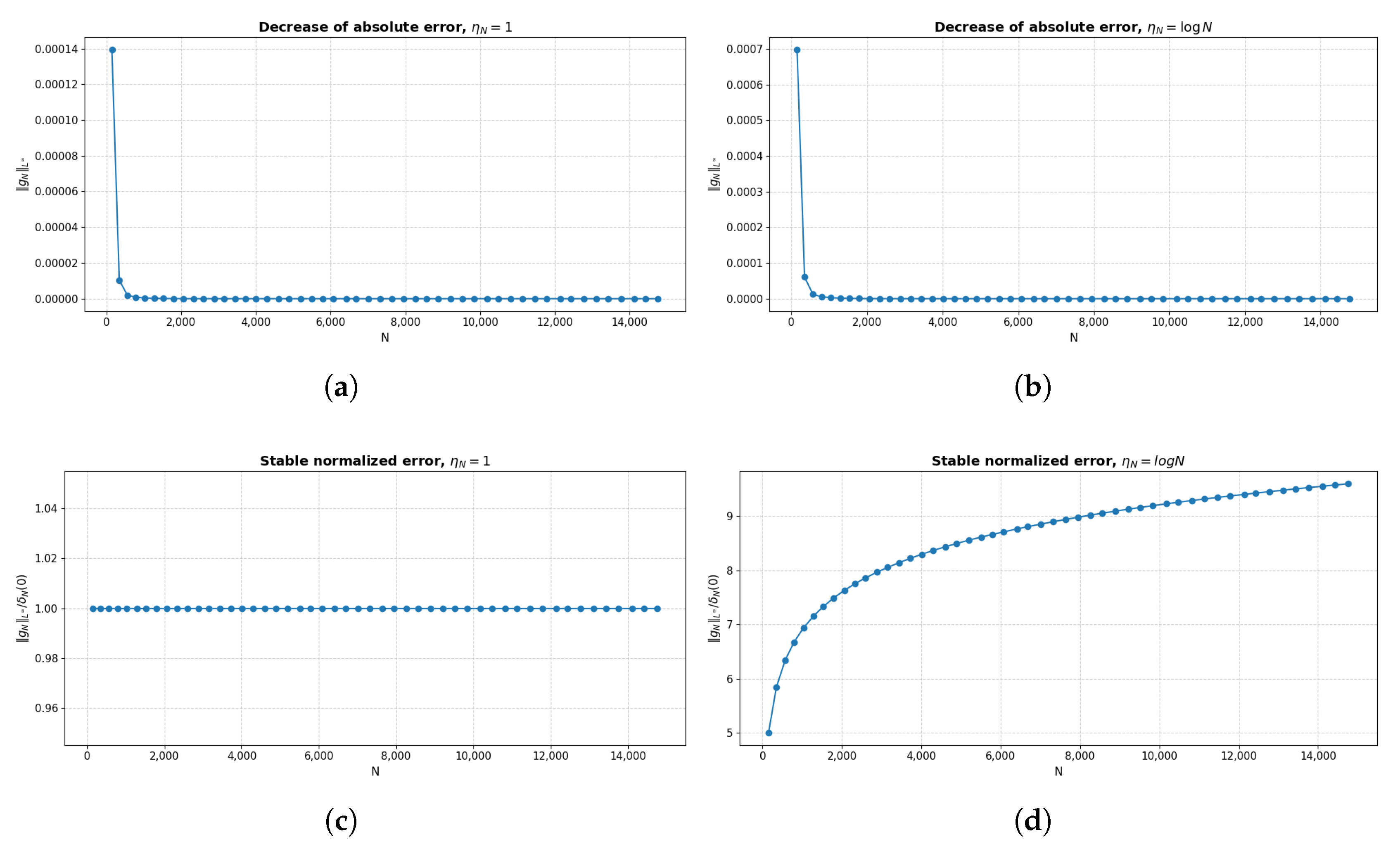
5. Numerical Implementation
6. Discussion
- The absolute errordecreases rapidly as in both numerical regimes corresponding to and (note the difference in scales in Figure 2a,b).
- The normalized value remains approximately constant with respect to N when , and increases when . This behavior confirms the theoretical results of Theorem 1 concerning the limiting recovery error under inaccurate information (the second parts of conditions C(N)D–2 and C(N)D–3).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Temirgaliyev, N. The concept of S. M. Voronin in the problem of comparisons of deterministic and random computation in the same terms. Bull. L. N. Gumilyov Eurasian Natl. Univ. Math. Comput. Sci. Mech. Ser. 2019, 128, 8–33. (In Russian) [Google Scholar]
- Temirgaliyev, N.; Zhubanysheva, A. Approximation Theory, Computational Mathematics and Numerical Analysis in New Conception of Computational (Numerical) Diameter. Bull. L. N. Gumilyov Eurasian Natl. Univ. Math. Comput. Sci. Mech. Ser. 2018, 124, 8–88. (In Russian) [Google Scholar] [CrossRef]
- Temirgaliev, N.; Zhubanysheva, A.Z. Computational (Numerical) Diameter in a Context of General Theory of a Recovery. Russ. Math. (Iz. VUZ) 2019, 63, 79–86. [Google Scholar] [CrossRef]
- Taugynbayeva, G.; Azhgaliyev, S.; Zhubanysheva, A.; Temirgaliyev, N. Full C(N)D-Study of Computational Capabilities of Lagrange Polynomials. Math. Comput. Simul. 2025, 227, 189–208. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. Über die beste Annäherung von Funktionen einer gegebenen Funktionenklasse. Ann. Math. 1936, 37, 107–110. [Google Scholar] [CrossRef]
- Sard, A. Best Approximate Integration Formulas; Best Approximation Formulas. Am. J. Math. 1949, 71, 80–91. [Google Scholar] [CrossRef]
- Nikol’skii, S.M. Concerning Estimation for Approximate Quadrature Formulas. Russ. Math. Surv. 1950, 5, 165–177. (In Russian) [Google Scholar]
- Stechkin, S.B. On the Best Approximation of Given Classes of Functions by Any Polynomials. Usp. Mat. Nauk 1954, 9, 133–134. (In Russian) [Google Scholar]
- Korobov, N.M. Number-Theoretical Methods in Approximate Analysis; Fizmatgiz: Moscow, Russia, 1963. (In Russian) [Google Scholar]
- Ioffe, A.D.; Tikhomirov, V.M. Duality of Convex Functions and Extremal Problems. Usp. Mat. Nauk 1968, 23, 51–116. (In Russian) [Google Scholar]
- Micchelli, C.A.; Rivlin, T.J. A Survey of Optimal Recovery. In Optimal Estimation in Approximation Theory; Micchelli, C.A., Rivlin, T.J., Eds.; Plenum Press: New York, NY, USA, 1977; pp. 1–54. [Google Scholar]
- Korneichuk, N.P. Exact Constants in Approximation Theory; Nauka: Moscow, Russia, 1987. (In Russian) [Google Scholar]
- Pietsch, A. Eigenvalues and s-Numbers; Geest and Portig: Leipzig, Germany; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
- Traub, J.F.; Wasilkowski, G.W.; Wozniakowski, H. Information-Based Complexity; Academic Press: New York, NY, USA, 1988. [Google Scholar]
- Novak, E.; Wozniakowski, H. Tractability of Multivariate Problems. Vol. 1. Linear Information; EMS Tracts Math. 6; European Mathematical Society Publish House: Zürich, Switzerland, 2008. [Google Scholar]
- Plaskota, L. Noisy Information and Computational Complexity; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Osipenko, K.Y. Best Approximation of Analytic Functions from Information about Their Values at a Finite Number of Points. Math. Notes 1976, 19, 17–23. [Google Scholar] [CrossRef]
- Magaril-Il’yaev, G.G.; Osipenko, K.Y. Optimal Recovery of Values of Functions and Their Derivatives from Inaccurate Data on the Fourier Transform. Sb. Math. 2004, 195, 1461–1476. [Google Scholar] [CrossRef]
- Marchuk, A.G.; Osipenko, K.Y. Best Approximation of Functions Specified with an Error at a Finite Number of Points. Math. Notes 1975, 17, 207–212. [Google Scholar] [CrossRef]
- Heinrich, S. Random Approximation in Numerical Analysis. In Functional Analysis; Bierstedt, K.D., Pietsch, A., Ruess, W.M., Vogt, D., Eds.; Marcel Dekker: New York, NY, USA, 1993; pp. 123–171. [Google Scholar]
- Smolyak, S.A. Quadrature and Interpolation Formulas for Tensor Products of Certain Classes of Functions. Dokl. Akad. Nauk SSSR 1963, 148, 1042–1045. [Google Scholar]
- Sherniyazov, K. Approximate Reconstruction of Functions and Solutions of Heat Conductivity Equations with Distribution Functions of Initial Temperatures from Classes E, SW and B. Ph.D. Thesis, Al-Farabi Kazakh National University, Almaty, Kazakhstan, 1998. (In Russian). [Google Scholar]
- Korobov, N.M. Trigonometric Sums and Their Applications; Nauka: Moscow, Russia, 1989. (In Russian) [Google Scholar]
- Kovaleva, I.M. Reconstruction and Integration over Domains of Functions from Anisotropic Korobov Classes. Ph.D. Thesis, Al-Farabi Kazakh National University, Almaty, Kazakhstan, 2002. (In Russian). [Google Scholar]
- Azhgaliev, S. Approximate Reconstruction of Functions and Solutions of the Heat Equation with Distribution Functions of Initial Temperatures from Classes W, B, SW and E from Linear Information. Ph.D. Thesis, Al-Farabi Kazakh National University, Almaty, Kazakhstan, 2000. (In Russian). [Google Scholar]
- Temirgaliev, N.; Sherniyazov, K.; Berikhanova, M. Exact Orders of Computational (Numerical) Diameters in Problems of Reconstructing Functions and Sampling Solutions of the Klein–Gordon Equation from Fourier Coefficients. Proc. Steklov Inst. Math. 2013, 282 (Suppl. 1), 165–191. (In Russian) [Google Scholar] [CrossRef]
- Temirgaliev, N. Computer (Computational) Diameter. Algebraic Number Theory and Harmonic Analysis in Reconstruction Problems (Quasi-Monte Carlo Method). Theory of Embeddings and Approximations. Fourier Series. Bull. L. N. Gumilyov Eurasian Natl. Univ. 2010, 194. [Google Scholar]
- Banach, S. The Lebesgue Integral in Abstract Space. In Theory of the Integral; Saks, S., Ed.; IL: Moscow, Russia, 1949; pp. 463–477. (In Russian) [Google Scholar]
- Sul’din, A.V. Wiener Measure and Its Applications to Approximation Methods. Izv. Vyss. Uchebnykh Zaved. Mat. 1959, 6, 145–158. (In Russian) [Google Scholar]
- Voronin, S.M.; Skalyga, V.I. Quadrature Formulas. Dokl. Akad. Nauk SSSR 1984, 276, 1038–1041. [Google Scholar] [CrossRef]
- Temirgaliev, N. On Some Problems of Numerical Integration. Vestn. Akad. Nauk KazSSR 1983, 12, 15–18. [Google Scholar]
- Temirgaliev, N. On the construction of probability measures of functional classes. Proc. Steklov Inst. Math. 1997, 218, 396–401. [Google Scholar]
- Nauryzbayev, N.; Shomanova, A.; Temirgaliyev, N. Average Square Errors by Banach Measure of Recovery of Functions by Finite Sums of Terms of Their Trigonometric Fourier Series. Bull. L. N. Gumilyov Eurasian Natl. Univ. Math. Comput. Sci. Mech. Ser. 2025, 150, 17–24. [Google Scholar]
- Liu, Y.; Li, X.; Li, H. N-Widths of Multivariate Sobolev Spaces with Common Smoothness in Probabilistic and Average Settings in the Sq Norm. Axioms 2023, 12, 698. [Google Scholar] [CrossRef]
- Fang, G.; Ye, P. Probabilistic and Average Linear Widths of Sobolev Spaces with Gaussian Measure in L∞-Norm. Constr. Approx. 2004, 20, 159–172. [Google Scholar]
- Tan, X.; Wang, Y.; Sun, L.; Shao, X.; Chen, G. Gel’fand-N-Width in Probabilistic Setting. J. Inequal. Appl. 2020, 2020, 143. [Google Scholar] [CrossRef]
- Liu, Y.; Li, H.; Li, X. Gel’fand Widths of Sobolev Classes of Functions in the Average Setting. Ann. Funct. Anal. 2023, 14, 14–31. [Google Scholar] [CrossRef]
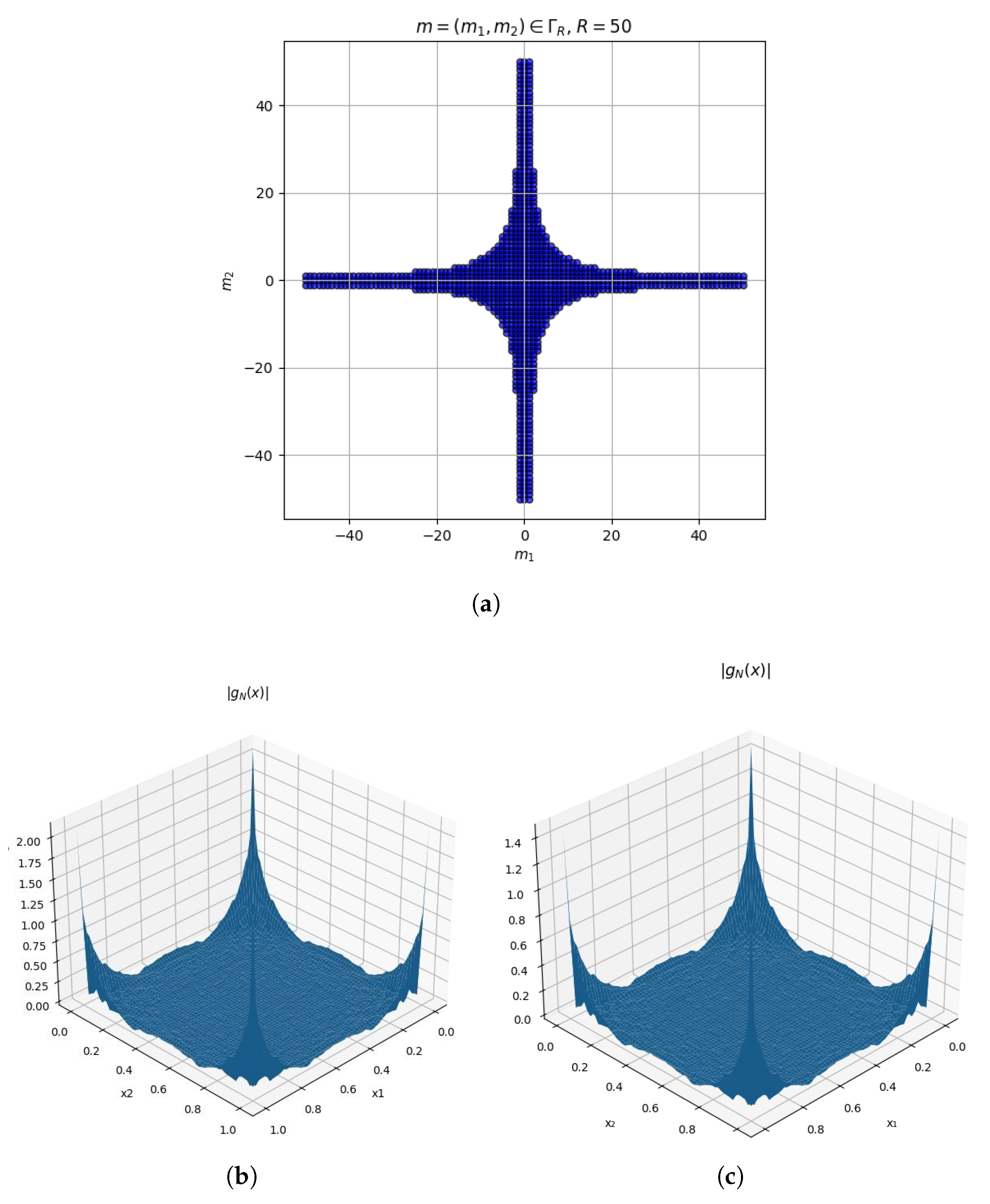
| R | for | for | for | for | |
|---|---|---|---|---|---|
| 10 | 149 | 1.89536 × | 1 | 9.48428 × | 5.003946306 |
| 20 | 345 | 2.83954 × | 1 | 1.6593 × | 5.843544417 |
| 30 | 565 | 8.94009 × | 1 | 5.66518 × | 6.336825731 |
| 40 | 793 | 3.9829 × | 1 | 2.65892 × | 6.675823222 |
| 50 | 1029 | 2.12459 × | 1 | 1.47369 × | 6.936342736 |
| 60 | 1285 | 1.23761 × | 1 | 8.85941 × | 7.158513997 |
| 70 | 1529 | 8.08639 × | 1 | 5.92924 × | 7.332369206 |
| 80 | 1793 | 5.46472 × | 1 | 4.09398 × | 7.491645474 |
| 90 | 2061 | 3.87329 × | 1 | 2.95568 × | 7.630946581 |
| 100 | 2329 | 2.86032 × | 1 | 2.21766 × | 7.75319427 |
| 110 | 2593 | 2.18982 × | 1 | 1.72132 × | 7.860570786 |
| 120 | 2889 | 1.67224 × | 1 | 1.33256 × | 7.9686657 |
| 130 | 3149 | 1.34806 × | 1 | 1.08584 × | 8.054840221 |
| 140 | 3437 | 1.08258 × | 1 | 8.81478 × | 8.142354277 |
| 150 | 3721 | 8.86906 × | 1 | 7.29192 × | 8.221747728 |
| 160 | 4009 | 7.3524 × | 1 | 6.09977 × | 8.296297113 |
| 170 | 4301 | 6.15869 × | 1 | 5.15273 × | 8.366602833 |
| 180 | 4605 | 5.18359 × | 1 | 4.3723 × | 8.434897949 |
| 190 | 4885 | 4.46519 × | 1 | 3.7927 × | 8.493924564 |
| 200 | 5193 | 3.82506 × | 1 | 3.27237 × | 8.555066844 |
| 210 | 5505 | 3.29935 × | 1 | 2.84187 × | 8.613412049 |
| 220 | 5785 | 2.90916 × | 1 | 2.52021 × | 8.66302364 |
| 230 | 6077 | 2.56718 × | 1 | 2.2366 × | 8.712266432 |
| 240 | 6413 | 2.23892 × | 1 | 1.96266 × | 8.766082459 |
| 250 | 6685 | 2.01433 × | 1 | 1.77414 × | 8.80762149 |
| 260 | 7009 | 1.78557 × | 1 | 1.58111 × | 8.854950317 |
| 270 | 7321 | 1.59793 × | 1 | 1.42191 × | 8.89850221 |
| 280 | 7641 | 1.43268 × | 1 | 1.281 × | 8.941283764 |
| 290 | 7949 | 1.29516 × | 1 | 1.16316 × | 8.980801414 |
| 300 | 8269 | 1.1709 × | 1 | 1.05618 × | 9.020268862 |
| 310 | 8565 | 1.07018 × | 1 | 9.69093 × | 9.055439411 |
| 320 | 8885 | 9.7429 × | 1 | 8.85836 × | 9.092119741 |
| 330 | 9217 | 8.86925 × | 1 | 8.09657 × | 9.128804884 |
| 340 | 9521 | 8.16154 × | 1 | 7.477 × | 9.161255164 |
| 350 | 9833 | 7.5139 × | 1 | 6.9079 × | 9.193499355 |
| 360 | 10,185 | 6.86552 × | 1 | 6.33597 × | 9.228671329 |
| 370 | 10,477 | 6.38497 × | 1 | 5.91052 × | 9.256937657 |
| 380 | 10,821 | 5.87651 × | 1 | 5.45883 × | 9.28924397 |
| 390 | 11,133 | 5.46251 × | 1 | 5.08979 × | 9.31766895 |
| 400 | 11,473 | 5.05589 × | 1 | 4.72612 × | 9.347751728 |
| 410 | 11,785 | 4.71866 × | 1 | 4.42355 × | 9.374582815 |
| 420 | 12,145 | 4.36699 × | 1 | 4.10701 × | 9.404672841 |
| 430 | 12,425 | 4.11804 × | 1 | 3.88227 × | 9.427465851 |
| 440 | 12,769 | 3.83826 × | 1 | 3.62899 × | 9.454775637 |
| 450 | 13,117 | 3.58125 × | 1 | 3.39562 × | 9.481664378 |
| 460 | 13,429 | 3.37061 × | 1 | 3.20383 × | 9.505171827 |
| 470 | 13,765 | 3.16244 × | 1 | 3.01377 × | 9.529884418 |
| 480 | 14,117 | 2.96292 × | 1 | 2.83111 × | 9.555135024 |
| 490 | 14,425 | 2.80233 × | 1 | 2.68371 × | 9.576718091 |
| 500 | 14,761 | 2.64053 × | 1 | 2.53484 × | 9.599743847 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhubanysheva, A.Z.; Taugynbayeva, G.E.; Nauryzbayev, N.Z.; Shomanova, A.A.; Apenov, A.T. Function-Theoretic and Probabilistic Approaches to the Problem of Recovering Functions from Korobov Classes in the Lebesgue Metric. Mathematics 2025, 13, 3363. https://doi.org/10.3390/math13213363
Zhubanysheva AZ, Taugynbayeva GE, Nauryzbayev NZ, Shomanova AA, Apenov AT. Function-Theoretic and Probabilistic Approaches to the Problem of Recovering Functions from Korobov Classes in the Lebesgue Metric. Mathematics. 2025; 13(21):3363. https://doi.org/10.3390/math13213363
Chicago/Turabian StyleZhubanysheva, Aksaule Zh., Galiya E. Taugynbayeva, Nurlan Zh. Nauryzbayev, Anar A. Shomanova, and Alibek T. Apenov. 2025. "Function-Theoretic and Probabilistic Approaches to the Problem of Recovering Functions from Korobov Classes in the Lebesgue Metric" Mathematics 13, no. 21: 3363. https://doi.org/10.3390/math13213363
APA StyleZhubanysheva, A. Z., Taugynbayeva, G. E., Nauryzbayev, N. Z., Shomanova, A. A., & Apenov, A. T. (2025). Function-Theoretic and Probabilistic Approaches to the Problem of Recovering Functions from Korobov Classes in the Lebesgue Metric. Mathematics, 13(21), 3363. https://doi.org/10.3390/math13213363






