Control of Predator Disease Dynamics Under Prey Refuge and Harvesting: A Fuzzy Computational Modeling Approach
Abstract
1. Introduction
- Firstly, we presented a crisp mathematical model that includes harvesting with diseases in the predator population and prey refuge.
- The crisp model is extended to the fuzzified model.
- The fuzzified model is then converted into a defuzzified model using the graded mean integrated value technique [49].
- Local stability analysis and bifurcation analysis is carried out in the research. In addition, reproduction numbers are proposed to analyze the dynamics of the system.
- Finally, extensive numerical simulations are carried out to investigate the dynamics of the system.
2. Models and Analysis
2.1. Basic Model
- The prey population exhibits a logistic growth pattern in the absence of predators. This growth is constrained by a carrying capacity and characterized by an inherent growth rate. The growth rate of the prey population declines as it approaches its carrying capacity.
- The disease is transmitted through direct contact between individuals. Specifically, the disease only affects the predator population and has no impact on the prey population.
- In this model, we assume that prey are less likely to be captured by predators as the prey population takes refuge and becomes inaccessible to the predators. Here, is the fraction of prey that is in refuge.
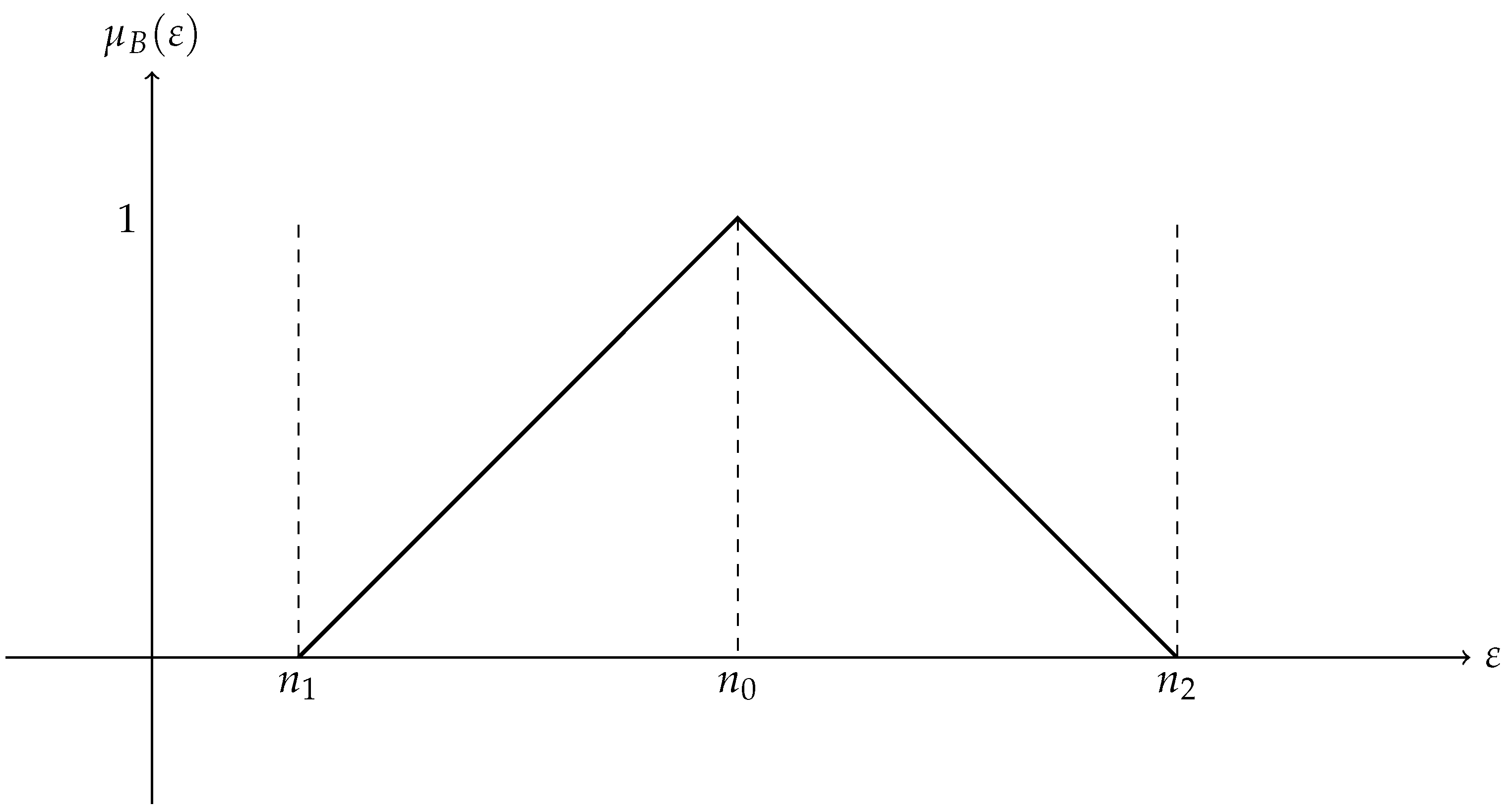
2.2. Fuzzy Model
2.3. Defuzzified Model
2.4. Basic Model Analysis
2.4.1. Equilibria
2.4.2. Biological Significance of Reproduction Numbers
2.4.3. Investigation the Stability and Existence of Equilibrium Points
- 1.
- ,
- 2.
- ,
- 3.
- < ,
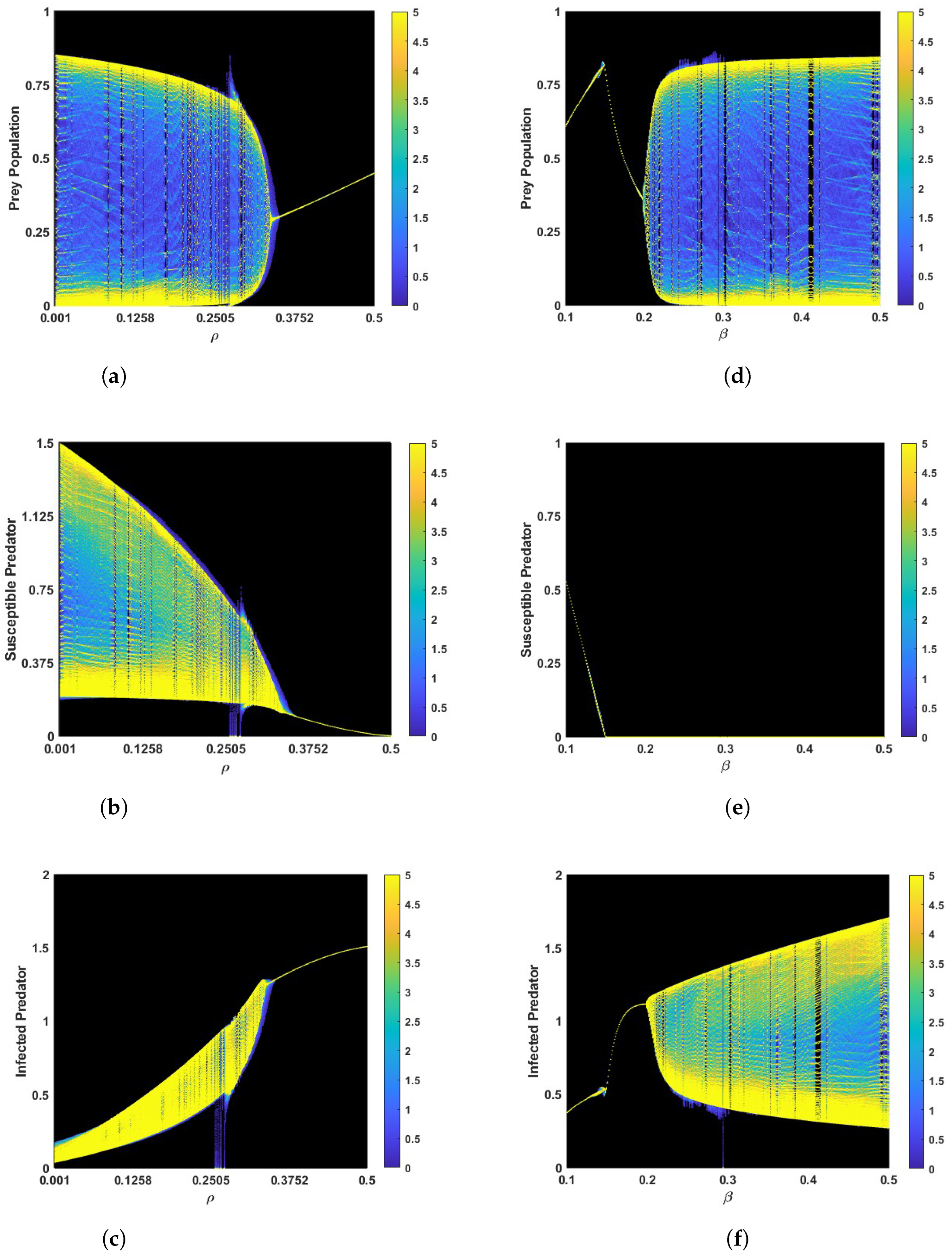
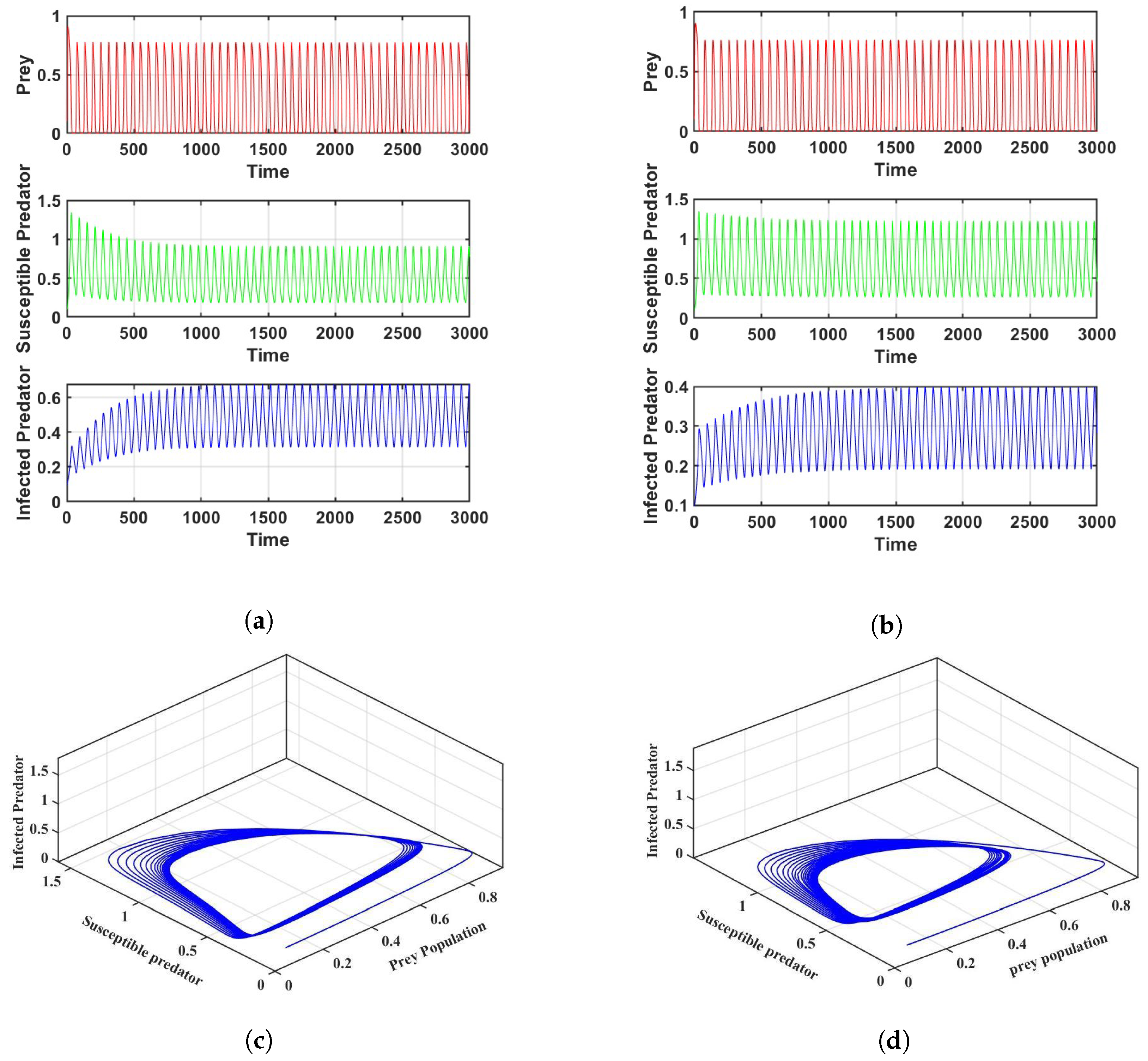
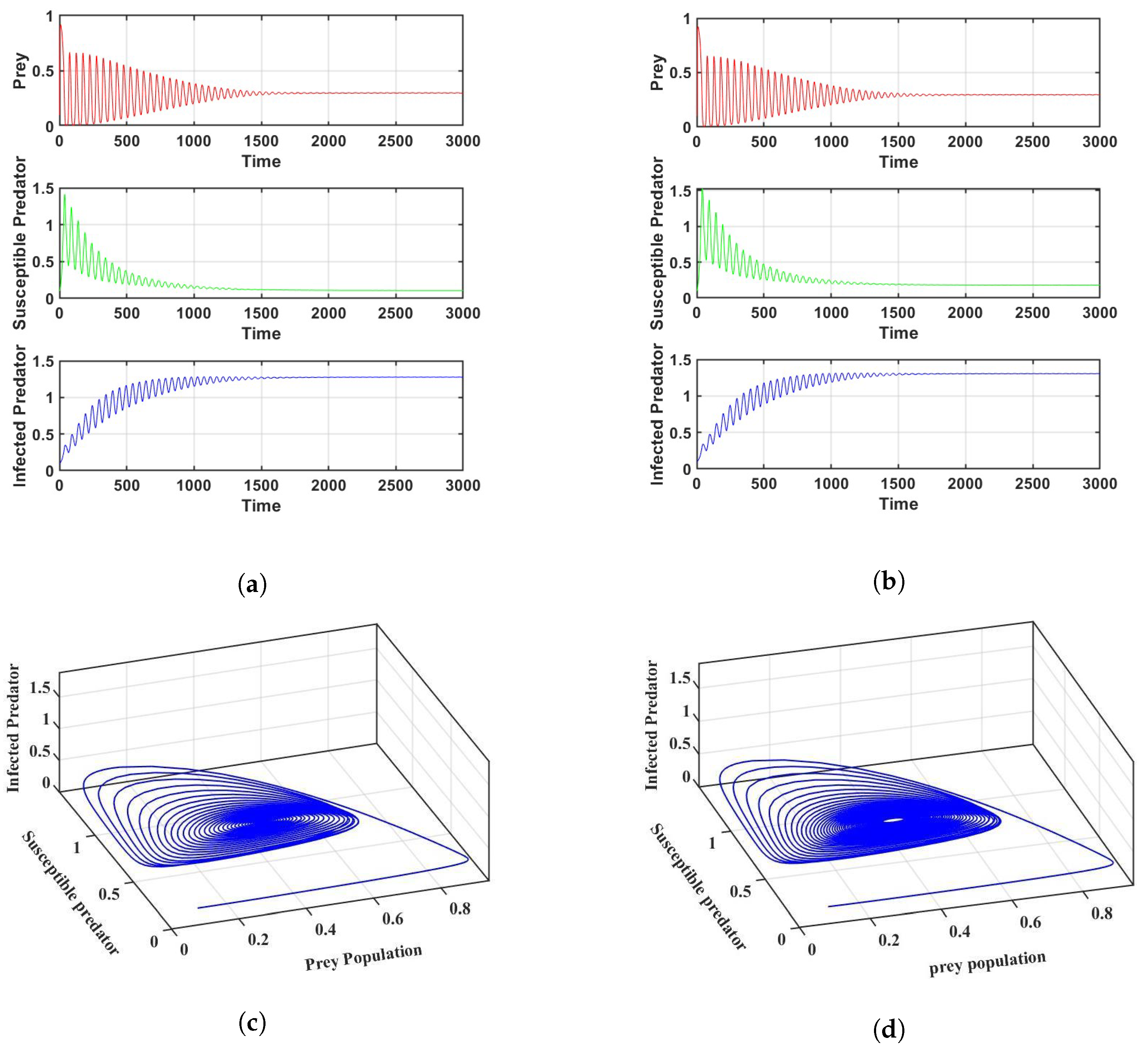
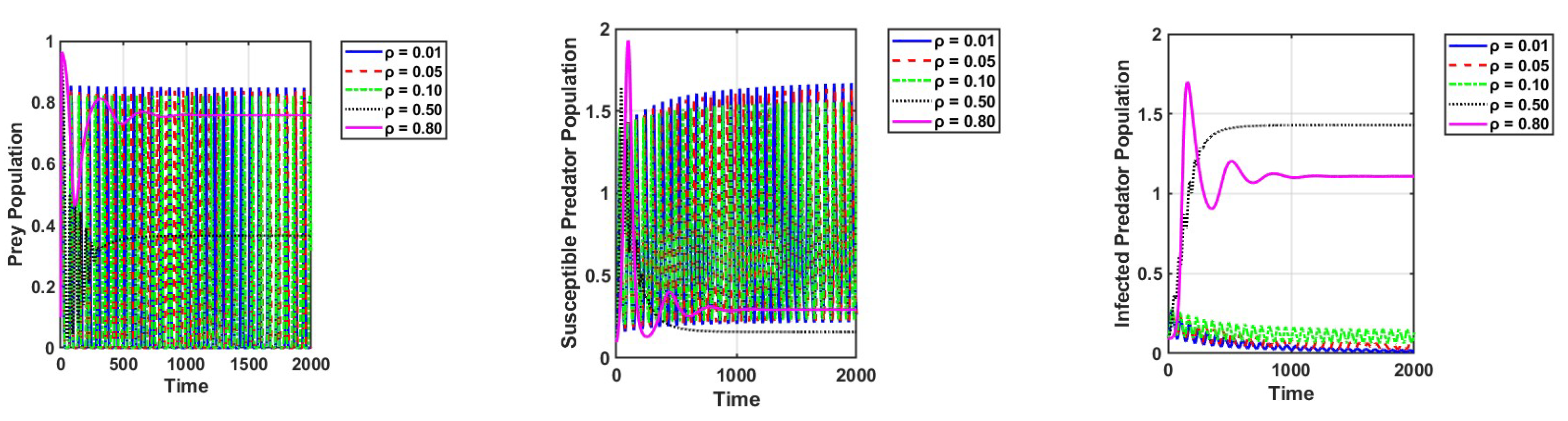
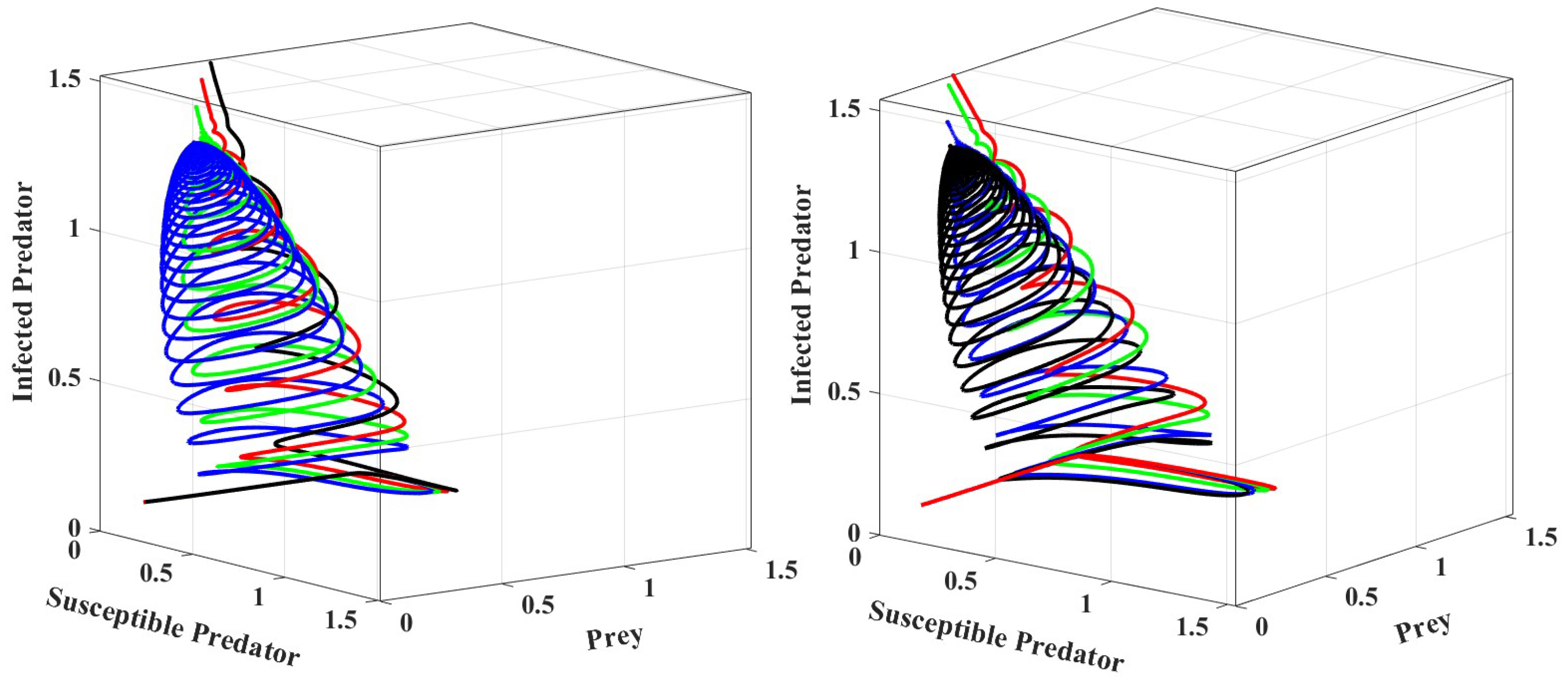
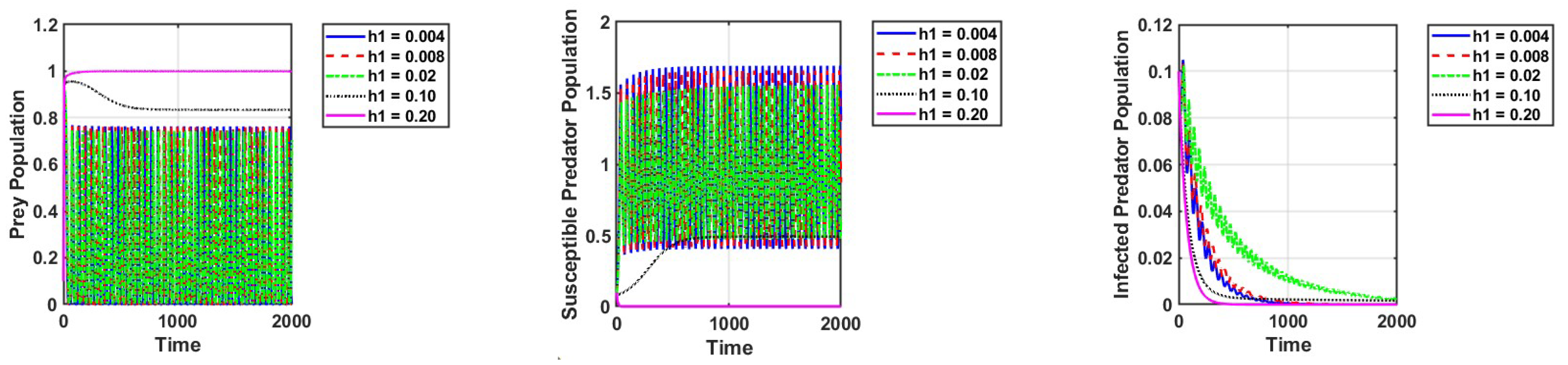
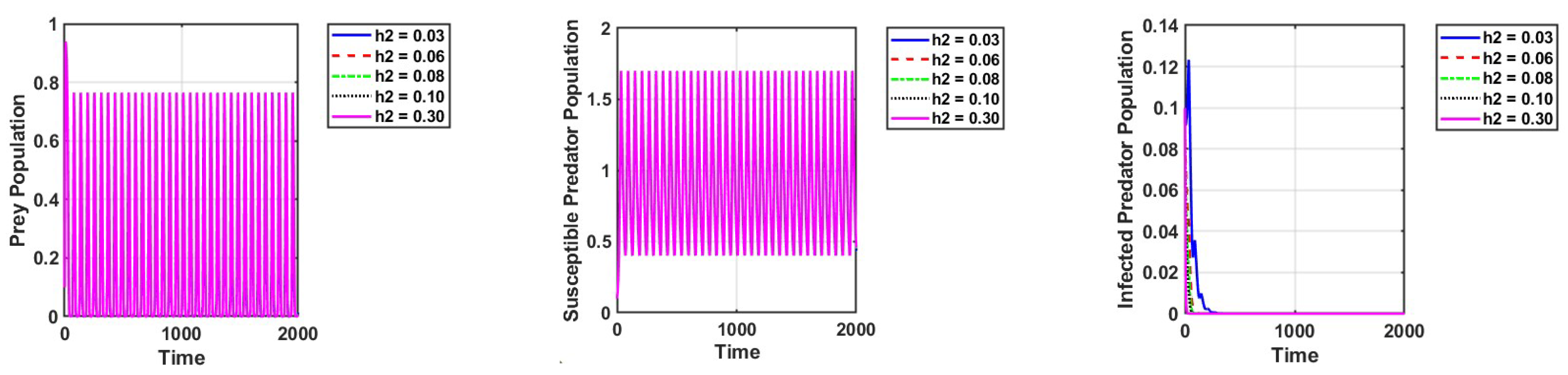
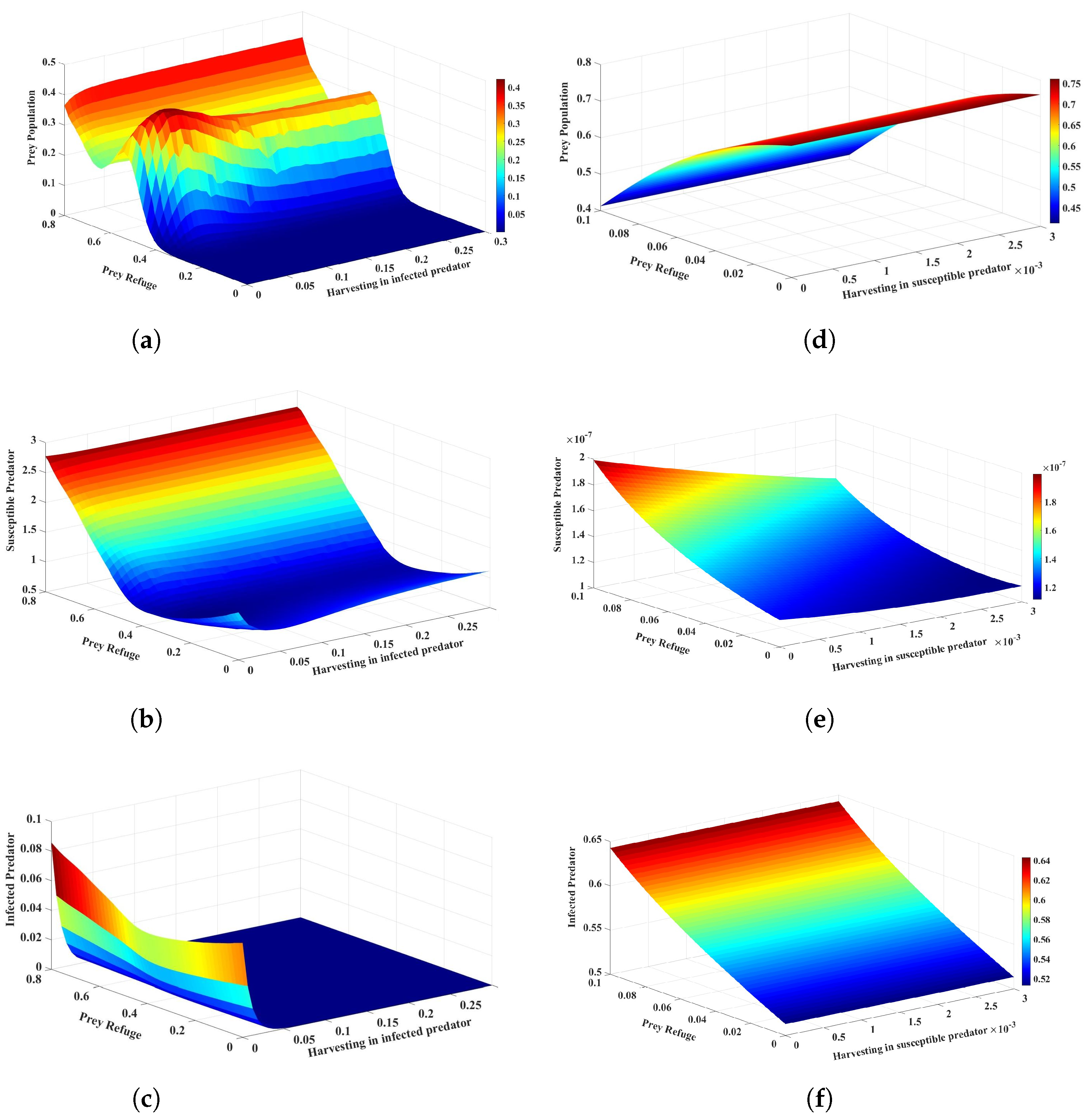
3. Numerical Simulations
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Stability Analysis of Equilibrium Points
References
- Sintunavarat, W.; Turab, A. Mathematical analysis of an extended SEIR model of COVID-19 using the ABC-fractional operator. Math. Comput. Simul. 2022, 198, 65–84. [Google Scholar] [CrossRef]
- Turab, A.; Shafqat, R.; Muhammad, S.; Shuaib, M.; Khan, M.F.; Kamal, M. Predictive modeling of hepatitis B viral dynamics: A caputo derivative-based approach using artificial neural networks. Sci. Rep. 2024, 14, 21853. [Google Scholar] [CrossRef]
- Paseka, R.E.; White, L.A.; de Waal, D.B.V.; Strauss, A.T.; González, A.L.; Everett, R.A.; Peace, A.; Seabloom, E.W.; Frenken, T.; Borer, E.T. Disease-mediated ecosystem services: Pathogens, plants, and people. Trends Ecol. Evol. 2020, 35, 731–743. [Google Scholar] [CrossRef] [PubMed]
- Keesing, F.; Belden, L.K.; Daszak, P.; Dobson, A.; Harvell, C.D.; Holt, R.D.; Hudson, P.; Jolles, A.; Jones, K.E.; Mitchell, C.E.; et al. Impacts of biodiversity on the emergence and transmission of infectious diseases. Nature 2010, 468, 647–652. [Google Scholar] [CrossRef] [PubMed]
- Anderson, R.M.; May, R.M. The invasion, persistence and spread of infectious diseases within animal and plant communities. Philos. Trans. R. Soc. Lond. Biol. Sci. 1986, 314, 533–570. [Google Scholar] [CrossRef]
- Lotka, A.J. Elements of Physical Biology; Williams and Wilkins: Baltimore, MD, USA, 1925. [Google Scholar] [CrossRef]
- Volterra, V. Fluctuations in the abundance of a species considered mathematically. Nature 1927, 119, 12–13. [Google Scholar] [CrossRef]
- Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. 1927, 115, 700–721. [Google Scholar] [CrossRef]
- Zhang, H.; Xu, G.J.; Sun, H. Biological control of a predator–prey system through provision of an infected predator. Int. J. Biomath. 2018, 11, 1850105. [Google Scholar] [CrossRef]
- Xiang, A.; Wang, L. Boundedness and stabilization in a predator–prey model with prey-taxis and disease in predator species. J. Math. Anal. Appl. 2023, 522, 126953. [Google Scholar] [CrossRef]
- Richards, R.L.; Elderd, B.D.; Duffy, M.A. Unhealthy herds and the predator–spreader: Understanding when predation increases disease incidence and prevalence. Ecol. Evol. 2023, 13, e9918. [Google Scholar] [CrossRef]
- Wilmers, C.C.; Post, E.; Peterson, R.O.; Vucetich, J.A. Predator disease out-break modulates top-down, bottom-up and climatic effects on herbivore population dynamics. Ecol. Lett. 2006, 9, 383–389. [Google Scholar] [CrossRef] [PubMed]
- Gulland, F.M.D. The impact of infectious diseases on wild animal populations: A review. Ecol. Infect. Dis. Nat. Popul. 1995, 1, 20–51. [Google Scholar] [CrossRef]
- Collyer, B.S.; Anderson, R.M. Probability distributions of helminth parasite burdens within the human host population following repeated rounds of mass drug administration and their impact on the transmission breakpoint. J. R. Soc. Interface 2021, 18, 20210200. [Google Scholar] [CrossRef]
- Byers, J.E. Marine parasites and disease in the era of global climate change. Annu. Rev. Mar. Sci. 2021, 13, 397–420. [Google Scholar] [CrossRef]
- Sapp, S.G.H.; Rascoe, L.N.; Wilkins, P.P.; Handali, S.; Gray, E.B.; Eberhard, M.; Woodhall, D.M.; Montgomery, S.P.; Bailey, K.L.; Lankau, E.W.; et al. Baylisascaris procyonis roundworm seroprevalence among wildlife rehabilitators, United States and Canada, 2012–2015. Emerg. Infect. Dis. 2016, 22, 2128. [Google Scholar] [CrossRef]
- Bauer, C. Baylisascariosis—Infections of animals and humans with ‘unusual’ roundworms. Vet. Parasitol. 2013, 193, 404–412. [Google Scholar] [CrossRef]
- Flegr, J.; Prandota, J.; Sovičková, M.; Israili, Z.H. Toxoplasmosis–a global threat. Correlation of latent toxoplasmosis with specific disease burden in a set of 88 countries. PLoS ONE 2014, 9, e90203. [Google Scholar] [CrossRef]
- McNair, J.N. The effects of refuges on predator-prey interactions: A reconsideration. Theor. Popul. Biol. 1986, 29, 38–63. [Google Scholar] [CrossRef]
- Gilliam, J.F.; Fraser, D.F. Habitat selection under predation hazard: Test of a model with foraging minnows. Ecology 1987, 68, 1856–1862. [Google Scholar] [CrossRef]
- Sagrario, G.; Ángeles, M.A.D.L.; Balseiro, E.; Ituarte, R.; Spivak, E. Macrophytes as refuge or risky area for zooplankton: A balance set by littoral predacious macroinvertebrates. Freshw. Biol. 2009, 54, 1042–1053. [Google Scholar] [CrossRef]
- Chen, W.C.; Yu, H.G.; Dai, C.J.; Guo, Q.; Liu, H.; Zhao, M. Stability and bifurcation in a predator–prey model with prey refuge. J. Biol. Syst. 2023, 31, 417–435. [Google Scholar] [CrossRef]
- Chatterjee, A.; Abbasi, M.A.; Venturino, E.; Zhen, J.; Haque, M. A predator–prey model with prey refuge: Under a stochastic and deterministic environment. Nonlinear Dyn. 2024, 112, 13667–13693. [Google Scholar] [CrossRef]
- Turab, A.; Sintunavarat, W. On the solutions of the two preys and one predator type model approached by the fixed point theory. Sādhanā 2020, 45, 211. [Google Scholar] [CrossRef]
- Turab, A.; Sintunavarat, W. On a solution of the probabilistic predator–prey model approached by the fixed point methods. J. Fixed Point Theory Appl. 2020, 22, 64. [Google Scholar] [CrossRef]
- Sharma, S.; Samanta, G.P. A Leslie–Gower predator–prey model with disease in prey incorporating a prey refuge. Chaos Solitons Fractals 2015, 70, 69–84. [Google Scholar] [CrossRef]
- Belew, B.; Yiblet, Y. Dynamical analysis of a Modified Leslie–Gower Predator-prey model with disease in prey incorporating a prey refuge and treatment. Int. J. Biomath. 2024, 21, 2450051. [Google Scholar] [CrossRef]
- Pradeep, M.S.; Nandha, G.T.; Sibabalan, M.; Yasotha, A. Bifurcation and Dynamic Analyses of a Diseased Predator-prey Model With Prey Refuge. Int. J. Appl. Comput. Math. 2023. [Google Scholar] [CrossRef]
- Lazaar, O.; Serhani, M. Stability and optimal control of a prey–predator model with prey refuge and prey infection. Int. J. Dyn. Control 2023, 11, 1934–1951. [Google Scholar] [CrossRef]
- Khan, M.; Sen, P.; Samanta, S. Stability and bifurcation analysis of an eco-epidemiological model with prey refuge. Nonlinear Stud. 2024, 31, 183–209. [Google Scholar] [CrossRef]
- Chauhan, R.P.; Singh, R.; Kumar, A.; Thakur, N.K. Role of prey refuge and fear level in fractional prey–predator model with anti-predator. J. Comput. Sci. 2024, 81, 102385. [Google Scholar] [CrossRef]
- Clark, C.W. Mathematical models in the Economics of Renewable Resources. SIAM Rev. 1979, 21, 81–99. [Google Scholar] [CrossRef]
- Hannesson, R. Optimal harvesting of ecologically interdependent fish species. J. Environ. Econ. Manag. 1983, 10, 329–345. [Google Scholar] [CrossRef]
- Ragozin, D.L.; Brown, G., Jr. Harvest policies and nonmarket valuation in a predator—Prey system. J. Environ. Econ. Manag. 1985, 12, 155–168. [Google Scholar] [CrossRef]
- Meng, X.Y.; Qin, N.N.; Huo, H.F. Dynamics analysis of a predator–prey system with harvesting prey and disease in prey species. J. Biol. Dyn. 2018, 12, 342–374. [Google Scholar] [CrossRef] [PubMed]
- Das, K.P. A study of harvesting in a predator–prey model with disease in both populations. Math. Methods Appl. Sci. 2016, 39, 2853–2870. [Google Scholar] [CrossRef]
- Jana, S.; Guria, S.; Das, U.; Kar, T.K.; Ghorai, A. Effect of harvesting and infection on predator in a prey–predator system. Nonlinear Dyn. 2015, 81, 917–930. [Google Scholar] [CrossRef]
- Themairi, A.A.; Alqudah, M.A. Predator-prey model of Holling-type II with harvesting and predator in disease. Ital. J. Pure Appl. Math. 2020, 43, 744–753. [Google Scholar]
- Das, D.K.; Das, K.; Kar, T.K. Dynamical behaviour of infected predator–prey eco-epidemics with harvesting effort. Int. J. Appl. Comput. Math. 2021, 7, 1–27. [Google Scholar] [CrossRef]
- Zadeh, L.A. The role of fuzzy logic in modeling, identification and control. In Fuzzy Sets, Fuzzy Logic, and Fuzzy Systems: Selected Papers; World Scientific: Waltham, MA, USA, 1996; pp. 783–795. [Google Scholar] [CrossRef]
- Gonzalez, A.; Pons, O.; Vila, M.A. Dealing with uncertainty and imprecision by means of fuzzy numbers. Int. J. Approx. Reason. 1999, 21, 233–256. [Google Scholar] [CrossRef]
- Oberguggenberger, M.; Pittschmann, S. Differential equations with fuzzy parameters. Math. Comput. Model. Dyn. Syst. 1999, 5, 181–202. [Google Scholar] [CrossRef]
- Yu, X.; Yuan, S.; Zhang, T. About the optimal harvesting of a fuzzy predator–prey system: A bioeconomic model incorporating prey refuge and predator mutual interference. Nonlinear Dyn. 2018, 94, 2143–2160. [Google Scholar] [CrossRef]
- Das, S.; Mahato, P.; Mahato, S.K. Disease control prey–predator model incorporating prey refuge under fuzzy uncertainty. Model. Earth Syst. Environ. 2021, 7, 2149–2166. [Google Scholar] [CrossRef]
- Das, S.; Mahato, P.; Mahato, S.K. A prey predator model in case of disease transmission via pest in uncertain environment. Differ. Equ. Dyn. Syst. 2023, 31, 457–483. [Google Scholar] [CrossRef]
- Kumar, A.; Malik, M.; Kang, Y. Dynamics of eco-epidemiological predator-prey model in fuzzy environment. Int. J. Biomath. 2025, 2550071. [Google Scholar] [CrossRef]
- Kaladhar, K.; Singh, K. Stability Analysis of a TS Prey-Predator Model with Disease in both Species using Fuzzy Impulsive Control. J. Environ. Account. Manag. 2024, 12, 231–247. [Google Scholar] [CrossRef]
- Ahmad, M.Z.; Hasan, M.K. Modeling of biological populations using fuzzy differential equations. In International Journal of Modern Physics: Conference Series; World Scientific Publishing Company: Waltham, MA, USA, 2012; Volume 9, pp. 354–363. [Google Scholar] [CrossRef]
- Chiao, K.P. Ranking interval type 2 fuzzy sets using parametric graded mean integration representation. In Proceedings of the 2016 International Conference on Machine Learning and Cybernetics (ICMLC), Jeju, Republic of Korea, 10–13 July 2016; Volume 2, pp. 606–611. [Google Scholar] [CrossRef]
- Das, K.P. Proper predation and disease transmission in predator population stabilize predator–prey oscillations. Differ. Equ. Dyn. Syst. 2020, 28, 295–313. [Google Scholar] [CrossRef]
- Clark, C.W. Mathematical Bioeconomics: The Optimal Management Resources; John Wiley & Sons: Hoboken, NJ, USA, 1976. [Google Scholar]
- Hsieh, Y.H.; Hsiao, C.K. Predator–prey model with disease infection in both population. Math. Med. Biol. J. IMA 2008, 25, 247–266. [Google Scholar] [CrossRef]
- Kooi, B.W.; van Voorn, G.A.; Das, K.P. Stabilization and complex dynamics in a predator–prey model with predator suffering from an infectious disease. Ecol. Complex. 2011, 8, 113–122. [Google Scholar] [CrossRef]
- Pielou, E.C. An Introduction to Mathematical Ecology; Wiley: Hoboken, NJ, USA, 1969. [Google Scholar] [CrossRef]
- Hethcote, H.W.; Wang, W.; Han, L.; Ma, Z. A predator–prey model with infected prey. Theor. Popul. Biol. 2004, 66, 259–268. [Google Scholar] [CrossRef]
- Behringer, M.J.B.I.V.D.C.; Valentine, M.M. Commercial sponge fishery impacts on the population dynamics of sponges in the Florida Keys, FL (USA). Fish. Res. 2017, 190, 113–121. [Google Scholar] [CrossRef]
| Notations | Explanation |
|---|---|
| B | Fuzzy set |
| Membership of fuzzy set B | |
| Defuzzified value of B | |
| M(x) | Left function of B |
| N(x) | Right function of B |
| Degree of optimism |
| Crisp Parameter | Fuzzy Parameter | Defuzzified Values |
|---|---|---|
| () | ||
| () | ||
| () | ||
| () | ||
| () | ||
| () | ||
| () | ||
| () | ||
| () | ||
| () | ||
| () |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, I.; Zhang, H.; Zhang, G.; Turab, A.; Wang, L.; Tiang, J.-J. Control of Predator Disease Dynamics Under Prey Refuge and Harvesting: A Fuzzy Computational Modeling Approach. Mathematics 2025, 13, 3362. https://doi.org/10.3390/math13213362
Ali I, Zhang H, Zhang G, Turab A, Wang L, Tiang J-J. Control of Predator Disease Dynamics Under Prey Refuge and Harvesting: A Fuzzy Computational Modeling Approach. Mathematics. 2025; 13(21):3362. https://doi.org/10.3390/math13213362
Chicago/Turabian StyleAli, Israr, Hui Zhang, Guobao Zhang, Ali Turab, Li Wang, and Jun-Jiat Tiang. 2025. "Control of Predator Disease Dynamics Under Prey Refuge and Harvesting: A Fuzzy Computational Modeling Approach" Mathematics 13, no. 21: 3362. https://doi.org/10.3390/math13213362
APA StyleAli, I., Zhang, H., Zhang, G., Turab, A., Wang, L., & Tiang, J.-J. (2025). Control of Predator Disease Dynamics Under Prey Refuge and Harvesting: A Fuzzy Computational Modeling Approach. Mathematics, 13(21), 3362. https://doi.org/10.3390/math13213362







