Perfect Divisions in (P₃ ∪ P₄, P₆,Bull)-Free Graphs

Abstract

A graph G is said to be perfect if $\omega \left(H\right)=\chi \left(H\right)$ for every induced subgraph H of G, where $\omega \left(H\right)$ and $\chi \left(H\right)$ denote the clique number and the chromatic number of H. We say that a graph G admits a perfect division if its vertex set can be partitioned into two subsets A and B such that $G\left[A\right]$ is perfect and $\omega \left(G\right[B\left]\right)<\omega \left(G\right)$. If every induced subgraph of G admits a perfect division, then G is called perfectly divisible. A graph $P_3\cup P_4$ is the disjoint union of paths $P_3$ and $P_4$. A bull refers to the graph consisting of a triangle with two disjoint pendant edges. A homogeneous set X is a proper subset of $V\left(G\right)$ with at least two vertices such that every vertex in $V\left(G\right)\setminus X$ is either complete or anticomplete to X. In this paper, we prove that every ($P_3\cup P_4,P_6$, bull)-free graph G with $\omega \left(G\right)\ge 3$ admits a perfect division, provided that G contains no homogeneous set. Moreover, we establish that this clique number condition is tight by presenting a counterexample with clique number of exactly 2.

1. Introduction

All graphs considered in this paper are finite and simple. Let G be a graph with vertex set $V\left(G\right)$ and edge set $E\left(G\right)$. Two vertices $u,v\in V\left(G\right)$ are adjacent if and only if $uv\in E\left(G\right)$. The degree of a vertex v, denoted by $d\left(v\right)$, is the number of vertices adjacent to v. The complement of G, denoted by $G^c$, is the graph on the same vertex set $V\left(G\right)$ such that $uv\in E\left(G^c\right)$ if and only if $uv\notin E\left(G\right)$.

Given two graphs H and G, we say that H is an induced subgraph of G if $V\left(H\right)\subseteq V\left(G\right)$ and, for any vertices $u,v\in V\left(H\right)$, the edge $uv\in E\left(H\right)$ if and only if $uv\in E\left(G\right)$. If G has an induced subgraph isomorphic to H, we say that G contains H; otherwise, G is said to be H-free. For a family of graphs $\mathcal{H}=\{H_1,H_2,\cdots \}$, the graph G is called $\left(\mathcal{H}\right)$-free if G is H-free for every $H\in \mathcal{H}$. For a subset $X\subseteq V\left(G\right)$, we write $G\left[X\right]$ to denote the subgraph of G induced by X.

For a positive integer k, let $P_k$ and $C_k$ denote the path and the cycle on k vertices, respectively. A path in a graph is a sequence of distinct vertices $p_1–p_2–\cdots –p_k$ such that $p_i$ is adjacent to $p_j$ if and only if $|i-j|=1$. Correspondingly, a cycle is a sequence of distinct vertices $c_1–c_2–\cdots –c_k–c_1$ such that $c_i$ is adjacent to $c_j$ if and only if $|i-j|\in \{1,k-1\}$. A hole is defined as an induced cycle of length at least 4. A hole is odd if its length is odd, and even otherwise. An antihole is an induced subgraph isomorphic to the complement of a cycle graph $C_k$ for some $k\ge 4$. It is odd or even according to the parity of k.

For two vertex-disjoint graphs $G_1$ and $G_2$, their union, denoted $G_1\cup G_2$, is the graph with vertex set $V\left(G_1\right)\cup V\left(G_2\right)$ and edge set $E\left(G_1\right)\cup E\left(G_2\right)$. An example is the graph $P_3\cup P_4$, illustrated in Figure 1. The bull (see Figure 1) is defined as the graph with vertex set $\{x_1,x_2,x_3,y,z\}$ and edge set $\{x_1{x}_2,x_1{x}_3,x_2{x}_3,x_{1}y,x_{2}z\}$. It consists of a triangle with two disjoint pendant edges.

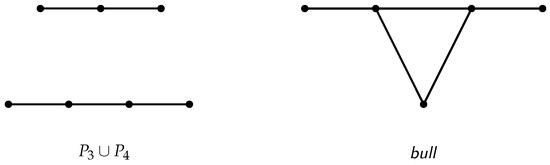
Figure 1. a $P_3\cup P_4$ and a bull.

Let A and B be two disjoint vertex subsets of a graph. We say that A is complete to B if every vertex in A is adjacent to all vertices in B. Conversely, A is anticomplete to B if there are no edges between A and B. A set $X\subseteq V\left(G\right)$ is said to be a homogeneous set if $2\le \left|X\right|<\left|V\right(G\left)\right|$ and every vertex in $V\left(G\right)\setminus X$ is either complete or anticomplete to X.

A stable set is a subset of vertices that are pairwise-nonadjacent. A clique $K_n$ is a graph on n vertices in which every pair of distinct vertices is adjacent. The clique number of G, denoted by $\omega \left(G\right)$, is the size of a largest clique in G. A graph is k-colorable if its vertices can be colored with k colors such that no two adjacent vertices share the same color. The chromatic number $\chi \left(G\right)$ is the smallest k such that G is k-colorable. It is well known that $\chi \left(G\right)\ge \omega \left(G\right)$. For a vertex set $X\subseteq V\left(G\right)$, we often use the shorthand $\chi \left(X\right)$ to denote $\chi \left(G\right[X\left]\right)$ and $\omega \left(X\right)$ for $\omega \left(G\right[X\left]\right)$.

A graph G is perfect if $\chi \left(H\right)=\omega \left(H\right)$ for every induced subgraph H of G. The celebrated Strong Perfect Graph Theorem [1] establishes that a graph is perfect if and only if it contains no odd hole and no odd antihole. As a natural extension of perfect graphs, Gyárfás [2,3] introduced the concept of $\chi$-boundedness. A class of graphs $\mathcal{G}$ is χ-bounded if there exists a function f such that $\chi \left(G\right)\le f\left(\omega \right(G\left)\right)$ for every $G\in \mathcal{G}$; such a function f is called a binding function. Clearly, the class of perfect graphs is $\chi$-bounded with $f\left(x\right)=x$. We refer the interested readers to [4,5,6] for more results and problems regarding $\chi$-boundedness.

In 2018, Hoàng [7] proposed the concept of perfect divisibility. A graph G is said to admit a perfect division if its vertex set can be partitioned into two sets A and B such that $G\left[A\right]$ is perfect and $\omega \left(G\right[B\left]\right)<\omega \left(G\right)$. We say that G is perfectly divisible if every induced subgraph of G admits a perfect division. Clearly, every perfect graph is perfectly divisible. As observed by Chudnovsky and Sivaraman [8], perfect divisibility implies a quadratic binding function, $\chi \left(G\right)\le \left({\displaystyle \genfrac{}{}{0pt}{}{\omega \left(G\right)+1}{2}}\right)$, which can be verified by a straightforward inductive argument.

Proposition 1

([8]). If G is a perfectly divisible graph, then $\chi \left(G\right)\le \left({\displaystyle \genfrac{}{}{0pt}{}{\omega \left(G\right)+1}{2}}\right)$.

Proof. 

We proceed by induction on $\omega \left(G\right)$. Let $X\subseteq V\left(G\right)$. Since G is a perfectly divisible graph, suppose that $G\left[X\right]$ is perfect and $\omega (G\setminus X)<\omega \left(G\right)$. Note that $G\setminus X$ is also perfectly divisible. By the inductive hypothesis, it follows that

$$\chi \left(G\right)\le \chi \left(X\right)+\chi (G\setminus X)\le \omega \left(X\right)+\left({\displaystyle \genfrac{}{}{0pt}{}{\omega (G\setminus X)+1}{2}}\right)\le \omega \left(G\right)+\left({\displaystyle \genfrac{}{}{0pt}{}{\omega \left(G\right)}{2}}\right)=\left({\displaystyle \genfrac{}{}{0pt}{}{\omega \left(G\right)+1}{2}}\right).$$

This completes the inductive step and the proof. □

There has been considerable recent interest in perfect divisibility. In [7,8,9,10,11,12,13], several classes of graphs have been proved to be perfectly divisible. For instance, Hoàng [7] proved that (banner, odd hole)-free graphs are perfectly divisible and proposed the following conjecture.

Conjecture 1

([7]). All odd hole-free graphs are perfectly divisible.

In [12], it is noted that Karthick, Kaufmann, and Sivaraman also posed a conjecture regarding fork-free graphs, which remains open. They [12] proved that the conjecture is true on (fork, F)-free graphs when $F\in \{P_6,\mathrm{co}\text{-}\mathrm{dart}, \mathrm{bull}\}$. They also showed that the classes of $(\mathrm{fork},F)$-free graphs, when $F\in \left\{\mathrm{dart},\mathrm{banner},\mathrm{co}\text{-}\mathrm{cricket}\right\}$, are either claw-free or perfectly divisible.

Conjecture 2

([12]). The class of fork-free graphs is perfectly divisible.

Chudnovsky and Sivaraman [8,14] obtained some structural property about bull-free graphs and established that all (odd hole, bull)-free graphs and $(P_5,\mathrm{bull})$-free graphs are perfect divisible. More recently, Deng and Chang [9] showed that every $(P_2\cup P_3,\mathrm{bull})$-free graph G with $\omega \left(G\right)\ge 3$ has a perfect division, provided that G contains no homogeneous set.

To date, most investigations into perfect divisibility have focused on graph classes defined by forbidding small induced subgraphs on 4 or 5 vertices. In this paper, we generalize the result of Deng and Chang [9] by proving that every $(P_3\cup P_4,P_6,\mathrm{bull})$-free graph G with $\omega \left(G\right)\ge 3$ admits a perfect division, under the same condition that G has no homogeneous set.

The study of perfect divisions in $(P_3\cup P_4,P_6,\mathrm{bull})$-free graphs is motivated by its algorithmic and structural implications. The existence of such a division provides a recursive framework for designing efficient algorithms for problems like graph coloring, where the problem can be decomposed into independent subproblems over structurally simpler components. Moreover, establishing perfect divisibility for graph classes defined by forbidden induced subgraphs represents a significant step in the systematic characterization of hereditary graph properties.

Theorem 1.

If G is a $(P_3\cup P_4,P_6,\mathit{bull})$-free graph with $\omega \left(G\right)\ge 3$, then either G contains a homogeneous set or G has a perfect division.

2. Notations and Technical Lemmas

For an induced subgraph H of a graph G, a vertex $x\in V\left(G\right)\setminus V\left(H\right)$ is called a center for H if it is complete to $V\left(H\right)$. Similarly, if x is anticomplete to $V\left(H\right)$, it is referred to as an anticenter for H.

For any subset $X\subseteq V\left(G\right)$, define $M_G\left(X\right)$ as the set of vertices in $V\left(G\right)\setminus X$ that are anticomplete to X, and $N_G\left(X\right)$ as the set of vertices that have a neighbor in X. Then, $(X,N_G\left(X\right),M_G\left(X\right))$ forms a partition of $V\left(G\right)$. When $X=\left\{v\right\}$ is a singleton, we simplify the notation to $N_G\left(v\right),M_G\left(v\right)$ for convenience. Where no confusion arises, we often omit the subscript G and write $N\left(v\right),M\left(v\right),N\left(X\right)$, and $M\left(X\right)$.

For a hole $C_5=v_1–v_2–v_3–v_4–v_5–v_1$, an i-clone is a vertex adjacent to $v_{i+1},v_{i-1}$ and nonadjacent to $v_{i+2},v_{i-2}$ (the indices are mod 5). An i-star is a vertex complete to $V\left(C_5\right)\setminus v_i$ and nonadjacent to $v_i$. A vertex is called a clone if it is an i-clone for some i, and a star if it is an i-star for some i.

To prove Theorem 1, we make essential use of the following results. The Strong Perfect Graph Theorem [1] allows us to reduce the proof of Theorem 1 to two main cases. Moreover, for bull-free graphs, Chudnovsky and Safra [15] established a sufficient condition for the existence of a homogeneous set.

Theorem 2

([1], The Strong Perfect Graph Theorem). A graph is perfect if and only if it does not contain an odd hole or odd antihole.

Lemma 1

([15]). If a bull-free graph G contains an odd hole or an odd antihole with a center and an anticenter, then G contains a homogeneous set.

3. The Structure of $\mathbf{(}{\mathit{P}}_{\mathbf{3}}\cup {\mathit{P}}_{\mathbf{4}},{\mathit{P}}_{\mathbf{6}},\mathbf{Bull}\mathbf{)}$-Free Graphs

The clique number condition of Theorem 1 is tight, as a counterexample exists when $\omega \left(G\right)=2$. Indeed, the Mycielski–Grötzsch graph, illustrated in Figure 2, is $(P_3\cup P_4,P_6,\mathrm{bull})$-free, contains no homogeneous set, and satisfies $\omega \left(G\right)=2$. However, it does not admit a perfect division.

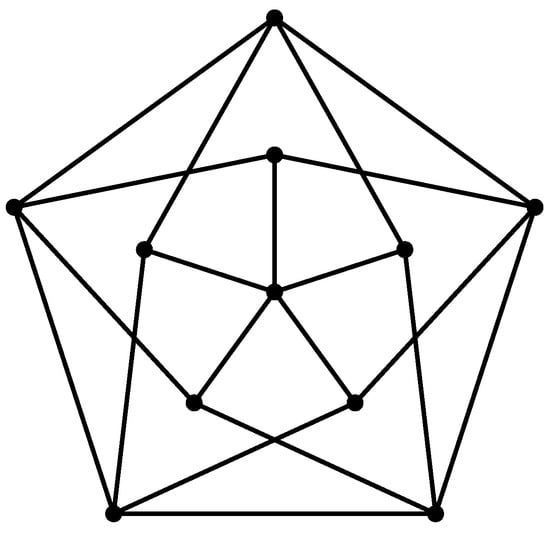
Figure 2. Mycielski–Grötzsch graph.

Proposition 2.

The Mycielski–Grötzsch graph does not admit a perfect division.

Proof. 

Let G be the Mycielski–Grötzsch graph. It is known that $\omega \left(G\right)=2$ and $\chi \left(G\right)=4$. Suppose, for contradiction, that G is perfectly divisible. Then, $V\left(G\right)$ can be partitioned into two sets A and B such that $G\left[A\right]$ is perfect and $\omega \left(G\right[B\left]\right)<2$. Since $G\left[A\right]$ is perfect, we have $\chi \left(G\right[A\left]\right)=\omega \left(G\right[A\left]\right)\le 2$. Moreover, since $\omega \left(G\right[B\left]\right)<2$, the induced subgraph $G\left[B\right]$ must be a stable set, implying $\chi \left(G\right[A\left]\right)=1$. Therefore,

$$\chi \left(G\right)\le \chi \left(G\right[A\left]\right)+\chi \left(G\right[B\left]\right)\le 2+1=3,$$

which contradicts the fact that $\chi \left(G\right)=4$. □

Consequently, we have identified a class of $(P_3\cup P_4,P_6,\mathrm{bull})$-free graphs which are not perfectly divisible. Nevertheless, requiring that $\omega \left(G\right)\ge 3$ and that G admits no homogeneous set suffices to guarantee the existence of a perfect division.

We now proceed to prove the main result of this paper.

Proof of Theorem 1.

Let G be a $(P_3\cup P_4,P_6,\mathrm{bull})$-free graph with $\omega \left(G\right)\ge 3$ and assume that G contains no homogeneous set. Then, G must be connected; otherwise, one of its components would constitute a homogeneous set. It suffices to show that there exists a vertex $v\in V\left(G\right)$ such that $G\left[M\right(v\left)\right]$ is perfect. In that case, the subgraph $G\left[\right\{v\}\cup M(v\left)\right]$ is perfect, and since $\omega \left(G\right[N\left(v\right)\left]\right)<\omega \left(G\right)$, the partition into $\left\{v\right\}\cup M\left(v\right)$ and $N\left(v\right)$ yields a perfect division of G.

Define

$$W:=\{x\in V(G)\mid N(x\left)\mathrm{contains}\mathrm{a}\mathrm{clique}\mathrm{of}\mathrm{size}\omega \right(G)-1\}.$$

Since G contains a clique of size $\omega \left(G\right)$, every vertex in this clique belongs to the set W. Therefore, W is non-empty. Choose a vertex $v\in W$ with maximum $\left|N\right(v\left)\right|$. We will show that $G\left[M\right(v\left)\right]$ is indeed perfect.

Suppose, for contradiction, that $G\left[M\right(v\left)\right]$ is not perfect. By the Strong Perfect Graph Theorem [1], it must contain an odd hole or an odd antihole. Since G is $P_6$-free, $G\left[M\right(v\left)\right]$ cannot contain a hole of length 7 or more. Noting that $C_5$ is isomorphic to its complement $C_5^c$, it follows that $G\left[M\right(v\left)\right]$ must contain either a $C_5$ or an odd antihole of length at least 7. Accordingly, the remainder of the proof is divided into two cases. The following claim will be used in both cases.

Claim 1.

For each vertex $x\in N\left(v\right)$, there exists a vertex $y\in N\left(v\right)$ such that y is nonadjacent to x.

Since $v\in W$, the neighborhood $N\left(v\right)$ contains a clique of size $\omega \left(G\right)-1$. Now, suppose for contradiction that there exists a vertex $x\in N\left(v\right)$ that is complete to $N\left(v\right)\setminus x$. Then, x also belongs to W. By the choice of v as a vertex in W with maximum degree, x cannot have any neighbor in $M\left(v\right)$; otherwise, we would have $\left|N\right(x\left)\right|>\left|N\right(v\left)\right|$. Under this condition, the set $\{v,x\}$ forms a homogeneous set, which contradicts the assumption that G contains no homogeneous set. This completes the proof of Claim 1.

Case 1.

$G\left[M\right(v\left)\right]$ contains an odd antihole H of length at least seven.

Let H be the odd antihole in $G\left[M\right(v\left)\right]$ with vertex set $V\left(H\right)=\{v_1,v_2,\cdots ,v_k\}$, where $k\ge 7$ is an odd integer. In H, two distinct vertices $v_i$ and $v_j$ are adjacent if and only if $|i-j|\not\equiv 1(modk)$.

Claim 2.

For each vertex $x\in N\left(v\right)$, $N\left(x\right)\cap V\left(H\right)$ is a stable set.

Suppose, for contradiction, that there exist two adjacent vertices in $N\left(x\right)\cap V\left(H\right)$. Without loss of generality, we may assume these are $v_1$ and $v_i$. If $i\le k-2$, then x must be adjacent to $v_{i+1}$; otherwise, the set {$x,v_1,v_i,v,v_{i+1}$} would induce a bull. Similarly, if $i+1\le k-2$, then x must be adjacent to $v_{i+2}$; otherwise, the set $x,v_1,v_{i+1},v,v_{i+2}$ would induce a bull. Repeating the argument, we conclude that x is complete to $v_i,\cdots ,v_{n-1}$.

By a symmetric argument applied in the reverse direction, x is also complete to $\{v_3,\cdots ,v_i\}$. Now, consider the induced graph $G\left[\{x,v_1,v_{k-1},v,v_2\}\right]$. To avoid inducing a bull, x must be adjacent to $v_2$. Similarly, by symmetry, x is also adjacent to $v_k$. Hence, x is a center for H, while v is an anticenter for H. By Lemma 1, this implies that G contains a homogeneous set, a contradiction. This completes the proof of Claim 2.

Let $x\in N\left(v\right)$. We proceed to consider all possible values of $\left|N\right(x)\cap V(H\left)\right|$ and show that all cases lead to a contradiction.

If $\left|N\right(x)\cap V(H\left)\right|\ge 3$, then since H is an odd antihole, it cannot contain three vertices that are nonadjacent to each other. Therefore, the set $N\left(x\right)\cap V\left(H\right)$ cannot be a stable set, contradicting Claim 2.

If $\left|N\right(x)\cap V(H\left)\right|=2$, assume without loss of generality that $N\left(x\right)\cap V\left(H\right)=\{v_1,v_2\}$. In this condition, the subgraph induced by $\{v_1,v_3,v_{k-1},x,v_k\}$ is a bull, yielding the desired contradiction.

If $\left|N\right(x)\cap V(H\left)\right|=1$, and assuming $N\left(x\right)\cap V\left(H\right)=\left\{v_1\right\}$, then the set $\{v,x,v_1,v_3,v_k,v_2\}$ induces a $P_6$, again a contradiction.

Therefore, $\left|N\right(x)\cap V(H\left)\right|=0$ for any vertex $x\in N\left(v\right)$. Now, by Claim 1, there exists a vertex $y\in N\left(v\right)$ nonadjacent to x. Since also $\left|N\right(y)\cap V(H\left)\right|=0$, the induced subgraph $G\left[\{x,v,y,v_2,v_4,v_1,v_3\}\right]$ is isomorphic to $P_3\cup P_4$, a final contradiction.

Case 2.

$G\left[M\right(v\left)\right]$ contains a $C_5$.

Let $V\left(C_5\right)=\{v_1,v_2,v_3,v_4,v_5\}$ with adjacency defined by $v_i{v}_j\in E\left(C_5\right)$ if and only if $|i-j|\equiv 1(mod5)$. Since $C_5$ is isomorphic to its complement, it is also an odd antihole. Consequently, the reasoning in the proof of Claim 2 applies directly, showing that for any vertex $x\in N\left(v\right)$, the set $N\left(x\right)\cap V\left(C_5\right)$ is a stable set.

Claim 3.

For each vertex $x\in N\left(v\right)$, we have $|N\left(x\right)\cap V\left(C_5\right)|=2$, and the two vertices in $N\left(x\right)\cap V\left(C_5\right)$ are nonadjacent.

Since $N\left(x\right)\cap V\left(C_5\right)$ is a stable set, we have $|N\left(x\right)\cap V\left(C_5\right)|\le 2$. If $|N\left(x\right)\cap V\left(C_5\right)|=1$, and assuming that $N\left(x\right)\cap V\left(C_5\right)=\left\{v_1\right\}$, then $G\left[\{v,x,v_1,v_2,v_3,v_4\}\right]$ is a $P_6$, leading to a contradiction.

If $|N\left(x\right)\cap V\left(C_5\right)|=0$, then by Claim 1, there exists a vertex $y\in N\left(v\right)$ such that y is nonadjacent to x. Note that $|N\left(y\right)\cap V\left(C_5\right)|\ne 1$, as the earlier argument (for the case $|N\left(x\right)\cap V\left(C_5\right)|=1$) applies symmetrically to y. If $|N\left(y\right)\cap V\left(C_5\right)|=0$, the induced subgraph $G\left[\{x,v,y,v_2,v_4,v_1,v_3\}\right]$ forms a $P_3\cup P_4$, a contradiction. If, instead, $|N\left(y\right)\cap V\left(C_5\right)|=2$, and assuming $N\left(y\right)\cap V\left(C_5\right)=\{v_1,v_3\}$, then $G\left[\{x,v,y,v_1,v_5,v_4\}\right]$ is a $P_6$, again a contradiction. Thus, Claim 3 is established.

By Claim 3, every vertex $x\in N\left(v\right)$ is a clone for the $C_5$, as defined in Section 2. A closer analysis of the graph’s structure yields the following.

Claim 4.

For any two adjacent vertices $x,y\in N\left(v\right)$, their neighborhood in $C_5$ coincides; that is, $N\left(x\right)\cap V\left(C_5\right)=N\left(y\right)\cap V\left(C_5\right)$.

Assume that x is a 1-clone. If y is a 2-clone, then the induced subgraph $G\left[\{v,x,y,v_3,v_5\}\right]$ forms a bull, a contradiction. If y is a 3-clone, then $G\left[\{x,y,v_2,v_3,v_5\}\right]$ is also a bull, again a contradiction. By symmetry, it follows that y cannot be a 4-clone or a 5-clone. Therefore, y must be a 1-clone, which proves Claim 4.

By the choice of vertex v, there exists a clique K of size $\omega \left(G\right)-1\ge 2$ in $G\left[N\right(v\left)\right]$. Let D denote the connected component of $G\left[N\right(v\left)\right]$ that contains K. We will show that D is precisely K.

Claim 5.

$D=K$.

If $D\ne K$, then D must contain a $P_3$. To see this, note that since D is connected and properly contains K, there exists a vertex $x\in D\setminus K$ that is not anticomplete to K. Moreover, x cannot be complete to K; otherwise, $K\cup \left\{x\right\}$ would form a clique of size $\omega \left(G\right)$ in D, a contradiction. Thus, there exists a vertex $y\in K$ adjacent to x, and a vertex $z\in K$ nonadjacent to x. Therefore, we get a $P_3=x–y–z$ in D.

By Claim 4, we may assume that every vertex in D is a 1-clone. It follows that $v_5$ and $v_2$ are both complete to D. Therefore, the neighborhoods $N\left(v_5\right)$ and $N\left(v_2\right)$ each contain a clique of size $\omega \left(G\right)-1$, which implies that $v_5,v_2\in W$. By the choice of v as a maximum degree vertex in W, we have $d\left(v\right)\ge d\left(v_5\right)$ and $d\left(v\right)\ge d\left(v_2\right)$. It follows that there exists a vertex $s\in N\left(v\right)$ such that s is nonadjacent to $v_5$, and likewise, a vertex $t\in N\left(v\right)$ nonadjacent to $v_2$.

By Claim 3, s is a clone for the $C_5$. We now examine the possible clone type of s. Note that s cannot be a 1-clone or 4-clone, since either case would require s to be adjacent to $v_5$. If s is a 5-clone, then {$x,y,z,v_1,s,v_4,v_3$} induces a $P_3\cup P_4$. If s is a 2-clone, then {$x,y,z,v_1,s,v_3,v_4$} also induces a $P_3\cup P_4$. In both situations, we obtain a contradiction. Hence, s must be a 3-clone.

By symmetry with the argument applied to $v_5$, we find that the vertex t which is nonadjacent to $v_2$ must be a 4-clone. According to Claim 4, t is nonadjacent to s. Therefore, {$x,y,z,s,v_4,v_3,t$} induces a $P_3\cup P_4$, contradicting the $P_3\cup P_4$-freeness of G. This completes the proof of Claim 5.

Let $x,y\in K$ be two distinct vertices, and consider the vertex set {$x,y$}. Since {$x,y$} is not a homogeneous set, there must exist a vertex u such that u is neither complete nor anticomplete to {$x,y$}. Without loss of generality, assume that u is adjacent to x and nonadjacent to y.

By Claim 5, we have $u\notin N\left(v\right)$, and by Claim 4, $u\notin C_5$. Therefore, $u\in M\left(v\right)\setminus C_5$. Now, suppose that $x,y$ is a 1-clone. Consider the set {$x,y,v_5,u,v_4$}. Since it does not induce a bull, u must be adjacent to at least one vertex from $\{v_5,v_4\}$. Similarly, considering {$x,y,v_2,u,v_3$}, which also cannot induce a bull, u must be adjacent to at least one vertex from $\{v_2,v_3\}$. It follows that $|N\left(u\right)\cap C_5|\ge 2$.

Claim 6.

u is not a clone for $C_5$.

Suppose that u is an i-clone. Then, the set $\{v_1,v_2,v_3,v_4,v_5,u\}\setminus v_i$ induces a hole of length 5, denoted by $C_5^{\prime }$. Note that $C_5^{\prime }$ is also contained in $M\left(v\right)$. Therefore, by Claim 4, we have $N\left(x\right)\cap V\left(C_5^{\prime }\right)=N\left(y\right)\cap V\left(C_5^{\prime }\right)$. But u is adjacent to x and nonadjacent to y, which leads to a contradiction.

Finally, we examine all possible values of $|N\left(u\right)\cap C_5|$ and show that each case leads to a contradiction.

If $|N\left(u\right)\cap C_5|=2$, then by Claim 6, the two vertices in $N\left(u\right)\cap C_5$ must be adjacent. Suppose $N\left(u\right)\cap C_5=\{v_i,v_{i+1}\}$ (indices are modulo 5), then the set {$u,v_i,v_{i+1},v_{i-1},v_{i+2}$} induces a bull, a contradiction.

If $|N\left(u\right)\cap C_5|=3$, again, by Claim 6, the three vertices in $N\left(u\right)\cap C_5$ cannot induce a $P_3$, as that would imply that u is a clone. Hence, we may assume $N\left(u\right)\cap C_5=\{v_i,v_{i+1},v_{i+3}\}$, then {$u,v_i,v_{i+1},v_{i-1},v_{i+2}$} induces a bull, a contradiction.

If $|N\left(u\right)\cap C_5|=4$, then u is a star for $C_5$. Since x and y are 1-clones, it suffices by symmetry to consider the cases where u is a 1-star, 2-star, or 3-star.

When u is a 1-star, the set {$u,x,v_5,v_1,v_3$} induces a bull. When u is a 2-star, the set {$u,v_5,v_1,v_3,y$} induces a bull. When u is a 3-star, the set {$u,v_5,v_4,v_3,y$} induces a bull. In every scenario, the resulting bull subgraph leads to a contradiction.

If $|N\left(u\right)\cap C_5|=5$, then u is a center for $C_5$ and v is an anticenter. By Lemma 1, G contains a homogeneous set, a contradiction.

As all cases lead to a contradiction, the proof of Theorem 1 is complete. □

4. Conclusions

In this paper, we have shown that every $(P_3\cup P_4,P_6,\mathrm{bull})$-free graph G with $\omega \left(G\right)\ge 3$ admits a perfect division, provided that G contains no homogeneous set. This result may be viewed as an extension of earlier work on perfect divisibility, and the condition on the clique number appears to be tight, as illustrated by the Mycielski–Grötzsch graph when $\omega \left(G\right)=2$. Our analysis relies on the structure imposed by the forbidden subgraphs and makes use of the Strong Perfect Graph Theorem, with the existence of a perfect division following from a contradiction reached in all other configurations.

It would be interesting to explore whether similar divisibility properties persist under weaker assumptions—for instance, whether the clique number condition might be relaxed in certain subfamilies of $(P_6,\mathrm{bull})$-free graphs. Another meaningful direction is to study the $\chi$-binding function for such graph classes. We hope that the structural insights gained in this study may support further investigations.