The Alternative Prioritization and Assessment System (ALPAS) Method for Environmental Performance Evaluation

Abstract

This study aims to evaluate the environmental performance of G7 countries using the Environmental Performance Index. To do this, we introduce a novel ranking multi-criteria method, Alternative Prioritization and Assessment System, for the first time in the literature. It offers a useful contribution to the multi-criteria decision-making field by tackling several ranking problems, such as low interpretability, a lack of dual evaluation metrics, and limited flexibility in data-driven scenarios. Moreover, three advanced multi-criteria decision-making weighting methods are used to assign weights to the environmental performance criteria. Therefore, the proposed Alternative Prioritization and Assessment System-based methodology evaluates the environmental performance of G7 countries in reaching sustainable development goals. The results show that the waste recovery rate is the paramount indicator, while unsafe drinking water has the least significance. Germany is ranked as the top-performing country, while Japan is ranked lowest. The key contribution of this research lies in the development and implementation of the Alternative Prioritization and Assessment System method, offering enhanced ranking stability, transparency, and dual-perspective evaluation. The use of the Environmental Performance Index further supports replicability and policy relevance. The proposed model can guide environmental policy formulation and benchmarking efforts among industrialized nations. It also provides a robust framework for cross-national sustainability comparisons in future research.

1. Introduction

The degradation of the environment has become a national concern as carbon emissions generated by industrial activities threaten sustainable development. A nation’s sustainable development is crucial, as the economy relies on the planet to supply resources such as food, materials, and energy. However, exclusively pursuing economic growth has severe repercussions for the planet and its inhabitants, especially for human lives.

Several studies have explored various solutions to address the environmental deterioration at the micro and macro levels. At the micro level, promoting consumer awareness about waste disposal practices [1], particularly plastic and electronics [2,3], can improve the environment. At the organizational level, transitioning to green supply chain operations can promote more sustainable operations [4]. Reverse logistics can connect consumers and organizations, promoting environmentally responsible consumption [5]. At the macroeconomic level, conservation of natural resources through technological innovation can enhance productivity and reduce energy consumption [6].

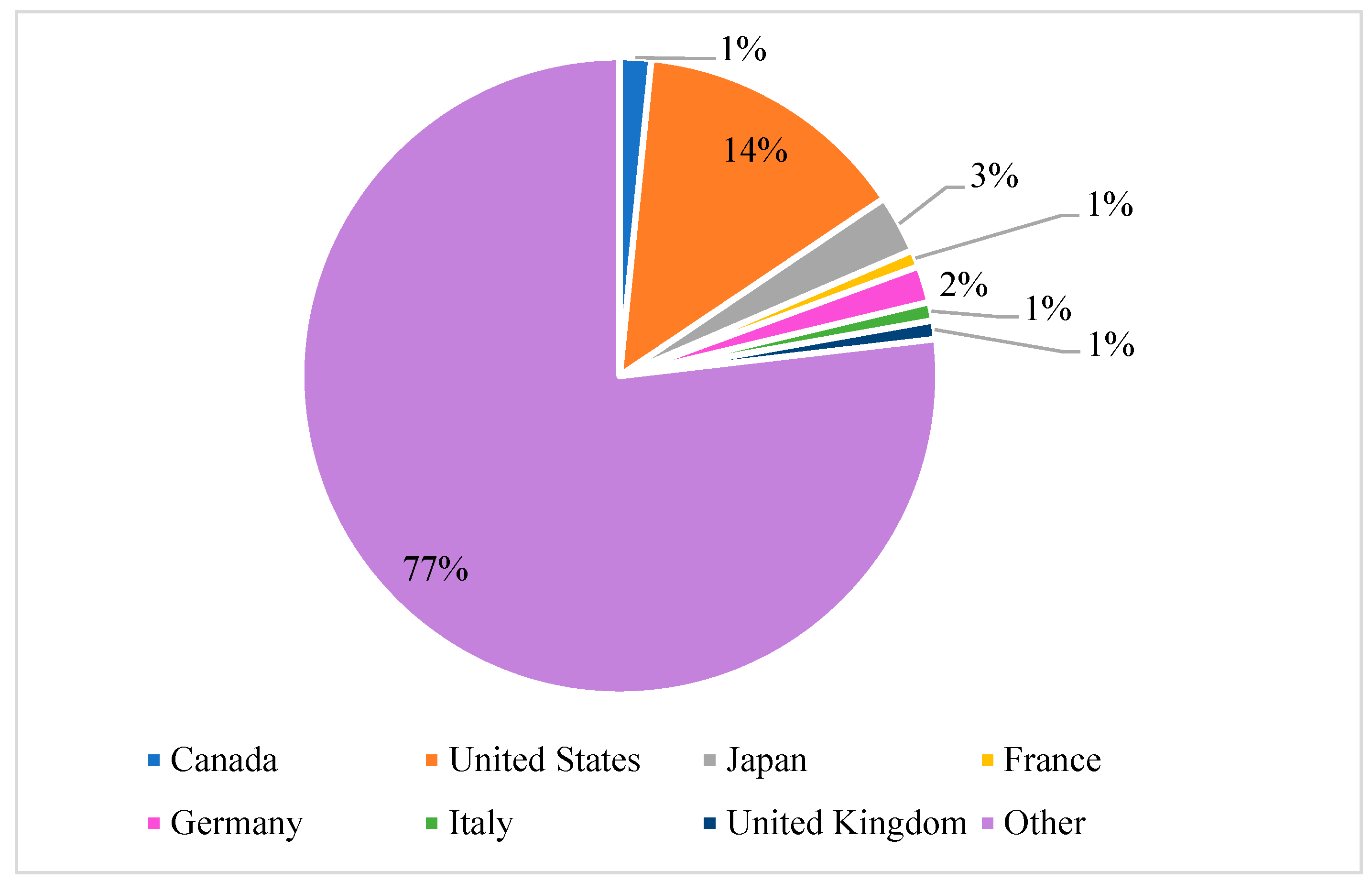
The G7 countries, comprising Canada, France, Germany, Italy, Japan, the United Kingdom, and the United States, are among the most developed in the world and are leaders in industrial development. They have exclusive environmental and economic designs that define their global impact. The G7 countries promote significant economic growth through high-volume international trade. This drives an increase in carbon emissions. The G7 countries account for 23% of total global emissions, 7619.3 MtCO₂eq, as seen in Figure 1, due to their industrial activities and consumption patterns [7]. Although the results are not precise, the G7 countries direct global environmental policies and plans through several initiatives, such as the Paris Agreement, aimed at decreasing carbon emissions. Onwe et al. [8] stated that nearly 70% of the global economy is driven to achieve net-zero emissions, in contrast to 30% when the United Kingdom assumed the presidency of the Conference of the Parties (COP). More than 80 nations have revised their Nationally Determined Contributions (NDCs), and all G7 nations have declared new NDC objectives to achieve net-zero emissions by 2050. The G7 nations, collectively representing over 50% of the global economy, have revised their 2030 objectives to align with the target of achieving net-zero emissions by 2050.

To deal with this degradation, several policies have been created. The United Nations Development Programme (UNDP) [9] stated that decreasing resource use with the implementation of circular economies will lead countries to a sustainable future as a result of low carbon release. Transition to the circular economy is expected to benefit countries economically (US$4.5 trillion), environmentally (carbon decrease), and socially (creating new jobs and job security). The United Nations Decade on Ecosystem Restoration 2021–2030 was prepared by the United Nations General Assembly to save and revive the ecosystems globally [10]. Nature Finance has become another initiative to conserve the environment [11]. It has been stated that dealing with degradation requires more effort. It needs a systemic transformation in the economy, in which the financial world must be linked to ecological targets. This shows that environmental degradation not only affects the environment and quality of life but also the economic stability of countries; therefore, there is a need for robust assessment methods.

Several studies have examined the impact of environmental deterioration due to emissions [12,13,14]. Whereas emissions illustrate the environmental impact, employing an alternative measure could provide different outcomes and more effectively elucidate the environmental impact. In recent decades, data-driven techniques have become a significant tool for assessing environmental problems and sustainability. Quantitative data were needed to identify targets presented in global sustainability initiatives, such as the Paris Conference in 2015. Countries have begun to utilize composite indices, such as the Sustainable Development Goals Index, to assess environmental issues, track trends, and analyze outcomes. The Environmental Performance Index (EPI) is the first of its kind, developed by a cooperation of Yale University, Columbia University, the World Economic Forum, and the EU’s Joint Research Centre to assess sustainability worldwide. It provides 24 criteria over two dimensions of sustainability for 180 countries. The primary motivation for using the EPI in this study is that it presents an international data set that provides information about the countries’ achievement level in the determined criteria, which shows the environmental targets set by relevant policies.

Numerous criteria in the EPI sometimes conflict with one another, leading to complexity in the analysis. To deal with this complexity, we propose an integrated multi-criteria decision-making (MCDM) methodology. MCDM techniques simplify the decision-making process in complex problems. This study introduces the Alternative Prioritization and Assessment System (ALPAS) method into the literature for the first time. To present its usefulness and applicability, an environmental performance evaluation is conducted. ALPAS addresses several ranking-related issues, including low interpretability, a lack of dual evaluation metrics, and limited adaptability to data-driven scenarios, thereby making it a valuable contribution to existing MCDM methods. Therefore, the primary goal of the research is to assess the green performance of the G7 countries with EPI data for 2024 using an integrated MCDM model that incorporates the Skewness Impact Through Distributional Evaluation (SITDE), the Logarithmic Decomposition of Criteria Importance (LODECI), the Logarithmic Percentage Change-driven Objective Weighting (LOPCOW), and the ALPAS methods. This study provides critical insights into environmental indicators, informs policy interventions aligned with global sustainability targets, and offers a methodological benchmark for future research and cross-country comparisons by focusing on the G7 countries using the latest EPI data. This model has several advantages. LOPCOW fills in the gap, assigns reasonable weights, and examines both positive and negative data [15]. The LODECI makes it easier to figure out the weights of the criteria [16]. The SITDE addresses built-in biases in symmetric assumption models and demonstrates its effectiveness with asymmetrical data distributions and skewed datasets [17].

This study makes several notable contributions. It creates a novel MCDM approach to assess the environmental performance of G7 countries. It aims to bridge the gap in the literature by introducing the novel ALPAS method for ranking alternatives, utilizing the LOPCOW, LODECI, and SITDE methodologies to calculate weights, presenting quantitative data for the environmental performance comparison of G7 countries, and developing a framework to measure environmental performance. This study aims to address the subsequent research inquiries:

RQ1: How can the environmental performance of G7 countries be effectively evaluated using EPI data with a multi-criteria decision-making approach?

RQ2: What is the relative importance of environmental indicators within the EPI framework when advanced objective weighting methods are used?

RQ3: How does the newly proposed ALPAS method compare to existing ranking methods regarding stability, transparency, and interpretability?

The remaining sections of the study are summarized. Section 2 presents a literature review. Section 3 explains MCDM methodologies. Section 4 applies the developed MCDM approach in a real case study. The Section 5 presents the results of the robustness check, and the final section provides the conclusion.

2. A Survey of MCDM Methods for Environmental Performance Evaluations

Several studies have assessed environmental performance using MCDM methods from different perspectives and employing various techniques. Cucchiella et al. [18] evaluated the environmental performance of European Union (EU) countries using the Analytic Hierarchy Process (AHP). The findings indicated that Northern European countries, such as Austria, Sweden, and Denmark, achieved the highest scores, while Poland, Estonia, and Malta scored the lowest. Hou et al. [19] analyzed the energy and environmental performances of South Asian countries using the Data Envelopment Analysis (DEA). They discovered that Bhutan does the best, followed by Nepal, and that Pakistan and India do the worst. Based on energy use, emissions, and economic–environmental efficiency, Iqbal et al. [20] ranked the countries with the most industries between 2013 and 2017. Although Poland, Australia, the US, and Japan had Strengths and Weaknesses, Mexico, Indonesia, and Brazil were the weakest countries. Using Entropy and Vlsekriterijumska Optimizacija I KOmpromisno Resenje (VIKOR) methods, Dang [21] investigated the environmental quality in countries that are part of the Organization for Economic Co-operation and Development (OECD). The results showed that Spain, Israel, Belgium, Japan, and the United States have the best environmental quality. Iceland, Australia, New Zealand, Canada, and Chile, on the other hand, were the worst countries. Lukáč et al. [22] employed the Ward Method and Euclidean Distance to group Slovakia, the Czech Republic, Hungary, and Poland with other OECD countries based on their EPI scores from 2008 to 2018. These countries were found to be in the second cluster. Matsumoto et al. [23] employed DEA to assess the environmental performance of EU countries from 2000 to 2017. The study’s results showed that Luxembourg does the best, followed by Denmark and Sweden. Nevertheless, Estonia had the worst performance, followed by the Czech Republic and Bulgaria. Sun et al. [24] employed DEA to assess the environmental performance of South Asian countries from 2001 to 2015. Bhutan, Nepal, and the Maldives performed the best, in that order. Pakistan and Sri Lanka had the worst environmental performance.

D’Adamo et al. [25] employed the AHP method to assess the sustainability performance of EU countries in environmental and energy issues. According to the research, Sweden, Finland, Denmark, and Austria performed better than other countries. However, Hungary, Romania, Cyprus, and Greece had the worst performance. Tutak et al. [26] employed Entropy and Complex Proportional Assessment (COPRAS) to assess the performance of EU countries in addressing energy and climate issues from 2009 to 2018. The results showed that Sweden and France performed the best, while Bulgaria and Cyprus performed the worst. Chen et al. [27] employed DEA to assess the environmental performance of 30 Chinese regions from the perspectives of efficiency and productivity. The results indicated that the eastern region is more effective at protecting the environment than the central and western regions. Gökgöz and Yalçın [28] compared the sustainability performance of G20 countries from energy and environmental perspectives between 2018 and 2021 using MCDM methods. The Criteria Importance Through Intercriteria Correlation (CRITIC) technique was used for weight calculation, while the VIKOR and Combined Compromise Solution (CoCoSo) techniques were employed for ranking the countries. Moreover, carbon emission was found to be the most significant criterion. Additionally, Brazil and the USA were determined to have the best environmental performances, while Saudi Arabia and China were ranked as the lowest performers. Eşiyok et al. [29] assessed the environmental performance of G7 countries and Turkey between 2010 and 2020, using the Global Green Growth Index, the Entropy and CRITIC techniques to calculate criterion weights, and the Evaluation based on Distance from Average Solution (EDAS) technique to rank the countries. The results suggest that Germany has the highest performance, while Turkey has the lowest. Malah et al. [30] established criteria to evaluate the sustainability performance of Moroccan regions and identified issues in achieving sustainable development in these regions. The results showed that 45% of regions have moderate to very high performance, while the remaining have low performance.

Ahmed et al. [31] evaluated the energy and environmental performance of BRICS countries with the Weighted Product Model (WPM), Simple Additive Weighting (SAW), Ideal Distance Weighting Method (WDI), and Multiplicative Data Envelopment Analysis (MDEA). It was found that Brazil is ranked first, whereas South Africa is ranked last overall. Anselmi et al. [32] evaluated the sustainability performance of EU countries with an MCDM approach. Their results showed that Sweden performed best, followed by the Netherlands, Denmark, and Finland. Bozkurt et al. [33] employed the CRITIC, Additive Ratio Assessment (ARAS), and Measurement Alternatives and Ranking according to Compromise Solution (MARCOS) techniques to assess the sustainable performance of the Fragile Five countries (Brazil, Turkey, Indonesia, India, and South Africa) with the SDGs. It was found that the best performances are in Turkey and Indonesia, among others. However, the worst performances were found to be in India and Brazil. Ecemiş et al. [34] developed an MCDM framework utilizing the CRITIC and TOmada de Decisão Interativa e Multicritério (TODIM) techniques to evaluate the performance of Turkey and Western Balkan states regarding the European Green Deal. The results highlighted that Montenegro and Bosnia and Herzegovina achieved the best performances. Kırda and Aytekin [35] employed several MCDM techniques to determine the environmental performance of 30 industrialized countries using the third version of Python-based software. It has been found that Sweden ranked the best, while India ranked the worst. Lacko et al. [36] analyzed the environmental efficiency of countries that joined the EU in 2004 and thereafter, using DEA. It was observed that Malta, Cyprus, Estonia, and the Czech Republic are the most environmentally efficient countries, whereas Bulgaria, Romania, and Croatia are the least efficient. Ozdemir et al. [37] examined the European Green Deal performance of the EU countries using the Method based on the Removal Effects of Criteria (MEREC) and Multi-Attributive Ideal–Real Comparative Analysis (MAIRCA) methods. The study findings indicated that the Netherlands and Sweden are the best-performing countries, while Ireland and Cyprus are the worst-performing. Senir [38] ranked the Eastern European countries with Entropy, COPRAS, and Weighted Aggregated Sum Product Assessment (WASPAS) techniques based on EPI. Regarding the study results, Slovenia, Estonia, and Latvia were among the top three countries. Tan et al. [39] assessed countries using the environmental, social, and governance criteria with the Performance Contribution Analysis (PCA), Clifford algebra method, and Entropy. The results showed that Finland and Sweden did the best. Gelmez et al. [40] developed an MCDM model that employed the Standard Deviation (SD), ARAS, and WASPAS methods to assess the environmental performance of OECD countries based on 10 criteria in the EPI. The study’s results showed that Sweden and Denmark performed the best of all the OECD countries. Karadag et al. [41] used the Best–Worst Method (BWM), Entropy, and the Ratio Product Model (RPM) to make a complete MCDM framework to see how well Turkey followed the European Green Deal from 2017 to 2021. The results showed that Turkey was the most compliant in 2021 and the least compliant in 2017. The Entropy and Preference Ranking Organization Method for Enrichment Evaluation (PROMETHEE) methods were employed by Karahan et al. [42] to compare Turkey’s environmental performance with that of Eastern European countries. The study suggested that Estonia presents the highest environmental performance and Bosnia and Herzegovina the lowest. Turkey shows low performance in the sixteenth order. Ottomano Palmisano et al. [43] employed the PROMETHEE II technique to evaluate the performance of the EU on the European Green Deal. The results emphasized that Sweden performs the best and Ireland performs the worst. Bajdor and Korpysa [44] analyzed the environmental performance of countries using SD and TOPSIS. The results suggest that Finland, France, and Germany have the highest performances, and the Czech Republic, Slovakia, and Hungary have the lowest. Karahan et al. [45] evaluated the environmental performance of the Turkic Republics based on CRITIC, Standard Deviation, MEREC, TOPSIS, ARAS, and Compromise Ranking of Alternatives from Distance to Ideal Solution (CRADIS) methods. It has been found that Kazakhstan and Uzbekistan have the best performance, while Azerbaijan and Kyrgyzstan have the lowest.

Recently, Chu et al. [46], Darzi [47], Longsheng and Shah [48], Ecer et al. [49], Barua Mimbela et al. [50], Deng et al. [51], and Karki et al. [52] also employed MCDM techniques to measure environmental performance in different perspectives, such as circular economy, pharmaceutics, sustainability, waste management, and banking.

2.1. Contributions and Novelties

The main motivation of this study is to develop a robust, transparent, and policy-relevant decision model to evaluate the environmental performance of G7 countries to deal with global sustainability challenges. The leading contributions and novelties of the research are as follows.

• The study introduces a new ranking method, ALPAS, to MCDM literature.
• It integrates LOPCOW, LODECI, and SITDE, three distinct objective weighting methods, for a more robust weight calculation.
• The model is applied to evaluate the environmental performance of G7 countries based on EPI.
• The ALPAS method uniquely combines utility and power scoring in decision-making, enhancing interpretability and ranking stability.
• A comprehensive robustness check (including sensitivity analysis with Bat Algorithm and rank reversal testing) is performed to verify model consistency.
• The study provides practical policy implications and cross-country benchmarking guidance for sustainable development strategies.

2.2. Insights from Literature Survey and Research Gap

These studies present MCDM techniques that effectively solve complex problems such as environmental performance analysis. However, there are several gaps in current studies. Although several studies have evaluated the environmental performance of countries, no study has specifically focused on the G7 countries. G7 countries are among the most economically developed nations; therefore, they play a significant role in shaping policy for environmental and sustainable development worldwide. They also have advanced industrial activities and consumption levels, which contribute to higher environmental impacts. For these reasons, the environmental performance analysis of G7 countries may give directions to global policies. Analyzing their environmental performance will help us clearly understand their strengths and weaknesses. Therefore, this analysis will not only contribute to the literature but also serve as a guide for practitioners, such as policymakers. Their environmental initiatives can serve as a model for other countries.

Commonly used methodologies such as AHP, DEA, Entropy, VIKOR, COPRAS, WASPAS, and MARCOS are limited to single score ranking; therefore, they lack dual evaluation (utility and power) metrics. Entropy, CRITIC, and AHP methods are sensitive to data shifts; thus, rankings become unstable with small changes in weights or indicators.

The studies analyzing the environmental performance of EU or OECD countries focus on regional groups, but there is no comprehensive study on G7 countries using integrated weighting and ranking techniques.

The studies using MCDM methods like ARAS, COPRAS, WASPAS, and VIKOR struggle with rank reversal problems and limited interpretability for policymakers.

The motivations and advantages of the methods used in the study are listed below.

The motivations for the LOPCOW method are as follows [15]:

• Traditional methods cannot sufficiently address imbalances arising from data size.
• Failure to consider positive and negative data together can lead to unrealistic results in the weighting of attributes.

The motivations for the LODECI method are as follows [16]:

• Some MCDM methods may disregard criteria with high contrast intensity.
• Unequal or unbalanced distribution of attribute weights creates inconsistency in the decision-making process.

The motivations for the SITDE method are as follows [17]:

• Traditional methods do not take into account asymmetry (skewness) in attribute distributions.
• There is a need for a new approach that will improve decision quality in asymmetric and unbalanced data sets.

The following motivations were utilized in the development of the ALPAS method:

• Traditional MCDM methods typically focus either solely on ideal/anti-ideal references or on the aggregation of additive/multiplicative values. ALPAS, however, aims to create a more holistic decision model by using these two approaches in a balanced manner.
• Although many methods in the literature are technically robust, they do not provide a clear and practical framework for decision-makers. ALPAS was developed to offer a more transparent approach that appeals to both academics and practitioners.

The advantages of the LOPCOW method are as follows [15]:

• It produces more reliable weights by eliminating the difference arising from the size of the data.
• It offers a more balanced approach by covering both positive and negative values.

The advantages of the LODECI method are as follows [16]:

• Distributes the weights of the criteria more evenly and balanced.
• Reflects the importance of the criteria more accurately by observing the contrast intensity under all conditions.

The advantages of the SITDE method are as follows [17]:

• It improves decision quality by taking into account skewness and asymmetric data distributions.
• It provides more comprehensive and balanced decision support with a multi-threshold structure.

The advantages of the ALPAS method are as follows:

• It produces more accurate results by evaluating both ideal and anti-ideal solutions together.
• It is less sensitive to small changes in reference values.
• Less variation in results under different scenarios increases confidence in the decision-making process.
• It evaluates alternatives more comprehensively by considering both utility and power scores.
• The calculation process is more understandable, allowing decision-makers to easily interpret the results.
• The method reaches the result with fewer complex steps in practice.
• It more clearly distinguishes between alternatives with similar scores.

As can be seen, each of the methods used in the study has at least one advantage. Therefore, this paper utilizes a novel integrated MCDM framework that includes the LOPCOW, LODECI, and SITDE methodologies to determine the criteria weights and the ALPAS technique to rank alternatives based on environmental performance.

• ALPAS ensures enhanced ranking stability, unlike traditional MCDM methods, which are sensitive to data shifts or minor changes in weights.
• It uses a dual-scoring mechanism (utility and power), providing a more nuanced and balanced evaluation than single-score systems.
• Unlike ARAS, COPRAS, or WASPAS, ALPAS adaptively derive ideal and anti-ideal values from the data, improving contextual relevance.
• The method demonstrates resistance to rank reversal, a known problem in many MCDM methods.
• ALPAS offers better interpretability and transparency, making the decision-making process more logical and transparent.
• The model shows strong performance in discriminating close alternatives, essential for policy applications where minor differences matter.

3. Materials and Methods

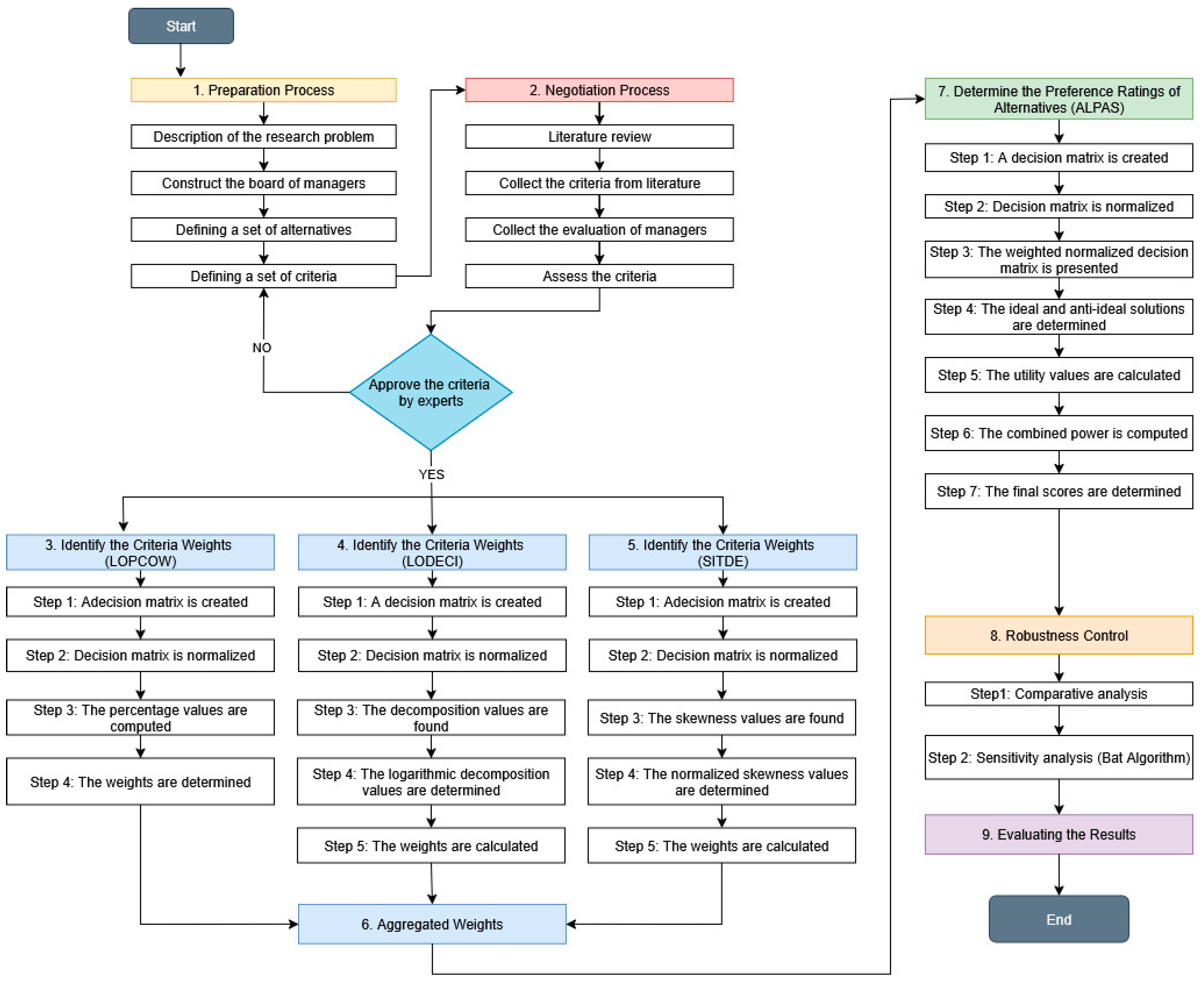
This study employs the LOPCOW, LODECI, and SITDE methodologies to determine the weights of EPI attributes while assessing the environmental performance of G7 countries using the newly developed ALPAS method. Figure 2 presents a flowchart of research methodology.

The ALPAS method presented in this paper aims to rank options by utilizing ideal and anti-ideal evaluations, along with a balanced normalization and weighting approach. ALPAS was created to address problems with traditional ranking methods, such as relying too heavily on evaluations based on distance or dominance. When there are closely valued alternatives, this can cause ranking problems or instability. One of ALPAS’s best features is that it focuses on both the usefulness and power of each option. These two factors are combined in a balanced way using equal coefficients. This two-layer evaluation makes the results more reliable and gives a more detailed picture of how well the alternatives perform. ALPAS also ensures that the steps for normalization and weighted assessment are clear and mathematically sound, which makes decisions more reliable in situations where problems are difficult to solve.

3.1. LOPCOW Method

The stages of the LOPCOW approach are defined below [15].

Stage 1-1: A decision matrix comprising options and attributes is established (Equation (1)). $b_{ij}$ is the value of the $jth$ criterion for $ith$ alternative.

$$B={\left[b_{ij}\right]}_{m\times n}, i=\mathrm{1,2},\dots ,m and j=\mathrm{1,2},\dots ,n$$

(1)

Stage 1-2: This matrix is normalized using Equations (2) and (3). $c_{ij}$ are the normalized values of $b_{ij}$.

$$c_{ij}={\displaystyle \frac{max\left(b_{ij}\right)-b_{ij}}{max\left(b_{ij}\right)-min\left(b_{ij}\right)}} if jϵNBAT$$

(2)

$$c_{ij}={\displaystyle \frac{b_{ij}-min\left(b_{ij}\right)}{max\left(b_{ij}\right)-min\left(b_{ij}\right)}} if jϵBNA$$

(3)

The NBAT and BNA are presented in Equations (2) and (3), respectively, where non-beneficial and beneficial attributes are denoted.

Stage 1-3: Calculating each attribute’s percentage values (${PV}_{ij}$) is performed as outlined in Equation (4).

$${PV}_{ij}=\left|ln\left({\displaystyle \frac{\sqrt{\frac{\sum _{i=1}^m{c}_{ij}^2}{m}}}{\sigma }}\right)·100\right|$$

(4)

where σ denotes the standard deviation and m signifies the number of options, respectively.

Stage 1-4: The weights of the attributes ($w_{jLOW}$) are computed concerning the LOPCOW method with Equation (5).

$$w_{jLOW}={\displaystyle \frac{{PV}_{ij}}{\sum _{j=1}^n{PV}_{ij}}}$$

(5)

3.2. LODECI Method

The LODECI method is an objective weighting technique, and the following steps outline its implementation [16].

Stage 2-1: The decision matrix is structured. Equation (1) illustrates the decision matrix.

Stage 2-2: The normalization of this decision matrix is achieved by applying Equations (6) and (7).

$$d_{ij}={\displaystyle \frac{min\left(b_{ij}\right)}{b_{ij}}} if jϵNBAT$$

(6)

$$d_{ij}={\displaystyle \frac{b_{ij}}{max\left(b_{ij}\right)}} if jϵBNA$$

(7)

Stage 2-3: The decomposition value (${DV}_{ij}$) is calculated using Equation (8).

$${DV}_{ij}=max\left\{\left|d_{ij}-d_{rj}\right|\right\} i\ne r$$

(8)

Stage 2-4: The logarithmic decomposition value ($L{DV}_j$) is computed with Equation (9).

$$L{DV}_j=ln\left(1+{\displaystyle \frac{{DV}_{ij}}{m}}\right)$$

(9)

Stage 2-5: The weights of the attributes ($w_{jLDC}$) are calculated according to the LODECI method with Equation (10).

$$w_{jLDC}={\displaystyle \frac{{LDV}_{ij}}{\sum _{j=1}^n{LDV}_{ij}}}$$

(10)

3.3. SITDE Method

The SITDE method is an objective weighting approach that considers the skewness values associated with the attributes. The following steps outline this method [17].

Stage 3-1: The decision matrix is established, and it is shown in Equation (1).

Stage 3-2: This decision matrix is normalized through Equations (6) and (7). Equation (7) is utilized for normalizing non-beneficial attributes, in contrast to the LODECI method, while Equation (6) is employed for normalizing beneficial attributes.

Stage 3-3: Equation (11) calculates the skewness values (${SN}_j$) for the attributes.

$${SN}_j={\displaystyle \frac{m}{(m-1)(m-2)}}\sum _{i=1}^m{\left({\displaystyle \frac{e_{ij}-{\overline{e}}_j}{{\sigma }_j}}\right)}^3$$

(11)

In Equation (11), $e_{ij}$, ${\overline{e}}_j$, and ${\sigma }_j$ denote the normalized value, the mean value, and the standard deviation of attribute $j$, respectively.

Stage 3-4: The normalized skewness for each attribute is calculated as outlined in Equation (12).

$${LSN}_j={log}_e\left|\left(\left({SN}_j+1\right)+\left(\left|min\left({SN}_j\right)\right|+1\right)\right)\right|$$

(12)

Stage 3-5: The weights of the attributes ($w_{jSDE}$) are calculated according to the SITDE method as detailed in Equation (13).

$$w_{jSDE}={\displaystyle \frac{{LSN}_j}{\sum _{j=1}^n{LSN}_j}}$$

(13)

The attribute weights derived from the LOPCOW method, the attribute weights derived from the LODECI method, and the attribute weights derived from the SITDE method are integrated using Equation (14).

$$w_{jINT}={\displaystyle \frac{1}{3}}\times \left(w_{jLOW}+w_{jLDC}+w_{jSDE}\right)$$

(14)

In Equation (14), $w_{jINT}$ presents the integrated weights of the $jth$ attribute.

3.4. ALPAS (ALternative Prioritization and Assessment System)

The steps of the ALPAS method are explained below.

Stage 4-1: The decision matrix is established (Equation (1)).

Stage 4-2: The values within the matrix will undergo normalization using Equations (15) and (16). $b_{ij}^{\prime }$ denotes normalized values of $b_{ij}$.

$$b_{ij}^{\prime }={\displaystyle \frac{b_{ij}}{max\left(b_{ij}\right)}}, if jϵBNA$$

(15)

$$b_{ij}^{\prime }={\displaystyle \frac{min\left(b_{ij}\right)}{b_{ij}}}, if jϵNBAT$$

(16)

Stage 4-3: Weighted normalized values ($y_{ij})$ are derived from Equation (17).

$$y_{ij}=w_{jINT}\times b_{ij}^{\prime }$$

(17)

Stage 4-4: The ideal and anti-ideal solutions for each attribute are determined with Equations (18) and (19).

$$I_j=max\left(y_{ij}\right) if jϵBNA, I_j=min\left(y_{ij}\right) if jϵNBAT$$

(18)

$$A{I}_j=min\left(y_{ij}\right) if jϵBNA, {AI}_j=max\left(y_{ij}\right) if jϵNBAT$$

(19)

Stage 4-5: Each option’s utility value ($S_i$) is calculated using Equation (20).

$$S_i=\sum _{j=1}^n\left({\displaystyle \frac{{(y}_{ij}+1)}{(I_j+1)}}-{\displaystyle \frac{{(AI}_j+1)}{{(y}_{ij}+1)}}\right)$$

(20)

Stage 4-6: The combined power ($P_i$) of each option is computed with Equation (21).

$$P_i=\alpha \times \sum _{j=1}^n(y_{ij}+1)+\beta \times {\left({\prod }_{j=1}^n\left(y_{ij}+1\right)\right)}^{1/n}$$

(21)

In Equation (21), $\alpha$ and $\beta$ values should be 0.5.

Stage 4-7: Each option’s final score ($G_i$) is computed with Equation (22).

$$G_i=\zeta \times S_i+\omega \times P_i$$

(22)

In Equation (22), $\zeta$ and $\omega$ values should be 0.5.

The option that received the highest final score is deemed the most excellent.

4. EPI Performance of G7 Countries

This section includes analyses of the environmental performance of G7 countries conducted using the LOPCOW, LODECI, SITDE, and ALPAS methods.

Initially, the attribute weights were determined using the LOPCOW, LODECI, and SITDE methods, which are objective weighting methods. Subsequently, the ALPAS method was employed to determine the countries’ environmental performance rankings and conduct a comparative sustainability assessment. The integration of MCDM techniques is intended to offer a more comprehensive and precise analysis of the environmental policies of the G7 countries at this stage of the study. This study considered the following attributes [53].

• CDA: Adjusted emission growth rate for carbon dioxide;
• FCL: Tree cover loss weighted by permanency;
• GTP: GHG growth rate adjusted by per capita emissions;
• HFD: Household solid fuels;
• HPE: Anthropogenic PM2.5 exposure;
• LED: Lead exposure;
• PAR: Protected area representativeness index
• RCY: Relative crop yield;
• SNM: Sustainable nitrogen management index;
• SPI: Species protection index;
• UWD: Unsafe drinking water;
• WPC: Waste generated per capita;
• WRR: Waste recovery rate;
• WWC: Wastewater collected;
• WWT: Wastewater treated.

The evaluation procedure resumed with 15 criteria, as the values of two criteria for the G7 countries were identical. Consequently, these criteria were excluded from the analysis. In the analysis, seven of the attributes (PAR, RCY, SNM, SPI, WRR, WWC, and WWT) are beneficial, whereas the other eight are associated with non-beneficial outcomes. The decision matrix is presented in

Table 1. Decision matrix.

	CDA	FCL	GTP	HFD	HPE
Canada	52.5	65.9	33.1	96.7	67
Germany	68.3	37.1	53.4	96.7	50
France	60.9	65.3	53.6	91.5	49
United Kingdom	74.3	45.6	61.6	98.8	52.1
Italy	55.9	61.3	48	79.3	31.7
Japan	63.1	76.4	52.8	86.7	42.2
United States	57.7	49.9	35.5	91.6	61.5
	LED	PAR	RCY	SNM	SPI
Canada	100	40.3	100	61.7	82.1
Germany	98.7	76.3	98.4	67.1	98.3
France	98.9	71.5	88.6	63.7	71.6
United Kingdom	99.8	60	100	56	57
Italy	83.6	55.4	70.3	41.7	57.6
Japan	100	25	89.8	50.3	58.9
United States	82.5	14.6	100	76.6	39.9
	UWD	WPC	WRR	WWC	WWT
Canada	99.7	17.6	24.4	98.3	84
Germany	100	19.7	98.9	99.3	97.3
France	87.6	23.9	75.2	100	82
United Kingdom	100	29.4	85.2	85.8	85.8
Italy	100	28.1	70.2	86.9	70
Japan	76.7	39.6	94.4	91.7	80.6
United States	100	13.3	44	78.2	67.7

Source: https://epi.yale.edu/ (accessed on 7 July 2025).

.

The weight of each attribute is determined by sequentially implementing the LOPCOW method, followed by the LODECI method, and concluding with the SITDE method, as applied to the decision matrix presented in Table 1.

Table 2. The weights of the attributes.

	${\mathit{w}}_{\mathit{j}\mathit{L}\mathit{O}\mathit{W}}$	${\mathit{w}}_{\mathit{j}\mathit{L}\mathit{D}\mathit{C}}$	${\mathit{w}}_{\mathit{j}\mathit{S}\mathit{D}\mathit{E}}$	${\mathit{w}}_{\mathit{j}\mathit{I}\mathit{N}\mathit{T}}$
CDA	0.0825	0.046	0.0722	0.0669
FCL	0.0679	0.078	0.0617	0.0692
GTP	0.0614	0.0755	0.0559	0.0643
HFD	0.0476	0.034	0.0491	0.0436
HPE	0.0688	0.0792	0.0617	0.0699
LED	0.0229	0.0356	0.0447	0.0344
PAR	0.0726	0.1152	0.0834	0.0904
RCY	0.1005	0.0531	0.0859	0.0798
SNM	0.0772	0.0669	0.0763	0.0735
SPI	0.0672	0.0848	0.0748	0.0756
UWD	0.0177	0.0445	0.0342	0.0321
WPC	0.0856	0.0941	0.072	0.0839
WRR	0.0839	0.1098	0.0857	0.0931
WWC	0.0795	0.0374	0.0734	0.0634
WWT	0.0647	0.0459	0.069	0.0599

presents the outcomes of the weighing methods and the integrated weights of the attributes.

The weights of the attributes, determined by integrating the outcomes of LOPCOW, LODECI, and SITDE, are aggregated into a unified weighting vector. This vector is then used to transform the raw decision matrix into a weighted normalized matrix, ensuring that each criterion’s relative importance is accurately reflected. The ALPAS method subsequently applies its dual-evaluation mechanism to this weighted matrix, producing composite scores that account for both utility and power relative to adaptive ideal/anti-ideal references. Thus, the ranking of the G7 countries directly reflects the optimized weighting of environmental criteria as derived from the integrated framework. Using Equation (14), attributes are ranked as follows: WRR, PAR, WPC, RCY, SPI, SNM, HPE, FCL, CDA, GTP, WWC, WWT, HFD, LED, and UWD (Table 2). Therefore, WRR is the most critical attribute, while UWD is the least critical. After determining the attribute weights, the ALPAS approach ranks the G7 countries. Equations (15) and (16) are employed to normalize the numbers presented in Table 1. To illustrate the calculations presented in Equations (15) and (16), Canada’s CDA and PAR attributes will be demonstrated, respectively.

$$b_{17}^{\prime }={\displaystyle \frac{b_{17}}{max\left(b_{ij}\right)}}={\displaystyle \frac{40.3}{76.3}}=0.5282$$

$$b_{11}^{\prime }={\displaystyle \frac{min\left(b_{ij}\right)}{b_{11}}}={\displaystyle \frac{52.5}{52.5}}=1$$

Other values are normalized identically.

Table 3. Normalized matrix.

	CDA	FCL	GTP	HFD	HPE
Canada	1	0.563	1	0.8201	0.4731
Germany	0.7687	1	0.6199	0.8201	0.634
France	0.8621	0.5681	0.6175	0.8667	0.6469
United Kingdom	0.7066	0.8136	0.5373	0.8026	0.6084
Italy	0.9392	0.6052	0.6896	1	1
Japan	0.8320	0.4856	0.6269	0.9146	0.7512
United States	0.9099	0.7435	0.9324	0.8657	0.5154
	LED	PAR	RCY	SNM	SPI
Canada	0.8250	0.5282	1	0.8055	0.8352
Germany	0.8359	1	0.9840	0.8760	1
France	0.8342	0.9371	0.8860	0.8316	0.7284
United Kingdom	0.8267	0.7864	1	0.7311	0.5799
Italy	0.9868	0.7261	0.7030	0.5444	0.5860
Japan	0.8250	0.3277	0.8980	0.6567	0.5992
United States	1	0.1913	1	1	0.4059
	UWD	WPC	WRR	WWC	WWT
Canada	0.7693	0.7557	0.2467	0.9830	0.8633
Germany	0.7670	0.6751	1	0.9930	1
France	0.8756	0.5565	0.7604	1	0.8428
United Kingdom	0.7670	0.4524	0.8615	0.8580	0.8818
Italy	0.7670	0.4733	0.7098	0.8690	0.7194
Japan	1	0.3359	0.9545	0.9170	0.8284
United States	0.7670	1	0.4449	0.7820	0.6958

presents the normalized matrix.

Equation (17) yields the weighted normalized values, whereas Equations (18) and (19) delineate the ideal and anti-ideal solutions for the criteria.

Table 4. The weighted normalized values and ideal and anti-ideal solutions.

	CDA	FCL	GTP	HFD	HPE
Canada	0.0669	0.039	0.0643	0.0357	0.0331
Germany	0.0514	0.0692	0.0398	0.0357	0.0443
France	0.0577	0.0393	0.0397	0.0378	0.0452
United Kingdom	0.0473	0.0563	0.0345	0.0350	0.0425
Italy	0.0628	0.0419	0.0443	0.0436	0.0699
Japan	0.0557	0.0336	0.0403	0.0398	0.0525
United States	0.0609	0.0515	0.0599	0.0377	0.0360
$I_j$	0.0473	0.0336	0.0345	0.0350	0.0331
${AI}_j$	0.0669	0.0692	0.0643	0.0436	0.0699
	LED	PAR	RCY	SNM	SPI
Canada	0.0284	0.0477	0.0798	0.0592	0.0631
Germany	0.0288	0.0904	0.0786	0.0644	0.0756
France	0.0287	0.0847	0.0707	0.0611	0.0551
United Kingdom	0.0284	0.0711	0.0798	0.0537	0.0438
Italy	0.0339	0.0656	0.0561	0.0400	0.0443
Japan	0.0284	0.0296	0.0717	0.0482	0.0453
United States	0.0344	0.0173	0.0798	0.0735	0.0307
$I_j$	0.0284	0.0904	0.0798	0.0735	0.0756
${AI}_j$	0.0344	0.0173	0.0561	0.0400	0.0307
	UWD	WPC	WRR	WWC	WWT
Canada	0.0247	0.0634	0.0230	0.0624	0.0517
Germany	0.0246	0.0566	0.0931	0.063	0.0599
France	0.0281	0.0467	0.0708	0.0634	0.0505
United Kingdom	0.0246	0.0380	0.0802	0.0544	0.0528
Italy	0.0246	0.0397	0.0661	0.0551	0.0431
Japan	0.0321	0.0282	0.0889	0.0582	0.0496
United States	0.0246	0.0839	0.0414	0.0496	0.0417
$I_j$	0.0246	0.0282	0.0931	0.0634	0.0599
${AI}_j$	0.0321	0.0839	0.0230	0.0496	0.0417

shows the weighted normalized values and the ideal and anti-ideal solutions.

Equation (20) is used to determine each country’s utility value ($S_i$). For illustration, the computation of Canada’s utility value is an example of this equation.

$$\begin{array}{cc}{S}_1=\hfill & {\displaystyle \sum _{j=1}^n}\left({\displaystyle \frac{{(y}_{ij}+1)}{\left(I_j+1\right)}}-{\displaystyle \frac{{(AI}_j+1)}{{(y}_{ij}+1)}}\right)\hfill \\ \hfill & =\left({\displaystyle \frac{\left(0.0669+1\right)}{\left(0.0473+1\right)}}-{\displaystyle \frac{\left(0.0669+1\right)}{\left(0.0669+1\right)}}\right)+\left({\displaystyle \frac{\left(0.039+1\right)}{\left(0.0336+1\right)}}-{\displaystyle \frac{\left(0.0692+1\right)}{\left(0.039+1\right)}}\right)+\dots \hfill \\ \hfill & +\left({\displaystyle \frac{\left(0.0517+1\right)}{\left(0.0599+1\right)}}-{\displaystyle \frac{\left(0.0417+1\right)}{\left(0.0517+1\right)}}\right)=-0.0327\hfill \end{array}$$

Once the utility values of all the countries have been determined, the combined power of all the countries is determined using Equation (21). The computation of Canada’s combined power illustrates this equation.

$$\begin{array}{cc}{P}_1=\hfill & \alpha \times {\displaystyle \sum _{j=1}^n}\left(y_{ij}+1\right)+\beta \times {\left({\prod }_{j=1}^n\left(y_{ij}+1\right)\right)}^{{\displaystyle \frac{1}{n}}}\hfill \\ \hfill & =0.5\times \left(\left(0.0669+1\right)+\left(0.039+1\right)+\dots +\left(0.0517+1\right)\right)\hfill \\ \hfill & +0.5\times {\left(\left(0.0669+1\right)\times \left(0.039+1\right)\times \dots \times \left(0.0517+1\right)\right)}^{{\displaystyle \frac{1}{15}}}=8.3959\hfill \end{array}$$

Equation (22) determines the final score for each country. By way of illustration, the computation of the combined power of Canada is an example of this equation.

$$G_1=\zeta \times S_1+\omega \times P_1=0.5\times -0.0327+0.5\times 8.3959=4.1816$$

Table 5. The results of ALPAS.

	${\mathit{S}}_{\mathit{i}}$	${\mathit{P}}_{\mathit{i}}$	${\mathit{G}}_{\mathit{i}}$	Rankings
Canada	−0.0327	8.3959	4.1816	3
Germany	0.2105	8.4668	4.3387	1
France	0.0325	8.4157	4.2241	2
United Kingdom	−0.0380	8.3959	4.1790	4
Italy	−0.0548	8.3899	4.1676	5
Japan	−0.1129	8.3744	4.1308	7
United States	−0.0675	8.3855	4.1590	6

presents the utility values, combined power values, and final scores for the G7 countries.

The following is a ranking of the G7 countries based on the ALPAS method: Germany, France, Canada, the United Kingdom, Italy, the United States, and Japan. Germany has been identified as the country with the highest environmental performance, whereas Japan has been recognized as the country with the lowest environmental performance.

5. Robustness Check

In this section, the robustness of the recently developed ALPAS method is investigated. To this end, it is compared with other methods to assess its responsiveness to attribute weight. Finally, the method is subjected to a rank reversal test.

5.1. Comparison Test

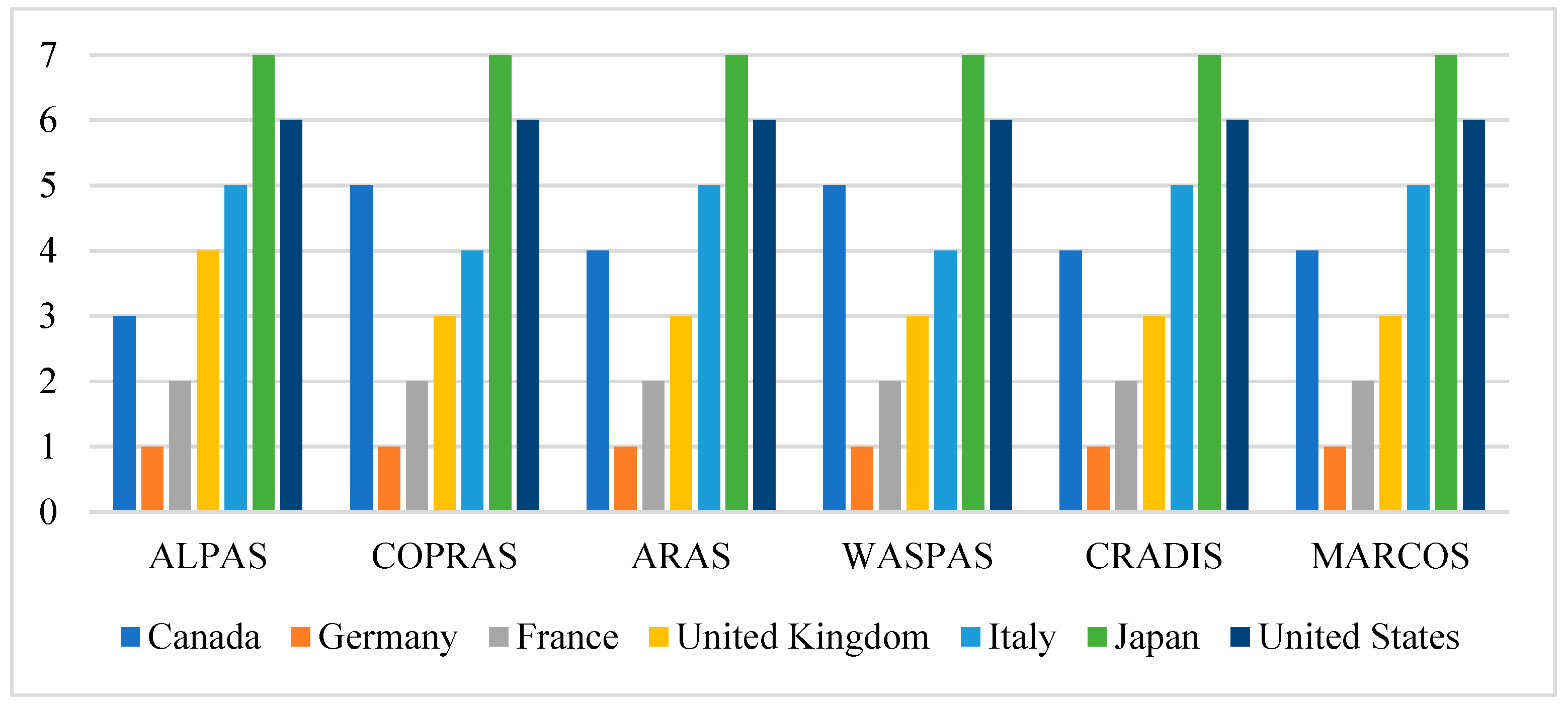
To validate the accuracy and consistency of the newly designed ALPAS approach, its results are compared with those of previous MCDM methods, including COPRAS, ARAS, WASPAS, CRADIS, and MARCOS. Figure 3 illustrates a comparison of the methods.

The comparison results illustrated in Figure 3 indicate that the proposed ALPAS method yields rankings that are markedly compatible with existing MCDM methodologies, including COPRAS, ARAS, WASPAS, CRADIS, and MARCOS. Germany regularly has the foremost position across all approaches, succeeded by France. This ranking has been derived from all employed MCDM approaches.

Moreover, Canada occupies the third position in the ALPAS technique, although it holds the fourth or fifth position in other MCDM methods. The United Kingdom is ranked fourth in the ALPAS method and third in other MCDM approaches. Italy is positioned fifth in the ALPAS, ARAS, CRADIS, and MARCOS methodologies, and fourth in the COPRAS and WASPAS methodologies. The United States and Japan occupied the sixth and seventh positions, respectively, in all MCDM methodologies. The comparative results confirm the superiority of ALPAS, as it mirrors the stable trends of established approaches while also offering significant methodological advancements.

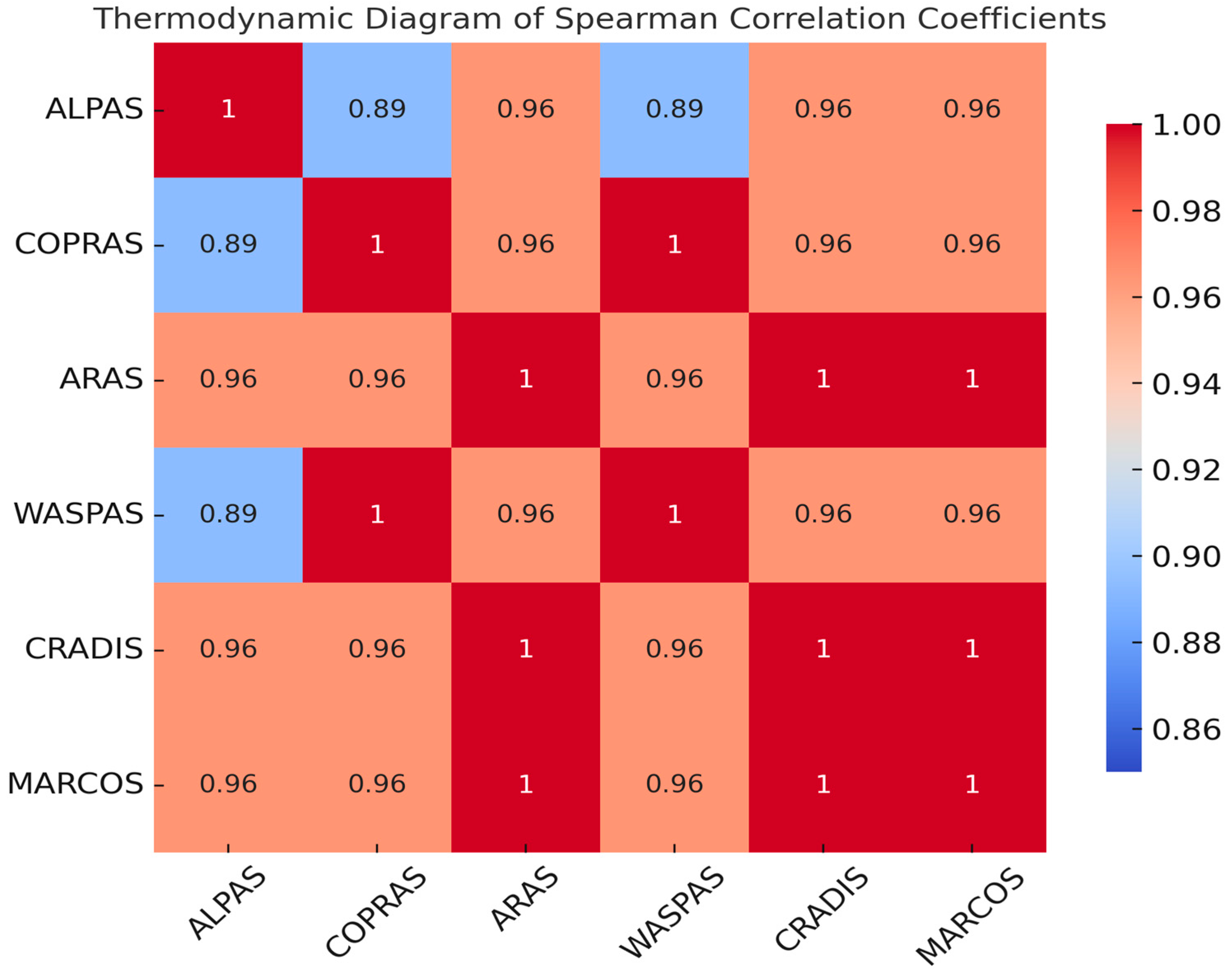
The methods’ comparison reveals the following Spearman Correlation Coefficients between the ALPAS method and other MCDM methods: ALPAS-COPRAS (0.8929), ALPAS-ARAS (0.9643), ALPAS-WASPAS (0.8929), ALPAS-CRADIS (0.9643), and ALPAS-MARCOS (0.9643). The results indicate a significant correlation between the outcomes of the developed ALPAS method and those obtained from other MCDM methods. The ALPAS method has demonstrated the capability to produce accurate and consistent results. Figure 4 presents the Thermodynamic Diagram of Spearman Correlation Coefficients.

In Equation (14), the arithmetic mean was employed to aggregate the weights. When the geometric mean is employed in place of the arithmetic mean, the ALPAS method and other MCDM methods: ALPAS-COPRAS (0.8929), ALPAS-ARAS (0.9643), ALPAS-WASPAS (0.8929), ALPAS-CRADIS (0.9643), and ALPAS-MARCOS (0.9643). If Zavadskas and Podvezko [54]’s weight combination method is used, the correlation coefficients between the ALPAS method and other MCDM methods are as follows: ALPAS-COPRAS (1.0000), ALPAS-ARAS (1.0000), ALPAS-WASPAS (0.9643), ALPAS-CRADIS (1.0000), and ALPAS-MARCOS (1.0000). The alteration of weight combination procedures has produced differing correlation coefficients between the ALPAS approach and other MCDM methods. This suggests that the ALPAS method may be susceptible to variations in weight combination techniques.

5.2. Sensitivity Analysis

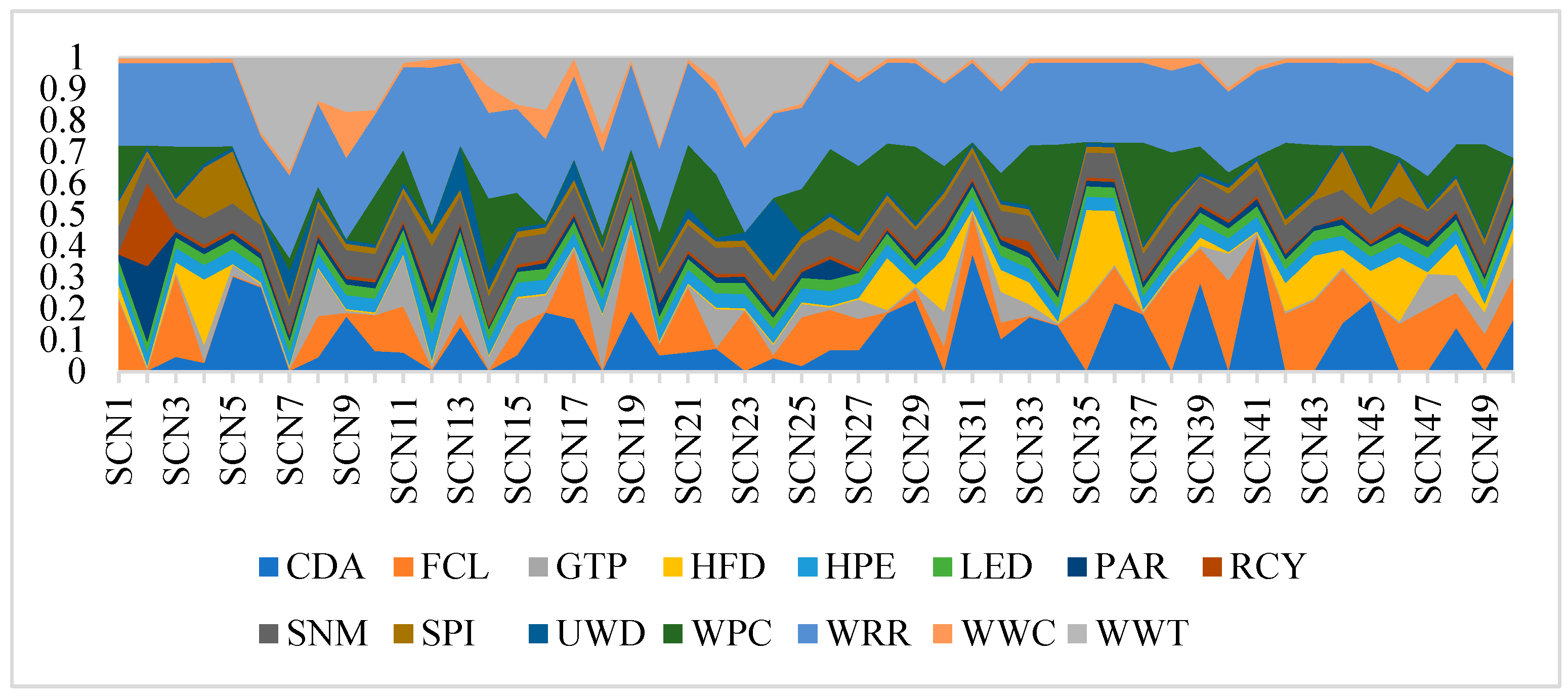
To test whether the ALPAS method is sensitive to changes in attribute weights, 50 criteria weight scenarios are formed with the Bat Algorithm. The attribute weights generated by the bat algorithm are presented in Figure 5.

The results of the sensitivity analysis are shown in Figure 6.

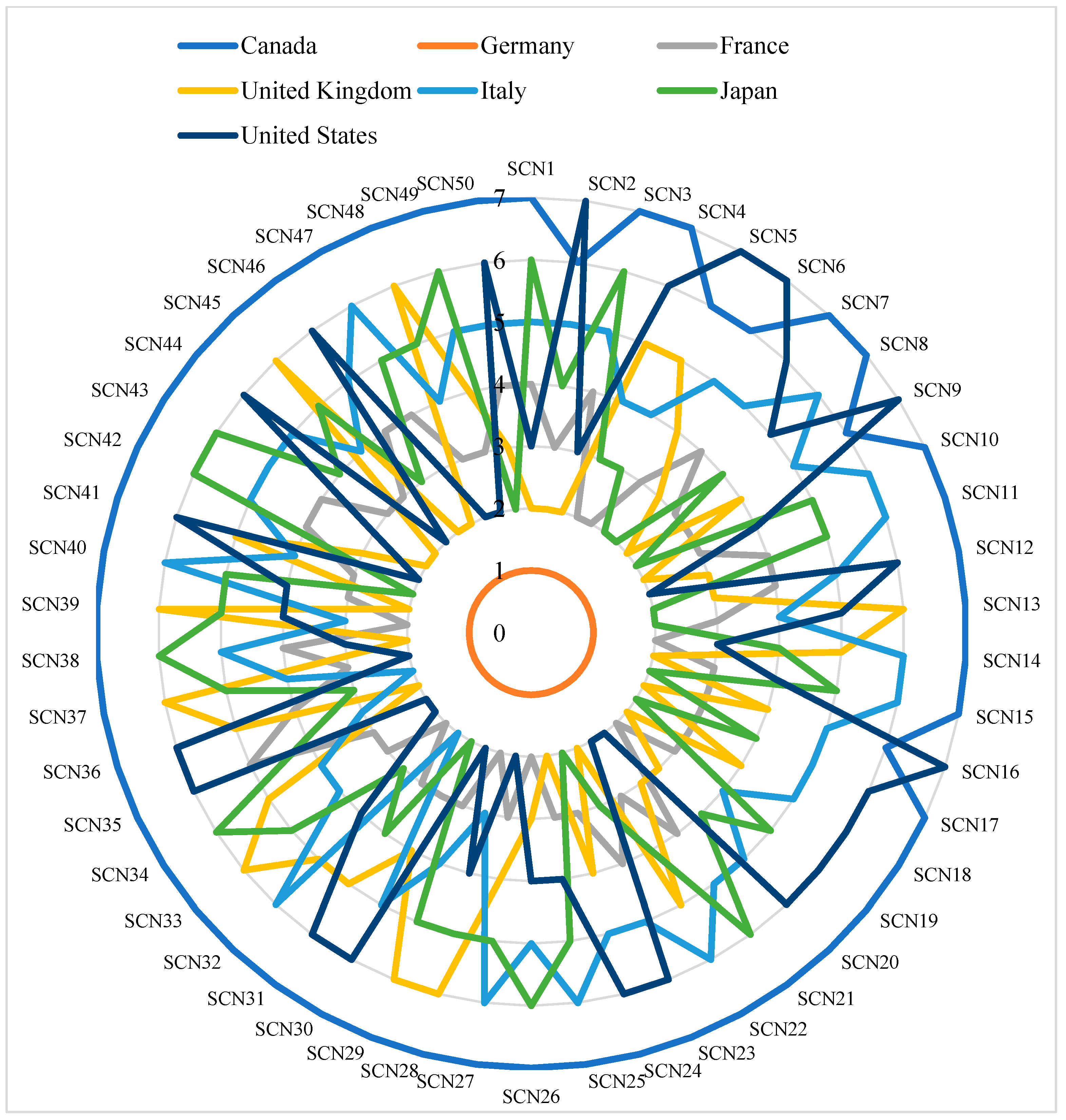
Once the weights of the criteria are changed, most of the rankings have changed. Germany is ranked 1st in all scenarios. France occupies the 5th position in SCN35, the 2nd position in SCN4-SCN5, SCN14, SCN20, SCN26, SCN28, SCN32, SCN39, the 4th position in SCN1, SCN3, SCN7, SCN11-SCN12, SCN21, SCN23, SCN36, SCN38, SCN42-SCN43, SCN46-SCN47, SCN50 scenarios, while ranking 3rd in the remaining scenarios. Italy is positioned 2nd in the SCN31 and SCN36, 3rd in the SCN28, SCN35, SCN39 scenarios, 4th in the SCN4-SCN5, SCN13, SCN19, SCN29, SCN33-SCN34, SCN37, SCN41, SCN45 SCN48 scenarios, 6th in the SCN8, SCN10-SCN11, SCN14-SCN15, SCN22, SCN25, SCN27, SCN32, SCN40, SCN47 scenarios, and 5th in the remaining scenarios. USA holds the 5th position in the SCN8, SCN13, 3rd position in the SCN19, SCN3, SCN14, SCN38, SCN43, SCN47 scenarios, ranks 4th in the SCN10, SCN15, SCN25- SCN26, SCN28, SCN32, SCN39-SCN40, 7th in the SCN2, SCN5-SCN6, SCN9, SCN16, 2nd in the SCN11, SCN21-SCN22, SCN27, SCN29, SCN33-SCN34, SCN37, SCN42, SCN45, SCN48-SCN49, and places 6th in the remaining scenarios. The United Kingdom achieves a ranking of 3rd in the SCN7, SCN11-SCN12, SCN20-SCN21, SCN26, SCN42, SCN50, 5th in the SCN4-SCN5, SCN22, SCN31, SCN34, SCN36, SCN41, 4th in the SCN6, SCN9, SCN16, SCN18, SCN24, SCN27, SCN30, SCN49, 6th in the SCN13, SCN28-SCN29, SCN33, SCN37, SCN39, SCN45, SCN48, while secures 2nd place in the remaining scenarios. Japan is ranked 3rd in the SCN4-SCN5, SCN23, SCN32, SCN36, SCN46, 6th in the SCN1, SCN3, SCN21, SCN26, SCN34, SCN38, SCN42-SCN43, SCN49, 4th in the SCN2, SCN8, SCN14, SCN17, SCN20, SCN22, SCN31, SCN35, SCN44, 2nd in the SCN6-SCN7, SCN9, SCN12-SCN13, SCN16, SCN18, SCN24, SCN30, SCN41, SCN50, and 5th in the remaining scenarios. Canada is ranked 6th in SCN2, SCN5-SCN6, SCN9, SCN16, and 7th in all other scenarios. The results indicate that the developed ALPAS method is sensitive to variations in the criterion weights.

5.3. Rank Reversal Test

As noted, the ALPAS method proposed countries’ rankings as Germany, France, Canada, the United Kingdom, Italy, the United States, and Japan. Various scenarios are formed to analyze whether the method has a rank reversal problem (

Table 6. Results of the rank reversal problem analysis.

	Original Rank	Scenario 1	Scenario 2	Scenario 3	Scenario 4	Scenario 4
Canada	3	3	3	3	3	Removed
Germany	1	1	1	1	1	1
France	2	2	2	2	2	2
United Kingdom	4	4	4	4	Removed	Removed
Italy	5	5	5	Removed	Removed	Removed
Japan	7	Removed	Removed	Removed	Removed	Removed
United States	6	6	Removed	Removed	Removed	Removed

). In the first scenario, the country with the worst performance, Japan, is removed from the analysis, and the analysis is repeated. The expectation is that the rankings of other countries do not change. After Japan, the United States is removed from the analysis in the second scenario, and the method is applied again. Similarly, the scenarios are prepared, the country with the worst performance is removed each time, and the analysis is repeated. Thus, the country rankings are determined based on the five scenarios presented in Table 6. The country rankings remain unchanged, indicating that the ALPAS method does not have a rank reversal problem.

Further,

Table 7. ALPAS vs. other MCDM methods.

	ALPAS	MARCOS	CRADIS	COPRAS	ARAS	WASPAS
Balanced use of ideal & anti-ideal solutions	✓	✓	✓	✗	✗	✗
Lower sensitivity to reference values	✓	✗	✗	✓	✓	✓
Enhanced ranking stability	✓	✓	✓	✗	✗	✗
Dual scoring mechanism (utility & power)	✓	✗	✗	✗	✗	✗
Better interpretability and transparency	✓	✗	✗	✗	✗	✗
Simplified computation	✓	✓	✗	✓	✓	✗
Improved discrimination among close alternatives	✓	✓	✓	✗	✗	✓
Resilience to weight distortions	✓	✓	✓	✓	✓	✗
Adaptive derivation of ideal/anti-ideal values (data-driven)	✓	✗	✓	✗	✓	✗

compares the newly developed ALPAS method with other MCDM methods.

Unlike COPRAS, ARAS, and WASPAS, which do not consistently use ideal and anti-ideal references, ALPAS employs a balanced approach. This enables more comprehensive decision-making by considering how close each alternative is to the best and worst possible cases. Similarly to COPRAS and ARAS, ALPAS is less influenced by slight shifts in reference values. Compared to MARCOS and CRADIS, ALPAS is more robust in dynamic or uncertain environments, where input data might vary slightly. ALPAS exhibits strong resistance to ranking reversal, similar to MARCOS and CRADIS, whereas COPRAS, ARAS, and WASPAS may produce inconsistent results. ALPAS offers more reliable and stable rankings across different scenarios. This is a unique strength of ALPAS. It is the only one of the six that uses utility and power scores to compare options. This provides a dual perspective that enhances the evaluation process and reduces confusion about rankings. Most traditional methods are not very clear, but ALPAS is designed to be easy to understand and follow. Its scoring and normalization steps are more logically organized, which makes it easier for decision-makers to see why specific options are ranked higher. ALPAS, like MARCOS, COPRAS, and ARAS, also support more straightforward calculations. It features a more advanced scoring system but lacks the same level of complexity as CRADIS and WASPAS. This makes it a good balance between being advanced and easy to use. Like MARCOS, CRADIS, and WASPAS, ALPAS does a good job of telling apart options that are very close in score. This makes it suitable for problems where minor differences are crucial, and decisions must be made with care. ALPAS, like MARCOS and CRADIS, is very resistant to changes in the criteria weight. On the other hand, WASPAS may have problems with rank stability when these changes happen, which gives ALPAS an advantage in situations where weighting is sensitive or depends on expertise. Unlike MARCOS, COPRAS, and WASPAS, ALPAS dynamically derives its reference values from the dataset. This data-driven nature enhances contextual relevance, particularly in complex or rapidly evolving decision-making environments.

6. Discussion and Implications

Among G7 countries, France has adopted strict environmental regulations to reduce energy use from fossil fuels by 40% by 2030, as outlined in the Law on Energy Transition for Green Growth of 2015 and the Law on Energy and Climate of 2019 [55]. Germany introduced the first climate legislation, the Climate Action Act, in 2019 to reduce carbon emissions by 55% compared to 1990 [56]. Although Italy, Japan, the United Kingdom, and the United States aim to achieve the targets outlined in the Paris Agreement, they continue to provide subsidies for fossil fuel energy [57]. Moreover, Japan is attempting to revive nuclear energy, which raises concerns about its environmental policy [58].

This study highlighted the waste recovery rate (WRR), the most important environmental factor, emphasizing the need for effective waste management strategies to improve national sustainability. On the other hand, unsafe drinking water (UWD) was the least important factor, perhaps reflecting the typically high standards of drinking water safety already achieved among these wealthy countries. The increasing relevance of WRR emphasizes the need for policymakers in G7 nations to prioritize the circular economy and waste management, thereby improving environmental outcomes. The high significance of the protected area representativeness index (PAR), waste generated per capita (WPC), relative crop yield (RCY), and species protection index (SPI) criteria present that agriculture efficiency, natural area, and species protection, and decreasing waste are important for increasing environmental performance in developed countries. Additionally, there is growing concern about maintaining equivalence between waste production and agricultural management. The medium significance of the anthropogenic PM2.5 exposure (HPE), adjusted emissions growth rate for carbon dioxide (CDA), and GHG growth rate adjusted by per capita emissions (GTP) criteria indicate that air pollution remains a concern for developed countries. The Sustainable Nitrogen Management Index (SNM) and Tree Cover Loss Weighted by Permanency (FCL) criteria are considered medium in significance. This shows that agricultural management has an average relevance to environmental performance. The lower significance of the wastewater collected (WWC), wastewater treated (WWT), household solid fuels (HSD), and lead exposure (LED) criteria indicate that G7 countries have a well-developed infrastructure and long-term applied measures; therefore, the importance of these criteria is no longer considered significant. These findings confirm that focusing solely on traditional environmental factors, such as wastewater and emissions, will not be sufficient; ecosystem integrity is also crucial for maintaining high environmental performance.

Under all the scenarios studied, Germany emerged as the top country in environmental performance. Germany’s comprehensive and proactive environmental laws, including the Climate Action Act of 2019, which aims to significantly cut carbon emissions, help explain its continual top ranking. Reflecting its dedication to the Paris Agreement goals, France has also demonstrated an outstanding performance, backed by stringent rules that significantly reduce fossil fuel consumption. Canada is ranked third. The analysis reveals that Canada’s economy is heavily reliant on energy-intensive industries. Canada ranks third due to its high emissions and other environmental impacts, despite excelling in other areas, such as protecting nature and building infrastructure. The United Kingdom is in fourth place. The United Kingdom did well in protecting nature, managing agriculture, and building infrastructure, but its performance was average due to pollution and waste caused by a high-consumption economy. Italy is set in the fifth order. Even though it performed well in terms of pollution and emissions, there are problems with infrastructure and agricultural management. Japan, on the other hand, came in last among the G7, indicating that its environmental policies were ineffective. Japan’s poor performance may be linked to issues with nuclear energy regulations and its reliance on fossil fuel subsidies. The United States also demonstrated poor environmental performance, underscoring the need for reform in its environmental policies, particularly in areas such as waste management and species conservation.

Eşiyok et al. [29] support these findings, as they found that Germany performs best. Further, Tutak et al. [26] presented that France performed well in environmental protection. On the other hand, these results contradict the findings of Iqbal et al. [20], Dang [21], and Gökgöz and Yalçın [28]. Iqbal et al. [20] indicated that the USA and Japan ranked the best. This is because they ordered the most industry-intensive countries, such as Brazil and Indonesia, which led to these countries using clean technologies performing better. Dang [21] ordered OECD countries and claimed that Japan and the USA had the highest performances, while Canada had the lowest. Gökgöz and Yalçın [28] ranked G20 countries and found that the US had the best performance, while Saudi Arabia and China had the worst. Assessing different sets of countries with different criteria led to contradictions with our results.

6.1. Managerial and Policy Implications

Germany’s success can be attributed to its comprehensive environmental legislation. Policymakers in other countries should adopt similar long-term emission reduction laws (e.g., the Climate Action Act). The importance of WRR (Waste Recovery Rate) indicates that waste management infrastructure must be prioritized. PAR (Protected Area Representativeness) suggests expanding and effectively managing conservation zones. High WPC (Waste Generated Per Capita) values indicate excessive consumption patterns; policies promoting circular economy principles should be introduced. Countries that ranked low (Japan, USA, Italy) should reassess fossil fuel subsidies, their energy mix, and conservation investments. International environmental bodies may consider adopting the ALPAS framework as a resource allocation and benchmarking decision-support tool.

With good environmental governance and aggressive application of solid policies for carbon emission reduction and sustainable resource management, Germany ranked as the best-performing nation. The outstanding performance of France underscored even more the need for strict environmental laws, especially those aimed at reducing emissions and the use of fossil fuels. Although both nations have good environmental standards, Canada and the United Kingdom hold middle rankings, suggesting that there is still much room for improvement, particularly in waste recovery efficiency and resource management. Ranked lowest were Italy, the United States, and Japan, which indicates significant gaps and opportunities for targeted interventions and policy changes. Japan’s underperformance highlights the need for a comprehensive review of environmental management policies, particularly regarding nuclear energy reliance and the preservation of protected areas. Most importantly, this study found that essential elements influencing environmental sustainability include waste recovery (WRR), the Protected Area Representativeness Index (PAR), and waste generated per capita (WPC). This emphasizes the need to prioritize these regions for legislators by utilizing creative technologies, sensible laws, and increased environmental infrastructure funding.

The results of this study have significant implications for the development of national and global environmental policy. Policymakers in underdeveloped nations may use these realizations to adopt excellent practices modeled by more successful countries, such as Germany and France. Also, this research supports cleaner environments, healthier communities, equitable access to resources, and global climate goals by offering policymakers a robust decision-support framework for environmental planning. Furthermore, international cooperation among the G7 countries could help to transmit knowledge and enable group advancement toward the objectives of global environmental sustainability.

6.2. Theoretical Implications

This paper comprehensively assesses the environmental performance of the G7 nations using an integrated MCDM methodology. The study specifically employed the LOPCOW, LODECI, and SITDE methods to determine the weights of environmental criteria. Although Jiang et al. [59] made significant contributions to LGDM (Large Group Decision Making) processes by considering uncertainty and multi-level linguistic environments, their focus was primarily on trust relationships between decision-makers and group dynamics. Therefore, their weighting approach is based on a hybrid structure (BWM and maximal deviation). In contrast, the contribution of this study is directed towards the structural characteristics of the data rather than group dynamics. Thanks to the integration of the LOPCOW, LODECI, and SITDE methods, deviations arising from the data scale are eliminated, contrast intensity is reflected in a more balanced manner, and decision quality is improved by taking into account the effect of distribution skewness. Thus, the proposed framework offers not only a hybrid weighting but also a robust, balanced, and more interpretable objective weighting mechanism that simultaneously addresses multidimensional data issues.

The ALPAS method was introduced to rank nations based on the EPI. The ALPAS method, as the core contribution of this study, provides a new perspective in MCDM-based ranking by integrating dual evaluation (utility and power), transparent normalization, and adaptive reference derivation. This study demonstrates its superior ranking stability and interpretability compared to established models such as MARCOS, CRADIS, COPRAS, ARAS, and WASPAS, validating its robustness through sensitivity analysis and rank reversal testing. Significant correlations are shown by the robustness of the ALPAS method being extensively evaluated against other accepted MCDM techniques (COPRAS, ARAS, WASPAS, CRADIS, and MARCOS). Under several attribute weighting scenarios, sensitivity analysis shows considerable variations in country rankings; nonetheless, Germany always maintains its top position. These differences highlight the importance of carefully selecting and weighing the criteria used in environmental performance assessments, as environmental rankings are susceptible to the allocation of weight to each criterion. Additionally, the fact that rank reversal does not occur in many testing environments strongly supports the reliability and durability of the ALPAS method. The ALPAS method is reliable and stable, which supports its use and effectiveness for assessing environmental performance. Because of this, researchers and policymakers can confidently use this method to make informed decisions and assess the environment with precision and reliability.

Beyond empirical validation, the study also makes a mathematical contribution. The optimization methodology underlying ALPAS extends traditional MCDM formulations by formalizing a novel dual-evaluation operator and incorporating an adaptive normalization scheme. Furthermore, the integrated weighting framework mathematically resolves three common data-related challenges: scale bias (via LOPCOW), unbalanced contrast intensity (via LODECI), and asymmetry in distribution (via SITDE). This demonstrates that the proposed method is not only effective in application but also expands the mathematical foundations of MCDM optimization models.

7. Conclusions

The primary objective of this study is to assess the environmental performance of the G7 countries. To examine important environmental elements and rank nations, this study introduces the ALPAS method. Then, it effectively employs an integrated MCDM methodology that combines ALPAS, LOPCOW, LODECI, and SITDE methodologies. The study identified Waste Recovery Rate (WRR), Protected Area Representativeness (PAR), and Waste Generated Per Capita (WPC) as the most important EPI indicators. Using the ALPAS method, Germany ranked 1st, followed by France and Canada. Japan was ranked last. Robustness analysis confirmed the validity and consistency of ALPAS rankings, as evidenced by Spearman correlation coefficients between ALPAS and other methods (e.g., ARAS, MARCOS), all of which were greater than 0.89. Sensitivity analysis using 50 scenarios (via the Bat Algorithm) confirmed Germany’s stable top performance, while the ranks of other countries varied slightly. The rank reversal test confirmed that excluding countries from the analysis did not alter the order of the remaining ones.

Nonetheless, this study has a few limitations. First, only objective weighting techniques were used to determine the criteria weights. Future studies can calculate the criteria weights with subjective or integrated (subjective and objective) techniques. Second, this study focuses on G7 countries; therefore, the results are limited to highly developed countries. Therefore, this analysis can be expanded by adding developing countries in future studies. Third, the criteria used in this study are taken from the EPI. Future studies could expand the scope by including other environmental parameters, investigating longitudinal data to track performance dynamics over time, and employing comparable robust approaches to those used by other worldwide groups or emerging nations. Further research should also examine the pragmatic outcomes of advised policies, enhancing knowledge of the effectiveness of strategic environmental projects. In addition to the integrated objective weighting and crisp evaluation approaches used in this study, future research could explore the application of fuzzy and grey extensions of MCDM methods. These approaches are particularly beneficial when data are uncertain, incomplete, or imprecise, a common issue in environmental studies that often involves expert judgments or qualitative assessments. Fuzzy MCDM methods (such as fuzzy AHP and fuzzy TOPSIS) can effectively handle linguistic terms and vague expressions, while grey system-based models (e.g., grey relational analysis and grey DEMATEL) are helpful when the dataset is limited or partially known. Incorporating these uncertain extensions into the environmental performance evaluation framework can enhance the realism and adaptability of assessments, particularly for emerging countries where precise data availability may be limited.