Research on a General State Formalization Method from the Perspective of Logic

Abstract

As information plays an ever more central role across disciplines, the lack of a precise and reusable definition of state impedes comparison, measurement, and verification. Building on Objective Information Theory (OIT), this paper proposes a logic-based framework that defines the state of an object or system at a time point (or interval) as the semantic valuation of a set of well-formed formulas over a given domain and interpretation. Within first-order and higher-order logic—extended to infinitary logic when needed—we show how finite and broad classes of infinite structures can be characterized, drawing on core results from model theory. We then instantiate the framework in economics, sociology, computer science, and natural language, demonstrating that logic provides a unifying language for representing, reasoning about, and relating states across domains. Finally, we refine OIT by supplying a universal state representation that supports cross-domain exchange, measurement, and verification.

1. Introduction

Information, matter, and energy are fundamental to nature, yet there is no cross-disciplinary consensus on what information is or how to define state precisely [1]. Classical information theory focuses on coding and communication efficiency and offers limited tools to characterize states at the levels of definition, analysis, and processing [2,3,4]. Objective Information Theory (OIT), grounded in a mapping between ontology and carrier, provides postulates, mathematical definitions, and measurement systems that unify diverse information principles [5,6,7]. However, OIT treats information as an enabling mapping between states without a rigorous and general definition of state itself, which hinders cross-domain comparability, logical inference about “the same state,” and precise measurement and verification of information mappings.

This paper proposes a universal, verifiable, and reusable definition of state: the state of an object or system at a time point (or interval) is the semantic valuation of a set of well-formed formulas over a given domain and interpretation. Leveraging results in model theory, we analyze when first-order and higher-order logic (and, when appropriate, infinitary logic) can fully characterize structures, from finite to broad classes of infinite ones. We then present representative cases from economics, sociology, computer science, and natural language to show that logic serves as a bridge for state representation across domains. Our contributions are:

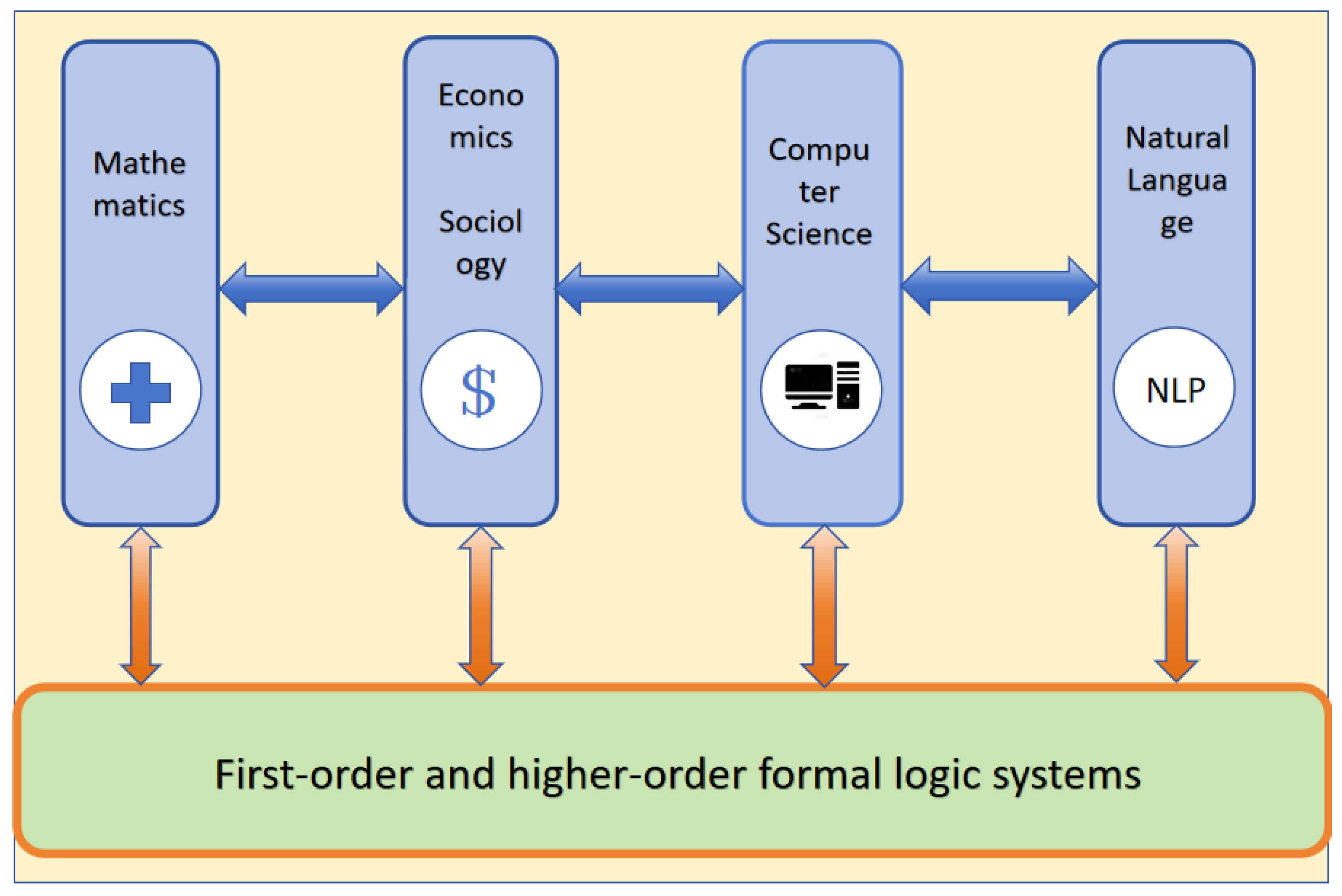
• a unified axiomatization of states as interpretations of formulas, with four axioms (parameter reference, property expressibility, logical closure, temporal causality) and an existence–uniqueness result up to logical equivalence that fills a gap in OIT;
• systematic links to model-theoretic milestones (categoricity, Skolem/non-categoricity, second-order Peano, Scott’s isomorphism theorem) and conditions for characterizing some uncountable structures;
• a cross-disciplinary case library for specification, verification, and measurement;
• an articulation of a deeper unity: many domain-specific notions of state admit uniform logical expression and transformation.

Figure 1 illustrates logic as a cross-domain bridge and a universal descriptive language.

2. Formal Expression of State

The information postulate emphasizes that the state of an ontology can be mapped to the state of a carrier. Establishing a formal representation for both is therefore essential. Mathematical logic, grounded in axiomatic systems and symbolic language, enables rigorous and unambiguous characterization of concepts, propositions, and reasoning, thereby avoiding the ambiguity of natural language and providing a precise tool for scientific inquiry. We first restrict attention to a first-order object language.

2.1. First-Order Formal System Definition

First-order predicate logic language has become a core tool for formal modeling and automatic reasoning in fields such as mathematics, information science, and artificial intelligence due to its strong expressiveness, clear structure, rigorous reasoning, good computability, and strong versatility [8]. First, we define the most basic symbols in the first-order formal system:

Definition 1

(Symbols in ${\mathcal{L}}^{\left(1\right)}$). ${\mathcal{L}}^{\left(1\right)}$ contains the following symbols:

• First-order variables: $x_1^{\left(1\right)},x_2^{\left(1\right)},\dots ;$
• First-order constants: $a_1^{\left(1\right)},a_2^{\left(1\right)},\dots ;$
• First-order function symbols: $f_1^{\left(1\right)1},f_2^{\left(1\right)1},\dots ,f_1^{\left(1\right)2},f_2^{\left(1\right)2},\dots$;
• brackets: (, );
• First-order predicate symbols: $A_1^{\left(1\right)1},A_2^{\left(1\right)1},\dots ,A_1^{\left(1\right)2},A_2^{\left(1\right)2},\dots$;
• Logical connectives: ∼ or ¬ (negation), → (implication);
• Quantifiers: ∀ (universal quantifier).

As usual, we define $\vee ,\wedge ,\leftrightarrow$, and ∃ from these primitives. Symbols such as = and ∈ are treated as predicate symbols.

Terms in a language are similar to nouns or noun phrases in a natural language, but terms and nouns (phrases) are not exactly the same. The main difference is that terms contain variables and are “compound” items constructed using variables.

Definition 2

(Terms in ${\mathcal{L}}^{\left(1\right)}$). The terms in ${\mathcal{L}}^{\left(1\right)}$ are generated as follows:

(1) 

Variables and constants are terms.

(2) 

If $f_i^{\left(1\right)n}$ ($n>0,i>0$) is a function symbol in ${\mathcal{L}}^{\left(1\right)}$ and $u_1,\dots ,u_n$ is a term in ${\mathcal{L}}^{\left(1\right)}$, then $f_i^{\left(1\right)n}(u_1,\dots ,u_n)$ is also a term in ${\mathcal{L}}^{\left(1\right)}$.

Next, we define atomic formulas. Atomic formulas are the most basic formulas in the language.

Definition 3

(Atomic formulas in ${\mathcal{L}}^{\left(1\right)}$). If $A_i^{\left(1\right)n}$ ($n>0,i>0$) is a predicate symbol in ${\mathcal{L}}^{\left(1\right)}$ and $u_1,\dots ,u_n$ is a term in ${\mathcal{L}}^{\left(1\right)}$, then $A_i^{\left(1\right)n}(u_1,\dots ,u_n)$ is an atomic formula in ${\mathcal{L}}^{\left(1\right)}$.

Definition 4

(Well-formed formulas in ${\mathcal{L}}^{\left(1\right)}$). The well-formed formula in ${\mathcal{L}}^{\left(1\right)}$ is defined as follows:

(1) 

Each atomic formula is a well-formed formula in ${\mathcal{L}}^{\left(1\right)}$;

(2) 

If $\mathcal{A}$ and $\mathcal{B}$ are well-formed formulas in ${\mathcal{L}}^{\left(1\right)}$, then $\sim \mathcal{A}$ and $\mathcal{A}\to \mathcal{B}$ are both well-formed formulas in ${\mathcal{L}}^{\left(1\right)}$;

(3) 

If $\mathcal{A}$ is a well-formed formula in ${\mathcal{L}}^{\left(1\right)}$ and u is a variable or function symbol in ${\mathcal{L}}^{\left(1\right)}$, then $(\forall u)\mathcal{A}$ is a well-formed formula in ${\mathcal{L}}^{\left(1\right)}$.

2.2. Recursive Definition of Higher-Order Formal Systems

Considering that first-order logic still has many shortcomings in terms of quantified objects, recursive induction, and other issues, such as its inability to fully express the concept of a set and its lack of direct characterization of higher-order properties, we need to expand the characterization capabilities of logical systems. Higher-order predicate logic (HOL) is an extension of first-order predicate logic. It allows quantification over predicates, functions, and even predicates about predicates. It offers greater expressive power, can formalize complex semantics in natural language and mathematics, and supports a richer set of logical tools and theoretical frameworks.

We obtain higher-order logic by iterating the construction above. Symbols, terms, atomic formulas, and wffs of order k are defined inductively from order $k-1$ (see Appendix A.1 for full details).

2.3. Interpretation of Formal Systems

Next, we can define the interpretation of the formal system.

Definition 5

(Interpretation of formal systems). An interpretation E of the formal system $\mathcal{L}$ is a two-tuple $E=\langle D_E,J\rangle$. Where:

• The domain $D_E$ is a non-empty set that contains the value range of all elements in $\mathcal{L}$, including individuals, properties, relations, and functions.
• The interpretation function J is a mapping that maps symbols in $\mathcal{L}$ to concrete semantics in the domain $D_E$ and is defined as follows:

  –

  Interpretation of constants and variables: Each constant $a_i^{\left(k\right)}$ is interpreted as an element in $D_E$, i.e., $J\left(a_i^{\left(k\right)}\right)\in D_E$; each variable $x_i^{\left(k\right)}$ is interpreted as an element in $D_E$, i.e., $J\left(x_i^{\left(k\right)}\right)\in D_E$.

  –

  Interpretation of function symbols: Each function symbol $f_i^{\left(k\right)n}$ is interpreted as a mapping from $D_E^n$ to $D_E$, that is, $J\left(f_i^{\left(k\right)n}\right):D_E^n\to D_E$.

  –

  Interpretation of predicate symbols: Each predicate symbol $A_i^{\left(k\right)n}$ is interpreted as a mapping from $D_E^n$ to $\{\mathit{True},\mathit{False}\}$, i.e., $J\left(A_i^{\left(k\right)n}\right):D_E^n\to \{\mathit{True},\mathit{False}\}$.

  –

  Interpretation of the terms:

  $$J\left(u\right)=\left\{\begin{array}{cc}J\left(a_i^{\left(k\right)}\right),\hfill & \mathit{if}u\mathit{is}\mathit{constant}{a}_i^{\left(k\right)}\hfill \\ J\left(x_i^{\left(k\right)}\right),\hfill & \mathit{if}u\mathit{is}\mathit{variable}{x}_i^{\left(k\right)}\hfill \\ J\left(f_i^{\left(k\right)n}\right)(J\left(u_1\right),\dots ,J\left(u_n\right)),\hfill & \mathit{if}u=f_i^{\left(k\right)n}(u_1,\dots ,u_n)\hfill \end{array}\right.$$

  –

  Interpretation of atomic formula:

  $$\mathit{if}\mathcal{A}=A_i^{\left(k\right)n}(u_1,\dots ,u_n),\mathit{then} J\left(\mathcal{A}\right)=J\left(A_i^{\left(k\right)n}\right)(J\left(u_1\right),\dots ,J\left(u_n\right)).$$

  –

  Interpretation of logical connectives:

  $$J(\sim \mathcal{A})=\mathit{True}\iff J\left(\mathcal{A}\right)=\mathit{False}$$

  $$J(\mathcal{A}\to \mathcal{B})=\mathit{True}\iff \left(J\right(\mathcal{A})\to J(\mathcal{B}\left)\right)=\mathit{True}$$

  –

  Interpretation of quantifiers: If $\mathcal{A}=(\forall u)\mathcal{B}$, where u is a variable or function symbol, then

  $$J\left(\mathcal{A}\right)=\mathit{True}\iff \forall d\in D_E, \mathit{when}u\mathit{is}\mathit{interpreted}\mathit{as}d,J\left(\mathcal{B}\right)=\mathit{True}$$

The interpretation of formal systems transforms the abstract syntax of formal logic into concrete semantics, serving as a crucial link between the “symbolic world” and the “real world.” It not only renders logical language meaningful but also provides a theoretical foundation for correct reasoning, modeling, verification, and automated applications. It is an essential concept in mathematical logic and information science.

2.4. Axiom System for Logical Expression of Ontology Components Under State Decomposition

In everyday usage, “state” is typically understood as something that pertains to a particular object, whose properties, meanings, and characteristics can be articulated and understood in natural language, that can be composed with other states to form new ones, and whose expression is inseparable from time and must respect temporal causality.

Let X denote a set of objects, T denote a set of time points or intervals, and L denote a higher-order formal system. In view of these properties of states, we propose the following four axioms [9]:

• Parameter Reference Axiom: Every object $x\in X$, every moment or period $t\in T$, and every function $f\in F$ is represented by a unique constant or term $c_x,c_t,c_f$ in L.
• Property Expressibility Axiom: The properties, form, value, relationship, and other attributes of a set of objects in the entire domain can be expressed through functions and predicates in the formal system.
• Logical Combination and the Closure Axiom:
  The generation rules of the state space $\mathcal{S}$ are limited to the following logical operations:
  • Implication: If $S_1,S_2\in \mathcal{S}$, then it implies that $S_1\to S_2$ is also a state of $\mathcal{S}$;
  • Negation: If $S\in \mathcal{S}$, then $\neg S\in \mathcal{S}$;
  • Quantification: if $S\left(x\right)$ is a state predicate, then $\forall xS\left(x\right)$ and $\exists xS\left(x\right)$ belong to S.
  Only finitely many applications of these operations may be used to generate new states.
• Temporal Causality Axiom: When any attribute, relationship, or state is established at a certain moment, its change or evolution at subsequent moments can be described by the formula in L.

Theorem 1.

If for any $x\in X,t\in T$, there exists at least one attribute, relation, or property that can be expressed by L, and satisfies the axioms of parameter reference, attribute expressibility, logical combination closure, and temporal causality, then all states of any object x at any time t can be uniquely characterized by a set of well-formed formulas ${\phi }_{S(x,t)}$ in L.

Proof of Theorem 1. 

According to the parameter reference axiom, the object x, time t, and the function f involved in the set can all be represented by unique terms $c_x,c_t,c_f$ in L.

Next, according to the property expressibility axiom, the various properties of the state set $S(x,t)$ can be expressed using functions and predicates in the formal system.

By definition, all expressions in the above state sets are atomic formulas in L. By logical combination and the closure axiom, any complex ontological state G can be recursively constructed from the base state by applying a finite number of generation rules expressible in L. Each generation rule is uniquely described by a well-formed formula and inference rule in L. Therefore, for any object x and time t, all its ontological states $S(x,t)$ can be uniquely mapped and characterized in L by the corresponding set of formulas ${\phi }_{S(x,t)}$, where ${\phi }_{S(x,t)}$ is recursively generated from the atomic formulas using logical rules.

In terms of uniqueness, the construction of $S(x,t)$ depends solely on x, t, and the set of ontological components. The representation of all predicates, functions, and parameters in L is uniquely determined by the axiomatic system. Therefore, ${\phi }_{S(x,t)}$ uniquely corresponds to $S(x,t)$ within L. If ${\phi }^{\prime },{\phi }^{″}\in L$ both characterize $S(x,t)$, then by the logical equivalence relation in L, ${\phi }^{\prime }\equiv {\phi }_{S(x,t)}\equiv {\phi }^{″}$, guaranteeing uniqueness.

Furthermore, the temporal causality axiom states that any time t can be expressed by a recursive or evolutionary formula in L. Specifically, for any $x\in X$, there exists a formula $\psi (x,t^{\prime },x,t)$ in L, such that $S(x,t^{\prime })$ is uniquely determined by $S(x,t)$ and related laws. Thus, any dynamic evolution of a system can be recursively expressed by a chain of well-formed formulas in L, and the history and future of its state can be reduced to the logical deduction of a set of formulas.

In summary, $S(x,t)$ can always be rigorously characterized by a unique set of well-formulated formulas in L under interpretation, and this expression holds true for any dynamic evolution. The theorem is proved. □

2.5. The State of an Object at a Specific Time

Then, according to the theorem, we give the definition of state:

Definition 6

(state). The state $S(x,t)$ of a set of objects x at a particular time set t is an interpretation of a set of well-formed formulas in the formal system $\mathcal{L}$ on the universe $x\times t$. The specific properties of x and t, as well as the choice of formula set and the definition of the interpretation, are determined by the specific application scenario.

OIT holds that information is an enabling mapping from state to state, but it does not itself answer what a “state” is. By Definition 6, we clarify the concept of state and decompose it, making the expressions of “state” and “information” more fine-grained, precise, and concrete, thereby achieving a logical closure within OIT.

Theorem 1 and Definition 6 show that, under the axioms of parameter reference, property expressibility, logical combination and closure, and temporal causality, for every object x at time t, there exists a set of formulas ${\phi }_S(x,t)$ that characterizes its state $S(x,t)$; moreover, this representation is unique up to logical equivalence. The formal representation of state is not only a technical tool but also a fundamental way for humans to understand and transform the world. It transforms intuitive concepts into precise mathematical objects, enabling rigorous reasoning and systematic analysis. As science and technology become increasingly complex, this formalization capability will continue to be a vital force driving the development of informatics and the progress of human civilization.

2.6. Relationship to and Distinctions from Existing Frameworks

We position our framework relative to established semantics as follows. Kripke semantics treats states as possible worlds with accessibility relations; in our setting, Kripke models arise as specific interpretations, but our focus is a uniform object–property–time semantics in first-/higher-order logic. LTL/CTL specifications embed as temporal fragments; dynamic logic modalities can be represented via interpretable predicates/functions; TLA+ is captured via state variables and a next relation; ASMs translate to predicate–function interpretations with update rules [10,11,12,13,14]. Our added value lies in a common semantic substrate and model-theoretic tools spanning finite, countable, and selected uncountable structures.

Next, we specify in detail the relationships and distinctions between this work and existing frameworks.

(1)

Modal logic (Kripke structures): Kripke semantics treats states as possible worlds and transitions as accessibility relations, focusing on “reachability/necessity.” In this paper, a state is defined as “the semantic object of formulas under an interpretation,” and Kripke structures can, when needed, be embedded as a specific interpretation (worlds = elements of the domain; R as relations induced by predicates/functions). Our main thrust, however, is to use logical expressive power to unify the semantic construction of “object–property–time,” rather than confining ourselves to the realm of accessibility. In other words, Kripke semantics is a specialized interpretation within our framework, while our framework natively supports higher-order properties, functions, and cross-domain mappings [15].

(2)

Linear/branching-time logics (LTL/CTL): LTL/CTL excel at temporal specifications and model checking, targeting safety/liveness over path- or tree-shaped time structures [16]. This paper incorporates the temporal dimension but does not fix time solely as a linear or branching transition system; instead, it incorporates “time” into the domain and interpretation and allows first-order/higher-order predicates to describe intrinsic mathematical properties and cross-domain relations of structures. For engineering use, LTL/CTL specifications can be regarded as a temporal subset of our state language, while our framework provides broader object-level semantics and model-theoretic tools (e.g., types, Scott sentences, and isomorphism metrics).

(3)

Dynamic logic (PDL, dynamic first-/higher-order logic): Dynamic logic takes program actions as modalities and is well-suited to characterize executable transformations. Our focus is the unified semantic definition and cross-domain representation of “state,” emphasizing that actions/processes are also treated as interpretable predicates/functions, thereby expressing object properties and evolution laws within a single language. By comparison, dynamic logic is strong in the calculational encapsulation of programmatic transformations, whereas this paper is strong in the semantic unification of cross-disciplinary objects and higher-order structures [17]. The two are complementary: embedding action semantics into our interpretive layer yields greater expressive power for complex object structures.

(4)

TLA+: TLA+ centers on state variables and the next-step relation and is well-suited for proving safety and liveness in concurrent/distributed systems [18]. In our approach, TLA+ states and the Next relation can be viewed as instances of interpretations of specific predicates/functions, thereby bringing TLA+ specifications under a unified logical semantics that can interoperate with state models in mathematics, economics, or natural language. Our added value lies in providing model-theoretic tools spanning finite/countable to certain uncountable structures (e.g., Scott sentences and approximation limits), as well as a dual-sided ontology–carrier expression and measurement of “information mappings.”

(5)

Abstract State Machines (ASM): ASM describes system behavior using refined states and transition rules [19]. We can translate ASM state families and update rules into a unified predicate–function interpretation with corresponding inferential commitments. The difference is that ASM targets execution-level abstractions for engineering modeling, whereas this paper provides a cross-disciplinary repository of semantic isomorphism and expressibility theorems, enabling states from mathematics/social sciences/language to be aligned and compared with engineering specifications such as ASM/TLA+ on a common semantic foundation.

In sum, this paper is not competing with these frameworks but provides a more general semantic substrate: it treats first-order/higher-order (and, when necessary, infinitary) logic as a “universal language of state,” viewing Kripke semantics, LTL/CTL, dynamic logic, TLA+, and ASM as subtheories or instances under specific signatures, semantics, and accessibility relations. When cross-domain problems require simultaneous treatment of higher-order properties, structural isomorphism, information mappings, and temporal evolution, our framework can integrate these methods within a single logical interpretation and model-theoretic toolbox, thereby enabling unified expression, comparison, and verification.

3. Mathematical Field State Expression

Mathematics, as a fundamental discipline, encompasses a wide range of branches and a vast system. Fundamental fields such as number theory focus on the properties of integers; algebra encompasses linear algebra (vector spaces and matrices), abstract algebra (groups, rings, and fields), and polynomial theory; and geometry includes Euclidean geometry and differential geometry (manifolds and curvature). Applied mathematics encompasses topology, probability theory and statistics (such as stochastic processes, Bayesian statistics, and the foundations of machine learning), and computational mathematics (numerical analysis, algorithm design, and scientific computing). Furthermore, new problems continue to emerge in discrete mathematics, mathematical physics, logic, and set theory.

From elementary arithmetic to cutting-edge research, mathematics demonstrates a progression in depth and abstraction, with numerous fields intersecting and integrating. Theorems, propositions, and formulas within each branch can be viewed as characterizing the “state” of certain mathematical objects. Broadly speaking, the state of mathematical objects is a core concept for understanding the dynamics, contextual dependence, and inherent connections of mathematical structures. Studying mathematical states not only helps focus on key properties and ignore minor details, but also helps grasp the essence of a problem, forming a crucial foundation for the development of mathematical theory.

3.1. Formalization of Finite Mathematical Structures

Finite structures are the foundation of discrete mathematics. Problems such as finite sets and their subsets, and the connectivity, coloring, and matching of graphs in finite graph theory are all inseparable from the study of finite structures. In addition, many “infinite” mathematical concepts originate from the generalization of finite structures [20,21,22].

Finite mathematical structures are not only an essential component of mathematics but also fundamental tools for understanding the complex world, solving practical problems, and advancing science and technology. Here, we provide a rigorous proof that finite mathematical structures can be formalized in a first-order manner.

Definition 7

(Finite structure). Let $\mathfrak{A}=\langle A,R_1^{\mathfrak{A}},\dots ,R_m^{\mathfrak{A}},f_1^{\mathfrak{A}},\dots ,f_n^{\mathfrak{A}},c_1^{\mathfrak{A}},\dots ,c_k^{\mathfrak{A}}\rangle$ be a finite structure, where: A is a finite set, $\left|A\right|=N$, $R_i^{\mathfrak{A}}\subseteq A^{a_i}$ is an $a_i$ ary-relation, $f_j^{\mathfrak{A}}:A^{b_j}\to A$ is a $b_j$ ary-function, and $c_l^{\mathfrak{A}}\in A$ is a constant.

Theorem 2

(First-order complete characterization of finite structures). If $\mathfrak{A}$ is a finite structure, then there exists a first-order language L and a set of L-sentences Γ such that for any L-structure $\mathfrak{B}$:

$$\mathfrak{B}\vDash \Gamma \mathit{if}\mathit{and}\mathit{only}\mathit{if}\mathfrak{B}\cong \mathfrak{A}$$

(1)

Proof of Theorem 2. 

The definition L includes:

• Relation symbols: $R_1,\dots ,R_m$ (with arity $a_1,\dots ,a_m$ respectively)
• Function symbols: $f_1,\dots ,f_n$ (with arity $b_1,\dots ,b_n$ respectively)
• Constant symbols: $c_1,\dots ,c_k$
• Individual constants: $d_1,\dots ,d_N$ (corresponding to each element in A)

• Let $A=\{{\alpha }_1,{\alpha }_2,\dots ,{\alpha }_N\}$; construct the following statement:

(${\Gamma }_1$) domain restriction statement:

$$\forall x\left(x=d_1\vee x=d_2\vee \dots \vee x=d_N\right)$$

(2)

(${\Gamma }_2$) element-wise distinction statement:

$$d_i\ne d_j(\mathrm{for}\mathrm{all}1\le i<j\le N)$$

(3)

(${\Gamma }_3$) relation characterization statement:

For each relation symbol $R_i$ and each tuple $({\alpha }_{j_1},\dots ,{\alpha }_{j_{a_i}})\in A^{a_i}$:

$$\left\{\begin{array}{cc}{R}_i(d_{j_1},\dots ,d_{j_{a_i}})\hfill & \mathrm{If}({\alpha }_{j_1},\dots ,{\alpha }_{j_{a_i}})\in R_i^{\mathfrak{A}}\hfill \\ \neg R_i(d_{j_1},\dots ,d_{j_{a_i}})\hfill & \mathrm{If}({\alpha }_{j_1},\dots ,{\alpha }_{j_{a_i}})\notin R_i^{\mathfrak{A}}\hfill \end{array}\right.$$

(4)

(${\Gamma }_4$) function characterization statement:

For each function symbol $f_j$ and each tuple $({\alpha }_{k_1},\dots ,{\alpha }_{k_{b_j}})\in A^{b_j}$:

$$f_j(d_{k_1},\dots ,d_{k_{b_j}})=d_l$$

(5)

where l satisfies $f_j^{\mathfrak{A}}({\alpha }_{k_1},\dots ,{\alpha }_{k_{b_j}})={\alpha }_l$

(${\Gamma }_5$) Constant Characterization Statement:

$$c_i=d_j\mathrm{where}j\mathrm{satisfies}{c}_i^{\mathfrak{A}}={\alpha }_j$$

(6)

We define $\Gamma =\{{\Gamma }_1,{\Gamma }_2,{\Gamma }_3,{\Gamma }_4,{\Gamma }_5\}$. Next, we prove two lemmas.

Lemma 1. 

If $\mathfrak{B}\vDash \Gamma$, then $\left|B\right|=N$.

Proof of Lemma 1. 

By (${\Gamma }_1$), $\forall x\in B,\exists i\in \{1,\dots ,N\},x=d_i^{\mathfrak{B}}$, so $\left|B\right|\le N$. By (${\Gamma }_2$), $d_i^{\mathfrak{B}}\ne d_j^{\mathfrak{B}}$ for all $i\ne j$, so $\left|B\right|\ge N$. Therefore, $\left|B\right|=N$. □

Lemma 2. 

If $\mathfrak{B}\vDash \Gamma$, then the map $h:A\to B$ defined as $h\left({\alpha }_i\right)=d_i^{\mathfrak{B}}$ is a bijection.

Proof of Lemma 2. 

This follows directly from Lemma 1 and (${\Gamma }_2$). □

Next, we can prove the consequence of Theorem 2:

(⇒) If $\mathfrak{B}\cong \mathfrak{A}$, then $\mathfrak{B}\vDash \Gamma$:

Let $g:A\to B$ be an isomorphic mapping. Definition of $\mathfrak{B}$:

• $d_i^{\mathfrak{B}}=g\left({\alpha }_i\right)$
• $R_i^{\mathfrak{B}},f_j^{\mathfrak{B}},c_l^{\mathfrak{B}}$ are defined by isomorphic correspondences.
  By the definition of isomorphism, $\mathfrak{B}$ satisfies all statements in $\Gamma$.
  (⇐) If $\mathfrak{B}\vDash \Gamma$, then $\mathfrak{B}\cong \mathfrak{A}$:
  By Lemma 2, $h:A\to B$ is defined as $h\left({\alpha }_i\right)=d_i^{\mathfrak{B}}$, which is a bijection.
  Verify that h maintains the relationship:
  For any $({\alpha }_{j_1},\dots ,{\alpha }_{j_{a_i}})\in A^{a_i}$:

  $$\begin{array}{cc}\hfill & ({\alpha }_{j_1},\dots ,{\alpha }_{j_{a_i}})\in R_i^{\mathfrak{A}}\hfill \\ \hfill & \iff \mathfrak{B}\vDash R_i(d_{j_1},\dots ,d_{j_{a_i}})(\mathrm{by}\left({\Gamma }_3\right))\hfill \\ \hfill & \iff (d_{j_1}^{\mathfrak{B}},\dots ,d_{j_{a_i}}^{\mathfrak{B}})\in R_i^{\mathfrak{B}}\hfill \\ \hfill & \iff (h\left({\alpha }_{j_1}\right),\dots ,h\left({\alpha }_{j_{a_i}}\right))\in R_i^{\mathfrak{B}}\hfill \end{array}$$

  (7)

Verify that h holds:

For any $({\alpha }_{k_1},\dots ,{\alpha }_{k_{b_j}})\in A^{b_j}$, let $f_j^{\mathfrak{A}}({\alpha }_{k_1},\dots ,{\alpha }_{k_{b_j}})={\alpha }_l$

From (${\Gamma }_4$):

$$\begin{array}{cc}\hfill & \mathfrak{B}\vDash f_j(d_{k_1},\dots ,d_{k_{b_j}})=d_l\hfill \\ \hfill & \iff f_j^{\mathfrak{B}}(d_{k_1}^{\mathfrak{B}},\dots ,d_{k_{b_j}}^{\mathfrak{B}})=d_l^{\mathfrak{B}}\hfill \\ \hfill & \iff f_j^{\mathfrak{B}}(h\left({\alpha }_{k_1}\right),\dots ,h\left({\alpha }_{k_{b_j}}\right))=h\left({\alpha }_l\right)\hfill \\ \hfill & \iff f_j^{\mathfrak{B}}(h\left({\alpha }_{k_1}\right),\dots ,h\left({\alpha }_{k_{b_j}}\right))=h\left(f_j^{\mathfrak{A}}({\alpha }_{k_1},\dots ,{\alpha }_{k_{b_j}})\right)\hfill \end{array}$$

(8)

Verify that h remains constant:this is directly derived from (${\Gamma }_5$).

Thus, h is an isomorphism, $\mathfrak{B}\cong \mathfrak{A}$. □

We now derive the following corollaries.

Corollary 1 (Uniqueness). 

The set of axioms Γ uniquely determines $\mathfrak{A}$ in the sense of logical equivalence.

Corollary 2 (Completeness). 

For any first-order property φ on $\mathfrak{A}$, either $\Gamma \vDash \phi$ or $\Gamma \vDash \neg \phi$.

Proof of Corollary 2. 

Let $\phi$ be any first-order sentence. Since $\phi$ is a sentence, either $\mathfrak{A}\vDash \phi$ or $\mathfrak{A}\vDash \neg \phi$ must hold.

If $\mathfrak{A}\vDash \phi$, then, by Theorem 1, any structure $\mathfrak{B}$ satisfying $\Gamma$ is isomorphic to $\mathfrak{A}$, so $\mathfrak{B}\vDash \phi$. Therefore, $\Gamma \vDash \phi$.

If $\mathfrak{A}\vDash \neg \phi$, then similarly, $\Gamma \vDash \neg \phi$. □

Corollary 3 (Decidability). 

The set $\{\phi :\Gamma \vDash \phi \}$ is decidable.

Proof of Corollary 3. 

By Corollary 2, for any sentence $\phi$, we can directly verify that $\mathfrak{A}\vDash \phi$ on the finite structure $\mathfrak{A}$. If true, then $\Gamma \vDash \phi$; otherwise, $\Gamma \vDash \neg \phi$. □

3.2. Previous Research on the Formalization of Infinite Structures

Naturally, we will wonder whether or not all infinite structures, except finite ones, can be completely characterized by a set of first-order logic formulas.

Generally speaking, the answer is no. In fact, according to the research results of Skolem et al., even countable structures cannot be guaranteed to be fully described by first-order logic [23].

Theorem 3 (Skolem). 

The standard natural numbers are countable structures that cannot be characterized by first-order categoricity.

We omit the proof. The main idea of the proof is to introduce infinite elements through extension theory. Then, we use the compactness theorem to derive a non-standard model and conclude.

Of course, if we expand the tools from first-order logic to higher-order logic, we can expand the characterization capabilities of the logical language [24,25]:

Theorem 4 (Peano). 

Under standard second-order semantics, the second-order Peano axioms categorically characterize the structure of natural numbers. That is, if quantification over set variables is allowed, then the sequence of natural numbers can be uniquely characterized by second-order logic.

This result highlights the greater expressive power of second-order logic under standard semantics. It not only solves the problem of characterizing natural numbers but also reveals a fundamental property of the expressive power of logical systems—higher-order logic possesses greater expressiveness than first-order logic.

However, despite its greater expressiveness, higher-order logic still cannot represent all countable structures. The boundaries of the logical structures that higher-order logic can represent remain unresolved. This result reflects the fundamental tension between computability and logical expressiveness. Even the most powerful logical systems cannot fully “tame” the complexity of infinite structures. This perhaps reveals a certain irreducible complexity of mathematical reality.

At present, the problem of expressing mathematical structures still depends on the work done by Scott in 1965 [26].

Scott first introduced the concept of infinite logic:

Definition 8 (Infinitary logic $L_{{\omega }_1\omega }$). 

The language $L_{{\omega }_1\omega }$ is defined by the following rules:

1. 

Contains all atomic formulas of first-order logic.

2. 

If $\{{\varphi }_i:i\in I\}$ is a set of formulas and $\left|I\right|\le {\aleph }_0$, then ${\bigwedge }_{i\in I}{\varphi }_i$ and ${\bigvee }_{i\in I}{\varphi }_i$ are also formulas.

3. 

If ϕ is a formula and x is a variable, then $\exists x\varphi$ and $\forall x\varphi$ are formulas.

4. 

Every formula contains only a finite number of free variables.

Furthermore, he proposed the crucial isomorphism theorem in the article.

Theorem 5 (Scott’s isomorphism theorem, 1965). 

Let $\mathfrak{A}$ be a countable structure and $\mathcal{L}$ be a countable language. Then, there exists a $L_{{\omega }_1\omega }$ sentence ${\varphi }_{\mathfrak{A}}$ (called a Scott sentence of $\mathfrak{A}$), such that:

For any structure $\mathfrak{B}$,

$$\mathfrak{B}\vDash {\varphi }_{\mathfrak{A}}\iff \mathfrak{B}\cong \mathfrak{A}$$

(9)

That is, ${\varphi }_{\mathfrak{A}}$ completely characterizes the structure $\mathfrak{A}$ in an isomorphic sense.

Scott’s isomorphism theorem is more than just a technical result; it reveals that infinitely long formulas are a natural tool for dealing with infinite structures, and that abstract existence can be transformed into concrete constructions.

Scott’s isomorphism theorem not only solves a specific mathematical problem but also, more importantly, opens up a whole new research paradigm, influencing multiple branches of mathematics and still guiding development in related fields today. This makes it one of the most important achievements in mathematical logic of the 20th century.

3.3. Formalization of Conditional Infinite Structures

To address the problem that infinite structures are difficult to characterize using logic, we present and prove a slightly weaker but still highly universal theorem. First, we provide several definitions.

Definition 9 (Relationship maintenance). 

Let $\mathfrak{M}=(M,R_1,R_2,\dots ,R_k)$ be a structure where $R_i$ is a $n_i$-ary relation. Let ${\{{\mathfrak{M}}_j=(M_j,R_1^j,R_2^j,\dots ,R_k^j)\}}_{j\in \mathbb{N}}$ be an approximate sequence.

Relationship maintenance means:

$$\forall i\in \{1,2,\dots ,k\},\forall j\in \mathbb{N}:R_i^j=R_i\upharpoonright M_j^{n_i}$$

(10)

then

$$R_i^j=\{(a_1,\dots ,a_{n_i})\in M_j^{n_i}:(a_1,\dots ,a_{n_i})\in R_i\}$$

(11)

Definition 10 (A precise definition of recursive approximation). 

The structure $\mathfrak{M}=(M,R_1,\dots ,R_k)$ satisfies recursive approximation if and only if:

There exists a sequence ${\left\{{\mathfrak{M}}_n\right\}}_{n\in \mathbb{N}}$ where every ${\mathfrak{M}}_n=(M_n,R_1^n,\dots ,R_k^n)$ satisfies:

1. 

Monotonicity: ${\mathfrak{M}}_n\subseteq {\mathfrak{M}}_{n+1}\subseteq \mathfrak{M}$

2. 

Countability: $|M_n|={\aleph }_0$ for all n

3. 

Recursion: There exists a recursive function that computes the Scott sentence for each ${\mathfrak{M}}_n$

4. 

Density: $\overline{{\bigcup }_n{M}_n}=M$(in appropriate topology)

5. 

Relationship maintenance: $R_i^n=R_i\upharpoonright M_n^{ar\left(R_i\right)}$ for all $i,n$, where $ar\left(R_i\right)$ denotes the number of elements of the relation $R_i$

6. 

Asymptotic uniqueness: Any two sequences are isomorphic to themselves or to each other after adding a finite number of elements from M.

Definition 11 (Topology of Scott’s sentence space). 

We define a topology on the space of Scott sentences, which makes the convergence exact. We assume that the space is complete under this topology.

Define $\mathcal{S}$ as the space of all Scott sentences. For $\varphi ,\psi \in \mathcal{S}$, define the distance:

$$d(\varphi ,\psi )=\sum _{k=1}^{\infty }{2}^{-k}·d_k(\varphi ,\psi )$$

(12)

where:

$$d_k(\varphi ,\psi )={\displaystyle \frac{|{\mathit{Tp}}_k\left(\varphi \right)▵{\mathit{Tp}}_k\left(\psi \right)|}{|{\mathit{Tp}}_k\left(\varphi \right)\cup {\mathit{Tp}}_k\left(\psi \right)|}}$$

(13)

Here, ${\mathit{Tp}}_k\left(\varphi \right)$ denotes the set of k-types that occur in a structure satisfying ϕ, and ${\mathit{Tp}}_k\left(\mathfrak{M}\right)$ contains the “complete description” of all possible k-tuples in the structure $\mathfrak{M}$.

Definition 12 (Local finiteness). 

$$\forall k,\forall l\in \mathbb{N},|{\mathit{Tp}}_k\left({\varphi }_l\right)|={\aleph }_0$$

(14)

and

$$\forall k,\forall l\in \mathbb{N},|{\mathit{Tp}}_k\left({\varphi }_{l+1}\right)-{\mathit{Tp}}_k\left({\varphi }_l\right)|<\infty$$

(15)

Theorem 6 (Higher-order characterization theorem for recursive approximate structures). 

Suppose $\mathfrak{M}$ is an uncountable structure that satisfies recursive approximation and local finiteness. Then, there exists a higher-order theory $T_{\mathfrak{M}}$ such that, for every structure $\mathfrak{N}$,

$$\forall \mathfrak{N}\left(\mathfrak{N}\vDash T_{\mathfrak{M}}\iff \mathfrak{N}\cong \mathfrak{M}\right)$$

(16)

Here, we assume that higher-order logic can be infinitely quantified, that is, it satisfies the properties of infinite logic. We prove this conclusion step by step. First, we prove that the recursive approximation sequence is inherently unique.

Lemma 3 (Normality of approximate sequences). 

Assume $\mathfrak{M}$ satisfies recursive approximation, and $\left\{{\mathfrak{M}}_n\right\}$ and $\left\{{\mathfrak{M}}_n^{\prime }\right\}$ are two approximate sequences that satisfy the condition. Then, there exists an increasing function $h:\mathbb{N}\to \mathbb{N}$, such that:

$${\mathfrak{M}}_n\cong {\mathfrak{M}}_{h\left(n\right)}^{\prime }\mathit{for}\mathit{all}n$$

(17)

Proof of Lemma 3. 

By density, monotonicity, and asymptotic uniqueness, for any ${\mathfrak{M}}_n$, there exists a sufficiently large m, such that ${\mathfrak{M}}_n$ can be embedded in ${\mathfrak{M}}_m^{\prime }$.

Vice versa. Combined with countability, we obtain an isomorphism. □

Next, we define limit operations and related concepts.

Definition 13 (Limits of structural sequences). 

Let $\left\{{\mathfrak{M}}_n\right\}$ be an increasing countable sequence of structures. Definition:

$$\underset{n\to \infty }{lim}{\mathfrak{M}}_n=\left(\bigcup _n{M}_n,\bigcup _n{R}_1^n,\dots ,\bigcup _n{R}_k^n\right)$$

(18)

If the union of every relation is well-defined in the limit.

Lemma 4 (Existence and uniqueness of limits). 

If $\left\{{\mathfrak{M}}_n\right\}$ satisfies the conditions for recursive approximation, then the limit exists and is isomorphic to the original structure $\mathfrak{M}$.

Proof of Lemma 4. 

Existence: By monotonicity, ${\bigcup }_n{M}_n$ is well-defined. The union of relations is well-defined by the relation-preserving property.

Uniqueness: By density, ${\bigcup }_n{M}_n$ is dense in M. If $\mathfrak{M}$ has appropriate continuity (implied by the recursive approximation), then it is uniquely determined by the dense substructure. □

Next, we need to verify the convergence of Scott’s sequence of sentence.

Theorem 7 (Convergence Theorem). 

Under the recursive approximation, if the local finiteness condition is additionally satisfied, then the Scott sentence sequence $\left\{{\varphi }_n\right\}$ converges to ${\varphi }_{\infty }$ in the defined topology.

Proof of Theorem 7. 

For fixed k, consider the sequence:

$${\mathrm{Tp}}_k\left({\varphi }_1\right)\subseteq {\mathrm{Tp}}_k\left({\varphi }_2\right)\subseteq \dots \subseteq {\mathrm{Tp}}_k\left({\varphi }_{k_m}\right)$$

(19)

For any $ϵ$, we can choose K so that ${\sum }_{k=K+1}^{\infty }{2}^{-k}<\epsilon /2$.

Since each inclusion is a subset relation, we can exploit local finiteness. Let $N_k$ exist, such that when $m,n\ge N_k$:

$$d_k({\varphi }_m,{\varphi }_n)<2^{(k-1)}ϵ/K$$

(20)

So, there exists $N=max\{N_1,N_2,\dots ,N_K\}$, such that when $m,n\ge N$:

$$d_k({\phi }_n,{\phi }_{)}<2^{(k-1)}ϵ/N\mathrm{for}\mathrm{all}k\le K$$

(21)

Thus:

$$\begin{array}{cc}\hfill d({\phi }_n,{\phi }_m)& =\sum _{k=1}^{\infty }{2}^{-k}·d_k({\phi }_n,{\phi }_m)\hfill \\ \hfill & =\sum _{k=1}^K{2}^{-k}·2^{(k-1)}\epsilon /K+\sum _{k=K+1}^{\infty }{2}^{-k}·d_k({\phi }_n,{\phi }_{\infty })\hfill \\ \hfill & \le \epsilon /2+\sum _{k=K+1}^{\infty }{2}^{-k}·1\hfill \\ \hfill & <\epsilon /2+\epsilon /2=\epsilon \hfill \end{array}$$

(22)

Thus, we obtain a Cauchy sequence. Based on completeness, we prove that this sequence has a limit. Let us assume that its limit is ${\varphi }_{\infty }$. □

Next, we can construct a complete characterization theory:

$$T_{\mathfrak{M}}=T_{\mathrm{approximation}}\cup T_{\mathrm{limit}}\cup T_{\mathrm{unique}}\cup {\varphi }_{\infty }$$

(23)

$$T_{\mathrm{approximation}}=\left\{\exists {\left\{{\mathfrak{M}}_n\right\}}_n.\mathrm{Satisfies}\mathrm{the}\mathrm{recursive}\mathrm{approximation}\mathrm{condition}\right\}$$

(24)

$$T_{\mathrm{limit}}=\left\{\mathfrak{M}=\underset{n\to \infty }{lim}{\mathfrak{M}}_n\right\}$$

(25)

$$T_{\mathrm{unique}}=\left\{\mathrm{The}\mathrm{approximation}\mathrm{sequence}\mathrm{is}\mathrm{unique}\mathrm{under}\mathrm{isomorphism}\right\}$$

(26)

Finally, we prove Theorem 6;

Proof of Theorem 6. 

Assume $\mathfrak{N}\vDash T_{\mathfrak{M}}$, then $\mathfrak{N}$ has an approximate sequence $\left\{{\mathfrak{N}}_n\right\}$ that satisfies the same conditions.

By ${\varphi }_1,\dots ,{\varphi }_{\infty }$, the Scott sentence for each ${\mathfrak{N}}_n$ is identical to the corresponding ${\mathfrak{M}}_n$. By Scott’s theorem, ${\mathfrak{N}}_n\cong {\mathfrak{M}}_n$ for all n.

Construct an isomorphic sequence $f_n:{\mathfrak{M}}_n\to {\mathfrak{N}}_n$. By monotonicity, consistency, and Lemma 4, $\left\{f_n\right\}$ can be combined into a global isomorphism:

$$f=\bigcup _n{f}_n:\mathfrak{M}\to \mathfrak{N}$$

(27)

Verifying that f is indeed an isomorphism: Injectivity, by the injectivity and density of each $f_n$; Surjectivity, by the surjectivity and limit properties of each $f_n$; Homomorphism, by the preservation of relations. □

At this point, we have rigorously proved the theorem and obtained the most abstract formula for $\mathfrak{M}$, ${\varphi }_{\infty }$. Clarifying ${\varphi }_{\infty }$ will help researchers understand the logical nature of infinite structures and facilitate deeper research.

3.4. Formalization of Phenomena in Mathematics

As shown in Figure 2, based on the formal characterization of finite and infinite mathematical structures, we finally conclude the following:

Theorem 8.

The following classes of structures are logically characterizable.

1. 

Finite structures. There exists a first-order language L and a set of sentences Γ such that for any L-structure $\mathfrak{B}$,

$$\mathfrak{B}\vDash \Gamma ⟺\mathfrak{B}\cong \mathfrak{A}$$

(a complete characterization up to isomorphism; see Theorem 2).

2. 

Countable structures. There exists a Scott sentence $\varphi \left(\mathfrak{A}\right)$ in $L_{{\omega }_1,\omega }$, such that

$$\mathfrak{B}\vDash \varphi \left(\mathfrak{A}\right)⟺\mathfrak{B}\cong \mathfrak{A}$$

(a complete characterization up to isomorphism; see Theorem 5).

3. 

Uncountable structures satisfying “recursive approximation + local finiteness”. There exists a higher-order theory $T_{\mathfrak{M}}$ (allowing countably infinite conjunctions), such that

$$\mathfrak{N}\vDash T_{\mathfrak{M}}⟺\mathfrak{N}\cong \mathfrak{M}$$

(see Theorems 6 and 7).

Our theory demonstrates that, within the appropriate framework, nearly all mathematical phenomena—particularly discrete, algebraic, and finitely generated phenomena—can be meaningfully logically characterized. This is an important theoretical achievement that expands our understanding of the extent to which mathematics can be formalized.

However, the richness and complexity of mathematics mean that finding a precise logical expression is difficult. As mathematics develops, modern mathematics presents new challenges. Problems such as the explosion of parameter space, the breakdown of intuition, and insufficient tools make characterizing high-dimensional and abstract problems particularly difficult. This reminds us that mathematics has both a formal side and a side beyond formalism. A perfect logical characterization may be a guiding principle, guiding us to continuously deepen our understanding, but it should not be mistaken for a fully achievable ultimate goal.

4. State Expression in Economics and Sociology

This section treats economics and sociology in parallel and begins with finite structures. Logical formalization in economics reduces ambiguity, enforces precise assumptions, and scales to multi-agent, multi-constraint settings. It also provides a common language to compare and integrate schools of thought. We begin with finite economic structures.

4.1. Logical Characterization in the Field of Economics

The logical characterization of economics is of fundamental significance to the development of the discipline and is also one of the hot issues in research [27,28,29]. First, logical representation can eliminate ambiguity and vagueness in economic theory. Traditional textual descriptions often allow for multiple interpretations, while logical formalization requires precise definitions of each concept and relationship, forcing theorists to clearly express their assumptions and reasoning. For example, when we say “demand is negatively correlated with price,” a logical representation requires us to specify under what conditions, for which goods, and over what timeframe this relationship holds true.

Furthermore, economics deals with complex systems involving multiple agents, multiple levels, and multiple variables, involving interactions between diverse actors such as consumers, businesses, and governments [30]. When a theory becomes complex, natural language descriptions often fail to accurately capture all logical relationships and constraints. Logical representations provide a structured approach to organizing these complex relationships, ensuring the internal consistency and integrity of the theory [31]. For example, when analyzing market equilibrium, we need to simultaneously consider multiple constraints, such as the supply equation, the demand equation, and market-clearing conditions. Logical representations can clearly demonstrate the logical dependencies between these conditions.

At the same time, considering that there are multiple schools and theoretical frameworks within economics, such as neoclassical economics, Keynesianism, institutional economics, etc. [32], different theoretical frameworks utilize different conceptual systems and analytical methods, making academic dialogue difficult. Logical representation provides a unified language for different theories, enabling theoretical comparison, integration, and synthesis. Researchers can more easily identify commonalities and divergences between different theories, promoting the integration and development of theories.

Therefore, the importance of logical characterization in the field of economics is self-evident. Here we first consider the logical characterization of finite economic structures.

Definition 14 (Economic structure). 

An economic structure $\mathfrak{S}$ can be represented as follows:

$$\mathfrak{S}=(A,R_1,R_2,\dots ,F_1,F_2,\dots ,P_1,P_2,\dots )$$

(28)

where:

• A is a set of agents (individuals, enterprises, institutions, etc.)
• $R_i$ is a relationship (social network, hierarchy, transaction relationship, etc.)
• $F_j$ is a function (utility function, production function, decision rule, etc.)
• $P_k$ is a process (market mechanism, institutional evolution, information dissemination, etc.)

Definition 15 (The logical language of economic structure). 

The basic language ${\mathcal{L}}_{SE}$ Contains:

Individual constants:

• $a_1,a_2,\dots$ represent specific agent individuals, enterprises, organizations, etc.

Variables:

• $x,y,z$ denote agent variables, t denotes time variables, and s denotes state variables.

Predicate symbols:

• $Agent\left(x\right)$: x is an agent.
• $Transitio{n}_{P_k}(s,s^{\prime })$: represents the transition from state s to state $s^{\prime }$ under process $P_k$.
• $TransitionConditio{n}_k(s,s^{\prime })$: indicates that the transition from state s to state $s^{\prime }$ under process $P_k$ satisfies the prescribed condition.

Theorem 9 (First-order representability of finite economic structures). 

Let $\mathfrak{S}=(A,R_1,R_2,\dots ,F_1,F_2,\dots ,P_1,P_2,\dots )$ be a finite economic structure, that is:

1. 

$\left|A\right|<\infty$ (Finite Agents)

2. 

Every relation $R_i$ and function $F_j$ is defined over a finite domain and has corresponding predicate and function representations in the base language.

3. 

The process $P_k$ involves finite states and finite time.

Then there exists a set of first-order formulas Φ, such that:

$$\forall \mathfrak{T},\mathfrak{T}\vDash \Phi \iff \mathfrak{T}\cong \mathfrak{S}$$

(29)

Proof of Theorem 9 

Domain characterization:

$${\varphi }_{\mathrm{domain}}=\forall x(Agent\left(x\right)\to \underset{i=1}{\overset{\left|A\right|}{\bigvee }}x=a_i)\wedge \underset{i\ne j}{\bigwedge }{a}_i\ne a_j$$

(30)

Characterization of relationships: For each relation $R_i\subseteq A^{n_i}$:

$${\varphi }_{R_i}=\forall x_1\dots x_{n_i}(R_i(x_1,\dots ,x_{n_i})\leftrightarrow \underset{(a_{j_1},\dots ,a_{j_{n_i}})\in R_i}{\bigvee }(x_1=a_{j_1}\wedge \dots \wedge x_{n_i}=a_{j_{n_i}}))$$

(31)

Function description: For each function $F_j:A^{m_j}\to D_j$ (where the range $D_j$ is finite):

$${\varphi }_{F_j}=\forall x_1\dots x_{m_j}\exists !y(F_j(x_1,\dots ,x_{m_j})=y\wedge y\in D_j)$$

(32)

Description of the process: For each process $P_k$, if it involves a finite state transition:

$${\varphi }_{P_k}=\forall s\forall s^{\prime }(Transitio{n}_{P_k}(s,s^{\prime })\to {\mathrm{TransitionCondition}}_k(s,s^{\prime }))$$

(33)

Complete formula:

$$\Phi =\{{\varphi }_{\mathrm{domain}},{\varphi }_{R_1},{\varphi }_{R_2},\dots ,{\varphi }_{F_1},{\varphi }_{F_2},\dots ,{\varphi }_{P_1},{\varphi }_{P_2},\dots \}$$

(34)

Since all components are finite, every formula is first-order, and $\Phi$ completely characterizes the structure $\mathfrak{S}$, we have proved the result. □

From the proof, we can see that structural finiteness has a profound impact on the construction of economic theory. It means that economic models need to pay more attention to boundary conditions, constrained optimization, and finite games. At the same time, finiteness also provides a more realistic foundation for economic analysis, making theoretical predictions more closely aligned with actual economic phenomena.

Theorem 10.

In the framework of first-order and higher-order logical theories, if the domains of the relations/functions involved in an economic structure, as well as the time/state sets, are all finite, then the structure can be completely characterized.

Given that empirical applications often fix finite sets of agents, goods, periods, and constraints, many practical economic models admit complete first-order specifications for a fixed instance.

Here, we give an example to verify how logic represents economic phenomena and structures. Lowercase letters represent variables.

Table 1. Predicate definition.

Symbol	Definition
$Demand(i,g,p,q)$	The quantity q demanded by consumer i for good g at price p is q
$Consumer\left(i\right)$	i is a consumer
$Good\left(g\right)$	g is a commodity
$Price\left(p\right)$	p is a valid price (non-negative)
$Quantity\left(q\right)$	q is a valid quantity (non-negative)
$MaximizesUtility(i,b,constraint)$	Consumer i chooses a bundle of goods b to maximize utility under constraints
$BudgetConstraint(i,p,income)$	Consumer i’s budget constraint under price p and income $income$
$Income\left(i\right)$	Income of consumer i
$Contains(b,g,q)$	The bundle b contains a quantity q of the good g
$Supply(f,g,p,q)$	The supply of good g by firm f at price p is q
$Firm\left(f\right)$	f is an enterprise (production unit)
$ProfitMaximizing(f,v,q_{bundle},p,w)$	Firm f chooses input v and output $q_{bundle}$ to maximize profit under price p and factor price w

gives the definition of predicates

Definition 16. Definition of Supply and Demand: 

$$\begin{array}{cc}\hfill Demand(i,g,p,q)& \leftrightarrow Consumer\left(i\right)\wedge Good\left(g\right)\wedge Price\left(p\right)\wedge Quantity\left(q\right)\wedge \hfill \\ \hfill & \exists b\left(MaximizesUtility\right(i,b,BudgetConstraint(i,p,\mathrm{Income}(i\left)\right))\wedge \hfill \\ \hfill & Contains(b,g,q))\hfill \end{array}$$

(35)

$$\begin{array}{cc}\hfill Supply(f,g,p,q)& \leftrightarrow Firm\left(f\right)\wedge Good\left(g\right)\wedge Price\left(p\right)\wedge Quantity\left(q\right)\wedge \hfill \\ \hfill & \exists v,q_{bundle}(ProfitMaximizing(f,v,q_{bundle},p,w)\wedge \hfill \\ \hfill & Contains(q_{bundle},g,q))\hfill \end{array}$$

(36)

In Appendix A.3, we present another example related to economics. Here, we outline its basic setup in Figure 3.

4.2. Logical Characterization in the Field of Sociology

The reason why social structures require logical representations is closely related to their inherent complexity and abstractness, and these needs are even more pressing than in economics [33].

Logical formalization in sociology reduces ambiguity, enforces precise assumptions, and scales to settings with many actors, relations, and constraints. Social phenomena typically involve multi-relational networks (e.g., kinship, power, exchange, culture), heterogeneous attributes, and context-dependent mechanisms. Natural-language descriptions often under-specify transitivity, symmetry, hierarchy, or diffusion effects; a logical representation makes such properties explicit and checkable. Just as in economics, a common logical language also facilitates comparison and integration across theoretical traditions (e.g., structuralism, network analysis, institutional theory), enabling cumulative, interoperable models.

We begin with finite social structures and show that, when agents, relations, and time/state sets are finite, they admit complete first-order specifications for a fixed instance. We then illustrate how typical sociological claims—such as influence through friendship ties, formation of network closures, or role/attribute constraints—translate into predicates and sentences that support reasoning, measurement, and verification [34].

The first-order logic description of social structure is similar to that of economic structure. Here, we only give the theorem.

Theorem 11 (First-order representability of finite social structures). 

Let $\mathfrak{S}=(A,R_1,R_2,\dots ,F_1,F_2,\dots ,P_1,P_2,\dots )$ be a finite social structure, that is:

1. 

$\left|A\right|<\infty$ (finite agent)

2. 

Each relation $R_i$ and function $F_j$ is defined over a finite domain and has corresponding predicate and function representations in the base language.

3. 

The process $P_k$ involves finite states and finite time.

Then, there exists a set of first-order formulas Φ such that:

$$\forall \mathfrak{T},\mathfrak{T}\vDash \Phi \iff \mathfrak{T}\cong \mathfrak{S}$$

(37)

Theorem 12.

In the framework of first-order and higher-order logical theories, if the domains of the relations/functions involved in an social structure, as well as the time/state sets, are all finite, then the structure can be completely characterized.

Similarly, considering the limitations of social structure, we can draw a conclusion. Within the theoretical framework of first-order and higher-order logic, almost all social structures can be fully characterized. Through logical representation, sociology can not only describe social phenomena more accurately but also discover hidden social laws, providing more powerful theoretical tools for understanding and improving social structure.

Here, we give an example of logical representation.

Table 2. Semantic interpretation table of sociological predicates.

Predicate	Semantic Meaning
$Friend(x,y)$	x and y are friends
$Smokes\left(x\right)$	x smokes
$Influenced(x,y)$	x is affected by y
$HigherSmokingProbability\left(x\right)$	x has a higher probability of smoking
$SocialNetwork(x,y)$	x and y are in the same social network

gives the definition of predicates.

Through the given predicate, we can express the state of the smoking phenomenon in sociology. Here, HigherSmokingProbability(x) is abbreviated as HSP(x).

Definition 17 (Expressions related to smoking). 

$$\begin{array}{cc}\hfill {\varphi }_1& =\forall x,y\left(Friend\right(x,y)\to Friend(y,x\left)\right)\hfill \end{array}$$

(38)

$$\begin{array}{cc}\hfill {\varphi }_2& =\forall x,y\left(Friend\right(x,y)\wedge Smokes(y)\to Influenced(x,y\left)\right)\hfill \end{array}$$

(39)

$$\begin{array}{cc}\hfill {\varphi }_3& =\forall x,y\left(Influenced\right(x,y)\to HSP(x\left)\right)\hfill \end{array}$$

(40)

$$\begin{array}{cc}\hfill {\varphi }_4& =\forall x,y,z\left(Friend\right(x,y)\wedge Friend(y,z)\to SocialNetwork(x,z\left)\right)\hfill \end{array}$$

(41)

To better demonstrate how our formalization can be applied to sociological practice—and to answer how a rigorous definition of state informs the choice of the eleven metrics in OIT—we present another example related to a census.

Table 3. Census information form.

Person	Age	Height	Gender	Occupation
A	22	179	Male	Student
B	54	158	Female	Teacher

gives an example of a census table.

In social surveys, researchers often need to tabulate extensive information about large populations—such as age, height, gender, and occupation—into tables or similar formats. Faced with a profusion of states and information, however, how to reasonably estimate information quantity has long been a challenge for sociologists.

When we translate the observed sociological states into logical statements, individuals naturally correspond to constants, while age, height, gender, occupation, and the like naturally correspond to predicates.

A row in the census table translates into a single existential statement over individual constants and attribute predicates, for example:

$$\exists x(x=a\wedge \mathrm{Age}(x,22)\wedge \mathrm{Height}(x,179)\wedge \mathrm{Male}(x)\wedge \mathrm{Occupation}(x,\mathrm{Student}\left)\right)$$

(42)

In this setting, according to the eleven metrics involved in OIT, the number of predicate types corresponds to variety; the number of instantiated records corresponds to volume. This yields a natural measurement of information and enables corresponding computations. In other words, formalization provides a measurable scale for the operationalization of concepts and variables in sociology and beyond, allowing researchers to use OIT’s metrics to quantify the uncertainty and structure inherent in observations, surveys, texts, or behavioral data.

5. Computer Field State Expression

In computer science, logic plays an irreplaceable role as a fundamental tool for expressing states. In program verification, Hoare logic precisely describes the state of each execution point of a program through preconditions, postconditions, and invariants, enabling rigorous proof of program correctness. In database systems, first-order logic is not only used to define the semantics of query languages but also characterizes the legal state space of data through integrity constraints. In the field of formal methods, temporal logic (such as LTL and CTL) can express the dynamic behavior and safety properties of systems in the time dimension, providing a mathematical foundation for modeling concurrent and real-time systems. Planning problems in artificial intelligence are essentially about finding a path from an initial state to a target state in the state space described by logic. In hardware design, Boolean logic directly corresponds to the physical state of circuits, enabling the design of complex digital systems. This abstract expressive power of logic not only provides a unified mathematical framework for modeling complex systems but, more importantly, enables automated reasoning and verification. From compiler optimization analysis to operating system resource management and from network protocol correctness verification to interpretability analysis of machine learning models, logic plays a critical role in translating intuitive concepts into computable forms [35,36,37].

5.1. Boolean Algebra and the Formalization of Computer Systems

Boolean algebra and logical representation are core areas of computer science and mathematical logic [38,39]. First, we verify that Boolean algebra can be formalized using first-order logic.

Theorem 13 (Axiomatizability of Boolean algebras in FOL). 

All axioms and operations of Boolean algebra can be expressed using first-order logic (FOL).

Proof of Theorem 13. 

Boolean algebra is defined as a set B, binary operations $\wedge ,\vee$, unary operations ¬, constants $0,1$, and the following axioms:

$$\begin{array}{cc}\hfill & \forall a,b\in B:a\wedge b=b\wedge a\hfill \end{array}$$

(43)

$$\begin{array}{cc}\hfill & \forall a\in B:a\vee \neg a=1\hfill \end{array}$$

(44)

$$\begin{array}{cc}\hfill & \forall a,b,c\in B:a\wedge (b\vee c)=(a\wedge b)\vee (a\wedge c)\mathrm{etc}.\hfill \\ \hfill \end{array}$$

(45)

Its axioms are first-order sentences; each algebra is an L-structure; hence, BA is axiomatizable in FOL. Therefore, the theorem is proved. □

Boolean algebra is the foundation of computer systems. The logic gates in digital circuits, conditional branching in programs, propositional calculus, and automata are all based on Boolean algebra. Operations, states, and transitions can all be reduced to Boolean algebraic expressions.

Because the entire content of Boolean algebra can be expressed using first-order logic, and computer systems can be reduced to Boolean algebraic structures, its core content can also be expressed using first-order logic. Practical applications such as model checking, hardware verification, and theorem proving have extensively employed first-order logic for modeling and reasoning.

Theorem 14.

Computer systems can be formally expressed in first-order logic.

5.2. Predicate Logic Description of a Turing Machine (TM)

Figure 4 shows a sketch of a Turing machine.

Definition 18.

Similar to finite state machines, Turing machines can be formally expressed. A deterministic Turing machine (DTM) can be represented as a seven-tuple:

$$M=(Q,\Gamma ,\Sigma ,\delta ,q_0,q_{\mathit{accept}},q_{\mathit{reject}})$$

(46)

where:

• Q is a finite state set.
• Γ is the set of tape symbols (including the blank symbol ⊔).
• $\Sigma \subseteq \Gamma$ is the set of input symbols (excluding ⊔).
• $\delta :Q\times \Gamma \to Q\times \Gamma \times \{L,R\}$ is the state transition function, where L and R indicate whether the read/write head moves left or right.
• $q_0\in Q$ is the initial state.
• $q_{\mathit{accept}},q_{\mathit{reject}}\in Q$ are the accept and reject states, respectively.

To represent a Turing machine, we can define the following predicates and give the corresponding state expressions:

Definition 19 (Predicate Definition and State Expression). 

The predicates and states in a Turing machine can be expressed as:

• State: $\mathit{State}\left(q\right)$ indicates that q is a state.

  $${\varphi }_1=\forall q(\mathit{State}\left(q\right)\to q\in Q)$$

  (47)
• Tape Symbol: $\mathit{TapeSymbol}\left(a\right)$ indicates that a is a tape symbol.

  $$\forall a\left(\mathit{TapeSymbol}\right(a)\to a\in \Gamma )$$

  (48)
• Tape content: $\mathit{Cell}(t,p,a)$ indicates that a is the tape symbol at time t and position p.

  $$\forall t\forall p\forall a\left(\mathit{Cell}\right(t,p,a)\to a\in \Gamma )$$

  (49)
• Read/Write Head Position: $\mathit{Head}(t,p)$ indicates that the head is at position p at time t.

  $$\forall t\exists p\mathit{Head}(t,p)$$

  (50)
• Transition function: $Transition(q,a,q^{\prime },a^{\prime },d)$ represents state transition, where d is the direction.

  $$\forall q\forall a\forall q^{\prime }\forall a^{\prime }\forall d(\mathit{Transition}(q,a,q^{\prime },a^{\prime },d)\leftrightarrow \delta (q,a)=(q^{\prime },a^{\prime },d))$$

  (51)
• Initial state: $Initial\left(q\right)$ represents the initial state q.

  $$\exists q_0(\mathit{Initial}\left(q_0\right)\wedge \mathit{State}\left(q_0\right))$$

  (52)
• Accept state (similar to the rejection state): $Accept\left(q\right)$ indicates that q is an accepting state.

  $$\forall q(\mathit{Accept}\left(q\right)\leftrightarrow q=q_{\mathit{accept}})$$

  (53)

Based on the above definition of predicates and the corresponding Turing machine state representation and state transition representation, we derive the theorem:

Theorem 15 (Turing Machine State Representation). 

For any Turing machine, its input, output, and state transition behavior over a relevant time set can be described using a state set.

Before Turing, concepts such as “computation,” “algorithm,” and “efficient process” were intuitive. Mathematicians knew what computation was but could not give a rigorous mathematical definition. The logical representation of the Turing machine was the first to transform these intuitive concepts into precise mathematical objects: state sets, symbol sets, transition functions, initial states, and accepting states. This formalization enables us to use mathematical methods to study the properties of computation itself [40].

5.3. Mathematical Formalization of Neural Networks

Neural networks (NNs) are machine learning models that mimic the structure and function of biological neural systems, capable of learning complex patterns from data and making predictions or decisions [41]. They are a core technology in deep learning and are widely used in fields such as computer vision, natural language processing, and speech recognition.

First, let us briefly introduce neural networks. A neural network can be represented as a function $\mathcal{N}:{\mathbb{R}}^n\to {\mathbb{R}}^m$, whose hierarchical structure is decomposed into:

$$\mathcal{N}\left(x\right)={\sigma }_L\left(W_L·{\sigma }_{L-1}\left(W_{L-1}\dots {\sigma }_1(W_{1}x+b_1)\dots \right)+b_L\right)$$

(54)

where: input layer: $x\in {\mathbb{R}}^n$, hidden layer: $h_l={\sigma }_l\left(W_l{h}_{l-1}\right)$, output layer: $\mathcal{N}\left(x\right)\in {\mathbb{R}}^m$, weight matrix: $W_l\in {\mathbb{R}}^{d_l\times d_{l-1}}$, bias vector: $b_l\in {\mathbb{R}}^{d_l}$, activation function: ${\sigma }_l:{\mathbb{R}}^{d_l}\to {\mathbb{R}}^{d_l}$

Single neuron calculation:

$$\sigma (w^{T}x+b)=\sigma \left(\sum _{i=1}^n{w}_i{x}_i+b\right)$$

(55)

Neural networks, by simulating the connections of the human brain, enable efficient modeling of complex data. With advances in computing power and algorithms (e.g., GPUs and attention mechanisms), their capabilities are continuously expanding, becoming the driving force behind the AI revolution.

Next, we demonstrate that the relevant aspects of neural networks can be formally expressed.

Proposition 1.

Neural networks can be formally expressed in first-order and higher-order logic.

Proof of Proposition 1. 

The first step is to logically represent a single neuron in a neural network.

Definition 20 (Neuron Triplet).

A neuron can be represented as $\mathcal{N}=(w,b,\sigma )$, where $w\in {\mathbb{R}}^n$ represents the weight vector, $b\in \mathbb{R}$ represents the bias term, and $\sigma :\mathbb{R}\to \mathbb{R}$ represents the activation function.

Using the neuron triple model, we can see that the neuron input–output relationship can be logically represented as follows:

$$\forall x\in {\mathbb{R}}^n,\exists z,a\in \mathbb{R},\left(z=\sum _{i=1}^n{w}_i{x}_i+b\right)\wedge \left(a=\sigma \left(z\right)\right)$$

(56)

Next, we express the activation function in the neural network. Activation functions are real-valued functions. Over real closed fields, one can encode piecewise-linear activations (e.g., ReLU) via linear constraints with slack variables; smooth activations require either algebraic approximations or $\delta$-decision procedures.

Finally, we demonstrate the logical representation of the network topology. Taking a simple fully connected layer as an example:

• Feedforward Network: $Connected(u,v)$ indicates the connection between $u,v$, and $Laye{r}_l$ indicates the lth layer.

  $$\begin{array}{cc}\hfill & \forall l\in \{1,...,L\},\forall u\in {\mathrm{Layer}}_l,\forall v\in {\mathrm{Layer}}_{l+1},\hfill \\ \hfill & \mathrm{Connected}(u,v)\wedge \neg \exists k<l\left(\mathrm{Connected}(v,{\mathrm{Layer}}_k)\right).\hfill \end{array}$$

  (57)
• Hierarchical Combination: $Network\left(x\right)$ indicates the hierarchical combination structure of x.

  $$\exists \mathrm{Network}:({\mathbb{R}}^{d_0}\to {\mathbb{R}}^{d_L}),\mathrm{Network}\left(x\right)={\sigma }_L\circ W_L\circ \dots \circ {\sigma }_1\circ W_1\left(x\right)$$

  (58)
• Combinatorial Completeness: If the lth layer can be represented as ${\Phi }_l$, then the $l+1$th layer can be represented as:

  $${\Phi }_{l+1}=\exists y_l,{\Phi }_l(x,y_l)\wedge \left(y_{l+1}={\sigma }_{l+1}(W_{l+1}{y}_l+b_{l+1})\right)$$

  (59)

This completes the argument. □

According to the theorem, from a theoretical perspective, there is a profound equivalence between neural networks and logical systems. Neural networks can discover strategic patterns that humans have never discovered. If these patterns can be expressed in logical form, they may be transformed into verifiable scientific theories. This fusion is not just a technological advancement; it also represents a deepening of our understanding of the nature of intelligence: intelligence requires both the ability to learn from experience and the ability to reason based on rules, and the logical representation of neural networks is the key bridge connecting the two.

5.4. Formal Expression of States in Computer Science

According to previous proofs, computer systems, Turing machines, and neural networks can all be formalized using first-order and higher-order logic. Scholars have also formalized phenomena such as computational concepts, programming languages, and algorithmic processes [9,42,43]. Accordingly, to better articulate the theoretical claims, we provide an example of how a finite automaton can be formally expressed, which is included in Appendix A.2.

Theorem 16.

The following mainstream models can be formalized within specified logical fragments:

1. 

Boolean circuits, finite automata, and finite-state concurrent models: first-order logic can completely characterize any fixed instance.

2. 

Turing machines’ state evolution and computability statements: their behavior and halting properties can be expressed in extensions of first-order or second-order arithmetic/set theory.

3. 

Neural networks (with finite depth/width over a given real field or its axiomatization): their topology and forward computation can be described in first- or higher-order logic.

Theorem 16 demonstrates that logic provides a unified framework for expressing different computational models. Logical formalization has transformed computer science from an engineering craft into a rigorous scientific discipline, providing powerful tools for understanding and controlling complex systems. Furthermore, emerging problems in computer science can be gradually formalized using the proof process of neural networks. Based on this, we draw a comprehensive conclusion.

6. State Expression in Natural Language Domain

Natural languages, such as Chinese, English, and Arabic, are the languages humans use in everyday life. They are essential tools for communicating ideas and conveying information. In contrast to formal languages, they possess unique properties. Natural languages are richly expressive, capable of expressing myriad worlds, complex emotions, and abstract concepts. This chapter introduces Montague semantics, explores the rules governing the grammar and semantic translation of natural languages, and achieves a formal understanding of natural languages through the principles of formalized mathematical logic.

6.1. Montague Semantics

Montague semantics, also known as Montague grammar, is a formalized approach to the study of natural semantics, particularly intensional semantics. It represents a new stage in the development of linguistics and logic.

Montague’s research began with the concept of categories, dividing English syntax into distinct categories. Montague introduced a system of syntactic categories and formation rules for English, defined meaningful expressions via recursion, interpreted them using model theory, and provided corresponding semantic translation rules [44].

Based on Montague’s work, Bennett conducted further research. He refined the English categories, dividing adjectives into separate categories; introduced more complex grammatical and semantic translation rules, expanding the rules from 17 to 35; and provided a solid theoretical foundation for language research using Montague semantics [45].

6.2. Study of English Ambiguity

Correctly handling linguistic ambiguity is an important indicator of semantic comprehension. Here, we use Montague grammar to provide an interpretation of ambiguity.

“At least one person likes the book” is a common ambiguous phrase in English. The ambiguity of “at least one person likes the book” stems from the ambiguity of the quantifier scope. Without context, “the book” could refer to a specific book or to a general term.

The semantics of the sentence “At least one person likes the book” can be formally modeled using the $\lambda$ calculus, with two possible interpretations: a broad interpretation and a narrow interpretation.

In the broad interpretation, “the book” refers to a specific book b. The logical form of the entire sentence is:

$$\exists x[ma{n}^{\prime }\left(x\right)\wedge lik{e}^{\prime }\left(\widehat{\phantom{x}}{b}^{\prime }\right)\left(x\right)]$$

(60)

where:

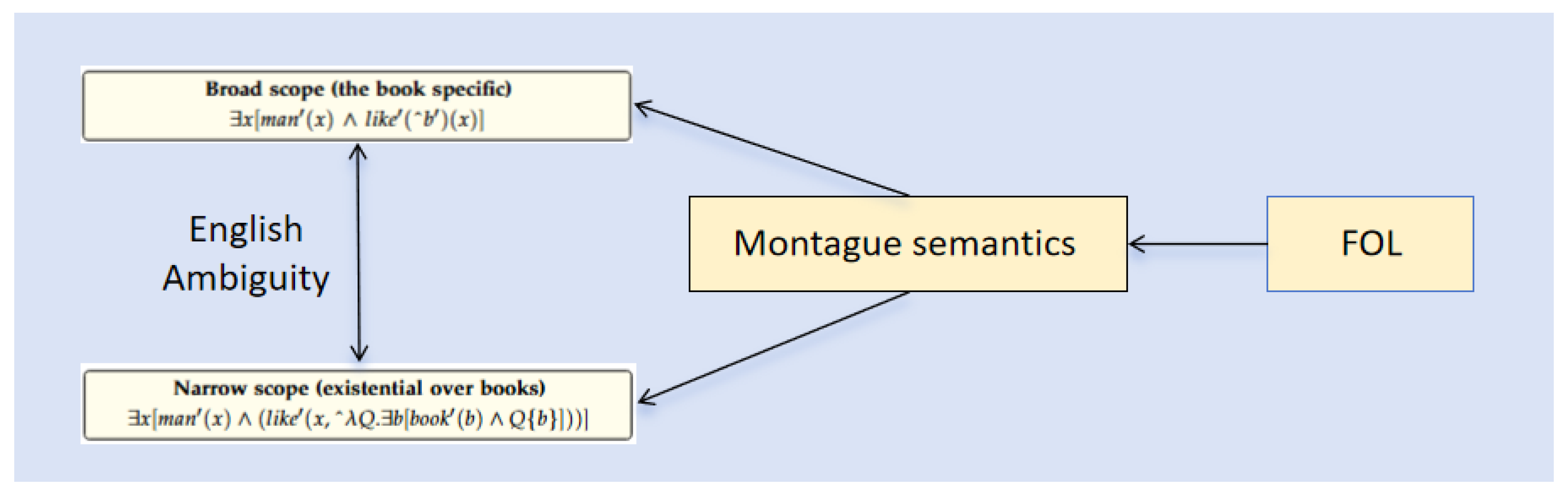
• $ma{n}^{\prime }\left(x\right)$ means x is a person;
• $lik{e}^{\prime }\left(\widehat{\phantom{x}}{b}^{\prime }\right)\left(x\right)$ means x likes a specific book b.

The specific $\lambda$ calculus combination process is as follows:

$$\begin{array}{cc}\hfill \mathrm{Like}& :lik{e}^{\prime }\hfill \\ \hfill \mathrm{The}\mathrm{book}& :b^{\prime }\hfill \\ \hfill \mathrm{Like}\mathrm{the}\mathrm{book}& :lik{e}^{\prime }\left(\widehat{\phantom{x}}{b}^{\prime }\right)\hfill \\ \hfill \mathrm{At}\mathrm{least}\mathrm{one}\mathrm{person}& :\lambda P.\exists x[ma{n}^{\prime }\left(x\right)\wedge P\left\{x\right\}]\hfill \\ \hfill \mathrm{Combination}\mathrm{result}& :\lambda P.\exists x[ma{n}^{\prime }\left(x\right)\wedge P\left\{x\right\}]\left(\widehat{\phantom{x}}lik{e}^{\prime }\left(\widehat{\phantom{x}}{b}^{\prime }\right)\right)\hfill \\ \hfill \lambda \mathrm{transposition}& :\exists x[ma{n}^{\prime }\left(x\right)\wedge \widehat{\phantom{x}}lik{e}^{\prime }\left(\widehat{\phantom{x}}{b}^{\prime }\right)\left\{x\right\}]\hfill \\ \hfill \mathrm{Bracket}\mathrm{convention}& :\exists x[ma{n}^{\prime }\left(x\right)\wedge \check{\phantom{x}}\widehat{\phantom{x}}lik{e}^{\prime }\left(\widehat{\phantom{x}}{b}^{\prime }\right)\left(x\right)]\hfill \\ \hfill \mathrm{Top}\mathrm{and}\mathrm{bottom}\mathrm{elimination}& :\exists x[ma{n}^{\prime }\left(x\right)\wedge lik{e}^{\prime }\left(\widehat{\phantom{x}}{b}^{\prime }\right)\left(x\right)]\hfill \end{array}$$

In the narrow-scope interpretation, “the book” is not a specific object but a quantifiable range. The logical form of the sentence is:

$$\exists x[ma{n}^{\prime }\left(x\right)\wedge \left(lik{e}^{\prime }(x,\widehat{\phantom{x}}\lambda Q.\exists b[boo{k}^{\prime }\left(b\right)\wedge Q\left\{b\right\}])\right)]$$

(61)

where:

• $boo{k}^{\prime }\left(b\right)$ indicates that b is a book;
• $\left(lik{e}^{\prime }(x,\widehat{\phantom{x}}\lambda Q.\exists b[boo{k}^{\prime }\left(b\right)\wedge Q\left\{b\right\}])\right)$ indicates that there exists at least one person x, there exists a book b, and this person likes book b.

The specific $\lambda$ calculus combination process is as follows:

$$\begin{array}{cc}\hfill \mathrm{Like}& :lik{e}^{\prime }\hfill \\ \hfill \mathrm{At}\mathrm{least}\mathrm{one}\mathrm{person}& :\lambda P.\exists x[ma{n}^{\prime }\left(x\right)\wedge P\left\{x\right\}]\hfill \\ \hfill \mathrm{The}\mathrm{book}\mathrm{exists}& :\lambda Q.\exists b[boo{k}^{\prime }\left(b\right)\wedge Q\left\{b\right\}]\hfill \\ \hfill \mathrm{Like}\mathrm{the}\mathrm{book}& :lik{e}^{\prime }(\widehat{\phantom{x}}\lambda Q.\exists b[boo{k}^{\prime }\left(b\right)\wedge Q\left\{b\right\}])\hfill \\ \hfill \mathrm{Combination}\mathrm{result}& :\lambda P.\exists x[ma{n}^{\prime }\left(x\right)\wedge P\left\{x\right\}]\left(\widehat{\phantom{x}}lik{e}^{\prime }(\widehat{\phantom{x}}\lambda Q.\exists b[boo{k}^{\prime }\left(b\right)\wedge Q\left\{b\right\}])\right)\hfill \\ \hfill \lambda \mathrm{Transposition}& :\exists x[ma{n}^{\prime }\left(x\right)\wedge \left(\widehat{\phantom{x}}lik{e}^{\prime }(\widehat{\phantom{x}}\lambda Q.\exists b[boo{k}^{\prime }\left(b\right)\wedge Q\left\{b\right\}])\right)\left\{x\right\}]\hfill \\ \hfill \mathrm{Bracket}\mathrm{convention}& :\exists x[ma{n}^{\prime }\left(x\right)\wedge \left(\check{\phantom{x}}\widehat{\phantom{x}}lik{e}^{\prime }(\widehat{\phantom{x}}\lambda Q.\exists b[boo{k}^{\prime }\left(b\right)\wedge Q\left\{b\right\}])\right)\left(x\right)]\hfill \\ \hfill \mathrm{Up}\mathrm{and}\mathrm{Down}\mathrm{Elimination}& :\exists x[ma{n}^{\prime }\left(x\right)\wedge \left(lik{e}^{\prime }(\widehat{\phantom{x}}\lambda Q.\exists b[boo{k}^{\prime }\left(b\right)\wedge Q\left\{b\right\}])\right)\left(x\right)]\hfill \\ \hfill \mathrm{Relational}\mathrm{notation}& :\exists x[ma{n}^{\prime }\left(x\right)\wedge \left(lik{e}^{\prime }(x,\widehat{\phantom{x}}\lambda Q.\exists b[boo{k}^{\prime }\left(b\right)\wedge Q\left\{b\right\}])\right)]\hfill \end{array}$$

As shown in Figure 5, by modeling the $\lambda$ calculus, the sentence “At least one person likes this book” can capture the following two semantic interpretations:

• Broad interpretation: There is at least one person who likes this particular book:

  $$\exists x[ma{n}^{\prime }\left(x\right)\wedge lik{e}^{\prime }\left(\widehat{\phantom{x}}{b}^{\prime }\right)\left(x\right)]$$

  (62)
• Narrow interpretation: There is a book and at least one person likes it:

  $$\exists x[ma{n}^{\prime }\left(x\right)\wedge \left(lik{e}^{\prime }(x,\widehat{\phantom{x}}\lambda Q.\exists b[boo{k}^{\prime }\left(b\right)\wedge Q\left\{b\right\}])\right)]$$

  (63)

Similarly, the ambiguous phenomenon of “Every student read a book” has been extensively studied and interpreted. The quantifier scope ambiguity involved in this issue is an active frontier in semantic research, continuing to drive theoretical and technological developments [46]. Studying such issues can further advance the research and development of natural semantics.

6.3. Optimizing Syntax and Semantic Translation Rules

Although Montague, Bennett, and others have established detailed rules for English semantics and grammar, which later generations can simply apply directly, many issues still need to be resolved in the actual translation process.

6.3.1. Conjunction Rules

Among Montague’s 17 rules, S11 and S12 deal with conjunction, defining parallel sentences and parallel verbs, respectively. Among Bennett’s 35 rules, S28 deals with conjunction, defining only parallel verbs. However, as we know, conjunctions of nouns and noun phrases occur very frequently in natural language. Surprisingly, neither Montague nor Bennett provide corresponding grammatical rules for this phenomenon. This is because conjunctions of nouns and noun phrases require the verb to become plural, and to simplify expression, no corresponding grammatical rules were defined. However, given the high frequency and widespread use of nouns and noun phrases, and to help beginners better grasp the relevant content, we provide the following additional rules:

Definition 21 (Grammatical Rules for Conjunction of Nouns and Noun Phrases). 

If $\alpha ,\beta \in P_{CN}$, then $F(\alpha ,\beta )\in P_{CN}$. If $\alpha ,\beta \in P_T$, then $F(\alpha ,\beta )\in P_T$. Here, $F(\alpha ,\beta )=\alpha and\beta$. And when the object of the conjunction becomes the subject, the corresponding verb becomes plural.

Definition 22 (Translation Rules for Conjunctions of Nouns and Noun Phrases). 

If $\alpha ,\beta \in P_{CN}$ or $\alpha ,\beta \in P_T$, and $\alpha ,\beta$ is translated as ${\alpha }^{\prime },{\beta }^{\prime }$, then $\alpha and\beta$ is translated as $\lambda P[{\alpha }^{\prime }\left(P\right)\wedge {\beta }^{\prime }\left(P\right)]$. When the conjunction object serves as the subject, the corresponding verb is translated into its plural form.

6.3.2. Adjective Rules

Among Bennett’s 35 rules, the one concerning adjectives is S10. We give its original definition:

Definition 23 (S10). 

If $\gamma \in P_{AJ}$ and $\zeta \in P_{CN}$, then $F_9(\gamma ,\zeta )\in P_{CN}$, where

(a) 

if γ contains an occurrence of a member of $B_{AJ/T}$, then $F_{\phi }(\gamma ,\zeta )=\zeta \gamma$;

(b) 

otherwise $F_9(\gamma ,\zeta )=\gamma \zeta$.

Bennett argues that using S10 can resolve the English grammatical phenomenon of adjective + noun. However, let us consider the following example: John’s mother. According to Bennett’s definition, John’s does not fall into the basic category of adjectives, so S10 cannot be used for translation. We must instead use S5.

Definition 24 (S5). 

If $\zeta \in P_{CN/T}$ and $\alpha \in P_T$, then $F_5(\zeta ,\alpha )\in P_{CN}$, where

(a) 

if $\alpha =h{e}_n$, then $F_5(\zeta ,\alpha )=\zeta \ast him$;

(b) 

otherwise $F_5(\zeta ,\alpha )=\zeta \alpha$.

Consider John’s mother to be equivalent to mother of John. This can be translated as:

$$\begin{array}{cc}\hfill \mathrm{mother}& :mothe{r}^{\prime }\hfill \\ \hfill \mathrm{John}& :\lambda P\left[P\right\{j\left\}\right]\hfill \\ \hfill \mathrm{mother}\mathrm{of}\mathrm{John}& :mothe{r}^{\prime }\left(\widehat{\phantom{x}}\left(\lambda P\left[P\left\{j\right\}\right]\right)\right)\hfill \end{array}$$

While there is certainly nothing wrong with translating “John’s mother” this way, treating “John’s mother” and “mother of John” as equivalent loses the distinction between the two grammatical structures. Furthermore, the resulting translation is often less concise and clear, hindering the reader’s intuitive understanding. Therefore, we provide supplementary rules for these situations.

Definition 25 (Grammar rule). 

If $\alpha \in P_{CN}$ or $\alpha \in P_T$, then $G_2\left(\alpha \right)\in P_{AJ}$, where

(a) 

If $\alpha =h{e}_n$, then $G_2\left(\alpha \right)=hi{s}_n$;

(b) 

Otherwise $G_2\left(\alpha \right)={\alpha }^{\prime }s$.

Definition 26 (Semantic Translation Rules). 

If $\alpha \in P_{CN}$ or $\alpha \in P_T$, and α is translated as ${\alpha }^{″}$, then

(a) 

$hi{s}_n$ is translated as ${hi{s}_n}^{\prime }$;

(b) 

John’s is translated as $\lambda P\left[P\left\{j^{\prime }s\right\}\right]$.

(c) 

In other cases, ${\alpha }^{\prime }s$ is translated as ${\alpha }^{″}{s}^{\prime }$.

Using the new rules, we can retranslate John’s mother:

$$\begin{array}{cc}\hfill \mathrm{mother}& :mothe{r}^{\prime }\hfill \\ \hfill \mathrm{John}’\mathrm{s}& :\lambda P\left[P\left\{j^{\prime }s\right\}\right]\hfill \\ \hfill \mathrm{John}’\mathrm{s}\mathrm{mother}& :\lambda P\left[P\left\{j\right\}\right]\left(\widehat{\phantom{x}}mothe{r}^{\prime }\right)\hfill \\ \hfill \lambda \mathrm{transposition}& :\widehat{\phantom{x}}mothe{r}^{\prime }\left\{j\right\}\hfill \\ \hfill \mathrm{Brackets},\mathrm{upper}\mathrm{and}\mathrm{lower}\mathrm{rules}& :mothe{r}^{\prime }\left(j^{\prime }s\right)\hfill \end{array}$$

In comparison, the translation using the new rules is more concise and clear, making it easier for readers to grasp the grammatical structure.

6.3.3. Clause Rules

For the sake of brevity, neither Montague nor Bennett discussed clause rules in detail, instead focusing on the typical relation “such that.” Some might question whether or not each clause has a specific function and introductory phrase, expressing different logical relationships depending on the context. Since their functions are not identical to “such that,” does this mean that the same rules cannot be applied universally?

Indeed, “such that” primarily expresses a result or condition. Commonly used attributive clauses, such as modifiers and adverbial clauses, often express time or cause, differ significantly from “such that.” However, these commonly used clauses are structurally simpler than standard relative clauses. Generally speaking, one can emulate Montague’s approach to translation by modifying or simplifying Montague’s rules or by transforming the clause form.

Here, we provide a case study: the man whom Mary loves.

$$\begin{array}{cc}\hfill & \mathrm{man}:ma{n}^{\prime }\hfill \\ \hfill & \mathrm{the}\mathrm{man}:\lambda P\exists y[\forall x[ma{n}^{\prime }\left(x\right)\leftrightarrow x=y]\wedge P\left\{y\right\}]\hfill \\ \hfill & \mathrm{Mary}:\lambda Q\left[Q\right\{m\left\}\right]\hfill \\ \hfill & \mathrm{loves}:lov{e}^{\prime }\hfill \\ \hfill & \mathrm{loves}\mathrm{the}\mathrm{man}:lov{e}^{\prime }\left(\widehat{\phantom{x}}(\lambda P\exists y[\forall x[ma{n}^{\prime }\left(x\right)\leftrightarrow x=y]\wedge P\left\{y\right\}])\right)\hfill \\ \hfill & \mathrm{Mary}\mathrm{loves}\mathrm{the}\mathrm{man}:\lambda Q\left[Q\left\{m\right\}\right]\left(\widehat{\phantom{x}}lov{e}^{\prime }\left(\widehat{\phantom{x}}(\lambda P\exists y[\forall x[ma{n}^{\prime }\left(x\right)\leftrightarrow x=y]\wedge P\left\{y\right\}])\right)\right)\hfill \\ \hfill & \lambda \mathrm{Transposition}:\widehat{\phantom{x}}\lambda P\exists y[\forall x[ma{n}^{\prime }\left(x\right)\leftrightarrow x=y]\wedge P\left\{y\right\}]\left)\right)\left\{m\right\}\hfill \\ \hfill & \mathrm{Brackets},\mathrm{upper}\mathrm{and}\mathrm{lower}\mathrm{rules}:\lambda P\exists y[\forall x[ma{n}^{\prime }\left(x\right)\leftrightarrow x=y]\wedge P\left\{y\right\}]\left)\right)\left(m\right)\hfill \\ \hfill & \lambda \mathrm{Transposition}:\exists y[\forall x[ma{n}^{\prime }\left(x\right)\leftrightarrow x=y]\wedge m\left\{y\right\}]\left)\right)\hfill \end{array}$$

Combined results:

$$\begin{array}{cc}\hfill & \lambda x_n[(\lambda P\exists y[\forall x[ma{n}^{\prime }\left(x\right)\leftrightarrow x=y]\wedge P\left\{y\right\}])\left(x_n\right)\wedge \hfill \\ \hfill & (\exists y[\forall x[ma{n}^{\prime }\left(x\right)\leftrightarrow x=y]\wedge m\left\{y\right\}])\left)\right]\hfill \end{array}$$

(64)

After $\lambda$ transposition, brackets, and upper and lower rules, the final result is:

$$\begin{array}{cc}\hfill & \lambda x_n[\exists y[\forall x[ma{n}^{\prime }\left(x\right)\leftrightarrow x=y]\wedge \check{\phantom{x}}{x}_n\left(y\right)])\wedge \hfill \\ \hfill & (\exists y[\forall x[ma{n}^{\prime }\left(x\right)\leftrightarrow x=y]\wedge \check{\phantom{x}}m\left(y\right)])\left)\right]\hfill \end{array}$$

(65)

The core insight of Montague semantics lies in placing natural language within a formal framework as rigorous as that of mathematics and logic. By supplementing these rules, scholars can better understand natural language through logic. Formal logic is not just an abstract mathematical tool; it is a key approach to understanding and modeling the most complex human cognitive abilities. As artificial intelligence progresses toward general intelligence, the formal methodology represented by Montague semantics will continue to play an irreplaceable role.

6.4. Formalization of Natural Languages

Scholars such as Montague have provided comprehensive tools and detailed introductions to the formalization of English, a natural language. Furthermore, combined with the rules subsequently added by scholars, it can be argued that English can be fully formalized. Similarly, other natural languages can be formalized using similar methods. Alternatively, given the intertranslatability between English and other languages, they can be directly converted into English for formalization.

In short, we can conclude the following:

Theorem 17.

Large fragments of natural languages can be formalized using first- and higher-order logic with appropriate extensions of symbols and rules; the scope of full formalization depends on the targeted phenomena and resources.

The importance of formalization of natural languages ultimately lies in the scientific method it provides for understanding the essence of human intelligence. Language is not only a tool for communication but also a vehicle for thought, a container for knowledge, and a medium for the transmission of culture. Formalizing language is a mathematical modeling of human cognitive abilities and a scientific exploration of the essence of intelligence.

7. Conclusions and Outlook

This paper systematically investigates the logical formalization of object states, proposing and demonstrating a rigorous and universally applicable formalization framework for revealing the nature of information and its interdisciplinary applications. The paper first reviews classical information theory and its shortcomings, noting the current lack of a unified and rigorous mathematical definition of the core concept of “state.”

To this end, this paper establishes a universal representation system for information states based on first-order and higher-order predicate logic, combined with modal logic and calculus, addressing the current lack of formal representations for states. This paper enumerates typical states from various fields, including mathematics, economics, sociology, computer science, and natural language, and rigorously proves that these states can be formalized using first-order and higher-order logic. Although this paper discusses the formalization of states in only four specific domains, these domains are highly representative. For any domain’s state, its numerical features can always be expressed mathematically, its attributes can always be represented by phenomena in economics and sociology, it can be implemented in computers, and its intention can be explained in natural language. In other words, the states of all domains can borrow the pattern we have proved to achieve formalization, thereby generalizing the formal expression of states from the particular to the general.

In this sense, logic has truly become a universal bridge connecting states across various fields, a universal language that enables communication across fields, and provides humanity with the most fundamental and powerful mathematical tools for understanding and transforming the world.

Through the formalization of states, objective information theory (OIT) has been further refined and developed, deepening research on the nature of information and expanding its scope from the classic Shannon framework. Many pressing problems in information science can be transformed into logical problems. By studying the properties of logical language and drawing on proven conclusions and axioms from logic, we can clarify the meaning of information and guide the development of information research.