Abstract
In the context of increasingly strong digital transformation and production automation, choosing the right palletizing robot plays a key role in optimizing operational efficiency in industrial chains. However, the wide variety of robot types and specifications complicates decision-making and increases the risk of biased judgments. To overcome this challenge, this study develops an objective multi-criteria decision-making (MCDM) framework that integrates two complementary methods for selecting the optimal industrial pal-letizing robot in the context of modern manufacturing that is increasingly dependent on intelligent automation solutions. Specifically, an improved CRITIC approach is employed to determine objective criteria weights by refining the measurement of contrast intensity and inter-criteria conflict, while normalization ensures comparability of heterogeneous robot parameters. CRADIS is then applied to rank the alternatives based on their relative closeness to the ideal solution. The contributions of this study are twofold: methodological, enhancing the objectivity and robustness of weighting through refined CRITIC and normalization, and practical, offering a reproducible evaluation framework for managers when choosing industrial robots. Application to eight palletizing robots demonstrates that “repeatability” and “power consumption” significantly influence rankings. Sensitivity analysis further confirms the model’s stability and reliability. These findings not only support evidence-based investment decisions but also provide a foundation for extending the method to other industrial technology selection problems.
MSC:
90B50
1. Introduction
In the context of the industrial revolution 5.0, global manufacturing is facing a historic turning point of comprehensive transformation, as advanced technologies such as artificial intelligence (AI), industrial Internet of Things (IIoT), machine learning, edge computing, and intelligent automation are increasingly widely applied throughout the entire manufacturing value chain [1]. One of the most prominent manifestations of this transformation is the dramatic increase in automation within smart factories, where industrial robots-particularly specialized robotic systems designed for handling and transporting materials, such as palletizing robots-serve as an indispensable central link [2,3]. The application of these robotic systems not only contributes to improving speed and accuracy in production operations but is also a key solution to help businesses reduce operating costs, optimize human resources, improve labor safety, and increase the ability to operate continuously in harsh working environments [4].
From a practical perspective, developed industrial countries such as Germany, Japan, the United States, and South Korea, as well as countries on the path to industrialization such as China, India, Brazil, and Vietnam, are all accelerating the digital transformation process in manufacturing through the integration of intelligent robotic systems in the operating chain [5,6]. In the post COVID-19 pandemic context and the increasingly serious shortage of technical labor, the need for robotic palletizing systems, with the ability to operate durably, accurately, and save space, has become an inevitable trend in the process of restructuring production towards comprehensive automation [7]. However, the transition to a highly automated production model is not only a technological issue but also a challenging strategic investment problem. Businesses face many barriers, such as high initial investment costs, system synchronization requirements, the ability to train and maintain technical staff, and the complexity of choosing the right technology for a specific production process.
In this context, the evaluation and selection of industrial palletizing robots cannot be approached in a single or intuitive manner but needs to be considered as a complex decision-making process, requiring the simultaneous consideration of multiple factors and multidimensional evaluation criteria. These factors include, but are not limited to, technical criteria such as maximum load, repeatability, manipulator reach, tip speed, and integration with control systems, as well as economic criteria such as investment costs, operating costs, average energy consumption, and maintenance costs [8]. Additionally, managers are increasingly focusing on qualitative criteria like safety level, programming flexibility, and adaptability to many types of products. Because of this complexity, Multi-Criteria Decision-Making (MCDM) methods have become ideal tools to support the process of analyzing, comparing and selecting robot options in a systematic and objective manner [9]. Unlike traditional approaches that rely on only one or a few single criteria, MCDM allows for the synthesis of quantitative and qualitative factors, fully reflecting the multidimensionality and practicality of the modern industrial production context [10].
Among the existing MCDM methods, CRITIC (CRiteria Importance Through Intercriteria Correlation) stands out as an objective weighting tool, using statistical methods to determine the importance of each criterion through two main parameters: standard deviation, indicating the ability to discriminate between options, and correlation coefficient, indicating the degree of independence or overlap between criteria [11]. This method has the outstanding advantage of not requiring subjective assessment from experts, thus minimizing personal bias. However, CRITIC also has certain limitations, especially the phenomenon of cancelation between positive and negative correlations during the calculation process, leading to distortion of the actual information value of some criteria of neutral or opposing nature. To improve this drawback, the study proposes an extended version of CRITIC, which integrates the concept of “distance” (distance-based refinement) to add an information dimension measuring the real dispersion between criteria [12]. This addition improves the accuracy of weight determination and helps to properly reflect the discriminating role of each criterion in the experimental dataset.
Additionally, to thoroughly rank robot options, the study introduces the CRADIS (Compromise Ranking of Alternatives from Distance to Ideal Solution) method, which is a contemporary decision-making technique gaining significant attention in the MCDM academic community [13,14]. CRADIS has the outstanding advantage of combining the distance to the ideal solution and the anti-ideal solution, thereby evaluating the suitability of each option based not only on the absolute closeness to the target but also on the distance from the worst options [15]. This helps create a ranking system that is balanced and meaningful in operational practice. However, CRADIS applications in the field of industrial robotics are still limited, especially in the context of evaluating palletizing robot lines with large differences in specifications, configurations and origins among different manufacturers.
From the above research gaps, this study proposes to develop an integrated model between the extended DR-CRITIC method and CRADIS, called the extended DR-CRITIC-CRADIS model, with the aim of objectively, comprehensively and with high reliability evaluating modern industrial palletizing robot solutions. This model allows us to take advantage of DR-CRITIC in determining criterion weights based on information level and data correlation and use CRADIS to rank alternatives based on overall distance to benchmark solutions. Combining the two methods will help overcome the shortcomings of each individual method while improving practical application and accuracy in assessment results.
The highlight of the study lies not only in the development of a new integrated model in the field of multi-criteria decision making but also in the application of this model to a less studied field, which is industrial palletizing robots. In addition, the study also proposes a flexible data normalization technique that is capable of handling heterogeneous datasets, a common problem in evaluating industrial equipment from multiple manufacturers. With a multidimensional and highly applicable approach, this study not only contributes theoretically to the field of MCDM, but also brings practical value to engineers, experts and policymakers in making investment decisions and developing smart manufacturing systems.
The paper is organized as follows: Section 2 reviews the literature related to MCDM and robot selection; Section 3 details the research methodology and proposed improvements; Section 4 analyzes the data and experimental results; Section 5 discusses the managerial and decision-making implications; and Section 6 draws conclusions and future research directions.
2. Literature Review
The rapid development of robotic technology in industrial applications has fueled extensive research interest in optimizing palletizing operations. Many works have focused on structural design, control strategy, energy efficiency and intelligent automation system for palletizing robots (PRs). Several studies have focused on optimizing the structure and dynamics of palletizing robots. Gao et al. proposed a motion analysis and trajectory model for a six-degree-of-freedom GLT palletizing robot, which was verified by simulation and experiment [16]. These studies emphasize the importance of accurate kinematic modeling in improving motion stability and structural efficiency. They collectively underline that structural optimization remains foundational to PR design, yet such approaches often remain narrowly focused on technical performance rather than multi-criteria operational evaluation. Supplement to this research direction, Choi & Suh designed the palletizing robot using a cable drive system and parallel gear joints, creating a lightweight, modular structure with high flexibility and scalability [17]. This work highlights a shift toward modularity and customization in robot design, supporting adaptability in fast-changing production environments. However, despite these advancements, the evaluation remains confined to structural robustness rather than incorporating decision-making frameworks that balance efficiency, scalability, and cost.
From the control system perspective, Nechita et al. applied a fuzzy logic-PID control algorithm on an FPGA hardware platform for a palletizing robot, and simulation results showed that this solution is suitable for a motion control system in a modern industrial environment [18]. Optimizing energy consumption is a key factor in robot deployment. In 2023, Sobaszek emphasized the importance of analyzing power consumption in robotized processes, showing the need to plan joint movements rationally [19]. Extending this direction of research, Deng et al. proposed an energy-saving planner based on the differential evolution algorithm, achieving up to 16% energy consumption reduction through robot trajectory optimization [20]. These studies mark energy efficiency as a growing research frontier, though the gap remains in systematically integrating energy criteria into broader multi-criteria evaluations of PRs. Robot optimization and job scheduling algorithms also attract much attention. Szczepanski et al. applied the Artificial Bee Colony algorithm to solve the multi-objective palletizing scheduling problem, significantly improving the number of palletized products and the overall efficiency of the robot. The proposed study integrates scheduling with path planning and speed configuration, forming a complex multi-objective nested optimization model, confirming the NP-hard nature of the problem [21]. This illustrates how metaheuristic optimization can enhance operational throughput, yet it still lacks connection to comprehensive evaluation frameworks where scheduling, energy, and cost trade-offs are assessed simultaneously.
In the context of collaborative robots (cobots), many studies emphasize flexibility and human orientation according to the Industry 5.0 trend. Dmytriyev et al. proposed a collaborative end-of-line robot model, which helps operators to be more proactive in their work and reduces system downtime [22]. At the same time, Kakade et al. reviewed the application of collaborative robots in flexible manufacturing, pointing out limitations such as low accuracy, a limited payload, and speed [23]. These findings stress the dual challenge of ensuring safety and efficiency while adapting robots to human-centric workspaces, which cannot be captured solely through technical performance metrics. On the machine vision and intelligent automation side, Valero et al. and Yoon et al. developed an RGB-D image processing method combined with deep learning such as Cycle-GAN and Mask R-CNN to detect and recognize cargo boxes in complex loading and unloading environments [24,25]. These studies contribute to improving the accuracy of robots in unstructured and highly noisy warehouse environments. Daios et al. focus on hybrid palletizing and sustainability, with an overview of exact algorithms, heuristics, AI, and quantum computing to optimize logistics efficiency [26]. Their review underscores the increasing importance of computational intelligence in addressing palletizing challenges, while simultaneously calling for frameworks that balance computational cost with practical applicability. The author points out that the balance between solution quality and computational power is the core factor in practical implementation. Finally, Mišković et al. present a model of an integrated robot system in a virtualized factory environment, using mobile robots and industrial manipulators linked via the OPIL IoT platform and the open-source software ROS (ROS industrial (ROS-I)) [27]. While such integration strengthens interoperability and digital connectivity, it does not yet provide standardized metrics for comparative evaluation across robot types and contexts, thus justifying the need for multi-criteria decision-making models. This model enables real-time task coordination and demonstrates scalability in smart manufacturing environments. However, there is still a lack of standardized quantitative and multi-criteria evaluation systems to comprehensively evaluate palletizing robots in different application contexts.
Although many studies have focused on aspects such as mechanical design, control algorithms, energy efficiency, and robot interoperability during palletizing, a research gap still exists regarding the construction of a comprehensive and quantitative evaluation system for selecting suitable palletizing robots in diverse industrial environments. Technical and technological factors are often analyzed separately, while few studies have combined these criteria in an integrated and objective decision-making framework. Therefore, the literature strongly suggests a pressing need to bridge the gap between technical performance improvements and systematic multi-criteria evaluation frameworks, ensuring that PRs are assessed not only for functionality but also for sustainability, cost, and adaptability.
The application of MCDM methods has been widespread in many different fields, demonstrating their effectiveness and ability to support solving complex decision-making problems. The literature review shows a rich diversity of MCDM methods, including adaptation and integration with other analytical tools to improve assessment accuracy and efficiency. Table 1 summarizes typical applications of the MCDM method in recent years, reflecting the increasingly expanding research trends and practical applications of this field.

Table 1.
MCDM application.
Xu et al. made notable contributions by combining IMF-SWARA and fuzzy CRADIS to assess the sustainability of mountain lodges [28]. The combination of expert weights and fuzzy operators emphasizes the role of contextual adaptation and accuracy in sustainability assessment. Similarly, the extension of MCDM models in fuzzy environments is further demonstrated by the study of Kamber et al. with the integration of Picture Fuzzy BWM and CODAS methods for selecting drip irrigation pumps [34]. Their approach effectively manages uncertainty in decision-making and is particularly relevant to industrial robot evaluation, where both performance and safety factors are difficult to quantify. The concepts of sustainability and accessibility are prominently mentioned in the study by Dadashzadeh et al. when the authors built a practical MCDM model to evaluate transport services in a comprehensive manner for disadvantaged groups [37]. This highlights the ability of MCDM to translate social objectives into quantitative criteria, reinforcing its suitability for multi-dimensional evaluation problems. Meanwhile, Momena et al. applied the CRITIC method combined with MULTIMOORA to evaluate the performance of supply chain companies [31]. The study underscores CRITIC’s strength in generating objective weights directly from data, a feature central to this research in minimizing subjectivity when evaluating industrial robots.
Another integrated approach was presented in the study by Hasankhani et al., where the authors combined SWOT, fuzzy MCDM, and game theory to select optimal waste treatment strategies in Iran [35]. This reflects the growing trend of linking MCDM with strategic and operational tools to enhance decision quality. From a global perspective, Kut & Pietrcha used CiteSpace software (version 6.3.R3 Advanced) to perform a bibliometric analysis of MCDM methods in environmental and energy engineering [32]. Their results reveal expanding geographical coverage and international collaboration, emphasizing the importance of transparency and reproducibility in model development. In national situations, such as the military field, Duško & Bozanic proposed the FUCOM-EWAA-COPRAS-G model to support decision-making in combat [36]. This framework ensures stability and verifiability, offering insights applicable to industrial robot evaluation where diverse and conflicting criteria coexist. From the perspective of sustainable development planning, Wang et al. combined MEREC and OCRA to assess the sustainable development level of countries in the Silk Road Economic Belt [33]. Their integration of an objective weighting method with a compensatory ranking method is conceptually aligned with the CRITIC-CRADIS approach proposed in this study.
From the perspective of human resource management, Stanujkic et al. applied the integration of PIPRECIA-S and WS-PLP to evaluate IT project management candidates [29]. The ability to balance tangible and intangible criteria parallels the challenge of industrial robot evaluation, which requires accounting for both technical and socio-economic dimensions. Meanwhile, Parvaneh et al. used an integrated MCDM model for selecting sustainable power generation technologies, illustrating the effectiveness of scenario-based sensitivity analysis in multi-stakeholder contexts [30]. Finally, Alamoodi et al. conducted a systematic review of health-related MCDM studies during the COVID-19 pandemic [38]. Their review classifies MCDM applications across diagnosis, treatment, safety, and resource allocation, showcasing the adaptability of MCDM in dynamic and high-risk environments. This adaptability provides a strong foundation for applying MCDM to modern manufacturing contexts, where rapid changes and risks are prevalent.
Overall, the reviewed literature demonstrates a clear shift towards hybrid MCDM models that prioritize objectivity, adaptability, and the capacity to handle uncertainty. The integration of objective weighting methods (CRITIC, MEREC, Entropy) with ranking approaches (TOPSIS, VIKOR, COPRAS, CRADIS) highlights a promising trajectory for industrial applications. However, few studies have explicitly extended these models to the evaluation of industrial palletizing robots, leaving a gap for developing tools that ensure accuracy, objectivity, and contextual sensitivity. Addressing this gap, the present study advances the CRITIC-CRADIS method for robot evaluation.
3. Methodology
The CRITIC method is an advanced decision-making tool developed to determine the weights of criteria objectively, independent of subjective assessment. This quantitative technique assesses the importance of each criterion by analyzing the degree of difference between decision alternatives and the correlation between criteria. Based on its ability to accurately quantify key properties, this method provides objective and reliable analysis, which is particularly useful in evaluating complex systems. However, a limitation of this method is that it is difficult to accurately reflect the total correlation level due to the cancelation between positive and negative correlations. To overcome this problem, the present study proposes an improved version of CRITIC, based on the concept of distance, which will be detailed in the following section [12]. Meanwhile, the CRADIS method has a different objective and is considered a powerful approach to assessing the performance of entities [14]. The main objective of this method is to determine the degree of deviation of the alternatives from the ideal and anti-ideal solutions. In addition, the method also determines the value of each alternative based on its closeness to the optimal alternative. By using multiple types of deviations, the method can calculate the overall value of each alternative. The objective weighting integration model proposed by the MCDM method in the flowchart Figure 1 provides a comprehensive analytical framework to handle complex decision-making situations.
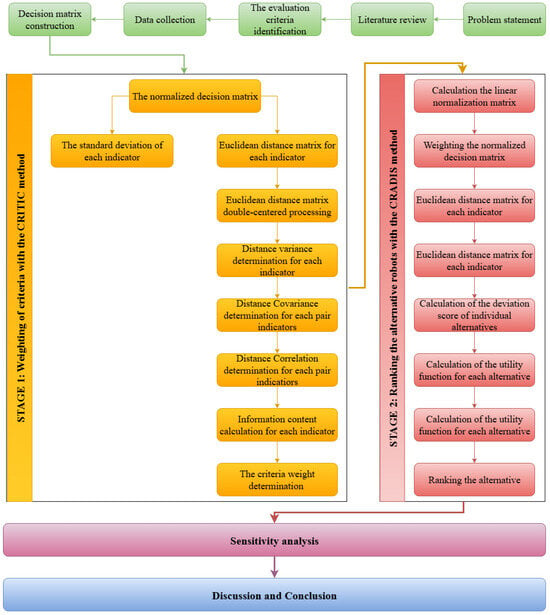
Figure 1.
The suggested objective weight MCDM methodology.
Furthermore, to ensure a comprehensive comparison, this study also implements other widely used MCDM methods such as TOPSIS, SAW, and EDAS. In the TOPSIS approach, the ideal solution represents the best performance values among all criteria (i.e., maximum for benefit criteria and minimum for cost criteria), while the anti-ideal solution represents the worst values. Each alternative is evaluated based on its Euclidean distance to these two reference points. The SAW method, by contrast, uses a simple additive weighting procedure in which all normalized criteria are multiplied by their corresponding weights and summed to determine the final performance score. Meanwhile, the EDAS method (Evaluation based on Distance from Average Solution) calculates the positive and negative distances of each alternative from the average performance solution, offering another perspective on the deviation-based evaluation process.
The implementation process of the proposed method will be presented in detail in the next section:
Step 1: Begin with an MCDM problem involving T alternatives and L criteria. The decision matrix (H) is defined in Equation (1), where the performance of the ith alternative () on the jth criterion is represented as .
Step 2: Define sets B and NB to represent beneficial and non-beneficial criteria, respectively. Normalize the decision matrix based on Equation (2), resulting in the normalized matrix shown in Equation (3).
Step 3: Compute the standard deviation for each criterion using Equation (4).
Step 4: Construct the Euclidean distance matrix for each criterion i using Equations (5) and (6), which assess the distances between the normalized values of the alternatives.
where
Step 5: Calculate the row-wise mean, column-wise mean, and the overall mean of each Euclidean distance matrix, as outlined in Equations (7)–(9).
Step 6: Apply the double-centering technique to each Euclidean distance matrix, producing double-centered matrices for all criteria, as illustrated in Equations (10) and (11).
where
Step 7: To determine the distance covariance () between criteria jth and kth, follow these sub-steps:
- Perform element-wise multiplication of the corresponding double-centered matrices.
- Calculate the meaning for the resulting matrix.
- Take the square root of the average value obtained.
Step 8: Use Equation (12) to compute the distance correlation () between criteria jth and kth.
Step 9: The informational content of criterion jth is calculated using Equation (13).
Step 10: Derive the objective weights for each criterion using Equation (14).
Step 11: Multiply the normalized decision matrix by the corresponding weights from the DR-CRITIC method to produce a weighted matrix, as shown in Equation (15).
Step 12: Identify the ideal and anti-ideal solutions from the weighted matrix using Equations (16) and (17). The ideal solution includes the highest values across all criteria, while the anti-ideal consists of the lowest.
Step 13: Measure the deviations of each alternative from both the ideal and anti-ideal solutions by subtracting weighted values from the maximum and minimum values, as per Equations (18) and (19).
Step 14: Sum these deviations to compute a score representing each alternative’s distance from the ideal and anti-ideal scenarios, following Equations (20) and (21).
Step 15: Using Equations (22) and (23), calculate the utility function for each alternative based on its deviation from optimal solutions.
where denotes the optimal alternative for the ideal case, and for the anti-ideal.
Step 16: Finally, compute the CRADIS method value for each alternative using Equation (24), and rank all options in descending order according to their corresponding values.
4. Numerical Results
4.1. Problem Description
Within the framework of this study, the identification and clustering of six indicators was carried out through a comprehensive and organized literature review process. The goal of this process is to ensure that each selected metric accurately reflects an important aspect of the decision-making process when evaluating a robot. The selection of indicators was not random but was based on their relevance and frequency of appearance in influential academic literature and up-to-date research in the relevant field. This systematic approach helps ensure that the selection criteria fully reflect the essential elements in evaluating and selecting the right palletizing robot for the modern industrial environment. The data of the indices are collected from reliable sources such as Robot Belt [39], JAKA [40], Universal Robots [41], FANUC [42], KUKA [43], in the latest period available.
As show in Table 2, The criteria provide an overview of the evaluation and selection of industrial palletizing robots. Details of the eight robots and six evaluation criteria are shown in Table 3. The selected robots are designed to stack pallets and perform automated tasks in industrial environments. R-1 Dobot CR20A: stacking, packaging, palletizing in automated lines. R-2 JAKA Zu 20: transportation, flexible production line support. R-3 Han’s Rbot Elfin-S30: heavy processing, industrial packaging. R-4 Universal Robots UR20: palletizing, CNC machining, quality control. R-5 FANUC CRX-25iA: palletizing, shipping, packaging in a human-occupied workspace. R-6 Siasun GCR5: small product packaging, quality inspection, electronic manufacturing support. R-7 Elite Robot EC66: inspection, packaging, semi-automatic production support. R-8 KUKA LBR iisy: precision assembly, testing, production support in industrial environments.

Table 2.
List of the criteria used in robot selection.

Table 3.
The decision matrix.
4.2. Single Indicator and Robots Discussion
Prior to implementing the study’s proposed methodology for evaluating multiple indicators, it is important to gain insights from each individual indicator.
In the modern industrial context, selecting the right robot is crucial in optimizing the production process and enhancing operational efficiency. Therefore, establishing a comprehensive and well-founded evaluation criteria system is an urgent requirement in industrial robot selection studies. The six core technical criteria identified in this study are payload, repeatability, load capacity, manipulator reach, maximum tip speed, and average power consumption. Each criterion reflects different important aspects of the robot’s performance and adaptability to the requirements in the real environment.
Payload (RC-1) refers to the maximum load that a robot can carry at the end of its operation, usually measured at the fully extended arm position. This is an important metric in applications that require heavy object handling, such as palletizing, internal logistics, or industrial packaging. A robot with a high payload will be able to handle various objects, contributing to increased flexibility in the production line.
Repeatability (RC-2) reflects the level of accuracy when the robot performs the same movement over many cycles. This criterion is especially important in processes that require high precision, such as electronic component assembly, printing, or robot-sensor coordination operations.
Load capacity (RC-3) is often considered an extension of payload, representing the overall load-carrying capacity of the entire manipulator system, including any supporting tools, end-effectors, or peripherals. This criterion is important in determining the structural strength of the robot and its ability to operate stably under variable load situations.
Manipulator reach (RC-4) represents the maximum working range that the robot can reach, from the center of the base to the furthest point that the manipulator arm can reach. The ability to reach further allows the robot to cover more space without moving the base, thereby reducing cycle times and optimizing the production floor layout.
Maximum tip speed (RC-5) represents the maximum tip speed at the end of the manipulator when the robot is operating at high intensity. This speed directly affects the efficiency of task processing in a unit of time, especially in high-speed production lines.
Finally, average power consumption (RC-6) is an important indicator that reflects the energy efficiency of robots. This criterion directly affects long-term operating costs and sustainability in production. Robots with low power consumption will be in line with the green transformation and energy-saving trend in Industry 5.0.
4.3. Multi-Indicator Efficiency Assessment
This section demonstrates the practical implementation of the proposed methods for assessing and selecting industrial palletizing robots. The dataset previously introduced is utilized to construct the decision matrix shown in Table 3, which forms the foundation of the evaluation. The normalized decision matrix, derived using Equations (2) and (3), is displayed in Table 4. To capture the variability of each criterion, the standard deviation is computed as per Equation (4), with the results also included in Table 4 for subsequent analysis. Following this, the Euclidean distances between the standardized values of the alternatives for each criterion are calculated using Equations (5) and (6), resulting in separate distance matrices for each criterion. As an illustration, Table 5 presents the Euclidean distance matrix corresponding to RC-1 (Payload). To correct potential biases and ensure robustness, double-centered distance matrices are then generated using Equations (7)–(11). This step involves adjusting each entry based on row and column means, which minimizes the impact of outliers or uneven data distributions. Table 6 provides an example of this process, showing the double-centered matrix for RC-1.

Table 4.
The Normalized Decision Matrix.

Table 5.
The Euclidean Distance Matrix for RC-1.

Table 6.
The Double-Centered Euclidean Distance Matrix for RC-1.
According to the content presented in Step 7 in Section 3, the process of calculating the distance covariance between each pair of indicators is performed to evaluate the level of distance association between the criteria in the dataset. With a total number of indicators (L = 6), the number of pairs of indicators that can be formed is 21 (based on the combination formula . Therefore, the process of calculating the covariance was repeated 21 times, corresponding to 21 different pairs of indicators. At each iteration, an element-wise multiplication matrix is constructed by applying Schur multiplication between two double-centered matrices of the pair of indicators under consideration. The results of these element-wise multiplications are used to determine the corresponding distance covariance value for each pair, resulting in a set of 21 values. Next, based on Equation (12), the distance correlation coefficients between pairs of indicators are calculated as shown in Table 7. These coefficients represent the degree of nonlinear correlation between the indicators in the distance space and are summarized and presented in detail in Table 6. Based on the distance correlation coefficients obtained together with the standard deviation of each indicator calculated in the previous steps, the process of determining the information content of each indicator is carried out according to Equation (13). Information content reflects the level of contribution and relative importance of each criterion in distinguishing between alternatives. Finally, this information is represented visually by graphs in Figure 2 to help readers observe and compare the level of influence of each criterion throughout the entire evaluation process.

Table 7.
The Distance Correlation Coefficient Between Indicators.
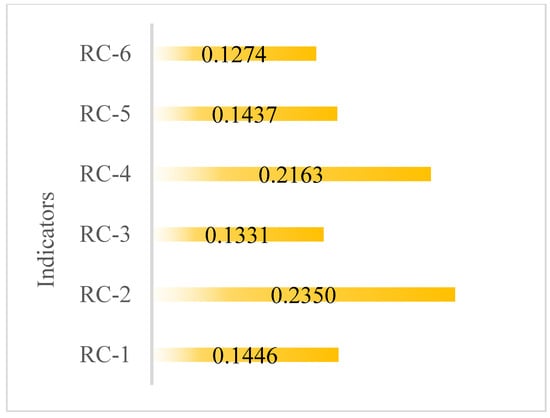
Figure 2.
The information content of indicators.
Based on the calculated results presented in Figure 3, RC-2 plays the most important role with 24% of the total weight. This analysis shows that RC-2 is a criterion that can clearly distinguish between robot options and is highly informative. RC-2 may involve a factor that has large variability and little correlation with the remaining criteria, thus playing a prominent role in classification and assessment. This is followed by RC-4, which at 22% also shows significant importance. The fact that RC-4 and RC-2 have the highest weights suggests that these are two key factors that should be given priority consideration in the robot selection process, as they have a large impact on the overall decision-making outcome. Meanwhile, RC-1 and RC-5, which account for 14% of the evaluation, represent a medium level of influence on the evaluation process. While these two criteria are not as prominent as RC-2 and RC-4, they still play a supporting role in creating a more comprehensive view of the performance and suitability of robots. In contrast, RC-3 and RC-6 both have the lowest weights, each criterion accounting for only 13%. This suggests that these criteria have relatively low variability or are highly correlated with other criteria, thereby reducing the discriminatory information they provide. However, this does not mean that RC-3 and RC-6 are not important, but rather that in this particular assessment context their role is secondary and can be seen as complementary to the primary criteria.
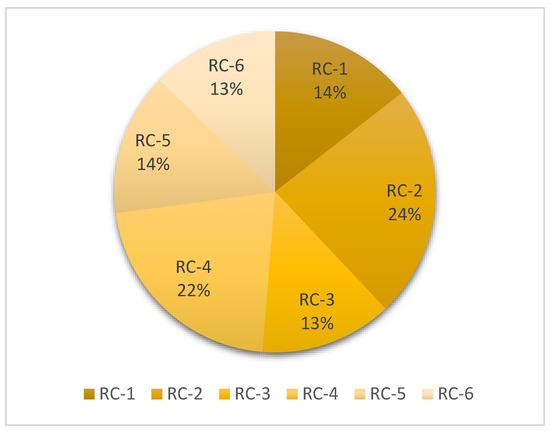
Figure 3.
Objective indicator weights derived from CRITIC.
With these weights established, the evaluation process will proceed. This process begins with the construction of a weighted decision matrix, in which the weight of each criterion is determined objectively through the CRITIC method. By integrating these weights shown in Equation (15), the post-normalized decision matrix is transformed into a weighted matrix, reflecting the relative importance of each criterion in the overall evaluation. Table 8 presents the results of this calculation. Next, determine the ideal solution and anti-ideal solution for each criterion, calculated according to Equations (16) and (17). For each column in the weighted matrix, the largest value is considered ideal, representing the highest achievable performance, while the smallest value is considered anti-ideal, representing the lowest performance. These two sets of values are used as reference standards for subsequent calculations and are presented in Table 9. Then, by calculating according to Equations (18) and (19), the deviation distances from each alternative to the ideal and anti-ideal values are calculated. For each element in the matrix, the deviation value is determined by taking the difference between the optimal (ideal or anti-ideal) value and the current value of the considered alternative. After determining the deviation distance of each option, the overall deviation score of each option is calculated according to Equations (20) and (21). The deviation values for each criterion are summed, thereby determining the total distance of each option to the ideal and anti-ideal points. The alternative that has a smaller deviation from the ideal and a larger deviation from the anti-ideal will be valued higher, as it represents a degree of asymptotic proximity to optimal performance in the multi-criteria space. Then, calculate the utility function for each option according to Equations (22) and (23), showing the relative relationship between each option and the optimal option. This function quantifies the overall closeness between a robot and the ideal solution. Table 10 shows the results of this calculation. Finally, calculate the total value of each option based on Equation (24). This value is an overall index representing the suitability of each robot in the context of industrial applications. These values are presented in Figure 4, where the option with the highest value is considered the top priority option.

Table 8.
Weighting the normalized decision matrix.

Table 9.
Determination of ideal and anti-ideal solutions.

Table 10.
Results of the CRADIS method.
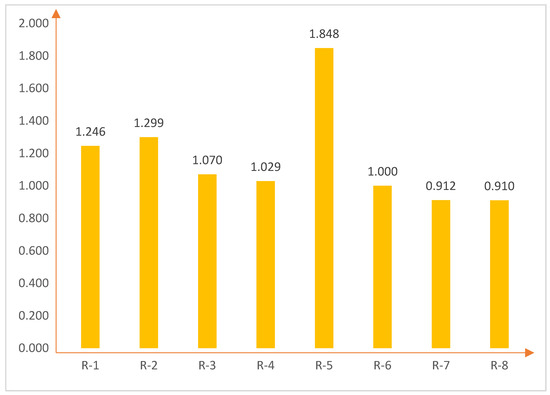
Figure 4.
Final evaluation scores using the DRCRITIC-CRADIS.
The final evaluation results are presented visually in Figure 4. The results show a clear differentiation in the priority levels among industrial palletizing robots, reflecting the comprehensiveness and high reliability of the CRITIC–CRADIS combination method in the context of multi-criteria decision making. Specifically, the R-5 robot stands out with the highest value of 1.848. These results show that the R-5 consistently outperforms many criteria, such as load capacity, maximum tip speed, repeatability, and average power consumption. The fact that the R-5 scores far above the rest reflects that it is the most optimal choice and can be considered as an ideal benchmark in the context of highly automated industrial applications.
Behind R-5 are robots R-2 (1.299) and R-1 (1.246), both of which have relatively high scores and demonstrate good competitiveness; however, they do not reach the level of overall superiority that R-5 achieves. It can be speculated that these robots still demonstrate high performance in some key criteria, but there may still be slight limitations in terms of secondary technical factors or integration capabilities in real-world environments.
The robot groups with average scores include R-3 (1.070), R-4 (1.029), and R-6 (1.000). The fact that these robots score so close together shows that they have similar levels of performance, but there is no outstanding factor that can create a breakthrough in the rankings. The R-6 score matches the average benchmark value (1.000), suggesting that the robot serves as a middle-ground option, neither too superior nor too severely limited technically.
Notably, the two robots, R-7 (0.912) and R-8 (0.910), ranked at the bottom of the rankings, indicating the lowest priority among the research options. This may be a consequence of these robots not performing well in important criteria or having a clear imbalance between performance factors, such as low speed, small payload, or suboptimal accuracy. The clear gap in scores compared to the leading group suggests that these robots may not be suitable for environments that require high precision and performance, such as those found in modern automated production lines.
4.4. Sensitivity Analysis
In this section, a sensitivity analysis is performed by comparing the distance-based refinement CRITIC-CRADIS method with three other popular multi-criteria decision-making (MCDM) methods, namely TOPSIS (Typical Similarity to Ideal Solution), SAW (Simple Weighted Algorithm), and EDAS (Evaluation based on Distance to Average Solution). These methods have been widely applied in many fields due to their transparency, ease of implementation, and high adaptability to many different decision-making situations. The quantitative evaluation and clear ranking between alternatives make these methods useful tools for both researchers and decision makers.
The results illustrated in Figure 5 show a clear variation in the evaluation results between the methods, indicating a significant influence of the chosen decision technique on the results. The DR-CRITIC-CRADIS method demonstrates a strong ability to discriminate among the alternatives, particularly because the R-5 option has a significantly higher value than the other methods. This reflects CRADIS’s keen ability to accurately detect and evaluate superior options.
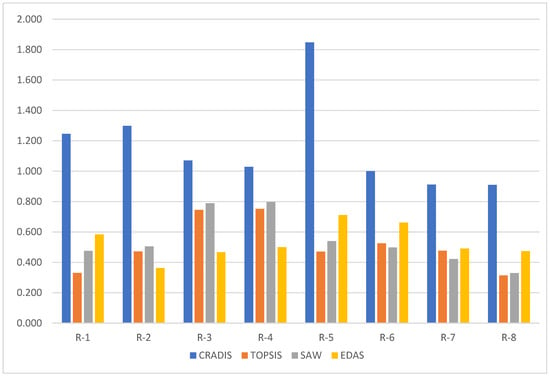
Figure 5.
Comparison of raking results across methods.
In addition, a clear difference can be seen between CRADIS and the remaining methods, such as TOPSIS, SAW and EDAS. While CRADIS shows a clear rank stratification, the remaining methods give uniform results with little variation. In options like R-3 and R-4, TOPSIS and SAW give approximately the same results, while CRADIS makes a significant difference. This shows that TOPSIS and SAW have lower sensitivity in identifying the advantages between the alternatives.
This variability underscores the inherent complexity of multi-criteria decision-making, highlighting the importance of choosing the right approach for specific goals and context. The distance-based refinement CRITIC-CRADIS not only demonstrates stability in its evaluation but also shows flexibility in responding to changes in weights and input data.
Furthermore, to quantitatively assess the consistency between the DR-CRITIC-CRADIS model and the benchmark MCDM methods, Spearman’s rank correlation coefficient (ρ) was calculated. The results reveal a moderate positive correlation between CRADIS and SAW (), whereas weaker correlations were found with EDAS () and TOPSIS (). These findings suggest that CRADIS maintains a distinct yet stable ranking pattern, confirming that it captures multi-criteria trade-offs differently from conventional normalization-based models. The inclusion of rank correlation analysis reinforces the robustness and credibility of the proposed method. The results are presented in Table 11.

Table 11.
Rank Correlation Coefficients among MCDM Methods.
5. Managerial Implications
The research results from the extended CRITIC-CRADIS model not only provide academic value but also have important managerial implications, especially for production managers and decision-making professionals in the field of industrial automation. Evaluating and comparing palletizing robots with the advanced MCDM method enables managers to gain a clearer understanding of each robot line’s overall performance, based on important technical criteria such as Payload, Repeatability, Load capacity, Manipulator reach, Maximum tip speed, and Average power consumption. The information is especially useful for businesses looking for effective automation solutions to improve productivity, reduce operating costs, and optimize supply chains.
The marked differences between the rankings of the methods (CRADIS, TOPSIS, SAW, and EDAS) show that choosing the appropriate MCDM method can significantly influence equipment investment decisions. CRADIS, which exhibits superior discrimination, provides a clearer and more comprehensive view of the performance gap between alternatives, helping managers make strategic and long-term robot purchasing decisions. Using objective weights from CRITIC also helps to limit bias in the evaluation process while increasing the transparency and reliability of the decision. In modern manufacturing environments where speed, precision, and energy efficiency play a key role, the results of this study can serve as a standard reference framework in developing evaluation criteria for autonomous robots, thereby standardizing the equipment selection process and enhancing the system in smart supply chain management.
Ultimately, managers can apply these results to restructure automation systems, rearrange production lines, and allocate investment budgets more efficiently. Applying the CRITIC-CRADIS model not only helps improve operational efficiency but also contributes to minimizing investment risks and creating sustainable competitive advantages in today’s volatile industrial environment.
6. Discussion
This research develops and implements an integrated evaluation framework for industrial palletizing robots by combining the distance-based refined CRITIC model with the CRADIS method, addressing the multi-criteria decision-making challenges in smart industrial environments. Choosing the right robot plays a key role in the automation of production, especially in the context of Industry 5.0, which is taking place strongly, leading to increasing requirements for performance, precision, energy savings, and system integration. Through the analysis of six key technical criteria, including payload, repeatability, load capacity, manipulator reach, maximum tip speed and average power consumption, the DR-CRITIC-CRADIS model has enabled a systematic, objective, and reliable evaluation process. DR-CRITIC takes on the role of quantifying the contrast and level of information conflict between criteria to determine objective weights, while CRADIS relies on the proximity to the ideal solution and the distance from the anti-ideal solution to rank the options appropriately. This combination helps overcome the limitations of traditional subjective weighting methods, such as AHP or BWM, and more accurately reflects the importance of each criterion in the context of real data.
After establishing methodological integration, the model was empirically tested to evaluate its effectiveness in differentiating industrial robots. The analysis results show that the FANUC CRX-25iA robot is the best choice among the surveyed options, excelling in high payload capacity, satisfactory repeatability, and fast operating speed. This not only demonstrates the superior technical capabilities of the FANUC CRX-25iA but also demonstrates the ability of the CRITIC-CRADIS model to deeply differentiate and evaluate options based on multidimensional criteria. Other robots, such as JAKA Zu 20 or Dobot CR20A are also ranked quite highly, showing fierce competition in the industrial equipment segment serving automatic production lines. In particular, the comparison of the results with other MCDM methods, such as TOPSIS, SAW, and EDAS, highlighted the stability and classification capacity of CRADIS, as this method demonstrated the sustainability of the ranking results even when there were small fluctuations in the weights or input data (shown through the sensitivity analysis). The DR-CRADIS model shows superiority in maintaining reasonable rankings without being too dependent on the absolute value of the criterion, thanks to the calculation feature based on the distance from the ideal solution. Furthermore, sensitivity analysis and evaluation of ranking changes under different weighting scenarios enhance the transparency and reliability of the proposed model. This is especially important for managers when making investment decisions that have long-term impacts on the operational capacity of the production line. In this way, the model does not stop at providing a ranking but also helps decision makers better understand the “fragility” of each option under changing environmental conditions.
In addition, although the analysis in this study was performed on eight representative industrial palletizing robots, the proposed DR-CRITIC–CRADIS framework is inherently scalable. Because both methods operate based on normalized and relative distance measures, the inclusion of additional alternatives would not affect the mathematical structure or the stability of the model. Sensitivity analysis results further confirm that the model maintains consistent ranking behavior even when input or weighting conditions vary, indicating its robustness for larger datasets.
Importantly, the comparative analysis presented in this study is not intended to claim the absolute superiority of the proposed DR-CRITIC–CRADIS framework over existing MCDM methods. Instead, the comparison serves to validate the framework’s robustness, consistency, and integration capability when combined with an objective weighting scheme. The main methodological contribution of this study lies in the refinement of the weighting process through the distance-based DR-CRITIC model, which enhances transparency and reduces subjective bias in multi-criteria decision-making. The subsequent stage of ranking using CRADIS merely demonstrates the model’s practical applicability rather than serving as a competitive benchmark. This clarification aligns the findings with the actual research objective—improving the reliability and interpretability of objective weighting in industrial decision-making contexts.
Additionally, while this study deliberately focuses on objective weighting to ensure methodological transparency and eliminate expert bias, it is acknowledged that integrating subjective or hybrid weighting schemes (e.g., AHP, BWM, or fuzzy extensions) could further enhance the managerial relevance of future applications. Such integration may help balance data-driven rigor with experiential judgment, improving the framework’s adaptability to real-world decision-making environments.
7. Conclusions
In the context of Industry 5.0, the global manufacturing industry is witnessing a strong transformation through the application of advanced technologies, such as automation, industrial robots, and artificial intelligence. In particular, robotic palletizing systems have become an indispensable part of the modern supply chain, contributing to improved efficiency, reduced labor costs, and optimized logistics operations. However, with the increasing variety of industrial robots on the market, selecting an optimal solution requires more objective and comprehensive evaluation methods. Stemming from that reality, this research is motivated with the aim of developing a robust analytical framework to support decision-making in palletizing robot selection.
Methodologically, the study proposes an extended integration between two MCDM methods, CRITIC and CRADIS, to evaluate industrial palletizing robots according to six technical criteria: payload, repeatability, load capacity, manipulator reach, maximum tip speed and average power consumption. The CRITIC method allows for the objective determination of the weight of each criterion based on the variance and correlation between the criteria, while CRADIS provides a ranking mechanism based on the distance from the ideal and anti-ideal solutions.
The analysis results show that the FANUC CRX-25iA robot is the most optimal solution in the dataset, continuously topping the rankings according to different priority levels. Notably, criteria such as repeatability and manipulator reach were identified as having the highest importance through DR-CRITIC weighting, reflecting the pivotal role of accuracy and operating range during loading and unloading operations. Sensitivity analysis also demonstrated the stability and reliability of the CRITIC-CRADIS method extension, as the rankings of the robots did not change significantly even with small adjustments in the criterion weights.
Academically, this study enriches the MCDM method repertoire by extending and integrating two highly reliable quantitative techniques and testing them in a new application area of industrial palletizing robot selection. The combination of distance-based refined CRITIC and CRADIS helps overcome the limitations of traditional subjective methods, creating a highly accurate assessment model that reflects the complexity and multidimensional relationships between technical criteria. In addition, this model is also customizable and applicable in other areas of engineering, manufacturing, logistics and smart industry.
In practice, the study provides an intuitive, effective, and easy-to-apply decision support tool for managers, automation engineers, and production planners. Based on this objective approach, businesses can choose the robot that suits their operational needs, optimizing initial investment costs as well as long-term operating efficiency. In addition, the research results also help simplify the process of comparing and evaluating robots in bidding or in the process of technological innovation of manufacturing enterprises.
Although this study primarily focused on technical and operational criteria to ensure methodological objectivity and data consistency, it is acknowledged that economic and safety factors also play essential roles in real-world industrial decision-making. These dimensions were not included in the present framework due to the lack of standardized and comparable datasets across the evaluated robots. Future research will aim to integrate these aspects into the CRITIC-CRADIS model to enhance its comprehensiveness and practical relevance.
Overall, despite these limitations, the proposed CRITIC-CRADIS framework demonstrates strong potential as a reliable, transparent, and adaptable MCDM tool. Future researchers could further expand its applicability by incorporating additional economic, social, or environmental factors and by comparing its performance with other MCDM techniques to strengthen the reliability and generalizability of the results. Moreover, as industrial data often involve uncertainty and imprecision, future studies could integrate fuzzy logic or rough set theory into the CRITIC–CRADIS model. Such integration would enable the framework to better capture the vagueness inherent in expert judgments and real-world measurements, thereby enhancing its robustness and decision-making accuracy. In general, this study can be considered foundational material for CRADIS application studies in other industrial fields, such as automation equipment selection, supply chain analysis, or advanced manufacturing technology evaluation.
Author Contributions
Conceptualization, H.-K.N., N.-L.N. and N.T.T.; methodology, H.-K.N.; validation, N.-L.N. and N.T.T.; formal analysis, N.-L.N.; data curation, H.-K.N.; writing—original draft preparation, H.-K.N.; writing—review and editing, H.-K.N. and N.T.T.; supervision, N.-L.N. and N.T.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research is funded by University of Economics Ho Chi Minh City-UEH, Vietnam.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed at the corresponding authors.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Kaur, N.; Sharma, A. Robotics and automation in manufacturing processes. In Intelligent Manufacturing; CRC Press: Boca Raton, FL, USA, 2025; pp. 97–109. [Google Scholar]
- Arents, J.; Greitans, M. Smart industrial robot control trends, challenges and opportunities within manufacturing. Appl. Sci. 2022, 12, 937. [Google Scholar] [CrossRef]
- Rainer, R.K., Jr.; Richey, R.G., Jr.; Chowdhury, S. How robotics is shaping digital logistics and supply chain management: An ongoing call for research. J. Bus. Logist. 2025, 46, e70005. [Google Scholar] [CrossRef]
- Zhang, H. Optimization and Efficiency Improvement of Robot-based Industrial Production Process. Int. J. New Dev. Eng. Soc. 2024, 8, 92–97. [Google Scholar] [CrossRef]
- Yun, J.J.; Zhao, X.; Koo, I.; Sadoi, Y.; Pyka, A. Open innovation and digital transformation in the automotive industry: A comparative analysis of South Korea, Japan and Germany. Eur. J. Innov. Manag. 2025. [Google Scholar] [CrossRef]
- Akbari, M.; Kok, S.K.; Hopkins, J.; Frederico, G.F.; Nguyen, H.; Alonso, A.D. The changing landscape of digital transformation in supply chains: Impacts of industry 4.0 in Vietnam. Int. J. Logist. Manag. 2024, 35, 1040–1072. [Google Scholar]
- Causa, O.; Abendschein, M.; Luu, N.; Soldani, E.; Soriolo, C. The post-COVID-19 rise in labour shortages. OECD Econ. Dep. Work. Pap. 2022. [Google Scholar] [CrossRef]
- Chodha, V.; Dubey, R.; Kumar, R.; Singh, S.; Kaur, S. Selection of industrial arc welding robot with TOPSIS and Entropy MCDM techniques. Mater. Today Proc. 2022, 50, 709–715. [Google Scholar]
- Taherdoost, H.; Madanchian, M. Multi-criteria decision making (MCDM) methods and concepts. Encyclopedia 2023, 3, 77–87. [Google Scholar] [CrossRef]
- Sahoo, S.K.; Goswami, S.S. A comprehensive review of multiple criteria decision-making (MCDM) Methods: Advancements, applications, and future directions. Decis. Mak. Adv. 2023, 1, 25–48. [Google Scholar] [CrossRef]
- Hosseinzadeh Lotfi, F.; Allahviranloo, T.; Pedrycz, W.; Shahriari, M.; Sharafi, H.; Razipour GhalehJough, S. The criteria importance through inter-criteria correlation (CRITIC) in uncertainty environment. In Fuzzy Decision Analysis: Multi Attribute Decision Making Approach; Springer: Berlin/Heidelberg, Germany, 2023; pp. 309–324. [Google Scholar]
- Wang, C.-N.; Syu, S.-D.; Nhieu, N.-L. Comparative analysis of telecommunications infrastructure resilience in BRICS nations: An integrated MCDM approach. IEEE Access 2024, 12, 35081–35096. [Google Scholar] [CrossRef]
- Chakraborty, S.; Chatterjee, P.; Das, P.P. Compromise Ranking of Alternatives from Distance to Ideal Solution (CRADIS) Method. In Multi-Criteria Decision-Making Methods in Manufacturing Environments; Apple Academic Press: Palm Bay, FL, USA, 2023; pp. 343–347. [Google Scholar]
- Yuan, J.; Chen, Z.; Wu, M. A novel distance measure and CRADIS method in picture fuzzy environment. Int. J. Comput. Intell. Syst. 2023, 16, 186. [Google Scholar] [CrossRef]
- Puška, A.; Božanić, D.; Mastilo, Z.; Pamučar, D. Extension of MEREC-CRADIS methods with double normalization-case study selection of electric cars. Soft Comput.- Fusion Found. Methodol. Appl. 2023, 27, 7097–7113. [Google Scholar] [CrossRef]
- Gao, R.; Zhang, W.; Wang, G.; Wang, X. Experimental research on motion analysis model and trajectory planning of GLT palletizing robot. Buildings 2023, 13, 966. [Google Scholar] [CrossRef]
- Choi, W.; Suh, J. Design and evaluation of a cable-actuated palletizing robot with geared rolling joints. IEEE/ASME Trans. Mechatron. 2024, 29, 3137–3145. [Google Scholar]
- Nechita, R.-M.; Cristoiu, C.; Mărgăritescu, M. Computational algorithm for evaluating gravitational and inertial loads acting on an industrial robot for palletizing operations. Stud. Univ. Babes-Bolyai Eng. 2024, 69, 15–31. [Google Scholar] [CrossRef]
- Sobaszek, Ł. Analysis of the Alternative Robotic Palletizing Processes in the Aspect of Electric Energy Consumption. Acta Mech. Slovaca 2023, 27, 42–47. [Google Scholar] [CrossRef]
- Deng, Y.; Zhou, T.; Zhao, G.; Zhu, K.; Xu, Z.; Liu, H. Energy saving planner model via differential evolutionary algorithm for bionic palletizing robot. Sensors 2022, 22, 7545. [Google Scholar] [CrossRef]
- Szczepanski, R.; Erwinski, K.; Tejer, M.; Bereit, A.; Tarczewski, T. Optimal scheduling for palletizing task using robotic arm and artificial bee colony algorithm. Eng. Appl. Artif. Intell. 2022, 113, 104976. [Google Scholar] [CrossRef]
- Dmytriyev, Y.; Carnevale, M.; Giberti, H. Enhancing flexibility and safety: Collaborative robotics for material handling in end-of-line industrial operations. Procedia Comput. Sci. 2024, 232, 2588–2597. [Google Scholar]
- Kakade, S.; Patle, B.; Umbarkar, A. Applications of collaborative robots in agile manufacturing: A review. Robot. Syst. Appl. 2023, 3, 59–83. [Google Scholar] [CrossRef]
- Valero, S.; Martinez, J.C.; Montes, A.M.; Marín, C.; Bolaños, R.; Álvarez, D. Machine vision-assisted design of end effector pose in robotic mixed depalletizing of heterogeneous cargo. Sensors 2025, 25, 1137. [Google Scholar] [CrossRef]
- Yoon, J.; Han, J.; Nguyen, T.P. Logistics box recognition in robotic industrial de-palletising procedure with systematic RGB-D image processing supported by multiple deep learning methods. Eng. Appl. Artif. Intell. 2023, 123, 106311. [Google Scholar] [CrossRef]
- Daios, A.; Kladovasilakis, N.; Kostavelis, I. Mixed palletizing for smart warehouse environments: Sustainability review of existing methods. Sustainability 2024, 16, 1278. [Google Scholar] [CrossRef]
- Mišković, D.; Milić, L.; Čilag, A.; Berisavljević, T.; Gottscheber, A.; Raković, M. Implementation of robots integration in scaled laboratory environment for factory automation. Appl. Sci. 2022, 12, 1228. [Google Scholar] [CrossRef]
- Xu, M.; Bai, C.; Shi, L.; Puška, A.; Štilić, A.; Stević, Ž. Assessment of mountain tourism sustainability using integrated fuzzy MCDM model. Sustainability 2023, 15, 14358. [Google Scholar] [CrossRef]
- Stanujkic, M.; Popovic, G.; Vukotic, S.; Karabasevic, D.; Stanujkic, D. Improvement of business decision-making in IT industry using the MCDM approach. Industrija 2023, 51, 73–88. [Google Scholar] [CrossRef]
- Parvaneh, F.; Hammad, A. Application of Multi-Criteria Decision-Making (MCDM) to select the most sustainable Power-Generating technology. Sustainability 2024, 16, 3287. [Google Scholar] [CrossRef]
- Momena, A.F.; Gazi, K.H.; Rahaman, M.; Sobczak, A.; Salahshour, S.; Mondal, S.P.; Ghosh, A. Ranking and challenges of supply chain companies using mcdm methodology. Logistics 2024, 8, 87. [Google Scholar] [CrossRef]
- Kut, P.; Pietrucha-Urbanik, K. Bibliometric Analysis of Multi-Criteria Decision-Making (MCDM) Methods in Environmental and Energy Engineering Using CiteSpace Software: Identification of Key Research Trends and Patterns of International Cooperation. Energies 2024, 17, 3941. [Google Scholar] [CrossRef]
- Wang, C.-N.; Nguyen, H.-K.; Nhieu, N.-L. Assessing sustainability on the modern Silk Road: An objective weighting methodological approach. PLoS ONE 2025, 20, e0324538. [Google Scholar] [CrossRef]
- Kamber, E.; Aydoğmuş, U.; Aydoğmuş, H.Y.; Gümüş, M.; Kahraman, C. Prioritization of drip-irrigation pump alternatives in agricultural applications: An integrated picture fuzzy BWM&CODAS methodology. Appl. Soft Comput. 2024, 154, 111308. [Google Scholar]
- Hasankhani, Z.; Zandieh, M.; Tirkolaee, E.B. Identification of optimal waste-to-energy strategies for sustainable development in Iran: SWOT analysis, hybrid MCDM methods, and game theory. Renew. Energy 2024, 237, 121564. [Google Scholar] [CrossRef]
- Duško, T.; Bozanic, D. Optimizing military decision-making: Application of the FUCOM–EWAA–COPRAS-G MCDM model. Acadlore Trans. Appl. Math. Stat. 2023, 1, 148–160. [Google Scholar]
- Dadashzadeh, N.; Sucu, S.; Pangbourne, K.; Ouelhadj, D. Socially Sustainable Mobility as a Service (MaaS): A practical MCDM framework to evaluate accessibility and inclusivity with application. Cities 2024, 154, 105360. [Google Scholar] [CrossRef]
- Alamoodi, A.; Zaidan, B.; Albahri, O.; Garfan, S.; Ahmaro, I.Y.; Mohammed, R.; Zaidan, A.; Ismail, A.R.; Albahri, A.; Momani, F. Systematic review of MCDM approach applied to the medical case studies of COVID-19: Trends, bibliographic analysis, challenges, motivations, recommendations, and future directions. Complex Intell. Syst. 2023, 9, 4705–4731. [Google Scholar] [CrossRef]
- Robot Belt. Available online: https://www.robotbelt.com/ (accessed on 3 July 2025).
- JAKA. Available online: https://robodk.com/robot/JAKA/Zu20 (accessed on 2 July 2025).
- Universal Robots. Available online: https://www.universal-robots.com/products/ur20/ (accessed on 1 July 2025).
- FANUC. Available online: https://crx.fanucamerica.com/crx-25ia/ (accessed on 1 July 2025).
- KUKA. Available online: https://url-shortener.me/5XHR (accessed on 1 July 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).