Product Design Decision-Making for Uncertain Environments: An Integrated Framework
Abstract
1. Introduction
2. Literature Review
2.1. Advances in QFD for Product Design
2.2. Fuzzy and Fuzzy Extensions
2.3. MCDM in Design Decision-Making
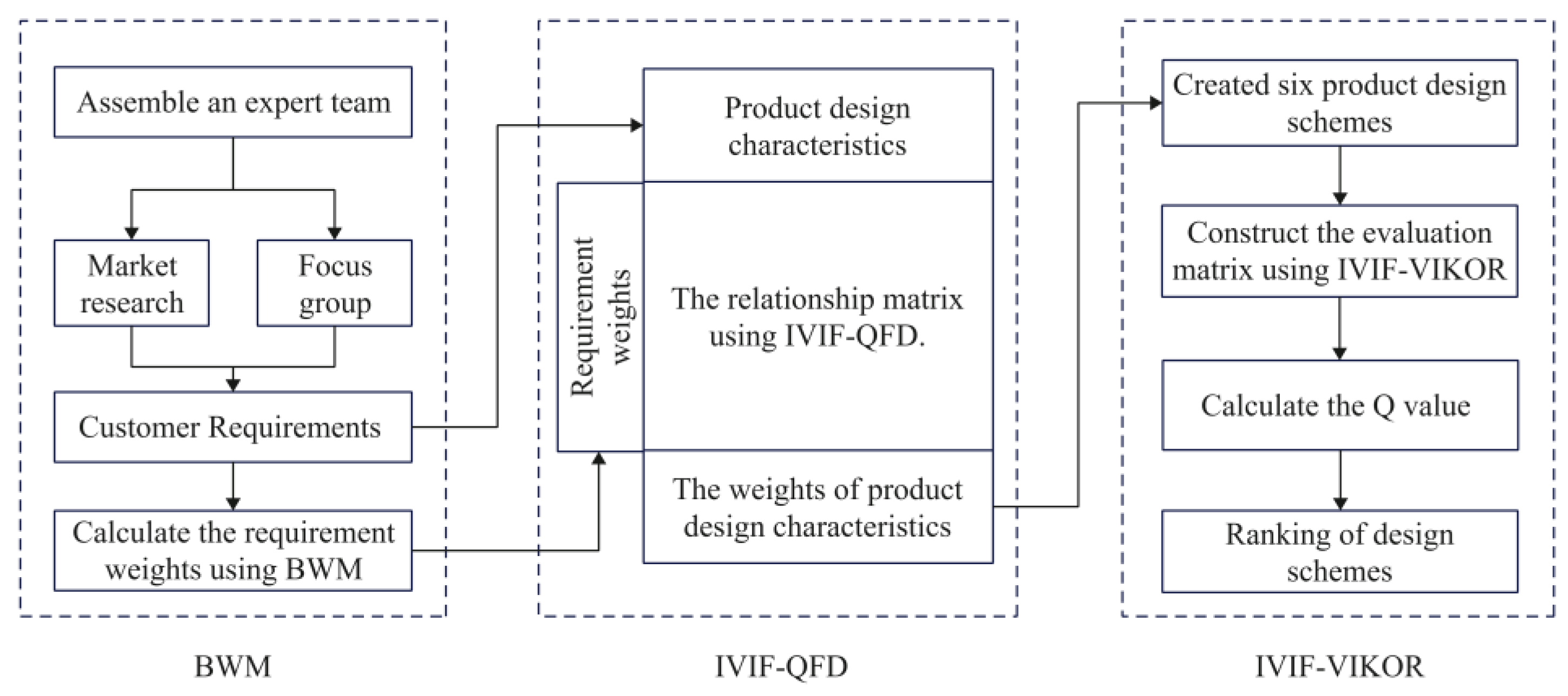
3. Proposed Framework
3.1. Application of BWM for Customer Requirement Weighting
- Best-to-Others (BO): Ratings comparing to each using a 1–9 scale, where 1 indicates equal importance and 9 extreme superiorities.
- Others-to-Worst (OW): Ratings comparing each to on the same scale.
3.2. Interval-Valued Intuitionistic Fuzzy
3.2.1. Preliminaries of Fuzzy Set Theory
3.2.2. Interval-Valued Intuitionistic Fuzzy Sets (IVIFS)
3.3. Ranking the Importance of DCs Using IVIF-QFD
3.4. Evaluating and Ranking Design Alternatives Using IVIF-VIKOR
- Determine the best and worst values for each criterion:
- 2.
- Compute the group utility and individual regret for each alternative:
- 3.
- Calculate the compromise index :
4. Case Study
4.1. Determine Customer Requirements and Design Characteristics
4.1.1. Assembling an Expert Team
4.1.2. Identify CRs and DCs
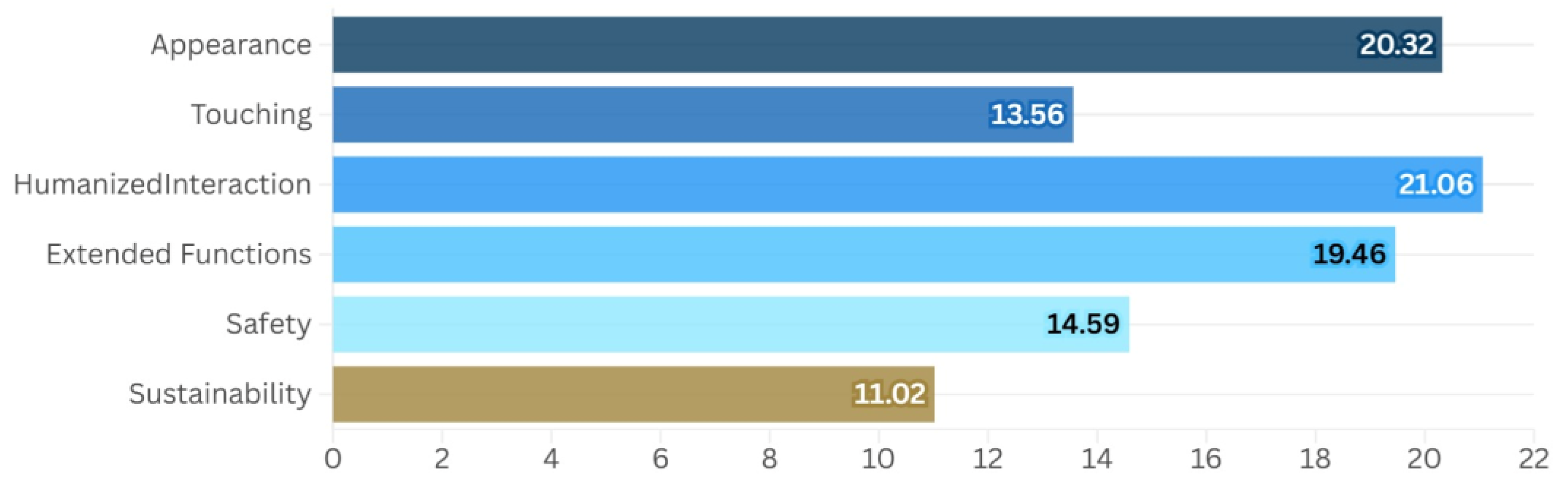
4.2. Calculating Customer Requirement Weights by BWM
4.3. Calculation of Design Characteristics Importance by IVIF-QFD
4.3.1. Constructing the CRs-DCs Relationship Matrix by IVIF
4.3.2. Defuzzified Relationship Matrix
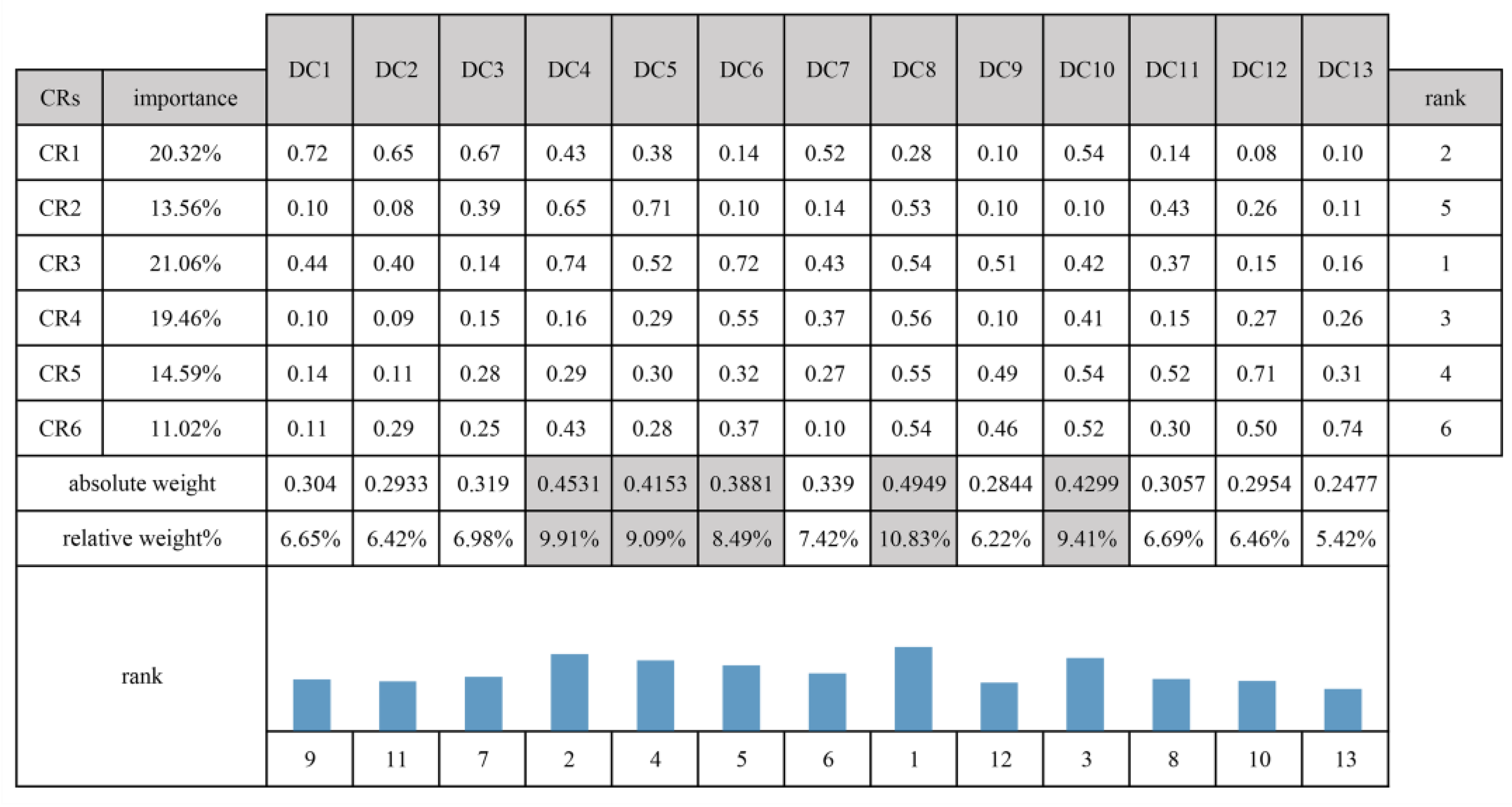
4.3.3. Calculating the Importance of Steering Wheel Design Characteristics
4.4. Design and Sequencing of Steering Wheel Conceptual Schemes
4.4.1. Six Steering Wheel Conceptual Design Schemes
4.4.2. Ranking of Design Schemes Using IVIF-VIKOR
5. Discussion
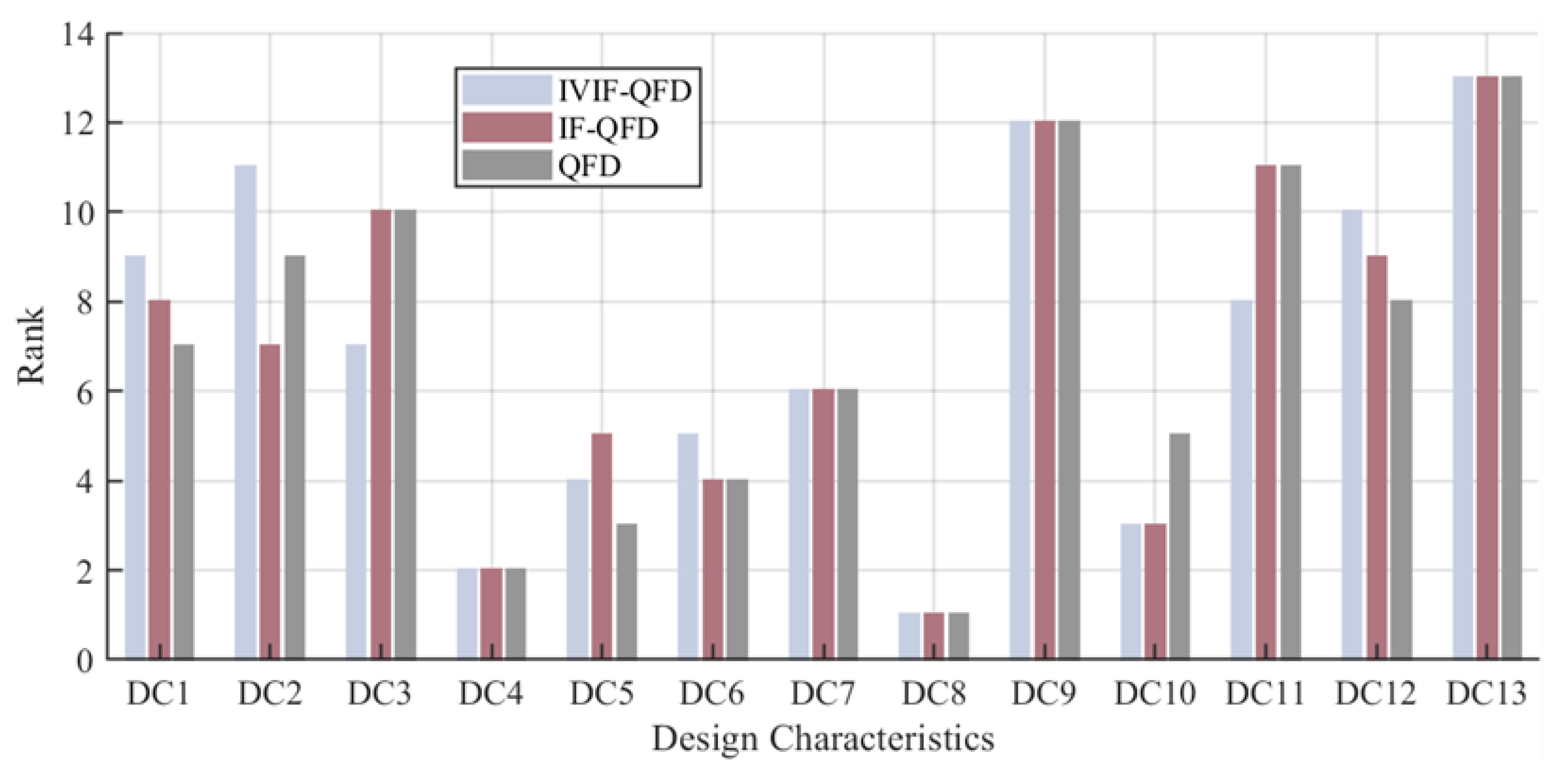
5.1. Comparative Analysis of IVIF-QFD, IF-QFD, QFD
5.2. Comparative Analysis of Different Decision-Making Frameworks
5.3. Sensitivity Analysis
6. Conclusions
6.1. The Benefits of This Research
6.2. Limitations of the Study and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Al-Ahwal, G.A.-S.; Salam, A.S.M.A.; Waheed, S.A. Design Research as competitive advantage in product design. Int. Des. J. 2021, 11, 207–221. [Google Scholar] [CrossRef]
- Ramasesh, R.; Tirupati, D.; Vaitsos, C.A. Modeling process-switching decisions under product life cycle uncertainty. Int. J. Prod. Econ. 2010, 126, 236–246. [Google Scholar] [CrossRef]
- Han, X.; Li, R.; Wang, J.; Ding, G.; Qin, S. A systematic literature review of product platform design under uncertainty. J. Eng. Des. 2020, 31, 266–296. [Google Scholar] [CrossRef]
- Shi, Y. Definition of Customer Requirements, Function Requirements, and Product Structures Based on Big Data and Data Mining Methods. Ph.D. Thesis, University of Manitoba, Winnipeg, MB, Canada, 2022. [Google Scholar]
- Ismail, G.; Taliep, N. The Delphi Method. In Handbook of Social Sciences and Global Public Health; Liamputtong, P., Ed.; Springer International Publishing: Cham, Switzerland, 2023; pp. 985–1003. [Google Scholar]
- Hamka, M. Application of fuzzy preference relations method in AHP to improve judgment matrix consistency. IOP Conf. Ser. Mater. Sci. Eng. 2020, 821, 012035. [Google Scholar] [CrossRef]
- Vaidya, O.S.; Kumar, S. Analytic hierarchy process: An overview of applications. Eur. J. Oper. Res. 2006, 169, 1–29. [Google Scholar] [CrossRef]
- Munier, N.; Hontoria, E. Uses and Limitations of the AHP Method; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Mi, X.; Tang, M.; Liao, H.; Shen, W.; Lev, B. The state-of-the-art survey on integrations and applications of the best worst method in decision making: Why, what, what for and what’s next? Omega 2019, 87, 205–225. [Google Scholar] [CrossRef]
- Chan, L.-K.; Wu, M.-L. Quality function deployment: A literature review. Eur. J. Oper. Res. 2002, 143, 463–497. [Google Scholar] [CrossRef]
- Ginting, R.; Ishak, A.; Malik, A.F.; Satrio, M.R. Product development with quality function deployment (QFD): A literature review. IOP Conf. Ser. Mater. Sci. Eng. 2020, 1003, 012022. [Google Scholar] [CrossRef]
- Beg, I.; Rashid, T. Group decision making using intuitionistic hesitant fuzzy sets. Int. J. Fuzzy Log. Intell. Syst. 2014, 14, 181–187. [Google Scholar] [CrossRef]
- Lu, S.; Zhou, J.; Ren, J. Alleviating Energy Poverty through Renewable Energy Technology: An Investigation Using a Best-Worst Method-Based Quality Function Deployment Approach with Interval-Valued Intuitionistic Fuzzy Numbers. Int. J. Energy Res. 2023, 2023, 8358799. [Google Scholar] [CrossRef]
- Yu, D.; Ye, T. Uncovering the academic evolution of VIKOR method: A comprehensive main path analysis. J. Oper. Res. Soc. 2025, 76, 393–409. [Google Scholar] [CrossRef]
- Jahan, A.; Mustapha, F.; Ismail, Y.; Sapuan, S.; Bahraminasab, M. A comprehensive VIKOR method for material selection. Mater. Des. 2011, 32, 1215–1221. [Google Scholar]
- Kim, J.H.; Ahn, B.S. The hierarchical VIKOR method with incomplete information: Supplier selection problem. Sustainability 2020, 12, 9602. [Google Scholar] [CrossRef]
- Chang, C.-L. A modified VIKOR method for multiple criteria analysis. Environ. Monit. Assess. 2010, 168, 339–344. [Google Scholar] [CrossRef] [PubMed]
- Akao, Y.; Mazur, G.H. The leading edge in QFD: Past, present and future. Int. J. Qual. Reliab. Manag. 2003, 20, 20–35. [Google Scholar] [CrossRef]
- Kang, X.; Yang, M.; Wu, Y.; Ni, B. Integrating Evaluation Grid Method and Fuzzy Quality Function Deployment to New Product Development. Math. Probl. Eng. 2018, 2018, 1–15. [Google Scholar] [CrossRef]
- Hauser, J.R. +e house of quality. Harv. Bus. Rev. 1988, 66, 63–73. [Google Scholar]
- English, J.R. Quality Function Deployment: Integrating Customer Requirements into Product Design. J. Qual. Technol. 2018, 25, 63–64. [Google Scholar] [CrossRef]
- Lai, X.; Xie, M.; Tan, T. Optimizing product design using the Kano model and QFD. In Proceedings of the 2004 IEEE International Engineering Management Conference, Singapore, 18–21 October 2004. [Google Scholar]
- Tu, N.; Zhang, T.; He, Q.; Zhang, H.; Li, Y. Applying combined AHP-QFD method in new product development: A case study in developing new sports earphone. In Proceedings of the MSIE 2011, Harbin, China, 8–11 January 2011. [Google Scholar]
- Karasan, A.; Ilbahar, E.; Cebi, S.; Kahraman, C. Customer-oriented product design using an integrated neutrosophic AHP & DEMATEL & QFD methodology. Appl. Soft Comput. 2022, 118, 108445. [Google Scholar] [CrossRef]
- Porto de Lima, B.; Da Silva, A.F.; Marins, F.A.S. New hybrid AHP-QFD-PROMETHEE decision-making support method in the hesitant fuzzy environment: An application in packaging design selection. J. Intell. Fuzzy Syst. 2022, 42, 2881–2894. [Google Scholar] [CrossRef]
- Yazdani, M.; Kahraman, C.; Zarate, P.; Onar, S.C. A fuzzy multi attribute decision framework with integration of QFD and grey relational analysis. Expert. Syst. Appl. 2019, 115, 474–485. [Google Scholar] [CrossRef]
- Ocampo, L.A.; Labrador, J.J.T.; Jumao-As, A.M.B.; Rama, A.M.O. Integrated multiphase sustainable product design with a hybrid quality function deployment—Multi-attribute decision-making (QFD-MADM) framework. Sustain. Prod. Consum. 2020, 24, 62–78. [Google Scholar] [CrossRef]
- Oglu, S.V.H. Decision Making Under Linguistic Uncertainty Conditions on Base of Generalized Fuzzy Numbers. World Sci. 2021, 8, 25–29. [Google Scholar]
- Zadeh, L. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Ramot, D.; Milo, R.; Friedman, M.; Kandel, A. Complex fuzzy sets. IEEE Trans. Fuzzy Syst. 2002, 10, 171–186. [Google Scholar] [CrossRef]
- Stojanović, N.; Laković, M. Q [ε]-FUZZY SETS. J. Korean Soc. Ind. Appl. Math. 2024, 28, 303–318. [Google Scholar]
- Singh, M.K. Application of Triangular Fuzzy Numbers in Taking Optimal Decision. In Decision Making in Inventory Management; Shah, N.H., Mittal, M., Cárdenas-Barrón, L.E., Eds.; Springer: Singapore, 2021; pp. 219–230. [Google Scholar]
- Sen, D.K.; Datta, S.; Mahapatra, S. Sustainable supplier selection in intuitionistic fuzzy environment: A decision-making perspective. Benchmarking Int. J. 2018, 25, 545–574. [Google Scholar] [CrossRef]
- Chen, L.; Liu, W.; Zhang, J. An interval type-2 fuzzy multi-criteria decision-making approach for patient bed allocation. Sci. Rep. 2025, 15, 21019. [Google Scholar] [CrossRef]
- Peng, J.-J.; Wang, J.-Q.; Wu, X.-H. Novel Multi-criteria Decision-making Approaches Based on Hesitant Fuzzy Sets and Prospect Theory. Int. J. Inf. Technol. Decis. Mak. 2016, 15, 621–643. [Google Scholar] [CrossRef]
- Kahraman, C.; Gündoğdu, F.K.; Karaşan, A.; Boltürk, E. Advanced fuzzy sets and multicriteria decision making on product development. In Customer Oriented Product Design: Intelligent and Fuzzy Techniques; Springer International Publishing: Cham, Switzerland, 2020; pp. 283–302. [Google Scholar]
- Khan, M.K.; Kamran Sajjad Ali Khan, M.; Aloqaily, A.; Mlaiki, N. Covering-Based Intuitionistic Hesitant Fuzzy Rough Set Models and Their Application to Decision-Making Problems. Symmetry 2024, 16, 693. [Google Scholar] [CrossRef]
- Ali, W.; Shaheen, T.; Haq, I.U.; Toor, H.G.; Akram, F.; Jafari, S.; Uddin, Z.; Hassan, M.M. Multiple-attribute decision making based on intuitionistic hesitant fuzzy connection set environment. Symmetry 2023, 15, 778. [Google Scholar] [CrossRef]
- Kahraman, C.; Onar, S.Ç.; Öztayşi, B. Interval valued intuitionistic fuzzy investment analysis: Application to CNC lathe selection. IFAC-Pap. 2016, 49, 1323–1328. [Google Scholar] [CrossRef]
- Caisucar, M.; Gaonkar, R.S.P. Uncertainty Identification in New Product Development. Ind. Eng. J. 2018, 10, 41–45. [Google Scholar] [CrossRef]
- Yang, Y.Z.; Yen, C.H. An AHP Method with Cosmetic Design Application. In Proceedings of the 2019 International Conference on Virtual Reality and Intelligent Systems (ICVRIS), Jishou, China, 14–15 September 2019; pp. 346–349. [Google Scholar] [CrossRef]
- Ayağ, Z.; özdem r, R. An analytic network process-based approach to concept evaluation in a new product development environment. J. Eng. Des. 2007, 18, 209–226. [Google Scholar] [CrossRef]
- Sharma, D.; Sridhar, S.; Claudio, D. Comparison of AHP-TOPSIS and AHP-AHP methods in multi-criteria decision-making problems. Int. J. Ind. Syst. Eng. 2020, 34, 203–223. [Google Scholar] [CrossRef]
- Yu, Z.; Zhao, W.; Guo, X.; Hu, H.; Fu, C.; Liu, Y. Multi-indicators decision for product design solutions: A TOPSIS-MOGA integrated model. Processes 2022, 10, 303. [Google Scholar] [CrossRef]
- Mousavi-Nasab, S.H.; Sotoudeh-Anvari, A. A comprehensive MCDM-based approach using TOPSIS, COPRAS and DEA as an auxiliary tool for material selection problems. Mater. Des. 2017, 121, 237–253. [Google Scholar] [CrossRef]
- Vinodh, S.; Girubha, R.J. PROMETHEE based sustainable concept selection. Appl. Math. Model. 2012, 36, 5301–5308. [Google Scholar] [CrossRef]
- Zhang, S.; Gao, H.; Wei, G.; Wei, Y.; Wei, C. Evaluation based on distance from average solution method for multiple criteria group decision making under picture 2-tuple linguistic environment. Mathematics 2019, 7, 243. [Google Scholar] [CrossRef]
- Zhu, G.-N.; Hu, J.; Qi, J.; Gu, C.-C.; Peng, Y.-H. An integrated AHP and VIKOR for design concept evaluation based on rough number. Adv. Eng. Inform. 2015, 29, 408–418. [Google Scholar] [CrossRef]
- Kirişci, M.; Demir, I.; Şimşek, N.; Topaç, N.; Bardak, M. The novel VIKOR methods for generalized Pythagorean fuzzy soft sets and its application to children of early childhood in COVID-19 quarantine. Neural Comput. Appl. 2022, 34, 1877–1903. [Google Scholar] [CrossRef]
- Park, J.H.; Cho, H.J.; Kwun, Y.C. Extension of the VIKOR method for group decision making with interval-valued intuitionistic fuzzy information. Fuzzy Optim. Decis. Mak. 2011, 10, 233–253. [Google Scholar] [CrossRef]
- Atanassov, K.T. Interval Valued Intuitionistic Fuzzy Sets. In Intuitionistic Fuzzy Sets: Theory and Applications; Atanassov, K.T., Ed.; Physica-Verlag HD: Heidelberg, Germany, 1999; pp. 139–177. [Google Scholar]
- Büyüközkan, G.; Uztürk, D. Smart Fridge Design with Interval-Valued Intuitionistic Fuzzy QFD. In Intelligent and Fuzzy Techniques in Big Data Analytics and Decision Making; Advances in Intelligent Systems and Computing; Springer International Publishing: Cham, Switzerland, 2020; Chapter 138; pp. 1170–1179. [Google Scholar]
- Karaşan, A.; Kahraman, C. A novel intuitionistic fuzzy DEMATEL—ANP—TOPSIS integrated methodology for freight village location selection. J. Intell. Fuzzy Syst. 2017, 36, 1335–1352. [Google Scholar] [CrossRef]
- Haktanir, E.; Kahraman, C. New product design using chebyshev’s inequality based interval-valued intuitionistic z-fuzzy qfd method. Informatica 2022, 33, 1–33. [Google Scholar] [CrossRef]
- Fu, S.; Xiao, Y.-Z.; Zhou, H.-J. Interval-valued intuitionistic fuzzy multi-attribute group decision-making method considering risk preference of decision-makers and its application. Sci. Rep. 2022, 12, 11597. [Google Scholar] [CrossRef] [PubMed]
- Park, H.; Megahed, A.; Yin, P.; Ong, Y.; Mahajan, P.; Guo, P. Incorporating experts’ judgment into machine learning models. Expert. Syst. Appl. 2023, 228, 120118. [Google Scholar] [CrossRef]
- Hariri, A.; Domingues, P.; Sampaio, P. Integration of multi-criteria decision-making approaches adapted for quality function deployment: An analytical literature review and future research agenda. Int. J. Qual. Reliab. Manag. 2023, 40, 2326–2350. [Google Scholar] [CrossRef]
- Schryen, G. Parallel computational optimization in operations research: A new integrative framework, literature review and research directions. Eur. J. Oper. Res. 2020, 287, 1–18. [Google Scholar] [CrossRef]



| Item | Content | Number of People | Percentage |
|---|---|---|---|
| Gender | Male | 24 | 63.16% |
| Female | 14 | 36.84% | |
| Driving Experience | <2 years | 8 | 21.05% |
| 2–5 years | 10 | 26.32% | |
| <5 years | 20 | 52.63% | |
| Occupation | Product design teacher | 14 | 36.84% |
| Taxi Driver | 14 | 36.84% | |
| Automotive Designer | 10 | 26.32% |
| Customer Requirements | No. | Design Characteristics |
|---|---|---|
| Appearance | DC1 | Stylish and attractive shape |
| DC2 | Reasonable color coordination | |
| DC3 | Premium materials and texture | |
| Touching | DC4 | Skin-friendly materials |
| DC5 | Ergonomic design | |
| Humanized Interaction | DC6 | Real-time feedback |
| DC7 | Touch buttons | |
| DC8 | Reasonable layout | |
| Extended Functions | DC9 | Adaptive adjustment |
| DC10 | Customizable buttons | |
| Safety | DC11 | Anti-slip design |
| DC12 | Fatigue-resistant design | |
| Sustainability | DC13 | Technological compatibility |
| E1 | E2 | E3 | E4 | E5 | E6 | E7 | E8 | E9 | E10 | E11 | E12 | E13 | E14 | E15 | E16 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| EPS | 0.085 | 0.093 | 0.075 | 0.094 | 0.089 | 0.094 | 0.089 | 0.094 | 0.083 | 0.086 | 0.083 | 0.083 | 0.075 | 0.089 | 0.075 | 0.090 |
| Cr | 0.028 | 0.031 | 0.025 | 0.031 | 0.03 | 0.031 | 0.03 | 0.031 | 0.028 | 0.029 | 0.028 | 0.028 | 0.025 | 0.03 | 0.025 | 0.03 |
| Linguistic Term | IVIF Number |
|---|---|
| Absolutely Low Importance (ALI)/Absolutely Low Relation (ALR) | (0.0,0.1),(0.8,0.9) |
| Very Low Importance (VLI)/Very Low Relation (VLR) | (0.1,0.2),(0.7,0.8) |
| Low importance (LI) /Low Relation (LR) | (0.2,0.3),(0.6,0.7) |
| Medium Low Importance (MLI) Medium Low Relation (MLR) | (0.3,0.4),(0.5,0.6) |
| Approximately Equal Importance (AEI)/Approximately Equal Relation (AER) | (0.4,0.5),(0.4,0.5) |
| Medium High Importance (MHI)/Medium High Relation (MHR) | (0.5,0.6),(0.3,0.4) |
| High Importance (HI)/High Relation (HR) | (0.6,0.7),(0.2,0.3) |
| Very High Importance (VHI)/Very High Relation (VHR) | (0.7,0.8),(0.1,0.2) |
| Absolutely High Importance (AHI)/Absolutely High Relation (AHR) | (0.8,0.9),(0.0,0.1) |
| CRs | DC1 | DC2 | DC3 | DC4 | DC5 | DC6 | DC7 | DC8 | DC9 | DC10 | DC11 | DC12 | DC13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CR1 | (0.69,0.79), (0.11,0.21) | (0.63,0.73), (0.17,0.27) | (0.65,0.75), (0.15,0.25) | (0.42,0.52), (0.38,0.48) | (0.37,0.47), (0.43,0.53) | (0.09,0.19), (0.71,0.81) | (0.51,0.61), (0.29,0.39) | (0.26,0.36), (0.54,0.64) | (0.04,0.14), (0.76,0.86) | (0.53,0.63), (0.27,0.37) | (0.10,0.20), (0.70,0.80) | (0.02,0.12), (0.78,0.88) | (0.05,0.15), (0.75,0.85) |
| CR2 | (0.04,0.14), (0.76,0.86) | (0.02,0.12), (0.78,0.88) | (0.38,0.48), (0.42,0.52) | (0.63,0.73), (0.17,0.27) | (0.68,0.78), (0.12,0.22) | (0.05,0.15), (0.75,0.85) | (0.09,0.19), (0.71,0.81) | (0.52,0.62), (0.28,0.38) | (0.05,0.15), (0.75,0.85) | (0.04,0.14), (0.76,0.86) | (0.42,0.52), (0.38,0.48) | (0.24,0.34), (0.56,0.66) | (0.06,0.16), (0.74,0.84) |
| CR3 | (0.43,0.53), (0.37,0.47) | (0.39,0.49), (0.41,0.51) | (0.10,0.20), (0.70,0.80) | (0.71,0.81), (0.09,0.19) | (0.51,0.61), (0.29,0.39) | (0.69,0.79), (0.11,0.21) | (0.42,0.52), (0.38,0.48) | (0.53,0.63), (0.27,0.37) | (0.50,0.60), (0.30,0.40) | (0.41,0.51), (0.39,0.49) | (0.36,0.46), (0.44,0.54) | (0.11,0.21), (0.69,0.79) | (0.12,0.22), (0.68,0.78) |
| CR4 | (0.05,0.15), (0.75,0.85) | (0.03,0.13), (0.77,0.87) | (0.11,0.21), (0.69,0.79) | (0.12,0.22), (0.68,0.78) | (0.27,0.37), (0.53,0.63) | (0.54,0.64), (0.26,0.36) | (0.36,0.46), (0.44,0.54) | (0.55,0.65), (0.25,0.35) | (0.05,0.15), (0.75,0.85) | (0.40,0.50), (0.40,0.50) | (0.11,0.21), (0.69,0.79) | (0.25,0.35), (0.55,0.65) | (0.24,0.34), (0.56,0.66) |
| CR5 | (0.09,0.19), (0.71,0.81) | (0.06,0.16), (0.74,0.84) | (0.26,0.36), (0.54,0.64) | (0.27,0.37), (0.53,0.63) | (0.28,0.38), (0.52,0.62) | (0.30,0.40), (0.50,0.60) | (0.25,0.35), (0.55,0.65) | (0.54,0.64), (0.26,0.36) | (0.48,0.58), (0.32,0.42) | (0.53,0.63), (0.27,0.37) | (0.51,0.61), (0.29,0.39) | (0.68,0.78), (0.12,0.22) | (0.29,0.39), (0.51,0.61) |
| CR6 | (0.06,0.16), (0.74,0.84) | (0.27,0.37), (0.53,0.63) | (0.23,0.33), (0.57,0.67) | (0.42,0.52), (0.38,0.48) | (0.26,0.36), (0.54,0.64) | (0.36,0.46), (0.44,0.54) | (0.04,0.14), (0.76,0.86) | (0.53,0.63), (0.27,0.37) | (0.45,0.55), (0.35,0.45) | (0.51,0.61), (0.29,0.39) | (0.28,0.38), (0.52,0.62) | (0.49,0.59), (0.31,0.41) | (0.71,0.81), (0.09,0.19) |
| Scheme | DC1 | DC2 | DC3 | DC4 | DC5 | DC6 | DC7 | DC8 | DC9 | DC10 | DC11 | DC12 | DC13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | (0.64,0.74) (0.16,0.26) | (0.61,0.71) (0.19,0.29) | (0.63,0.73) (0.17,0.27) | (0.53,0.63) (0.27,0.37) | (0.63,0.73) (0.17,0.27) | (0.58,0.68) (0.22,0.32) | (0.29,0.39) (0.51,0.61) | (0.47,0.57) (0.33,0.43) | (0.38,0.48) (0.42,0.52) | (0.53,0.63) (0.27,0.37) | (0.64,0.74) (0.16,0.26) | (0.53,0.63) (0.27,0.37) | (0.28,0.38) (0.52,0.62) |
| B | (0.59,0.69) (0.21,0.31) | (0.53,0.63) (0.27,0.37) | (0.53,0.63) (0.27,0.37) | (0.61,0.71) (0.19,0.29) | (0.62,0.72) (0.18,0.28) | (0.54,0.64) (0.26,0.36) | (0.54,0.64) (0.26,0.36) | (0.62,0.72) (0.18,0.28) | (0.42,0.52) (0.38,0.48) | (0.53,0.63) (0.27,0.37) | (0.64,0.74) (0.16,0.26) | (0.54,0.64) (0.26,0.36) | (0.62,0.72) (0.18,0.28) |
| C | (0.47,0.57) (0.33,0.43) | (0.49,0.59) (0.31,0.41) | (0.51,0.61) (0.29,0.39) | (0.53,0.63) (0.27,0.37) | (0.55,0.65) (0.25,0.35) | (0.54,0.64) (0.26,0.36) | (0.61,0.71) (0.19,0.29) | (0.55,0.65) (0.25,0.35) | (0.14,0.24) (0.66,0.76) | (0.33,0.43) (0.47,0.57) | (0.14,0.24) (0.66,0.76) | (0.15,0.25) (0.65,0.75) | (0.21,0.31) (0.59,0.69) |
| D | (0.47,0.57) (0.33,0.43) | (0.51,0.61) (0.29,0.39) | (0.52,0.62) (0.28,0.38) | (0.18,0.28) (0.62,0.72) | (0.57,0.67) (0.23,0.33) | (0.54,0.64) (0.26,0.36) | (0.54,0.64) (0.26,0.36) | (0.18,0.28) (0.62,0.72) | (0.19,0.29) (0.61,0.71) | (0.53,0.63) (0.27,0.37) | (0.49,0.59) (0.31,0.41) | (0.14,0.24) (0.66,0.76) | (0.18,0.28) (0.62,0.72) |
| E | (0.58,0.68) (0.22,0.32) | (0.29,0.39) (0.51,0.61) | (0.59,0.69) (0.21,0.31) | (0.33,0.43) (0.47,0.57) | (0.54,0.64) (0.26,0.36) | (0.53,0.63) (0.27,0.37) | (0.25,0.35) (0.55,0.65) | (0.42,0.52) (0.38,0.48) | (0.29,0.39) (0.51,0.61) | (0.14,0.24) (0.66,0.76) | (0.53,0.63) (0.27,0.37) | (0.22,0.32) (0.58,0.68) | (0.47,0.57) (0.33,0.43) |
| F | (0.54,0.64) (0.26,0.36) | (0.52,0.62) (0.28,0.38) | (0.31,0.41) (0.49,0.59) | (0.49,0.59) (0.31,0.41) | (0.58,0.68) (0.22,0.32) | (0.52,0.62) (0.28,0.38) | (0.50,0.59) (0.30,0.41) | (0.64,0.74) (0.16,0.26) | (0.37,0.47) (0.43,0.53) | (0.54,0.64) (0.26,0.36) | (0.62,0.72) (0.18,0.28) | (0.47,0.57) (0.33,0.43) | (0.33,0.43) (0.47,0.57) |
| Scheme | DC1 | DC2 | DC3 | DC4 | DC5 | DC6 | DC7 | DC8 | DC9 | DC10 | DC11 | DC12 | DC13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 0.66 | 0.63 | 0.65 | 0.54 | 0.65 | 0.60 | 0.31 | 0.48 | 0.39 | 0.54 | 0.66 | 0.54 | 0.30 |
| B | 0.61 | 0.54 | 0.54 | 0.63 | 0.64 | 0.55 | 0.55 | 0.64 | 0.43 | 0.54 | 0.66 | 0.55 | 0.64 |
| C | 0.48 | 0.50 | 0.52 | 0.54 | 0.56 | 0.55 | 0.63 | 0.56 | 0.18 | 0.35 | 0.18 | 0.19 | 0.24 |
| D | 0.48 | 0.52 | 0.53 | 0.21 | 0.59 | 0.55 | 0.55 | 0.21 | 0.22 | 0.54 | 0.50 | 0.18 | 0.21 |
| E | 0.60 | 0.31 | 0.61 | 0.35 | 0.55 | 0.54 | 0.28 | 0.43 | 0.31 | 0.18 | 0.54 | 0.25 | 0.48 |
| F | 0.55 | 0.53 | 0.33 | 0.50 | 0.60 | 0.53 | 0.51 | 0.66 | 0.38 | 0.55 | 0.64 | 0.48 | 0.35 |
| Scheme | Group Utility Value (S) | Individual Regret Value (R) | Compromise Ranking Index (Q) | Rank |
|---|---|---|---|---|
| A | 0.189496 | 0.067824 | 0.109194 | 2 |
| B | 0.154588 | 0.060662 | 0 | 1 |
| C | 0.602021 | 0.081791 | 0.657825 | 4 |
| D | 0.650322 | 0.108298 | 0.983119 | 6 |
| E | 0.667644 | 0.094074 | 0.850702 | 5 |
| F | 0.381027 | 0.084927 | 0.475369 | 3 |
| Model | Average Value | Standard Deviation | IVIF-QFD | IF-QFD | QFD |
|---|---|---|---|---|---|
| IVIF-QFD | 7.000 | 3.894 | 1 | ||
| IF-QFD | 7.000 | 3.894 | 0.896 ** | 1 | |
| QFD | 7.000 | 3.894 | 0.901 ** | 0.962 ** | 1 |
| Scheme | IVIF-COPRAS | Rank | IVIF-TOPSIS | Rank | Proposed Framework | Rank |
|---|---|---|---|---|---|---|
| A | 0.816175 | 2 | 0.713419 | 2 | 0.109193 | 2 |
| B | 0.847632 | 1 | 0.7709815 | 1 | 0 | 1 |
| C | 0.644881 | 5 | 0.4312833 | 4 | 0.657824 | 4 |
| D | 0.563214 | 6 | 0.400109 | 5 | 0.983118 | 6 |
| E | 0.746638 | 4 | 0.3792867 | 6 | 0.850702 | 5 |
| F | 0.802472 | 3 | 0.5813431 | 3 | 0.475368 | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, W.; Cui, X.; Peng, H. Product Design Decision-Making for Uncertain Environments: An Integrated Framework. Mathematics 2025, 13, 3257. https://doi.org/10.3390/math13203257
Xu W, Cui X, Peng H. Product Design Decision-Making for Uncertain Environments: An Integrated Framework. Mathematics. 2025; 13(20):3257. https://doi.org/10.3390/math13203257
Chicago/Turabian StyleXu, Weifeng, Xiaomin Cui, and Haitao Peng. 2025. "Product Design Decision-Making for Uncertain Environments: An Integrated Framework" Mathematics 13, no. 20: 3257. https://doi.org/10.3390/math13203257
APA StyleXu, W., Cui, X., & Peng, H. (2025). Product Design Decision-Making for Uncertain Environments: An Integrated Framework. Mathematics, 13(20), 3257. https://doi.org/10.3390/math13203257






