Joint Wavelet and Sine Transforms for Performance Enhancement of OFDM Communication Systems
Abstract
1. Introduction
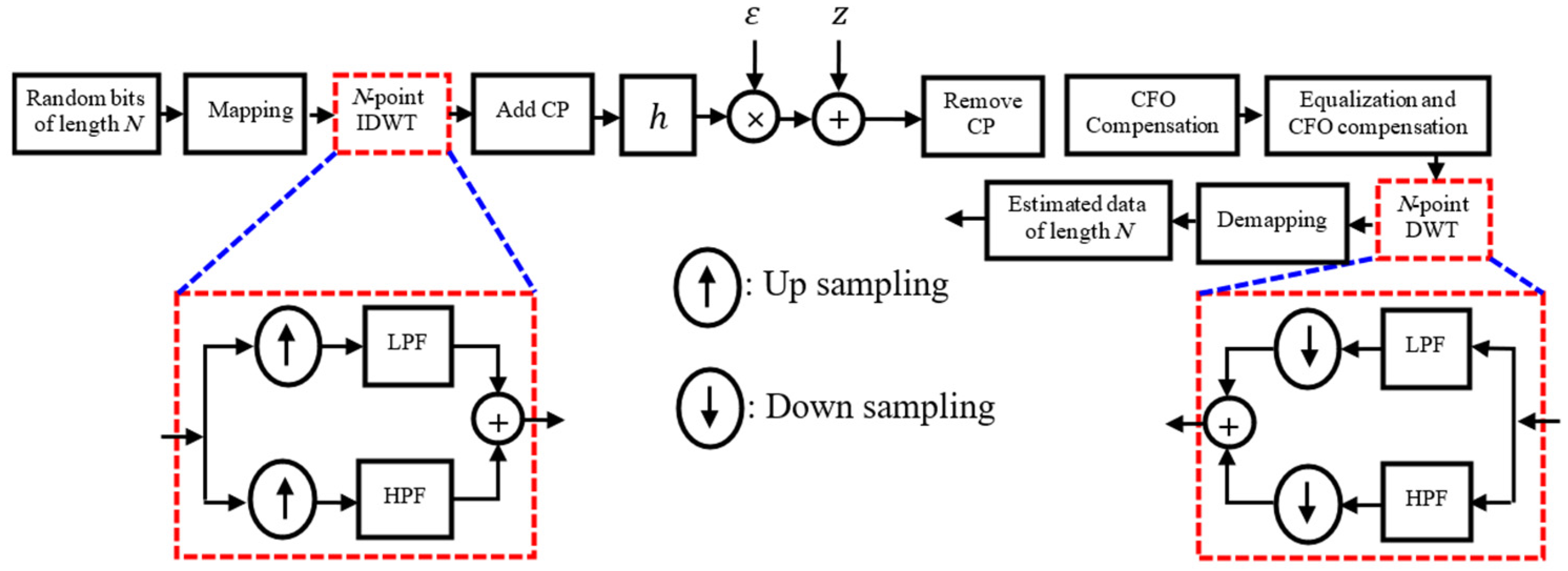
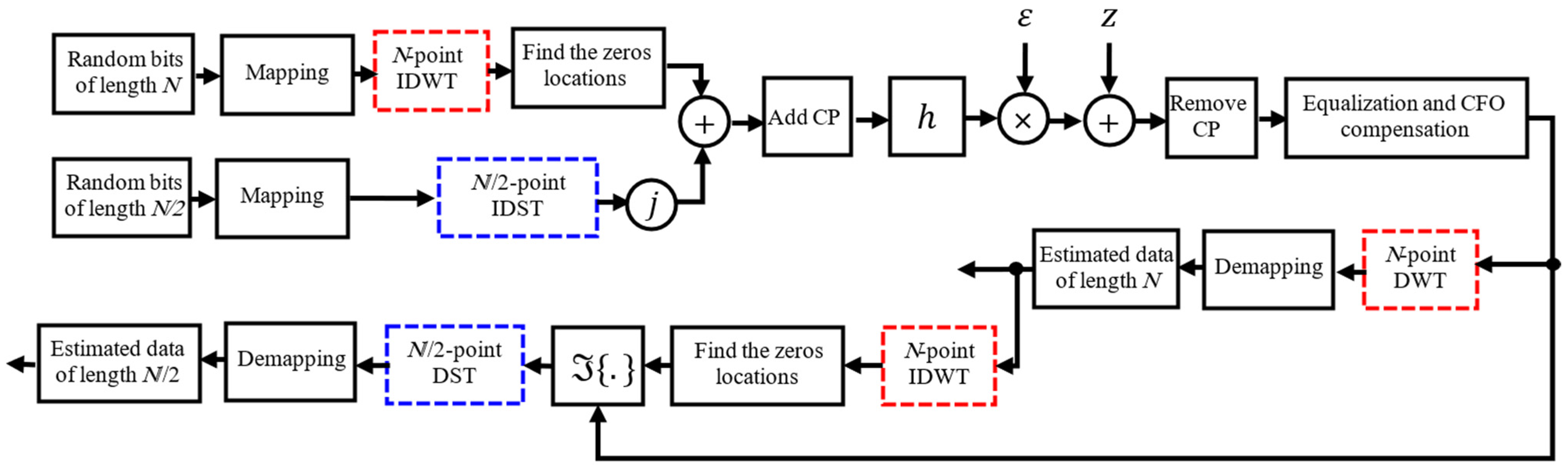
2. Proposed DWT-OFDM System Model
3. Simulation Results and Analysis
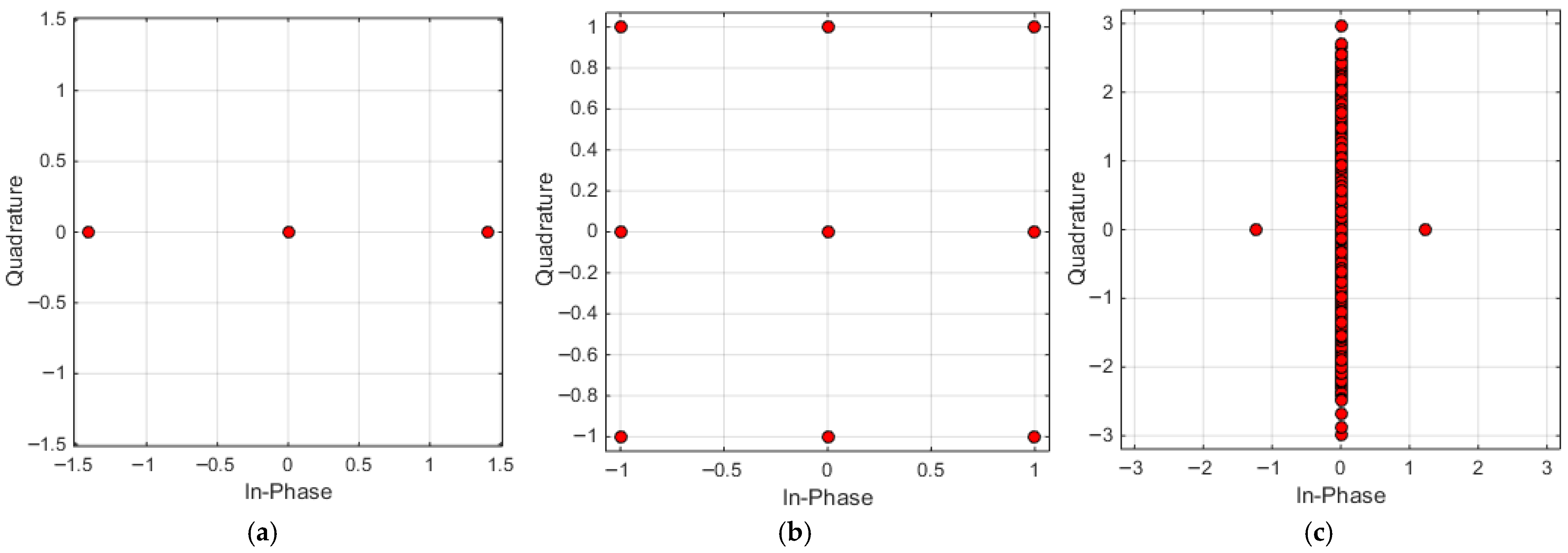
3.1. Transmission Capacity
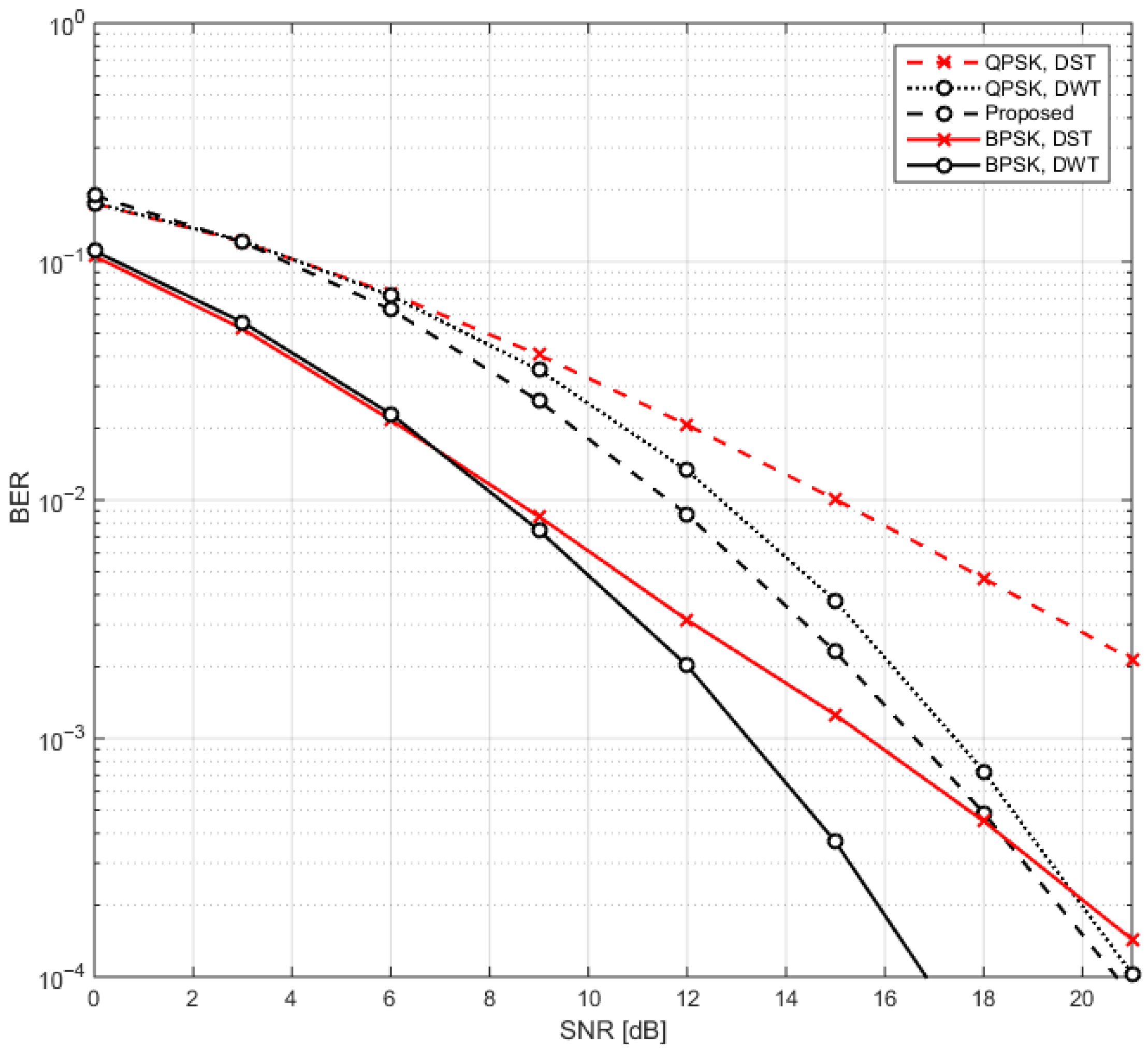
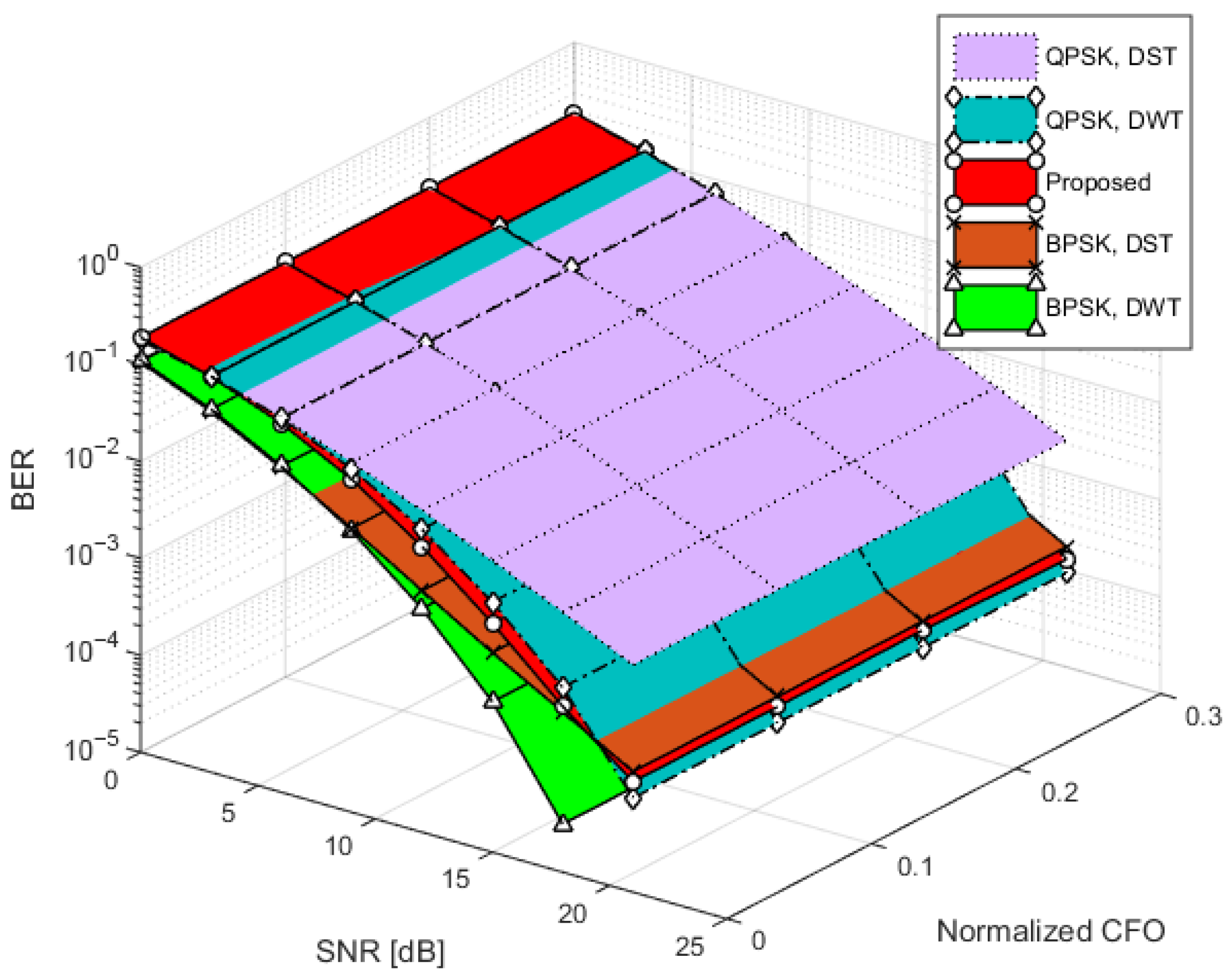
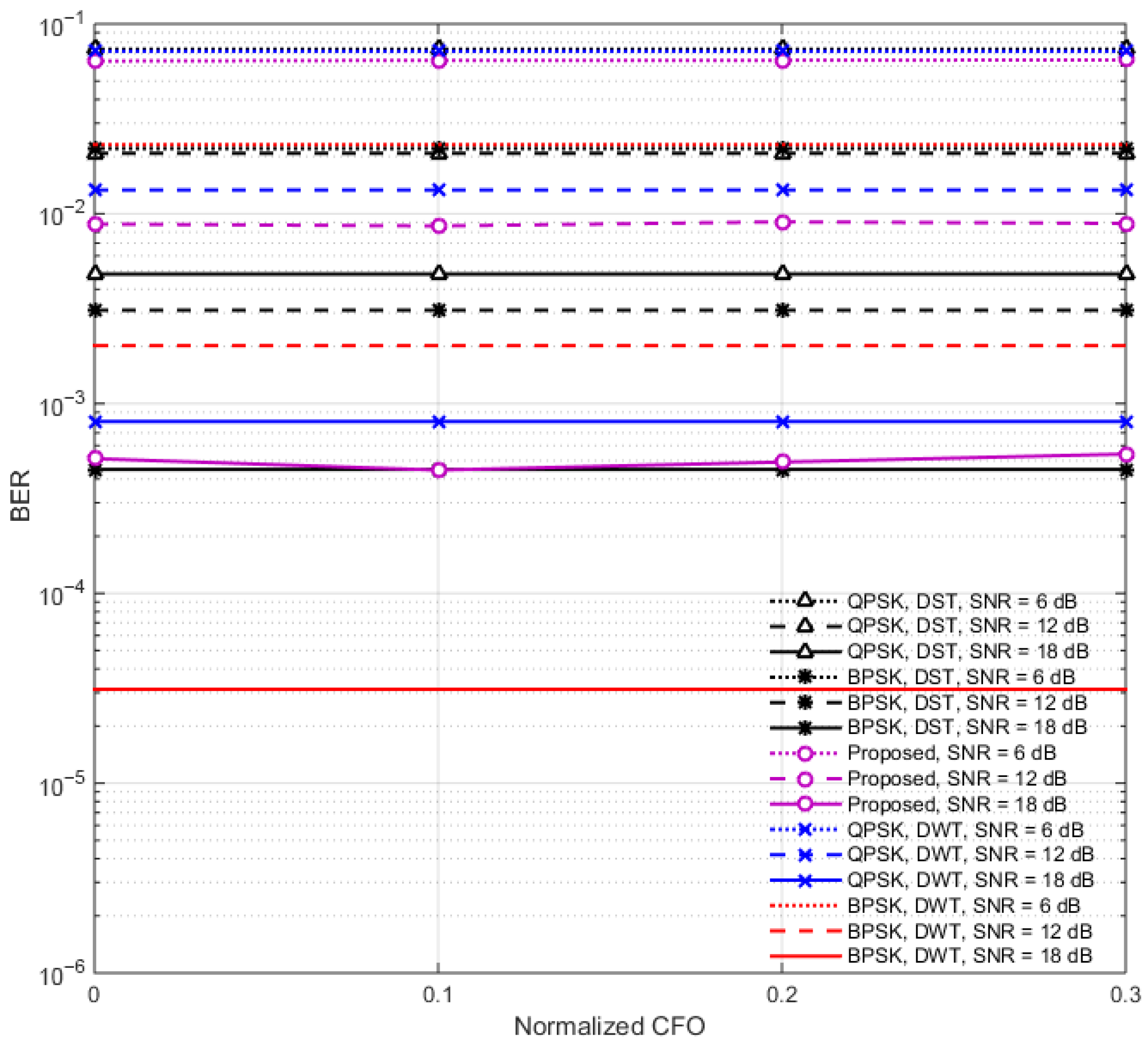
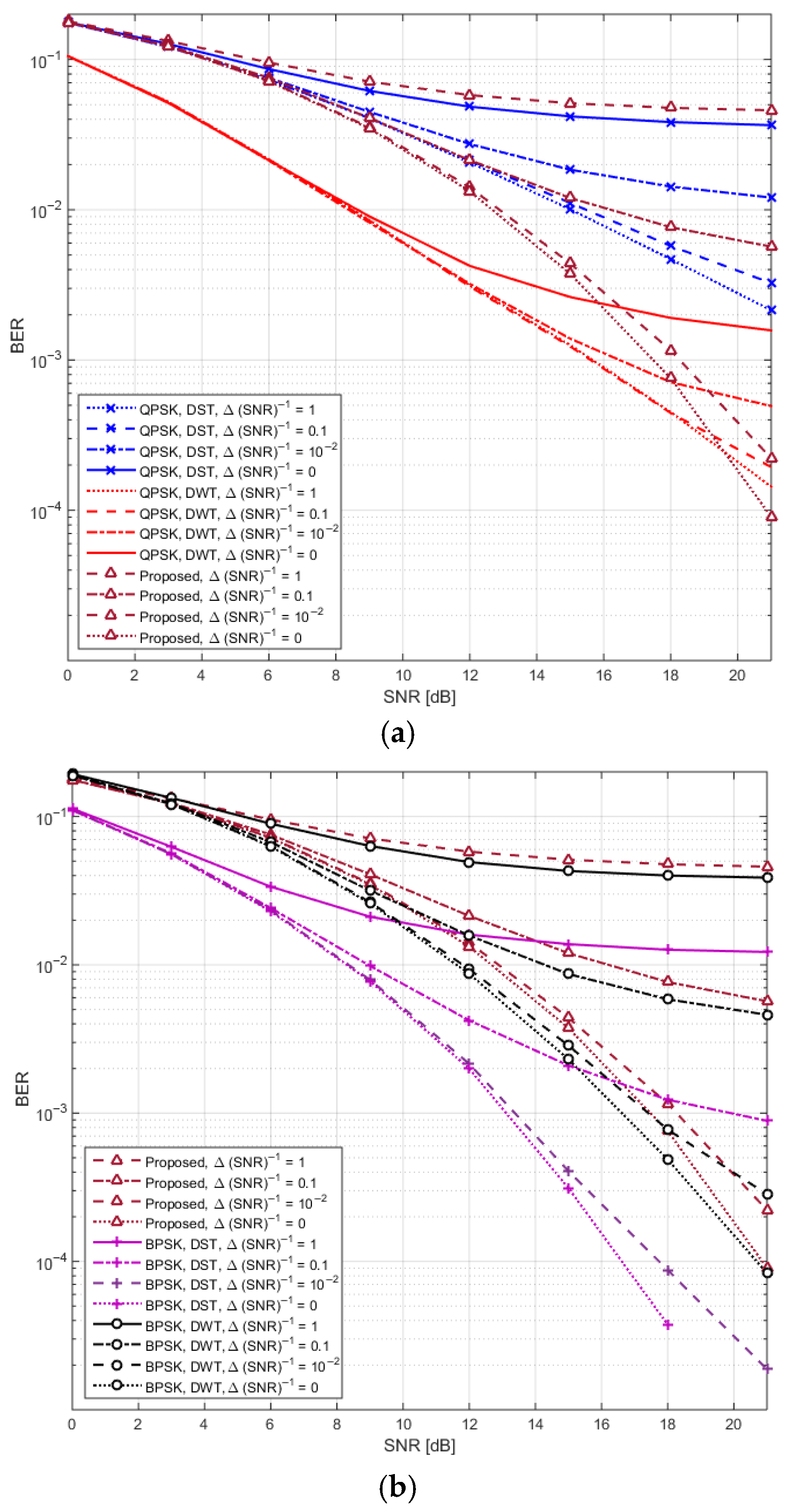
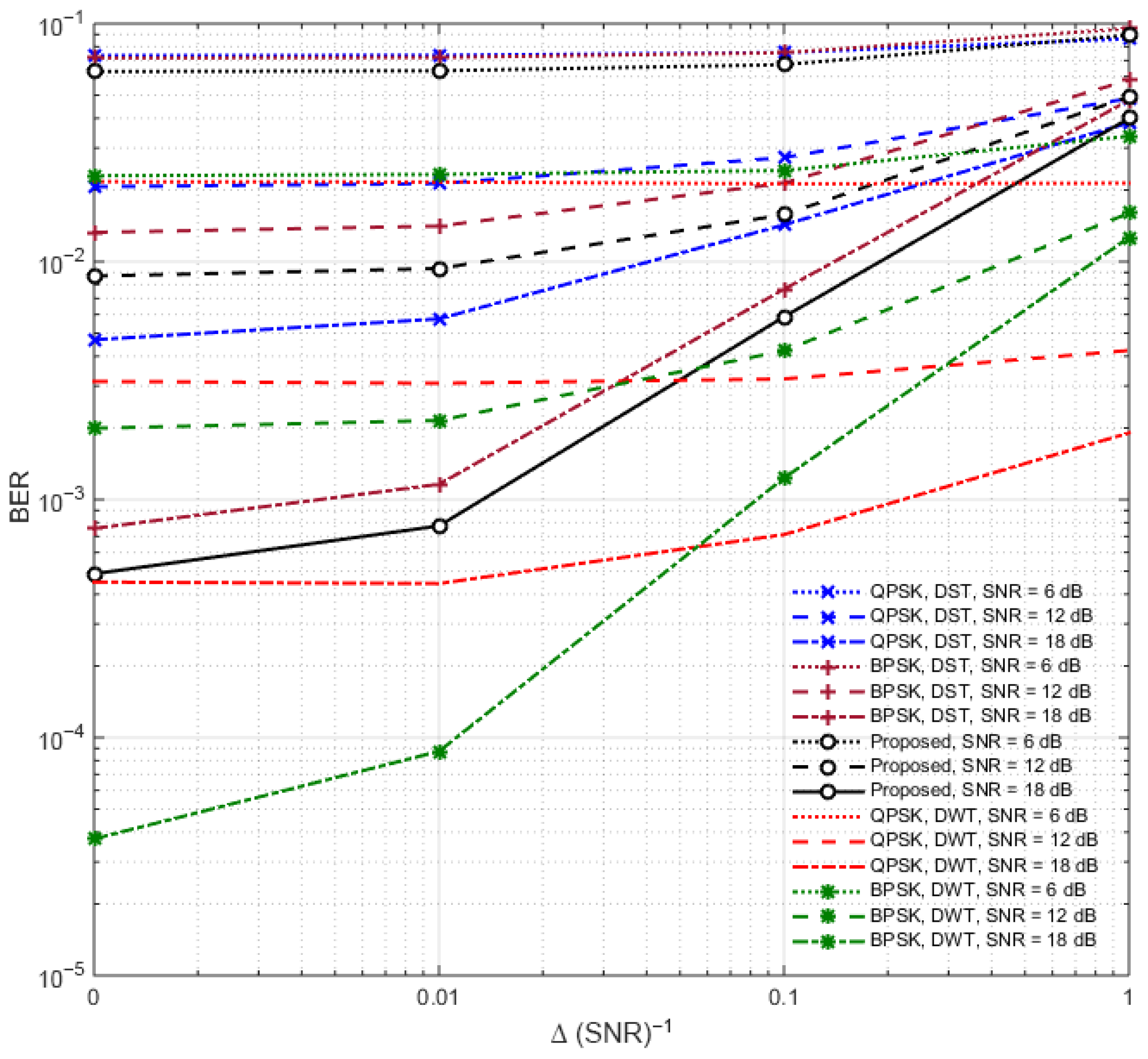
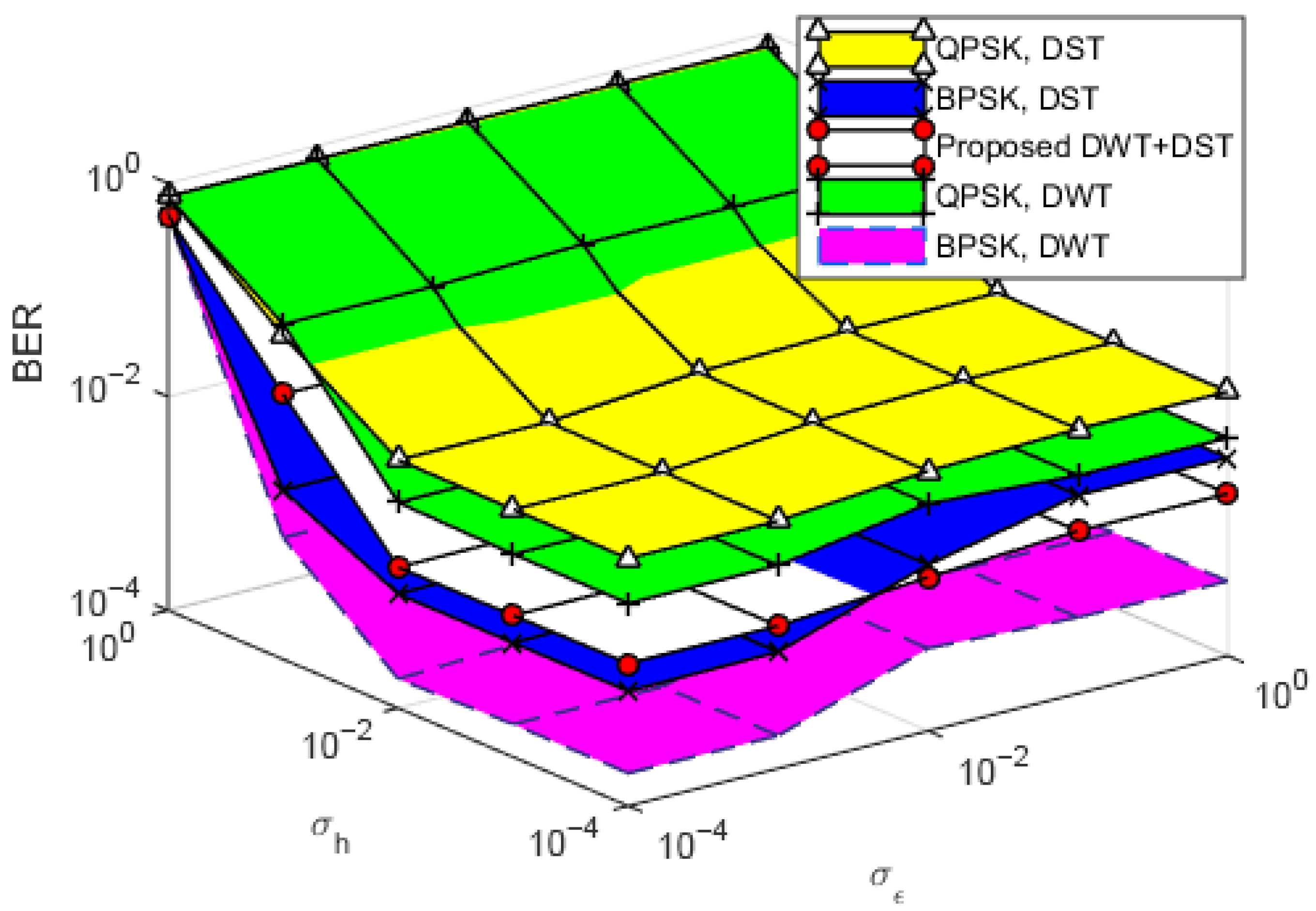
3.2. BER Performance
3.3. Accuracy Calculation
3.4. Transmitted Power
4. Conclusions
5. Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| OFDM | Orthogonal Frequency Division Multiplexing |
| DWT | Discrete Wavelet Transform |
| DFT | Discrete Fourier Transform |
| DST | Discrete Sine Transform |
| BER | Bit-Error-Rate |
| BPSK | Binary Phase Shift Keying |
| QPSK | Quadrature Phase Shift Keying |
| FDM | Frequency Division Multiplexing |
| CP | Cyclic Prefix |
| MIMO | Multiple-Input–Multiple-Output |
| PAPR | Peak-to-Average Power Ratio |
| LPF | Low-Pass Filter |
| HPF | High-Pass Filter |
| CFO | Carrier Frequency Offset |
| SNR | Signal-to-Noise Ratio |
| AWGN | Additive White Gaussian Noise |
| IDST | Inverse Discrete Sine Transform |
| IDWT | Inverse Discrete Wavelet Transform |
| IM/DD | Intensity Modulation/Direct Detection |
| VLC | Visible Light Communication |
References
- Hassan, E.S. Multi-Carrier Communication Systems with Examples in MATLAB®: A New Perspective; CRC Press: Boca Raton, FL, USA; Taylor & Francis: Oxfordshire, UK, 2019; Volume 47, pp. 26–35. ISBN 9781498735322. [Google Scholar]
- Yılmaz, G.; Yılmaz, A.Ö. Quasi-Newton FDE in One-bit Pseudo-Randomly Quantized Massive MIMO-OFDM Systems. IEEE Commun. Lett. 2024, 28, 917–921. [Google Scholar] [CrossRef]
- Ramadan, K.; Hassan, E.S. Linear WDE for Performance Enhancement of MIMO-OFDM System in the Presence of Co-CFO. Def. Technol. J. 2025, 51, 51–66. [Google Scholar] [CrossRef]
- Arabian, F.; Shoushtari, M. A Comparative Study of Waveforms Across Mobile Cellular Generations: From 0G to 6G and Beyond. Telecom 2025, 6, 67. [Google Scholar] [CrossRef]
- Lian, D.; Gao, Y.; Lian, J.; Li, Y. Joint DFT and Spacetime Coding for MU-OFDM in Power-Constrained Optical Wireless Communication Systems. Photonics 2025, 12, 11. [Google Scholar] [CrossRef]
- Cao, Z.; Tureli, U.; Yao, Y. Low-complexity orthogonal spectral signal construction for generalized OFDMA uplink with frequency synchronization errors. IEEE Trans. Veh. Technol. 2007, 56, 1143–1154. [Google Scholar] [CrossRef]
- Zhang, C.; Baharudin, M.A.B.; Guo, T.; Wang, J.; Jia, Z. A Survey on the Latest Developments of OFDM Schemes for Optimizing the Capacity and Reliability of Visible Light Communication (VLC) Systems. KSII Trans. Internet Inf. Syst. 2025, 19, 1625. [Google Scholar] [CrossRef]
- Wan, Y.; Hu, Z.; Liu, A.; Du, R.; Han, T.X.; Quek, T.Q.S. OFDM-Based Multiband Sensing For ISAC: Resolution Limit, Algorithm Design, and Open Issues. IEEE Veh. Technol. Mag. 2024, 19, 51–59. [Google Scholar] [CrossRef]
- Yeh, H.-G. Architectures for MIMO-OFDM Systems in Frequency-Selective Mobile Fading Channels. IEEE Trans. 2015, 62, 1189–1193. [Google Scholar] [CrossRef]
- Li, P.; Pan, W.; Zou, X.; Yan, L. Low-Complexity Adaptive Frequency-Domain Nonlinear Equalization for Analog RoF Mobile Fronthaul Using FFT/IFFT-Assisted Channel Aggregation. J. Light. Technol. 2022, 40, 1072–1082. [Google Scholar] [CrossRef]
- Kansal, K.; Berra, S.; Mounir, M.; Miglani, R.; Dinis, R.; Rabie, K. Performance Analysis of Massive MIMO-OFDM System Incorporated with Various Transforms for Image Communication in 5G Systems. Electronics 2022, 11, 621. [Google Scholar] [CrossRef]
- Ding, Y.; Deng, H.; Xie, Y.; Wang, H.; Sun, S. Time-Varying Channel Estimation Based on Distributed Compressed Sensing for OFDM Systems. Sensors 2024, 24, 3581. [Google Scholar] [CrossRef]
- Lalitha, H.; Kumar, N. Carrier frequency synchronization for WLAN systems based on MIMO-OFDM-IM. EURASIP J. Wirel. Commun. Netw. 2024, 2024, 77. [Google Scholar] [CrossRef]
- Sreeraj, S.J.; Lakshman, B.; Ganti, R.; Nirmalathas, A.; Koilpillai, R.D.; Venkitesh, D. Optical Upconversion of OFDM Signals for Next Generation Fronthauling Using Frequency Doubling and Quadrupling. IEEE Access 2024, 12, 39300–39312. [Google Scholar] [CrossRef]
- Mohammed, M. Theoretical Analysis and Simulation of IM/DD Optical OFDM Systems; McMaster Universit: Hamilton, ON, Canada, 2011; Available online: http://www.academia.edu/19322099 (accessed on 25 August 2025).
- Wen, M.; Li, J.; Cheng, X.; Cheng, X. ICI Cancellation Techniques Based on Data Repetition for OFDM Systems. In Radio Access Network Slicing and Virtualization for 5G Vertical Industries; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2021; pp. 1–24. [Google Scholar] [CrossRef]
- Farhang-Boroujeny, B. Ofdm versus filter bank multicarrier. IEEE Signal Process. Mag. 2011, 28, 92–112. [Google Scholar] [CrossRef]
- Liu, X.; Lu, H.; He, Y.; Wu, F.; Zhang, C.; Wang, X. Analysis on the Effect of Phase Noise on the Performance of Satellite Communication and Measurement System. Symmetry 2023, 15, 2053. [Google Scholar] [CrossRef]
- Zhu, C.; He, P.; Wu, S.; Wang, G. An Integrated Orthogonal Frequency-Division Multiplexing Chirp Waveform Processing Method for Joint Radar and Communication Based on Low-Density Parity-Check Coding and Channel Estimation. Electronics 2024, 13, 334. [Google Scholar] [CrossRef]
- Rizwana, A.; Srivastava, A. PAPR Reduction of OFDM Signal Through DFT Precoding and GMSK Pulse Shaping in Indoor VLC. IEEE Access 2020, 8, 122092–122103. [Google Scholar] [CrossRef]
- Cinemre, I.; Hacioglu, G.; Mahmoodi, T. QCTP: A Novel Pre-Coding Approach for PAPR Reduction in IM/DD Systems. IEEE Access 2024, 12, 115588–115596. [Google Scholar] [CrossRef]
- Bouhlel, A.; Sakly, A.; Mansouri, N. Performance Comparison of DWT Based MIMO OFDM and FFT Based MIMO OFDM. Procedia Comput. Sci. 2015, 73, 266–273. [Google Scholar] [CrossRef][Green Version]
- Dang, S.; Zhou, J.; Shihada, B.; Alouini, M. Toward Spectral and Energy Efficient 5G Networks Using Relayed OFDM with Index Modulation. Front. Commun. Netw. 2021, 2, 635295. [Google Scholar] [CrossRef]
- Trivedi, V.K.; Ramadan, K.; Kumar, P.; Dessouky, M.I.; El-Samie, F.E.A. Trigonometric transforms and precoding strategies for OFDM-based uplink hybrid multi-carrier nonorthogonal multiple access. Trans. Emerg. Telecommun. Technol. 2019, 30, e3694. [Google Scholar] [CrossRef]
- Cinemre, I.; Hacioglu, G. A DCT/DST Based Fast OFDM Method in IM/DD Systems. IEEE Commun. Lett. 2021, 25, 3013–3016. [Google Scholar] [CrossRef]
- Dissanayake, S.D.; Armstrong, J. Comparison of ACO-OFDM, DCO-OFDM and ADO-OFDM in IM/DD Systems. J. Light. Technol. 2013, 31, 1063–1072. [Google Scholar] [CrossRef]
- Bhadoria, M.P.; Pandey, G.; Dixit, A. Performance evaluation of visible light communication for DCO and ACO optical OFDM techniques. In Proceedings of the 2019 National Conference on Communications (NCC), Bangalore, India, 20–23 February 2019. [Google Scholar]
- Androw, S.; Derd, H. Enhancing the performance of optical VLC system based on asymmetric symmetric subcarriers OFDM. Int. J. Commun. Syst. 2020, 33, e4226. [Google Scholar]
- Vappangi, S.; Mani, V.V. A Power efficient DST-based multicarrier and multiple access systems for VLC. In Proceedings of the 2018 IEEE International Conference on Advanced Networks and Telecommunications Systems (ANTS), Indore, India, 16–19 December 2018. [Google Scholar]
- Baig, I.; ul Hasan, N.; Zghaibeh, M.; Khan, I.U.; Saand, A.S. A DST precoding based uplink NOMA scheme for PAPR reduction in 5G wireless network. In Proceedings of the 2017 7th International Conference on Modeling, Simulation, and Applied Optimization (ICMSAO), Sharjah, United Arab Emirates, 4–6 April 2017. [Google Scholar]
- Dent, P.; Bottomley, G.E.; Croft, T. Jakes Fading Model Revisited. Electron. Lett. 1993, 29, 1162–1163. [Google Scholar] [CrossRef]


| Feature | Advantages | Potential Limitations |
|---|---|---|
| Use of DWT instead of DFT | Improved spectral efficiency and time–frequency localization; better resilience to multipath | Increased computational complexity in some implementations |
| Dual Modulation via IDWT and IDST | zero elements to transmit additional data (imaginary part), increasing throughput by 50% | Requires precise synchronization between real and imaginary paths; implementation complexity |
| Power Efficiency | Maintains similar power efficiency as traditional OFDM systems | No specific gain in power efficiency, equivalent to conventional methods |
| BER Performance | BER lies between BPSK and QPSK, offering a middle ground between robustness and data rate | Not as robust as pure BPSK in harsh conditions |
| Data Rate and BER Trade-off | Supports flexible trade-off configurations depending on application needs | Needs adaptive control or additional logic to optimize the trade-off in real-time |
| Consideration of Multipath, Noise, and CFO | Designed to handle realistic channel impairments, including CFO and multipath | Performance may still degrade at high CFO unless mitigation is properly tuned |
| Robustness to Estimation Uncertainties | Demonstrates low BER degradation (<3.4%) under moderate estimation errors, outperforming QPSK schemes | Slightly more degradation than BPSK systems |
| Scheme | % Degradation | |||
|---|---|---|---|---|
| Proposed (DWT + DST) | 0.00216 | 0.03571 | 0.03355 | 3.36% |
| DWT + QPSK | 0.00791 | 0.15247 | 0.14456 | 14.46% |
| DWT + BPSK | 0.00020 | 0.00211 | 0.00191 | 0.19% |
| DST + QPSK | 0.02077 | 0.11775 | 0.09698 | 9.70% |
| DST + BPSK | 0.00119 | 0.00941 | 0.00822 | 0.82% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramadan, K.; Aqeel, I.; Hassan, E.S. Joint Wavelet and Sine Transforms for Performance Enhancement of OFDM Communication Systems. Mathematics 2025, 13, 3258. https://doi.org/10.3390/math13203258
Ramadan K, Aqeel I, Hassan ES. Joint Wavelet and Sine Transforms for Performance Enhancement of OFDM Communication Systems. Mathematics. 2025; 13(20):3258. https://doi.org/10.3390/math13203258
Chicago/Turabian StyleRamadan, Khaled, Ibrahim Aqeel, and Emad S. Hassan. 2025. "Joint Wavelet and Sine Transforms for Performance Enhancement of OFDM Communication Systems" Mathematics 13, no. 20: 3258. https://doi.org/10.3390/math13203258
APA StyleRamadan, K., Aqeel, I., & Hassan, E. S. (2025). Joint Wavelet and Sine Transforms for Performance Enhancement of OFDM Communication Systems. Mathematics, 13(20), 3258. https://doi.org/10.3390/math13203258







