Accurate and Scalable DV-Hop-Based WSN Localization with Parameter-Free Fire Hawk Optimizer

Abstract

Wireless Sensor Networks (WSNs) have emerged as a foundational technology for monitoring and data collection in diverse domains such as environmental sensing, smart agriculture, and industrial automation. Precise node localization plays a vital role in WSNs, enabling effective data interpretation, reliable routing, and spatial context awareness. The challenge intensifies in range-free settings, where a lack of direct distance data demands efficient indirect estimation methods, particularly in large-scale, energy-constrained deployments. This work proposes a hybrid localization framework that integrates the distance vector-hop (DV-Hop) range-free localization algorithm with the Fire Hawk Optimizer (FHO), a nature-inspired metaheuristic method inspired by the predatory behavior of fire hawks. The proposed FHODV-Hop method enhances location estimation accuracy while maintaining low computational overhead by inserting the FHO into the third stage of the DV-Hop algorithm. Extensive simulations are conducted on multiple topologies, including random, circular, square-grid, and S-shaped, under various network parameters such as node densities, anchor rates, population sizes, and communication ranges. The results show that the proposed FHODV-Hop model achieves competitive performance in Average Localization Error (ALE), localization ratio, convergence behavior, computational, and runtime efficiency. Specifically, FHODV-Hop reduces the ALE by up to 35% in random deployments, 25% in circular networks, and nearly 45% in structured square-grid layouts compared to the classical DV-Hop. Even under highly irregular S-shaped conditions, the algorithm achieves around 20% improvement. Furthermore, convergence speed is accelerated by approximately 25%, and computational time is reduced by nearly 18%, demonstrating its scalability and practical applicability. Therefore, these results demonstrate that the proposed model offers a promising balance between accuracy and practicality for real-world WSN deployments.

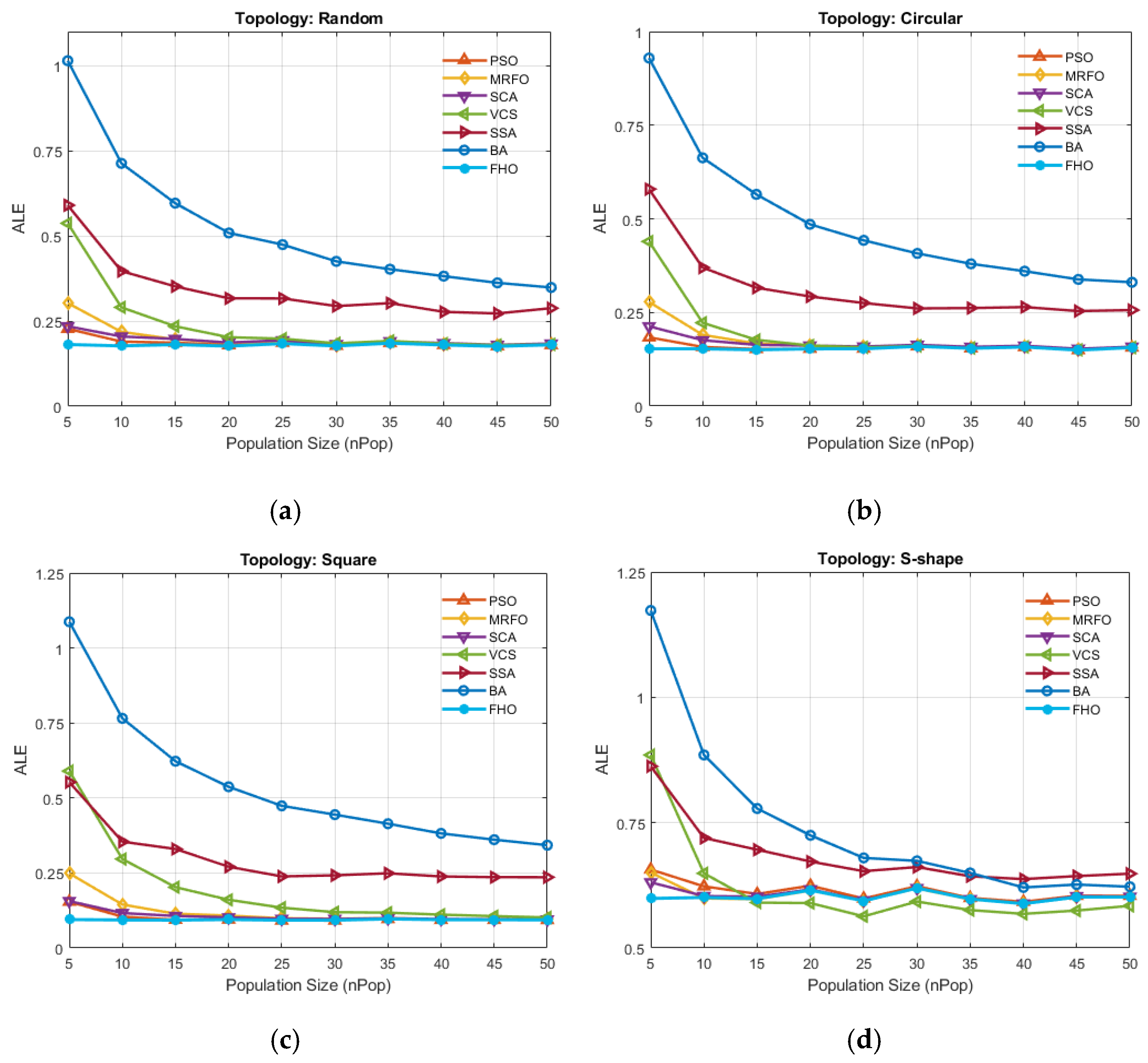
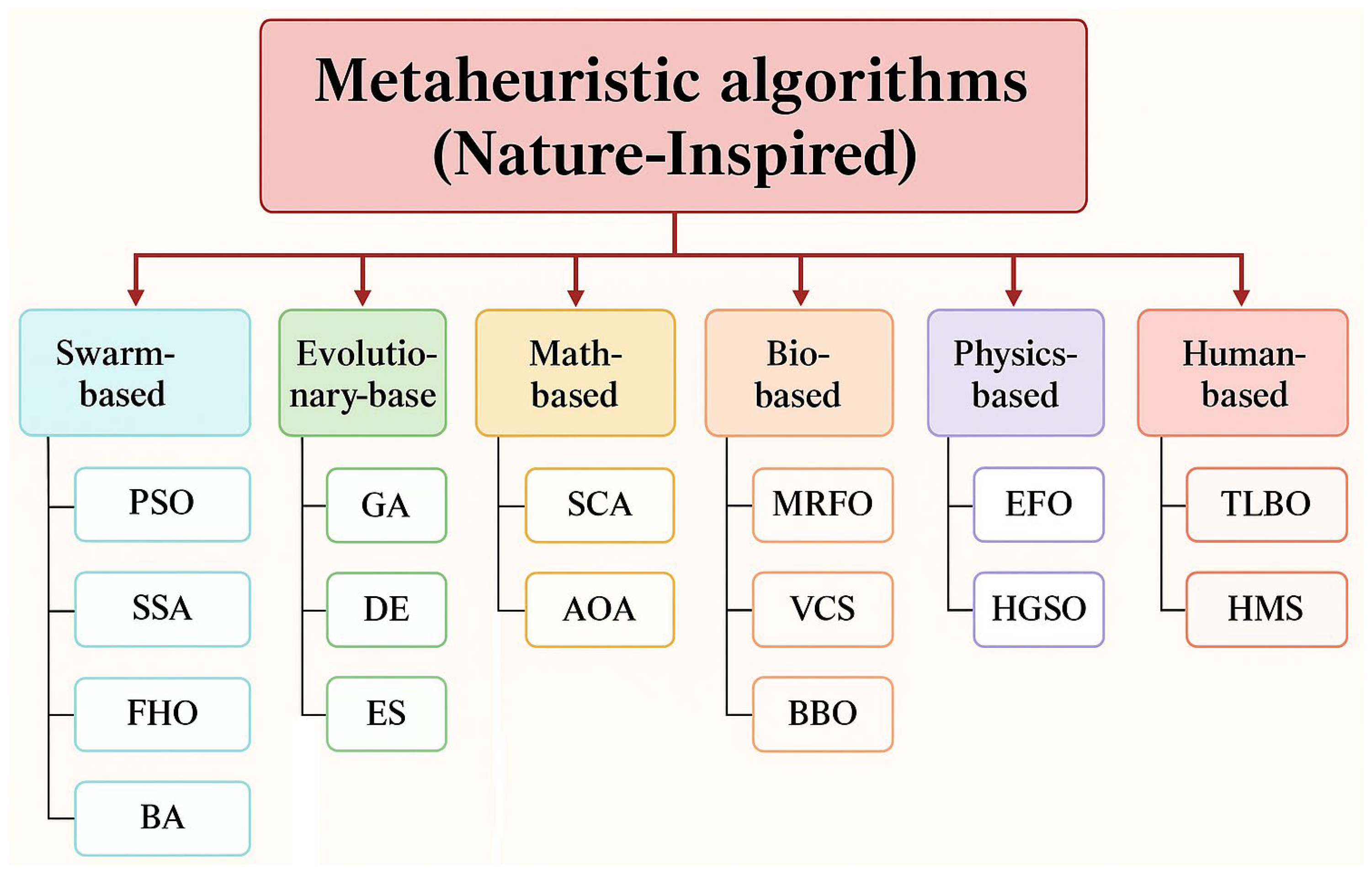
1. Introduction

Wireless Sensor Networks (WSNs) consist of large numbers of interconnected sensor nodes that collaboratively sense the environment and forward the collected information [1]. Each node operates under stringent resource limitations, including restricted energy, memory, and processing capacity, which makes sustaining reliable network performance particularly challenging [2]. By relying on multi-hop communication and flexible topologies, WSNs can function effectively across wide areas without the need for fixed infrastructure, even under dynamic environmental conditions [3,4]. These features have established WSNs as a practical solution for diverse applications, ranging from environmental and disaster monitoring to healthcare, defense, agriculture, industrial automation, and smart-city systems [5,6].

As WSNs are increasingly deployed in mission-critical applications, accurate knowledge of sensor node positions has become essential. In many cases, identifying the source of an event is as important as the sensed data itself [7,8]. Localization in WSNs refers to the process of estimating the geographical coordinates of sensor nodes within the network. The process differentiates between anchor nodes (ANs), whose positions are known in advance, and unknown nodes (UNNs), which infer their locations relative to ANs [9]. Although the Global Positioning System (GPS) provides high positional accuracy, equipping every sensor with GPS modules is impractical due to cost, limited battery life, and the frequent unavailability of signals in indoor or obstructed environments. Consequently, WSN localization methods are expected to achieve reliable performance with minimal hardware support, low energy consumption, and resilience across diverse operating conditions [10,11].

Various localization techniques—categorized as range-based and range-free—have been developed to overcome GPS limitations. Range-based methods, such as those using Received Signal Strength Indicator (RSSI), Time of Arrival (TOA), Time Difference of Arrival (TDOA), or Angle of Arrival (AOA), provide high accuracy but demand extra hardware and strict synchronization, which raise both complexity and energy use [12]. Range-free techniques, by contrast, rely only on simple network metrics like hop count or connectivity, making them more practical for resource-constrained deployments [13]. Prominent range-free algorithms include Centroid, Approximate Point in Triangle (APIT), Amorphous, and notably, the Distance Vector-Hop (DV-Hop), DV-HopMax algorithm [14]. DV-Hop is particularly appealing due to its simple implementation, low computational overhead, and robustness across large-scale networks. It operates in three stages: (1) broadcasting hop counts from ANs to all nodes, (2) estimating the average per-hop distance using known AN coordinates, and (3) position estimation of UNNs using multi-lateration [15].

Although DV-Hop is widely used, its third stage—position estimation—often produces considerable error, since a global average hop distance cannot accurately capture irregular topologies or uneven AN placement [16]. To address these limitations without adding hardware, researchers have explored deterministic refinements. Examples include AN selection strategies that optimize reference nodes [17,18], and cluster-based recalibration methods that enhance accuracy in heterogeneous networks [19].

Deterministic adjustments alone often struggle in dynamic or irregular deployments. As a result, metaheuristic algorithms have emerged as effective alternatives for refining DV-Hop’s third phase, as they can search the solution space more adaptively and reduce reliance on static hop estimates [20]. Metaheuristic algorithms are broadly categorized into several groups based on their inspiration sources [21,22]. As illustrated in Figure 1, these include:

• Physics-inspired algorithms: Electromagnetic field optimization (EFO) [23] and Henry Gas Solubility Optimization (HGSO) [24].
• Evolutionary algorithms: Genetic Algorithm (GA) [25], Differential Evolution (DE) [26], and Evolutionary Strategy (ES) [27].
• Swarm intelligence-based algorithms: Particle Swarm Optimization (PSO) [28], Salp Swarm Algorithm (SSA) [29], Fire Hawk Optimizer (FHO) [30], and Bat Algorithm (BA) [31].
• Mathematics-based algorithms: Sine Cosine Algorithm (SCA) [32] and Arithmetic Optimization Algorithm (AOA) [33].
• Bio-inspired algorithms: Manta Ray Foraging Optimization (MRFO) [34], Virus Colony Search (VCS) [35], Biogeography-Based Optimization (BBO) [36].
• Human-based algorithms: Teaching-Learning-Based Optimization (TLBO) [37] and Human Mental Search (HMS) [38].

Figure 1. A detailed taxonomy of nature-inspired optimizers [39,40].

Figure 1. A detailed taxonomy of nature-inspired optimizers [39,40].

Figure 1 outlines the taxonomy of nature-inspired optimization methods, though only a limited subset has been applied to DV-Hop. Their performance differs with algorithmic design, parameter sensitivity, and suitability for WSN constraints. A more comprehensive review of these studies is provided in the Related Work section.

While numerous studies have targeted various phases of the DV-Hop algorithm—such as AN deployment optimization in Step 1 or adaptive hop-size estimation in Step 2—comparatively fewer have focused exclusively on enhancing Step 3, where the positions of UNNs are determined. In the limited works that address this stage, metaheuristic optimization has been applied; however, the comparative performance of recently developed optimizers remains largely unexplored, particularly across diverse network topologies and operational scenarios. To address this gap, we propose an enhanced DV-Hop localization framework in which the parameter-free FHO is integrated into the position-estimation phase. FHO is a swarm intelligence algorithm inspired by the cooperative hunting behavior of fire hawks (FHs). Its parameter-free nature eliminates the need for manual tuning, making it highly suitable for real-world deployments where minimal human intervention and robustness are critical. Although WSN localization has been widely investigated, many real-world deployments continue to demand lightweight, hardware-independent solutions capable of operating under dynamic network conditions. The proposed FHODV-Hop framework is designed to address precisely such scenarios—including post-disaster monitoring, precision agriculture, and long-span infrastructure surveillance—where the use of additional ranging equipment is often impractical, costly, or infeasible. Under these constraints, the parameter-free design of FHO offers a distinct practical advantage by enabling reliable convergence without manual hyperparameter tuning, thereby improving adaptability to heterogeneous node distributions and noisy hop-based distance estimations. Furthermore, its balanced exploration–exploitation mechanism and fast convergence characteristics offer potential advantages over many classical metaheuristics in range-free localization contexts [30].

Accordingly, this study is guided by the following hypothesis and research questions:

Hypothesis: Integrating the parameter-free FHO into the third phase of DV-Hop will significantly enhance localization accuracy without increasing hardware cost, while preserving competitive convergence speed and computational efficiency across different topologies.

Research Questions:

RQ1: Can the integration of a parameter-free optimizer such as FHO into the third phase of DV-Hop achieve higher localization accuracy than classical and state-of-the-art metaheuristics?

RQ2: How does the proposed FHODV-Hop perform under varying network topologies and operational conditions in terms of ALE, convergence rate, and computational time?

FHO has recently been explored in WSN research, most notably in routing-oriented applications such as cluster-based trusted path formation (e.g., [41]). These works leverage FHO to improve forwarding and trust management but do not address localization. To the best of our knowledge, this work is the first to apply FHO within the context of DV-Hop or any other range-free WSN localization framework. The proposed method enhances localization accuracy purely at the algorithmic level, without altering the hardware infrastructure or sensor configuration. This distinction is critical: while routing tasks optimize link- or cluster-level decisions, our approach formulates localization as a bounded coordinate optimization problem solved in DV-Hop Step-3, thereby opening a novel direction for parameter-free FHO in WSN localization.

A comprehensive set of experiments was conducted to evaluate the method under fair and consistent conditions, including a deployment area of 100 × 100 m², communication range (CR) of 30 m, and a beacon node ratio of 30%. The algorithm was benchmarked against classical DV-Hop and six widely used metaheuristics: PSO, MRFO, SCA, VCS, SSA, and BA. Performance was analyzed across four distinct topologies—random, circular, square-grid, and S-shaped—using metrics such as Average Localization Error (ALE), convergence speed, and computational time.

The main contributions of this paper are as follows:

• First integration of the parameter-free FHO algorithm into DV-Hop localization, offering enhanced stability and reduced sensitivity to parameter tuning.
• Demonstration of notable accuracy improvements without additional hardware costs.
• Fair and comprehensive comparison with multiple state-of-the-art metaheuristics across diverse deployment scenarios.
• Validation of FHODV-Hop as a low-cost, robust, and scalable localization solution for practical WSNs.
• Systematic performance analysis of both previously used and entirely new metaheuristics for DV-Hop, including the first joint evaluation of MRFO and VCS in this context.

The remainder of this paper is organized as follows: Section 2 reviews prior work on DV-Hop localization with metaheuristic optimization techniques; Section 3 presents the fundamental concepts of DV-Hop localization and the FHO; Section 4 introduces the proposed FHODV-Hop framework and its algorithmic integration; Section 5 describes the experimental setup, simulation parameters, and evaluation metrics. Section 5 also discusses the simulation results across different topologies and parameters. Section 6 concludes the paper and outlines future research directions.

2. Related Works

In recent years, numerous enhancements have been proposed to improve the accuracy of DV-Hop, one of the most widely adopted range-free localization algorithms in WSNs. Owing to its simplicity and minimal hardware requirements, DV-Hop remains widely used; however, its performance is often limited by error accumulation across different stages. To address these limitations, many studies have incorporated metaheuristic optimization into the DV-Hop framework, targeting various phases of the algorithm. These hybrid approaches leverage the global search capabilities of metaheuristics to reduce localization errors and enhance robustness under diverse deployment conditions.

This section provides a systematic, chronological review of studies that combine DV-Hop with metaheuristics, focusing on their optimization strategies, evaluation methods, and key findings. The review places particular emphasis on improvements to Step 3 (position estimation), while also including selected Step 2 enhancements where hop-size correction is integrated with or compared to metaheuristic-based optimization. The inclusion of these works is intended to offer a comprehensive view of how DV-Hop has been refined across its stages. By contrast, recent localization studies that do not extend DV-Hop, or that focus exclusively on AN deployment or range-based methods, are excluded as they fall outside the scope of this review.

A summary of the most prominent contributions is presented in

Table 1. Summary of DV-Hop hybrid localization algorithms in the recent literature.

Algorithm	DV-Hop Phase	Strengths	ALE Improvement (vs. DV-Hop)	Limitations	Ref.
GADV-Hop	Step 3	Improved location accuracy; GA-based global search	≈25–35% lower ALE	Limited evaluation on topologies and parameters	[42], (2015)
OCSDV-Hop	Step 3	Outperforms classical DV-Hop; effective exploitation	≈7–27% lower ALE	Insufficient analysis of correction validity	[43], (2017)
SFLA/GA-PSO-DV-Hop	Steps 2 & 3	Improves accuracy using hybrid methods at different steps	≈30–45% lower ALE	Higher computational complexity	[44], (2017)
PSODV-Hop	Step 3	Lower error using PSO fitness-based optimization	≈25–40% lower ALE	Single topology; lacks generalizability	[45], (2018)
CTODV-Hop	Step 3	Efficient coordinate estimation via Elite guidance using CTO, a little-studied metaheuristic	≈30–45% lower ALE	Limited analysis of parameter/topology effects	[46], (2021)
SSADV-Hop	Steps 2 & 3	Accurate hop and location estimation using SSA	≈35–45% lower ALE	Hop correction not mathematically analyzed, higher complexity than DV-Hop	[47], (2021)
TSA-HHO-DV-Hop	Step 3	Improved accuracy via hybrid optimizer and strategies	≈35–45% lower ALE	Increased computational complexity	[48], (2022)
SCADV-Hop	Steps 2 & 3	Effective correction and position estimation; fast convergence	≈35–45% lower ALE	Limited algorithm comparison	[49], (2022)
MSSADV-Hop	Steps 2 & 3	Enhanced accuracy via hop correction and multi-objective fitness	≈20–50% lower ALE	Generalizability not fully analyzed	[50], (2023)
GOADV-Hop	Step 3	Improved accuracy and stability over DV-Hop via GOA-based position estimation	≈35–50% lower ALE	Single topology and limited parameters	[51], (2024)
LF-SOADV-Hop	Step 3	Independent effect analysis of each strategy	≈30–45% lower ALE	Unclear interaction effects	[52], (2024)
MSMAO-DV-Hop	Steps 2 & 3	Accurate hop correction and optimization; strong convergence	≈30–50% lower ALE	High complexity for large-scale WSNs	[53], (2025)
POADV-Hop	Step 2	Significant reduction in hop-size induced error; effective in UWSNs	≈30–45% lower ALE	Focused only on hop-size; no Step 3 optimization	[54], (2025)
VVS-HCO-DV-Hop	Steps 2 & 3	Faster convergence; robust against local minima; improved accuracy under anisotropic radio conditions; energy-efficient	≈25–45% lower ALE	Increased algorithmic complexity; requires careful parameter tuning	[55], (2025)

.

In [42], the position estimation phase is modeled as an optimization problem, aiming to minimize the distance error relative to the ANs. To enhance localization accuracy, GADV-Hop—an improved variant of the DV-Hop algorithm incorporating a GA—is introduced. This approach initializes the population within a constrained search region defined by three ANs, effectively reducing the solution space and expediting convergence. The GA’s evolutionary mechanisms, including selection, crossover, and mutation, are then employed to further minimize the estimation error inherent in the DV-Hop algorithm. Simulations performed in MATLAB 2021b show that the GADV-Hop algorithm provides lower ALE compared to the classical DV-Hop and a previously proposed GA-based method. However, the proposed approach has not been tested in different network environments, and the number of studies used for comparison is small.

In [43], a new metaheuristic algorithm, called Oriented Cuckoo Search (OCS), is proposed to improve the positioning accuracy of the DV-Hop algorithm. OCS is enhanced by adding an oriented strategy to the classical Cuckoo Search algorithm and is specifically applied in the position estimation step of DV-Hop. The optimization process is based on a fitness function that aims to minimize the distance errors between UNN and ANs. While simulations reveal that the OCS-based method provides lower mean location error and faster convergence compared to classical DV-Hop and other metaheuristic algorithms, most studies focused on accuracy over large areas. Still, they did not evaluate the performance in complex terrain conditions.

In [44], different evolutionary algorithms were integrated at various stages to improve the accuracy of the DV-Hop algorithm. In the second stage, the Shuffled Frog Leaping Algorithm (SFLA) was used to reduce the error in HopSize calculations due to its advantages of ease of implementation and rapid convergence. In the final stage, the hybrid GA-PSO algorithm was implemented to prevent the high error generated by the least squares method (LSM). While GA is preferred for efficiently exploring a large solution space, PSO is used for the refinement of elite individuals. Simulation results show that the proposed approach achieves lower localization errors than the traditional DV-Hop algorithm. However, while it offers enhanced accuracy and better energy efficiency, these gains come at the cost of increased computational complexity.

In [45], the third step of the DV-Hop algorithm, the location estimation process, was optimized using the Particle Swarm Optimization (PSO) algorithm to improve localization accuracy. PSO’s population-based exploration–exploitation balance allowed for more precise estimation of the locations of UNNs. For this purpose, instead of the classical LSM, the sum of the squared errors between the actual and estimated distances was used as the fitness function. Simulation results indicate that the proposed approach offers lower average location errors than the classical DV-Hop. However, the tests were conducted only on a specific topology, and the effect of network structure on algorithm performance was not systematically investigated, which may limit the generalizability of the method to different distribution scenarios.

In [46], the location estimation step was optimized using the Class Topper Optimization (CTO) algorithm to increase the accuracy of the DV-Hop algorithm. HopCount and HopSize calculations were performed using the classic DV-Hop structure, intervening only in the coordinate estimation process of UNNs. The CTO algorithm offers an exploration-exploitation strategy based on guiding individuals by using the highest-performing student in the class as a guide. However, this study did not analyze the parameters and topology sensitivity in detail, increasing the risk of the method yielding unstable results in different application scenarios.

In [47], a new localization approach, SSIDV-Hop, is presented by integrating an improved version of the DV-Hop algorithm with the Squirrel Search Algorithm (SSA). In the first stage, the distances between UNNs and ANs are estimated more accurately using improved average hop distances obtained from neighboring ANs. Then, instead of the classical LSM, positions are optimized using SSA, applying a fitness function that weights the squared error between the AN and UNNs. However, although an improvement in hop distance is stated, the impact of this correction is not further explored through detailed mathematical analysis. Although simulations confirm that the proposed method outperforms existing approaches in accuracy, stability, and convergence speed, these enhancements are accompanied by a higher computational cost.

In [48], a hybrid architecture was created by combining the Tunicate Swarm Algorithm (TSA) and Harris Hawk Optimization (HHO) algorithms. This architecture was then enhanced by adding a phase and integrated with the DV-Hop algorithm. The proposed positioning algorithm was evaluated in different scenarios using metrics such as node positioning error, mean positioning error, and positioning error variance. Experimental findings revealed the positive effects of the presented contributions on algorithm performance. However, this study hybridized the TSA and HHO algorithms and added random strategy selection, new phases, and numerous control parameters. This strategy faces the risk of increased computational costs.

In [49], a two-stage approach is presented that focuses on both improving hop distances and optimizing position estimation to improve the accuracy of the DV-Hop algorithm. In the first stage, instead of the traditional fixed average hop distance, a correction method based on the statistical properties of the hop distances obtained from ANs is developed, aiming to reduce the hop size error. However, since the validity of this correction across various scenarios, such as different network topologies and node densities, has not been comprehensively analyzed, some limitations in the generalizability of the method may arise. In the second stage, the coordinates of UNNs are optimized using the Sine Cosine Algorithm (SCA) instead of the classical LSM. SCA’s structure, which balances exploration and exploitation, was effective in improving the accuracy of position estimation. Simulations revealed that the proposed method offers lower positioning error, faster convergence, and better stability compared to the classical DV-Hop and some existing advanced algorithms. However, the fact that comparative analyses are limited to a few algorithms makes it difficult to evaluate the relative superiority of the proposed approach over more current methods.

In [50], an approach that includes improvements for both hop distance estimation and location optimization is proposed to improve the positioning accuracy of the DV-Hop algorithm. First, a more adaptable structure is created for hop size calculation using a weighted average of hop distances from ANs instead of the traditional fixed average. Subsequently, the coordinates of UNNs are optimized using the Multi-Objective Salp Swarm Algorithm (MSSA) within a multi-objective fitness function. This structure improves overall accuracy by considering error, distance, and energy factors together. However, because the effect of hop distance correction on different topologies and node distributions is not thoroughly analyzed, the generalizability of this improvement may be limited in some scenarios. Simulation results show that the proposed method offers higher accuracy and better stability compared to the classic DV-Hop and some advanced variants.

In [51], to improve the accuracy of the classical DV-Hop algorithm, the location estimation process is optimized using the Grasshopper Optimization Algorithm (GOA). The first two stages of DV-Hop (hop count and average step distance calculation) were performed using the traditional method, but in the third stage, the determination of the coordinates of UNNs was converted to an optimization-based approach. Accordingly, the fitness function generated for each UNN was solved using GOA to minimize the sum of squared error between the estimated location and the distances from the ANs. Simulations have shown that the proposed GOADV-Hop structure produces lower average location error and more stable results compared to the classical DV-Hop algorithm. However, the fact that the algorithm has been tested only on a single topology and limited parameters limits the scope of the evaluation in terms of generalizability.

In [52], the authors developed a localization approach based on the Seagull Optimization Algorithm (SOA) to improve location accuracy in WSNs. The proposed method is enhanced by two independent strategies: a Logistic Chaotic Map to increase the diversity of the initial population, and a Lévy Flight-based location update mechanism to extend the discovery process. Both strategies were implemented separately, and their effects were analyzed independently. However, in such multi-strategy integrations, the impact of interactions can often remain unclear. Therefore, more in-depth testing is needed to confirm that each component is equally effective when used together.

In [53], the authors proposed both an improvement based on hop distance correction and integrating the multi-strategy Aquila Optimizer into the location estimation process to improve the accuracy of the DV-Hop algorithm. They aim to reduce the error using a weighted average approach in hop distance estimation, and improve location estimation through an optimizer structure. Thanks to the multi-strategy structure of MSMAO, high accuracy and strong convergence properties are achieved, and comparisons with various competing methods confirm this superiority. However, it should be noted that the multi-component optimization structure used may increase computational complexity and lead to limitations in some applications, especially in large-scale network scenarios.

In [54], the authors introduced POADV-Hop, in which the Pelican Optimization Algorithm is employed to refine hop-size estimation in underwater WSNs. By minimizing hop-size errors, their approach significantly improves localization precision compared to the classical DV-Hop baseline. The method demonstrated its effectiveness under harsh aquatic environments, although it remains focused exclusively on Step 2 optimization without further refinement at the position estimation stage. In [55], the authors proposed VVS-HCO-DV-Hop, an enhanced hybrid model that integrates a variable velocity strategy into Human Conception Optimization. The approach simultaneously addresses hop-size correction (Step 2) and position estimation (Step 3), accelerating convergence while avoiding premature stagnation. Experimental results confirmed notable improvements in accuracy and robustness under anisotropic channel conditions, though the method introduces additional algorithmic complexity relative to conventional DV-Hop extensions.

Previous research on DV-Hop enhancement has generally followed two primary directions: either refining the hop size estimation in the second phase or optimizing the position estimation in the third phase using metaheuristic approaches. While both directions offer performance gains, position-level optimization has attracted growing interest due to its direct impact on localization accuracy. However, many existing studies have been narrow in scope, often evaluating a single optimizer under specific network conditions or topological scenarios. This fragmented assessment has hindered broader insights into the comparative strengths of different algorithms across diverse deployments. Addressing this gap, our study establishes a unified and comprehensive evaluation framework that systematically benchmarks multiple metaheuristic algorithms under consistent experimental parameters and varied topologies.

Within this context, it is important to recognize that several parameter-free optimizers have been proposed in the literature, most notably TLBO [37] and Jaya [56]. TLBO was historically the first fully parameter-free method and has been adapted to DV-Hop Step-3 [57], but its evaluation remained limited to sparse random scenarios without broad comparative benchmarking. Although Jaya is also parameter-free, it has primarily been applied in range-based localization and, to our knowledge, has not yet been integrated into DV-Hop. Building on such precedents, this study investigates the recent FHO as a modern parameter-free candidate for range-free WSNs. FHO uniquely combines swarm-intelligence search dynamics with a parameter-free structure, yielding a balanced interplay of exploration and exploitation that enables it to adapt effectively to noisy and resource-constrained environments while avoiding premature stagnation. In contrast to TLBO and Jaya, whose parameter-free nature is based largely on deterministic update rules, FHO employs a fire-spreading mechanism that introduces stochastic diversification without sacrificing convergence stability. This distinctive design underpins FHO’s practical advantages over earlier parameter-free optimizers when integrated into the DV-Hop framework. More importantly, by positioning FHO within a spectrum of low-parameter (SCA, SSA), moderately and highly parameterized (PSO, MRFO, VCS, BA), and parameter-free designs, this study explicitly clarifies where a contemporary parameter-free optimizer stands in terms of localization accuracy, convergence behavior, and robustness.

Extensive experiments conducted under standardized conditions across multiple topologies demonstrate that FHO consistently outperforms many classical methods, offering a compelling alternative for range-free localization. By isolating the third phase, the study enables clear attribution of performance improvements to the applied optimization strategy while simultaneously advancing the discussion on how modern parameter-free designs compare against low- and high-parameter metaheuristics. This contribution not only highlights FHO’s potential but also lays a solid foundation for future multi-phase or hybrid enhancements.

3. Materials and Methods

This section firstly defines the problem of WSN localization and then presents two algorithms: the traditional DV-Hop and FHO algorithms.

3.1. WSN Localization Problem

In a two-dimensional WSN, the localization task involves determining the spatial coordinates of UNNs using a subset of ANs. Let the network contain $N_a$ ANs and $N_u$ UNNs, such that the initial configuration of the network can be expressed as a vector $\mathit{\theta }=[Z_1, Z_2,\dots , Z_{N_a+N_u }]$, where each node $Z_i$ is defined by its coordinate pair ${[x_i,y_i]}^T, \left(i=\mathrm{1,2},\dots ,N_a+N_u\right)$.

The positions of the $N_a$ ANs are known and denoted as $\left(x_1,y_1\right), \left(x_2,y_2\right),\dots , \left(x_{N_a },y_{N_a}\right).$ The objective is to accurately estimate the coordinates of the remaining n nodes, labeled as $\left(x_{N_a+1},y_{N_a+1}\right), \left(x_{N_a+2},y_{N_a+2}\right),\dots , \left(x_{N_a+N_u },y_{N_a+N_u }\right)$, based on the geometric information from the ANs and the available inter-node distance measurements.

Formally, the localization of a UNN can be modeled as a function of the known AN positions and their respective distances to the UNN. This relationship is expressed as:

$$\left(x,y\right)=F_i\left(x_i,y_i,d_{u,i}\right), \mathrm{for} i=1, 2,\dots ,N_a$$

(1)

where $\left(x,y\right)$ denotes the coordinates of a UNN to be estimated, $\left(x_i,y_i\right)$ represents the position of the i-th AN, and $d_{u,i}$ is the estimated distance between the UNN and AN i. The function $F_i\left(·\right)$ encapsulates the localization model, which is typically nonlinear due to the Euclidean nature of distance estimations in the plane [58]. It should be noted that Equation (1) provides a general mathematical representation of the localization problem, where distances are expressed in their ideal Euclidean form. However, in DV-Hop and other range-free methods, these distances are not directly measurable. Instead, they are approximated using hop counts and the average hop-size (as defined in Equation (3)). Thus, Equation (1) serves as a theoretical formulation, while Equation (3) captures the practical realization in the DV-Hop context.

We consider a static 2D WSN with ANs and UNNs. Localization relies solely on AN beacons and hop-based distances; no sink or base station is involved in DV-Hop or our optimization step. If a sink exists for data collection, it plays no role in the localization pipeline.

3.2. DV-Hop Algorithm

The DV-Hop algorithm [15] is a fundamental range-free localization technique extensively employed in WSNs due to its simplicity, scalability, and independence from physical ranging hardware such as ultrasonic or RSSI-based devices. It determines the positions of UNNs using only the network’s connectivity information and the known coordinates of a limited number of ANs. Unlike range-based techniques, it does not rely on direct distance measurements. Instead, each node estimates its distance to the ANs by calculating the minimum hop count and multiplying it by the average hop distance. This average is derived from the known positions of ANs. Finally, the coordinates of each UNN are estimated using the LSM. The DV-Hop localization process is structured into three primary steps, outlined as follows:

Step 1: (Obtaining the minimum hop count)

In this step, each node calculates the minimum hop count required to reach every AN. The process begins with each AN broadcasting a message containing its coordinates and an initial hop count of zero. When neighboring nodes receive this message, they increase the hop count by one and forward the message. Upon receiving such a message—whether the recipient is an AN or a UNN—the node stores the sender’s coordinates and updates its hop count accordingly. This procedure establishes a hop count field, representing the shortest number of hops between a node and each AN. If a node receives multiple messages from the sameAN, it compares the newly received hop count with the stored one; if the new value is smaller, it updates its record and rebroadcasts the message. Otherwise, the message is ignored. By the end of this step, all nodes in the network will have recorded the minimum hop counts to all reachable ANs.

Step 2: (Computation of average hop distances)

Once all ANs have received hop counts from other ANs, they proceed to estimate a critical parameter: the average physical distance per hop, often referred to as the HopSize. This value is derived using the actual Euclidean distances between AN pairs and the associated hop counts computed during the first step. For an AN $a_i$, the hop size is calculated as follows:

$${HopSize}_i={\displaystyle \frac{\sum d_{i,j}}{\sum {HopCount}_{i, j}}}={\displaystyle \frac{{\sum }_{j=1 j\ne i}^{N_a}\sqrt{{(x_i-x_j)}^2+{(y_i-y_j)}^2}}{{\sum }_{j=1 j\ne i}^{N_a}{HopCount}_{i, j}}}$$

(2)

where $(x_i,y_i)$ and $(x_j,y_j)$ are the coordinates of ANs $a_i$ and $a_j$, ${HopCount}_{i, j}$ is the minimum number of hops between them and $N_a$ is the total number of ANs. This hop size is then broadcasted throughout the network, allowing UNNs to estimate their distance to AN $a_i$. The mean hop distance corresponding to the nearest AN is adopted as the representative average hop distance for each UNN. Accordingly, the estimated distance $d_{u,i}$ between an UNN $u$ and an AN $a_i$ is calculated as shown in Equation (3):

$$d_{u,i}={HopCount}_{u,i}\times {HopSize}_i$$

(3)

where ${HopCount}_{u,i}$ denotes the minimum hop from UNN u and AN $a_i$.

Step 3: (Position estimation)

After obtaining distances to at least three non-collinear ANs, an UNN computes its position using multilateration. The classic method is the LSM, minimizing the error between estimated and real distances. Each AN $a_i (i=1, 2,\dots ,N_a)$ defines a nonlinear equation. If an UNN detects at least $N_a$ ANs, $N_a>2$, it computes its coordinates $x_u$ and $y_u$ by solving a system of nonlinear equations:

$$\begin{gathered} {\left(x_u- x_1\right)}^2+ {\left(y_u- y_1\right)}^2= d_{u,1}^2 \\ {\left(x_u- x_2\right)}^2+ {\left(y_u- y_2\right)}^2= d_{u,2}^2 \\ ⋮ \\ {\left(x_u- x_{N_a}\right)}^2+ {\left(y_u- y_{N_a}\right)}^2= d_{u,N_a}^2 \end{gathered}$$

(4)

Each AN contributes one equation, yielding a total of $N_a$. By designating one as a reference and subtracting it from the others, we obtain ($N_a$ − 1) independent linearized equations. This transformation converts the nonlinear system into the following form:

$$\begin{gathered} 2x_u\left(x_1- x_{N_a}\right)+2y_u\left(y_1- y_{N_a}\right)={x_1}^2+{y_1}^2+d_{u{,N}_a}^2-d_{u,1}^2-{x_{N_a}}^2-{y_{N_a}}^2 \\ 2x_u\left(x_2- x_{N_a}\right)+2y_u\left(y_2- y_{N_a}\right)={x_2}^2+{y_2}^2+d_{u,N_a}^2-d_{u,2}^2-{x_{N_a}}^2-{y_{N_a}}^2 \\ ⋮ \\ 2x_u\left(x_{N_a-1}- x_{N_a}\right)+2y_u\left(y_{N_a-1}- y_{N_a}\right)={x_{N_a-1}}^2+{y_{N_a-1}}^2+d_{u,N_a}^2-d_{u,N_a-1}^2-{x_{N_a}}^2-{y_{N_a}}^2 \end{gathered}$$

(5)

This results in a linear system that can be represented in matrix form as:

$$A·X=b$$

(6)

where $X$ represents the coordinates $(x_u,y_u)$ of the UNN to be estimated. $b$ is a vector containing constants derived from the equations and including distances squared. $A$ is a matrix of coefficients representing the positions of the ANs. The matrices $A$, $X$ and $b$ are given by Equations (7), (8), and (9), respectively.

$$A=\left[\begin{array}{cc}2\left(x_1-x_{N_a}\right)& 2\left(y_1-y_{N_a}\right)\\ 2\left(x_2-x_{N_a}\right)& 2\left(y_2-y_{N_a}\right)\\ ⋮& ⋮\\ 2\left(x_{N_a-1}-x_{N_a}\right)& 2\left(y_{N_a-1}-y_{N_a}\right)\end{array}\right]$$

(7)

$$b=\left[\begin{array}{c}{x_1}^2+{y_1}^2+d_{u,N_a}^2-d_{u,1}^2-{x_{N_a}}^2-{y_{N_a}}^2\\ {x_2}^2+{y_2}^2+d_{u,N_a}^2-d_{u,2}^2-{x_{N_a}}^2-{y_{N_a}}^2\\ ⋮\\ {x_{N_a-1}}^2+{y_{N_a-1}}^2+d_{u,N_a}^2-d_{u,N_a-1}^2-{x_{N_a}}^2-{y_{N_a}}^2\end{array}\right]$$

(8)

$$X=\left[\begin{array}{c}{x}_u\\ y_u\end{array}\right]$$

(9)

The LSM is subsequently employed to solve this overdetermined system, yielding the estimated position $X^{\ast }$ of the UNN:

$$X^{\ast }={\left(A^{T}A\right)}^{-1}{A}^{T}b$$

(10)

where the superscript $T$ indicates the transpose of a matrix [15].

Error Analysis of DV-Hop

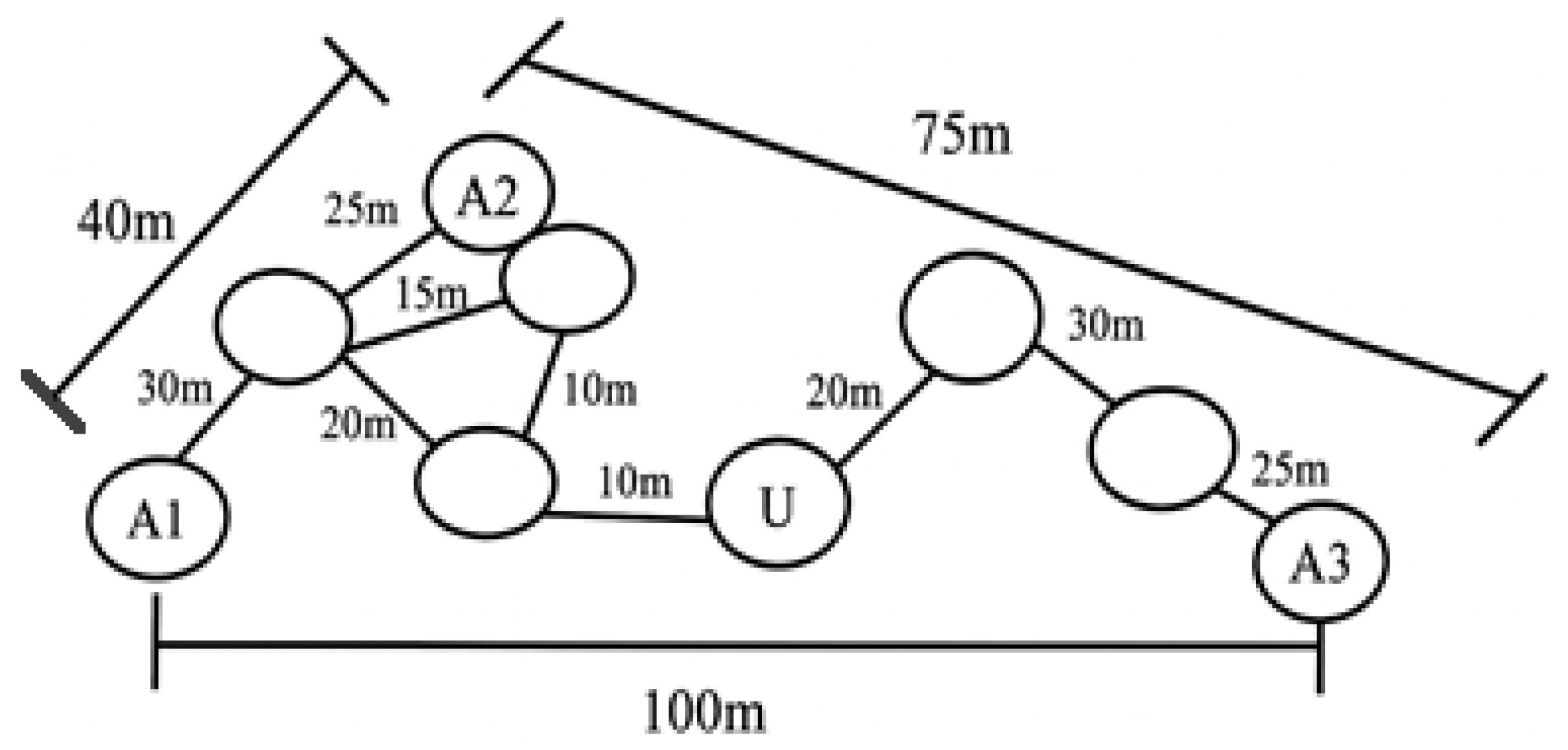
The DV-Hop algorithm assumes that the minimum-hop path between two nodes is approximately equivalent to a straight-line connection. However, this assumption often deviates from real-world conditions due to the influence of network topology, which causes each hop length to vary. Consequently, the estimated distance between an UNN and an AN, calculated using a uniform hop size, can significantly differ from the actual Euclidean distance. This deviation is referred to as the ranging or positioning error, which constitutes the primary source of overall localization inaccuracy. To illustrate this issue, consider the scenario in Figure 2. ANs are labeled as A₁, A₂, and A₃, and the UNN is denoted as U. Each anchor knows the number of hops to other anchors, and the hop count represents the number of intermediate links between them. In the standard DV-Hop process, each anchor computes its hop size as follows:

Figure 2. Error analysis of DV-Hop algorithm [45].

Figure 2. Error analysis of DV-Hop algorithm [45].

• For A₁: (40 + 100)/(2 + 6) = 17.50
• For A₂: (40 + 75)/(2 + 5) = 16.42
• For A₃: (75 + 100)/(5 + 6) = 15.90

After computing these values, anchors broadcast their respective hop sizes throughout the network. The UNN stores the first received hop size and uses it for all subsequent distance estimations. In this example, node U is 2 hops from A₂ and 3 hops from both A₁ and A₃. Since it first receives the hop size from A₂, it adopts 16.42 as its hop size value. Using this, the estimated distances are:

• U–A₂: 2 × 16.42 = 32.84
• U–A₁: 3 × 17.50 = 52.50
• U–A₃: 3 × 15.90 = 47.70

However, the actual Euclidean distance between U and A₂ is 55, while the estimated distance is 32.84, leading to a positioning error of 22.16, which is nearly 40% of the true value. This large error propagates into the final position estimation of the UNN, leading to substantial localization inaccuracies. In conclusion, the precision of the DV-Hop algorithm is highly sensitive to these positioning errors [45].

While DV-Hop offers a hardware-independent and scalable approach to node localization, its accuracy is often compromised by the accumulation of errors in hop-based distance estimation. Metaheuristic algorithms that leverage global search capabilities to improve location accuracy are employed in the coordinate estimation phase to mitigate this limitation. In this study, the FHO, distinguished by its balanced exploration–exploitation behavior and parameter-free design, is used to reduce localization errors in the third step of the DV-Hop algorithm.

3.3. Fire Hawk Optimizer

The Fire Hawk Optimizer (FHO), introduced by Azizi et al. in 2023 [30], is a swarm intelligence-driven metaheuristic algorithm inspired by the distinctive hunting strategy of certain raptor species, including whistling kites, black kites, and brown falcons. These birds display a remarkable behavior in which they intentionally carry burning twigs in their beaks or claws to start fires in unburned areas. This tactic flushes out concealed prey such as reptiles and rodents, significantly improving their chances of a successful hunt.

The FHO algorithm mimics this unique natural behavior by modeling the dynamics of fire propagation and prey pursuit. It initiates the search process with a population of candidate solutions (X), symbolizing the spatial positions of FHs and their preys within the optimization landscape. These initial positions are assigned through a randomized initialization strategy, setting the stage for the iterative optimization process.

$$X=\left[\begin{array}{c}{X}_1\\ X_2\\ ⋮\\ X_i\\ ⋮\\ X_N\end{array}\right]=\left[\begin{array}{c}{x_1}^1{x_1}^2\cdots {x_1}^j\cdots {x_1}^D\\ {x_2}^1{x_2}^2\cdots {x_2}^j\cdots {x_2}^D\\ \dots \\ {x_i}^1{x_i}^2\cdots {x_i}^j\cdots {x_i}^D\\ ⋮\\ {x_N}^1{x_N}^2\cdots {x_N}^j\cdots {x_N}^D\end{array}\right],\left\{\begin{array}{c}i=1, 2,\dots ,N.\\ j=1, 2,\dots ,D.\end{array}\right.$$

(11)

$${x_i}^j\left(0\right)=x_{i,min}^j+rand.\left(x_{i,max}^j-x_{i,min}^j\right),\left\{\begin{array}{c}i=1, 2,\dots ,N.\\ j=1, 2,\dots ,D.\end{array}\right.$$

(12)

Here, $X_i$ denotes the i-th candidate solution within the search space, while $x_{i,min}^j$ and $x_{i,max}^j$ represent the lower and upper bounds of its j-th decision variable, respectively. The variable rand corresponds to a uniformly distributed random number in the range [0, 1]. The notation ${x_i}^j$ indicates the j-th decision variable of the i-th solution candidate, and ${x_i}^j\left(0\right)$ refers to initial position of these candidates. D expresses the dimensionality of the problem, and N defines the total number of solution candidates in the search space.

In the subsequent stage, each candidate solution is evaluated using the objective function. According to their fitness values, the population is divided into two separate categories: FHs and prey. Individuals with better fitness are classified as FHs, whereas those with lower performance are considered prey, as determined by the following equations:

$$PR=\left[\begin{array}{c}{PR}_1\\ {PR}_2\\ ⋮\\ {PR}_k\\ ⋮\\ {PR}_m\end{array}\right],k =1, 2,\dots ,m, FH=\left[\begin{array}{c}{FH}_1\\ {FH}_2\\ ⋮\\ {FH}_l\\ ⋮\\ {FH}_n\end{array}\right],l =1, 2,\dots ,n$$

(13)

Here, ${FH}_l$ denotes the l-th FH within a population of n FHs, while ${PR}_k$ denotes the k-th prey among a total of m prey individuals. In the subsequent step, the algorithm computes the distance between each FH and its corresponding prey, with $D_k^l$ representing this distance, as formulated in the following equation:

$$D_k^l={\left(x_2- x_1\right)}^2+ {\left(y_2- y_1\right)}^2, \left\{\begin{array}{c}l=1, 2,\dots ,n.\\ k=1, 2,\dots ,m.\end{array}\right.$$

(14)

In this context, $(x_1, y_1)$ and $(x_2, y_2)$ correspond to the spatial coordinates of the FHs and prey, respectively. The parameters m and n represent the total number of prey and FHs within the search space.

In the following stage, each FH collects flaming sticks from the central fire to ignite its designated region, thereby forcing prey to escape. Additionally, a FH may acquire burning material from the territories of other hawks to initiate fires in its own area. These natural behaviors are mathematically modeled in FHO by updating the positions of FHs using the following formulation:

$${FH}_l^{new}={FH}_l+\left(r_1\times GB-r_2\times {FH}_{Near}\right), l=1, 2,\dots ,n.$$

(15)

Here, ${FH}_l^{new}$ denotes the updated position vector of the l-th FH (${FH}_l$), while ${FH}_{Near}$ refers to another FH within the population. The term GB represents the global best solution in the search space, symbolizing the main fire source. The coefficients $r_1$ and $r_2$ are uniformly distributed random numbers in the interval (0, 1), which regulate the hawk’s movement toward the main fire and nearby FHs’ regions.

In the following stage of the algorithm, the behavioral response of prey within a FH’s territory becomes central to the position-update mechanism. When a prey encounters a burning stick dropped by a FH, it may instinctively try to flee, hide, or unintentionally approach the predator. These natural reactions are mathematically captured in the equation below to steer the position adjustment process.

$${PR}_q^{new}={PR}_q+\left(r_3\times {FH}_l-r_4\times {SP}_l\right),\left\{\begin{array}{c}l=1, 2,\dots ,n.\\ q=1, 2,\dots ,m.\end{array}\right.$$

(16)

Here, ${PR}_q^{new}$ denotes the updated position vector of the q-th prey (${PR}_q$) residing within the territory of the l-th FH (${FH}_l$). The terms $r_3$ and $r_4$ are uniformly distributed random variables in the interval (0, 1), introducing stochasticity into the prey’s movement. Moreover, ${SP}_l$ represents a safe point within the l-th FH’s territory, calculated as follows:

$${SP}_l={\displaystyle \frac{{\sum }_{q=1}^r{PR}_q}{r}},\left\{\begin{array}{c}l=1, 2,\dots ,n.\\ q=1, 2,\dots ,r.\end{array}\right.$$

(17)

In this context, ${PR}_q$ refers to the q-th prey located within the domain of the l-th FH. In addition, prey may occasionally move into regions controlled by other FHs. Simultaneously, some prey might attempt to approach FHs that are obstructed by neighboring hawks, aiming to reach a safer zone outside the immediate territory. These behavioral patterns are captured in the position update mechanism through the application of the following equation:

$${PR}_q^{new}={PR}_q+\left(r_5\times {FH}_{Alter}-r_6\times SP\right)\left\{\begin{array}{c}l=1, 2,\dots ,n.\\ q=1, 2,\dots ,r.\end{array}\right.$$

(18)

Here, ${PR}_q^{new}$ denotes the updated position vector of the q-th prey (${PR}_q$) within the region of the l-th FH (${FH}_l$). The term $SP$ represents a secure location situated beyond the boundaries of ${FH}_l$’s territory. ${FH}_{Alter}$ refers to another FH present in the search space. The variables $r_5$ and $r_6$ are uniformly distributed random numbers within the range (0, 1), governing the movement of prey toward alternative FHs or external safe zones. The safe point $SP$ is computed as follows:

$$SP={\displaystyle \frac{{\sum }_{k=1}^m{PR}_k}{m}}, k=1, 2,\dots ,m.$$

(19)

where ${PR}_k$ denotes the k-th prey in the search space.

The candidate solutions are iteratively refined until a predefined termination criterion is satisfied, after which the algorithm outputs the best-obtained solution [30,59]. The overall procedure of the FHO is summarized in Algorithm 1, adapted and reformulated based on the original version proposed by Azizi et al. [30].

Algorithm 1: Fire Hawk Optimizer (general form, adapted from [30])

Input: Problem dimension (D), number of agents (N), maximum iterations (T), search space bounds: lower (Xmin) and upper (Xmax) Output: Final global best solution GB

1. Initialize the positions of all solution candidates Xi ∈ [Xmin, Xmax] using Equation (12) 2. Evaluate the fitness of each candidate solution 3. Identify the best solution GB (Global Best) as the main fire 4. Set iteration counter t ← 1 5. while t ≤ T do    6. Randomly select n FHs from the population    7. Classify the remaining (N − n = m) individuals as Preys (PR)    8. Compute distances between FHs and Preys using Equation (14)    9. Assign each Prey to the nearest FH to define their territory    10. for each FHl = 1 to n do     11. Update the position of FHl using main fire GB and another hawk Equation (15)     12. for each prey q in territory of FHl do      13. Compute a safe zone SP1 within FHl’s territory Equation (17)      14. Update the position of the prey using Equation (16)      15. Compute an external safe point SP outside FHl’s territory Equation (19)      16. Update the position of the prey using Equation (18)

end for     end for

17. Recalculate fitness values of updated FHs and Preys    18. Update GB if a better solution is found    19. t ← t + 1

end while

4. Proposed Work

To improve the localization accuracy of the traditional DV-Hop algorithm without compromising its range-free nature, this study introduces a hybrid method that integrates the FHO into the third phase of the DV-Hop procedure. The first two stages—hop count dissemination and average hop distance estimation—are retained without modification, ensuring low hardware dependency and reduced communication overhead. In contrast, the third stage, which conventionally estimates UNN positions via multilateration, is reformulated as a constrained nonlinear optimization problem. The objective is to minimize the cumulative error between the estimated Euclidean distances (derived from hop-based approximations) and the candidate positions of UNNs.

To solve this problem, FHO is employed as a population-based metaheuristic optimizer. A separate FHO instance is initialized for each UNN, where every firehawk in the population represents a possible coordinate pair within the deployment region. The fitness of each candidate is evaluated by computing its distance discrepancy concerning reachable ANs. Through an iterative process inspired by the cooperative hunting behavior of FHs, the population converges toward the optimal solution by dynamically balancing exploration and exploitation. FHO’s fast convergence, low parameter sensitivity, and adaptability to irregular search landscapes make it particularly well-suited for DV-Hop-based localization, where AN density, topology irregularities, or environmental uncertainties often hinder accuracy. The proposed FHODV-Hop hybrid model effectively reduces localization error by tailoring FHO to refine each UNN’s coordinates independently while preserving the core benefits of range-free localization schemes. The overall procedure is structured into steps, as detailed below:

Step 1: (Construction of the Hop Count Matrix)

Each AN in the network initiates a controlled flood of its identity, position, and a hop count initialized to zero. Upon receiving a broadcast, an intermediate node increments the hop count by one and relays the message. Every node records only the minimum number of hops it receives from each AN, leading to the construction of a hop count (HC) vector for each UNN:

$${HC}_u=\left[{HC}_{u,1},{HC}_{u,2},\dots ,{HC}_{u,N_a}\right]$$

(20)

where ${HC}_{u,i}$ represents the minimum number of hops from UNN $u$ to AN $i,$ ($i=\mathrm{1,2},\dots ,N_a)$, and $N_a$ is the total number of ANs.

Step 2: (Estimation of Average Hop Size)

To translate hop counts into approximate physical distances, each AN calculates an average hop size using the locations of neighboring ANs as in Equation (2). This ${HopSize}_i$ scalar value is broadcast across the network. Each UNN receives multiple such values and adopts the first one received, denoted as ${HopSize}_u$. This allows UNN u to estimate its distance to AN i as in Equation (3). These estimated distances serve as proxies for the true Euclidean distances, forming the basis for position estimation.

Step 3: (Reformulation as an Optimization Problem)

The process of determining the coordinates of a UNN is framed as an optimization problem, aiming to minimize the total deviation between the estimated Euclidean distances and those derived from hop counts:

$$\underset{\mathit{x}}{\mathit{min}}f\left(\mathit{x}\right)={\sum }_{i=1}^{N_a}\left(\sqrt{{\left(x-x_i\right)}^2+{\left(y-y_i\right)}^2}-{d_i}^2\right)$$

(21)

Here, $\mathit{x}=[x,y]$ is the candidate position of the UNN, and ${(x}_i,y_i)$ denotes the coordinates of AN i. The error term penalizes spatial inconsistencies between calculated and actual distances, forming a nonlinear least-squares objective function.

Step 4: (Initialization of FHO Population)

To solve the optimization problem, the FHO is employed. A population of N candidate solutions is initialized randomly over the 2D search space ${[0,areaSize]}^2$. Each candidate ${{\mathit{x}}_{\mathit{i}}=(x}_i,y_i)$ is initialized using:

$$x_j^i\left(0\right)=x_{j,min}^i+rand.{(x}_{j,max}^i-x_{j,min}^i)$$

(22)

where $i=1, 2,\dots ,N$ is the candidate index and $j=1, 2$ indicates the coordinate dimension (x or y), and $rand$ is a uniformly distributed random number in the interval [0, 1]. This ensures a uniform and unbiased distribution of initial solutions throughout the search domain.

Step 5: (Fitness Evaluation Based on DV-Hop Localization Error)

Each candidate solution (position) ${\mathit{x}}_{\mathit{i}}$ is evaluated using the objective function $f\left(\mathit{x}\right)$ defined in Step 3. Based on fitness values, the population is divided into two disjoint sets: 1. Fire Hawks (FHs)—candidates with better fitness (lower error), 2. Preys (PRs)—candidates with worse fitness (higher error) (as represented in Equation (13) with n FHs and m PRs, where $n+m=N$). This division simulates the predator–prey interaction mechanism that characterizes the FHO algorithm.

Step 6: (Distance Computation Between FHs and Preys)

Each FH computes the Euclidean distance to prey individuals to identify interaction opportunities using Equation (14). In this step, the coordinates are taken directly from the corresponding candidate solutions. This step allows hawks to detect prey proximity, analogous to tracking promising or poor solutions.

Step 7: (FH Position Update Toward the Global Best)

FHs adjust their positions by gravitating toward the global best solution $GB$ while simultaneously referencing the position of a neighboring hawk ${FH}_{Near}$ using Equation (15). This equation facilitates exploitation by refining elite solutions, and the stochastic terms $r_1,r_2\in \left(\mathrm{0,1}\right)$ introduce variability that promotes convergence without stagnation.

Step 8: (Prey Position Update Within Local Territory)

Prey individuals adapt their positions by considering both the dominant ${FH}_l$ in their region and a locally defined safe position ${SP}_l$ using Equations (16) and (17). The safe position ${SP}_l$ is the centroid of prey in the local territory, promoting group cohesion and stabilizing local search dynamics. This step allows hawks to detect prey proximity, analogous to tracking promising or poor solutions.

Step 9: (Prey Exploration Beyond Local Territories)

To enhance global exploration and mitigate premature convergence, prey may migrate beyond their original territory by referencing an alternative FH and a global safe zone $SP$ using Equations (18) and (19). This process dynamically balances exploration and exploitation, enhancing diversification by guiding the optimizer beyond local optima and ensuring sensitivity to diverse regions of the search space.

Step 10: (Final Position Selection)

For each UNN, the optimization process runs independently for a predefined number of iterations or until convergence. Upon completion, the candidate solution yielding the lowest DV-Hop-based error ${(x}_u^{est},y_u^{est})$ is selected as the final position estimate, and the results for all UNNs are aggregated into a unified position matrix.

By embedding FHO into the third phase of the DV-Hop algorithm, the proposed hybrid framework delivers an adaptive and range-free localization solution tailored for WSNs. This integration transforms the position estimation step into a population-based optimization process that autonomously operates for each UNN. The synergy between FHO’s search dynamics and DV-Hop’s topological foundations enables accurate coordinate estimation even in networks with irregular node distribution or complex topologies, where classical methods often underperform. The hybrid framework maintains a strong equilibrium between global search and local refinement, promoting effective convergence to optimal solutions while mitigating the risk of premature stagnation. Each component of the FHO algorithm is meticulously aligned with the DV-Hop structure, preserving its range-free nature and supporting scalable deployment across varying network densities. As a result, the proposed method offers both high localization resolution and methodological consistency, making it a viable candidate for real-world, topology-agnostic localization tasks. As shown in

Table 2. Mapping of key FHO parameters to their roles in DV-Hop-based WSN localization.

FHO Parameter	Meaning in Optimization Process	Corresponding Concept in WSN Localization
Population size (N)	Number of solutions evaluated per iteration	Candidate position estimates per UNN
Maximum iterations (T)	Total optimization cycles	Allowed computation budget
Search space ([0, D]2)	Defined range of possible solutions	Deployment area boundaries
Candidate solution ($X^{\mathrm{\ast }}$)	Individual solution vector explored by the optimizer	Estimated coordinates ${(x}_u^{est},y_u^{est})$
Objective function (f(X))	Fitness to be minimized	Localization error
Global best solution (GB)	Optimal solution identified	Final estimated position
Convergence criterion	Termination condition of the search	Stop condition based on accuracy or iterations

, the core parameters of the FHO are mapped to their functional roles within the DV-Hop localization framework. This mapping bridges the gap between algorithmic configuration and real-world deployment, showing how choices such as population size, search domain, and iteration budget translate into practical aspects of WSN operation, including the number of position estimates, the sensing field dimensions, and the computational effort required for localization. Integrating this correspondence into the methodological flow enhances the transparency of the proposed approach and clarifies how the optimization process is grounded in realistic WSN scenarios.

FHODV-Hop is realized as a network-layer localization service that builds on standard DV-Hop operations. Steps 1–2 (hop counting and hop-size estimation) remain unchanged and provide the connectivity-derived inputs used by Step 3. In Step 3, position estimation for each unknown node is cast as a bounded, population-based optimization over [0, D]²: the fitness is the least-squares misfit between anchor distances and hop-based distance estimates, and the FHO iterates for at most T cycles with population N to return the best coordinate GB. The procedure is range-free and does not modify PHY/MAC or routing; it consumes only the outputs of Steps 1–2 and produces final coordinates for dissemination at the network layer. Execution can be centralized (e.g., controller/base station) or distributed across capable nodes; for reproducibility, our experiments adopt a centralized solver, but the design is agnostic to this choice. Under this arrangement, FHODV-Hop composes cleanly with existing DV-Hop implementations and remains compatible with standard WSN protocol stacks.

The proposed FHODV-Hop algorithm is summarized in Algorithm 2. For compactness, Algorithm 2 references previously defined equations rather than reproducing them in full. All formulas cited (e.g., distance estimation, multilateration objective, and FHO update rule) are explicitly provided in Section 3. To ensure that the algorithm remains internally consistent and easily interpretable without requiring the reader to search backwards in the text, short identifiers have been added next to particularly important equations.

Algorithm 2: FHODV-Hop (FHO adapted for WSN localization scenario)

Input: Node coordinates (nodePos), AN indices (beaconIdx), UNN indices (unknownIdx), Deployment area (areaSize), Number of FHO agents (population size, N), Maximum number of iterations (T), Search space bounds = [0, areaSize] (Xmin, Xmax). Output: Final estimated positions of UNNs Procedure:

1. Construct the Hop Count matrix for each UNN (Equation (20)) 2. Estimate average hop sizes at each AN using Equation (2) and broadcast 3. Estimate distances from UNNs to ANs using DV-Hop rule: $d_{u,i}={HopCount}_{u,i}\times {HopSize}_i$ (Equation (3)) 4. If at least three ANs are available for a given UNN, reformulate position estimation as a nonlinear optimization problem: $\underset{\mathit{x}}{\mathit{min}}f\left(\mathit{x}\right)={\sum }_{i=1}^{N_a}\left(\sqrt{{\left(x-x_i\right)}^2+{\left(y-y_i\right)}^2}-{d_i}^2\right)$ (Equation (21)) (objective function) Otherwise, apply centroid fallback. 5. for each UNN do    6. Initialize FHO population uniformly in [0, areaSize] using Equation (22)    7. Evaluate fitness of each candidate (Equation (21))    8. Identify the global best solution GB    9. Set iteration t ← 1    10. while t ≤ T do     11. Select n FHs randomly from population     12. Assign remaining (N-n = m) as Preys (Equation (13))     13. Compute distances between each FH and Prey (Equation (14))     14. Assign Preys to closest FH to define territories     15. for each FHl do      16. Update position of FHl using GB and another hawk ${FH}_l^{new}={FH}_l+\left(r_1\times GB-r_2\times {FH}_{Near}\right), l=1, 2,\dots ,n.$ (Equation (15)      17. for each prey PRq in territory of FHl do       18. Compute local safe zone SP1 (Equation (17))       19. Update prey locally using Equation (16)       20. Compute global safe point SP2 (Equation (19))       21. Update prey globally using Equation (18)

end for     end for

22. Re-evaluate fitness and update GB if better    23. t ← t + 1

end while

24. Select GB as final estimate for current UNN

end for

25. Aggregate estimates of all UNNs into estimatedPos 26. return estimatedPos

For clarity, the mathematical symbols employed in the DV-Hop and FHODV-Hop formulations are summarized in

Table 3. Notation table.

Symbol	Definition
${\mathit{N}}_{\mathit{a}}$	Number of ANs
${\mathit{N}}_{\mathit{u}}$	Number of UNNs
${\mathit{H}\mathit{o}\mathit{p}\mathit{C}\mathit{o}\mathit{u}\mathit{n}\mathit{t}}_{\mathit{u},\mathit{i}}$ (${\mathit{H}\mathit{C}}_{\mathit{u},\mathit{i}}$)	Minimum hop count between UNN u and AN i
${\mathit{H}\mathit{o}\mathit{p}\mathit{S}\mathit{i}\mathit{z}\mathit{e}}_{\mathit{i}}$	Average hop distance computed at AN i
${\mathit{H}\mathit{o}\mathit{p}\mathit{C}\mathit{o}\mathit{u}\mathit{n}\mathit{t}}_{\mathit{i},\mathit{j}}$	The minimum number of hops between AN i and AN j
${\mathit{d}}_{\mathit{u},\mathit{i}}$	Estimated distance between UNN u and AN i
D	Dimensionality of the optimization problem (decision variables; D = 2 for coordinates)
N	Total number of candidate solutions (population size)
n	Number of FHs (elite solutions) selected from population
N–n or m	Number of Preys (remaining individuals with lower fitness)
${\mathit{x}}_{\mathit{i},\mathit{m}\mathit{i}\mathit{n}}^{\mathit{j}}$ and ${\mathit{x}}_{\mathit{i},\mathit{m}\mathit{a}\mathit{x}}^{\mathit{j}}$	the lower and upper bounds of its j-th decision variable, respectively.
${\mathit{F}\mathit{H}}_{\mathit{l}}$	Position vector of the l-th FH
${\mathit{F}\mathit{H}}_{\mathit{A}\mathit{l}\mathit{t}\mathit{e}\mathit{r}}$	Another FH present in the search space
${\mathit{P}\mathit{R}}_{\mathit{q}}$	Position vector of the q-th Prey
GB	Global best solution (main fire source)
${\mathit{S}\mathit{P}}_{\mathit{l}}$	Safe point within the territory of FH l
$\mathit{S}\mathit{P}$	A secure location situated beyond the boundaries of ${\mathit{F}\mathit{H}}_{\mathit{l}}$’s territory
T	Maximum number of iterations
${\mathbf{X}}^{\mathbf{\ast }},{(\mathit{x}}_{\mathit{u}}^{\mathit{e}\mathit{s}\mathit{t}},{\mathit{y}}_{\mathit{u}}^{\mathit{e}\mathit{s}\mathit{t}})$	The estimated location of UNN u
${(\mathit{x}}_{\mathit{u}}^{\mathit{a}\mathit{c}\mathit{t}},{\mathit{y}}_{\mathit{u}}^{\mathit{a}\mathit{c}\mathit{t}})$	The actual location of UNN u
M	The number of times the algorithm is tested on independent random distributions

below. This table consolidates the notation used in Section 3 and Section 4, ensuring consistent interpretation before proceeding to the experimental results.

5. Experimental Design and Performance Evaluation

To evaluate the performance and flexibility of the proposed algorithm, simulations are conducted across four commonly adopted network topologies: random, circular, square grid, and S-shaped. In WSNs, the spatial arrangement of nodes significantly influences localization accuracy, especially for range-free approaches such as DV-Hop enhanced with metaheuristic optimization techniques. These classical topologies are employed to represent diverse deployment scenarios, enabling a comprehensive analysis of algorithm performance under varying conditions of connectivity, node density, and geometric structure.

• Random topology

In this topology, nodes are distributed uniformly at random across the deployment area, reflecting scenarios with minimal control over placement—such as post-disaster zones or aerial sensor drops. This randomness induces heterogeneous neighbor relationships and unpredictable hop-count distributions, significantly challenging localization algorithms that rely solely on connectivity rather than ranging estimates. Random deployment remains a core baseline in many localization studies due to its relevance to real-world unstructured deployments [60].

2.

Circular topology

In this configuration, nodes are arranged radially around a central AN point, often representing a base station or high-priority node. The geometry facilitates more balanced propagation of AN-derived information and promotes isotropic connectivity across the network. Circular layouts are pertinent to surveillance and area-covering applications where symmetry and centralized coordination enhance localization quality [61].

3.

Square grid topology

Square grid deployment places nodes in a regularly spaced lattice across the field, simulating structured and planned deployments typical in agricultural monitoring, smart buildings, or urban sensing infrastructure. This deterministic arrangement supports predictable multi-hop paths and uniform connectivity, leading to stable localization performance and reduced positional ambiguity. Thus, it often serves as a theoretical ideal against which other topologies are benchmarked [62].

4.

S-shape topology

In this topology, nodes roughly follow a sinusoidal trajectory, with small perturbations to emulate deployment along winding terrains—such as pipelines, riverbanks, or roadways. This layout introduces irregular node density, asymmetric connectivity, and elongated hop distributions. It constitutes a stringent test for localization schemes, particularly those dependent on hop-based distance estimation, by exposing them to highly anisotropic network structures [63].

All simulation tests were conducted under identical network and algorithmic parameters to ensure fairness and comparability with prior literature. A 100 × 100 m² area was used to emulate small-to-medium WSN applications such as environmental monitoring. In each scenario, 100 nodes were deployed with a 30% AN ratio and a 25 m CR, consistent with IEEE 802.15.4-based nodes. The AN ratio was chosen as a balanced trade-off between localization accuracy and hardware cost, while node densities from 10 to 400 captured both sparse and dense deployments. The reasons for choosing the AN and CR ratios in this way can be easily seen in the relevant simulation results below, which examine the effect of these parameters on ALE. Four topologies—Random, Circular, Square-grid, and S-shaped—were tested to represent diverse practical layouts. Each configuration was repeated 50 times, and average results were reported to ensure statistical robustness.

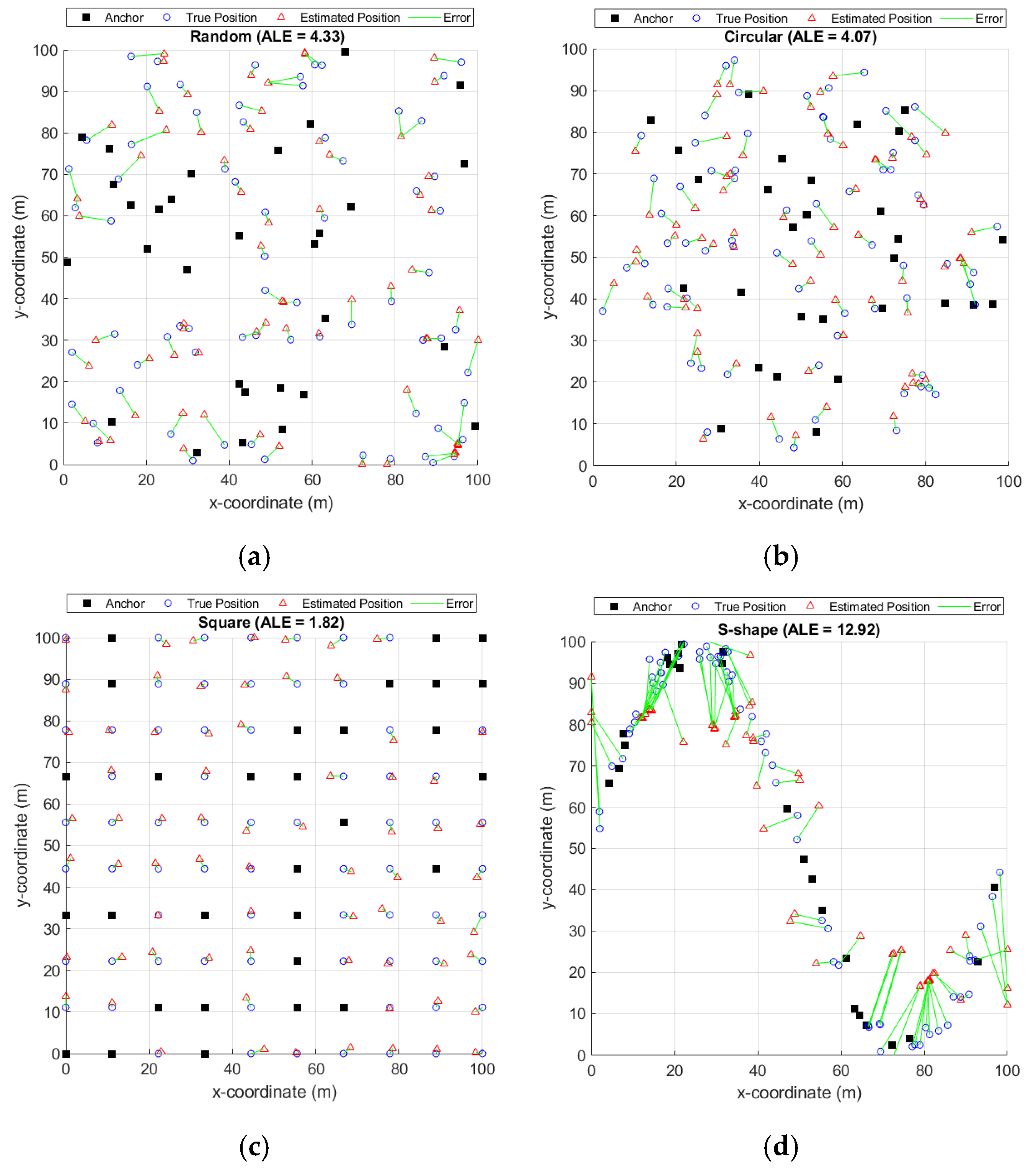
Examples of the FHODV-Hop algorithm in these topologies are shown in Figure 3. Black squares denote ANs, blue circles the true positions of UNNs, red triangles their estimated locations, and green lines the localization errors, with corresponding ALE values given in the captions. Among the topologies, the square-grid offered the most favorable localization conditions, whereas the S-shaped layout posed the greatest challenge.

Using different evaluation criteria, the proposed FHODV-Hop algorithm is compared with the original DV-Hop and its hybrid versions with PSO [28], MRFO [34], SCA [32], VCS [35], SSA [29], and BA [31]. These algorithms were selected not only for their prevalence in DV-Hop literature but also for their capacity to introduce new insights, ensuring that the experimental scope remains distinct from the literature review. This separation avoids redundancy while maintaining fairness and clarity. Comprehensive simulation experiments were carried out in MATLAB 2021b under identical conditions to guarantee reproducibility, using a desktop computer with an Intel(R) Core(TM) i7-4790 @ 3.60 GHz, 16 GB RAM, and Windows 10.

The baseline DV-Hop algorithm was implemented in its canonical form. In the third phase, where UNN positions are estimated, seven metaheuristics were integrated: PSO, MRFO, SCA, VCS, FHO, SSA, and BA. Each UNN was optimized independently by minimizing the mean squared error between anchor-to-node distances derived from hop counts and those implied by candidate solutions. The deployment area bounded the search domain, and infeasible solutions were clipped to the nearest feasible value. To ensure consistency, if fewer than three ANs were available, the centroid of accessible ANs was used as a fallback. At the same time, the deployment area center was applied when no ANs were reachable.

To ensure fairness, all algorithms were tested under identical conditions, using a population size of 30 with a fixed maximum of 50 iterations. Initial solutions were uniformly distributed within the search space, and the stopping criterion was defined as the maximum number of iterations.

Table 4. Experimental parameters.

Parameter	Value
CR	10–60 (m)
Total number of nodes	50–300
AN ratio	10–60%
Monitoring area	100 × 100 (m2)
Population Size	5–50
Number of iterations	50
Topologies	Random, Circular, Square-grid, S-shape

outlines the WSN configuration settings, while the parameter values of the metaheuristic algorithms were taken from their original papers. To ensure reproducibility, all algorithmic parameters are explicitly stated below.

• PSO: acceleration coefficients $C_1=C_2=2.05$, inertia weight decreased linearly from 0.9 to 0.4 [28].
• MRFO: included chain, cyclone, and somersault phases with somersault factor $S=2$ [34].
• SCA: employed sine–cosine position updates with control parameter ${\mathit{r}}_1$ decreasing linearly from 2 to 0 [32].
• VCS: parameterized with $\beta =0.2$, $\gamma =1.5$, and $\mu =0.5$ [35].
• SSA: leader–follower chain dynamics with $c_1=2\mathrm{e}\mathrm{x}\mathrm{p}[-{\left({\displaystyle \frac{4t}{MaxIt}}\right)}^2]$ [29].
• BA: loudness $A=0.9$ decreasing with $\alpha =0.9$, pulse rate $r=0.1$ increasing with $\gamma =0.9$, frequency range $Q\in [0, 2]$ and a local random walk factor of 0.001 [31].

The parameter settings for each metaheuristic were carefully chosen to ensure both fairness and methodological consistency across all algorithms. Instead of arbitrary tuning, we adopted the default configurations reported in the original papers and widely cited implementations. This strategy prevents overfitting to particular topologies and supports transparent, reproducible comparisons under a uniform computational budget. Common settings such as population size, iteration limit, initialization scheme, boundary handling, and stopping criterion guaranteed equal search effort across all methods, while algorithm-specific defaults preserved the exploration–exploitation balance intended by their designers. Notably, the FHO maintains its parameter-free nature, which avoids manual calibration altogether and demonstrates its practical advantage for real-world WSN localization where minimal user intervention is desired.

In this study, FHO was integrated into DV-Hop for the first time. Unlike most metaheuristics, it requires no control parameters, enhancing practicality in real-world deployments. Candidate updates follow a best-directed step toward the global optimum, complemented by Gaussian perturbation $(\mathit{\sigma }=0.05\times \left(\mathit{u}\mathit{b}-\mathit{l}\mathit{b}\right))$ to maintain diversity and avoid premature convergence. This combination of exploitation and exploration enables both rapid convergence and robust performance. Compared to classical parameter-dependent optimizers, FHO provides stronger reproducibility, lower implementation complexity, and suitability for large-scale WSN applications where parameter tuning is impractical.

5.1. Performance Metrics

The effectiveness of the proposed FHODV-Hop algorithm is assessed based on three primary metrics: ALE (m), localization success ratio, and computational time. The definitions of these evaluation criteria are as follows:

5.1.1. Average Localization Error (ALE)

ALE serves as a core metric for evaluating localization performance by calculating the average difference between the actual and estimated positions of sensor nodes. Lower ALE values indicate higher localization precision. The metric is computed using the following equation:

$$ALE={\displaystyle \frac{{\sum }_{u=1}^{N_u}\sqrt{{\left(x_u^{est}-x_u^{act}\right)}^2+{\left(y_u^{est}-y_u^{act}\right)}^2}}{CR\times N_u}}$$

(23)

where ${(x}_u^{est},y_u^{est})$ is the estimated location UNN u, ${(x}_u^{act},y_u^{act})$ denotes its actual location, $N_u$ refers the total number of UNNs that can be localized, and $CR$ indicates the CR used in the network.

All algorithms were evaluated over 50 independent trials, each using randomly generated WSN node distributions appropriate to the nature of the topology of interest. Multiple statistical indicators are utilized to assess the performance and reliability of the proposed methods.

• Mean: To achieve a reliable assessment, each algorithm is tested across 50 independent random deployments of WSN nodes (M = 50). To ensure a consistent evaluation of localization accuracy, the average ALE value—defined in Equation (24)—is calculated.

$$Mean={\displaystyle \frac{1}{M}}{\sum }_{i=1}^M{f}_{\ast }^i$$

(24)

where $f_{\ast }^i$ indicates the ALE value corresponding to the best solution obtained during the i-th run.

2.

Standard deviation (STD): The standard deviation (STD) is used to assess the stability and robustness of the algorithm. A lower STD indicates that the optimization method consistently converges to similar solutions across multiple runs, which is more desirable than the erratic performance associated with higher STD values. The STD is computed using the following formula:

$$STD=\sqrt{{\displaystyle \frac{1}{M-1}}\sum {(f_{\ast }^i-Mean)}^2}$$

(25)

3.

t-tests: To assess whether the observed differences in localization accuracy across algorithms are statistically meaningful, an independent two-sample t-test was conducted. This test compares the mean values of two independent groups under the assumption of normally distributed data with equal variances. A significance level of α = 0.05 was adopted. The t-statistic is calculated as follows:

$$t={\displaystyle \frac{{\overline{X}}_1-{\overline{X}}_2}{\sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}}}$$

(26)

where ${\overline{X}}_1$ and ${\overline{X}}_2$ represent the sample means, $s_1^2$ and $s_2^2$  denote the sample variances, and $n_1$, $n_2$ are the sample sizes of the two groups. A p-value below 0.05 indicates a statistically significant difference between the compared methods.

Mean ALE values were calculated to represent average accuracy, while STD quantified robustness across multiple trials. To assess statistical significance between algorithms, independent two-sample t-tests (with Welch’s correction where necessary) were employed at a 0.05 level. Although these methods are widely accepted, they rely on assumptions of normality and variance, which represent their primary limitations.

5.1.2. Localization Success Ratio

The localization success ratio represents the proportion of nodes correctly positioned by the algorithm relative to the total number of nodes. A higher value signifies the algorithm’s effectiveness in accurately estimating a larger number of node locations [20,64].

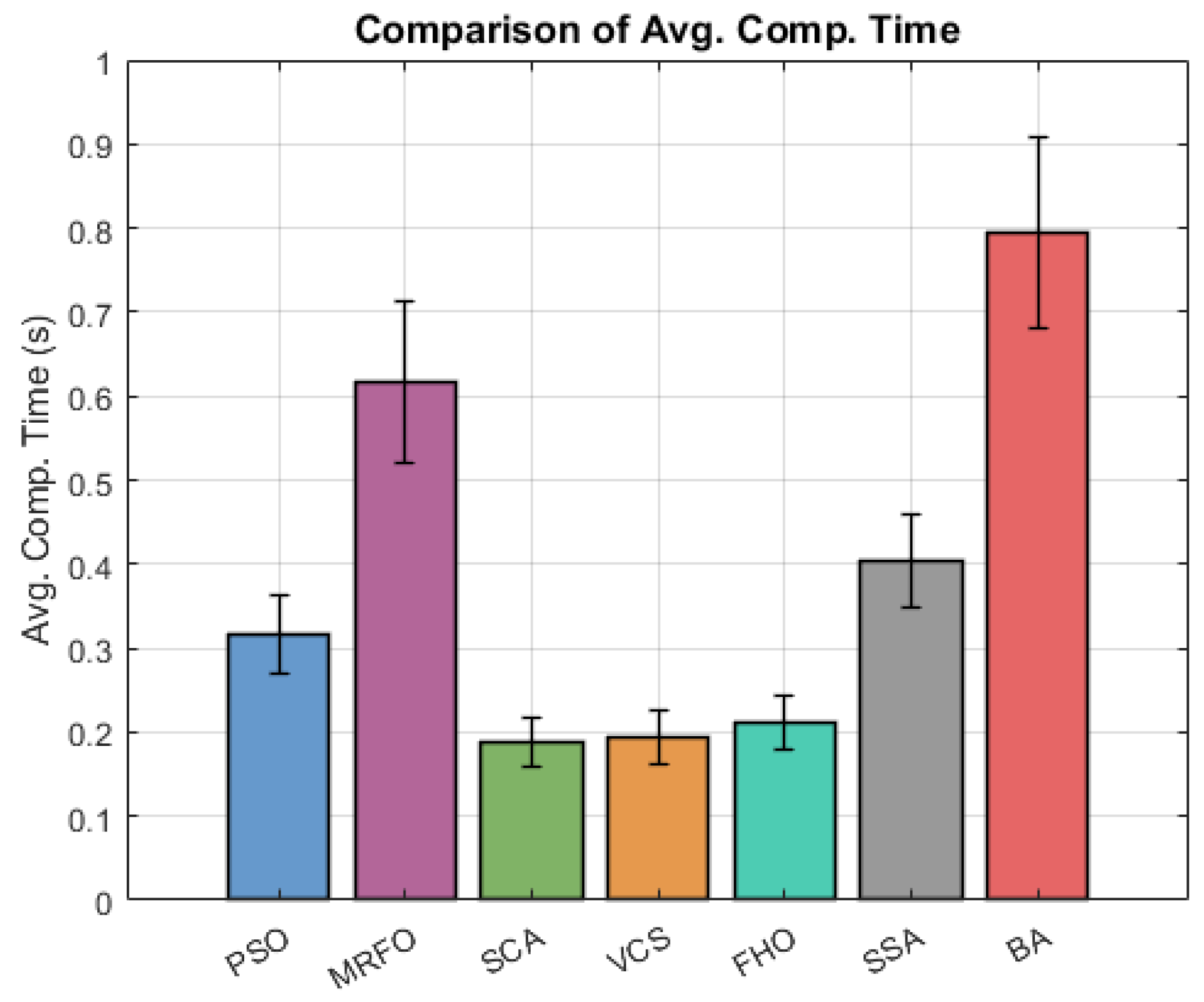
5.1.3. Computational Cost Analysis

Computational cost refers to the overall resource expenditure of an algorithm in solving a given problem and is a critical metric for evaluating its efficiency, particularly in scenarios that demand scalability or real-time applicability. It is typically quantified by measuring the total processing effort required to execute all algorithmic steps from start to finish. Since a single measurement can be influenced by transient system conditions, computational cost is commonly evaluated across multiple independent runs, with the mean and STD reported in line with recommendations from the literature [65].

Such multiple iteration-based cost analyses enable fair comparisons of algorithms not only in terms of accuracy but also in terms of computational burden. A lower computational cost generally corresponds to reduced energy consumption, which is particularly important in resource-constrained systems such as WSNs and directly influences the practical applicability of an algorithm [66].

In addition to empirical runtime comparisons, computational cost in WSN localization is typically evaluated along two complementary dimensions. First, theoretical computational complexity analysis provides insight into the scalability of algorithms by expressing their cost in terms of population size, iteration budget, and network scale. This allows researchers to classify different metaheuristics within comparable complexity classes and anticipate their behavior under larger deployments. Second, energy consumption analysis bridges algorithmic performance with practical feasibility, since even moderate increases in runtime can translate into significant energy expenditure on resource-constrained sensor nodes. Together, these perspectives highlight that an algorithm must not only achieve accuracy but also remain computationally tractable and energy-aware, ensuring its applicability in real-world WSN scenarios.

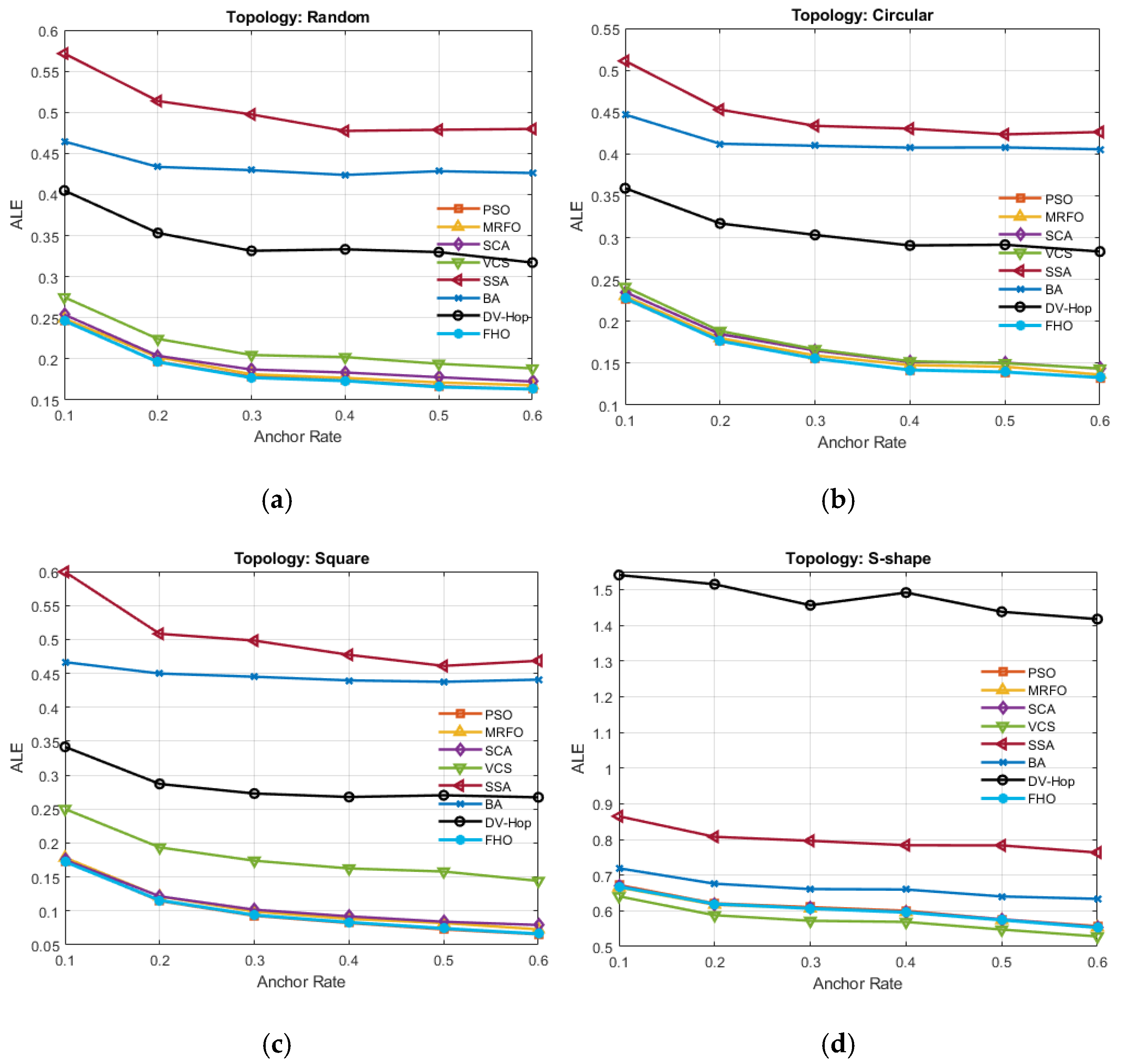
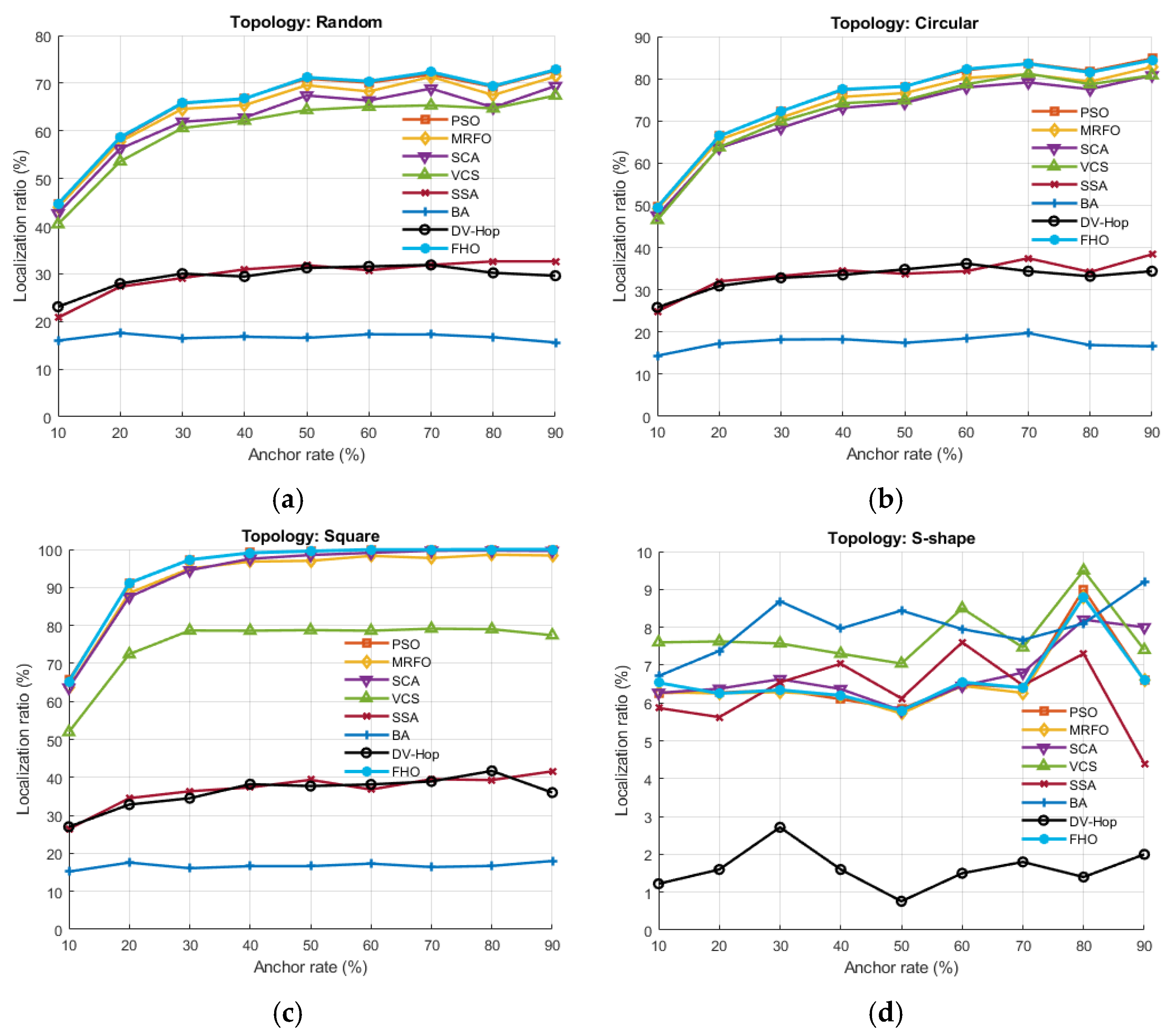
5.2. Effect of the Percentage of ANs on ALE

The number of ANs in the network plays a crucial role in determining localization accuracy. This section explores the impact of varying the AN ratio on the overall performance of the localization process. In the experiment, 100 sensor nodes were randomly deployed across various topologies within a 100 m × 100 m² sensing region, each node having a CR of 25 m. The AN ratio was gradually increased from 10% to 60% in steps of 10% to assess its effect on localization error. The results are presented in Figure 4 and

Table 5. Top three Algorithms (Mean ± STD) per Topology and AN Rate.

Topology: Random
AN Rate	1st	2nd	3rd
10%	FHO (0.2464 ± 0.0424)	PSO (0.2467 ± 0.0418)	MRFO (0.2490 ± 0.0405)
20%	FHO (0.1962 ± 0.0274)	PSO (0.1968 ± 0.0273)	MRFO (0.2021 ± 0.0274)
30%	FHO (0.1772 ± 0.0221)	PSO (0.1782 ± 0.0226)	MRFO (0.1814 ± 0.0232)
40%	FHO (0.1733 ± 0.0221)	PSO (0.1737 ± 0.0225)	MRFO (0.1770 ± 0.0232)
50%	FHO (0.1658 ± 0.0386)	PSO (0.1668 ± 0.0387)	MRFO (0.1713 ± 0.0383)
60%	FHO (0.1632 ± 0.0204)	PSO (0.1634 ± 0.0203)	MRFO (0.1679 ± 0.0205)
Topology: Circular
AN Rate	1st	2nd	3rd
10%	PSO (0.2268 ± 0.0312)	FHO (0.2276 ± 0.0320)	MRFO (0.2303 ± 0.0314)
20%	PSO (0.1765 ± 0.0220)	FHO (0.1766 ± 0.0219)	MRFO (0.1800 ± 0.0223)
30%	FHO (0.1556 ± 0.0189)	PSO (0.1556 ± 0.0190)	MRFO (0.1594 ± 0.0186)
40%	PSO (0.1418 ± 0.0158)	FHO (0.1419 ± 0.0158)	MRFO (0.1478 ± 0.0170)
50%	PSO (0.1393 ± 0.0162)	FHO (0.1395 ± 0.0163)	MRFO (0.1459 ± 0.0181)
60%	FHO (0.1326 ± 0.0165)	PSO (0.1329 ± 0.0162)	MRFO (0.1364 ± 0.0180)
Topology: Square Grid
AN Rate	1st	2nd	3rd
10%	FHO (0.1724 ± 0.0244)	PSO (0.1726 ± 0.0240)	MRFO (0.1786 ± 0.0287)
20%	PSO (0.1147 ± 0.0129)	FHO (0.1156 ± 0.0124)	MRFO (0.1213 ± 0.0132)
30%	PSO (0.0928 ± 0.0110)	FHO (0.0938 ± 0.0109)	MRFO (0.0991 ± 0.0107)
40%	PSO (0.0821 ± 0.0081)	FHO (0.0832 ± 0.0079)	MRFO (0.0884 ± 0.0090)
50%	PSO (0.0728 ± 0.0083)	FHO (0.0742 ± 0.0083)	MRFO (0.0821 ± 0.0111)
60%	PSO (0.0655 ± 0.0063)	FHO (0.0662 ± 0.0055)	MRFO (0.0729 ± 0.0075)
Topology: S-Shape
AN Rate	1st	2nd	3rd
10%	VCS (0.6407 ± 0.0939)	MRFO (0.6654 ± 0.0960)	FHO (0.6675 ± 0.0994)
20%	VCS (0.5877 ± 0.0796)	MRFO (0.6169 ± 0.0856)	FHO (0.6193 ± 0.0878)
30%	VCS (0.5721 ± 0.0578)	FHO (0.6066 ± 0.0655)	MRFO (0.6067 ± 0.0664)
40%	VCS (0.5690 ± 0.0431)	FHO (0.5958 ± 0.0619)	MRFO (0.5962 ± 0.0617)
50%	VCS (0.5476 ± 0.0574)	MRFO (0.5740 ± 0.0802)	FHO (0.5742 ± 0.0798)
60%	VCS (0.5282 ± 0.0606)	FHO (0.5532 ± 0.0661)	MRFO (0.5535 ± 0.0661)

.

The data presented in Table 5 and Figure 4 thoroughly illustrate the impact of AN density on localization accuracy across different deployment topologies. As the AN ratio increases from 10% to 60%, all algorithms generally exhibit improved localization accuracy, manifested by declining normalized ALE values. This trend confirms the expected outcome: a higher density of ANs enhances spatial reference quality, enabling more reliable distance estimations and reducing cumulative hop errors. This improvement is particularly evident in structured topologies such as circular and square grid, where uniform connectivity allows algorithms to leverage AN information more effectively. Across the entire spectrum of AN ratios and topologies, FHODV-Hop consistently ranks among the top three performers. In the random topology, FHO secures the first rank at all AN ratios, with ALE values steadily decreasing from 0.2464 ± 0.0424 at 10% to 0.1632 ± 0.0204 at 60%, outperforming PSO and MRFO in every configuration. This consistent superiority demonstrates FHO’s robustness and adaptability in unstructured and irregular node deployments. Notably, the gap between FHO and its closest competitors remains statistically minimal, underscoring its competitive edge even under increased AN availability.

In the circular topology, PSO narrowly surpasses FHO in most configurations. However, the differences are marginal and, in some cases, statistically insignificant (e.g., at 30%, both PSO and FHO report nearly identical errors of 0.1556). FHO still retains a strong second-place position in four out of six settings and outperforms all others at the 60% AN level, demonstrating its ability to match or exceed PSO in highly symmetric environments. The square grid topology follows a similar pattern, with PSO slightly outperforming FHO across most configurations. Nevertheless, the margin is consistently narrow—at 60%, PSO achieves 0.0655 ± 0.0063, while FHO records 0.0662 ± 0.0055. FHO’s close pursuit of the top performer highlights its exceptional suitability for deterministic and highly structured layouts, where algorithmic precision can be fully capitalized. In the S-shape topology, which introduces complex path geometries and connectivity irregularities, VCS emerges as the dominant algorithm. Still, FHO remains highly competitive, appearing in the top three in all AN settings. For instance, at a 30% AN rate, FHO records 0.6066 ± 0.0655, only slightly trailing VCS. Even in challenging scenarios, this consistent high-ranking performance underscores FHO’s structural resilience and generalization capability.

Further supporting these findings, the combined analysis of the ALE ± STD values and performance trends confirms FHODV-Hop as the most consistently competitive algorithm. According to the tabulated results, it ranks first in 11 out of 24 configurations and maintains a top-three presence in all 24. While PSO demonstrates strength in symmetric topologies and VCS dominates the S-shape configuration, FHO delivers across-the-board stability and excellence. In contrast, SSA and BA exhibit underwhelming performance across all scenarios, with higher ALE values and limited responsiveness to increasing AN density—highlighting their lack of adaptability to varying network structures.

In conclusion, the visual and statistical evidence reinforce FHODV-Hop’s position as a leading solution for range-free localization. Its remarkable consistency, structural versatility, and high localization accuracy make it especially suited for real-world WSN deployments under diverse and dynamic AN configurations.

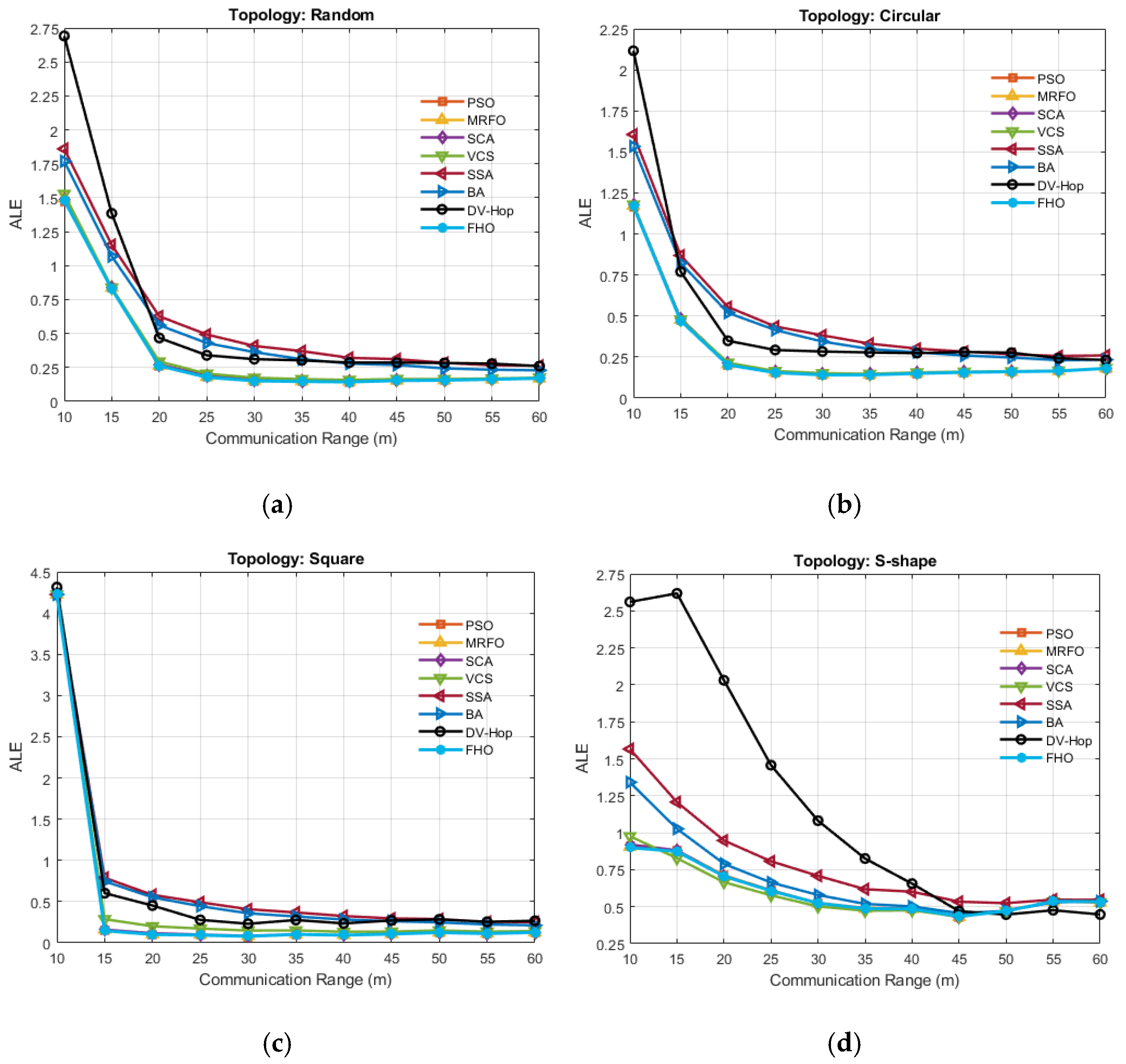
5.3. Effect of CR on ALE

This experiment examines how changes in CR influence the localization accuracy of various algorithms within a WSN comprising 100 sensor nodes and a fixed 30% AN ratio. The CR varies from 10 m to 60 m in steps of 10 m. ALE values are shown in Figure 5, and a statistical analysis of the three best performances obtained in each topology, which is not apparent in these figures, is summarized in

Table 6. Top three Algorithms (Mean ± STD) per Topology and CR.

Topology: Random
CR	1st	2nd	3rd
15	FHO (0.8285 ± 0.3455)	PSO (0.8364 ± 0.3510)	VCS (0.8380 ± 0.3336)
25	FHO (0.1777 ± 0.0301)	PSO (0.1784 ± 0.0300)	MRFO (0.1817 ± 0.0300)
35	FHO (0.1466 ± 0.0162)	PSO (0.1469 ± 0.0163)	MRFO (0.1497 ± 0.0177)
45	FHO (0.1530 ± 0.0199)	PSO (0.1530 ± 0.0198)	MRFO (0.1541 ± 0.0205)
55	FHO (0.1625 ± 0.0223)	PSO (0.1626 ± 0.0221)	MRFO (0.1629 ± 0.0215)
Topology: Circular
CR	1st	2nd	3rd
15	FHO (0.4710 ± 0.1916)	PSO (0.4736 ± 0.1978)	MRFO (0.4789 ± 0.1952)
25	PSO (0.1545 ± 0.0148)	FHO (0.1548 ± 0.0147)	MRFO (0.1581 ± 0.0143)
35	PSO (0.1414 ± 0.0150)	FHO (0.1415 ± 0.0150)	MRFO (0.1436 ± 0.0151)
45	PSO (0.1569 ± 0.0177)	FHO (0.1569 ± 0.0179)	MRFO (0.1584 ± 0.0177)
55	PSO (0.1642 ± 0.0206)	FHO (0.1647 ± 0.0210)	MRFO (0.1654 ± 0.0205)
Topology: Square Grid
CR	1st	2nd	3rd
15	PSO (0.1455 ± 0.0257)	FHO (0.1471 ± 0.0256)	SCA (0.1601 ± 0.0243)
25	PSO (0.0930 ± 0.0098)	FHO (0.0938 ± 0.0093)	MRFO (0.0992 ± 0.0103)
35	PSO (0.1019 ± 0.0125)	FHO (0.1024 ± 0.0122)	MRFO (0.1058 ± 0.0130)
45	PSO (0.1064 ± 0.0126)	FHO (0.1066 ± 0.0125)	SCA (0.1091 ± 0.0126)
55	PSO (0.1123 ± 0.0100)	FHO (0.1124 ± 0.0100)	SCA (0.1134 ± 0.0098)
Topology: S-Shape
CR	1st	2nd	3rd
15	VCS (0.8279 ± 0.1314)	FHO (0.8734 ± 0.1711)	MRFO (0.8753 ± 0.1689)
25	VCS (0.5768 ± 0.0711)	FHO (0.6071 ± 0.0757)	MRFO (0.6073 ± 0.0757)
35	VCS (0.4725 ± 0.0484)	MRFO (0.4312 ± 0.0499)	FHO (0.4867 ± 0.0568)
45	SCA (0.4297 ± 0.0514)	MRFO (0.4300 ± 0.0500)	PSO (0.4319 ± 0.0536)
55	DV-Hop (0.4761 ± 0.0714)	BA (0.5293 ± 0.0506)	VCS (0.5350 ± 0.0551)

. The findings highlight key trends in how each algorithm responds to changes in CR under multiple deployment topologies.

The graphical trends confirm that increasing the CR leads to a consistent improvement in localization accuracy for all algorithms. This enhancement is attributed to the higher number of 1-hop connections in the network, which reduces the cumulative hop distances and leads to more precise distance estimations. This behavior is particularly visible in Random and Circular topologies, where spatial uniformity allows longer CRs to maximize their effect.

The comparative evaluation based on ALE ± STD values across CRs from 15 m to 55 m reveals that the FHODV-Hop consistently demonstrates robust localization performance across various topologies. In the Random topology, FHO secures the first rank across all five CRs, clearly outperforming its closest competitors, such as PSO and MRFO. Its dominant position is particularly evident at CR = 15 m and CR = 25 m, where it achieves the lowest normalized ALE values of 0.8285 ± 0.3455 and 0.1777 ± 0.0301, respectively. Although PSO narrowly leads in most CR settings in the Circular topology, FHO remains highly competitive by consistently occupying the second rank, with minimal differences from the best-performing algorithm. For instance, at CR = 25 m, FHO’s normalized ALE is 0.1548 ± 0.0147, virtually matching PSO’s 0.1545 ± 0.0148. This indicates that FHO retains excellent accuracy in structured and symmetric deployment scenarios. In Square Grid topology, PSO again holds the top position across all CR values, yet FHO persistently remains in second place. The difference in localization accuracy between FHO and PSO is marginal, especially at CR = 25 m (FHO: 0.0938 ± 0.0093, PSO: 0.0930 ± 0.0098) and CR = 35 m (FHO: 0.1024 ± 0.0122, PSO: 0.1019 ± 0.0125). This proximity underscores FHO’s high efficiency in grid-like arrangements, where predictable connectivity aids precise localization. The S-shape topology, characterized by irregular connectivity and high path asymmetry, presents the most challenging scenario. Here, FHO ranks second at low CR values (e.g., CR = 15 m: 0.8734 ± 0.1711) and maintains a top-three presence at CR = 25 m and 35 m. Although VCS slightly outperforms FHO in early stages, FHO still offers strong adaptability and reliable results. Importantly, even when it does not achieve the top rank, FHO’s normalized error remains within acceptable limits, indicating robustness to topological complexity.

Overall, the combined insights from Table 6 indicate that FHO ranks within the top 3 in 19 out of 20 configurations, including first place in 6 cases and second in 9 others. This remarkable consistency across all topologies and CRs highlights FHO’s excellent generalization capability, structural adaptability, and high localization accuracy. While other algorithms like PSO or VCS excel in specific topologies, FHO offers the most balanced and reliable performance, making it a top-tier candidate for real-world, range-free WSN localization tasks under diverse deployment conditions.

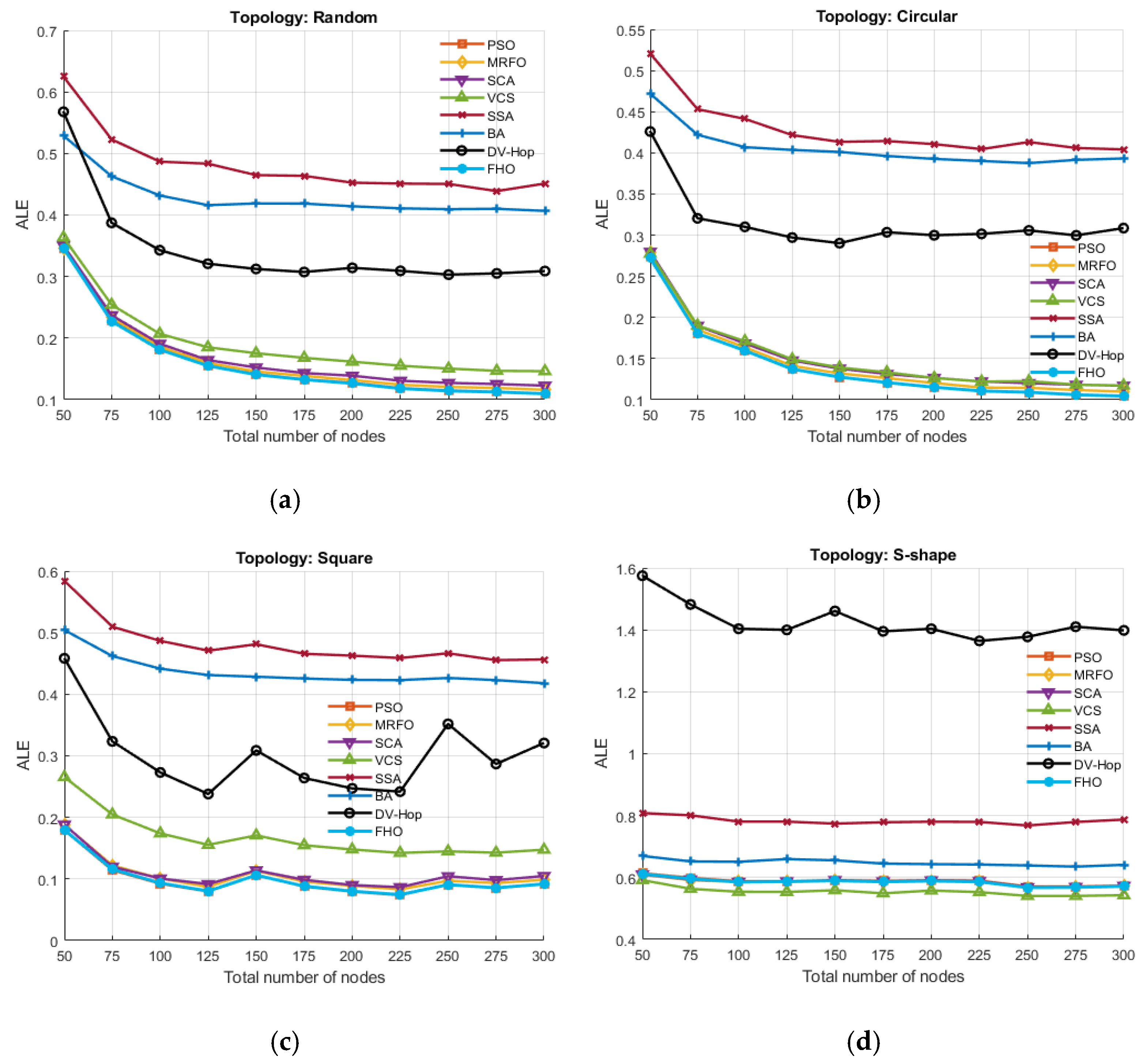
5.4. Effect of Varying Total Number of Nodes on ALE

This section analyzes the performance of the FHODV-Hop algorithm under different network sizes and compares its results with those of existing approaches. The experiment was carried out using a fixed set of 30 ANs and a CR of 25 m, while the total number of nodes varied from 50 to 300. This configuration allowed for a thorough assessment of the proposed algorithm’s efficiency. The corresponding results are illustrated in Figure 6 and a statistical analysis of the three best performances obtained in each topology, which is not apparent in these figures, is summarized in

Table 7. Top three Algorithms (Mean ± STD) per Topology and Total Number of Nodes.

Topology: Random
Node Count	1st	2nd	3rd
100	FHO (0.1813 ± 0.0288)	PSO (0.1821 ± 0.0293)	MRFO (0.1859 ± 0.0287)
150	FHO (0.1407 ± 0.0118)	PSO (0.1414 ± 0.0116)	MRFO (0.1458 ± 0.0129)
200	FHO (0.1264 ± 0.0094)	PSO (0.1273 ± 0.0095)	MRFO (0.1319 ± 0.0093)
250	FHO (0.1142 ± 0.0080)	PSO (0.1150 ± 0.0079)	MRFO (0.1207 ± 0.0087)
300	FHO (0.1097 ± 0.0071)	PSO (0.1102 ± 0.0071)	MRFO (0.1161 ± 0.0074)
Topology: Circular
Node Count	1st	2nd	3rd
100	PSO (0.1596 ± 0.0326)	FHO (0.1598 ± 0.0327)	MRFO (0.1638 ± 0.0325)
150	PSO (0.1275 ± 0.0114)	FHO (0.1276 ± 0.0114)	MRFO (0.1320 ± 0.0114)
200	PSO (0.1151 ± 0.0097)	FHO (0.1153 ± 0.0096)	MRFO (0.1204 ± 0.0100)
250	PSO (0.1091 ± 0.0068)	FHO (0.1092 ± 0.0068)	MRFO (0.1145 ± 0.0071)
300	PSO (0.1043 ± 0.0072)	FHO (0.1045 ± 0.0072)	MRFO (0.1099 ± 0.0070)
Topology: Square Grid
Node Count	1st	2nd	3rd
100	PSO (0.0923 ± 0.0098)	FHO (0.0933 ± 0.0091)	SCA (0.1007 ± 0.0098)
150	PSO (0.1059 ± 0.0123)	FHO (0.1061 ± 0.0120)	MRFO (0.1131 ± 0.0126)
200	PSO (0.0794 ± 0.0077)	FHO (0.0800 ± 0.0076)	MRFO (0.0888 ± 0.0085)
250	FHO (0.0907 ± 0.0065)	PSO (0.0909 ± 0.0068)	MRFO (0.0971 ± 0.0072)
300	PSO (0.0916 ± 0.0056)	FHO (0.0918 ± 0.0056)	MRFO (0.0987 ± 0.0057)
Topology: S-Shape
Node Count	1st	2nd	3rd
100	VCS (0.5541 ± 0.0565)	FHO (0.5855 ± 0.0554)	MRFO (0.5856 ± 0.0547)
150	VCS (0.5590 ± 0.0436)	MRFO (0.5894 ± 0.0500)	FHO (0.5899 ± 0.0514)
200	VCS (0.5581 ± 0.0449)	MRFO (0.5888 ± 0.0499)	FHO (0.5890 ± 0.0507)
250	VCS (0.5407 ± 0.0334)	FHO (0.5675 ± 0.0394)	MRFO (0.5676 ± 0.0394)
300	VCS (0.5430 ± 0.0275)	FHO (0.5718 ± 0.0285)	MRFO (0.5721 ± 0.0285)

.

The experimental results shown in Table 7 and Figure 6 offer a detailed assessment of how changes in the total node count affect localization accuracy under various network topologies. As node density increases from 100 to 300, most algorithms experience a notable decline in ALE, indicating improved spatial resolution and network connectivity. This behavior reflects the scalability and robustness of algorithms when deployed in larger WSNs. Across all topologies, the FHO consistently ranks among the top performers, highlighting its adaptability and precision. FHO maintains a commanding lead in the Random topology, outperforming all other methods at every node count level. Its ALE values drop steadily from 0.1813 ± 0.0288 at 100 nodes to 0.1097 ± 0.0071 at 300 nodes, demonstrating excellent scalability. The consistent margin by which FHO surpasses competitors like PSO and MRFO underlines its strong generalization capability in unstructured environments. In the Circular topology, PSO slightly edges out FHO in all configurations; however, the difference remains marginal (e.g., at 300 nodes, PSO: 0.1043 ± 0.0072 vs. FHO: 0.1045 ± 0.0072). This near parity suggests that FHO retains high precision in symmetric and uniformly distributed node arrangements. Notably, FHO’s performance scales reliably with network size, retaining its second-place position with minimal standard deviation. For the Square Grid topology, PSO again dominates, but FHO closely follows with nearly indistinguishable results. At 300 nodes, FHO achieves a normalized ALE of 0.0918 ± 0.0056 compared to PSO’s 0.0916 ± 0.0056. This tight performance margin highlights FHO’s effectiveness in structured environments, where deterministic connectivity patterns enable high localization accuracy. The S-shape topology poses a more complex scenario due to its irregular and asymmetric layout. In this setting, VCS slightly outperforms FHO and MRFO, particularly at lower node counts. However, FHO consistently holds a top-three position across all configurations. For example, at 250 and 300 nodes, FHO’s normalized errors are 0.5675 ± 0.0394 and 0.5718 ± 0.0285, respectively—very close to the best-performing algorithm, VCS. These results demonstrate FHO’s robustness even under challenging deployment geometries.

Overall, FHO appears in the top three rankings for all topologies and node counts (20 out of 20 cases), securing first place in 6, second in 12, and third in 2 instances. This level of consistency underscores FHO’s exceptional scalability, resilience to deployment irregularities, and suitability for real-world localization tasks. While certain algorithms like PSO and VCS may excel in specific structured settings, FHO’s across-the-board reliability makes it a superior choice for range-free localization in diverse WSN environments.

5.5. Effect of Varying Population Size on ALE

In nature-inspired optimization algorithms, the population size (nPop) is a key factor in maintaining a balance between exploration and exploitation throughout the search process. Within the scope of range-free localization in WSNs, choosing an appropriate population size is especially important, as it significantly impacts both the accuracy and convergence characteristics of the position estimation procedure. In WSNs, evaluating the sensitivity of ALE to changes in nPop is essential not only for performance optimization but also for understanding the algorithm’s scalability and computational efficiency. A robust algorithm is expected to maintain high localization accuracy even as the population size varies—minimizing the need for extensive tuning in practical deployments. This characteristic is particularly relevant for energy- and resource-constrained WSN environments, where computational budgets are limited and runtime scalability is critical [67].

Figure 7 illustrates the ALE variation of different metaheuristic optimization approaches applied to the DV-Hop range-free localization technique with respect to the population size. In this experiment, the total number of nodes is 100, the AN ratio is 30%, and the CR is 25. The experimental analysis across four distinct topologies—random, circular, square grid, and S-shape—reveals that among the evaluated methods, the FHODV-Hop algorithm exhibits exceptional robustness to changes in population size. Unlike most algorithms whose ALE fluctuates with increasing nPop, FHO consistently maintains a nearly flat performance curve across all topologies, with ALE values showing minimal change from nPop = 5 to nPop = 50. This stability is particularly notable in the other three topologies except the S-shape, where FHO’s normalized ALE remains almost unchanged over the entire range of tested population sizes. Such behavior demonstrates the algorithm’s insensitivity to population scaling and its capacity to deliver reliable localization results without requiring parameter fine-tuning.

Importantly, while FHO performs quite consistently across all tested population sizes (reaching nearly optimal ALE values even when nPop = 5 and smaller), several other competitive algorithms, such as PSO, MRFO, and VCS, start to improve significantly after the population size exceeds about 20. In these mid-to-high population regimes (nPop ≥ 20), certain high-performing algorithms—such as PSO, MRFO, and VCS—begin to exhibit localization accuracy that is virtually indistinguishable from that of FHO in most topologies. This convergence becomes particularly evident beyond nPop = 20, where their normalized ALE values consistently align with those of FHO across the remaining population range. For instance, in structured topologies like Circular and Square Grid, PSO and MRFO maintain low and stable ALE values that mirror FHO’s performance from nPop = 20 onward. However, it is important to emphasize that while these algorithms converge in terms of mean localization error, they do not always replicate FHO’s robustness in terms of stability across runs or topologies. In complex and irregular layouts such as the S-shape, PSO, MRFO, and VCS also display stable localization performance beyond nPop = 20, with relatively minor variations across increasing population sizes. However, FHO still stands out by achieving this stability earlier and maintaining a consistently low error profile across the entire population range, further highlighting its robustness to topological complexity and population scaling.

From a practical standpoint, FHO’s invariance to population size substantially reduces the complexity of hyperparameter tuning, thereby enhancing its suitability for real-world WSN deployments. Notably, this robustness is not achieved at the expense of accuracy. On the contrary, FHO consistently delivers top-tier localization performance across all population sizes and topological configurations, reinforcing its adaptability and scalability as a range-free solution. This convergence behavior is clearly illustrated in Figure 7, where FHO achieves its optimal ALE values at very low population sizes (as early as nPop < 5) and maintains this accuracy stably throughout the entire nPop range. FHO has a deterministic and adaptive structure, where each individual directly seeks the best solution when updating its position. This approach reduces the need for variation due to population size, enabling early convergence. Furthermore, because local exploitation capacity is strong, the need for exploration can be limited. This allows for near-optimal solutions to be generated even in small populations. In comparison, while other strong algorithms—such as PSO, MRFO, and VCS—tend to converge after nPop ≥ 20, their early-stage variability and occasional sensitivity to network topology distinguish FHO as the more dependable option under diverse deployment conditions.

In addition to its invariance to population size, FHO’s rapid convergence at low nPop values implies limited sensitivity to the maximum number of iterations. Optimal ALE values are typically reached well before the iteration limit, confirming that FHODV-Hop is robust to both population and iteration settings.

5.6. Effect of Varying AN Rates on Localization Ratio

Localization ratio is a critical performance indicator that reflects the percentage of UNNs successfully localized within a network. It serves as a measure of algorithm robustness and practical applicability, particularly in sparse or irregular deployments. This metric is influenced by factors such as the AN density and the network topology, and is commonly used to evaluate the effectiveness of localization schemes under varying conditions. By analyzing the localization ratio across different AN rates, one can assess the scalability and reliability of the proposed method in real-world WSN scenarios.

A threshold-based approach is employed to distinguish between nodes that are successfully localized and those that are not, enabling the evaluation of the localization ratio. Following the execution of the localization algorithm, each estimated position is compared to the corresponding true position. If the Euclidean distance between them exceeds a specified threshold, the node is deemed not localized; otherwise, it is classified as successfully localized. In this study, a node is considered successfully localized if the error remains within 20% of the CR. The experimental setup consisted of a WSN comprising 100 nodes deployed within the sensing field, with a fixed communication radius of 30 m. To assess the scalability and effectiveness of the proposed algorithm under varying AN densities, the AN ratio was systematically adjusted from 10% to 90%. This configuration enabled a thorough evaluation of the algorithm’s localization performance across different levels of reference node availability.

The findings presented in Figure 8 provide an analysis of how varying the AN ratio affects the localization rate in different topologies. The evaluation across diverse topologies reveals the substantial influence of AN density and network geometry on localization performance. All metaheuristic algorithms benefit noticeably from increased AN rates in the random topology. FHO demonstrates an early advantage with 44.64% localization at just 10% AN density and maintains this lead at 90% with 72.80%, slightly outperforming PSO and MRFO. In contrast, DV-Hop and BA lag considerably, peaking at only 29.60% and 15.60%, respectively, underscoring their limited adaptability in unstructured environments. In the circular topology, the relative rankings remain consistent. PSO reaches a marginally higher peak of 84.80%, closely followed by FHO at 84.40%. FHO’s accuracy improves steadily from 49.58% to the top level, indicating stable convergence even in symmetric layouts. Traditional methods again underperform; while DV-Hop reaches 34.40%, BA shows an unresponsive behavior to increasing AN density, reflecting its inconsistency in regular topologies.

The square topology further reinforces the effectiveness of metaheuristic methods. Both PSO and FHO reach complete localization (100%) at the highest AN level, with FHO progressing from 65.27% at the lowest AN ratio. MRFO and SCA also perform reliably, exceeding 97% from 60% ANs onward. Meanwhile, VCS shows moderate improvement but plateaus at 79.13%, suggesting less affinity for grid-like structures. DV-Hop and BA continue to trail behind, with maximum localization ratios of only 36.00% and 18.00%, respectively. The S-shape topology presents the most complex scenario due to its geometric irregularity and fragmented connectivity. All algorithms experience reduced localization ratios; nonetheless, metaheuristic approaches retain a clear edge. FHO maintains stable and competitive results across AN rates, with values generally ranging between 5.80% and 6.60%, and peaking at 8.80% at 80% AN density. VCS occasionally surpasses others, achieving a maximum of 9.50%, but displays higher variability. MRFO and SCA produce results in a similar range to FHO, indicating a shared resilience in complex layouts. DV-Hop, by contrast, rarely exceeds 2%, and BA, while occasionally reaching high values like 9.20%, fails to show a consistent trend.

Overall, the results emphasize the advantages of metaheuristic algorithms under varying spatial configurations. Among them, FHO consistently performs near the top across all scenarios, demonstrating strong generalization ability without requiring topology-specific tuning.

5.7. Average Computational Cost Analysis

A comprehensive evaluation of localization algorithms requires examining both empirical runtime behavior and theoretical computational complexity. In resource-constrained environments such as WSNs, a method must not only achieve high localization accuracy but also operate within practical time and energy limits. For this reason, average computational cost analysis—commonly expressed in execution time—serves as a key metric for assessing an algorithm’s efficiency and applicability to real-time or energy-sensitive deployments.

However, execution time alone may not fully reveal how an algorithm scales as the network grows or as the optimization settings change. Therefore, this study complements empirical runtime measurements with a theoretical complexity analysis of each method’s Step-3 estimation phase. While runtime reflects the algorithm’s real-world responsiveness under a given setup, complexity analysis offers a more abstract but generalized view of its intrinsic computational demands. These dual perspectives provide a deeper understanding of the trade-offs between localization accuracy and processing overhead. Accordingly, this section presents a comparative analysis of the average computational cost—both measured and theoretical—for various metaheuristic techniques integrated into the DV-Hop framework. The analysis of average computational cost further strengthens the position of FHO as a well-balanced and robust localization strategy.

5.7.1. Average Computational Time and Energy Consumption Analysis

The results of the execution time are shown in Figure 9. These results were obtained by averaging 50 run repetitions in an environment with a total number of nodes of 100, an AN ratio of 30%, and a CR of 25%.

With an average execution time of 0.2108 s, FHO achieves a notable balance between computational efficiency and localization accuracy. Although SCA (0.1879 s) and VCS (0.1936 s) show slightly lower average runtimes, their overall localization accuracy across different topologies and AN rates remains inferior, suggesting that their faster execution comes at the cost of reduced estimation quality. FHO consistently ranks among the top in terms of localization precision while also maintaining stable computational behavior, as reflected by its low STD (0.0322 s). This reliability is particularly important in real-time or resource-limited WSNs. Algorithms like PSO (0.3155 s, std = 0.0465 s) and MRFO (0.6165 s, std = 0.0975 s), despite their widespread use, demonstrate higher computational demands and variability, which may hinder scalability in practical deployments.

The error bars in the corresponding runtime figure visualize these standard deviations, highlighting FHO’s predictable performance. Meanwhile, PSO, despite its competitive performance in structured environments, suffers from a significantly higher runtime, which limits its applicability in time-sensitive or resource-constrained deployments.

Using the measured runtime of 0.2108 s, the computational energy of FHODV-Hop can be quantified on TelosB-class motes. The MSP430F1611 microcontroller consumes ≈ 330 µA/MHz; at 8 MHz this corresponds to 2.64 mA [68]. With a 3 V supply, the compute-only energy is therefore E = 3 V × 2.64 mA × 0.2108 s ≈ 1.67 mJ. In a pessimistic case where the CC2420 radio remains in continuous RX mode (18.8 mA) [69], the total current rises to ≈ 21.4 mA, yielding E = 3 V × 21.4 mA × 0.2108 s ≈ 13.6 mJ. Both values fall well within the energy budget of TelosB motes powered by AA batteries, whose capacity is typically in the range of 5–8 Wh [70], confirming the feasibility of FHODV-Hop under realistic deployment conditions. FHO’s linear memory footprint (<1 kB for typical nPop = 20) and parameter-free update rule indicate energy- and memory-feasible operation on constrained WSN hardware, consistent with the low-variance runtimes reported in this section.

Taken together, the results confirm FHO as a computationally efficient and consistently accurate solution, outperforming alternatives not just in estimation quality, but also in runtime consistency—key factors for real-world WSN applications.

5.7.2. Theoretical Computational Complexity Analysis

Since step 1 (hop count propagation) and step 2 (average hop distance estimation) of the DV-Hop algorithm are implemented identically across all methods, the difference in computational cost arises exclusively from step 3, where the positions of UNNs are estimated. In the baseline DV-Hop approach, this step is handled using a linearized LS solution. Each UNN solves a set of equations based on its estimated distances to known ANs. Solving the resulting normal equations involves matrix inversion, yielding a per-node computational complexity of approximately O(k³), and a total cost of O(U·k³) across the network. Here, U denotes the number of UNNs and k the number of ANs used per estimate.

In FHODV-Hop, Step 3 is replaced by node-wise optimization using the FHO. Each UNN is optimized independently over M iterations using a population of n_pop candidate solutions. The fitness of each candidate is calculated based on its estimated distance errors with respect to k ANs. This yields a per-node complexity of O(M·n_pop·k), and a total cost of O(U·M·n_pop·k) for the network. Memory usage grows linearly with the population size per node, and full population sorting is avoided due to best-agent tracking.

Although all compared metaheuristics (PSO, MRFO, SCA, VCS, SSA, BA) share the same fitness evaluation structure and thus belong to the same asymptotic complexity class, they differ notably in their parametrization and update overheads. Several methods rely on multiple control parameters—such as inertia weights, adaptive learning coefficients, or frequency terms—which increase the constant-factor cost per iteration. In contrast, FHO’s parameter-free structure eliminates this computational burden, leading to simpler iterations and reducing both execution time and deployment effort. A summary of Step-3 computational characteristics across algorithm families is provided in

Table 8. Summary of Step-3 Computational Characteristics by Algorithm Class.

Algorithm Type	Representative Methods	Complexity	Parametrization	Practical Overhead
Deterministic (Baseline)	DV-Hop (LS)	O(U·k3)	None	Very low (matrix-based)
Parameter-Free Metaheuristic	FHO	O(U·M·npop·k)	None	Low (simple updates, no tuning)
Low-Parameter Metaheuristics	SCA, SSA	O(U·M·npop·k)	1–2 parameters	Moderate (lightweight updates)
High-Parameter Metaheuristics	PSO, MRFO, VCS, BA	O(U·M·npop·k)	3–5+ parameters	High (multiple updates and tuning steps)

, highlighting their complexity class, parameter requirements, and practical implications:

In summary, while all metaheuristic-based methods scale linearly with the number of UNNs under fixed M, n_pop, and k, the internal design of FHO offers a clear advantage. Its lightweight update mechanism and zero tuning requirement result in faster and more stable performance within the same complexity class, making FHODV-Hop a highly scalable and robust alternative for large-scale WSN localization tasks. These advantages are consistently reflected in both the average computational time analysis and the theoretical computational complexity assessment, where FHO demonstrates coherent improvements over its counterparts. Moreover, the overall findings show that the two types of analyses complement and reinforce each other, further validating the reliability of the proposed approach.

5.8. Statistical Significance Analysis Using t-Tests

To assess statistical significance, independent two-sample t-tests (Welch’s correction, without assuming equal variances) were conducted by taking FHODV-Hop as the reference algorithm. In addition to significance testing, we also computed effect sizes (Cohen’s d) and 95% confidence intervals (CIs) for the mean differences between FHODV-Hop and the baseline algorithms, thereby quantifying both the magnitude and precision of the observed effects. This approach ensured a rigorous comparison of ALE values obtained under varying numbers of UNNs. As presented in

Table 9. Statistical comparison (t-tests) of FHODV-Hop against other algorithms based on ALE under varying numbers of UNNs, including effect sizes (Cohen’s d) and 95% confidence intervals.

Topology	Algorithm vs. FHO	p-Value	Cohen’s d	95% CI
Random	DV-Hop	1.94 × 10−5	−0.93	[−10.11, −0.73]
	PSO	9.87 × 10−1	−0.01	[−3.46, 3.41]
	MRFO	9.02 × 10−1	−0.04	[−3.62, 3.30]
	SCA	8.16 × 10−1	−0.06	[−3.69, 3.14]
	VCS	5.34 × 10−1	−0.18	[−4.06, 2.59]
	SSA	7.71 × 10−11	−2.05	[−10.73, −4.71]
	BA	2.06 × 10−8	−1.76	[−9.26, −3.48]
Circular	DV-Hop	1.52 × 10−4	−1.17	[−7.92, −1.49]
	PSO	9.93 × 10−1	−0.00	[−2.77, 2.77]
	MRFO	9.27 × 10−1	−0.04	[−2.88, 2.64]
	SCA	8.30 × 10−1	−0.07	[−2.99, 2.49]
	VCS	8.21 × 10−1	−0.07	[−2.96, 2.46]
	SSA	2.78 × 10−11	−2.28	[−9.39, −4.51]
	BA	7.92 × 10−10	−2.17	[−8.61, −3.98]
Square	DV-Hop	1.21 × 10−3	−2.77	[−7.06, −3.90]
	PSO	9.98 × 10−1	0.03	[−0.73, 0.80]
	MRFO	9.28 × 10−1	−0.18	[−0.94, 0.60]
	SCA	9.01 × 10−1	−0.23	[−0.96, 0.53]
	VCS	3.76 × 10−1	−1.52	[−2.84, −0.88]
	SSA	1.82 × 10−7	−8.33	[−10.58, −8.73]
	BA	4.87 × 10−6	−8.39	[−9.32, −7.69]
S-shape	DV-Hop	4.81 × 10−12	−17.05	[−21.68, −19.74]
	PSO	8.60 × 10−1	−0.20	[−0.31, 0.18]
	MRFO	9.81 × 10−1	0.06	[−0.22, 0.26]
	SCA	9.58 × 10−1	−0.09	[−0.27, 0.21]
	VCS	4.39 × 10−1	1.96	[0.42, 1.00]
	SSA	2.38 × 10−18	−13.88	[−5.14, −4.58]
	BA	6.04 × 10−4	−5.25	[−1.86, −1.37]

, FHODV-Hop demonstrates statistically significant improvements over the baseline DV-Hop algorithm across all topologies (p < 0.001). For example, in the Random topology, FHODV-Hop vs. DV-Hop yielded Cohen’s d = −0.93 with a 95% CI [−10.11, −0.73], which constitutes a large effect size according to Cohen’s benchmark. Similar strong effect sizes were obtained across the other topologies (all d < −0.80), further reinforcing the robustness of the observed improvements. It also consistently outperforms SSA and BA (p < 0.001), confirming its robustness compared to these metaheuristics. These results were associated with medium-to-large effect sizes (Cohen’s d < −0.80 in most cases), and the 95% CIs did not cross zero, indicating that the superiority of FHODV-Hop is not only statistically significant but also practically meaningful.

When compared with widely recognized optimizers such as PSO, MRFO, SCA, and VCS, no statistically significant differences were observed (p > 0.05). Consistently, the effect sizes for these comparisons were close to zero and the 95% CIs crossed zero, confirming that the differences are negligible in practical terms. This indicates that FHODV-Hop consistently achieves performance at least comparable to, and in several cases exceeding, that of these state-of-the-art methods. In addition, FHODV-Hop preserves the distinctive advantage of being parameter-free, which eliminates the need for manual tuning and enhances adaptability in practical deployments.

Beyond this core test, other experimental analyses conducted under diverse network settings (e.g., AN density, population size, and CR variations) produced similar conclusions, reinforcing that FHODV-Hop maintains its robustness and competitiveness across a broad range of conditions. Since these findings align with the results reported in Table 9, they are not reproduced in detail here for brevity. For instance, under increased CR values, FHODV-Hop consistently retained statistically significant advantages over DV-Hop with large effect sizes.

6. Conclusions and Future Work

6.1. Study Limitations and Discussions

This study proposed an enhanced range-free localization framework, FHODV-Hop, which integrates the FHO into the third phase of the classical DV-Hop algorithm. The objective was to improve localization accuracy without relying on range-based distance measurements, thereby ensuring applicability in cost-sensitive and energy-constrained WSNs. The proposed algorithm was rigorously evaluated under multiple network conditions and benchmarked against both the original DV-Hop and several well-established metaheuristic-based variants.

Simulation results across four canonical topologies—random, circular, square grid, and S-shaped—demonstrated that FHODV-Hop consistently achieves lower ALE and higher localization success rates. In particular, when compared to the baseline DV-Hop algorithm, FHODV-Hop yields significant performance gains. For instance, under standard conditions, the proposed method reduces ALE by approximately 44% to 60%, depending on the topology and AN density. This considerable improvement illustrates FHO’s ability to guide the search process more effectively toward optimal node positions, even in complex and irregular deployment scenarios.

In addition to delivering accurate results, FHODV-Hop exhibits favorable computational properties. Although based on an optimization process, it maintains competitive execution times and demonstrates low variance across repeated runs, highlighting both efficiency and robustness. Its consistent behavior under different node densities and CRs indicates strong scalability for practical WSN deployments, while dependable accuracy at low AN ratios emphasizes its suitability for cost-sensitive scenarios. Furthermore, its parameter-free design eliminates the need for manual configuration, enhancing adaptability and making it particularly valuable in contexts where reliability and ease of implementation are essential.

At the same time, we acknowledge that, like other DV-Hop enhancements, FHODV-Hop cannot fully eliminate the hop-size bias of the original algorithm. Its accuracy remains affected by AN density and spatial distribution, which may cause fluctuations in irregular or sparse networks. While these limitations indicate that some weaknesses of DV-Hop persist, they are modest compared to the improvements in accuracy, efficiency, and stability introduced by the FHO-based enhancement. Taken together, FHODV-Hop offers a balanced trade-off between practicality and performance, reinforcing its value as a low-cost, scalable, and reliable localization solution for WSNs.

Beyond simulation outcomes, the findings of this study have direct implications for real-world biomimetic and engineering contexts. Accurate and low-cost localization is essential in applications such as environmental monitoring, precision agriculture, industrial automation, and swarm robotics, where large numbers of nodes must operate autonomously under limited energy and hardware resources. By eliminating parameter tuning and ensuring stable performance across diverse network conditions, FHODV-Hop reduces deployment complexity and accelerates adaptation to dynamic environments. In biomimetic design, where systems often emulate collective intelligence and robustness found in nature, the parameter-free and cooperative search dynamics of FHO align closely with principles of adaptability and self-organization. These properties make FHODV-Hop a strong candidate for large-scale, real-time deployments in WSNs and related biomimetic systems.

Also, this study directly fulfills its original aim by showing that the integration of FHO into DV-Hop enhances localization accuracy while preserving low-cost and parameter-free operation. The consistent performance across different topologies and AN densities confirms that FHODV-Hop achieves a balanced trade-off between practicality and innovation, thereby validating the novelty claims outlined in the introduction and positioning it as a meaningful advancement over existing DV-Hop-based methods.

An additional set of challenges arises when considering the transition from controlled simulations to practical deployments. First, the communication overhead of metaheuristic-driven localization may become non-negligible, since repeated message exchanges can strain bandwidth in dense or resource-limited networks, potentially constraining scalability. Second, real deployments are inherently exposed to packet loss; missing hop-count or distance data may lead to unstable or biased position estimates, and FHODV-Hop’s resilience under such conditions requires further validation. Finally, most current evaluations, including ours, are confined to two-dimensional layouts, whereas many emerging applications—such as UAV swarms, underwater sensor arrays, and smart buildings—demand reliable operation in three-dimensional spaces. Extending FHODV-Hop to such scenarios while keeping accuracy and efficiency intact represents a key step toward real-world applicability.

Notably, in the S-shape topology, FHODV-Hop achieved lower relative gains than other scenarios. This can be attributed to the irregular geometry and long curved paths of the topology, which amplify hop-size bias and introduce uneven anchor-to-node distances. These structural factors inherently limit the accuracy of hop-based multilateration, explaining why FHODV-Hop, despite improving over DV-Hop, did not outperform all competing optimizers in this specific case.

These limitations highlight not only the persistent challenges of DV-Hop but also the directions where future hybrid strategies—such as combining statistical hop-size correction with metaheuristic optimization—could yield further accuracy gains.

6.2. Future Research Directions

For future possible works, several promising research directions emerge. For example:

• The use of VCS and MRFO metaheuristics to improve the performance of DV-Hop and similar localization techniques can be further investigated.
• In particular, the superior performance achieved by VCS on irregular topologies such as the S-shape, highlighted by the results obtained in this study, remains a research topic that deserves detailed investigation.
• A natural next step is to mitigate the hop-size bias of DV-Hop more explicitly. Hybrid approaches that integrate statistical correction mechanisms (e.g., average hop-size refinement) with optimization-based position estimation could address this limitation more effectively, improving both robustness and scalability.
• Extending the algorithm to three-dimensional environments could address localization challenges in UAV-based sensing or underwater sensor networks.
• Future research should systematically investigate the communication burden introduced by optimization-driven localization in dense or bandwidth-constrained sensor networks and assess FHODV-Hop’s tolerance to packet loss under realistic conditions. Such analyses would provide a clearer understanding of the algorithm’s robustness and scalability, thereby facilitating its transition from simulation environments to practical large-scale deployments.
• Incorporating energy awareness into the optimization objective may further enhance the algorithm’s practicality in resource-limited contexts.
• Additionally, adopting multi-objective optimization strategies could enable simultaneous minimization of ALE and energy consumption.
• As a natural extension, future work will systematically evaluate other parameter-free optimizers—such as TLBO and Jaya—within the same unified DV-Hop Step-3 framework. This comparative analysis will further clarify the role of parameter-free designs relative to low- and high-parameter metaheuristics, thereby deepening insights into their practical value for range-free WSN localization.
• Finally, integrating learning-based dynamic parameter control may improve convergence behavior under rapidly changing network conditions.

These directions open the door for even more intelligent and adaptive localization systems in future WSN applications.