Two-Party Quantum Private Comparison Protocol for Direct Secret Comparison

Abstract

In this paper, we leverage the properties of the swap test to evaluate the similarity of two qubits and propose a two-party quantum private comparison (QPC) protocol involving a semi-trusted third party (TP). The TP facilitates the comparison between participants without accessing their private information, other than the final comparison results. Our protocol encodes participants’ secret integers directly into the amplitudes of single-photon states and introduces a novel method for secret-to-secret comparison rather than the traditional bit-to-bit comparison, resulting in improved scalability. To ensure security, the encoded single-photon states are concealed using rotation operations. The comparison results are derived through the implementation of the swap test. A simulation on the IBM Quantum Platform demonstrates the protocol’s feasibility, and a security analysis confirms its robustness against potential eavesdropping and participant attacks. Compared with existing QPC protocols that employ bit-to-bit comparison methods, our approach offers improved practicality and scalability. Specifically, it integrates single-photon states, rotation operations, and the swap test as key components for direct secret comparison, facilitating easier implementation with quantum technology.

1. Introduction

Quantum information science has progressed significantly, particularly in quantum cryptography, which utilizes quantum mechanics for enhanced security compared with classical methods that depend on mathematical complexity. Following Bennett and Brassard’s introduction of the first unconditional quantum cryptographic protocol in 1984 [1], a variety of protocols have been developed to tackle different cryptographic tasks, including quantum key distribution (QKD) [2,3,4,5,6], quantum secret sharing (QSS) [7,8,9,10], quantum key agreement (QKA) [11,12], quantum secure direct communication (QSDC) [13,14,15,16], and quantum private set intersection (QPSI) [17,18,19,20].

Secure multiparty computation (MPC) is a cryptographic framework that enables multiple parties to compute a function collaboratively while keeping their inputs confidential. A key development in this area is the private comparison proposed by Yao in the context of the millionaires’ problem [21], which allows two millionaires to determine who is wealthier without disclosing their actual wealth. Boudot et al. [22] later expanded this concept to the socialist millionaires’ problem, where two parties seek to establish whether their wealth is equal without revealing specific amounts. This issue has garnered significant attention in the cryptographic community, leading to various privacy-enhancing solutions. However, Lo [23] identified a significant limitation in two-party settings: it is fundamentally impossible to securely evaluate a computational function without compromising privacy. To overcome this challenge, the involvement of a semi-honest third party (TP) is crucial. The TP facilitates secure comparisons while potentially attempting to glean information about the participants’ inputs.

The security of private comparison protocols relies on unproven mathematical assumptions, making them susceptible to threats from quantum computers, which exploit quantum mechanics for efficient parallel computation. Notably, the Shor algorithm [24] can factor large integers in polynomial time, rendering classical public-key cryptographic systems like RSA vulnerable to quantum attacks. Additionally, the Grover algorithm [25] poses a significant risk to symmetric-key cryptography by enabling faster search and function inversion, effectively reducing the effective key length of symmetric algorithms by half. In response to these vulnerabilities, quantum private comparison (QPC) has been developed. QPC utilizes quantum mechanics to enhance security features, ensuring that sensitive information remains confidential throughout the comparison process.

The first quantum private comparison (QPC) protocol was developed by Yang and Wen [26], utilizing EPR pairs for quantum information transmission along with decoy photons and a one-way hash function for security. Since then, various QPC protocols have emerged, employing different quantum states such as single particles [27,28,29,30,31,32], Bell states [33,34,35,36,37,38,39,40], and multi-particle entangled states [41,42,43,44,45,46,47,48,49,50,51,52,53]. Beyond merely comparing equality, researchers have also explored protocols for comparing the sizes of secret integers. For instance, Lin et al. [54] proposed a size comparison QPC protocol using d-level Bell states, while Guo et al. [55] utilized entanglement swapping of d-level Bell states. Yu et al. [56] introduced a similar protocol with d-level single-particle states, and Ye and Ye [57] presented two multiparty QPC protocols involving one or two semi-honest TPs. Additionally, Song et al. [58] developed an multiparty quantum private comparison (MQPC) using single-particle states.

The swap test [59], a fundamental algorithm in quantum computing, has become a key focus in the development of quantum cryptographic protocols. Its primary objective is to assess the similarity between two qubits. By measuring the probability of the ancilla qubit being in the $\left|1\right.⟩$ or $\left|0\right.⟩$ state, the square of the inner product of the two qubits is determined. Building on the principles of the swap test, various applications such as quantum signatures [60], quantum machine learning [61], and the blind millionaires’ problem [62] have been proposed.

The previously discussed QPC protocols focus on converting secret integers into binary representations and comparing these classical bits (0 or 1) using a bit-by-bit approach, which inherently limits their scalability. Additionally, many existing QPC protocols employ multi-qubit states and d-dimensional states, which further constrain their practicality due to the complexities associated with manipulating these states. To overcome these limitations, we propose a two-party quantum private comparison (QPC) protocol that utilizes the swap test to evaluate the similarity of two encoded qubits. This process involves a semi-honest third party (TP) who facilitates the comparison between participants without accessing their private information, except for the final comparison results. In our protocol, the two participants encode their secret integers directly into the amplitudes of single-photon states through rotation operations, significantly enhancing scalability by eliminating the need for binary representations. The encoded single-photon states are secured through these rotation operations before being sent to the TP, who then derives the comparison results using the swap test. A simulation conducted on the IBM Quantum Platform confirms the feasibility of our protocol, and security analysis demonstrates its resilience against potential eavesdropping and participant attacks. Compared with existing QPC protocols that rely on bit-by-bit comparison methods, our approach offers improved practicality and scalability. Specifically, it integrates single-photon states, rotation operations, and the swap test as essential components for direct secret comparison, making it easier to implement with modern technology.

The remainder of this paper is structured as follows. Section 2 introduces the swap test and rotation operation. A detailed description of the proposed QPC protocol is provided in Section 3. Section 4 and Section 5 present the simulation and analysis, respectively. Section 6 offers a comparison with existing protocols, and, finally, Section 7 concludes the paper.

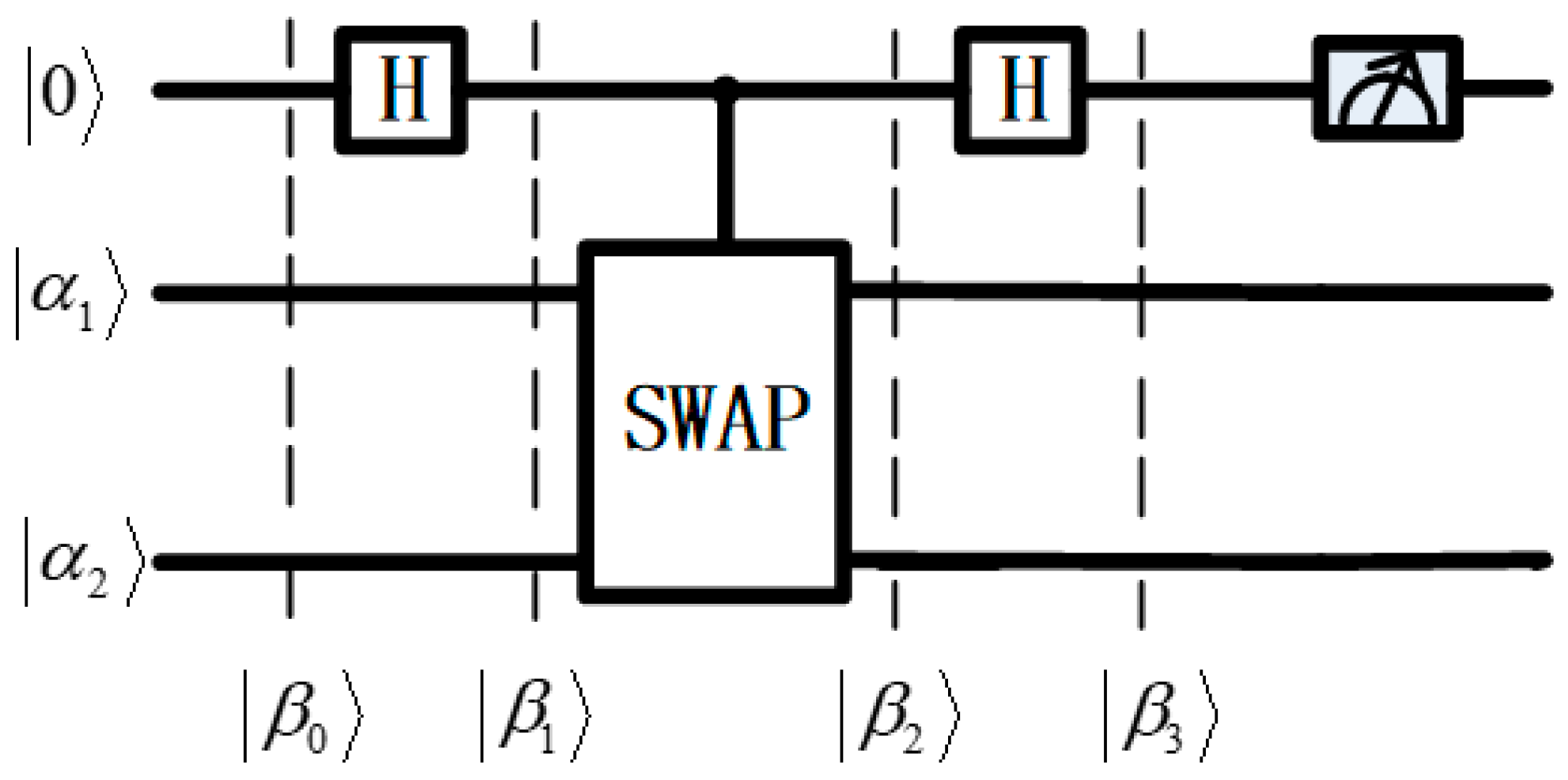
2. Swap Test and Rotation Operation

2.1. Swap Test

The swap test was first introduced in [59] and is designed to assess the similarity between two arbitrary qubits. By measuring the probability that the ancilla qubit is in either state |1⟩ or state |0⟩, we can determine the square of the inner product of the two qubits [63]. The quantum circuit implementing the swap test is illustrated in Figure 1.

The initial quantum states are composed by two quantum states $\left|{\alpha }_1\right.⟩$ and $\left|{\alpha }_2\right.⟩$, as well as an ancillary state $\left|0\right.⟩$. That is,

$$\left|{\beta }_0\right.〉=\left|0\right.〉\otimes \left|{\alpha }_1\right.〉\otimes \left|{\alpha }_2\right.〉=\left|0,{\alpha }_1,{\alpha }_2\right.〉$$

(1)

When performing a Hadamard operation on the ancillary state $\left|0\right.⟩$, the initial quantum state $\left|{\beta }_0\right.⟩$ is converted as

$$\left|{\beta }_1\right.〉=\left(H\otimes I\otimes I\right)\left|{\beta }_0\right.〉={\displaystyle \frac{1}{\sqrt{2}}}\left(\left|0\right.〉+\left|1\right.〉\right)\otimes \left|{\alpha }_1\right.〉\otimes \left|{\alpha }_2\right.〉={\displaystyle \frac{1}{\sqrt{2}}}\left(\left|0,{\alpha }_1,{\alpha }_2\right.〉+\left|1,{\alpha }_1,{\alpha }_2\right.〉\right)$$

(2)

When performing the controlled-swap gate where the ancillary is the control qubit, $\left|{\beta }_1\right.⟩$ is transformed into

$$\left|{\beta }_2\right.〉={\displaystyle \frac{1}{\sqrt{2}}}\left|0\right.〉\otimes \left|{\alpha }_1\right.〉\otimes \left|{\alpha }_2\right.〉+{\displaystyle \frac{1}{\sqrt{2}}}\left|1\right.〉\otimes \left|{\alpha }_2\right.〉\otimes \left|{\alpha }_1\right.〉={\displaystyle \frac{1}{\sqrt{2}}}\left(\left|0,{\alpha }_1,{\alpha }_2\right.〉+\left|1,{\alpha }_2,{\alpha }_1\right.〉\right)$$

(3)

When performing the Hadamard operation on the ancillary state $\left|0\right.⟩$ again, $\left|{\beta }_2\right.⟩$ is converted as

$$\begin{array}{ll}\left|{\beta }_3\right.〉& =\left(H\otimes I\otimes I\right)\left|{\beta }_2\right.〉={\displaystyle \frac{1}{\sqrt{2}}}\left({\displaystyle \frac{\left|0\right.〉+\left|1\right.〉}{\sqrt{2}}}\otimes \left|{\alpha }_1\right.〉\otimes \left|{\alpha }_2\right.〉+{\displaystyle \frac{\left|0\right.〉-\left|1\right.〉}{\sqrt{2}}}\otimes \left|{\alpha }_2\right.〉\otimes \left|{\alpha }_1\right.〉\right)\\ & ={\displaystyle \frac{1}{2}}\left|0\right.〉\otimes \left|{\alpha }_1\right.〉\otimes \left|{\alpha }_2\right.〉+{\displaystyle \frac{1}{2}}\left|1\right.〉\otimes \left|{\alpha }_1\right.〉\otimes \left|{\alpha }_2\right.〉+{\displaystyle \frac{1}{2}}\left|0\right.〉\otimes \left|{\alpha }_2\right.〉\otimes \left|{\alpha }_1\right.〉-{\displaystyle \frac{1}{2}}\left|1\right.〉\otimes \left|{\alpha }_2\right.〉\otimes \left|{\alpha }_1\right.〉\\ & ={\displaystyle \frac{1}{2}}\left|0\right.〉\left(\left|{\alpha }_1,{\alpha }_2\right.〉+\left|{\alpha }_2,{\alpha }_1\right.〉\right)+{\displaystyle \frac{1}{2}}\left|1\right.〉\left(\left|{\alpha }_1,{\alpha }_2\right.〉-\left|{\alpha }_2,{\alpha }_1\right.〉\right)\end{array}$$

(4)

When performing a projective measurement on the ancillary state with an operator $M=\left|1\right.⟩\left.⟨1\right|$, the probability that the ancillary state is in state $\left|1\right.⟩$ can be given by

$$\begin{array}{l}P\left(\left|1\right.〉\right)=\left.〈{\beta }_3\right|M^{†}M\left|{\beta }_3\right.〉=\left.〈{\beta }_3\right|M\left|{\beta }_3\right.〉\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}={\displaystyle \frac{1}{4}}\left(\left.〈1,{\alpha }_1,{\alpha }_2\right|-\left.〈1,{\alpha }_2,{\alpha }_1\right|\right)\otimes \left|1\right.〉\left.〈1\right|\otimes \left(\left|1,{\alpha }_1,{\alpha }_2\right.〉-\left|1,{\alpha }_2,{\alpha }_1\right.〉\right)\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}={\displaystyle \frac{1}{4}}\left(\left.〈{\alpha }_1,{\alpha }_2\right|-\left.〈{\alpha }_2,{\alpha }_1\right|\right)\otimes \left(\left|{\alpha }_1,{\alpha }_2\right.〉-\left|{\alpha }_2,{\alpha }_1\right.〉\right)\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}={\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{2}}{\left|〈{\alpha }_1|{\alpha }_2〉\right|}^2\end{array}$$

(5)

According to Equation (5), we can deduce that

$${\left|〈{\alpha }_1|{\alpha }_2〉\right|}^2=1-2P\left(\left|1\right.〉\right)$$

(6)

2.2. Rotation Operation

The rotation operation around the Y-axis can be written as

$$R_y\left(\theta \right)=\left(\begin{array}{cc}\cos {\displaystyle \frac{\theta }{2}}& -\sin {\displaystyle \frac{\theta }{2}}\\ \sin {\displaystyle \frac{\theta }{2}}& \cos {\displaystyle \frac{\theta }{2}}\end{array}\right)$$

(7)

$R_y\left(\theta \right)$ is a unitary operation since ${R_y}^{†}\left(\theta \right)R_y\left(\theta \right)=R_y\left(-\theta \right)R_y\left(\theta \right)=I$. For quantum states $\left|1\right.⟩$ and $\left|0\right.⟩$, when performing the rotation operation on them, we can obtain

$$R_y\left(\theta \right)\left|1\right.〉=\left(\begin{array}{cc}\cos {\displaystyle \frac{\theta }{2}}& -\sin {\displaystyle \frac{\theta }{2}}\\ \sin {\displaystyle \frac{\theta }{2}}& \cos {\displaystyle \frac{\theta }{2}}\end{array}\right)\left(\begin{array}{c}0\\ 1\end{array}\right)=\left(\begin{array}{c}-\sin {\displaystyle \frac{\theta }{2}}\\ \cos {\displaystyle \frac{\theta }{2}}\end{array}\right)=-\sin {\displaystyle \frac{\theta }{2}}\left|0\right.〉+\cos {\displaystyle \frac{\theta }{2}}\left|1\right.〉$$

(8)

$$R_y\left(\theta \right)\left|0\right.〉=\left(\begin{array}{cc}\cos {\displaystyle \frac{\theta }{2}}& -\sin {\displaystyle \frac{\theta }{2}}\\ \sin {\displaystyle \frac{\theta }{2}}& \cos {\displaystyle \frac{\theta }{2}}\end{array}\right)\left(\begin{array}{c}1\\ 0\end{array}\right)=\left(\begin{array}{c}\cos {\displaystyle \frac{\theta }{2}}\\ \sin {\displaystyle \frac{\theta }{2}}\end{array}\right)=\cos {\displaystyle \frac{\theta }{2}}\left|0\right.〉+\sin {\displaystyle \frac{\theta }{2}}\left|1\right.〉$$

(9)

From Equations (8) and (9), we can know that the single-photon states $\left|1\right.⟩$ and $\left|0\right.⟩$ are concealed. Without knowing the angle $\theta$, $\left|1\right.⟩$ and $\left|0\right.⟩$ cannot be recovered.

To obtain the initial single-photon states $\left|1\right.⟩$ and $\left|0\right.⟩$, we need to rotate the resulting state with an angle of $\theta$ in the opposite direction. That is, the rotation angle is $-\theta$.

$$R_y\left(-\theta \right)\left(-\sin {\displaystyle \frac{\theta }{2}}\left|0\right.〉+\cos {\displaystyle \frac{\theta }{2}}\left|1\right.〉\right)=\left(\begin{array}{cc}\cos {\displaystyle \frac{-\theta }{2}}& -\sin {\displaystyle \frac{-\theta }{2}}\\ \sin {\displaystyle \frac{-\theta }{2}}& \cos {\displaystyle \frac{-\theta }{2}}\end{array}\right)\left(\begin{array}{c}-\sin {\displaystyle \frac{\theta }{2}}\\ \cos {\displaystyle \frac{\theta }{2}}\end{array}\right)=\left(\begin{array}{c}0\\ 1\end{array}\right)=\left|1\right.〉$$

(10)

$$R_y\left(-\theta \right)\left(\cos {\displaystyle \frac{\theta }{2}}\left|0\right.〉+\sin {\displaystyle \frac{\theta }{2}}\left|1\right.〉\right)=\left(\begin{array}{cc}\cos {\displaystyle \frac{-\theta }{2}}& -\sin {\displaystyle \frac{-\theta }{2}}\\ \sin {\displaystyle \frac{-\theta }{2}}& \cos {\displaystyle \frac{-\theta }{2}}\end{array}\right)\left(\begin{array}{c}\cos {\displaystyle \frac{\theta }{2}}\\ \sin {\displaystyle \frac{\theta }{2}}\end{array}\right)=\left(\begin{array}{c}1\\ 0\end{array}\right)=\left|0\right.〉$$

(11)

Furthermore, the rotation operation can also be used to encode the secret integer. For instance, for the integer 10, we can consider it as ${\displaystyle \frac{\pi }{10}}$, which serves as the angle of the rotation operation performed on quantum state $\left|0\right.⟩$. Then, the encoded single-photon state is $R_y\left({\displaystyle \frac{\pi }{10}}\right)\left|0\right.⟩=\mathit{cos}{\displaystyle \frac{\pi }{20}}\left|0\right.⟩+\mathit{sin}{\displaystyle \frac{\pi }{20}}\left|1\right.⟩$.

3. The Proposed QPC Protocol

The primary objective of the QPC protocol is to determine whether the secrets x and y held by Alice and Bob are equal with the assistance of a semi-honest third party (TP). The TP is expected to adhere to the protocol as designed and will not collude with the participants. However, despite following the rules, the TP may still attempt to extract additional information from the data it processes. This determination is achieved without either party disclosing any information about their respective secrets to one another, the TP, or any external observers. The protocol guarantees several key properties:

Privacy: Each participant’s secret remains confidential throughout the entire process.

Correctness: The protocol’s comparison result accurately indicates whether the secrets are equal.

Fairness: Both parties receive the comparison result simultaneously, ensuring that neither participant has an advantage over the other.

The protocol assumes the availability of a noise-free and lossless quantum channel, which allows for the transmission of quantum states without any degradation. Furthermore, it presumes that the classical channel used for communication between the parties is authenticated during transmission.

The detailed steps of the proposed QPC protocol are as follows, and its diagram is depicted in Figure 2.

Step 1. Alice and Bob share an angle ${\theta }_{AB}\in \left.[\mathrm{0,2}\pi \right)$ through a QKD protocol. Then, Alice (Bob) converts her (his) secret x (y) into an angle ${\theta }_A={\displaystyle \frac{\pi }{x}}$ (${\theta }_B={\displaystyle \frac{\pi }{y}}$). Specifically, if x = 0 (y = 0), then ${\theta }_A=0$ ${(\theta }_B=0).$ Finally, Alice (Bob) performs the rotation operation with the angle ${\theta }_A+{\theta }_{AB}$ ${(\theta }_B+{\theta }_{AB})$ on quantum state $\left|0\right.⟩$ to obtain the encoded single-photon state $\left|{\alpha }_A\right.⟩$ $\left(\left|{\alpha }_B\right.⟩\right)$.

$$\begin{array}{ll}\left|{\alpha }_A\right.〉& =R_y\left({\theta }_A+{\theta }_{AB}\right)\left|0\right.〉=\left(\begin{array}{cc}\cos \left({\displaystyle \frac{\pi }{2x}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)& -\sin \left({\displaystyle \frac{\pi }{2x}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\\ \sin \left({\displaystyle \frac{\pi }{2x}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)& \cos \left({\displaystyle \frac{\pi }{2x}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\end{array}\right)\left(\begin{array}{c}1\\ 0\end{array}\right)=\left(\begin{array}{c}\cos \left({\displaystyle \frac{\pi }{2x}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\\ \sin \left({\displaystyle \frac{\pi }{2x}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\end{array}\right)\\ & =\cos \left({\displaystyle \frac{\pi }{2x}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\left|0\right.〉+\sin \left({\displaystyle \frac{\pi }{2x}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\left|1\right.〉=\cos \left({\displaystyle \frac{\pi }{2x}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\left|0\right.〉+\sin \left({\displaystyle \frac{\pi }{2x}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\left|1\right.〉\end{array}$$

(12)

$$\begin{array}{ll}\left|{\alpha }_B\right.〉& =R_y\left({\theta }_B+{\theta }_{AB}\right)\left|0\right.〉=\left(\begin{array}{cc}\cos \left({\displaystyle \frac{\pi }{2y}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)& -\sin \left({\displaystyle \frac{\pi }{2y}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\\ \sin \left({\displaystyle \frac{\pi }{2y}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)& \cos \left({\displaystyle \frac{\pi }{2y}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\end{array}\right)\left(\begin{array}{c}1\\ 0\end{array}\right)=\left(\begin{array}{c}\cos \left({\displaystyle \frac{\pi }{2y}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\\ \sin \left({\displaystyle \frac{\pi }{2y}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\end{array}\right)\\ & =\cos \left({\displaystyle \frac{\pi }{2y}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\left|0\right.〉+\sin \left({\displaystyle \frac{\pi }{2y}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\left|1\right.〉=\cos \left({\displaystyle \frac{\pi }{2y}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\left|0\right.〉+\sin \left({\displaystyle \frac{\pi }{2y}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\left|1\right.〉\end{array}$$

(13)

Step 2. Alice (Bob) randomly generates her (his) own secret key ${\theta }_{AO}\in \left.[\mathrm{0,2}\pi \right)$ (${\theta }_{BO}\in \left.[\mathrm{0,2}\pi \right))$. She (he) performs the rotation operation with the angle ${\theta }_{AO}$ $\left({\theta }_{BO}\right)$ on the encoded single-photon state $\left|{\alpha }_A\right.⟩$ $\left(\left|{\alpha }_B\right.⟩\right)$. The resulting single-photon state is denoted as $\left|{\chi }_A\right.⟩$ $\left(\left|{\chi }_B\right.⟩\right)$.

$$\begin{array}{ll}\left|{\chi }_A\right.〉& =R_y\left({\theta }_{AO}\right)\left|{\alpha }_A\right.〉=\left(\begin{array}{cc}\cos {\displaystyle \frac{{\theta }_{AO}}{2}}& -\sin {\displaystyle \frac{{\theta }_{AO}}{2}}\\ \sin {\displaystyle \frac{{\theta }_{AO}}{2}}& \cos {\displaystyle \frac{{\theta }_{AO}}{2}}\end{array}\right)\left(\begin{array}{c}\cos \left({\displaystyle \frac{\pi }{2x}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\\ \sin \left({\displaystyle \frac{\pi }{2x}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\end{array}\right)=\left(\begin{array}{c}\cos \left({\displaystyle \frac{{\theta }_{AO}}{2}}+{\displaystyle \frac{\pi }{2x}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\\ \sin \left({\displaystyle \frac{{\theta }_{AO}}{2}}+{\displaystyle \frac{\pi }{2x}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\end{array}\right)\\ & =\cos \left({\displaystyle \frac{{\theta }_{AO}}{2}}+{\displaystyle \frac{\pi }{2x}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\left|0\right.〉+\sin \left({\displaystyle \frac{{\theta }_{AO}}{2}}+{\displaystyle \frac{\pi }{2x}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\left|1\right.〉\end{array}$$

(14)

$$\begin{array}{ll}\left|{\chi }_B\right.〉& =R_y\left({\theta }_{BO}\right)\left|{\alpha }_B\right.〉=\left(\begin{array}{cc}\cos {\displaystyle \frac{{\theta }_{BO}}{2}}& -\sin {\displaystyle \frac{{\theta }_{BO}}{2}}\\ \sin {\displaystyle \frac{{\theta }_{BO}}{2}}& \cos {\displaystyle \frac{{\theta }_{BO}}{2}}\end{array}\right)\left(\begin{array}{c}\cos \left({\displaystyle \frac{\pi }{2y}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\\ \sin \left({\displaystyle \frac{\pi }{2y}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\end{array}\right)=\left(\begin{array}{c}\cos \left({\displaystyle \frac{{\theta }_{BO}}{2}}+{\displaystyle \frac{\pi }{2y}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\\ \sin \left({\displaystyle \frac{{\theta }_{BO}}{2}}+{\displaystyle \frac{\pi }{2y}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\end{array}\right)\\ & =\cos \left({\displaystyle \frac{{\theta }_{BO}}{2}}+{\displaystyle \frac{\pi }{2y}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\left|0\right.〉+\sin \left({\displaystyle \frac{{\theta }_{BO}}{2}}+{\displaystyle \frac{\pi }{2y}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\left|1\right.〉\end{array}$$

(15)

Step 3. To prevent eavesdropping, Alice (Bob) prepares a decoy-photon sequence $D_A \left(D_B\right)$, randomly selecting from four nonorthogonal states $\left\{\left|0\right.⟩,\left|1\right.⟩,\left|+\right.⟩,\left|-\right.⟩\right\}$. Alice (Bob) inserts $D_A$ into $\left|{\chi }_A\right.⟩$ ($D_B$ into $\left|{\chi }_B\right.⟩$) at random positions. Throughout this process, Alice (Bob) carefully records the states and positions of the decoy photons. After the insertion of the decoy photons, the modified sequence is denoted as $S_A \left(S_B\right)$. Alice (Bob) then sends $S_A \left(S_B\right)$ to the TP for further processing.

Step 4. After confirming that the trusted party (TP) has received the sequences $S_A \left(S_B\right)$, Alice (Bob) will publicly disclose the measurement bases for measuring the decoy photons. Specifically, the Z-basis was utilized for measuring states $\left|0\right.⟩$ and $\left|1\right.⟩$, and the X-basis was used for measuring states $\left|+\right.⟩$ and $\left|-\right.⟩$. Alice (Bob) will also publish the positions of the decoy photons $D_A \left(D_B\right)$. The TP then performs quantum measurements on the decoy photons $D_A$ and $D_B$ to obtain the measurement results. These results are sent back to Alice and Bob, who can detect the presence of an eavesdropper (commonly referred to as “Eve”) by comparing the measurement results with the initially prepared decoy photons. If the error rate exceeds a pre-agreed threshold, Alice and Bob will conclude that the communication has been compromised and will restart the protocol from Step 2. Conversely, if the error rates for both Alice and Bob are acceptable, the TP will send a confirmation message back to them. Subsequently, Alice announces her key ${\theta }_{AO}$ and Bob announces his key ${\theta }_{BO}$ to the TP.

Step 5. The TP recovers $\left|{\chi }_A\right.⟩$ $\left(\left|{\chi }_B\right.⟩\right)$ by discarding all decoy photons in $S_A \left(S_B\right)$. The TP then performs the rotation operation with the angle ${-\theta }_{AO}$ $\left({-\theta }_{BO}\right)$ on $\left|{\chi }_A\right.⟩$ $\left(\left|{\chi }_B\right.⟩\right)$ to obtain the encoded single-photon state $\left|{\alpha }_A\right.⟩$ $\left(\left|{\alpha }_B\right.⟩\right)$. This process can be given by

$$\begin{array}{l}{R}_y\left(-{\theta }_{AO}\right)\left|{\chi }_A\right.〉=\left(\begin{array}{cc}\cos {\displaystyle \frac{-{\theta }_{AO}}{2}}& -\sin {\displaystyle \frac{-{\theta }_{AO}}{2}}\\ \sin {\displaystyle \frac{-{\theta }_{AO}}{2}}& \cos {\displaystyle \frac{-{\theta }_{AO}}{2}}\end{array}\right)\left(\begin{array}{c}\cos \left({\displaystyle \frac{{\theta }_{AO}}{2}}+{\displaystyle \frac{\pi }{2x}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\\ \sin \left({\displaystyle \frac{{\theta }_{AO}}{2}}+{\displaystyle \frac{\pi }{2x}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\end{array}\right)=\left(\begin{array}{c}\cos \left({\displaystyle \frac{\pi }{2x}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\\ \sin \left({\displaystyle \frac{\pi }{2x}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\end{array}\right)\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}=\cos \left({\displaystyle \frac{\pi }{2x}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\left|0\right.〉+\sin \left({\displaystyle \frac{\pi }{2x}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\left|1\right.〉=\left|{\alpha }_A\right.〉\end{array}$$

(16)

$$\begin{array}{l}{R}_y\left(-{\theta }_{BO}\right)\left|{\chi }_B\right.〉=\left(\begin{array}{cc}\cos {\displaystyle \frac{-{\theta }_{BO}}{2}}& -\sin {\displaystyle \frac{-{\theta }_{BO}}{2}}\\ \sin {\displaystyle \frac{-{\theta }_{BO}}{2}}& \cos {\displaystyle \frac{-{\theta }_{BO}}{2}}\end{array}\right)\left(\begin{array}{c}\cos \left({\displaystyle \frac{{\theta }_{BO}}{2}}+{\displaystyle \frac{\pi }{2y}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\\ \sin \left({\displaystyle \frac{{\theta }_{BO}}{2}}+{\displaystyle \frac{\pi }{2y}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\end{array}\right)=\left(\begin{array}{c}\cos \left({\displaystyle \frac{\pi }{2y}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\\ \sin \left({\displaystyle \frac{\pi }{2y}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\end{array}\right)\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}=\cos \left({\displaystyle \frac{\pi }{2y}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\left|0\right.〉+\sin \left({\displaystyle \frac{\pi }{2y}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\left|1\right.〉=\left|{\alpha }_B\right.〉\end{array}$$

(17)

Finally, the TP performs the swap test on $\left|{\alpha }_A\right.⟩$ and $\left|{\alpha }_B\right.⟩$ and measures the ancillary quantum state to obtain the measurement results.

Step 6. By executing Steps 2–5 a total of λ times, the process allows the TP to gather multiple measurement results from the ancillary quantum state. Once one of the measurement results appears as $\left|1\right.⟩$, TP can conclude that $x\ne y$; otherwise, $x=y$. The TP announces the comparison result to Alice and Bob at the same time.

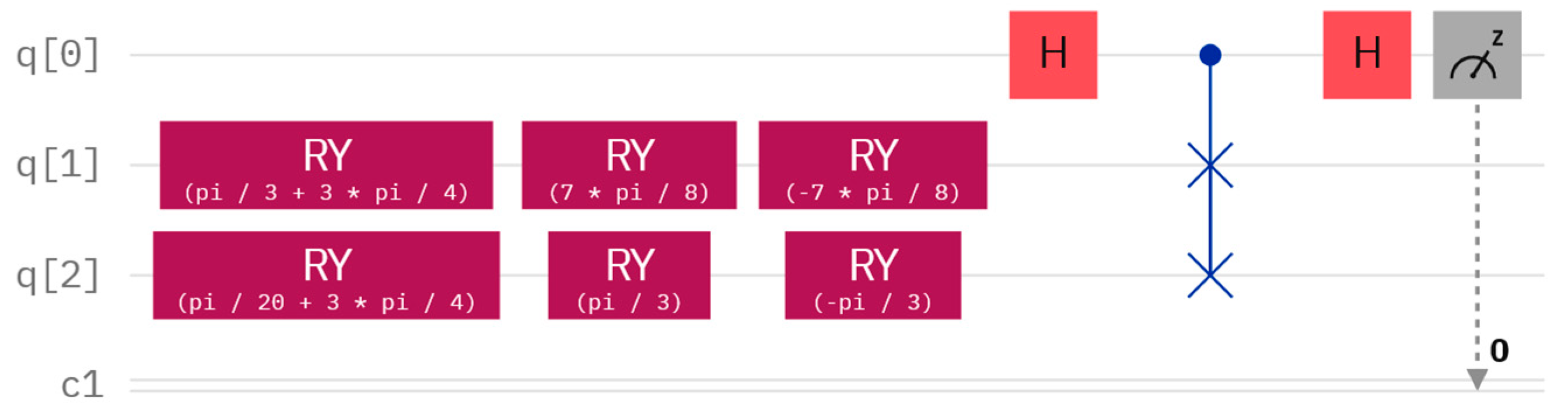
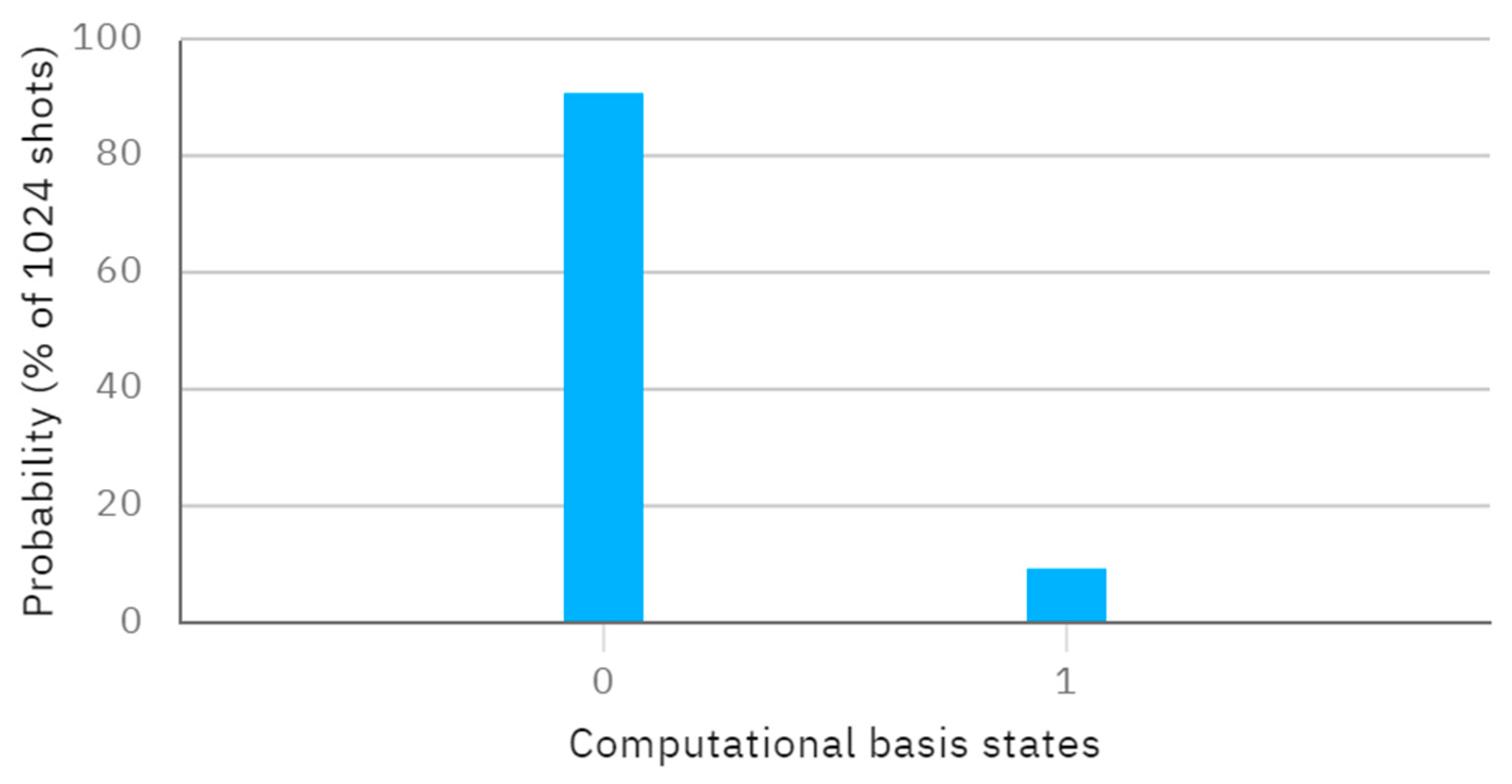
4. Simulation

Consider a case in which Alice and Bob hold their own secret x = 3 and y = 20, respectively, and they want to determine whether $x=y$ without revealing x and y to each other, the TP, and any eavesdropper.

According to the protocol description, we assume that Alice and Bob share an angle ${\theta }_{AB}={\displaystyle \frac{3\pi }{4}}$ through a QKD protocol. Alice (Bob) converts her (his) secret x (y) into an angle ${\theta }_A={\displaystyle \frac{\pi }{3}}$ (${\theta }_B={\displaystyle \frac{\pi }{20}}$). When performing the rotation operation with the angle ${\theta }_A={\displaystyle \frac{\pi }{3}}$ (${\theta }_B={\displaystyle \frac{\pi }{20}}$) on quantum state $\left|0\right.⟩$, the encoded single-photon state $\left|{\alpha }_A\right.⟩\left(\left|{\alpha }_B\right.⟩\right)$ can be expressed as

$$\begin{array}{ll}\left|{\alpha }_A\right.〉& =R_y\left({\displaystyle \frac{\pi }{3}}+{\displaystyle \frac{3\pi }{4}}\right)\left|0\right.〉=\left(\begin{array}{cc}\cos \left({\displaystyle \frac{\pi }{6}}+{\displaystyle \frac{3\pi }{8}}\right)& -\sin \left({\displaystyle \frac{\pi }{6}}+{\displaystyle \frac{3\pi }{8}}\right)\\ \sin \left({\displaystyle \frac{\pi }{6}}+{\displaystyle \frac{3\pi }{8}}\right)& \cos \left({\displaystyle \frac{\pi }{6}}+{\displaystyle \frac{3\pi }{8}}\right)\end{array}\right)\left(\begin{array}{c}1\\ 0\end{array}\right)=\left(\begin{array}{c}\cos \left({\displaystyle \frac{\pi }{6}}+{\displaystyle \frac{3\pi }{8}}\right)\\ \sin \left({\displaystyle \frac{\pi }{6}}+{\displaystyle \frac{3\pi }{8}}\right)\end{array}\right)\\ & =\cos \left({\displaystyle \frac{\pi }{6}}+{\displaystyle \frac{3\pi }{8}}\right)\left|0\right.〉+\sin \left({\displaystyle \frac{\pi }{6}}+{\displaystyle \frac{3\pi }{8}}\right)\left|1\right.〉=\cos \left({\displaystyle \frac{\pi }{6}}+{\displaystyle \frac{3\pi }{8}}\right)\left|0\right.〉+\sin \left({\displaystyle \frac{\pi }{6}}+{\displaystyle \frac{3\pi }{8}}\right)\left|1\right.〉\end{array}$$

(18)

$$\begin{array}{ll}\left|{\alpha }_B\right.〉& =R_y\left({\displaystyle \frac{\pi }{20}}+{\displaystyle \frac{3\pi }{4}}\right)\left|0\right.〉=\left(\begin{array}{cc}\cos \left({\displaystyle \frac{\pi }{40}}+{\displaystyle \frac{3\pi }{8}}\right)& -\sin \left({\displaystyle \frac{\pi }{40}}+{\displaystyle \frac{3\pi }{8}}\right)\\ \sin \left({\displaystyle \frac{\pi }{40}}+{\displaystyle \frac{3\pi }{8}}\right)& \cos \left({\displaystyle \frac{\pi }{40}}+{\displaystyle \frac{3\pi }{8}}\right)\end{array}\right)\left(\begin{array}{c}1\\ 0\end{array}\right)=\left(\begin{array}{c}\cos \left({\displaystyle \frac{\pi }{40}}+{\displaystyle \frac{3\pi }{8}}\right)\\ \sin \left({\displaystyle \frac{\pi }{40}}+{\displaystyle \frac{3\pi }{8}}\right)\end{array}\right)\\ & =\cos \left({\displaystyle \frac{\pi }{40}}+{\displaystyle \frac{3\pi }{8}}\right)\left|0\right.〉+\sin \left({\displaystyle \frac{\pi }{40}}+{\displaystyle \frac{3\pi }{8}}\right)\left|1\right.〉=\cos \left({\displaystyle \frac{\pi }{40}}+{\displaystyle \frac{3\pi }{8}}\right)\left|0\right.〉+\sin \left({\displaystyle \frac{\pi }{40}}+{\displaystyle \frac{3\pi }{8}}\right)\left|1\right.〉\end{array}$$

(19)

Following that, we assume that Alice (Bob) generates her (his) own secret key ${\theta }_{AO}={\displaystyle \frac{7\pi }{8}}$ (${\theta }_{BO}={\displaystyle \frac{\pi }{3}})$. When performing the rotation operation with the angle ${\theta }_{AO}={\displaystyle \frac{7\pi }{8}}$ (${\theta }_{BO}={\displaystyle \frac{\pi }{3}})$ on the encoded single-photon state $\left|{\alpha }_A\right.⟩$ $\left(\left|{\alpha }_B\right.⟩\right)$, the resulting single-photon state $\left|{\chi }_A\right.⟩\left(\left|{\chi }_B\right.⟩\right)$ can be given by

$$\begin{array}{ll}\left|{\chi }_A\right.〉& =R_y\left({\theta }_{AO}\right)\left|{\alpha }_A\right.〉=\left(\begin{array}{cc}\cos {\displaystyle \frac{7\pi }{16}}& -\sin {\displaystyle \frac{7\pi }{16}}\\ \sin {\displaystyle \frac{7\pi }{16}}& \cos {\displaystyle \frac{7\pi }{16}}\end{array}\right)\left(\begin{array}{c}\cos \left({\displaystyle \frac{\pi }{6}}+{\displaystyle \frac{3\pi }{8}}\right)\\ \sin \left({\displaystyle \frac{\pi }{6}}+{\displaystyle \frac{3\pi }{8}}\right)\end{array}\right)=\left(\begin{array}{c}\cos \left({\displaystyle \frac{7\pi }{16}}+{\displaystyle \frac{\pi }{6}}+{\displaystyle \frac{3\pi }{8}}\right)\\ \sin \left({\displaystyle \frac{7\pi }{16}}+{\displaystyle \frac{\pi }{6}}+{\displaystyle \frac{3\pi }{8}}\right)\end{array}\right)\\ & =\cos \left({\displaystyle \frac{7\pi }{16}}+{\displaystyle \frac{\pi }{6}}+{\displaystyle \frac{3\pi }{8}}\right)\left|0\right.〉+\sin \left({\displaystyle \frac{7\pi }{16}}+{\displaystyle \frac{\pi }{6}}+{\displaystyle \frac{3\pi }{8}}\right)\left|1\right.〉\end{array}$$

(20)

$$\begin{array}{ll}\left|{\chi }_B\right.〉& =R_y\left({\theta }_{BO}\right)\left|{\alpha }_B\right.〉=\left(\begin{array}{cc}\cos {\displaystyle \frac{\pi }{6}}& -\sin {\displaystyle \frac{\pi }{6}}\\ \sin {\displaystyle \frac{\pi }{6}}& \cos {\displaystyle \frac{\pi }{6}}\end{array}\right)\left(\begin{array}{c}\cos \left({\displaystyle \frac{\pi }{40}}+{\displaystyle \frac{3\pi }{8}}\right)\\ \sin \left({\displaystyle \frac{\pi }{40}}+{\displaystyle \frac{3\pi }{8}}\right)\end{array}\right)=\left(\begin{array}{c}\cos \left({\displaystyle \frac{\pi }{6}}+{\displaystyle \frac{\pi }{68}}+{\displaystyle \frac{3\pi }{8}}\right)\\ \sin \left({\displaystyle \frac{\pi }{6}}+{\displaystyle \frac{\pi }{68}}+{\displaystyle \frac{3\pi }{8}}\right)\end{array}\right)\\ & =\cos \left({\displaystyle \frac{\pi }{6}}+{\displaystyle \frac{\pi }{40}}+{\displaystyle \frac{3\pi }{8}}\right)\left|0\right.〉+\sin \left({\displaystyle \frac{\pi }{6}}+{\displaystyle \frac{\pi }{40}}+{\displaystyle \frac{3\pi }{8}}\right)\left|1\right.〉\end{array}$$

(21)

Without considering the eavesdropping in Step 3 and Step 4 for simplification, the TP can recover $\left|{\chi }_A\right.⟩$ $\left(\left|{\chi }_B\right.⟩\right)$ in Step 5. When performing the rotation operation with the angle $-{\displaystyle \frac{7\pi }{8}}$ $(-{\displaystyle \frac{\pi }{3}})$ on $\left|{\chi }_A\right.⟩$ $\left(\left|{\chi }_B\right.⟩\right)$ to obtain the encoded single-photon state $\left|{\alpha }_A\right.⟩\left(\left|{\alpha }_B\right.⟩\right)$, this process can be written as

$$\begin{array}{l}{R}_y\left(-{\theta }_{AO}\right)\left|{\chi }_A\right.〉=\left(\begin{array}{cc}\cos {\displaystyle \frac{-7\pi }{16}}& -\sin {\displaystyle \frac{-7\pi }{16}}\\ \sin {\displaystyle \frac{-7\pi }{16}}& \cos {\displaystyle \frac{-7\pi }{16}}\end{array}\right)\left(\begin{array}{c}\cos \left({\displaystyle \frac{7\pi }{16}}+{\displaystyle \frac{\pi }{6}}+{\displaystyle \frac{3\pi }{8}}\right)\\ \sin \left({\displaystyle \frac{7\pi }{16}}+{\displaystyle \frac{\pi }{6}}+{\displaystyle \frac{3\pi }{8}}\right)\end{array}\right)=\left(\begin{array}{c}\cos \left({\displaystyle \frac{\pi }{6}}+{\displaystyle \frac{3\pi }{8}}\right)\\ \sin \left({\displaystyle \frac{\pi }{6}}+{\displaystyle \frac{3\pi }{8}}\right)\end{array}\right)\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}=\cos \left({\displaystyle \frac{\pi }{6}}+{\displaystyle \frac{3\pi }{8}}\right)\left|0\right.〉+\sin \left({\displaystyle \frac{\pi }{6}}+{\displaystyle \frac{3\pi }{8}}\right)\left|1\right.〉=\left|{\alpha }_A\right.〉\end{array}$$

(22)

$$\begin{array}{l}{R}_y\left(-{\theta }_{BO}\right)\left|{\chi }_B\right.〉=\left(\begin{array}{cc}\cos {\displaystyle \frac{\pi }{6}}& -\sin {\displaystyle \frac{\pi }{6}}\\ \sin {\displaystyle \frac{\pi }{6}}& \cos {\displaystyle \frac{\pi }{6}}\end{array}\right)\left(\begin{array}{c}\cos \left({\displaystyle \frac{\pi }{6}}+{\displaystyle \frac{\pi }{68}}+{\displaystyle \frac{3\pi }{8}}\right)\\ \sin \left({\displaystyle \frac{\pi }{6}}+{\displaystyle \frac{\pi }{68}}+{\displaystyle \frac{3\pi }{8}}\right)\end{array}\right)=\left(\begin{array}{c}\cos \left({\displaystyle \frac{\pi }{40}}+{\displaystyle \frac{3\pi }{8}}\right)\\ \sin \left({\displaystyle \frac{\pi }{40}}+{\displaystyle \frac{3\pi }{8}}\right)\end{array}\right)\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}=\cos \left({\displaystyle \frac{\pi }{40}}+{\displaystyle \frac{3\pi }{8}}\right)\left|0\right.〉+\sin \left({\displaystyle \frac{\pi }{40}}+{\displaystyle \frac{3\pi }{8}}\right)\left|1\right.〉=\left|{\alpha }_B\right.〉\end{array}$$

(23)

When performing the swap test on $\left|{\alpha }_A\right.⟩$ and $\left|{\alpha }_B\right.⟩$ and measuring the ancillary quantum state, the probability that the measurement results are $\left|1\right.⟩$ is

$$\begin{array}{ll}P\left(\left|1\right.〉\right)& ={\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{2}}{\left|〈\left(\cos \left({\displaystyle \frac{\pi }{6}}+{\displaystyle \frac{3\pi }{8}}\right)\left.〈0\right|+\sin \left({\displaystyle \frac{\pi }{6}}+{\displaystyle \frac{3\pi }{8}}\right)\left.〈1\right|\right)|\cos \left({\displaystyle \frac{\pi }{40}}+{\displaystyle \frac{3\pi }{8}}\right)\left|0\right.〉+\sin \left({\displaystyle \frac{\pi }{40}}+{\displaystyle \frac{3\pi }{8}}\right)\left|1\right.〉〉\right|}^2\\ & ={\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{2}}\left|\cos \left({\displaystyle \frac{\pi }{6}}+{\displaystyle \frac{3\pi }{8}}\right)\cos \left({\displaystyle \frac{\pi }{40}}+{\displaystyle \frac{3\pi }{8}}\right)+\sin \left({\displaystyle \frac{\pi }{6}}+{\displaystyle \frac{3\pi }{8}}\right)\sin \left({\displaystyle \frac{\pi }{40}}+{\displaystyle \frac{3\pi }{8}}\right)\right|\\ & ={\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{2}}{\left|\cos \left({\displaystyle \frac{\pi }{6}}-{\displaystyle \frac{\pi }{40}}\right)\right|}^2={\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{2}}{\cos }^2\left({\displaystyle \frac{\pi }{6}}-{\displaystyle \frac{\pi }{40}}\right)={\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{2}}{\cos }^2\left({\displaystyle \frac{17\pi }{120}}\right)=0.09267\end{array}$$

(24)

Since the probability that the measurement results appear to be $\left|1\right.⟩$ is not 0, we can conclude that $x\ne y$.

The quantum circuit implementation of the above process for determining whether $x=y$ is shown in Figure 3. The measurement results obtained by executing the quantum circuit on the IBM Quantum Experience are presented in Figure 4.

According to the measurement results, we find that quantum state $\left|1\right.⟩$ appears. This indicates that $x\ne y$.

Therefore, we verify the feasibility of the proposed protocol by performing a quantum circuit to compare x = 3 and y = 20 on the IBM Quantum Platform.

5. Analysis

5.1. Correctness

When performing the swap test on $\left|{\alpha }_A\right.⟩$ and $\left|{\alpha }_B\right.⟩$, the probability of $\left|1\right.⟩$ appearing can be expressed as

$$\begin{array}{ll}P\left(\left|1\right.〉\right)& ={\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{2}}{\left|〈\left(\cos \left({\displaystyle \frac{\pi }{2x}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\left.〈0\right|+\sin \left({\displaystyle \frac{\pi }{2x}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\left.〈1\right|\right)|\cos \left({\displaystyle \frac{\pi }{2y}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\left|0\right.〉+\sin \left({\displaystyle \frac{\pi }{2y}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\left|1\right.〉〉\right|}^2\\ & ={\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{2}}\left|\cos \left({\displaystyle \frac{\pi }{2x}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\cos \left({\displaystyle \frac{\pi }{2y}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)+\sin \left({\displaystyle \frac{\pi }{2x}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\sin \left({\displaystyle \frac{\pi }{2y}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\right|\\ & ={\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{2}}{\left|\cos \left({\displaystyle \frac{\pi }{2x}}-{\displaystyle \frac{\pi }{2y}}\right)\right|}^2={\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{2}}{\cos }^2\left({\displaystyle \frac{\pi }{2x}}-{\displaystyle \frac{\pi }{2y}}\right)\end{array}$$

(25)

From Equation (25), we can know that $P\left(\left|1\right.⟩\right)=0$ if and only if $x=y$. Therefore, we can conclude that $x\ne y$ once the measurement results appear as $\left|1\right.⟩$; otherwise, $x=y$.

5.2. Security

For the proposed QPC protocol, the attacks mainly come from the external adversary often referred to as Eve, who may intercept the quantum sequence transmitted in the quantum channel and the participants who utilize their intermediate calculation results to uncover the private information. In the following, we will show that our protocol is secure against these attacks.

5.2.1. External Attacks

External attacks refer to Eve’s attempts to perform various common attack strategies, including intercept-resend, direct measurement, entangle-measure, and Trojan horse attacks, to extract information about the participants’ secret integer to the greatest extent possible. However, the participants’ secret integer is encoded as a single-photon state, which is transmitted to the TP. The TP’s own secret key and decoy photon technology can be used to effectively prevent eavesdropping during this process. The following cases consider different attack strategies.

• Case I. The intercept-resend attack

During this attack, Eve attempts to intercept the sequences $S_A$ and $S_B$, measure them on a guessed measurement basis, and resend two fake sequences to the TP. $S_A$ and $S_B$ consist of decoy photons that are randomly chosen from four nonorthogonal states $\left\{\left|0\right.⟩,\left|1\right.⟩,\left|+\right.⟩,\left|-\right.⟩\right\}$, which are used to enhance security against eavesdropping. After intercepting the quantum sequences, Eve can measure them but cannot distinguish between the decoy photons and the actual encoded qubits since Eve lacks knowledge of the specific positions of the decoy photons. Her measurements introduce disturbances that can be detected by Alice and Bob, thereby resulting in the termination of this protocol. For instance, for a decoy photon in state $\left|+\right.⟩$, if Eve chooses the X basis to measure it, she will pass the eavesdropping detection with a probability of 100%. Conversely, if Eve selects the Z basis to measure it, she will pass the eavesdropping detection with a probability of 50%. For Alice, the probability of choosing the X basis or the Z basis is 50%. Therefore, the probability that Eve can pass the eavesdropping detection is ${\displaystyle \frac{1}{2}}\times 1+{\displaystyle \frac{1}{2}}\times {\displaystyle \frac{1}{2}}={\displaystyle \frac{3}{4}}$. For m decoy photons, the probability of this attack being detected is $1-{\left({\displaystyle \frac{3}{4}}\right)}^m$. As the number of decoy photons m increases sufficiently, the probability of detecting an intercept-resend attack approaches 1. This enhancement in detection capability means that Eve, attempting to execute the intercept-resend strategy, is unable to extract any meaningful information regarding Alice’s or Bob’s encoded qubits.

• Case II. The direct measure attack

In a direct measurement attack, Eve intercepts the sequences $S_A$ and $S_B$ from Alice and Bob, respectively, and conducts measurements on them. However, without prior knowledge of the positions of the decoy photons, Eve faces significant challenges in accurately distinguishing between these decoys and the actual encoded qubits. Eve might attempt to substitute the original quantum sequences with a fabricated version when sending them to the TP. After the TP confirms the receipt of the sequence, Alice and Bob will disclose the positions of the decoy photons. At this stage, Eve can eliminate the decoy photons from $S_A$ and $S_B$ to obtain encoded single-photon states $\left|{\chi }_A\right.⟩$ and $\left|{\chi }_B\right.⟩$. Eve can then proceed to measure them using the measurement operator $M=\left|1\right.⟩\left.⟨1\right|$, allowing her to derive the measurement outcomes $MA$ and $MB$ corresponding to Alice’s and Bob’s encoded qubits, respectively.

$$\begin{array}{ll}M& A=\left|{\chi }_A\right.〉\left|1\right.〉\left.〈1\right|\left|{\chi }_A\right.〉\\ & =\left(\cos \left({\displaystyle \frac{{\theta }_{AO}}{2}}+{\displaystyle \frac{\pi }{2x}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\left.〈0\right|+\sin \left({\displaystyle \frac{{\theta }_{AO}}{2}}+{\displaystyle \frac{\pi }{2x}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\left.〈1\right|\right)\left|1\right.〉\left.〈1\right|\cos \left({\displaystyle \frac{{\theta }_{AO}}{2}}+{\displaystyle \frac{\pi }{2x}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\left|0\right.〉+\sin \left({\displaystyle \frac{{\theta }_{AO}}{2}}+{\displaystyle \frac{\pi }{2x}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\left|1\right.〉\\ & ={\sin }^2\left({\displaystyle \frac{{\theta }_{AO}}{2}}+{\displaystyle \frac{\pi }{2x}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\end{array}$$

(26)

$$\begin{array}{ll}MB& =\left|{\chi }_B\right.〉\left|1\right.〉\left.〈1\right|\left|{\chi }_B\right.〉\\ & =\left(\cos \left({\displaystyle \frac{{\theta }_{BO}}{2}}+{\displaystyle \frac{\pi }{2y}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\left.〈0\right|+\sin \left({\displaystyle \frac{{\theta }_{BO}}{2}}+{\displaystyle \frac{\pi }{2y}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\left.〈1\right|\right)\left|1\right.〉\left.〈1\right|\cos \left({\displaystyle \frac{{\theta }_{BO}}{2}}+{\displaystyle \frac{\pi }{2y}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\left|0\right.〉+\sin \left({\displaystyle \frac{{\theta }_{BO}}{2}}+{\displaystyle \frac{\pi }{2y}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\left|1\right.〉\\ & ={\sin }^2\left({\displaystyle \frac{{\theta }_{BO}}{2}}+{\displaystyle \frac{\pi }{2y}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\end{array}$$

(27)

However, the measurement outcome $MA$($MB)$ is intrinsically linked to the keys ${\theta }_{AO}\left({\theta }_{BO}\right)$ and ${\theta }_{AB}$. Consequently, Eve cannot deduce the confidentiality of Alice’s or Bob’s secret integer without possessing knowledge of these keys.

• Case III. The entangle-measure attack

In the entangle-measure attack, Eve intercepts the transmitted qubits and applies a unitary operation $U_O$ to entangle her ancilla qubits $\left|e_i\right.⟩$ with the intercepted qubits. When performing the unitary operation $U_O$ on the intercepted qubits in states $\left\{\left|0\right.⟩,\left|1\right.⟩,\left|+\right.⟩,\left|-\right.⟩\right\}$ and $\left|e_i\right.⟩$, the process can be described as follows:

$$U_O\left|0\right.〉\left|e_i\right.〉=c_{00}\left|0\right.〉\left|e_{00}\right.〉+c_{01}\left|1\right.〉\left|e_{01}\right.〉$$

(28)

$$U_O\left|1\right.〉\left|e_i\right.〉=c_{10}\left|0\right.〉\left|e_{10}\right.〉+c_{11}\left|1\right.〉\left|e_{11}\right.〉$$

(29)

$$\begin{array}{ll}{U}_O\left|+\right.〉\left|e_i\right.〉& ={\displaystyle \frac{1}{\sqrt{2}}}\left(U_O\left|0\right.〉\left|e_i\right.〉+U_O\left|1\right.〉\left|e_i\right.〉\right)\\ & ={\displaystyle \frac{1}{\sqrt{2}}}\left(c_{00}\left|0\right.〉\left|e_{00}\right.〉+c_{01}\left|1\right.〉\left|e_{01}\right.〉+c_{10}\left|0\right.〉\left|e_{10}\right.〉+c_{11}\left|1\right.〉\left|e_{11}\right.〉\right)\\ & ={\displaystyle \frac{1}{2}}\left|+\right.〉\left(c_{00}\left|e_{00}\right.〉+c_{01}\left|e_{01}\right.〉+c_{10}\left|e_{10}\right.〉+c_{11}\left|e_{11}\right.〉\right)\\ & +{\displaystyle \frac{1}{2}}\left|-\right.〉\left(c_{00}\left|e_{00}\right.〉-c_{01}\left|e_{01}\right.〉+c_{10}\left|e_{10}\right.〉-c_{11}\left|e_{11}\right.〉\right)\end{array}$$

(30)

$$\begin{array}{ll}{U}_O\left|-\right.〉\left|e_i\right.〉& ={\displaystyle \frac{1}{\sqrt{2}}}\left(U_O\left|0\right.〉\left|e_i\right.〉-U_O\left|1\right.〉\left|e_i\right.〉\right)\\ & ={\displaystyle \frac{1}{\sqrt{2}}}\left(c_{00}\left|0\right.〉\left|e_{00}\right.〉+c_{01}\left|1\right.〉\left|e_{01}\right.〉-c_{10}\left|0\right.〉\left|e_{10}\right.〉-c_{11}\left|1\right.〉\left|e_{11}\right.〉\right)\\ & ={\displaystyle \frac{1}{2}}\left|+\right.〉\left(c_{00}\left|e_{00}\right.〉+c_{01}\left|e_{01}\right.〉-c_{10}\left|e_{10}\right.〉-c_{11}\left|e_{11}\right.〉\right)\\ & +{\displaystyle \frac{1}{2}}\left|-\right.〉\left(c_{00}\left|e_{00}\right.〉-c_{01}\left|e_{01}\right.〉-c_{10}\left|e_{10}\right.〉+c_{11}\left|e_{11}\right.〉\right)\end{array}$$

(31)

Four quantum states $\{\left|e_{00}\right.⟩,\left|e_{01}\right.⟩,\left|e_{10}\right.⟩,\left|e_{11}\right.⟩\}$ are pure states uniquely defined by the unitary operation $U_O$, with coefficients that satisfy the conditions ${\left|c_{00}\right|}^2+{\left|c_{01}\right|}^2=1$ and ${\left|c_{10}\right|}^2+{\left|c_{11}\right|}^2=1$. Specifically, we have ${\left|c_{00}\right|}^2={\left|c_{11}\right|}^2=F$ and ${\left|c_{01}\right|}^2={\left|c_{10}\right|}^2=D$, where F represents fidelity and D denotes the quantum bit error rate (QBER). When the decoy photon is in the states $\left\{\left|0\right.⟩,\left|1\right.⟩\right\}$, the probability of obtaining the correct result is F. In contrast, when the decoy photon is in the states $\left\{\left|+\right.⟩,\left|-\right.⟩\right\}$, the probability of correctness drops to $1/2$. Therefore, for a decoy photon, the probability of obtaining the result successfully is written as

$$P_{\mathrm{successful}}={\displaystyle \frac{1}{2}}\left(F+{\displaystyle \frac{1}{2}}\right)$$

(32)

The probability of detecting Eve is given by

$$P_{\mathrm{detected}}=1-p^m$$

(33)

where m represents the number of decoy photons. As m increases sufficiently, the probability of detecting Eve approaches 1.

When performing the entangle-measure attack on single-photon states $\left|{\chi }_A\right.⟩$ and $\left|{\chi }_B\right.⟩$, the process can be given by

$$\begin{array}{l}{U}_o\left(\left|{\chi }_A\right.〉\left|e_i\right.〉\right)=U_O\left(\cos \left({\displaystyle \frac{{\theta }_{AO}}{2}}+{\displaystyle \frac{\pi }{2x}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\left|0\right.〉+\sin \left({\displaystyle \frac{{\theta }_{AO}}{2}}+{\displaystyle \frac{\pi }{2x}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\left|1\right.〉\right)\left|e_i\right.〉\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}=\left|0\right.〉\left(c_{00}\cos \left({\displaystyle \frac{{\theta }_{AO}}{2}}+{\displaystyle \frac{\pi }{2x}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\left|e_{00}\right.〉+c_{10}\sin \left({\displaystyle \frac{{\theta }_{AO}}{2}}+{\displaystyle \frac{\pi }{2x}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\left|e_{10}\right.〉\right)\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}+\left|1\right.〉\left(c_{01}\cos \left({\displaystyle \frac{{\theta }_{AO}}{2}}+{\displaystyle \frac{\pi }{2x}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\left|e_{01}\right.〉+c_{11}\sin \left({\displaystyle \frac{{\theta }_{AO}}{2}}+{\displaystyle \frac{\pi }{2x}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\left|e_{11}\right.〉\right)\end{array}$$

(34)

$$\begin{array}{ll}{U}_o\left(\left|{\chi }_B\right.〉\left|e_i\right.〉\right)& =U_O\left(\cos \left({\displaystyle \frac{{\theta }_{BO}}{2}}+{\displaystyle \frac{\pi }{2y}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\left|0\right.〉+\sin \left({\displaystyle \frac{{\theta }_{BO}}{2}}+{\displaystyle \frac{\pi }{2y}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\left|1\right.〉\right)\left|e_i\right.〉\\ & =\left|0\right.〉\left(c_{00}\cos \left({\displaystyle \frac{{\theta }_{BO}}{2}}+{\displaystyle \frac{\pi }{2y}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\left|e_{00}\right.〉+c_{10}\sin \left({\displaystyle \frac{{\theta }_{BO}}{2}}+{\displaystyle \frac{\pi }{2y}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\left|e_{10}\right.〉\right)\\ & +\left|1\right.〉\left(c_{01}\cos \left({\displaystyle \frac{{\theta }_{BO}}{2}}+{\displaystyle \frac{\pi }{2y}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\left|e_{01}\right.〉+c_{11}\sin \left({\displaystyle \frac{{\theta }_{BO}}{2}}+{\displaystyle \frac{\pi }{2y}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\left|e_{11}\right.〉\right)\end{array}$$

(35)

To pass the eavesdropping detection, the coefficients in Equations (34) and (35) should satisfy $c_{10}=c_{01}=0$ and $c_{00}=c_{11}=1$. Therefore, Equations (34) and (35) can be written as

$$U_o\left(\left|{\chi }_A\right.〉\left|e_i\right.〉\right)=\cos \left({\displaystyle \frac{{\theta }_{AO}}{2}}+{\displaystyle \frac{\pi }{2x}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\left|0\right.〉\left|e_{00}\right.〉+\sin \left({\displaystyle \frac{{\theta }_{AO}}{2}}+{\displaystyle \frac{\pi }{2x}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\left|1\right.〉\left|e_{11}\right.〉$$

(36)

$$U_o\left(\left|{\chi }_B\right.〉\left|e_i\right.〉\right)=\cos \left({\displaystyle \frac{{\theta }_{BO}}{2}}+{\displaystyle \frac{\pi }{2y}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\left|0\right.〉\left|e_{00}\right.〉+\sin \left({\displaystyle \frac{{\theta }_{BO}}{2}}+{\displaystyle \frac{\pi }{2y}}+{\displaystyle \frac{{\theta }_{AB}}{2}}\right)\left|1\right.〉\left|e_{11}\right.〉$$

(37)

From Equations (34) and (35), we know that the resulting quantum states are directly related to ${\theta }_{AO},{ \theta }_{BO}$ and ${ \theta }_{AB}$. However, Eve has no chance of obtaining ${\theta }_{AO},{ \theta }_{BO}$, and ${ \theta }_{AB}$; therefore, it is impossible for Eve to deduce Alice’s and Bob’s secret integer.

• Case IV. The Trojan horse attacks

The Trojan horse attacks, including the invisible photon eavesdropping attack and the delay-photon attack [64], mainly work in two-way quantum communication when a quantum sequence is transmitted in a bidirectional quantum channel. However, the quantum sequences $S_A$ and $S_B$ are transmitted in a unidirectional quantum channel to the TP. This indicates that our protocol is a one-way communication protocol, which can prevent the Trojan horse attacks automatically.

Based on the analysis presented above, external eavesdropping performed by Eve cannot be used to successfully acquire the participants’ secret integer.

5.2.2. Participant Attacks

Participant attacks are, in fact, more formidable than outsider attacks. For participants, they have a chance of knowing some immediate results and can legally utilize this information to infer the participant’s secret integer. The following two cases of participant attacks are considered.

• Case 1. Attacks from Alice (Bob)

In this protocol, the quantum sequence $S_A$ ($S_B$) encoding the secret integer is transmitted to the TP, whose security is ensured by the decoy state technology and the rotation operation with the angle on the secret key. The role of Alice in this protocol is analogous to that of Bob. We assume that Bob intercepts the sequence $S_A$ like Eve does and resends a fake sequence to the TP who will then announce the positions of the decoy photons in $S_A$. Bob can recover the quantum state $\left|{\chi }_A\right.⟩$ by discarding all decoy photons in $S_A$. Even though this behavior has been detected, Bob has obtained the quantum state $\left|{\chi }_A\right.⟩$ and can deduce the secret integer x. $\left|{\chi }_A\right.⟩$ is generated by performing the rotation operation with the angle ${\theta }_{AO}$ on the encoded single-photon state $\left|{\alpha }_A\right.⟩$, and ${\theta }_{AO}$ will not be published once the quantum channel is not secure. Therefore, Bob has no chance of obtaining ${\theta }_{AO}$, resulting in the quantum state $\left|{\chi }_A\right.⟩$ being concealed. Additionally, the quantum state $\left|{\chi }_A\right.⟩$, in fact, is unknown to the other participants, and an unknown quantum state is indistinguishable. This results in it being impossible for Bob to steal Alice’s secret integer x. A similar analysis can be conducted on Alice with respect to stealing Bob’s secret integer y. To conclude, x and y remain confidential throughout the whole process.

• Case 2. Attacks from the TP

The TP is expected to adhere to the protocol as designed and will not collude with the participants. However, despite following the rules, the TP may still attempt to extract additional information from the data it processes. Although the TP has knowledge of $\left|{\alpha }_A\right.⟩$ ($\left|{\alpha }_B\right.⟩)$, which are generated by performing the rotation operation with the angle ${\theta }_A+{\theta }_{AB}$ ${(\theta }_B+{\theta }_{AB})$ on quantum state $\left|0\right.⟩$, she cannot extract Alice’s or Bob’s private information without access to the shared secret key ${\theta }_{AB}$. Without knowing ${\theta }_{AB}$, $\left|{\alpha }_A\right.⟩$ ($\left|{\alpha }_B\right.⟩)$ is unknown to the TP. Since an unknown quantum state is indistinguishable, the TP has no chance of knowing Alice’s secret integer x and Bob’s secret integer y. Therefore, the participants’ secret integers remain undisclosed to the TP.

5.3. Fairness

The fairness of the protocol is guaranteed by the introduction of a TP who announces the comparison result to both Alice and Bob. This simultaneous disclosure ensures that neither participant has an advantage over the other.

6. Comparison

A comparison between our protocol and several existing QPC protocols is presented in

Table 1. A comparison between our protocol and several existing QPC protocols.

Protocol	Quantum States Used	Need of Entanglement Swapping	Quantum Communication Methods	Technology Used	Quantum Measurement Method	Comparison Method
Ref. [26]	EPR pairs	No	Two-way	Unitary operations and hash function	Bell-basis	Bit-to-bit
Ref. [27]	Single photon	No	Two-way	Unitary operations	Single-particle	Bit-to-bit
Ref. [41]	GHZ states	No	Two-way	Rotation operations	GHZ-basis	Bit-to-bit
Ref. [42]	Four-particle cluster and extended Bell state	Yes	One-way	quantum-one-time pad	Bell-basis and extended-Bell-basis	Bit-to-bit
Ref. [43]	hyper-entangled GHZ states	Yes	One-way	quantum-one-time pad	Bell-basis	Bit-to-bit
Ref. [54]	d-dimensional Bell state	No	One-way	Unitary operation	Single-particle	Bit-to-bit
Ours	Single photon	No	One-way	Rotation operation	Single-particle	Secret-to-secret

, focusing on the quantum states used, the need for entanglement swapping, quantum communication methods, the technology used, the quantum measurement method, and the comparison method.

According to Table 1, our protocol offers several advantages over existing QPC protocols, including the following:

(1)

It uses a novel method for secret-to-secret comparison rather than the traditional bit-to-bit comparison, resulting in improved scalability;

(2)

It does not require entanglement swapping technology and integrates single-photon states, rotation operations, and the swap test as key components, facilitating easier implementation with quantum technology;

(3)

All qubits are transmitted using one-way communication, eliminating the need for wavelength quantum filters and photon number splitters to mitigate Trojan horse attacks;

(4)

It employs single-particle measurements instead of Bell-basis measurements, thereby reducing the measurement requirements.

7. Conclusions

In this paper, we propose a two-party quantum private comparison (QPC) protocol that utilizes the properties of the swap test to evaluate the similarity of two qubits. The participants compare their secret integers by encoding these integers directly into the amplitudes of single-photon states, which are concealed using rotation operations. Without knowledge of the rotation angles, the encoded single-photon states remain secure. By introducing a semi-honest third party (TP) to facilitate the comparison between participants without accessing their private information, the protocol ensures fairness. Simulations conducted on the IBM Quantum Platform demonstrate the protocol’s feasibility, while a security analysis confirms its resilience against potential eavesdropping and participant attacks. Compared with existing QPC protocols that employ bit-to-bit comparison methods, our approach offers enhanced practicality and scalability. The integration of single-photon states, rotation operations, and the swap test as key components for direct secret comparison simplifies implementation with modern technology. In the future, we will focus on applying this protocol to the areas of quantum voting and quantum auctions, exploring its potential to enhance security and privacy in these critical applications.