Two-Party Quantum Private Comparison Protocol for Direct Secret Comparison
Abstract
1. Introduction
2. Swap Test and Rotation Operation
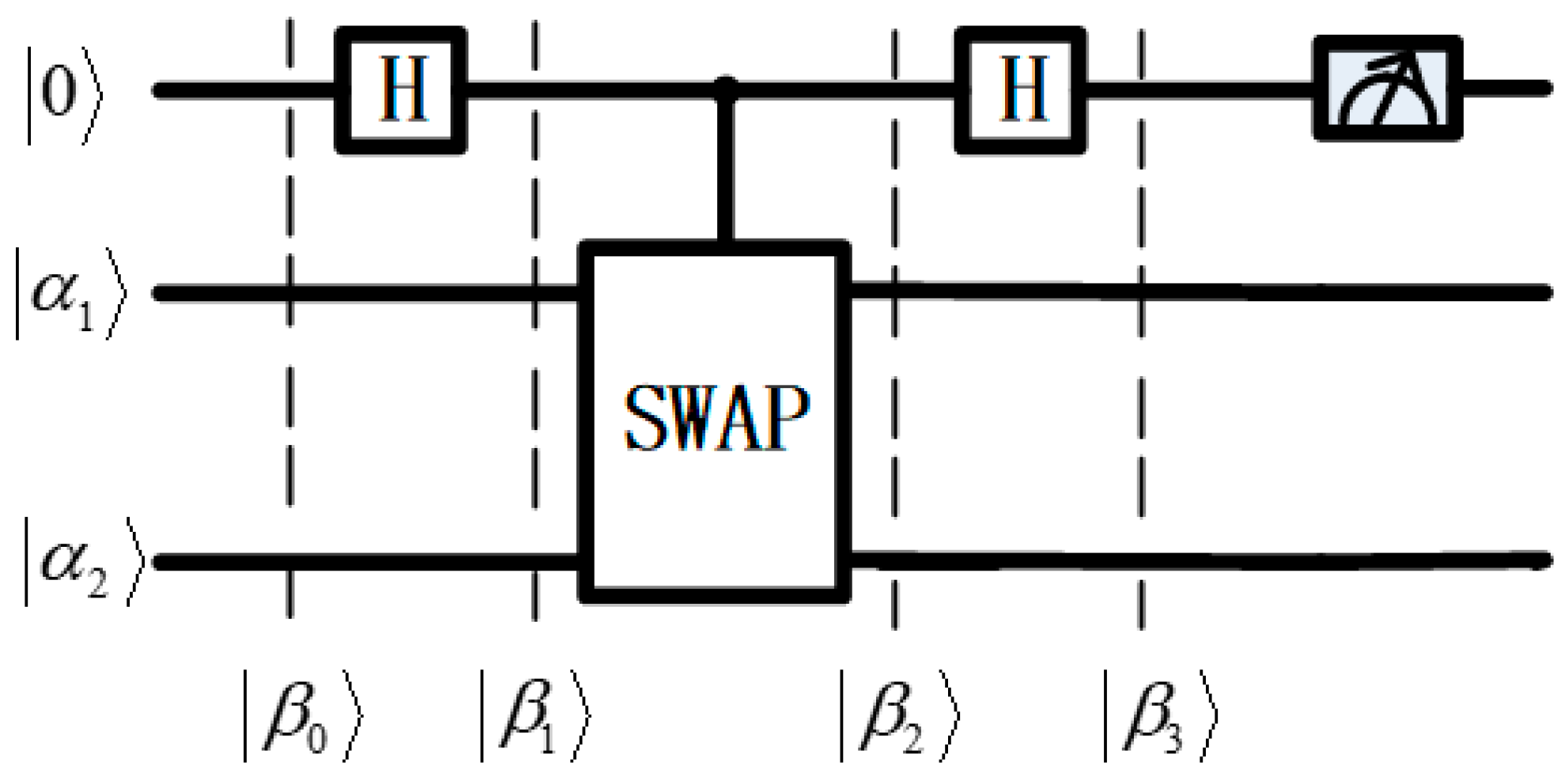
2.1. Swap Test
2.2. Rotation Operation
3. The Proposed QPC Protocol
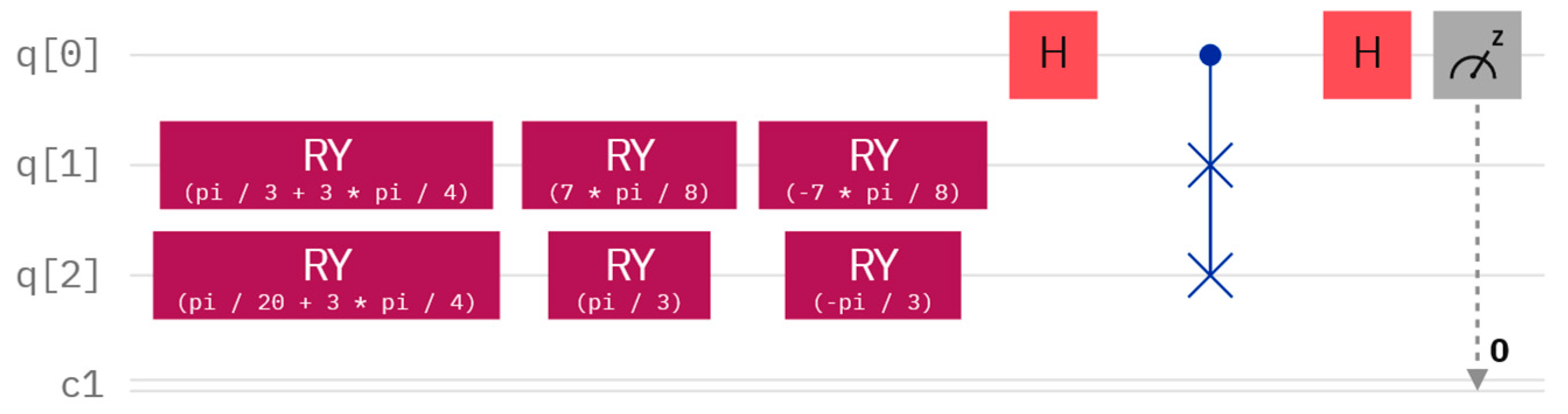
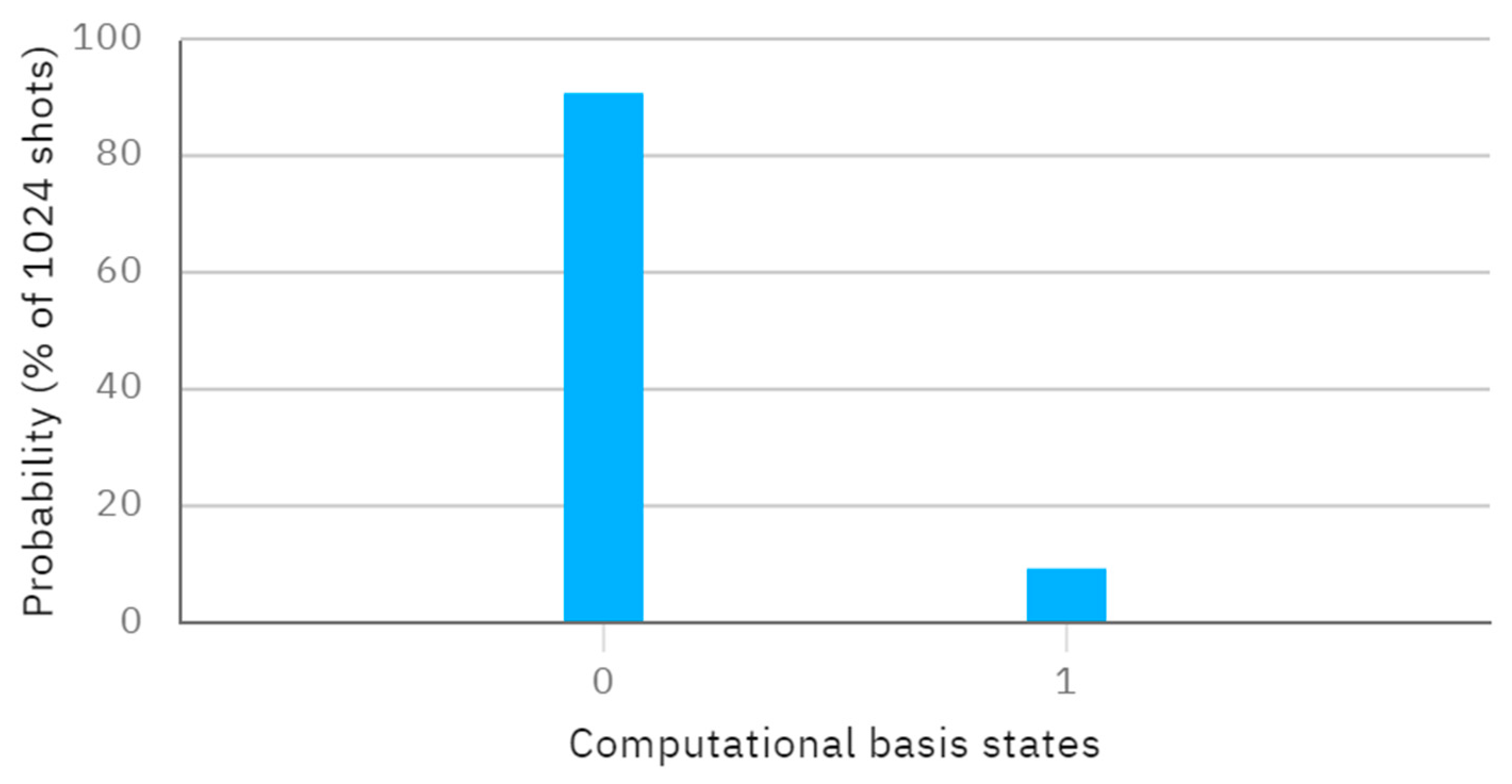
4. Simulation
5. Analysis
5.1. Correctness
5.2. Security
5.2.1. External Attacks
- Case I. The intercept-resend attack
- Case II. The direct measure attack
- Case III. The entangle-measure attack
- Case IV. The Trojan horse attacks
5.2.2. Participant Attacks
- Case 1. Attacks from Alice (Bob)
- Case 2. Attacks from the TP
5.3. Fairness
6. Comparison
- (1)
- It uses a novel method for secret-to-secret comparison rather than the traditional bit-to-bit comparison, resulting in improved scalability;
- (2)
- It does not require entanglement swapping technology and integrates single-photon states, rotation operations, and the swap test as key components, facilitating easier implementation with quantum technology;
- (3)
- All qubits are transmitted using one-way communication, eliminating the need for wavelength quantum filters and photon number splitters to mitigate Trojan horse attacks;
- (4)
- It employs single-particle measurements instead of Bell-basis measurements, thereby reducing the measurement requirements.
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bennett, C.H.; Brassard, G. Quantum cryptography: Public key distribution and coin tossing. In Proceedings of the IEEE International Conference on Computers Systems and Signal Processing, Bangalore, India, 10–12 December 1984; pp. 175–179. [Google Scholar]
- Zhang, W.; van Leent, T.; Redeker, K. A device-independent quantum key distribution system for distant users. Nature 2022, 607, 687–691. [Google Scholar] [CrossRef] [PubMed]
- Xu, F.; Ma, X.; Zhang, Q. Secure quantum key distribution with realistic devices. Rev. Mod. Phys. 2020, 92, 025002. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, W.J.; Jiang, C. Experimental twin-field quantum key distribution over 1000 km fiber distance. Phys. Rev. Lett. 2023, 130, 210801. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.Z.; Zhang, Y.Z.; Zhen, Y.Z. Toward a photonic demonstration of device-independent quantum key distribution. Phys. Rev. Lett. 2022, 129, 050502. [Google Scholar] [CrossRef] [PubMed]
- Mehic, M.; Niemiec, M.; Rass, S. Quantum key distribution: A networking perspective. ACM Comput. Surv. (CSUR) 2020, 53, 1–41. [Google Scholar] [CrossRef]
- Tsai, C.W.; Yang, C.W.; Lin, J. Multiparty mediated quantum secret sharing protocol. Quantum Inf. Process. 2022, 21, 63. [Google Scholar] [CrossRef]
- Hu, W.W.; Zhou, R.G.; Li, X. A novel dynamic quantum secret sharing in high-dimensional quantum system. Quantum Inf. Process. 2021, 20, 159. [Google Scholar] [CrossRef]
- Wang, S.; Liu, B.; Huang, W. Memory-free quantum secret sharing protocol with collective detection. Quantum Inf. Process. 2023, 22, 181. [Google Scholar] [CrossRef]
- Shen, A.; Cao, X.Y.; Wang, Y. Experimental quantum secret sharing based on phase encoding of coherent states. Sci. China Phys. Mech. Astron. 2023, 66, 260311. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, S.B.; Chang, Y. Quantum key agreement protocol based on quantum search algorithm. Int. J. Theor. Phys. 2021, 60, 838–847. [Google Scholar] [CrossRef]
- Karim, F.; Abulkasim, H.; Alabdulkreem, E. Improvements on new quantum key agreement protocol with five-qubit Brown states. Mod. Phys. Lett. A 2022, 37, 2250128. [Google Scholar] [CrossRef]
- Sheng, Y.B.; Zhou, L.; Long, G.L. One-step quantum secure direct communication. Sci. Bull. 2022, 67, 367–374. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Sun, Z.; Qi, R. Realization of quantum secure direct communication over 100 km fiber with time-bin and phase quantum states. Light Sci. Appl. 2022, 11, 83. [Google Scholar] [CrossRef]
- Cao, Z.; Lu, Y.; Chai, G. Realization of quantum secure direct communication with continuous variable. Research 2023, 6, 0193. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Zhang, S.; Chang, Y. Quantum secure direct communication based on quantum homomorphic encryption. Mod. Phys. Lett. A 2021, 36, 2150263. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, W.; Zhang, S. Quantum multi-party private set intersection using single photons. Phys. A Stat. Mech. Its Appl. 2024, 649, 129974. [Google Scholar] [CrossRef]
- Debnath, S.K.; Dey, K.; Kundu, N. Feasible private set intersection in quantum domain. Quantum Inf. Process. 2021, 20, 41. [Google Scholar] [CrossRef]
- Liu, W.J.; Li, W.B.; Wang, H.B. An improved quantum private set intersection protocol based on hadamard gates. Int. J. Theor. Phys. 2022, 61, 53. [Google Scholar] [CrossRef]
- Chen, Y.; Situ, H.; Huang, Q. A novel quantum private set intersection scheme with a semi-honest third party. Quantum Inf. Process. 2023, 22, 429. [Google Scholar] [CrossRef]
- Yao, A.C. Protocols for secure computations. In Proceedings of the 23rd IEEE Symposium on Foundations of Computer Science (FOCS’ 82), Washington, DC, USA, 3–5 November 1982; p. 160. [Google Scholar]
- Boudot, F.; Schoenmakers, B.; Traore, J. A fair and efficient solution to the socialist millionaires’ problem. Discret. Appl. Math. 2001, 111, 23–36. [Google Scholar] [CrossRef]
- Lo, H.K. Insecurity of quantum secure computations. Phys. Rev. A 1997, 56, 1154–1162. [Google Scholar] [CrossRef]
- Shor, P.W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM Rev. 1999, 41, 303–332. [Google Scholar] [CrossRef]
- Grover, L.K. Quantum mechanics helps in searching for a needle in a haystack. Phys. Rev. Lett. 1997, 79, 325. [Google Scholar] [CrossRef]
- Yang, Y.G.; Wen, Q.Y. An efficient two-party quantum private comparison protocol with decoy photons and two-photon entanglement. J. Phys. A Math. Theor. 2009, 42, 055305. [Google Scholar] [CrossRef]
- Hou, M.; Wu, Y. Single-photon-based quantum secure protocol for the socialist millionaires’ problem. Front. Phys. 2024, 12, 1364140. [Google Scholar] [CrossRef]
- Liu, B.; Gao, F.; Jia, H.Y. Efficient quantum private comparison employing single photons and collective detection. Quantum Inf. Process. 2013, 12, 887–897. [Google Scholar] [CrossRef]
- Chen, X.B.; Su, Y.; Niu, X.X. Efficient and feasible quantum private comparison of equality against the collective amplitude damping noise. Quantum Inf. Process. 2014, 13, 101–112. [Google Scholar] [CrossRef]
- Liu, B.; Xiao, D.; Huang, W. Quantum private comparison employing single-photon interference. Quantum Inf. Process. 2017, 16, 180. [Google Scholar] [CrossRef]
- Kou, T.Y.; Che, B.C.; Dou, Z. Efficient quantum private comparison protocol utilizing single photons and rotational encryption. Chin. Phys. B 2022, 31, 060307. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, W.F.; Zhang, S.B. Efficient multiparty quantum private comparison protocol based on single photons and rotation encryption. Quantum Inf. Process. 2023, 22, 272. [Google Scholar] [CrossRef]
- Wen, L.; Wang, Y.B.; Wei, C. Quantum private comparison protocol based on Bell entangled states. Commun. Theor. Phys. 2012, 57, 583. [Google Scholar]
- Tseng, H.Y.; Lin, J.; Hwang, T. New quantum private comparison protocol using EPR pairs. Quantum Inf. Process 2012, 11, 373–384. [Google Scholar] [CrossRef]
- Hou, M.; Sun, S.Y.; Zhang, W. Quantum private comparison for the socialist millionaire problem. Front. Phys. 2024, 12, 1408446. [Google Scholar] [CrossRef]
- Hou, M.; Wu, Y. New Quantum Private Comparison Using Bell States. Entropy 2024, 26, 682. [Google Scholar] [CrossRef] [PubMed]
- Lang, Y.F. Quantum private comparison using single bell state. Int. J. Theor. Phys. 2021, 60, 4030–4036. [Google Scholar] [CrossRef]
- Lang, Y.F. Quantum gate-based quantum private comparison. Int. J. Theor. Phys. 2020, 59, 833–840. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, S.B.; Chang, Y. Efficient quantum private comparison based on entanglement swapping of bell states. Int. J. Theor. Phys. 2021, 60, 3783–3796. [Google Scholar] [CrossRef]
- Hou, M.; Wu, Y. Efficient Quantum Private Comparison with Unitary Operations. Mathematics 2024, 12, 3541. [Google Scholar] [CrossRef]
- Hou, M.; Wu, Y.; Zhang, S. Efficient Quantum Private Comparison Based on GHZ States. Entropy 2024, 26, 413. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Chen, X.; Li, H. Efficient quantum private comparison protocol based on the entanglement swapping between four-qubit cluster state and extended Bell state. Quantum Inf. Process. 2019, 18, 158. [Google Scholar] [CrossRef]
- Gianni, J.; Qu, Z. New quantum private comparison using hyperentangled ghz state. J. Quantum Comput. 2021, 3, 45–54. [Google Scholar] [CrossRef]
- Chen, X.B.; Xu, G.; Niu, X.X.; Wen, Q.Y.; Yang, Y.X. An efficient protocol for the private comparison of equal information based on the triplet entangled state and single-particle measurement. Opt. Commun. 2010, 283, 1561–1565. [Google Scholar] [CrossRef]
- Ye, T.Y.; Ji, Z.X. Two-party quantum private comparison with five-qubit entangled states. Int. J. Theor. Phys. 2017, 56, 1517–1529. [Google Scholar] [CrossRef]
- Sun, Q. Quantum private comparison with six-particle maximally entangled states. Mod. Phys. Lett. A 2022, 37, 2250149. [Google Scholar] [CrossRef]
- Ji, Z.X.; Zhang, H.G.; Fan, P.R. Two-party quantum private comparison protocol with maximally entangled seven-qubit state. Mod. Phys. Lett. A 2019, 34, 1950229. [Google Scholar] [CrossRef]
- Fan, P.; Rahman, A.U.; Ji, Z. Two-party quantum private comparison based on eight-qubit entangled state. Mod. Phys. Lett. A 2022, 37, 2250026. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, S.B.; Cheng, W. Quantum Private Comparison Based on GHZ-type States. In Proceedings of the 2021 IEEE AFRICON, Arusha, Tanzania, 13–15 September 2021; pp. 1–4. [Google Scholar]
- Ji, Z.; Zhang, H.; Wang, H. Quantum private comparison protocols with a number of multi-particle entangled states. IEEE Access 2019, 7, 44613–44621. [Google Scholar] [CrossRef]
- Hou, M.; Wu, Y.; Zhang, S. New Quantum Private Comparison Using Four-Particle Cluster State. Entropy 2024, 26, 512. [Google Scholar] [CrossRef]
- Chang, Y.; Zhang, W.B.; Zhang, S.B. Quantum private comparison of equality based on five-particle cluster state. Commun. Theor. Phys. 2016, 66, 621. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, S.; Xia, J. Efficient Quantum Private Comparison Using Locally Indistinguishable Orthogonal Product States. In Proceedings of the 8th International Conference on Artificial Intelligence and Security, Qinghai, China, 15–20 July 2022; Springer International Publishing: Cham, Switzerland, 2022; pp. 260–273. [Google Scholar]
- Lin, S.; Sun, Y.; Liu, X.F. Quantum private comparison protocol with d-dimensional Bell states. Quantum Inf. Process. 2013, 12, 559–568. [Google Scholar] [CrossRef]
- Guo, F.Z.; Gao, F.; Qin, S.J. Quantum private comparison protocol based on entanglement swapping of d-level Bell states. Quantum Inf. Process. 2013, 12, 2793–2802. [Google Scholar] [CrossRef]
- Yu, C.H.; Guo, G.D.; Lin, S. Quantum private comparison with d-level single-particle states. Phys. Scr. 2013, 88, 065013. [Google Scholar] [CrossRef]
- Ye, C.Q.; Ye, T.Y. Multi-party quantum private comparison of size relation with d-level single-particle states. Quantum Inf. Process. 2018, 17, 252. [Google Scholar] [CrossRef]
- Song, X.L.; Wen, A.J.; Gou, R. Multiparty quantum private comparison of size relation based on single-particle states. IEEE Access 2019, 7, 142507–142514. [Google Scholar] [CrossRef]
- Buhrman, H.; Cleve, R.; Watrous, J. Quantum fingerprinting. Phys. Rev. Lett. 2001, 87, 167902. [Google Scholar] [CrossRef] [PubMed]
- Kang, M.S.; Choi, H.W.; Pramanik, T. Universal quantum encryption for quantum signature using the swap test. Quantum Inf. Process. 2018, 17, 254. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, S.; Lin, C. Quantum Fuzzy Support Vector Machine for Binary Classification. Comput. Syst. Sci. Eng. 2023, 45, 2783–2794. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, W.; Zhang, S. Practical quantum protocols for blind millionaires’ problem based on rotation encryption and swap test. Phys. A Stat. Mech. Its Appl. 2024, 637, 129614. [Google Scholar] [CrossRef]
- Huang, X.; Chang, Y.; Cheng, W. Quantum private comparison of arbitrary single qubit states based on swap test. Chin. Phys. B 2022, 31, 040303. [Google Scholar] [CrossRef]
- Li, Z.H.; Wang, L.; Xu, J. Counterfactual trojan horse attack. Phys. Rev. A 2020, 101, 022336. [Google Scholar] [CrossRef]

| Protocol | Quantum States Used | Need of Entanglement Swapping | Quantum Communication Methods | Technology Used | Quantum Measurement Method | Comparison Method |
|---|---|---|---|---|---|---|
| Ref. [26] | EPR pairs | No | Two-way | Unitary operations and hash function | Bell-basis | Bit-to-bit |
| Ref. [27] | Single photon | No | Two-way | Unitary operations | Single-particle | Bit-to-bit |
| Ref. [41] | GHZ states | No | Two-way | Rotation operations | GHZ-basis | Bit-to-bit |
| Ref. [42] | Four-particle cluster and extended Bell state | Yes | One-way | quantum-one-time pad | Bell-basis and extended-Bell-basis | Bit-to-bit |
| Ref. [43] | hyper-entangled GHZ states | Yes | One-way | quantum-one-time pad | Bell-basis | Bit-to-bit |
| Ref. [54] | d-dimensional Bell state | No | One-way | Unitary operation | Single-particle | Bit-to-bit |
| Ours | Single photon | No | One-way | Rotation operation | Single-particle | Secret-to-secret |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, M.; Wu, Y. Two-Party Quantum Private Comparison Protocol for Direct Secret Comparison. Mathematics 2025, 13, 326. https://doi.org/10.3390/math13020326
Hou M, Wu Y. Two-Party Quantum Private Comparison Protocol for Direct Secret Comparison. Mathematics. 2025; 13(2):326. https://doi.org/10.3390/math13020326
Chicago/Turabian StyleHou, Min, and Yue Wu. 2025. "Two-Party Quantum Private Comparison Protocol for Direct Secret Comparison" Mathematics 13, no. 2: 326. https://doi.org/10.3390/math13020326
APA StyleHou, M., & Wu, Y. (2025). Two-Party Quantum Private Comparison Protocol for Direct Secret Comparison. Mathematics, 13(2), 326. https://doi.org/10.3390/math13020326






