On the Exponential Atom-Bond Connectivity Index of Graphs
Abstract
1. Introduction
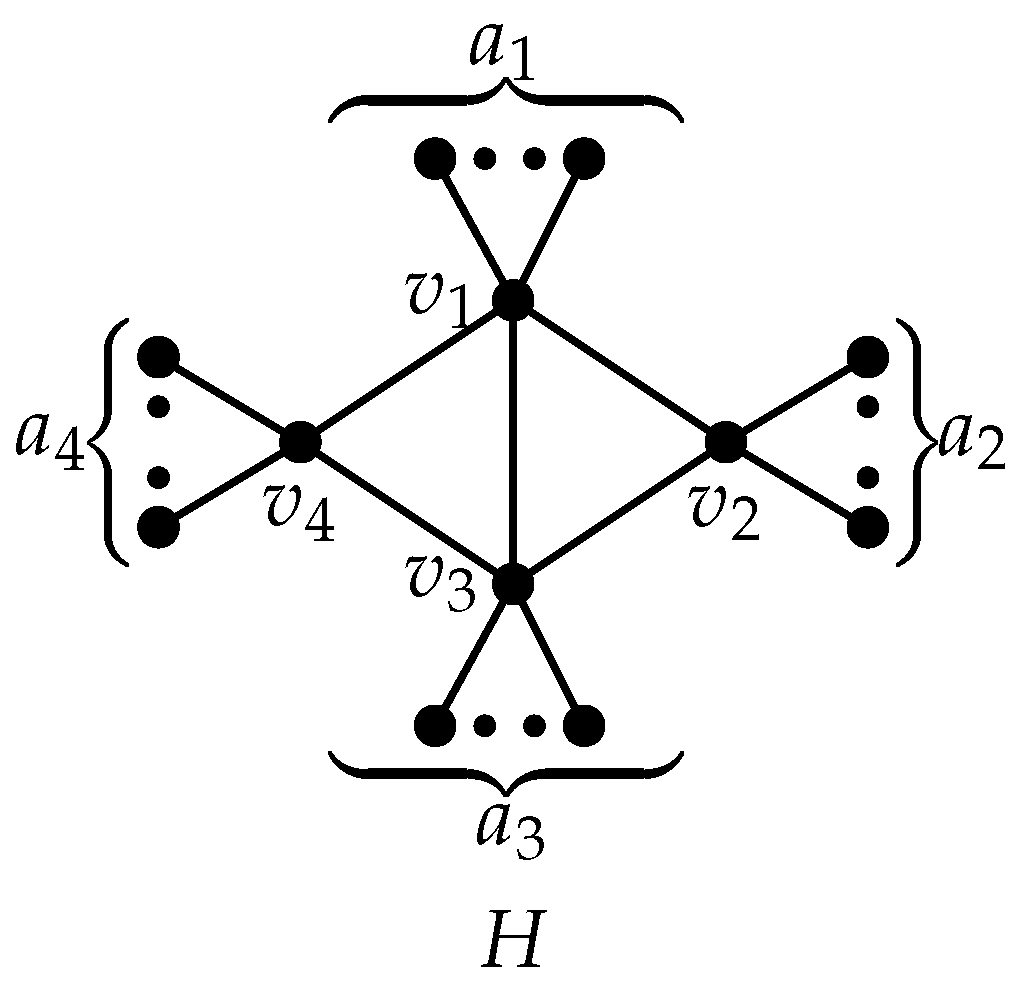
2. On the Second Maximal Trees of Exponential Atom-Bond Connectivity Index
3. Upper Bounds on of Unicyclic and Bicyclic Graphs
4. Some Relations Between and ABC() of Graphs
5. Conclusions and Future Work
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| q | f (6, q) |
|---|---|
| 1 | 11.189 |
| 2 | 10.998 |
| q | |
|---|---|
| 1 | 13.84 |
| 2 | 13.564 |
| q | f (46, q) |
|---|---|
| 1 | 119.614 |
| 2 | 119.159 |
| 3 | 118.923 |
| 4 | 118.778 |
| 5 | 118.68 |
| 6 | 118.608 |
| 7 | 118.554 |
| 8 | 118.512 |
| 9 | 118.478 |
| 10 | 118.45 |
| 11 | 118.428 |
| 12 | 118.409 |
| 13 | 118.393 |
| 14 | 118.38 |
| 15 | 118.37 |
| 16 | 118.361 |
| 17 | 118.354 |
| 18 | 118.348 |
| 19 | 118.344 |
| 20 | 118.341 |
| 21 | 118.339 |
| 22 | 118.338 |
| q | |
|---|---|
| 1 | 116.897 |
| 2 | 116.441 |
| 3 | 116.206 |
| 4 | 116.061 |
| 5 | 115.963 |
| 6 | 115.892 |
| 7 | 115.838 |
| 8 | 115.795 |
| 9 | 115.762 |
| 10 | 115.735 |
| 11 | 115.712 |
| 12 | 115.694 |
| 13 | 115.678 |
| 14 | 115.666 |
| 15 | 115.655 |
| 16 | 115.647 |
| 17 | 115.64 |
| 18 | 115.635 |
| 19 | 115.631 |
| 20 | 115.628 |
| 21 | 115.627 |
References
- Todeschini, R.; Consonni, V. Handbook of Molecular Descriptors; Wiley-VCH: Weinheim, Germany, 2000. [Google Scholar]
- Furtula, B.; Gutman, I.; Dehmer, M. On structure-sensitivity of degree-based topological indices. Appl. Math. Comput. 2013, 219, 8973–8978. [Google Scholar] [CrossRef]
- Gutman, I.; Trinajstić, N. Graph theory and molecular orbitals. Total π-electron energy of alternant hydrocarbons. Chem. Phys. Lett. 1972, 17, 535–538. [Google Scholar] [CrossRef]
- Randić, M. On characterization of molecular branching. J. Am. Chem. Soc. 1975, 97, 6609–6615. [Google Scholar] [CrossRef]
- Zhong, L. The harmonic index for graphs. Appl. Math. Lett. 2012, 25, 561–566. [Google Scholar] [CrossRef]
- Chen, X. General sum-connectivity index of a graph and its line graph. Appl. Math. Comput. 2023, 443, 127779. [Google Scholar] [CrossRef]
- Zhou, B.; Trinajstić, N. On a novel connectivity index. J. Math. Chem. 2009, 46, 1252–1270. [Google Scholar] [CrossRef]
- Das, K.C.; Mondal, S. On neighborhood inverse sum indeg index of molecular graphs with chemical significance. Inf. Sci. 2023, 623, 112–131. [Google Scholar] [CrossRef]
- Vukičević, D.; Furtula, B. Topological index based on the ratios of geometrical and arithmetical means of end-vertex degrees of edges. J. Math. Chem. 2009, 46, 1369–1376. [Google Scholar] [CrossRef]
- Estrada, E.; Torres, L.; Rodríguez, L.; Gutman, I. An atom-bond connectivity index: Modelling the enthalpy of formation of alkanes. Indian J. Chem. 1998, 37A, 849–855. [Google Scholar]
- Li, F.; Ye, Q. Extremal graphs with given parameters in respect of general ABS index. Appl. Math. Comput. 2024, 482, 128974. [Google Scholar] [CrossRef]
- Xing, R.; Zhou, B.; Dong, F. On atom–bond connectivity index of connected graphs. Discret. Appl. Math. 2011, 159, 1617–1630. [Google Scholar] [CrossRef]
- Albalahi, A.M.; Milovanović, E.; Ali, A. General atom-bond sum-connectivity index of graphs. Mathematics 2023, 11, 2494. [Google Scholar] [CrossRef]
- Gutman, I. Geometric approach to degree-based topological indices: Sombor indices. MATCH Commun. Math. Comput. Chem. 2021, 86, 11–16. [Google Scholar]
- Furtula, B.; Graovac, A.; Vukičević, D. Augmented Zagreb index. J. Math. Chem. 2010, 48, 370–380. [Google Scholar] [CrossRef]
- Dehmer, M.; Grabner, M. The discrimination power of molecular identification numbers revisited. MATCH Commun. Math. Comput. Chem. 2013, 69, 785–794. [Google Scholar]
- Dehmer, M.; Grabner, M.; Varmuza, K. Information indices with high discriminative power for graphs. PLoS ONE 2012, 7, e31214. [Google Scholar] [CrossRef]
- Konstantinova, E.V. On some applications of information indices in chemical graph theory. In General Theory of Information Transfer and Combinatorics; Ahlswede, R., Ed.; Lecture Notes of Computer Science; Springer: Berlin/Heidelberg, Germany, 2006; pp. 831–852. [Google Scholar]
- Rada, J. Exponential vertex-degree-based topological indices and discrimination. MATCH Commun. Math. Comput. Chem. 2019, 82, 29–41. [Google Scholar]
- Carballosa, W.; Quintana, Y.; Rodríguez, J.M.; Sigarreta, J.M. Exponential topological indices: Optimal inequalities and applications. J. Math. Chem. 2023, 61, 933–949. [Google Scholar] [CrossRef]
- Cruz, R.; Monsalve, J.; Rada, J. Trees with maximum exponential Randić index. Discrete Appl. Math. 2020, 283, 634–643. [Google Scholar] [CrossRef]
- Cruz, R.; Rada, J. The path and the star as extremal values of vertex-degree-based topological indices among trees. MATCH Commun. Math. Comput. Chem. 2019, 82, 715–732. [Google Scholar]
- Das, K.C.; Elumalai, S.; Balachandran, S. Open problems on the exponential vertex-degree-based topological indices of graphs. Discret. Appl. Math. 2021, 293, 38–49. [Google Scholar] [CrossRef]
- Das, K.C.; Mondal, S.; Huh, D. On the exponential augmented Zagreb index of graphs. J. Appl. Math. Comput. 2024, 70, 839–865. [Google Scholar] [CrossRef]
- Das, K.C.; Mondal, S. On exponential geometric-arithmetic index of graphs. J. Math. Chem. 2023, 62, 2740–2760. [Google Scholar] [CrossRef]
- Das, K.C.; Mondal, S. On EAZ index of unicyclic and bicyclic graphs, general graphs in terms of the number of cut edges. J. Appl. Math. Comput. 2024, 70, 2995–3010. [Google Scholar] [CrossRef]
- Das, K.C.; Mondal, S.; Huh, D. Open Problem on the Maximum Exponential Augmented Zagreb Index of Unicyclic Graphs. Comput. Appl. Math. 2024, 43, 317. [Google Scholar] [CrossRef]
- Eliasi, M. Unicyclic and bicyclic graphs with maximum exponential second Zagreb index. Discret. Appl. Math. 2022, 307, 172–179. [Google Scholar] [CrossRef]
- Gao, W.; Gao, Y. The extremal trees for exponential vertex-degree-based topological indices. Appl. Math. Comput. 2024, 472, 128634. [Google Scholar] [CrossRef]
- Mondal, S.; Das, K.C. Complete Solution to Open Problems on Exponential Augmented Zagreb Index of Chemical Trees. Appl. Math. Comput. 2024, 482, 128983. [Google Scholar] [CrossRef]
- Xu, C.; Horoldagva, B.; Buyantogtokh, L. The exponential second Zagreb index of (n,m)-graphs. Mediterr. J. Math. 2023, 20, 181. [Google Scholar] [CrossRef]
- Zeng, M.; Deng, H. An open problem on the exponential of the second Zagreb index. MATCH Commun. Math. Comput. Chem. 2021, 85, 367–373. [Google Scholar]
- Cruz, R.; Monsalve, J.; Rada, J. On chemical trees that maximize atom-bond connectivity index, its exponential version, and minimize exponential geometric-arithmetic index. MATCH Commun. Math. Comput. Chem. 2020, 84, 691–718. [Google Scholar]
- Bondy, J.A.; Murty, U.S.R. Graph Theory with Applications; Macmillan Press: New York, NY, USA, 1976. [Google Scholar]
- Wolfram Research, Inc. Mathematica, Version 7.0; Wolfram Research, Inc.: Champaign, IL, USA, 2008. [Google Scholar]
- Stein, W.A. Sage Mathematics Software, Version 6.8; The Sage Development Team, 2015. Available online: http://www.sagemath.org (accessed on 21 December 2024).

| n | q | Maximum Value of | |
|---|---|---|---|
| (DSn−q−2,q) | |||
| 6 | 2 | 10.998 | 11.189 |
| 7 | 2 | 13.564 | 13.84 |
| 8 | [2,3] | 16.191 | 16.514 |
| 9 | [2,3] | 18.848 | 19.2 |
| 10 | [2,4] | 21.523 | 21.894 |
| 11 | [2,4] | 24.208 | 24.594 |
| 12 | [2,5] | 26.9 | 27.297 |
| 13 | [2,5] | 29.598 | 30.003 |
| 14 | [2,6] | 32.299 | 32.711 |
| 15 | [2,6] | 35.004 | 35.421 |
| 16 | [2,7] | 37.71 | 38.132 |
| 17 | [2,7] | 40.418 | 40.843 |
| 18 | [2,8] | 43.128 | 43.556 |
| 19 | [2,8] | 45.838 | 46.269 |
| 20 | [2,9] | 48.55 | 48.983 |
| 21 | [2,9] | 51.262 | 51.697 |
| 22 | [2,10] | 53.975 | 54.412 |
| 23 | [2,10] | 56.688 | 57.127 |
| 24 | [2,11] | 59.402 | 59.843 |
| 25 | [2,11] | 62.116 | 62.558 |
| 26 | [2,12] | 64.831 | 65.274 |
| n | q | Maximum Value of | |
|---|---|---|---|
| (DSn−q−2,q) | |||
| 27 | [2,12] | 67.546 | 67.99 |
| 28 | [2,13] | 70.261 | 70.706 |
| 29 | [2,13] | 72.976 | 73.423 |
| 30 | [2,14] | 75.692 | 76.139 |
| 31 | [2,14] | 78.408 | 78.856 |
| 32 | [2,15] | 81.124 | 81.572 |
| 33 | [2,15] | 83.84 | 84.289 |
| 34 | [2,16] | 86.556 | 87.006 |
| 35 | [2,16] | 89.272 | 89.723 |
| 36 | [2,17] | 91.989 | 92.44 |
| 37 | [2,17] | 94.705 | 95.157 |
| 38 | [2,18] | 97.422 | 97.875 |
| 39 | [2,18] | 100.139 | 100.592 |
| 40 | [2,19] | 102.856 | 103.309 |
| 41 | [2,19] | 105.573 | 106.027 |
| 42 | [2,20] | 108.29 | 108.744 |
| 43 | [2,20] | 111.007 | 111.461 |
| 44 | [2,21] | 113.724 | 114.179 |
| 45 | [2,21] | 116.441 | 116.897 |
| 46 | [2,22] | 119.159 | 119.614 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Das, K.C. On the Exponential Atom-Bond Connectivity Index of Graphs. Mathematics 2025, 13, 269. https://doi.org/10.3390/math13020269
Das KC. On the Exponential Atom-Bond Connectivity Index of Graphs. Mathematics. 2025; 13(2):269. https://doi.org/10.3390/math13020269
Chicago/Turabian StyleDas, Kinkar Chandra. 2025. "On the Exponential Atom-Bond Connectivity Index of Graphs" Mathematics 13, no. 2: 269. https://doi.org/10.3390/math13020269
APA StyleDas, K. C. (2025). On the Exponential Atom-Bond Connectivity Index of Graphs. Mathematics, 13(2), 269. https://doi.org/10.3390/math13020269






