Abstract
The existing quantitative geography literature contains a dearth of articles that span spatial autocorrelation (SA), a fundamental property of georeferenced data, and spatial optimization, a popular form of geographic analysis. The well-known location–allocation problem illustrates this state of affairs, although its empirical geographic distribution of demand virtually always exhibits positive SA. This latent redundant attribute information alludes to other tools that may well help to solve such spatial optimization problems in an improved, if not better than, heuristic way. Within a proof-of-concept perspective, this paper articulates connections between extensions of the renowned Majority Theorem of the minisum problem and especially the local indices of SA (LISA). The relationship articulation outlined here extends to the p = 2 setting linkages already established for the p = 1 spatial median problem. In addition, this paper presents the foundation for a novel extremely efficient p = 2 algorithm whose formulation demonstratively exploits spatial autocorrelation.
Keywords:
local spatial autocorrelation; majority theorem; spatial autocorrelation; spatial median; spatial optimization MSC:
62H11; 90C27
1. Introduction
One big data era theme lacking sufficient research efforts is the inter-disciplinary intersection of applied probability, statistics, and operations research dealing with spatial optimization involving the servicing of large numbers of demand locations with multiple supplier facilities. Its high dimensionality (e.g., see []) derives from its number of demand points, n, coupled with its number of spatial median supply locations, a solution requiring numerically intensive work because of it being a daunting combinatorial problem (e.g., see [,]). This paper exploits spatial statistics (e.g., []) to propose and develop new methodologies and theories to resolve such real-life challenges. In doing so, it advances a data-driven decision-making spatial optimization process.
Griffith et al. [] discuss that the integration of spatial optimization and spatial statistics can bring synergetic effects to answering optimal location siting questions, such as optimal location–allocation problems, adopting insightful findings from their individual separately developed literatures. Location problems face computational challenges, especially when they involve large numbers of demand and central facility (i.e., median) locations. Hence, studies often present heuristic solutions with improved initial solutions (e.g., []) or constraints that reflect spatial characteristics such as distance thresholds (e.g., []) and spatial contiguity (e.g., []). Some studies (e.g., [,]) further discuss that the spatial patterns of weight surfaces have an impact on location problem solutions. However, these narratives focus on explaining associations between these two components, and generally lack incorporating spatial patterns into spatial optimization model formulations. Such spatial patterns are often attributable to latent spatial autocorrelation (SA), which is a central concept in spatial statistics. Spatial statistical models incorporate SA terms, which are often specified with correlation parameters and linear combinations of spatial neighboring observation attribute values (e.g., spatial optimization demand point weights), extending traditional statistical models such as those for spatial regression techniques created from conventional linear and generalized regression specifications (e.g., []).
Griffith et al. [], augmenting Griffith [], Griffith et al. [], and Lee et al. [], document a relatively newly verbalized relationship between the p = 1 minisum solution [i.e., the spatial median, the answer to a problem for which Drezner et al. [] provide a thorough review] and local SA (note: local SA is the key ingredient for global SA because its manifestation is a particular mosaic of organized local SA clusters, as Moran eigenvector spatial filtering demonstrates (e.g., global, regional, and local components for positive SA; see []); the significant local SA clusters are extreme neighboring location dis/similar attribute point pairs, which are positioned at the opposite ends of a Moran scatterplot trendline data cloud, as well as pairs substantially deviating orthogonally in either direction from the trendline itself). In doing so, they link their discovery to its associated legendary majority theorem (MT-1; [,] p. 30, [] p. 148]). The formulation of MT-1 can be found in Griffith et al. []. This theorem states that when the weight on a single demand point is greater than half of the sum of the weights on all n demand points, then this demand point location is the optimal solution of the p = 1 spatial median problem, which finds a solution that minimizes the sum of weighted distances [i.e., it is a minisum problem (see [] for its proof)]. One compelling feature of this MT-1 known analytical result is that it enables easily verifiable numerical experiments. These most recent efforts also produced a new egalitarian theorem (ET-1), describing essentially the opposite circumstances depicted by the MT situation.
The selected operations research literature furnishes a contextualizing backdrop to this mostly ignored liaison in an interface between global/local SA and optimization. In Computers & Operations Research, Williams [] pp. 496–497 speculates about this association in global SA environments. Thirteen European Journal of Operational Research articles span mentioning (e.g., [] p. 263) to extensively employing (e.g., []) it when such global manifestations exist—with its localized attention focusing on scattered micro groupings rather than a solitary macro (i.e., global) map pattern of weights. Ten Annals of Operations Research papers published between 2000 and 2023 also recognize SA, from incorporating it into natural resource optimization models [] p. 77, through missing values imputation [] and utilizing the local indicators of SA (LISA) as objectives in a multicriteria framework [], to geographic-clustering-informed spatial optimization []. And, a set of three papers appearing in Operational Research that range from acknowledging without explicitly accounting for it [], through optimizing the hot/cold spot geographic clusters it spotlights [], to again exploiting it to spatially interpolate missing values []. In other words, SA has become a more exposed spatial optimization concern during the last quarter century, with a much greater interest in it materializing in the past decade. Nevertheless, the connection between SA and spatial optimization still remains under investigation. Current studies appearing in the existing literature are often limited to speculative links between the two, or to utilizing spatial statistical tools for either missing value imputations or the identification of geographic clustering patterns. The practical application of SA to enhance spatial optimization has largely been unincorporated into the specifications of spatial optimization models []. Additionally, the increasing complexities of analytical solutions for spatial optimization—particularly with the problem size growth as well as the growth itself—have posed significant challenges. These complexities have hindered theoretical and/or conceptual developments in this field, despite contributions by some recent studies [,,]. This literature gap underscores the need for further exploration of the integration of these two research areas.
1.1. The Objective of This Paper
This paper extends MT-1 to a novel p = 2 MT conjecture (MTC-2), while also postulating a conjectural extension of ET-1 to the p = 2 case (ETC-2). Restricting attention here to the p = 2 case allows a more comprehensive examination of the simplest situation (e.g., exact solutions are feasible for massive numbers of demand locations), in which competitive allocations of demand points occur. A noteworthy ET-1 implication arising from the generalization of a single dominant weight demand point to a coterminous geographic cluster of extremely large weight points collectively being dominant is that spatial optimization potentially misidentifies this swath of similar nearby outlier value weights with local positive SA (the Getis-Ord Gi* local SA statistic can furnish insights into this scenario []). The MTC-2 model accommodates collective dominating weights rather than relying on a single dominating weight. It incorporates the observation that p = 2 solutions tend to emerge on opposite sides of the p = 1 solution, reminiscent of the first and third quartiles positioning themselves on both sides of a univariate median. Additionally, the MT-1 model can be leveraged to identify a single dominating weight within each of the two resulting subgroups, enhancing its scalability for spatial optimization. These foci are the original contributions of this paper that differentiate it from its earlier p = 1 counterpart. A principal motivation latent in this confluence nucleus is a necessity to address the gap between location–allocation research and the increasing recognition that SA is everywhere in the real world, and, paralleling the universal role of means and variances in data analyses, is a fundamental property of geospatial data that virtually always merits acknowledgment.
Of course, other issues may be relevant, too, such as the MAUP [], whose aggregation error (e.g., using the average distance and average weight for each individual point in a local geographic distribution) impacts on optimal solutions and already has a lengthy discussion appearing in the literature (e.g., []). Meanwhile, Lee et al. [], for example, investigate the relationships between the MAUP and global SA. Although these and other topics are important, and deserve careful and detailed further examination, they are beyond the scope of this paper, and as such, constitute future research pursuits. The findings reported in this paper are scalable in geographic resolution, planar surface partitioning, and geographic scale, and hence should be robust to these three particular data features.
The research problem addressed in this paper is to determine the optimal locations {(Uj, Vj), j = 1, 2} on a continuous surface for two facilities, with no constraint on capacity (i.e., uncapacitated location–allocation problems), to serve a geographically distributed set of demand points [finding a pair of points (p = 2) on a continuous surface that jointly minimize the sum of weighted Euclidean distances to them from a designated set of demand points], which may be stated in the objective function form as follows:
where λij denotes a pair of dichotomous 0–1 indicator variables for each location i, with λi1 = 1 if its allocation is to the first facility (j = 1) or λi2 = 1 if its allocation is to the second facility (j = 2), (ui, vi) are the posited set of n demand point Cartesian coordinates, and wi > 0 is the weight quantifying demand at point i.
The point (Uj, Vj) also is the spatial median for the demand points constituting the allocation to facility j (i.e., λij = 1). One challenging difficulty here is that the objective function (1) minimum is not necessarily unique (see Figure 1, which also illustrates that the magnitude of non-uniqueness can be a function of geographic region shape [,] pp. 76–77); this feature is more notorious for uniform distribution contexts. Furthermore, if = 0, then the spatial median (Uj, Vj) coincides with the location (ui, vi) of demand point i; in contrast, obviously if wi = 0, then location i effectively disappears from the set of demand points in this spatial optimization problem, regardless of the location of its accompanying point. Solving this p = 2 median problem essentially reduces to, in a methodical way, iteratively allocating each of n demand points to one of two nonoverlapping coterminous geographic regions (note: this situation spawned the p = 2 specific TWAIN algorithm, an implementation of this conceptualization that very efficiently solves the p = 2 median problem [] p. 210), and then applying the Kuhn–Kuenne [] algorithm (note: an independent rediscovery—e.g., [] p. 835—of the Weiszfeld [] algorithm for optimally solving the p = 1 Weber problem case, as was also conducted by Miehle [], by Cooper [], and by Vergin and Rodgers [], among others) to the subset of points contained in each region [initiating this computation with each region’s spatial mean [i.e., bivariate weighted arithmetic average ] to compute its spatial median (note: an equivalent statistical solution is to set a nonlinear regression’s left-hand side response variable Y identically equal to 0 (i.e., it becomes a constant), and its right-hand side to . This specification yields the parameter estimates Uj and Vj for the spatial median (Uj, Vj), j = 1, 2); the iteration involving reallocations and spatial median [i.e., , where di denotes the Euclidean distance for each of the p allocation regions] recalculations continues until convergence.
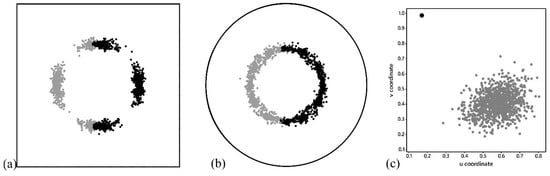
Figure 1.
Geographic distributions of 1000 p = 2 solutions for a uniform distribution of demand across a regular hexagonal lattice; gray and black filled circles, respectively, denote the first and second of a spatial median pair (post-sorted by axes positions). Left (a): a unit square landscape (n = 144); equally likely north-south or east-west solutions. Middle (b): a unit circle landscape (n = 112); very many (e.g., an infinite number of) equally likely essentially inner-circle-diameter-length separated solution pairs. Right (c): a single dominant weight (denoted by a solid black circle; the MT case) demand location held constant (n = 100) across simulation replications.
1.2. The Content Organized of This Paper
This paper has four ensuing sections. The next one addresses solving the uncapacitated p = 2 median problem. Its sequel summarizes the special formal mathematical properties of this p = 2 median problem. Next, arguments are put forth establishing the solution utility of a specific spatial statistical tool (i.e., local SA indices) in the presence of two dominant demand point weights in a p = 2 median problem. The final section enumerates salient conclusions and implications.
2. Solving the Uncapacitated p = 2 Median Problem
Rushton et al. [] furnished a number of Fortran computer code programs to calculate the exact solutions for this problem, including TWAIN, that very efficiently solves only the p = 2 case. The number of possible distinct two-group demand point combinations is 2n [one of these is the empty set, which when subtracted yields (2n − 1)]; the subset number of non-empty two-group combinations (i.e., a requirement for the existence of two central facilities) is the Stirling number of the second kind (i.e., 2n−1 − 1; note: using p = 2 location–allocation phraseology and a combinatorial mathematics context, it is the number of ways to partition—i.e., group—a set of n demand points into 2 non-empty subsets—i.e., each subset must contain at least one demand point; see []); subtraction of the one is for the empty set, whereas the loss of the other 16 (for the n = 5 case) combinations is because allocating k demand points to one group and (5 − k) to the other is the same as allocating (5 − k) to one group and k to the other, k = 1, 2, …, 4. In other words, five of these possibilities have one demand point in one and four in the other group, where the group order is unimportant, and ten of these combinatoric possibilities have two in one and three in the other group, again with the group order being unimportant.
The planar surface upon which the p = 2 spatial median problem resides allows a further reduction in the number of candidate solution combinations to nC2 = n (n − 1)/2 []; for the illustrative example in this section, the number of geographic assessments is n (n − 1)/2 = 5 (5 − 1)/2 = 10. This is a count of the number of possible pairs of points supporting the construction of a Thiessen polygon boundary separating them into groups (re all points within a Thiessen polygon are closer to its designated generator point than to any other point on a planar surface, using the Euclidean distance metric). TWAIN is the algorithm used to obtain solutions of this type reported in this paper.
The conceivable partitionings for a randomly selected specimen unit square example appear in Figure 2; the various Thiessen polygon boundary lines traversing this geographic landscape are superimposed perpendicular bisectors (the corresponding equation comes from []) for the 10 possible point pairs.
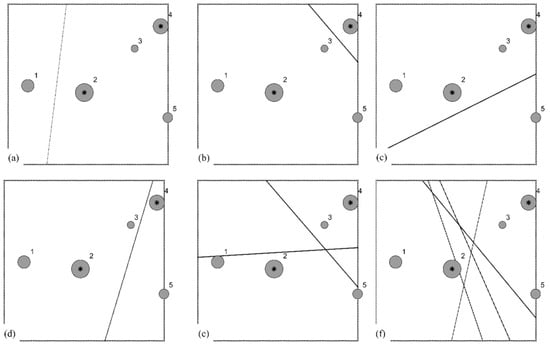
Figure 2.
The geographic distribution of all possible non-empty planar groups of a specimen set of five demand points in a unit square: gray circles are proportional to weight quantities, asterisks denote the pair of optimal spatial medians, and the line transects are the perpendicular bisectors of straight lines connecting a pair of designated demand points; the integer name order of weights is {6, 14, 2, 10, 5}. Top left (a): {1; 2, 3, 4, 5}. Top middle (b): {4; 1, 2, 3, 5}. Top right (c): {5; 1, 2, 3, 4}. Bottom left (d): {4, 5; 1, 2, 3}. Bottom middle (e): {3, 4; 1, 2, 5} from two partitionings; the optimal solution. Bottom right (f): {1, 2; 3, 4, 5} from four partitionings.
The specimen set of demand points portrayed in Figure 2 also has a primary (#2, w = 14) and a secondary (#4, w = 10) dominant weight; for the optimal solution, 14 > 6 + 5, and 10 > 2. Table 1 tabulates all possible planar and non-empty set outcomes, demonstrating that this TWAIN solution approach eliminates by fiat five infeasible combinations of demand points from the number of non-empty two-group possibilities, as well as another four lacking a Thiessen polygon derivable combination. In other words, four partitionings automatically yield the optimal solution, and five additional partitionings iterate to the optimal solution. A substantial reduction in the original number of necessitated branch-and-bound executions to achieve optimality occurs with this tactic, making much larger demand point sets amenable to solving. Note that the optimal solutions in each of the two subgroups can be derived from MT-1. For example, MT-1 indicates that the optimal p = 1 solutions in each Thiessen polygon in Figure 2b are #2 and #4, respectively, because their weights are greater than 50% of the sum of all weights within each Thiessen polygon. This reflection provides some insight, paralleling how MT-2 is derivable from MT-1, which is presented in Section 3.

Table 1.
Enumeration of TWAIN-inspired Figure 2 specimen demand point set combinations.
3. Special Formal Mathematical Properties of the p = 2 Median Problem
The past, present, and continual future improvement of computing environments (e.g., Moore’s Law; note: the number of transistors in a dense integrated circuit (i.e., a chip) doubles roughly every two years, a claim holding since 1975 []) has been a boon to spatial optimization; in particular, the growth in the size of solvable problems attributable to computational advances (e.g., computing power and sophisticated solution algorithms/procedures) increasingly pushes the boundaries of tractability outward. In combination, the refinements advocated by these developments rationalized the implementation and performance of spatial optimization in geographic information systems (GISs), allowing such geospatial analyses to contribute to both GIScience theory and practice. This section expressly adds to this theory part by creating several innovative conjectures that serendipitously allude to global and local SA.
3.1. An ETC-2 Proposition
Griffith et al. [] provide a theorem stating that the p = 1 solution concentrates in the center of a set of demand points with either a constant, or, on average, an identically distributed random variable (RV; the arithmetic mean is a constant) weight across them. Neither LISA [], highlighting geographically clustering contrasting weights, nor Gi* [], highlighting geographically clustering similar weights, statistics identify at least a potential solution point in these settings because global SA is zero, and hence, local SA fluctuates within the bounds of independent stochastic behavior. However, such a geospatial landscape is empirically unlikely, in general, because most socio-economic/demographic attributes display moderate, and most remotely sensed quantities display very strong, global positive SA. Nevertheless, this situation is enlightening to examine because it both is theoretically interesting and illuminating, and establishes a null hypothesis type of benchmark for comparative purposes with landscapes containing strong global SA.
The following is a formal conjecture statement verbalizing the p = 2 spatial median problem affiliated with the preceding constant weights scenario:
Conjecture 1
(Egalitarian, p = 2; ETC-2). For an n destination p = 2 source location–allocation (i.e., p-median) problem in continuous space, with n > 2 and Euclidean distance, if all weights wi (i = 1, 2, …, n) are identical (i.e., the same value) and form a uniform geographic distribution across the landscape, then the subsets-generated optimal spatial median pair locate on opposite sides of a geographic landscape (à la geographic market area conceptualizations; see [,]), with a straight line connecting these two locations being (nearly) collinear with the p = 1 spatial median for that landscape, which lies between them. (Note: three points are collinear if their composite pairwise interpoint connections fall on the same single straight line; Appendix A summarizes an exploratory investigation about conditions coexisting with this property).
Rationale for Conjecture 1.
For a unit square. Bisecting a square creates equal area shapes ranging from a rectangle of dimension 1-by-½ (or vice versa), with centroid (xcentroid, ycentoid) = (½, ¼), through a trapezoid sequence of dimension 1-by-(½ − c)-&-(½ + c), with centroid (,) for 0 < c < ½, to a right triangle of dimension 1-by-1, with centroid (⅔, ⅓). Based upon integrating the Euclidean distance function , the average within region distance incrementally increases from roughly 0.297 for each rectangle, to approximately 0.366 for each triangle. the pair of optimal locations is either the set {(½, ¼), (½, ¾)} or {(¼, ½), (¾, ½)}, depending upon whether the two rectangles are the products of a horizontal or a vertical division; see Figure 1a.
For a unit circle Bisecting a circle creates equal area semicircles. Without loss of generality, considering the pair whose diameters are parallel to the horizontal axis, having respective centroids (½, ), the average distance increases from roughly 0.292 for the centroid focal point, to approximately 0.354 for the center of the circle focal point, and, in the reverse vertical direction, 0.851 for the semicircle pinnacle focal point. Any other pair of semicircles is obtainable by rotating the aforesaid centroids to a specified angle. numerous pairs of optimal locations form an inner circle of radius ; see Figure 1b.
Figure 1 exemplifies this general situation. The unit square solution aligns with the quartiles of the horizontal or vertical axes (re the solution lacks uniqueness), reminiscent of the socially optimal Hotelling problem outcome []. The unit circle optimal locations almost share this trait, locating, for example, at 0.29 and 0.71 along the horizontal axis interval [0, 1].
A principal implication from ETC-2, beyond the existence of multiple optima, is that a pronounced tendency exists for p = 2 spatial medians to disperse, hinting that the expression (1) metric term potentially governs its associated weights term wi, a noteworthy finding. In addition, just like for ET-1, ETC-2 implies a corollary for identically distributed RV weights (because their expected values also are constant weights, as previously discussed; see Appendix A).
3.2. More About the Collinearity Conjecture
The preceding collinearity of p = 1 and p = 2 optimal solution coordinate pairs appears to be an exploitable property for efficiently and effectively solving a p = 2 location–allocation problem. However, doing so requires preprocessing calculations of the p = 1 solution as well as the weighted spatial mean (which almost always is the adopted initial starting solution for the Kuhn–Kuenne algorithm), and the angle of rotation and major axis vertices of a directional ellipse (see [,,]) portraying the geographic orientation of the n weights, both of which are simple and fast computations. The final solution begins with these aforementioned vertices as an initial solution for a call to a heuristic algorithm such as ALTERN [], followed by 179 equal incremental clockwise angle increases (i.e., +1° tracking a semi-circle) to establish sequential initial heuristic algorithm solutions, each succeeded by a call to ALTERN. In other words, the optimal guided systematic search strategy here involves about a sixth as many calls to ALTERN as the common random search approach; a more sophisticated implementation of this novel algorithm should reduce this number of calls (e.g., if the search rotation fails to change the initial allocation of demand points to initializing centers, then an ALTERN call is not made) while increasing its success rate from near to exactly 100%.
Figure 3a visualizes aspects of the solution approach proposed here. This illustration depicts a tendency for the major axis of a directional ellipse to align with a prominent SA map pattern. It also shows the near-collinearity of the p = 1 and p = 2 solution coordinate pairs. Some software packages, such as ESRI© ArcMap, present this type of analysis in terms of a clockwise rotation from the vertical axis. Figure 4 portrays a systematic search counterclockwise rotation around a given dataset’s p = 1 optimal solution, initiated with the directional ellipse major axis vertices. This strategy requires only a semicircle search region because each of these two points aligns with and locates on the opposite side of their affiliated p = 1 solution coordinates (see the dyad connections portrayed in Figure 4a). The Table 2 tabulations reinforce a contention that this restricted search, which executes 180 calls to a location–allocation heuristic algorithm (e.g., ALTERN), considerably outperforms the popular practice of executing thousands―here 1000―of random calls to the same heuristic algorithm. Moreover, a p = 1 solution provides discoverable and useful information about its associated p = 2 solution.
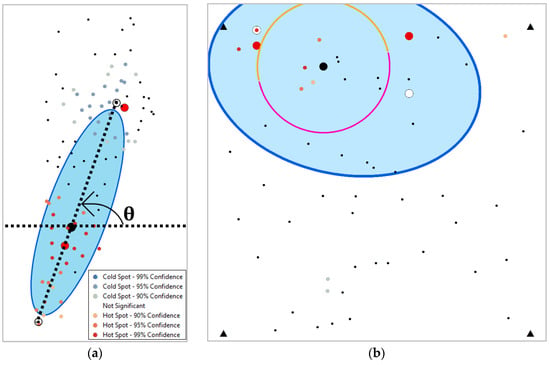
Figure 3.
Selected directional ellipse empirical applications; black dots denote the 50 weight locations, solid black filled circles denote p = 1 solutions, solid red filled circles denote p = 2 solutions, and graduated orange and gray dots, respectively, denote cold and hot spots. Left (a): Goodwin’s [] example; black dotted lines denote counterclockwise horizontal axis rotation through angle θ with the pair of ellipse vertices circled. Right (b): failed solution unit square (borders designated by corner solid black triangles) linear trend weights (n = 50) simulation case; filled white circles denote an incorrect p = 2 local minimum solution, and merged pink-orange semicircles denote the employed rotation search tack.
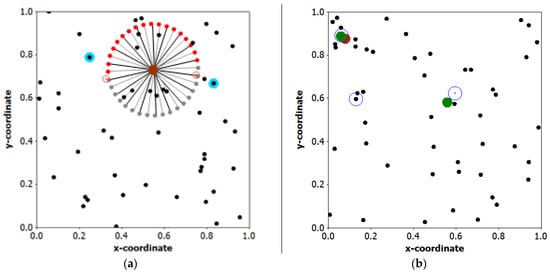
Figure 4.
Unit square specimen point patterns; black dots denote the 50 weighted locations, and brown and blue filled circles, respectively, denote the p = 1 and p = 2 solutions. Left (a): A successful rotation search example; red circled dots denote the directional ellipse vertices, and each black/gray linked red-gray point pair denotes an incrementally rotated (here by 10°) initial ALTERN solution. Right (b): p = 1, 2, and 3 solutions, strong spatial autocorrelation, n = 50; blue circled dots denote the p = 3 solution.

Table 2.
Exploratory collinearity algorithm and random search comparisons; 100 replications, a unit square geographic landscape, and Poisson distributed weights of at least one.
Table 2 corroborates the general contention that SA furnishes invaluable but, to date, mostly overlooked information about spatial optimization and its accompanying optimal solutions, an assertion supported by circumstantial evidence appearing in Figure 3 (i.e., the colocation of hot/cold spots and p = 2 solution coordinate pairs). In addition, Table 2 reports optimization achievement frequencies, buttressing the notion that exploiting p = 1 and p = 2 (near-)collinearity improves the efficiency and success rate of finding an optimal solution with ALTERN, vis-à-vis random searching, by as much as a factor of roughly 1.5 (e.g., from 61 to 98; the random, n = 100 scenario). As an aside, supplemental simulations for n = 50 with 10,000 replications verify the general nature of these results, yielding the new proposed algorithm success rates by weight category type of approximately 97.6% for linear, 97.7% for quadratic, 98.0% for periodic, and 97.9% for random. This discovery should be transformative, and hence should motivate much more future research about the relationships between spatial autocorrelation and spatial optima. Nevertheless, this pursuit merits further work, given that the systematic search based upon the map pattern presented in this section of this paper fails to uncover the p = 2 solution for every one of the studied random coordinate sets (sampled from a bivariate uniform distribution) and weights [sampled from a spatially (un)autocorrelated Poisson RV] case (e.g., Figure 3b); the culprit could be edge effects or more extensive deviation from collinearity (see Figure 3b). This particular analysis employed the Overton-Stehman [] simulation experiment design. Interestingly, the last Table 2 column reveals that the random search sometimes (although apparently rarely) identifies an optimal solution not found by the systematic search.
3.3. A Conjecture Relating to MT-1 for the p = 2 Spatial Median Problem
The fundamental change from p = 1 to p = 2 is the addition of a second central facility (i.e., another subset with a spatial median). Consequently, if any demand point k has a dominant weight that axiomatically places the p = 1 optimal solution there because wk is greater than the sum of the remaining (n − 1) weights, then partitioning the demand points into two subsets (see the preceding section) only reinforces demand point k’s wk dominance within its neighborhood subset of points, which is <(n − 1) in size, regardless of the extent of its subset. Figure 1c embodies this notion, stressing the dispersive nature of the p = 2 pair of optimal locations, and documenting the continuance of the MT-1 solution in a p = 2 context. The p = 1 spatial optimization–SA relationships already uncovered by Griffith et al. [] transfer to this p = 2 situation. Furthermore, the following conjecture encapsulates a more sweeping insinuation:
Conjecture 2
(MT-1 for p = 2; MTC-1&2). For an n destination p = 1 source location–allocation (i.e., p-median) problem in continuous space, with n > 1 and Euclidean distance, if a single dominant weight wk > , then the optimal location set for any uncapacitated p ≥ 1 medium problem contains the demand point (xk, yk) as one of its entries.
Conceptualization for Conjecture 2.
If wk is dominant among a set of n demand point weights, it is dominant among any subset of these weights (i.e., being greater than the sum of all of them means being greater than the sum of any subset of them).
This conjecture is not cast as a theorem here because, although its rationale signals that it is true, it lacks a formal and complete proof for all 1 ≤ p < n; however, it is true for p = n because all demand points by themselves become optimal locations [i.e., expression (1) becomes zero].
One immediate consequence of this location–allocation property is that the p = 2 problem reduces in size from a maximum of n(n − 1)/2 to (n − 1), converting it from order O(n2) to O(n): the only perpendicular bisector construction necessary is for those links connecting the dominant weight demand point and the (n − 1) other demand points. Accordingly, the feasible problem size in terms of n now rivals that for the p = 1 problem. Meanwhile, local SA is informative during the initial screening for dominance of a set of weights (see []).
3.4. An MTC-2 Formulation
MT-1 states that a single wk needs to compose a majority of the sum of a given set of weights. Griffith et al. [] show that collective dominance can exist when this total is uniformly spread across all entries in a relatively compact geographic cluster of demand points; the p = 1 optimization mechanics detects this cluster in terms of global positive SA. Expanding to the p = 2 problem invokes its dispersive property to avoid this mechanical reaction. Assigning 50%+ of the total weights to a sole dominant weight allows a minimum of 25%+ for the other dominant weight; the expectation is that each comprises 50%+ of the total sum of weights in its respective subregion. The binary indicator variable λij (j = 1, 2) in expression (1) designates this regionalization duet, with subregions H and K, respectively, labeling the demand points symbolized by λi1 and λi2, and housing weights wh and wk. Adhering to the preceding Thiessen polygon viewpoint promoted by TWAIN, if two weights exist such that each conforms to these two percentage conditions, then their corresponding demand points are the pair of optimal locations:
Conjecture 3
(Majority for p = 2; MTC-2). For an n destination p = 2 source location–allocation (i.e., p-median) problem in continuous space (see Figure 2 and Figure 3), with n > 2 sufficiently large and Euclidean distance, if two distinct weights are such that wh > (i ≠ h) and wk > (i ≠ k), with wh/ + wk/ < 1, and wh > (i ≠ h) and wk > (i ≠ k), with their collocated demand points (xh, yh) and (xk, yk) located on opposite sides of the transect passing through the p = 1 spatial median for an underlying continuous demand surface perpendicular to the straight line connecting them (see the spatial economics market area literature; i.e., realizations are samples from a two-dimensional population), then this pair of demand points also is the set of the optimal locations (i.e., subset spatial medians) solution.
Rationale for Conjecture 3.

This is an asymptotic consequence. The sum of the two dominant weights needs to exceed 50%, to which MT-1 attests. Then, in an ideal situation (e.g., n is large), the dominant weight affiliated with each subset has to constitute more than 50% of its weight sum for MT-1 also to apply to it. These necessary percentages increase for smaller n (see Table 3) because integer weight sums distribute across fewer locations, causing indivisibility/lumpiness complications (i.e., designated precise percentages are not always attainable—e.g., half of an odd number is not an integer, resulting in the closest possible empirical majority percentage to 50% necessarily being greater than it).

Table 3.
The random distribution of weights is w ~ Poisson (μ = 4) + 1; 1000 replications.
Remark for Conjecture 3.
Simulation experiments imply that the percentage for MT-1-oriented dominant weight wh decreases from 50% to 25% with increasing n, being approximately 25% for a sufficiently large n (e.g., 200); the accompanying secondary dominant weight, wk, appears to be a minimum of 25% (see Table 3), as long as the two percentages sum to at least 50% in total, as well as for each of their subsets of weights; this is a very appealing feature because a large n is a chief source of computational difficulties. Bounds for these percentages merit future research attention (Table 3 reports selective confirmatory instances).
This is a completely new finding that offers a transformative possibility for parts of spatial optimization.
Table 3 tabulates selected confirmatory MTC-2 output from a collection of simulation experiments employing 1000 replications; these are merely a handful of the total number of completed experiments, some involving as many as 10,000 replications, used to crystalize the conjecture theorized in this section (note: one noteworthy finding undocumented in Table 1 is that when the aggregate percentage of total weight for (wh + wk) is less than 50%, none of the MTC-2 solutions materialize—or at least their emergence probability is extraordinarily low (i.e., extremely difficult to detect)—although conjectures MTC-1&2 certainly hold). The distance separating the two globally quasi-dominant weights relates to the underlying population spatial median of a demand points generating process, as well as coincides with the dispersive nature of the p = 2 solution, emphasizing that the mechanics of TWAIN may well routinely confuse nearby outlier weights with local positive SA. The reported distance measures also reflect the dispersion tendency of p = 2 optimal solution pairs (the prevailing population spatial median constrains the distance between dominant demand points; note: when the distance between two dominant demand weight locations is too small, then the probability of them being the optimal solution may be less than 1), with particular reference to the preceding unit square answers concerning uniqueness questions. Another conspicuous feature is the average percentages for the pair of dominant weights, which very closely approximates their respective input parameter values. Finally, the number of demand points captured by each dominant demand point’s Thiessen polygon demarcated geographic subregion relates to its relative magnitude.
Although MTC-2 might not appear to yield a theoretical solution by simple inspection as does MT-1 (e.g., for MT-1, summing the weights and checking to see if any one of them is greater than half of that calculated total), the procedure implementing MTC-2 is the following sequence of three steps for a reasonably large n (future research needs to establish a threshold for this n):
- Step 1:
- sum the weights and check to see if each of any two of them is greater than a specified percentage of that calculated total (each of the two weights must be at least 25% of the computed sum);
- Step 2:
- if Step 1 identifies two weights, check that their respective positions are on opposite sides of the geographic landscape’s transect passing through the p = 1 spatial median perpendicular to the straight line connecting; and,
- Step 3:
- if Step 2 conditions hold, construct a perpendicular bisector of the line connecting the two identified demand points (this construction can be completed with a GIS Thiessen polygon tool; it is equivalent to allocating each demand point to its closest of the two dominant weight points), and then check to see if each identified weight is at least 50% of its respective subset’s total weight sum.
If Step 1 validates that one of the two largest weights exceeds 50% of the total demand, then, at a minimum, invoking MTC-1&2 allows a reduction in the complexity of the problem to be solved. If Step 1 validates that both of the two largest weights exceed the prespecified percentages (at least 25%) of the total demand, MTC-2 potentially furnishes the solution to the problem, depending upon n. However, if no validation occurs, then an exact or heuristic solution algorithm, such as TWAIN [] and ALTERN, must provide the location–allocation problem solution.
4. Local SA in the Presence of a Two Dominant Demand Point Weights in a p = 2 Median Problem
The ultimate purpose of this paper is to demonstrate how this MTC-2 mathematical solution coincides with the local SA latent in dominant geographic clusters of weights, paralleling and expanding the MT-1 findings by Griffith et al. []. Its rationale builds upon the expectation that because spatial optimization identifies favored points in a geographic landscape, often in terms of their aggregate accessibility, these preferential points relate to local SA statistics. As noted previously, two popular indices quantify this notion. The local Getis-Ord Gi* statistic []—which includes the attribute value yi of random variable (RV) Y in its calculation—a ratio of the sum of a local subset to the total of a given attribute’s values in a geographic landscape (i.e., ); this local SA statistic can highlight geographic clusters of similar attribute values (i.e., hot and cold spots), like a coterminous geographic cluster of weights forming a collectively dominant region [], but not outliers like the dispersed pair of dominant weights in MTC-2. In other words, MTC-2, like MT-1, tends to relate to concentrations of contrasting high–low weights. The alternative second popular index is the local indices of SA (LISA; []) related to the Moran scatterplot [], in which the second and fourth quadrants of its graph, respectively, identify concentrations of relatively high and low neighboring values (i.e., global negative SA). A fundamental advantage of this index is that, because it involves cross-product calculations, it is able to differentiate between a spatial outlier and other more similar (i.e., high–high and low–low) values in local neighborhoods. This local SA statistic may be defined for the RV Y and binary 0–1 spatial weight matrix (SWM) C in its z-score form as follows:
where cij is the (i, j) cell entry in SWM C, and denotes the arithmetic mean of RV Y. This quantity is called local Moran’s I, which indicates a correlation between the ith observation in a geographic distribution and the average of its neighbors’ values, all expressed in their z-score forms. This measure is a localized index of the global Moran’s I, this latter composite statistic being the same as the mean of its constituent local Morna’s I values. Similarity between neighboring demand weights leads to positive SA, whereas dissimilarity leads to negative SA; noteworthy is that this formula has essentially the same form as Pearson’s well-known product–moment correlation coefficient. Local SA is commonly used to detect localized SA patterns: positive SA for spatial clusters and negative SA for spatial outliers. A LISA map can represent the spatial patterns of weights associated with demands, which in turn can impact location model solutions. Although spatial patterns of demands points and SA in weight surfaces have been recognized in spatial optimization (e.g., []), local SA indices have not been utilized in spatial optimization model specifications. Only recently, Griffith [] articulates some of the more conspicuous relationships between local SA indices on spatial optimization.
This is the popular local SA index used in this paper for traditional MTC-2 settings (i.e., geographic landscapes with a more dispersed distribution of demand points). Griffith et al. [] furnish details about it for MT-1 that extend to MTC-2 because the positions of a pair of dominant weights are located on opposite sides of the transect passing through a geographic landscape’s population spatial median that is perpendicular to a straight line connecting them. Accordingly, given that peripheral demand points pull optimal locations toward multiple landscape borders, the case of nearby dominant weight locations never materializes.
In keeping with the construction of Figure 5c,f, empirical LISA calculations utilized a distance threshold such that all neighboring points within a specified radius greater than zero had an SWM value of one rather than zero. Table 4 reports these thresholds whose judicious selection ensured that each demand point had at least one neighboring point. As Figure 5 entries demonstrate, the geographic distributions of LISA tend to constitute two groups, the pair coinciding with the MTC-2 optimal locations, and essentially all others; these were the criteria used to classify the LISA for comparison purposes (see Table 4). Not surprisingly, the LISA groups neither conform to bell-shaped curves nor display constant variance (i.e., they are non-normal RVs), compelling the application of non-parametric statistical techniques. Table 4 tabulates analysis of variance type of output for Kruskal–Wallis treatments of these data. The computed chi-square statistics based upon 1000 observations are roughly a thousand times greater than even the rather extreme null hypothesis α = 0.01 critical value of 6.635; in other words, the LISA results are tremendously inconsistent with a null hypothesis stating that they are the same for the MTC-2 optimal and the (n − 2) other demand point locations (and certainly satisfy a practical decision-making criterion such as being at least four times greater than the designated critical value []).
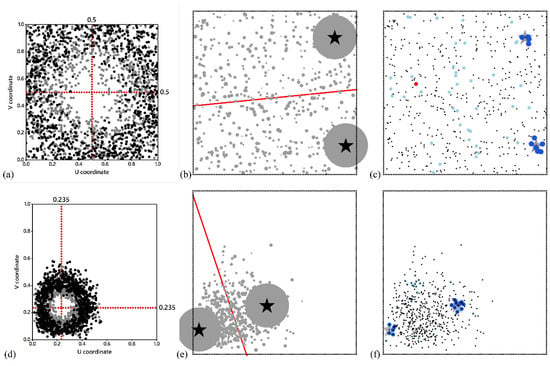
Figure 5.
Specimen n = 500 simulated datasets; the top row displays a uniform, whereas the bottom row displays a skewed, random points realization (medians denoted by superimposed red dotted lines), with a 1 to 15 nondominant weights range for illustrative purposes. Left top (a) uniform vs. bottom (d) skewed: benchmark distributions of 1000 (n = 100) simulated p = 2 solutions, respectively, denoted by filled gray and black circles. Middle top (b) uniform vs. bottom (e) skewed: distributions of n = 500 demand points with their weights depicted by proportional gray filled circles, their superimposed Thiessen polygon partitionings denoted by red lines, and their two dominant weight locations denoted by filled black stars. Right top (c) uniform/bottom (f) skewed: LISA maps with a high–low (HL) outlier denoted by red in the uniform distribution results appear only in (c), whereas the two clusters of low–high (LH) outliers denoted by dark blue (the optimal solutions), and a scattering of low–low (LL) weights denoted by light blue appear in (f).

Table 4.
Kruskal–Wallis results for difference of MTC-2 and all other LISA, for two distinct underlying geographic distributions of random demand point locations; 1000 replications.
Specimen LISA Examples for n = 500
Ostresh [] mentions n = 100 as a relatively large problem. Here, thanks to the advent of superior computer technology, the basis of Figure 5 output is n = 500 (and some Appendix A output is for n = 729); his computing time estimation equation predicts the solution should take approximately 166,250 s, whereas this solution took on the order of 100 s of CPU time on a modern (albeit not state-of-the-art) desktop computer—in contrast, MTC-2 demonstrates a greater reduction of this time to just a few seconds. Figure 5a,d illustrate the gap within the unit square geographic landscape arising from the dispersive nature of the p = 2 solution. Figure 5b,e reproduce the type of Thiessen polygon partitioning appearing in Figure 2 for n = 5. Figure 5c,f exemplify the coinciding of extreme low–high (LH) LISA (residing in the third quadrant of the Moran scatterplot) with the dominant weights.
5. Conclusions
This paper complements Griffith et al. [] by summarizing new research examining as well as establishing additional relationships between spatial optimization and global and local SA. This is its primary novelty, one translated into an implementable heuristic algorithm enhancement, with demonstrable (e.g., see Table 2) over unsupervised heuristic executions, a common practice. It formulates and then utilizes the MTC-2, so that the optimization solution is known theoretically, to further establish a proof of concept. Its primary conclusion, a spectacular finding, is that the p = 2 spatial median pair co-locate with local SA hot spots. Other important findings include the following: (1) supplemental documentation that the LISA are the appropriate local SA statistics for assessing a MTC-2 geographic landscape; and, (2) distance separating optimal location pairs plays an important role in the MTC-2 context. The collection essentially is the new findings’ contribution of this paper.
Another important class of conclusions pertains to MTC-2-competing alternative optimal location propensities, summarized here in the newly posited ETC-2. These two innovative conjectures add to the corpus of existing ones, such as MT-1 and those already devised by Cooper []. Following Cooper’s logic, another conjecture would be that the pair of subset spatial means provide an upper bound for the p = 2 objective function value. The simulation experiments employed in the research foundation for this paper corroborate this contention.
Future research should articulate linkages between salient properties of the subset spatial medians, such as those enumerated in Griffith et al. [], and global and local SA. Other fruitful research endeavors would be establishing more precise percentage bounds for the necessary sizes of the MTC-2 weights (see Table 3), and the minimum threshold or context for the value of n that ensures weights just exceeding 25% are sufficient to guarantee MTC-2. Other future research themes meriting pursuit include the following: extending p = 2 discoveries to p > 2 (e.g., converting this and other conjectures proposed in this paper to theorem status), or, rather than a forward procedure, developing a backward procedure to eliminate non-feasible solutions in which any optimal locations among p cannot reside with regard to MTC-2 and ETC-2, thus narrowing the extent of the spatial medians’ solution space. Both proposals craft a more detailed understanding of the role of the ETC-2 with regard to spatial optimization solutions, composing a more comprehensive classification of spatial optimization solution guidance offered by LISA and local Gi* statistics, and compiling an ample assortment of empirical evidence-based confirmations of the theoretical contentions presented in this paper. The age of the spatial optimization-SA interface is here!
Future research also should compare the branch-and-bound based solutions and TWAIN solutions with the enhanced ALTERN algorithm presented here. Ostresh [] already furnishes a comparison of these first two solution techniques. His analyses can be updated to include much larger problems that advances in computer technology over the past decades now readily enable as well as a much more diverse set of point demand weights, and then extended to include comparisons with the bolstered heuristic. Other possible future research endeavors include making the proposed algorithm more comprehensive, allowing it, for example, to incorporate other forms of spatial dependence (e.g., higher-order spatial autocorrelation), or adapting it for different types of location–allocation problems (e.g., maximizing coverage, facility location with multiple objectives).
Author Contributions
Conceptualization, D.A.G., Y.C. and H.K.; methodology, D.A.G., Y.C. and H.K.; software, D.A.G.; validation, D.A.G.; formal analysis, D.A.G., Y.C. and H.K.; investigation, D.A.G., Y.C. and H.K.; resources, D.A.G., Y.C. and H.K. data curation, D.A.G.; writing—original draft preparation, D.A.G.; writing—review and editing, D.A.G., Y.C. and H.K.; visualization, D.A.G.; supervision, D.A.G., Y.C. and H.K.; project administration, D.A.G., Y.C. and H.K.; funding acquisition, D.A.G., Y.C. and H.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the United States National Science Foundation, grant number BCS-1951344. Any opinions, findings, and conclusions or recommendations expressed in this article are those of the authors, and do not necessarily reflect the views of the National Science Foundation.
Data Availability Statement
All data were simulated with standard pseudo-random number generators; anyone with spatial data simulation experience is capable of repeating the exercises with the information appearing in this article. Computer Code Information (Appendix B).
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Collinearity of p = 1 and p = 2 Solutions: Simulation Evidence
If three points on a planar surface are perfectly collinear, then Euclidean geometry dictates that the following conditions hold: (1) the absolute value of the determinant of the matrix constructed by stacking the three coordinates—(xi, yi), i = 1, 2, 3—augmented with a 3-by-1 column vector of ones, 1, equals zero [i.e., designating the location–allocation solution by (x2, y2) for p = 1, and {(x1, y1), (x3, y3)} for p = 2, given the hypothesis that the location of the former solution point is between the two points constituting the latter solution, = 0]; (2) the triangle constructed by designating the three solution coordinates as its vertices has zero area; and, (3) = 0 defines a pertinent Euclidean distance segmentation comparison. Employing a unit square geographic landscape, for simplicity, the respective approximate worst-case scenario minimum upper limits for these three quantities in the given geographic landscape are as follows: 0.5, 0.25, and 0.4142. Each lower limit is zero. Table A1 tabulates output from an exploratory simulation experiment (i.e., only 100 replications)—the computation of each p = 2 solution becomes increasingly numerically intensive as n increases. This exploration is sufficient here because the goal is to uncover trends, not optimize precision. Exact collinearity renders a triplet of zero values; few results attain this status. In contrast, the preponderance of near-zero numbers supports a contention that virtually all cases achieve near-collinearity status: the three points always almost or unerringly fall on the same straight line. Furthermore, replacing constant weights with ones that vary as an independent and identically distributed random variable slightly increases outcome variability while preserving this near-collinearity property, as does supplanting a uniform with a random distribution of demand point coordinates. These trace random effects appear to decrease with an increasing number of demand points. As an aside, another property is that the slopes of each of the two aforementioned line segments are equal; this property is computationally more difficult to demonstrate numerically because p-median solutions arranged in parallel with the vertical axis of a geographic landscape have (near-)infinite slopes, which can distort calculations by grossly magnifying slight differences.

Table A1.
Exploratory simulation results for a unit square geographic landscape; a maximum of 100 replications.
Table A1.
Exploratory simulation results for a unit square geographic landscape; a maximum of 100 replications.
| Geographic Point Pattern Distribution | Collinearity (# of Replicates) | # of Demand Points | Demand Point Weights | Collinearity Index | ||
|---|---|---|---|---|---|---|
| Matrix Determinant | Triangle Area | Distance Segments Sum | ||||
| uniform | exact † (0) | 36 | i | *** | *** | *** |
| near (100) | 0.0001 (0.0001) | 0.0001 (<0.0001) | 0 (***) | |||
| exact † (1) | 400 | 0 | 0 | 0 | ||
| near (99) | 0.0000 (<0.0000) | 0.0000 (<0.0000) | 0 (***) | |||
| exact † (0) | 729 | *** | *** | *** | ||
| near (100) | 0.0002 (0.0001) | 0.0001 (0.0001) | 0 (***) | |||
| random | exact † (0) | 36 | *** | *** | *** | |
| near (100) | 0.0081 (0.0065) | 0.0040 (0.0032) | 0.0013 (0.0020) | |||
| exact † (1) | 400 | 0 | 0 | 0 | ||
| near (99) | 0.0032 (0.0026) | 0.0016 (0.0013) | 0.0002 (0.0004) | |||
| exact † (0) | 729 | *** | *** | *** | ||
| near (100) | 0.0019 (0.0014) | 0.0010 (0.0007) | 0.0001 (0.0001) | |||
| uniform | exact † (0) | 36 | wi~1 + Poisson (μ) | *** | *** | *** |
| near (100) | 0.0072 (0.0056) | 0.0036 (0.0028) | 0.0013 (0.0016) | |||
| exact † (0) | 400 | *** | *** | *** | ||
| near (100) | 0.0011 (0.0009) | 0.0006 (0.0004) | 0.0000 (<0.0001) | |||
| exact † (1) | 729 | 0 | 0 | 0 | ||
| near (99) | 0.0008 (0.0007) | 0.0004 (0.0003) | 0.0000 (<0.0001) | |||
| random | exact † (0) | 36 | *** | *** | *** | |
| near (100) | 0.0097 (0.0069) | 0.0049 (0.0035) | 0.0018 (0.0022) | |||
| exact † (0) | 400 | *** | *** | *** | ||
| near (100) | 0.0030 (0.0025) | 0.0015 (0.0012) | 0.0002 (0.0004) | |||
| exact † (0) | 729 | *** | *** | *** | ||
| near (100) | 0.0023 (0.0016) | 0.0011 (0.0008) | 0.0001 (0.0002) | |||
† to five decimal places. *** denotes missing entries because of a lack of data.
Appendix B. Computer Code Information
No general scripts exist for this research. Rather, it utilized customized publicly available and proprietary computer software.
Figure 1 Simulation
The foundational computer program code modified for this work is TWAIN, with its Fortran script retrieved from Ostresh [] via digital page scanning followed by optical character recognition (OCR) conversion to courier font text. The resulting customized computer program was executed with a Fortran 77 compiler. The customizations involved the following:
- insertion of a DO loop enables repeated optimizations to generate the simulation experiment replications;
- IMSL random number generator RNBET samples coordinates from either a uniform (parameters: α = 1, β = 1) or a skewed distribution (parameters: α = 9, β = 5);
- IMSL random number generator RNPOI samples weights from a Poisson distribution (parameter: μ = 4); the mean was 1 added to it, increasing it to μ = 5, to ensure all weights are positive.
References
- Carmona-Benítez, R. Dimensionality-reduction procedure for the capacitated p-median transportation inventory problem. Mathematics 2020, 8, 471. [Google Scholar] [CrossRef]
- Janáček, J.; Kvet, M.; Czimmermann, P. Kit of uniformly deployed sets for p-Location problems. Mathematics 2023, 11, 2418. [Google Scholar] [CrossRef]
- Lopes, C.; Rodrigues, A.; Romanciuc, V.; Ferreira, J.; Öztürk, E.; Oliveira, C. Divide and conquer: A location-allocation approach to sectorization. Mathematics 2023, 11, 2553. [Google Scholar] [CrossRef]
- Giraldo, R.; Leiva, V.; Castro, C. An overview of kriging and cokriging predictors for functional random fields. Mathematics 2023, 11, 3425. [Google Scholar] [CrossRef]
- Griffith, D.; Chun, Y.; Kim, H. Spatial autocorrelation informed approaches to solving location–allocation problems. Spat. Stat. 2022, 50, 100612. [Google Scholar] [CrossRef]
- Lee, C.; Griffith, D.; Chun, Y.; Kim, H. Effects of geographically stratified random sampling initial solutions on solving a continuous surface p-median location problem using the ALTERN heuristic. Spat. Stat. 2023, 57, 10076. [Google Scholar] [CrossRef]
- Church, R.L. BEAMR: An exact and approximate model for the p-median problem. Comput. Oper. Res. 2008, 35, 417–426. [Google Scholar] [CrossRef]
- Kim, K.; Chun, Y.; Kim, H. p-Functional Clusters Location Problem for Detecting Spatial Clusters with Covering Approach. Geogr. Anal. 2017, 49, 101–121. [Google Scholar] [CrossRef]
- Griffith, D. Articulating spatial statistics and spatial optimization relationships: Expanding the relevance of statistics. Stats 2021, 4, 850–867. [Google Scholar] [CrossRef]
- Kim, D.; Chun, Y.; Griffith, D. Impacts of spatial imputation on location-allocation problem solutions. Spat. Stat. 2024, 59, 100810. [Google Scholar] [CrossRef]
- Anselin, L. Thirty years of spatial econometrics. Pap. Reg. Sci. 2010, 89, 3–26. [Google Scholar] [CrossRef]
- Griffith, D.; Chun, Y.; Kim, H. The majority theorem for the single (p = 1) median problem and local spatial autocorrelation. Geogr. Anal. 2022, 55, 107–124. [Google Scholar] [CrossRef]
- Drezner, Z.; Klamroth, K.; Schobel, A.; Wesolowsky, G. Chapter 1: The Weber problem. In Facility Location: Applications and Theory; Drezner, Z., Hamacher, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 1–24. [Google Scholar]
- Griffith, D. Interpreting of Moran eigenvector maps with the Getis-Ord Gi* statistic. Prof. Geogr. 2021, 73, 447–463. [Google Scholar] [CrossRef]
- Witzgall, C. Optimal Location of a Central Facility: Mathematical Models and Concepts; NBS Report 8388; U. S. National Bureau of Standards: Washington, DC, USA, 1964.
- Körner, M.-C. Minisum Hyperspheres; Springer: New York, NY, USA, 2011. [Google Scholar]
- Tuy, H. Convex Analysis and Global Optimization, 2nd ed.; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Williams, J. Optimal reserve site selection with distance requirements. Comput. Oper. Res. 2008, 35, 488–498. [Google Scholar] [CrossRef]
- Kim, Y.-H.; Bettinger, P.; Finney, M. Spatial optimization of the pattern of fuel management activities and subsequent effects on simulated wildfires. Eur. J. Oper. Res. 2009, 197, 253–265. [Google Scholar] [CrossRef]
- Calabrese, R. Contagion effects of UK small business failures: A spatial hierarchical autoregressive model for binary data. Eur. J. Oper. Res. 2023, 305, 989–997. [Google Scholar] [CrossRef]
- Hof, J.; Bevers, M. Direct spatial optimization in natural resource management: Four linear programming examples. Ann. Oper. Res. 2000, 95, 67–81. [Google Scholar] [CrossRef]
- Griffith, D. Using estimated missing spatial data with the 2-median model. Ann. Oper. Res. 2003, 122, 233–247. [Google Scholar] [CrossRef]
- García-Alonso, C.; Pérez-Naranjo, L.; Fernández-Caballero, J. Multiobjective evolutionary algorithms to identify highly autocorrelated areas: The case of spatial distribution in financially compromised farms. Ann. Oper. Res. 2014, 219, 187–202. [Google Scholar] [CrossRef]
- Chai, N.; Gong, Z.; Bai, C.; Abedin, M.; Shi, B. A socio-technology perspective for building a Chinese regional green economy. Ann. Oper. Res. 2023. [Google Scholar] [CrossRef]
- Milliken, G.; Willers, J.; McCarter, K.; Jenkins, J. Designing experiments to evaluate the effectiveness of precision agricultural practices on research fields: Part 1 concepts for their formulation. Oper. Res. 2010, 10, 329–348. [Google Scholar] [CrossRef]
- Nepomuceno, T.; Costa, A. Spatial visualization on patterns of disaggregate robberies. Oper. Res. 2019, 19, 857–886. [Google Scholar] [CrossRef]
- Vavatsikos, A.; Sotiropoulou, K.; Tzingizis, V. GIS-assisted suitability analysis combining PROMETHEE II, analytic hierarchy process and inverse distance weighting. Oper. Res. 2022, 22, 5983–6006. [Google Scholar] [CrossRef]
- Oh, C.; Kim, H.; Chun, Y. An efficient solving approach for the p-dispersion problem based on the distance-based spatially informed property. Geogr. Anal. 2024, 56, 600–623. [Google Scholar] [CrossRef]
- Ord, J.; Getis, A. Local spatial autocorrelation statistics: Distributional issues and an application. Geogr. Anal. 1995, 27, 286–306. [Google Scholar] [CrossRef]
- Duque, J.; Laniado, H.; Polo, A. S-maup: Statistical test to measure the sensitivity to the modifiable areal unit problem. PLoS ONE 2018, 13, e0207377. [Google Scholar] [CrossRef]
- Hodgson, M.; Shmulevitz, F.; Körkel, M. Aggregation error effects on the discrete-space p-median model. Can. Geogr. 2008, 41, 415–428. [Google Scholar] [CrossRef]
- Lee, S.-I.; Lee, M.; Chun, Y.; Griffith, D. Uncertainty in the effects of the modifiable areal unit problem under different levels of spatial autocorrelation: A simulation study. Int. J. Geogr. Inf. Sci. 2019, 33, 1135–1154. [Google Scholar] [CrossRef]
- Demetriou, D.; Stillwell, J.; See, L. A GIS-based shape index for land parcels. In Proceedings of the First International Conference on Remote Sensing and Geoinformation of the Environment (RSCy2013), Paphos, Cyprus, 8–10 April 2013; Volume 8795, pp. 421–430. [Google Scholar] [CrossRef]
- Church, R.; Murray, A. Location Covering Models: History, Applications and Advancements; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Ostresh, L. An efficient algorithm for solving the two center location-allocation problem. J. Reg. Sci. 1975, 15, 209–216. [Google Scholar] [CrossRef]
- Kuhn, H.; Kuenne, R. An efficient algorithm for the numerical solution of the generalized Weber problem in spatial economics. J. Reg. Sci. 1962, 4, 21–33. [Google Scholar]
- Murray, A.; Church, R.; Feng, X. Single facility siting involving allocation decisions. Eur. J. Oper. Res. 2020, 284, 834–846. [Google Scholar] [CrossRef]
- Weiszfeld, E. Sur le point pour lequel la somme des distances de n points donnés est minimum. Tohoku Math. J. 1937, 43, 355–386. [Google Scholar]
- Miehle, W. Link-length minimization in networks. Oper. Res. 1958, 6, 232–243. [Google Scholar] [CrossRef]
- Cooper, L. Location-allocation problems. Oper. Res. 1963, 11, 331–343. [Google Scholar] [CrossRef]
- Vergin, R.; Rogers, J. An algorithm and computational procedure for locating economic facilities. Manag. Sci. 1967, 13, B-240–B-254. [Google Scholar] [CrossRef]
- Rushton, G.; Goodchild, M.; Ostresh, L. (Eds.) Computer Programs for Location-Allocation Problems; Monograph #6; Department of Geography, University of Iowa: Iowa City, IA, USA, 1973. [Google Scholar]
- Goldberg, K.; Newman, M.; Haynsworth, E. §24.1.4: Stirling numbers of the second kind. In Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; Abramowitz, M., Stegun, I., Eds.; Dover: New York, NY, USA, 1972; pp. 824–825. [Google Scholar]
- Meracalculator. Perpendicular Bisector Calculator. How Long Can a Spinoff Like ‘Better Call Saul’ Last? FiveThirtyEight. 2024. Available online: https://www.meracalculator.com/graphic/perpendicularbisector.php (accessed on 29 October 2024).
- Burg, D.; Ausubel, J. Moore’s Law revisited through Intel chip density. PLoS ONE 2021, 16, e0256245. [Google Scholar] [CrossRef]
- Anselin, L. Local indicators of spatial association—LISA. Geogr. Anal. 1995, 27, 93–115. [Google Scholar] [CrossRef]
- Fetter, F. The economic law of market areas. Q. J. Econ. 1924, 38, 520–529. [Google Scholar] [CrossRef]
- Hyson, C.; Hyson, W. The economic law of market areas. Q. J. Econ. 1950, 64, 319–327. [Google Scholar] [CrossRef]
- Meager, K.; Teo, E.; Xie, T. Socially-optimal locations of duopoly firms with non-uniform consumer densities. Theor. Econ. Lett. 2014, 4, 431–445. [Google Scholar] [CrossRef][Green Version]
- Gong, J. Clarifying the standard deviational ellipse. Geogr. Anal. 2002, 34, 155–167. [Google Scholar] [CrossRef]
- Wang, B.; Shi, W.; Miao, Z. Confidence analysis of standard deviational ellipse and its extension into higher dimensional Euclidean space. PLoS ONE 2015, 10, e0118537. [Google Scholar] [CrossRef] [PubMed]
- Goodwin, R. Data features of the weighted standard deviational curve. In Proceedings of the 6th International Conference on Agro-Geoinformatics, Fairfax, VA, USA, 7–10 August 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 76–80. Available online: https://ieeexplore.ieee.org/document/8046253 (accessed on 5 January 2025).
- Cooper, L. Heuristic methods for location-allocation problems. SIAM Rev. 1964, 6, 37–53. [Google Scholar] [CrossRef]
- Overton, S.; Stehman, S. Properties of designs for sampling continuous spatial resources from a triangular grid. Commun. Stat. 1993, 22, 251–264. [Google Scholar] [CrossRef]
- Anselin, L. The Moran Scatterplot as an ESDA tool to assess local instability in spatial association. In Spatial Analytical Perspectives on GIS in Environmental and Socio-Economic Sciences; Fischer, M., Scholten, H., Unwin, D., Eds.; Taylor & Francis: London, UK, 1996; pp. 111–125. [Google Scholar]
- Tong, D.; Murray, A. Spatial optimization in geography. Ann. Am. Assoc. Geogr. 2012, 102, 1290–1309. [Google Scholar] [CrossRef]
- Ryan, T. Modern Regression Analysis; Wiley: New York, NY, USA, 2009. [Google Scholar]
- Ostresh, L. TWAIN-exact solution to the two source location-allocation problem. In Computer Programs for Location-Allocation Problems; Rushton, G., Goodchild, M.F., Ostresh, L.M., Jr., Eds.; Monograph No. 6; Department of Geography, University of Iowa: Iowa City, IA, USA, 1973; pp. 15–28. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).