An Adaptive Large Neighborhood Search for a Green Vehicle Routing Problem with Depot Sharing
Abstract
1. Introduction
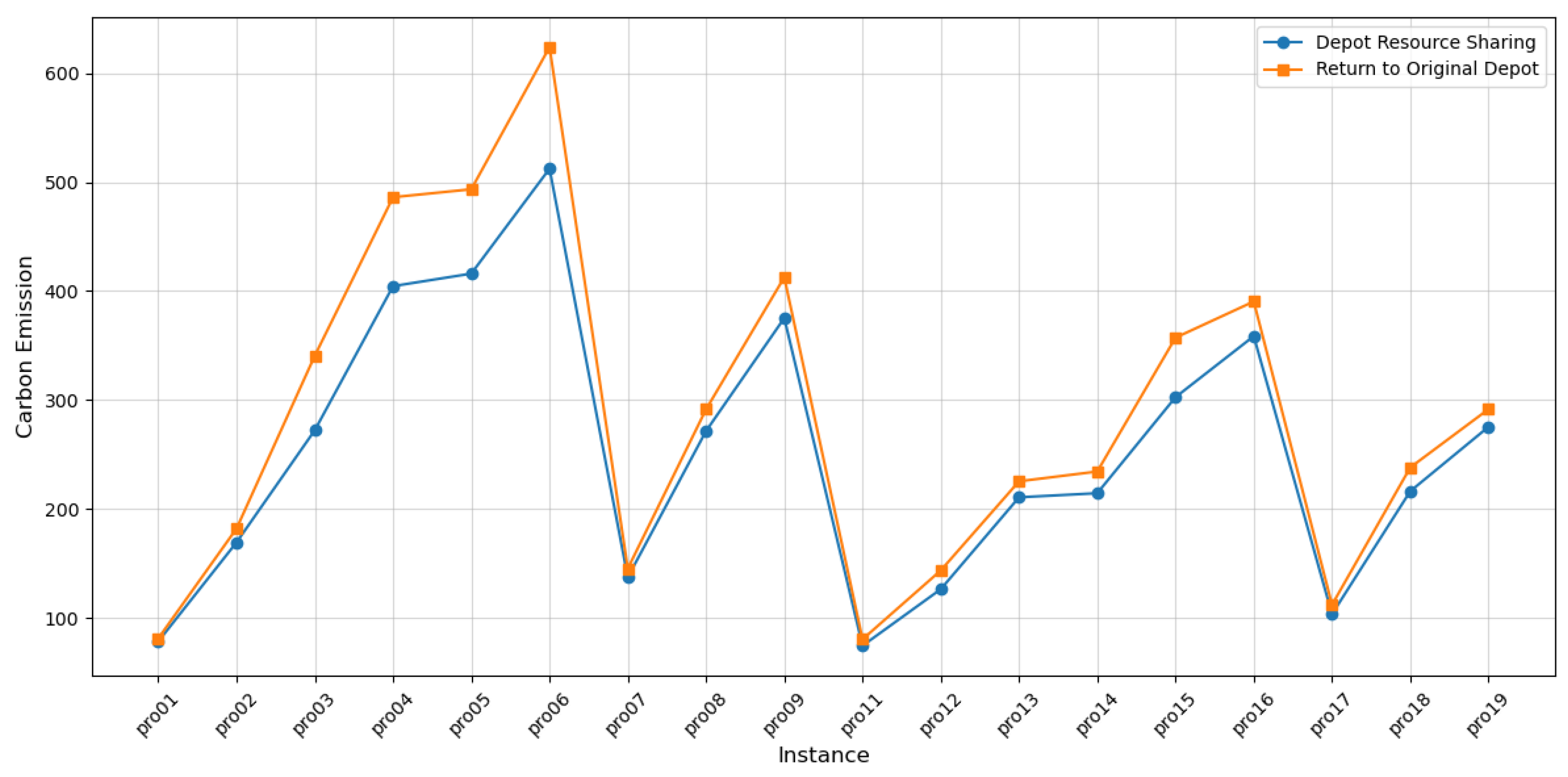
- The GVRPDS is presented in this manuscript, in which vehicles choose a nearby depot for return, thereby shortening the distance traveled by vehicles returning to depots and reducing carbon emissions.
- A carbon emission model of vehicle, which is positively correlated with fuel consumption based on vehicle load and distance, is established for calculating emissions during logistics distribution.
- An improved adaptive large neighborhood search algorithm is proposed to solve this GVRPDS, in which the Split strategy and two new operators are proposed to accelerate the convergence and to jump out of the local optimal solution.
2. Literature Review
3. Description and Formulation of GVRPDS
3.1. Problem Description
3.2. Mathematical Model
3.2.1. Carbon Emission Evaluation
3.2.2. Optimization Model Formulation
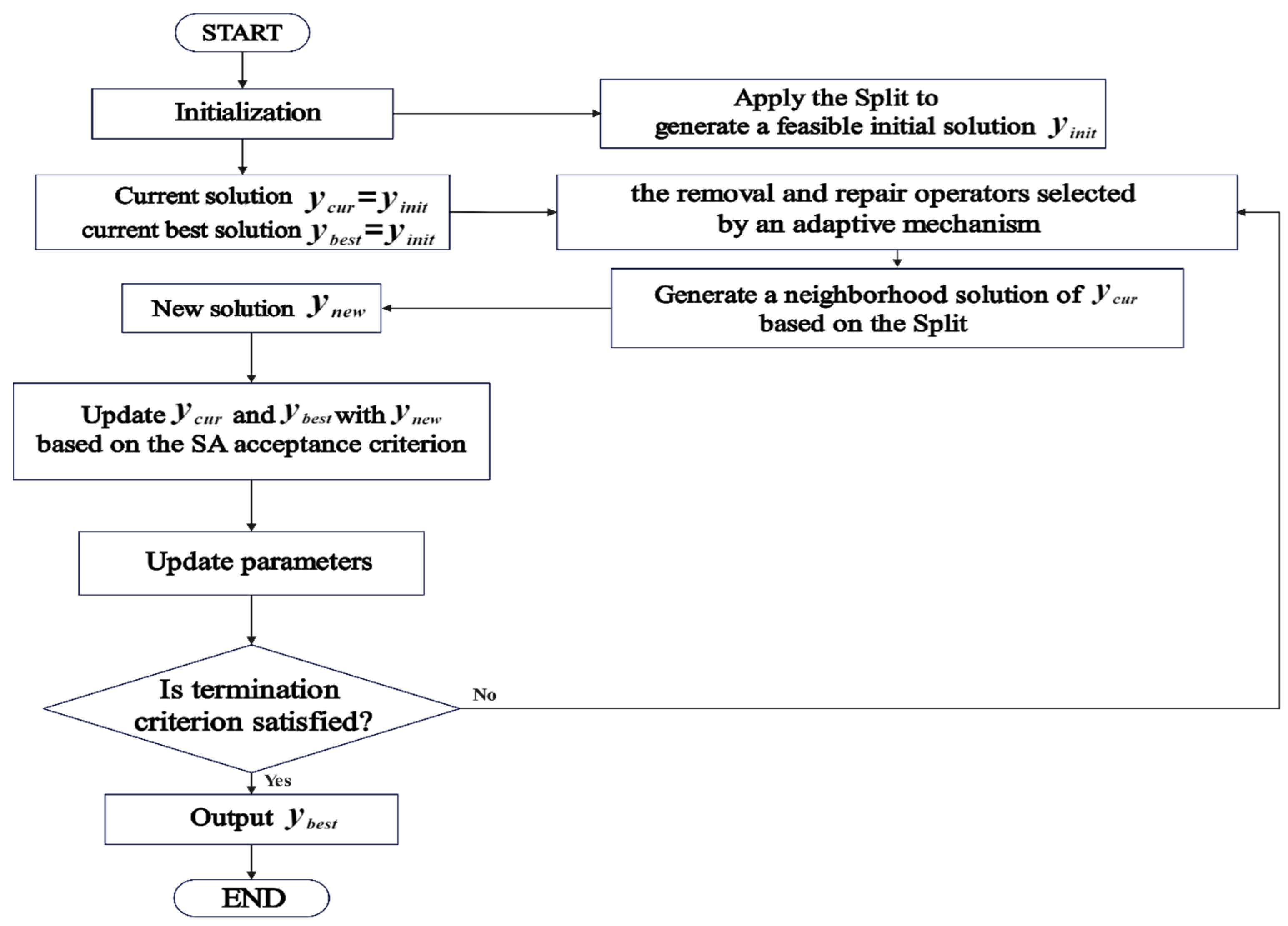
4. The Improved ALNS for the GVRPDS
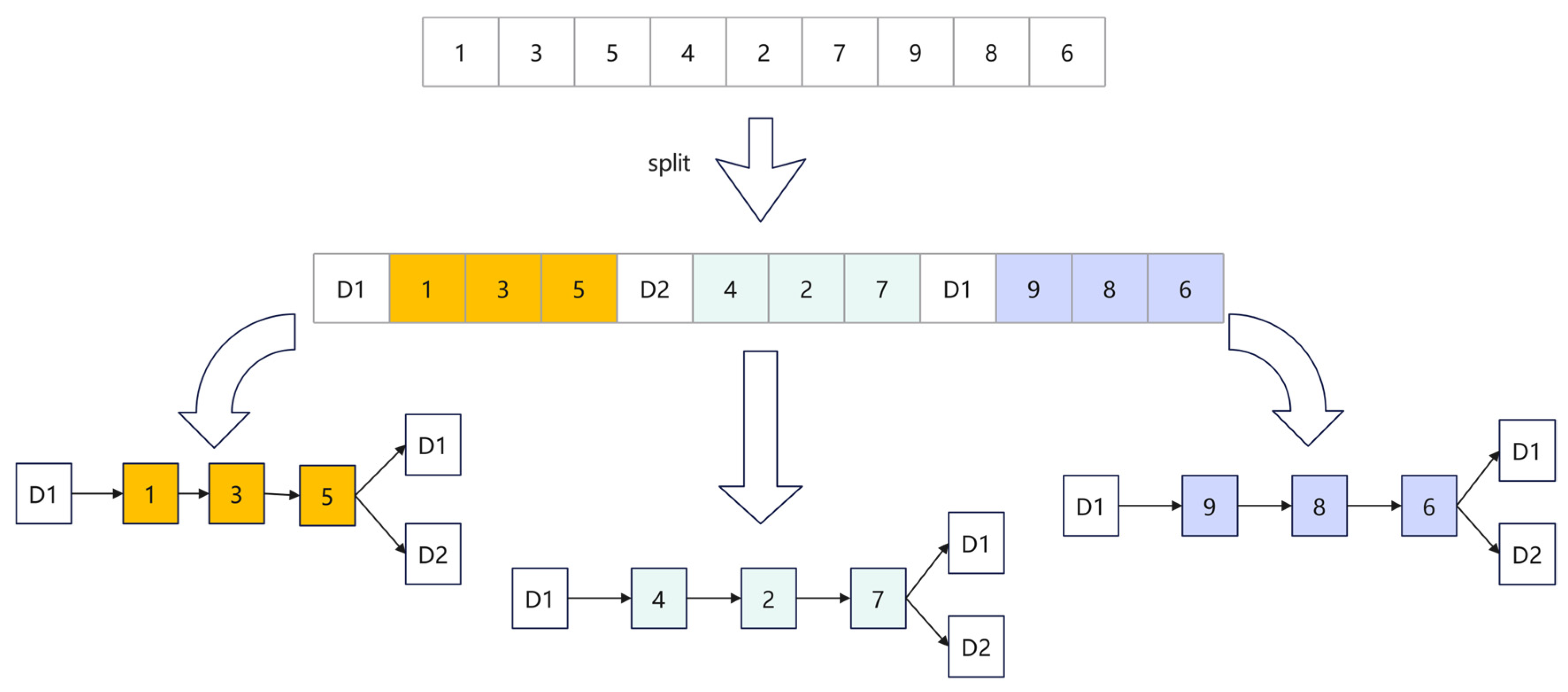
4.1. The Split for the GVRPDS
4.2. Encoding and Decoding
4.3. The Initial Solution
4.4. Search Mechanism
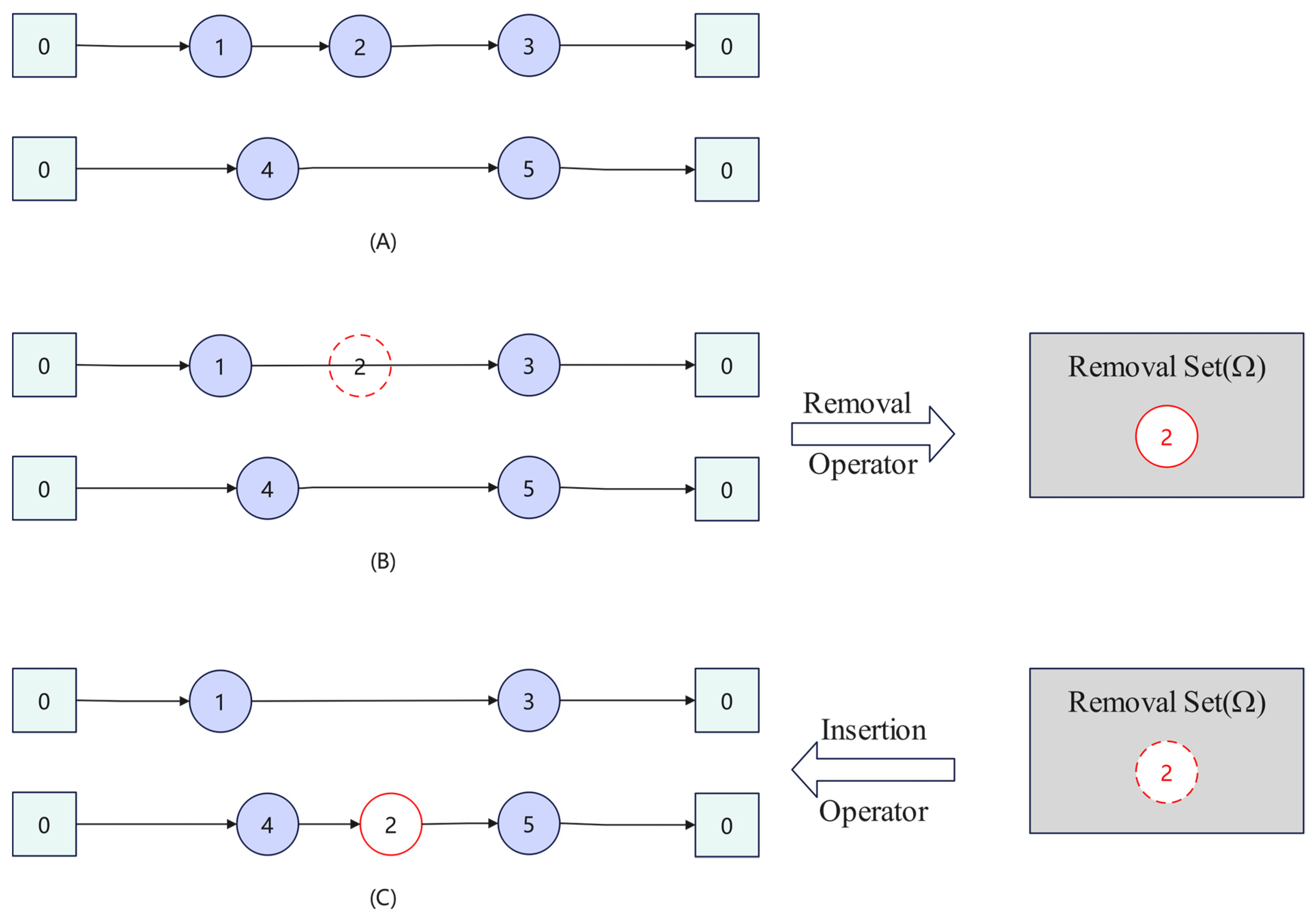
4.4.1. Removal Operators
| Algorithm 1 | Carbon emission-optimization removal |
| Input: | , , |
| Output: | , ; |
| 1. | 0; |
| 2. | while) do |
| 3. | Current iteration count + 1; |
| 4. | ; |
| 5. | ) do |
| 6. | , ; |
| 7. | foreach) do |
| 8. | foreach) do |
| 9. | if) then |
| 10. | if) then |
| 11. | ; |
| 12. | Return to step 2; |
4.4.2. Repair Operators
4.5. Adaptive Weighting Mechanism
- (1)
- If , the corresponding operators get points.
- (2)
- If the corresponding operators get points.
- (3)
- If , but is still accepted as , the corresponding operators get points.
4.6. Acceptance and Stopping Criteria
5. Experiments and Analyses
5.1. Instances Generation
5.2. Parameter Setting
5.3. SALNS Performance Evaluation
5.3.1. Comparisons SALNS with ALNS
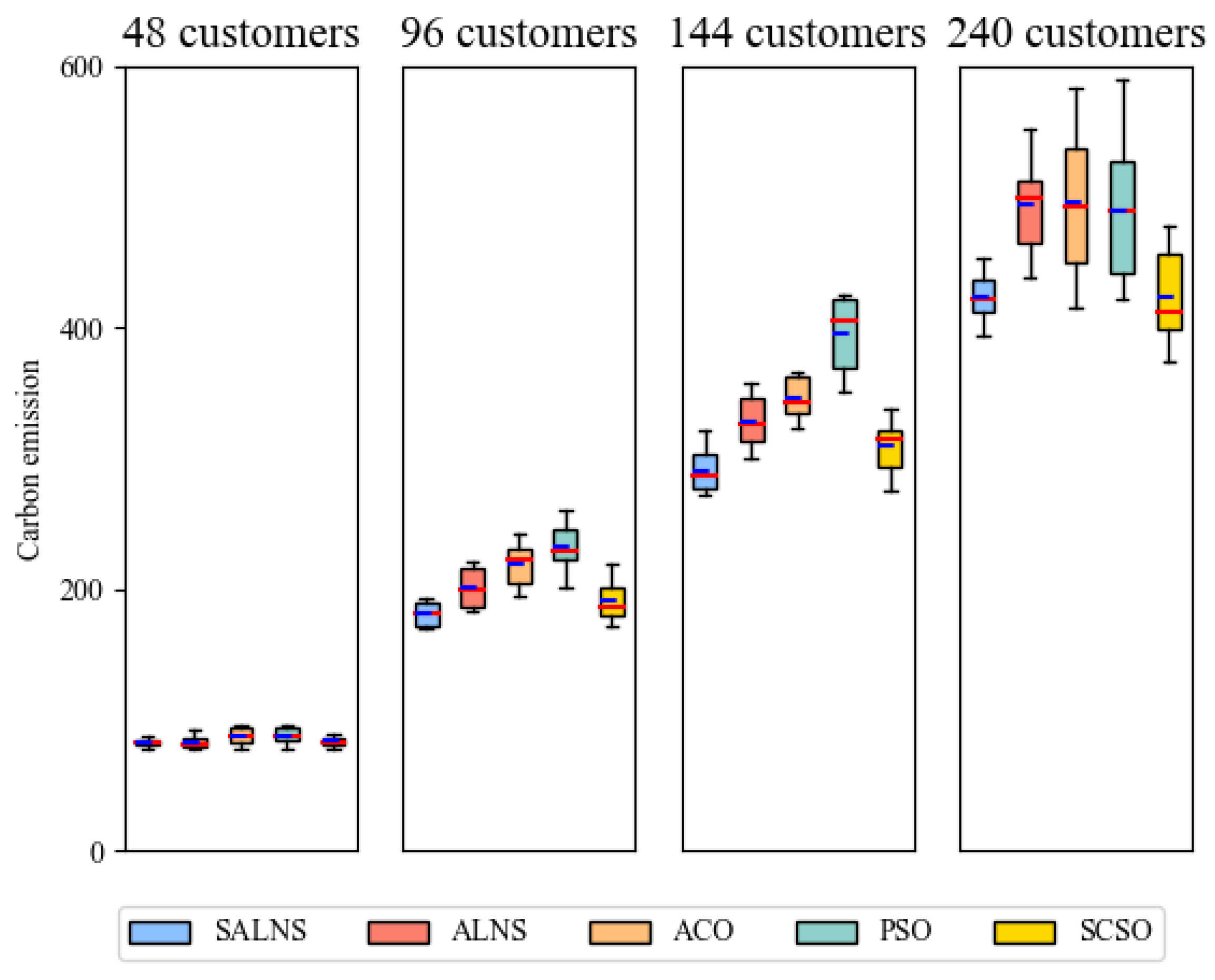
5.3.2. Comparisons with Meta-Heuristic Algorithms
5.4. Evaluation of Question Features
5.5. The Sensitivity Analysis of Model Parameters
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Choi, D.; Gao, Z.; Jiang, W. Attention to Global Warming. Rev. Financ. Stud. 2020, 33, 1112–1145. [Google Scholar] [CrossRef]
- Zhang, W.; Gajpal, Y.; Appadoo, S.S.; Wei, Q. Multi-Depot Green Vehicle Routing Problem to Minimize Carbon Emissions. Sustainability 2020, 12, 3500. [Google Scholar] [CrossRef]
- Duan, H.; Zhou, S.; Jiang, K.; Bertram, C.; Harmsen, M.; Kriegler, E.; Van Vuuren, D.P.; Wang, S.; Fujimori, S.; Tavoni, M.; et al. Assessing China’s Efforts to Pursue the 1.5 °C Warming Limit. Science 2021, 372, 378–385. [Google Scholar] [CrossRef] [PubMed]
- Erdoğan, S.; Miller-Hooks, E. A Green Vehicle Routing Problem. Transp. Res. Part E Logist. Transp. Rev. 2012, 48, 100–114. [Google Scholar] [CrossRef]
- Moghdani, R.; Salimifard, K.; Demir, E.; Benyettou, A. The Green Vehicle Routing Problem: A Systematic Literature Review. J. Clean. Prod. 2021, 279, 123691. [Google Scholar] [CrossRef]
- Nura, A.; Abdullahi, S. A Systematic Review of Multi-Depot Vehicle Routing Problems. Syst. Lit. Rev. Meta-Anal. J. 2022, 3, 51–60. [Google Scholar] [CrossRef]
- Eglese, R.; Bektas, T. Chapter 15: Green Vehicle Routing. In Vehicle Routing: Problems, Methods, and Applications, 2nd ed.; Toth, P., Vigo, D., Eds.; MOS-SIAM Series on Optimization; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2014; pp. 437–458. [Google Scholar] [CrossRef]
- Lahyani, R.; Gouguenheim, A.-L.; Coelho, L.C. A Hybrid Adaptive Large Neighbourhood Search for Multi-Depot Open Vehicle Routing Problems. Int. J. Prod. Res. 2019, 57, 6963–6976. [Google Scholar] [CrossRef]
- Alinaghian, M.; Shokouhi, N. Multi-Depot Multi-Compartment Vehicle Routing Problem, Solved by a Hybrid Adaptive Large Neighborhood Search. Omega 2018, 76, 85–99. [Google Scholar] [CrossRef]
- Mühlbauer, F.; Fontaine, P. A Parallelised Large Neighbourhood Search Heuristic for the Asymmetric Two-Echelon Vehicle Routing Problem with Swap Containers for Cargo-Bicycles. Eur. J. Oper. Res. 2021, 289, 742–757. [Google Scholar] [CrossRef]
- Prins, C.; Lacomme, P.; Prodhon, C. Order-First Split-Second Methods for Vehicle Routing Problems: A Review. Transp. Res. Part C Emerg. Technol. 2014, 40, 179–200. [Google Scholar] [CrossRef]
- Lin, C.; Choy, K.L.; Ho, G.T.; Chung, S.H.; Lam, H.Y. Survey of Green Vehicle Routing Problem: Past and Future Trends. Expert Syst. Appl. 2014, 41, 1118–1138. [Google Scholar] [CrossRef]
- Bektaş, T.; Laporte, G. The Pollution-Routing Problem. Transp. Res. Part B Methodol. 2011, 45, 1232–1250. [Google Scholar] [CrossRef]
- Park, Y.; Chae, J. A Review of the Solution Approaches Used in Recent G-VRP (Green Vehicle Routing Problem). Int. J. Adv. Logist. 2014, 3, 27–37. [Google Scholar] [CrossRef]
- Rezaei, N.; Ebrahimnejad, S.; Moosavi, A.; Nikfarjam, A. A Green Vehicle Routing Problem with Time Windows Considering the Heterogeneous Fleet of Vehicles: Two Metaheuristic Algorithms. Eur. J. Ind. Eng. 2019, 13, 507–535. [Google Scholar]
- Schneider, M.; Stenger, A.; Goeke, D. The Electric Vehicle-Routing Problem with Time Windows and Recharging Stations. Transp. Sci. 2014, 48, 500–520. [Google Scholar] [CrossRef]
- Amiri, A.; Amin, S.H.; Zolfagharinia, H. A Bi-Objective Green Vehicle Routing Problem with a Mixed Fleet of Conventional and Electric Trucks: Considering Charging Power and Density of Stations. Expert Syst. Appl. 2023, 213, 119228. [Google Scholar] [CrossRef]
- Liu, Y.; Yu, Y.; Zhang, Y.; Baldacci, R.; Tang, J.; Luo, X.; Sun, W. Branch-Cut-and-Price for the Time-Dependent Green Vehicle Routing Problem with Time Windows. INFORMS J. Comput. 2023, 35, 14–30. [Google Scholar] [CrossRef]
- Ghannadpour, S.F. Evolutionary Approach for Energy Minimizing Vehicle Routing Problem with Time Windows and Customers’ Priority. Int. J. Transp. Eng. 2019, 6, 237–264. [Google Scholar]
- Lu, F.; Du, Z.; Wang, Z.; Wang, L.; Wang, S. Towards Enhancing the Crowdsourcing Door-to-Door Delivery: An Effective Model in Beijing. JIMO 2025, 21, 2371–2395. [Google Scholar] [CrossRef]
- Yang, D.; Hyland, M.F.; Jayakrishnan, R. Tackling the Crowdsourced Shared-Trip Delivery Problem at Scale with a Novel Decomposition Heuristic. Transp. Res. Part E Logist. Transp. Rev. 2024, 188, 103633. [Google Scholar] [CrossRef]
- Cassidy, P.J.; Bennett, H.S. TRAMP—A Multi-Depot Vehicle Scheduling System. J. Oper. Res. Soc. 1972, 23, 151–163. [Google Scholar] [CrossRef]
- Yu, B.; Yang, Z.-Z.; Xie, J.-X. A Parallel Improved Ant Colony Optimization for Multi-Depot Vehicle Routing Problem. J. Oper. Res. Soc. 2011, 62, 183–188. [Google Scholar] [CrossRef]
- Özger, A. Multi-Depot Heterogeneous Fleet Vehicle Routing Problem with Time Windows: Airline and Roadway Integrated Routing. Int. J. Ind. Eng. Comput. 2022, 13, 435–456. [Google Scholar]
- Fan, H.; Yang, X.; Li, D.; Li, Y.; Liu, P.; Wu, J.X. Half-Open Multi-Depot Vehicle Routing Problem Based on Joint Distribution Mode of Fresh Food. Comput. Integ. Manufact. Syst 2019, 25, 256–266. [Google Scholar]
- Schmidt, C.E.; Silva, A.C.; Darvish, M.; Coelho, L.C. Time-Dependent Fleet Size and Mix Multi-Depot Vehicle Routing Problem. Int. J. Prod. Econ. 2023, 255, 108653. [Google Scholar] [CrossRef]
- Soriano, A.; Gansterer, M.; Hartl, R.F. The Multi-Depot Vehicle Routing Problem with Profit Fairness. Int. J. Prod. Econ. 2023, 255, 108669. [Google Scholar] [CrossRef]
- Salehi Sarbijan, M.; Behnamian, J. Feeder Vehicle Routing Problem in a Collaborative Environment Using Hybrid Particle Swarm Optimization and Adaptive Learning Strategy. Environ. Dev. Sustain. 2023, 1–41. [Google Scholar] [CrossRef]
- Jabir, E.; Panicker, V.V.; Sridharan, R. Design and Development of a Hybrid Ant Colony-Variable Neighbourhood Search Algorithm for a Multi-Depot Green Vehicle Routing Problem. Transp. Res. Part D Transp. Environ. 2017, 57, 422–457. [Google Scholar] [CrossRef]
- Shen, L.; Tao, F.; Wang, S. Multi-Depot Open Vehicle Routing Problem with Time Windows Based on Carbon Trading. Int. J. Environ. Res. Public Health 2018, 15, 2025. [Google Scholar] [CrossRef]
- Qin, G.; Tao, F.; Li, L. A Vehicle Routing Optimization Problem for Cold Chain Logistics Considering Customer Satisfaction and Carbon Emissions. Int. J. Environ. Res. Public Health 2019, 16, 576. [Google Scholar] [CrossRef]
- Wen, M.; Sun, W.; Yu, Y.; Tang, J.; Ikou, K. An Adaptive Large Neighborhood Search for the Larger-Scale Multi Depot Green Vehicle Routing Problem with Time Windows. J. Clean. Prod. 2022, 374, 133916. [Google Scholar] [CrossRef]
- Ropke, S.; Pisinger, D. An Adaptive Large Neighborhood Search Heuristic for the Pickup and Delivery Problem with Time Windows. Transp. Sci. 2006, 40, 455–472. [Google Scholar] [CrossRef]
- Chen, S.; Chen, R.; Wang, G.-G.; Gao, J.; Sangaiah, A.K. An Adaptive Large Neighborhood Search Heuristic for Dynamic Vehicle Routing Problems. Comput. Electr. Eng. 2018, 67, 596–607. [Google Scholar] [CrossRef]
- Liu, R.; Tao, Y.; Xie, X. An Adaptive Large Neighborhood Search Heuristic for the Vehicle Routing Problem with Time Windows and Synchronized Visits. Comput. Oper. Res. 2019, 101, 250–262. [Google Scholar] [CrossRef]
- Azi, N.; Gendreau, M.; Potvin, J.-Y. An Adaptive Large Neighborhood Search for a Vehicle Routing Problem with Multiple Routes. Comput. Oper. Res. 2014, 41, 167–173. [Google Scholar] [CrossRef]
- Gu, W.; Cattaruzza, D.; Ogier, M.; Semet, F. Adaptive Large Neighborhood Search for the Commodity Constrained Split Delivery VRP. Comput. Oper. Res. 2019, 112, 104761. [Google Scholar] [CrossRef]
- Sacramento, D.; Pisinger, D.; Ropke, S. An Adaptive Large Neighborhood Search Metaheuristic for the Vehicle Routing Problem with Drones. Transp. Res. Part C Emerg. Technol. 2019, 102, 289–315. [Google Scholar] [CrossRef]
- Koç, Ç.; Bektaş, T.; Jabali, O.; Laporte, G. The Impact of Depot Location, Fleet Composition and Routing on Emissions in City Logistics. Transp. Res. Part B Methodol. 2016, 84, 81–102. [Google Scholar] [CrossRef]
- Scora, G.; Barth, M. Comprehensive Modal Emissions Model (Cmem), Version 3.01. User Guide; Centre for Environmental Research and Technology, University of California,: Riverside, CA, USA, 2006; Volume 1070, p. 1580. [Google Scholar]
- Demir, E.; Bektaş, T.; Laporte, G. An Adaptive Large Neighborhood Search Heuristic for the Pollution-Routing Problem. Eur. J. Oper. Res. 2012, 223, 346–359. [Google Scholar] [CrossRef]
- Niu, Y.; Yang, Z.; Chen, P.; Xiao, J. Optimizing the Green Open Vehicle Routing Problem with Time Windows by Minimizing Comprehensive Routing Cost. J. Clean. Prod. 2018, 171, 962–971. [Google Scholar] [CrossRef]
- Desrochers, M. An algorithm for the shortest path problem with resource constraints. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Ann Arbor, MI, USA, 5–9 June 1988; pp. 3454–3461. [Google Scholar]
- Mancini, S. A Real-Life Multi Depot Multi Period Vehicle Routing Problem with a Heterogeneous Fleet: Formulation and Adaptive Large Neighborhood Search Based Matheuristic. Transp. Res. Part C Emerg. Technol. 2016, 70, 100–112. [Google Scholar] [CrossRef]
- Ky Phuc, P.N.; Phuong Thao, N.L. Ant Colony Optimization for Multiple Pickup and Multiple Delivery Vehicle Routing Problem with Time Window and Heterogeneous Fleets. Logistics 2021, 5, 28. [Google Scholar] [CrossRef]
- Ramadhani, B.N.I.F.; Garside, A.K. Particle Swarm Optimization Algorithm to Solve Vehicle Routing Problem with Fuel Consumption Minimization. J. Optimasi Sist. Ind. 2021, 20, 1–10. [Google Scholar] [CrossRef]
- Seyyedabbasi, A.; Kiani, F. Sand Cat Swarm Optimization: A Nature-Inspired Algorithm to Solve Global Optimization Problems. Eng. Comput. 2023, 39, 2627–2651. [Google Scholar] [CrossRef]

| Notation | Meaning | |
|---|---|---|
| Sets Nodes parameters Vehicle parameters Variables | The depot set The customer set The vertex set The vehicle set earliest service time latest service time Depot D parking space capacity Number of vehicles in depot D The capacity of the vehicle k ) ) ) ) The rolling resistance coefficient The aerodynamic drag coefficient ) Road angle ) ) The efficiency of the vehicle drive train The efficiency for diesel engines ) The fuel-to-air mass ratio ) , 0 otherwise | Values 5000 0.2 36.67 6.9 0.01 0.7 9.81 0 8.0 1.20 0.45 0.45 0 1:14.7 737 4.4 |
| Instances | Number | Depot | Vehicle | Capacity | ||
|---|---|---|---|---|---|---|
| pro01 | 48 | 4 | 3 | 4 | 8 | 200 |
| pro02 | 96 | 6 | 4 | 4 | 12 | 195 |
| pro03 | 144 | 8 | 6 | 4 | 16 | 150 |
| pro04 | 192 | 10 | 8 | 4 | 20 | 185 |
| pro05 | 240 | 12 | 10 | 4 | 24 | 180 |
| pro06 | 288 | 14 | 12 | 4 | 28 | 175 |
| pro07 | 72 | 5 | 4 | 6 | 12 | 200 |
| pro08 | 144 | 8 | 6 | 6 | 18 | 190 |
| pro09 | 216 | 11 | 10 | 6 | 24 | 180 |
| pro11 | 48 | 4 | 3 | 4 | 8 | 200 |
| pro12 | 96 | 6 | 4 | 4 | 12 | 195 |
| pro13 | 144 | 8 | 6 | 4 | 16 | 150 |
| pro14 | 192 | 10 | 8 | 4 | 20 | 185 |
| pro15 | 240 | 12 | 10 | 4 | 24 | 180 |
| pro16 | 288 | 14 | 12 | 4 | 28 | 175 |
| pro17 | 72 | 5 | 4 | 6 | 12 | 200 |
| pro18 | 144 | 8 | 6 | 6 | 18 | 190 |
| pro19 | 216 | 11 | 10 | 6 | 24 | 180 |
| Notation | Description | Value |
|---|---|---|
| Worst-case number of corrupts | [5, 10] | |
| Regret value the number of corruptions | 5 | |
| Weight decay ratio | 0.1 | |
| Rate of annealing | 0.9 | |
| Weight adjustment step size | 5 |
| Instances | SALNS | ALNS | |||
|---|---|---|---|---|---|
| Carbon Emission | Time | Carbon Emission | Time | ||
| pro01 | 78.5 | 1.1 | 78.5 | 1.3 | 0.00% |
| pro02 | 169.4 | 5.7 | 182.6 | 6.7 | 7.23% |
| pro03 | 272.3 | 15.9 | 300.5 | 16.4 | 9.38% |
| pro04 | 404.5 | 24.2 | 465.6 | 28.5 | 13.12% |
| pro05 | 416.0 | 43.4 | 470.2 | 48.0 | 11.49% |
| pro06 | 512.3 | 62.3 | 603.7 | 65.6 | 15.14% |
| pro07 | 137.3 | 4.9 | 137.3 | 5.2 | 0.00% |
| pro08 | 271.5 | 17.0 | 292.3 | 21.6 | 7.12% |
| pro09 | 375.2 | 27.8 | 400.9 | 30.3 | 6.41% |
| pro11 | 74.5 | 0.8 | 74.5 | 1.0 | 0.00% |
| pro12 | 126.4 | 5.9 | 144.3 | 6.0 | 12.40% |
| pro13 | 210.7 | 14.4 | 230.7 | 15.2 | 8.67% |
| pro14 | 214.5 | 25.5 | 243.6 | 29.7 | 11.95% |
| pro15 | 302.6 | 46.3 | 321.8 | 52.3 | 5.97% |
| pro16 | 358.6 | 65.4 | 415.4 | 75.4 | 13.67% |
| pro17 | 103.5 | 4.3 | 115.9 | 4.7 | 10.70% |
| pro18 | 216.3 | 16.0 | 242.7 | 17.1 | 10.88% |
| pro19 | 275.4 | 66.7 | 302.3 | 70.5 | 8.90% |
| Instances | General | COR | EOR | |||
|---|---|---|---|---|---|---|
| Carbon Emission | Time | Carbon Emission | Time | Carbon Emission | Time | |
| pro01 | 78.5 | 1.3 | 78.5 | 1.1 | 78.5 | 1.2 |
| pro02 | 176.7 | 6.2 | 172.6 | 6.3 | 173.4 | 6.2 |
| pro03 | 294.3 | 16.4 | 284.5 | 16.2 | 287.3 | 16.3 |
| pro04 | 409.5 | 28.5 | 405.6 | 25.5 | 407.6 | 26.5 |
| pro05 | 430.2 | 48.0 | 420.2 | 47.0 | 421.2 | 46.1 |
| pro06 | 528.5 | 65.6 | 523.7 | 65.3 | 518.7 | 64.6 |
| pro07 | 137.3 | 5.2 | 137.3 | 5.0 | 137.3 | 5.0 |
| pro08 | 290.3 | 21.6 | 284.3 | 20.6 | 286.6 | 19.6 |
| pro09 | 402.9 | 30.3 | 394.9 | 28.3 | 395.3 | 29.3 |
| Instances | SALNS | ACO | PSO | SCSO | ||||
|---|---|---|---|---|---|---|---|---|
| Carbon Emission | Time | Carbon Emission | Time | Carbon Emission | Time | Carbon Emission | Time | |
| pro01 | 78.5 | 1.1 | 78.5 | 1.3 | 78.5 | 1.2 | 78.5 | 1.1 |
| pro02 | 169.4 | 5.7 | 194.2 | 6.6 | 201.2 | 7.2 | 172.3 | 5.8 |
| pro03 | 272.3 | 15.9 | 323.5 | 18.7 | 350.3 | 17.0 | 275.4 | 19.3 |
| pro04 | 404.5 | 24.2 | 433.1 | 27.0 | 436.2 | 31.2 | 402.1 | 34.7 |
| pro05 | 416.0 | 43.4 | 446.2 | 50.2 | 452.6 | 48.1 | 412.3 | 45.6 |
| pro06 | 512.3 | 62.3 | 570.8 | 65.4 | 563.6 | 63.2 | 524.2 | 65.2 |
| pro07 | 137.3 | 4.9 | 145.1 | 5.1 | 227.3 | 5.4 | 134.2 | 5.6 |
| pro08 | 271.5 | 17.0 | 323.6 | 24.3 | 342.5 | 23.1 | 300.4 | 18.4 |
| pro09 | 375.2 | 27.8 | 412.2 | 33.4 | 420.5 | 30.3 | 430.2 | 35.6 |
| pro11 | 74.5 | 0.8 | 74.5 | 1.1 | 74.5 | 0.9 | 74.5 | 0.7 |
| pro12 | 126.4 | 5.9 | 137.4 | 6.4 | 144.3 | 7.9 | 127.4 | 5.6 |
| pro13 | 210.7 | 14.4 | 218.3 | 15.8 | 224.3 | 16.8 | 208.4 | 17.3 |
| pro14 | 214.5 | 25.5 | 232.2 | 26.9 | 253.6 | 26.7 | 223.5 | 27.4 |
| pro15 | 302.6 | 46.3 | 371.6 | 50.9 | 360.6 | 53.2 | 345.2 | 56.3 |
| pro16 | 358.6 | 65.4 | 403.7 | 70.7 | 433.9 | 73.2 | 385.2 | 72.8 |
| pro17 | 103.5 | 4.3 | 121.3 | 5.2 | 125.6 | 5.1 | 105.3 | 4.4 |
| pro18 | 216.3 | 16.0 | 256.5 | 19.2 | 260.3 | 18.8 | 224.9 | 16.6 |
| pro19 | 275.4 | 66.7 | 301.6 | 70.3 | 315.6 | 73.4 | 295.4 | 75.3 |
| Instances | 30 km/h | 40 km/h | 50 km/h | |||
|---|---|---|---|---|---|---|
| Carbon Emission | Distance | Carbon Emission | Distance | Carbon Emission | Distance | |
| pro01 | 83.4 | 645.2 | 78.5 | 610.4 | 71.4 | 594.4 |
| pro02 | 183.6 | 1369.3 | 169.4 | 1274.3 | 153.6 | 1185.0 |
| pro03 | 300.5 | 1944.4 | 272.3 | 1775.7 | 258.1 | 1347.2 |
| pro04 | 432.1 | 2597.2 | 404.5 | 2383.7 | 384.6 | 2234.9 |
| pro05 | 440.2 | 2674.1 | 416.0 | 2400.5 | 396.7 | 2356.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Z.; Lou, P.; Hu, J.; Zeng, Y.; Fan, C. An Adaptive Large Neighborhood Search for a Green Vehicle Routing Problem with Depot Sharing. Mathematics 2025, 13, 214. https://doi.org/10.3390/math13020214
Wu Z, Lou P, Hu J, Zeng Y, Fan C. An Adaptive Large Neighborhood Search for a Green Vehicle Routing Problem with Depot Sharing. Mathematics. 2025; 13(2):214. https://doi.org/10.3390/math13020214
Chicago/Turabian StyleWu, Zixuan, Ping Lou, Jianmin Hu, Yuhang Zeng, and Chuannian Fan. 2025. "An Adaptive Large Neighborhood Search for a Green Vehicle Routing Problem with Depot Sharing" Mathematics 13, no. 2: 214. https://doi.org/10.3390/math13020214
APA StyleWu, Z., Lou, P., Hu, J., Zeng, Y., & Fan, C. (2025). An Adaptive Large Neighborhood Search for a Green Vehicle Routing Problem with Depot Sharing. Mathematics, 13(2), 214. https://doi.org/10.3390/math13020214






