Exploring the Structure of Possibility Multi-Fuzzy Soft Ordered Semigroups Through Interior Ideals

Abstract

This paper aims to introduce a novel idea of possibility multi-fuzzy soft ordered semigroups for ideals and interior ideals. Various results, formulated as theorems based on these concepts, are presented and further validated with suitable examples. This paper also explores the broad applicability of possibility multi-fuzzy soft ordered semigroups in solving modern decision-making problems. Furthermore, this paper explores various classes of ordered semigroups, such as simple, regular, and intra-regular, using this innovative method. Based on these concepts, some important conclusions are drawn with supporting examples. Moreover, it defines the possibility of multi-fuzzy soft ideals for semiprime ordered semigroups.

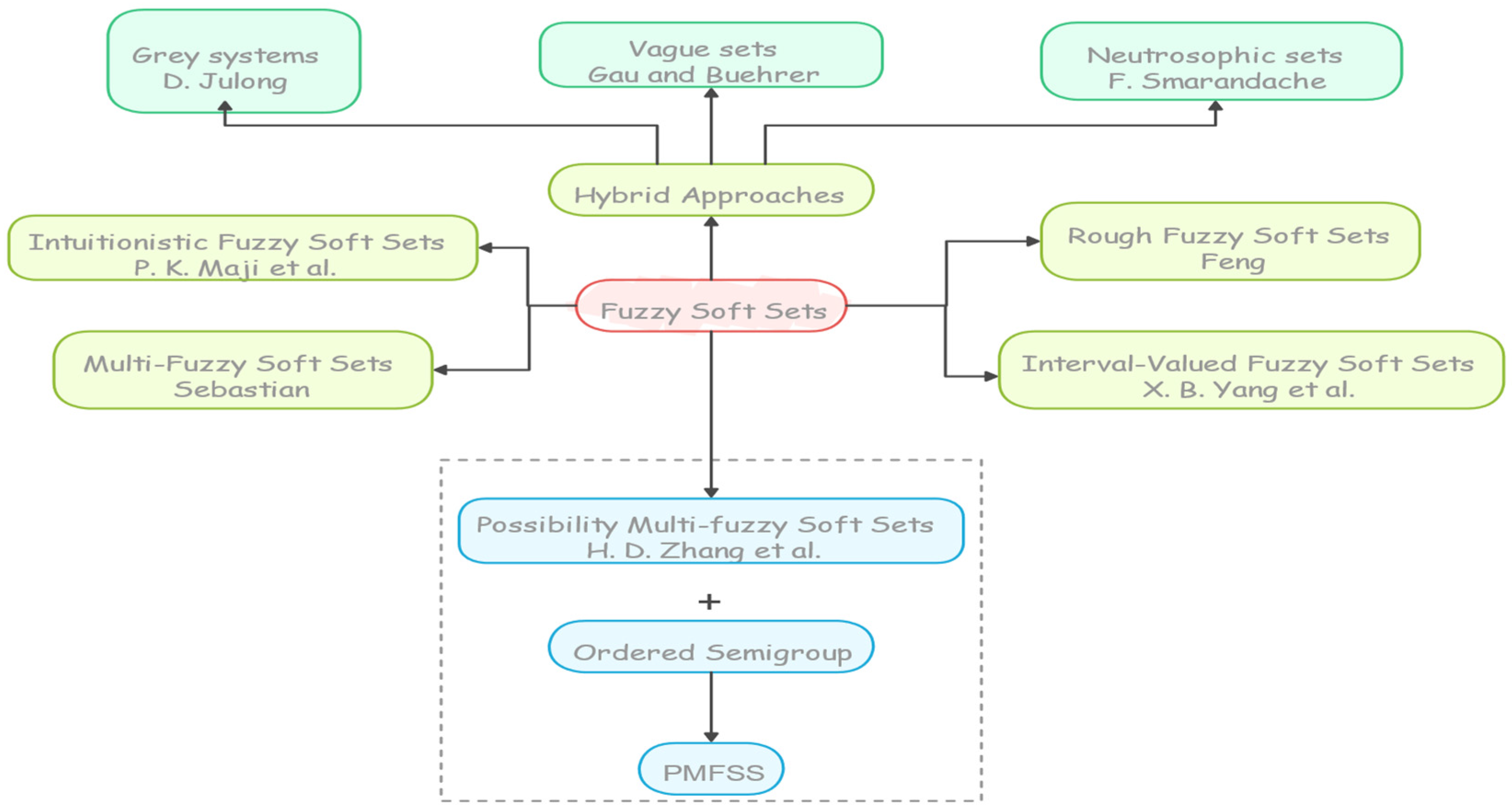
1. Introduction

Traditional mathematical tools of the classical approach are inadequate in handling the modern problems of applied sciences more precisely. Therefore, Zadeh initiated a novel approach called fuzzy mathematics [1]. This theory was further applied by scientists to solve numerous problems in artificial intelligence, control engineering, management sciences, robotics, and operational research.

Later, Moldstov initiated the soft set concept that extended fuzzy set theory by providing a parameterization tool [2,3]. Using Moldstov’s approach, Maji et al. solved various physical decision sciences problems [4,5]. Alkalzaleh et al. gave a new generalization to the soft sets approach, known as soft multisets [6]. Well ahead, Maji et al. broached the fuzzy soft set concept, providing a parametrization tool for fuzzy set theory, which improved its applications in decision sciences [7]. Different generalizations to fuzzy soft sets were made recently, like interval-valued fuzzy soft sets [8], intuitionistic fuzzy soft sets [9], multi-fuzzy soft sets [10], neutrosophic sets [11], vague soft expert sets [12], and many more [13,14,15,16,17,18,19,20,21,22,23,24]. Recently, S. Alkhazaleh and A.R. Salleh introduced the concept of soft expert sets and related their application to decision-making problems [25].

Possibility fuzzy soft set is also one of the generalized concepts used in solving decision-making problems and medical diagnoses introduced by Alkhalzaleh [26]. Recently, Zhang et al. proposed the possibility of multi-fuzzy soft sets and mentioned some of their applications [27]. The possibility multi-fuzzy soft sets theory precisely provides multi-membership values and possible membership values for all the elements in a universal set that leads the experts to choose the most appropriate results in decision sciences.

Algebraic structures are the main logistic tools for solving modern engineering problems and in various fields of applied sciences, which is why researchers are working on coupling these algebraic structures with modern methods of applied sciences. Initially, the concept of fuzzy sets in terms of semigroups was defined by Kuroki, who also related fuzzy ideals with semigroups [28,29,30]. Later, some properties of fuzzy sets in ordered groupoids were studied [31]. Kehayopulu and Tsingelis initiated the idea of fuzzy bi-ideals in ordered semigroups and also studied interior ideals for the same approach [32,33]. Khan et al. studied fuzzy interior ideals for ordered semigroups [34]. Jun et al. coupled the soft set theory with ordered semigroups [35]. Other researchers picked up the same concept and combined fuzzy soft sets with ordered semigroups [36,37]. Recently, Habib et al. initiated the idea of possibility fuzzy and multi-fuzzy soft ordered semigroups and possibility fuzzy soft ideals and related some of their applications via different operations [38,39,40]. Figure 1 illustrates a flow chart of fuzzy soft set theory, with the dotted section representing our proposed theory.

Figure 1. Flow chart of fuzzy soft set [8,9,10,11,12,16,17,25].

The traditional fuzzy set theory has been widely used to model uncertainty by assigning a single membership value to each element in a set, reflecting its degree of belonging to that set. However, applying fuzzy sets to complex, real-world decision-making problems often requires modelling multiple criteria, alternatives, and uncertainty in a more flexible manner.

To address these limitations, this paper relates a novel concept, the possibility multi-fuzzy soft set, which combines the advantages of fuzzy sets and soft sets but with significant enhancements. Unlike traditional fuzzy sets, which assign a single membership value to each element, the possibility multi-fuzzy soft set assigns multiple membership values for each component, representing the degree of membership under different possibilities or criteria.

Furthermore, this paper explores the potential of multi-fuzzy soft sets by extending this concept to ordered semigroups and ideals, making it suitable for more complex mathematical applications. In particular, we show how these sets can be used to model decision-making problems in algebraic structures, such as ordered semigroups, in a simplified example.

The paper demonstrates that this extended flexibility in representing uncertainty and possibility provides a powerful tool for solving complex decision-making problems that involve multiple alternatives and criteria, which are often not fully captured by traditional fuzzy logic approaches.

The primary objectives of this research approach are outlined as follows:

• Introduce possibility multi-fuzzy soft sets: develop this concept in relation to ordered semigroups and clarify its applications in decision sciences.
• Define possibility multi-fuzzy soft ideals: establish definitions for left (and right) ideals and interior ideals, examining their interconnections through illustrative examples.
• Propose new concepts: introduce possibility multi-fuzzy soft ideals and interior ideals for various classes, including regular and intra-regular ordered semigroup relations.
• Characterize simple ordered semigroups: Present a novel method for characterizing these semigroups using possibility multi-fuzzy soft ideals and interior ideals.
• Explore possibility multi-fuzzy soft semiprime ideals: initiate this concept and assess its relevance within intra-regular and regular ordered semigroups.

This paper comprises the following sections. In Section 2, some important definitions are mentioned that will be further used to understand the new concepts. Section 3 introduces a novel concept of PMFSS, and some related theorems are included. In Section 4, the authors will explain the idea of possibility multi-fuzzy soft interior ideals in ordered semigroups. Later, the concept of possibility multi-fuzzy soft ideals and its relation with possibility multi-fuzzy soft interior ideals is generated. Further, union and intersection properties are defined in terms of these notions and are validated with suitable examples. Section 5 includes the concept of possibility multi-fuzzy soft simple for ordered semigroups. Lastly, in Section 6, the relation of semiprime possibility multi-fuzzy soft ideals is defined and supported by suitable lemma and theorems. The authors also build the relation for intra-regular and regular ordered semigroups for the PMFSS approach.

2. Preliminaries

In this section, the authors restate essential definitions and lemmas that form the foundational framework for developing new and fundamental concepts later in the paper. Additionally, two comparison tables are included to provide a comprehensive analysis of related concepts, highlighting distinctions and contextual relevance to the proposed methodology.

In this paper, we introduce and explore the concept of possibility multi-fuzzy soft sets, a generalization of fuzzy and soft set theories.

A possibility multi-fuzzy soft set is a generalized structure where each element of a universe has multiple membership values representing different degrees of possibility, thus allowing for greater flexibility and precision in modelling uncertainty. This is particularly useful in decision-making processes where various possibilities must be evaluated simultaneously.

Definition 1

([27]). Let $U=\{u_1,u_2,\dots ,u_r\}$ be a universal set and $N=\left\{n_1,n_2,\dots ,n_q\right\}$ be a set of parameters. Consider the mapping

$${\overline{\Gamma }}_{\overline{f}}:N\to M^{p}FS(U)\times M^{p}FS(U)$$

($M^{p}FS\left(U\right)$ represents the set of all multi-fuzzy subsets of U with dimension p).

Then, ${\overline{\Gamma }}_{\overline{f}}(n_i)=(\overline{\Gamma }(n_i)(u),\overline{f}(n_i)(u))$ $\forall u\in U$ is known as a possibility multi-fuzzy soft set and is denoted by $({\overline{\Gamma }}_{\overline{f}},N)$. Possibility multi-fuzzy soft sets define both the multi-degree of membership value and its possible membership value for an element, denoted by $\overline{\Gamma }(n_i)$ and $\overline{f}(n_i)$, respectively.

$${\overline{\Gamma }}_{\overline{f}}(n_i)=\{({\displaystyle \frac{u}{{\nu }_{\overline{\Gamma }(n_i)}(u),{\nu }_{\overline{f}(n_i)}(u)}}):u\in U\}.$$

In its generalized form, a possibility multi-fuzzy soft set is expressed as

$${\overline{\Gamma }}_{\overline{f}}\left(n_i\right)=\{({\displaystyle \frac{u_1}{\overline{\Gamma }\left(n_i\right)(u_1)}},\overline{f}\left(n_i\right)(u_1)),({\displaystyle \frac{u_2}{\overline{\Gamma }\left(n_i\right)(u_2)}},\overline{f}\left(n_i\right)(u_2)),\dots \dots ,({\displaystyle \frac{u_r}{\overline{\Gamma }\left(n_i\right)(u_r)}},\overline{f}\left(n_i\right)(u_r))\}$$

where $i=1,2,\dots ,q$.

Theorem 1

([27]). Let $({\overline{\Gamma }}_{\overline{f}},N)$ and $({\overline{\zeta }}_{\overline{g}},N)$ be two possibility multi-fuzzy soft sets defined over U. If

• $\overline{\Gamma }\left(n\right)\subseteq \overline{\zeta }\left(n\right)$.
• $\overline{f}\left(n\right)\subseteq \overline{g}\left(n\right)\forall n\in N$.

then${\overline{\Gamma }}_{\overline{f}}\subseteq {\overline{\zeta }}_{\overline{g}}$ (${\overline{\Gamma }}_{\overline{f}}$is a subset of ${\overline{\zeta }}_{\overline{g}}$).

Theorem 2

([27]). The union of two possibility multi-fuzzy soft sets ${\overline{\Gamma }}_{\overline{f}}$ and ${\overline{\zeta }}_{\overline{g}}$, defined over U, is represented as ${\overline{\Gamma }}_{\overline{f}}\cup {\overline{\zeta }}_{\overline{g}}={\overline{\sigma }}_{\overline{h}}$, where ${\overline{\sigma }}_{\overline{h}}:N\to M^{p}FS\left(U\right)\times M^{p}FS\left(U\right),$ defined by ${\overline{\sigma }}_{\overline{h}}(n)=(\overline{\sigma }\left(n\right)\left(u\right),\overline{h}\left(n\right)\left(u\right))$, must satisfy the following conditions:

• $\overline{\Gamma }(n)\cup \overline{\zeta }(n)=\overline{\eta }(n)$.
• $\overline{h}\left(n\right)=\overline{f}\left(n\right)\cup \overline{g}\left(n\right)\forall n\in N$.

Theorem 3

([27]). Let $({\overline{\Gamma }}_{\overline{f}},N)$ and  $({\overline{\zeta }}_{\overline{g}},N)$ be two possibility multi-fuzzy soft sets defined over U. Then, their intersection is defined as ${\overline{\Gamma }}_{\overline{f}}\cap {\overline{\zeta }}_{\overline{g}}={\overline{\sigma }}_{\overline{h}}$, where ${\overline{\sigma }}_{\overline{h}}:N\to M^{p}FS(U)\times M^{p}FS(U)$, defined by ${\overline{\sigma }}_{\overline{h}}(n)=\overline{(\sigma }(n)(u),\overline{h}(n)(u))$, must satisfy the following conditions:

• $\overline{\Gamma }(n)\cap \overline{\zeta }(n)=\overline{\eta }(n)$.
• $\overline{h}\left(n\right)=\overline{f}\left(n\right)\cap \overline{g}\left(n\right)\forall n\in N.$

Theorem 4

([27]).  Let $({\overline{\Gamma }}_{\overline{f}},N)$ and $({\overline{\zeta }}_{\overline{g}},M)$ be two possibility multi-fuzzy soft sets defined over U. Then, the AND operation is defined as

$$({\overline{\Gamma }}_{\overline{f}},N)\wedge ({\overline{\zeta }}_{\overline{g}},M)=({\overline{\sigma }}_{\overline{h}},O)\forall O=N\times M,$$

where ${\overline{\sigma }}_{\overline{h}}(n,m)=\overline{(\sigma }(n,m)(u),\overline{h}(n,m)(u))$,$\forall (n,m)\in N\times M$ is such that

$$\overline{\sigma }(n,m)=\overline{\Gamma }(n)\cap \overline{\zeta }(m)$$

$$\overline{h}\left(n,m\right)=\overline{f}\left(n\right)\cap \overline{g}\left(m\right).$$

We then extend this framework to ordered semigroups, algebraic structures equipped with a binary operation and a partial order.

An ordered semigroup is a semigroup $\left(Z,\cdot \right)$ in which an order relation $\le$is defined over its elements, and this order relation is compatible with the semigroup operation: for all $z_1,z_2\in Z$,$z_1\le z_2$ implies $z_{1}a\le z_{2}a$ or $a{z}_1\le a{z}_2$ [41]. If$A^2\subseteq A$, then A is called a subsemigroup of Z for any non-empty subset A of $\left(Z,\cdot ,\le \right)$.

In particular, we examine how these structures interact with ideals and interior ideals to provide more efficient solutions to decision-making problems under uncertainty.

Definition 2.

Let L be a non-empty subset of Z. Then, L is called a left (resp. right) ideal of Z if $ZL\subseteq L$ (resp.$LZ\subseteq L$), and for all $z\in Z,x\in L$the next implication holds:$z\le x\Rightarrow z\in L$. If L is both a left and right ideal of Z, then it is called an ideal of Z and is represented by $L⊲Z$. Left (respectively right) ideals are denoted by $L{⊲}_{l}Z$ (resp.$L{⊲}_{r}Z$) [42].

Definition 3.

A non-empty subset A of an ordered semigroup Z is called an interior ideal of Z if

• $A^2\subseteq A$.
• For all $z\in Z$and$a\in A$,$z\le a\Rightarrow z\in A$.
• $ZAZ\subseteq A.$

An ordered semigroup Z is called semiprime if, for all non-empty subsets L of Z, we have $A^2\subseteq L$, for all $\forall A\subseteq Z$ [43].

Z is regular [41] if $\forall a\in Z$; we have $a\le aza,$which means that for all $a\in Z,$ $a\in \left(aZa\right]$, or equivalently,$\forall A\subseteq Z$,$A\subseteq (AZA]$.

If $\forall a\in Z$, there exists $y\in Z$such that $a\le y{a}^2$ (resp.$a\le a^{2}y$); then, Z is called left (resp right) regular. In other words, if $\forall a\in Z$, we have$a\in ({Za}^2]$(resp. $a\in (a^{2}Z]$), or equivalently if $\forall A\subseteq Z$, we have $A\subseteq ({ZA}^2]$ (resp.$A\subseteq (A^{2}Z]$). Z is known as completely regular if it is both left and right regular.

For every left (resp. right) ideal L of Z, Z is called left (resp. right) simple if and only if L = Z [44]. If an ordered semigroup Z is both right and left simple, then Z is simple.

Definition 4

([2]). Let U be a universal set, and let N denote a set of parameters. If M is a subset of N, then the pair$(f,M)$ is called a soft set, where f is a mapping from M to P(U), i.e., $f:M\to P\left(U\right)$.

Definition 5

([36]). Let$(f,M)$ be a soft set over Z, where M is a set of parameters. Then,  $(f,M)$ is called a soft ordered semigroup if $\forall n\in M,f(n)$is non-empty, and $f(n)$ is a subsemigroup of Z.

Theorem 5

([35]). Let $(f,N)$be a soft set over Z. Then, $(f,N)$ is a soft left (resp. right) ideal over Z if and only if $f(n)\forall n\in N$ is a fuzzy soft left (resp. right) ideal over Z.

Theorem 6

([35]). Let $(f,N)$ be a soft set over Z. Then, $(f,N)$ is a semiprime soft left (resp. right) ideal over Z if and only if $f(n)$ is a semiprime ideal over Z,$\forall n\in N$.

Also,$z^2\in f\left(n\right)$,$\forall z\in Z$.

Possibility multi-fuzzy soft sets [25], bipolar fuzzy sets [14], and intuitionistic fuzzy sets [11] are advanced mathematical tools designed to address uncertainty and imprecision. Table 1 elaborates a detailed comparison based on their key characteristics, applications, and advantages.

Table 1. Comparison Table.

Feature	Possibility Multi-Fuzzy Soft Sets	Bipolar Fuzzy Sets	Intuitionistic Fuzzy Sets
Core concept	Combines multi-fuzzy sets, soft set theory, and possibility theory to handle complex uncertainties.	Represents both positive and negative membership values.	Uses membership, non-membership, and hesitation values.
Membership representation	Multi-valued membership functions influenced by parameters of soft sets.	Positive and negative membership functions.	Membership and non-membership functions with hesitation.
Complexity handling	High, capable of addressing multi-criteria and parameterized uncertainty.	Moderate, focuses on duality of perspectives.	Moderate, focuses on hesitation or ambiguity.
Mathematical framework	Extends soft sets using multi-fuzzy and possibility logic.	Built on bipolar fuzzy logic.	Built on intuitionistic fuzzy logic.
Level of uncertainty	Rich models layered and parameterized uncertainties.	Moderate, dual aspects of uncertainty.	Balanced accounts for both ambiguity and hesitation.
Applications	Decision sciences, optimization, and multi-criteria analysis (MCA).	Sentiment analysis, conflict resolution, and evaluation systems.	Medical diagnostics, pattern recognition, and risk assessment.
Example use case	Ranking projects based on multi-criteria under vague conditions.	Modelling approvals and rejections simultaneously.	Assessing a candidate’s suitability with incomplete information.
Strengths	Highly flexible, parameter-driven framework for complex systems.	Effectively models dualistic problems.	Explicitly models ambiguity and hesitation.
Weaknesses	More complex implementation and interpretation.	Limited to bipolar scenarios.	Less flexible for multi-dimensional uncertainty.

A comparison table is presented below as Table 2 to elucidate the distinctions between general type 2 fuzzy logic systems (GT2 FLS) [45] and the proposed possibility multi-fuzzy soft sets in terms of membership value assignment. This table highlights their unique approaches to handling uncertainty and multi-criteria decision making, offering insights into their strengths and applications.

Table 2. Key differences in membership value assignment.

Aspect	General Type-2 FLS	Proposed System (PMFSS)
Membership representation	Interval-based with secondary membership	Multiple discrete membership values
Additional measure	Probability associated with each interval value	Possibility measure for each membership
Focus	Captures uncertainty through intervals and FOUs	Models’ multi-criteria decision scenarios
Flexibility	Accounts for uncertainty granularity	Handles multi-criteria and contextual data
Examples of use	Control systems, robotics, and real-time decisions	Algebraic structures and decision sciences

3. Possibility Multi-Fuzzy Soft Ordered Semigroups

Definition 6

([41]). Let $({\overline{\Gamma }}_{\overline{f}},N)$ be a possibility multi-fuzzy soft set of Z, defined by ${\overline{\Gamma }}_{\overline{f}}:N\to M^{p}FS(Z)\times M^{p}FS(Z)$, where $M^{p}FS\left(Z\right)$ denotes the multi-fuzzy subsets of Z and $(\overline{\Gamma }\left(n\right),\overline{f}\left(n\right))$ define the degree of membership value and possible membership value. Then, for any set of parameters $n\in N$, $({\overline{\Gamma }}_{\overline{f}},N)$ is called a possibility multi-fuzzy soft ordered semigroup of Z, if $(\overline{\Gamma }\left(n\right),\overline{f}\left(n\right))$ is non-empty and also ${\overline{\Gamma }}_{\overline{f}}\left(n\right)\left(z_1{z}_2\right)\ge {\overline{\Gamma }}_{\overline{f}}\left(z_1\right)\wedge {\overline{\Gamma }}_{\overline{f}}\left(z_2\right)\forall z_1,z_2\in Z.$ Thus$,({\overline{\Gamma }}_{\overline{f}},N)$ is a fuzzy subsemigroups of Z.

Unless otherwise specified, a possibility multi-fuzzy soft ordered semigroup is referred to as a PMFSS.

Example 1.

Let $Z=\left\{z_1,z_2,z_3,z_4\right\}$ be an ordered semigroup defined as in Table 3 and under the following ordered relation:

$$\le :=\left\{\right(z_1,z_1),(z_2,z_2),(z_3,z_3),(z_4,z_4),(z_1,z_2\left)\right\}.$$

Table 3. Multiplication table of Z.

.	${\mathit{z}}_1$	${\mathit{z}}_2$	${\mathit{z}}_3$	${\mathit{z}}_4$
$z_1$	$z_1$	$z_1$	$z_1$	$z_1$
$z_2$	$z_1$	$z_1$	$z_1$	$z_1$
$z_3$	$z_1$	$z_1$	$z_2$	$z_1$
$z_4$	$z_1$	$z_1$	$z_2$	$z_2$

For parameters$N=\{n_1,n_2,n_3\}$, $({\overline{\Gamma }}_{\overline{f}},N)$ is defined as ${\overline{\Gamma }}_{\overline{f}}:N\to M^{p}FS(Z)\times M^{p}FS(Z)$, where $({\overline{\Gamma }}_{\overline{f}},N)$ is a possibility multi-fuzzy soft set over Z.

Here, we obtain

$$\begin{array}{l}{\overline{\Gamma }}_{\overline{f}}(n)\\ =\left[\begin{array}{cccc}(0.9,0.7,0.4),(0.8,0.6,0.5)& (0.8,0.6,0.3),(0.7,0.5,0.4)& (0.5,0.3,0.2),(0.6,0.4,0.3)& (0.4,0.2,0.1),(0.6,0.4,0.3)\\ (0.5,0.7,0.8),(0.6,0.7,0.7)& (0.3,0.6,0.6),(0.4,0.6,0.4)& (0.2,0.5,0.5),(0.3,0.5,0.2)& (0.2,0.3,0.4),(0.3,0.4,0.4)\\ (0.8,0.7,0.7),(0.7,0.6,0.6)& (0.7,0.6,0.5),(0.6,0.5,0.4)& (0.5,0.3,0.2),(0.5,0.4,0.3)& (0.4,0.3,0.1),(0.5,0.3,0.2)\end{array}\right]\end{array}$$

Since ${\overline{\Gamma }}_{\overline{f}}(n)$ is non-empty and also ${\overline{\Gamma }}_{\overline{f}}\left(n\right)\left(z_1{z}_2\right)\ge {\overline{\Gamma }}_{\overline{f}}\left(z_1\right)\wedge {\overline{\Gamma }}_{\overline{f}}\left(z_2\right)\forall z_1,z_2\in Z$, it follows that $({\overline{\Gamma }}_{\overline{f}},N)$ is a fuzzy subsemigroup of Z. Hence, $({\overline{\Gamma }}_{\overline{f}},N)$ is a possibility multi-fuzzy soft ordered semigroup over Z, by Definition 6.

Definition 7.

Let $({\overline{\Gamma }}_{\overline{f}},N)$ be a PMFSS over Z for a set of parameters N. Then, the possibility multi-fuzzy soft level set of $({\overline{\Gamma }}_{\overline{f}},N)$ for all $t\in \left[\mathrm{0,1}\right]$ is defined by

$$\mathfrak{A}({\overline{\Gamma }}_{\overline{f}};t)=\{z\in Z|\overline{\psi }(z)\ge t,\overline{f}(z)\ge t\}.$$

Further, we stated the following theorems based on the notion of PMFSS.

Theorem 7.

Let $({\overline{\Gamma }}_{\overline{f}},N)$ and $({\overline{\zeta }}_{\overline{g}},M)$ be a PMFSS over Z. Then, $({\overline{\Gamma }}_{\overline{f}},N)\wedge ({\overline{\zeta }}_{\overline{g}},M)$ is also a PMFSS over Z.

Proof. 

The AND operation in possibility multi-fuzzy soft sets is defined by $\left({\overline{\Gamma }}_{\overline{f}},N\right)\wedge \left({\overline{\zeta }}_{\overline{g}},M\right)=({\overline{\sigma }}_{\overline{h}},O)$, where $O=N\times M$ and ${\overline{\sigma }}_{\overline{h}}(n,m)={\overline{\Gamma }}_{\overline{f}}(n)\cap {\overline{\zeta }}_{\overline{g}}(m)$, $\forall (n,m)\in N\times M$. Since $({\overline{\Gamma }}_{\overline{f}},N)$ and $({\overline{\zeta }}_{\overline{g}},M)$ are PMFSSs over Z, thereby the definition of PMFSSs ${\overline{\Gamma }}_{\overline{f}}(n)$ and ${\overline{\zeta }}_{\overline{g}}(m)$ are multi-fuzzy subsemigroups of Z, and their intersection is also a fuzzy subsemigroup of Z. Hence, ${\overline{\sigma }}_{\overline{h}}(n,m)=(\overline{\sigma }(n,m)(z),\overline{h}\left(n,m\right)\left(z)\right)\forall z\in Z$ is also a fuzzy subsemigroup of Z. Thus, $\left({\overline{\Gamma }}_{\overline{f}},N\right)\wedge \left({\overline{\zeta }}_{\overline{g}},M\right)=({\overline{\sigma }}_{\overline{h}},O)$ is also a PMFSS over Z. □

Example 2.

Let $({\overline{\Gamma }}_{\overline{f}},N)$ be a PMFSS over Z as defined in Example 1. Then, we define a mapping ${\overline{\zeta }}_{\overline{g}}:M\to M^{n}FS(Z)\times M^{n}FS(Zby$ ${\overline{\zeta }}_{\overline{g}}(m)=\overline{\zeta }(m)(z),\overline{g}(m)(z)$ for all $z\in Z$.

$${\overline{\zeta }}_{\overline{g}}(m)=\left[\begin{array}{c}(0.8,0.7,0.4)(0.7,0.6,0.5)(0.7,0.5,0.3)(0.6,0.6,0.4)(0.6,0.4,0.2)(0.5,0.4,0.3)(0.6,0.4,0.2)(0.5,0.3,0.2)\\ (0.7,0.7,0.8)(0.6,0.5,0.7)(0.6,0.6,0.7)(0.5,0.4,0.6)(0.3,0.5,0.6)(0.4,0.2,0.2)(0.5,0.5,0.1)(0.6,0.2,0.3)\\ (0.9,0.8,0.6)(0.8,0.7,0.6)(0.6,0.7,0.6)(0.6,0.6,0.5)(0.4,0.6,0.2)(0.3,0.4,0.2)(0.3,0.3,0.2)(0.3,0.3,0.2)\end{array}\right]$$

Then, ${\overline{\zeta }}_{\overline{g}}\left(m\right)isnonempty$and ${\overline{\zeta }}_{\overline{g}}(m)(z),\forall z\in Z$ are fuzzy subsemigroups of Z. Hence, $\left({\overline{\zeta }}_{\overline{g}},M\right)$ is a PMFSS over Z.

Then, we can define the corresponding AND operation by $\left({\overline{\Gamma }}_{\overline{f}},N\right)\wedge \left({\overline{\zeta }}_{\overline{g}},M\right)=({\overline{\sigma }}_{\overline{h}},O)$, where ${\overline{\sigma }}_{\overline{h}}$ for all pairs of parameters can be concluded as follows.

In matrix form

$${\overline{\mathsf{\sigma }}}_{\overline{\mathrm{h}}}=\left[\begin{array}{cccc}(0.8,0.7,0.4),(0.7,0.6,0.5)& (0.7,0.5,0.3),(0.6,0.5,0.4)& (0.5,0.3,0.1),(0.5,0.4,0.3)& (0.4,0.2,0.1),(0.5,0.3,0.2)\\ (0.7,0.7,0.4),(0.6,0.5,0.5)& (0.6,0.6,0.3),(0.5,0.4,0.4)& (0.3,0.3,0.2),(0.4,0.2,0.2)& (0.4,0.2,0.1),(0.6,0.2,0.3)\\ (0.9,0.7,0.4),(0.8,0.6,0.5)& (0.6,0.6,0.3),(0.6,0.5,0.4)& (0.4,0.3,0.2),(0.3,0.4,0.2)& (0.3,0.2,0.1),(0.3,0.3,0.2)\\ (0.5,0.7,0.4),(0.6,0.6,0.5)& (0.3,0.5,0.3),(0.4,0.6,0.4)& (0.2,0.4,0.2),(0.3,0.4,0.2)& (0.2,0.3,0.2),(0.3,0.3,0.2)\\ (0.5,0.7,0.8),(0.6,0.5,0.7)& (0.3,0.6,0.6),(0.4,0.4,0.4)& (0.2,0.5,0.5),(0.3,0.2,0.2)& (0.2,0.3,0.1),(0.3,0.2,0.3)\\ (0.5,0.7,0.6),(0.6,0.7,0.6)& (0.3,0.6,0.6),(0.4,0.6,0.4)& (0.2,0.5,0.2),(0.3,0.4,0.2)& (0.2,0.3,0.2),(0.3,0.3,0.2)\\ (0.8,0.7,0.4),(0.7,0.6,0.5)& (0.7,0.6,0.3),(0.6,0.5,0.4)& (0.5,0.3,0.2),(0.5,0.4,0.3)& (0.4,0.3,0.1),(0.5,0.3,0.2)\\ (0.7,0.7,0.7),(0.6,0.5,0.6)& (0.6,0.6,0.5),(0.5,0.4,0.4)& (0.3,0.3,0.2),(0.4,0.2,0.2)& (0.4,0.3,0.1),(0.5,0.2,0.2)\\ (0.8,0.7,0.6),(0.7,0.6,0.6)& (0.6,0.6,0.5),(0.6,0.5,0.4)& (0.4,0.3,0.2),(0.3,0.4,0.2)& (0.3,0.3,0.1),(0.3,0.3,0.2)\end{array}\right]$$

as ${\overline{\sigma }}_{\overline{h}}(n,m)\ne \varphi$, ${\overline{\sigma }}_{\overline{h}}(n,m)$ is a multi-fuzzy subsemigroup of Z. Thus, $\left({\overline{\Gamma }}_{\overline{f}},N\right)\wedge \left({\overline{\zeta }}_{\overline{g}},M\right)=({\overline{\sigma }}_{\overline{h}},O)$ is also possibility multi-fuzzy soft ordered semigroup over Z.

Theorem 8.

Let $({\overline{\Gamma }}_{\overline{f}},N)$ and $({\overline{\zeta }}_{\overline{g}},M)$ be PMFSSs over Z. Then, for all $M\cap N=\varphi$, $({\overline{\Gamma }}_{\overline{f}},N)\vee ({\overline{\zeta }}_{\overline{g}},M)$ is also a PMFSS over Z.

Proof. 

The proof of this theorem is straightforward and follows directly from the steps outlined in Theorem 7. □

4. Application of Possibility Multi-Fuzzy Soft Ordered Semigroup

Consider a set $Z=\{B_1,B_2,B_3\}$ representing three football players. To evaluate their performance in the last five matches, we define a multiplication table (Table 4) and an ordered relation to compare their overall performance:

$$\le :=\left\{\right(B_1,B_1),(B_2,B_2),(B_3,B_3),(B_1,B_3),\left(B_2,B_3)\right\}.$$

Table 4. Multiplication table for players.

.	B1	B2	B3
B1	B1	B2	B3
B2	B2	B2	B3
B3	B3	B3	B3

From this relation, it is clear that $B_3$ is the most suitable player due to its dominance in the hierarchy.

Let us define a possibility multi-fuzzy soft set by a mapping ${\overline{\Gamma }}_{\overline{f}}:N\to M^{p}FS(Z)\times M^{p}FS(Z)$ with index $p$ = 2 and the $N=\{n\}$ parameter, where $n$ represents skills (attacking and defense). Then, ${\overline{\Gamma }}_{\overline{f}}(n)=(\overline{\Gamma }(n)(B_i),\overline{f}(n)(B_i))$ for all $B_i\in Z$and $n\in N$ where $i=1,2,3$.

$${\overline{\Gamma }}_{\overline{f}}=\left[\begin{array}{ccc}(0.4,0.1),(0.6,0.3)& (0.6,0.3),(0.7,0.5)& (0.8.0.9),(0.9,1.0)\end{array}\right].$$

Hence, ${\overline{\Gamma }}_{\overline{f}}\left(n\right)\left(z_1{z}_2\right)\ge {\overline{\Gamma }}_{\overline{f}}\left(z_1\right)\wedge {\overline{\Gamma }}_{\overline{f}}\left(z_2\right)\forall z_1,z_2\in Z$, satisfies the criteria for a fuzzy subsemigroup of Z. Hence, $({\overline{\Gamma }}_{\overline{f}},N)$ is a possibility multi-fuzzy soft ordered semigroup over Z as per Definition 6. Here, $({\overline{\Gamma }}_{\overline{f}},N)$ is defined on the basis of data provided by the first observer or the committee member.

Similarly, let us define a possibility multi-fuzzy soft set $({\overline{\zeta }}_{\overline{g}},M)$ by a mapping ${\overline{\zeta }}_{\overline{g}}:M\to M^{p}FS(Z)\times M^{p}FS(Z)$, where $({\overline{\zeta }}_{\overline{g}},M)$ is defined as the second committee member and $\mathrm{N}=\mathrm{M}$

$${\overline{\zeta }}_{\overline{g}}=\left[\begin{array}{ccc}(0.3,0.1),(0.4,0.4)& (0.7,0.6),(0.6,0.6)& (0.8.0.8),(0.9,0.8)\end{array}\right].$$

In addition, $({\overline{\zeta }}_{\overline{g}},M)$ also satisfies the possibility multi-fuzzy soft ordered semigroup criteria. In order to evaluate the results on the basis of combined scoring AND operation of PMFSS, we consider $({\overline{\sigma }}_{\overline{h}},O)=({\overline{\Gamma }}_{\overline{f}},N)\wedge ({\overline{\zeta }}_{\overline{g}},M)$, or simply we can write

$${\overline{\sigma }}_{\overline{h}}={\overline{\Gamma }}_{\overline{f}}\wedge {\overline{\zeta }}_{\overline{g}}$$

$${\overline{\sigma }}_{\overline{h}}=\left[\begin{array}{ccc}(0.3,0.1)(0.4,0.3)& (0.6,0.3),(0.6,0.5)& (0.8.0.8),(0.9,0.8)\end{array}\right].$$

This clearly indicates that both the multi-membership value and the possible multi-membership value for the third player are the highest. Therefore, the committee should select the third player as the star player.

5. Possibility Multi-Fuzzy Soft Interior Ideals

This section of the paper elaborates the concepts of possibility multi-fuzzy soft left (and right) ideals as well as possibility multi-fuzzy soft interior ideals. Furthermore, accompanied by appropriate examples for clarification, various classes of ordered semigroups, including simple, regular, and intra-regular relations, are defined.

Definition 8.

Let $({\overline{\Gamma }}_{\overline{f}},N)$ be a PMFSS over Z. Then, for any possibility multi-fuzzy soft set $({\overline{\zeta }}_{\overline{g}},L)$ over Z, $({\overline{\zeta }}_{\overline{g}},L)$ is called a possibility multi-fuzzy soft left ideal (resp. right ideal) of $({\overline{\Gamma }}_{\overline{f}},N)$ if $L\subseteq N$and for every $n\in L$, and ${\overline{\zeta }}_{\overline{g}}(n)$ is a multi-fuzzy soft left ideal (resp. right ideal) of ${\overline{\Gamma }}_{\overline{f}}\left(n\right).$In this case, we write $({\overline{\zeta }}_{\overline{g}},L){⊲}_l({\overline{\Gamma }}_{\overline{f}},N)$ (resp. ($({\overline{\zeta }}_{\overline{g}},L){⊲}_r({\overline{\Gamma }}_{\overline{f}},N)$)). Furthermore, $({\overline{\zeta }}_{\overline{g}},L)$ is called a possibility multi-fuzzy soft ideal of $({\overline{\Gamma }}_{\overline{f}},N)$ if it is both a left and right ideal of $({\overline{\Gamma }}_{\overline{f}},N)$, and this is denoted by $({\overline{\zeta }}_{\overline{g}},L)⊲({\overline{\Gamma }}_{\overline{f}},N)$.

Example 3.

Let $Z=\left\{z_1,z_2,z_3,z_4\right\}$ be an ordered semigroup defined as in Table 5 and under the following ordered relation:

$$\le :=\left\{\right(z_1,z_1),(z_2,z_2),(z_3,z_3),(z_4,z_4),(z_1,z_2\left)\right\}.$$

Table 5. Multiplication table of Z.

.	${\mathit{z}}_1$	${\mathit{z}}_2$	${\mathit{z}}_3$	${\mathit{z}}_4$
$z_1$	$z_1$	$z_1$	$z_1$	$z_1$
$z_2$	$z_1$	$z_1$	$z_1$	$z_1$
$z_3$	$z_1$	$z_1$	$z_1$	$z_2$
$z_4$	$z_1$	$z_1$	$z_2$	$z_3$

Let $({\overline{\Gamma }}_{\overline{f}},N)$ be a PMFSS over Z with parameters $N=\{n_1,n_2,n_3\}$; here, $p$ = 3.

Let L be a subset of N. Then, $({\overline{\zeta }}_{\overline{g}},L)$ is also a possibility multi-fuzzy soft set defined by a mapping ${\overline{\zeta }}_{\overline{g}}:L\to M^{p}FS(Z)\times M^{p}FS(Z)$, where ${\overline{\zeta }}_{\overline{g}}(n)=(\overline{\zeta }(n)(z_i),\overline{g}(n)\left(z_i)\right)\forall z_i\in Z$. Here, ${\overline{\zeta }}_{\overline{g}}(n)(z_i\cdot z_j)\ge {\overline{\zeta }}_{\overline{g}}(n)(z_i)\forall z_i,z_j\in Z$; hence, ${\overline{\zeta }}_{\overline{g}}(n)$ is a possibility multi-fuzzy soft right ideal of $({\overline{\Gamma }}_{\overline{f}},N)$.

$$\begin{array}{l}{\overline{\zeta }}_{\overline{g}}(n)\\ =\left[\begin{array}{cccc}(0.8,0.7,0.6),(0.7,0.5,0.4)& (0.7,0.6,0.4),(0.6,0.4,0.4)& (0.5,0.4,0.4),(0.5,0.4,0.3)& (0.5,0.3,0.2),(0.4,0.4,0.3)\\ (0.6,0.6,0.4),(0.6,0.4,0.4)& (0.5,0.4,0.4),(0.4,0.4,0.3)& (0.4,0.3,0.3),(0.3,0.3,0.1)& (0.4,0.3,0.2),(0.1,0.1,0.1)\\ (0.7,0.7,0.6),(0.7,0.6,0.5)& (0.6,0.5,0.5),(0.5,0.5,0.4)& (0.5,0.4,0.3),(0.4,0.4,0.2)& (0.4,0.3,0.2),(0.4,0.4,0.1)\end{array}\right]\end{array}$$

Similarly, ${\overline{\zeta }}_{\overline{g}}(n)(z_i\cdot z_j)\ge {\overline{\zeta }}_{\overline{g}}(n)(z_j)$ implies that ${\overline{\zeta }}_{\overline{g}}(n)$ is a possibility multi-fuzzy soft left ideal of $({\overline{\Gamma }}_{\overline{f}},N)$. Thus, it is concluded that $({\overline{\zeta }}_{\overline{g}},L)⊲({\overline{\Gamma }}_{\overline{f}},N)$.

Theorem 9.

Let $({\overline{\Gamma }}_{\overline{f}},N)$ be a PMFSS over Z, and let $L_1$ and $L_2$be the parameters contained in N, and also$L_1\cap L_2\ne \varphi$. Then, the following statements hold:

• If$({\overline{\zeta }}_{\overline{g}}{|}_1,L_1){⊲}_l({\overline{\Gamma }}_{\overline{f}}N)$ and$({\overline{\zeta }}_{\overline{g}}{|}_2,L_2){⊲}_l({\overline{\Gamma }}_{\overline{f}},N)$ then$({\overline{\zeta }}_{\overline{g}}{|}_1,L_1)\cap ({\overline{\zeta }}_{\overline{g}}{|}_2,L_2){⊲}_l({\overline{\Gamma }}_{\overline{f}},N)$.
• If$\left({\overline{\zeta }}_{\overline{g}}{|}_1,L_1\right){⊲}_r\left({\overline{\Gamma }}_{\overline{f}},N\right)$and$({\overline{\zeta }}_{\overline{g}}{|}_2,L_2){⊲}_r({\overline{\Gamma }}_{\overline{f}},N)$ then$({\overline{\zeta }}_{\overline{g}}{|}_1,L_1)\cap ({\overline{\zeta }}_{\overline{g}}{|}_2,L_2){⊲}_r({\overline{\Gamma }}_{\overline{f}},N).$

Proof. 

Let $({\overline{\zeta }}_{\overline{g}}{|}_1,L_1)$ and $({\overline{\zeta }}_{\overline{g}}{|}_2,L_2)$ be possibility multi-fuzzy soft sets of Z, and their intersections are defined as $({\overline{\zeta }}_{\overline{g}}{|}_1,L_1)\cap ({\overline{\zeta }}_{\overline{g}}{|}_2,L_2)=({\overline{\zeta }}_{\overline{g}},L)$, where $L_1\cap L_2=L$. Then, for any n of L, it follows that either n belongs to $L_1$ or to $L_2$. If $n\in L_1$, then ${\overline{\zeta }}_{\overline{g}}(n)={\overline{\zeta }}_{\overline{g}}{|}_1(n)$, and if $n\in L_2$, then ${\overline{\zeta }}_{\overline{g}}(n)={\overline{\zeta }}_{\overline{g}}{|}_2(n)$. As $L\subseteq N$, we can conclude that $({\overline{\zeta }}_{\overline{g}},L)$ is a PMFSS over Z. Since $({\overline{\zeta }}_{\overline{g}}{|}_1,L_1){⊲}_l({\overline{\Gamma }}_{\overline{f}},N)$, it follows that $({\overline{\zeta }}_{\overline{g}},L){⊲}_l({\overline{\Gamma }}_{\overline{f}},N)$ as $({\overline{\zeta }}_{\overline{g}}{|}_1,L_1)\cap ({\overline{\zeta }}_{\overline{g}}{|}_2,L_2)=({\overline{\zeta }}_{\overline{g}},L){⊲}_l({\overline{\Gamma }}_{\overline{f}},N)$.

Similarly, we can prove that $({\overline{\zeta }}_{\overline{g}}{|}_1,L_1)\cap ({\overline{\zeta }}_{\overline{g}}{|}_2,L_2){⊲}_r({\overline{\Gamma }}_{\overline{f}},N).$ □

Theorem 10.

Let $({\overline{\zeta }}_{\overline{g}},M)$ and $({\overline{\sigma }}_{\overline{h}},O)$be two possibility multi-fuzzy soft sets over Z, where $M\cap O=\varphi$, and let $({\overline{\Gamma }}_{\overline{f}},N)$ be a PMFSS over Z. Then, the following statements hold:

• If $({\overline{\zeta }}_{\overline{g}},M)$ and $({\overline{\sigma }}_{\overline{h}},O)$ are a possibility multi-fuzzy soft left ideal of $\left({\overline{\Gamma }}_{\overline{f}},N\right)$, then their union $({\overline{\zeta }}_{\overline{g}},M)\cup ({\overline{\sigma }}_{\overline{h}},O)$is also a possibility multi-fuzzy soft left ideal of $({\overline{\Gamma }}_{\overline{f}},N)$, denoted by $({\overline{\zeta }}_{\overline{g}},M)\cup ({\overline{\sigma }}_{\overline{h}},O){⊲}_l({\overline{\psi }}_{\overline{f}},N)$.
• If$({\overline{\zeta }}_{\overline{g}},M)$ and$({\overline{\sigma }}_{\overline{h}},O)$ are a possibility multi-fuzzy soft right ideal of $\left({\overline{\Gamma }}_{\overline{f}},N\right),$ then their union$({\overline{\zeta }}_{\overline{g}},M)\cup ({\overline{\sigma }}_{\overline{h}},O)$is also a possibility multi-fuzzy soft right ideal of $({\overline{\Gamma }}_{\overline{f}},N)$, denoted by $({\overline{\zeta }}_{\overline{g}},M)\cup ({\overline{\sigma }}_{\overline{h}},O){⊲}_r({\overline{\Gamma }}_{\overline{f}},N)$.

Proof. 

Let the union of two possibility multi-fuzzy soft sets $({\overline{\zeta }}_{\overline{g}},M)$ and $({\overline{\sigma }}_{\overline{h}},O)$ be equal to $({\overline{\varpi }}_{\overline{k}},V)$, denoted by $({\overline{\zeta }}_{\overline{g}},M)\cup ({\overline{\sigma }}_{\overline{h}},O)=({\overline{\varpi }}_{\overline{k}},V),$ where for all $n\in V$, $M\cup O=V$.

$${\overline{\varpi }}_{\overline{k}}(n)=\left\{\begin{array}{c}{\overline{\zeta }}_{\overline{g}}(n)\\ {\overline{\sigma }}_{\overline{h}}(n)\\ {\overline{\zeta }}_{\overline{g}}(n)\cup {\overline{\sigma }}_{\overline{h}}(n)\end{array}\right.if\begin{array}{c}n\in M\backslash O,\\ n\in O\backslash M,\\ n\in M\cap O.\end{array}$$

Since $M\cap O=\varphi ,$ either n belongs to M or to O. If n belongs to M, then ${\overline{\varpi }}_{\overline{k}}(n)={\overline{\zeta }}_{\overline{g}}(n)$, where ${\overline{\zeta }}_{\overline{g}}(n)$is a multi-fuzzy soft left ideal of ${\overline{\Gamma }}_{\overline{f}}(n)$. Therefore, ${\overline{\varpi }}_{\overline{k}}(n)$ is also a multi-fuzzy soft left ideal of ${\overline{\Gamma }}_{\overline{f}}(n)$. Hence, $({\overline{\varpi }}_{\overline{k}},V){⊲}_l({\overline{\Gamma }}_{\overline{f}},N)$. If n belongs to O, then ${\overline{\varpi }}_{\overline{k}}(e)={\overline{\sigma }}_{\overline{h}}(e)$, where ${\overline{\sigma }}_{\overline{h}}(n)$ is a multi-fuzzy soft left ideal of ${\overline{\Gamma }}_{\overline{f}}(n)$. So, ${\overline{\varpi }}_{\overline{k}}(n)$ is also a multi-fuzzy soft left ideal of ${\overline{\Gamma }}_{\overline{f}}(n)$. Therefore, $({\overline{\varpi }}_{\overline{k}},V){⊲}_l({\overline{\Gamma }}_{\overline{f}},N)$. As a result, $({\overline{\zeta }}_{\overline{g}},M)\cup ({\overline{\sigma }}_{\overline{h}},O){⊲}_l({\overline{\Gamma }}_{\overline{f}},N)$. □

Theorem 11.

Let $({\overline{\Gamma }}_{\overline{f}},N)$ be a PMFSS over Z. Then, $({\overline{\Gamma }}_{\overline{f}},N)$ is said to be a possibility multi-fuzzy soft interior ideal of Z if

• ${\overline{\Gamma }}_{\overline{f}}\left(n\right)\left(z_1{z}_2\right)\ge {\overline{\Gamma }}_{\overline{f}}\left(z_1\right)\wedge {\overline{\Gamma }}_{\overline{f}}\left(z_2\right)\forall z_1,z_2\in Z$.
• ${\overline{\Gamma }}_{\overline{f}}(n)(z_{1}a{z}_2)\ge {\overline{\Gamma }}_{\overline{f}}(n)(a)$ $\forall a,z_1,z_2\in Z$.

Example 4.

Let $Z=\left\{x_1,x_2,x_3,x_4\right\}$ be an ordered semigroup defined as in Table 6 and under the following ordered relation:

$$\le :=\left\{\right(x_1,x_1),(x_2,x_2),(x_3,x_3),(x_4,x_4),(x_1,x_2\left)\right\}.$$

Table 6. Multiplication table of Z.

.	$\mathit{x}$1	${\mathit{x}}_2$	${\mathit{x}}_3$	${\mathit{x}}_4$
$x$1	$x$1	$x$1	$x$1	$x$1
$x_2$	$x$1	$x$1	$x$1	$x$1
$x_3$	$x$1	$x$1	$x$1	$x_2$
$x_4$	$x$1	$x$1	$x_2$	$x_3$

Let $({\overline{\Gamma }}_{\overline{f}},N)$ be a PMFSS over Z with parameters $N=\{n_1,n_2,n_3\}$. The mapping ${\overline{\Gamma }}_{\overline{f}}:N\to F(Z)\times I(Z)$ is defined as ${\overline{\Gamma }}_{\overline{f}}(n)=(\overline{\psi }(n)(x_i),\overline{f}(n)(x_i))\forall x_i\in Z$, where

$${\overline{\Gamma }}_{\overline{f}}(n)=\left[\begin{array}{cccc}(0.8,0.7),(0.7,0.6)& (0.7,0.5),(0.6,0.4)& (0.5,0.4),(0.5,0.3)& (0.4,0.2),(0.4,0.1)\\ (0.7,0.6),(0.7,0.5)& (0.6,0.4),(0.6,0.4)& (0.5,0.3),(0.5,0.3)& (0.3,0.2),(0.1,0.1)\\ (0.5,0.5),(0.5,0.4)& (0.4,0.3),(0.4,0.3)& (0.3,0.2),(0.3,0.2)& (0.2,0.1),(0.2,0.1)\end{array}\right].$$

We have ${\overline{\Gamma }}_{\overline{f}}(n)(x_i{x}_j)\ge {\overline{\Gamma }}_{\overline{f}}(x_i)\wedge {\overline{\Gamma }}_{\overline{f}}\left(x_j\right)\forall x_i,x_j\in Z$; thus, it is a fuzzy subsemigroup of Z. Also, ${\overline{\Gamma }}_{\overline{f}}(n)(x_{i}a{x}_j)\ge {\overline{\Gamma }}_{\overline{f}}(n)(a)$,$\forall a,x_i,x_j\in Z$. Thus, Definition 8 is satisfied, so $({\overline{\Gamma }}_{\overline{f}},N)$ is a possibility multi-fuzzy soft interior ideal of Z.

Definition 9.

A possibility multi-fuzzy soft set $({\overline{\Gamma }}_{\overline{f}},N)$ is a possibility multi-fuzzy soft interior ideal over Z if and only if for every $n\in N,$ ${\overline{\Gamma }}_{\overline{f}}(n)$ is a possibility multi-fuzzy soft interior ideal over Z.

Lemma 1.

Every possibility multi-fuzzy soft right and left ideal of Z is also a possibility multi-fuzzy soft interior ideal of Z.

Proof. 

The proof of Lemma 1 is straightforward and can be readily understood by referring to Example 5 provided below. □

Example 5.

Let an ordered semigroup $Z=\left\{x_1,x_2,x_3,x_4\right\}be$ defined as in Example 4. Let $({\overline{\Gamma }}_{\overline{f}},N)$ be a possibility multi-fuzzy soft set over Z with parameters $N=\{n_1,n_2\}$. Then, a mapping ${\overline{\Gamma }}_{\overline{f}}:N\to F(Z)\times I(Z)$ is defined by ${\overline{\Gamma }}_{\overline{f}}(n)=(\overline{\Gamma }(n)(x_i),\overline{f}(n)(x_i))\forall x_i\in Z$, where

$${\overline{\Gamma }}_{\overline{f}}(n)=\left[\begin{array}{cccc}(0.9,0.8)(0.8,0.8)& (0.6,0.5)(0.7,0.6)& (0.5,0.5)(0.6,0.5)& (0.3,0.2)(0.3,0.2)\\ (0.7,0.6)(0.7,0.5)& (0.6,0.4)(0.6,0.4)& (0.3,0.2)(0.4,0.2)& (0.4,0.3)(0.4,0.3)\end{array}\right]$$

We have ${\overline{\Gamma }}_{\overline{f}}(n)(x_i\cdot x_j)\ge {\overline{\Gamma }}_{\overline{f}}(n)\left(x_i\right)\forall x_i,x_j\in Z,$ and thus the definition of a multi-fuzzy soft right ideal is satisfied. Similarly, ${\overline{\Gamma }}_{\overline{f}}(n)(x_i\cdot x_j)\ge {\overline{\Gamma }}_{\overline{f}}(n)(x_j)$ implies that ${\overline{\Gamma }}_{\overline{f}}(n)$ also satisfies the condition of a multi-fuzzy soft left ideal of Z. We have ${\overline{\Gamma }}_{\overline{f}}(n)(x_{i}a{x}_j)\ge {\overline{\Gamma }}_{\overline{f}}(n)(a)$,$\forall a,x_i,x_j\in Z$. Thus, $({\overline{\Gamma }}_{\overline{f}},N)$ is also a possibility multi-fuzzy soft interior ideal of Z.

Clearly, every possibility multi-fuzzy soft ideal of Z is also a possibility multi-fuzzy soft interior ideal of Z. However, the converse does not hold universally, as illustrated in the following example.

Example 6.

Let an ordered semigroup $Z=\{x_1,x_2,x_3,x_4\}$ be defined as described in Example 4. Let $({\overline{\Gamma }}_{\overline{f}},N)$ be a possibility multi-fuzzy soft set over Z with parameters $N=\{n_1,n_2\}$ and ${\overline{\Gamma }}_{\overline{f}}:N\to F(Z)\times I(Z)$ and be defined by ${\overline{\Gamma }}_{\overline{f}}(n)=(\overline{\Gamma }(n)(x_i),\overline{f}\left(n)\left(x_i\right)\right)\forall x_i\in Z$, where

$${\overline{\Gamma }}_{\overline{f}}(n)=\left[\begin{array}{cccc}(0.9,0.8)(0.8,0.8)& (0.5,0.6)(0.5,0.4)& (0.6,0.7)(0.6,0.5)& (0.3,0.2)(0.4,0.2)\\ (0.7,0.6)(0.7,0.5)& (0.4,0.4)(0.5,0.3)& (0.5,0.5)(0.6,0.4)& (0.3,0.3)(0.4,0.1)\end{array}\right]$$

We have ${\overline{\Gamma }}_{\overline{f}}\left(n\right)\left(x_i{x}_j\right)\ge {\overline{\Gamma }}_{\overline{f}}\left(x_i\right)\wedge {\overline{\Gamma }}_{\overline{f}}\left(x_j\right)\forall x_i,x_j\in Z$. Also,${\overline{\Gamma }}_{\overline{f}}(n)(x_{i}a{x}_j)\ge {\overline{\Gamma }}_{\overline{f}}(n)(a)$, $\forall a,x_i,x_j\in Z$. Thus, $({\overline{\Gamma }}_{\overline{f}},N)$ is a possibility multi-fuzzy soft interior ideal of Z. But ${\overline{\Gamma }}_{\overline{f}}(n)$ does not satisfy the condition of a multi-fuzzy soft left ideal of Z since ${\overline{\Gamma }}_{\overline{f}}(n)(x_i\cdot x_j)\ngeqq {\overline{\Gamma }}_{\overline{f}}(n)(x_j)$. Hence, $({\overline{\Gamma }}_{\overline{f}},N)$ is not a possibility multi-fuzzy soft ideal of Z.

Proposition 1.

Every possibility multi-fuzzy soft interior ideal is a possibility multi-fuzzy soft right and left ideal of Z if Z is regular.

Proof. 

For a regular ordered semigroup Z, let $({\overline{\Gamma }}_{\overline{f}},N)$ be a possibility multi-fuzzy soft interior ideal, and then by the definition of regular, we can write $z_1\le z_{1}a{z}_1$, where $z_1,z_2\in Z$ and $a\in Z$. Further, by using Lemma 1, the following inequality holds:

$${\overline{\Gamma }}_{\overline{f}}(n)(z_1{z}_2)\ge {\overline{\Gamma }}_{\overline{f}}(n)((z_1{az}_1)z_2)={\overline{\Gamma }}_{\overline{f}}(n)((z_{1}a)z_1{z}_2)\ge {\overline{\Gamma }}_{\overline{f}}(n)(z_1)$$

Similarly, ${\overline{\Gamma }}_{\overline{f}}(n)(z_1{z}_2)\ge {\overline{\Gamma }}_{\overline{f}}(n)(z_1(z_2{az}_2))={\overline{\Gamma }}_{\overline{f}}(n)(z_1{z}_2({az}_2))\ge {\overline{\Gamma }}_{\overline{f}}(n)(z_2)$.

Thus, ${\overline{\Gamma }}_{\overline{f}}(n)(z_1{z}_2)\ge {\overline{\Gamma }}_{\overline{f}}(n)(z_1)$, and also ${\overline{\Gamma }}_{\overline{f}}(n)(z_1{z}_2)\ge {\overline{\Gamma }}_{\overline{f}}(n)(z_2)\forall z_1,z_2\in Z$ and $n\in N.$ In other words, ${\overline{\Gamma }}_{\overline{f}}(n)$ is a possibility multi-fuzzy soft right and left ideal of Z. □

Corollary 1.

In regular ordered semigroups, both the concepts of possibility multi-fuzzy soft ordered semigroups for ideals and interior ideal must be satisfied over Z.

Theorem 12.

Let $({\overline{\Gamma }}_{\overline{f}},N)$ and $({\overline{\zeta }}_{\overline{g}},M)$ be two possibility multi-fuzzy soft left (resp. right) ideals of Z, and $({\overline{\sigma }}_{\overline{h}},O)=({\overline{\Gamma }}_{\overline{f}},N)\wedge ({\overline{\zeta }}_{\overline{g}},M)$ is also a possibility multi-fuzzy soft left (resp. right) ideal of Z for all $M\cap N\ne \varphi$.

Proof. 

By using Theorem 7, for any two PMFSSs $({\overline{\Gamma }}_{\overline{f}},N)$ and $({\overline{\zeta }}_{\overline{g}},M)$ of Z, the And operation is defined by ${\overline{\Gamma }}_{\overline{f}}(n)\wedge {\overline{\zeta }}_{\overline{g}}(n)={\overline{\sigma }}_{\overline{h}}(n)$ for all $n\in O.$ Then, ${\overline{\sigma }}_{\overline{h}}(n)$ is also a PMFSS of Z. Since ${\overline{\Gamma }}_{\overline{f}}(n)$ and ${\overline{\zeta }}_{\overline{g}}(n)$ are both possibility multi-fuzzy soft left (resp. right) ideals of Z, then ${\overline{\sigma }}_{\overline{h}}(n)$ is also a possibility multi-fuzzy soft left (resp. right) ideal of Z for all $O=M\cap N$ and $n\in O$. Thus, ${\overline{\sigma }}_{\overline{h}}(n)$ is a possibility multi-fuzzy soft left (resp. right) ideal of Z. Accordingly, ${\overline{\Gamma }}_{\overline{f}}(n)\wedge {\overline{\zeta }}_{\overline{g}}(n)={\overline{\sigma }}_{\overline{h}}(n)$ is a possibility multi-fuzzy soft left (resp. right) ideal of Z. □

Theorem 13.

Let $({\overline{\Gamma }}_{\overline{f}},N)$ and $({\overline{\zeta }}_{\overline{g}},M)$ be two possibility multi-fuzzy soft left (resp. right) ideals of Z. Then, $({\overline{\sigma }}_{\overline{h}},O)=({\overline{\Gamma }}_{\overline{f}},N)\vee ({\overline{\zeta }}_{\overline{g}},M)$is also a possibility multi-fuzzy soft left (resp. right) ideal of Z for all $M\cap N=\varphi$.

Proof. 

The proof follows directly from Theorem 8. □

6. Possibility Multi-Fuzzy Soft Simple Ordered Semigroup

Let $({\overline{\Gamma }}_{\overline{f}},N)$ be a possibility multi-fuzzy soft set over an ordered semigroup Z. For all $y\in Z$and $l\in N$, define a mapping ${\overline{\Gamma }}_{\overline{f}}:N\to {\mathsf{ƛ}}_y,$where $({\mathsf{ƛ}}_y(l),M)$is a PMFSS over Z, and it is defined by

$${\mathsf{ƛ}}_y(l):=\mathsf{\{}a\in Z|{\overline{\Gamma }}_{\overline{f}}(l)(a)\ge {\overline{\Gamma }}_{\overline{f}}(l)\left(y)\right\},\forall l\in M$$

Proposition 2.

Let $({\overline{\Gamma }}_{\overline{f}},N)$ be a possibility multi-fuzzy soft set over an ordered semigroup Z. Then, $({\mathsf{ƛ}}_y,M)$ is a soft right ideal of Z.

Proof. 

Let $\left({\overline{\Gamma }}_{\overline{f}},N\right)$ be a possibility multi-fuzzy soft right ideal over Z. If ${\mathrm{ƛ}}_y(l)\ne \varphi$ for every $y\in Z$ and $l\in M$ and if ${\overline{\Gamma }}_{\overline{f}}(l)(y)\ge {\overline{\Gamma }}_{\overline{f}}(l)(y)$, then we have $y\in {\mathrm{ƛ}}_y(l)$ and ${\mathrm{ƛ}}_y(l)\ne \varphi$. Let $a\in {\mathrm{ƛ}}_y(l).$ Then, for any $t\in Z$,$t\le a$, it is implied that $t\in {\mathrm{ƛ}}_y(l)(\forall l\in M)$. Since $t\le a$ and $\left({\overline{\Gamma }}_{\overline{f}},N\right)$ is a possibility multi-fuzzy soft right ideal over Z, it follows that for every $l\in M$, we have

${\overline{\Gamma }}_{\overline{f}}(l)(t)\ge {\overline{\Gamma }}_{\overline{f}}(l)(a)$ as$l\in {\mathsf{ƛ}}_y(l)$

$${\overline{\Gamma }}_{\overline{f}}(l)(a)\ge {\overline{\Gamma }}_{\overline{f}}(l)(y)$$

$${\overline{\Gamma }}_{\overline{f}}(l)(t)\ge {\overline{\Gamma }}_{\overline{f}}(l)(y).$$

Hence, $t\in {\mathrm{ƛ}}_y(l)$.

Now, suppose that $a\in {\mathsf{ƛ}}_y(l)$ for every $l\in M$and $t\in Z.$Then, $at\in {\mathsf{ƛ}}_y(l)$. Since $({\overline{\Gamma }}_{\overline{f}},N)$ is a possibility multi-fuzzy soft right ideal over Z, it follows that

$${\overline{\Gamma }}_{\overline{f}}(l)(at)\ge {\overline{\Gamma }}_{\overline{f}}(l)(a)\mathrm{as}a\in {\mathsf{ƛ}}_y(l)$$

$${\overline{\Gamma }}_{\overline{f}}(l)(a)\ge {\overline{\Gamma }}_{\overline{f}}(l)(y)$$

So, ${\overline{\Gamma }}_{\overline{f}}(l)(at)\ge {\overline{\Gamma }}_{\overline{f}}(l)(y)$.

Therefore, $at\in {\mathsf{ƛ}}_y(l)$.

We have ${\mathrm{ƛ}}_y(l)Z\subseteq {\mathrm{ƛ}}_y(l)$, and hence ${\mathrm{ƛ}}_y(l)$ is a soft right ideal of Z.

Likewise, the proposition can be easily proven for left ideals using the same approach as in the above proof. □

Theorem 14.

Let $({\overline{\Gamma }}_{\overline{f}},N)$ be a possibility multi-fuzzy soft ideal over an ordered semigroup Z. Then, $({\mathsf{ƛ}}_y,M)$ is a soft ideal of Z for all $y\in Z$.

Definition 10.

Let $({\overline{\Gamma }}_{\overline{f}},N)$ be a PMFSS over an ordered semigroup Z. Then, Z is called possibility multi-fuzzy left (resp. right) simple if and only if $({\overline{\Gamma }}_{\overline{f}},N)$ is a possibility multi-fuzzy soft left (resp. right) simple ideal over Z, with ${\overline{\Gamma }}_{\overline{f}}(l)(y_1)={\overline{\Gamma }}_{\overline{f}}(l)(y_2),\forall y_1,y_2\in Z$, and$l\in N$.

An ordered semigroup Z is called possibility multi-fuzzy soft simple if it is both possibility multi-fuzzy soft left simple and possibility multi-fuzzy soft right simple.

Example 7.

Let $Z=\{z_1,z_2,z_3\}$be an ordered semigroup defined as in Table 7 and under the following ordered relation.

Table 7. Multiplication table of Z.

.	${\mathit{z}}_1$	${\mathit{z}}_2$	${\mathit{z}}_3$
$z_1$	$z_1$	$z_2$	$z_3$
$z_2$	$z_2$	$z_2$	$z_3$
$z_3$	$z_3$	$z_3$	$z_3$

$$\le :=\left\{\right(z_1,z_1),(z_2,z_2),(z_3,z_3),(z_1,z_3),(z_2,z_3\left)\right\}.$$

Let $({\overline{\Gamma }}_{\overline{f}},N)$ be defined by a mapping ${\overline{\Gamma }}_{\overline{f}}:N\to F(Z)\times I(Z)$ with N parameters.

$${\overline{\Gamma }}_{\overline{f}}(n)=(\overline{\Gamma }(n)(z_i),\overline{f}\left(n)\left(z_i\right)\right)\forall z_i\in Z$$

where

$${\overline{\Gamma }}_{\overline{f}}(n)=\left[\begin{array}{ccc}(0.9,0.7),(0.6,0.7)& (0.9,0.7),(0.6,0.7)& (0.9,0.7),(0.6,0.7)\\ (0.2,0.5),(0.1.0.5)& (0.2,0.5),(0.1.0.5)& (0.2,0.5),(0.1.0.5)\end{array}\right].$$

Here,

${\overline{\Gamma }}_{\overline{f}}(n)(z_i{z}_j)\ge {\overline{\Gamma }}_{\overline{f}}(z_i)\wedge {\overline{\Gamma }}_{\overline{f}}(z_j)\forall z_i,z_j\in Z$. ($({\overline{\Gamma }}_{\overline{f}},N)$ is a multi-fuzzy subsemigroup of Z).

${\overline{\Gamma }}_{\overline{f}}(n)(z_i{z}_j)\ge {\overline{\Gamma }}_{\overline{f}}(n)(z_i)$ $(({\overline{\Gamma }}_{\overline{f}},N)$ is a possibility multi-fuzzy soft right ideal of Z).

${\overline{\Gamma }}_{\overline{f}}(n)(z_i{z}_j)\ge {\overline{\Gamma }}_{\overline{f}}(n)(z_j)$ $(({\overline{\Gamma }}_{\overline{f}},N)$ is a possibility multi-fuzzy soft left ideal of Z).

Also, ${\overline{\Gamma }}_{\overline{f}}(n)(z_i)={\overline{\Gamma }}_{\overline{f}}(n)(z_j),\forall z_i,z_j\in Z$, and $n\in N$.

Hence, $({\overline{\Gamma }}_{\overline{f}},N)$ is a possibility multi-fuzzy soft simple of Z.

Theorem 15.

An ordered semigroup Z is possibility multi-fuzzy soft simple if and only if Z is soft simple.

Proof. 

Let $({\overline{\Gamma }}_{\overline{f}},N)$ be a PMFSS, which satisfies the conditions for left and right ideals over an ordered semigroup Z. By Theorem 14, $({\mathsf{ƛ}}_{y_1},M)$ is a soft ideal of Z for all $y_1,y_2\in Z$. Since Z is soft simple, it follows that ${\mathsf{ƛ}}_{y_1}(l)=Z\mathrm{f}\mathrm{o}\mathrm{r}l\in M$, and for all $y_2\in {\mathsf{ƛ}}_{y_1}(l)$ we have, ${\overline{\Gamma }}_{\overline{f}}(l)(y_1)\ge {\overline{\Gamma }}_{\overline{f}}(l)(y_2)\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}l\in N.$ Similarly, ${\overline{\Gamma }}_{\overline{f}}(l)(y_2)\ge {\overline{\Gamma }}_{\overline{f}}(l)(z_1)$, and thus ${\overline{\Gamma }}_{\overline{f}}(l)(y_1)={\overline{\Gamma }}_{\overline{f}}(l)(y_2)$. Therefore, Z is a possibility multi-fuzzy soft simple.

Conversely, let $(\mathrm{ƛ},M)$ be a soft ideal over Z such that $\mathrm{ƛ}(l)\ne Z\mathrm{f}\mathrm{o}\mathrm{r}l\in M$. Since$(\mathrm{ƛ},M)$ is a soft ideal over Z, it follows that $\mathrm{ƛ}(l)$ is a soft ideal over Z. By Theorem 5, every soft ideal is also a fuzzy soft ideal; hence, ${\overline{\zeta }}_{\mathrm{ƛ}(m)}(l)$ is a fuzzy ideal of Z and ${\overline{g}}_{\mathrm{ƛ}(m)}(l)$ is a multi-fuzzy ideal of Z $\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}l\in N.\mathrm{T}\mathrm{h}\mathrm{i}\mathrm{s}$ implies that ${\overline{\zeta }}_{\overline{g}}{|}_{\mathrm{ƛ}(m)}(l)$ is a possibility multi-fuzzy ideal of Z. Since Z is fuzzy simple, ${\overline{\zeta }}_{\overline{g}}{|}_{\mathrm{ƛ}(m)}(l)$ must be a constant function, i.e., ${\overline{\zeta }}_{\overline{g}}{|}_{\mathrm{ƛ}(m)}(l)(y_1)={\overline{\zeta }}_{\overline{g}}{|}_{\mathrm{ƛ}(m)}(l)(y_2)$ for all $y_1,y_2\in Z$. Thus, for any $a\in \mathrm{ƛ}(m),$we can write ${\overline{\zeta }}_{\overline{g}}{|}_{\mathrm{ƛ}(m)}(l)(y_1)={\overline{\zeta }}_{\overline{g}}{|}_{\mathrm{ƛ}(m)}(l)(y_2)=1,$ and therefore $a\in \mathrm{ƛ}(m).$ Thus, $Z=\mathrm{ƛ}(m)$, which leads to a contradiction, so Z is a soft simple. □

Theorem 16.

For an ordered semigroup Z, Z is soft simple if and only if for every possibility multi-fuzzy soft interior ideal $({\overline{\Gamma }}_{\overline{f}},N)$ over Z, ${\overline{\Gamma }}_{\overline{f}}(l)(y_1)={\overline{\Gamma }}_{\overline{f}}(l)(y_2)foralll\in N$ and $y_1,y_2\in Z$.

Proof. 

Let $({\overline{\Gamma }}_{\overline{f}},N)$ be a possibility multi-fuzzy soft interior ideal over Z, and assume that Z is soft simple. Then, $Z=Z{y}_{2}Z{\mathrm{for}\mathrm{all}y}_2\in Z.$ Thus $y_1\le a{y}_{2}b$ for any $a,b\in Z$. Since $({\overline{\Gamma }}_{\overline{f}},N)$ is a possibility multi-fuzzy soft interior ideal over Z, we have

$${\overline{\Gamma }}_{\overline{f}}(l)(y_1)\ge {\overline{\Gamma }}_{\overline{f}}(l)({ay}_{2}b)$$

$${\overline{\Gamma }}_{\overline{f}}(l)({ay}_{2}b)={\overline{\Gamma }}_{\overline{f}}(l)(a(y_{2}b))$$

$${\overline{\Gamma }}_{\overline{f}}(l)(a(y_{2}b))\ge {\overline{\Gamma }}_{\overline{f}}(l)(y_2)$$

$${\overline{\Gamma }}_{\overline{f}}(l)(y_1)\ge {\overline{\Gamma }}_{\overline{f}}(l)(y_2)$$

Similarly, following the same reasoning, we have

$${\overline{\Gamma }}_{\overline{f}}(l)(y_2)\ge {\overline{\Gamma }}_{\overline{f}}(l)(y_1).$$

Therefore

$${\overline{\Gamma }}_{\overline{f}}(l)(y_1)={\overline{\Gamma }}_{\overline{f}}(l)(y_2).$$

Conversely, let $({\overline{\Gamma }}_{\overline{f}},N)$ be a possibility multi-fuzzy soft interior ideal over Z and suppose that ${\overline{\Gamma }}_{\overline{f}}(l)(y_1)={\overline{\Gamma }}_{\overline{f}}(l)(y_2)\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}l\in N$. Then,$\mathrm{b}\mathrm{y}\mathrm{P}\mathrm{r}\mathrm{o}\mathrm{p}\mathrm{o}\mathrm{s}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}1,({\overline{\Gamma }}_{\overline{f}},N)$ is also a possibility multi-fuzzy soft ideal over Z. By Theorem 15, Z is a possibility multi-fuzzy soft simple with ${\overline{\Gamma }}_{\overline{f}}(l)(y_1)={\overline{\Gamma }}_{\overline{f}}(l)(y_2)$. Hence, an ordered semigroup Z is a soft simple. □

Theorem 17.

For an ordered semigroup Z, Z is intra-regular if for every possibility multi-fuzzy soft ideal  $({\overline{\Gamma }}_{\overline{f}},N)$ over Z, ${\overline{\Gamma }}_{\overline{f}}(l)(y)={\overline{\Gamma }}_{\overline{f}}(l)(y^2),\forall l\in N$, and $y\in Z$.

Proof. 

Suppose that $({\overline{\Gamma }}_{\overline{f}},N)$ is a possibility multi-fuzzy soft ideal. For an intra-regular ordered semigroup Z, for all $y\in Z$, there exist $a,b\in Z$such that $y\le a{y}^{2}b$. Since $({\overline{\Gamma }}_{\overline{f}},N)$ is a possibility multi-fuzzy soft ideal of Z, we have

$${\overline{\Gamma }}_{\overline{f}}(l)(y)\ge {\overline{\Gamma }}_{\overline{f}}(l)({ay}^{2}b)$$

$${\overline{\Gamma }}_{\overline{f}}(l)({ay}^{2}b)={\overline{\Gamma }}_{\overline{f}}(l)(a(y^{2}b))$$

Since $({\overline{\Gamma }}_{\overline{f}},N)$ is a possibility multi-fuzzy soft left ideal, we have

$${\overline{\Gamma }}_{\overline{f}}(l)(a(y^{2}b))\ge {\overline{\Gamma }}_{\overline{f}}(l)(y^{2}b)$$

Since $({\overline{\Gamma }}_{\overline{f}},N)$ is also a possibility multi-fuzzy soft right ideal, we obtain

$${\overline{\Gamma }}_{\overline{f}}(l)(y^{2}b)\ge {\overline{\Gamma }}_{\overline{f}}(l)(y^2)$$

Thus, we conclude that

$${\overline{\Gamma }}_{\overline{f}}(l)(y)\ge {\overline{\Gamma }}_{\overline{f}}(l)(y^2)$$

Since

$$\{{\overline{\Gamma }}_{\overline{f}}(l)(y)\ge {\overline{\Gamma }}_{\overline{f}}(l)(y^2)={\overline{\Gamma }}_{\overline{f}}(l)(y\cdot y)\ge {\overline{\Gamma }}_{\overline{f}}(l)(y)\},$$

it follows that

$${\overline{\Gamma }}_{\overline{f}}(l)(y)={\overline{\Gamma }}_{\overline{f}}(l)(y^2)$$

Hence, the result follows. □

7. Semiprime Possibility Multi-Fuzzy Soft Ideals

Definition 11.

Let $({\overline{\Gamma }}_{\overline{f}},N)$ be a possibility multi-fuzzy soft ideal of Z. Then, $({\overline{\Gamma }}_{\overline{f}},N)$ is a semiprime possibility multi-fuzzy soft ideal of Z if and only if ${\overline{\Gamma }}_{\overline{f}}(n)(z)\ge {\overline{\Gamma }}_{\overline{f}}(n)(z^2)$ for all $n\in N$ and $z\in Z.$ In other words, $({\overline{\Gamma }}_{\overline{f}},N)$ is a semiprime possibility multi-fuzzy ideal of Z.

Lemma 2.

Let $(f,M)$ be a soft set over Z. Then, $(f,M)$ is a semiprime soft ideal over Z if and only if $({\overline{\Gamma }}_{\overline{f}},N)$ is a semiprime possibility multi-fuzzy soft ideal over Z.

Proof. 

Suppose that $(f,M)$ is a semiprime soft ideal over Z. By Theorem 6, $f(n)$ is also a semiprime soft ideal over Z. If $z\in Z$such that $z^2\in \overline{\psi }(n)$ and $z^2\in \overline{f}(n),\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{n}$ for possible multi-membership value, we have ${\overline{\Gamma }}_{\overline{f}}(n)(z^2)=1$,$\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}n\in N$. Since $f(n)$is a semiprime ideal and $z\in {\overline{\Gamma }}_{\overline{f}}(n)$, it follows that

$${\overline{\Gamma }}_{\overline{f}}(n)(z)=1={\overline{\Gamma }}_{\overline{f}}(n)(z^2).$$

Suppose now that $z^2\notin {\overline{\Gamma }}_{\overline{f}}(n)$. Then

$${\overline{\Gamma }}_{\overline{f}}(n)(z)\ge 0={\overline{\Gamma }}_{\overline{f}}(n)(z^2)$$

Thus, ${\overline{\Gamma }}_{\overline{f}}(n)$is a semiprime possibility multi-fuzzy soft ideal over Z, meaning that $({\overline{\Gamma }}_{\overline{f}},N)$ is a semiprime possibility multi-fuzzy soft ideal over Z.

Conversely, let $({\overline{\Gamma }}_{\overline{f}}(n),N)$be a semiprime possibility multi-fuzzy soft ideal over Z. This implies that $z^2\in {\overline{\Gamma }}_{\overline{f}}(n)$ for all $n\in M$, so

$${\overline{\Gamma }}_{\overline{f}}(n)(z^2)=1.$$

We have

$${\overline{\Gamma }}_{\overline{f}}(n)(z)\ge {\overline{\Gamma }}_{\overline{f}}(n)(z^2)=1$$

We concluded that ${\overline{\Gamma }}_{\overline{f}}(n)(z)=1,\mathrm{a}\mathrm{n}\mathrm{d}$thus$z\in {\overline{\Gamma }}_{\overline{f}}(n)$. Therefore, ${\overline{\Gamma }}_{\overline{f}}(n)$ is a semiprime soft ideal over Z, implying that $f(n)$ or $(f,M)$ is a semiprime soft ideal over Z. □

Theorem 18.

Every possibility multi-fuzzy soft left or right ideal $({\overline{\Gamma }}_{\overline{f}},N)$ over Z is semiprime if Z is left or right regular, respectively.

Proof. 

Let $({\overline{\Gamma }}_{\overline{f}},N)$ be a possibility multi-fuzzy soft left ideal over Z, and suppose that Z is a left regular ordered semigroup. By definition, for every $a\in Z$, there exist $z\in Z$ such that $a\le z{a}^2$. Then

$${\overline{\Gamma }}_{\overline{f}}(n)(a)\ge {\overline{\Gamma }}_{\overline{f}}(n)({za}^2)\ge {\overline{\Gamma }}_{\overline{f}}(n)(a^2).$$

Since ${\overline{\Gamma }}_{\overline{f}}(n)$ is a possibility multi-fuzzy soft left ideal, $\left({\overline{\Gamma }}_{\overline{f}},N\right)$ is also a possibility multi-fuzzy soft left ideal. Similarly, following the same reasoning, we can prove that for an ordered semigroup Z, Z is right regular if every possibility multi-fuzzy soft right ideal $({\overline{\Gamma }}_{\overline{f}},N)$ over Z is semiprime. □

Theorem 19.

An ordered semigroup Z is intra-regular if every possibility multi-fuzzy soft left (resp. right) ideal over Z is semiprime.

Proof. 

The proof is straightforward and directly follows from Theorem 18. □

8. Conclusions

This research aims to broaden the scope of possibility multi-fuzzy soft sets by integrating them into the context of ordered semigroups, thus offering a more comprehensive framework. Since fuzzy soft sets play an important role in solving various applications in decision sciences, error correcting codes, etc., a novel subsystem of the fuzzy soft set approach named possibility multi-fuzzy soft ordered semigroups has been introduced to solve these problems more accurately and precisely. Further, the concept of the possibility multi-fuzzy ideals and interior ideals in ordered semigroups is broached. The authors characterize various classes of ordered semigroups in terms of this new approach, including regular and intra-regular ordered semigroups. The idea of a possibility multi-fuzzy soft simple ordered semigroup has been presented and validated with several theorems and examples. Different relations pertinent to simple, intra-regular, and regular ordered semigroups within the premises of PMFSSs are established. Lastly, semiprime ideals for PMFSSs have been introduced and supported with several theorems. This research is poised to provide a new platform for deriving diverse applications in decision making using PMFSS theory. Future research will include exploring concepts such as possibility multi-fuzzy soft bi-ideals, possibility multi-fuzzy soft generalized bi-ideals, possibility multi-fuzzy soft quasi-ideals, and so on. Overall, this research contributes to the advancement of decision-making methodologies by providing a theoretical framework that can be applied across various domains, with potential implications for practical problem-solving analyses.