Miss-Triggered Content Cache Replacement Under Partial Observability: Transformer-Decoder Q-Learning

Abstract

Content delivery networks (CDNs) face steadily rising, uneven demand, straining heuristic cache replacement. Reinforcement learning (RL) is promising, but most work assumes a fully observable Markov Decision Process (MDP), unrealistic under delayed, partial, and noisy signals. We model cache replacement as a Partially Observable MDP (POMDP) and present the Miss-Triggered Cache Transformer (MTCT), a Transformer-decoder Q-learning agent that encodes recent histories with self-attention. MTCT invokes its policy only on cache misses to align compute with informative events and uses a delayed-hit reward to propagate information from hits. A compact, rank-based action set (12 actions by default) captures popularity–recency trade-offs with complexity independent of cache capacity. We evaluate MTCT on a real trace (MovieLens) and two synthetic workloads (Mandelbrot–Zipf, Pareto) against Adaptive Replacement Cache (ARC), Windowed TinyLFU (W-TinyLFU), classical heuristics, and Double Deep Q-Network (DDQN). MTCT achieves the best or statistically comparable cache-hit rates on most cache sizes; e.g., on MovieLens at $M=600$, it reaches $0.4703$ (DDQN $0.4436$, ARC $0.4513$). Miss-triggered inference also lowers mean wall-clock time per episode; Transformer inference is well suited to modern hardware acceleration. Ablations support $CL=50$ and show that finer action grids improve stability and final accuracy.

1. Introduction

The rapid growth of internet and mobile traffic has increased the load on content delivery networks (CDNs). As of 2024, about 5.5 billion people (68%) use the internet and roughly 57% are mobile users [1,2]. Over the same period, monthly mobile data traffic rose from 58.2 exabytes in 2020 to 165.7 exabytes in 2024 and is projected to reach 430 exabytes by 2030 [3]. These trends call for caching policies that track rapid, uneven shifts in content popularity without incurring high online overheads.

Reinforcement learning (RL) offers a data-driven alternative to classical policies such as least recently used (LRU) and least frequently used (LFU). Model-free value methods like Deep Q-Network (DQN) [4] and Double DQN (DDQN) [5] can adapt to changing demand, but much prior work assumes a fully observable Markov Decision Process (MDP). In production CDNs, signals are often delayed, partial, or noisy, so the agent observes compressed or lagged statistics rather than the true state. This motivates a partially observable formulation.

We model cache replacement as a Partially Observable MDP (POMDP) and introduce the Miss-Triggered Cache Transformer (MTCT), a Transformer-decoder Q-learning agent that encodes recent observation histories via self-attention. MTCT invokes its policy only on cache misses, aligning updates with informative events and reducing the online inference rate to approximately $1-C_{\mathrm{HIT}}$. A delayed-hit reward carries cache-hit information into miss-triggered updates to stabilize learning under partial observability. The action space is a compact rank–evict grid (12 actions by default) that trades off popularity and recency while keeping decision complexity independent of capacity.

We evaluate MTCT on a real trace (MovieLens) and two synthetic workloads (Mandelbrot–Zipf, Pareto). Baselines include modern admission/replacement methods—Adaptive Replacement Cache (ARC) and Windowed TinyLFU (W-TinyLFU)—and classical heuristics. We also compare against RL baselines, including DDQN and a miss-triggered DDQN control that shares the trigger schedule and replay protocol with MTCT. Across most cache sizes, MTCT attains the best or statistically comparable hit rates. On MovieLens, it is consistently top (e.g., $M=600$: $0.4703$ vs. DDQN $0.4436$, ARC $0.4513$); on synthetic workloads, ARC/W-TinyLFU are strong at small to mid capacities, with gaps narrowing or reversing as M grows. Despite using a higher-capacity network, the mean wall-clock time per training episode is lower than DDQN due to miss-triggered inference and parallelizable decoder execution.

We also study design choices via ablations. Varying the context length shows four regimes with a stable plateau for $CL\in [30,70]$, supporting $CL=50$ as a practical default. Adjusting action-set granularity (3/7/12) shows that finer grids improve final accuracy and reduce run-to-run variance, whereas very coarse grids converge faster but to lower fixed points. Under distribution shift on Mandelbrot–Zipf, MTCT achieves the strongest end-of-training averages among compared methods and suggests benefits from prioritized or recency-aware replay to speed post-shift adaptation.

Contributions. We formulate cache replacement under partial observability as a POMDP and instantiate it with a MTCT. The policy is invoked only on cache misses, focusing computation on informative events and reducing the online inference rate to approximately $1-C_{\mathrm{HIT}}$. A delayed-hit reward carries cache-hit feedback into miss-triggered updates, improving stability. We introduce a compact, rank-based action space (12 actions by default) and examine 3/7/12 variants to assess the effect of action-granularity. Against Adaptive Replacement Cache (ARC), Windowed TinyLFU (W-TinyLFU), classical heuristics, and both standard and miss-triggered DDQN, MTCT attains higher hit rates on MovieLens and best or statistically comparable results on the synthetic workloads. It also lowers mean per-episode wall-clock time relative to standard DDQN (with rare exceptions in Appendix B).

2. Related Work

2.1. Cache Management Policies and Related Work

Research on content caching is commonly grouped by admission, eviction, and replacement. Admission policies decide whether a requested object should enter the cache; eviction policies choose a victim when the cache is full; replacement policies couple admission and eviction into a unified decision.

Admission. RL-Cache learns admission directly from request traces with model-free RL [6]. Song et al. [7] formulate proactive mobile caching as an MDP to minimize long-term energy. Wang et al. [8] address long horizons via subsampling and Advantage Actor–Critic (A2C). Niknia et al. [9] combine Double Deep Q-Learning with transfer learning for adaptive edge caching. Srinivasan et al. [10] use LSTM-augmented A2C to cope with non-stationarity in wireless settings.

Eviction. Zhou et al. [11] propose 3L-Cache, applying object-level RL with bidirectional sampling and gradient boosting. Alabed et al. [12] present RLCache, managing admission, eviction, and TTL via multi-task RL. Yang et al. [13] introduce MAT, which mixes heuristics and RL to reduce prediction cost for eviction. Wang et al. [14] develop DeepChunk, a DQN-based scheme for chunk-level caching in wireless systems. Sun et al. [15] report a DQN-driven cache manager with strong adaptability across workloads.

Replacement. Zhong et al. [16] use the Wolpertinger architecture to tackle large discrete action spaces in DRL-based caching. Nguyen et al. [17] (RL-Bélády) unify admission and eviction for CDNs. Zhou et al. [18] propose Catcher, an end-to-end DRL caching system that generalizes across cache sizes and workloads. Wang et al. [19] study multi-agent DRL for cooperative edge caching; Lyu et al. [20] extend this with an actor–critic design for dynamic environments. Abdo et al. [21] present a Q-learning framework that integrates admission and replacement in fog computing.

Building on this line of work, we take a replacement-oriented view and address partial observability directly: we cast cache replacement as a POMDP and learn a policy that couples admission and rank-based eviction. Our formulation differs from fully observable MDP approaches by explicitly encoding recent observation histories and invoking the policy only on cache misses, aligning decision rate with $1-C_{\mathrm{HIT}}$.

2.2. MDP-Based Caching Research and Its Limitations

2.2.1. Markov Decision Processes (MDPs)

Owing to their tractability and well-established solution methods [22], Markov Decision Processes (MDPs) have been widely adopted in content caching research. An MDP is defined by the tuple $\langle S,A,P,R,\gamma \rangle$, where S is the state space, A the action space, P the state-transition probability, R the reward function, and $\gamma \in [0,1)$ the discount factor. In this setting, the agent fully observes the current state $s\in S$ and selects actions $a\in A$ to maximize expected long-term reward. The state-value function under a fixed policy $\pi$ is

$$V^{\pi }\left(s\right)=\mathbb{E}\left[\sum _{t=0}^{\infty }{\gamma }^t{r}_t|s_0=s,\pi \right],$$

(1)

and the optimal value function is $V^{*}\left(s\right)={max}_{\pi }{V}^{\pi }\left(s\right)$. Here, $r_t$ denotes the immediate reward at step t.

Building on this framework, prior studies have proposed a range of MDP-based caching methods. RL-Cache [6] learns admission policies directly from traces, while Song et al. [7] applied an MDP model to proactive caching in mobile networks. To address scalability, Wang et al. [8] introduced subsampling with Advantage Actor–Critic (A2C), and Srinivasan et al. [10] used LSTM-augmented A2C to adapt under non-stationary demand. Zhou et al. [11] further developed 3L-Cache, combining object-level RL with bidirectional sampling for efficient replacement.

2.2.2. Semi-Markov Decision Processes (SMDPs)

While MDPs assume fixed decision intervals, real caching systems often feature variable timing between events. Semi-Markov Decision Processes (SMDPs) extend MDPs by allowing flexible holding times between decisions [23].

Let ${\tau }_k$ denote the random holding time between the k-th and $(k+1)$-th decision steps, and define the elapsed time up to decision step t as

$$T_t=\sum _{k=0}^{t-1}{\tau }_k,$$

(2)

so that $T_0=0$. The state-value function under policy $\pi$ is

$$V^{\pi }\left(s\right)=\mathbb{E}\left[\sum _{t=0}^{\infty }{\gamma }^{T_t}{r}_t|s_0=s,\pi \right],$$

(3)

where $\gamma \in [0,1)$ is the discount factor and $r_t$ the immediate reward at decision step t. The optimal value function is $V^{*}\left(s\right)={max}_{\pi }{V}^{\pi }\left(s\right)$. By raising $\gamma$ to the realized elapsed time $T_t$, this formulation correctly accounts for irregular decision intervals. Such flexibility makes SMDPs particularly suitable for irregular or event-driven caching systems; for example, Niknia et al. [9] applied an SMDP-based approach to edge caching with irregularly timed requests.

2.2.3. Limitations of MDP/SMDP Approaches

While MDPs and SMDPs provide mathematically well-defined objectives (Equations (1) and (3)) and established solution techniques, both rely on the assumption of full state observability. In practice, this assumption rarely holds in CDN environments with distributed caches, delayed telemetry, and noisy logs. As Kaelbling et al. [22] noted, full observability is convenient for analysis but uncommon in real systems.

Empirical evidence from other domains supports this limitation. In partially observable Atari tasks with flickering inputs, Hausknecht and Stone [24] showed that memoryless DQN agents degrade sharply, whereas adding recurrence (DRQN) restores stability under observation aliasing. Across broader POMDP benchmarks, Toro Icarte et al. [25] reported that reactive (memoryless) policies are unreliable and that learned memory is required for stable generalization. From a theoretical perspective, Liu et al. [26] demonstrated that MDP-based learners can be sample-inefficient or unstable under partial observability unless restrictive revealing conditions are satisfied. More recently, Esslinger et al. [27] found that Transformer-based memory (DTQN) is particularly effective, coping with occlusion and noise while outperforming recurrent baselines in learning speed and robustness.

Taken together, these findings indicate that cache control under delayed and partial measurements is better modeled as a POMDP, where incorporating learned memory into the policy is essential. Motivated by this evidence, our work adopts a Transformer decoder as the memory module and trains it with miss-triggered updates tailored to event-driven CDN caching.

2.3. Memory-Based Approximation for POMDP Caching

2.3.1. POMDP Definition and Exact-Solution Complexity

A Partially Observable Markov Decision Process (POMDP) is defined by the tuple $\mathcal{P}=\langle S,A,P,R,\gamma ,O,Z\rangle$, where S is the latent state space, A the action space, $P(s^{\prime }\mid s,a)$ the state-transition probability, R the reward function, $\gamma \in [0,1)$ the discount factor, O the observation space, and $Z(o\mid s,a)$ the observation (emission) model. Because the true state is unobserved, the agent maintains a belief distribution $b_t=P(s_t\mid o_{1:t},a_{1:t-1})$, updated by Bayes’ rule [22]. The value function over belief states is

$$V\left(b\right)=\underset{\pi }{max}\mathbb{E}\left[\sum _{t=0}^{\infty }{\gamma }^t{r}_t|b_0=b,\pi \right].$$

(4)

Solving the corresponding continuous-state Bellman equation exactly is computationally intractable: grid-based or point-based methods must quantize the belief simplex, and the number of grid points grows exponentially with $\left|S\right|$. This curse of dimensionality renders exact POMDP solvers impractical for real-time CDN caching, where state dimensionality (thousands of objects) and request dynamics are large and fast.

2.3.2. Memory-Based Approximation

To avoid intractable belief updates (Section 2.3.1), we adopt a memory-based approximation that compresses the most recent L interaction steps into a learned memory vector. At decision time t, define the history

$$h_t=\left(o_{t-L+1},o_{t-L+2},\dots ,o_{t-1},o_t\right).$$

(5)

Toro Icarte et al. [25] showed that memoryless policies degrade under partial observability, whereas learned memory (e.g., LSTM) restores stability and generalization. Parisotto et al. [28] introduced Gated Transformer-XL (GTrXL), which augments Transformer-XL with GRU-style gating and a revised normalization scheme; on DMLab-30, GTrXL outperformed LSTM-based agents, indicating that gated self-attention can serve as an efficient memory mechanism for POMDPs.

2.3.3. Advantages of Transformer Architectures in RL for Caching

A Transformer decoder applies causal self-attention to the fixed-length observation history $h_t$ (Equation (5)), producing a compact memory embedding $m_t={\mathrm{TransformerDecoder}}_{\theta }\left(h_t\right)$. Unlike recurrent networks, parallel attention avoids stepwise recurrence, mitigates vanishing gradients, and enables faster convergence. Causal masking preserves temporal order while allowing flexible reference to informative past events—useful in sequential decision problems such as caching. We concatenate $m_t$ with the current cache features $s_t$ and approximate the action–value function as

$$Q\left([s_t;m_t],a\right)\approx \mathbb{E}\left[r_t+\gamma \underset{a^{\prime }}{max}Q\left([s_{t+1};m_{t+1}],a^{\prime }\right)\right].$$

(6)

The policy then selects $a_t\in arg{max}_{a}Q([s_t;m_t],a)$.

Adaptation for Content Caching

We augment the Transformer inputs with cache-specific metadata (e.g., popularity statistics, categorical tags, timestamps, and derived features), and tailor the reward and decision timing to CDN dynamics. These adaptations guide the learned memory to capture both temporal and structural regularities under partial observability, yielding a practical cache-replacement method for deployment.

3. Problem Formulation

3.1. System Model

We study a single edge-server cache of capacity M, where all content items have unit size so that the cache can hold at most M objects. Time is modeled in discrete steps $t\in \{1,2,\dots ,T\}$, each corresponding to the arrival of a request $R_t$ drawn from a predefined workload (see Section 3.2 for formal definitions and Section 5.1 for preparation details).

• Cache hit: If $R_t\in {\mathrm{CIM}}_t$, the request is served from the edge cache, minimizing latency. Here, ${\mathrm{CIM}}_t$ (Contents in Memory at time t) denotes the set of objects currently stored in the cache.
• Cache miss: If $R_t\notin {\mathrm{CIM}}_t$, the requested object is fetched from the CDN, inserted into the cache (evicting one item if $\left|{\mathrm{CIM}}_t\right|=M$), and then served, incurring additional response delay and backhaul traffic.

The cache-replacement policy is invoked only on cache misses, so decisions are made precisely when previously unseen content arrives. We adopt a model-free reinforcement learning setting in which the next state $s_{t+1}$ under $(s_t,a_t)$ is determined by the simulator or trace, without explicit transition probabilities.

The effectiveness of a caching policy $\pi$ is primarily evaluated by the long-run cache-hit rate:

$$C_{\mathrm{HIT}}={\displaystyle \frac{1}{T}}\sum _{t=1}^T\mathbf{1}\left\{R_t\in {\mathrm{CIM}}_t\right\},$$

(7)

where $\mathbf{1}\{·\}$ is the indicator function and T the total number of requests. This metric directly captures how effectively the policy exploits capacity to reduce latency and bandwidth usage. To complement hit rate, we also report auxiliary metrics (e.g., average miss latency and total backhaul traffic) in our experiments.

3.2. Request Workload Models

We evaluate the learned policies under three representative request workloads. Each workload is executed independently (no mixing). Let N denote the catalog size (the number of unique content items). Detailed workload parameters and preprocessing steps for MovieLens are provided in Section 5.1.

• MovieLens workload [29]: A real-world request trace derived from MovieLens, replayed as a request sequence to reflect realistic user behavior.
• Mandelbrot–Zipf workload: A synthetic workload in which each request index $i\in \{1,\dots ,N\}$ is sampled according to

  $$P_{\mathrm{Zipf}}\left(i\right)={\displaystyle \frac{{(i+q)}^{-s}}{{\displaystyle \sum _{j=1}^N{(j+q)}^{-s}}}},$$

  (8)

  where $s>0$ is the skewness exponent and $q\ge 0$ is an offset controlling the head–tail balance.
• Pareto workload: A synthetic workload in which request index $i\in \{1,\dots ,N\}$ follows

  $$P_{\mathrm{Pareto}}\left(i\right)={\displaystyle \frac{\alpha x_m^{\alpha }{i}^{-(\alpha +1)}}{{\displaystyle \sum _{j=1}^N\alpha x_m^{\alpha }{j}^{-(\alpha +1)}}}}={\displaystyle \frac{i^{-(\alpha +1)}}{{\displaystyle \sum _{j=1}^N{j}^{-(\alpha +1)}}}},$$

  (9)

  where $\alpha >0$ is the shape parameter and $x_m>0$ the minimum-index cutoff.

By separating workload specification from the POMDP formulation in Section 3, we ensure that the state, action, observation, reward definitions, and miss-triggered decision timing remain fixed, while workload variation is controlled entirely through the request-generation process.

3.3. State and Observation

In our POMDP formulation, we distinguish between the latent environment state $s_t$, which the agent cannot fully observe, and the partial observation $o_t$ that the agent actually receives and uses for decision making.

3.3.1. Environment State

We represent the true environment state as

$$s_t=\left[{\mathrm{CF}}_t,{\mathrm{CP}}_t\right],$$

where

• Content Features (${\mathrm{CF}}_t$): Metadata for all N catalog entries, including each item’s identifier, popularity score, and genre tag. Together, these describe the catalog at time t.
• Content Popularity (${\mathrm{CP}}_t$): A full vector of popularity scores for every item, spanning both the catalog and the cache. We distinguish two components:
  • catalog popularity: Scores for all N items in the catalog.
  • cache popularity: Scores for the up to M items currently stored in the cache.

Although $s_t$ captures the complete system state, including precise popularity statistics, it remains hidden from the agent.

3.3.2. Observation

At each decision step, the agent observes a compressed feature vector

$$o_t=\left[{\mathrm{CRF}}_t,{\mathrm{CCP}}_t\right],$$

where

• Current-Request Features (${\mathrm{CRF}}_t$): Identifier of the requested item $R_t$, its popularity rank, genre tag, and request timestamp.
• Compressed Content Popularity (${\mathrm{CCP}}_t$): Six summary statistics of ${\mathrm{CP}}_t$: the mean, top-10% mean, and bottom-10% mean, each computed over (i) the entire catalog and (ii) the cached subset.

Thus, the agent bases its decisions on the compact observation $o_t$, rather than the full latent state $s_t$. This design reflects partial observability while retaining the most informative signals, enabling efficient and stable learning of cache-replacement policies.

3.4. Action Space

We invoke the policy only on cache misses (i.e., $R_t\notin {\mathrm{CIM}}_t$), never on hits. To keep decision complexity independent of capacity M, we use a fixed action set $A=\{0,1,\dots ,11\}$. On each miss, the agent selects one action $a_t\in A$:

• $a_t=0$: Do not cache the missed item (admission suppressed).
• $1\le a_t\le 5$: Rank cached items by ascending estimated popularity,

  $$\left[i_1,\dots ,i_M\right]=Rank\left({\mathrm{CIM}}_t;\mathrm{ascending}\mathrm{popularity}\right),$$

  and evict $i_{a_t}$.
• $6\le a_t\le 11$: Rank cached items by recency (least recently used first),

  $$\left[j_1,\dots ,j_M\right]=Rank\left({\mathrm{CIM}}_t;\mathrm{LRU}\right),$$

  and evict $j_{a_t-5}$.

• Recency, tie-breaking, and clamping.

Let $\tau \left(x\right)$ be the last access time (in steps) of item x, and define $r_t\left(x\right)=t-\tau \left(x\right)$ (larger means less recent use). Sorting by $\mathrm{LRU}$ is equivalent to ordering by non-increasing $r_t$, so $j_1=arg{max}_x{r}_t\left(x\right)$. Ties in either ranking are broken deterministically by (i) smaller item ID, then (ii) earlier insertion time. If a requested rank k exceeds M, we clamp to $k^{\prime }=min\{k,M\}$ for determinism.

This rank–evict grid subsumes classical heuristics as special cases: $\mathrm{LFU}$ corresponds to $a_t=1$, and $\mathrm{LRU}$ to $a_t=6$. Confining decisions to a small, semantically meaningful set that balances long-term popularity and short-term recency reduces exploration variance and stabilizes Q-learning as M grows. We also evaluate reduced action sets with $\left|A\right|\in \{3,7,12\}$ under identical protocols (see Section 5.4).

3.5. Reward Function

Let ${\delta }_1<{\delta }_2<\cdots <{\delta }_K$ denote the strictly increasing sequence of cache-miss time steps, a subsequence of the global timeline $t\in \{1,2,\dots ,T\}$. The policy is updated only at these miss steps, but cache hits between misses still contribute to the reward. At miss step ${\delta }_k$, the reward is defined as

$$r_{{\delta }_k}=r_{\mathrm{hit},{\delta }_k}+r_{\mathrm{miss}}+r_{\mathrm{add},{\delta }_k}+\left(r_{r_L}+r_{r_M}+r_{r_S}\right)+r_{\mathrm{totalP}}.$$

(10)

• Cache-hit window reward $r_{\mathrm{hit},{\delta }_k}$: The number of cache hits occurring between the previous miss ${\delta }_{k-1}$ and the current miss ${\delta }_k$,

  $$r_{\mathrm{hit},{\delta }_k}=\sum _{t={\delta }_{k-1}+1}^{{\delta }_k-1}\mathbf{1}\left(R_t\in {\mathrm{CIM}}_t\right).$$

  (11)
• Cache-miss penalty $r_{\mathrm{miss}}$: A fixed negative penalty applied at each cache miss.
• Delayed-hit bonus $r_{\mathrm{add},{\delta }_k}$: Within a fixed horizon H, cache hits on items admitted after ${\delta }_{k-H+1}$ yield additional reward, reinforcing effective recent admissions.
• Multi-scale request-matching rewards $(r_{r_L},r_{r_M},r_{r_S})$: Fractions of hits measured over long, medium, and short recent-request windows.
• Global-popularity alignment $r_{\mathrm{totalP}}$: A reward proportional to the overlap between cached items and globally popular content, promoting adaptation to long-term demand.

This composite reward integrates immediate reuse $\left(r_{\mathrm{hit}}\right)$, short- to long-term request matching $\left(r_{r_{*}}\right)$, and popularity alignment $\left(r_{\mathrm{add}},r_{\mathrm{totalP}}\right)$, guiding the agent to trade off short-term responsiveness against sustained cache efficiency under partial observability.

3.6. Learning Objective

Building on the miss-triggered reward scheme (Section 3.5), the objective is to learn a policy $\pi$ that maximizes the expected average reward per miss:

$${\rho }^{\pi }=\underset{K\to \infty }{lim}{\displaystyle \frac{1}{K}}{\mathbb{E}}_{\pi }\left[\sum _{k=1}^K{r}_{{\delta }_k}\right],$$

(12)

where ${\delta }_1<{\delta }_2<\cdots <{\delta }_K$ are the miss steps in an episode of length T, and $r_{{\delta }_k}$ is given by (10). The optimal policy is then

$${\pi }^{*}=arg\underset{\pi }{max}{\rho }^{\pi }.$$

(13)

This objective is closely related to the cache-hit rate $C_{\mathrm{HIT}}$, since

$${\rho }^{\pi }\approx {\displaystyle \frac{H}{K}}={\displaystyle \frac{C_{\mathrm{HIT}}}{1-C_{\mathrm{HIT}}}},$$

(14)

where H and K denote the total numbers of hits and misses, respectively (so $T=H+K$ and $C_{\mathrm{HIT}}=H/T$). Thus, maximizing ${\rho }^{\pi }$ is essentially aligned with maximizing $C_{\mathrm{HIT}}$. This formulation also satisfies the Bellman optimality condition under miss-triggered updates. In practice, we implement this objective using DDQN and perform value updates only at miss steps ${\delta }_k$ (see Section 4).

4. Proposed Framework: Miss-Triggered Cache Transformer

This section introduces the MTCT, a framework designed to align learning and decision-making with cache-miss events, thereby capturing partial observability in CDN environments more effectively. The framework consists of three components: (1) a Miss-Triggered Decision Mechanism, which activates policy inference and updates only upon cache misses; (2) Miss-Triggered Delayed-Hit Reward Learning, which accumulates hit-window rewards and incorporates delayed-hit bonuses to reinforce effective caching decisions; and (3) Transformer Decoder Memory Approximation, which embeds fixed-length sequences of observations and actions via a lightweight Transformer decoder to approximate POMDP belief updates.

The rest of this section is structured as follows. Section 4.1 outlines the overall process flow. Section 4.2 explains the agent’s internal data pipeline. Section 4.3 details the Miss-Triggered Delayed-Hit Reward Learning scheme. Finally, Section 4.4 describes aggregation of partial observations into state representations.

4.1. MTCT Framework Process Flow Overview

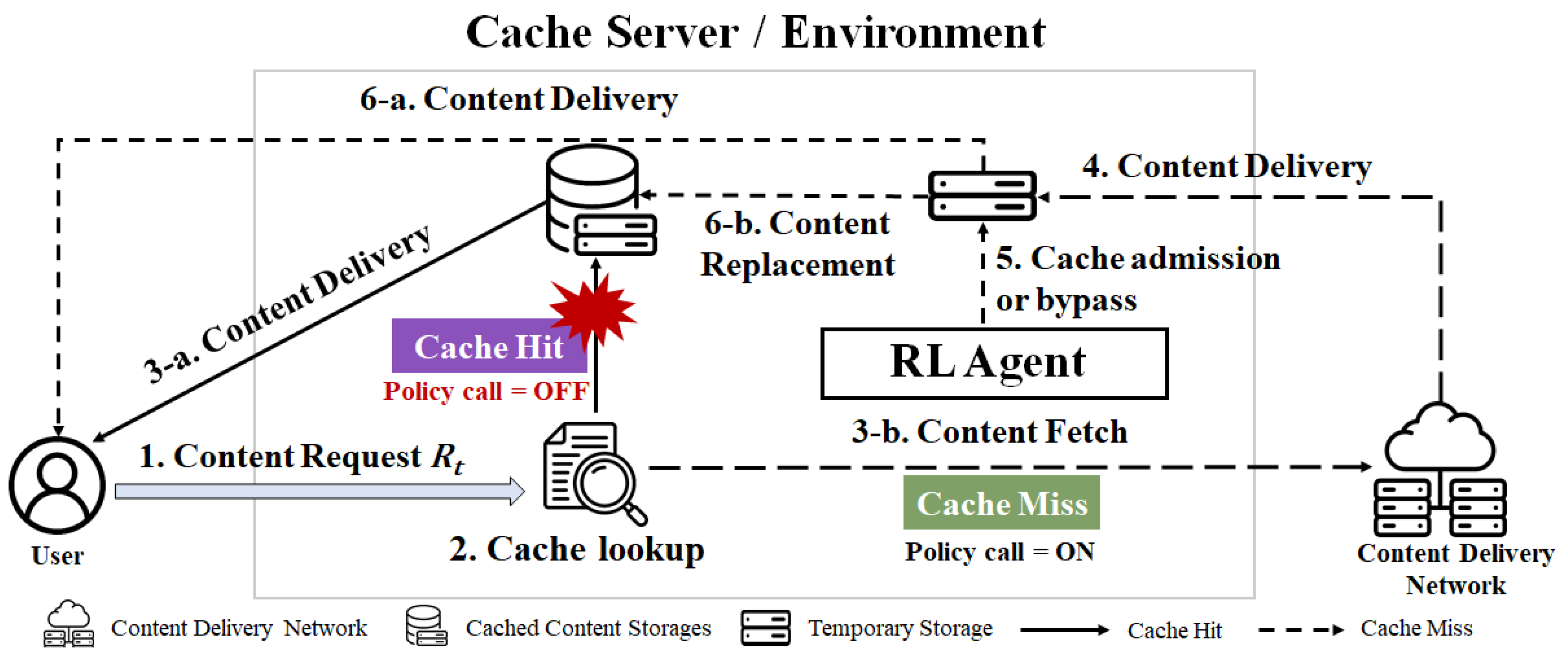
Figure 1 illustrates the processing steps of a content request under the miss-triggered framework at the edge cache server. When a request $R_t$ arrives, the system follows a pipeline that confines policy inference and model updates to cache-miss events, minimizing computational overhead. The stages of this workflow are summarized in Figure 1 and detailed below.

• Request and cache lookup (Steps 1–2). The system registers the user request $R_t$ and checks whether the requested content is present in ${\mathrm{CIM}}_t$.
• Cache hit (Step 3-a). If the item is found, it is served immediately with no policy call. Metadata such as recency or popularity may be updated.
• Cache miss and CDN fetch (Steps 3-b, 4). If the item is absent, it is retrieved from the CDN/origin and placed in a temporary buffer.
• MTCT agent decision (Step 5). After the fetch, the MTCT agent decides whether to admit the item into the cache. If admitted, the agent also selects a victim for eviction.
• Delivery and update (Steps 6-a, 6-b). The content is delivered to the user regardless of admission. If admitted, the item replaces the chosen victim in the cache; otherwise, the temporary copy is discarded.

This miss-triggered pipeline ensures that policy inference and updates occur only when necessary, focusing learning on the most informative events while avoiding unnecessary computation during cache hits.

4.2. Agent Data Processing Flow

Figure 2 summarizes the pipeline in five stages, described below.

• 1. Request and cache lookup (red). A user request $R_t$ arrives and the cache is queried. No policy call occurs at this stage.
• 2. Internal state update (gray). Popularity and recency metadata in the internal state $s_t$ are updated.
  Hit case: if $R_t\in {\mathrm{CIM}}_t$, metadata and counters for Miss-Triggered Delayed-Hit Reward Learning (MTDHRL; Section 4.3) are updated, and the request is served from the cache. No observation construction, policy inference, or replay write occurs.
  Miss case: if $R_t\notin {\mathrm{CIM}}_t$, miss-related counters and statistics are updated, and the pipeline proceeds to Stage 3.
• 3. History integration (brown). A partial observation $o_t$ is constructed via State Aggregation (Section 4.4) and appended to the last $CL-1$ observations to form

  $$h_t=\left\{o_{t-CL+1},\dots ,o_t\right\},$$

  represented as a tensor of shape $[1,CL,\text{obs\_dim}]$, where $CL$ is the context length.
• 4. Inference and action/transition (green). The policy consumes the history tensor and produces Q-value estimates $\{Q_{t-CL+1},\dots ,Q_t\}$. The cache operation is chosen by $a_t=arg{max}_a{Q}_t\left(a\right)$ and executed (bypass or admit+evict; rank-based). The transition $\left(o_{t-1},a_{t-1},r_{t-1},o_t\right)$ from the previous miss is written to the replay buffer.
• 5. Replay learning and target update (apricot). Mini-batches of size $B_s$ consisting of $CL$-step sequences are sampled from replay to compute the temporal-difference loss against a target network. Input tensors have shape $[B_s,CL,\text{obs\_dim}]$. Policy parameters are updated by gradient descent, and the target network is synchronized periodically. Training is miss-triggered, so hit-only intervals incur no forward or backward passes.

This design ensures that computation and learning are concentrated on cache-miss events, reducing overhead during hits while preserving the information needed for stable training under partial observability.

Algorithmic overview. The overall MTCT operation is summarized in Algorithm 1. The pseudocode below follows the same miss-triggered loop as Figure 2: by design, hits do not invoke the policy, whereas misses trigger observation/history assembly, action selection, a replay write, and a small number of learner steps. For each request, the cache is checked first; on a hit, we refresh metadata and update delayed-reward counters only. On a miss, we form $o_t$ and update the fixed-length history $h_t$ with the most recent $CL$ observations. The agent then chooses either to bypass or to admit with a rank-based eviction (e.g., least popular or least recently used ranks). At the miss, the credited reward aggregates immediate reuse since the last miss, a miss penalty, and delayed-hit bonuses that attribute subsequent hits to recent admissions. We append one transition (from the previous miss) to the replay buffer. We perform G gradient steps with temporal-difference targets and synchronize the target network every K misses. This event-driven schedule concentrates computation on informative events while still propagating information from hit intervals via delayed-reward bookkeeping.

Algorithm 1 MTCT online loop (miss-triggered).

1: Init $\theta$; $\overline{\theta }\leftarrow \theta$; replay $\mathcal{D}$; counters   2: for each request $R_t$ do   3:       if $R_t\in {\mathrm{CIM}}_t$ then                                    ▹ hit   4:           OnHit   5:           continue   6:       else                                         ▹ miss   7:           $o_t\leftarrow$ BuildObs   8:           $h_t\leftarrow$ AssembleHistory$(o_t,CL)$   9:           $a_t\leftarrow arg{max}_a{Q}_{\theta }(h_t,a)$ 10:         Execute($a_t$)                        ▹ bypass or admit + evict (rank-based) 11:         $r_t\leftarrow$ ComputeReward$(\text{hit-window},\text{miss-pen},\text{delayed-hit},\dots )$ 12:         ReplayWrite($(h_{t-1},a_{t-1},r_{t-1},h_t)$ if previous step was a miss) 13:         for $g=1$ to G do 14:            sample $(h,a,r,h^{\prime })\sim \mathcal{D}$;   $y\leftarrow r+\gamma {max}_{a^{\prime }}{Q}_{\overline{\theta }}(h^{\prime },a^{\prime })$ 15:            $\theta \leftarrow \theta -\eta {\nabla }_{\theta }{\left(Q_{\theta }(h,a)-y\right)}^2$ 16:         end for 17:         if $\text{miss\_count}modK=0$ then $\overline{\theta }\leftarrow \theta$ 18:         end if 19:     end if 20: end for 21: function  OnHit 22:     serve from cache; update recency/popularity; update delayed-reward counters 23:     /* no policy call, no history build, no replay write, no update */ 24: end function

4.3. Miss-Triggered Delayed-Hit Reward Learning (MTDHRL)

To exploit the high information content of cache misses while minimizing overhead, all policy inference and learning are triggered exclusively at miss events $\left\{{\delta }_k\right\}$. Cache hits between misses still carry useful information, so we aggregate them into two delayed-reward components credited at the next miss.

• Hit-window reward $r_{\mathrm{hit},{\delta }_k}$. This term counts the number of cache hits that occurred between the previous miss ${\delta }_{k-1}$ and the current miss ${\delta }_k$ (see Equation (11), Section 3.5). For example, if the 5th miss occurs at request $R_{15}$ and the 6th miss at $R_{20}$, then all hits from $R_{16}$ to $R_{19}$ are accumulated as $r_{\mathrm{hit},{\delta }_6}=4$. This signal reflects short-term reuse efficiency.
• Additional delayed-hit bonus $r_{\mathrm{add},{\delta }_k}$. Over a fixed horizon of the past H miss events $\{{\delta }_{k-H},\dots ,{\delta }_{k-1}\}$, any cache hits on items admitted during those misses earn extra reward, credited at the current miss ${\delta }_k$. For example, with $H=2$, if the 6th miss occurs at $R_{20}$ and items admitted at the 4th and 5th misses subsequently hit between $R_{16}$–$R_{19}$, then $r_{\mathrm{add},{\delta }_6}=2$. This signal propagates medium-term impact of admission decisions.

By consolidating hit-window and delayed-hit bonuses into miss-triggered updates, MTDHRL avoids per-hit policy calls while still incorporating both immediate and delayed information from cache hits. These aggregated rewards are stored with their associated transitions in the replay buffer and used during Q-learning updates. The Transformer decoder processes only the observation history for Q-value estimation. This design reduces computational overhead and enables the agent to capture long-term dependencies between replacement actions and their delayed outcomes, leading to efficient and stable cache-management policies under partial observability.

4.4. State Aggregation

In our POMDP formulation, the full environment state $s_t=[{\mathrm{CF}}_t,{\mathrm{CP}}_t]$ includes both catalog-level and cache-level popularity information. At each time step t, we maintain two vectors: a catalog-level popularity vector of length N and a cache-level vector of length M for items in ${\mathrm{CIM}}_t$. Directly using these high-dimensional vectors is computationally expensive, so we summarize them with six scalar statistics that capture overall, head, and tail popularity for both scopes (

Table 1. Summary statistics for the Compressed Content Popularity vector ${\mathrm{CCP}}_t$.

Symbol	Description
${\mu }_{\mathrm{all}}$	Mean popularity of all N catalog items at time t.
${\mu }_{\mathrm{cache}}$	Mean popularity of the M items currently stored in the cache.
${\mu }_{\mathrm{all},\mathrm{top}}$	Mean popularity of the top $10\%$ of catalog items.
${\mu }_{\mathrm{cache},\mathrm{top}}$	Mean popularity of the top $10\%$ of cached items.
${\mu }_{\mathrm{all},\mathrm{bot}}$	Mean popularity of the bottom $10\%$ of catalog items.
${\mu }_{\mathrm{cache},\mathrm{bot}}$	Mean popularity of the bottom $10\%$ of cached items.

).

Using these six statistics, we define the Compressed Content Popularity vector as

$${\mathrm{CCP}}_t=\left[{\mu }_{\mathrm{all}},{\mu }_{\mathrm{cache}},{\mu }_{\mathrm{all},\mathrm{top}},{\mu }_{\mathrm{cache},\mathrm{top}},{\mu }_{\mathrm{all},\mathrm{bot}},{\mu }_{\mathrm{cache},\mathrm{bot}}\right],$$

which replaces the raw popularity vectors. This representation reduces input dimensionality and accelerates both Transformer inference and training updates. It also smooths out noise in item-level popularity while highlighting head (top-10%) and tail (bottom-10%) trends, guiding the agent toward the most impactful cache-management decisions. Combined with Miss-Triggered Delayed-Hit Reward Learning, this state aggregation contributes to stable and efficient policy learning under partial observability.

In summary, the MTCT framework integrates Miss-Triggered Delayed-Hit Reward Learning, Transformer-based memory approximation, and state aggregation to address the challenges of partial observability and high-dimensional cache states. The next section evaluates these contributions empirically across diverse workloads and baselines.

5. Experiments

5.1. Experimental Environment and Workloads

All experiments were conducted on a workstation with an NVIDIA GeForce RTX 3060 Ti GPU (NVIDIA Corporation, Santa Clara, CA, USA), 32 GB DDR5-5600 RAM (2 × 16 GB; Samsung Electronics, Suwon-si, Republic of Korea), and an Intel Core i5-13500 CPU (Intel Corporation, Santa Clara, CA, USA). We evaluate the proposed framework on three representative workloads:

• MovieLens Latest Small [29]: We construct the request trace by mapping each rating event to a movie request and sorting events by Unix timestamp in ascending order (ties resolved by the original event index). The rating values themselves are not used. Movie metadata is merged with a three-dimensional PCA projection of one-hot genre vectors, and UTC temporal features (date, weekday, time of day) are added. The resulting trace covers requests from 610 users.
• Synthetic Mandelbrot–Zipf: We generated a catalog of $N=3000$ items and simulated $\mathrm{300,000}$ requests from 5000 users based on a Mandelbrot–Zipf popularity model $(s=1.2,q=0.5)$. Users were divided into heavy ($40\%$), light ($40\%$), and minor ($20\%$) groups. Request counts were drawn from Poisson distributions and scaled to match the total volume. Heavy and light users sampled items with probabilities proportional to the Zipf exponents, while minor users sampled by normalized rank to emphasize long-tail items. The final traces were temporally shuffled and augmented with PCA-reduced genre features, home region, age group, time class, weekend flag, and request location.
• Synthetic Pareto: Using the same procedure, we generated another $N=3000$-item catalog and $\mathrm{300,000}$ requests following a Pareto popularity distribution $(\alpha =1.2)$. All other user-group assignments and preprocessing steps matched those of the Mandelbrot–Zipf workload, thereby isolating the effect of the popularity distribution.

Table 2. Core hyperparameters for MTCT and the DDQN baseline. The symbol N/A denotes not applicable.

Hyperparameter	MTCT	DDQN (MLP)
Optimizer	Adam	Adam
Learning rate	$1\times {10}^{-4}$	$1\times {10}^{-3}$
Batch size	32	32
Target network update interval (steps)	1000	1000
Context/history length ($CL$)	50	N/A
Model dimension ($D_{\mathrm{model}}$)	64	N/A
Number of layers/blocks	2 decoder blocks	3 hidden layers
Number of attention heads	8	N/A
Activation (core)	ReLU (FFN/head)	ReLU
Input embedding dimension	8	128 (outer embed)
Hidden layer sizes	N/A	$[128,128,64]$

lists the core hyperparameters used for MTCT and the DDQN baseline. Based on these configurations, we conducted evaluations covering multiple criteria, including cache-hit rate, wall-clock training time, and sensitivity to context length. The results reported in Section 5.3 are all derived under these controlled experimental settings.

5.2. Comparison Baselines

We evaluate three baseline families to fairly contextualize MTCT.

(A)

Modern caching/admission policies (non-RL).

We focus in the main text on two widely adopted, high-performing representatives that cover complementary design axes—adaptive replacement and admission filtering:

• ARC [30]: An adaptive replacement that balances recency and frequency via two main lists (recent/frequent) and two ghost lists remembering evicted items; self-tunes the balance based on ghost hits ($O\left(1\right)$ amortized).
• W-TinyLFU [31]: An admission policy combining a small recency window with an approximate frequency filter (count-min sketch, optionally a doorkeeper); paired with an LRU/ARC back end to protect against one-hit wonders.

Additional modern policies (LRU-K [32], 2Q [33], LeCaR [34], etc.) are evaluated in Appendix B, where we also provide method descriptions and comparisons beyond ARC/W-TinyLFU. Full hyperparameter specifications for all modern baselines, including window ratios, back-end choices, and sketch dimensions for W-TinyLFU, are documented in Appendix B.4.

(B)

Classical heuristics (for continuity).

• FIFO: Evicts the oldest resident (queue-based); oblivious to locality (lower-bound reference).
• LRU: Removes the least recently used item; strong with short-term locality, slower under long-range gaps.
• LFU: Evicts the lowest access count; strong under stable popularity/heavy tails, brittle under abrupt shifts.
• Thompson Sampling: Bandit-style admission/eviction; adapts but requires posterior updates and is prior-sensitive.
• Random: Uniform victim; very low overhead, typically weakest, used as a sanity check.

(C)

RL baselines (with and without memory).

• DDQN (MLP): A standard value-based agent that approximates caching as an MDP using aggregated features $({\mathrm{CRF}}_t,{\mathrm{CCP}}_t)$ as a proxy state; three actions $a_t\in \{0,1,2\}$ for bypass/LRU/LFU; invokes the policy at every cache event (hits and misses); no sequence memory or delayed-hit credit assignment.
• DDQN (miss-triggered; control): Same MLP, optimizer, replay, targets, and loss as above, but policy calls, replay writes, and updates occur only at miss steps $\left\{{\delta }_k\right\}$, matching MTCT’s trigger schedule and miss-window transitions. This isolates the contribution of Transformer-based memory under an identical decision cadence.

• Reporting policy. In the main text, we report ARC and W-TinyLFU alongside classical heuristics and RL baselines; additional modern policies and ablations are documented in Appendix B, with full hyperparameter tables in Appendix B.4. Wall-clock analyses by cache size appear in Appendix A.1.
• Evaluation setup. Unless otherwise stated, RL baselines use the same observation features, replay sampling, target-update cadence, and evaluation seeds. DDQN variants adopt a three-way action space, whereas MTCT uses the 12-action grid by default; MTCT and the miss-triggered DDQN control invoke the policy only on misses, while the standard DDQN acts at every cache event. We compute the final cache-hit rate as the mean over the last 10 episodes of each run and report results as mean ± s.d. across the number of runs indicated in each study (for example, 10 runs for the context-length sweep; 5 runs for reward and distribution-shift ablations; and 5 runs for the action-set study), and the corresponding numerical summaries are presented in the Results tables and figures where those artifacts are first introduced. End-of-training averages are summarized in the corresponding tables.

5.3. Evaluation

We evaluate MTCT under cache capacities $M\in \{100,200,300,400,500,600\}$ with a fixed context length $CL=50$. For each M and method, we run 10 independent trials and report the cache-hit rate $C_{\mathrm{HIT}}$ (Equation (7)) averaged over the last 10 evaluation episodes.

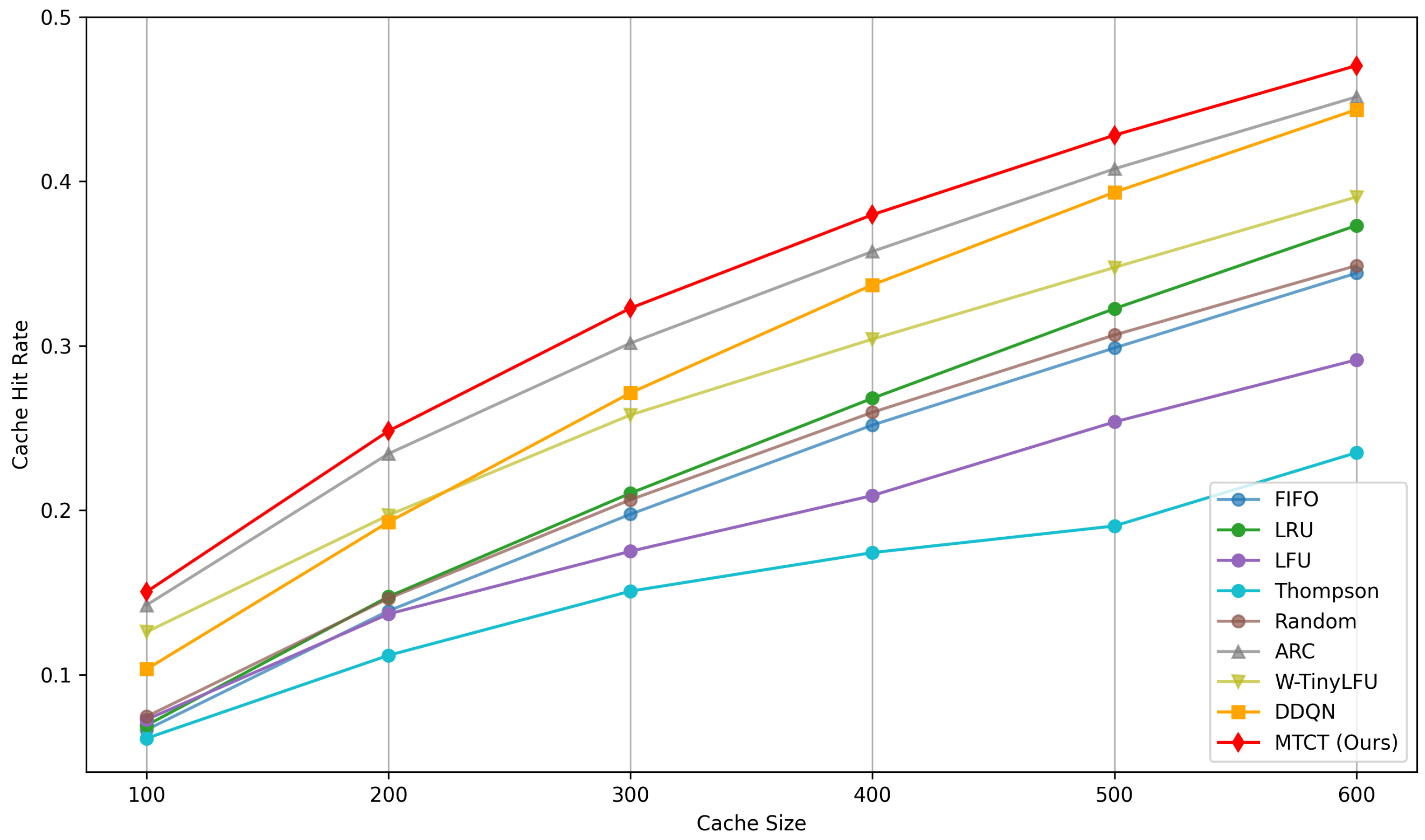
Figure 3, Figure 4 and Figure 5 plot the mean $C_{\mathrm{HIT}}$ versus cache size on MovieLens (real trace) and two synthetic workloads (Mandelbrot–Zipf, Pareto). Overall, MTCT attains the best or statistically comparable (within one s.d.) hit rates on most cache sizes. On the synthetic workloads, the modern admission/replacement baselines ARC and W-TinyLFU are highly competitive at small to mid capacities, whereas MTCT catches up or leads as M grows. On MovieLens, MTCT is consistently top across all M.

Table 3. Cache hit rates $C_{\mathrm{HIT}}$ by workload and cache size M. For DRL methods (DDQN, MTCT), values are the mean over the last 10 episodes of each run, reported as mean ± s.d. across 10 runs. The best mean value for each workload and cache size is shown in bold.

Workload	M	FIFO	LRU	LFU	Thompson	Random	ARC	W-TinyLFU	DDQN	MTCT (Ours)
Mandelbrot–Zipf	100	0.3895	0.4332	0.4668	0.1136	0.3900	0.5156	0.5413	0.5102 ± 0.0002	0.5376 ± 0.0011
	200	0.4627	0.5029	0.5194	0.2100	0.4622	0.5656	0.5961	0.5666 ± 0.0010	0.5960 ± 0.0005
	300	0.5078	0.5453	0.5494	0.3684	0.5083	0.5956	0.6286	0.6218 ± 0.0134	0.6302 ± 0.0001
	400	0.5437	0.5794	0.5854	0.5799	0.5437	0.6181	0.6523	0.6280 ± 0.0034	0.6550 ± 0.0000
	500	0.5738	0.6079	0.6124	0.6076	0.5733	0.6371	0.6716	0.6591 ± 0.0117	0.6749 ± 0.0001
	600	0.6000	0.6331	0.6421	0.6335	0.6001	0.6541	0.6882	0.6847 ± 0.0070	0.6917 ± 0.0001
Pareto	100	0.4175	0.4569	0.4887	0.0900	0.4176	0.5341	0.5580	0.5155 ± 0.0007	0.5232 ± 0.0011
	200	0.4846	0.5210	0.5317	0.1832	0.4844	0.5802	0.6094	0.5713 ± 0.0004	0.6088 ± 0.0017
	300	0.5271	0.5616	0.5668	0.5614	0.5273	0.6082	0.6399	0.6081 ± 0.0018	0.6414 ± 0.0016
	400	0.5607	0.5935	0.6001	0.5925	0.5607	0.6293	0.6621	0.6361 ± 0.0018	0.6512 ± 0.0007
	500	0.5890	0.6205	0.6213	0.6152	0.5889	0.6476	0.6803	0.6711 ± 0.0012	0.6791 ± 0.0010
	600	0.6142	0.6443	0.6549	0.6379	0.6138	0.6639	0.6958	0.6822 ± 0.0008	0.6961 ± 0.0007
MovieLens	100	0.0665	0.0692	0.0727	0.0613	0.0726	0.1423	0.1260	0.1033 ± 0.0051	0.1504 ± 0.0036
	200	0.1388	0.1475	0.1369	0.1118	0.1444	0.2344	0.1970	0.1928 ± 0.0052	0.2482 ± 0.0047
	300	0.1976	0.2104	0.1750	0.1508	0.2044	0.3016	0.2579	0.2713 ± 0.0078	0.3229 ± 0.0065
	400	0.2518	0.2681	0.2089	0.1742	0.2575	0.3573	0.3040	0.3370 ± 0.0076	0.3797 ± 0.0070
	500	0.2987	0.3226	0.2537	0.1904	0.3045	0.4076	0.3476	0.3933 ± 0.0089	0.4280 ± 0.0074
	600	0.3441	0.3731	0.2914	0.2350	0.3467	0.4513	0.3905	0.4436 ± 0.0097	0.4703 ± 0.0086

provides the detailed per-workload results. On MovieLens, MTCT is consistently the top performer across all M (e.g., $M=600$: MTCT $0.4703$ vs. DDQN $0.4436$, ARC $0.4513$, W-TinyLFU $0.3905$). On Mandelbrot–Zipf, W-TinyLFU slightly exceeds MTCT at small M (e.g., $M=100$), while the gap narrows and reverses by $M=600$ (MTCT $0.6917$ vs. $0.6882$). On Pareto, W-TinyLFU often remains ahead through mid-to-large capacities (e.g., $M=400,500$), with a virtual tie at $M=600$ (MTCT $0.6961$ vs. $0.6958$).

Complementing Table 3,

Table 4. Macro-averaged improvements of MTCT over baselines (percentage points, pp). Per-workload rows average over $M\in \{100,200,300,400,500,600\}$; Macro Avg averages over all workloads and M (18 settings total).

	FIFO	LRU	LFU	Thompson	Random	ARC	W-TinyLFU	DDQN
Mandelbrot–Zipf	$+11.80$	$+8.06$	$+6.83$	$+21.21$	$+11.80$	$+3.32$	$+0.12$	$+1.92$
Pareto	$+10.11$	$+6.70$	$+5.61$	$+18.66$	$+10.12$	$+2.28$	$-0.76$	$+1.93$
MovieLens	$+11.70$	$+10.14$	$+14.35$	$+17.93$	$+11.16$	$+1.75$	$+6.27$	$+4.30$
Macro Avg	$+11.20$	$+8.30$	$+8.93$	$+19.27$	$+11.02$	$+2.45$	$+1.88$	$+2.72$

reports macro-averaged improvements (percentage points, pp) of MTCT over the baselines across cache sizes $M\in \{100,200,300,400,500,600\}$. On Pareto, MTCT averages $0.76$ pp below W-TinyLFU; however, across all workloads and capacities (18 settings), MTCT attains $+1.88$ pp over W-TinyLFU, with gains of $+11.20$, $+8.30$, $+8.93$, $+19.27$, $+11.02$, $+2.45$, and $+2.72$ pp vs. FIFO, LRU, LFU, Thompson, Random, ARC, and DDQN, respectively.

5.3.1. Discussion of Figure 3, Figure 4 and Figure 5

Each plot shows mean curves (no error bands) to maximize readability. As M increases, all methods improve monotonically, but the relative ordering varies by workload. On MovieLens, MTCT is consistently the top curve across M. On Mandelbrot–Zipf and Pareto, W-TinyLFU leads at small M. On Pareto, it remains ahead at mid capacities (e.g., $M=400,500$). At the largest M, the curves converge: Pareto is a near tie, while MTCT holds a slight lead on Mandelbrot–Zipf. For variability and per-run dispersion, please refer to Table 3 (mean ± s.d. across 10 runs).

5.3.2. Wall-Clock Efficiency

While our main focus is on cache-hit rates, we also measured the mean wall-clock time per training episode under the hardware/software setup described in Section 5.1. Detailed breakdowns by cache size are reported in Appendix A.1. In brief, MTCT consistently requires less training time per episode than DDQN, confirming that miss-triggered decision making reduces policy-call overhead while maintaining high hit rates (see

Table 5. Mean wall-clock time (seconds) per training episode across workloads. Detailed results by cache size are reported in Appendix A.1.

Workload	DDQN (Baseline)	MTCT (Ours)
Mandelbrot–Zipf	376.47 ± 115.19	216.14 ± 76.09
Pareto	340.82 ± 102.33	201.67 ± 69.24
MovieLens	298.21 ± 88.11	187.92 ± 64.75

for workload-level means; detailed per-M results in Appendix A.1).

5.4. Ablation Studies

To further analyze the design of MTCT, we conduct ablation studies along four axes: (i) history length, (ii) reward shaping, (iii) robustness to distributional shifts, and (iv) sensitivity to the action-set design.

5.4.1. Sensitivity to Context Length

To examine the effect of history length, we fixed the cache size at $M=600$ and varied the context length $CL$.

Table 6. Sensitivity to context length $CL$ on MovieLens at cache size $M=600$. Values are mean ± s.d. of $C_{\mathrm{HIT}}$ across 10 runs (each run averaged over its final 10 episodes).

$\mathit{CL}$	Mean ± s.d.
1	0.3979 ± 0.0014
5	0.4003 ± 0.0344
10	0.4257 ± 0.0457
32	0.4699 ± 0.0030
50	0.4703 ± 0.0004
64	0.4700 ± 0.0025
128	0.4492 ± 0.0401
256	0.4393 ± 0.0460

and Figure 6 summarize representative results. Performance is poor for very short contexts ($CL\le 5$), indicating that the agent lacks sufficient temporal information to capture request dynamics. In particular, $CL=1$ effectively collapses the POMDP into a degenerate MDP approximation, serving as a lower bound on achievable performance. As $CL$ increases, accuracy improves steadily and stabilizes near $0.47$ for $CL\in [30,70]$, with small standard deviations. Beyond $CL\approx 100$, performance degrades slightly (e.g., $0.4492$ at $CL=128$, $0.4393$ at $CL=256$), suggesting diminishing returns and over-smoothing when the history window is too long. These trends justify adopting $CL=50$ as the default in the main experiments, balancing accuracy, stability, and computational cost. See

Table A2. Cache-hit rate $C_{\mathrm{HIT}}$ under varying context lengths $CL$ at $M=600$. Values are mean ± s.d. across the final 10 evaluation episodes per run.

$\mathit{CL}$	Mean ± s.d.	$\mathit{CL}$	Mean ± s.d.
1	0.3979 ± 0.0014	32	0.4699 ± 0.0030
2	0.4025 ± 0.0154	50	0.4703 ± 0.0004
4	0.3984 ± 0.0369	64	0.4700 ± 0.0025
5	0.4003 ± 0.0344	70	0.4695 ± 0.0027
8	0.4182 ± 0.0459	100	0.4502 ± 0.0379
10	0.4257 ± 0.0457	128	0.4492 ± 0.0401
16	0.4257 ± 0.0520	150	0.4496 ± 0.0394
20	0.4340 ± 0.0702	200	0.4371 ± 0.0456
30	0.4703 ± 0.0023	250	0.4443 ± 0.0452
		256	0.4393 ± 0.0460

in Appendix A for the complete grid.

5.4.2. Reward Ablations

To isolate the effect of individual shaping terms, we conducted ablations on MovieLens at $M=600$.

Table 7. Reward ablation on MovieLens ($M=600$). We report mean cache-hit rate ($C_{\mathrm{HIT}}$) over the final 10 episodes, averaged across 5 runs per variant. “Full” denotes the complete MTCT reward; variants drop one or more delayed/auxiliary terms. $\mathrm{\Delta }$ is the difference vs. Full in pp.

Variant	${\mathit{C}}_{\mathbf{HIT}}$ (Mean ± s.d.)	$\mathbf{\Delta }$ vs. Full (pp)
Full (MTCT reward)	0.4703 ± 0.0086	0.0
w/o Multi-scale request matching	0.4519 ± 0.0408	−1.8
w/o Global popularity alignment	0.4334 ± 0.0497	−3.7
w/o All delayed-hit rewards	0.4341 ± 0.0503	−3.6

shows that removing the multi-scale request-matching term reduces accuracy by about $1.8\mathrm{pp}$, while dropping global popularity alignment has a larger impact ($-3.7\mathrm{pp}$). Eliminating both delayed-hit rewards ($r_{\mathrm{hit},{\delta }_k}$ and $r_{\mathrm{add},{\delta }_k}$) similarly causes a $\sim 3.6\mathrm{pp}$ loss, highlighting their joint importance. These results suggest that (i) popularity-aware alignment is critical in long-tail workloads like MovieLens, (ii) multi-scale request matching stabilizes short- vs. medium-term reuse signals, and (iii) delayed-hit propagation is necessary to capture temporal effects of admission decisions beyond immediate hits. Overall, the full composite reward yields the most accurate and stable policy. The advantage of delayed-hit is not limited to stationary settings: on the non-stationary Mandelbrot–Zipf trace, MTCT attains $0.5166$ vs. $0.4881$ without delayed-hit ($+2.85\mathrm{pp}$) with markedly lower run-to-run s.d. ($0.0001$ vs. $0.0391$); see

Table 8. Stationary vs. non-stationary at $M=600$: overall hit rate for heuristics and DRL methods. Each entry averages the final 10 episodes of each run and is reported as mean ± s.d. across 5 runs.

Mandelbrot–Zipf ($\mathit{\alpha }$)	ARC	W-TinyLFU	DDQN	Miss-DDQN	MTCT (Ours)	MTCT-w/o Delayhit
1.2	0.6529	0.6740	0.6642 ± 0.0198	0.6630 ± 0.0198	0.6857 ± 0.0000	N/A
$1.0\to 0.6$	0.4679	0.5041	0.4893 ± 0.0133	0.4600 ± 0.0080	0.5166 ± 0.0001	0.4881 ± 0.0391

.

5.4.3. Distribution-Shift Robustness (Mandelbrot–Zipf)

We evaluate robustness under evolving access dynamics using a lightweight Mandelbrot workload. It mirrors Section 5.1 but runs for $\mathrm{100,000}$ requests (vs. $\mathrm{300,000}$ in the main workloads). We vary the popularity exponent $\alpha$ across segments. In the stationary setting, $\alpha =1.2$. In the piecewise non-stationary schedule, the first $\mathrm{50,000}$ requests use $\alpha =1.0$, and the remaining $\mathrm{50,000}$ use $\alpha =0.6$. 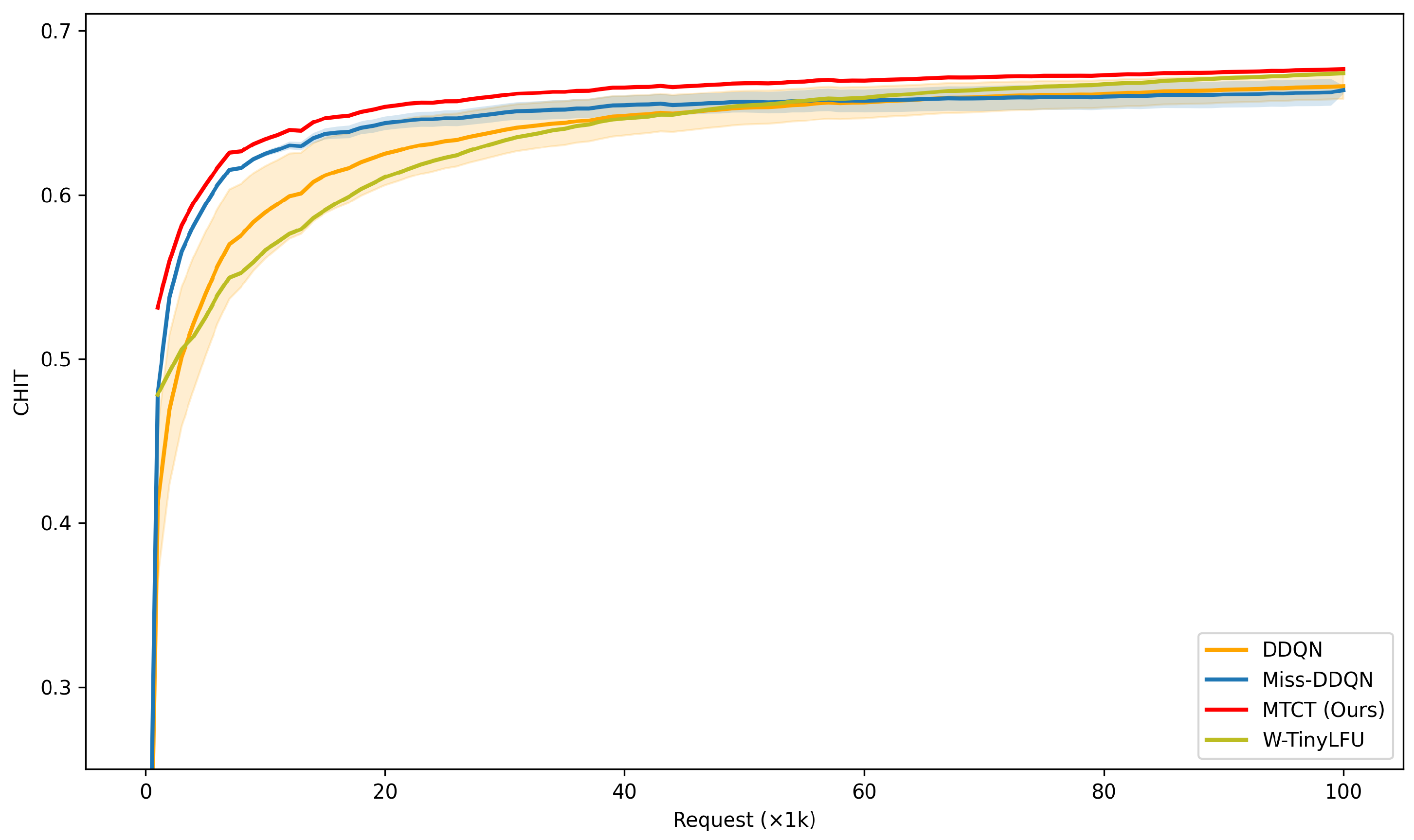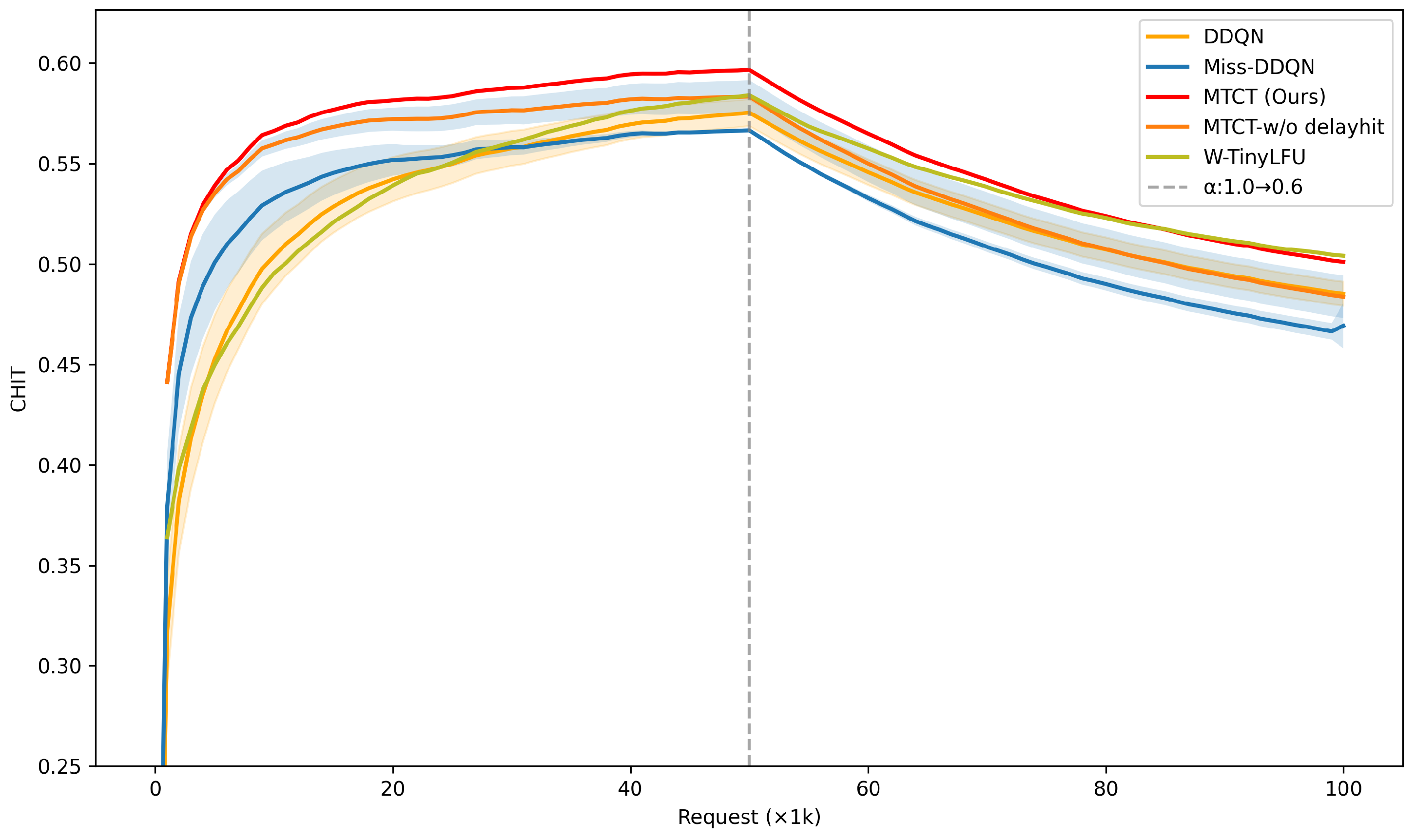Table 8 confirms that MTCT achieves the highest hit rates under both settings, with the largest margins in the non-stationary case where heuristic and DRL baselines degrade more severely. Figure 7 and Figure 8 provide per-1k breakdowns: under stationarity, MTCT converges fastest and maintains the highest performance across the full trace. Under non-stationarity, all methods drop after the distribution shift, and MTCT—while still best on average—also exhibits a gradual decline in later requests. This indicates that, although miss-triggered sequence modeling improves robustness, a uniform replay buffer can overweight outdated experience, slowing adaptation to newly shifted popularity. A natural extension is to replace uniform replay with prioritized or recency-aware sampling to better align learning with current request distributions.

5.4.4. Action-Set Sensitivity

To assess robustness of the action-space design, we vary the granularity of rank-based eviction choices on MovieLens with $M=600$, keeping the training and evaluation protocol fixed. As reported in

Table 9. Action-set sensitivity on MovieLens at $M=600$: last-10-episode mean $C_{\mathrm{HIT}}$ (mean ± s.d.) across 5 runs per action-set size.

Action Set Size	Mean ${\mathit{C}}_{\mathbf{HIT}}$ ± s.d.
3	0.4197 ± 0.0466
7	0.4532 ± 0.0414
12 (base)	0.4703 ± 0.0021

, finer granularity consistently improves terminal performance and reduces variability: the 12-action configuration attains the highest final hit rate ($+5.1\mathrm{pp}$ over 3 actions; $+1.7\mathrm{pp}$ over 7 actions) and shows the smallest run-to-run spread. By contrast, the 3-action configuration tends to converge earlier to a lower fixed point with larger variance. This pattern is consistent with reduced expressivity and action aliasing—distinct states that require different popularity–recency trade-offs collapse to the same choice—together with coarser credit assignment that limits the diversity of TD targets and weakens the effect of exploration. The 7-action setting offers a middle ground, whereas 12 actions recover the full benefit of rank-based control and stabilize learning. Accordingly, the main results adopt the 12-action grid as the default.

6. Discussion

6.1. Overall Performance and Workload Dependence

Across the three workloads, MTCT is competitive with state-of-the-art heuristics and RL baselines and attains the best or statistically comparable hit rates on most cache sizes. On the real trace (MovieLens), MTCT is consistently the top method across all M, highlighting the benefit of miss-triggered sequence modeling and delayed-hit credit assignment under non-stationary, long-tail demand. On the synthetic workloads (Mandelbrot–Zipf, Pareto), modern admission/replacement policies—particularly W-TinyLFU and ARC—are highly competitive at small to mid capacities; gaps narrow or reverse as M increases, with a slight MTCT lead by $M=600$ on Mandelbrot–Zipf and a near-tie on Pareto. We note one exception visible in Appendix B: on MovieLens at $M=600$, LRU–K ($K=2$) slightly exceeds MTCT (0.4765 vs. 0.4703;

Table A3. Appendix—Additional heuristics (overall cache-hit rates). We report LRU–K ($K=2$), 2Q, and LeCaR across workloads and cache sizes M. The rightmost column reprints the best modern heuristic from the main text (ARC or W-TinyLFU) for quick reference; see Table 3 and Table A4. Bold indicates the best mean within each workload–capacity row.

Workload	M	LRU–K ($\mathit{K}=2$)	2Q	LeCaR	Best Modern (Main)
Mandelbrot–Zipf	100	0.5027	0.5013	0.4571	W-TinyLFU 0.5413
	200	0.5558	0.5539	0.5183	W-TinyLFU 0.5961
	300	0.5898	0.5868	0.5573	W-TinyLFU 0.6286
	400	0.6172	0.6122	0.5887	W-TinyLFU 0.6523
	500	0.6404	0.6332	0.6149	W-TinyLFU 0.6716
	600	0.6608	0.6520	0.6392	W-TinyLFU 0.6882
Pareto	100	0.5217	0.5207	0.4787	W-TinyLFU 0.5580
	200	0.5704	0.5695	0.5359	W-TinyLFU 0.6094
	300	0.6028	0.6004	0.5730	W-TinyLFU 0.6399
	400	0.6290	0.6241	0.6024	W-TinyLFU 0.6621
	500	0.6510	0.6447	0.6282	W-TinyLFU 0.6803
	600	0.6705	0.6626	0.6506	W-TinyLFU 0.6958
MovieLens	100	0.1307	0.1328	0.0761	ARC 0.1423
	200	0.2297	0.2218	0.1540	ARC 0.2344
	300	0.3086	0.2894	0.2211	ARC 0.3016
	400	0.3740	0.3424	0.2837	ARC 0.3573
	500	0.4279	0.3889	0.3410	ARC 0.4076
	600	0.4765	0.4311	0.3934	ARC 0.4513

). Nonetheless, aggregated over cache sizes and workloads, MTCT remains the most consistent top performer.

6.2. Wall-Clock Efficiency

In addition to accuracy, MTCT reduces episode time relative to a standard DDQN, consistent with the fact that policy-call volume scales with the miss rate $(\propto 1-C_{\mathrm{HIT}})$. Concentrating computation on informative miss events lowers overhead without sacrificing final quality; detailed breakdowns by cache size confirm this trend (Appendix A.1).

6.3. Ablations: Context Length and Reward Shaping

On MovieLens, varying the context length reveals four regimes. Very short histories ($CL\le 5$) underperform and are unstable. Short-to-intermediate windows ($CL=8–20$) improve steadily but still show larger variance. A plateau appears for $CL\in [30,70]$ around $C_{\mathrm{HIT}}\approx 0.47$ with minimal variance. Excessively long windows ($CL\gtrsim 100$) yield a mild decline, consistent with over-smoothing. These trends justify adopting $CL=50$ as a practical default. Reward ablations further show that removing multi-scale request matching or global popularity alignment reduces $C_{\mathrm{HIT}}$ by about $1.8\mathrm{pp}$ and $3.7\mathrm{pp}$, respectively, and turning off delayed-hit components yields a similar $\sim 3.6\mathrm{pp}$ drop, confirming their complementary roles.

6.4. Robustness Under Distribution Shift

On a lightweight Mandelbrot–Zipf variant with a piecewise shift in the popularity exponent, MTCT maintains the strongest end-of-training averages among compared methods in both stationary and non-stationary settings. Learning curves sampled every 1k requests show that all methods suffer a drop at the shift point; MTCT still leads on average but also exhibits a gradual late-stage decline. This suggests that a uniform replay buffer can overweight stale experience; prioritized or recency-aware sampling is a natural extension to accelerate adaptation without sacrificing stability.

6.5. Action-Space Design

A controlled study on MovieLens at $M=600$ shows that a finer, semantically structured action grid improves terminal accuracy and stability. The 12-action design achieves the highest final hit rate and the smallest run-to-run variance, while the 3-action variant converges faster but to a lower fixed point with larger variance—consistent with reduced expressivity (action aliasing) and coarser credit assignment. We therefore adopt 12 actions as the default, while noting that lower-resolution settings may remain attractive under strict latency/compute budgets.

6.6. Limitations and Future Work

Our study has three primary limitations. (1) Byte-awareness and object-size heterogeneity. We assume unit-size objects and optimize request hit rate; this simplifies analysis but departs from real systems where object sizes vary, byte-hit rate matters, and TTL/invalidations are present. Evaluating MTCT under byte-aware objectives, realistic size distributions, and TTLs—including multi-tier or distributed cache hierarchies—is an important next step. It is also necessary to validate performance on larger-scale industrial datasets to confirm practical applicability. (2) Replay and adaptation under drift. While miss-triggered updates improve efficiency, our uniform replay can overweight stale experience after distributional shifts. Prioritized or recency-aware sampling, as well as adaptive buffers, are natural extensions to accelerate adaptation without sacrificing stability. (3) Scope of RL baselines. We compared against strong modern heuristics (ARC, W-TinyLFU) and MLP-based DDQN (including a miss-triggered control), but we did not undertake a head-to-head comparison among memory-based RL architectures (e.g., DRQN/LSTM-Q, DTQN/GTrXL). This omission is by design: our focus is to establish the benefit of a POMDP formulation with miss-triggered, Transformer-decoder Q-learning over MDP approximations for caching. A comprehensive architecture study across memory-based RL methods is left to future work. (4) Practical deployment considerations. Beyond single-node experiments, real-world deployment requires attention to scalability in distributed settings and cross-cache communication overheads. We emphasize keeping policy invocation miss-triggered to avoid adding latency on the hit path, and leave a systematic, at-scale evaluation of these systems-level choices to future work.

7. Conclusions

We presented MTCT, a cache-replacement framework that marries a POMDP formulation with Transformer-based memory, miss-triggered decision scheduling, compact popularity features, and delayed-hit credit assignment. By invoking the policy only on informative miss events and propagating hit information through delayed rewards, MTCT aligns computation with signal and stabilizes training under partial observability.

Across MovieLens (real trace) and the Mandelbrot–Zipf and Pareto workloads, MTCT achieves the best or statistically comparable hit rates on most cache sizes while reducing per-episode wall-clock time relative to DDQN. On synthetic workloads, strong modern heuristics (ARC, W-TinyLFU) are highly competitive at small to mid capacities, with gaps narrowing or reversing as M grows; on MovieLens, MTCT remains consistently top across all M, with rare exceptions noted in Appendix B. Ablations corroborate these findings: four context-length regimes support $CL=50$ as a practical default, finer 12-action grids improve terminal accuracy and stability over coarser sets, and MTCT retains an edge under distributional shift albeit with room to accelerate post-shift adaptation.

Future work proceeds along four axes. First, we move beyond unit-size objects to byte-aware objectives, realistic TTL/invalidations, and multi-tier deployments. Second, we replace uniform replay with prioritized or recency-aware sampling and explore adaptive buffers to improve responsiveness under drift. Third, we broaden comparisons to alternative memory-based RL architectures (e.g., DRQN/LSTM-Q, DTQN/GTrXL) to more fully map the design space. These directions will test MTCT’s generality and scalability in realistic CDN settings while deepening our understanding of memory and decision scheduling in learning-based caching. Finally, we will evaluate practical deployment considerations—scalability in distributed settings and cross-cache communication overheads—while keeping policy invocation miss-triggered to preserve hit-path latency.