This section elaborates on the design principles and technical details of the proposed framework, which explicitly distinguishes itself from existing federated fine-tuning approaches in three key aspects:
3.1. Overall Model Architecture
This paper proposes a federated fine-tuning framework for large language models in privacy-sensitive scenarios. For the first time, cross-client gradient updates are explicitly mapped to a global interaction graph (The global interaction graph is introduced to address the challenge of fragmented and locally-biased representations under heterogeneous data distributions. It explicitly models high-order dependencies across clients, enabling consistent knowledge alignment and improving global semantic coherence). A linear alignment module and a graph representation learning component are introduced to capture high-order dependencies under heterogeneous distributions. Based on this structure, we design a graph-importance-driven structural pruning (Structural pruning reduces communication and computation bottlenecks by removing redundancy and retaining critical structures) strategy. Only sub-blocks with the highest semantic relevance are unfrozen, balancing parameter efficiency and communication compression. A hierarchical secure channel (The hierarchical secure channel mitigates multi-level privacy risks and adapts to network heterogeneity while ensuring secure transmission) and a minimum exposure gradient embedding mechanism are also integrated to mitigate potential privacy leakage risks.
The proposed framework unifies graph learning, scalable federated optimization, and
LoRA-based fine-tuning. It provides a low-barrier solution for large model customization on resource-constrained devices. This design also lays the groundwork for future studies on high-fidelity knowledge sharing in distributed settings. Low-Rank Adaptation (LoRA) is adopted in our framework to enable efficient fine-tuning of large-scale language models in resource-constrained federated learning environments. LoRA decomposes the weight update into a pair of low-rank matrices, which are trained while keeping the original pre-trained weights frozen. This approach significantly reduces the number of trainable parameters and memory footprint while preserving the expressive power of the base model. In our scenario, LoRA is particularly suitable because each federated client often has limited computational capacity and communication bandwidth. By applying LoRA to selected model layers, we achieve efficient parameter updates with minimal communication cost, making the method well-suited for cross-client training where privacy, scalability, and deployment efficiency are critical. The overall architecture is illustrated in
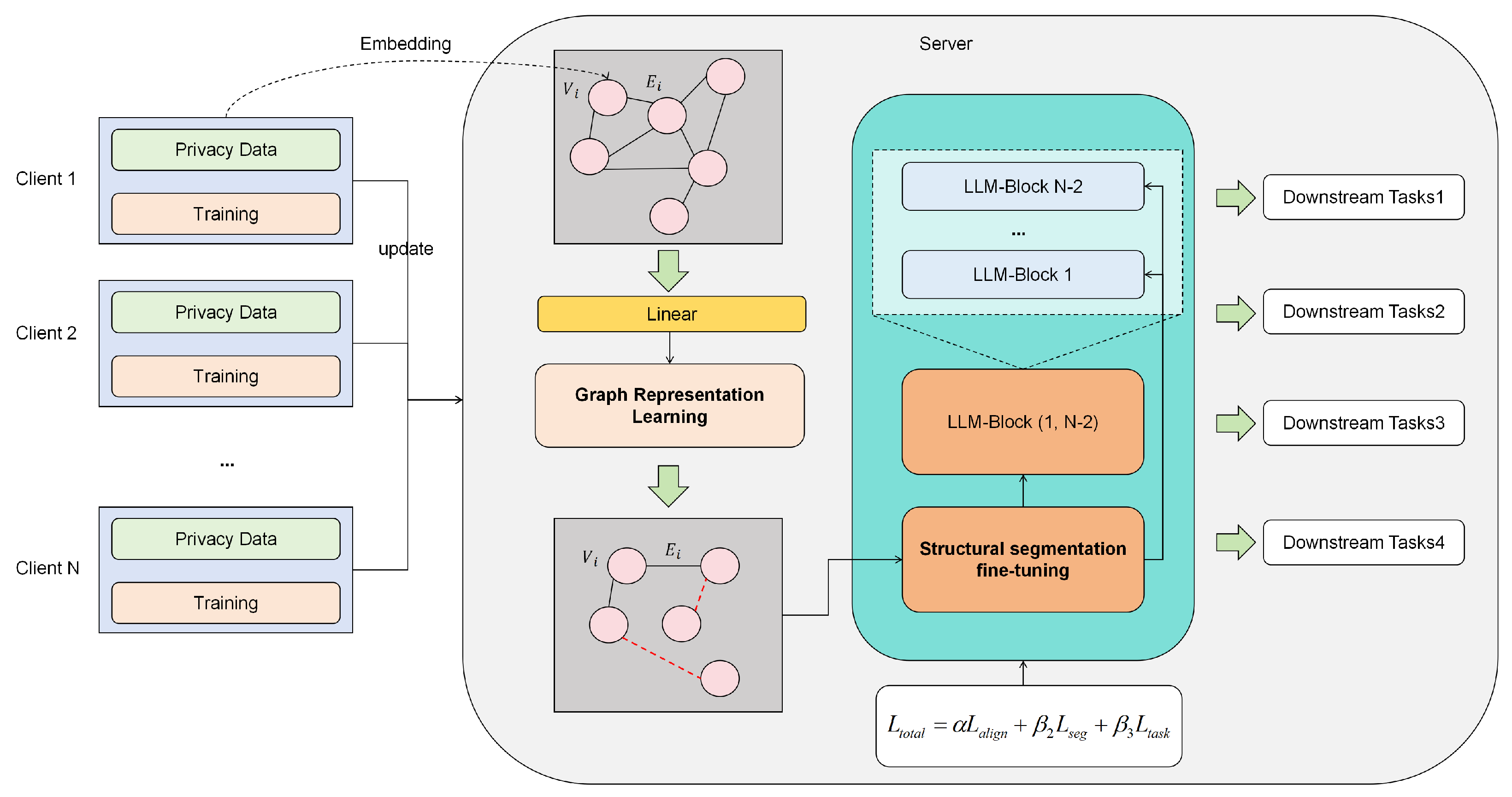
Figure 1. The proposed framework first constructs a graph-based representation space to capture structural relationships among clients and then applies the structural segmentation framework to selectively update parameters. The arrows in the figure depict the direction of information flow, while the color coding differentiates between communication, local optimization, and auxiliary operations. This design facilitates both structure-aware knowledge sharing and task-specific adaptation.
The proposed framework integrates graph representation learning and structural segmentation to address both semantic consistency and heterogeneous adaptation in federated large language model (LLM) fine-tuning. The architecture consists of three main components: (1) graph representation learning to capture high-order semantic dependencies across distributed clients, (2) structural segmentation to adapt model components to heterogeneous environments, and (3) optimization strategies for privacy preservation and communication efficiency. The global server coordinates the training process, while client-specific graphs encode the structural and semantic characteristics of local data. Details of the graph representation process are provided in the following subsection.
3.2. Graph Representation Learning
To enhance representation learning in federated semantic alignment scenarios, this paper introduces a graph representation learning module as a structural foundation. The input graph is denoted as
, where the node set is
and the edge set is
. Here, each edge
represents the structural or semantic relationship between node
and node
, such as feature similarity, dependency links, or interaction frequency, enabling the model to capture both local and global dependencies. Each node has a feature vector
. For clarity, we provide a brief example illustrating the text-to-graph transformation. Consider the sentence “Privacy constraints influence model optimization in federated learning”. Each content-bearing word or recognized named entity is treated as a node, such as privacy constraints, model optimization, and federated learning. Edges are established based on syntactic dependencies and semantic co-occurrence, for instance linking privacy constraints to model optimization due to the causal relation implied in the sentence. This representation preserves both local phrase-level structures and global semantic dependencies, facilitating downstream structural segmentation and alignment. The initial node embeddings are obtained through the following mapping:
where
denotes the raw feature vector of node
i.
is a standard multi-layer perceptron used to project raw features into the initial embedding space. The same MLP (Multi-Layer Perceptron) parameters are shared across all nodes and applied independently to each
, so Equation (
1) represents the per-node form of the mapping. In practice, all node features can be stacked into a matrix
and processed in parallel to obtain
.
After initialization, the model captures local topological information by applying multi-layer message passing. Node states are updated using the structural neighborhood. The propagation mechanism at the
l-th layer is defined as
Derivation of Equation (
2). Let
be the adjacency matrix of
and
be the degree matrix with
. Adding self-loops yields
and
. Define the symmetrically normalized propagation matrix
A graph convolution/message-passing layer then takes the matrix form
where
. Expanding the
i-th row gives
If self-loops are omitted, replacing
with
yields
which is Equation (
2). The symmetric factor
arises from
and stabilizes feature propagation across nodes with different degrees (bounded operator norm), preventing high-degree nodes from dominating the aggregation.
where
is the set of neighbors of node
i,
and
are their degrees,
is the learnable weight matrix at layer
l, and
is a nonlinear activation function.
After stacking multiple layers, the final node representation
is obtained, serving as the base of fine-grained structural encoding:
where
denotes the hidden state of node
i at the final GNN (Graph Neural Network) layer indexed by
L, serving as its learned representation. Here,
l in Equation (
4) is a generic layer index (
), while
L specifically denotes the total number of GNN layers, i.e., the index of the last layer whose output is used as the final embedding.
To encode graph-level semantics while capturing localized structural patterns, the constructed global interaction graph is further partitioned into multiple subgraphs through a structure-preserving clustering procedure. This partitioning enables the model to focus on semantically coherent regions within the global topology, enhancing representation granularity. Assume that the global graph
G is divided into subgraphs
. The representation of each subgraph is computed as
The
function in Equation (
5) serves the purpose of compressing node-level embeddings within a subgraph into a single, fixed-dimensional subgraph representation. This operation enables the model to capture high-level semantic information of the entire subgraph, which is crucial for subsequent multi-scale feature integration and task-specific prediction. Functionally,
acts as a permutation-invariant pooling operator that ensures the aggregated result is independent of the ordering of nodes.
From an algorithmic perspective, common implementations include mean pooling, sum pooling, or max pooling. For instance, in the case of mean pooling, the representation of subgraph
is computed as
where
is the number of nodes in subgraph
and
is the learned embedding of node
i from the final GNN layer. Such aggregation condenses the distributed node information into a compact vector that preserves the global semantics of the subgraph.
Based on these aggregated features, a multi-scale structure fusion module is constructed to integrate embeddings from different granularity levels. The fused representation is defined as
The fused representation is fed into a structure-aware refinement module. A shallow mapping
generates intermediate representations:
where
is the fused subgraph embedding after multi-scale integration, and
is a task-specific transformation function.
In the refinement stage, the output passes through multiple task-specific heads. Structural node embeddings are routed to task-specific branches to produce output embeddings:
where
is the prediction head for task
t, mapping the shared representation
to the corresponding output space.
Formulas (
6)–(
8) together describe the forward propagation process of a basic neural network applied to subgraph representations. Specifically, Equation (
6) serves as the input layer, where multi-scale subgraph embeddings
are integrated through learnable weights
and attention coefficients
. Equation (
7) acts as the hidden layer, transforming the fused embedding
into a task-shared representation
via a nonlinear mapping
. Finally, Equation (
8) represents the output layer, where the shared representation
is projected into the output space of task
t through the task-specific head
. This sequence illustrates how information flows from integrated subgraph features to task-specific predictions.
The final outputs are connected to the structural segmentation module. This builds a semantic bridge between structural partitioning and downstream tasks. It also provides a unified representation and structural discriminative basis for federated optimization. The model architecture diagram is shown in
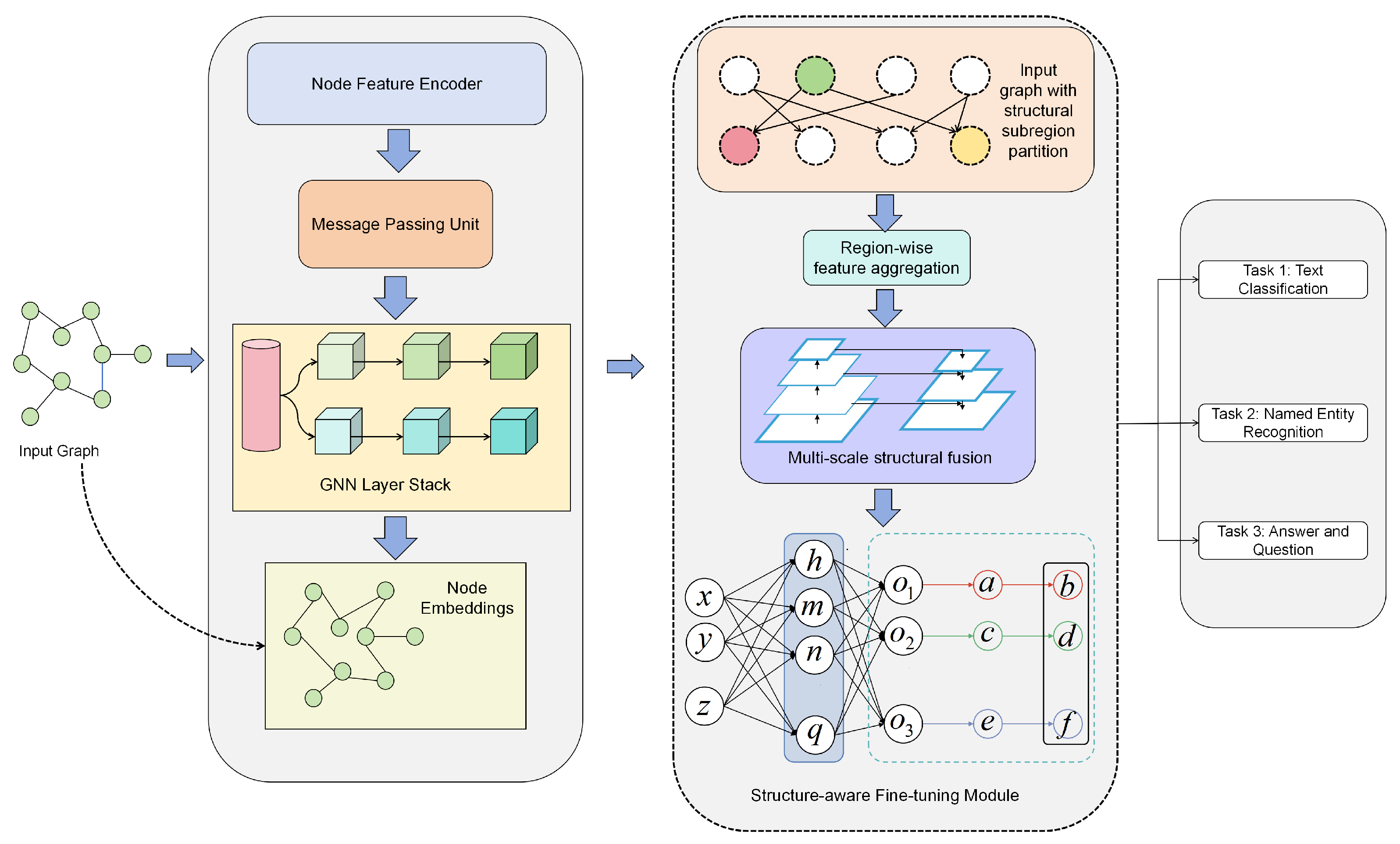
Figure 2. In the figure we can see, the left panel implements the Graph Representation Learning pipeline. The input client graph (green nodes with black edges) is first processed by a node feature encoder to obtain initial node states. A message passing unit aggregates neighborhood information, and a stacked GNN propagates multi-hop signals to produce node embeddings. The dashed feedback arrow indicates an optional refinement step in which the learned embeddings can adjust or regularize the input graph before the next round. The right panel corresponds to the Structural Segmentation Framework. The input graph is partitioned into structural subregions; features are aggregated region-wise and then fused across multiple scales to capture both local and global dependencies. The structure-aware fine-tuning module receives the fused representation and performs selective parameter updates on the large language model according to segment importance and sensitivity, while the remaining parts stay frozen to preserve general knowledge. Finally, the module outputs task-level representations (
), which are routed to task-specific parameter groups (a–f) and heads to serve downstream tasks (text classification, named entity recognition, sentiment analysis, and prompt completion). Solid arrows denote forward feature flow, whereas dashed arrows mark auxiliary or feedback links used for iterative refinement.
In this stage, each client constructs a semantic–structural graph from its local dataset, where nodes represent task-specific entities or feature tokens, and edges encode semantic correlations and structural dependencies. A graph neural network (GNN) backbone is then applied to capture high-order interactions, producing embeddings that preserve both semantic coherence and structural relationships. These embeddings are aggregated at the server to form a unified representation space that aligns cross-client semantics. The generated graph embeddings are subsequently leveraged in the structural segmentation process, enabling fine-grained adaptation across heterogeneous model components.
3.3. Structural Segmentation Framework
To enable adaptability of large language models to complex structural information and enhance local responsiveness, this paper proposes a structural segmentation enhancement mechanism. The model architecture diagram is shown in
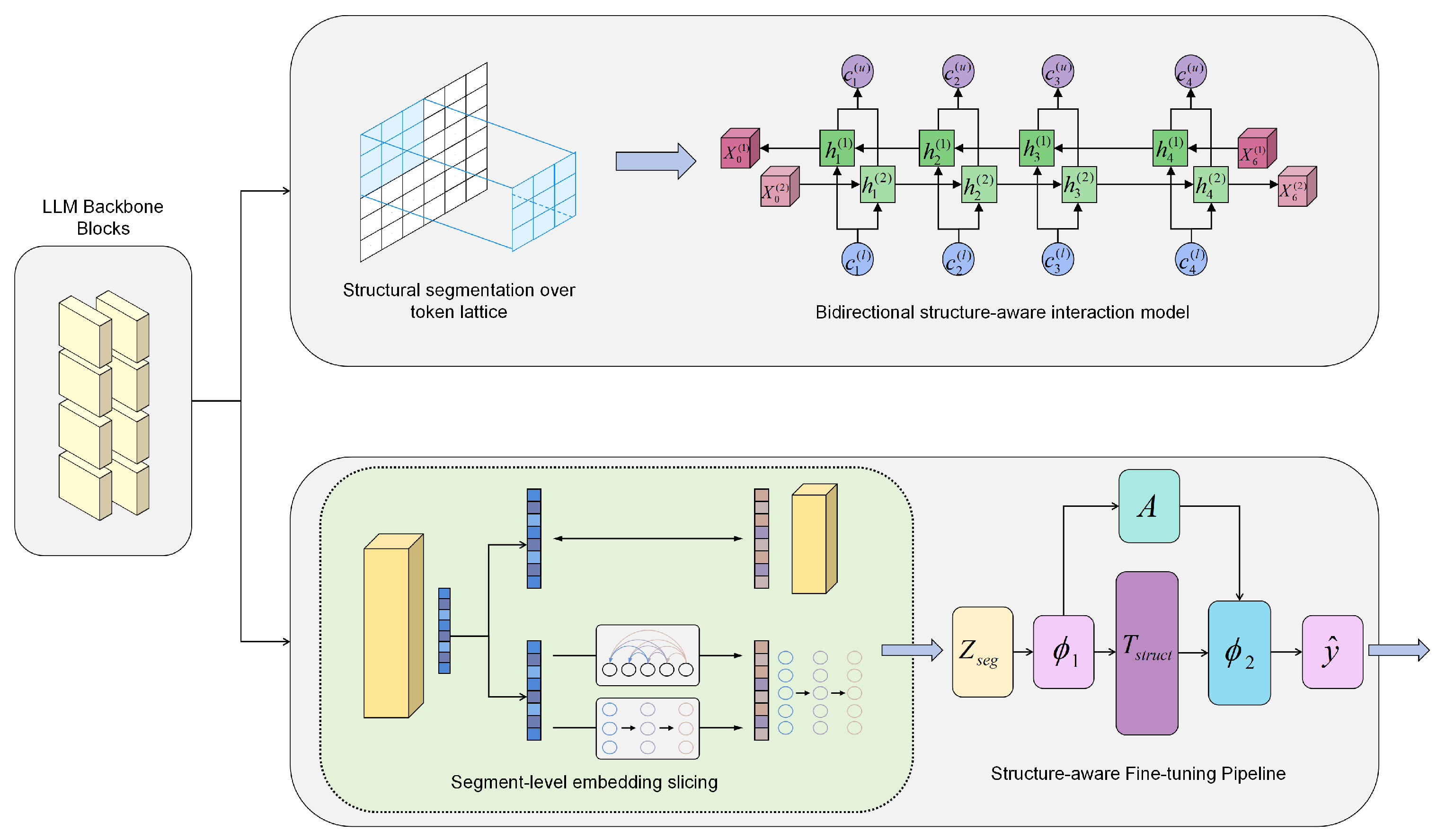
Figure 3. As can be seen from the figure, the upper pathway instantiates the Structural Segmentation Framework on top of the LLM backbone. Tokens are first organized into a lattice and then partitioned into structural segments. The bidirectional structure-aware interaction model updates hidden states along two complementary streams, enabling information to flow in both directions across adjacent segments. Contextual coefficients modulate each step so that segment interactions reflect local cues and long-range dependencies. The lower pathway performs segment-level embedding slicing. Layerwise token embeddings are grouped according to the segmentation map, refined within each segment, and aligned across neighboring segments. Bidirectional arrows indicate that the slicing and refinement steps can be iterated until stable segment representations are obtained. The result is a compact segment representation
that preserves structure while reducing redundancy. The structure-aware fine-tuning pipeline then applies selective updates. A lightweight controller
A configures two adapter-like parameter groups
and
. A structural transformation module
enforces consistency with the segmentation, guiding the update path toward structure-preserving changes. Only the selected parameters are unfrozen, while the rest of the backbone remains fixed to retain general knowledge. The head produces the final prediction
. Solid arrows denote the forward information flow between modules, and dashed boundaries indicate the scope of each functional block.
The output representations from the LLM backbone are partitioned into a set of structural segments
. Each segment corresponds to a subregion of consecutive tokens. Given a sequence of length
T, the segment boundary is defined by
. The segmentation operation is expressed as
where
denotes the token sequence belonging to the
k-th structural segment, bounded by start index
and end index
.
Each structural segment
is passed into a structure-aware encoder for bidirectional interactive modeling. This forms upward and downward structural paths denoted by
and
, respectively. The contextual information is propagated through forward and backward GRU (Gated Recurrent Unit) as follows:
where
processes the input sequence in the forward direction, updating hidden state
based on current token
and previous hidden state
.
where
processes the input sequence in the backward direction, updating hidden state
based on current token
and next hidden state
.
The two paths are concatenated to form the joint structural representation
, which is used for segment-level information integration and module-wise embedding enhancement:
where
denotes concatenation, producing a bi-directional representation of token
i.
Based on this structural modeling, a Segment-level Slicing mechanism is introduced. It selects structural feature regions from key blocks of the LLM backbone using a segment index set
, producing multi-scale embedding representations:
where
is the matrix of layerwise embeddings, and
is the index set specifying which embeddings belong to each segment.
The sliced representation is projected by a nonlinear mapping function
and then passed to the structure transformation module
for enhancement:
where
transforms the segment representation, and
enforces structural consistency based on the segmentation map.
To further improve the precision of local structural consistency modeling, an auxiliary structure-aware module
A is introduced and optimized in parallel with the main branch:
where
is a lightweight controller producing auxiliary parameters or adjustments from the segment embeddings.
The final representation is projected into the task-specific output space through
, generating the prediction
while preserving the granularity of structural segments:
where
maps the structure-aware representation to the final task prediction.
The structural segmentation path and the LLM backbone form a complementary interaction in the overall framework. This approach strengthens structural semantic granularity and provides a unified interface for multi-task structural transfer and personalized fine-tuning.
The structural segmentation framework decomposes the LLM into functional modules, such as attention layers, feed-forward blocks, and embedding layers, based on the semantic–structural cues provided by the graph embeddings. This decomposition allows selective fine-tuning of model segments according to client-specific resource constraints, data distributions, and privacy requirements. By aligning the segmentation strategy with the graph-derived semantic structure, the framework ensures that parameter updates are both computationally efficient and semantically consistent across clients.
3.5. Training Objectives
To jointly optimize the graph representation and structural segmentation modules, we design an end-to-end differentiable training objective. The goal is to preserve semantic consistency while improving generalization under multi-source tasks. Specifically, the total loss consists of three parts: alignment loss
, segmentation consistency loss
, and task-driven loss
. The total objective is defined as
where
denotes the overall optimization objective of the proposed framework. It is composed of three components:
encourages embedding consistency among structurally connected nodes in the graph,
measures the accuracy of the predicted structural segmentation against the ground truth, and
corresponds to the primary task-specific loss (e.g., cross-entropy for classification or mean squared error for regression). The non-negative coefficients
,
, and
control the relative contribution of each term, enabling a balance between structural preservation, segmentation quality, and downstream task performance. By jointly optimizing these components, the model aligns structural information with task objectives while maintaining robust segment-level representations.
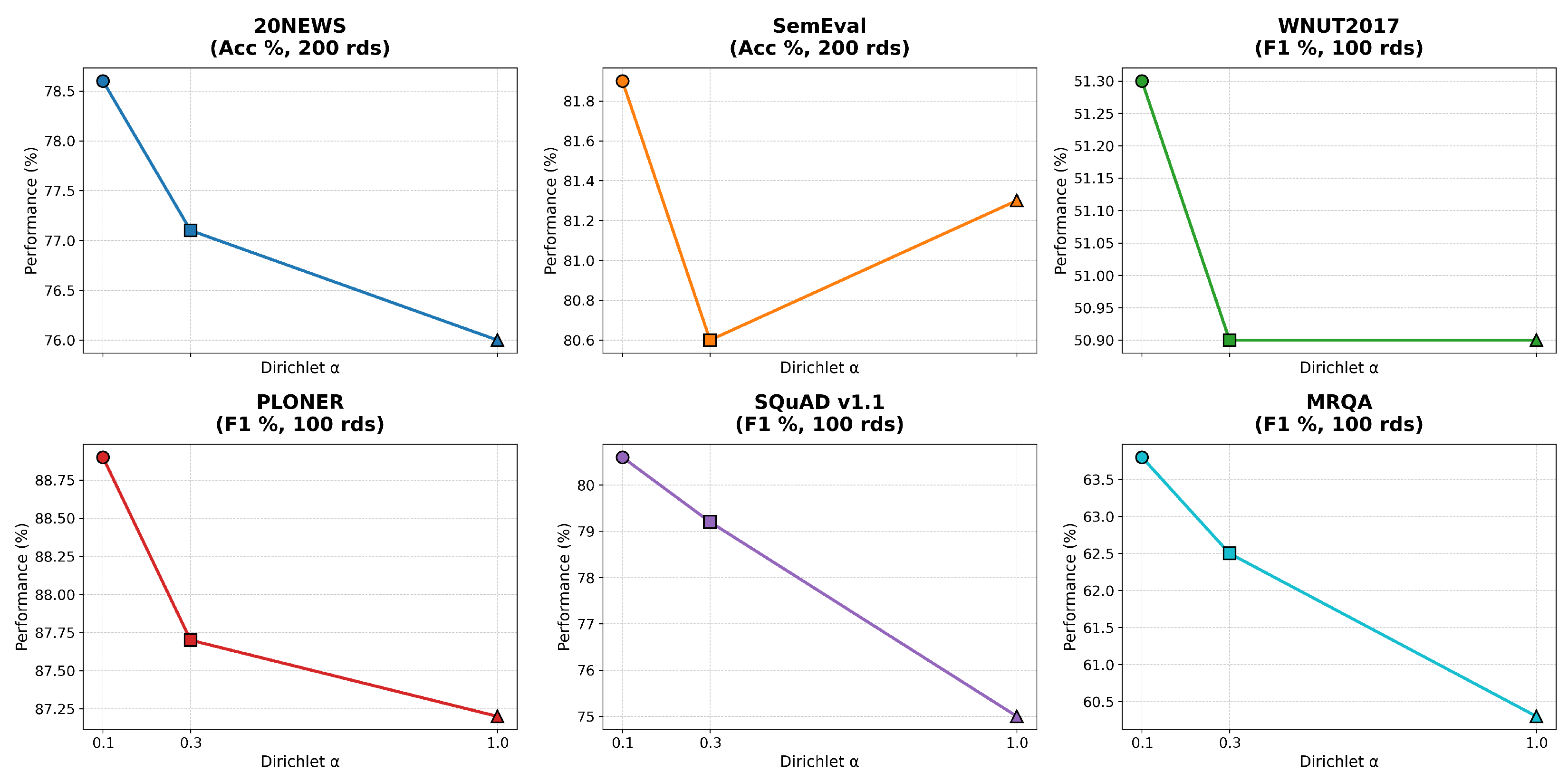
We treat as hyperparameters and determine them via a small grid search on the validation splits of 20NEWS and SEMEVAL (RoBERTa backbone), under the constraint . The search ranges are with the heuristic to prioritize the task-driven objective. The best configuration is then fixed and reused across all tasks and backbones. This choice reflects the roles of and as structural regularizers, while drives the primary optimization target. We also observed that moderate perturbations (±0.1) to any do not change the relative ranking of methods.
For graph representation learning, we introduce the structural alignment loss
to ensure consistency within the global graph space. Let
and
be two semantically adjacent nodes, with embeddings
and
. The loss is defined as
where
denotes the set of edges in the constructed client interaction graph, and
is the total number of such edges. For each connected pair of nodes
,
and
represent their respective learned embedding vectors. This term computes the mean squared
distance between connected node embeddings, encouraging semantically related or structurally linked clients to maintain similar representations. By minimizing this distance, the model aligns local feature spaces across clients, which promotes consistent structural semantics, reduces distributional shifts, and enhances the transferability and robustness of the learned graph representations in a federated environment.
For the structural segmentation module, we design a fine-grained consistency loss
. It constrains structural boundaries across layers for the same semantic unit. Let the input sequence be divided into
m structural fragments
, with representations
and decoder outputs
. The loss is defined as
where
m denotes the number of structural segments within the input sequence or graph,
represents the predicted embedding vector for the
k-th segment generated by the model, and
is the corresponding ground-truth segment embedding. This term measures the mean squared
distance between predicted and target segment embeddings, thereby assessing how accurately the model reconstructs the structural configuration in the semantic space. By minimizing this loss, the model learns to preserve fine-grained structural boundaries and semantic consistency across segments, which is particularly important when multi-scale information fusion might otherwise distort local representations. As a result,
plays a key role in maintaining representation fidelity and ensuring that the structural segmentation framework produces semantically coherent and structurally accurate embeddings.
Finally, different are instantiated per downstream task (e.g., cross-entropy for classification, token-level cross-entropy for NER, and span extraction losses for QA) to match task requirements.