A Novel Consensus Considering Endo-Confidence with Double-Hierarchy Hesitant Fuzzy Linguistic Term Set and Its Application
Abstract
1. Introduction
- (1)
- Objective expression of DMs’ confidence. Although prior studies have incorporated confidence into MAGDM consensus models—based on generalized fuzzy numbers [31], linguistic distribution evaluations, numerical information [21], and probabilistic linguistic term sets [28], most approaches rely on self-reported self-confidence, which lacks objectivity and is vulnerable to manipulation. While Li et al. [28] introduced endo-confidence (i.e., confidence derived from the evaluation information itself), their operationalization is limited to probabilistic linguistic circumstances. We extend this line by defining and extracting endo-confidence under DHHFLTS, leveraging the semantics of double-hierarchy modifiers and hesitation structure to obtain a confidence signal that is comparable across DMs.
- (2)
- Consensus threshold determination. In consensus processes, higher confidence should imply greater credibility of original evaluations, hence more opinions can be retained and fewer forced adjustments are warranted. Conversely, more confident DMs are typically less willing to revise their assessments, implying higher adjustment costs. Therefore, the consensus threshold should increase as experts’ confidence increases [32,33]. However, existing studies usually exogenously set the threshold (often provided by DMs themselves) and do not couple it with confidence levels. We develop a method under DHHFLTS to determine an endo-confidence-aware threshold that links the threshold to objectively extracted confidence, aligning with both accuracy and adjustment-cost considerations.
- (3)
- Feedback mechanism under DHHFLTS. Traditional feedback mechanisms often overlook DMs’ willingness to adjust while striving for higher consensus. Some works incorporate confidence via optimization models that implicitly assume self-confidence amplifies information loss between additive preference relations and individual vectors [15,18,19]. Yet when confidence is expressed linguistically, subscripts remain qualitative and cannot precisely reflect degrees, risking questionable modeling assumptions. Other studies employ identification/direction rules to decide who should adjust and how, based on peer or collective assessments [17,19,21,22]. More recent advances propose dual-strategy CRP in probabilistic linguistic MCGDM [34] and cost-sensitive two-stage dynamic consensus with subgroup strategies and incomplete preferences [35]. However, these models do not exploit the richer semantics of DHHFLTS. We propose a two-stage feedback mechanism tailored to DHHFLTS that (i) identifies adjustment targets using endo-confidence-weighted distances to the consensus set, and (ii) gives direction and magnitude suggestions that minimize information loss while respecting confidence-dependent willingness to adjust.
- (1)
- Endo-confidence extraction from DHHFLTS. We define a computation of endo-confidence directly from double-hierarchy hesitant linguistic information, capturing (i) the semantic precision of adverb–adjective modifiers and (ii) the degree of hesitation in the provided assessments. This yields an objective, comparable confidence signal for all DMs.
- (2)
- Confidence-coupled consensus control. We design a rule to determine the consensus threshold as a function of endo-confidence, so that higher-confidence evaluations are retained with fewer forced changes. Expert weights are determined jointly by endo-confidence and entropy, aligning credibility with informational richness.
- (3)
- Two-stage feedback mechanism under DHHFLTS. We propose an identification–direction scheme that (i) forms an adjustment set using confidence-weighted distances to the consensus region and establishes an adjustment order, and (ii) provides directional suggestions that minimize information loss while respecting confidence-dependent willingness to adjust.
- (4)
- Operator refinements for DHHFLTS calculus. We refine the transformation function and introduce a well-defined addition operator for DHLTs, improving the rationality and stability of computations involved in aggregation and feedback within the DHHFLTS framework.
2. The Double-Hierarchy Hesitant Fuzzy Linguistic Term Set
2.1. The Definition of Double-Hierarchy Hesitant Fuzzy Linguistic Term Set
2.2. The Improved Operators and the Comparative Method
- (1)
- If , there is .
- (2)
- If , there is .
- (3)
- If , there is .
- (1)
- If , then is superior to , that is .
- (2)
- Similarly, if , then is inferior to , that is .
- (3)
- If , then
- (a)
- If , then is inferior to , that is .
- (b)
- If , then is superior to , that is .
- (c)
- If , then is equivalent with , that is .
2.3. The Novel Method to Add the DHLTs and the Corresponding Distance Measurement
- (1)
- If there is only one term in , that is , we should add the number of DHLTs to .
- (2)
- If there is and is an integer multiple of , then we repeat each term in for times in order not to change the original evaluation and rank all the DHLTs according to the membership degree in non-descending order.
- (3)
- If there is and is not an integer multiple of , then we repeat each term in for times and add the number of DHLTs to , where is calculated by Equation (14). We rank all the DHLTs according to the membership degree in non-descending order and set in this paper.
- (1)
- If we use the method proposed in [39] to add the DHLTs, then we get , and the Hamming-Hausdorff distance between and are .
- (2)
- If we use the proposed method in this paper, then we can find that in this example, is an integer multiple of , and we need to repeat each term in for time. Then, we get , and the Hamming-Hausdorff distance between and are .
3. Consensus Decision-Making with Endo-Confidence Based on Double-Hierarchy Hesitant Fuzzy Linguistic Term Set
3.1. The Measurement of Endo-Confidence Level Based on Double-Hierarchy Hesitant Fuzzy Linguistic Term Set
- (1)
- The accuracy of the expert’s description of the evaluation information
- (2)
- The hesitance degree of experts in evaluation information
- (1)
- If there is , then it means that gives only one DHLT to evaluate the decision-making object. Then, is completely sure about the evaluation information and there is .
- (2)
- If there is , then it means that thinks that all terms in DHHFLTS can evaluate the decision-making object. Then, is completely uncertain about the evaluation information and there is .
- (3)
- In other cases, the endo-confidence level of is somewhere between the above two cases, and there is .
3.2. The Determination of Expert’s Weight with Endo-Confidence Level
3.2.1. The Weight Based on Endo-Confidence Level
- (1)
- The weight changes continuously with the increase (decrease) of endo-confidence and they have a positive correlation.
- (2)
- Experts with higher endo-confidence have a decisive role in the decision-making results. However, the experts with lower endo-confidence are often affected by others and change their evaluations, thus the impact on the final result is small.
3.2.2. The Weight Based on Entropy
3.3. How to Determine the Consensus Threshold Based on Endo-Confidence Level
3.4. The Feedback Mechanism for the DHHFLTS
- (1)
- If , then we need to reduce the value of the second hierarchy of the DHLT .
- (a)
- If the adjusted membership degree of the DHLT is not less than the expected value of the collective evaluation information, that is , then we take the DHLT as the adjusted one and further obtain the updated DHHFLE .
- (b)
- If the adjusted membership degree of the DHLT is smaller than the expected value of the collective evaluation information, that is , then we select the DHLT with the smallest distance from as the adjusted DHLT and further obtain the updated DHHFLE . If there are two DHLTs whose distance from are equal, in order to reduce the loss of original information, we choose the one which is closer to the original evaluation as the adjusted DHLT and further obtain the updated DHHFLE .
- (2)
- If , then we need to increase the value of the second hierarchy of the DHLT .
- (a)
- If the adjusted membership degree of the DHLT is not more than the expected value of the collective evaluation information, that is , then we take the DHLT as the adjusted one and further obtain the updated DHHFLE .
- (b)
- If the adjusted membership degree of the DHLT is bigger than the expected value of the collective evaluation information, that is , then we select the DHLT with the smallest distance from as the adjusted DHLT and further obtain the updated DHHFLE . Similarly, if there are two DHLTs whose distance from are equal, in order to reduce the loss of original information, we choose the one which is closer to the original evaluation as the adjusted DHLT and further obtain the updated DHHFLE .
- (3)
- If , then the DHLT should not be changed, and we should further modify other DHLTs in the DHHFLE .
- (1)
- If , then we need to reduce the value of the first hierarchy of the DHLT . In order to minimize the loss of evaluation and retain more original information, we modify the DHLT to and the following rules are provided:
- (a)
- If , then we take the DHLT as the adjusted one and further obtain the updated DHHFLE .
- (b)
- If the adjusted membership degree of the DHLT is smaller than the expected value of the collective evaluation information, that is , then we can obtain the DHLT with the smallest distance from and denote it as . If there are two DHLTs whose distance from are equal, then we choose the one which is closer to the original evaluation and denote it as . Then, we compare the distance between the DHLT in obtained in Stage 1 and the expected value of the collective evaluation information with the distance between and the DHLT , and select the smaller one as the adjusted DHLT. We can further obtain the updated DHHFLE .
- (2)
- If , then we need to increase the value of the first hierarchy of the DHLT . Then, we modify the DHLT to and the following rules are provided:
- (a)
- If , then we choose the DHLT as the adjusted one and further obtain the updated DHHFLE .
- (b)
- If , then we can obtain the DHLT with the smallest distance from and denote it as . If there are two DHLTs whose distance from are equal, then we choose the one which is closer to the original evaluation and denote it as . Then, we compare the distance between the DHLT in obtained in Stage 1 and the expected value of the collective evaluation information with the distance between and the DHLT , and select the smaller one as the adjusted DHLT. We can further obtain the updated DHHFLE .
- (3)
- If , then the DHLT does not change, and we should further modify other DHLTs in the DHHFLE .
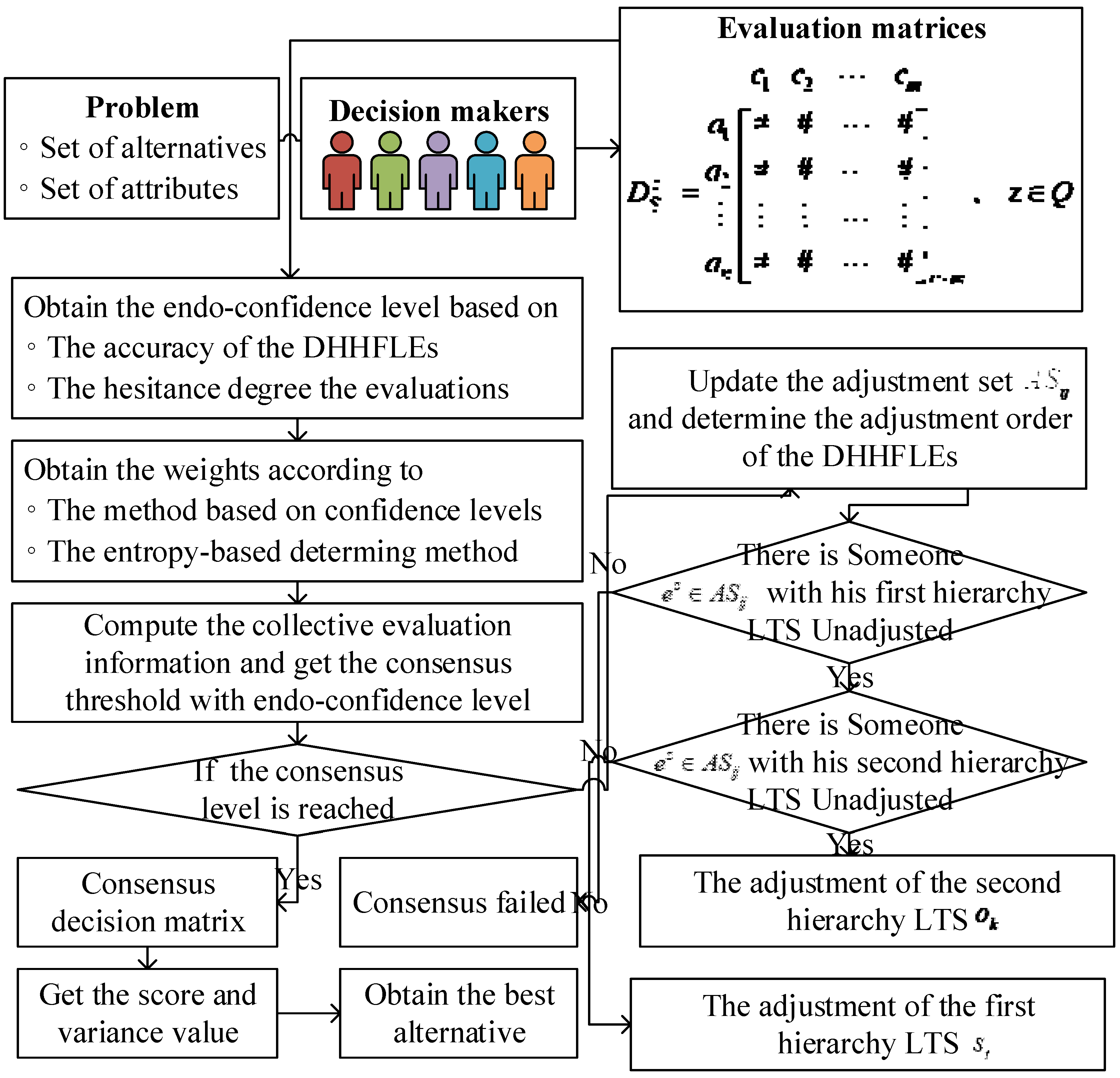
3.5. Selection Process
| Algorithm 1. Consensus decision-making process under DHHFLTS with endo-confidence |
| Input: , , , , , , and . |
| Output: The ranking results of the alternatives and the best choice. |
| Step 1. Get the endo-confidence level and respectively according to the accuracy of their description and the degree of hesitation. Then, we acquire the endo-confidence by Equation (19). |
| Step 2. Obtain the weight based on endo-confidence by Equations (20) and (21) and weight based on entropy by Equations (22)–(25). Then, we compute the weight of by Equation (26). |
| Step 3. Calculate the collective evaluation information and the collective distance by Equations (27) and (28) respectively. Then, we get the consensus threshold by Equations (29) and (30). If there is for , then go to Step 6 to get the best alternative; Otherwise, continue to the next step. The decision-making process should terminate if all experts in the adjustment set has adjusted the evaluation in Stage 2, but the consensus does not reach. |
| Step 4. Get the adjustment set according to the distance and further obtain the adjustment order of the DHHFLEs. Then, we use the two-stage adjustment mechanism to correct the evaluations, in other words, to obtain and . Notice that in both stages, the expert can only adjust his/her evaluation once. |
| Step 5. Go back to repeat Steps 2–3. |
| Step 6. When the consensus reaches, we obtain the overall information for by Equation (31), and get the best alternative by comparing their score values and variance values. |
| Step 7. End. |
- (1)
- Endo-confidence refresh. Endo-confidence levels are defined from the accuracy and hesitation of the DHHFLTS (Equations (16)–(19)). Whenever a DHHFLE is edited in the identification-direction rules, the corresponding are re-evaluated from the updated linguistic elements. Thus, confidence always reflects the current (not outdated) information state.
- (2)
- Expert weights reallocation. Expert weights are determined jointly by endo-confidence and entropy (see Equations (20)–(26)). After the refresh of , the expert-level weights are recomputed and normalized according to the same formulas, so that more reliable (higher-confidence) evaluations preserve influence, while less reliable ones are automatically down-weighted.
- (3)
- Consensus threshold stability. Although the consensus threshold is defined as a function of endo-confidence (Equation (30)), in the adjustment phase is fixed once it is initialized. This design ensures that the acceptance region remains stable during iterations, which is essential for guaranteeing convergence. Endo-confidence and weights are refreshed after each edit, but the threshold serves as a stationary benchmark rather than a moving target.
4. Illustrative Example
4.1. The Selection Process of Transportation with the Proposed Method
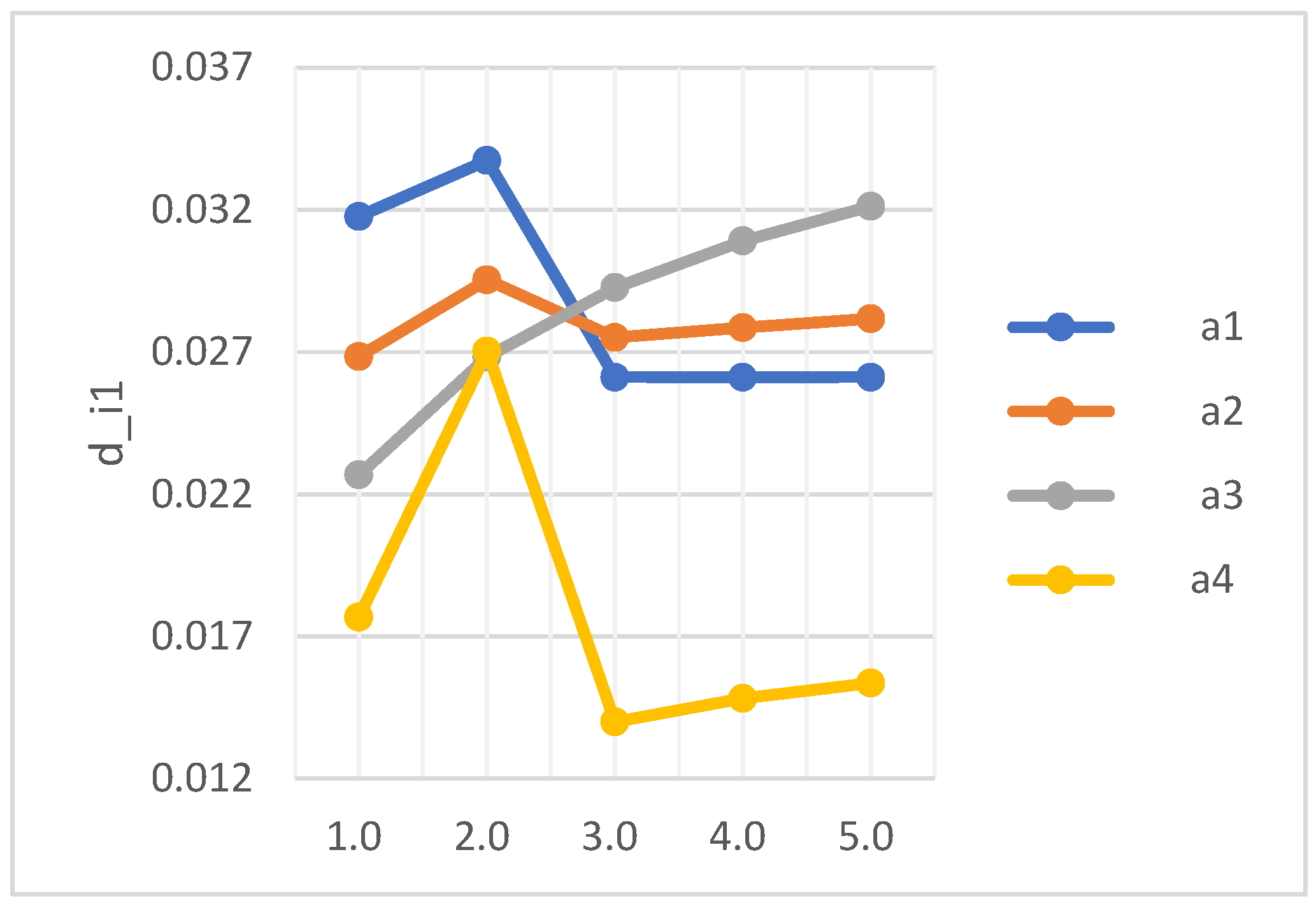
4.2. Sensitive Analysis
- (1)
- Analysis of the parameter
- (2)
- Analysis of the parameter
4.3. Comparative Analysis
5. Conclusions
5.1. Summary
5.2. Limitations and Future Work
- (1)
- Dependence on the linguistic–numeric mapping. The proposed framework relies on the transformation functions , (Equation (6)) that map double-hierarchy linguistic terms into a numerical scale. While this design ensures mathematical tractability and allows the use of distance measures (Equation (15)) and aggregation operators (Equations (9)–(11)), it also introduces sensitivity to the choice of linguistic granularity and scale calibration. In practice, experts from different cultural or organizational backgrounds may interpret the same double-hierarchy linguistic terms differently, potentially leading to inconsistencies. Future research could explore data-driven calibration or adaptive learning of the linguistic–numeric mapping to enhance robustness and cross-context applicability.
- (2)
- Simplifying assumptions in endo-confidence measurement. The endo-confidence level is quantified using two components: accuracy and hesitation (Equations (16)–(19)). This formulation is theoretically grounded and computationally efficient, yet it abstracts away other psychological or contextual factors that may influence confidence in real decision-making, such as social influence, risk preference, or time pressure. Moreover, the balance between accuracy and hesitation is fixed in this study, while in practice their relative importance may vary across domains. Extending the model to incorporate additional determinants of confidence, or to adaptively weight accuracy and hesitation, would improve realism and generalizability.
- (3)
- Scalability and computational aspects. Although the model performs well in small- and medium-sized group decision-making, large-scale MAGDM scenarios with hundreds of decision makers pose additional challenges. The iterative CRP requires repeated computation of distances (Equation (15)) and weight updates (Equations (20)–(23)), which can become computationally demanding as the group size increases. While clustering techniques can mitigate complexity, the current paper does not provide a systematic scalability analysis. Future work could investigate parallel computing strategies, approximate distance measures, or hierarchical consensus structures to ensure efficiency in very large-scale applications.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Demir, G.; Chatterjee, P.; Pamucar, D. Sensitivity analysis in multi-criteria decision making: A state-of-the-art research perspective using bibliometric analysis. Expert Syst. Appl. 2024, 237, 121660. [Google Scholar] [CrossRef]
- Qin, J.D.; Li, M.X.; Liang, Y.Y. Minimum cost consensus model for CRP-driven preference optimization analysis in large-scale group decision making using Louvain algorithm. Inf. Fusion 2022, 80, 121–136. [Google Scholar] [CrossRef]
- Gai, T.T.; Chiclana, F.; Jin, W.D.; Zhou, M.; Wu, J. A transformation method of non-cooperative to cooperative behavior by trust propagation in social network group decision making. IEEE Trans. Fuzzy Syst. 2025, 33, 2238–2250. [Google Scholar] [CrossRef]
- Wu, Q.; Liu, X.W.; Zhou, L.G.; Tao, Z.F.; Qin, J.D. A quantum framework for modeling interference effects in linguistic distribution multiple criteria group decision making. IEEE Trans. Syst. Man Cybern.-Syst. 2022, 52, 3492–3507. [Google Scholar] [CrossRef]
- Sun, X.L.; Zhu, J.J.; Wang, J.P.; Pérez-Gálvez, I.J.; Cabrerizo, F.J. Consensus-reaching process in multi-stage large-scale group decision-making based on social network analysis: Exploring the implication of herding behavior. Inf. Fusion 2024, 104, 102184. [Google Scholar] [CrossRef]
- Ji, Y.; Xu, Y.; Qu, S.J.; Xu, Z.S.; Wu, Z.; Nabe, M. A novel two-stage multi-criteria decision-making method based on interval-valued Pythagorean fuzzy aggregation operators with self-confidence levels. Arab. J. Sci. Eng. 2020, 46, 1561–1584. [Google Scholar] [CrossRef]
- Liu, X.; Xu, Y.J.; Ge, Y.; Zhang, W.K.; Herrera, F. A group decision making approach considering self-confidence behaviors and its application in environmental pollution emergency management. Int. J. Environ. Res. Public Health 2019, 16, 385. [Google Scholar] [CrossRef]
- Dong, Y.C.; Liu, W.Q.; Chiclana, F.; Kou, G.; Herrera-Viedma, E. Are incomplete and self-confident preference relations better in multicriteria decision making? A simulation-based investigation. Inf. Sci. 2019, 492, 40–57. [Google Scholar] [CrossRef]
- Zeng, S.Z.; Peng, X.M.; Baležentis, T.; Streimikiene, D. Prioritization of low-carbon suppliers based on Pythagorean fuzzy group decision making with self-confidence level. Econ. Res.-Ekon. Istraz. 2019, 32, 1073–1087. [Google Scholar] [CrossRef]
- Gou, X.; Xu, X.; Deng, F.; Zhou, W.; Herrera-Viedma, E. Medical health resources allocation evaluation in public health emergencies by an improved ORESTE method with linguistic preference orderings. Fuzzy Optim. Decis. Mak. 2024, 23, 1–27. [Google Scholar] [CrossRef]
- Fan, S.; Zhang, H.J.; Tang, H.L. A linguistic hierarchy model with self-confidence preference relations and its application in co-regulation of food safety in China. Int. J. Environ. Res. Public Health 2019, 16, 2918. [Google Scholar] [CrossRef] [PubMed]
- Liu, B.S.; Jiao, S.X.; Shen, Y.H.; Chen, Y.; Wu, G.B.; Chen, S. A dynamic hybrid trust network-based dual-path feedback consensus model for multi-attribute group decision-making in intuitionistic fuzzy environment. Inf. Fusion 2022, 80, 266–281. [Google Scholar] [CrossRef]
- Liu, W.Q.; Wu, Y.Z.; Chen, X.; Chiclana, F. Managing heterogeneous preferences and multiple consensus behaviors with self-confidence in large-scale group decision making. Inf. Fusion 2024, 107, 102289. [Google Scholar] [CrossRef]
- Ding, Z.G.; Chen, X.; Dong, Y.C.; Herrera, F. Consensus reaching in social network DeGroot model: The roles of the self-confidence and node degree. Inf. Sci. 2019, 486, 62–72. [Google Scholar] [CrossRef]
- Liu, X.; Xu, Y.J.; Montes, R.; Herrera, F. Social network group decision making: Managing self-confidence-based consensus model with the dynamic importance degree of experts and trust-based feedback mechanism. Inf. Sci. 2019, 505, 215–232. [Google Scholar] [CrossRef]
- Ding, R.X.; Yang, B.; Yang, G.R.; Li, M.N.; Wang, X.; Chiclana, F. A confidence and conflict-based consensus reaching process for large-scale group decision-making problems with intuitionistic fuzzy representations. IEEE Trans. Fuzzy Syst. 2024, 32, 3420–3432. [Google Scholar] [CrossRef]
- Liu, W.Q.; Zhang, H.J.; Chen, X.; Yu, S. Managing consensus and self-confidence in multiplicative preference relations in group decision making. Knowl.-Based Syst. 2018, 162, 62–73. [Google Scholar] [CrossRef]
- Zhang, H.J.; Li, C.C.; Liu, Y.T.; Dong, Y.C. Modeling personalized individual semantics and consensus in comparative linguistic expression preference relations with self-confidence: An optimization-based approach. IEEE Trans. Fuzzy Syst. 2021, 29, 627–640. [Google Scholar] [CrossRef]
- Gou, X.J.; Xu, Z.S.; Wang, X.X.; Liao, H.C. Managing consensus reaching process with self-confident double hierarchy linguistic preference relations in group decision making. Fuzzy Optim. Decis. Mak. 2021, 20, 51–79. [Google Scholar] [CrossRef]
- Han, Y.; Ji, Y.; Qu, S.J. ELICIT trust-driven robust consensus model in social network linguistic large-scale group decision-making. Expert Syst. Appl. 2025, 293, 129053. [Google Scholar] [CrossRef]
- Xu, X.H.; Du, Z.J.; Chen, X.H.; Cai, C.G. Confidence consensus-based model for large-scale group decision making: A novel approach to managing non-cooperative behaviors. Inf. Sci. 2019, 477, 410–427. [Google Scholar] [CrossRef]
- Liu, X.; Xu, Y.J.; Herrera, F. Consensus model for large-scale group decision making based on fuzzy preference relation with self-confidence: Detecting and managing overconfidence behaviors. Inf. Fusion 2019, 52, 245–256. [Google Scholar]
- Zou, W.C.; Wan, S.P.; Dong, J.Y. Trust evolution based minimum adjustment consensus framework with dynamic limited compromise behavior for probabilistic linguistic large scale group decision-making. Inf. Sci. 2024, 652, 119724. [Google Scholar]
- Tu, Y.; Song, J.J.; Xie, Y.T.; Zhou, X.Y.; Lev, B. Facilitating large-scale group decision-making in social networks: A bi-level consensus model with social influence. Inf. Fusion 2024, 105, 102258. [Google Scholar] [CrossRef]
- Tan, X.; Zhu, J.J.; Palomares, I.; Liu, X. On consensus reaching process based on social network analysis in uncertain linguistic group decision making: Exploring limited trust propagation and preference modification attitudes. Inf. Fusion 2022, 78, 180–198. [Google Scholar] [CrossRef]
- Gou, X.J.; Liao, H.C.; Xu, Z.S.; Herrera, F. Double hierarchy hesitant fuzzy linguistic term set and MULTIMOORA method: A case of study to evaluate the implementation status of haze controlling measures. Inf. Fusion 2017, 38, 22–34. [Google Scholar] [CrossRef]
- Gou, X.; Xu, Z.; Liao, H.; Herrera, F. Probabilistic double hierarchy linguistic term set and its use in designing an improved VIKOR method: The application in smart healthcare. J. Oper. Res. Soc. 2021, 72, 2611–2630. [Google Scholar] [CrossRef]
- Li, W.Q.; Li, L.H.; Xu, Z.S.; Tian, X.L. Large-scale consensus with endo-confidence under probabilistic linguistic circumstance and its application. Econ. Res.-Ekon. Istraz. 2022, 35, 2039–2072. [Google Scholar]
- Tian, X.; Li, W.; Xu, Z.; Kou, G.; Nie, C. An endo-confidence-based consensus with hierarchical clustering and automatic feedback in multi-attribute large-scale group decision-making. Inf. Sci. 2022, 608, 1702–1730. [Google Scholar]
- Tian, X.; Li, W.; Li, L.; Kou, G.; Ye, C. A consensus model under framework of prospect theory with acceptable adjustment and endo-confidence. Inf. Fusion 2023, 97, 101808. [Google Scholar] [CrossRef]
- Guha, D.; Chakraborty, D. Fuzzy multi attribute group decision making method to achieve consensus under the consideration of degrees of confidence of experts’ opinions. Comput. Ind. Eng. 2011, 60, 493–504. [Google Scholar] [CrossRef]
- Hinsz, V.B. Cognitive and consensus processes in group recognition memory performance. J. Personal. Soc. Psychol. 1990, 59, 705–718. [Google Scholar]
- Wan, S.P.; Yan, J.; Dong, J.Y. Personalized individual semantics based consensus reaching process for large-scale group decision making with probabilistic linguistic preference relations and application to COVID-19 surveillance. Expert Syst. Appl. 2022, 191, 116328. [Google Scholar] [CrossRef]
- Wan, S.P.; Zou, W.C.; Dong, J.Y.; Gao, Y. Dual strategies consensus reaching process for ranking consensus based probabilistic linguistic multi-criteria group decision-making method. Expert Syst. Appl. 2025, 262, 125342. [Google Scholar] [CrossRef]
- Zhan, J.X.; Cai, M.J. A cost-minimized two-stage three-way dynamic consensus mechanism for social network-large scale group decision-making: Utilizing K-nearest neighbors for incomplete fuzzy preference relations. Expert Syst. Appl. 2025, 263, 125705. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its applications to approximate reasoning—I. Inf. Sci. 1975, 8, 199–249. [Google Scholar] [CrossRef]
- Xia, M.M.; Xu, Z.S. Hesitant fuzzy information aggregation in decision making. Int. J. Approx. Reason. 2011, 52, 395–407. [Google Scholar] [CrossRef]
- Gou, X.J.; Xu, Z.S. Double hierarchy linguistic term set and its extensions: The state-of-the-art survey. Int. J. Intell. Syst. 2021, 36, 832–865. [Google Scholar] [CrossRef]
- Gou, X.J.; Xu, Z.S.; Liao, H.C.; Herrera, F. Multiple criteria decision making based on distance and similarity measures under double hierarchy hesitant fuzzy linguistic environment. Comput. Ind. Eng. 2018, 126, 516–530. [Google Scholar] [CrossRef]
- Pastore, R.E.; Scheirer, C.J. Signal detection theory: Considerations for general application. Psychol. Bull. 1974, 81, 945. [Google Scholar] [CrossRef]
- Koriat, A. The self-consistency model of subjective confidence. Psychol. Rev. 2012, 119, 80. [Google Scholar] [CrossRef] [PubMed]
- Herrera, F.; Martínez, L. A 2-tuple fuzzy linguistic representation model for computing with words. IEEE Trans. Fuzzy Syst. 2002, 8, 746–752. [Google Scholar]
- Wan, S.P.; Wu, H.; Dong, J.Y. An integrated method for complex heterogeneous multi-attribute group decision-making and application to photovoltaic power station site selection. Expert Syst. Appl. 2024, 242, 122456. [Google Scholar]
- Moslem, S. A novel parsimonious spherical fuzzy analytic hierarchy process for sustainable urban transport solutions. Eng. Appl. Artif. Intell. 2024, 128, 107447. [Google Scholar]
- Yue, C.; Huang, R.; Towey, D.; Xian, Z.; Wu, G. An entropy-based group decision-making approach for software quality evaluation. Expert Syst. Appl. 2024, 238, 121979. [Google Scholar]
- Akram, Z.; Ahmad, U.; Alcantud, J.C.R. Multi-criteria decision-making for the selection of best airport ground access mode with a new fuzzy rough-entropy based method. Eng. Appl. Artif. Intell. 2024, 135, 108843. [Google Scholar]
- Khan, M.J.; Ding, W.; Jiang, S.; Akram, M. Group decision making using circular intuitionistic fuzzy preference relations. Expert Syst. Appl. 2025, 270, 126502. [Google Scholar] [CrossRef]
- Gou, X.J.; Xu, Z.S.; Herrera, F. Consensus reaching process for large-scale group decision making with double hierarchy hesitant fuzzy linguistic preference relations. Knowl.-Based Syst. 2018, 157, 20–33. [Google Scholar]
- Gou, X.J.; Liao, H.C.; Xu, Z.S.; Min, R.; Herrera, F. Group decision making with double hierarchy hesitant fuzzy linguistic preference relations: Consistency based measures, index and repairing algorithms and decision model. Inf. Sci. 2019, 489, 93–112. [Google Scholar] [CrossRef]
- Wang, H.; Liao, H.C.; Huang, B.; Xu, Z.S. Determining consensus thresholds for group decision making with preference relations. J. Oper. Res. Soc. 2020, 72, 2290–2300. [Google Scholar] [CrossRef]
- Wang, H.; Yu, D.J.; Xu, Z.S. A novel process to determine consensus thresholds and its application in probabilistic linguistic group decision-making. Expert Syst. Appl. 2021, 168, 114315. [Google Scholar] [CrossRef]
- Fan, S.; Liang, H.; Li, C.C.; Chiclana, F.; Pedrycz, W.; Dong, Y.C. Optimal resources allocation to support the consensus reaching in group decision making. Inf. Fusion 2024, 110, 102451. [Google Scholar] [CrossRef]
- Tian, Z.P.; Xu, F.X.; Nie, R.X.; Wang, X.K.; Wang, J.Q. An adaptive consensus model for multi-criteria sorting under linguistic distribution group decision making considering decision-makers’ attitudes. Inf. Fusion 2024, 108, 102406. [Google Scholar]
- Schönherr, S.; Pikkemaat, B. Young peoples’ environmentally sustainable tourism attitude and responsible behavioral intention. Tour. Rev. 2024, 79, 939–952. [Google Scholar]
- Kim, M.J.; Hall, C.M.; Chung, N.; Kim, M.; Sohn, K. What makes tourists use public transport? Value-belief-norm theory, environmental, social, and governance factors, and the sustainable development goals. J. Travel Res. 2024, 63, 1426–1441. [Google Scholar]
- Zhang, B.W.; Liang, H.M.; Zhang, G.Q. Reaching a consensus with minimum adjustment in MAGDM with hesitant fuzzy linguistic term sets. Inf. Fusion 2018, 42, 12–23. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, H.; Tian, X.; Liu, L.; Li, W. A Novel Consensus Considering Endo-Confidence with Double-Hierarchy Hesitant Fuzzy Linguistic Term Set and Its Application. Mathematics 2025, 13, 3200. https://doi.org/10.3390/math13193200
Xu H, Tian X, Liu L, Li W. A Novel Consensus Considering Endo-Confidence with Double-Hierarchy Hesitant Fuzzy Linguistic Term Set and Its Application. Mathematics. 2025; 13(19):3200. https://doi.org/10.3390/math13193200
Chicago/Turabian StyleXu, Honghai, Xiaoli Tian, Li Liu, and Wanqing Li. 2025. "A Novel Consensus Considering Endo-Confidence with Double-Hierarchy Hesitant Fuzzy Linguistic Term Set and Its Application" Mathematics 13, no. 19: 3200. https://doi.org/10.3390/math13193200
APA StyleXu, H., Tian, X., Liu, L., & Li, W. (2025). A Novel Consensus Considering Endo-Confidence with Double-Hierarchy Hesitant Fuzzy Linguistic Term Set and Its Application. Mathematics, 13(19), 3200. https://doi.org/10.3390/math13193200





