Nyström-Based 2D DOA Estimation for URA: Bridging Performance–Complexity Trade-Offs

Abstract

To address the computational efficiency challenges in two-dimensional (2D) direction-of-arrival (DOA) estimation, a two-stage framework integrating the Nyström approximation with subspace decomposition techniques is proposed in this paper. The methodology strategically integrates the Nyström approximation with subspace decomposition techniques to bridge the critical performance–complexity trade-off inherent in high-resolution parameter estimation scenarios. In the first stage, the Nyström method is applied to approximate the signal subspace while simultaneously enabling construction of a reduced rank covariance matrix, which effectively reduces the computational complexity compared with eigenvalue decomposition (EVD) or singular value decomposition (SVD). This innovative approach efficiently derives two distinct signal subspaces that closely approximate those obtained from the full-dimensional covariance matrix but at substantially reduced computational cost. The second stage employs a sophisticated subspace-based estimation technique that leverages the principal singular vectors associated with these approximated subspaces. This process incorporates an iterative refinement mechanism to accurately resolve the paired azimuth and elevation angles comprising the 2D DOA solution. With the use of the Nyström approximation and reduced rank framework, the entire DOA estimation process completely circumvents traditional EVD/SVD operations. This elimination constitutes the core mechanism enabling substantial computational savings without compromising estimation accuracy. Comprehensive numerical simulations rigorously demonstrate that the proposed framework maintains performance competitive with conventional high-complexity estimators while achieving significant complexity reduction. The evaluation benchmarks the method against multiple state-of-the-art DOA estimation techniques across diverse operational scenarios, confirming both its efficacy and robustness under varying signal conditions.

1. Introduction

A two-dimensional (2D) direction-of-arrival (DOA) estimation of a uniform rectangular array (URA) is a technique employed in signal processing to localize signals in space. In general, DOA estimation techniques are used to find the DOA of a signal from a specific angle or direction. It also arises in various applications such as radar, sonar, and mobile communications [1,2,3,4]. The URA is a type of antenna array that consists of multiple rows and columns of sensor elements. The URA-based DOA estimation methods are generally used when the signal in question is arriving from a 2D plane. And the signals may have multiple angles or directions that need to be located and identified. Using a URA, signals from different directions can be separated and processed individually, providing accurate localization information.

Traditional subspace-based methods, such as Multiple Signal Classification (MUSIC) [5] and Estimation of Signal Parameters via Rotational Invariance Techniques (ESPRIT) [6], form the cornerstone of DOA estimation. For instance, the MUSIC algorithm estimates the 2D DOA from a URA by exploiting the noise subspace derived from the received data covariance matrix [7]. However, a significant drawback of 2D MUSIC is its reliance on an exhaustive 2D spectral search, which incurs prohibitively high computational complexity, especially for high-resolution estimation or large arrays. In order to reduce the computational burden, search-free methods, such as 2D ESPRIT [8], and approaches leveraging the Matrix Pencil (MP) method [9,10], have been developed to circumvent the need for grid searches. While these methods offer substantial complexity reductions, they can introduce other challenges; for example, the technique in [10] requires an additional pairing step due to the separate estimation of the two spatial parameters. Furthermore, a critical limitation of many proposed high-resolution methods, including those mentioned, is their dependence on a relatively large number of statistically independent snapshots to accurately estimate the data covariance matrix. Achieving computational efficiency and robustness under snapshot scarcity is paramount for practical direction-finding systems deployed in real-world scenarios. Some physical constraints, such as rapidly time-varying channels in mobile communications or sonar applications, will often severely restrict the number of available snapshots. And this challenge is particularly acute in applications like automotive radar, where the ability to resolve multiple sources from a single snapshot is essential. Consequently, some significant research efforts have been developed to deal with algorithms capable of operating effectively with very limited data, including compressed sensing techniques [11,12] and specialized methods explicitly designed for the demanding single snapshot scenario [13,14,15].

To tackle the computational complexity and performance constraints, researchers have proposed diverse solutions in recent URA 2D DOA estimation studies. The problem has been effectively linked to compressive sensing through trilinear modeling [16], where a proposed algorithm achieves superior angle estimation performance compared to ESPRIT while eliminating spectral peak searching and maintaining low computational complexity. Similarly, an efficient orthogonal matching pursuit (OMP)-based method [17] reduces computational burden by strategically pruning the complete dictionary’s atom count. Beyond standard array configurations, significant work addressing practical imperfections is developed in [18], where a low-complexity joint 2D DOA estimation and self-calibration framework for URA is proposed, with gain-phase errors by modeling the array as a Kronecker product of two ULAs. This approach reconstructs the destroyed rotational invariance factor using well-calibrated auxiliary elements and constrained optimization. For coherent sources, novel PARAFAC techniques are applied to electromagnetic vector sensor (EMVS) arrays with URA geometry [19]; these methods overcome source matrix rank deficiency through data rearrangement, preserving all available measurements without resorting to smoothing-based dimension reduction. Concurrently, deep neural networks (DNNs) have emerged as promising alternatives for DOA estimation, demonstrating considerable potential in handling complex scenarios [20]. However, these data-driven approaches often incur substantially higher computational complexity during both training and inference compared to classical algorithmic methods, presenting a significant trade-off between adaptability and real-time efficiency. To challenge the computation complexity problem, we recently developed a novel method that combines the Nyström approximation with a unitary transformation approach, which significantly reduced the computational burden while maintaining estimation accuracy [21].

In this paper, a computationally efficient approach for 2D DOA estimation of signals impinging on a URA under the challenging single snapshot scenario is proposed. The proposed method leverages the Nyström approximation technique [22,23] to address the inherent complexity limitations of traditional high-resolution estimators:

(1) The Nyström method is first applied to the single snapshot of received data to approximate the subspace of the signal, which reduces the computational complexity compared with eigenvalue decomposition (EVD) or singular value decomposition (SVD) in obtaining the covariance matrix required for subspace decomposition.

(2) Building upon this approximated subspace, the 2D DOA parameters are then estimated through a novel process that exploits the principal singular vectors inherent to the subspace structure.

(3) The estimation framework inherently preserves the geometric relationship between the two spatial dimensions, ensuring that the azimuth and elevation parameters are automatically paired during the estimation process, which reduces the complexity again with high estimation accuracy.

The rest of this paper is organized as follows. In Section 2, the array signal model is introduced. The Nyström approximation method and singular value decomposition are applied to obtain the signal subspace, which is used by a method utilizing the principal singular vectors to obtain the 2D DOA estimation in Section 3. Computer simulations are performed in Section 4 to check the performance of the proposed method and its comparison with some existing algorithms. The conclusion is drawn in Section 5.

Notation

In this paper, the boldface lowercase letters denote vectors and boldface uppercase letters denote matrices. Superscripts such as ${\left(\right)}^T$, ${\left(\right)}^{*}$, ${\left(\right)}^H$, ${\left(\right)}^{†}$, and ${\left(\right)}^{-1}$ represent transpose, complex conjugate, Hermitian transpose, pseudo inverse, and matrix inverse, respectively. $\mathbb{E}$ denotes the expectation operator and is the diagonal matrix operator. The $\widehat{a}$ denotes an estimate of a. ${\mathbf{I}}_m$ is the $m\times m$ identity matrix, and $\mathbb{C}$ denotes the set of complex numbers.

2. Signal Model

We consider a URA with $M\times N$ omnidirectional antennas with interelement spacing d. Assume there are P far-field narrowband signal sources impinging on the URA from the directions $({\varphi }_p,{\theta }_p)$, with $p=1,2,\cdots ,P$. We set the first sensor as the reference sensor. Then the single snapshot received signal of the sensor at $(m,n)$ is defined as

$$\begin{array}{cc}\hfill x_{m,n}=& s_{m,n}+q_{m,n}\hfill \\ \hfill =& \sum _{p=1}^P{s}_p{e}^{-j\frac{2\pi }{\lambda }(m-1)dsin{\varphi }_{p}cos{\theta }_p}{e}^{-j\frac{2\pi }{\lambda }(n-1)dsin{\varphi }_{p}sin{\theta }_p}\hfill \\ \hfill & +q_{m,n},\hfill \end{array}$$

(1)

where $s_p$ is the wavefront of the pth signal, $\lambda$ is the wavelength of the impinging wavefront, and $q_{m,n}$ is the noise, which is white Gaussian; the noise power is assumed to be ${\sigma }^2$. Then the task of the 2D DOA estimation problem is to estimate the DOA, which is $({\varphi }_p,{\theta }_p)$, from the received signals.

3. Algorithm Development

In order to analyze the signal, we first express the signal in (1) into a matrix form as

$$\mathbf{X}=\mathbf{S}+\mathbf{Q},$$

(2)

where the matrices come from the elements of the signal and the noise, ${\left[\mathbf{X}\right]}_{m,n}=x_{m,n}$, ${\left[\mathbf{S}\right]}_{m,n}=s_{m,n}$, and ${\left[\mathbf{Q}\right]}_{m,n}=q_{m,n}$

After receiving the signal $\mathbf{X}$, the traditional method usually computes the covariance matrix with multiple snapshots, but here, we are considering single snapshot signals; we do not have enough snapshots to denoise the signal by computing the covariance matrix. On the other hand, the signal matrix can be factorized as

$$\mathbf{S}=\mathbf{G}\mathbf{\Sigma }\mathbf{H},$$

(3)

where

$$\mathbf{G}=[{\mathbf{g}}_1{\mathbf{g}}_2\cdots {\mathbf{g}}_P],$$

(4)

$$\mathbf{\Sigma }=\mathrm{diag}\left([s_1{s}_2\cdots s_P]\right),$$

(5)

$$\mathbf{G}=[{\mathbf{h}}_1{\mathbf{h}}_2\cdots {\mathbf{h}}_P],$$

(6)

$${\mathbf{g}}_p={[{\mu }_P{\mu }_P^2\cdots {\mu }_P^M]}^T,$$

(7)

$${\mathbf{h}}_P={[{\nu }_P{\nu }_P^2\cdots {\nu }_P^N]}^T,$$

(8)

where ${\mu }_p={\displaystyle \frac{2\pi }{\lambda }}dsin{\varphi }_{p}cos{\theta }_p$, ${\nu }_p={\displaystyle \frac{2\pi }{\lambda }}dsin{\varphi }_{p}sin{\theta }_p$. ${(·)}^T$ is the transpose operator. We see that the elements in ${\mathbf{g}}_P$ and ${\mathbf{h}}_P$ have linear prediction (LP) relations.

3.1. Nyström Approximation Method

We apply the Nyström method to approximate the signal subspace. In the Nyström method, the signal matrix $\mathbf{X}={\left[{\mathbf{x}}_1,{\mathbf{x}}_2,\cdots ,{\mathbf{x}}_M\right]}^T$ is first decomposed into two parts [23]:

$${\mathbf{X}}_{new}=\left[\begin{array}{c}{\mathbf{X}}_1\\ {\mathbf{X}}_2\end{array}\right],$$

(9)

where ${\mathbf{X}}_1$ is the first K rows and ${\mathbf{X}}_2$ is the remaining $(M-K)$ elements of $\mathbf{X}$, respectively.

$$\begin{array}{ccc}\hfill {\mathbf{X}}_1& =& \mathbf{X}(1:K,:),\hfill \end{array}$$

(10)

$$\begin{array}{ccc}\hfill {\mathbf{X}}_2& =& \mathbf{X}(K+1:M,:).\hfill \end{array}$$

(11)

${\mathbf{x}}_1,{\mathbf{x}}_2,\cdots ,{\mathbf{x}}_M$ are the row vectors of $\mathbf{X}$. Here K is a user-defined parameter satisfying $K\in (1,2,\cdots ,M)$. We then use ${\mathbf{X}}_1$ and ${\mathbf{X}}_2$ to compute the covariance matrices as follows:

$${\mathbf{R}}_{11}=\mathbb{E}\left[{\mathbf{X}}_1{\mathbf{X}}_1^H\right],$$

(12)

$${\mathbf{R}}_{21}=\mathbb{E}\left[{\mathbf{X}}_2{\mathbf{X}}_1^H\right].$$

(13)

In real-world scenarios, signals are often contaminated with noise, making it difficult to obtain the correlation matrices described above directly. As a result, an approximation approach is commonly utilized, which is

$${\mathbf{R}}_{11}={\displaystyle \frac{1}{N}}\left[{\mathbf{X}}_1{\mathbf{X}}_1^H\right],$$

(14)

$${\mathbf{R}}_{21}={\displaystyle \frac{1}{N}}\left[{\mathbf{X}}_2{\mathbf{X}}_1^H\right].$$

(15)

Typically, the matrix ${\mathbf{R}}_{11}$ needs to have full rank before proceeding with data processing. To achieve this, we set K to be larger than P but less than $minM,N$, i.e., $P<K\le min\{M,N\}$. Through simulations, we have confirmed that the value of K does not need to increase with an increase in the number of array sensors, M. Instead, a specific value of K is sufficient for accurate DOA estimation while decreasing computational complexity.

To obtain the signal subspace, we can utilize eigenvalue decomposition (EVD) on ${\mathbf{R}}_{11}$ and ${\mathbf{R}}_{21}$  [24]:

$${\mathbf{R}}_{11}={\mathbf{U}}_{11}{\mathsf{\Lambda }}_{11}{\mathbf{U}}_{11}^H,$$

(16)

where ${\mathbf{U}}_{11}\in {\mathbb{C}}^{K\times K}$ is the singular vector matrix and ${\mathsf{\Lambda }}_{11}\in {\mathbb{C}}^{K\times K}$ is the corresponding eigenvalue matrix. And let ${\mathbf{U}}_{21}={\mathbf{R}}_{21}{\mathbf{U}}_{11}{\mathsf{\Lambda }}_{11}^{-1}$. Then the relationship of ${\mathbf{R}}_{21}$, ${\mathbf{U}}_{11}$, and ${\mathsf{\Lambda }}_{11}$ is obtained with the use of (16):

$${\mathbf{R}}_{21}{\mathbf{U}}_{11}={\mathbf{U}}_{21}{\mathsf{\Lambda }}_{11}.$$

(17)

We then construct a new matrix with ${\mathbf{U}}_{11}$ and ${\mathbf{U}}_{21}$:

$$\mathbf{U}=\left[\begin{array}{c}{\mathbf{U}}_{11}\\ {\mathbf{U}}_{21}\end{array}\right].$$

(18)

With (17), we rewrite (18) as

$$\mathbf{U}=\left[\begin{array}{c}{\mathbf{U}}_{11}\\ {\mathbf{R}}_{21}{\mathbf{U}}_{11}{\mathsf{\Lambda }}_{11}^{-1}\end{array}\right].$$

(19)

On the other hand, to orthogonalize $\mathbf{U}$, we assume a matrix $\mathbf{D}$, which is computed from

$$\mathbf{D}=\mathbf{U}{\mathsf{\Lambda }}_{11}^{\frac{1}{2}},$$

(20)

and another matrix $\mathbf{W}$:

$$\mathbf{W}={\mathbf{D}}^H\mathbf{D}.$$

(21)

If we use EVD to decompose $\mathbf{W}$, then

$$\mathbf{W}={\mathbf{U}}_D{\mathsf{\Lambda }}_D{\mathbf{U}}_D^H,$$

(22)

where ${\mathsf{\Lambda }}_D=\mathrm{diag}\left[{\lambda }_{D1},{\lambda }_{D2},\cdots ,{\lambda }_{DK}\right]$ is the eigenvalue matrix with ${\lambda }_{D1}\le {\lambda }_{D2}\le \cdots \le {\lambda }_{DK}$, and ${\mathbf{U}}_D$ comes from the corresponding eigenvector matrix ${\mathbf{U}}_D=[{\mathbf{u}}_{D1},{\mathbf{u}}_{D2},\cdots ,{\mathbf{u}}_{DK}]$. Its elements ${\mathbf{u}}_{Di}(i=1,2,\cdots ,K)$ are the ith eigenvector. As the signal number is known to be P, we use the first P column vectors of matrix $\mathbf{Y}$ to construct the subspace of the signal, $\mathbf{Y}=\mathbf{D}{\mathbf{U}}_D$ [23], and since

$$span\left\{{\tilde{\mathbf{U}}}_s\right\}=span\left\{\mathbf{S}\right\},$$

(23)

where ${\tilde{\mathbf{U}}}_s=\mathbf{Y}(:,1:P)$, we receive the subspace of the signal.

3.2. Reduced Rank Covariance Matrix Construction

If we directly compute the covariance matrix of ${\mathbf{X}}_{new}$, we obtain

$${\mathbf{R}}_{new}=\left[\begin{array}{cc}{\mathbf{R}}_{11}& {\mathbf{R}}_{12}\\ {\mathbf{R}}_{21}& {\mathbf{R}}_{22}\end{array}\right],$$

(24)

where

$${\mathbf{R}}_{12}=\mathbb{E}\left[{\mathbf{X}}_1{\mathbf{X}}_2^H\right],$$

(25)

$${\mathbf{R}}_{22}=\mathbb{E}\left[{\mathbf{X}}_2{\mathbf{X}}_2^H\right].$$

(26)

and if we perform the EVD on ${\mathbf{R}}_{new}$, we can also obtain the signal subspace of the DOA, but in the Nyström method  [25], ${\mathbf{R}}_{22}$ is replaced by ${\mathbf{R}}_{21}^H{\mathbf{R}}_{11}^{-1}{\mathbf{R}}_{12}$; then the covariance matrix becomes

$${\mathbf{R}}_{newc}=\left[\begin{array}{cc}{\mathbf{R}}_{11}& {\mathbf{R}}_{12}\\ {\mathbf{R}}_{21}& {\mathbf{R}}_{21}^H{\mathbf{R}}_{11}^{-1}{\mathbf{R}}_{12}\end{array}\right],$$

(27)

and so we use ${\mathbf{R}}_{22}$ and ${\mathbf{R}}_{21}^H{\mathbf{R}}_{11}^{-1}{\mathbf{R}}_{12}$ to construct a new matrix ${\mathbf{R}}_{rr}$, which is called a reduced rank covariance matrix:

$${\mathbf{R}}_{rr}={\mathbf{R}}_{22}+{\mathbf{R}}_{21}{\mathbf{R}}_{11}^{-1}{\mathbf{R}}_{12},$$

(28)

where ${\mathbf{R}}_{rr}$ is a matrix with size $(M-K)\times (M-K)$, and it contains the information of the DOA as ${\mathbf{R}}_{new}$, with a lower rank. And we perform the EVD on ${\mathbf{R}}_{rr}$, where we can obtain the signal subspace:

$${\mathbf{R}}_{rr}={\mathbf{U}}_{rr}{\mathsf{\Lambda }}_{rr}{\mathbf{U}}_{rr}^H,$$

(29)

where ${\mathbf{U}}_{rr}$ contains the signal subspace of the signal.

3.3. DOA Estimation

After receiving the signal’s subspace with (23) in Section 3.1 and (29) in Section 3.2, we can perform some existing subspace-based methods to estimate the 2D DOA; however, some of the methods are time-consuming or need an extra parameter matching process. To solve the 2D DOA estimation problem, we apply a principal singular value-based method  [26]. We assume the obtained signal subspace is ${\mathbf{U}}_s$, and

$${\mathbf{U}}_s=[{\mathbf{u}}_1{\mathbf{u}}_2\cdots {\mathbf{u}}_P].$$

(30)

With (23), we know that ${\mathbf{U}}_s$ contains the information of ${\mu }_p$. And the elements in ${\mathbf{U}}_s$ satisfy the LP conditions. So we have the LP property as

$$\begin{array}{cc}\hfill & \sum _{l=1}^P\alpha {\left[{\mathbf{u}}_p\right]}_{m-l}=0,\hfill \\ \hfill & {\alpha }_0=1,p=1,2,\cdots ,P,m=P+1,\cdots ,K,\hfill \end{array}$$

(31)

where ${\alpha }_l$ are factors of LP. The ${\mathbf{u}}_p$ can be obtained by solving the polynomial

$$\sum _{l=1}^P{\alpha }_l{z}^{P-l}=0,$$

(32)

where the roots of the polynomial are $z=e^{j{\mu }_p}$. Then with (31), we have the LP error vector $\mathbf{e}$ as  [26]

$$\mathbf{e}=\mathbf{B}\underset{-}{\mathbf{-}}\mathbf{f},$$

(33)

where

$$\mathbf{B}={[{\mathbf{B}}_1^T{\mathbf{B}}_2^T\cdots {\mathbf{B}}_P^T]}^T,$$

$$\mathbf{f}={[{\mathbf{f}}_1^T{\mathbf{f}}_2^T\cdots {\mathbf{f}}_P^T]}^T,$$

$$\mathbf{b}={[{\alpha }_1{\alpha }_2\cdots {\alpha }_P]}^T,$$

$${\mathbf{f}}_p=-{\left[{\left[{\mathbf{u}}_p\right]}_{P+1}{\left[{\mathbf{u}}_p\right]}_{P+2}{\left[{\mathbf{u}}_p\right]}_M\right]}^T,$$

and

$${\mathbf{B}}_p=\left[\begin{array}{cccc}{\left[{\mathbf{u}}_p\right]}_P& {\left[{\mathbf{u}}_p\right]}_{P-1}& \cdots & {\left[{\mathbf{u}}_p\right]}_1\\ {\left[{\mathbf{u}}_p\right]}_{P+1}& {\left[{\mathbf{u}}_p\right]}_P& \cdots & {\left[{\mathbf{u}}_p\right]}_2\\ ⋮& ⋮& \ddots & ⋮\\ {\left[{\mathbf{u}}_p\right]}_{K-1}& {\left[{\mathbf{u}}_p\right]}_{K-2}& \cdots & {\left[{\mathbf{u}}_p\right]}_{K-P}\end{array}\right].$$

To solve the problem in (33), we use the weighted least squares (WLS) method; we first define a symmetric weighted matrix $\mathbf{W}$, then the estimate of $\mathbf{b}$, denoted as $\widehat{\mathbf{b}}$, which is

$$\widehat{\mathbf{b}}=arg\underset{\mathbf{b}}{min}{\mathbf{e}}^H\mathbf{W}\mathbf{e}={\mathbf{B}}^H\mathbf{W}\mathbf{f}/\left({\mathbf{B}}^H\mathbf{W}\mathbf{B}\right).$$

(34)

To construct the weighted matrix, we first define a Toeplitz matrix $\mathbf{C}$:

$$\begin{array}{cc}\hfill \mathbf{C}=\mathrm{Toeplitz}(& {\left[{\mathbf{b}}_p{\mathbf{0}}_{1\times (K-P-1)}\right]}^T,[b_p\hfill \\ \hfill & b_{p-1}\cdots b_{1}1{\mathbf{0}}_{1\times (M-P-1)}\left]\right),\hfill \end{array}$$

(35)

with $\mathbf{0}$ denoting the zero matrix with all elements with 0 in it, and ${\mathbf{u}}_s=[{\mathbf{u}}_1^T{\mathbf{u}}_2^T\cdots ,{\mathbf{u}}_P^T]$; then $\mathbf{W}$ is constructed  [26]:

$$\begin{array}{cc}\hfill \mathbf{W}=& {\sigma }^2{\left[\mathbb{E}\left\{\mathbf{e}{\mathbf{e}}^H\right\}\right]}^{-1}\hfill \\ \hfill =& {\sigma }^2{\left[\mathbb{E}\left\{\mathbf{C}{\mathbf{u}}_s{\mathbf{u}}_s{\mathbf{C}}^H\right\}\right]}^{-1}\hfill \\ \hfill \approx & \mathrm{diag}\left(\left[{\lambda }_1^2{\lambda }_2^2\cdots ,{\lambda }_P^2\right]\right)\otimes {\left(\mathbf{C}{\mathbf{C}}^H\right)}^{-1},\hfill \end{array}$$

(36)

where ⊗ is the Kronecker product. After the estimate of $\widehat{\mathbf{b}}$ is received, we use it to reconstruct $\mathbf{W}$, and we iterate the process to expect a better estimate. We then use the final $\widehat{\mathbf{b}}$ to solve (32) and assume the roots are ${\widehat{r}}_p$; then the estimate is

$${\widehat{\mu }}_p=\angle \left({\widehat{r}}_p\right),$$

(37)

where ∠ is the phase angle operator; we finally receive the estimate of ${\mu }_p$. On the other hand, to estimate ${\nu }_p$, we can still use $\mathbf{X}$, but the accuracy is not guaranteed. Then we use both the estimated ${\widehat{\mu }}_p$ and $\mathbf{X}$ to improve the accuracy. We substitute ${\mu }_p$ into $\mathbf{X}$ to obtain the subspace ${\mathbf{Y}}_2$ only containing the information of ${\nu }_p$:

$${\mathbf{Y}}_2={\mathbf{X}}^T{\left({\widehat{\mathbf{G}}}^{†}\right)}^T,$$

(38)

where ^† is the pseudo inverse operator, and $\widehat{\mathbf{G}}$ is the estimate of $\mathbf{G}$ constructed with ${\widehat{r}}_p$; we then follow the process from (31) to (37) to obtain the estimate of ${\nu }_p$, denoted by ${\widehat{\nu }}_p$. Then the estimation of the 2D DOA is computed from ${\widehat{\mu }}_p$ and ${\widehat{\nu }}_p$ as

$${\widehat{\varphi }}_p={\displaystyle \frac{\lambda }{2\pi d}}arcsin\left(\sqrt{{\widehat{\mu }}_p^2+{\widehat{\nu }}_p^2}\right),$$

(39)

and

$${\widehat{\theta }}_p=arctan\left({\displaystyle \frac{{\widehat{\nu }}_p}{{\widehat{\mu }}_p}}\right).$$

(40)

As $\widehat{\nu }$ is estimated with the use of ${\widehat{\mu }}_p$ and signal subspace, the proposed methodology inherently ensures automatic pairing of azimuth and elevation angles through the structural relationship embedded in the estimated spatial parameter. This intrinsic pairing mechanism eliminates the need for explicit parameter matching by preserving the geometric correspondence between the two angular dimensions during the estimation process. Crucially, as the signal subspace is initially obtained through the Nyström approximation, which is a low-complexity alternative to conventional subspace decomposition methods, the algorithm completely avoids performing SVD during the critical DOA estimation phase. This strategic bypassing of SVD operations constitutes the primary source of computational savings, particularly impactful in real-time applications where iterative parameter estimation is required. The complete steps of our approaches, detailing both the Proposed Algorithm 1 (utilizing the Nyström approximation) and the Proposed Algorithm 2 (employing the reduced rank covariance matrix method) are systematically presented in Algorithms 1 and 2, which, respectively, outline the algorithmic steps.

Algorithm 1 (utilizing the Nyström approximation)

Step 1: Decompose $\mathbf{X}$ into two sub-matrices ${\mathbf{X}}_1$ and ${\mathbf{X}}_2$

and construct ${\mathbf{X}}_{new}$ as (9).

Step 2: Perform EVD on ${\mathbf{R}}_{11}$ and ${\mathbf{R}}_{21}$ and construct $\mathbf{U}$ with (19).

Step 3: Construct $\mathbf{D}$ in (20), construct $\mathbf{Y}$, and obtain

the subspace of the signal.

Step 4: Compute ${\widehat{\mu }}_p$ and ${\widehat{\nu }}_p$ using (30) to (38).

Step 5: Estimate 2D DOA with (39) and (40).

Algorithm 2 (employing the reduced rank covariance matrix method)

Step 1: Decompose $\mathbf{X}$ into two sub-matrices ${\mathbf{X}}_1$ and ${\mathbf{X}}_2$

and construct ${\mathbf{X}}_{new}$ as (9).

Step 2: Construct ${\mathbf{R}}_{newc}$ in (27).

Step 3: Construct ${\mathbf{R}}_{newc}$ with (28) and perform EVD on ${\mathbf{R}}_{rr}$ to

obtain the signal’s subspace.

Step 4: Compute ${\widehat{\mu }}_p$ and ${\widehat{\nu }}_p$ using (30) to (38).

Step 5: Estimate 2D DOA with (39) and (40).

3.4. Computational Complexity Analysis

The computational complexity of the proposed method is evaluated in terms of floating-point operations (flops), following standard practice in computational analysis. The dominant computational cost arises from the Nyström approximation used to construct the equivalent signal subspace. Specifically, computing ${\mathbf{R}}_{11}$ and ${\mathbf{R}}_{12}$ require $\mathcal{O}\left(N{K}^2\right)$ and $\mathcal{O}(MNK-N{K}^2)$ flops, respectively, while the subsequent subspace construction via the Nyström method incurs additional $\mathcal{O}\left(M{K}^2\right)$ operations. Thus, the overall complexity of the proposed approach is $\mathcal{O}(MNK+M{K}^2)$. In comparison, conventional methods exhibit significantly higher computational demands: ESPRIT requires $\mathcal{O}\left(M^2{N}^2\right)$ [27], and ML estimation typically scales as $\mathcal{O}\left(M^3{N}^3\right)$ multiplications [28]. The conventional 2D DOA based on OMP has TQ atoms; the most time-consuming step is to search for atoms in the complete dictionary. In each iteration, the conventional method searches atoms at a cost of $\mathcal{O}\left(MNTQ\right)$, resulting in a total complexity of $\mathcal{O}\left(PMNTQ\right)$ [17]. When estimating 2D DOA, the traditional MP method has similar complexity to the ESPRIT method, but it requires parameter pairing, which has higher computational complexity than ESPRIT [9]. These theoretical advantages are validated through simulation results presented in the final experiment of Section 4, demonstrating substantial runtime reductions without sacrificing estimation accuracy.

4. Simulation Results

This section presents a comprehensive computer simulation study designed to rigorously evaluate the performance of the proposed 2D DOA estimation framework for the URA signal under the single snapshot scenario. To establish meaningful benchmarks, the proposed approach is compared against two well-established high-resolution ESPRIT algorithms [27] and the ML method [28], together with the MP [9] and OMP [17] methods. For clarity within the results, the two variants of the proposed methodology are denoted as Proposed 1 (utilizing the Nyström approximation) and Proposed 2 (employing the reduced rank covariance matrix method). The primary performance metric is the Root Mean Square Error (RMSE), computed using the estimated DOA and the real DOA. The signal-to-noise ratio (SNR) is SNR = $10log({\sigma }_s^2/{\sigma }_n^2)$ (dB). The signals’ and noises’ power are denoted as ${\sigma }_s^2$ and ${\sigma }_n^2$, respectively. We set the 2D DOA of the URA as $\theta =[5°30°]$ and $\varphi =[15°45°]$. The RMSE is computed as

$$\begin{array}{c}\hfill \mathrm{RMSE}=\sqrt{\mathbb{E}\left\{{\displaystyle \frac{1}{P_1}}{\displaystyle \sum _{p_1=1}^{P_1}}[{({\widehat{\theta }}_{i,p_1}-{\theta }_i)}^2+{({\widehat{\varphi }}_{i,p_1}-{\varphi }_i)}^2]\right\}}.\end{array}$$

The computer simulations are conducted using $P_1=200$ Monte Carlo trials, as increasing the number of trials does not yield a significant improvement in the results.

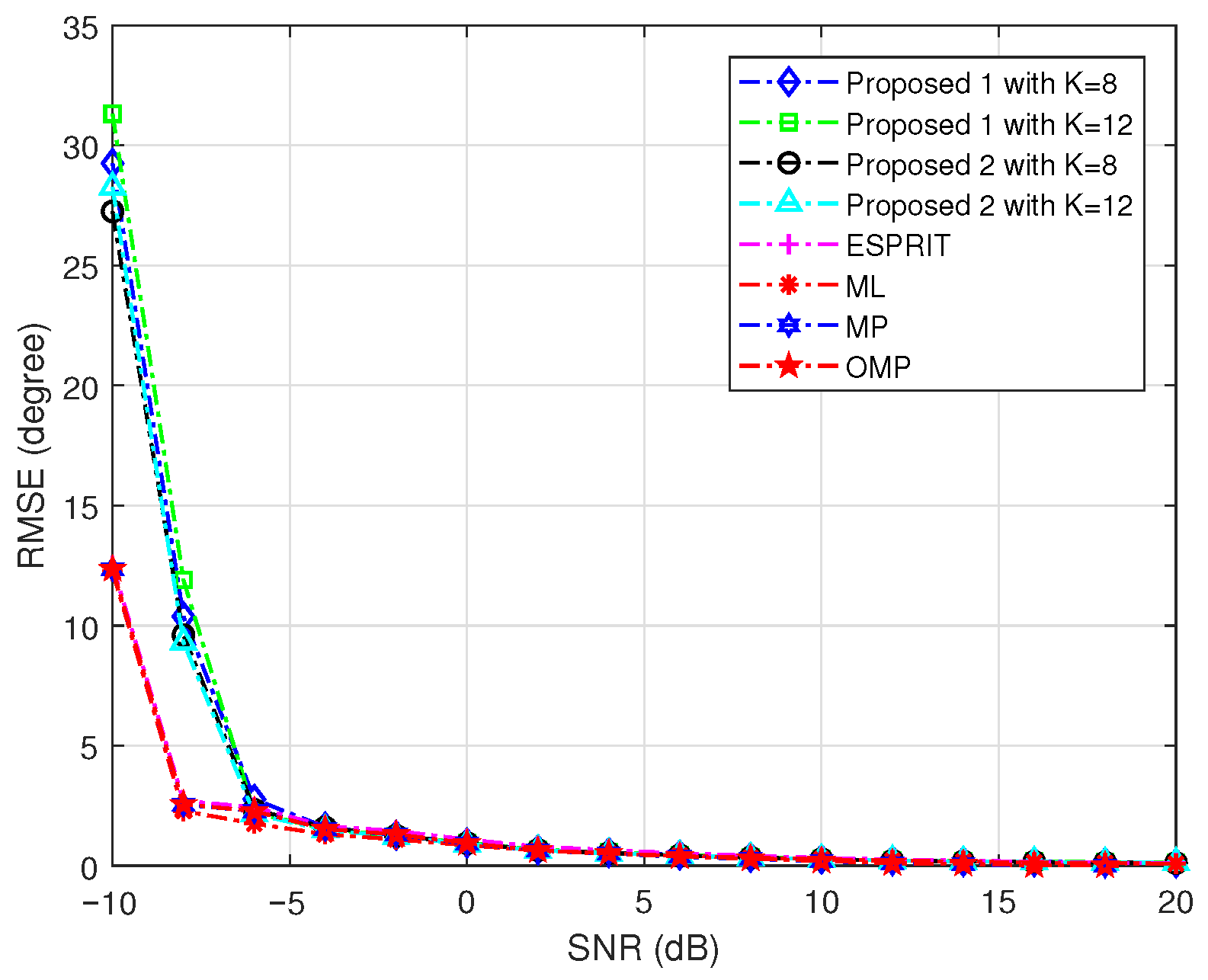
We begin by comparing the RMSE versus the SNR of the methods mentioned above. Simulations are conducted over an SNR range spanning from $-10$ dB to 20 dB, with the URA size fixed at $M=16$. As the Nyström approximation requires selecting the parameter K, we investigate its impact by employing two distinct values: $K_1=8$ and $K_2=12$. This allows for a direct comparison of the proposed approach’s sensitivity to this key parameter. The comparative RMSE results are presented in Figure 1. As shown in the figure, the RMSE of the proposed algorithms with $K_1$ and $K_2$ attains the ML at an SNR larger than $-5$ dB, where the ML method is usually used as the benchmark when estimating parameters. And the proposed method with different values of K has comparable performance with ESPRIT, ML, MP, and OMP methods in large SNR cases. Additionally, we observe that the performance does not change significantly with an increase in K in larger SNR situations. It should be noted that the results of Proposed 1 and Proposed 2 are similar. Therefore, in the following simulations, we include the results with two different values of K, and unless otherwise stated, the other parameters remain the same in the following experiments.

To rigorously assess the robustness of the proposed method under different source configurations, a second simulation is conducted where the DOAs are altered to $\theta =[10°50°]$ and $\varphi =[20°70°]$. This configuration tests the algorithms’ ability to resolve sources with significantly different angular separations in both azimuth and elevation dimensions. All other experimental parameters, including the SNR range, array size, number of snapshots, and the tested K values, remain identical to the first simulation. The resulting RMSE performance, illustrated in Figure 2, demonstrates that the proposed methods maintain accuracy comparable to the other methods across the evaluated SNR range. This consistent performance under altered source geometry provides strong empirical verification of the proposed method’s inherent accuracy, effectiveness, and robustness in diverse localization scenarios. The close alignment of the results between Proposed 1 and Proposed 2, as well as the minimal performance variation with K, further reinforces the reliability of the approach.

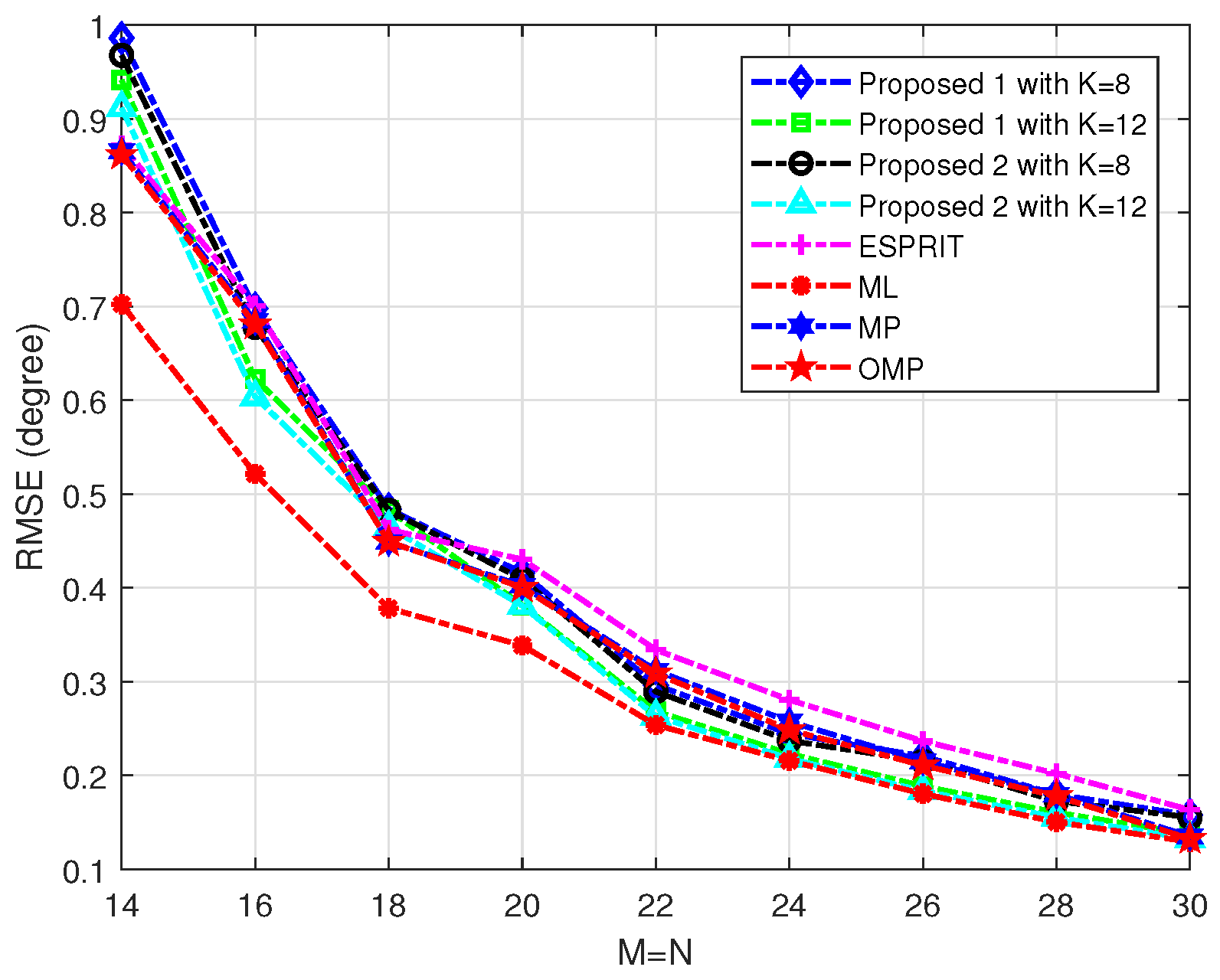
The subsequent experiment investigates the impact of array aperture on estimation accuracy by evaluating the RMSE as a function of the number of array elements, denoted as M. We systematically vary M from 14 to 30, maintaining all other parameters consistent with those in the first simulation. The resulting performance trends are illustrated in Figure 3. We can observe that the RMSE performance of all evaluated methods exhibits a consistent monotonic improvement as the number of array elements M increases, highlighting the expected benefit of enhanced spatial resolution provided by larger apertures. And more notably, the proposed method with $K_2=12$ demonstrates superior accuracy compared to both the variant using $K_1=8$ and the ESPRIT algorithm for array sizes exceeding $M=18$ while having similar performance to the other method. This performance advantage of the $K_2$ configuration becomes increasingly pronounced with a larger M, suggesting that a higher K is better suited to leverage the increased information available from larger arrays for achieving lower estimation error.

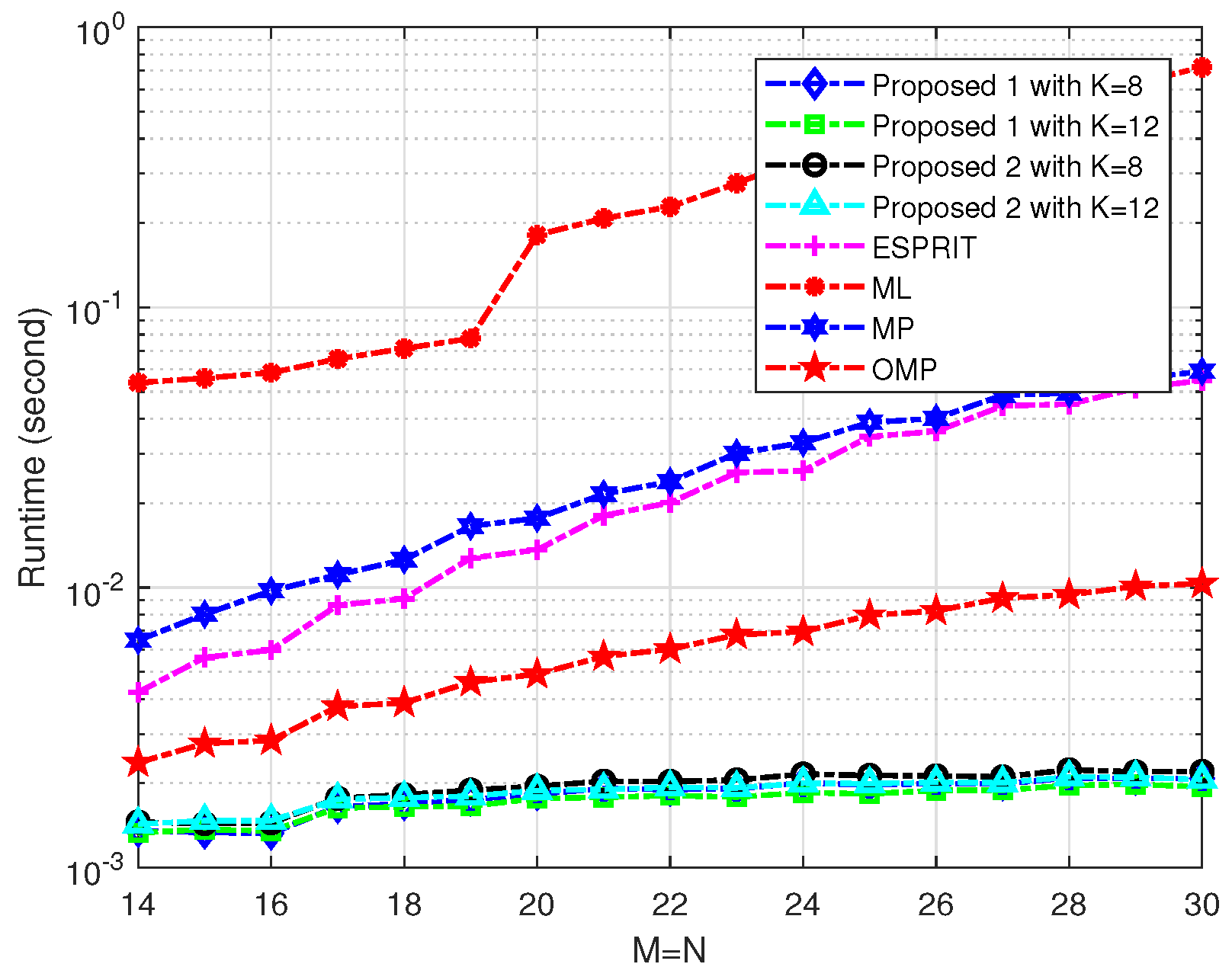
In the final experiment, we compare the runtime of all the methods mentioned above to evaluate their computational complexity. We use average CPU runtime as the performance metric to provide an estimate of the complexity. The runtime comparison is shown in Figure 4. The results show that the proposed method is much faster than the ESPRIT, ML, MP, and OMP methods. We also observe that the proposed methods with different values of K have similar complexities, indicating that an increase in K does not significantly affect the complexity of the proposed method. To give a further detailed view, we also give the runtime under different array sizes in

Table 1. Comparison of runtime (seconds).

Method	M = 18	M = 22	M = 28
Proposed 1 with K = 8	0.0017	0.0020	0.0021
Proposed 2 with K = 8	0.0018	0.0022	0.0022
ESPRIT	0.0091	0.0261	0.0451
ML	0.0713	0.3426	0.5527
MP	0.0125	0.0239	0.0494
OMP	0.0039	0.0060	0.0094

. The proposed methods demonstrate significant advantages in computational speed: for M = 28, Proposed 1 and Proposed 2 achieve runtimes of 0.0021s and 0.0022s, respectively, which are $21.5$ and $20.5$ faster than ESPRIT ($0.0451s$), and $263$ and $251$ faster than ML ($0.5527s$). Notably, the runtime difference between Proposed 1 and Proposed 2 remains negligible across all M values (e.g., $0.0017$ s vs. $0.0018$ s for $M=18$), suggesting that parameter K has minimal impact on complexity. This empirical evidence confirms that our method achieves state-of-the-art efficiency while maintaining competitive accuracy. This again indicates that the proposed method is a fast approach with comparable performance compared to some of the existing methods.

5. Conclusions

This paper introduces computationally efficient approaches for estimating the 2D DOA of signals impinging on a URA, specifically designed to bridge the critical performance–complexity trade-off inherent in such estimation problems. The proposed method leverages the Nyström approximation technique combined with a reduced rank covariance matrix framework. This foundation enables the derivation of two distinct signal subspaces approximating those obtained from the full array covariance matrix but at a significantly lower computational cost. This technique utilizes the principal singular vectors associated with the approximated signal subspaces and incorporates an iterative refinement process to accurately resolve the 2D DOA parameters. A key advantage of the proposed framework is that, because the essential signal subspaces are directly obtained via the efficient Nyström method, the computationally intensive EVD/SVD operations traditionally required during the DOA estimation phase are entirely circumvented. This elimination of EVD/SVD constitutes the primary mechanism for achieving substantial computational savings. Compared to conventional methods, the proposed method achieves high complexity with reduced complexity. The efficacy and robustness of the proposed method are evaluated through several numerical simulations.