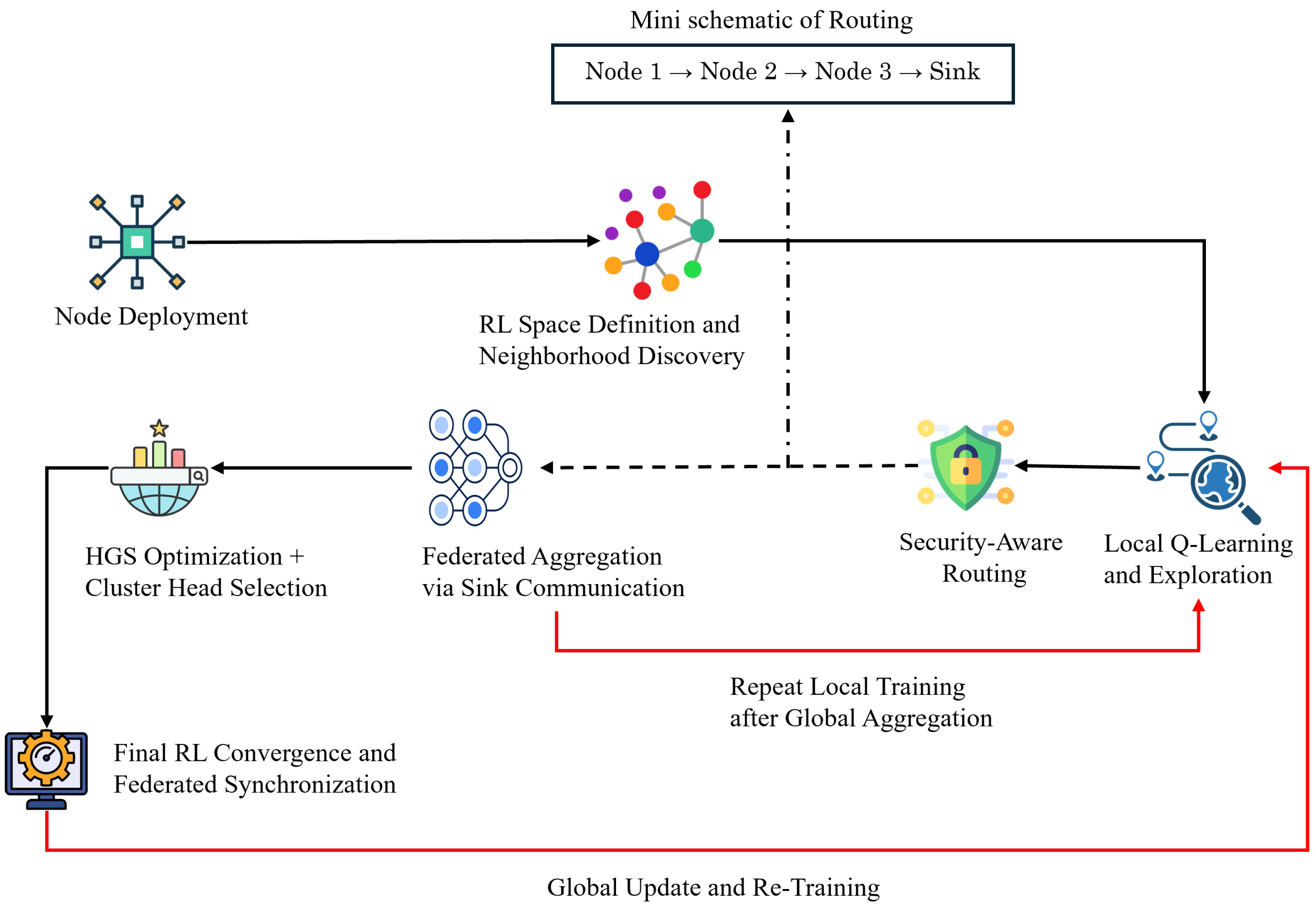
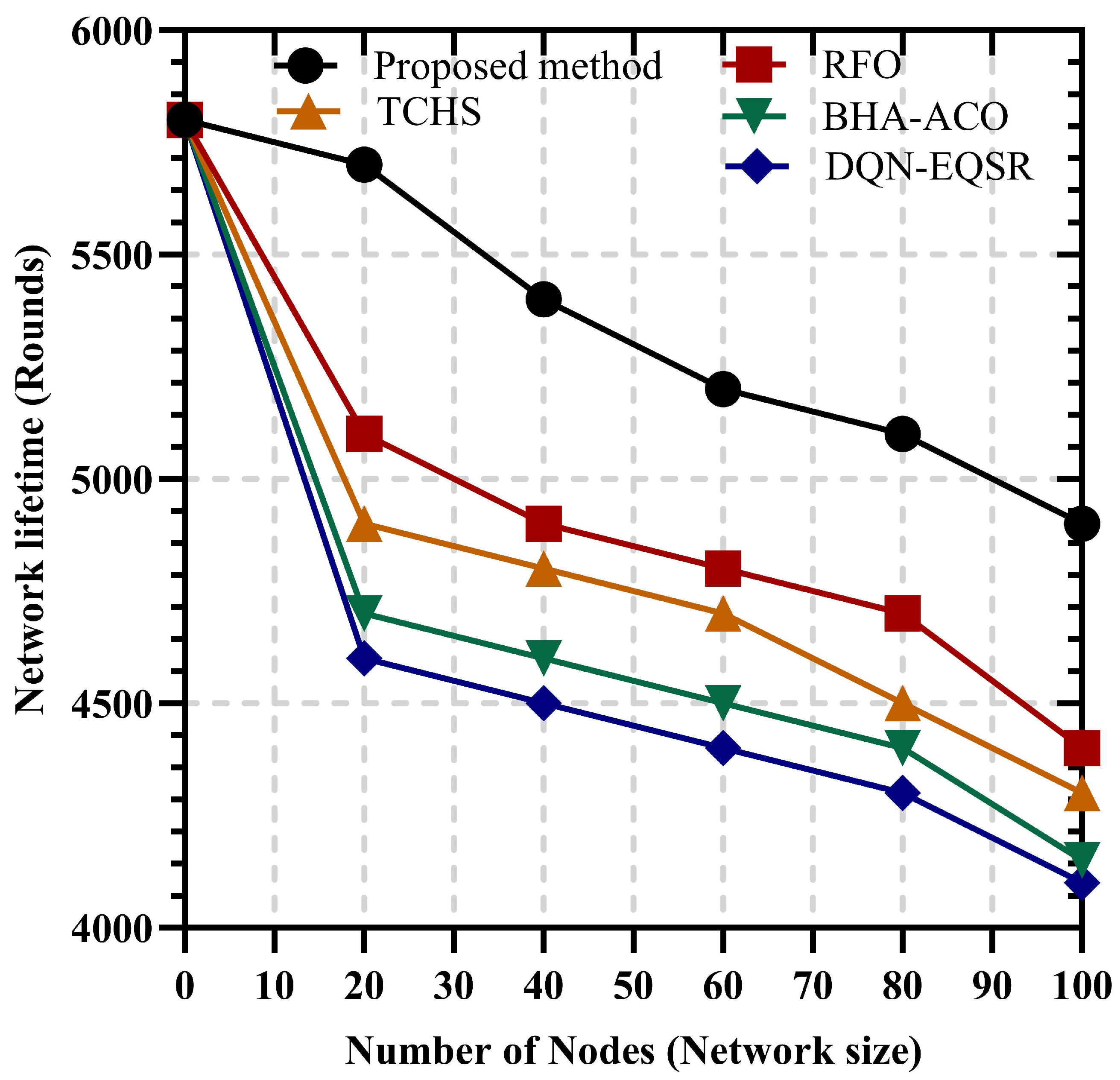
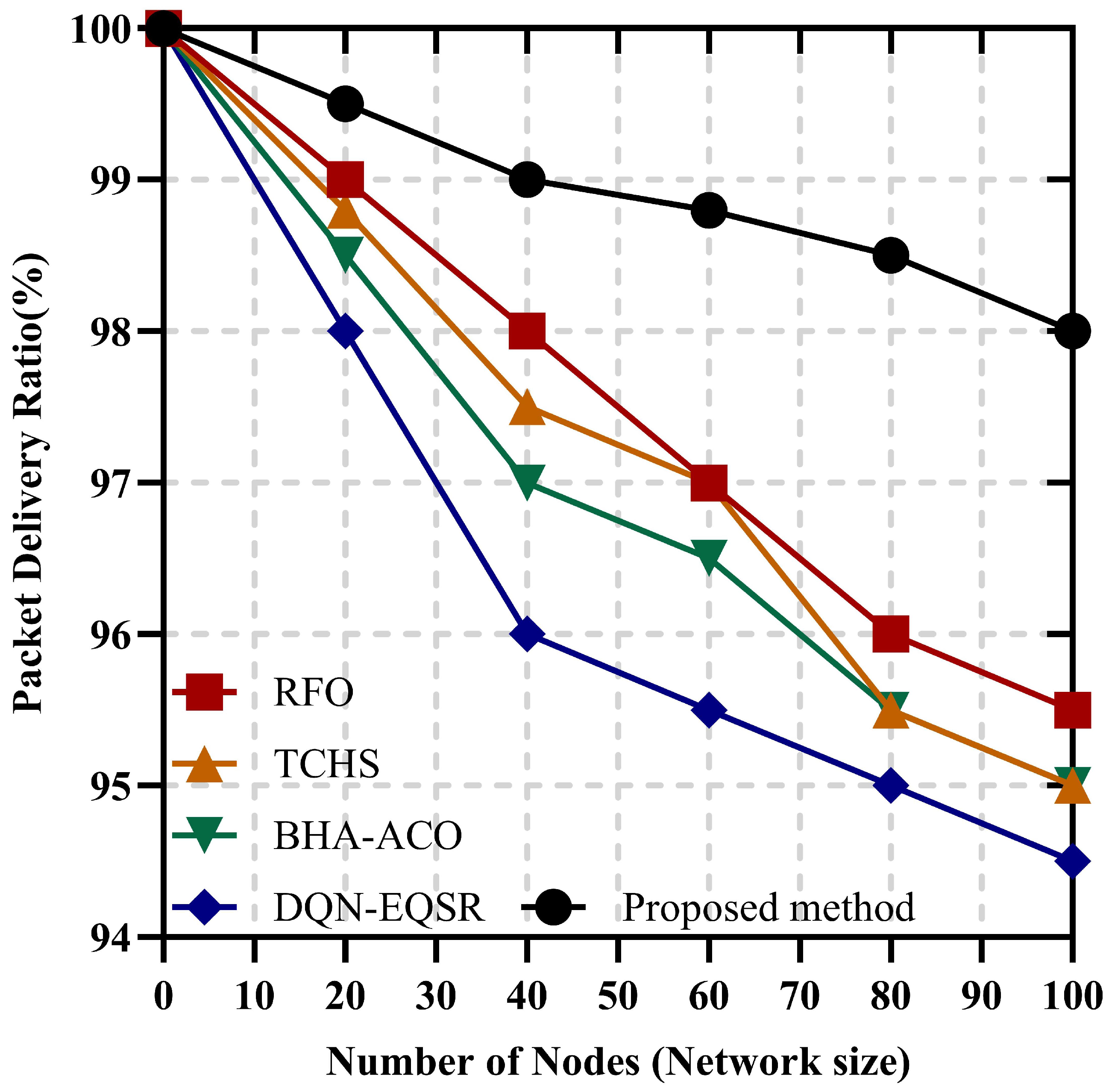
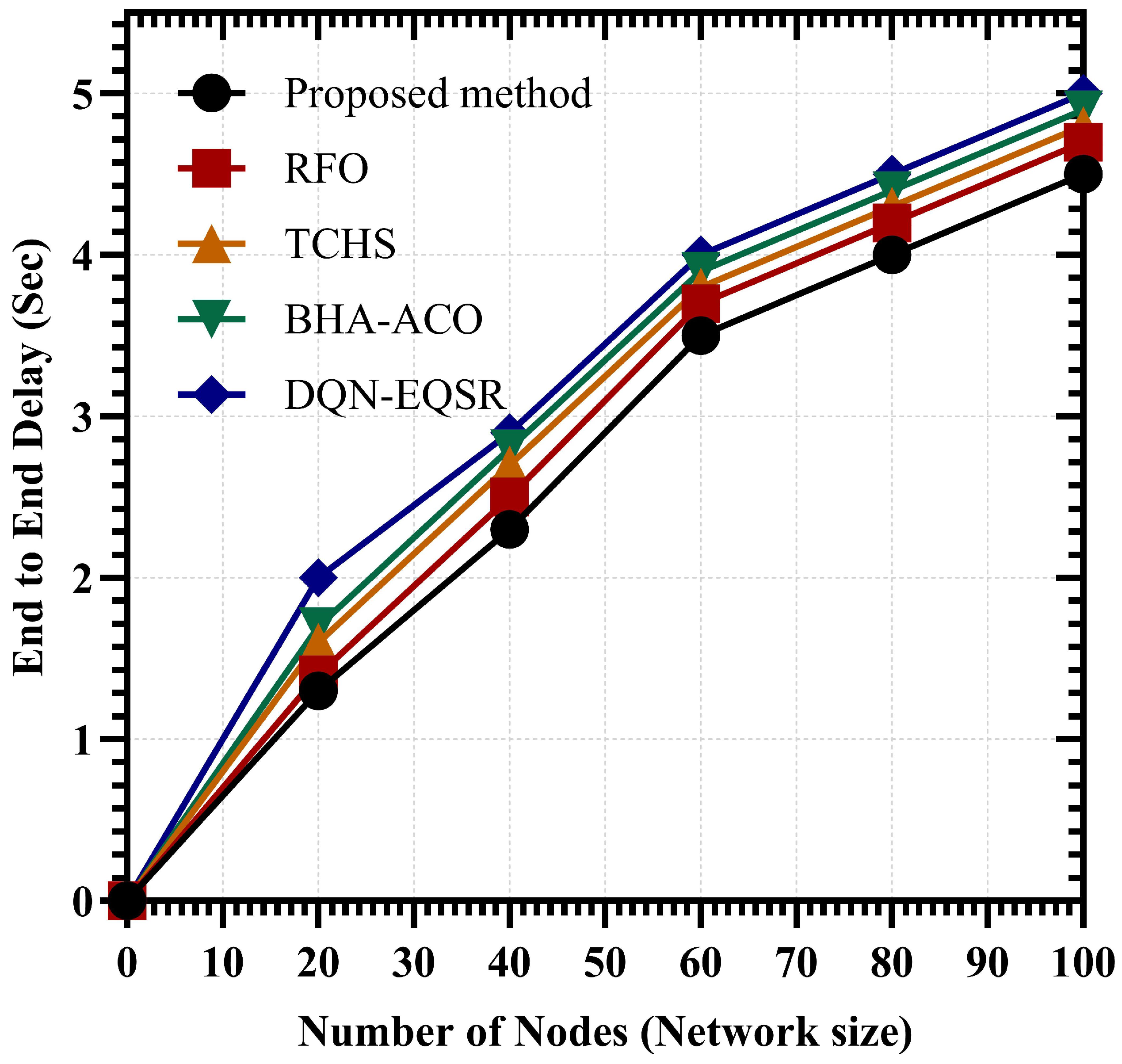
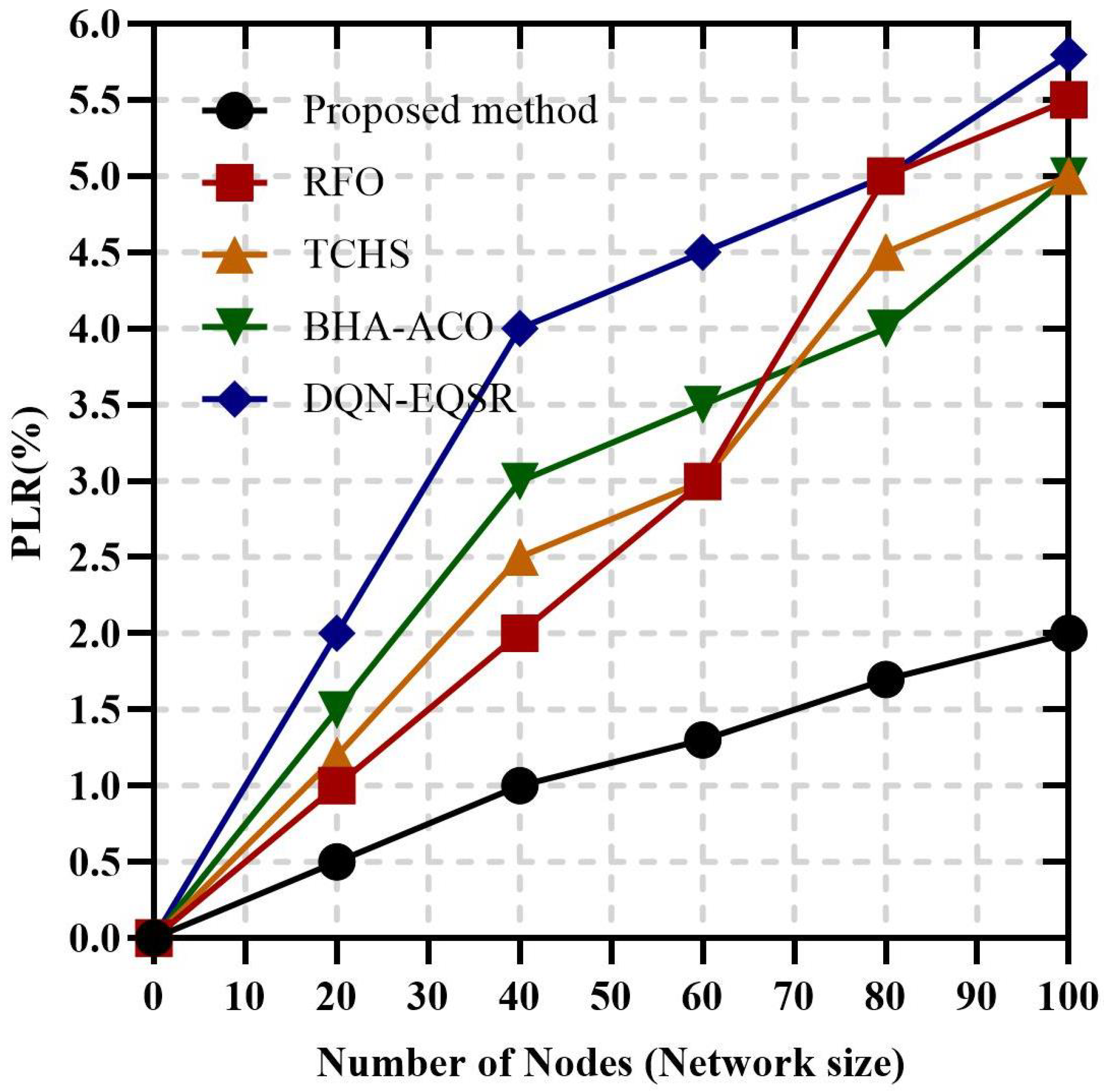
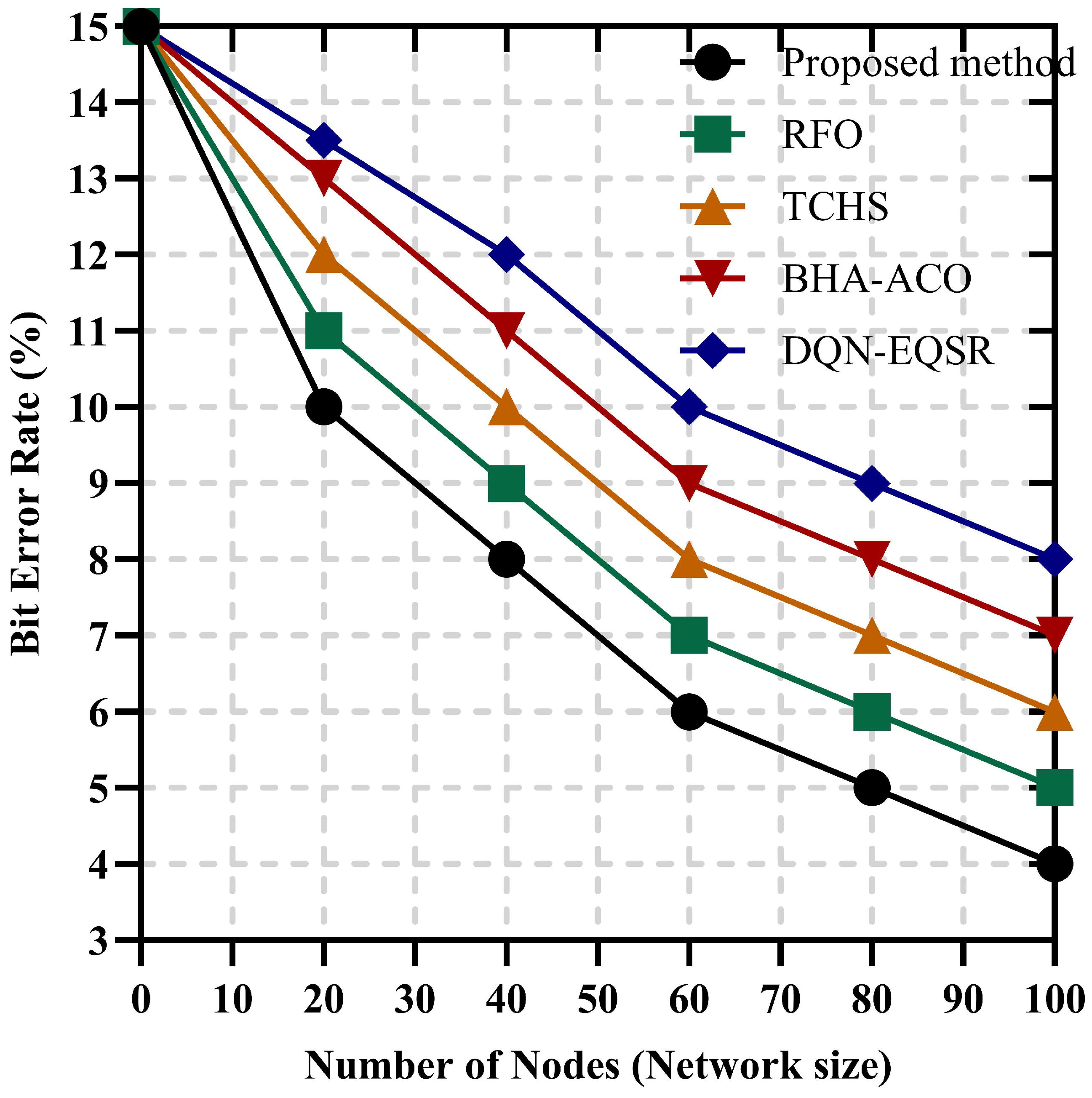
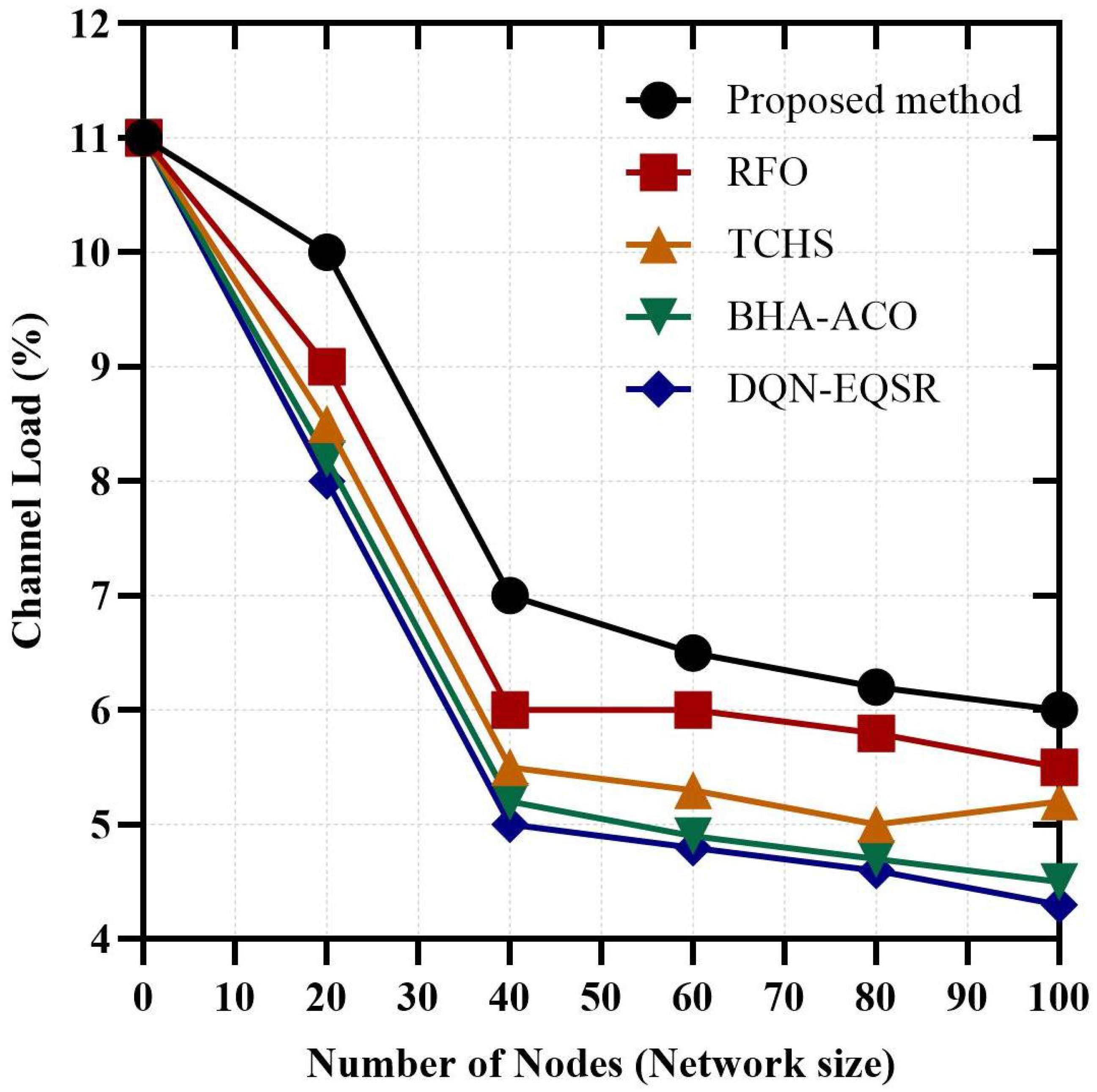
3.7. Proposed Method
Step 1: Initial Modeling of Nodes, Network Topology, and Physical Resources.
We consider a static WSN deployed in a rectangular region with a single sink at (extension to multiple sinks is straightforward). Nodes are placed i.i.d. uniformly at random in and have limited battery, compute, and memory resources.
Node positions and initial energy. Let
N be the number of sensor nodes. The position of node
i is
, and all nodes start with the same initial energy:
We assume ideal localization (each node knows
and the sink broadcasts
); if localization noise is present, it can be modeled as
with
.
Distance and neighborhood. The Euclidean distance between nodes
i and
j is
A directed link
is feasible if
, where
is the PHY-layer communication range.
Radio/energy model. We adopt the first-order radio model with a free-space/multipath crossover distance
. Let
k be the packet size in bits,
the electronics energy per bit (TX/RX),
and
the amplifier coefficients for free-space (
) and multipath (
) propagation, respectively. The per-packet transmit and receive energies are:
If on-node processing is non-negligible, we include a per-bit CPU cost
so that the processing energy for
k bits is
.
Battery dynamics. Let
and
denote the sets of packets transmitted to and received by node
i during slot/epoch
t, and let
be the corresponding TX distances. The battery recursion is
with node
i considered dead when
. Control traffic (e.g., HELLO/ACK, FRL uploads) is accounted for by using (
6) and (7) with the appropriate control packet sizes.
Step 2: Neighbor Discovery and Initialization of Communication Metrics.
Each node discovers neighbors and initializes link metrics (distance, reliability, trust primitives) using a lightweight HELLO/ACK procedure over IEEE 802.15.4 Carrier-Sense Multiple Access with Collision Avoidance (CSMA/CA).
MAC/PHY and timing. Time is partitioned in discovery periods of length . To reduce collisions, each node transmits one HELLO per period at time where is a jitter (). We use unslotted CSMA/CA with maximum re-transmissions for data/ACK frames. Let and be the HELLO and ACK payload sizes (bits).
Control frame formats. Node i broadcasts ( is a local timestamp). Upon reception, neighbor j unicasts .
Neighbor set and distances. The (directed) neighbor set of i at period t is . Distances follow Step 1: , .
Link reliability estimator. Let
indicate whether a valid ACK from
j to
i was received in period
t. We maintain both a sliding-window estimator over the last
periods and an EWMA:
with
. A link is considered usable if
. Neighbors that fail to respond for
consecutive periods are pruned.
RTT and RSSI sampling. For each ACK, node i estimates Round-Trip Time , and records receiver-side RSSI (from the radio), yielding time series and .
Lightweight anomaly detector (for trust primitives). Per link
, define residuals for a generic scalar metric
, where
. Maintain EWMA mean/variance:
with
. The standardized residual is
(
small). We flag an anomaly on
at time
t if either
or the windowed loss
exceeds
, for at least
M consecutive periods. The Boolean flag
is passed to Step 4’s trust update.
Control plane energy accounting. Let
denote the one-shot success probability for
transmissions in period
t (estimated by
or PHY metrics). The expected number of transmissions (including CSMA/CA retries, truncated at
) is
. Assuming a fixed broadcast range
for HELLOs, the expected control energy of node
i per discovery period is
which is debited in the battery recursion (Equation (
9)).
Initialization of trust primitives. Behavioral trust is initialized neutrally: () and will be updated in Step 4 using , , and RTT residuals. Algorithm 6 presents the neighbor discovery and metric initialization procedure.
Step 3: Defining the Reinforcement Learning Space for Network Nodes (Modeling RL Agents).
Each node is modeled as an RL agent that selects its next-hop parent based on local state features. To ensure tractability, continuous state variables are discretized into finite bins, enabling tabular Q-learning.
State space. The state of agent
i at time
t is represented as:
: residual energy of node i, discretized into bins (e.g., 10 uniform bins between 0 and ).
: distance to sink, discretized into concentric rings .
: queue congestion index, discretized into levels (e.g., ).
: path quality score (delay/PDR composite), mapped to bins using quantiles or thresholds.
: estimated end-to-end security probability from i to the sink, discretized into intervals in .
Thus, the effective state space is finite with cardinality .
Action space. At each step, node
i selects one neighbor as the next-hop parent:
Here,
is the neighbor set from Step 2 and
is the minimum energy threshold for participation.
Reward function. The reward encourages low-energy, low-delay, and secure routing. To avoid mixing different physical units, each term is normalized:
where:
: transmit energy consumed by node i in epoch t, normalized by a maximum reference .
: End-to-End Delay from node i to sink in epoch t, normalized by a maximum tolerable delay .
: path-level security probability, computed as in Step 4, normalized relative to the threshold .
The weights
satisfy
, balancing the trade-offs among energy, delay, and security.
| Algorithm 6 Neighbor discovery and metric initialization (per period of length ) |
![Mathematics 13 03196 i006 Mathematics 13 03196 i006]() |
Decision policy. Each agent follows an
-greedy policy over its Q-table:
The exploration rate
decays over time, ensuring sufficient exploration initially while converging toward exploitation of high-value routes.
Step 4: Security Evaluation and Path Trustworthiness Assessment.
To ensure that the paths chosen in Step 3 remain resilient against misbehavior and channel anomalies, each node maintains a dynamic trust score per link .
Hybrid link trust. For each neighbor
, node
i computes a hybrid link trust:
where:
is the historical trust, estimated from the smoothed link reliability ).
is the behavioral trust, adapted from anomaly detector outputs ().
balances long-term reliability vs. short-term anomaly evidence.
Behavioral trust update. At each discovery period, behavioral trust is updated as:
with
the penalty decrement and
the recovery increment.
Path-level security aggregation. To avoid underflow from multiplicative products, path security is aggregated in the log domain:
This formulation yields the geometric mean of link trust scores, ensuring longer paths are not unfairly penalized while still reflecting weak links.
Constraint vs. reward. To avoid double counting, we enforce a
constraint-only role for security: a candidate path
p is admissible if
otherwise, it is excluded from the action set
in Step 3. This ensures that the reward need not include a separate security term, keeping objectives decoupled.
Parameter ranges. Typical values are: (balance), – (penalty), – (recovery), and – (acceptance threshold). These can be tuned in the simulation setup. Algorithm 7 describes the process of security evaluation and trust updating.
Step 5: Local Q-Learning Model Training for Nodes.
Each node trains its own Q-learning agent over the discretized state/action space defined in Step 3, subject to the admissibility constraints from Step 4. Learning proceeds in episodes, where each episode corresponds to a sequence of packet transmissions and acknowledgments until either the sink is reached or a timeout occurs.
Q-learning update. At each decision epoch
t, node
i observes its current state
, selects an action
, obtains a normalized reward
(Equation Step 3), and observes the next state
. Its Q-table is updated as:
where:
is the learning rate at epoch t, scheduled to decay as with , .
is the discount factor, typically .
reflects normalized energy, delay, and path security feasibility (from Steps 1–4).
| Algorithm 7 Security evaluation and trust update |
![Mathematics 13 03196 i007 Mathematics 13 03196 i007]() |
Exploration-exploitation policy. Node
i selects actions using an
-greedy rule:
where
decays over episodes, e.g.,
, with
,
.
Stopping criterion and practical convergence. Unlike infinite-horizon Markov Decision Processes (MDPs), WSN agents operate under finite energy budgets and time-varying topologies. Thus, we adopt empirical convergence: training stops after episodes or when the Q-values stabilize, i.e., for M consecutive episodes, with . This practical stopping rule avoids reliance on ergodicity assumptions that are unrealistic in battery-limited WSNs.
Q-table structure and memory footprint. Each Q-table has dimension , where is the product of the discretization bins from Step 3, and is the number of admissible neighbors. For example, with , , , , , we obtain . If the average neighbor set has , the Q-table has, at most, entries. With each Q-value stored as a 4-byte float, the per-node memory requirement is kB, feasible for constrained sensor platforms with ≥128 kB RAM.
Step 6: Adaptive Federated Aggregation of Q-Learning Models.
To align local policies across the WSN without transmitting raw data, we adopt FRL. Each node periodically uploads a compressed summary of its Q-table after local training, and the sink aggregates these contributions into a global Q-model. This reduces energy overhead compared to centralized training, while ensuring robustness across heterogeneous nodes.
Aggregation model. After local training episode
, node
i has a Q-table
. The sink aggregates them as:
where
and
. Thus, nodes with more reliable contributions influence the global model more.
Adaptive weighting. We define
based on both residual energy and local performance:
where:
: residual energy of node i, consistent with the radio/battery model (Step 1).
: average return of node i’s policy, i.e., the mean episodic reward over the last episodes (normalized to ).
: trade-off weights with .
Temporal process. Federated exchange occurs every
local episodes. To reduce communication cost, only nonzero entries or quantized Q-values are transmitted, incurring energy consumption
where
is the payload size (bits),
is the distance to sink, and
is the expected re-transmissions.
Local synchronization. Upon receiving the global Q-table, each node blends it with its local table using a Polyak update (to prevent catastrophic forgetting):
This ensures stability while gradually aligning local policies with the global one.
Stopping condition. Aggregation continues until either (i) the global Q-values stabilize (), or (ii) the average number of alive nodes drops below a threshold. Algorithm 8 presents the adaptive federated aggregation of local Q-learning models.
Step 7: Optimization of Clustering and Routing Using Hunger Games Search.
To this end, we apply a binary variant of the HGS algorithm to jointly optimize CH selection and routing paths. The resulting topology minimizes energy consumption, delay, and vulnerability, while ensuring structural feasibility.
Chromosome representation. Each candidate solution is encoded as:
A binary CH vector where if node i is a CH and otherwise.
A directed binary routing matrix , where denotes a parent-child link .
Feasibility constraints. Each solution
must satisfy:
Infeasible candidates are repaired (reassigning orphan nodes) or penalized in the fitness score.
| Algorithm 8 Adaptive federated aggregation of Local Q-Learning Models |
![Mathematics 13 03196 i008 Mathematics 13 03196 i008]() |
Fitness function. The objective is to minimize:
Metrics are defined as:
HGS update mechanism (binary variant). In the continuous HGS update, candidate solutions evolve via:
To preserve binary encoding, we apply a sigmoid mapping and Bernoulli sampling:
then sample
. This ensures binary Cluster Head assignments.
The hunger factor is computed as:
where
reflects the fitness-induced hunger of solution
i.
Step 8: Integrating HGS Output with Reinforcement Learning for Faster Convergence and Structured Stability.
The binary HGS optimization yields an initial Cluster Head assignment and a feasible routing matrix . These outputs are now used to warm-start the Q-learning agents of Step 5, ensuring that training begins from a near-optimal topology rather than from a random policy. This accelerates convergence and improves stability in the early phases of federated aggregation.
Inputs. The initialization procedure uses:
: optimized CH selection vector.
: optimized directed routing matrix.
: residual energy of all nodes (Step 1).
: per-node security index (Step 4).
Q-table initialization. For each node
i, the Q-table entries corresponding to admissible actions
are initialized as:
where
are bounded constants (e.g.,
,
). This ensures that routes favored by HGS start with higher expected utility.
Policy initialization. The initial decision policy is biased toward the HGS solution:
where
allows limited exploration from the start. This avoids purely deterministic choices and ensures that suboptimal HGS assignments can still be corrected.
Effect on convergence. With HGS-guided initialization, the number of training episodes needed to reach a near-optimal policy is reduced. There exists
such that:
meaning that the hybrid HGS-RL process attains an
-close approximation of the optimal Q-function faster than a random-start Q-learning agent. This warm-start effect improves energy efficiency by reducing the number of early, exploratory transmissions that would otherwise consume scarce battery resources.
Step 9: Adaptive Re-Aggregation of Learning Policies after HGS-RL Convergence.
After nodes complete their local HGS-guided Q-learning episodes, a second federated aggregation is performed to refine and synchronize policies. This re-aggregation stage ensures that energy-depleted nodes do not dominate decisions, while reinforcing secure and reliable routes across the network.
Inputs. Each node provides:
Its locally updated Q-table , which reflects both RL training and HGS initialization.
Residual energy .
Reliability score defined as the Packet Delivery Ratio (PDR) over the last transmissions.
Security index .
Adaptive weighting. The global aggregation weights are computed as:
with
. This ensures balanced contributions from energy-rich, reliable, and secure nodes.
Global aggregation. The sink computes the new federated Q-function:
Local synchronization. Instead of overwriting local tables, each node blends the global update into its own Q-table:
This prevents catastrophic forgetting and ensures smoother convergence. Algorithm 9 presents the adaptive re-aggregation of HGS-RL Q-tables.
| Algorithm 9 Adaptive re-aggregation of HGS-RL Q-tables |
![Mathematics 13 03196 i009 Mathematics 13 03196 i009]() |