Abstract
Magnetohydrodynamic (MHD) flow and heat transfer in porous media are central to many engineering applications, including heat exchangers, MHD generators, and polymer processing. This study examines the boundary layer flow and thermal behavior of an electrically conducting viscous fluid over a porous stretching tube. The model accounts for nonlinear thermal radiation, internal heat generation/absorption, and Darcy–Forchheimer drag to capture porous medium resistance. Similarity transformations reduce the governing equations to a system of coupled nonlinear ordinary differential equations, which are solved numerically using the BVP4C technique with Response Surface Methodology (RSM) and sensitivity analysis. The effects of dimensionless parameters magnetic field strength (M), Reynolds number (Re), Darcy–Forchheimer parameter (Df), Brinkman number (Br), Prandtl number (Pr), nonlinear radiation parameter (Rd), wall-to-ambient temperature ratio (rw), and heat source/sink parameter (Q) are investigated. Results show that increasing M, Df, and Q suppresses velocity and enhances temperature due to Lorentz and porous drag effects. Higher Re raises pressure but reduces near-wall velocity, while rw, Rd, and internal heating intensify thermal layers. The entropy generation analysis highlights the competing roles of viscous, magnetic, and thermal irreversibility, while the Bejan number trends distinctly indicate which mechanism dominates under different parameter conditions. The RSM findings highlight that rw and Rd consistently reduce the Nusselt number (Nu), lowering thermal efficiency. These results provide practical guidance for optimizing energy efficiency and thermal management in MHD and porous media-based systems.:
Keywords:
stretching porous cylindrical surface; inclined magnetic field; heat source/sink parameter; Darcy–Forchheimer parameter; entropy generation analysis; nonlinear radiation MSC:
76W05; 65L10
1. Introduction
This study holds broad practical significance in industrial and engineering systems where fluid flow, heat transfer, and electromagnetic effects are of critical importance. Its relevance spans polymer and fiber manufacturing, metallurgical operations, cooling of cylindrical reactor components, and biomedical devices, all of which demand precise regulation of thermal and flow characteristics. In addition, applications in porous media, such as oil recovery and groundwater filtration, benefit from these insights by enhancing efficiency, safety, and overall performance. Since the 1980s, a wide range of analytical, computational, and theoretical investigations have progressively advanced this field, shedding light on the complex interplay of viscosity, thermal diffusion, magnetic forces, porous structures, and nanoparticle suspensions.
The research journey began with Brucker [1], who underlined the importance of viscous dissipation in natural convection through porous materials, thereby laying the groundwork for more accurate and physically consistent thermal modeling in porous domains. Extending this foundation, Chamkha [2] investigated chemically reactive and thermally generating boundary layers in porous MHD environments, thereby highlighting the influence of both chemical kinetics and thermal energy sources on magnetized convective transport. A notable contribution came from Ishak et al. [3], who analyzed magnetohydrodynamic (MHD) flow along a stretching cylinder, and their findings demonstrated that parameters such as the Prandtl and Reynolds numbers, along with magnetic field intensity, strongly regulate the momentum and thermal boundary layers. This line of inquiry was further advanced by Mukhopadhyay [4], who studied axisymmetric convection within porous settings under variable surface temperature conditions and compared the heat transfer between curved and flat geometries, ultimately noting that cylindrical configurations are superior in facilitating enhanced thermal transport. Along similar lines, Prasad et al. [5] emphasized the combined roles of viscous dissipation, resistive heating, and internal heat generation in porous cylinders, while also bringing attention to the critical influence of Darcy and Forchheimer drag terms in capturing the complexity of porous structures.
Subsequent research expanded the scope of investigations by addressing different orientations and geometrical configurations of cylinders. Hayat et al. [6] considered convective flow across inclined cylinders, with special emphasis on the effects of Soret and Dufour mechanisms, while Salimipour [7] examined mixed convection in horizontal cylinders to better understand combined buoyancy and forced convection effects. Furthermore, Ali et al. and Butt et al. [8,9] incorporated non-uniform cylindrical geometries into their analysis, thereby attempting to capture more realistic heat and mass exchange mechanisms associated with curved geometries encountered in practical systems. With the advancement of nanofluid research, Saeed et al. [10] in 2020 investigated hybrid nanofluids in porous stretching cylinders, demonstrating their thermal enhancement potential, while Mishra and Kumar [11] examined the combined effects of velocity and thermal slip in the presence of viscous dissipation and Joule heating, thereby contributing to the understanding of slip-flow conditions in porous cylinders.
In more recent years, there has been a significant shift toward incorporating advanced nanofluid formulations and non-Newtonian rheological models in the study of porous cylindrical flows. Awan et al. [8] and Dharmendar Reddy et al. [12] contributed to this domain by analyzing hybrid and Ellis fluids under porous and electromagnetic influences, whereas Madkhali et al. [13] further extended the scope by examining ternary nanoparticles in MHD flows through porous geometries. In a related development, Kumar et al. [14] investigated Williamson fluid transport and its thermal behavior over a permeable stretching cylinder, explicitly considering the combined influences of magnetic fields, viscous dissipation, Joule heating, and heat generation/absorption, thereby providing insights into the relationship between rheological properties and transport performance. Complementing this, Murthy et al. [15] explored mixed convective radiative motion of Casson fluid with Joule heating and chemical reactions over a stretched cylinder by applying the double-diffusive Cattaneo–Christov framework, and their findings, validated against earlier reports, indicated that both temperature and concentration fields decrease significantly when larger thermal and solutal relaxation parameters are employed.
The role of porous medium resistance and non-Fourier effects in cylindrical transport problems has also been actively pursued. Zegeye et al. [16] analyzed convective transport of Williamson nanofluid with variable thermal conductivity through a Darcy–Forchheimer porous layer over an unsteady stretching cylindrical sheet, and their results revealed that Biot numbers significantly enhance mass transfer, whereas heat transfer responds differently, while higher unsteadiness parameters lead to substantial increases in wall friction. Similarly, Jan et al. [17] investigated ternary hybrid nanofluids using a non-similarity analysis framework, whereas Mohanty et al. [18] specifically addressed entropy generation metrics in nonlinear radiative cross-ternary nanofluid flows, thereby highlighting the thermodynamic irreversibility in such advanced nanofluid systems. The comparative study conducted by Mahboobtosi et al. [19] demonstrated the improved thermal and kinetic performance of ternary suspensions in contrast to single and binary counterparts, further consolidating the case for multi-component nanofluids. Meanwhile, Shankar Goud [20] analyzed the effect of a magnetic dipole on magneto-thermal transport within a deformable cylinder, which was found to have direct implications for magnetotherapy and spectroscopy, and the observed outcomes highlighted the sensitivity of flow and heat distribution to physical parameters in such magnetized systems.
A growing body of work has specifically focused on entropy generation in porous cylindrical flows. Faisal [21] examined entropy generation with activation energy for viscous fluid double diffusion over a stretching cylinder using non-Fourier and non-Fick models, and the homotopy analysis revealed that entropy declines near the surface with stronger unsteady stretching but increases further away, while both concentration and temperature grow with the stretching factor. Similarly, Gogoi et al. [22] studied unsteady thin liquid film flow over a porous heated stretching cylinder using full Navier–Stokes equations with the Crank–Nicolson approach, showing that film thinning is reduced by higher porosity and Hartmann number, while injection enlarges the film thickness, suction decreases it, and thermocapillary effects vary with heating or cooling conditions. Hybrid nanofluid research has also been enriched by Nabwey et al. [23], who analyzed Cu–Al2O3/Williamson fluid flow past an inclined stretching cylinder in a porous structure, with magnetic and Joule heating effects included, and their results demonstrated that Biot and Eckert numbers increase surface temperature, Lewis number decreases concentration, curvature enhances concentration, while skin friction rises with magnetic field strength but decreases with higher curvature. Similarly, Ramireddy et al. [24] studied blood-based hybrid nanofluids containing silver and gold nanoparticles over a stretched porous cylinder under the combined influences of magnetic fields, convection, Joule heating, stratification, and nonlinear radiation, and their outcomes showed that curvature strongly impacts velocity and temperature distributions, while the Nusselt number increases by 17% at φ1 = 0.15 compared to the base fluid, thereby highlighting biomedical relevance.
Further contributions include Ramasekhar et al. [25], who analyzed magnetohydrodynamic Casson hybrid nanofluid over a stretching cylinder in the presence of porous media and heat source/sink, motivated by applications in restricted blood circulation studies, and they reported that magnetic fields raise velocity but reduce temperature, heat generation increases temperature, and both skin friction and Nusselt numbers improve with parameter variations. Sobhanapuram et al. [26] studied Williamson nanofluid with variable thermal conductivity through a Darcy–Forchheimer porous medium over an unsteady stretching cylindrical sheet using the Cattaneo–Christov model, and they found that larger unsteady parameters increase wall friction and boundary layer thicknesses, while Biot numbers significantly influence convective heat and mass transfer. Similarly, Faraz et al. [27] analyzed Maxwell nanofluid containing single-walled and multi-walled carbon nanotubes in sodium alginate over a stretchable cylinder under the combined effects of thermal radiation, magnetic field, and viscous dissipation, reporting that temperature rises with Eckert number, curvature, and radiation but decreases with nanoparticle concentration, while skin friction grows with curvature, magnetic intensity, and Maxwell parameter, and Nusselt number decreases with Eckert number, nanoparticle concentration, and Maxwell effects. Finally, Wang et al. [28] investigated ultra-thin film dynamics of ternary nanofluids under nonlinear radiation, emphasizing their direct applications in solar and combustion system technologies.
Across these decades, three emerging themes are evident:
- Thermal entropy generation (Faisal [21]; Mohanty [18]) is critical for assessing system irreversibility and improving efficiency in both engineering and biomedical systems.
- Magnetized radiative flows (Murthy [15]; Nabwey [23]; Ramasekhar [25]) demonstrate strong control over velocity, temperature, and concentration, with applications in cooling technologies, magnetotherapy, and energy conversion.
- RSM analysis (Farooq [29]), although not directly addressed in earlier works, has gained traction in recent nanofluid and hybrid fluid studies as a robust statistical framework to optimize multi-parameter interactions, validate numerical models, and guide industrial design strategies. RSM enables systematic evaluation of parameter interactions, sensitivity analysis, and predictive modeling, which are especially valuable in hybrid nanofluid systems where multiple competing effects coexist. By bridging numerical and experimental studies, RSM offers a practical pathway to translate theoretical models into industrial-scale applications.
Although extensive studies have addressed MHD flows and heat transfer over cylindrical and porous surfaces, significant research gaps remain. Most previous works have primarily focused on velocity and temperature distributions without incorporating the influence of pressure variations, despite their critical role in convective transport. Similarly, studies on MHD flow often assume a perpendicular magnetic field, whereas the effect of an inclined magnetic field—highly relevant in real industrial systems—has received limited attention. Although entropy generation has been explored in certain contexts, a comprehensive analysis incorporating entropy generation with Bejan number and Darcy–Forchheimer drag to capture the effects of complex porous structures in stretching cylinders under nonlinear radiation and internal heat generation remains largely unreported in the literature.
- How do pressure variations evolve in the boundary layer flow of an electrically conducting viscous fluid over a porous stretching cylinder?
- What is the influence of an inclined magnetic field on velocity, temperature, and pressure distributions compared to the conventional normal field case?
- How do entropy generation and the Bejan number respond to variations in key dimensionless parameters such as M, Re, Df, Br, Rd, Q and rw?
Objectives of the Study
- To analyze the combined effects of aligned magnetic field, nonlinear thermal radiation, and internal heat generation on fluid flow and heat transfer over a porous stretching cylinder.
- To study the influence of key dimensionless parameters on velocity and temperature profiles.
- To compute skin friction coefficient and Nusselt number to quantify wall shear stress and surface heat transfer.
- To establish trends that may assist in optimizing industrial and engineering applications involving curved surfaces, magnetic fields, and porous media.
Problem Formulation
The problem considers a steady, axisymmetric, laminar flow of an incompressible, electrically conducting fluid induced by a porous stretching cylindrical tube of radius a. Let be the velocity component along the coordinate axes where the axial coordinate is denoted by z, and the radial coordinate by r. The stretching occurs in the axial direction, and the surface temperature of the tube is held constant at Tw, while the ambient fluid temperature is T∞ with Tw > T∞. An inclined magnetic field Bo is applied at different angles of . The motion of the fluid is caused by stretching cylinder in the axial direction.
Assumptions:
- Viscous dissipation, Ohmic heating, and Hall effects are negligible.
- The fluid moves within a porous medium influenced by Darcy–Forchheimer resistance.
- Heat transfer includes nonlinear thermal radiation and heat source/sink effects.
- The Cylinder is stretched with a uniform velocity in the axial direction, denoted by , where c is constant.
- The flow is axisymmetric, i.e., the azimuthal axis ( does not affect field variables (There is no -momentum equation). Since the flow is induced only by the stretching motion of the cylinder. Hence, the axial pressure gradient is inactive. Ishak et al. [3].
Figure 1 illustrates the geometry of the physical problem, showing the schematic representation of the stretching cylindrical embedded in a porous medium along with the applied boundary conditions.
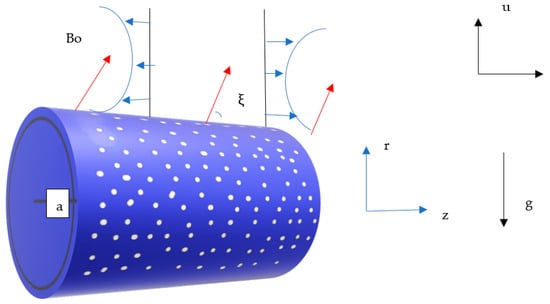
Figure 1.
Physical Model.
The governing equations are given by
Continuity equation:
Momentum equation:
Energy Equation:
Subject to the boundary condition
Similarity transformation
Using the above similarity variables, the transformed non-dimensional equations are
where .
The transformed boundary condition are
Skin friction coefficient .
The Rosseland approximation is used to model thermal radiation by transforming the radiative heat flux into a diffusion-like form, based on the assumption of an optically thick medium.
Numerical Procedure
As a result of nonlinear and coupled nature of the governing equations, finding analytical solutions for the boundary value problem described by Equations (1)–(5) is not feasible. A practical strategy involves converting the system into an equivalent set of first-order differential equations, which facilitates numerical analysis. The BVP4C technique is well-adapted for addressing such transformed problems. Similarly, the shooting method handles the ordinary differential Equations (7)–(9) with boundary conditions (10) by initially reformulating them into a compatible first-order system, as detailed below.
Corresponding boundary conditions are
Figure 2 presents the computational flow chart, which outlines the step-by-step procedure adopted in formulating, transforming, and numerically solving the governing equations using the BVP4C method.
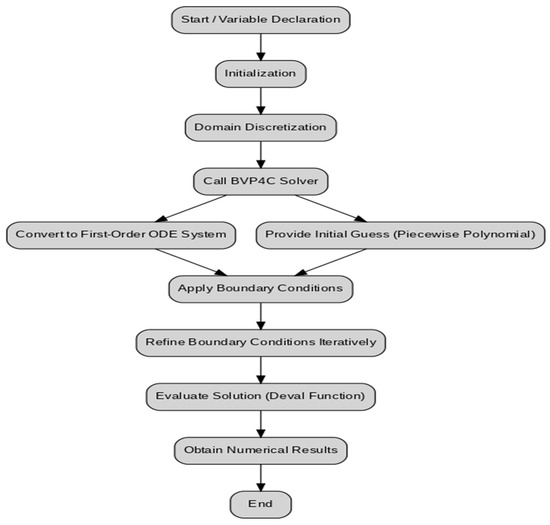
Figure 2.
Flow chart.
2. Results and Discussion
The results presented in Table 1 for in the absence of energy equation and other physical parameters with boundary conditions show good agreement with the findings of other authors, thereby confirming the accuracy and reliability of the present numerical approach.

Table 1.
Comparison of the results for , Pr = 0.7 in the absence of other physical parameters.
The graphical results presented in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18 and Figure 19 illustrate the impact of various parameters on the velocity and temperature profiles within the boundary layer of an electrically conducting fluid flow over a stretching tube.
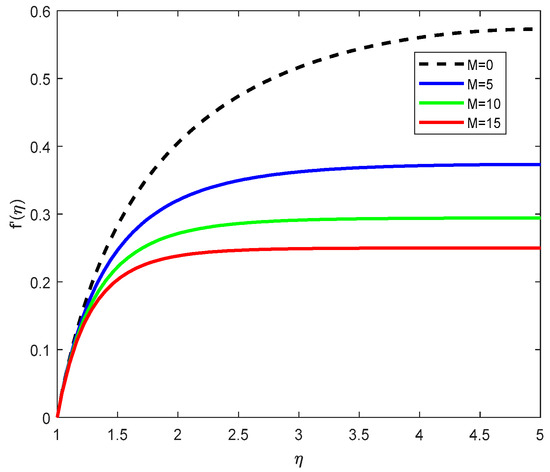
Figure 3.
Velocity Profiles f with various Magnetic parameter M.
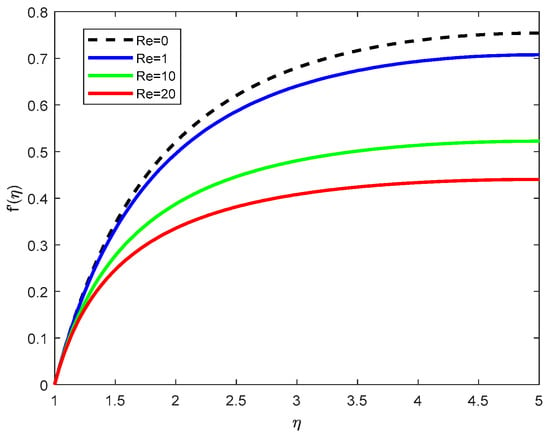
Figure 4.
Velocity Profiles f with various Reynolds number Re.
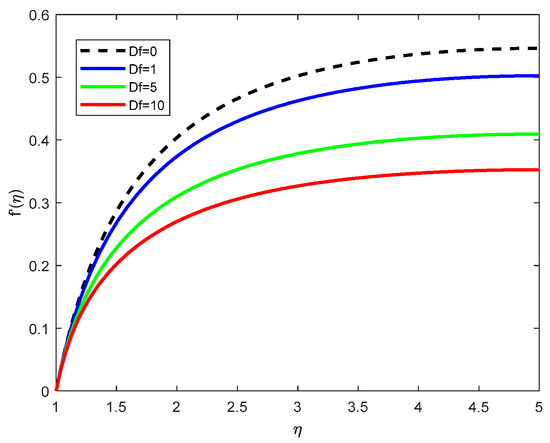
Figure 5.
Velocity Profiles f with various Darcy–Forchheimer parameters Df.
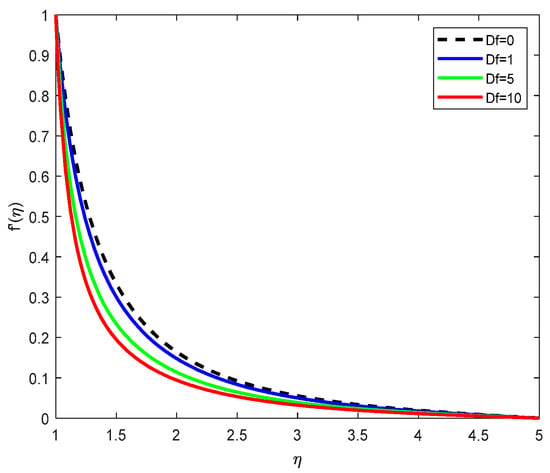
Figure 6.
Velocity Profiles of various Darcy–Forchheimer parameters.
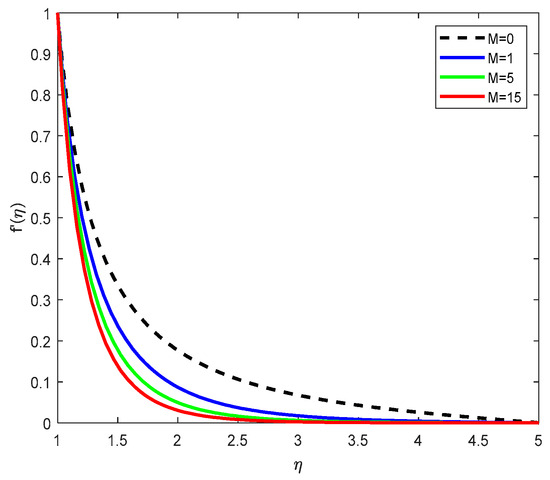
Figure 7.
Velocity Profiles with parameter M.
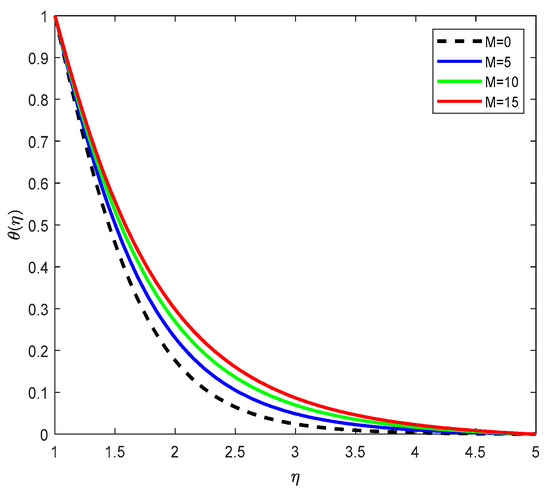
Figure 8.
Temperature Profiles with parameter M.
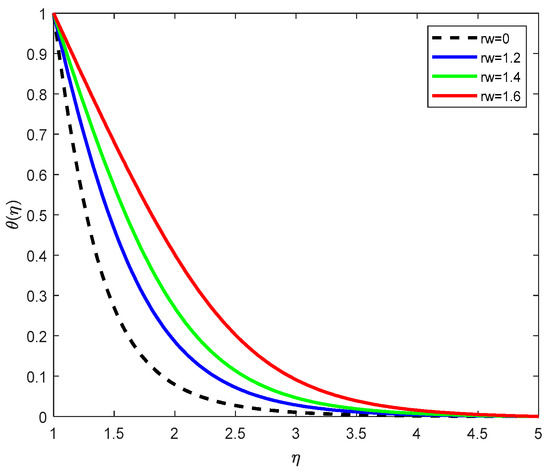
Figure 9.
Temperature Profiles with various rw temperature ratios.
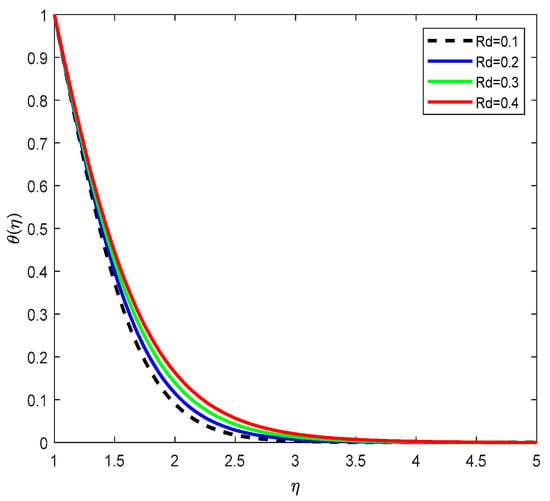
Figure 10.
Temperature Profiles with various Rd, Radiation Parameters.
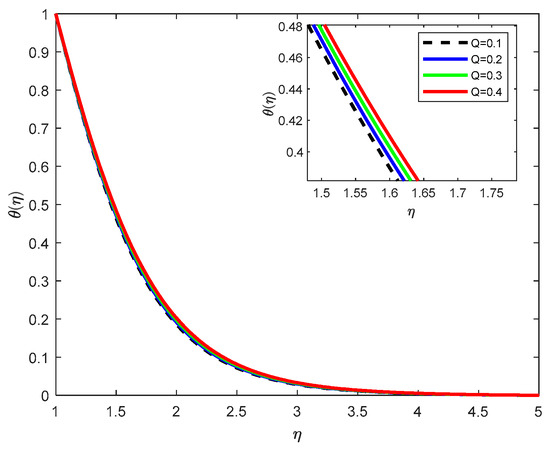
Figure 11.
Temperature Profiles with various Q, Heat Source/sink parameters.
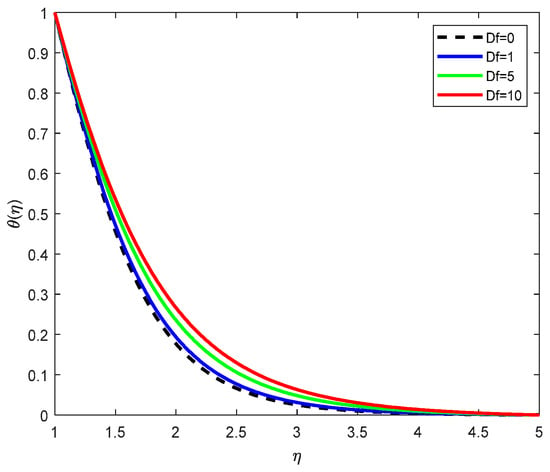
Figure 12.
Temperature Profiles with various Darcy–Forchheimer parameters.
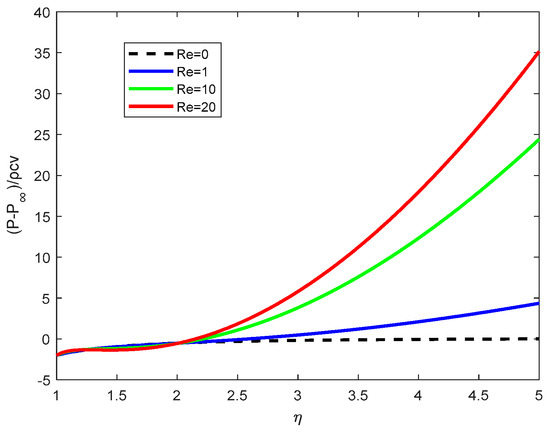
Figure 13.
Pressure distribution with various Re, Reynolds numbers.
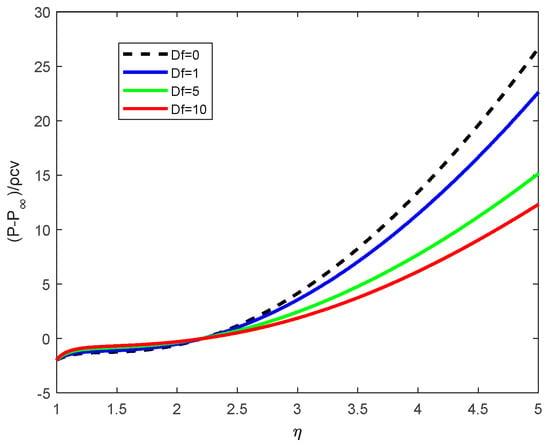
Figure 14.
Pressure distribution with various Df, Darcy–Forchheimer parameters.
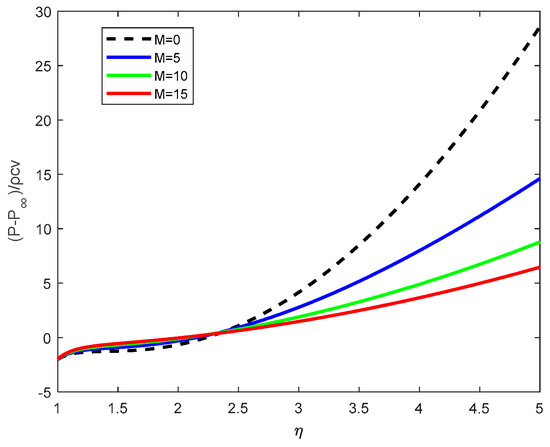
Figure 15.
Pressure distribution with various Magnetic parameters, M.
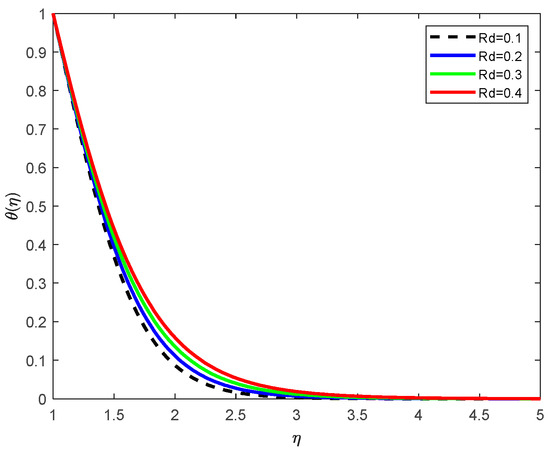
Figure 16.
Temperature Profiles with various Rd, Radiation Parameters when π/4.
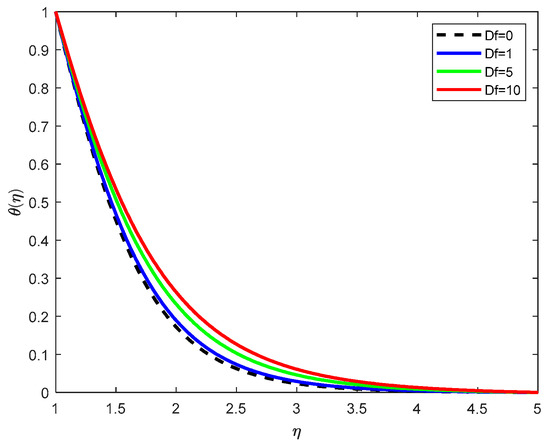
Figure 17.
Temperature Profiles with various Darcy–Forchheimer parameters when π/4.
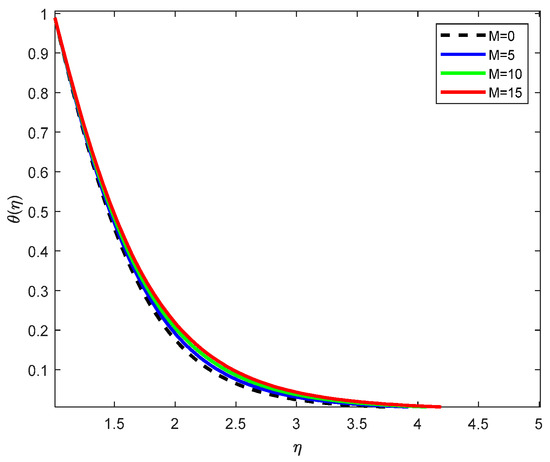
Figure 18.
Temperature Profiles with various Magnetic parameters when π/6.
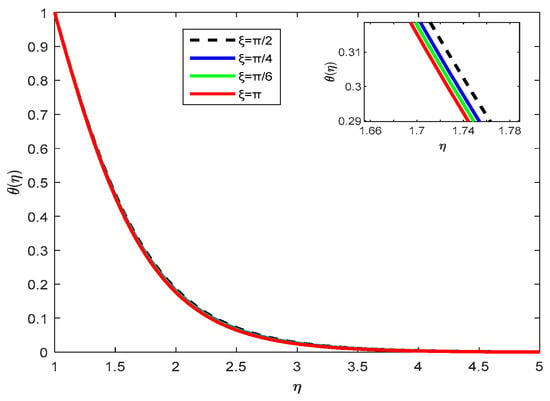
Figure 19.
Temperature Profiles with various values.
Figure 3 illustrates the effect of the magnetic parameter on the velocity profile It is observed that the velocity decreases with increasing . This is attributed to the Lorentz force generated by the interaction between the magnetic field and the electrically conducting fluid. The Lorentz force acts as a resistive drag, opposing the fluid motion and thereby reducing the velocity within the boundary layer. As a result, stronger magnetic fields significantly suppress the flow.
Figure 4 presents the variation in velocity with the Reynolds number An increase in corresponds to a higher ratio of inertial to viscous forces. However, in boundary layer flows over curved or rotating surfaces, a higher Reynolds number often implies a thinner boundary layer and enhanced inertial resistance, leading to a reduction in the flow velocity near the surface due to stronger momentum diffusion effects.
Figure 5 shows the influence of the Darcy–Forchheimer parameter on the velocity As this parameter increases, the velocity decreases. This is because the Darcy–Forchheimer model incorporates both permeability resistance (Darcy) and inertial drag (Forchheimer) within porous media. Higher values signify greater flow resistance through the porous medium, which causes a considerable reduction in fluid motion.
Graphs depicting velocity, temperature and concentration profiles
M = 0.8; Re = 10; Df = 0.5; K = 2; Pr = 0.7; Rd = 0.5; Q = 0.1; rw = 1.2;
Figure 6 further examines the impact of the Darcy–Forchheimer parameter, but on the velocity gradient . The trend similarly shows a decline in with increasing parameter values. This indicates that the rate of change in velocity near the wall also diminishes due to intensified frictional and inertial resistance in the porous medium, ultimately leading to a slower momentum transfer across the boundary layer.
Figure 7 shows that as the magnetic parameter M increases, the velocity of the fluid decreases. This behavior is expected due to the presence of the Lorentz force generated by the magnetic field, which acts in opposition to the motion of the conducting fluid. As M increases, the resistive magnetic damping effect becomes more dominant, reducing the fluid motion near the surface and across the boundary layer.
Figure 8 demonstrates that increasing the magnetic parameter M results in an increase in the temperature profile. This is a consequence of the suppressed convective motion caused by the magnetic field, which reduces the convective cooling effect. As the flow is slowed down by the magnetic field, less heat is convicted away from the heated surface, leading to a thicker thermal boundary layer and higher fluid temperatures.
Figure 9 shows that the temperature increases with the wall-to-ambient temperature ratio . A higher indicates a larger difference between the wall temperature and the ambient temperature. This intensifies the thermal gradient and leads to more heat being conducted into the fluid. As a result, the temperature distribution in the boundary layer rises significantly with increasing
Figure 10 indicates that an increase in the nonlinear radiation parameter leads to a higher temperature distribution. Thermal radiation contributes additional energy to the system, especially when the radiation term is nonlinear, thus enhancing the thermal energy content of the fluid. This results in a thicker thermal boundary layer and elevated temperature profiles.
Figure 11 shows that increasing the heat source/sink parameter also raises the temperature of the fluid. A positive denotes internal heat generation, which adds thermal energy directly into the fluid, thereby raising the temperature within the boundary layer. This effect becomes more pronounced as increases, especially near the wall region.
Figure 12 illustrates the influence of the Darcy–Forchheimer parameter on temperature. As increases, representing higher resistance due to porous medium effects, the temperature profile increases. This is because the flow resistance reduces the fluid velocity, which weakens convective heat transfer. As a result, the retained heat raises the fluid temperature across the thermal boundary layer.
The influence of key physical parameters on pressure distribution, Bejan number, and entropy generation number based on Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18 and Figure 19. The analysis is carried out with respect to varying Reynolds numbers , Darcy–Forchheimer parameters , magnetic parameters , and Brinkman numbers .
Figure 13 shows that as the Reynolds number increases, the pressure distribution increases significantly. Physically, a higher Reynolds number implies stronger inertial forces, which lead to increased fluid motion and higher resistance in terms of pressure.
Figure 14 illustrates that increasing the Darcy–Forchheimer parameter causes the pressure distribution to decrease. This behavior is due to increased porous medium resistance, which suppresses the flow, resulting in lower pressure build-up.
Figure 15 indicates that pressure distribution decreases with an increase in the magnetic parameter . This can be attributed to the Lorentz force, which acts opposite to the flow direction and inhibits the fluid motion, thereby reducing the pressure gradient.
Figure 16 illustrates the variation in temperature with respect to the nonlinear radiation parameter under the influence of magnetic field inclination at an angle ξ = π/4. The results show that the temperature within the thermal boundary layer increases as Rd increases. This is due to the enhanced thermal energy transfer via radiation, which becomes more pronounced with higher values. The effect is further amplified by the inclined magnetic field, which exerts a Lorentz force that suppresses fluid motion and convective heat loss. As a result, the temperature distribution rises sharply, indicating thicker thermal boundary layers and stronger thermal gradients near the surface.
Figure 17 presents the impact of the Darcy–Forchheimer parameter on the temperature distribution for a magnetic field inclined at ξ = π/4. An increase in , which characterizes resistance due to both Darcy permeability and inertial drag, leads to elevated temperatures throughout the boundary layer. In the presence of magnetic field inclination, this resistance effect is compounded. The inclined magnetic force directionally restricts fluid motion, further suppressing convective heat transport. This reduction in convective cooling enhances thermal energy accumulation in the fluid, especially near the wall region, thereby increasing the temperature profile significantly with higher values.
Figure 18 shows how the magnetic parameter influences temperature variation when the magnetic field is inclined at ξ = π/6. The results demonstrate that temperature increases noticeably with increasing M. The inclined magnetic field intensifies the Lorentz force acting opposite to the flow direction, diminishing fluid velocity and weakening convective heat transfer. This effect is more pronounced at ξ = π/6, as the inclination introduces asymmetry in the flow and alters the thermal boundary layer development. The combined effect of magnetic resistance and angular influence leads to higher fluid temperatures, especially near the stretching surface.
Figure 19 as the magnetic field inclination angle ξ decreases from π to π/2, π/4, and π/6, the temperature within the boundary layer decreases. This is due to the weaker damping effect of the magnetic field on the fluid motion at lower inclination angles, which enhances convective heat transfer and cools the system more effectively.
Key Physical Insights
- Magnetic field : Suppresses velocity but increases temperature due to reduced convection, acting as a dual control mechanism on momentum and energy transfer.
- Darcy–Forchheimer drag : Weakens flow but enhances thermal buildup, highlighting porous media’s role in entropy generation.
- Reynolds number : Strengthens inertial resistance, reducing velocity near the wall while raising pressure and shear stress.
- Nonlinear radiation & heat source : Significantly increase thermal energy, expanding the thermal boundary layer and amplifying entropy generation.
- Magnetic inclination (ξ): Alters Lorentz force distribution, shifting momentum suppression and thermal retention depending on angle.
Overall, the interaction of these parameters governs entropy generation and Bejan number variations. Higher magnetic damping, porous resistance, and radiation favor heat accumulation and entropy production, while higher Reynolds number promotes momentum-driven transport but reduces thermal retention.
Entropy Generation Analysis and Bejan Number Formulation
The entropy generation rate in a viscous, electrically conducting fluid under the influence of a magnetic field comprises three primary contributions: thermal conduction, fluid friction, and magnetic effects.
where is the ambient fluid temperature, is thermal conductivity, is dynamic viscosity, is electrical conductivity, is the magnetic field strength, and is the velocity component in the axial direction.
By introducing appropriate non-dimensional variables, the entropy generation rate can be reformulated in dimensionless form as
where ,
is the entropy generation number. Equation (13) can be written in the form:
where ,
- and
- .
Here represents the total fluid friction and magnetic field contribution to entropy.
A useful dimensionless quantity known as the Bejan number is defined to evaluate the relative contribution of heat transfer to total entropy generation:
By definition, the Bejan number ranges from 0 to 1. A value greater than 0.5 indicates that heat transfer irreversibility dominates, while a value less than 0.5 suggests that viscous and magnetic dissipations are more significant. When Be = 0.5, the irreversibility from thermal and frictional/magnetic effects is equal.
Figure 20 shows that the Bejan number decreases with increasing Brinkman number This shows that entropy generation due to fluid friction and magnetic effects becomes more dominant compared to thermal irreversibility, reducing the relative contribution of heat transfer to total entropy generation.
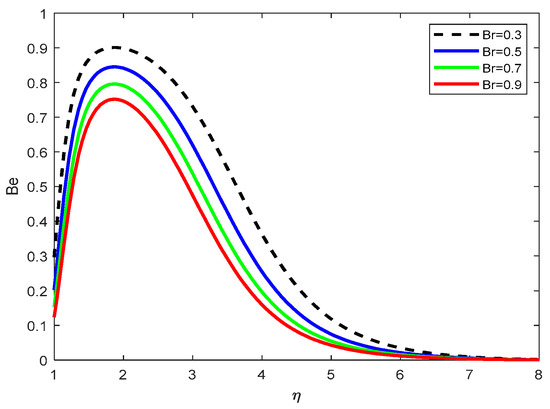
Figure 20.
Bejan number variation for .
Figure 21 reveals that the Bejan value increases with increasing magnetic parameter . This indicates that the heat transfer irreversibility becomes more significant compared to magnetic and frictional dissipation as the magnetic field strength increases, possibly due to enhanced thermal gradients.
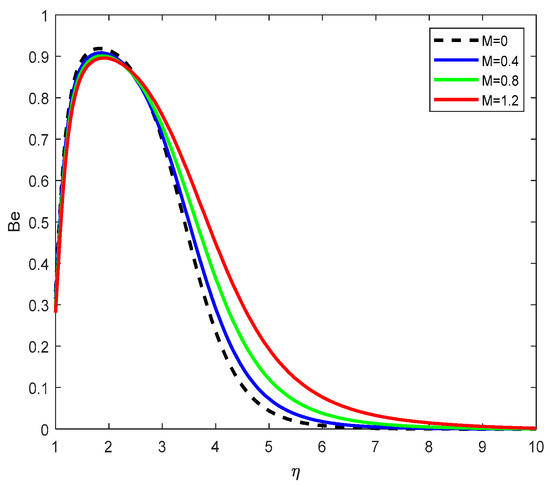
Figure 21.
Bejan variation for varying .
Figure 22 demonstrates that the entropy generation number increases with increasing magnetic parameter . The magnetic field introduces additional resistance (via the Lorentz force), which enhances internal friction and consequently increases overall entropy generation.
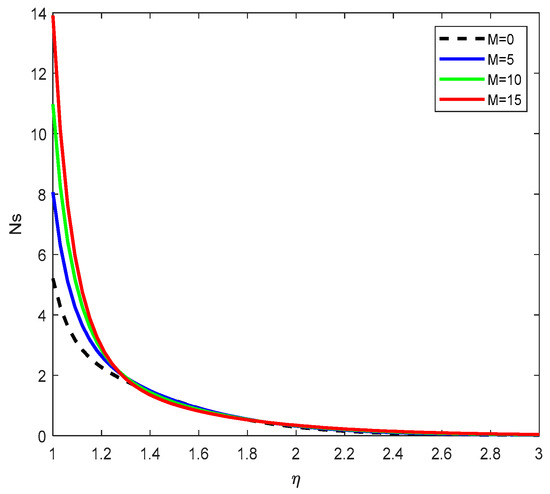
Figure 22.
Entropy generation variation for .
Figure 23 confirms that entropy generation enhances with an increase in the Brinkman number A higher indicates greater viscous dissipation effects relative to heat conduction, thereby enhancing the entropy generation rate.
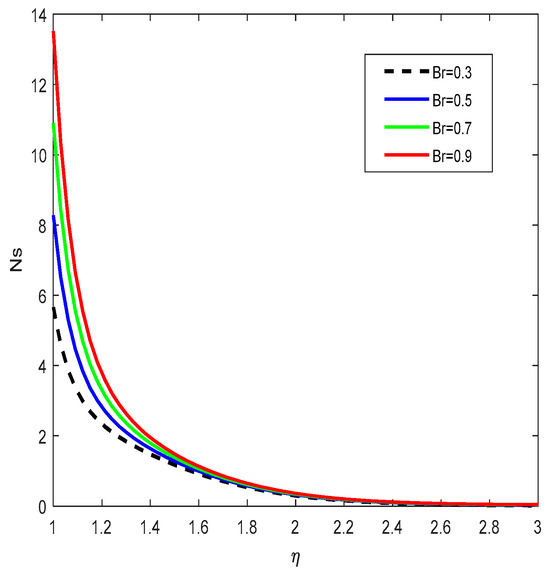
Figure 23.
Entropy generation variation for .
Figure 24 depicts that entropy generation increases with increasing Darcy–Forchheimer parameter . The intensified resistance due to the porous structure leads to more flow obstruction and internal friction, contributing to higher irreversibility.
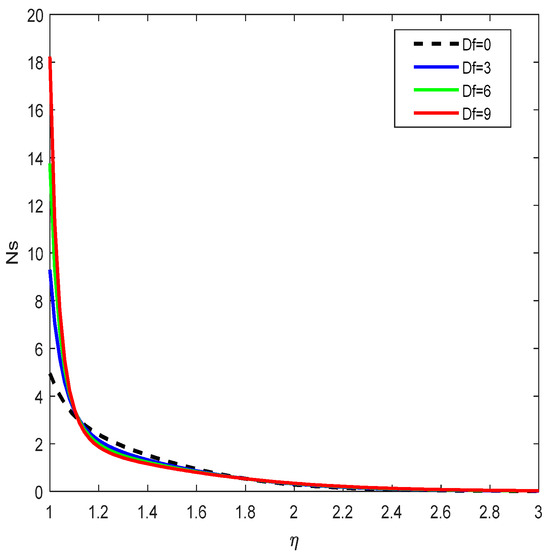
Figure 24.
Entropy generation variation for .
The entropy generation and Bejan number profiles show insensitivity to further increases in the similarity variable limit (η → ∞) as depicted in the figures, thereby confirming the stability and reliability of the obtained results.
3. Key Findings
Velocity Profiles:
The velocity of the fluid decreases with increasing magnetic parameter due to the Lorentz force, which imparts a damping effect opposing the flow. Similarly, higher Darcy–Forchheimer parameter values—representing porous medium resistance—significantly suppress fluid motion, and increasing Reynolds number (Re) also leads to reduced near-wall velocities due to enhanced inertial resistance and boundary layer thinning.
Temperature Distributions:
The thermal boundary layer thickens with increasing nonlinear radiation parameter heat source (Q), and wall-to-ambient temperature ratio . These parameters elevate the temperature by weakening convective cooling and enhancing thermal energy input or retention in the system.
Pressure Behavior:
Pressure increases with , driven by stronger inertial effects, while it decreases with both and , owing to greater drag forces and magnetic damping, respectively.
Entropy Generation and Irreversibility:
The entropy generation number rises with increasing (Brinkman number), and , indicating intensified thermal and viscous dissipation. The Bejan number decreases with , revealing a shift toward dominance of fluid friction and magnetic reversibility. Conversely, it increases with suggesting that heat transfer irreversibility becomes more prominent under stronger magnetic effects.
Table 2 represents numerical values for Skin Friction and Nusselt number. The numerical results reveal clear trends in how various physical parameters influence the flow and heat transfer characteristics in the problem.

Table 2.
Numerical values for Skin Friction and Nusselt number. .
As the magnetic parameter increases, the skin friction coefficient (0) becomes increasingly negative, indicating greater resistance to the fluid motion due to the Lorentz force. Concurrently, the Nu, which represents the rate of heat transfer at the wall, decreases steadily. This shows that the application of a magnetic field suppresses both momentum and thermal transport due to magnetic damping effects.
The wall-to-ambient temperature ratio which represents the thermal difference between the tube surface and the ambient fluid, significantly affects heat transfer but not the flow field. As increases, the value of (0) remains constant and then increases, implying that the flow is affected. However, the Nu decreases sharply, indicating that increasing the wall temperature relative to the ambient reduces the thermal gradient at the surface, and thus, the rate of heat transfer.
The nonlinear thermal radiation parameter also demonstrates a clear impact on the thermal field. As increases, the Nu decreases, showing that enhanced radiation leads to increased internal energy transport, which in turn reduces the effectiveness of convective heat transfer.
With regard to the heat source/sink parameter , an increase in leads to a consistent decline in the Nu. This suggests that the presence of a heat source within the fluid domain reduces the thermal gradient near the surface, thereby diminishing the overall heat transfer rate.
The Darcy–Forchheimer parameter , which accounts for resistance due to a porous medium, influences both the velocity and thermal fields. As increases, the magnitude of (0) becomes more negative, indicating stronger resistance to flow due to nonlinear drag. Simultaneously, the Nu decreases slightly, suggesting a mild reduction in heat transfer efficiency.
The Prandtl number which represents the ratio of momentum diffusivity to thermal diffusivity, has a pronounced effect on the heat transfer rate. As increases, the Nu increases significantly. This implies that fluids with higher Prandtl numbers (such as oils) have thinner thermal boundary layers, resulting in higher temperature gradients at the surface and hence, more efficient heat transfer.
Lastly, the Reynolds number , indicative of the flow’s inertial effects, shows that increasing Re enhances both the surface shear stress and the Nu. This means that higher flow velocities improve both the rate of momentum transfer and convective heat transfer.
In summary, the magnetic parameter, heat source, radiation, Darcy–Forchheimer drag, and temperature ratio primarily reduce heat transfer rates, while higher Prandtl and Reynolds numbers enhance it. The flow resistance increases notably with magnetic and porous medium effects, while heat transfer is most sensitive to the wall temperature ratio, radiation, and Prandtl number.
4. Response Surface Methodology (RSM)
RSM is used to optimize the response by systematically exploring the relationships and interactions among the influencing factors. It is particularly advantageous in the context of experimental design and process optimization.
In this study, RSM is utilized to establish the functional relationship between the critical parameters—namely, Darcy–Forchheimer number , radiation parameter , and wall radius —and the resulting response variables. Table 3 depicts the range and levels of the selected parameters, while Table 4 presents the corresponding response values obtained from 20 experimental runs. A multivariate regression model has been developed to express the response variables as functions of the identified parameters.

Table 3.
Effective Parameter Ranges.

Table 4.
Coded Values (.
Model Accuracy
The accuracy of the regression models is assessed using an analysis of variance table and residual analysis, as presented in Table 5. Statistical measures such as p-values and F-values are employed to evaluate the significance of individual terms and the overall variability within the dataset. In this context, model terms with an F-value greater than 1 and a p-value less than 0.05 are considered statistically significant and retained. Consequently, the squared term g2 and interaction terms such as Df2 and Rd2 are excluded from the Nusselt number (Nu) model due to their lack of relevance.

Table 5.
Analysis of variance, ANOVA, for the rate of heat transfer ().
Figure 25 presents the residual plots. Although a few residuals deviate more significantly, the overall trend supports the model’s adequacy and predictive capability. These observations collectively validate the effectiveness of the quadratic model in capturing the underlying response behavior, affirming its appropriateness for engineering applications in this study.
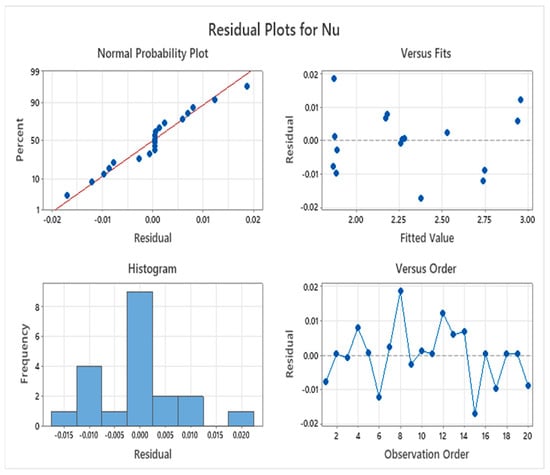
Figure 25.
Residual Plots for .
Degrees of Freedom: DoF; Mean Squares: MS; Sum of Squares: SS. The reduced regression model for , as derived from Table 5, is provided.
Figure 25 represents residual plots for . In the normal probability plot, the red line denotes the ideal normal distribution, while the blue points represent residuals closely following it. The dotted lines in the residuals versus fits and versus order plots mark the zero-residual level, around which the blue points are randomly scattered, confirming normality, independence, and randomness of errors.
Figure 26, Figure 27 and Figure 28 display the contour and three-dimensional surface plots for the Nusselt number (Nu), providing a visual depiction of how interaction effects influence heat transfer performance.
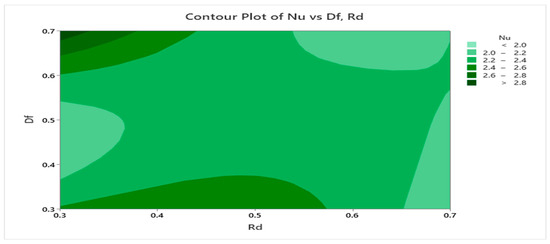
Figure 26.
Contour Plot of vs , .
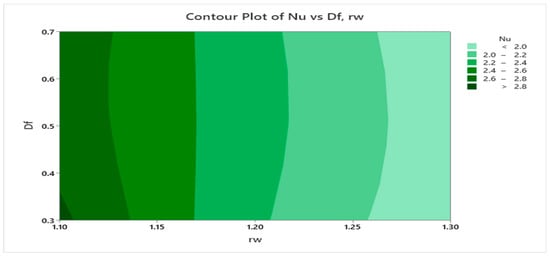
Figure 27.
Contour Plot of vs , .
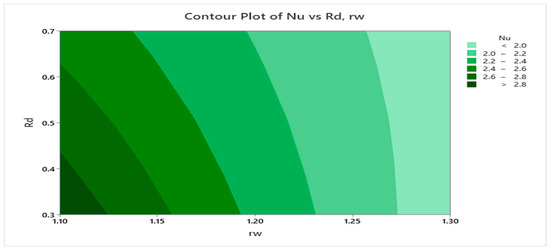
Figure 28.
Contour Plot of vs , .
In Figure 26, it is evident that both the Darcy–Forchheimer number (Df) and the radiation parameter (Rd) positively contribute to enhancing Nu. The maximum frictional effect is observed when Df reaches its upper limit, while Rd is at a reduced level.
Figure 27 presents the coupled influence of the Darcy–Forchheimer parameter (Df) and wall-to-ambient temperature ratio (rw) on the Nusselt number (Nu). It is evident that superior heat transfer performance is obtained when both parameters are maintained at relatively low levels. Increasing Df intensifies the inertial resistance within the porous medium, thereby attenuating convective transport and leading to a decline in Nu. Likewise, larger rw values reduce the curvature-driven thinning of the thermal boundary layer, which further suppresses the surface heat transfer rate.
In Figure 28, the interaction between Rd and rw is analyzed. The graphical trend suggests that Nu improves as both parameters decrease, highlighting their inverse relationship with the response variable.
Figure 29, Figure 30 and Figure 31 collectively present the sensitivity of the Nusselt number (Nu) with respect to the temperature ratio (rw), radiation parameter (Rd), and Darcy–Forchheimer parameter (Df). The results show that both rw and Rd exhibit consistently negative sensitivities, indicating that an increase in either parameter reduces heat transfer performance. A larger temperature ratio weakens the surface temperature gradient or alters the flow geometry in a manner that diminishes convective efficiency, while higher radiation levels shift the thermal balance toward radiative dominance, thereby suppressing convective transport and thickening the thermal boundary layer. In contrast, the sensitivity of Nu to the Darcy–Forchheimer parameter (Df) remains negligible, suggesting that inertial resistance introduced by the porous medium exerts minimal influence on the heat transfer process under the studied conditions. These findings highlight that temperature ratio and radiation are the critical parameters controlling heat transfer behavior, whereas the effect of porous medium resistance is relatively insignificant.
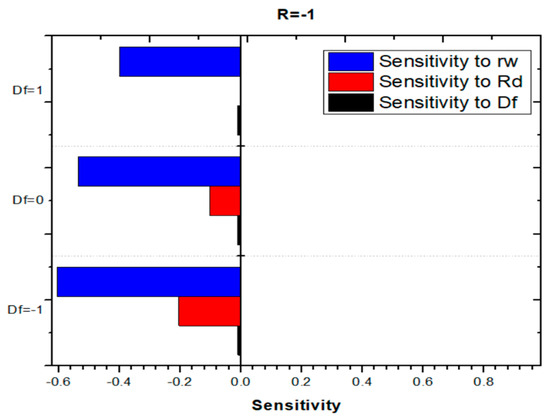
Figure 29.
Sensitivity of the Nusselt number () to Darcy–Forchheimer parameter ().
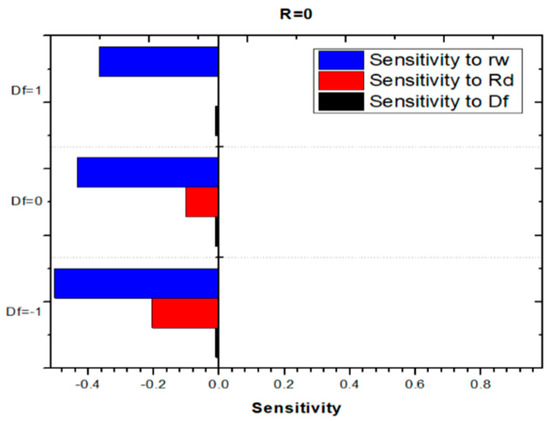
Figure 30.
Sensitivity of the Nusselt number () to radiation parameter ().
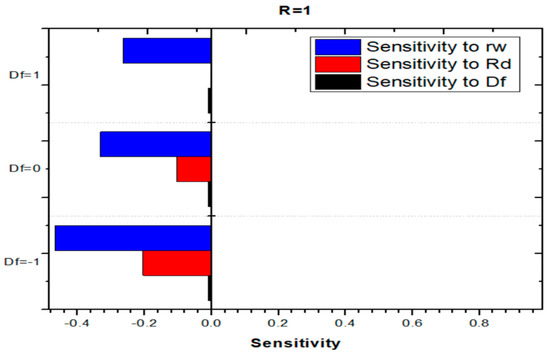
Figure 31.
Sensitivity of the Nusselt number () to temperature ratio ().
5. Interpretation
The findings highlight that both and negatively affect Nu, pointing to a reduction in thermal efficiency with increasing values of these parameters. Meanwhile, Df appears to play a negligible role in influencing Nu within the investigated range.
6. Conclusions
This study presents a comprehensive numerical investigation of the heat transfer and boundary layer flow characteristics of an electrically conducting viscous fluid over a stretching tube, incorporating the effects of aligned magnetic fields, nonlinear thermal radiation, heat generation/absorption, and porous medium resistance modeled through the Darcy–Forchheimer formulation. Such analyses are particularly relevant to polymer extrusion, wire coating, and metal drawing industries, where precise control of heat transfer in electrically conducting and radiative fluids is crucial for maintaining material quality during manufacturing processes. The analysis was conducted using a transformed system of nonlinear ordinary differential equations solved with robust numerical techniques.
The findings reveal that increasing magnetic field intensity and porous medium resistance significantly suppress fluid velocity and reduce wall shear stress due to the enhanced electromagnetic drag and nonlinear inertial resistance. Thermal performance is strongly influenced by parameters such as Rd, Q, and rw, which tend to increase the thermal boundary layer thickness and reduce the surface heat transfer rate, as indicated by the decreasing Nusselt number. The Prandtl number enhances heat transfer efficiency by thinning the thermal boundary layer, whereas higher Reynolds numbers amplify both shear stress and heat transfer rate, highlighting the importance of flow inertia in convective processes. These results have direct implications in nuclear reactor cooling, geothermal heat extraction, and chemical reactors with porous catalytic beds, where controlling heat transfer and surface shear is critical for system efficiency and safety.
Entropy generation analysis shows that the magnetic parameter, Brinkman number, and Darcy–Forchheimer parameter increase the total entropy production, with the Bejan number effectively quantifying the dominance of thermal versus frictional and magnetic irreversibility. Specifically, the Bejan number decreases with Br, indicating increased dominance of viscous and magnetic entropy generation, while it increases with M due to stronger thermal gradients caused by flow suppression. Such entropy minimization analyses are highly useful in designing energy-efficient cooling systems, optimizing magnetohydrodynamic (MHD) pumps, and improving thermal management in electronic and electrochemical devices, where reducing irreversibility is essential for maximizing performance and reliability.
The Response Surface Methodology (RSM) analysis further supports these observations by providing quantitative insights into interaction effects and parameter sensitivities. It demonstrates that the wall-to-ambient temperature ratio (rw) and the nonlinear radiation parameter (Rd) consistently exert negative effects on the Nusselt number (Nu), thereby reducing thermal efficiency, whereas the Darcy–Forchheimer parameter (Df) shows only minimal influence within the investigated range. Sensitivity studies indicate that heat transfer performance is particularly vulnerable to increases in rw and Rd, underscoring the need for careful thermal management in practical applications.
From a physical standpoint, these results imply that higher magnetic fields and porous resistance enhance stability but at the cost of reduced fluid transport and cooling efficiency. Similarly, while nonlinear radiation enriches thermal energy retention, it suppresses convective cooling, which is undesirable in high-efficiency systems. These insights are vital for the design of magnetohydrodynamic (MHD) generators, advanced heat exchangers, nuclear cooling systems, and porous media-based energy devices.
In conclusion, this study not only identifies the controlling role of electromagnetic and porous effects in curved geometries but also emphasizes the delicate balance between heat transfer enhancement and entropy minimization. The RSM analysis strengthens the predictive capability of the model and provides a framework for optimization in industrial and energy-related applications.
The present investigation is limited to steady, laminar, axisymmetric boundary layer flow over a porous stretching cylinder, with the induced magnetic field, Hall effects, and viscous dissipation neglected for simplification. The analysis is based on a single-phase nanofluid model without considering particle–fluid interactions at the microscale. Future research could extend the present model to unsteady or turbulent regimes, incorporate additional effects, such as slip boundary conditions and multi-phase nanofluids.
It is also acknowledged that, due to the novelty of the entropy generation and Bejan number analysis in this configuration, external benchmarks for these fields are currently unavailable.
Author Contributions
Conceptualization, S.V., B.P., S.S.K.R. and S.V.V.; Methodology, S.V., B.P., S.S.K.R. and S.V.V.; Software, S.V., B.P. and S.S.K.R.; Validation, S.V., B.P. and S.S.K.R.; Formal analysis, S.V., B.P., S.S.K.R. and S.V.V.; Investigation, S.V., B.P. and S.S.K.R.; Resources, F.H.H.A.M. and B.S.; Data curation, S.V. and S.S.K.R.; Writing—original draft, S.V., B.P. and S.S.K.R.; Writing—review & editing, S.V., S.S.K.R. and S.V.V.; Visualization, S.S.K.R. and B.S.; Supervision, S.S.K.R. and S.V.V.; Project administration, F.H.H.A.M.; Funding acquisition, F.H.H.A.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia [Grant No. KFU253491].
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare that they have no conflicts of interest related to this study.
Nomenclature
| Symbol | Description |
| a | Radius of the cylindrical surface (m) |
| B0 | Aligned magnetic field strength (T) |
| c | Constant associated with axial stretching rate s−1 |
| Cf | Non-dimensional coefficient indicating wall shear stress (skin-friction) |
| f | Stream-function expressed in non-dimensional form |
| k | Thermal conductivity of the fluid (W·m−1·K−1) |
| M | Hartmann number representing magnetic field interaction |
| Nu | Local Nusselt number indicating surface heat transfer rate |
| p | Pressure within the fluid flow (Pa) |
| Pr | Prandtl number, defined as the ratio ν/α |
| qw | Heat flux at the surface of the cylinder (W·m−2) |
| Re | Reynolds number, indicating inertial to viscous force ratio |
| T | Temperature of the fluid at a given location (K) |
| Tw | Prescribed temperature at the cylinder surface (K) |
| T∞ | Temperature of the surrounding undisturbed fluid (K) |
| (u, w) | Velocity components in radial and axial directions, respectively (m·s−1) |
| (r, z) | Cylindrical coordinate system (radial and axial positions) |
| α | Thermal diffusivity of the fluid (m2·s−1) |
| η | Similarity transformation variable |
| θ | Non-dimensional temperature variable |
| σ | Electrical conductivity of the fluid (sm−1) |
| ν | Kinematic viscosity (ν = μ/ρ) (m2·s−1) |
| μ | Fluid’s dynamic viscosity (Pa.s) |
| ψ | Stream-function in dimensional form (m2·s−1) |
| τw | Shear stress exerted at the cylinder surface |
| ρ | Density of the fluid (kgm−3) Angle of inclination |
| Subscript | Meaning |
| w | Evaluated at the cylinder surface |
| ∞ | Evaluated in the free stream (far from the surface) |
| Parameter | Description |
| Q | Internal heat generation/absorption parameter |
| Df | Darcy–Forchheimer porous medium parameter |
| Rd | Non-linear radiation parameter |
| Wall-to-ambient temperature ratio (Tw⁄T∞) | |
| M | Magnetic parameter (listed above for completeness) |
| Entropy generation rate (W·m−3·K−1) | |
| Dimensionless temperature difference | |
| Dimensionless parameter | |
| Entropy due to heat transfer (W/(m3K)) | |
| (W/(m3K)) | |
| (W/(m3K)) |
References
- Brucker, J. A Correlation by Natural Convection for Heat Transfer from Horizontal Cylinders That Accounts for Viscous Dissipation. Int. J. Heat Mass Transf. 1983, 26, 709–716. [Google Scholar] [CrossRef]
- Chamkha, A.J. Heat and Mass Transfer from Mhd Flow Over a Moving Permeable Cylinder with Heat Generation or Absorption and Chemical Reaction. Commun. Numer. Anal. 2011, 2011, 1–20. [Google Scholar] [CrossRef]
- Ishak, A.; Nazar, R.; Pop, I. Magnetohydrodynamic (Mhd) Flow and Heat Transfer Due to A Stretching Cylinder. Energy Convers. Manag. 2008, 49, 3265–3269. [Google Scholar] [CrossRef]
- Mukhopadhyay, S. Mixed Convection Boundary Layer Flow Along a Stretching Cylinder in Porous Medium. J. Pet. Sci. Eng. 2012, 96–97, 73–78. [Google Scholar] [CrossRef]
- Prasad, R.; Rao, S.; Bég, A. Computational Analysis of Viscous Dissipation and Joule-Heating Effects on Non-Darcy Mhd Natural Convection Flow from A Horizontal Cylinder in Porous Media with Internal Heat Generation. Theor. Appl. Mech. 2014, 41, 37–70. [Google Scholar] [CrossRef]
- Hayat, T.; Saeed, Y.; Asad, S.; Alsaedi, A. Convective Heat and Mass Transfer in Flow by An Inclined Stretching Cylinder. J. Mol. Liq. 2016, 220, 573–580. [Google Scholar] [CrossRef]
- Salimipour, E. A Numerical Study on The Fluid Flow and Heat Transfer from A Horizontal Circular Cylinder Under Mixed Convection. Int. J. Heat Mass Transf. 2019, 131, 365–374. [Google Scholar] [CrossRef]
- Awan, A.U.; Ali, B.; Shah, S.A.A.; Oreijah, M.; Guedri, K.; Eldin, S.M. Numerical Analysis of Heat Transfer in Ellis Hybrid Nanofluid Flow Subject to A Stretching Cylinder. Case Stud. Therm. Eng. 2023, 49, 103222. [Google Scholar] [CrossRef]
- Butt, A.S.; Ali, A.; Mehmood, A. Numerical Investigation of Magnetic Field Effects on Entropy Generation in Viscous Flow Over a Stretching Cylinder Embedded In A Porous Medium. Energy 2016, 99, 237–249. [Google Scholar] [CrossRef]
- Saeed, A.; Tassaddiq, A.; Khan, A.; Jawad, M.; Deebani, W.; Shah, Z.; Islam, S. Darcy-Forchheimer Mhd Hybrid Nanofluid Flow and Heat Transfer Analysis Over a Porous Stretching Cylinder. Coatings 2020, 10, 391. [Google Scholar] [CrossRef]
- Mishra, A.; Kumar, M. Velocity and Thermal Slip Effects on Mhd Nanofluid Flow Past a Stretching Cylinder with Viscous Dissipation and Joule Heating. SN Appl. Sci. 2020, 2, 1350. [Google Scholar] [CrossRef]
- Reddy, Y.D.; Goud, B.S.; Nisar, K.S.; Alshahrani, B.; Mahmoud, M.; Park, C. Heat Absorption/Generation Effect on Mhd Heat Transfer Fluid Flow Along a Stretching Cylinder with A Porous Medium. Alex. Eng. J. 2023, 64, 659–666. [Google Scholar] [CrossRef]
- Madkhali, H.A.; Ahmed, M.; Nawaz, M.; Alharbi, S.O.; Alqahtani, A.S.; Malik, M.Y. Numerical Study on The Role of Ternary Nanoparticles on Heat Transfer Enhancement in Mhd Flow of Cross-Rheological-Fluid. Case Stud. Therm. Eng. 2023, 51, 103579. [Google Scholar] [CrossRef]
- Kumar, P.; Yadav, R.S.; Makinde, O.D. Numerical Study of Williamson Fluid Flow and Heat Transfer Over a Permeable Stretching Cylinder with The Effects of Joule Heating And Heat Generation/Absorption. Heat Transf. 2023, 52, 3372–3388. [Google Scholar] [CrossRef]
- Murthy, D.V.N.S.R.; Babu, P.R.S.; Srinivasulu, C. Cattaneo-Christov Model for Mixed Convective Radiative Flow of Casson Fluid with Joule Heating in The Presence Of Chemical Reaction Over A Stretching Cylinder. JP J. Heat Mass Transf. 2023, 34, 153–181. [Google Scholar] [CrossRef]
- Zegeye, G.B.; Haile, E.; Awgichew, G. Combined Effects of Joule Heating and Binary Chemical Reaction of Mhd Williamson Nanofluid On Darcy–Forchheimer Porous Medium Past Unsteady Stretching Cylinder. Int. J. Thermofluids 2023, 20, 100474. [Google Scholar] [CrossRef]
- Jan, A.; Mushtaq, M.; Hussain, M. Heat Transfer Enhancement of Forced Convection Magnetized Cross Model Ternary Hybrid Nanofluid Flow Over a Stretching Cylinder: Non-Similar Analysis. Int. J. Heat Fluid Flow 2024, 106, 109302. [Google Scholar] [CrossRef]
- Mohanty, D.; Mahanta, G.; Shaw, S. Irreversibility and Thermal Performance of Nonlinear Radiative Cross-Ternary Hybrid Nanofluid Flow About a Stretching Cylinder with Industrial Applications. Powder Technol. 2024, 433, 119255. [Google Scholar] [CrossRef]
- Mahboobtosi, M.; Hosseinzadeh, K.; Ganji, D.D. Investigating the Convective Flow of Ternary Hybrid Nanofluids and Single Nanofluids Around a Stretched Cylinder: Parameter Analysis And Performance Enhancement. Int. J. Thermofluids 2024, 23, 100752. [Google Scholar] [CrossRef]
- Goud, B.S.; Dharmaiah, G.; Hendy, A.S.; Ali, M.R. Flow Over a Stretchable Cylinder with Nonlinear Heat Sources/Sinks: Magnetic Dipoles Application. Case Stud. Therm. Eng. 2024, 54, 104038. [Google Scholar] [CrossRef]
- Faisal, M.; Ahmad, I.; Awan, M.A. Analysis of Entropy Generation and Activation Energy In Unsteady Double Diffusive Flow Over A Stretching Cylinder. Heat Transf. 2024, 53, 646–665. [Google Scholar] [CrossRef]
- Gogoi, P.P. Thermocapillary Thin Film Flow Upon a Porous Heated Stretchable Cylinder. Heat Transf. 2024, 53, 73–96. [Google Scholar] [CrossRef]
- Nabwey, H.A.; El-Hakiem, A.M.A.; Khan, W.A.; Abdelrahman, Z.M.; Rashad, A.M.; Hawsah, M.A. Magnetic Williamson Hybrid Nanofluid Flow Around an Inclined Stretching Cylinder with Joule Heating in A Porous Medium. Chem. Eng. J. Adv. 2024, 18, 100604. [Google Scholar] [CrossRef]
- Ramireddy, P. The Impression of Thermal Stratification and Joule Heating on Hybrid Nanofluid Over a Porous Stretching Cylinder. JP J. Heat Mass Transf. 2025, 38, 47–76. [Google Scholar] [CrossRef]
- Ramasekhar, G.; Divya, A.; Selvi, P.D.; Narayanagari, R.; Reddy, R.C.S.; Jakeer, S.; Reddy, S.R.R.; Suneetha, S.; Shah, N.A.; Ahmed, S.F. Exploring the Role of Casson Hybrid Nanofluid Flow Through a Stretching Cylinder with A Significant Impact of Heat Source/Sink: A Computational Analysis. Aip Adv. 2025, 15, 035120. [Google Scholar] [CrossRef]
- Sobhanapuram, S.; Devi, S.R.; Ganteda, C.; Kottapalli, R.; Govindan, V.; Byeon, H.; Pimpunchat, B. On Cattaneo-Chrystov Heat Flux Model for Nanofluid Flow on Darcy–Forchheimer Porous Medium Past Unsteady Stretching Cylinder. Int. J. Thermofluids 2025, 26, 101101. [Google Scholar] [CrossRef]
- Faraz, M.; Park, J.M. Thermal and Mhd Behavior of Cnt Maxwell Nanofluid Over a Stretchable Cylinder. J. Radiat. Res. Appl. Sci. 2025, 18, 101326. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, L.; Nazir, F.; Ahmed, J.; Mohamed, A.; Khan, I.; Elseesy, I.E. Heat Transfer in Transient Motion of Thin Film Coatings with Copper (Cu), Aluminium Oxide (Al2o3) And Molybdenum Disulfide (MoS2) Nanoparticles Over a Stretching Cylinder. Case Stud. Therm. Eng. 2025, 69, 105951. [Google Scholar] [CrossRef]
- Farooq, U.; Imran, M.; Fatima, N. Computational Insights into The Thermal Behavior of Swcnt-Fe3O4 and Mwcnt-Cuo Hybrid Nanofluids in Stretching Cylinder with Response Surface Methodology. Multiscale Multidiscip. Model. Exp. Des. 2025, 8, 221. [Google Scholar] [CrossRef]
- Wang, C.Y. Fluid Flow Due to A Stretching Cylinder. Phys. Fluids 1988, 31, 466–468. [Google Scholar] [CrossRef]
- Ahmed, S.E.; Hussein, A.K.; Mohammed, H.A.; Sivasankaran, S. Boundary Layer Flow and Heat Transfer Due to Permeable Stretching Tube in The Presence of Heat Source/Sink Utilizing Nanofluids. Appl. Math. Comput. 2014, 238, 149–162. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).