Investigating the Performance of Longitudinal Groove on Noise Reduction in a NACA0015 Hydrofoil Using Computational Fluid Dynamics
Abstract
1. Introduction
2. Formulation
2.1. Momentum Change by Convection
2.2. Derivation of Forcing Terms
2.2.1. Gravity
2.2.2. Pressure
2.2.3. Viscosity
2.3. Ffowcs Williams-Hawkings (FW-H) Equation
3. Numerical Model
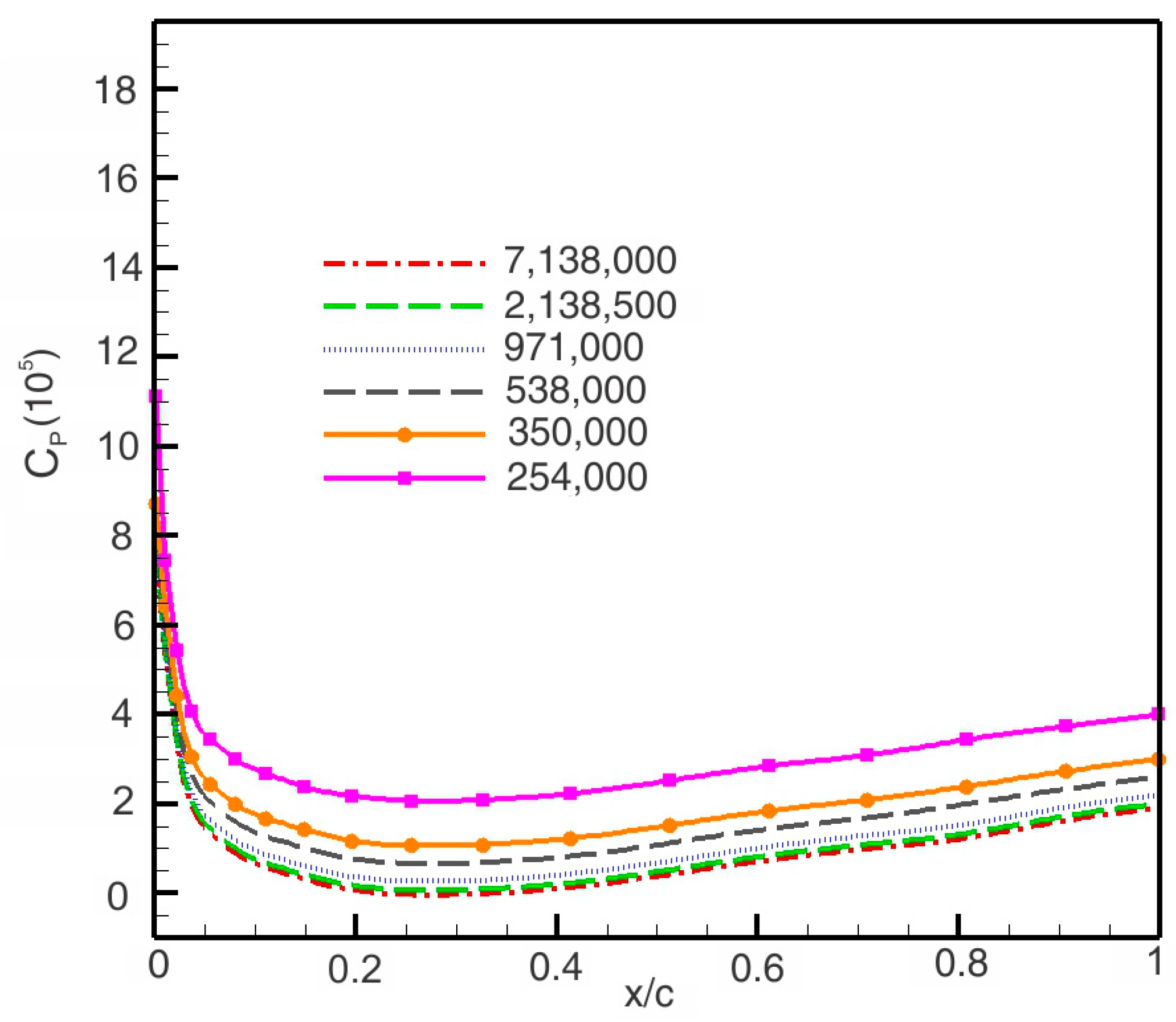
4. Mesh Independence
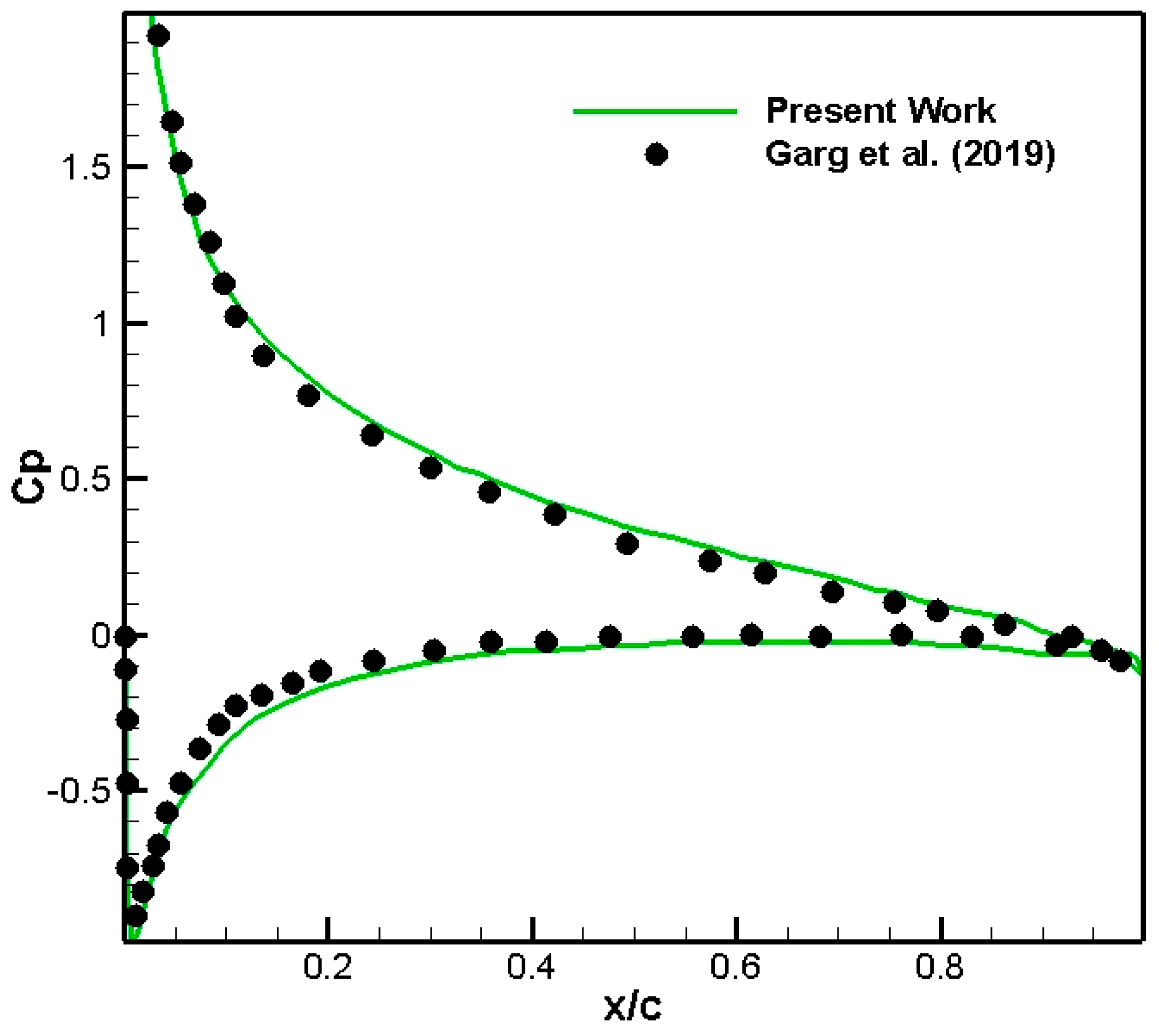
5. Validation
6. Results
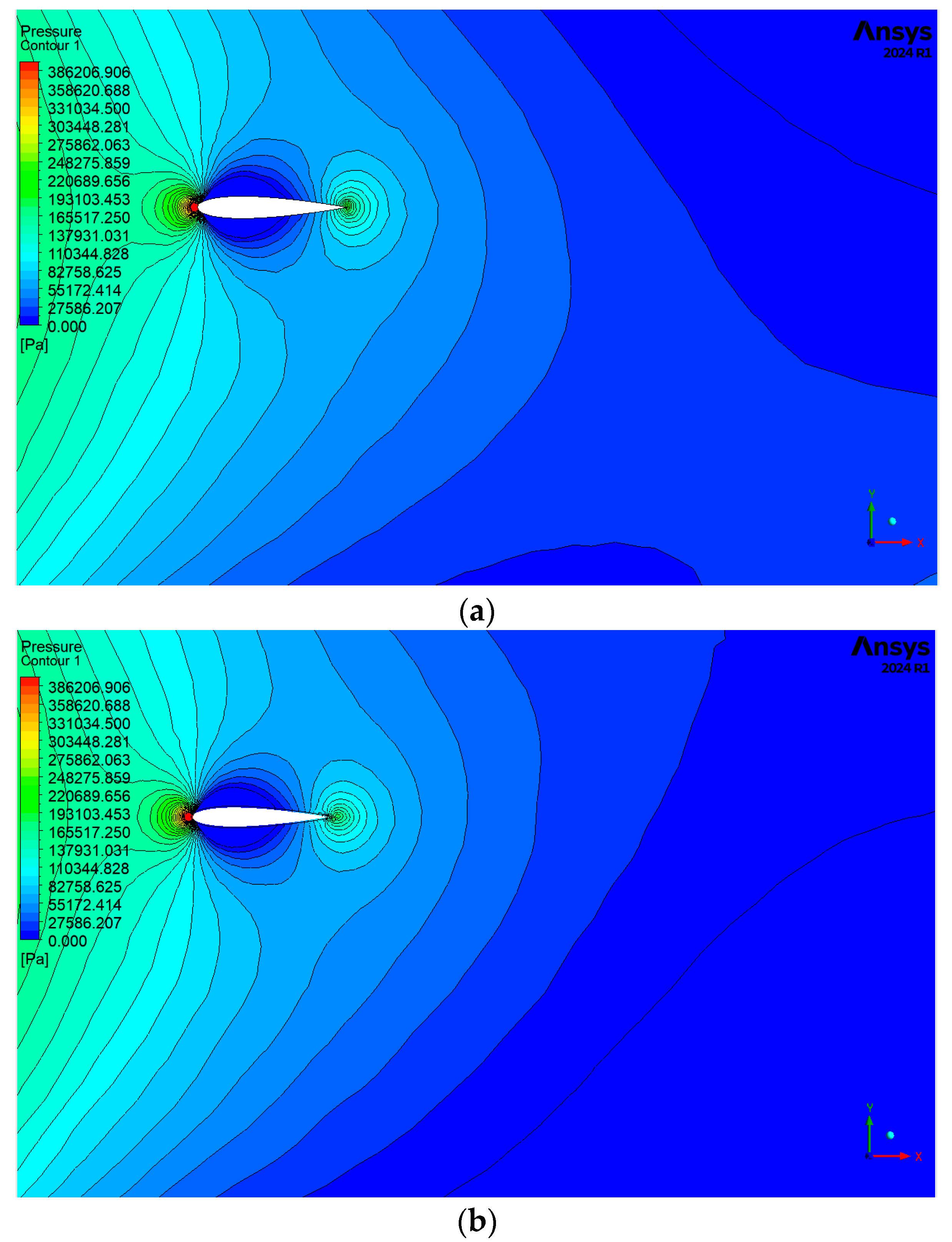
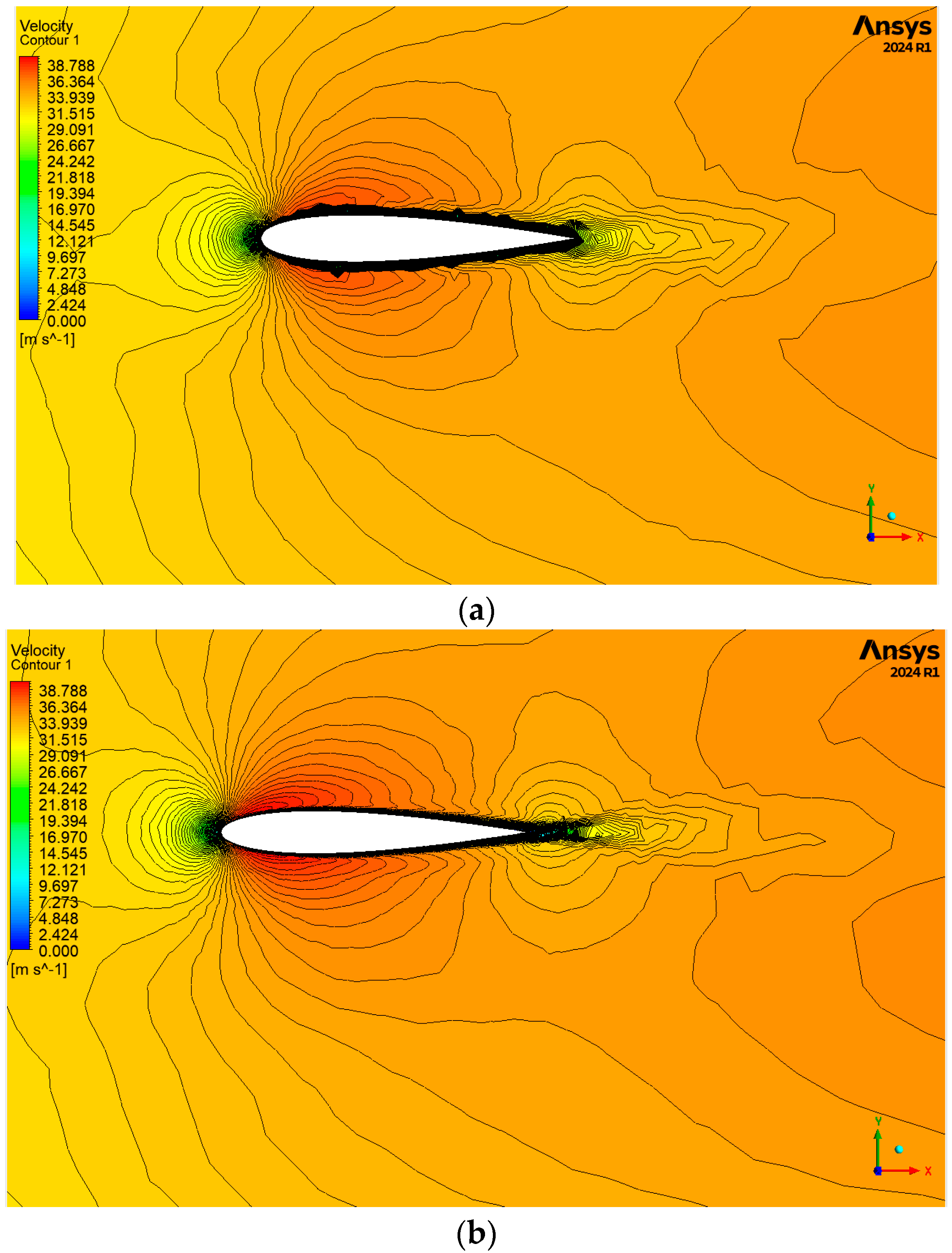
6.1. Contours
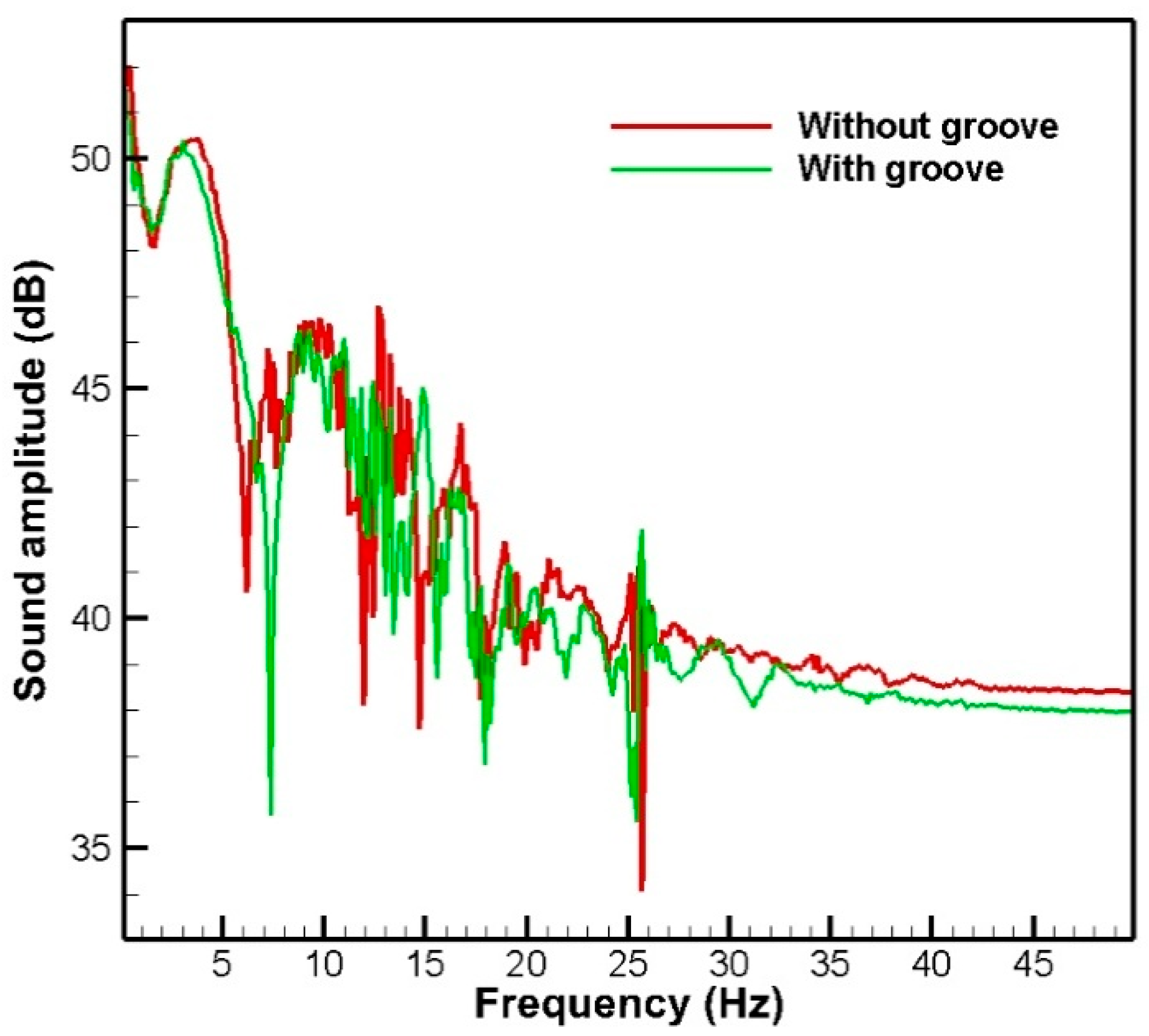
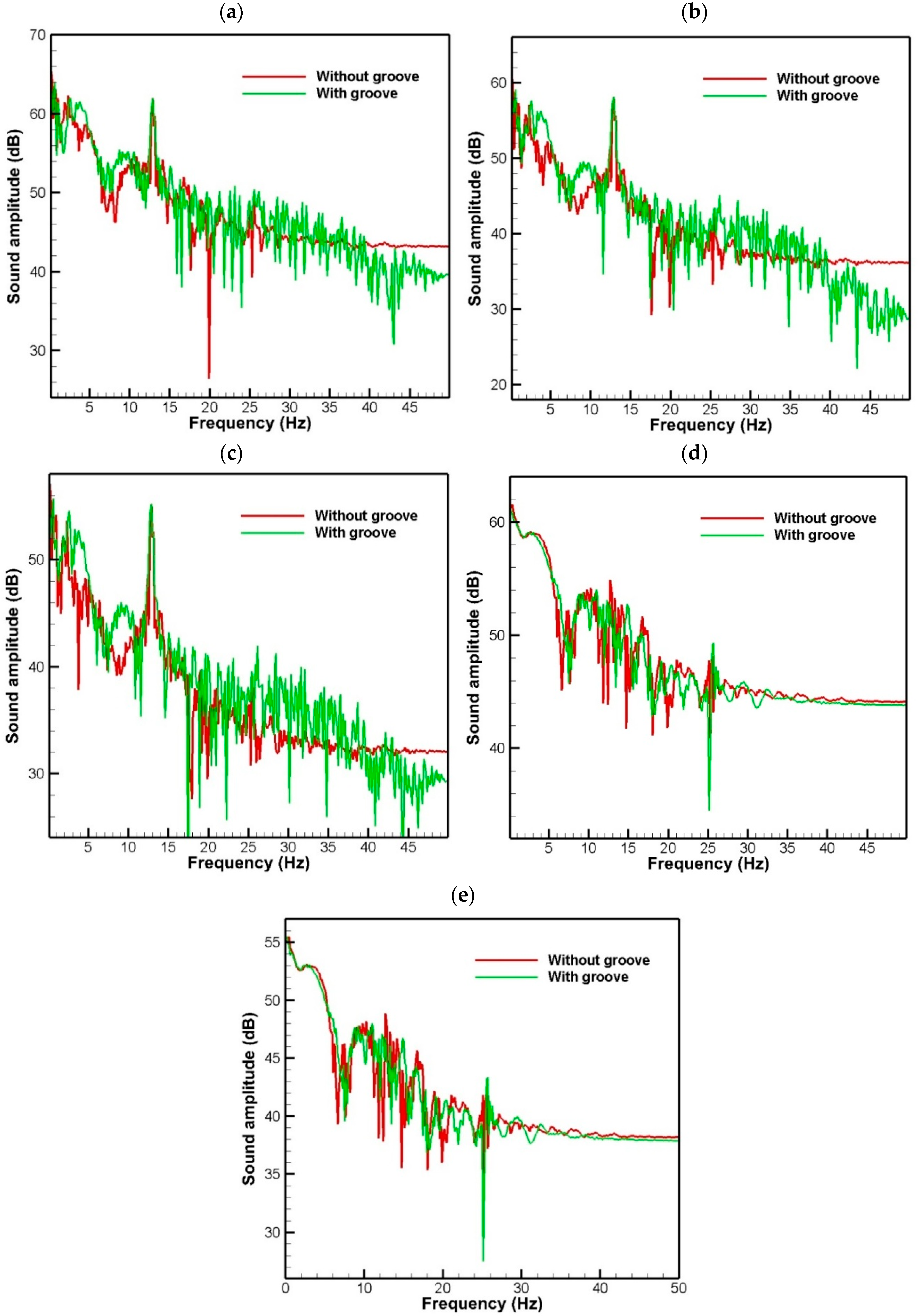
6.2. Noise Intensity by Frequency in Different Receivers
7. Conclusions
- At low frequencies (up to approximately 10 Hz), the noise intensity of the ungrooved hydrofoil is higher than that of the grooved hydrofoil, but in the frequency range of 10 to 20 Hz, the noise intensity of the grooved hydrofoil increases significantly and exceeds that of the ungrooved hydrofoil.
- At frequencies above 20 Hz, the noise intensity of both hydrofoils is approximately equal and does not change much.
- In general, it can be said that the use of grooves in the hydrofoil can increase the noise intensity in some frequency ranges (especially in the range of 10 to 20 Hz). However, at lower and higher frequencies, it has a good effect on noise reduction.
- The presence of grooves on the surface of the hydrofoil can change the flow pattern around it. This change can lead to a reduction in vortices and turbulence in the flow, which in turn affects the amount of noise generated.
- In the area behind the airfoil and close to it, the flow turbulence is high and the presence of grooves cannot control or greatly affect the noise generated in this area.
- As the distance of the noise receivers from the hydrofoil increases, the intensity of the received noise decreases at all frequencies.
- The area of the low-pressure region behind the hydrofoil decreases in the grooved state compared to the low-pressure state, which indicates an improvement in the performance of the hydrofoil in this regard.
- In the area behind the grooved hydrofoil, the lines of velocity alignment are more regular than in the ungrooved hydrofoil. This indicates the positive effect of the groove created on the hydrofoil on the downstream flows passing through it.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Taha, Z.; Ya, T.T.; Sawada, T. Numerical investigation on the performance of Wells turbine with non-uniform tip clearance for wave energy conversion. Appl. Ocean Res. 2011, 33, 321–331. [Google Scholar] [CrossRef]
- Luo, Y.; Wang, Z.; Liu, X.; Xiao, Y.; Chen, C.; Wang, H.; Yan, J. Numerical prediction of pressure pulsation for a low head bidirectional tidal bulb turbine. Energy 2015, 89, 730–738. [Google Scholar] [CrossRef]
- Heo, M.-W.; Kim, K.-Y.; Kim, J.-H.; Choi, Y.S. High-efficiency design of a mixed-flow pump using a surrogate model. J. Mech. Sci. Technol. 2016, 30, 541–547. [Google Scholar] [CrossRef]
- Zhang, W.; Yu, Z.; Zhu, B. Characteristic analysis on the pressure fluctuation in the impeller of a low specific speed mixed flow pump. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2016; p. 012035. [Google Scholar]
- Zhang, W.; Yu, Z.; Zhu, B. Influence of tip clearance on pressure fluctuation in low specific speed mixed-flow pump passage. Energies 2017, 10, 148. [Google Scholar] [CrossRef]
- Wang, J.; Sundén, B.; Zeng, M.; Wang, Q.-W. Influence of different rim widths and blowing ratios on film cooling characteristics for a blade tip. J. Heat Transf. 2012, 134, 061701. [Google Scholar] [CrossRef]
- Danlos, A.; Méhal, J.-E.; Ravelet, F.; Coutier-Delgosha, O.; Bakir, F. Study of the cavitating instability on a grooved Venturi profile. J. Fluids Eng. 2014, 136, 101302. [Google Scholar] [CrossRef]
- Qian, Z.; Wang, Z.; Guo, Z.; Dong, J.; Lu, J. Analysis of silt abrasion of the impeller ring in a centrifugal pump with J-grooves. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2016; p. 012021. [Google Scholar]
- Lidtke, A.K.; Turnock, S.R.; Humphrey, V.F. Characterisation of sheet cavity noise of a hydrofoil using the Ffowcs Williams–Hawkings acoustic analogy. Comput. Fluids 2016, 130, 8–23. [Google Scholar] [CrossRef]
- Kim, S.; Cheong, C.; Park, W.-G.; Seol, H. Numerical investigation of cavitation flow around hydrofoil and its flow noise. Trans. Korean Soc. Noise Vib. Eng. 2016, 26, 141–147. [Google Scholar] [CrossRef][Green Version]
- Liu, Y.; Tan, L. Method of C groove on vortex suppression and energy performance improvement for a NACA0009 hydrofoil with tip clearance in tidal energy. Energy 2018, 155, 448–461. [Google Scholar] [CrossRef]
- Huang, Z.; Han, Y.; Tan, L.; Huang, C. Influence of T-shape tip clearance on energy performance and broadband noise for a NACA0009 hydrofoil. Energies 2019, 12, 4066. [Google Scholar] [CrossRef]
- Dang, Z.; Mao, Z.; Tian, W. Reduction of hydrodynamic noise of 3d hydrofoil with spanwise microgrooved surfaces inspired by sharkskin. J. Mar. Sci. Eng. 2019, 7, 136. [Google Scholar] [CrossRef]
- Kundu, P.; Sarkar, A.; Nagarajan, V. Improvement of performance of S1210 hydrofoil with vortex generators and modified trailing edge. Renew. Energy 2019, 142, 643–657. [Google Scholar] [CrossRef]
- Hu, Z.; Huang, C.; Huang, Z.; Zhang, J. A method of bending shrinkage groove on vortex suppression and energy improvement for a hydrofoil with tip gap. Processes 2020, 8, 1299. [Google Scholar] [CrossRef]
- Liu, Y.; Tan, L. Influence of C groove on suppressing vortex and cavitation for a NACA0009 hydrofoil with tip clearance in tidal energy. Renew. Energy 2020, 148, 907–922. [Google Scholar] [CrossRef]
- Xie, X.; Chang, S.; Wang, C.; Guo, C. Numerical simulation of hydrodynamic performance of hydrofoil with inner groove. Chin. J. Ship Res. 2020, 15, 127–134. [Google Scholar]
- Huang, Z.; Huang, Z.; Fan, H. Influence of C groove on energy performance and noise source of a NACA0009 hydrofoil with tip clearance. Renew. Energy 2020, 159, 726–735. [Google Scholar] [CrossRef]
- Tirandazi, P.; Hidrovo, C.H. Study of drag reduction using periodic spanwise grooves on incompressible viscous laminar flows. Phys. Rev. Fluids 2020, 5, 064102. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, D.; Wang, F.; Zhang, G.; van Esch, B.B. Vortex suppression of the tip leakage flow over a NACA0009 hydrofoil via a passive jet induced by the double-control-hole. Ocean. Eng. 2021, 237, 109647. [Google Scholar] [CrossRef]
- Bi, Z.; Zhang, L.; Shao, X. Numerical study of suppression mechanism of two types of grooves on the TLV. Ocean Eng. 2021, 224, 108637. [Google Scholar] [CrossRef]
- Wang, W.; Li, Z.; Liu, M.; Ji, X. Influence of water injection on broadband noise and hydrodynamic performance for a NACA66 (MOD) hydrofoil under cloud cavitation condition. Appl. Ocean Res. 2021, 115, 102858. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, W.; Fang, D.; Sun, M.; Liu, J.; Song, D.; Zhang, X. Vortex suppression and flow pattern analysis of a hydrofoil with parallel grooves. Processes 2021, 9, 816. [Google Scholar] [CrossRef]
- Li, D.; Yang, Q.; Yang, W.; Chang, H.; Wang, H. Bionic leading-edge protuberances and hydrofoil cavitation. Phys. Fluids 2021, 33, 093317. [Google Scholar] [CrossRef]
- Kouser, T.; Xiong, Y.; Yang, D.; Peng, S. Numerical study on drag reduction and wake modification for the flows over a hydrofoil in presence of surface heterogeneity. Adv. Mech. Eng. 2022, 14, 16878140221075306. [Google Scholar] [CrossRef]
- Jiang, J.-W.; Xie, C.-M.; Xu, L.-H.; Li, L.; Huang, W.-X. The groove at blade tip designed for suppression of tip-leakage vortex may bring the risk of inducing new cavitation. Phys. Fluids 2022, 34, 121701. [Google Scholar] [CrossRef]
- Chada, J.S.R.; Rao, B.R. Study of flow pattern on a hydrofoil with structural and profile modification. J. Mech. Energy Eng. 2022, 6, 27–32. [Google Scholar] [CrossRef]
- Han, Y.; Liu, Y.; Tan, L. Method of variable-depth groove on vortex and cavitation suppression for a NACA0009 hydrofoil with tip clearance in tidal energy. Renew. Energy 2022, 199, 546–559. [Google Scholar] [CrossRef]
- Jia, J.; Zhang, J.; Huang, Z. Cavitation flow and broadband noise source characteristics of NACA66 hydrofoil with a V groove on the suction surface. Ocean Eng. 2022, 266, 112889. [Google Scholar] [CrossRef]
- Wang, L.; Luo, X.; Feng, J.; Lu, J.; Zhu, G.; Li, C. Numerical evaluation of suppression mechanism of shark-inspired riblet on tip leakage vortex of a NACA0009 hydrofoil with tip clearance. Ocean Eng. 2022, 244, 110288. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, J.; Huang, Z.; Wang, L.; Li, W.; Lan, G. Large eddy simulation on the cavitation flow and noise characteristics of a NACA0009 hydrofoil with different tip clearance sizes. J. Fluids Eng. 2023, 145, 011204. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, X.; Yang, C.; Tang, J.; Huang, Z. Cavitation flow and noise reduction design of bionic hydrofoil based on orthogonal optimization. Phys. Fluids 2023, 35, 115132. [Google Scholar] [CrossRef]
- Wang, L.; Luo, X.; Lu, J.; Feng, J.; Zhu, G.; Wang, W.; Wang, K. Effect of asymmetrical tip clearances on energy performance and cavitation characteristics of NACA0009 hydrofoil in tidal energy. J. Mech. Sci. Technol. 2023, 37, 4717–4728. [Google Scholar] [CrossRef]
- Gu, Y.; Ma, L.; Yu, S.; Yan, M.; Wu, D.; Mou, J. Surface cavitation flow characterization of jet hydrofoils based on vortex identification method. Phys. Fluids 2023, 35, 012112. [Google Scholar] [CrossRef]
- Huang, C.; Sun, M.; Lv, X.; Wu, X.; Yang, Q. Energy performance and flow characteristics of a NACA0009 hydrofoil with bending shrinkage groove and tip winglet. Ocean Eng. 2023, 279, 114588. [Google Scholar] [CrossRef]
- Dong, L.; Chenhao, L. Investigation on the effect of different groove depth and width on the tip clearance leakage flow of hydrofoil. J. Phys. Conf. Ser. 2024, 2752, 012195. [Google Scholar] [CrossRef]
- Wang, L.; Mi, J.; Luo, X.; Yao, L.; Feng, J.; Zhu, G.; Li, C. Numerical investigation the shape of groove on tip leakage vortex suppression of a NACA0009 hydrofoil. J. Phys. Conf. Ser. 2024, 2707, 012063. [Google Scholar] [CrossRef]
- Gu, F.; Shi, L.; Shen, X.; Zhang, G.; Geng, L.; Zhang, D.; van Esch, B.B. A novel flow control method suppressing tip leakage vortex of a hydrofoil applied for ducted devices. Ocean Eng. 2024, 311, 118920. [Google Scholar] [CrossRef]
- Wang, L.; Feng, J.; Lu, J.; Zhu, G.; Wang, W. Novel bionic wave-shaped tip clearance toward improving hydrofoil energy performance and suppressing tip leakage vortex. Energy 2024, 290, 130261. [Google Scholar] [CrossRef]
- Gang, Y.; Zhou, Z.; Li, J.; Peng, L.; Liu, D.; Liu, X.; Pang, J. Analysis of hydrofoil tip leakage vortex dynamic characteristics. Adv. Mech. Eng. 2024, 16, 16878132241293622. [Google Scholar] [CrossRef]
- Timoshevskiy, M.; Zapryagaev, I.; Pervunin, K.; Markovich, D. Longitudinal grooves for hampering cavitation development: Experiments on a 2D hydrofoil. In AIP Conference Proceedings; AIP Publishing LLC: Melville, NY, USA, 2018; p. 030003. [Google Scholar]
- Maung, P.; Prusty, B.; White, J.; David, M.; Phillips, A.; John, N.S. Structural performance of a shape-adaptive composite hydrofoil using automated fibre placement. Eng. Struct. 2019, 183, 351–365. [Google Scholar] [CrossRef]
- Kadivar, E.; Ochiai, T.; Iga, Y.; el Moctar, O. An experimental investigation of transient cavitation control on a hydrofoil using hemispherical vortex generators. J. Hydrodyn. 2021, 33, 1139–1147. [Google Scholar] [CrossRef]
- Zaresharif, M.; Ravelet, F.; Kinahan, D.J.; Delaure, Y. Cavitation control using passive flow control techniques. Phys. Fluids 2021, 33, 121301. [Google Scholar] [CrossRef]
- Xu, L.; Liu, Y.; Cheng, H.; Ji, B.; Peng, X. Suppression effect on TLV cavitation of overhanging grooves with different tab orientations: An experimental investigation. Ocean Eng. 2022, 266, 113125. [Google Scholar] [CrossRef]
- Nichik, M.Y.; Timoshevskiy, M.V.; Pervunin, K.S. Effect of an end-clearance width on the gap cavitation structure: Experiments on a wall-bounded axis-equipped hydrofoil. Ocean Eng. 2022, 254, 111387. [Google Scholar] [CrossRef]
- Skripkin, S.G.; Starinskiy, S.V.; Tsoy, M.A.; Vasiliev, M.M.; Kravtsova, A.Y. Effect of a textured surface on the occurrence and development of cavitation on the hydrofoil. Phys. Fluids 2023, 35, 025109. [Google Scholar] [CrossRef]
- Cao, Y.-T.; Xu, L.-H.; Peng, X.-X. An experimental study on the impact behavior of cavitation inside tip clearance of a hydrofoil. J. Hydrodyn. 2023, 35, 1208–1214. [Google Scholar] [CrossRef]
- Qiu, N.; Xu, P.; Zhu, H.; Zhou, W.; Xun, D.; Li, M.; Che, B. Cavitation morphology and erosion on hydrofoil with slits. Int. J. Mech. Sci. 2024, 275, 109345. [Google Scholar] [CrossRef]
- Tsoy, M.; Skripkin, S.; Kravtsova, A. Cavitating flow around a low aspect ratio NACA0012 hydrofoil with regular grooves. J. Phys. Conf. Ser. 2024, 2752, 012189. [Google Scholar] [CrossRef]
- Li, Y.; Chen, H.; Wang, J.; Chen, D. Effect of grooves on cavitation around the body of revolution. J. Fluids Eng. 2010, 132, 011301. [Google Scholar] [CrossRef]
- Kang, D.; Arimoto, Y.; Yonezawa, K.; Horiguchi, H.; Kawata, Y.; Hah, C.; Tsujimoto, Y. Suppression of cavitation instabilities in an inducer by circumferential groove and explanation of higher frequency components. Int. J. Fluid Mach. Syst. 2010, 3, 137–149. [Google Scholar] [CrossRef]
- Mita, J.R.; Qu, W.; Kobayashi, M.H.; Pfefferkorn, F.E. Experimental study and numerical analysis of water single-phase pressure drop across an array of circular micro-pin-fins. In Proceedings of the ASME/JSME Thermal Engineering Joint Conference, Washington, DC, USA, 8–13 August 2011; p. T10131. [Google Scholar]
- Danlos, A.; Ravelet, F.; Coutier-Delgosha, O.; Bakir, F. Cavitation regime detection through Proper Orthogonal Decomposition: Dynamics analysis of the sheet cavity on a grooved convergent–divergent nozzle. Int. J. Heat Fluid Flow 2014, 47, 9–20. [Google Scholar] [CrossRef]
- Komárek, M.; Sedlář, M.; Vyroubal, M.; Zima, P.; Müller, M.; Pálka, T. Preparation of experimental and numerical research on unsteady cavitating flow around hydrofoil. EPJ Web Conf. EDP Sci. 2015, 92, 02036. [Google Scholar] [CrossRef]
- Cheng, H.; Long, X.; Ji, B.; Peng, X.; Farhat, M. Suppressing tip-leakage vortex cavitation by overhanging grooves. Exp. Fluids 2020, 61, 159. [Google Scholar] [CrossRef]
- Fei, Z.; Zhang, R.; Xu, H.; Mu, T. Investigation of the groove effect on the tip leakage vortex flow. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2021; p. 012004. [Google Scholar]
- Roohi, E.; Zahiri, A.P.; Passandideh-Fard, M. Numerical simulation of cavitation around a two-dimensional hydrofoil using VOF method and LES turbulence model. Appl. Math. Model. 2013, 37, 6469–6488. [Google Scholar] [CrossRef]
- Ye, C.; Wang, F.; Wang, C.; van Esch, B.P. Assessment of turbulence models for the boundary layer transition flow simulation around a hydrofoil. Ocean Eng. 2020, 217, 108124. [Google Scholar] [CrossRef]
- Garg, N.; Pearce, B.W.; Brandner, P.A.; Phillips, A.W.; Martins, J.R.; Young, Y.L. Experimental investigation of a hydrofoil designed via hydrostructural optimization. J. Fluids Struct. 2019, 84, 243–262. [Google Scholar] [CrossRef]
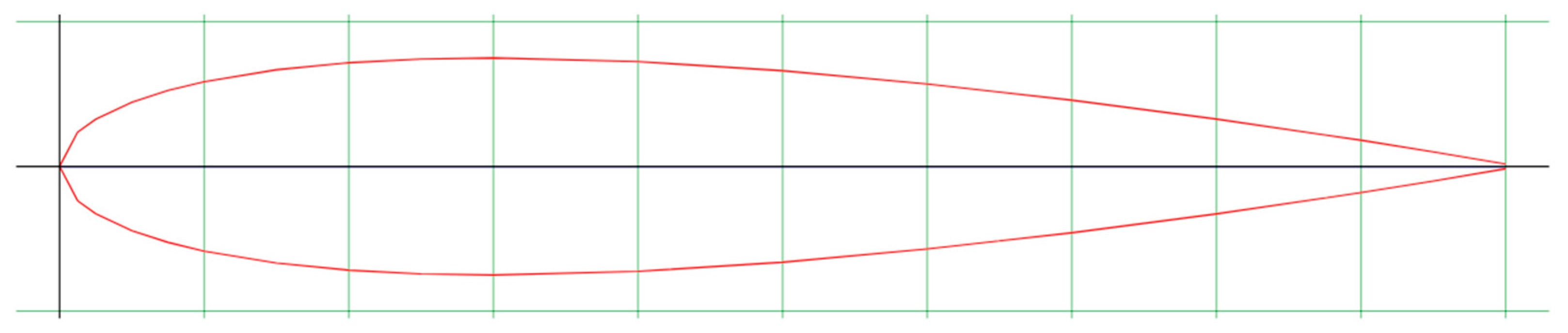
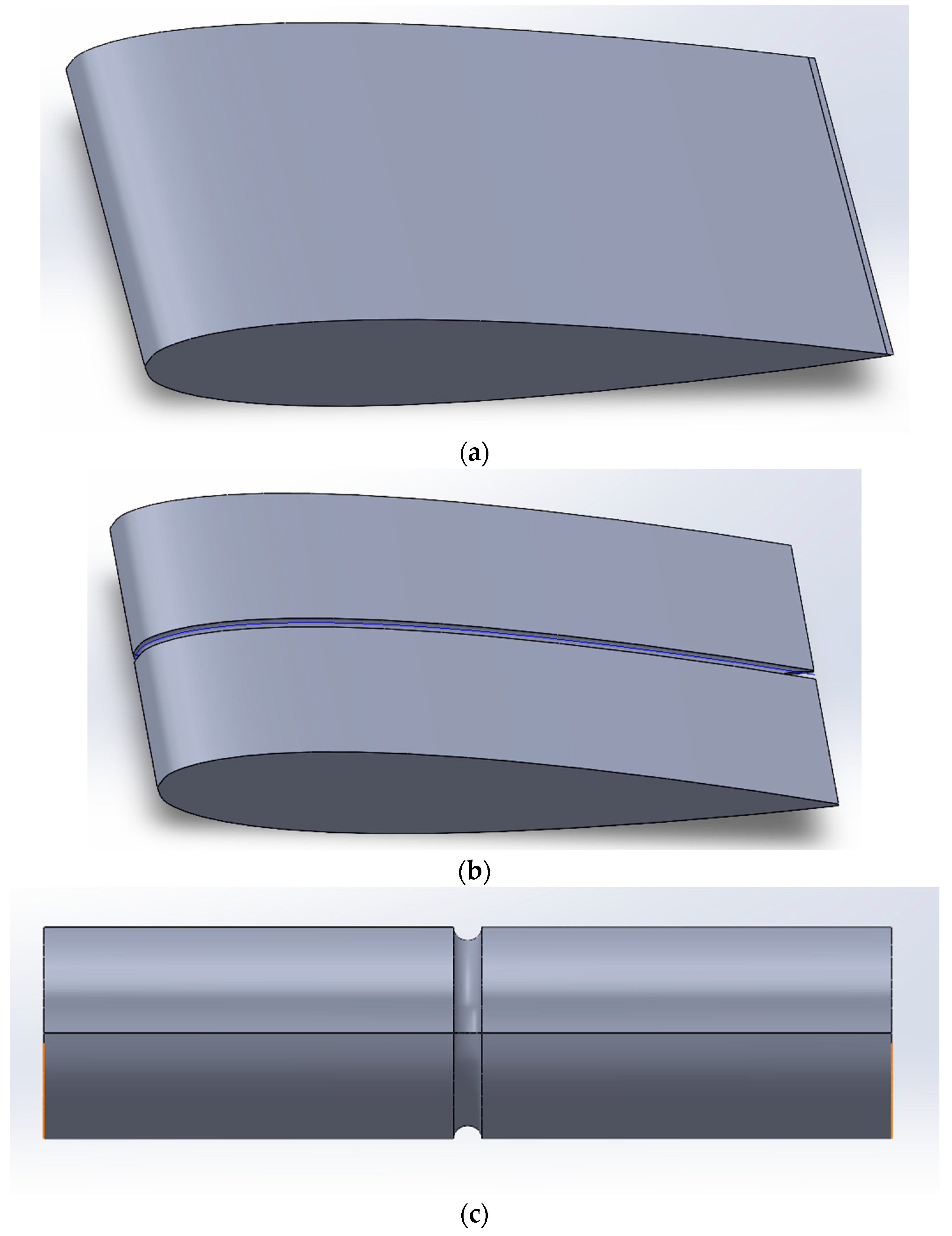
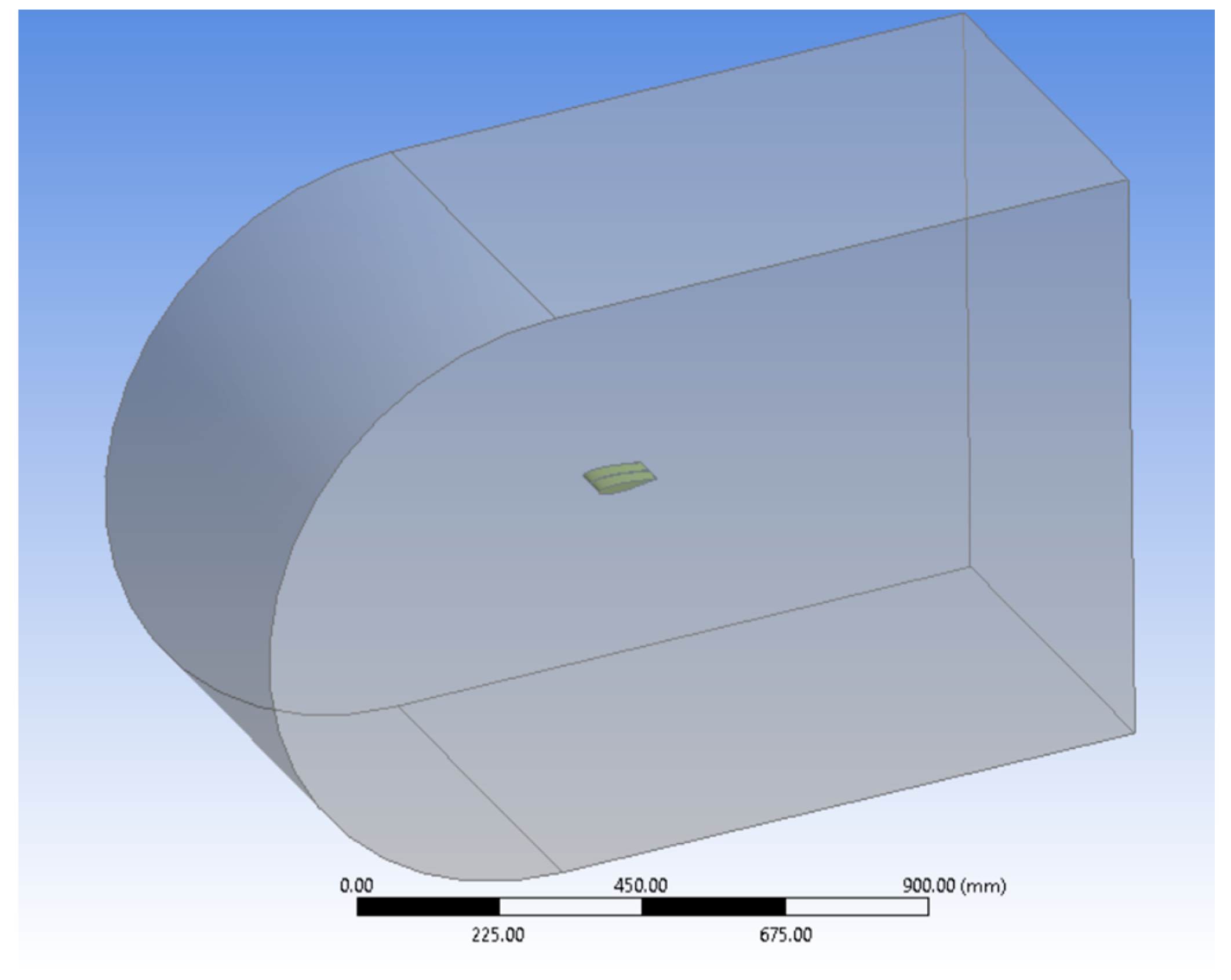


| Number of Noise Receivers | X (mm) | Y (mm) | Z (mm) |
|---|---|---|---|
| 1 | −200 | 0 | 0 |
| 2 | −100 | 0 | 0 |
| 3 | 200 | 0 | 0 |
| 4 | 300 | 0 | 0 |
| 5 | 400 | 0 | 0 |
| 6 | 600 | 0 | 0 |
| 7 | 100 | 100 | 0 |
| 8 | 100 | 200 | 0 |
| 9 | 100 | 300 | 0 |
| 10 | 100 | 0 | 130 |
| 11 | 100 | 0 | 230 |
| Number of Receiver | Minimum of Sound Amplitude | Average of Sound Amplitude | ||
|---|---|---|---|---|
| Without Groove | With Groove | Without Groove | With Groove | |
| 1 | 34.06037 | 35.55114 | 41.35454 | 40.95443 |
| 2 | 39.50958 | 40.11554 | 48.07069 | 47.78734 |
| 3 | 37.35591 | 32.37408 | 44.56235 | 44.9629 |
| 4 | 25.81683 | 21.96079 | 37.79089 | 36.98377 |
| 5 | 23.47688 | 22.68428 | 32.83075 | 31.56271 |
| 6 | 7.094681 | 4.227746 | 25.19589 | 22.42847 |
| 7 | 26.38985 | 30.73397 | 47.55033 | 47.31445 |
| 8 | 29.163 | 22.09035 | 41.03336 | 40.93716 |
| 9 | 27.61235 | 17.29411 | 37.16866 | 38.01303 |
| 10 | 40.88711 | 34.45841 | 47.72337 | 47.57785 |
| 11 | 34.90629 | 27.47563 | 41.76771 | 41.61544 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raju, S.S.K.; Firouzi, N.; Mukahal, F.H.H.A.; Podulka, P. Investigating the Performance of Longitudinal Groove on Noise Reduction in a NACA0015 Hydrofoil Using Computational Fluid Dynamics. Mathematics 2025, 13, 3125. https://doi.org/10.3390/math13193125
Raju SSK, Firouzi N, Mukahal FHHA, Podulka P. Investigating the Performance of Longitudinal Groove on Noise Reduction in a NACA0015 Hydrofoil Using Computational Fluid Dynamics. Mathematics. 2025; 13(19):3125. https://doi.org/10.3390/math13193125
Chicago/Turabian StyleRaju, S. Suresh Kumar, Nasser Firouzi, Fatemeh H. H. Al Mukahal, and Przemysław Podulka. 2025. "Investigating the Performance of Longitudinal Groove on Noise Reduction in a NACA0015 Hydrofoil Using Computational Fluid Dynamics" Mathematics 13, no. 19: 3125. https://doi.org/10.3390/math13193125
APA StyleRaju, S. S. K., Firouzi, N., Mukahal, F. H. H. A., & Podulka, P. (2025). Investigating the Performance of Longitudinal Groove on Noise Reduction in a NACA0015 Hydrofoil Using Computational Fluid Dynamics. Mathematics, 13(19), 3125. https://doi.org/10.3390/math13193125








