Abstract
The growing demand for reliable long-term traffic forecasting has become increasingly critical in the development of intelligent transportation systems (ITS). However, capturing both strong periodic patterns and long-range temporal dependencies presents a significant challenge, and existing approaches often fail to balance these factors effectively, resulting in unstable or suboptimal predictions. To address this issue, we propose MixModel, a novel hybrid framework that integrates TimesNet and Informer to leverage their complementary strengths. Specifically, the TimesNet branch extracts periodic variations through frequency-domain decomposition and multi-scale convolution, while the Informer branch employs ProbSparse attention to efficiently capture long-range dependencies across extended horizons. By unifying these capabilities, MixModel achieves enhanced forecasting accuracy, robustness, and stability compared with state-of-the-art baselines. Extensive experiments on real-world highway datasets demonstrate the effectiveness of our model, highlighting its potential for advancing large-scale urban traffic management and planning. To the best of our knowledge, MixModel is the first hybrid framework that explicitly bridges frequency-domain periodic modeling and efficient long-range dependency learning for long-term traffic forecasting, establishing a new benchmark for future research in Intelligent Transportation Systems.
Keywords:
artificial intelligence; deep learning; pattern recognition; time-series forecasting; traffic flow prediction MSC:
68T07; 62H12; 68T09
1. Introduction
Accurate traffic flow forecasting plays a crucial role in Intelligent Transportation Systems (ITS), enabling traffic authorities to implement proactive control strategies, reduce congestion, and improve road safety. Reliable forecasts allow for better planning of traffic signal timing, congestion management, and route recommendations, ultimately leading to enhanced mobility and reduced environmental impact.
Traditional statistical approaches, such as Auto-Regressive Integrated Moving Average (ARIMA) and Kalman filtering, have been widely used in early traffic forecasting studies [1]. While these methods are effective in modeling linear temporal dependencies, they struggle with the highly nonlinear, non-stationary patterns inherent in real-world traffic data, especially during peak hours and under irregular traffic events.
The advent of deep learning has led to significant advancements in traffic forecasting [2]. Recurrent Neural Networks (RNNs), including Long Short-Term Memory (LSTM) networks [3] and Gated Recurrent Units (GRUs) [4], have demonstrated the ability to model temporal dependencies, while Convolutional Neural Networks (CNNs) [5] have been applied to extract spatial features from road networks. More recently, Transformer-based models [6] have achieved success in long-term forecasting tasks due to their ability to capture global dependencies efficiently.
In the context of long-term traffic forecasting, the challenges are multi-faceted: traffic flows exhibit strong periodic structures (e.g., daily and weekly cycles) while also showing irregular variations that disrupt these patterns. Capturing both aspects within a single model has proven difficult, as most approaches tend to emphasize one side of the problem. To address this imbalance, researchers have explored hybrid or specialized designs—some focusing on multi-horizon modeling, others on periodic encodings, decomposition techniques, or graph-based fusion—to strike a better balance between periodicity and irregular dynamics. The following studies exemplify these efforts.
Lin and Tseng [7] proposed a Transformer-based travel time prediction framework that integrates both short-term and long-term horizons. Their encoder–decoder design allowed the model to capture immediate fluctuations while also learning temporal dynamics across extended horizons, thereby reducing accumulated error in multi-step forecasts. The study validated its effectiveness in urban travel time prediction, showing improved accuracy compared with conventional Transformer baselines. However, the model was primarily evaluated on travel time datasets rather than freeway traffic flow, and it did not explicitly incorporate periodic structures such as daily or weekly cycles. As such, while it improved temporal adaptability, its effectiveness in domains dominated by strong periodic patterns—like freeway traffic—remains uncertain.
Lin and Tseng [8] further advanced this direction by developing the Periodic Transformer Encoder (PTE), an encoder-only Transformer variant that integrates periodic representations directly into the architecture. By embedding periodic priors into the attention mechanism, PTE achieved stronger long-range forecasting capability with reduced complexity compared with traditional encoder–decoder frameworks. The design highlighted that periodic structures are critical in long-term sequence prediction and can be explicitly modeled within Transformer-based architectures. Nevertheless, while PTE effectively addressed periodicity, it did not provide a mechanism to handle irregular traffic fluctuations, limiting its robustness in freeway environments where disruptions frequently break periodic cycles.
Zuo et al. [9] introduced a hybrid TimesNet–SARIMA–VMD framework for metro passenger flow forecasting. Their approach began with Variational Mode Decomposition (VMD) to separate traffic sequences into intrinsic mode functions, isolating different components of variation. TimesNet was applied to capture periodic elements, while SARIMA modeled residual trend dynamics. This decomposition–forecasting pipeline achieved more than 50% error reduction compared with single-model approaches, underscoring the power of combining frequency decomposition with statistical modeling. However, the reliance on decomposition and SARIMA makes the framework domain-specific, as metro flows are relatively more structured than freeway traffic. In freeway datasets, irregular events and unstable fluctuations would reduce the reliability of such decomposition, limiting the model’s applicability.
Qian and Zhu [10] proposed MeshHSTGT, a complex hybrid model that integrates TimesNet with Graph Convolutional Networks (GCNs), Gated Recurrent Units (GRUs), and a Transformer-based fusion module. This comprehensive design combined frequency-domain periodic modeling, spatial graph learning, short-term sequential modeling, and global dependency capture in one framework. Experimental results demonstrated consistent improvements in MAE and RMSE across large-scale traffic datasets, illustrating the benefit of multi-branch integration. Yet, this benefit came at the cost of dramatically increased model complexity: the architecture required high memory usage, longer training times, and greater inference latency. Such complexity raises concerns about scalability and real-time feasibility for freeway-scale ITS deployments.
Song et al. [11] extended the Informer model by integrating Graph Attention Networks (GAT), resulting in GAT–Informer. This framework was designed to simultaneously capture spatial dependencies among traffic nodes and long-range temporal dependencies. By enhancing Informer with graph attention, the model successfully accounted for local interactions and global sequence patterns, yielding improved accuracy in scenarios affected by external influences such as accidents or regional demand shifts. Despite these strengths, GAT–Informer’s improvements are primarily in spatial–temporal fusion; it does not explicitly model periodic frequency-domain characteristics, leaving part of the forecasting challenge unresolved in freeway contexts where daily and weekly cycles are highly pronounced.
The Mixer–Informer framework [12] focused on electric vehicle (EV) charging load forecasting by combining a Mixer module for feature fusion with Informer for long-sequence modeling. The Mixer module was responsible for integrating heterogeneous feature sets, while Informer captured extended temporal dependencies. Results showed superior adaptability to complex multivariate series compared with baseline Informer models, making it suitable for EV load forecasting tasks. However, the application domain is far from freeway traffic prediction, and the framework still lacks explicit periodic modeling. While Mixer improved feature fusion, it did not directly address the dual need for modeling periodicity and long-range irregularities in traffic forecasting.
These studies collectively illustrate the diverse strategies that researchers have explored to balance periodicity and long-range dependencies in traffic forecasting. Multi-horizon designs improved adaptability across timescales, periodic encodings enhanced the modeling of recurring cycles, decomposition methods isolated different signal components, and graph-based approaches strengthened spatial–temporal interactions. Yet, these approaches also share common limitations: many are domain-specific (e.g., metro systems or EV demand), others focus on only one side of the problem (either periodicity or long-range dependencies), and some increase model complexity to levels that hinder scalability in real-world ITS deployments.
Recent studies on traffic forecasting have increasingly adopted graph neural networks (GNNs) and spatio-temporal graph transformers to capture spatial correlations across irregular road networks. While these methods provide flexible representations, they often suffer from high computational overhead and require dense, high-quality sensor coverage of the entire network. Such requirements limit their scalability for freeway-scale deployment, where road topology is relatively simple and sensor distribution is sparse. In contrast, our work focuses on long-term temporal forecasting with a lightweight dual-branch design, leaving the integration of advanced graph modules as a promising but complementary direction for future extensions.
Most of the research on traffic forecasting has focused on short-term horizons, typically ranging from a few minutes to several hours. In contrast, long-term traffic prediction research is comparatively sparse, even though it is critical for strategic decision-making in areas such as congestion management, infrastructure planning, and policy evaluation [13]. This imbalance constitutes the research gap: existing methods are well developed for short-term prediction, but they often fail to address the challenges of extended horizons where error accumulation and non-stationarity become severe.
Existing models can generally be grouped into three directions. Some approaches such as TimesNet and the Periodic Transformer Encoder [7,8,9] emphasize periodicity, which makes them effective for daily and weekly cycles but less robust when traffic is disrupted by irregular events like accidents or holiday surges. Other approaches such as Informer and GAT-Informer [11,14] focus on capturing long-range dependencies efficiently, yet they overlook explicit periodic signals, which reduces accuracy in recurring peak periods. More complex hybrids such as MeshHSTGT and Mixer-Informer [10,12] combine multiple modules to achieve higher accuracy, but they also introduce heavy computational cost that limits practical deployment in freeway-scale systems. These limitations point to an unresolved challenge in freeway traffic forecasting. What is still lacking is a lightweight yet effective framework that can simultaneously capture periodic structures and irregular long-range variations in freeway traffic. MixModel addresses this gap by integrating TimesNet and Informer through an adaptive projection–fusion–residual mechanism, which balances periodicity and long-term dependencies without excessive model complexity.
The main motivation of this work is to address this underexplored long-term setting, particularly for freeway-scale forecasting in Taiwan. Traffic on national freeways exhibits both strong periodic cycles (e.g., daily and weekly commuting patterns) and irregular disruptions (e.g., accidents, holidays, and lane closures). Capturing these dual dynamics over multiple days is essential for practical planning yet remains insufficiently studied.
Recent advances in other domains also demonstrate the rapid evolution of Transformer-based designs. The knowledge embedding Transformer for medical question answering [15] highlights how domain-specific embeddings improve interpretability and accuracy, while the joint multi-scale multimodal Transformer for emotion recognition using consumer devices [16] shows the benefit of integrating multi-scale temporal signals with multimodal features. These studies emphasize that continuous architectural innovations are essential, suggesting that traffic forecasting can also benefit from models that integrate multiple perspectives of temporal dynamics.
Building on these insights, and in response to the shortcomings of existing traffic forecasting approaches, we propose MixModel as a dual-branch hybrid framework that integrates TimesNet [17] and Informer [14] to fully exploit their complementary strengths. The TimesNet branch captures recurring periodic patterns through frequency-domain decomposition and multi-scale convolution, while the Informer branch efficiently models long-range dependencies using ProbSparse attention. By unifying these two perspectives within a single architecture, MixModel directly addresses the dual challenge of periodicity and long-range forecasting. Moreover, instead of incorporating external features such as weather or event data, we extend the conventional 4D temporal feature space into an 11D representation composed entirely of enriched time-based attributes (e.g., peak/off-peak indicators, weekend/weekday cycles, seasonal encodings). This design enhances the model’s ability to capture irregular traffic behavior without relying on auxiliary datasets, making the framework lightweight, scalable, and broadly applicable.
Based on the proposed MixModel, the contributions of this article can be summarized as follows:
- Long-Term Forecasting Focus: Unlike most prior works that emphasize short-term horizons, this study directly targets the underexplored challenge of long-term traffic forecasting. By modeling both periodic cycles and irregular disruptions over extended horizons, MixModel provides stable and interpretable predictions that support freeway-scale planning and policy evaluation.
- Hybrid Architecture: We design a dual-branch MixModel that combines TimesNet [17] and Informer [14], enabling simultaneous modeling of periodic patterns and long-range dependencies.
- Extended Temporal Feature Space: We enhance the model input with additional temporal attributes beyond the conventional 4D setting, providing richer contextual information for prediction.
- Comprehensive Evaluation: We conduct extensive experiments on real-world freeway traffic datasets, comparing MixModel against standalone TimesNet [17], standalone Informer [14], and the baseline MixModel configuration.
- Performance Gains: Experimental results demonstrate that the proposed approach achieves lower forecasting errors, particularly in multi-day horizon predictions.
2. Materials and Methods
2.1. Dataset
This study utilized a real-world freeway traffic dataset collected from the National Freeway Bureau in Taiwan. The dataset contains multi-sensor measurements including traffic volume and average speed recorded at 5 min intervals across multiple highway sections [18]. To support long-term forecasting tasks, we aggregated these 5 min records into hourly values. Hence, the input length L = 168 corresponds to 7 days of hourly sequences. In addition, we selected a representative subset of sensor stations with continuous data availability over a 10-month period, covering both weekdays and weekends to account for commuting patterns and seasonal variations.
The raw dataset underwent several preprocessing steps before being fed into the models [2]. Missing values were handled using linear interpolation for short gaps (less than 30 min) and forward filling for longer gaps. Outlier values caused by sensor malfunction were identified through threshold-based filtering (removing values exceeding ±3 standard deviations from the mean) and replaced with interpolated estimates [19]. All continuous numerical features were normalized to the [0,1] range using Min-Max scaling to improve model training stability [2].
This normalization process also alleviates data imbalance between peak and off-peak traffic flows, preventing extreme values from dominating the loss function. Model optimization was conducted using the MSE loss, which penalizes large deviations more heavily and ensures stable convergence across both high- and low-flow periods.
Even after preprocessing, freeway traffic data remain challenging for long-term forecasting due to several inherent characteristics. Traffic flows exhibit strong periodic patterns such as morning and evening commuting peaks and weekly cycles, yet these regular structures are frequently disrupted by irregular fluctuations, including sudden surges during holidays, accidents, or lane closures caused by maintenance. Moreover, the fine-grained 5 min sampling interval produces very long input sequences for multi-day forecasting, which increases computational demand and amplifies error accumulation over extended horizons.
Generalization is another challenge. Highway sections differ in geography, commuter density, and urban development. These differences make it difficult for one model to perform uniformly.
To address this, MixModel was tested on multiple samples. The results confirmed stable performance. Future work will extend evaluation to broader regions to further validate generalization.
Data collected from different highway sections also reveal heterogeneity in geography, urban development, and commuter behavior, making it difficult for a single model to generalize uniformly across locations. The selected stations include both metropolitan freeway segments around Taipei and intercity highway sections connecting northern and southern Taiwan. These locations differ in commuter density, land use, and long-distance travel demand. For example, urban sections typically exhibit highly regular peak–off-peak cycles, while rural segments are more sensitive to irregular surges caused by holiday travel or accidents. This diversity improves the representativeness of the dataset but also introduces potential bias, since models may perform better on stable urban flows than on more volatile rural traffic. These characteristics underscore the necessity of a forecasting framework that not only captures recurring periodicity but also adapts to irregular variations, motivating the integration of enriched temporal features and a hybrid architecture in our proposed MixModel.
Freeway traffic is inherently non-stationary. Daily, weekly, and seasonal patterns are frequently disrupted by accidents, holidays, or unexpected demand surges. In addition, sparse data often occurs due to missing sensor reports or measurement errors, which complicates long-term forecasting.
To address these issues, MixModel incorporates 11-dimensional temporal features that encode calendar effects such as weekdays, weekends, and seasonal cycles. These features provide contextual information that helps the model adapt to shifts in distribution. Sparse data problems are mitigated through interpolation of short gaps and forward filling of longer gaps, while normalization balances extreme peaks and off-peak flows.
2.2. Feature Engineering
The baseline MixModel (4D) configuration used the following four temporal features [20]:
- Hour of day (0–23);
- Day of week (0–6);
- Workday flag (binary);
- Holiday flag (binary).
To enhance the model’s temporal representation, we extended the feature space to 11 dimensions in the MixModel-11D configuration [21]. The additional seven features are:
- 5.
- Month of year (1–12);
- 6.
- Season (Spring, Summer, Autumn, Winter; encoded as integers 0–3);
- 7.
- Week of year (1–52);
- 8.
- Day of month (1–31);
- 9.
- Weekend flag (binary);
- 10.
- Morning rush hour flag (binary; 6–9 AM);
- 11.
- Evening rush hour flag (binary; 4–7 PM).
Categorical features such as month, season, and day of week were one-hot encoded before being concatenated with continuous features [2]. This extended temporal encoding allows the model to capture not only short-term patterns such as daily cycles but also longer-term seasonal dynamics, thereby providing richer contextual information for traffic forecasting [22].
Beyond the dimensional expansion itself, we explicitly considered the rationale behind each newly introduced feature and the practical benefits it provides. The conventional 4D setting captures only basic daily and weekly cycles, which we found insufficient for representing longer-term or more irregular variations in freeway traffic. Guided by both exploratory analysis of Taiwan freeway data and prior findings such as Ma et al. [23], we extended the input to 11D in order to capture seasonal effects, holiday surges, workday versus weekend commuting patterns, and rush-hour peaks. In this way, the feature design was not arbitrary but grounded in empirical evidence and theoretical support, ensuring that each added dimension contributes to predictive accuracy while retaining interpretability.
The feature, Month of year (1–12), reflects gradual changes in traffic intensity across months. For instance, traffic in summer months may decrease due to school vacations, whereas December often experiences spikes related to holiday shopping and travel. Incorporating this signal allows the model to differentiate traffic patterns even if they occur on the same weekday and time of day but belong to different months.
While the month feature, Season (Spring, Summer, Autumn, Winter), captures finer granularity, seasonal encoding provides a broader grouping that emphasizes recurring long-term patterns. For example, commuter flows in winter may be lighter in the evenings due to shorter daylight hours, while summer weekends often see increased recreational travel. Seasonality thus acts as a complementary macro-level signal to stabilize long-horizon forecasts.
Weekly indexing, Week of year (1–52), captures mid-range fluctuations that are not visible in daily or monthly features. A typical case is the Lunar New Year period in Taiwan, which usually occurs around late January or early February. Even though the specific dates change each year, the week of year indicator helps the model identify and generalize across such recurring holiday peaks. Similarly, long weekends and school breaks often fall in specific weeks, producing distinct traffic surges.
Day of month (1–31) highlights intra-month variability, which can be significant in certain contexts. For example, the end of the month often coincides with payroll cycles, leading to increased traffic in commercial districts. By encoding the day of month, the model gains the ability to pick up on these subtle but recurring behavioral patterns that would otherwise be masked by daily or weekly indicators alone.
While the baseline 4D setting already distinguishes between workdays and holidays, explicitly separating weekends is important because Saturday and Sunday traffic often differs sharply from official public holidays. For instance, weekend congestion patterns may include heavier outbound traffic on Saturday mornings and return flows on Sunday evenings, which are distinct from the one-off peaks of long holidays. Weekend flag (binary) ensures that routine weekly leisure traffic is clearly recognized.
One of the most predictable and policy-relevant patterns is the weekday morning commute. Encoding this period explicitly highlights its significance and ensures that the model pays additional attention to morning peaks, where forecasting errors could have the most severe consequences for congestion management. Morning rush-hour flag (binary; 6–9 AM) allows the model to emphasize short, sharp increases in flow that occur with remarkable regularity.
Complementing the morning peak, the evening rush hour is often more irregular due to overtime work, social activities, or shopping trips. By flagging this period, Evening rush-hour flag (binary; 4–7 PM), the model learns to expect higher variability and can adapt its predictions accordingly. Capturing both morning and evening rush periods separately is especially valuable for long-term forecasting, where daily peak patterns might otherwise be averaged out and diluted.
Unlike approaches that rely on external data such as weather or event reports, our feature design is entirely self-contained and requires only the raw traffic dataset. As long as timestamps are available—a property of virtually all traffic data—the full set of 11 temporal features can be automatically derived (e.g., month, season, week of year, day of week, holiday flag, rush-hour indicators). This self-sufficiency addresses three common issues in traffic forecasting: (1) the data availability problem, since external variables are often missing across regions or periods; (2) the data reliability problem, as auxiliary sources may be inconsistent or delayed; and (3) the data alignment problem, where external features differ in resolution or coverage. By avoiding these pitfalls, MixModel ensures consistent and portable feature construction across datasets. Moreover, the 11D features remain interpretable—each corresponds to a meaningful temporal pattern familiar to commuters and traffic managers—allowing the model to capture routine cycles as well as irregular variations. This richer yet self-contained design bridges the gap between model accuracy and real-world usability, offering a framework that transportation agencies can directly deploy even in data-scarce environments.
2.3. Model Architecture
Figure 1 presents the overall architecture of the proposed MixModel, which adopts a dual-branch design combining TimesNet [17] and Informer [14] to leverage their complementary strengths. The Data Preprocessing Layer incorporates the newly designed 11-dimensional feature construction module, which enriches the input representation by combining raw traffic measurements (flow, speed, occupancy) with derived temporal indicators, in particular, the preprocessing layer not only integrates the 11D temporal encoding but also embeds categorical indicators into continuous vectors and normalizes numerical inputs, this ensures that heterogeneous features are aligned in scale and representation before entering the two branches, thereby improving stability during training and preventing bias toward any specific feature type.
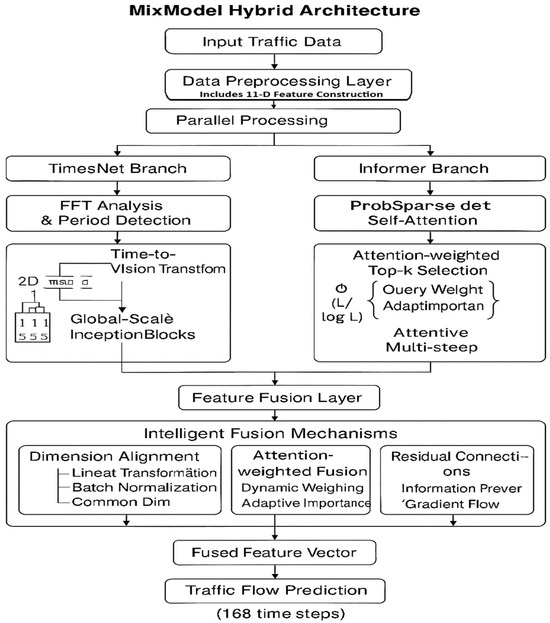
Figure 1.
The architecture of the proposed MixModel, integrating TimesNet and Informer branches. The Data Preprocessing Layer incorporates the newly designed 11-dimensional feature construction module, enabling richer input representation for enhanced predictive performance (168 time steps).
2.3.1. TimesNet Branch
The TimesNet branch applies Fast Fourier Transform (FFT) to project the input sequence into the frequency domain, enabling efficient extraction of periodic components [17]. Formally, an input sequence is transformed as shown in Equation (1) [17]
The formulation can be interpreted as follows. In this equation, InputSequence denotes the raw traffic input, and represents the Fourier transform operator. This corresponds to the FFT module in Figure 1 (TimesNet branch).
After projection, the frequency-domain representation is further processed through multi-scale convolutional kernels, as expressed in Equation (2) [17]
This equation shows how frequency features are filtered at multiple scales. Here, represents convolution kernels with different receptive fields, and denotes the convolution operator. This corresponds to the Multi-scale Convolution module in Figure 1. Through this design, TimesNet excels at extracting strong and recurring cycles from highway traffic flow.
TimesNet is particularly advantageous in scenarios where traffic flow is dominated by periodic structures. Daily commuting peaks, weekly cycles, and recurring seasonal trends can be effectively extracted through its frequency-domain decomposition and multi-scale convolution design. However, real traffic conditions also involve irregular or long-range variations that periodic modeling alone cannot capture. To address this limitation, we introduce the Informer branch.
2.3.2. Informer Branch
The Informer branch adapts the Transformer architecture with ProbSparse attention. This mechanism reduces computation while preserving the ability to capture long-range dependencies. The attention mechanism is defined in Equation (3) [14]
The meaning of this formulation is as follows. Query, Key, and Value represent the query, key, and value matrices, while denotes the key dimension. This corresponds to the Attention module in Figure 1 (Informer branch).
In a standard Transformer, each time step compares itself with all others, leading to quadratic complexity for a sequence length . For example, if , this requires about one million pairwise interactions. ProbSparse attention prunes redundant comparisons, lowering the cost to . For , this reduces the effort to around 10,000 computations—two orders of magnitude smaller. In simpler terms, instead of checking every time step against every other one, the model focuses only on the most informative comparisons.
This efficiency is crucial in traffic forecasting, where (7 days of hourly predictions) and multiple sensor stations are involved. Without ProbSparse, long-horizon forecasts would be computationally infeasible.
The decoder of Informer then generates the entire prediction horizon at once, as shown in Equation (4) [14]
This formulation indicates that produces the 168-step forecast in a single forward pass. This corresponds to the Decoder module in Figure 1.
Convolutional Neural Networks (CNNs) and Recurrent Neural Networks (RNNs), including LSTMs and GRUs, have demonstrated strong performance in short-term traffic forecasting by capturing local spatial features and immediate temporal dependencies. However, their effectiveness diminishes as the prediction horizon extends, due to limited receptive fields in CNNs and vanishing gradients in RNNs.
To address longer horizons, Informer demonstrates clear advantages for long-term forecasting with extended sequences and irregular variations. Its ProbSparse attention mechanism reduces the computational burden of processing multi-day inputs while retaining essential dependencies, and its generative decoder maintains temporal consistency by producing the entire horizon at once, thereby avoiding step-by-step error accumulation. Nevertheless, Informer does not explicitly capture strong periodic signals, which are prominent in freeway traffic. To overcome this limitation, MixModel introduces an intelligent fusion mechanism that integrates Informer with TimesNet, enabling the model to jointly exploit long-range irregularities and recurring periodic patterns.
2.3.3. Intelligent Fusion Mechanism
While TimesNet excels at capturing periodic structures through frequency-domain decomposition and multi-scale convolution, and Informer is particularly effective in modeling long-range dependencies within extended sequences, each branch emphasizes a different dimension of traffic dynamics. In real-world freeway environments, traffic conditions result from the interplay between recurring cycles and irregular disruptions. For instance, weekday morning rush hours follow predictable rhythms but can be disrupted by accidents or weather, while large-scale holiday migrations create multi-day deviations beyond weekly cycles. To effectively integrate these complementary representations, we introduce the projection–fusion–residual mechanism, illustrated in Figure 2. The outputs of TimesNet and Informer are first projected into a shared latent space, dynamically balanced through adaptive fusion with weight vector , and then combined with residual connections to preserve branch-specific information. This process yields a unified representation that directly contributes to the final forecast.
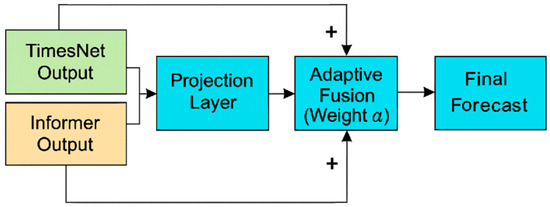
Figure 2.
Illustration of the projection–fusion–residual mechanism in MixModel. The outputs of TimesNet and Informer are first projected into a shared latent space. An adaptive weight vector dynamically balances the two representations, followed by residual integration to preserve original branch information. The unified representation is then passed to the final forecasting layer.
Motivated by these dynamics, we design the projection–fusion–residual mechanism as shown in Figure 2. To rigorously describe this process, Equations (5)–(7) formalize the projection, adaptive fusion with weight , and residual integration across the two branches.
To reconcile these complementary perspectives, MixModel employs an intelligent fusion mechanism. First, the hidden representations from both branches are projected into a common latent space, as defined in Equation (5).
Here, is the input sequence, where denotes the sequence length and is the feature dimension. The matrices are learnable projection weights. They align the outputs of TimesNet and Informer into the same latent space. forming the Projection Layer shown in Figure 2.
Next, an adaptive weighting balances the contributions of the two branches, as expressed in Equation (6).
In this expression, is a learnable attention vector, and represents element-wise multiplication. Each component acts as a gate that controls the relative contribution of TimesNet and Informer in the corresponding latent dimension. This design enables fine-grained balancing. It provides greater flexibility than a single global weight, as implemented in the Adaptive Fusion (Weight α) module of Figure 2.
Finally, residual connections are incorporated to stabilize training and preserve contextual cues, as formulated in Equation (7).
Here, denotes the concatenation of the two projected vectors. The mapping matrix transforms this concatenated vector back to the -dimensional space. The residual connection with ensures that the fused representation is preserved in the final output. realized through the Residual Connection and Final Forecast in Figure 2.
In summary, MixModel integrates frequency-domain periodic modeling (TimesNet) with efficient long-range dependency learning (Informer). Through adaptive fusion, the architecture ensures robust predictions across both routine traffic cycles and unexpected disruptions. Unlike previous hybrid approaches that typically concatenate or sequentially stack heterogeneous modules (e.g., CNN+Transformer, GCN+LSTM), MixModel introduces a projection–fusion–residual mechanism in a shared latent space. The learnable fusion vector enables fine-grained, element-wise balancing between periodic and irregular features, providing more flexibility than static concatenation or fixed global weighting. This design highlights the novelty of MixModel, as it not only combines complementary feature extraction strategies but also integrates them through an adaptive and interpretable fusion process.
2.4. Complexity Considerations
The dual-branch design of MixModel inevitably introduces additional operations compared to single-branch models. However, the overhead remains marginal because the fusion mechanism only relies on lightweight linear mappings and residual connections, rather than heavy modules such as multi-layer graph convolutions.
Our prior conference study [24] reported that Informer achieves favorable long-horizon accuracy while requiring fewer computational resources than sequence-based or graph-based baselines such as LSTM and STGCN. This observation highlights Informer as an efficient yet powerful foundation for long-term traffic forecasting. Building upon this, MixModel incorporates Informer as one branch and enhances it with TimesNet through the projection–fusion–residual mechanism. The additional cost introduced by Equations (5)–(7) is limited to simple linear transformations, meaning that MixModel maintains efficiency comparable to a single Informer branch while delivering improved accuracy through dual-branch integration.
More complex hybrid frameworks, such as MeshHSTGT [10], demonstrate that integrating multiple modules (e.g., GCN, GRU, and Transformer) can lead to high accuracy but at the expense of greater computational demand. In contrast, MixModel achieves a more balanced trade-off by selectively combining two complementary branches with minimal overhead, making it a practical and scalable choice for freeway-scale forecasting.
2.5. Training Settings
Both MixModel-4D and MixModel-11D were trained using the Mean Squared Error (MSE) loss function [19]. The Adam optimizer was employed with an initial learning rate of 0.0005, decayed by a factor of 0.5 every 10 epochs without improvement [2]. Each model was trained for a maximum of 100 epochs with early stopping (patience = 15 epochs) based on validation loss [2].
The dataset was split chronologically into training (70%), validation (15%), and testing (15%) sets [18]. Batch size was set to 32, and gradient clipping with a maximum norm of 5.0 was applied to prevent exploding gradients [2]. All experiments were conducted on a workstation equipped with an NVIDIA GeForce RTX 4070 GPU, 32 GB of RAM, and running PyTorch 2.2.0 on Python 3.10.
Like other deep learning frameworks, MixModel is influenced by hyperparameter choices. In our validation experiments, changing the batch size from 16 to 64 or adjusting dropout between 0.1 and 0.3 altered MSE by less than 2%, indicating limited sensitivity. Optimizer parameters such as β values also had negligible impact. By contrast, learning rate and hidden dimension exerted stronger influence. For example, raising the learning rate from 0.0005 to 0.002 led to unstable convergence with validation loss fluctuating by more than 10%. Similarly, increasing the hidden dimension from 256 to 512 raised GPU memory usage by over 40% while improving accuracy by less than 1%. These results suggest that MixModel is relatively robust to most hyperparameter variations, but careful tuning of learning rate and representation size is essential for optimal performance.
3. Results
3.1. Evaluation Metrics
We used Mean Squared Error (MSE) as the primary evaluation metric to measure the difference between predicted and actual traffic values [18,19]. MSE is widely adopted in time series forecasting tasks because it directly penalizes larger deviations, making it especially suitable for evaluating long-term predictions where accumulated errors may become critical. Since all traffic data were normalized using Min-Max scaling, MSE provides a consistent and comparable measure across different models and samples.
Lower MSE values indicate higher prediction accuracy. In addition to the overall numerical comparison, visual inspection was performed to assess how well each model captured both daily cycles and irregular fluctuations in traffic flow [1].
3.2. Best-Sample Evaluation
Figure 3 presents the forecasting results of MixModel-4D on two additional test samples. Both cases confirm that the model consistently tracks actual traffic dynamics. The predicted curves capture daily cycles and peak variations with reasonable accuracy. The mean squared errors (MSEs) for Sample 1 (0.0692) and Sample 2 (0.0703) are slightly higher than that of Sample 3. Nevertheless, the results of Samples 1 and 2 demonstrate that MixModel-4D delivers stable accuracy across different test cases. These findings indicate that the predictive advantage of MixModel-4D is not confined to a single sample. Among the three, Sample 3 achieves the lowest error and therefore serves as the representative case for detailed comparison.
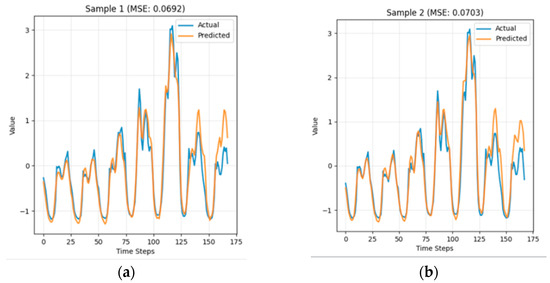
Figure 3.
Forecasting results of MixModel-4D for additional test samples over a 7-day horizon: (a) Sample 1 (MSE = 0.0692); (b) Sample 2 (MSE = 0.0703).
In Figure 3, the horizontal axis represents time steps across the 7-day forecasting horizon, and the vertical axis denotes traffic volume recorded by the freeway sensor. The blue curve corresponds to the ground-truth traffic flow, while the orange curve shows the predictions generated by MixModel-4D. This setting provides a direct comparison of actual and predicted traffic variations across multiple peak and off-peak periods.
The results for Sample 3 demonstrate the strongest case. The predicted curve closely follows the actual traffic flow, successfully capturing both daily commuting cycles and variations in peak intensity. Deviations appear mainly during abrupt surges, such as sudden traffic spikes caused by external events. Overall, the alignment confirms that Sample 3 yields the best performance, providing a clear view of MixModel-4D’s architectural advantages in handling both regular and irregular traffic patterns.
By focusing on a best-performing sample, we can more clearly evaluate how each model leverages its architectural advantages under optimal conditions.
From the results in Table 1, it is clear that hybrid MixModel architectures outperform their standalone counterparts. Informer [14], despite its strength in capturing long-range dependencies, shows higher error compared to MixModel-4D and MixModel-11D, particularly because it struggles to fully capture short-term periodicity. TimesNet [17], on the other hand, models periodic patterns well but lacks the flexibility to adapt to sudden, non-periodic traffic changes. The MixModel-4D effectively integrates both strengths, while the MixModel-11D leverages additional temporal features to further improve performance [20,21].

Table 1.
Best-sample MSE results for Sample 3 across four model configurations.
Beyond the architectural effect, enriching the temporal encoding from 4D to 11D provides stronger contextual cues (month, season, week-of-year, day-of-month, weekend, and rush-hour flags). As shown by Table 1, MixModel-11D lowers MSE from 0.057 (MixModel-4D) to 0.014—a 75.44% relative reduction—and achieves 84.44% and 89.15% reductions versus Informer and TimesNet, respectively, underscoring its advantage for multi-day forecasting.
3.3. Visual Comparison
Figure 4 shows the predicted and actual traffic flow for Sample 3 over a 7-day (168 h) forecast horizon for each model. The x-axis represents the forecasted time in hours, while the y-axis shows the normalized traffic flow values.
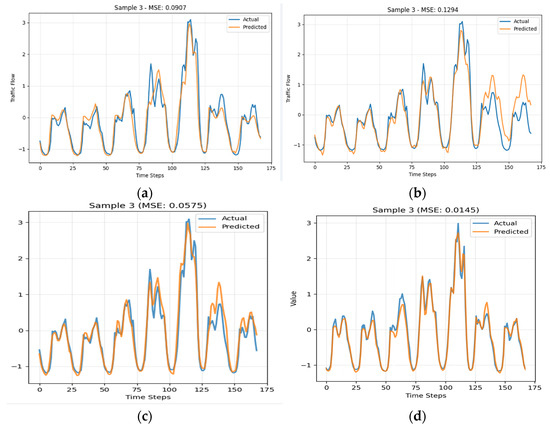
Figure 4.
Forecast results for Sample 3 over a 7-day horizon: (a) Informer; (b) TimesNet; (c) MixModel-4D; (d) MixModel-11D predictions vs. ground truth.
In Figure 4a (Informer [14]), the model correctly captures the general shape of the traffic flow curve, including the location of morning and evening peaks. However, peak amplitudes are often underestimated, and the transition between low and high traffic periods is overly smoothed, leading to reduced accuracy during rapid traffic changes.
In Figure 4b (TimesNet [17]), the model accurately represents daily cyclical patterns and maintains stable predictions for recurring peaks. Nevertheless, its performance degrades when traffic patterns deviate from regular cycles, such as during holidays or unusual congestion events, leading to mismatches in certain valleys and peaks.
Figure 4c (MixModel-4D) demonstrates a more balanced prediction profile. By combining TimesNet’s [17] periodic modeling and Informer’s [14] long-range dependency capture, this configuration better aligns peak timing and magnitude with the ground truth. Peak values are more accurately predicted, and off-peak traffic levels are closer to actual measurements, reducing both overestimation and underestimation errors.
Finally, Figure 4d (MixModel-11D) shows the most accurate alignment with ground truth across the entire forecast horizon. The inclusion of 11 temporal features [25,26] enables the model to differentiate between weekdays, weekends, and specific rush-hour intervals. This richer temporal context allows the model to anticipate subtle changes in traffic patterns, such as slightly earlier peak formation on Fridays or prolonged evening congestion during certain seasons. The result is a curve that tracks both the timing and amplitude of peaks and valleys more precisely than all other configurations.
3.4. Observations
Hybrid Advantage: The fusion of TimesNet [17] and Informer [14] consistently outperforms standalone models, confirming the benefit of combining frequency-domain periodic modeling with attention-based long-sequence modeling [6,25].
Feature Dimension Impact: Expanding from 4D to 11D features provides additional contextual awareness [25,26], which is particularly effective in capturing typical but recurring patterns such as seasonal effects and weekend traffic surges [22].
Peak Period Accuracy: MixModel-11D significantly reduces underestimation during morning peaks and overestimation during night-time lows, leading to smoother and more realistic forecast curves [26].
Practical Implication: The improvement in prediction accuracy can enhance freeway traffic management systems by enabling more precise allocation of resources such as dynamic lane control and congestion-based tolling.
4. Discussion
The results from our experiments demonstrate that integrating TimesNet [17] and Informer [14] into a single hybrid framework brings significant advantages. TimesNet [17] alone captures recurring traffic cycles through frequency-domain decomposition but often struggles with sudden irregular changes. Informer [14], on the other hand, models long-range dependencies effectively but lacks the ability to fully exploit short-term periodicity. By merging these complementary strengths, the proposed MixModel achieves a balanced forecasting capability, handling both stable daily patterns and unpredictable fluctuations with improved accuracy.
Expanding the model’s feature space from 4 to 11 dimensions further enhances its predictive power [20,21]. The additional temporal and contextual variables allow the model to differentiate between weekday and weekend traffic behaviors, recognize seasonal shifts, and anticipate subtle variations such as earlier congestion on Fridays or extended evening rush hours in certain months [22]. This richer representation results in a closer match between predicted and actual traffic curves across the entire forecast horizon.
These findings are consistent with prior studies where hybrid designs combining convolutional components and attention-based mechanisms [6,14], or employing multi-scale temporal representations [17], benefit from richer feature inputs [25]. Our results confirm that when the architecture is capable of extracting meaningful patterns, increasing feature diversity directly contributes to improved robustness under diverse traffic conditions [21,26].
Although the best-sample evaluation highlights each model’s maximum potential accuracy [21], it also points to challenges in real-world deployment. Traffic conditions can be disrupted by accidents, weather changes, or special events, making it essential for forecasting systems to maintain stability in less-than-ideal scenarios [1]. In such contexts, the MixModel-11D’s richer feature set offers a distinct advantage by providing additional contextual cues for decision-making.
However, these benefits come with trade-offs. The increase in feature dimensionality raises computational demands during both training and inference [2], which can be a limiting factor for applications requiring low-latency predictions on resource-constrained devices. Furthermore, the present study focuses solely on freeway traffic data. Whether similar performance gains can be achieved in other transportation contexts, such as urban road networks or multimodal transit systems, remains an open question.
Future research could address these limitations by optimizing the computational efficiency of MixModel-11D for deployment on edge computing platforms [5], exploring domain adaptation strategies to transfer learned patterns between different geographic regions or transport modes [25], and incorporating exogenous factors such as weather forecasts, event schedules, and incident reports into the model’s input space [26]. Such developments could lead to forecasting systems that are accurate, robust, and adaptable across a wide range of operational environments.
5. Conclusions
In this paper, we proposed MixModel, a dual-branch framework that integrates TimesNet and Informer through an intelligent fusion mechanism for long-term freeway traffic forecasting. The architecture leverages frequency-domain decomposition to capture periodic structures and ProbSparse attention to efficiently model long-range dependencies.
Experimental results on real-world highway datasets demonstrate that MixModel significantly outperforms strong baselines, including single-branch models and reduced feature settings. In particular, the incorporation of 11-dimensional temporal features and adaptive fusion (Equations (1)–(7)) yields clear improvements in both accuracy and robustness, especially for multi-day horizons where error accumulation is critical.
Nevertheless, this study is limited to freeway sensor networks with relatively simple spatial structures. Its applicability to irregular and more complex urban road networks has not yet been verified, and further validation is required to confirm its effectiveness in such scenarios.
The strength of MixModel lies in its ability to integrate complementary modules in a lightweight architecture. It simultaneously captures stable periodic patterns and irregular disruptions. Beyond empirical performance, MixModel underscores the practical value of jointly modeling periodic and irregular dynamics in traffic forecasting. The framework is well suited to large-scale freeway management. Accurate and efficient long-term predictions enable congestion mitigation, infrastructure planning, and policy evaluation.
Author Contributions
Conceptualization, H.-T.C.L. and S.L.; methodology, C.-C.T.; software, C.-C.T.; validation, C.-C.T.; formal analysis, C.-C.T.; investigation, C.-C.T.; resources (dataset provision), K.-T.W.; data curation, K.-T.W.; writing—original draft preparation, C.-C.T.; writing—review and editing, S.L., H.-T.C.L. and C.-C.T.; visualization, C.-C.T.; supervision, S.L.; project administration, S.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are openly available in [Freeway Bureau, MOTC, Taiwan], at [URL: https://www.freeway.gov.tw/english/, (accessed on 31 August 2025)], reference number [M08A]. [Freeway Bureau, MOTC, Taiwan] [https://www.freeway.gov.tw/english/, (accessed on 31 August 2025)] [M08A].
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice, 3rd ed.; OTexts: Melbourne, Australia, 2021; Available online: https://otexts.com/fpp3/ (accessed on 25 March 2025).
- Zhang, A.; Lipton, Z.C.; Li, M.; Smola, A.J. Dive into Deep Learning; Cambridge University Press: Cambridge, UK, 2021; Available online: https://d2l.ai/ (accessed on 25 March 2025).
- Hochreiter, S.; Schmidhuber, J. "Long Short-Term Memory," in Neural Computation; MIT Press: Cambridge, MA, USA, 1997; Volume 9, pp. 1735–1780. [Google Scholar] [CrossRef]
- Cho, K.; van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning Phrase Representations using RNN Encoder–Decoder for Statistical Machine Translation. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), Doha, Qatar, 25–29 October 2014; pp. 1724–1734. Available online: https://aclanthology.org/D14-1179/ (accessed on 31 August 2025).
- Bai, S.; Kolter, J.Z.; Koltun, V. An Empirical Evaluation of Generic Convolutional and Recurrent Networks for Sequence Modeling. arXiv 2018, arXiv:1803.01271. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention Is All You Need. In Proceedings of the Advances in Neural Information Processing Systems 30 (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; pp. 5998–6008. [Google Scholar]
- Lin, H.-T.C.; Dai, H.; Tseng, V.S. Short-Term and Long-Term Travel Time Prediction Using Transformer-Based Techniques. Appl. Sci. 2024, 14, 4913. [Google Scholar] [CrossRef]
- Lin, H.-T.C.; Tseng, V.S. Periodic Transformer Encoder for Multi-Horizon Travel Time Prediction. Electronics 2024, 13, 2094. [Google Scholar] [CrossRef]
- Zuo, T.; Tang, S.; Zhang, L.; Kang, H.; Song, H.; Li, P. An Enhanced TimesNet-SARIMA Model for Predicting Outbound Subway Passenger Flow with Decomposition Techniques. Appl. Sci. 2025, 15, 2874. [Google Scholar] [CrossRef]
- Qian, S.; Zhu, X. MeshHSTGT: Hierarchical Spatio-Temporal Fusion for Mesh Network Traffic Forecasting. Sci. Rep. 2025, 15, 20411. [Google Scholar] [CrossRef] [PubMed]
- Song, Y.; Luo, R.; Zhou, T.; Zhou, C.; Su, R. Graph Attention Informer for Long-Term Traffic Flow Prediction under the Impact of Sports Events. Sensors 2024, 24, 4796. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.; Jiang, B.; Wang, Q. Mixer-Informer-Based Two-Stage Transfer Learning for Long-Sequence Load Forecasting in Newly Constructed EV Charging Stations. arXiv 2025, arXiv:2505.06657. [Google Scholar]
- Toba, A.-L.; Kulkarni, S.; Khallouli, W.; Pennington, T. Long-Term Traffic Prediction Using Deep Learning Long Short-Term Memory. Smart Cities 2025, 8, 126. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual Event, 2–9 February 2021; Volume 35, pp. 11106–11115. [Google Scholar] [CrossRef]
- Zhu, X.; Khan, M.; Taleb-Ahmed, A.; Othmani, A. Advancing medical question answering with a knowledge embedding transformer. PLoS ONE 2025, 20, e0329606. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.; Ahmad, J.; Gueaieb, W.; De Masi, G.; Karray, F.; El Saddik, A. Joint Multi-Scale Multimodal Transformer for Emotion Using Consumer Devices. IEEE Trans. Consum. Electron. 2025, 71, 1092–1101. [Google Scholar] [CrossRef]
- Wu, H.; Xu, J.; Wang, J.; Long, M. TimesNet: Temporal 2D-Variation Modeling for General Time Series Analysis. In Proceedings of the International Conference on Learning Representations (ICLR), Kigali, Rwanda, 1–5 May 2023. [Google Scholar]
- Makridakis, S.; Spiliotis, E.; Assimakopoulos, V. The M4 Competition: Results, Findings, Conclusion and Way Forward. Int. J. Forecast. 2020, 36, 54–74. [Google Scholar] [CrossRef]
- Barnett, V.; Lewis, T. Outliers in Statistical Data, 3rd ed.; Wiley: Chichester, UK, 1994; Available online: https://www.wiley.com/en-us/Outliers+in+Statistical+Data%2C+3rd+Edition-p-9780471930945 (accessed on 25 March 2025).
- Li, S.; Jin, X.; Xuan, Y.; Zhou, X.; Chen, W.; Wang, Y.-X.; Yan, X. Enhancing the Locality and Breaking the Memory Bottleneck of Transformer on Time Series Forecasting. In Proceedings of the Advances in Neural Information Processing Systems 32 (NeurIPS 2019), Vancouver, BC, Canada, 8–14 December 2019; pp. 5244–5254. Available online: https://papers.nips.cc/paper_files/paper/2019/hash/6775a0635c302542da2c32aa19d86be0-Abstract.html (accessed on 25 March 2025).
- Chen, Y.; Kang, Y.; Chen, Y.; Wang, Z. Probabilistic Forecasting with Temporal Convolutional Neural Network. Neurocomputing 2020, 399, 491–501. [Google Scholar] [CrossRef]
- Lai, G.; Chang, W.-C.; Yang, Y.; Liu, H. Modeling Long- and Short-Term Temporal Patterns with Deep Neural Networks. In Proceedings of the 41st International ACM SIGIR Conference on Research and Development in Information Retrieval (SIGIR ’18), Ann Arbor, MI, USA, 8–12 July 2018; pp. 95–104. [Google Scholar] [CrossRef]
- Ma, D.; Song, X.B.; Zhu, J.; Ma, W. Input Data Selection for Daily Traffic Flow Forecasting through Contextual Mining and Intra-Day Pattern Recognition. Expert Syst. Appl. 2021, 176, 114902. [Google Scholar] [CrossRef]
- Wu, K.-T.; Lin, S. An Integrated Traffic Forecasting Framework for Taiwan’s Highways. In Proceedings of the International Conference on Information, Communication and Signal Processing (ICICSP), Xi’an, China, 12–14 September 2025. [Google Scholar]
- Guo, T.; Lin, T.; Antulov-Fantulin, N. Exploring Interpretable LSTM Neural Networks over Multi-Variable Data. arXiv 2019, arXiv:1905.12034. [Google Scholar] [CrossRef]
- Wu, Z.; Pan, S.; Chen, F.; Long, G.; Zhang, C.; Yu, P.S. A Comprehensive Survey on Graph Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 4–24. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).