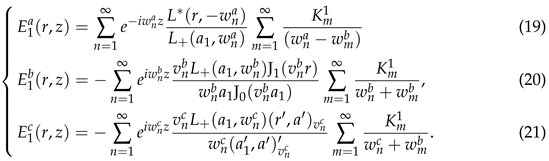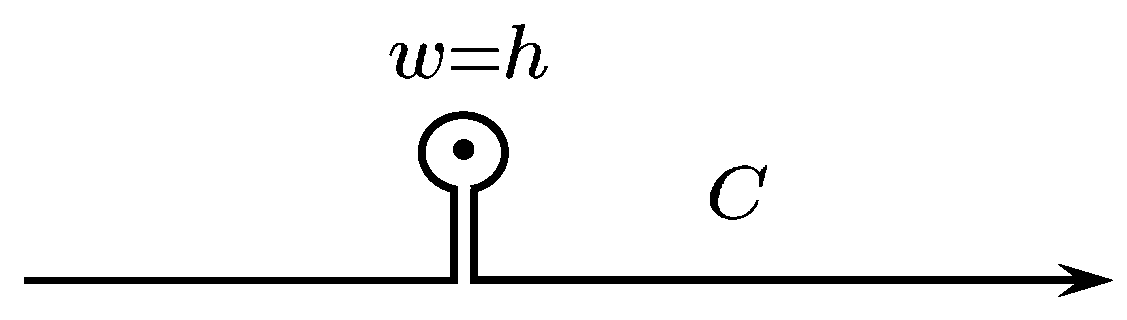Diffraction by Circular Pin: Wiener–Hopf Method

Abstract

In this paper, the boundary value problem of wave diffraction on a semi-infinite circular pin is solved using the Wiener–Hopf method with compensation of eigenmodes. The solution to the problem is presented as an infinite series defined by a recurrence formula. The reliability and accuracy of the solution are verified numerically in terms of fulfillment of the law of energy conservation. Sufficiently reliable results are obtained at the first iteration. The method used for solving this problem can be applied to solving diffraction problems on axisymmetric volumetric structures.

1. Introduction

Diffraction of waves by obstacles is a fundamental problem of wave physics, which finds its applications in acoustics, electromagnetism, and hydrodynamics.

The theoretical foundations for the diffraction of waves by a circular cylinder were laid by Gustav Kirchhoff [1] and Lord Rayleigh [2] (1878) in their seminal works.

A solution for a perfectly conducting cylinder was obtained by Sommerfeld [3] (1896) and later improved by Stratton [4].

It is well known that one of the two existing rigorous methods in the theory of wave diffraction is the classical Wiener–Hopf (W-H) method [5] (1931) for solving singular integral equations. This mathematical method was systematized for its application in the diffraction theory by Noble (1958) in his famous book [6]. An early application to canonical diffraction problems can be found in the work of Jones (1952) [7], which is a key to solving diffraction problems taking into account the singularity, the Meixner condition at the edge [8].

The W-H method was developed by Weinstein (1969) [9], who was one of the first to apply it to waveguide problems and generalized the factorization method for internal obstacles. The applications of the W-H method to waveguide problems were extended by Mittra and Lee [10], and a modification of the method was made by Hurd [11]. The W-H method remains a powerful tool for solving diffraction problems, especially for canonical shapes such as half-planes, wedges, and cylindrical pins. However, its analytical elegance loses its attractiveness when it comes into contradiction with practical limitations, which encourages researchers to use numerical methods.

Recent advances in fast numerical methods, used particularly to solve boundary integral equations arising in scattering problems, have significantly reduced the computational cost of simulations [12,13,14]. However, for instance, the boundary element method can suffer from ill-conditioning at certain frequencies (fictitious eigenfrequencies) unless regularization techniques are applied. In recent publications [15,16,17], the scope of the W-H method was extended by using numerical and analytical–numerical approaches.

Consequently, a straightforward analytical solution to the axisymmetric key problem of diffraction on a perfectly conducting volumetric structure, for instance, on a semi-infinite round pin, remains a topical problem.

In attempt to solve this problem, the authors come across serious difficulties, which mainly concern the reliable solution of infinite algebraic equations. For example, in [10], the solution is reduced to solving a system of nonlinear algebraic equations, which is extremely time-consuming for numerical calculations.

As mentioned in [18], the solution was limited to the case of a thin rod. A similar problem was also considered in [19,20] using the interpolation method of factorization, related to the W-H method, where a numerical–analytical method of generalized stitching was proposed for solving systems of linear algebraic equations, the cumbersomeness and complexity of which increases significantly with an increase in the accuracy of the obtained solution.

In this paper, in order to find an analytical solution to the boundary value problem for the pin, we choose as its reference the well-known problem of diffraction on a thin, perfectly conducting, semi-infinite (SI) circular waveguide, coaxially located inside an infinite circular waveguide, which has a strict solution in the framework of the W-H method.

A specific feature of this problem is that its solutions are expressed through its eigenvalues and functions, as a result of which the longitudinal boundary conditions are satisfied automatically, due to the Bessel functions. Therefore, as an initial approximation, it is advisable to choose a solution to the reference problem. Then we only have to satisfy the boundary condition at the edge of the pin.

To achieve this goal, a new method is proposed that step by step provides suppression of all eigenmodes of the reference problem in the region inside the pin.

The idea of the method of compensating eigenmodes is realized by constructing an analytical W-H source located inside a SI cylinder very close to the edge of the pin, which radiates the same eigenmodes in antiphase. Although all modes of the reference problem are eliminated, the secondary modes appear as a result of interaction of the analytical source (AS) with the source located at the end of the SI cylinder. Each mode of the AS, running onto the end of the SI cylinder, is transformed into eigenmodes of neighboring regions, including all spatial modes in the pin region.

We keep in mind that according to the law of conservation of energy, the total power of the transformed secondary modes must be less than the power of one mode of the AS. This approach to suppression of eigenmodes is supported by the fact that the reflection coefficient of waves from the end of a SI thin cylinder is usually negligible when the wave is incident from the right. It is also justified by calculations showing that the diffraction effect of the incident wave in the opposite direction becomes insignificant with an increase in frequency $\omega$ (or wave number k).

Therefore, according to the method of successive approximations, the procedure of suppression of eigenmodes should be repeated cyclically as many times as required until complete suppression of the modes in the pin region.

In Section 2, the formulation of the boundary value problem (BVP) is reduced to a system of paired singular integral equations, and some important notations are introduced.

In Section 3, it is shown how the W-H method is used to solve the auxiliary problem of wave diffraction at the end of a semi-infinite circular waveguide of ideal conductivity, placed coaxially inside an infinite waveguide. In the subsections, eigenvalues and functions of the boundary value problem are obtained in the form of eigenmodes for each region of the waveguide in cases where a single mode is incident on the end of the semi-infinite waveguide both from the left and from the right.

The solution to the BVP in the form of an infinite series is considered in Section 4, where the method of compensating eigenmodes of the reference problem obtained strictly by the W-H method is described in detail.

Section 5 and Section 6 contain the discussion of the obtained results, estimation of the convergence of the solution and conclusions.

2. Statement of the Boundary Value Problem

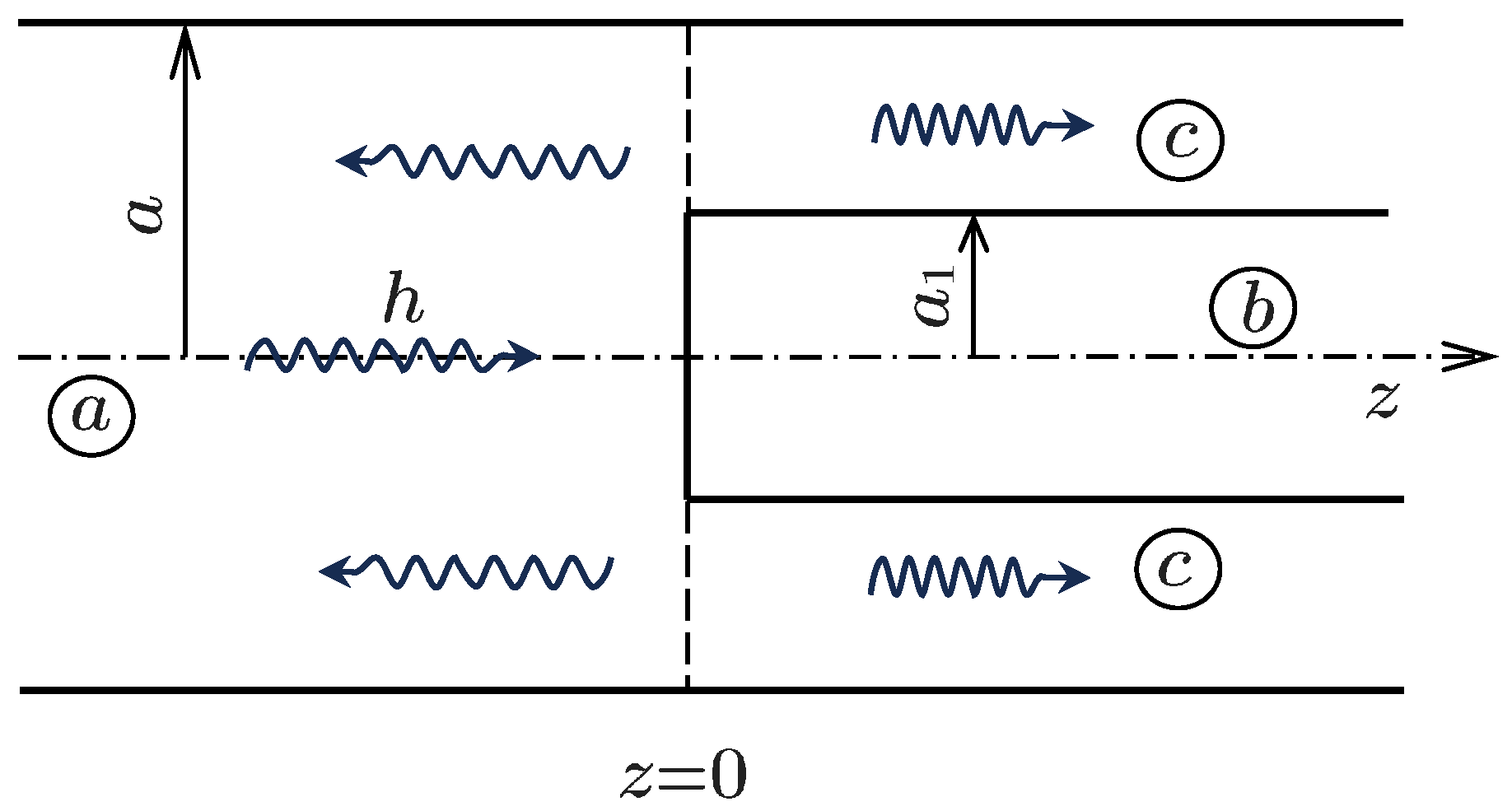
We let a TE-wave with a longitudinal wave number h and a unit amplitude be incident from the left on the end of a perfectly conducting SI pin of radius $a_1$, coaxially located inside an infinite circular waveguide of radius a (see Figure 1)

$$\begin{array}{c}\hfill E_{\phi }^i(r,z)={\mathrm{J}}_1\left(Vr\right)e^{ihz},\end{array}$$

(1)

where $V=\sqrt{k^2-h^2}$ is one of the roots of the first-order Bessel function ${\mathrm{J}}_1\left(va\right)$, $k=\omega /c$, and $z=0$ is the location of the end of the pin, which coincides with the origin of the coordinate system.

The BVP satisfies the electrodynamic boundary conditions, i.e., there is no tangential component of the electric field on the conducting surface [21]

$$E_{\phi }(r,z)+E_{\phi }^i(r,z)=0,0\le r\le a_1,0\le z;r=a,-\infty <z<\infty ,$$

(2)

including the end of the pin ($z=0$). Here,

$$E_{\phi }(r,z)=\underset{-\infty }{\overset{\infty }{\int }}{e}^{iwz}L(r,w)F\left(w\right)dw$$

(3)

is a diffracted field of waves scattered by a SI pin, $F\left(w\right)$ is the Fourier component of the current density.

$$L(r,w)={\displaystyle \frac{1}{{\mathrm{J}}_1\left(va\right)}}\left\{\begin{array}{c}{\mathrm{J}}_1\left(vr\right)(a_1^{\prime },a^{\prime }),r\le a_1,\hfill \\ {\mathrm{J}}_1\left(v{a}_1\right)(r_1^{\prime },a^{\prime }),r\ge a_1.\hfill \end{array}\right.$$

(4)

The combination of Bessel functions and their derivatives are denoted as

$$\begin{array}{cc}\hfill & (r^{\prime },a^{\prime })={\mathrm{J}}_1\left(vr\right){\mathrm{Y}}_1\left(va\right)-{\mathrm{J}}_1\left(va\right){\mathrm{Y}}_1\left(vr\right),\hfill \\ \hfill & (a_1,a^{\prime })={\mathrm{J}}_0\left(v{a}_1\right){\mathrm{Y}}_1\left(va\right)-{\mathrm{J}}_1\left(va\right){\mathrm{Y}}_0\left(v{a}_1\right),\hfill \end{array}$$

${\mathrm{Y}}_0$ and ${\mathrm{Y}}_1$ are the Neumann functions of zero and first order.

Then the boundary value problem can be reduced to a pair of integral W-H equations

$$\{\begin{array}{}\mathrm{(5a)}& \underset{C}{\int }{e}^{iwz}L\left(r,w\right)F\left(w\right)dw=0,0\le r\le a_1,z\ge 0,\mathrm{(5b)}& \underset{C}{\int }{e}^{iwz}F\left(w\right)dw=0,z<0,\end{array}$$

where C is the integration contour (see Figure 2), which consists of the real axis and a narrow loop enclosing the point $w=h$ from above, the first equation coincides with Expression (2), and the second means the absence of currents in the empty space for $z<0$.

For convenience, we divide the space inside the waveguide into three regions (see Figure 1).

$\left(a\right)$: $\{0\le r\le a,z\le 0\}$, $\left(b\right)$: $\{0\le r\le a_1,0\le z\}$$\left(c\right)$: $\{a_1\le r\le a,0\le z\}$, where spatial eigenmodes with transverse and longitudinal wave numbers $v_n^{\ell }$ and $w_n^{\ell }$ can propagate, $\ell =a,b,c$, $(n=1,2,\dots )$, where $w_n^{\ell }=\sqrt{k^2-v_n^{\ell 2}}$, $v_n^{a,b}$ are the roots of the Bessel functions ${\mathrm{J}}_1\left(va\right)$ and ${\mathrm{J}}_1\left(v{a}_1\right)$, respectively, and $v_n^c$ are the roots of the combinations of the Bessel functions $(a_1^{\prime },a^{\prime })$.

3. Excitation of Eigenmodes Inside a Circular Waveguide

The solution of the BVP is constructed on the basis of well-known analytical solutions obtained by the W-H method, the problem of wave diffraction on a SI thin circular cylinder located coaxially inside an infinite waveguide, where the cylindrical surfaces of the waveguides have perfect conductivity (see Figure 3). This problem is considered as a reference when constructing the solution because its eigenvalues and functions automatically satisfy the longitudinal boundary conditions of the stated problem along the z axis.

Therefore, we first consider the eigenmodes in each region from a methodological point of view, when a single eigenmode runs onto the open end of a thin semi-infinite cylinder from the left as well as from the right.

3.1. TE-Wave Diffraction on a Thin Perfectly Conducting SI Waveguide

We let a TE-wave with a unit amplitude and a wave number h (see (1), Figure 3) impinge on the open end of a semi-infinite waveguide of radius $a_1$, coaxially located inside an infinite circular waveguide of radius a, from the left.

The azimuthal component of the electric field of the scattered wave is described by the expression

$$E_{\phi }(r,z)=\underset{-\infty }{\overset{\infty }{\int }}{e}^{iwz}L(r,w)F_0\left(w\right)dw.$$

(6)

The BVP, due to the boundary conditions $E_{\phi }^i(a_1,z)+E_{\phi }(a_1,z)=0$ at $z\ge 0$, $r=a_1$ as well as the absence of surface currents in the extension of the cylinder, is reduced to solving the paired W-H integral equations

$$\{\begin{array}{}\mathrm{(7a)}& \underset{C}{\int }{e}^{iwz}L\left(a_1,w\right)F_0\left(w\right)=0,z\ge 0,\mathrm{(7b)}& \underset{C}{\int }{e}^{iwz}{F}_0\left(w\right)dw=0,z<0,\end{array}$$

where C is the integration contour in (5), $F_0\left(w\right)$ is the sought Fourier component of the current density, and $L(a_1,w)$ is the kernel of the integral equation. Note that the modified Fourier transform can be found in the works of L. Weinstein [9].

The system of integral Equation (7) has an exact solution

$$F_0\left(w\right)={\displaystyle \frac{K_0}{2\pi i(w-h)L_{-}(a_1,w)}}$$

(8)

obtained by the W-H method using the factorization of the kernel [9,22]

$$L(a_1,w)=L_{-}(a_1,w)L_{+}(a_1,w),$$

(9)

where the function $L_{-}$ is analytic in the lower half-plane (LHP) of the complex variable w and $L_{+}$ is, respectively, analytic in the upper half-plane (UHP).

From the methodological point of view, it should be mentioned that the function $F_0\left(w\right)$ corresponds to the analytical W-H source localized at the end of a SI cylinder (at $z=0$).

The accuracy of the solution is checked directly by substituting solution $F_0$ into System (7). Indeed, as the integration contour C in (8) should be closed in UHP w, the integrand is analytic inside the closed contour C, and therefore the Cauchy integral is zero. In the second Equation (7b), the integrand is also analytic inside the integration contour when the contour C is closed in the LHP w.

The constant

$$K_0=-{\displaystyle \frac{{\mathrm{J}}_1\left(V{a}_1\right)}{L_{+}(a_1,h)}}$$

(10)

is determined by the amplitude of the incident wave in integrating the field over the loop of the contour C.

It should be noted that the solution $F_0\left(w\right)\sim w^{-1/2}$ for $\left|w\right|\to \infty$ automatically satisfies the Meixner condition [8] on a sharp edge, which determines the uniqueness of the solution for the system of singular integral Equation (7).

Using the residue theory, the azimuthal component of the electric field (6) of the scattered wave can be calculated in the form of a sum of eigenmodes in each region:

(a) $0\le r\le a,z<0$

$$E_0^a(r,z)=K_0\sum _{n=1}^{\infty }{e}^{-i{w}_n^{a}z}{\displaystyle \frac{v_n^a{\mathrm{J}}_1\left(v_n^{a}r\right){(a_1^{\prime },a^{\prime })}_{v_n^a}}{w_n^{a}a(w_n^a+h)L_{-}(a_1,-w_n^a){\mathrm{J}}_0\left(v_n^{a}a\right)}};$$

(11)

(b) $0\le r\le a_1,z>0$

$$E_0^b(r,z)=-K_0\sum _{m=1}^{\infty }{e}^{i{w}_m^{b}z}{\displaystyle \frac{v_m^b{L}_{+}(a_1,w_m^b){\mathrm{J}}_1\left(v_m^{b}r\right)}{w_m^b{a}_1(w_m^b-h){\mathrm{J}}_0\left(v_m^b{a}_1\right)}};$$

(12)

(c) $a_1\le r\le a,z>0$

$$E_0^c(r,z)=-K_0\sum _{n=1}^{\infty }{e}^{i{w}_m^{c}z}{\displaystyle \frac{v_m^c{L}_{+}(a_1,w_m^c){(r^{\prime },a^{\prime })}_{v_m^c}}{w_m^c(w_m^c-h){(a_1^{\prime },a^{\prime })}_{v_m^c}^{\prime }}},$$

(13)

where

$$\begin{array}{c}{L}^{*}(r,-w_n^a)=\underset{w\to -w_n^a}{lim}(w+w_n^a)L(r,w)={\displaystyle \frac{v_n^a{\mathrm{J}}_1\left(v_n^{a}r\right){(a_1^{\prime },a^{\prime })}_{v_n^a}}{w_n^{a}a{\mathrm{J}}_0\left(v_n^{a}a\right)}},\\ {(a_1^{\prime },a^{\prime })}^{\prime }=a_1(a_1,a^{\prime })+a(a_1^{\prime },a).\end{array}$$

(14)

3.2. The Wave Impinges the Open End of the Waveguide from the Right

We let the mth mode with the amplitude ${\tilde{B}}_m$ of the electric field

$$E_{\phi }^i(r,z)={\tilde{B}}_m{\mathrm{J}}_1\left(v_m^{b}r\right)e^{-i{w}_m^{b}z}$$

(15)

from the AS (${\tilde{B}}_m\equiv B_m^{j}exp\left(i{w}_m^b\delta \right)$, located inside the semi-infinite cylinder at the point $z=\delta >0$, impinge on its end from the right (see Figure 3). In this case, the system of paired integral equations takes the same form as (7)

$$\left\{\begin{array}{c}{\displaystyle \underset{C_1}{\int }{e}^{iwz}L(a_1,w)F_1\left(w\right)dw=0,z\ge 0,}\hfill \\ {\displaystyle \underset{C_1}{\int }{e}^{iwz}{F}_1\left(w\right)dw=0,z<0}\hfill \end{array}\right.$$

(16)

with the exception of the integration contour $C_1$ (see Figure 4), which mainly passes along the real axis of the complex plane w and in a narrow loop goes around the point $-w_m^b$ from below.

The solution of System (16) is

$$F_1\left(w\right)={\displaystyle \frac{K_m^1}{2\pi i(w+w_m^b)L_{-}(a_1,w)}}.$$

(17)

The constant

$$K_m^1={\tilde{B}}_m{L}_{+}(a_1,w_m^b){\displaystyle \frac{{\mathrm{J}}_1\left(v_m^{b}a\right)}{{(a_1^{\prime },a^{\prime })}_{v_m^b}}}$$

(18)

is determined by calculating the integral over the narrow loop of the contour $C_1$, which corresponds to the amplitude ${\tilde{B}}_m$ of the incident mode.

The azimuthal component of the electric field (6) of scattered waves can be calculated using the theory of residues through the eigenmodes of the regions:

4. Solution of the Problem

The solution $F\left(w\right)$ only needs to satisfy one boundary condition at the end of the pin, along the radius at the point z = 0, since the above-mentioned eigenmodes automatically satisfy the longitudinal boundary conditions on the waveguide walls.

Let us represent the solution $F\left(w\right)$ in (5) as the sum of a sequence

$$F\left(w\right)=F_0\left(w\right)+\sum _{j=1}^{\infty }{F}_j\left(w\right)=F_0\left(w\right)+F_1\left(w\right)+F_2\left(w\right)+\dots .$$

(22)

The convergence of the solution F is ensured through the Fourier components of the surface currents $F_j$ ($j=1,2,\dots$), which in the region (b) successively destroy all the eigenmodes excited by the analytical source, i.e., the sought function $F_1\left(w\right)$ in (17) must update $F_0\left(w\right)$ (8), and the one following it must update the previous term by damping its eigenmode amplitude, etc.

It can be noted that the second Equation (5b) of the system is satisfied automatically due to the analyticity of the function

$$F_j\left(w\right)={\displaystyle \frac{K_m^j}{2\pi i(w+w_m^b)L_{-}(a_1,w)}}{K}_m^j=\mathrm{const}$$

(23)

in LHP w. We keep in mind that the function $F_1\left(w\right)$ in (16) is the initial term of the sequence ($j=1$).

The first Equation (5a) of the system can be conveniently represented as the sum of a series with coefficients $K_m^j$

$$E_0^b(r,z)+\sum _{j=1}^{\infty }{E}_j^b(r,z)=0(0\le r\le a_1,z\ge 0)$$

(24)

by calculating the integral using the residue theory in (5a), where

$$E_j^b(r,z)=-\sum _{n=1}^{\infty }{e}^{i{w}_n^{b}z}{\displaystyle \frac{v_n^b{L}_{+}(a_1,w_n^b){\mathrm{J}}_1\left(v_n^{b}r\right)}{w_n^b{a}_1{\mathrm{J}}_0\left(v_n^b{a}_1\right)}}\sum _{m=1}^{\infty }{\displaystyle \frac{K_m^j}{w_n^b+w_m^b}}.$$

(25)

As the fields of scattered eigenmodes $E_j^b$ and $E_{j+1}^b$ must cancel each other, it is reasonable to determine the values of the amplitudes $B_n^j$ from the relation

$$-E_{j-1}^b(r,z)=\sum _{n=1}^{\infty }{B}_n^j{e}^{i{w}_n^b|z-\delta |}{\mathrm{J}}_1\left(v_n^{b}r\right),B_n^j=\mathrm{const},\delta >0.$$

(26)

It should be borne in mind that the limit transition $\delta \to 0$ is performed only in the final results, and AS placed at the point $z=\delta$ inside the SI cylinder (in the region $\left(b\right)$).

Let the fields of the mth mode $E_0^b(r,z)$ in (12) and the AS $E_1^b(r,z)$ in (26) at $j=1$ completely eliminate each other at the point $z=0$. This enables us to obtain the constant in the first approach

$$B_m^1=K_0{\displaystyle \frac{v_m^b{L}_{+}(a_1,w_m^b)e^{-i{w}_m^b\delta }}{w_m^b{a}_1(w_m^b-h){\mathrm{J}}_0\left(v_m^b{a}_1\right)}}({\tilde{B}}_m=B_m^j{e}^{i{w}_m^b\delta }).$$

(27)

Substituting this expression instead of ${\tilde{B}}_m$ in (18), we find

$$K_m^1=K_0{\displaystyle \frac{L_{+}^2(a_1,w_m^b)}{(w_m^b-h)L^{*}(a_1,-w_m^b)}},$$

(28)

where $L^{*}(a_1,-w_m^b)=\underset{w\to -w_m^b}{lim}{(w+w_m^b)}^{-1}L(a_1,w)$.

Similarly, from Expressions (25) and (26) (for $j=2$), we can determine the following constant

$$B_n^2=e^{-i{w}_n^b\delta }{\displaystyle \frac{v_n^b{L}_{+}(a_1,w_n^b)}{w_n^b{a}_1{\mathrm{J}}_0\left(v_n^b{a}_1\right)}}\sum _{m=1}^{\infty }{\displaystyle \frac{K_m^1}{w_n^b+w_m^b}},$$

(29)

which corresponds to the amplitude of the field of the second analytical source $E_2^b$.

Next, it is useful to establish a recurrence relation between constants $K_m^2$ and $K_m^1$

$$K_m^2={\displaystyle \frac{L_{+}^2(a_1,w_m^b)}{L^{*}(a_1,-w_m^b)}}\sum _{n=1}^{\infty }{\displaystyle \frac{K_n^1}{w_n^b+w_m^b}},$$

(30)

which follows from (29) and the expression (at $j=2$)

$$\begin{array}{cc}\hfill & K_m^j=B_m^j{e}^{i{w}_m^b\delta }{L}_{+}(a_1,w_m^b){\displaystyle \frac{{\mathrm{J}}_1\left(v_m^{b}a\right)}{{(a_1^{\prime },a^{\prime })}_{v_m^b}}}.\hfill \end{array}$$

(31)

The above relationship connects the amplitude of the incident current wave $F_j$ with the scattered radiation field through the integral over the circuit loop $C_1$ and transforms into the expression (18) at $j=1$.

Thus, using the induction method, we can obtain the following recurrent formula:

$$K_m^{j+1}={\displaystyle \frac{L_{+}^2(a_1,w_m^b)}{L^{*}(a_1,-w_m^b)}}\sum _{n=1}^{\infty }{\displaystyle \frac{K_n^j}{w_n^b+w_m^b}}$$

(32)

for all terms of the series.

Thus, the diffraction fields for regions are expressed by the terms of the sequence

$$\{\begin{array}{}\mathrm{(33a)}& E_{\phi }^a(r,z)=E_0^a(r,z)+\sum _{j=1}^{\infty }{E}_{\mathrm{j}}^a(r,z),\mathrm{(33b)}& E_{\phi }^b(r,z)=E_0^b(r,z)+\sum _{j=1}^{\infty }{E}_{\mathrm{j}}^b(r,z)=0,\mathrm{(33c)}& E_{\phi }^c(r,z)=E_0^c(r,z)+\sum _{j=1}^{\infty }{E}_{\mathrm{j}}^c(r,z),\end{array}$$

where

$$\begin{array}{cc}\hfill & E_j^a(r,z)=\sum _{n=1}^{N_a}{e}^{-i{w}_n^{a}z}{\displaystyle \frac{L^{*}(r,-w_n^a)}{L_{+}(a_1,w_n^a)}}\sum _{m=1}^{N_b}{\displaystyle \frac{K_m^j}{w_n^a-w_m^b}},\hfill \end{array}$$

(34)

$$\begin{array}{cc}\hfill & E_j^b(r,z)=-\sum _{n=1}^{N_b}{e}^{i{w}_n^{b}z}{\displaystyle \frac{v_n^b{L}_{+}(r,w_n^b){\mathrm{J}}_1\left(v_n^{b}r\right)}{w_n^b{a}_1{\mathrm{J}}_0\left(v_n^b{a}_1\right)}}\sum _{m=1}^{N_b}{\displaystyle \frac{K_m^j}{w_n^b+w_m^b}},\hfill \end{array}$$

(35)

$$\begin{array}{cc}\hfill & E_j^c(r,z)=-\sum _{n=1}^{N_c}{e}^{i{w}_n^{c}z}{\displaystyle \frac{v_n^c{L}_{+}(a_1,w_n^c){(r^{\prime },a^{\prime })}_{v_n^c}}{w_n^c{(a_1^{\prime },a^{\prime })}_{v_n^c}^{\prime }}}\sum _{m=1}^{N_b}{\displaystyle \frac{K_m^j}{w_n^c+w_m^b}}.\hfill \end{array}$$

(36)

As all eigenmodes must be completely suppressed both inside the region $\left(b\right)$ and on the pin surface, it can be assumed that all boundary conditions of the BVP are satisfied.

It should be noted that the continuity of the fields at the point of discontinuity of the boundary conditions at the boundary of the regions $\left(a\right)$ and $\left(c\right)$ ($z=0,a_1\le r\le a$) is ensured automatically, as the fields of the AS are continuous everywhere, and the boundary condition $E_{\phi }^b=0$ at the end of the pin is satisfied by virtue of the sequence in (33b).

Thus, expressions for the electric field (33a) and (33c) are found for the spatial modes of regions $\left(a\right)$ and $\left(c\right)$ in the form of exponentially converging series.

Therefore, when summing up the series, we can limit ourselves to its initial $N_a$ or $N_c$ terms, which correspond to the number of running modes in regions $\left(a\right)$ and $\left(c\right)$, respectively.

It should be noted that the Meixner condition [8]

$$F\left(w\right)\simeq w^{-2/3},\left|w\right|\to \infty$$

(37)

is provided by shifting the zeros of the factorized Bessel function ${\mathrm{J}}_1{\left(v_m^b{a}_1\right)}_{-}$ by the value $▵w_m^b=i\pi /\left(6a_1\right)$ at $\left|w\right|\to \infty$.

5. Discussion

The solution $F\left(w\right)$ in (22) is presented as an infinite series, each term of which is an exact solution to the reference problem obtained by the W-H method. In this case, the fulfillment of the boundary condition $E_{\phi }^b=0$ on the surface of the end face of the pin ($z=0$, $0\le r\le a_1$) in (33b) is ensured by the AS located on the right near the point $z=0$ in the region $\left(b\right)$.

The convergence of the solution in (33) can be clearly interpreted in terms of the transformation and reflection of the incident wave at the end of a SI cylinder.

It is obvious that the smaller the wave reflection coefficient, the better the convergence of the solution. Indeed, with an increase in the value of the wave number k, the wave transmission coefficient by power tends to unity, which is confirmed by numerical calculations.

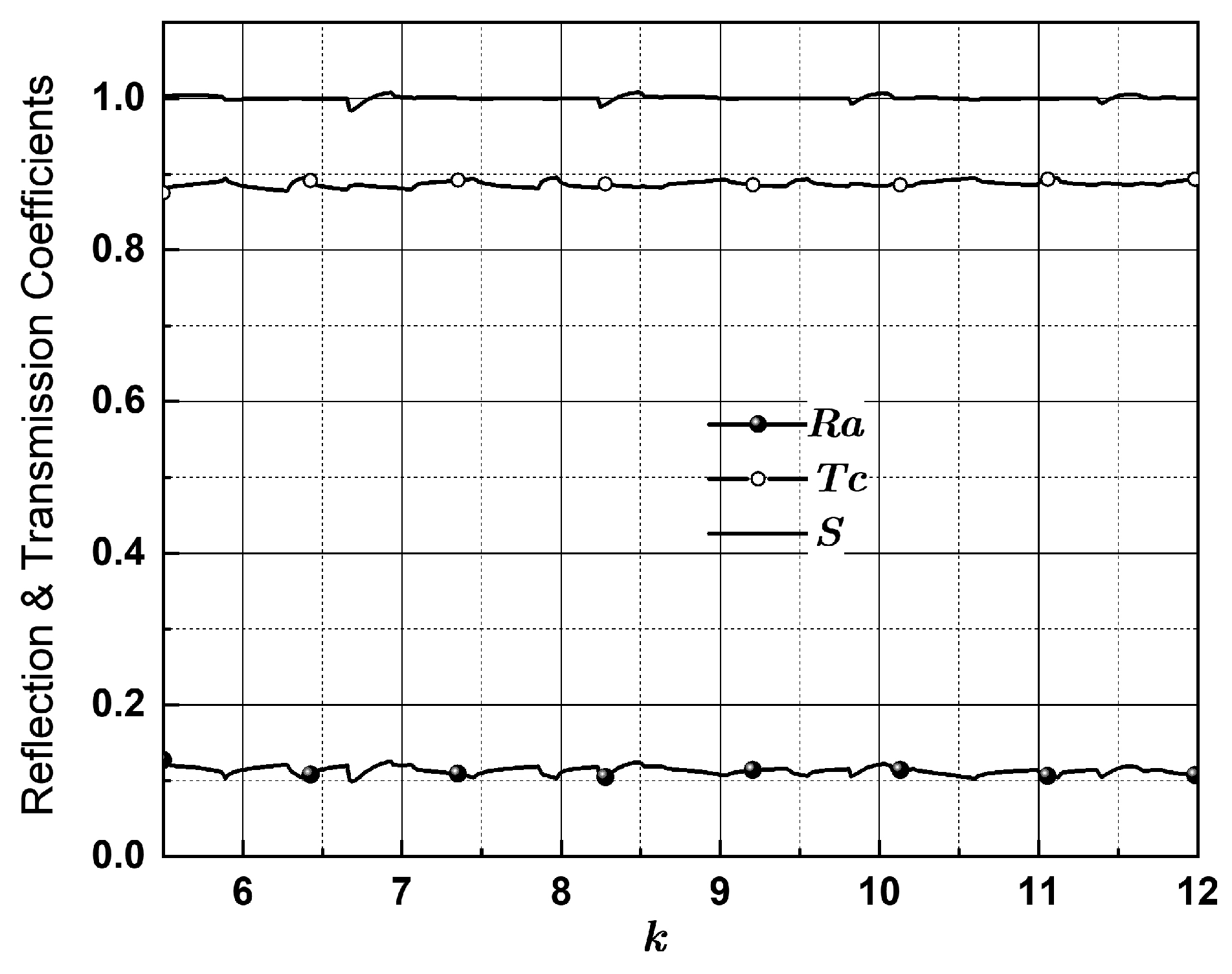
Figure 5 demonstrates the dependence of transmission $T_c$ and reflection $R_a$ coefficients on power taking into account the two initial terms of the solution ($F_0$ and $F_1$), where $a=6$, $a_1=2$ are the radii of the outer and inner waveguides, and $S=T_c+R_a$ is the total power of all transformed modes after diffraction of the incident mode, normalized to unity ($S_0=1$ is the power of the incident mode with (longitudinal) wave number h).

Figure 5 shows that the solution complies with the law of conservation of energy with an accuracy of a fraction of a percent, with the exception of periodic bursts, the relative deviation of which is an order of magnitude greater—about a percent.

It can be noted that the onset of the burst coincides with the zero value of the longitudinal wave number $w_m^b=\sqrt{k^2-v_m^{b2}}\simeq 0$ $(m=1,2,\dots )$, which usually entails a maximum increase in the reflection coefficient of waves from the end of the SI cylinder. As a result, the fraction of the energy of one eigenmode converted into the modes of neighboring regions $\left(a\right)$ and $\left(c\right)$ decreases sharply and as a rule the efficiency of mode suppression decreases.

In Figure 5, we can find the frequency region of the maximum deviation of the function $S\left(k\right)$ from unity

$$k\in \bigcup _{m=1}^{N_b}\left[v_m^b,\sqrt{v_m^{b2}+1}\right](k=\omega /c),$$

(38)

where the values of the longitudinal wave number $w_m^b$ fall in the interval $[0,1]$, as $w_m^b$ is in the denominator $K_m^j$.

Apparently, the denominator $(w_n^a-w_m^b)$ in the expression $E_j^a$ (35) also contributes to the weakening of the convergence of the solution, which is observed in the graph of the functions $R_a\left(k\right)$ or $S\left(k\right)$.

However, the calculation of scattered wave fields in the remaining part of the frequency range demonstrates a fast convergence and allows us to obtain a result with a given accuracy.

Based on the law of energy conservation, the relative error can be defined as

$$\eta \left(k\right)=\left(1-S\left(k\right)\right)100\%,$$

(39)

It should be noted that in the multimode regime, the maximum deviation from the true solution in the graph decreases with increasing k.

6. Conclusions

An analytical solution to the problem of wave diffraction at the end of a circular pin with ideal conductivity is obtained by the method of damping eigenmodes in the form of an infinite series using a recurrent formula.

The method of suppression of eigenmodes is based on the use of AS modes in the problem of wave diffraction on a SI thin cylinder of ideal conductivity, solved by the W-H method. The auxiliary AS is located inside the SI cylinder close to the end surface.

The reliability and accuracy of the obtained analytical solutions are verified numerically in terms of fulfillment of the energy conservation law at the values of the radii $a=6$, $a_1=2$. For this purpose, on the segment $k\in [5.5,12]$, two frequency ranges of solution convergence are identified and their boundaries are determined. In the first range, the relative calculation error is about one percent in the form of a splash in the graph, and in the second, the calculation accuracy is an order of magnitude higher than in the first one, which is seen even at the first iteration. It is numerically established that in the multimode mode, the calculation accuracy increases as k increases.

It should be noted that the proposed method can be further expanded to solving axisymmetric thick diaphragm problems, as they are also based on the W-H method. For example, the standard method for solving a similar problem of wave diffraction on a section of a circular cylinder is a key to considering the problem of a volumetric resonator with supply waveguides.