Physics-Informed Feature Engineering and R²-Based Signal-to-Noise Ratio Feature Selection to Predict Concrete Shear Strength

Abstract

Accurate prediction of reinforced concrete shear strength is essential for structural safety, yet datasets often contain a mix of raw geometric and material properties alongside physics-informed engineered features, making optimal feature selection challenging. This study introduces a statistically principled framework that advances feature reduction for neural networks in three novel ways. First, it extends the artificial neural network-based signal-to-noise ratio (ANN-SNR) method, previously limited to classification, into regression tasks for the first time. Second, it couples ANN-SNR with a confidence-interval (CI)-based stopping rule, using the lower bound of the baseline ANN’s R² confidence interval as a rigorous statistical threshold for determining when feature elimination should cease. Third, it systematically evaluates both raw experimental variables and physics-informed engineered features, showing how their combination enhances both robustness and interpretability. Applied to experimental concrete shear strength data, the framework revealed that many low-SNR features in conventional formulations contribute little to predictive performance and can be safely removed. In contrast, hybrid models that combined key raw and engineered features consistently yielded the strongest performance. Overall, the proposed method reduced the input feature set by approximately 45% while maintaining results statistically indistinguishable from baseline and fully optimized models (R² ≈ 0.85). These findings demonstrate that ANN-SNR with CI-based stopping provides a defensible and interpretable pathway for reducing model complexity in reinforced concrete shear strength prediction, offering practical benefits for design efficiency without compromising reliability.

1. Introduction

Overly simplified models, limited generalizability, and uncertainty in design predictions are common consequences of data scarcity in civil engineering. Data scarcity exists due to the realities of civil engineering experimentation, which is both costly and time-consuming. Thus, traditional design equations are based on sparse datasets and rely heavily on conservative assumptions. While these models provide safe lower-bound estimates, they often fail to capture complex nonlinear interactions among geometric and material properties, potentially leading to inefficient or unconservative designs.

Mathematical models are central to structural engineering [1] and provide analytical frameworks to estimate performance characteristics. However, traditional models are often built on idealized assumptions and calibrated using limited datasets, which constrains their ability to generalize across a broad range of conditions. In many domains, this has led to a shift toward data-centric modeling, where models are driven by observed data rather than fixed assumptions. For this, this research explores a compiled database of 1200+ observations across 49 studies on concrete shear strength [2].

Due to their ability to model any measurable underlying function to an arbitrary degree of accuracy, artificial neural networks (ANNs) are of interest herein. Appropriately constructed, ANNs are universal approximators [3] however, their nonlinear and black-box nature has made their adoption slow in safety-critical applications, such as civil engineering [4] To address these competing limitations, black-box interpretability versus feature transparency, this study advances the mathematical modeling of reinforced concrete shear strength by integrating ANNs for modeling, feature engineering, feature selection, and hyperparameter optimization.

To address black-box concerns, this research evaluates both raw and physics-informed engineered features, assessing their combined influence on reinforced concrete shear strength prediction. Model configuration is systematically optimized through Bayesian hyperparameter search, ensuring robust selection of network architecture and learning parameters. For feature selection, we extend signal-to-noise ratio (SNR) screening, previously confined to classification [5] to regression tasks, and develop a novel R² confidence-interval-based stopping rule that defines statistical equivalence to a full model. Applied to reinforced concrete data, this integrated framework enables systematic reduction in features while maintaining predictive performance.

Taken together, this paper contributes to the integration of feature engineering, mathematical learning models, optimization methods, and statistically principled feature selection to advance a long-standing, data-scarce problem in structural engineering. By balancing predictive accuracy with model parsimony, the ANN framework achieves accuracy surpassing traditional code-based formulas while clarifying the relative influence of key design variables through a transparent, data-driven approach.

2. Motivation: Concrete Shear Strength

Figure 1 illustrates a typical reinforced concrete beam subjected to shear loading, highlighting key geometric and reinforcement parameters used in shear strength estimation. Traditional methods for predicting shear strength rely on simplified models rooted in engineering mechanics and calibrated with empirical data from laboratory tests. These models typically aim to ensure safety by providing conservative lower-bound estimates of the shear capacity.

The traditional method used to calculate the lower bound on concrete shear strength is defined as standard ACI 318-14 [7]:

$$V_n=V_c+V_S$$

(1)

where $V_c$ is the concrete contribution and $V_S$ is the transverse steel contribution [2,8] In (1), the concrete contribution is defined as

$$V_c=2\lambda \sqrt{f_c^{’}}·bd$$

(2)

where $\lambda$ is an effect size, $f_c^{’}$ is the compressive strength of concrete, $b$ is the beam width, and $d$ is the beam depth [2,8] The steel contribution is then defined as

$$V_S={\displaystyle \frac{A_v{f}_{y}d}{s}}$$

(3)

where $A_v$ is the shear reinforcement, $f_y$ is the yield strength of the sheer reinforcement, $d$ is the effective depth of the beam, and $s$ is the spacing of the shear reinforcement [2,8]

2.1. Experimental Dataset

As mentioned across multiple studies of concrete shear strength, cf. [2,6,9] limited large datasets exist for modeling. Thus, aggregating data from multiple studies is common practice. Of interest herein is using the compiled dataset introduced in [2] which was taken from multiple publications, including [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50]. This resulted in a total dataset of 1259 samples from 49 studies published between 1951 and 2004. Notably, this further creates a heterogeneous dataset as some studies were interested in different geometries, sizes, and questions related to constructing concrete beams. Overall, this aggregation provides both statistical diversity necessary for machine learning, albeit at the cost of possibly introducing additional variability.

A description of variables, their ranges, and units is presented in

Table 1. Concrete Shear Strength Database Variables, from [2].

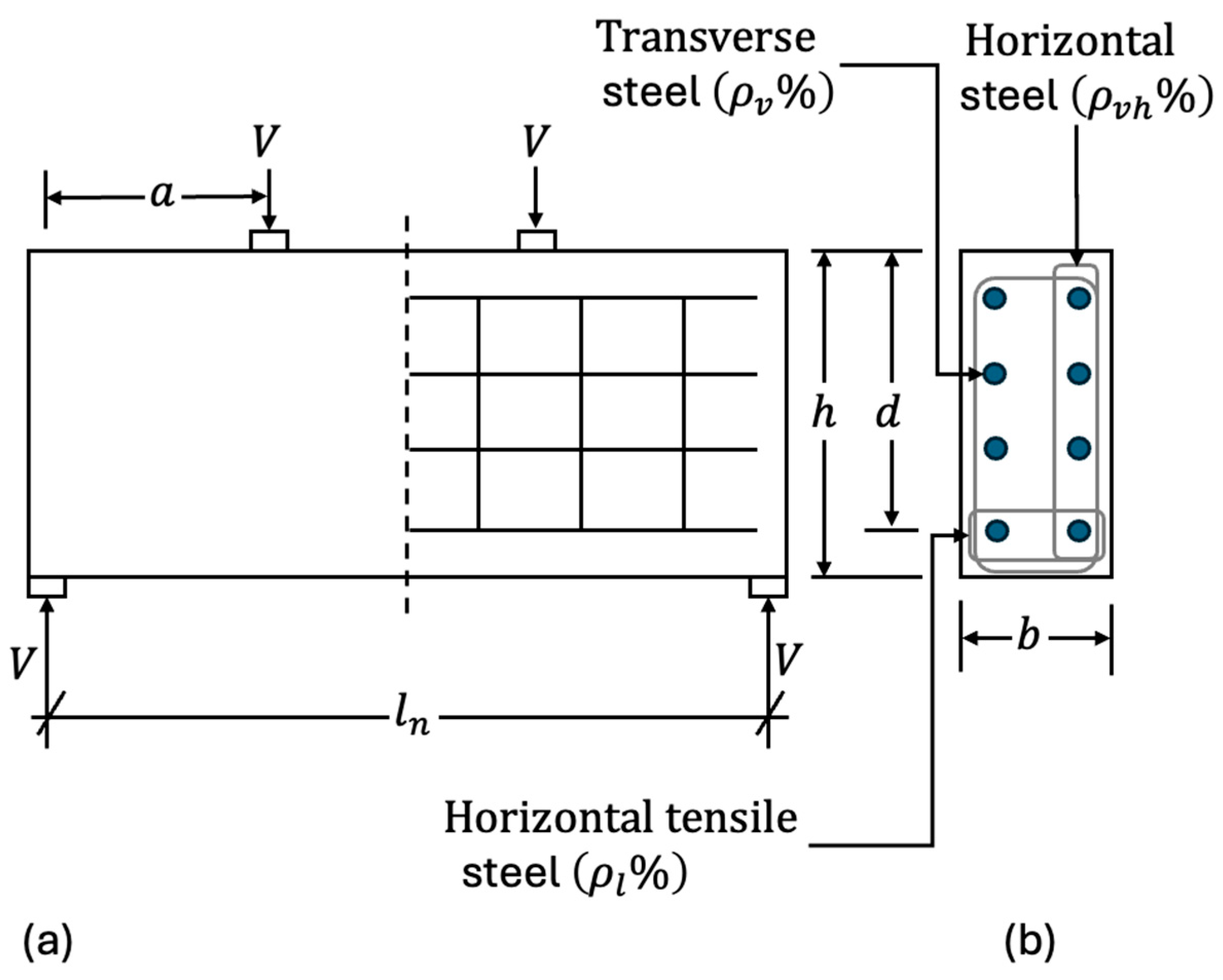
Variable	Description	[Range] (S.D.) and Units
$b$	Width of the beam	[1.5, 79.1] (4.45) inches
$d$	Effective depth of the beam	[0.8, 118.1] (10.12) inches
$f_c^{’}$	Compressive strength of concrete used in the beam	[880, 18,170] (0.31) psi
$f_y$	Yield strength of the shear reinforcement	[20.3, 258] (20.54) ksi
${\rho }_l$	Longitudinal reinforcement ratio (steel reinforcement by area of concrete)	[0.001, 0.070] (0.012)
${\rho }_v$	Vertical shear reinforcement ratio	[0.001, 0.029] (0.003)
${\rho }_{vh}$	Longitudinal shear reinforcement ratio	[0, 0.077] (0.004)
$a$	Shear span (distance from the applied load and the support)	[2.4, 708.6] (40.78) inches
${\displaystyle \raisebox{1ex}{$a$}\!\left/ \!\raisebox{-1ex}{$d$}\right.}$	Shear span-to-depth ratio	[0.27, 9.7] (1.82)
$l_n$	Clear span of the beam	[5.6, 1417.2] (81.5) inches
$V_{test}$	Measured shear strength of the specimen at the face of the support	[0.33, 502.35] (53.78) kips
$V_{pred}$	Predicted shear strength at the face of the support (by sources)	[0.20, 828.21] (44.49) kips

. Notably, the issues in traditional prediction methods are seen even in the data summary of Table 1, with the maximum predicted value of shear strength from the studies, $V_{pred}$, being 60+% larger than the maximum tested value, $V_{test}$.

2.2. Performance Metrics

For regression tasks in concrete shear strength estimation, performance is typically evaluated by regressive [2,17] Consistent with [2,17] the coefficient of determination (R²) is the standard metric in concrete shear strength prediction studies, and it provides a direct measure of variance explained by the model. In practical terms, R² measures how much of the variation in shear strength data is explained by the model. An R² close to 1 means the model predictions closely follow the experimental results, while lower values indicate larger unexplained differences. R² is defined as

$$R^2=1-{\displaystyle \frac{{\sum }_i{\left(y_i-{\widehat{y}}_i\right)}^2}{{\sum }_i{\left(y_i-\mu \right)}^2}}$$

(4)

where $y_i$ are the actual values, ${\widehat{y}}_i$ are the predicted values, and $\mu$ are the mean values [51]. Notably, R² is not a perfect measure, e.g. it does not capture curvilinear relationships, and it can imply relationships that are not there [51]. As a result, a qualitative assessment of performance is needed by observing real versus predicted and parameter estimate plots.

Given the stochastic nature of many AI algorithms in randomized training and sensitivity to starting points, multiple replications and then computing confidence intervals (CIs) for the performance metrics are useful evaluation tools. For R², the confidence interval used is computed by first computing the mean and standard deviation:

$${\widehat{R}}^2={\displaystyle \frac{1}{n}}\sum _{i=1}^n{R}_i^2 and \widehat{s}=\sqrt{{\displaystyle \frac{1}{n-1}}\sum _{i=1}^n{\left(R_i^2-{\widehat{R}}^2\right)}^2}$$

(5)

where n is the number of replications. The mean confidence interval for R² used herein employs a t-score to permit small replication number estimates of the mean R². Consistent with general mean CIs, this was computed as

$$CI=\left[{\widehat{R}}^2-t_{n-\mathrm{1,1}-{\displaystyle \frac{\alpha }{2}}}{\displaystyle \frac{\widehat{s}}{\sqrt{n}}}, \hspace{1em}{\widehat{R}}^2+t_{n-\mathrm{1,1}-{\displaystyle \frac{\alpha }{2}}}{\displaystyle \frac{\widehat{s}}{\sqrt{n}}},\right]$$

(6)

with $t_{n-\mathrm{1,1}-{\displaystyle \frac{\alpha }{2}}}$ being the Student t quantile.

2.3. ANNs for Concrete Shear Strength Modeling

ANNs have seen limited but focused applicability in civil engineering. ANNs are of interest due to their ability to model complex nonlinear data problems, but hesitation exists due to the general black-box nature of ANN algorithms. Londhe et al. [4] provide a comprehensive and recent review of ANN methodologies in civil engineering, highlighting applications ranging from structural health monitoring to concrete strength prediction, and emphasizing the flexibility of ANNs to handle incomplete or noisy data.

In the specific domain of reinforced concrete shear strength prediction, Sanad and Saka [6] pioneered the use of ANNs for shear strength prediction, and then Young et al. [2] pioneered the exploration of ANN hyperparameter design for more accurate shear strength prediction. Young et al. [2] further focused on how input variables such as beam dimensions and material properties influence predictions. Their work demonstrated that ANNs can achieve high predictive accuracy while also revealing variable importance, setting a precedent for knowledge discovery in model outputs.

Markou and Bakas [52] extended this work by applying AI algorithms, including ANNs, to a large synthetic database of slender reinforced concrete beams generated via 3D nonlinear finite element analysis. Their study underscored the potential of combining simulation-derived datasets with AI to improve prediction quality for configurations not well-represented in experimental data.

More recently, Murphy and Paal [8] introduced a hybrid transfer learning and physics-informed feature engineering approach for modeling the shear strength of concrete walls. By embedding physics-based data features as inputs to opaque machine learning neural networks, they demonstrated that feature engineering grounded in structural mechanics can improve both predictive accuracy and model interpretability.

2.4. Physics-Informed Feature Engineering

Murphy and Paal [8] developed a feature engineering strategy whereby physics-defined features were applied as input data to conventional ANNs. This concept aims to craft features that are more relevant and incorporate subject matter expertise for the ANN to model. Of interest herein is extending this consideration by incorporating these features and understanding their relevance for predictive tasks.

The engineered features from [8] include a calculation of the total shear capacity from concrete and reinforcement:

$$p_0=\left({\alpha }_c\lambda \sqrt{f_c^{’}}+{\rho }_t{f}_{y }\right)A_{cv}$$

(7)

where $A_{cv}$ is a cross-sectional area and assumed herein as $A_{cv}=bd$, ${\alpha }_c\lambda \sqrt{f_c^{’}}$ is associated with concrete strength and ${\rho }_t{f}_{y }$ is associated with reinforcement strength. In addition to $p_0$, ref. [8] defines the following additional features:

$$p_1={\alpha }_c\lambda \sqrt{f_c^{’}}$$

(8)

$$p_2={\alpha }_c\lambda \sqrt{f_c^{’}}{A}_{cv}$$

(9)

$$p_3={\rho }_t{f}_{y }$$

(10)

$$p_4={\rho }_t{f}_{yt }{A}_{cv}$$

(11)

where $p_1$ is the contribution of strength from concrete, $p_2$ scales $p_1$ by area, $p_3$ represents the reinforcement ratio and yield stress product, and $p_4$ scales $p_3$ by area.

3. Methodology

3.1. Artificial Neural Networks

Artificial Neural Networks (ANNs) are a class of supervised machine learning methods inspired by the structure and learning processes of biological neural systems [53] They are typically nonlinear models that learn mappings between input and output data by adapting the weights of connections among layers (input, hidden, and output) during training. Through this process, ANNs construct a mathematical model that captures complex patterns and relationships within the data.

A wide variety of ANN approaches exist, e.g., see [53], however, given the relatively small scale of the dataset and the absence of temporal or spatial structure in the features, a feedforward ANN provides an appropriate balance between model complexity and predictive capacity. Notably, when appropriately constructed, a feedforward ANN can serve as a provably optimal universal approximator [3]. However, simplicity is relative, and even a relatively simple feedforward ANN has considerable hyperparameters to choose from, which greatly influence performance. These include the number of hidden nodes, the type of functions in each node, the training approach, the training objective, and the number of iterations.

3.2. Hyperparameter Determination

AI/ML algorithmic results are often only as good as the settings used to train these algorithms. Such hyperparameters can be numerous, and determining their appropriate values is a discipline in itself. While general taxonomies of these approaches exist [54] these methods can largely be separated into model-free and model-based approaches. Model-free approaches can range from scientific grid searches to experiential/haphazard and random methods. Model-based approaches have generally outperformed model-free approaches and employ a wrapper function around the algorithm of interest and use a concerted search strategy [54].

Bayesian optimization (BO) is one of the most competitive model-based hyperparameter determination methods [55]. BO employs a sequential search strategy for optimizing expensive, black-box functions, with the objective function (typically) being the validation performance of a learning algorithm as a function of its hyperparameters, a function which is usually noisy, non-convex, and lacks a closed-form expression or gradient information. BO addresses this by fitting a probabilistic surrogate model (also known as a response surface model) to predict the objective function and by using an acquisition function to decide which hyperparameter setting to evaluate next.

3.3. Feature Saliency in Artificial Neural Networks

In many data-driven applications, experiments often aim to collect large volumes of data under the assumptions that it will be difficult, if not impossible, to collect additional data later and that more data will lead to better modeling capabilities. However, this often results in having more data than necessary. The consequence of this can be not only larger datasets than needed but also the inclusion of redundant, irrelevant, and low-quality data [56]. Thus, feature selection and feature extraction methods are commonly employed to mitigate these issues by, respectively, identifying and retaining only the most informative variables or transforming data to a more useful representation [57].

Feature extraction is the process of transforming raw data into a reduced set of informative features that capture the most relevant characteristics of the original data. These transformations often aim to maximize data variance, improve class separability, or reduce dimensionality, and possibly enhance the performance and efficiency of learning algorithms. However, these methods can create less interpretable features and cause the resultant models to be less explainable. This is in contrast to feature selection, which retains a subset of the original variables and preserves their interpretability, which is thus of interest.

Feature selection for ANN applications can take the form of filter-based approaches, which aim to provide feature relevance ranking before the ANN model is run [58] post-classifier methods which incorporate a sensitivity analysis [2] and combined model-saliency approaches, which simultaneously train and compute saliency [5] Due to their ability to intrinsically capture the importance of each feature to a model, the combined ANN-SNR approach is of interest herein.

ANN-SNR feature selection is an extension of [59,60] and is a weight-based approach for feature selection. The ANN-SNR approach adds a noise feature to the dataset, and then the ANN is trained. After training, the weights of each node are compared against the trained weights of the noise-related nodes using an SNR calculation:

$$SN{R}_i=10{\log }_{10}\left({\displaystyle \frac{{\sum }_{j=1}^J{\left(w_{i,j}^1\right)}^2}{{\sum }_{j=1}^J{\left(w_{N,j}^1\right)}^2}}\right)$$

(12)

where $SN{R}_i$ is the SNR value in dB for the i-th feature, J is the number of hidden nodes, $w_{i,j}^1$ is the first layer weight between node i and node j, and $w_{N,j}^1$ is the first layer weight from the noise node N to node j [5,57].

Consistent with [57] when using ANN-SNR, the data set is standardized, and one random normal data vector, N(0,1), is added to the dataset as the noise feature. After training an ANN and computing, by (12), the SNR values for each feature, features with higher SNR values are considered like signals that stand out clearly above background noise, whereas features with comparatively low SNR values are like weak signals that add little to the prediction. Removing the weakest features step by step helps isolate the variables that truly matter. The process of (12) is applied in a backward selection manner for all data until only one non-noise feature remains, with the noise features retained. The accuracy of each iteratively explored model is evaluated, and the best set of data features is selected.

It should be noted that the SNR values reported in ANN-SNR applications are relative measures derived from ANN weights and input variability, and are not directly comparable to signal-to-noise ratios in communication systems. Their absolute magnitude is less important than their ranking, since the method eliminates features with the lowest relative SNR.

3.4. ANN-SNR Predictive Stopping Rules

In general, finding the smallest feature set that provides for a model statistically similar results (or better) to a model trained on the entire feature set is of interest. For regression tasks, this involves selecting the smallest feature set whose mean R² remains within or above the full model’s 95% CI lower bound on the R². This approach is two-stage: first exploring all subsets through iterative elimination and then validating the best candidate with full optimization to ensures that the final model balances parsimony and statistical equivalence, producing a reduced yet defensible representation of the original ANN model.

The process in Figure 2 captures the end-to-end approach, beginning with finding the baseline performance through BO to optimize an initial ANN with all k features to determine l best algorithmic settings. The ANN with the l optimized settings is then trained on all k features for p replications to compute the baseline mean R² and its 95% confidence interval. Next, setup for the ANN-SNR approach is performed with data features that are standardized, and at the initialization of the ANN-SNR backward feature selection loop, a synthetic noise variable ($\mu =0, \sigma =1$) is added. TRACE is initialized as an empty record to track subsets and their R² values. An ANN with l settings is trained on [F, noise], and the resulting R² is recorded in TRACE along with the current subset. Features are then ranked based on their signal-to-noise ratio (SNR), derived from the ANN’s first-layer weights to quantify relative feature importance as seen in Equation (12), and the lowest-ranked feature is eliminated from F. This cycle continues until only one feature remains in F.

After the loop terminates, TRACE contains the record of all candidate feature subsets and their associated R² values. From TRACE, the smallest subset whose mean R² remains above the baseline confidence interval threshold is selected as the final reduced feature set. The final ANN is then re-optimized with BO using this reduced F, and its predictive performance (R² and CI) is reported. The best result from this provides m algorithm settings.

4. Results

Results are presented for the baseline dataset and architecture, first refined using Bayesian Optimization (BO) to identify optimal hyperparameters. The optimized model was then subjected to ANN-SNR feature selection to produce a parsimonious feature set while maintaining predictive accuracy. Once a parsimonious feature set is found, results are presented for algorithms and feature sets. For all analyses, MATLAB 2025a on a MacBook Pro (Apple M4 Max, 48 GB RAM) was used.

4.1. Baseline Results

The baseline results,

Table 2. Baseline results summary from [2].

Algorithm	Features	Architecture	R2
Baseline [2]	$b,d,f_c^{’},f_y,{\rho }_l,{\rho }_v,{\rho }_{vh},a$,$l_n$,${\displaystyle \raisebox{1ex}{$a$}\!\left/ \!\raisebox{-1ex}{$d$}\right.}$	logsig [7, 4] LM with MSE	Mean R2: 0.866 Range R2: [0.841, 0.892]
Baseline [2]	$b,d,f_c^{’},f_y,{\rho }_l,{\rho }_v,a$,$l_n$	logsig [7, 4] LM with MSE	Mean R2: 0.877 Range R2: [0.832, 0.903]

, are drawn from Young et al. [2] and represent a two-hidden-layer feedforward neural network (7 and 4 neurons) trained using the Levenberg–Marquardt (LM) algorithm with mean squared error (MSE) as the performance function. Two feature sets were tested: (1) the full set of experimental variables, and (2) a reduced set obtained via post hoc sensitivity analysis feature selection. The reduced feature set achieved a slightly higher mean coefficient of determination (R² = 0.877, range: 0.832–0.903) compared to the full set (R² = 0.866, range: 0.841–0.892). Although these differences were not statistically significant, they indicate that targeted feature selection can yield practically meaningful improvements in model accuracy.

Because ANN performance is inherently stochastic, with outcomes sensitive to initialization, training order, and software platform, BO was used to refine hyperparameters for the baseline architecture rather than relying on fixed settings. BO was applied to identify the best-performing configuration for each feature subset, ensuring that subsequent SNR-based feature selection (ANN-SNR) operated on an optimized baseline model rather than one influenced by suboptimal tuning. The hyperparameters tuned in this process are summarized in

Table 3. Bayesian Optimization (BO) search space.

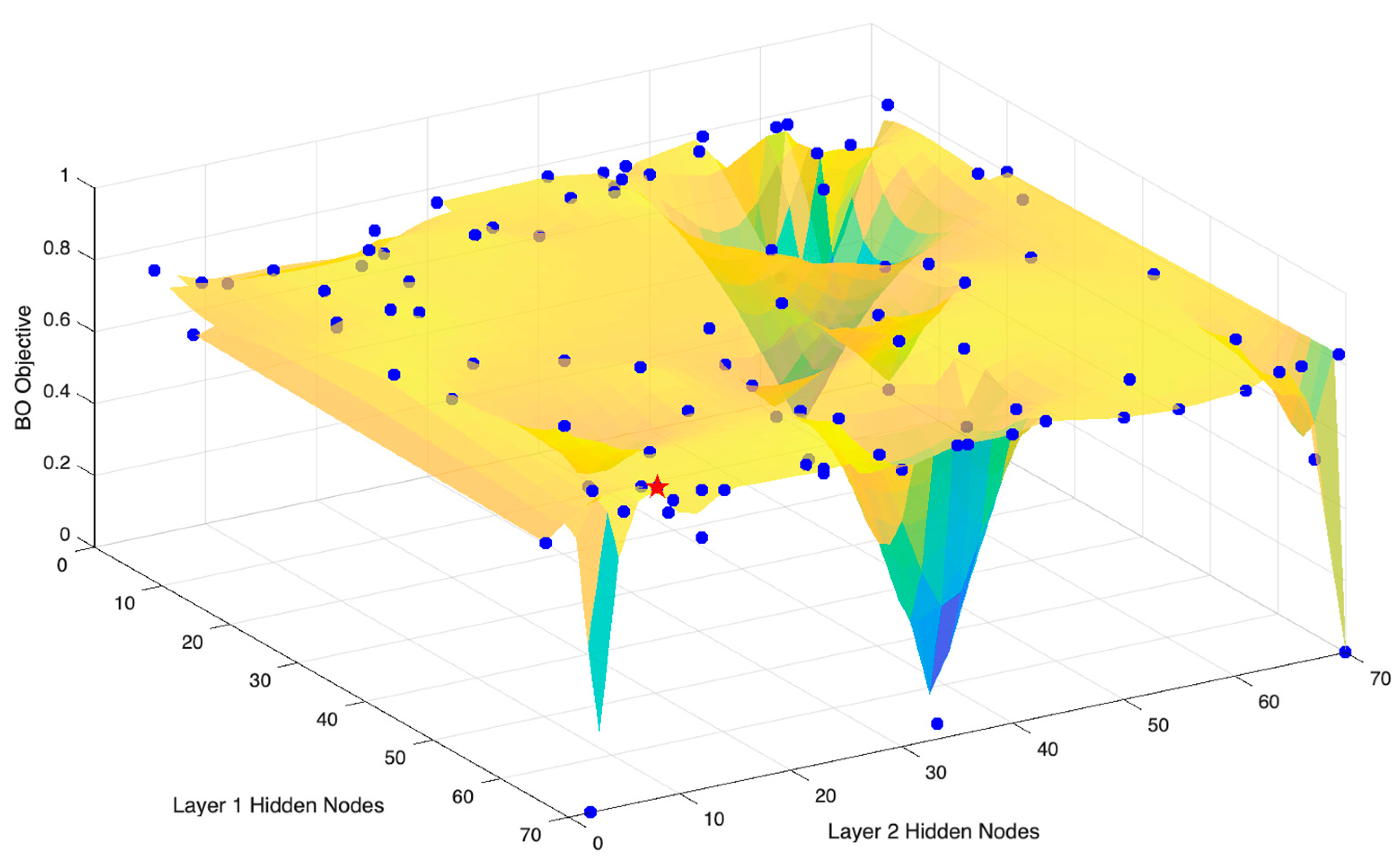
Hyperparameter	Description	Range
Layer 1 nodes	Neurons in the first hidden layer; controls initial feature extraction.	[3, 70]
Layer 2 nodes	Neurons in the second hidden layer; refines and combines features.	[1, 70]
Activation function	Nonlinear function used for each node in the hidden layers	[tansig, logsig, poslin]
Regularization	L2 penalty to improve generalization and reduce overfitting	[0, 0.4]
Training	Training algorithm used	[LM, BR, SCG]
Patience	Maximum epochs before training stops	[4000, 5000]
Performance Metric	Error function for optimization	[MAE, MSE, MSEReg]
BO Iterations	Iterations for BO to search over this space	100

.

The hyperparameters in Table 3 define the structure and learning behavior of the artificial neural network (ANN). The number of neurons in the first and second hidden layers controls the model’s capacity to detect and refine nonlinear relationships, with higher values allowing more complex feature representations at the risk of overfitting. Activation functions (tansig, logsig, poslin) introduce nonlinearity, enabling the network to model complex behaviors beyond simple linear mappings. Regularization applies an L2 penalty to the weight magnitudes, helping improve generalization to unseen data. Training algorithms (LM, BR, SCG) balance convergence speed, stability, and robustness differently, while the patience setting determines the maximum number of epochs before stopping to prevent excessive or premature termination of training. The choice of performance metric (MAE, MSE, MSEReg) directly influences the optimization process, shaping the trade-off between penalizing large deviations and ensuring overall robustness to variability in the data.

Once the BO process was completed, the BO recommendation was rerun for 5 iterations to get performance results.

Table 4. Results summary for BO determined optimal settings for given features after 100 iterations, with R² results from 5 replications of each feature and algorithmic setting combination.

Algorithm	Features	Architecture	R2
BO-ANN	$b,d,f_c^{’},f_y,{\rho }_l,{\rho }_v,{\rho }_{vh},a$,$l_n$,${\displaystyle \raisebox{1ex}{$a$}\!\left/ \!\raisebox{-1ex}{$d$}\right.}$	tansig [68, 15] LM with MAE Reg = 0.005395	Mean R2: 0.8564 95% CI: [0.8208, 0.8920]
BO-ANN Engineered	$p_0, p_1, p_2, p_3, p_4$	tansig [61, 14] LM with MAE Reg = 0.0017861	Mean R2: 0.6518 95% CI: [0.5524, 0.7512]
BO-ANN Hybrid	$b,d,f_c^{’},f_y,{\rho }_l,{\rho }_v,{\rho }_{vh},a$,$l_n$,${\displaystyle \raisebox{1ex}{$a$}\!\left/ \!\raisebox{-1ex}{$d$}\right.},p_0, p_1, p_2, p_3, p_4$	tansig [64, 24] LM with MAE Reg = 0.0015075	Mean R2: 0.8428 95% CI: [0.8181, 0.8675]

presents the results from this analysis along with the features used, the architecture recommended, and R² with a 95% t-score mean confidence interval. Results for the original feature set, BO-ANN, were statistically comparable to the baseline (mean R² = 0.8564, 95% CI: [0.8208, 0.8920]), suggesting that the baseline network was already close to optimal for the given data and feature set. When BO was applied exclusively to the engineered features ($p_0$–$p_4$) from Murphy and Paal [8]. BO-ANN Engineered, performance decreased substantially (mean R² = 0.6518, 95% CI: [0.5524, 0.7512]). This reflects the apparent limited predictive power of these engineered features when used in isolation. Finally, combining the original experimental features with the engineered features in a single feature set and applying Bayesian optimization produced results from the algorithm BO-ANN Hybrid (mean R² = 0.8428, 95% CI: [0.8181, 0.8675]), which was statistically indistinguishable from both the baseline and BO-only approaches. This indicates that, for this dataset, engineered features did not significantly enhance predictive accuracy when combined with the original variables.

4.2. ANN-SNR Feature Selection

The architectures identified by BO from Table 4 served as the starting point for the ANN–SNR procedure. As discussed previously, ANN-SNR introduces a synthetic noise variable, and the signal-to-noise ratio (SNR) of each feature was computed after training. Features were iteratively removed based on the lowest SNR, with the model retrained at each step.

Table 5. Results summary for BO-ANN with iterative ANN-SNR feature selection process.

Iteration	Features and SNR (dB)										R2
	$\mathit{b}$	$\mathit{d}$	${\mathit{f}}_{\mathit{c}}^{\mathit{’}}$	${\mathit{f}}_{\mathit{y}}$	${\mathit{\rho }}_{\mathit{l}}$	${\mathit{\rho }}_{\mathit{v}}$	${\mathit{\rho }}_{\mathit{v}\mathit{h}}$	$\mathit{a}$	${\mathit{l}}_{\mathit{n}}$	$\mathit{a}/\mathit{d}$
1	0.16	−0.03	0.31	−1.6	0.21	−1.07	−0.85	−0.51	−0.58	−0.34	0.841
2	1.08	−0.42	0.63	-	−1.44	0.09	−0.77	−0.19	−0.64	−0.57	0.867
3 1	−0.41	−0.57	0.74	-	-	−0.09	−1.06	−0.18	0.25	−0.55	0.843
4 1	1.16	0.53	1.02	-	-	−0.05	-	0.45	1.32	1.23	0.822
5	1.99	0.79	3.24	-	-	-	-	1.29	1.14	0.97	0.722
6	−0.86	-	−0.51	-	-	-	-	−0.53	−0.72	−0.74	0.541
7	0.96	-	1.33	-	-	-	-	1.41	0.86	1.38	0.682
8	−1.17	-	−1.40	-	-	-	-	−0.17	-	−1.04	0.754
9	−0.82	-	-	-	-	-	-	−0.05	-	0.98	0.547
10	-	-	-	-	-	-	-	0.98	-	0.59	0.576
11	-	-	-	-	-	-	-	-	-	−0.72	0.022

¹ Final selected sets, in bold, that balanced parsimony and accuracy.

presents the results of this process. SNR values (in dB) are reported for each feature at the time of elimination, with negative values indicating a weaker and noisier contribution to output prediction. The corresponding R² values quantify predictive accuracy after each removal. Performance peaked early in the elimination process, with iteration 2 (R² = 0.867) exceeding the original full-feature BO–ANN model. Iterations 3 and 4 produced the most parsimonious feature sets while maintaining high accuracy, within or above the model’s CI (R² = 0.843 and R² = 0.822, respectively). Based on the criterion of selecting the smallest feature subset whose performance remained within the confidence interval (CI) of the baseline BO–ANN model, both iterations 3 and 4 qualified as final candidates. Beyond iteration 4, further removals caused a marked decline in accuracy, indicating that variables with moderate SNR still contributed essential predictive information. The finding that not all experimental variables are salient aligns with Young et al. [2]; however, this analysis specifically identifies $f_y$ and ${\rho }_l$ as unimportant, in contrast to [2], which flagged ${\rho }_{vh}$ and $a/d$ as low-value features.

Table 6. Results summary for BO-ANN Engineered with ANN-SNR feature selection process.

Iteration	Features and SNR (dB)					R2
	${\mathit{p}}_0$	${\mathit{p}}_1$	${\mathit{p}}_2$	${\mathit{p}}_3$	${\mathit{p}}_4$
1 1	1.14	0.37	−0.58	0.16	−0.49	0.591
2	−0.51	−0.97	-	−1.33	0.17	0.526
3	0.44	−1.07	-	-	0.26	0.481
4	−0.01	-	-	-	0.41	0.356
5	-	-	-	-	−0.42	0.202

¹ Final selected set, in bold, to be within the original CI has no features removed.

summarizes the results of BO-ANN Engineered, which explored only engineered features and the ANN-SNR feature selection process to find a parsimonious set. Each row corresponds to an iteration that reports the signal-to-noise ratio (SNR, in dB) for individual engineered features ($p_0$–$p_4$) and the corresponding model R². Notably, R² values start considerably lower than BO-ANN, as presented in Table 5, and results in Table 6 rapidly decline across all iterations. Overall, these results suggest that the engineered features, in isolation, have limited predictive value and that feature removal or degradation in SNR correlates with a loss in model fit. The analysis showed that the smallest feature set falling within the model’s confidence interval occurred in the first iteration, which retained all original features.

Table 7. Results summary for BO-ANN Hybrid with iterative ANN-SNR feature selection process.

Iter	Features and SNR (dB)															R2
	$\mathit{b}$	$\mathit{d}$	${\mathit{f}}_{\mathit{c}}^{\mathit{’}}$	${\mathit{f}}_{\mathit{y}}$	${\mathit{\rho }}_{\mathit{l}}$	${\mathit{\rho }}_{\mathit{v}}$	${\mathit{\rho }}_{\mathit{v}\mathit{h}}$	$\mathit{a}$	${\mathit{l}}_{\mathit{n}}$	$\mathit{a}/\mathit{d}$	${\mathit{p}}_0$	${\mathit{p}}_1$	${\mathit{p}}_2$	${\mathit{p}}_3$	${\mathit{p}}_4$
1	14.3	12.1	9.92	13.7	11.7	23.1	20.35	11.5	15.2	25.1	15.7	16.4	15.7	14.8	19.5	0.78
2	11.5	10.4	-	9.9	5.69	17.5	14.5	13.4	14.3	21.4	9.66	18.7	9.65	2.89	5.35	0.841
3	11.7	15.7	-	9.57	2.41	13.29	8.52	11.73	10.35	15.7	5.34	18.98	5.34	-	6.91	0.804
4	5.44	−0.61	-	−0.99	-	9.74	4.94	4.46	−1.54	11.55	1.38	5.95	1.38	-	8.57	0.786
5	4.01	-	-	−0.81	-	3.18	3.47	3.44	-	6.70	4.71	6.85	1.83	-	4.36	0.799
6	6.97	-	-	-	-	11.83	9.63	8.13	-	15.87	6.59	13.10	6.59	-	12.2	0.818
7	11.89	-	-	-	-	17.04	12.47	8.02	-	18.27	14.07	16.08	-	-	16.83	0.812
8 1	−1.46	-	-	-	-	0.37	2.74	-	-	6.15	−0.37	1.60	-	-	4.11	0.832
9	-	-	-	-	-	18.89	16.41	-	-	20.39	15.39	18.37	-	-	21.24	0.801
10	-	-	-	-	-	22.80	16.95	-	-	23.11	-	21.82	-	-	21.35	0.805
11	-	-	-	-	-	3.28	-	-	-	5.73	-	4.67	-	-	5.86	0.763
12	-	-	-	-	-	-	-	-	-	21.64	-	10.54	-	-	17.88	0.659
13	-	-	-	-	-	-	-	-	-	16.3	-	-	-	-	14.53	0.652
14	-	-	-	-	-	-	-	-	-	1.9	-	-	-	-	-	0.162

¹ Final selected set, in bold, that balanced parsimony and accuracy and is within the original CI.

summarizes the performance of the BO–ANN Hybrid model during iterative ANN–SNR feature selection. This model starts with both the original features and all engineered feature set. SNR values (in dB) for each feature reflect their relative contribution at the point of removal, with negative or near-zero SNR indicating limited signal strength relative to noise. Notably, performance initially improved with iteration 2 and several mid-stage iterations (3, 5, 6, 7, 9, 10) maintained R² values around or above 0.80. The final stopping point was iteration 8, which represented the smallest feature set that still had performance (R² = 0.832) within (or above) the model’s confidence interval. This subset ($b$, ${\rho }_v$, ${\rho }_{vh}$, $a/d$, $p_0$, $p_4$) achieved a balance between parsimony and accuracy as well as between raw data features and engineered features. Compared to models using only engineered or original features, the hybrid set demonstrated greater resilience to feature removal, indicating redundancy between engineered and original variables. However, excessive removal beyond the confidence-interval threshold caused sharp performance declines (R² < 0.70), showing that certain moderate-SNR features still provided complementary predictive information.

With the final recommended feature sets and BO-optimized architectures, the algorithms were rerun for five independent replications, this time without the synthetic noise variable, to produce the final results summarized in

Table 8. Results summary for BO determined optimal algorithms for given features after 100 iterations, with R² results from 5 replications of each feature and algorithmic setting combination.

Algorithm	Features	Architecture	R2
BO-ANN-SNR3	$b,d,f_c^{’},{\rho }_v,{\rho }_{vh},a,l_n, a/d$	tansig [68, 15] LM with MAE Reg = 0.005395	Mean R2: 0.8358 95% CI: [0.8160, 0.8556]
BO-ANN-SNR4	$b,d,f_c^{’},{\rho }_{vh},a$,$l_n$,${\displaystyle \raisebox{1ex}{$a$}\!\left/ \!\raisebox{-1ex}{$d$}\right.}$	tansig [68, 15] LM with MAE Reg = 0.005395	Mean R2: 0.7824 95% CI: [0.7494, 0.8154]
BO-ANN-SNR Engineered	$p_0, p_1, p_2, p_3, p_4$	tansig [61, 14] LM with MAE Reg = 0.0017861	Mean R2: 0.6518 95% CI: [0.5524, 0.7512]
BO-ANN-SNR Hybrid	$b,{\rho }_v, {\rho }_{vh},{\displaystyle \raisebox{1ex}{$a$}\!\left/ \!\raisebox{-1ex}{$d$}\right.}, p_0,p_1,p_4$	tansig [64, 24] LM with MAE Reg = 0.015075	Mean R2: 0.8524 95% CI: [0.8312, 0.8736]

. Similarly to Table 4, performance metrics were averaged across replications to provide stable estimates. For each algorithm–feature configuration, the table reports the BO-optimized ANN architecture (hidden layer sizes, activation function, and regularization parameter) along with the resulting mean R² and 95% confidence interval (CI).

Figure 3 illustrates the BO search surface for the BO–ANN–SNR₃ configuration, plotted over the number of hidden nodes in the first and second layers. Each blue marker represents an individual trial evaluated during the optimization, while the surface provides an interpolated landscape of the BO objective. The red marker denotes the best-performing configuration identified by BO. As shown, the BO–ANN–SNR₃ model achieved its best performance with a two-layer configuration of 68 and 15 hidden nodes using a tansig activation function and LM with MAE regularization. This result not only validates the utility of BO for architecture selection but also demonstrates how Figure 3 can serve as a representative example of the tuning process applied across all feature sets reported in Table 8.

Figure 3 highlights two important aspects of the optimization process. First, the search surface is nonconvex and irregular, with multiple local peaks and valleys. Notably, this is also for only 2 of the 8 hyperparameters BO is optimizing over, Table 3, and the entire relationship is more complex and hyperdimensional. This underscores the difficulty of tuning ANN architectures using manual or grid search methods, since small changes in the number of hidden nodes can lead to large and unpredictable swings in performance. Second, BO is shown to be effective at navigating this complex landscape: rather than exhaustively testing every possibility, BO strategically samples promising regions, converging on an architecture that balances predictive accuracy and model simplicity.

Results, Table 8 and Figure 3, indicate that the BO–ANN–SNR₃ model, using the feature set ($b,d,f_c^{’},{\rho }_v,{\rho }_{vh},a,l_n, a/d$), achieved a mean R² of 0.8358 with a 95% CI of [0.8160, 0.8556], demonstrating strong predictive accuracy. Removing one additional feature, ${\rho }_v$, to form the BO–ANN–SNR₄ model with feature set ($b,d,f_c^{’},{\rho }_{vh},a$,$l_n$,${\displaystyle \raisebox{1ex}{$a$}\!\left/ \!\raisebox{-1ex}{$d$}\right.}$) reduced performance noticeably to a mean R² of 0.7824, CI [0.7494, 0.8154], suggesting that ${\rho }_v$ contributed to improved predictions despite moderate SNR. By contrast, the engineered-only feature set ($p_0, p_1, p_2, p_3, p_4$), yielded the weakest performance (mean R² of 0.6518, CI [0.5524, 0.7512]), showing that, in isolation, composite physics-informed variables possibly remove nonlinear interactions that the ANN can otherwise exploit.

The BO tuned model BO-ANN-SNR Hybrid provided a hybrid configuration with a feature set containing both raw and engineered features ($b,{\rho }_v, {\rho }_{vh},{\displaystyle \raisebox{1ex}{$a$}\!\left/ \!\raisebox{-1ex}{$d$}\right.}, p_0,p_1,p_4$) achieved the highest performance, with a mean R² of 0.8524, CI [0.8312, 0.8736], exceeding all other tested combinations. Notably, this result exceeded all other reduced-feature models and fell within the performance range of the baseline BO–ANN models. These findings reinforce that combining select raw and engineered features yields the most balanced outcome: preserving interpretability and parsimony while maintaining accuracy that is statistically indistinguishable from the full feature set.

5. Discussion

When comparing the original baseline ANN models (Table 2) with the BO-optimized ANN models (Table 4) and the BO–ANN–SNR reduced-feature models (Table 8), performance remains statistically comparable despite substantial reductions in the number of input features. The original baseline configurations achieved mean R² values between 0.866 and 0.877, with confidence intervals overlapping those of the BO-optimized ANN models. For example, the top performing BO–ANN configuration in Table 4 reached a mean R² of 0.8564 (95% CI: [0.8208, 0.8920]), fully overlapping the baseline intervals, indicating no statistically significant loss in predictive accuracy despite feature reduction.

Against prior literature (summary presented in

Table 9. Results summary for best methods explored in this work along with published baselines, results from this work in bold.

Algorithm	Features	R2
BO-ANN-SNR3	8 raw data features	Mean R2: 0.8358 95% CI: [0.8160, 0.8556]
BO-ANN	10 raw data features	Mean R2: 0.8564 95% CI: [0.8208, 0.8920]
BO-ANN-SNR Hybrid	7 features: 4 raw, 3 engineered	Mean R2: 0.8524 95% CI: [0.8312, 0.8736]
Best-Young [2]	8 raw data features	Mean R2: 0.877 Range R2: [0.832, 0.903]
Best-Murphy and Paal [8]	18 data features: 17 raw, 1 engineered	Max R2: 0.877

), the proposed framework demonstrates equivalence while improving efficiency. Compared to the results of Young et al. [2] where we recomputed a mean best R² of 0.877 with a wide range [0.832–0.903], the BO-ANN-SNR₃ model achieved a similar accuracy (mean R² = 0.852, CI [0.831–0.874]) with one fewer feature and a much narrower confidence interval. This suggests that while the maximum performance in Young et al. [2] may appear higher, it is less stable across replications. In contrast, BO-ANN-SNR₃ offers comparable predictive capability with improved reproducibility and statistical transparency, making it a more defensible choice for engineering applications.

Likewise, results from Murphy and Paal [8] included one algorithm with a maximum R² of 0.877; however, the algorithm of Murphy and Paal [8] used 18 input variables, including variables not under consideration herein, and a much more complex transfer learning algorithm. By comparison, the BO-ANN-SNR Hybrid model achieved statistically similar performance (mean R² = 0.852, CI [0.831–0.874]) with fewer than half as many features (7). Importantly, the hybrid configuration confirms that near-equivalent accuracy can be achieved with substantially fewer inputs, improving parsimony and interpretability without sacrificing reliability.

Additional insights are provided by examining engineered features in isolation. When used alone, the engineered set produced substantially lower predictive accuracy (R² ≈ 0.65). This likely reflects two factors: first, the formulations condense multiple raw variables into composite terms, which may remove nonlinear interactions that ANNs can otherwise exploit; and second, aggregating features such as $f_c^{’}$ into composite/hybrid features may obscure important relationships between material strength and geometric dimensions. Including these engineered features alongside raw variables, however, preserved that information and improved robustness. The SNR-based feature reduction further confirmed that many variables contribute little to modeling and can be removed without degrading performance. Importantly, the hybrid feature set achieved the strongest performance among reduced-feature models, underscoring two critical insights: firstly, that retaining salient variables with strong statistical signal and domain relevance is essential, and secondly, that combining raw and engineered features leverages the strengths of both, maximizing predictive accuracy while enhancing interpretability. Such a balanced feature set ensures the model remains not only a powerful predictor but also a transparent analytical tool, while enabling dimensionality reduction that improves efficiency and practicality for engineering applications.

Some limitations should be acknowledged. The primary contribution of this work is the adaptation of ANN-SNR for regression, making feature saliency intrinsic to the ANN itself. Accordingly, comparisons are drawn primarily to other ANN-based studies (e.g., Young et al. [2] and Murphy & Paal [8]), which provide the most relevant context. External feature selection methods such as principal component analysis (PCA) could be an alternative; however, PCA would involve a further rendering of features to be more abstract and less explainable. Further, LASSO (Least Absolute Shrinkage and Selection Operator) could provide an additional alternative to feature saliency; however, LASSO assumes linearity in relationships whereas the ANN approach can capture nonlinear relationships. Finally, methods such as random forests could provide external measures of feature importance through impurity-based rankings or permutation testing; however, their interpretations would not be intrinsic to the neural network itself. In contrast, the ANN-SNR framework derives feature saliency directly from ANN weights and integrates it into the feature reduction process, producing interpretability that is consistent with the deployed model and grounded in the nonlinear structure of the ANN. Another limitation lies in dataset heterogeneity: the 1259 samples were aggregated from 49 experimental programs, each with its own testing protocols and material characterizations. While such heterogeneity could introduce bias, aggregated datasets are the accepted practice in AI/ML applications to reinforced concrete, see [2,6,8], precisely because individual programs rarely provide sufficient observations for data-driven modeling.

6. Conclusions

The results demonstrate the value of engineered features, and selecting salient features is critical to achieving models that are both accurate and interpretable. The analysis shows that eliminating low-value variables can significantly reduce dimensionality without compromising accuracy. Furthermore, the superior performance of the hybrid feature set highlights the value of combining original raw variables with thoughtfully engineered features; this approach not only preserves physical interpretability for domain experts but also leverages transformations that can capture nonlinear relationships more effectively. The findings suggest that feature engineering should be approached as a complementary process to statistical selection, rather than as a replacement, to maximize both predictive strength and interpretability.

The work further introduced ANN-SNR feature selection for prediction and developed a stopping rule for feature elimination whereby one stops at the smallest set of features whose performance remains within or above the full model’s confidence interval. This criterion ensures that dimensionality reduction does not come at the expense of statistically significant performance loss, providing a defensible balance between parsimony and accuracy.

Future work should focus on developing physics-informed ANN methodologies, e.g., [61], that more directly integrate engineered features derived from governing equations and domain principles, such as detailed physics models as seen in [62]. Such approaches could yield models that are not only high-performing but also grounded in physically meaningful relationships, enhancing both trustworthiness and explanatory power. A further understanding of data heterogeneity and developing stratified models within more homogeneous subsets to further isolate any effects of heterogeneity is a direction of possible interest to the field. Additionally, exploring automated pipelines that merge physics-based transformations with modern optimization strategies, such as Bayesian optimization and SNR-based filtering, could provide a systematic way to design compact yet powerful models for complex engineering prediction tasks.