Equilibrium Dynamics in the CR3BP with Radiating Primary and Oblate Secondary Using the Rotating Mass Dipole Model

Abstract

In this study, we numerically investigate the equilibrium dynamics of a rotating system consisting of two masses connected by a massless rod within the framework of the circular restricted three-body problem. The larger primary is modeled as a radiating body and the smaller as an oblate spheroid. We explore the influence of the involved parameters, i.e., mass ratio ($\mu$), force ratio (k), radiation pressure factor ($q_1$), and oblateness coefficient ($A_2$), on the number, positions, and linear stability of equilibrium points. Zero velocity curves are presented in the equatorial plane for varying values of the Jacobi constant. Up to five equilibrium points are identified of which three are collinear ($L_1$, $L_2$, $L_3$) and two are non-collinear ($L_4$, $L_5$). The positions of all equilibria shift under variations in the perturbing parameters. While the collinear points are generally unstable, $L_1$ can exhibit stability for certain combinations of $\mu$, k, and $q_1$. The non-collinear points may also be stable under specific conditions with stability zones expanding with increased parameter values. The model is applied to the irregular, elongated asteroid 951 Gaspra, for which five equilibrium points are found. Despite positional dependence on oblateness and radiation, the perturbations do not significantly affect the equilibrium points’ stability and the motion near them remains linearly unstable. The Lyapunov families of periodic orbits emanating from the collinear equilibria of this particular system are also investigated.

1. Introduction

The circular restricted three-body problem (CR3BP), which describes the motion of an infinitesimal mass under the gravitational influence of two massive bodies in circular orbits about their common center of mass, is a classical model that approximates many real-world celestial systems. It admits five equilibrium points (EPs), three of which are collinear ($L_1$, $L_2$, $L_3$) and are unstable for $0<\mu \le 0.5$, and two are triangular ($L_4$, $L_5$), which are stable when the mass ratio $\mu$ is below Routh’s critical value ${\mu }_0=0.03852\dots$ [1]. However, the classical CR3BP assumes spherical, purely gravitating primaries and neglects other physical forces, limiting its applicability to more realistic settings. In many astrophysical systems, such as star-dust interactions or binary asteroid environments, non-gravitational effects like radiation pressure can significantly alter particle dynamics. Radzievskii [2] was among the first to include radiation forces in the CR3BP, giving rise to the photogravitational CR3BP. Since then, various studies have incorporated radiating primaries either individually or jointly [3,4,5]. Moreover, more complex configurations, such as the photogravitational restricted four-body problem, have been proposed to model systems with multiple massive bodies and external forces [6,7,8]. These extensions aim to bridge the gap between idealized and physically rich dynamical models, underscoring the significance of photogravitational effects which are an essential aspect of the present study.

While the classical CR3BP assumes perfectly spherical primaries, many celestial bodies, such as Earth, Jupiter, or Saturn, are better represented as oblate spheroids due to rotationally induced flattening. This has led to extensive research incorporating oblateness to enhance dynamical realism [9,10,11,12,13]. Sharma [14] examined the planar CR3BP with a radiating larger primary and an oblate smaller one, revealing the presence of retrograde elliptic periodic orbits and showing that increasing oblateness and radiation reduces the critical mass for triangular point stability. Other studies have analyzed related configurations that combine radiation and oblateness effects, focusing on the existence, linear stability, and periodic motion near the EPs [15,16,17]. These contributions underscore the relevance and importance of combining photogravitational and oblateness effects, an approach that is central to the model investigated in this study.

The solar system contains various types of celestial bodies, including numerous elongated objects, such as certain asteroids, comets, and dwarf planets. Asteroids, in particular, hold substantial scientific and practical value, especially as many are found in binary or multiple systems [18,19]. Modeling the dynamics around irregularly shaped bodies has become a key focus in celestial mechanics, with particular attention given to contact binaries and simplified representations, such as two-connected-mass systems also referred to as rotating mass dipoles. The rotating dipole model, where two masses are linked by a rigid rod, has been explored in several works [20,21], primarily to analyze the equilibrium point structure and stability for slow and fast rotating configurations. Their results showed that only the $L_1$ point can be stable. As a generalization of the CR3BP, the rotating mass dipole model extends classical methods to more complex geometries and is particularly useful for studying the dynamics near elongated bodies.

Zeng et al. [22] investigated a synchronous asteroid system modeled as a rotating dipole and later improved the model by incorporating oblateness and adopting a dipole segment framework [23,24,25,26,27]. Related studies have addressed specific cases such as orbital motion around contact binaries like asteroid 1996 HW1 [28] or used polyhedral methods to compute the number and distribution of EPs for a sample of 23 irregular bodies [29], showing that these systems typically have four unstable external EPs. Jiang et al. [30] derived the characteristic equations governing equilibria near rotating asteroids to investigate periodic orbits and associated manifolds. Santos et al. [31] studied the restricted synchronous three-body problem in the context of elongated binary asteroid systems and analyzed the location and stability of EPs. Most recently, Vincent et al. [32] considered a system with an oblate larger primary and a synchronous dipole secondary, computing Lyapunov families emanating from the EPs. Although many studies have investigated equilibrium structures and their stability in rotating dipole systems with oblate primaries, the combined effects of radiation and oblateness have received comparatively limited attention. This also motivates the present work.

This work extends the rotating dipole model introduced by Zeng et al. [24] by treating the primary body as a radiating source rather than a gravitational point mass. Near the surface of asteroids, particles are influenced by a combination of perturbative forces that can result in impacts with the body or escape from its gravitational field. Characterizing these effects is crucial for determining the existence and extent of regions that support stable natural orbits. Prior investigations have highlighted the prominent role of solar radiation pressure and non-spherical gravitational potentials in shaping particle dynamics. Hamilton and Burns [33] studied stability zones around asteroid 951 Gaspra by modeling the asteroid as a point mass under solar radiation. Considering that many asteroids exhibit significant geometric irregularities, we model the smaller primary as an oblate spheroid and include radiation pressure from the larger primary. The system is framed within a modified photogravitational CR3BP, incorporating a rotating mass dipole to represent a slow-spinning elongated body inspired by asteroid 951 Gaspra. The goal is to investigate how mass distribution, rotational coupling, oblateness, and radiative effects influence the location and stability of EPs as well as the Lyapunov periodic orbits emanating from them.

The structure of the paper is organized as follows. Section 2 introduces the mathematical formulation of the dynamical model. In Section 3, we determine the positions of the collinear and non-collinear EPs and describe the associated regions of motion. Section 4 is devoted to the linear stability analysis of these points, while Section 5 provides a numerical application using the physical parameters of asteroid 951 Gaspra. Finally, Section 6 and Section 7 offer a discussion of the results and summarize the main conclusions of the study.

2. Equations of Motion and the Jacobian-Type Integral

The originally proposed rotating mass dipole model comprises two finite bodies, $M_1$ and $M_2$, maintained at a fixed distance d along the horizontal x-axis by a massless, rigid connector (see [20]). In our study, the more massive primary $M_1$ is modeled as a radiating source while the less massive $M_2$ is treated as an oblate spheroid. This formulation generalizes the work of Zeng et al. [24] by introducing radiation pressure effects on $M_1$. The primaries revolve in circular orbits around their mutual center of mass and an infinitesimal third body $m_3$ moves under their gravitational influence without perturbing their motion. The system is rendered dimensionless by selecting the total mass M as the unit of mass, the separation d as the unit of length, and ${\omega }^{-1}$ as the time unit, where $\omega$ is the angular velocity of rotation. This choice normalizes the rotation period to $2\pi$. Let $r_1$, $r_2$, and r denote the distances from the infinitesimal body $m_3$ to $m_1$, $m_2$, and the system’s origin, respectively. The mass ratio is defined as $0<\mu =m_2/(m_1+m_2)\le 1/2$, yielding $m_1=1-\mu$ and $m_2=\mu$. Accordingly, the primaries are positioned at $(-\mu ,0,0)$ and $(1-\mu ,0,0)$ in the rotating reference frame. The oblateness of the smaller primary is quantified by the dimensionless coefficient $A_2=(A_E^2-A_P^2)/\left(5d^2\right)$, where $A_E$ and $A_P$ denote the equatorial and polar radii of $M_2$, respectively, while the coefficient satisfies $0\le A_2\ll 1$ [14].

Following the formulation established by Prieto-Llanos and Gómez-Tierno [20] and Zeng et al. [24], the equations of motion for the infinitesimal body, subject to the combined influences of radiation from $M_1$ and the oblateness of $M_2$, are expressed as:

$$\ddot{x}-2\omega \dot{y}={\displaystyle \frac{\partial U}{\partial x}}=U_x,\ddot{y}+2\omega \dot{x}={\displaystyle \frac{\partial U}{\partial y}}=U_y,\ddot{z}={\displaystyle \frac{\partial U}{\partial z}}=U_z,$$

(1)

where U is the effective potential (or generalized gravitational potential) given as

$$U={\displaystyle \frac{{\omega }^2(x^2+y^2)}{2}}+k{\omega }^2\left({\displaystyle \frac{1-\mu }{r_1}}+{\displaystyle \frac{\mu }{r_2}}+{\displaystyle \frac{A_2\mu }{2r_2^3}}-{\displaystyle \frac{3\mu A_2{z}^2}{2r_2^5}}\right).$$

(2)

The perturbed mean motion of the primaries, $\omega$, also known as the constant angular velocity of the primary is given by

$${\omega }^2=1+{\displaystyle \frac{3A_2}{2}},$$

(3)

while

$$r_1^2={(x+\mu )}^2+y^2+z^2,r_2^2={(x+\mu -1)}^2+y^2+z^2.$$

(4)

We note that in this formulation $\omega$ is obtained directly from Equation (3) through the oblateness coefficient $A_2$ in nondimensional units, rather than being assigned from external measurements. The dimensionless quantity $k={\displaystyle \frac{GM}{{\omega }^2{d}^3}}$ [24] is the force ratio and represents the ratio between gravitational and centrifugal forces. Here, $M=m_1+m_2$ is the total mass of the system, G is the gravitational constant ($G=6.67408\times {10}^{-11}{\mathrm{m}}^3{\mathrm{kg}}^{-1}{\mathrm{s}}^{-2}$), and d is the fixed separation between the two masses. The value of k characterizes the rotational state of the system, since the connected massless rod transmits either tensile or compressive internal forces in addition to gravity, depending on the value of force ratio. In particular, when $k=1$, gravitational and centrifugal forces are balanced and the primaries rotate about their center of mass without internal stress. For $k<1$, centrifugal force dominates, tending to separate the components, while for $k>1$, gravitational attraction dominates, resulting in compression [20,24]. Depending on the system considered, one needs to choose the appropriate value of k. When the shapes of the primaries are included, only the gravitational term $GM$ is modified but not the ratio (e.g., in the Earth–Moon system, Earth’s oblateness modifies $G{M}_{\mathrm{earth}}$ with terms including $J_2$ perturbations but the ratio $\left(GM\right)/\left({\omega }^2{d}^3\right)$ remains unchanged). In this study, we adopt smaller values of k to simulate a realistic rotating dipole configuration which is consistent with previous investigations. It is important to note that k also provides an indication of the dipole’s spin state, i.e., lower values of k correspond to fast rotation, while higher values imply slower rotation. The case $k>1$ is considered more typical, as most known dumbbell-shaped binary asteroids rotate slowly and experience a compressive force between their components.

When the primary body $m_1$ is assumed to emit radiation, the effect of radiation pressure on a particle can be represented following the classical photogravitational framework (e.g., [2]). Let $F_r$ and $F_g$ denote the radiation and gravitational forces acting on the particle, respectively. The radiation pressure is incorporated through the mass reduction factor $q_1=1-b_1$, where $b_1=F_r/F_g$ is the radiation coefficient. In the limiting case $q_1=1$, the radiation force vanishes and the system reduces to the classical gravitational problem. For values $q_1\in (0,1)$, gravity dominates over radiation, if $q_1=0$, the two forces are in balance, and when $q_1<0$, radiation pressure exceeds the gravitational attraction. In this study, we consider the physically realistic case where gravity prevails, i.e., $q_1\in (0,1]$. It is worth noting that for a fixed gravitational force, increasing radiation pressure corresponds to a decrease in the mass reduction factor $q_1$.

Therefore, incorporating the effects of radiation pressure from the larger primary and the oblateness of the smaller primary, the equations of motion (1) are modified and take the following form:

$$\ddot{x}-2\omega \dot{y}={\displaystyle \frac{\partial U}{\partial x}}=U_x,\ddot{y}+2\omega \dot{x}={\displaystyle \frac{\partial U}{\partial y}}=U_y,\ddot{z}={\displaystyle \frac{\partial U}{\partial z}}=U_z,$$

(5)

with

$$U={\displaystyle \frac{{\omega }^2(x^2+y^2)}{2}}+k{\omega }^2\left[{\displaystyle \frac{q_1(1-\mu )}{r_1}}+{\displaystyle \frac{\mu }{r_2}}+{\displaystyle \frac{A_2\mu }{2r_2^3}}-{\displaystyle \frac{3\mu A_2{z}^2}{2r_2^5}}\right].$$

(6)

The corresponding energy integral, known as the Jacobi integral, is given by:

$$C=2U-{\Gamma }^2,$$

(7)

where its explicit form is expressed as:

$$C={\omega }^2(x^2+y^2)+2k{\omega }^2\left[{\displaystyle \frac{q_1(1-\mu )}{r_1}}+{\displaystyle \frac{\mu }{r_2}}+{\displaystyle \frac{A_2\mu }{2r_2^3}}-{\displaystyle \frac{3\mu A_2{z}^2}{2r_2^5}}\right]-({\dot{x}}^2+{\dot{y}}^2+{\dot{z}}^2)$$

(8)

with ${\Gamma }^2={\dot{x}}^2+{\dot{y}}^2+{\dot{z}}^2$, where $\dot{x}$, $\dot{y}$, and $\dot{z}$ are the velocities of the relative motion and C is the Jacobian constant, sometimes referred to as a pseudo-integral. The Jacobi constant determines the allowable regions of motion bounded by the zero velocity surfaces. It serves as a fundamental tool for understanding orbital dynamics, particularly in relation to equilibrium configurations and their stability and is crucial for deep space exploration. Note that the equations of motion (5) define a dynamical system with three degrees of freedom in the rotating frame, corresponding to the coordinates $(x,y,z)$ of the infinitesimal body. When motion is restricted to the equatorial plane ($z=0$), the problem reduces to two degrees of freedom.

The free parameters involved in Equations (5) are k, $\mu$, $q_1$, and $A_2$. Unlike the classical CRTBP where the zero-velocity curves (ZVCs) are primarily shaped by the mass ratio $\mu$, the structure of the ZVCs in the present model depends on all four parameters. Two formulations of the rotating dipole model exist: the reduced model, defined in dimensionless units, and the simplified model, expressed in SI units. The reduced model involves only two parameters ($\mu$ and k) whereas the simplified model incorporates five $(\mu ,k,\omega ,d$ and $M)$. Despite these differences, the reduced model is equivalent to the simplified one under appropriate scaling, enabling the rotating mass dipole framework to approximate the external gravitational potential of natural elongated bodies when suitable parameter values are chosen.

We note that when the larger primary is not a source of radiation, i.e., $q_1=1$, the equations of motion reduce to those derived by Zeng et al. [24]. If, in addition, $A_2=0$ and $k\ne 1$, the system coincides with the formulation presented in [20], while the classical gravitational CR3BP is recovered when $q_1=1$, $k=1$, and $A_2=0$. Therefore, the rotating dipole model presented here constitutes a generalization of the classical CR3BP, encompassing photogravitational effects, oblateness, and asymmetric mass distribution. Moreover, in the limiting case of zero tensile force in the connecting rod, the equations of motion become analogous to those studied in [14,15,16].

Therefore, to investigate the influence of the problem parameters, in what follows, the investigated region of k is set to be $k\in (0,9.0]$ [24], representing a wide range for a realistic rotating dipole (rotation rate) of the asteroid without excluding analysis for higher values of k. The admissible region for the mass parameter $\mu$ is $\mu \in (0,0.5]$, while the admissible regions for the oblate small primary and radiating bigger primary are specified as $0\le A_2\le 0.2$ and $0<q_1\le 1$, respectively. It should be noted that the upper bound $A_2=0.2$ corresponds to the theoretical maximum of the oblateness coefficient, arising in the extreme case where the polar radius of the body vanishes and the equatorial radius becomes equal to the separation distance R between the two primaries. In realistic planetary systems, the oblateness values are much smaller, i.e., $0<A_2\ll 1$. In this work, the extended interval $0\le A_2\le 0.2$ is considered in order to investigate the qualitative influence of strong oblateness and to ensure that the dynamical behavior of the model is examined both within and beyond the range of commonly observed values. This choice also allows for the possibility that highly irregular small bodies, such as asteroids, comets, or contact binaries, may be effectively represented by larger oblateness coefficients than planets.

3. Locations of Equilibrium Points

It is well known that the classical CR3BP admits five EPs, denoted by $L_i$ for $i=1,\dots ,5$, for any combination of primary masses. Three of these points lie along the x-axis and are referred to as the collinear points ($L_1$, $L_2$, $L_3$), while the remaining two lie off the axis forming equilateral configurations with the primaries and are known as the triangular points ($L_4$, $L_5$) [34]. In the case of the gravitational rotating mass dipole problem, the number and location of the EPs depend sensitively on the values of the force ratio k and the mass parameter $\mu$ [20]. In particular, it has been shown that the triangular EPs disappear when $k<0.125$. Equilibrium points correspond to stationary solutions in the rotating (body-fixed) frame, where both velocity and acceleration vanish. In the context of the modified CR3BP considered here, their number and precise locations are determined by solving the nonlinear system:

$$\ddot{x}=\ddot{y}=\ddot{z}=0=\dot{x}=\dot{y}=\dot{z},U_x=0=U_y=U_z,$$

(9)

such that,

$$\begin{array}{cc}\hfill U_x& ={\omega }^2\left\{x-k\left[{\displaystyle \frac{q_1(1-\mu )(x+\mu )}{r_1^3}}+{\displaystyle \frac{\mu (x+\mu -1)}{r_2^3}}+3A_2\mu (x+\mu -1)\left({\displaystyle \frac{1}{2r_2^5}}-{\displaystyle \frac{5z^2}{2r_2^7}}\right)\right]\right\},\hfill \\ \hfill U_y& ={\omega }^{2}y\left\{1-k\left[{\displaystyle \frac{q_1(1-\mu )}{r_1^3}}+{\displaystyle \frac{\mu }{r_2^3}}+3A_2\mu \left({\displaystyle \frac{1}{2r_2^5}}-{\displaystyle \frac{5z^2}{2r_2^7}}\right)\right]\right\},\hfill \\ \hfill U_z& =-{\omega }^{2}kz\left[{\displaystyle \frac{q_1(1-\mu )}{r_1^3}}+{\displaystyle \frac{\mu }{r_2^3}}+A_2\mu \left({\displaystyle \frac{9}{2r_2^5}}-{\displaystyle \frac{15z^2}{2r_2^7}}\right)\right].\hfill \end{array}$$

(10)

The EPs in the equatorial plane $(x,y\ne 0)$ are solutions of the first two equations of (10) since the third equation is true for $z=0$. Consequently, in the synodic (rotating) frame, the equilibria are of the form $(x_0,y_0,0)$ and are determined by solving the conditions for stationary motion, namely, $U_x=0$, $U_y=0$, which explicitly take the form:

$$U_x={\omega }^2\left\{x-k\left[{\displaystyle \frac{q_1(1-\mu )(x+\mu )}{r_1^3}}+{\displaystyle \frac{\mu (x+\mu -1)}{r_2^3}}+{\displaystyle \frac{3A_2\mu (x+\mu -1)}{2r_2^5}}\right]\right\},$$

(11)

$$U_y={\omega }^{2}y\left\{1-k\left[{\displaystyle \frac{q_1(1-\mu )}{r_1^3}}+{\displaystyle \frac{\mu }{r_2^3}}+{\displaystyle \frac{3A_2\mu }{2r_2^5}}\right]\right\},$$

(12)

with $r_1^2={(x+\mu )}^2+y^2$, $r_2^2={(x+\mu -1)}^2+y^2$.

Equations (11) and (12) indicate that the positions of the EPs depend on the values of the mass ratio $\mu$, force ratio k, oblateness coefficient $A_2$, and radiation pressure parameter $q_1$. Accordingly, we investigate the existence and configuration of EPs under varying parameter sets where two distinct cases arise, specifically, the collinear and non-collinear EPs. The collinear points are obtained when $y=0$ whereas non-collinear points arise when $y\ne 0$. These equations can be tackled analytically using Taylor series expansions of $r_1$ and $r_2$ along with suitable approximations (see, e.g., [20,21]); however, in the present study, we opt for a numerical approach. Using the Newton iterative method, we find that the system admits five EPs. In particular, three collinear points, $L_1$, $L_2$, and $L_3$, aligned along the x-axis, and two non-collinear points, $L_4$ and $L_5$.

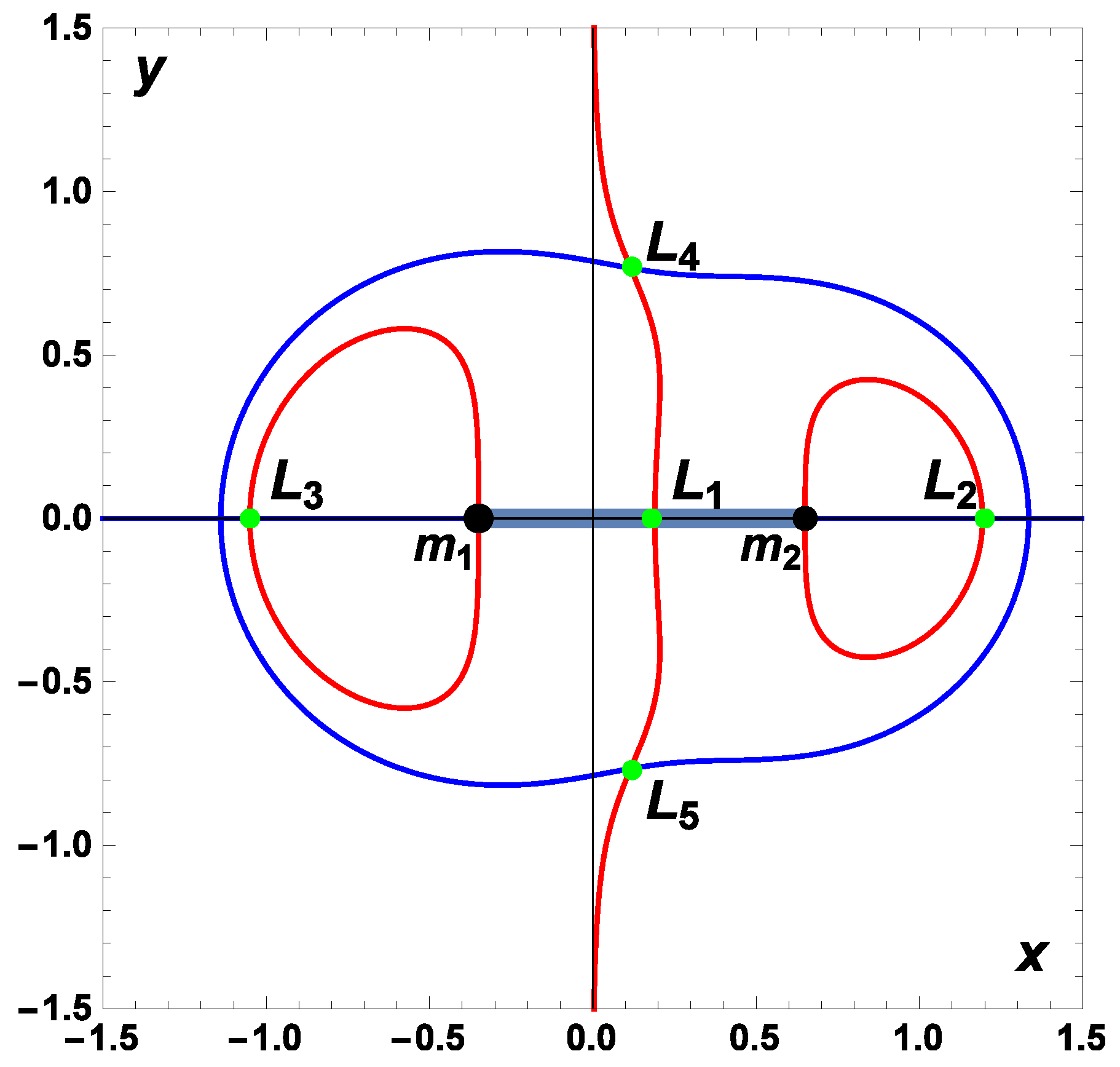
The configuration of the EPs and the positions of the primaries in the equatorial ($xy$) plane are shown in Figure 1 for the representative parameter set $\mu =0.35$, $q_1=0.9$, $k=0.8$, and $A_2=0.01$, obtained by numerically solving the nonlinear system (11) and (12). Throughout this study, we adopt the following labelling convention according to which $L_1$ lies between the two primaries, $L_2$ is located to the right of $m_2$ (the oblate secondary), and $L_3$ lies to the left of $m_1$ (the radiating primary). The triangular points $L_4$ and $L_5$ are symmetrically positioned above and below the x-axis, respectively. Beyond the iterative method employed in this work, various analytical and numerical techniques have been developed to determine the location and number of libration points in related dynamical models (see, e.g., [22]). In particular, the topological degree theory provides a powerful alternative framework for establishing the existence and count of collinear EPs in systems such as the rotating mass dipole, as demonstrated in [35].

In the gravitational CR3BP with a rotating mass dipole, it is known that the existence of triangular EPs requires the force ratio to satisfy the condition $k>0.125$ [20]. When $k<0.125$, the triangular points $L_4$ and $L_5$ merge with the inner collinear point $L_1$, resulting in their disappearance. As the parameters of the present system are varied, the gravitational potential and the overall dynamical structure of the system are correspondingly modified.

Next, we investigate how the oblateness coefficient ($A_2$), radiation pressure factor ($q_1$), force ratio (k), and mass ratio ($\mu$) affect the positions of the five EPs. To illustrate the impact of these parameters, we compute the coordinates of the EPs for eight representative cases involving different combinations of their values, as shown in

Table 1. The exact positions of the five EPs $L_i$, $i=1,2,\dots ,5$ under effects of various parameters.

Case	${\mathit{A}}_2$	${\mathit{q}}_1$	k	$\mathsf{\mu }$	${\mathit{L}}_1$	${\mathit{L}}_2$	${\mathit{L}}_3$	${\mathit{L}}_{4,5}$
1	0	1	1	0.05	0.715225	1.228094	$-1.020830$	$0.450000,\pm 0.866025$
2	0.01	0.9	0.5	0.25	0.318541	1.130414	$-0.884736$	$0.223731,\pm 0.602337$
	0.1				0.277441	1.204443	$-0.885375$	0.186006, ±0.630181
	0.2				0.250000	1.250000	$-0.886084$	0.152524, ±0.652077
3	0.01	0.9	0.5	0.25	0.318541	1.130414	$-0.884736$	$0.223731,\pm 0.602337$
		0.5			0.245200	1.119030	$-0.764154$	0.128541, ±0.503545
		0.2			0.140769	1.110880	$-0.618767$	0.037837, ±0.364134
4	0.01	0.9	0.5	0.25	0.318541	1.130414	$-0.884736$	$0.223731,\pm 0.602337$
			1		0.338707	1.269630	$-1.072750$	0.211146, ±0.848242
			5		0.356049	1.839471	$-1.734490$	0.145853, ±1.602800
5	0.01	0.9	0.5	0.01	0.728301	1.107730	$-0.770963$	0.463731, ±0.602337
				0.05	0.632563	1.150505	$-0.789672$	0.423731, ±0.602337
				0.25	0.318541	1.130414	$-0.884736$	0.223731, ±0.602337
6	0.01	0.9	0.5	0.25	0.318541	1.130414	$-0.884736$	0.223731, ±0.602337
		0.5	1		0.266601	1.245951	$-0.921530$	0.060041, ±0.730640
		0.2	5		0.175717	1.678121	$-1.187550$	$-0.716988$, ±0.884264
7	0.01	0.9	0.5	0.25	0.318541	1.130414	$-0.884736$	0.223731, ±0.602337
	0.1		1		0.290264	1.332430	$-1.073622$	0.171197, ±0.868771
	0.2		5		0.267860	1.897480	$-1.737384$	0.058239, ±1.621930
8	0.01	0.9	0.5	0.25	0.318541	1.130414	$-0.884736$	0.223731, ±0.602337
	0.1	0.5	1		0.227390	1.313372	$-0.922735$	0.020092, ±0.746332
	0.2	0.2	5		0.116930	1.762270	$-1.195463$	$-0.804602$, ±0.832116

. Each parameter is varied independently to assess its specific influence on the equilibrium configuration relative to the classical case. Arbitrary values have been used for the perturbing and mass parameters. So, whenever we need a fixed set of involved parameters values, we will adopt that we have $A_2=0.01$, $q_1=0.9$, $k=0.5$, and $\mu =0.25$. The considered cases are:

• Case 1: Classical Newtonian configuration $(A_2=0$, $q_1=1$, $k=1)$
• Case 2: Varying the oblateness coefficient of the smaller primary ($A_2$ only)
• Case 3: Varying the radiation pressure factor of the larger primary ($q_1$ only)
• Case 4: Varying the force ratio parameter (k only)
• Case 5: Varying the mass ratio of the system ($\mu$ only)
• Case 6: Simultaneous variation of k and $q_1$
• Case 7: Simultaneous variation of k and $A_2$
• Case 8: Simultaneous variation of $q_1$, $A_2$ and k

It can be seen from Table 1 that each parameter under consideration significantly influences the location of the EPs. In the unperturbed classical configuration (Case 1), the EPs retain their classical coordinates, consistent with the results in [34]. In Case 2, when only the oblateness coefficient of the smaller primary increases while all other parameters remain fixed, the collinear points $L_2$ and $L_3$ shift outward (away from $m_1$ and $m_2$, respectively) whereas $L_1$ moves inward (closer to the origin). Simultaneously, the triangular points $L_4$ and $L_5$ are displaced perpendicularly to the x-axis, moving outward along the y-direction. A similar trend is observed in Case 4, where increasing the force ratio k causes most EPs to move away from the line connecting the primaries. Notably, $L_1$ in this case tends to migrate toward the smaller primary, $m_2$. In addition, as k increases, the triangular points shift farther from the larger primary $m_1$ along the y-axis.

Table 1 also reveals the effect of radiation pressure from the larger primary in isolation (Case 3). As the radiation effect increases (i.e., as $q_1$ decreases), the collinear points $L_1$ and $L_3$ shift closer to the radiating primary $m_1$ while $L_2$ moves toward the center of the oblate secondary $m_2$. The triangular points $L_4$ and $L_5$ approach the x-axis, indicating a reduction in both their x- and y-coordinates. In the limit of strong radiation (small $q_1$), the triangular equilibria tend to collapse toward the massive primary $m_1$ along the y-axis, highlighting the dominance of photogravitational effects in shaping their positions. Also, increasing the mass parameter while keeping the other parameters fixed (Case 5) influences the collinear points in distinct ways. Specifically, $L_1$ shifts closer to the origin while $L_2$ initially moves away from the oblate secondary $m_2$ and then reverses direction, approaching it again. In contrast, $L_3$ steadily moves away from the more massive primary $m_1$. The triangular points $L_4$ and $L_5$ remain nearly unchanged in the y-direction, exhibiting only slight displacement along the x-axis.

Additionally, when both the radiation pressure from the larger primary and the force ratio are increased while keeping the other parameters fixed (Case 6), the collinear EPs $L_2$ and $L_3$ shift outward, moving away from the centers of the oblate secondary $m_2$ and the radiating primary $m_1$, respectively, while $L_1$ moves closer to the origin. Simultaneously, the triangular points $L_4$ and $L_5$ are displaced away from the x-axis and shift to the left, increasing their separation from the line connecting the two primaries. A comparable displacement pattern is observed in Case 7, where the oblateness coefficient of the smaller primary and the force ratio are varied jointly. The same qualitative behavior persists in Case 8, where all three parameters, oblateness, radiation pressure, and force ratio, are varied in combination. In this scenario, $L_1$ continues to migrate toward the origin, $L_2$ and $L_3$ retreat further from $m_2$ and $m_1$, respectively, and the non-collinear points $L_4$ and $L_5$ exhibit a pronounced leftward drift away from the x-axis.

In the same vein, our numerical computations indicate that when the radiation parameter $q_1$ approaches zero (e.g., $q_1\le 0.016$), while all other parameters remain fixed, the non-collinear points $L_4$ and $L_5$ collapse onto the collinear point $L_1$. Consequently, the system admits only three EPs, all of which are collinear ($L_1$, $L_2$, $L_3$). A similar phenomenon has been observed in the photogravitational CR3BP, where increasing the radiation pressure (i.e., decreasing the values of the radiation factors $q_1$ and $q_2$) causes the triangular points $L_4$ and $L_5$ to migrate toward the inner collinear point $L_1$ and ultimately vanish upon coalescence with it. This transition is accompanied by a transfer of linear stability from the triangular points to $L_1$ [3].

In Figure 2 (left panel), we illustrate the location of the collinear EPs as the radiation pressure increases (Case 3), keeping the remaining parameters equal to $\mu =0.25$, $A_2=0.01$, and $k=0.5$. It is observed that as the radiation parameter $q_1$ decreases, the negative outer collinear point approaches the corresponding primary, while also, the inner point $L_1$ shifts toward the position $x=-\mu$ of the secondary. In the same figure (right panel), the positions of the non-collinear points are plotted for varying $q_1$. As the radiation pressure intensifies (i.e., as $q_1$ decreases), the triangular points $L_4$ and $L_5$ approach the line joining the primaries, with $L_4$ located above and $L_5$ below the x-axis. Eventually, for $q_1\le 0.016$, these points coalesce with the collinear point $L_1$, indicating the disappearance of the triangular equilibria. Based on these results, we conclude that radiation pressure has an obvious effect on the positions of the five EPs. In particular, the locations of the collinear points $L_1$ and $L_3$ exhibit greater sensitivity to variations in radiation pressure compared to $L_2$. This behavior is also clearly illustrated in Table 1 (Case 3) and corroborated by the trends shown in Figure 2.

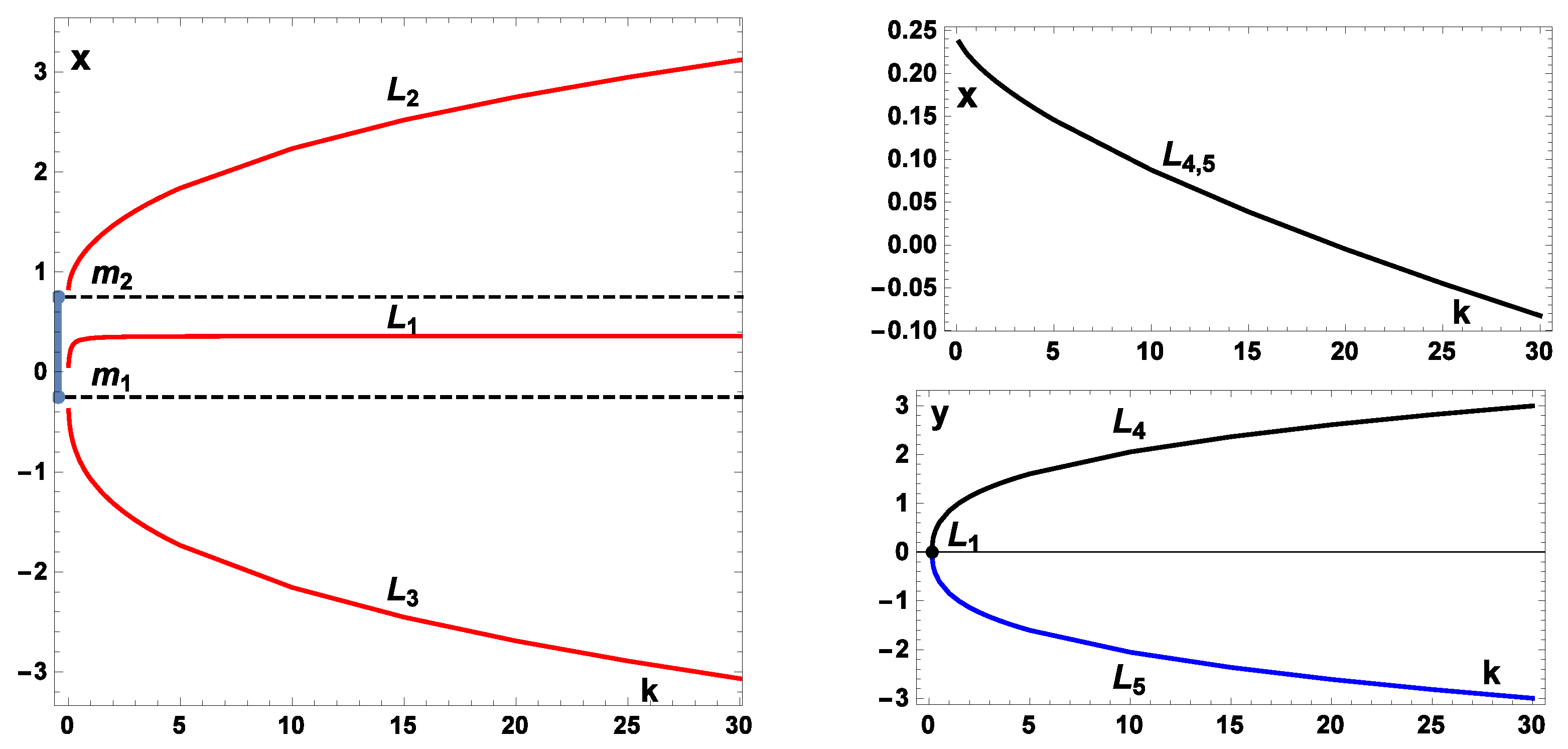
Similarly, the parameter-dependent behavior discussed in Case 4 of Table 1 is illustrated in Figure 3, where the positions of the five EPs $L_i$, $i=1,\dots ,5$ are plotted as a function of the force ratio k. In the left panel of this figure, we depict the variation of the collinear points along with the fixed locations of the two primaries for constant values of $\mu =0.25$, $A_2=0.01$, and $q_1=0.9$. As k increases from near zero to large values, $L_2$ and $L_3$ diverge toward positive and negative infinity, respectively, while the inner point $L_1$ asymptotically approaches the oblate primary $m_2$. The right panel shows the corresponding locations of the non-collinear points $L_4$ and $L_5$, which also diverge along the y-axis as k increases, and coalesce with $L_1$ when $k\le 0.129$. The trends depicted in Figure 3 qualitatively confirm the behavior outlined in Table 1 (Case 4), highlighting that $L_2$ and $L_3$ exhibit significantly greater sensitivity to variations in k compared to $L_1$.

We now turn our attention to the contours of the effective potential surface defined by the Jacobi integral (7), projected onto the $xy$-plane for zero kinetic energy. These contours define the ZVCs which enclose regions where the motion of the infinitesimal body is energetically allowed or forbidden. The structure of these regions is essential for understanding the particle’s dynamical behavior under various perturbing influences and it significantly differs from that of the classical RTBP. In particular, the presence of the force ratio k modifies the system even when the radiation pressure and oblateness effects are absent (i.e., $q_1=1$, $A_2=0$), resulting in ZVCs that deviate from the classical form.

Figure 4 illustrates the ZVCs and the positions of the EPs for fixed mass and force ratios ($\mu =0.25$ and $k=0.5$, respectively) while varying the values of the radiation factor $q_1$ and the oblateness coefficient $A_2$. These curves separate the configuration space into accessible regions and forbidden zones where motion is not allowed. As the Jacobi constant C varies, these regions expand or contract and may reduce to isolated points for critical values of C. Notably, the ZVCs remain symmetric with respect to both coordinate axes, as in the classical rotating dipole model. From Figure 4, several key effects can be observed. In panel (a), the ZVCs resemble those of the gravitational rotating dipole. When radiation pressure is introduced from the larger primary (see panel (b), $q_1<1$), the lobe around that primary shrinks, indicating a reduced sphere of influence due to the repelling effect of radiation. In contrast, the inclusion of oblateness in the smaller primary (see panel (c), $A_2>0$) results in the expansion of the lobe around it, showing that oblateness tends to enlarge the domain of influence of the oblate body. These results highlight that both radiation and oblateness can significantly modify the topology of the ZVCs and, in particular, large deviations from the purely gravitational case result in notable changes in the shape and extent of the energetically allowed regions.

4. Linear Stability of the Equilibrium Points

To analyze the linear stability of EPs, we shift the origin of the coordinate system to a given equilibrium point $L_i$ by introducing the transformations $x=x_{L_i}+\xi$, $y=y_{L_i}+\eta$ and $z=z_{L_i}+\zeta$, where $i=1,2,\dots ,5$. Substituting into the equations of motion and retaining only first-order terms yields the linearized system:

$$\overrightarrow{\dot{X}}=A\overrightarrow{X},\overrightarrow{X}={(\xi ,\eta ,\zeta ,\dot{\xi },\dot{\eta },\dot{\zeta })}^T$$

(13)

where $\xi$, $\eta$, and $\zeta$ denote small perturbations about the EPs $L_i$, while $x_{L_i},y_{L_i},z_{L_i}$ are the coordinates of $L_i$. The vector $\overrightarrow{X}$ represents the state of the infinitesimal body relative to the equilibrium position and the time-independent coefficient matrix A is written as:

$$A=\left(\begin{array}{cc}{0}_{3\times 3}& I_{3\times 3}\\ U_{3\times 3}& {\varpi }_{3\times 3}\end{array}\right)$$

(14)

where ${\mathbf{0}}_{3\times 3}$ and $I_{3\times 3}$ denote the $3\times 3$ zero and identity matrices, respectively. The remaining submatrices are defined as:

$$U=\left(\begin{array}{ccc}{U}_{xx}^{\left(0\right)}& U_{xy}^{\left(0\right)}& U_{xz}^{\left(0\right)}\\ U_{xy}^{\left(0\right)}& U_{yy}^{\left(0\right)}& U_{yz}^{\left(0\right)}\\ U_{xz}^{\left(0\right)}& U_{yz}^{\left(0\right)}& U_{zz}^{\left(0\right)}\end{array}\right),\varpi =\left(\begin{array}{ccc}0& 2\omega & 0\\ -2\omega & 0& 0\\ 0& 0& 0\end{array}\right)$$

(15)

where superscript “(0)” indicates evaluation at the EP $L_i$. Due to the system’s symmetry with respect to the $xy$-plane, where all EPs lie on the plane $(x_0,y_0,0)$, the vertical dynamics decouple from the planar motion. As a result, the z and $\dot{z}$ components can be neglected and the associated mixed partial derivatives $U_{xz}$, $U_{yz}$, and $U_{zz}$ vanish at each EP. This allows the dynamical system to be reduced to a four-dimensional form. Under this reduction, the characteristic equation corresponding to the linearized system (13) becomes:

$${\lambda }^4+(4{\omega }^2-U_{xx}^{\left(0\right)}-U_{yy}^{\left(0\right)}){\lambda }^2+U_{xx}^{\left(0\right)}{U}_{yy}^{\left(0\right)}-{\left[U_{xy}^{\left(0\right)}\right]}^2=0,$$

(16)

where $\lambda$ denotes the eigenvalues of the linearized system. Their real parts correspond to the local Lyapunov exponents, which determine the growth or decay rates of perturbations in the vicinity of the equilibrium point. Introducing the substitution $\Lambda ={\lambda }^2$ simplifies the characteristic equation to the form:

$${\Lambda }^2+\alpha \Lambda +\beta =0,$$

(17)

where the involved coefficients

$$\alpha =4{\omega }^2-U_{xx}^{\left(0\right)}-U_{yy}^{\left(0\right)},\beta =U_{xx}^{\left(0\right)}{U}_{yy}^{\left(0\right)}-{\left[U_{xy}^{\left(0\right)}\right]}^2,$$

depend on the four parameters $\mu$, k, $A_2$, $q_1$ and the coordinates, $x_0(\mu ,k,A_2,q_1)$ and $y_0(\mu ,k,A_2,q_1)$, of the EPs. The solution of the quadratic Equation (17) is

$${\Lambda }_{1,2}=\pm {\displaystyle \frac{1}{\sqrt{2}}}\sqrt{-\alpha \pm \sqrt{\Delta }},\Delta ={\alpha }^2-4\beta .$$

(18)

The nature of the eigenvalues derived from Equations (18) or (13) determines the linear stability of the EPs. Stability in the linearized sense is achieved only when all four eigenvalues are purely imaginary, implying the absence of exponential growth or decay in the local dynamics. In this case, the eigenvalues are of the form:

$${\lambda }_{1,2}=\pm i{\Lambda }_1,{\lambda }_{3,4}=\pm i{\Lambda }_2.$$

(19)

From Equation (16), the following three conditions are known to be both necessary and sufficient for linear stability [1]:

$$\alpha >0,\beta >0,{\alpha }^2-4\beta >0.$$

(20)

These criteria must all be satisfied simultaneously to ensure that the EP is linearly stable. If any of them is violated, at least one eigenvalue will have a non-zero real part, leading to unbounded motion and thus instability. It is also noted that the mixed second partial derivatives of the effective potential $U(x,y)$ at the EPs satisfy $U_{xy}^{\left(0\right)}=U_{yx}^{\left(0\right)}=0$ for collinear points, while $U_{xy}^{\left(0\right)}=U_{yx}^{\left(0\right)}\ne 0$ for non-collinear points. The second-order partial derivatives evaluated at each equilibrium location are given by:

$$\begin{array}{cc}\hfill U_{xx}^{\left(0\right)}=& {\omega }^2-{\omega }^{2}k[{\displaystyle \frac{q_1(1-\mu )}{r_{10}^3}}-{\displaystyle \frac{3q_1(1-\mu ){(x_0+\mu )}^2}{r_{10}^5}}+{\displaystyle \frac{\mu }{r_{20}^3}}\hfill \\ \hfill & \phantom{{\omega }^2}-{\displaystyle \frac{3\mu {(x_0+\mu -1)}^2}{r_{20}^5}}+{\displaystyle \frac{3A_2\mu }{2r_{20}^5}}-{\displaystyle \frac{15A_2\mu {(x_0+\mu -1)}^2}{2r_{20}^7}}],\hfill \end{array}$$

(21)

$$U_{yy}^{\left(0\right)}={\omega }^2-{\omega }^{2}k\left[{\displaystyle \frac{q_1(1-\mu )}{r_{10}^3}}-{\displaystyle \frac{3q_1(1-\mu )y_0^2}{r_{10}^5}}+{\displaystyle \frac{\mu }{r_{20}^3}}-{\displaystyle \frac{3\mu y_0^2}{r_{20}^5}}+{\displaystyle \frac{3A_2\mu }{2r_{20}^5}}-{\displaystyle \frac{15A_2\mu y_0^2}{2r_{20}^7}}\right],$$

(22)

$$U_{xy}^{\left(0\right)}=U_{yx}^{\left(0\right)}=3k{\omega }^2{y}_0\left[{\displaystyle \frac{q_1(1-\mu )(x_0+\mu )}{r_{10}^5}}+{\displaystyle \frac{\mu (x_0+\mu -1)}{r_{20}^5}}+{\displaystyle \frac{5A_2\mu (x_0+\mu -1)}{2r_{20}^7}}\right],$$

(23)

where

$$r_{10}^2={(x_0+\mu )}^2+y_0^2,r_{20}^2={(x_0+\mu -1)}^2+y_0^2.$$

4.1. Stability of Collinear Equilibrium Points

In the present model, and based on Equation (16), the collinear EPs satisfy $U_{xy}^{\left(0\right)}=U_{yx}^{\left(0\right)}=0$, simplifying the constant term of the characteristic equation. Our analysis reveals that the EPs $L_2$ and $L_3$ are generically linearly unstable. This conclusion holds throughout the full range of parameters explored, namely, the radiation pressure factor $q_1$, mass ratio $\mu$, oblateness coefficient $A_2$, and force ratio k, since at least one eigenvalue consistently possesses a positive real part or is a positive real root. In contrast, the inner collinear point $L_1$ may admit linear stability under certain parameter conditions. Specifically, there exist intervals of $\mu$, k, $A_2$, and $q_1$ for which the stability criteria in Equation (20) are simultaneously satisfied.

Table 2. Stability of collinear EPs $L_2$ and $L_3$ with varying mass parameter, force ratio, oblateness, and varying radiation.

$\mathsf{\mu }$	k	${\mathit{A}}_2$	${\mathit{q}}_1$	${\mathit{L}}_2$		${\mathit{L}}_3$
				${\mathsf{\lambda }}_{\mathbf{1},\mathbf{2}}$	${\mathsf{\lambda }}_{\mathbf{3},\mathbf{4}}$	${\mathsf{\lambda }}_{\mathbf{1},\mathbf{2}}$	${\mathsf{\lambda }}_{\mathbf{3},\mathbf{4}}$
0.1	0.1	0	1	$\pm 4.047472$	$\pm 3.057622\mathrm{i}$	$\pm 0.766698$	$\pm 1.165033\mathrm{i}$
0.2	5	0.02	0.8	$\pm 1.016742$	$\pm 1.261251\mathrm{i}$	$\pm 0.506785$	$\pm 1.092103\mathrm{i}$
0.3	10	0.04	0.6	$\pm 0.886314$	$\pm 1.218123\mathrm{i}$	$\pm 0.495653$	$\pm 1.101833\mathrm{i}$
0.4	30	0.06	0.4	$\pm 0.712818$	$\pm 1.172016\mathrm{i}$	$\pm 0.235988$	$\pm 1.058346\mathrm{i}$
0.5	50	0.08	0.1	$\pm 0.730999$	$\pm 1.189650\mathrm{i}$	$\pm (0.205720\pm 0.822165\mathrm{i})$

presents the eigenvalues ${\lambda }_i,i=1,2,3,4,$ associated with $L_2$ and $L_3$ for the parameter ranges $0.1\le \mu \le 0.5$, $0.1\le k\le 50$, $0\le A_2\le 0.08$ and $0.01\le q_1\le 1$. No case was found where all four eigenvalues are purely imaginary, confirming the persistent instability of $L_2$ and $L_3$, in agreement with earlier findings in [20,21].

Table 3. Stability of the collinear EP $L_1$ with and without radiation pressure for varying mass parameter and varying force ratio. The point $L_1$ is stable on the darkly shaded roots.

${\mathit{A}}_2=0.05$		${\mathsf{\lambda }}_{\mathit{i}}{\mathit{L}}_1({\mathit{q}}_1=1)$		${\mathsf{\lambda }}_{\mathit{i}}{\mathit{L}}_1({\mathit{q}}_1=0.2)$
$\mathsf{\mu }$	$\mathit{k}$	${\mathsf{\lambda }}_{\mathbf{1},\mathbf{2}}$	${\mathsf{\lambda }}_{\mathbf{3},\mathbf{4}}$	${\mathsf{\lambda }}_{\mathbf{1},\mathbf{2}}$	${\mathsf{\lambda }}_{\mathbf{3},\mathbf{4}}$
0.01	0.01	±0.394602 i	$\pm \mathbf{0}.\mathbf{983554}\mathbf{i}$	$\pm \mathbf{0}.\mathbf{537780}\mathbf{i}$	$\pm \mathbf{0}.\mathbf{931528}\mathbf{i}$
0.025	0.03	$\pm \mathbf{0}.\mathbf{512399}\mathbf{i}$	$\pm \mathbf{0}.\mathbf{942035}\mathbf{i}$	$\pm (0.111084\pm 0.785184\mathrm{i})$
0.05	0.06	$\pm \mathbf{0}.\mathbf{575967}\mathbf{i}$	$\pm \mathbf{0}.\mathbf{909410}\mathbf{i}$	$\pm (0.226204\pm 0.825855\mathrm{i})$
0.1	0.09	$\pm \mathbf{0}.\mathbf{513775}\mathbf{i}$	$\pm \mathbf{0}.\mathbf{923822}\mathbf{i}$	$\pm (0.305789\pm 0.874188\mathrm{i})$
0.15	0.1	$\pm \mathbf{0}.\mathbf{437769}\mathbf{i}$	$\pm \mathbf{0}.\mathbf{937597}\mathbf{i}$	$\pm (0.345913\pm 0.909256\mathrm{i})$
0.2	0.12	$\pm 0.446152$	$\pm 1.049560\mathrm{i}$	$\pm (0.356031\pm 0.913036\mathrm{i})$
0.25	0.14	$\pm 0.813497$	$\pm 1.154710\mathrm{i}$	$\pm (0.356773\pm 0.902091\mathrm{i})$
0.3	0.16	$\pm 1.081698$	$\pm 1.254075\mathrm{i}$	$\pm (0.345006\pm 0.876729\mathrm{i})$
0.35	0.18	$\pm 1.302160$	$\pm 1.346910\mathrm{i}$	$\pm (0.308887\pm 0.834110\mathrm{i})$
0.4	0.2	$\pm 1.488120$	$\pm 1.432198\mathrm{i}$	$\pm (0.208490\pm 0.765541\mathrm{i})$

shows the stability region for $L_1$ in the scenarios where $q_1=1$ (non-radiating primary) and $q_1=0.2$ (strongly radiating primary), with fixed oblateness $A_2=0.05$ and varying $\mu$ and k in the intervals $0.01\le \mu \le 0.4$ and $0.01\le k\le 0.2$. The results indicate that $L_1$ is conditionally stable for small values of k, consistent with the conclusions of [21]. Moreover, the influence of radiation pressure significantly reduces the extent of the stability region, i.e., when the primary is radiating ($q_1=0.2$), the zone of stability is notably smaller than in the non-radiating case ($q_1=1$). Overall, the stability region associated with $L_1$ contracts as the parameters $\mu$ and k increase. In the tabulated results, bold roots correspond to stable configurations, while not bold roots represent instability of the EPs.

4.2. Stability of Non-Collinear Equilibrium Points

We focus our stability analysis on the triangular EP $L_4$, since the behavior at $L_5$ is equivalent due to the system’s inherent symmetry. For non-collinear points, the linearized dynamics are governed by the coefficient matrix A, as defined in Equations (14) and (21)–(23). Numerical computations reveal that the triangular EPs are conditionally stable over a broad range of the system’s parameters, including the mass ratio $\mu$, oblateness coefficient $A_2$, force ratio k, and radiation pressure factor $q_1$. The extent of the stability region is sensitive to the variation in each of these parameters.

Table 4. The roots of Equation (16) and the locations $(x_0,\pm y_0)$ of the EPs $L_4\left(5\right)$ for varying $\mu$ and k when $A_2=0.05$, for $q_1=1$ and $q_1=0.32$.

${\mathit{q}}_1$	$\mathsf{\mu }$	k	${\mathit{L}}_{4,5}({\mathit{x}}_0,\pm {\mathit{y}}_0)$	${\mathsf{\lambda }}_{1,2},{\mathsf{\lambda }}_{3,4}$	Stability
1	0.01	0.25	(0.468081, ±0.410230)	±0.336744 i,$\pm \mathbf{0}.\mathbf{979018}\mathbf{i}$	Stable
	0.2	0.5	(0.277105, ±0.634296)	$\pm (0.624166,\pm 0.951633\mathrm{i})$	Unstable
	0.25	1	(0.226403, ±0.879227)	$\pm (0.594443,\pm 0.934292)$	Unstable
	0.30	10	(0.175328, ±2.101350)	$\pm (0.261339,\pm 0.775063\mathrm{i})$	Unstable
	0.35	20	(0.125209, ±2.672500)	$\pm (0.109969,\pm 0.738801\mathrm{i})$	Unstable
	0.45	30	(0.025160, ±3.070690)	$\pm \mathbf{0}.\mathbf{614067}\mathbf{i},\pm \mathbf{0}.\mathbf{830964}\mathbf{i}$	Stable
0.32	0.01	0.25	(0.362488, ±0.216601)	$\pm \mathbf{0}.\mathbf{253532}\mathbf{i},\pm \mathbf{1}.\mathbf{003790}\mathbf{i}$	Stable
	0.2	0.5	(0.109486, ±0.446028)	$\pm (0.638559,\pm 0.961134\mathrm{i})$	Unstable
	0.25	1	(−0.039676, ±0.650851)	$\pm (0.635450,\pm 0.960903\mathrm{i})$	Unstable
	0.30	10	(−1.059700, ±1.262692)	$\pm (0.166316,\pm 0.748389\mathrm{i})$	Unstable
	0.35	20	(−1.835275, ±1.114030)	$\pm \mathbf{0}.\mathbf{349744}\mathbf{i},\pm \mathbf{0}.\mathbf{972186}\mathbf{i}$	Stable
	0.45	30	(−2.543801, ±0.364654)	$\pm \mathbf{0}.\mathbf{086041}\mathbf{i},\pm \mathbf{1}.\mathbf{029650}\mathbf{i}$	Stable

presents the stability domain of $L_4$ for various combinations of the perturbing parameters. With $A_2$ fixed at $0.05$ and $\mu$, k varying within the intervals $0.01\le \mu \le 0.45$ and $0.25\le k\le 30$, the stability regions are shown for the representative cases $q_1=1$ (no radiation) and $q_1=0.32$ (moderate radiation). The results clearly indicate that increased radiation pressure enhances the size of the stability region. In particular, for the lower radiation parameter ($q_1=0.32$), the area of stable configurations grows compared to the purely gravitational case ($q_1=1$). In this table, bold roots indicate parameter combinations yielding linear stability, while non-bold roots correspond to unstable configurations. Moreover, we observe that as $q_1$ decreases (i.e., as radiation pressure increases), the stability zone associated with $L_4$ expands for many combinations of $\mu$ and k. Additionally, the influence of the force ratio k becomes apparent, since even for values of $\mu$ exceeding the classical Routh stability threshold ($\mu >0.03852$), the non-collinear points can remain stable. This finding aligns with earlier results reported in [20].

5. Numerical Application to Slow Rotating Asteroid 951 Gaspra

Asteroid 951 Gaspra is selected as a case study because its irregular, elongated shape makes it a natural candidate for approximation by a rotating mass dipole. Earlier investigations have already highlighted its suitability for such modeling. Zeng et al. [22] adopted the dipole framework to link the dynamics of simplified elongated systems with real asteroids and Wang et al. [29] analyzed Gaspra’s gravitational environment using a polyhedral shape model, confirming the existence and distribution of equilibrium points. These studies indicate that the dipole approximation captures the essential external dynamical features of asteroid 951 Gaspra with reasonable accuracy. In the present work, the asteroid is represented by two point masses at the endpoints of a rigid rod, rotating uniformly about their common center of mass. The separation distance d is chosen so that the computed equilibrium point locations best match those obtained from polyhedral models, and once d is fixed, the corresponding force ratio k follows directly. Specifically, the physical parameters adopted here are taken from the latter works and are summarized in

Table 5. The main parameters of 951 Gaspra [22,29].

Asteroid	$\mathsf{\mu }$	k	T (Hours)	M (kg)	d (km)
951 Gaspra	0.2496003	5.3814122	7.042	$2.31959126\times {10}^{15}$	7.7649056

, which provides the simplified representation used in our analysis.

It should be emphasized that the adopted Gaspra system remains an idealized configuration, designed to highlight the dynamical aspects addressed in the present work. The mass parameter and force ratio were fixed from observational constraints, while the radiation and oblateness parameters were varied in order to study the system’s dynamics in a broader sense and to cover other potential or hypothetical configurations. This approach preserves the simplicity of the CR3BP framework while extending its applicability beyond the classical formulation. Although the dipole model reduces computational effort and simplifies the gravitational function, it should be regarded as a first-order approximation to the complex gravitational field of a real asteroid.

Finally, we note that all computations are carried out in nondimensional form. Accordingly, the mean motion $\omega$ is determined through Equation (3) from the chosen values of $A_2$ and no observational spin rate of Gaspra is imposed. Refined formulations of mean motion that incorporate additional perturbations, such as eccentricity and higher-order oblateness, have been proposed in the literature (e.g., [36]). These formulations are appropriate for the elliptic restricted three-body problem, whereas in the present work, we adopt the standard circular model. The results presented here are therefore consistent with the classical framework, while also being compatible with possible future extensions based on such refined expressions.

5.1. Location of EPs at Different Values of $q_1$ and $A_2$

Based on the parameters listed in Table 5, we now compute the EPs of the 951 Gaspra system for different values of the radiation pressure factor $q_1$ and the oblateness coefficient $A_2$. This numerical analysis examines how these perturbation parameters influence both the location and the linear stability of the EPs. It is worth noting that most prior investigations have focused exclusively on EPs located outside the surface of small bodies, often disregarding interior equilibria. While such an omission may be justified for large, nearly spherical planets where a single interior equilibrium point typically exists near the center, it becomes inadequate for highly irregular objects like asteroids. In these cases, internal EPs can exhibit complex spatial distributions and their stability characteristics may reveal important information about the internal structure, stress fields, and potential failure modes of the body [29]. Notably, despite the inclusion of non-spherical effects and radiative forces, our results confirm that all five EPs remain confined to the $xy$-plane and occupy the same positions as in the purely planar case.

Table 6. Coordinates of the EPs $L_i,i=1,2,\dots ,5$ in the rotating frame for classical case and varying oblateness and radiation parameters for the asteroid 951 Gaspra with $\mu =0.2496003$, $k=5.3814122$.

${\mathit{A}}_2$	${\mathit{q}}_1$	${\mathit{L}}_1$	${\mathit{L}}_2$	${\mathit{L}}_3$	${\mathit{L}}_{4,5}$
0	1	$0.380196013$	$1.89729285$	$-1.82642454$	$0.25039970,\pm 1.67955035$
$0.01$	$0.9$	$0.356997199$	$1.87630078$	$-1.77439241$	$0.14127030,\pm 1.64615016$
$0.05$		$0.326779394$	$1.88944441$	$-1.77500836$	$0.12174051,\pm 1.65066539$
$0.1$		$0.301818156$	$1.90469828$	$-1.77577732$	$0.09814389,\pm 1.65579714$
$0.15$		$0.283373806$	$1.91885897$	$-1.77654518$	$0.07537126,\pm 1.66041672$
$0.2$		$0.268608044$	$1.93209959$	$-1.77731195$	$0.05334691,\pm 1.66457598$
$0.01$	$0.9$	$0.356997199$	$1.87630078$	$-1.77439241$	$0.14127030,\pm 1.64615016$
	$0.7$	$0.327774092$	$1.82761856$	$-1.65776264$	$-0.07952086,\pm 1.54663533$
	$0.5$	$0.287574561$	$1.77879796$	$-1.51762834$	$-0.32275525,\pm 1.38895192$
	$0.3$	$0.225523173$	$1.73017543$	$-1.33601936$	$-0.60192988,\pm 1.11895205$
	$0.15$	$0.142943813$	$1.69407440$	$-1.14047314$	$-0.85655216,\pm 0.70608406$

presents the computed positions of the EPs for asteroid 951 Gaspra, considering both the classical case and a range of assumed values for the oblateness and radiation pressure parameters. Since the precise shape and oblateness of asteroids are often difficult to determine, it is important to investigate the system’s behavior across a spectrum of plausible values for the oblateness coefficient. The solar radiation pressure factor is defined as $q_1=1-b_1$, where $b_1=L_{\otimes }/\left(2\pi G{m}_{1}c\overline{k}\right)$ depends on several physical constants: the solar luminosity $L_{\otimes }$, gravitational constant G, mass of the primary $m_1$, speed of light c, and the mass-to-area ratio of the particle $\overline{k}$ [37]. The solar luminosity itself can be estimated using the Stefan–Boltzmann law as $L_{\otimes }=4\pi {\overline{R}}_{\otimes }^2\sigma T_{\otimes }^4$ where $\sigma$ is the Stefan–Boltzmann constant.

According to Table 6, when perturbative effects are neglected (i.e., the sphere–sphere configuration), the computed coordinates of the EPs are in exact agreement with those reported in [22]. The apparent differences in sign are due solely to a difference in the labeling convention. Similar results were found in [28] for the contact binary asteroid 1996 HW1, where a polyhedral shape model was employed. In this study, we adopt the labeling convention in which $L_1$ lies between the two primaries, $L_2$ is located to the right of $m_2$ (the smaller, oblate primary), $L_3$ lies to the left of $m_1$ (the larger, radiating primary), while the triangular EPs $L_4$ and $L_5$ are positioned symmetrically above and below the line joining the primaries, exhibiting north–south symmetry. The inclusion of oblateness and radiation pressure causes a noticeable shift in the locations of all five EPs. Specifically, increasing the oblateness coefficient of the smaller primary (with the radiation parameter held fixed) causes the collinear points $L_2$ and $L_3$ to move farther away from $m_2$ and $m_1$, respectively, while $L_1$ shifts closer to the origin. Simultaneously, $L_4$ and $L_5$ move away from the x-axis toward the y-axis. Increasing the radiation pressure factor of the larger primary (while keeping the oblateness coefficient fixed) causes $L_1$ and $L_3$ to shift toward $m_1$ and $L_2$ to move closer to the center of $m_2$. In this case, the triangular EPs $L_4$ and $L_5$ move toward the x-axis and closer to the line joining the primaries, indicating a reduction in both their x- and y-coordinates.

5.2. Stability of EPs at Different Values of $q_1$ and $A_2$

The linear stability of the EPs can be assessed using the linearized system defined by Equation (13). In this context, the characteristic equation associated with the coefficient matrix A is given by:

$$({\lambda }^2-U_{zz}^{\left(0\right)})({\lambda }^4+(4{\omega }^2-U_{xx}^{\left(0\right)}-U_{yy}^{\left(0\right)}){\lambda }^2+U_{xx}^{\left(0\right)}{U}_{yy}^{\left(0\right)}-{\left(U_{xy}^{\left(0\right)}\right)}^2)=0,$$

(24)

where $U_{xx}^{\left(0\right)},U_{yy}^{\left(0\right)},U_{xy}^{\left(0\right)},\dots ,U_{zz}^{\left(0\right)}$ denote the second-order partial derivatives of the effective potential evaluated at the equilibrium point. These derivatives are explicitly given by:

$$U_{xz}^{\left(0\right)}=U_{yz}^{\left(0\right)}=U_{zx}^{\left(0\right)}=U_{zy}^{\left(0\right)}=0,U_{xy}^{\left(0\right)}=U_{yx}^{\left(0\right)},$$

(25)

$$U_{zz}^{\left(0\right)}=-{\omega }^{2}k\left[{\displaystyle \frac{q_1(1-\mu )}{r_{10}^3}}+{\displaystyle \frac{\mu }{r_{20}^3}}+{\displaystyle \frac{9A_2\mu }{2r_{20}^5}}\right],$$

(26)

where

$$r_{10}^2={(x_0+\mu )}^2+y_0^2+z_0^2,r_{20}^2={(x_0+\mu -1)}^2+y_0^2+z_0^2$$

(27)

and the expressions for $U_{xx}^{\left(0\right)}$, $U_{yy}^{\left(0\right)}$, and $U_{xy}^{\left(0\right)}$ are provided in Equations (21), (22), and (23), respectively. It is worth noting that asteroids exhibit a spatial mass distribution in three dimensions; however, at the EPs, motion confined to the $xy$-plane does not couple with motion in the z-direction (see, e.g., [22,28]). Recall also here that an equilibrium point is linearly stable if all eigenvalues ${\lambda }_i$$(i=1,2,\dots ,6)$ of the linearized system have non-positive real parts. If at least one eigenvalue has a positive real part, the equilibrium point is linearly unstable.

The eigenvalues ${\lambda }_i$$(i=1,2,\dots ,6)$ associated with the linearized system (24) are computed numerically in the vicinity of asteroid 951 Gaspra.

Table 7. Stability of the EPs $L_i,i=1,2,\dots ,5$ in the asteroid 951 Gaspra with $\mu =0.2496003$, $k=5.3814122$ for $A_2=0$, and $q_1=1$ (classical case).

${\mathit{L}}_{\mathit{i}}$	${\mathsf{\lambda }}_{1,2}$	${\mathsf{\lambda }}_{3,4}$	${\mathsf{\lambda }}_{5,6}$
$L_1$	$\pm 9.143780839714$	$\pm 6.55509535574\mathrm{i}$	$\pm 6.52988919675\mathrm{i}$
$L_2$	$\pm 0.862046356230$	$\pm 1.20193940585\mathrm{i}$	$\pm 1.13950234091\mathrm{i}$
$L_3$	$\pm 0.542551099779$	$\pm 1.08896935233\mathrm{i}$	$\pm 1.05285680202\mathrm{i}$
$L_{4,5}$	$-0.32411351501\pm 0.77784932385\mathrm{i}$	$0.32411351501\pm 0.77784932385\mathrm{i}$	$\pm 1.00000000000\mathrm{i}$

,

Table 8. Effects of oblateness of asteroid 951 Gaspra with $\mu =0.2496003$, $k=5.3814122$ on stability of EPs $L_i,i=1,2,\dots ,5$ for $q_1=0.9$.

${\mathit{L}}_{\mathit{i}}$	${\mathsf{\lambda }}_{1,2}$	${\mathsf{\lambda }}_{3,4}$	${\mathsf{\lambda }}_{5,6}$
$A_2=0.01$
$L_1$	$\pm 9.207479282446$	$\pm 6.43254624004\mathrm{i}$	$\pm 6.41010845931\mathrm{i}$
$L_2$	$\pm 0.915762399656$	$\pm 1.22292267911\mathrm{i}$	$\pm 1.16209926349\mathrm{i}$
$L_3$	$\pm 0.547463395326$	$\pm 1.09720224086\mathrm{i}$	$\pm 1.06087923621\mathrm{i}$
$L_{4,5}$	$-0.33570115889\pm 0.78674504439\mathrm{i}$	$0.33570115889\pm 0.78674504439\mathrm{i}$	$\pm 1.00747208398\mathrm{i}$
$A_2=0.1$
$L_1$	$\pm 11.53161906265$	$\pm 7.41410872421\mathrm{i}$	$\pm 7.40247962075\mathrm{i}$
$L_2$	$\pm 1.033163408304$	$\pm 1.26721723903\mathrm{i}$	$\pm 1.23913321438\mathrm{i}$
$L_3$	$\pm 0.580782175934$	$\pm 1.16575483281\mathrm{i}$	$\pm 1.12863597226\mathrm{i}$
$L_{4,5}$	$-0.36833593376\pm 0.83527919817\mathrm{i}$	$0.36833593376\pm 0.83527919817\mathrm{i}$	$\pm 1.07238052948\mathrm{i}$
$A_2=0.2$
$L_1$	$\pm 13.31902662039$	$\pm 8.36018184928\mathrm{i}$	$\pm 8.35134145939\mathrm{i}$
$L_2$	$\pm 1.15311726225$	$\pm 1.31928122737\mathrm{i}$	$\pm 1.31700516567\mathrm{i}$
$L_3$	$\pm 0.61518626521$	$\pm 1.23693150399\mathrm{i}$	$\pm 1.19929208435\mathrm{i}$
$L_{4,5}$	$-0.401907187146\pm 0.88552816509\mathrm{i}$	$0.401907187146\pm 0.88552816509\mathrm{i}$	$\pm 1.14017542510\mathrm{i}$

and

Table 9. Effects of radiation of asteroid 951 Gaspra with $\mu =0.2496003$, $k=5.3814122$ on stability of EPs $L_i,i=1,2,\dots ,5$ for $A_2=0.01$.

${\mathit{L}}_{\mathit{i}}$	${\mathsf{\lambda }}_{1,2}$	${\mathsf{\lambda }}_{3,4}$	${\mathsf{\lambda }}_{5,6}$
$q_1=0.7$
$L_1$	$\pm 8.382551209356$	$\pm 5.89739503290\mathrm{i}$	$\pm 5.87233832234\mathrm{i}$
$L_2$	$\pm 1.003626347008$	$\pm 1.25864176493\mathrm{i}$	$\pm 1.19368729614\mathrm{i}$
$L_3$	$\pm 0.547354202897$	$\pm 1.09712617238\mathrm{i}$	$\pm 1.06085143892\mathrm{i}$
$L_{4,5}$	$-0.34729476063\pm 0.79176142085\mathrm{i}$	$0.34729476063\pm 0.79176142085\mathrm{i}$	$\pm 1.00747208398\mathrm{i}$
$q_1=0.5$
$L_1$	$\pm 7.487999334294$	$\pm 5.31395290762\mathrm{i}$	$\pm 5.28546054660\mathrm{i}$
$L_2$	$\pm 1.101195705488$	$\pm 1.30009047661\mathrm{i}$	$\pm 1.23160058061\mathrm{i}$
$L_3$	$\pm 0.540350217049$	$\pm 1.09495647629\mathrm{i}$	$\pm 1.05941830247\mathrm{i}$
$L_{4,5}$	$-0.34978030887\pm 0.79285481727\mathrm{i}$	$0.34978030887\pm 0.79285481727\mathrm{i}$	$\pm 1.00747208398\mathrm{i}$
$q_1=0.15$
$L_1$	$\pm 5.63625242226$	$\pm 4.09987782710\mathrm{i}$	$\pm 4.06126287112\mathrm{i}$
$L_2$	$\pm 1.29935435360$	$\pm 1.38934445712\mathrm{i}$	$\pm 1.31658282220\mathrm{i}$
$L_3$	$\pm 0.40173247733$	$\pm 1.05718095825\mathrm{i}$	$\pm 1.03540588171\mathrm{i}$
$L_{4,5}$	$-0.178884330465\pm 0.73367029412\mathrm{i}$	$0.178884330465\pm 0.73367029412\mathrm{i}$	$\pm 1.00747208398\mathrm{i}$

present the results corresponding to the equilibrium point coordinates given in Table 6, both for the classical configuration and for selected values of the perturbing parameters, with all other parameters held constant. In all examined cases, the collinear points $L_1$, $L_2$, and $L_3$ exhibit positive real eigenvalues, indicating instability, and correspond to Case 2 in the classification introduced by Jiang et al. [30] and Wang et al. [29]. The triangular points $L_4$ and $L_5$ also exhibit instability, characterized by complex conjugate eigenvalues with positive real parts, placing them in Case 5 of the same classification scheme. These results suggest that the inclusion of perturbative effects, such as oblateness and radiation pressure, does not significantly alter the inherent instability of the EPs in the vicinity of asteroid 951 Gaspra, that is, the perturbations considered in this study do not qualitatively change the linear stability behavior of the system. Consequently, the motion of an infinitesimal particle near any of the five EPs remains linearly unstable under the influence of these forces and the computed positions and the stability characteristics of the EPs are consistent with prior results reported in [22,29,30].

5.3. Lyapunov Families at Different Values of $q_1$ and $A_2$

It is known that periodic orbits are key dynamical features in celestial mechanics, providing insight into the local structure of phase space around EPs. In particular, the Lyapunov families of the CR3BP emerging from the collinear points are of special interest due to their role in organizing nearby motion. Additionally, they serve as useful reference trajectories in mission design, enabling efficient transfers in the vicinity of small bodies [34,38].

So, in this subsection, we examine how variations in the radiation pressure factor $q_1$ and the oblateness coefficient $A_2$ affect the evolution of the Lyapunov families originating from the collinear EPs of the adopted dynamical model. The mass parameter $\mu$ and the force ratio k are kept fixed at the values corresponding to asteroid 951 Gaspra, namely, $\mu =0.2496003$ and $k=5.3814122$, so that the influence of $q_1$ and $A_2$ can be isolated. By systematically varying these two perturbation parameters, we aim to characterize the resulting changes in the characteristic curves of the Lyapunov families and to identify qualitative trends in their dynamical behavior. The focus here is on understanding the local dynamics in the vicinity of the collinear points under different perturbative conditions, rather than on deriving any specific astronomical application.

Figure 5 illustrates the Lyapunov families computed for asteroid 951 Gaspra under several combinations of the radiation pressure factor $q_1$ and the oblateness coefficient $A_2$. The characteristic curves are represented in the plane of initial conditions $(C,x_0)$, where C is the Jacobi constant and $x_0$ denotes the first vertical intersection of the periodic orbit with the Ox-axis. The shaded hatched regions correspond to energetically forbidden domains for the motion of the massless body, while the red dashed horizontal lines mark the positions of the two primaries in the rotating frame. For each Lyapunov family, the continuous blue curves trace the initial conditions of the periodic orbits at their first vertical intersection with the $Ox$-axis, while the continuous purple curves (labeled with the subscript cut) indicate the subsequent vertical intersections with the same axis at the half-period $t=T/2$. This representation provides direct visualization of how the families emerge from the collinear EPs, evolve, and terminate in the plane of initial conditions.

In the unperturbed configuration, shown in Figure 5a with $q_1=1.0$ and $A_2=0.0$, all three Lyapunov families terminate in collision with one of the primaries. Specifically, family b, emanating from the collinear point $L_3$, evolve until its periodic orbits collide to the larger primary $m_1$ at their second vertical intersection with the $Ox$-axis. Family c, originating from the interior point $L_1$, exhibits an analogous behaviour, ending in collision with the smaller primary $m_2$ also at its orbits’ second vertical intersection. In contrast, family a, emerging from $L_2$, collides with the larger primary $m_1$ at its orbits’ first vertical intersection. These results reflect the classical termination modes expected in the CR3BP without the additional perturbations of radiation pressure or oblateness.

Introducing oblateness alone, as in Figure 5b with $q_1=1.0$ and $A_2=0.1$, deforms the geometry of the characteristic curves while preserving their qualitative termination types. The b-family extends further in the $(C,x_0)$ plane, developing an additional intersection with the $Ox$-axis, thus producing a triple-intersection multiplicity, before colliding to $m_1$ at an oblique intersection. The c-family follows essentially the same termination pattern with $m_2$ as in the unperturbed case, while the a-family also undergoes changes in its intersection sequence (exhibiting triple periodic orbits) before ending in an oblique impact with $m_1$.

When radiation pressure is introduced in combination with oblateness, as in Figure 5c with $q_1=0.7$ and $A_2=0.1$, a clear qualitative change emerges for the exterior families. Both the b- and a-families no longer terminate in collision. Instead, their trajectories asymptotically approach the triangular EPs $L_4$ and $L_5$, producing branches in the $(C,x_0)$ plane that spiral toward these points in phase space. This asymptotic behaviour suggests the presence of invariant manifolds guiding the motion toward the vicinity of the triangular points. The c-family, however, remains unaffected in its qualitative dynamics, continuing to terminate in collision with $m_2$. A further increase in oblateness to $A_2=0.2$ while keeping $q_1=0.7$, as in Figure 5d, and a subsequent increase in radiation strength to $q_1=0.5$ with $A_2=0.2$, as in Figure 5e, do not produce new qualitative changes either in the topology of the characteristic curves or in their termination types. In both configurations, the c-family consistently ends in collision with the smaller primary, while families b and a retain their asymptotic approach to the triangular points.

Overall, the numerical results indicate that radiation pressure primarily modifies the termination behaviour of the exterior families, replacing collision trajectories with asymptotic approaches to $L_4$ and $L_5$, while oblateness does not essentially change the form of their characteristic curves in the considered plane of initial conditions $(C,x_0)$.

We have also studied the horizontal stability of all the computed members of the Lyapunov families [39]. To do so, we integrate the planar equations of motion (8), simultaneously with the equations of variation; thus, we are able to determine the stability indexes $a_h$, $b_h$, $c_h$, and $d_h$ with the accuracy of the numerical integration [40]. We recall that a periodic orbit is horizontally stable when $\frac{1}{2}|a_h+d_h|<1$ and unstable otherwise. In the case of symmetric orbits, it is $a_h=d_h$, so the condition reduces to $|a_h|<1$ for stability and $|a_h|>1$ for instability.

Figure 6 presents the horizontal stability analysis of the Lyapunov families for all parameter combinations considered in the previous discussion. The horizontal axis shows the half period $T/2$, which allows the evolution of the orbital period along each family to be visualized, while the vertical axis indicates the stability index. Due to the large variations in $a_h$, we plot instead the transformed quantity $A_h={log}_{10}\left(a_h+\sqrt{a_h^2+1}\right)$, which preserves the stability information while compressing extreme values. In this representation, stability occurs when $|A_h|<{log}_{10}\left(1+\sqrt{2}\right)\approx 0.38278$. The top-left panel corresponds to the family emerging from $L_3$, the top-right to the family emanating from the interior point $L_1$, and the bottom panel to the family originating from $L_2$. Each panel uses a colour code to distinguish the parameter sets where black indicates $q_1=1.0$ and $A_2=0.0$, blue shows $q_1=1.0$ and $A_2=0.1$, purple marks $q_1=0.7$ and $A_2=0.1$, violet corresponds to $q_1=0.7$ and $A_2=0.2$, and orange refers to $q_1=0.5$ and $A_2=0.2$. The results show that the Lyapunov families from $L_3$ and $L_2$ contain extended stable parts with the stability index remaining below the threshold value, indicating the existence of stable periodic orbits. In contrast, the family from $L_1$ always remains unstable for all computed orbits across all parameter choices. Furthermore, for the b- and a-families, the orbital period increases, reflecting the asymptotic approach of their members toward the triangular EPs $L_4$ and $L_5$ identified in the characteristic diagrams of Figure 5.

This asymptotic behaviour is also illustrated in Figure 7 for the Gaspra system with $q_1=0.5$ and $A_2=0.2$. Panel (a) shows a representative orbit near the termination point of the Lyapunov family emerging from the collinear equilibrium point $L_3$, while panel (b) displays a corresponding orbit near the termination point of the Lyapunov family emanating from $L_2$. The initial conditions for the $L_3$ orbit are:

$$T/2=20.00579585,x_0=-2.42960066,{\dot{y}}_0=1.64955137,C=8.47000952,$$

while for the $L_2$ orbit, the relevant conditions are:

$$T/2=20.00853983,x_0=1.12506374,{\dot{y}}_0=3.60027727,C=8.46391340.$$

In both cases, the orbits, plotted as continuous blue lines, exhibit the asymptotic spiraling behaviour characteristic of the termination of these families around the triangular points $L_4$ and $L_5$. The primary bodies are marked with black dots, the schematic representation of the rotating mass dipole system is shown in gray, while the triangular EPs are indicated by magenta dots. These examples confirm that the Lyapunov families originating from the exterior collinear EPs terminate through asymptotic approach to the triangular points rather than through collision with the primaries.

Table 10. Sample members of the Lyapunov family b emanating from $L_3$ in the Gaspra system ($\mu =0.2496003$, $k=5.3814122$) for different values of $q_1$ and $A_2$.

Parameters	$\mathit{T}/2$	${\mathit{x}}_0$	${\dot{\mathit{y}}}_0$	${\mathit{x}}_{\mathbf{cut}}$	C	${\mathit{a}}_{\mathit{h}}$
$q_1=1.0,A_2=0.0$	$2.88505403$	$-1.87212500$	$0.10002047$	$-1.78060126$	$9.49689300$	$11.4496$
$q_1=1.0,A_2=0.1$	$2.69521525$	$-1.87065000$	$0.10043335$	$-1.78493129$	$10.93094619$	$11.4002$
$q_1=0.7,A_2=0.1$	$2.69674887$	$-1.70224000$	$0.10036330$	$-1.61651489$	$9.06792711$	$11.4113$
$q_1=0.7,A_2=0.2$	$2.54312503$	$-1.70180000$	$0.10091292$	$-1.62067552$	$10.26359292$	$11.3212$
$q_1=0.5,A_2=0.2$	$2.55354253$	$-1.56251240$	$0.10022848$	$-1.48160865$	$8.70047919$	$10.8167$

,

Table 11. Sample members of the Lyapunov family c emanating from $L_1$ in the Gaspra system ($\mu =0.2496003$, $k=5.3814122$) for different values of $q_1$ and $A_2$.

Parameters	$\mathit{T}/2$	${\mathit{x}}_0$	${\dot{\mathit{y}}}_0$	${\mathit{x}}_{\mathbf{cut}}$	C	${\mathit{a}}_{\mathit{h}}$
$q_1=1.0,A_2=0.0$	$0.47952069$	$0.37869600$	$0.10002047$	$0.38181769$	$20.21501451$	$3194.9988$
$q_1=1.0,A_2=0.1$	$0.40892992$	$0.31127700$	$0.10887571$	$0.31353733$	$25.51868622$	$9226.5867$
$q_1=0.7,A_2=0.1$	$0.46000815$	$0.27470200$	$0.10598196$	$0.27754288$	$20.40523932$	$7769.4599$
$q_1=0.7,A_2=0.2$	$0.40610643$	$0.24283710$	$0.10297203$	$0.24505252$	$24.54229176$	$9876.9084$
$q_1=0.5,A_2=0.2$	$0.44606062$	$0.20885500$	$0.10572411$	$0.21164879$	$20.14406813$	$8471.2730$

and

Table 12. Sample members of the Lyapunov family a emanating from $L_2$ in the Gaspra system ($\mu =0.2496003$, $k=5.3814122$) for different values of $q_1$ and $A_2$.

Parameters	$\mathit{T}/2$	${\mathit{x}}_0$	${\dot{\mathit{y}}}_0$	${\mathit{x}}_{\mathbf{cut}}$	C	${\mathit{a}}_{\mathit{h}}$
$q_1=1.0,A_2=0.0$	$2.61422210$	$1.85779000$	$0.10001890$	$1.93648249$	$9.69969467$	$45.1649$
$q_1=1.0,A_2=0.1$	$2.50922774$	$1.89119800$	$0.10000302$	$1.96306789$	$11.25375340$	$70.6495$
$q_1=0.7,A_2=0.1$	$2.41643274$	$1.82606100$	$0.10023956$	$1.89325798$	$9.95306181$	$118.8104$
$q_1=0.7,A_2=0.2$	$2.32926560$	$1.85915000$	$0.10006317$	$1.92106974$	$11.37462299$	$178.0334$
$q_1=0.5,A_2=0.2$	$2.26732125$	$1.81935000$	$0.10031023$	$1.87805493$	$10.38332237$	$261.1440$

present representative members of the Lyapunov families originating from the collinear EPs of the Gaspra system for all examined combinations of the radiation factor and oblateness coefficient, namely, $q_1=1$, $A_2=0$; $q_1=1$, $A_2=0.1$; $q_1=0.7$, $A_2=0.1$; $q_1=0.7$, $A_2=0.2$; and $q_1=0.5$, $A_2=0.2$. For each orbit, the tables list the half period $T/2$ together with the initial position and velocity components $(x_0,{\dot{y}}_0)$ at the first perpendicular intersection with the $Ox$-axis at which the values of the remaining components are zero. In addition, the coordinate $x_{\mathrm{cut}}$ which specifies the orbital amplitude along the $Ox$-axis, the associated Jacobi constant C, and the horizontal stability index $a_h$ are also provided.

6. Discussion

The equilibrium dynamics of a modified rotating mass dipole system within the framework of the photogravitational CR3BP was investigated. The model incorporates a radiating primary and an oblate secondary, connected by a massless rod capable of transmitting internal forces in addition to gravity. This configuration generalizes classical formulations and captures a broader range of physical scenarios, including cases where the rod exerts no tension, thereby reducing the system to earlier models in the literature. Our analysis reveals that the existence and stability of EPs are strongly influenced by the system’s parameters, i.e., the mass ratio, the oblateness of the secondary, the force ratio, and the radiation pressure factor. We identified five EPs, three collinear and two non-collinear, whose positions are significantly affected by variations in these parameters. In particular, the introduction of oblateness and radiation causes noticeable shifts from the equilibrium configurations known in the classical CR3BP. These perturbations also modify the structure of the ZVCs, altering the regions of allowed motion for the infinitesimal third body. Regarding linear stability, we found that the collinear points $L_2$ and $L_3$ remain consistently unstable across a wide range of parameter values. In contrast, the collinear point $L_1$ and the non-collinear points $L_4$ and $L_5$ exhibit conditional stability, depending on specific combinations of the perturbation parameters.

We applied the developed model to the asteroid 951 Gaspra by incorporating indicative perturbation parameters into the analysis. Using estimated physical properties of the asteroid, we identified three collinear and two non-collinear EPs. In the unperturbed case, the computed equilibrium positions are consistent with those reported in earlier studies, confirming the validity of our approach. However, the inclusion of oblateness and radiation pressure leads to noticeable shifts in the equilibrium locations, highlighting the sensitivity of the dynamical structure to such perturbations. Our stability analysis indicates that the collinear points $L_1$, $L_2$, and $L_3$ consistently exhibit positive real eigenvalues, indicating instability. The non-collinear points $L_4$ and $L_5$ possess complex conjugate eigenvalues with positive real parts, characterizing them as complex unstable.

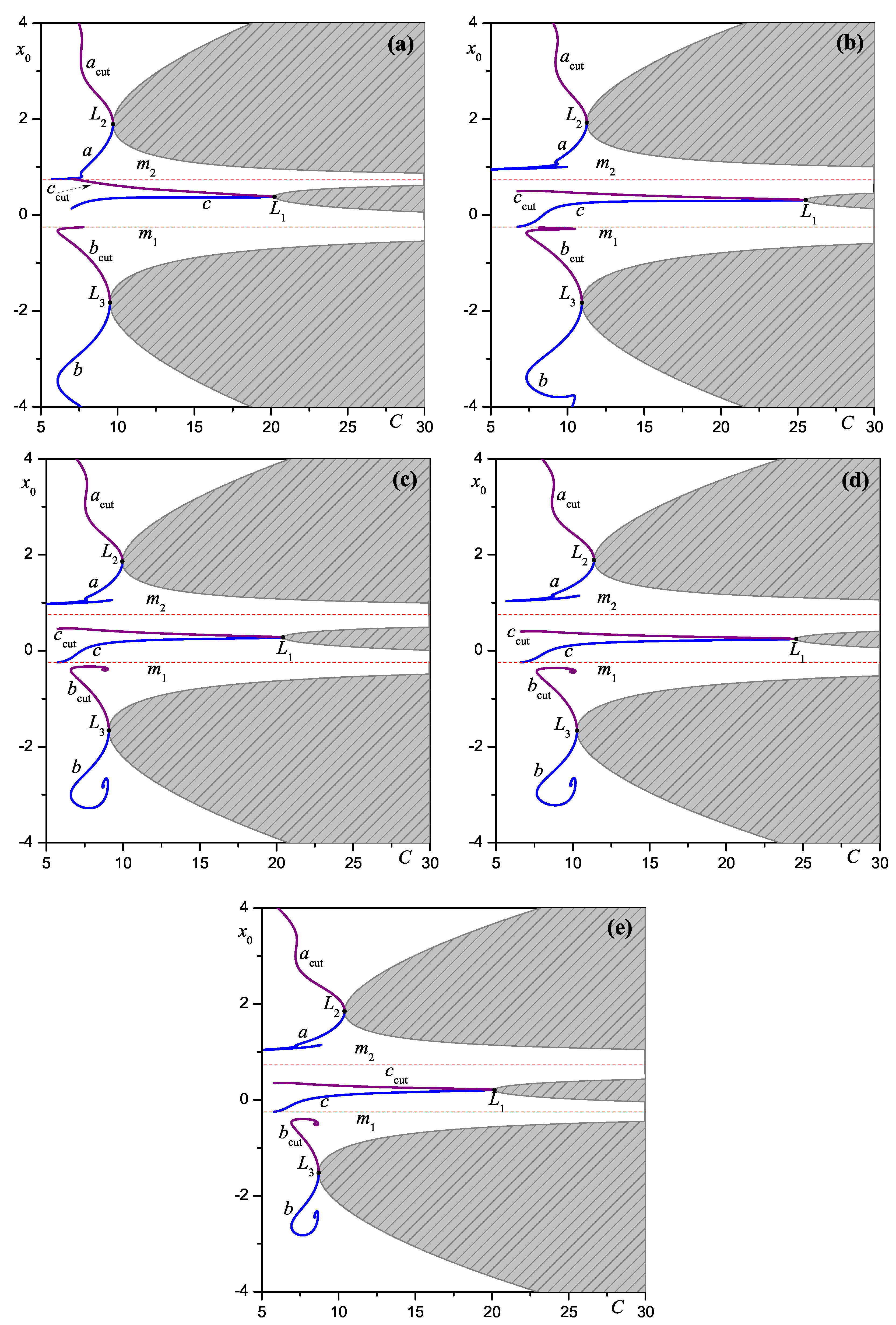
In addition to the equilibrium analysis of the asteroid 951 Gaspra, we investigated the Lyapunov families of periodic orbits associated with the collinear EPs. The numerical results show that in the unperturbed configuration, all three families (a, b, and c) terminate in collision with one of the primaries. The inclusion of oblateness primarily reshapes the characteristic curves, modifying their intersection patterns in the $(C,x_0)$ plane but without changing their termination modes. By contrast, radiation pressure induces a qualitative transition for families a and b, emanating from the exterior EPs $L_2$ and $L_1$, respectively, replacing collision terminations with asymptotic spiral orbits around the triangular EPs $L_4$ and $L_5$. Family c, emerging from the interior equilibrium point $L_1$, retains its collisional termination with the smaller primary in all cases. Horizontal stability analysis further revealed that the a- and b-families contain extended segments of stable periodic orbits, whereas the c-family remains unstable throughout.

7. Conclusions

This study investigated the equilibrium dynamics of a rotating mass dipole system in the photogravitational CR3BP, extending earlier formulations by incorporating both radiation pressure and oblateness. The analysis showed that these perturbations influence not only the positions of the equilibrium points but also their stability properties. In particular, we found that the inner collinear point $L_1$ can become stable when the triangular points $L_4$ and $L_5$ coalesce with it, transferring their stability to the collinear configuration. This shows how the combined action of gravitational asymmetries and radiative effects can influence the dynamics near elongated celestial bodies.

The application of the model to asteroid 951 Gaspra demonstrated the potential of the dipole approximation, within its idealized assumptions, to capture key aspects of the dynamical environment of an elongated body. In this representation, the mass parameter and force ratio were fixed from observational constraints, whereas the radiation and oblateness coefficients were varied to explore the system’s response more broadly and to encompass potential or hypothetical configurations. The results showed that these perturbations displace the equilibrium configurations and reshape the associated Lyapunov families, modifying their geometry, stability, and their termination behavior, but without removing the intrinsic instability of the equilibria near Gaspra. Overall, the results emphasize both the sensitivity of small-body dynamics to physical asymmetries and the value of simplified CR3BP-based models, which, despite their idealized nature, can still provide useful insight into the complex gravitational environment of irregular asteroids.

A natural extension of the present work is to study the invariant manifolds of the collinear equilibria themselves, which can provide valuable information on the local and global dynamics of the system. Also, the stable and unstable manifolds associated with the Lyapunov orbits around the collinear equilibria could be investigated to gain deeper insight into the transport mechanisms and dynamical pathways in their vicinity. Beyond this, further investigations may address the global dynamical structure more broadly, including the onset of chaotic behavior, resonance phenomena, and long-term orbital stability. Such studies could employ tools such as Poincaré maps defined on appropriate surfaces of section, numerical exploration of chaotic trajectories, and frequency-domain techniques to characterize dominant frequencies and resonance effects. These directions would provide a more comprehensive picture of the nonlinear dynamics, complementing the local analysis of equilibria and periodic orbits developed in this work.