Abstract
Creative insight is a core phenomenon of human cognition, often characterized by the sudden emergence of novel and contextually appropriate ideas. Classical models based on symbolic search or associative networks struggle to capture the non-linear, context-sensitive, and interference-driven aspects of insight. In this work, we propose a computational model of insight generation grounded in continuous-time quantum walks over weighted semantic graphs, where nodes represent conceptual units and edges encode associative relationships. By exploiting the principles of quantum superposition and interference, the model enables the probabilistic amplification of semantically distant but contextually relevant concepts, providing a plausible account of non-local transitions in thought. The model is implemented using standard Python 3.10 libraries and is available both as an interactive fully reproducible Google Colab notebook and a public repository with code and derived datasets. Comparative experiments on ConceptNet-derived subgraphs, including the Candle Problem, 20 Remote Associates Test triads, and Alternative Uses, show that, relative to classical diffusion, quantum walks concentrate more probability on correct targets (higher AUC and peaks reached earlier) and, in open-ended settings, explore more broadly and deeply (higher entropy and coverage, larger expected radius, and faster access to distant regions). These findings are robust under normalized generators and a common time normalization, align with our formal conditions for transient interference-driven amplification, and support quantum-like dynamics as a principled process model for key features of insight.
Keywords:
quantum walks; creative insight; conceptual networks; cognitive modeling; quantum-inspired computation MSC:
91E10
1. Introduction: When Ideas Collapse into Insight
Creative insight is widely recognized as a fundamental yet elusive aspect of human cognition. It is typically characterized as a sudden and often unexpected transition from a state of cognitive impasse to one of solution or conceptual clarity [1,2]. The phenomenology of insight has been documented across diverse domains, including problem solving, metaphor generation, scientific discovery, and artistic production [3,4,5]. Despite its centrality in mental life, modeling insight computationally remains an open and challenging problem [2,6,7,8].
Several theoretical accounts have sought to explain the mechanisms underlying insight, ranging from heuristic-based symbolic search to associative network models that rely on spreading activation within a conceptual space [9,10]. However, these models often struggle to capture the non-linear, discontinuous, and context-sensitive nature of creative transitions [4,11]. More recent approaches have proposed dual-process theories that distinguish between fast associative mechanisms and slower controlled processes [10,12]. Yet, even dual-process frameworks face limitations in formally accounting for the dynamics of sudden restructuring or emergence that characterize genuine insight episodes [4,13].
An alternative line of research has emerged over the past two decades that leverages the mathematical formalism of quantum theory, originally developed for physics, as a modeling framework for cognitive phenomena that exhibit contextuality, interference, and probabilistic emergence [6,14,15]. In particular, quantum models have been applied to concept combination, decision-making under ambiguity, and the role of context in mental representation [1,6,16]. Within this tradition, a growing body of work has suggested that creative cognition, and especially insight, may benefit from a quantum-theoretic treatment [1,3,17]. These models typically rely on the notions of superposition, collapse, and entanglement to capture the emergence of novel ideas from latent cognitive states.
The present work is situated within this broader line of quantum-inspired cognitive modeling. It builds upon previous efforts to represent conceptual dynamics in Hilbert space [1,14], extending them through the use of quantum walks on semantic graphs as a means to simulate the exploratory processes that precede insight. Rather than postulating insight as a discrete event imposed by an external rule or threshold, we aim to show that its probabilistic emergence can be modeled as an endogenous property of a quantum dynamical system navigating a structured conceptual landscape.
In this paper, we develop a quantum-inspired account of insight that moves beyond a purely conceptual proposal. We first establish, in a precise mathematical form, when and how interference can generate short-time amplifications of activation, conditions that make remote but contextually appropriate concepts temporarily more accessible. Building on this foundation, we introduce a set of quantitative observables and nonparametric statistics that let us read the model empirically rather than impressionistically, separating target-centric behavior from open-ended exploration. We then put the framework to work on large empirically derived ConceptNet subgraphs spanning three settings, an illustrative Candle instance, twenty Remote Associates Test triads, and Alternative Uses—always comparing continuous-time quantum walk (CTQW) with classical diffusion (CRW) under identical initial conditions and a common spectrum-scaled time normalization. Across these conditions, CTQW reliably concentrates more probability on single-solution targets and reaches higher peaks sooner, while in open-ended tasks it explores both more broadly and more deeply within the same temporal budget. The pattern is robust to normalized generator choices and small variations in the rate parameter once time is scaled by the operator spectrum.
The paper is organized as follows. We begin by locating our contribution within the existing literature (Section 2), setting the stage with essentials from semantic networks, quantum walks, and the cognitive motivation that ties them together. Section 3 then fixes notation and modeling choices and, to keep the paper accessible, folds in a brief primer for non-specialists alongside a short note on feasibility and implementation. With this scaffold in place, Section 4 develops the mathematical core—our propositions on time averaging and transient amplification—while Section 5 lays out the quantitative yardsticks and statistical procedures that will anchor the claims. Section 6 and Section 7 introduce the operational CTQW/CRW setup and the Candle case study. Section 8 scales up to ConceptNet-derived subgraphs, detailing the datasets, experimental setup, and results for Candle, twenty RAT triads, and Alternative Uses. Section 9 closes with a discussion of the implications and potential future directions.
2. Background
This section situates our contribution by reviewing the ingredients we rely on and the work we build upon. We first recall semantic networks and their cognitive motivation, then provide a brief primer on continuous-time quantum walks to orient non-specialist readers, and summarize prior quantum-inspired approaches to cognition. We conclude with a concise statement of the objectives and contributions that structure the remainder of the paper.
2.1. Limitations of Classical and Associative Models
Creative insight has long been approached through symbolic search methods, including heuristic-based rule systems and systematic problem decomposition; however, these frameworks often fail to account for sudden restructuring or remote idea emergence, leading to overly deterministic and serial explanations of insight [18]. Associative network models, anchored in spreading activation through conceptual memory, posit that solutions arise by traversing paths of semantic proximity, but they often produce gradual local transitions and struggle to predict sudden leaps to distant concepts [9,19]. Moreover, such models are inherently limited in capturing non-linear dynamics and context-dependent restructuring [11].
Dual-process theories have enriched the account by distinguishing between fast intuitive mechanisms and slower analytic processes [10,12], but they still fall short in formalizing how intuitive restructuring leads abruptly to insight without external triggers or threshold rules [2,13].
Other computational frameworks, such as random-walk-based exploration or Markov chain Monte Carlo (MCMC) models, simulate search over semantic networks, yet these methods exhibit a strong bias toward local search and rarely yield the large sudden transitions characteristic of insight episodes [20].
Finally, although process modeling frameworks attempt to integrate dynamic cognitive steps into unified models, many remain simulation-bound and unable to generalize across domains, often neglecting the emergent interference-driven transitions that insight displays [19].
Thus, while classical, associative, and heuristic-based models offer useful approximations of creative cognition, they systematically underperform in modeling the non-local, interference-driven, and contextual emergence dynamics that define genuine insight.
2.2. Quantum Cognition as a Modeling Framework
Classical models struggle with discontinuity, context sensitivity, and non-local effects in cognition. Quantum-theoretic formalisms address these features by providing a probabilistic calculus with contextuality, interference, entanglement, and superposition [6,14,21]. Within quantum cognition, such tools have explained decision-making paradoxes (e.g., conjunction/disjunction effects and sure-thing violations) that are difficult for classical Bayesian accounts [6,22]. Crucially, quantum models offer structural mechanisms—state superposition and context-dependent projection—that accommodate incompatible or non-compositional cognitive states [1,16].
This perspective extends to conceptual combination: rather than static symbols, concepts are represented as state vectors in a Hilbert space whose actualization depends on measurement context, supporting flexible context-sensitive meanings [1,16].
These characteristics align with the phenomenology of insight: multiple candidate interpretations can coexist and interact prior to a context-driven actualization (collapse) into a single solution. In what follows, we leverage these principles at the process level, using interference and superposition to model how remote yet context-appropriate candidates can transiently gain probability in semantic networks [1,14,19].
2.3. Proposed Model and Contributions
We model creative insight as continuous-time quantum walks (CTQWs) on weighted semantic graphs: concepts are nodes, associative relations are weighted edges, and a quantum state evolves under a graph-derived Hamiltonian. Interference—rather than purely local diffusion—governs how activation redistributes over time.
Within this process-level view, insight is a probabilistic actualization (collapse) of a conceptually remote but structurally supported node whose salience is transiently amplified by constructive interference. This connects Hilbert-space accounts of concept representation [1,22] to a dynamic mechanism for semantic search.
To evaluate the model, we provide open executable materials (Colab notebook and code) and run paired CTQW–CRW comparisons under matched initial states and an auto-normalized horizon. Beyond a small illustrative graph for the Candle Problem, we use ConceptNet k-hop subgraphs across three settings: Candle, 20 Remote Associates Test triads, and Alternative Uses. We quantify target-centric outcomes (AUC, peak probability, time-of-peak, and time-to-threshold) and exploration behavior (entropy, coverage, expected radius, and time-to-depth), following the formal definitions and statistics in Section 5.
Empirically, we observe systematic statistically significant differences between CTQW and CRW on these graphs: CTQW can transiently increase the probability of reaching remote task-relevant nodes compared to the classical baseline (see Section 8).
This work advances the field of quantum cognitive modeling through the following contributions:
- Formal analysis. Proposition 1 (time-averaged CTQW distribution via spectral projectors) and Proposition 2 (sufficient condition for transient interference-based amplification), and discussion of generators (; robustness checks with ) and time normalization.
- Quantitative framework. Target-centric (AUC, peak, time-of-peak, time-to-threshold, and first-hitting) and exploration metrics (entropy, coverage, expected radius, and time-to-deep-layer), with paired CTQW–CRW statistics (Wilcoxon; bootstrap CIs).
- Empirical validation at scale. Paired comparisons on ConceptNet-derived subgraphs for Candle, 20 RAT triads, and AUs using identical graphs, initial states, and normalized horizons; robust effects across normalized generators.
- Reproducibility. Public code, derived datasets, and a Colab notebook that reproduce all the figures and tables.
These contributions aim to bridge the gap between abstract quantum cognitive theory and implementable computational models, offering new tools for the formal analysis of creative cognition.
3. From Semantics to Superposition: Unified Notation and Setup
We represent task-relevant conceptual knowledge as a finite undirected weighted graph with nodes. Nodes correspond to concepts, and edge weights encode associative strength obtained from empirical resources (e.g., co-occurrence statistics, psycholinguistic word-association norms, WordNet, and ConceptNet) or from synthetic constructions designed to probe specific topologies (small-world, scale-free, and modular). The (symmetric) adjacency matrix is , with for and otherwise; the diagonal degree matrix is , with ; the (combinatorial) Laplacian is . These matrices are real-symmetric (hence Hermitian) and admit an orthonormal eigenbasis. In what follows, we work in the node (computational) basis (bra–ket notation), identifying with the i-th canonical basis vector when convenient. We associate each concept node with a basis vector , forming an orthonormal computational basis. Orthogonality here reflects perfect discriminability of labels at readout and is a representational choice common in quantum walks on graphs; semantic relatedness is encoded in the graph (edge weights) and hence in the Hamiltonian, not as basis overlap. This avoids double counting similarity in both the state space and the dynamics. The framework can be generalized to non-orthogonal concept states with positive-definite Gram matrix . One may work with the G-inner product (so that H is Hermitian with respect to G) or equivalently pass to an orthonormal basis via a whitening transform , setting and . In that representation, our spectral statements and projector formulas apply as usual, while measurement is represented by a POVM over . For clarity—and because our empirical nodes are discrete identifiers—we adopt the orthonormal coding throughout and let the graph weights govern similarity and interference via H.
This graph is not a passive store but the substrate on which conceptual dynamics unfold. The classical baseline is continuous-time diffusion governed by the heat equation , with solution . The classical baseline follows the diffusion dynamics in Equation (17), where probabilities evolve under the graph Laplacian. It provides an interference-free spread of activation that respects local conservation and yields smooth relaxation. In the quantum account adopted here, conceptual dynamics are modeled by a continuous-time quantum walk (CTQW) on G. The cognitive state evolves unitarily as
The cognitive state evolves according to the unitary dynamics in Equation (1), which defines the continuous-time quantum walk on the semantic graph.
The choice emphasizes direct adjacency-mediated transitions, whereas emphasizes diffusion-like propagation with a tunable rate. For , any global scaling can be absorbed into the time unit, so we set without loss of generality; for , we keep explicit to control the propagation rate. Unless otherwise stated, the initial condition is localized on a source node , namely ; we occasionally discuss more diffuse or context-biased superpositions when theoretically informative. The instantaneous probability of observing node i at time t is
while in the classical model we denote by the i-th component of with the same source (the Dirac unit vector at s). When a set of targets is designated by the task (e.g., solution concepts), we aggregate mass as and . Proximity in the graph serves as a proxy for cognitive accessibility, yet weights need not be mere distances: they may encode familiarity, typicality, cue validity, or other psychologically meaningful factors.
Equation (2) provides the node-wise probabilities of the quantum walk, obtained as the squared modulus of the amplitude at node i. These are the directly observable quantities that we compare against the classical baseline.
The Hilbert space picture makes the cognitive reading explicit. Each concept is a basis state, and a mental configuration is a normalized superposition
in which amplitudes quantify the momentary potential of concepts to be actualized. Localized states model focused search; broader superpositions capture exploratory modes and context sensitivity. Under the graph-induced Hamiltonian, amplitudes propagate along multiple paths and combine with phases; when phases align, constructive interference can transiently amplify probability on conceptually “remote” nodes, offering a mechanistic route to sudden restructuring episodes often described as insight. Conversely, destructive interference can suppress otherwise accessible alternatives. Beyond single concepts, entanglement-like structures (e.g., compositional subspaces for co-activated pairs) can model joint contextualization, whereby meanings are not merely additive but depend on relational constraints.
This representational stance departs from static symbol manipulation: conceptual content is not a fixed object but a context-sensitive process realized as state evolution. It aligns with empirical and phenomenological accounts of creative thought in which breakthroughs arise from reconfigurations among seemingly unrelated elements rather than from linear associative chains. Importantly, while some illustrations will use small hand-crafted networks to elucidate mechanisms, the same formalism applies to graphs derived from empirical linguistic data, opening a path to hybrid approaches that combine principled quantum dynamics with data-driven semantic structure.
To summarize performance over a finite horizon , we will report both level and latency measures on designated targets. For a single target r,
approximated in practice on a uniform grid (, ) by Riemann sums. Given a decision threshold , the (first) time-to-threshold is
As shown in Equation (4), AUC integrates the probability mass on the target node over the normalized horizon, providing a level-based summary of accessibility. Equation (5) defines the time-to-threshold metric, i.e., the first time a node’s probability exceeds a chosen level . This captures the latency with which a solution becomes salient.
Unless otherwise indicated, all CTQW/CRW comparisons use the same graph, source node, and time horizon; we vary , the Hamiltonian choice (A vs L), and and assess sensitivity accordingly. This unified setup provides the bridge from semantic structure to superposed cognitive dynamics, which we analyze mathematically in the next section and evaluate empirically thereafter.
4. Mathematical Analysis
We now formalize two aspects that distinguish continuous-time quantum walks (CTQWs) on semantic graphs from classical diffusion (CRW): (i) the structure of the long-time average distribution, and (ii) the possibility of transient phase-driven amplification on semantically remote targets. Throughout, we refer to the unified notation of Section 3.
Proposition 1
(Time-averaged CTQW distribution). Let H be a Hermitian graph Hamiltonian, either or with , and let be its spectral decomposition into orthogonal projectors onto eigenspaces associated with distinct eigenvalues λ. For any initial state and node ,
Equation (6) provides the long-time average probability of observing node r, which depends only on the spectral projectors of H. In particular, only intra-eigenspace coherences contribute to the time average, while interference across distinct eigenvalues washes out.
Proof.
Expand the unitary evolution in the eigenbasis of H: . Then, Squaring the modulus and integrating over t kills oscillatory cross-terms with frequencies by the Riemann–Lebesgue lemma; only terms with survive, yielding . Degeneracies are handled by the projector at fixed . The statement holds identically for and for ; in the latter case, the scaling rescales time but does not affect the infinite-time average. □
The next result isolates a sufficient spectral condition under which interference can produce transient probability gains on a target r relative to diffusion. Intuitively, if at least two eigenmodes connect source s and target r with comparable weights, their phases can align and yield a constructive cross-term that has no classical analogue.
Proposition 2
(Transient interference-based amplification). Let with , and consider the transition amplitude where and is an orthonormal eigenbasis of H. Assume there exist two indices such that , and the residual spectral weight is finite. Then, there exists a time such that
Moreover, for the classical heat kernel with the same initial condition,
where and . For all ,
Consequently, if , then there exists a time at which .
Observe that Equation (7) provides a lower bound on the quantum probability at the target, showing that constructive interference of multiple contributing amplitudes can guarantee a non-trivial activation. Equation (8) expresses the classical diffusion probability in the eigenbasis of the Laplacian, where decay is governed by the eigenvalues . Equation (9) provides an upper bound for the classical probability at node r, showing that it can never exceed the cumulative spectral weight B.
Proof.
Write , where and . Choose so that the two dominant terms are phase-aligned; i.e., with , which maximizes to . Then, by the reverse triangle inequality,
and squaring provides the stated lower bound: For the classical case, the heat kernel has no oscillatory cross-terms; by the triangle inequality, If the quantum lower bound exceeds B, the claimed strict inequality follows. □
Equation (10) makes explicit that the contribution of the two principal modes adds at least ; i.e., interference can secure a non-trivial amplitude even in the presence of residual spectral mass.
Corollary 1
(Graph-level sufficient condition). Suppose there exist two internally vertex-disjoint paths in G with distinct effective lengths/weights (so that the spectrum of H induces at least two eigenmodes with nonzero overlaps at s and r). Then, under mild non-degeneracy of the corresponding overlaps and sufficiently small residual spectral mass R, the condition of Proposition 2 holds; hence, there exists a time with .
Proof.
Two distinct families of paths typically generate distinct spectral contributions with nonzero overlaps at both s and r; for generic positive weights, this yields with . The disjointness assumption controls interference with other modes, making R small on small-to-moderate graphs or on well-separated path families. A full proof can be provided under specific regularity assumptions. □
Remark 1
(Choice of H and role of ). The statements above are agnostic to whether or . Proposition 1 depends only on the spectral projectors of H; scaling rescales phases but leaves the infinite-time average invariant. In Proposition 2, γ shifts the alignment time through , thereby modulating when amplification occurs, not whether the constructive cross-term can arise. Empirically, we therefore expect similar qualitative effects under both and , with different peak timings and bandwidths; this is consistent with the experimental sensitivity analyses reported later.
Implications for experiments.
Proposition 1 justifies reporting long-horizon summaries (e.g., AUC) together with transient metrics since persistent biases are tied to spectral weight within degenerate eigenspaces. Proposition 2 and Corollary 1 motivate seeking semantic subgraphs where multiple path families connect source and target (e.g., via alternative associative routes). Under such conditions, CTQWs admit time windows where target probability exceeds the diffusion baseline, a signature we quantify in the experimental sections.
To quantify these effects, we adopt the level and latency metrics defined in Section 5.
5. Metrics and Statistics
We summarize model behavior over a finite horizon using level and latency metrics on designated targets in the unified notation of Section 3. Let an experimental instance specify a graph , a source , and a target (or target set) (resp. ). Time is discretized as for , with .
Time is discretized on a uniform grid over the auto-normalized horizon in Equation (4), ensuring comparability across graphs and operators.
To begin with, we quantify overall target activation through the area under the curve (AUC). Specifically, for a single target r,
approximated by Riemann sums We also report the normalized AUC . For a set of targets R, replace with the aggregate .
As defined in Equation (11), AUC summarizes the total probability mass accrued on the target over the horizon , providing a level-based measure complementary to peak and latency metrics.
Beyond cumulative mass, we also track the most salient activation by considering peak probability and its timing. On the grid,
As per Equation (12), we summarize level and latency via the peak value and its earliest occurrence time on the sampled grid (for ties, we pick the earliest time).
In addition to peak-based measures, we evaluate latency more directly via time-to-threshold metrics. Given , define the first-passage time
Equation (13) defines the instance-level time-to-threshold, namely the earliest time within at which the target probability exceeds .
On the grid, we use linear interpolation: if , set
Equation (14) specifies the linear interpolation used to estimate the threshold-crossing time between two consecutive grid points.
If the threshold is not reached by T, we record a right-censored observation and report both the reach rate and the conditional summary of on the subset that reaches . In the main text, we use .
To compare quantum and classical dynamics on the same instances, we analyze paired differences across metrics. For each instance j, we form paired differences
and, for each , on the subset, where both are uncensored. We summarize paired differences by median and interquartile range (IQR). For inference, we use the two-sided Wilcoxon signed-rank test on each metric family, reporting the exact (or continuity-corrected) p-value and the effect size
where Z is the Wilcoxon test statistic normalized, and is the number of nonzero paired differences. Equation (16) defines the standardized effect size r, obtained from the test statistic Z and the effective sample size . In numerical simulations, Equation (8) makes explicit that CRW trajectories are convex combinations of exponential decays. Unlike the constructive interference bound in Equation (7), the CRW distribution is limited by the static spectral sum in Equation (9), which restricts its capacity to amplify remote nodes.
For robust inference, we complement paired statistics with confidence intervals obtained via resampling. We report confidence intervals for medians and for median paired differences via nonparametric bootstrap with resamples (BCa intervals unless otherwise noted). For reach rates , we provide exact binomial CIs; when comparing reach rates between QW and CRW on paired instances, we report McNemar’s exact test.
Finally, to account for multiple hypotheses and ensure consistent reporting, we apply standard correction procedures.
Within each task family (e.g., Candle, RAT, and AUs), we adjust for multiple -levels and metric families using the Holm–Bonferroni procedure over the corresponding set of hypotheses. While Equation (6) characterizes asymptotic behavior, our empirical metrics (AUC, peak, and threshold) focus on finite-horizon dynamics. Unless stated otherwise, all tables report medians and paired effect sizes r; figures display distributions (violin/box) of paired differences and time-series exemplars. All tests are two-sided.
6. Walking the Unseen Paths
Before the full model and results, we collect the operational ingredients of continuous-time quantum walks (CTQWs) and contrast them with classical diffusion, keeping only what is used later for Figures 2 and 3. On a semantic graph with adjacency A, degree D, normalized adjacency , and normalized Laplacian , the CTQW evolves unitarily, as described in Equation (1), and is read out on nodes via the Born rule (Equation (2)). Unnormalized generators are reported as robustness checks. The matched classical continuous-time random walk (CRW) evolves a probability vector on the same graph and from the same initial mass as
While CRW is stochastic and diffusive, CTQW is unitary and phase-bearing: amplitudes traveling along multiple paths can interfere constructively or destructively, yielding transient non-classical propagation and potential non-local reinforcement.
To enable comparisons across graphs and generators, we adopt an auto-normalized horizon
with the spectral radius and fixed across all experiments; CTQW and CRW are sampled on the same time grid with step . Under this convention, scaling (e.g., ) re-parameterizes time without changing qualitative interference patterns up to discretization.
Both CTQW and CRW are sampled on the same grid within the auto-normalized horizon of Equation (4) so that scale effects due to are controlled.
Nodes are concepts, edges carry associative weights, and is the computational basis. Initial states encode the task context (localized cue or superposition). Unless stated otherwise, we read a designated target and report target-centric metrics (AUC, peak, time-of-peak, and time-to-threshold) and exploration metrics (entropy, coverage, expected radius, and time-to-depth) as formally defined in Section 5. In cognitive terms, interference can concentrate probability on remote yet context-appropriate candidates, offering a process-level account of discontinuity and restructuring at commitment; a compact interpretation is provided in Section 9/Appendix A.
The classical baseline is the continuous-time random walk (CRW) in Equation (17), which is stochastic and diffusive: probability mass spreads locally and tends to privilege high-degree or nearby nodes. By contrast, the CTQW in Equation (1) is unitary and phase-bearing, so amplitudes traveling along multiple paths can interfere constructively or destructively. Under identical graphs, initial states, and the auto-normalized horizon in Equation (18), this contrast can yield transient non-classical propagation—most notably, a non-local reinforcement of structurally supported yet semantically remote nodes. In the experiments, we make the comparison explicit by pairing CTQW and CRW trajectories on the same time grid and then reading the same target-centric and exploration metrics (Section 5).
Within a semantic network, the initial state encodes task context (localized cue or superposition), and the CTQW evolves multiple candidates in superposition until commitment at readout. Interference can concentrate probability on remote yet context-appropriate nodes, offering a process-level account of apparent discontinuity and restructuring at commitment. In this study, the interpretation is kept operational: claims are tied to numbered quantities—AUC, peak, time-of-peak, time-to-threshold, and exploration measures—and to the spectral statements proved earlier (propositions), which together predict when transient amplification should emerge on a given graph (see Section 5 for metric definitions and Section 8 for empirical tests). A compact non-technical discussion is deferred to Section 9/Appendix A.
The framework is quantum-inspired and operational. Amplitudes evolve unitarily on a graph-induced real-symmetric d-sparse generator (robustness checks with ); spectra lie in for and for . We adopt the auto-normalized horizon (Equation (18)) and sample all trajectories on a uniform grid shared by CTQW and CRW. Simulations are executed classically via sparse actions of the matrix exponential (e.g., expm_multiply), with per-step cost and tolerance-controlled Krylov subspaces; unit-norm preservation provides a runtime diagnostic, and empirical scaling is reported in Section 8.1. A hardware realization would amount to implementing with standard Hamiltonian-simulation techniques for d-sparse Hermitian matrices; our claims here concern the process model and its testable signatures on semantic graphs.
7. Modeling and Visualizing Insight Dynamics via Quantum Walks
In this section, we present a computational simulation designed to explore the dynamic behavior of concept activation during insight problem solving. The Candle Problem, a well-known cognitive task requiring representational change, serves as our case study. By modeling the underlying semantic structure as a graph of conceptual associations, we compare the trajectories of a classical random walk and a continuous-time quantum walk initiated from a key element in the problem.
Our aim is to evaluate whether the quantum dynamics can account for the emergence of non-obvious yet functional associations. We construct a semantic network encoding the problem space and examine how each model distributes probability over time across conceptual nodes. This approach allows us to investigate whether quantum interference and coherence can facilitate representational restructuring, thereby offering a computational perspective on creative insight.
The proposed model and the associated simulations are fully accessible and reproducible via an interactive Google Colab notebook [23].
7.1. The Candle Problem: A Case of Insight
The Candle Problem, originally introduced by Karl Duncker in the 1940s [24], is a classical experimental paradigm used to study the phenomenon of creative insight. In its standard formulation, participants are presented with a candle, a box of tacks, and a book of matches. They are asked to attach the candle to a vertical wall in such a way that it does not drip wax onto the table below. Most participants initially attempt to affix the candle using the tacks or melt it with the matches, leading to an impasse. The insight-based solution involves emptying the box of tacks and repurposing it as a shelf for the candle, thus overcoming functional fixedness and reinterpreting the box’s role from a container to a support.
This problem has been widely studied in the psychology of problem solving and creativity as a prototypical example of representational restructuring [25,26]. It exemplifies key features of insight: a period of unsuccessful search, a mental impasse, and a sudden restructuring that redefines object affordances. Notably, the solution often emerges not through incremental reasoning but via a discontinuous shift in conceptual representation [27].
Recent cognitive models have sought to formalize the mechanisms underlying such restructuring, including dual-process theories [12], spreading activation in semantic networks [9], and Bayesian approaches [28]. However, these frameworks often struggle to account for the non-local interference-driven dynamics that characterize true insight episodes.
In this section, we adopt the Candle Problem as a case study to evaluate our quantum-inspired model of creative cognition. We propose that a continuous-time quantum walk over a structured semantic graph can capture the non-linear dynamics required for a distant but contextually relevant concept, such as shelf, to become salient. Thus, we aim to simulate the cognitive reconfiguration that underlies the insight moment in this canonical task.
7.2. Modeling and Simulating Conceptual Dynamics
To formalize the conceptual landscape of the Candle Problem, we define a weighted semantic graph , where each node represents a concept relevant to the problem scenario (e.g., box, container, support, and shelf) and each edge is assigned a positive weight reflecting associative or semantic proximity. The adjacency matrix A is then provided by for connected nodes and otherwise; the corresponding Laplacian is , with and . This representation provides the substrate for the continuous-time quantum walk dynamics of Equations (1) and (2) and the classical diffusion baseline of Equation (17).
The illustrative graph contains approximately ten nodes, chosen to balance expressiveness and interpretability. Importantly, there is no direct edge between the initial concept (box) and the target solution concept (shelf), so any successful trajectory must pass through intermediate associations, such as platform, support, or stand. This topological constraint operationalizes the idea of insight as a non-local interference-driven transition.
Edge weights were assigned heuristically, following prior work on semantic networks and spreading-activation models [9,28]. For transparency, the exact weights are reported in Figure 1 (annotated edges) so that the reader can directly reconstruct the adjacency matrix used in the simulations. The network was implemented in Python with the NetworkX library, allowing reproducible analysis and visualization.
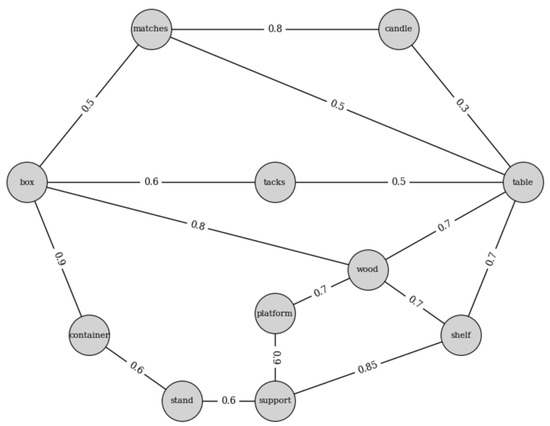
Figure 1.
Semantic network used to model the conceptual space of the Candle Problem. Nodes are concepts, and weighted edges denote associative or functional proximity. The initial node box is not directly connected to the solution node shelf, requiring indirect activation through intermediates such as wood, support, and platform. Edge weights are shown along the connections and correspond to the entries of the adjacency matrix used for simulation.
To explore the dynamic behavior of conceptual activation within the semantic network, we implemented both classical and quantum walk simulations in Python. Quantum dynamics follow the continuous-time quantum walk of Equation (1), with readout probabilities provided by Equation (2), starting from the localized initial state (Section 4). Probabilities are sampled on a uniform time grid with horizon (spectral normalization; see Section 4).
The matched classical baseline is the continuous-time random walk governed by Equation (17), with localized at box. This process lacks interference and yields diffusive spreading.
Both models were run in a reproducible Google Colab environment using NumPy 2.3, SciPy 1.16, NetworkX 3.5, and Matplotlib 3.10. For each , we record the node-wise probabilities and visualize them as heatmaps.
Figure 2 shows the temporal evolution of the quantum walk probability distribution reflecting the numerical values from Equations (1), (2), and (17). The heatmap values correspond to the computed for each node i and time step . Starting from the localized state on box, the system spreads across the network; after sufficient evolution, the shelf node emerges with elevated probability, illustrating the potential of quantum dynamics to support non-local semantic activation relevant for insight.
To enable a direct comparison with the classical diffusion baseline, we report in Figure 3 the probability distributions obtained from Equations (1), (2), and (17) at four representative time instants: the initial state (), two mid-trajectory snapshots ( and in normalized units), and the final horizon (). For each instant, the node-wise probabilities and are directly computed from the simulated dynamics and plotted side by side. These snapshots are sampled on the same time grid used for Figure 2 and correspond to the auto-normalized horizon described in Section 4. Each classical snapshot in Figure 3 is computed from Equation (3) on the same time grid used for the quantum evolution.
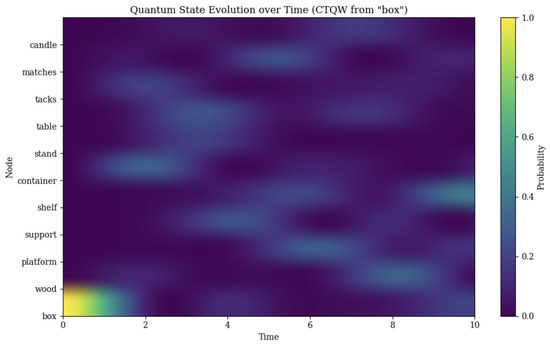
Figure 2.
Heatmap of the quantum probability distribution over the semantic graph. The walker starts at the box node. Over time, amplitudes evolve by Equation (1), with readout via Equation (2). The shelf node shows a marked late-time increase, consistent with interference-driven amplification of remote but context-appropriate concepts.
These results substantiate the analytical conditions derived in Section 4: in the presence of multiple paths, the CTQW can transiently amplify the probability of reaching semantically remote but contextually appropriate nodes. In contrast, the CRW follows a diffusion pattern that distributes mass more evenly and lacks the constructive interference required for focused emergence. This difference is also reflected in the quantitative metrics reported in Section 8.3 (e.g., higher AUC and earlier peak times under CTQW). The sharper rise on shelf under CTQW corresponds to higher and earlier , as defined in Equation (12).
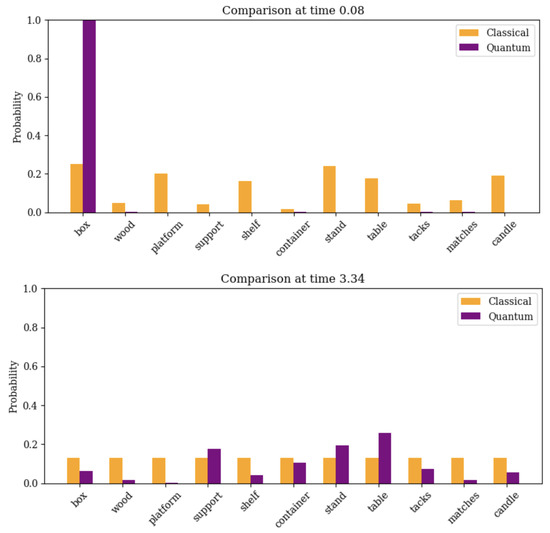
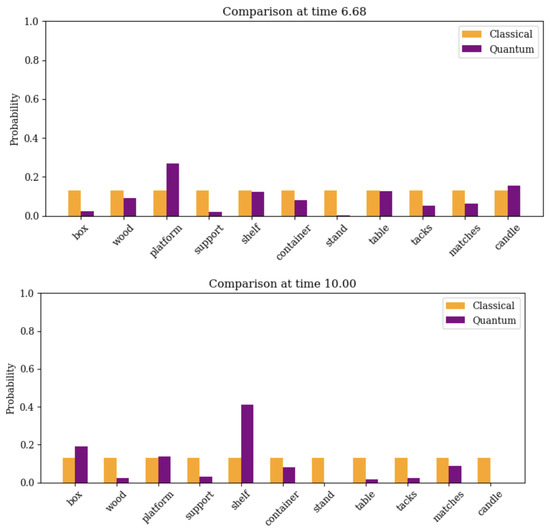
Figure 3.
Side-by-side comparison of probability distributions obtained from Equations (1), (2), and (17). At , the CTQW remains localized on the box node, while the CRW has already diffused to neighbors. At , the CTQW reaches semantically distant nodes with non-negligible probability on support, stand, and table. At , constructive interference amplifies activation on platform and shelf, whereas the CRW shows a flatter spread. At , the CTQW exhibits a clear peak on the shelf node, consistent with interference-driven amplification predicted by Proposition 2; the CRW maintains a uniform distribution.
7.3. Interpretation and Implications
The simulation results offer a concrete instantiation of how quantum dynamics over a semantic network can enable the emergence of remote associations that are functionally relevant to insight problem solving. In the context of the Candle Problem, the observed convergence of probability on the shelf node, despite the absence of direct connections from the initial concept box, illustrates the capacity of quantum walks to navigate conceptual structures in a non-local and interference-based manner.
8. Extended Experimental Results
We complement illustrative toy examples with three task families widely used in the insight and creativity literature: the Candle Problem, Remote Associates Test (RAT) triads, and Alternative Uses (AUs). In all cases, the semantic substrate is obtained from ConceptNet 5.7 (English) via k-hop neighborhoods () around task-specific seeds, followed by weight symmetrization and normalization (row-stochastic by default) and the removal of self-loops (see Section 3). A repository with the full dataset and Python scripts is available in [29], while basic graph statistics for the resulting subgraphs are reported in Table 1.

Table 1.
Statistics of the k-hop semantic subgraphs extracted from ConceptNet for each task instance. Columns report the number of nodes (), edges (, undirected, weighted), edge density (all graphs are sparse), the size of the largest connected component (“largest_cc”; equal to indicates a single giant component), and the average degree . For Candle and AUs, we aggregate the task terms into one seed set and extract the neighborhood; for RAT, we build one subgraph per triad from the three cues (and candidate solution). Graph sizes span to nodes with average degree typically in the 10–12 range, reflecting the high sparsity typical of large semantic networks. These graphs constitute the common backbone on which CTQW and CRW are compared under identical initial conditions and time normalization (see Section 5).
RAT tasks probe the ability to connect three cue words via a single associative bridge (e.g., cottage–swiss-cake →cheese). We use a set of 20 English triads (see repository seeds) and, for each triad, derive a dedicated subgraph by taking the union of k-hop neighborhoods around the three cues. The solution word (target) is included only for evaluation, not as a seed. RAT triads are ideal to test scalability beyond a single illustrative case since they require converging on a specific remote concept while navigating a moderately sized semantic region. They also support paired statistical comparisons (CTQW vs. diffusion) across multiple independent instances (Section 5).
AU tasks evoke divergent thinking by prompting many uses for a common object (e.g., brick, paperclip, newspaper, rope, shoe, bottle, cup, spoon, fork, pencil, book, and towel). Here, we treat the object name(s) as seeds and extract a broader semantic neighborhood capturing materials, functions, locations, and affordances. While AUs are not single-target problems, they provide a stress test for whether quantum dynamics preferentially amplify non-obvious “remote” regions of the graph. In analyses, we therefore report aggregate target sets or exemplar remote nodes and summarize level/latency metrics accordingly (Section 5).
For all families, we rely on ConceptNet relations from a standard whitelist (e.g., RelatedTo, IsA, UsedFor, PartOf, CapableOf, AtLocation, HasA, Causes, and Synonym); weights are symmetrized (max) when edges exist in both directions and then normalized. The exact seeds, scripts, and per-graph summaries are included in the repository for full reproducibility. ConceptNet data are used under CC BY–SA; we provide attribution and links in the repository README.
Across all subgraphs, we verify that graphs are non-empty, densities fall in , the largest connected component typically covers the majority of nodes, and average degree exceeds 1; detailed counts are provided in Table 1. These checks ensure that subsequent CTQW vs. diffusion comparisons operate on meaningful semantic neighborhoods rather than on degenerate or overly fragmented graphs.
8.1. Experimental Setup
We evaluate continuous-time quantum walks (CTQWs) against classical diffusion (CRW) on the ConceptNet-derived k-hop subgraphs described above. Notation and metrics follow Section 3 and Section 5. Unless otherwise noted, CTQW and CRW are run on the same graphs, with the same initial states and time grid.
Our main results use graph-normalized operators to make scales comparable across instances: (i) the normalized adjacency (normA); and (ii) the normalized Laplacian with a small rate parameter (normL, i.e., ). In sensitivity checks, we also report the unnormalized choices and (extended Tables in [29]). For normL, we sweep over a few small values (e.g., ).
For the Candle Problem, we initialize a localized state on the source concept (e.g., ) and use the standard solution node as target (e.g., or available variant). For RAT triads, we model simultaneous cue presentation by the equal-phase superposition
with the triad’s solution as target. For AUs (no single target), we initialize on the object name (e.g., ) and evaluate exploration metrics rather than target-centric ones.
To avoid arbitrary scale effects, the horizon is set by the operator’s spectral radius: (autoT), with fixed (we use in our runs). Probability trajectories are sampled on a uniform grid for with depending on the experiment. CTQW evolution uses the action of the matrix exponential via expm_multiply applied to ; CRW uses the heat-kernel action computed analogously. We monitor unit-norm preservation for CTQW (tolerances ).
For Candle and RAT (single-solution tasks), we report the target-centric metrics of Section 5: AUC on the solution node, peak probability, and time-of-peak; we also track time-to-threshold (Equation (5)) for and first-hitting time with discrete readout. Paired differences (QW−CRW) are formed per instance (per triad for RAT), and nonparametric Wilcoxon signed-rank tests and BCa bootstrap CIs are computed across instances when sample sizes permit. AUC values in Equation (11) are evaluated on the sampled grid by Riemann sums over the auto-normalized horizon (Equation (4)).
For AUs (open-ended), we use exploration metrics defined in Section 5: mean entropy over time, coverage (number of nodes that ever exceed a small activation threshold ), expected radius (mean shortest-path distance from the source, in hops), and time to a “deep layer” (first time the expected radius reaches a graph-dependent threshold , e.g., a high distance percentile). As in the target-centric case, we aggregate paired differences (QW−CRW) across sources and use Wilcoxon tests where applicable.
8.2. Operator Ablation: Adjacency vs. Laplacian
We compare quantum generators that are standard in graph-based CTQW: (i) the (symmetric) normalized adjacency and (ii) the normalized Laplacian (used as with small ). All ablations use identical graphs and initial states and a shared spectral time normalization to remove arbitrary scale effects; small sweeps are included for Laplacian forms.
Since , Laplacian-based CTQW differs from adjacency-based CTQW by an on-site diagonal term D. In unitary dynamics, diagonal entries act as local phase rates (“site energies”): nodes with larger degree accumulate phase faster, which can dephase interference at hubs and modulate path combination. By contrast, adjacency-based CTQW has no such degree-dependent on-site term and tends to privilege path multiplicity more directly. Normalization () reduces degree heterogeneity and bounds the spectrum, allowing fairer cross-graph comparison.
Adjacency-based dynamics () emphasize direct associative transitions and multi-path reinforcement, aligning with a view of insight as rapid re-combination of strongly cued associations. Laplacian-based dynamics () impose a degree-sensitive “cost of connectivity,” potentially tempering hub dominance and favoring selective routes. Both are plausible: we therefore let data arbitrate under matched conditions.
For single-solution tasks (Candle and RAT), we compute AUC on the target, peak probability, and time-of-peak. For AUs, we use mean entropy, coverage, expected radius, and time to a deep layer (Section 5). We report paired differences per instance and Wilcoxon signed-rank tests with %QW-better.
8.3. Results
The compact summaries used in the main text (Table 2, Table 3 and Table 4) display medians of paired differences (QW−CRW), interquartile ranges, and, when applicable, Wilcoxon p-values and the percentage of instances in which QW outperforms CRW (with “lower is better” for time metrics). Extended results, i.e., operator sweeps, additional thresholds, full per-instance tables, and confidence intervals, are provided in [29].

Table 2.
Candle (illustrative case). Median differences (QW−CRW) on AUC, peak probability, and time-of-peak for a single derived semantic graph of the Candle Problem. Positive deltas on AUC/peak indicate higher transient concentration on the solution node under CTQW, while a negative delta on time-of-peak indicates an earlier peak (faster buildup). As this is a single-graph demonstration, the table complements the qualitative time-series by indicating direction and magnitude of the effect under identical initial conditions and time grid.

Table 3.
RAT (20 triads). Paired comparison between CTQW and CRW on target-centric metrics. The table reports the median paired difference (QW−CRW) across triads for AUC, peak probability, and time-of-peak. Positive deltas indicate that CTQW accumulates more probability mass on the correct target (AUC) or attains a higher maximum activation (peak), while negative deltas for time-of-peak indicate that CTQW reaches its peak earlier (i.e., faster) than CRW. Values are computed on identical semantic graphs, with the same initial state and time grid. These medians summarize the direction and magnitude of the effect across triads; inferential statistics (e.g., Wilcoxon signed-rank tests) are reported in Section 8.

Table 4.
Alternative Uses (AUs). Exploration-oriented metrics without a single target. The table reports the median difference (QW−CRW) across sources for four complementary measures: (i) entropy (mean over time), capturing the diversity of the explored probability distribution; (ii) coverage, the number of nodes that exceed a small activation threshold at least once; (iii) expected radius (mean), the average topological distance from the source weighted by activation; and (iv) time to deep layer, the first time the expected radius reaches a graph-dependent threshold (e.g., a high distance percentile). Positive deltas for entropy/coverage/radius indicate broader and deeper exploration under CTQW; negative deltas for the time metric indicate faster progression to distant regions. All runs use the same graphs, initial states, and temporal discretization to ensure a fair comparison.
For the Candle dataset, regarding the ConceptNet-derived subgraph for the Candle Problem, CTQW shows a transient amplification on the solution node relative to CRW: a higher area under the curve (AUC) and a higher probability peak reached earlier. These effects are summarized in the compact table (Table 2), which reports the median differences (QW−CRW) for AUC, peak, and time-of-peak. As this is a single-graph demonstration, we use Candle chiefly as a qualitative exemplar; extended numeric diagnostics (including full time-series) are provided in [29]. The differences in AUC (Equation (11)) indicate that CTQW concentrates more probability on the solution node relative to CRW. The observed concentration patterns are consistent with the spectral decomposition in Equation (6), which predicts stable long-term distributions tied to eigenstructure, while the observed amplification of the shelf node is consistent with the interference bound derived in Equation (7). Differences in AUC (Equation (11)) indicate higher mass concentration on the solution node under CTQW. Median paired differences in and (Equation (12)) favor CTQW, indicating stronger and earlier concentration on the solution node.
In the case of the RAT dataset, for each triad, we computed paired differences between CTQW and CRW on target-centric metrics (AUC, peak, and time-of-peak). The compact summary (Table 3) reports the median paired difference (QW−CRW) across the 20 triads (and Wilcoxon p-values when applicable). The pattern is consistent with the interference-based account: medians are positive for AUC (Equation (4)) and peak (CTQW concentrates more mass and attains a higher maximum on the correct target) and negative for time-of-peak (CTQW reaches that peak earlier). Across the 20 triads, paired AUC differences computed via Equation (11) are consistently positive, supporting stronger target accumulation for CTQW. Threshold-based and first-hitting times are less sensitive in cases where targets remain below fixed thresholds; we therefore include their full details in [29] and do not emphasize them in the main text. Across triads, CTQW attains larger and smaller (Equation (12)) than CRW.
In the case of the AUS dataset, without a unique target, we evaluate exploration on ConceptNet-derived AUS graphs across multiple sources (e.g., brick, paperclip, newspaper, rope, and shoe). The compact summary (Table 4) aggregates the median differences (QW−CRW) for four interpretable measures: mean entropy (diversity of the explored distribution), coverage (number of nodes ever exceeding a small activation threshold), expected radius (mean topological distance from the source), and time to a deep layer (first time the expected radius reaches a graph-dependent threshold). The medians are positive for entropy/coverage/radius and negative for time-to-depth, indicating that CTQW explores more broadly and reaches distant regions faster. Per-source breakdowns and additional metrics (e.g., entropy peak, and radius peak) are reported in [29]. For divergent tasks, the metric of Equation (13) captures the onset of activation across sets of remote nodes.
All the comparisons use identical graphs, identical initial conditions (source node or superposition of cues for RAT), and identical temporal discretization. The qualitative pattern does not depend on the specific generator (normalized adjacency, normA; normalized Laplacian, normL at small ), and the time normalization mitigates spurious scale effects. The location and sign of the observed advantages match the conditions for the transient interference-driven amplification presented in our analysis (Section 4).
Taken together, the three datasets paint a coherent picture. On single-solution tasks (Candle and RAT), CTQW concentrates more probability on the correct target and reaches stronger peaks earlier than CRW (Table 2 and Table 3). On open-ended tasks (AUs), CTQW explores broader and deeper regions of the semantic graph in the same time budget (Table 4). Extended tables with per-triad and per-source results, as well as additional metrics and confidence intervals, are provided in [29].
Regarding the ablation results, under identical initial states and spectral time normalization, CTQWs with and yield qualitatively similar advantages over CRW on single-solution tasks, with effect sizes that vary across datasets. Where differences arise, tends to accentuate multi-path reinforcement (higher peaks), while can produce slightly earlier or more selective amplification when high-degree hubs would otherwise dominate. On AUs, both generators broaden exploration relative to CRW; often shows larger coverage/radius, whereas reduces hub bias. These patterns are consistent with the diagonal degree term present in Laplacian-based dynamics (Section 8.2).
9. Discussion and Outlook: Quantum Paths to Creativity
The results presented here support accounts of insight as representational restructuring, an abrupt reorganization that makes previously remote solution paths salient. CRW typically yields gradual locality-driven spread in conceptual space. In contrast, our CTQW formalism introduces superposition and interference between semantic trajectories, enabling transient concentration on semantically distant context-appropriate ideas without sequential traversal of all the intermediates.
Across three families of tasks, the empirical patterns match the qualitative predictions of our analysis (Section 4). On single-solution problems, CTQW concentrates more probability on the correct node and does so earlier than CRW. In the illustrative Candle graph, the compact summary (Table 2) shows CTQW exceeding CRW on AUC and peak probability and achieving an earlier time-of-peak. More importantly, on RAT triads (20 instances), the paired deltas (QW−CRW) in Table 3 have positive medians for AUC and peak and negative medians for time-of-peak, indicating stronger and earlier target activation under CTQW. These effects are precisely the kind of transient amplification predicted by our sufficient conditions (Proposition 2). Threshold-based and first-hitting metrics are less diagnostic when targets remain below strict thresholds; detailed values for those measures are therefore reported in [29] rather than emphasized here.
On open-ended AUs, where no single target exists, CTQW exhibits broader and deeper exploration over the same time budget. The summary in Table 4 shows positive median deltas for mean entropy, coverage, and expected radius, and negative deltas for time to a deep layer, indicating that CTQW spreads diversity more widely and reaches distant regions faster than CRW. Together, these findings link the formal notion of interference-enabled amplification to observable advantages in both target-centric (Candle and RAT) and AU settings.
All the CTQW–CRW comparisons were performed on identical graphs with identical initial states and matched time grids (Section 8.1). We also normalized horizons via the operator spectral radius (autoT), reducing spurious scale differences across instances. Hence, the observed gains are not attributable to graph size or trivial timing choices; rather, they emerge when—per our analysis—the topology supports constructive phase alignment along multiple paths.
First, Candle is a single-graph demonstration; we therefore treat it as qualitative evidence, with quantitative strength coming from RAT (paired across 20 triads) and aggregated AU sources. Second, thresholded metrics (time-to-threshold; first-hitting) can underreport quantum advantages when activation remains below preset levels; extended tables in [29] document these cases. Third, ConceptNet-derived subgraphs inherit biases from the source resource (edge types; coverage). Future work should replicate additional semantic networks and psycholinguistic association norms. Finally, while we established robustness across generators (normalized adjacency and normalized Laplacian with small ), effect sizes can vary with operator choice and local spectral structure—an expected consequence of the phase geometry emphasized in our propositions.
The consistent advantages of CTQW on AUC/peak/timing (single-solution tasks) and exploration breadth/depth (AUs) suggest a common mechanism: interference distributes, and then selectively re-concentrates, probability mass in a way that diffusion alone cannot. This yields two testable predictions for human cognition: (i) when restructuring succeeds, activation of the correct solution should exhibit sharper and earlier peaks relative to closely matched control conditions; and (ii) in open-ended ideation, the early-time diversity and reach of candidate ideas should be higher under contexts that encourage superposed (rather than serial) processing modes.
The immediate avenues include (i) extending the analyses to empirically curated networks (e.g., word-association norms) to improve ecological validity; (ii) hybrid classical–quantum models, where diffusion sets a baseline and interference modulates context-dependent leaps; (iii) measurement protocols (readout frequency/strength) and open-system variants to emulate attentional collapse and noise; and (iv) behavioral studies designed to track time-resolved activation patterns against our model’s predictions. On the computational side, our formulation offers a clear path to carefully controlled ablations (path multiplicity; spectral overlaps) that can further connect the theorems to the effect sizes observed in Table 2, Table 3 and Table 4.
Author Contributions
Conceptualization, A.P. and S.F.; methodology, A.P. and S.F.; software, A.P. and S.F.; validation, A.P. and S.F.; formal analysis, A.P. and S.F.; investigation, A.P. and S.F.; resources, A.P. and S.F.; data curation, A.P. and S.F.; writing—original draft, A.P. and S.F.; writing—review and editing, A.P. and S.F.; visualization, A.P. and S.F.; supervision, A.P. and S.F.; project administration, A.P. and S.F.; funding acquisition, A.P. and S.F. All authors have read and agreed to the published version of the manuscript.
Funding
Simone Faro is supported by the National Centre for HPC, Big Data and Quantum Computing, Project CN00000013, affiliated with Spoke 10, co-funded by the European Union-NextGenerationEU. Arianna Pavone is supported by PNRR project ITSERR—Italian Strengthening of the ESFRI RI RESILIENCE.
Data Availability Statement
The data presented in this study are openly available in 1. Simulating the Candle Problem with Quantum Walks at https://colab.research.google.com/drive/1mBfkXOBIrES3DZ3Je8__vTsCGKuEWidV?usp=sharing (accessed on 25 July 2025) [23]; 2. Modeling the Emergence of Insight via Quantum Interference on Semantic Graphs at https://www.ariannapavone.com/semantic_khop_pipeline/ (accessed on 25 July 2025) [29].
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Cognitive Interpretation: Emergence and Collapse
In the context of creative cognition, insight is often preceded by a phase of mental exploration during which multiple ideas, associations, or partial solutions coexist in a state of uncertainty or ambiguity. This cognitive condition—commonly experienced as a feeling of being “on the verge” of a solution—can be interpreted as a form of conceptual superposition, where various representational possibilities are simultaneously active at a subthreshold level [1,30].
Unlike classical symbolic models that assume a determinate search path or a single active hypothesis at each step [18], quantum-inspired frameworks allow for cognitive states to be represented as linear combinations of conceptual alternatives, each with an associated probability amplitude [6,22]. In this view, the mind does not hold one candidate idea at a time but rather navigates a space of coexisting potentials, shaped by both semantic structure and contextual modulation [1,31].
Such superposed conceptual states are inherently latent: they do not correspond to explicit conscious thoughts but rather form a distributed substrate of activation across the semantic network. This latent structure is sensitive to subtle relational patterns in the graph and evolves under the dynamics of interference, where amplitudes can constructively or destructively combine [32,33]. Crucially, the representation of ideas in this framework is not static or pre-formed but dynamically encoded as a weighted superposition of semantic possibilities that may or may not become actualized depending on contextual interactions.
This perspective aligns with phenomenological accounts of creativity, where the generation of insight is not the result of linear deduction or exhaustive search but a reconfiguration of latent knowledge into a coherent new form [19]. The superposition framework thus provides a formal means to capture the openness and indeterminacy of early-stage creative thinking—prior to the moment of recognition or problem resolution.
In the quantum walk model presented here, this superpositional structure emerges naturally from the system’s evolution. As the walk propagates over the semantic graph, amplitudes are distributed across multiple conceptual nodes, reflecting a cognitive state in which several candidate ideas are simultaneously entertained. The structure and connectivity of the graph modulate how these amplitudes accumulate or cancel, laying the groundwork for the eventual emergence of a dominant interpretation.
In quantum theory, the evolution of a system is governed by the linear superposition of probability amplitudes, which can interfere constructively or destructively depending on the phase relationships of the paths involved. In the cognitive domain, this principle provides a compelling mechanism for modeling the emergence of novel ideas that are not the result of direct incremental reasoning but rather indirect context-sensitive combination of latent associations [1,6].
Within our framework, the propagation of a conceptual quantum walk over a semantic graph leads to the accumulation of amplitudes on multiple nodes. Each possible path from the initial concept to a target node contributes an amplitude that may enhance or suppress the overall probability of activation for that node depending on its interference with other paths [32,34]. This dynamic departs fundamentally from classical spreading activation models, which treat paths as additive and context-independent [9,19].
Interference effects in the quantum model enable the emergence of semantically remote yet contextually relevant ideas—those that classical models would deem unreachable or improbable within a local search neighborhood. For example, in a semantic graph where the concept “unexpected solution” lies at a distance from the initial node “problem,” a quantum walk may yield a high activation probability for the former due to constructive interference, while the same node would be virtually unreachable via a classical random walk [35].
Crucially, the structure of the semantic graph and the relative weights of its edges encode the semantic and associative relationships among concepts. These features modulate the evolution of amplitudes over time, effectively shaping the interference pattern. Additionally, contextual information—such as task constraints, framing effects, or recent cognitive history—can be integrated into the system by modifying the initial state or the Hamiltonian operator, influencing the trajectory of activation in a manner analogous to quantum measurement biasing outcomes [6,14].
The amplitude-based dynamics yield a probability distribution over the conceptual space that is highly sensitive to both structural and contextual constraints. Rather than simulating a fixed sequence of ideas, the system evolves toward a set of cognitively plausible candidates, each weighted by the cumulative effect of quantum interference. This formalism captures not only the flexibility and unpredictability of creative ideation but also the internal coherence that often characterizes moments of insight—where an idea emerges as both surprising and appropriate within its context.
In this sense, interference serves not merely as a computational artifact but as a mechanism of cognitive selection by which the mind—modeled as a dynamical quantum system—amplifies semantically meaningful possibilities while suppressing irrelevant or incoherent alternatives. This process sets the stage for the final act of selection or “collapse”, which will be discussed in the following section.
Appendix A.1. The Cognitive Interpretation of Collapse
In quantum mechanics, measurement induces a collapse of the system’s wave function, selecting a single outcome from a superposition of possibilities. Although the precise mechanisms behind this process remain debated in physics, the mathematical notion of collapse provides a useful metaphor—and potentially a formal mechanism—for modeling the cognitive moment of insight [1,36].
Within our framework, collapse is not imposed externally but interpreted as the culmination of amplitude dynamics governed by the structure of the semantic graph and modulated by interference and context. The idea that “an insight occurs” corresponds to a sudden transition from a distributed state of conceptual uncertainty to a sharply localized state in which a previously latent idea becomes cognitively salient and subjectively experienced as a solution or revelation.
This perspective resonates with phenomenological accounts of insight as a discrete often affectively charged moment of reorganization or restructuring [25,26]. The transition is not necessarily the result of exhaustive search or linear reasoning but rather a convergence process in which certain nodes in the conceptual graph accumulate sufficient amplitude—due to constructive interference—to cross an implicit threshold for conscious access [19].
Importantly, collapse in this context does not imply determinism or finality. Rather, it reflects a context-sensitive actualization of one among many latent possibilities, where the selected idea is both shaped by and shapes the current cognitive landscape. In this view, insight is not an isolated event but the emergent output of a dynamic interplay between semantic structure, probabilistic dynamics, and contextual constraints.
Moreover, this approach captures the dual character of creative insight: its unexpectedness (emerging from non-local indirect interference patterns) and its appropriateness (amplified by coherent semantic trajectories). The collapse to a remote but contextually fitting node formalizes this duality within a unified probabilistic framework—offering a computational account of how novelty and relevance co-emerge in the creative process.
Thus, the notion of collapse serves not only as a metaphor but as a functional element in modeling how cognition resolves ambiguity and navigates conceptual complexity. It marks the point at which the exploratory dynamics of superposition and interference give rise to a stable reportable outcome: the idea that “makes sense” and completes the creative arc.
Appendix A.2. Insight as Non-Deterministic Emergence
Creative insight resists deterministic explanation. Even when a solution is eventually reached, the cognitive path that leads to it is rarely linear, repeatable, or predictable. Instead, insight often appears as a spontaneous surprising event—emerging from a complex interplay of associations, memory traces, and contextual cues. Capturing this character of non-deterministic emergence is a central goal of our quantum walk-based model.
Unlike rule-based symbolic frameworks or stochastic local search methods, our model does not rely on pre-defined heuristics or fixed evaluation criteria to guide exploration. Instead, the dynamics are encoded in the structure of the semantic graph and governed by the mathematical evolution of a quantum state. The outcome—i.e., the activated concept—is not selected by an external controller but emerges probabilistically through the internal dynamics of amplitude distribution, modulated by constructive and destructive interference [6,22].
This emergence is not arbitrary: it reflects both the global structure of the conceptual landscape and the contextual features embedded in the initial conditions or system parameters. The insight that “pops out” is not drawn at random but reflects a non-classical probability distribution shaped by semantic proximity, network topology, and contextual phase alignment [1,32]. In this sense, the model bridges the gap between predictive constraints and creative unpredictability.
Importantly, this approach aligns with a growing body of theoretical work suggesting that cognitive creativity arises not from deterministic computation but from interference-driven dynamics in which novel states emerge through a superpositional recombination of latent representations [14,36]. The probabilistic nature of quantum walks thus provides not only modeling convenience but a principled framework for understanding why insight feels both surprising and inevitable once achieved.
By treating insight as a contextual selection among dynamically evolving possibilities, our model accounts for the core phenomenological properties of creative cognition: the absence of stepwise derivation, the irreducibility to single-path search, and the sudden appearance of coherence. This positions quantum walks not just as computational abstractions but as process-level analogs of real mental dynamics involved in idea generation and problem restructuring.
This theoretical account sets the stage for our empirical validation: in the next section, we implement and simulate the behavior of quantum walks on structured semantic graphs, demonstrating how non-local activation and emergent conceptual focus can be instantiated within a computational framework.
References
- Gabora, L. Steps Toward Quantum Computational Creativity. In Proceedings of the 14th International Conference on Computational Creativity (ICCC 2023), Toronto, ON, Canada, 19–23 June 2023; AAAI Press: Washington, DC, USA, 2023; pp. 278–284. [Google Scholar]
- Jordanous, A.; Keller, B. Modelling creativity: Identifying key components through a corpus-based approach. PLoS ONE 2016, 11, e0162959. [Google Scholar] [CrossRef] [PubMed]
- Mannone, M.; Chella, A.; Pilato, G.; Seidita, V.; Vella, F.; Gaglio, S. Modeling Robotic Thinking and Creativity: A Classic–Quantum Dialogue. Mathematics 2024, 12, 642. [Google Scholar] [CrossRef]
- Simonton, D.K. Creative thought as blind-variation and selective-retention: Combinatorial models of exceptional creativity. Phys. Life Rev. 2010, 7, 156–179. [Google Scholar] [CrossRef] [PubMed]
- Kaufman, J.C.; Glăveanu, V.P. An Overview of Creativity Theories. In Creativity: An Introduction; Kaufman, J.C., Sternberg, R.J., Eds.; Cambridge University Press: Cambridge, UK, 2021; pp. 17–30. [Google Scholar]
- Busemeyer, J.R.; Bruza, P.D. Quantum Models of Cognition and Decision; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Colton, S.; Wiggins, G.A. Computational Creativity: The Final Frontier? In Proceedings of the 20th European Conference on Artificial Intelligence 2012, Montpellier, France, 27–31 August 2012; pp. 21–26. [Google Scholar]
- Pavone, A.; Plebe, A. How Neurons in Deep Models Relate with Neurons in the Brain. Algorithms 2021, 14, 272. [Google Scholar] [CrossRef]
- Mednick, S.A. The associative basis of the creative process. Psychol. Rev. 1962, 69, 220–232. [Google Scholar] [CrossRef] [PubMed]
- Sowden, P.T.; Pringle, A.; Gabora, L. The shifting sands of creative thinking: Connections to dual-process theory. Think. Reason. 2015, 21, 40–60. [Google Scholar] [CrossRef]
- Hélie, S.; Sun, R. Incubation, insight, and creative problem solving: A unified theory and a connectionist model. Psychol. Rev. 2010, 117, 994–1024. [Google Scholar] [CrossRef] [PubMed]
- Evans, J.S.B.T.; Stanovich, K.E. Dual-Process Theories of Higher Cognition: Advancing the Debate. Perspect. Psychol. Sci. 2013, 8, 223–241. [Google Scholar] [CrossRef] [PubMed]
- Beaty, R.E.; Kenett, Y.N. Associative thinking at the core of creativity. Trends Cogn. Sci. 2023, 27, 671–683. [Google Scholar] [CrossRef] [PubMed]
- Aerts, D. Quantum structure in cognition. J. Math. Psychol. 2009, 53, 314–348. [Google Scholar] [CrossRef]
- Pothos, E.M.; Busemeyer, J.R. Can quantum probability provide a new direction for cognitive modeling? Behav. Brain Sci. 2013, 36, 255–274. [Google Scholar] [CrossRef] [PubMed]
- Aerts, D.; Aerts, S.; Gabora, L. Experimental evidence for quantum structure in cognition. In Proceedings of the International Symposium on Quantum Interaction, Berlin, Germany, 25–27 March 2009; pp. 59–70. [Google Scholar]
- Miranda, E.R. (Ed.) Quantum Computer Music: Foundations, Methods and Advanced Concepts; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Newell, A. Human Problem Solving; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1972. [Google Scholar]
- Gabora, L. Revenge of the ‘neurds’: Characterizing creative thought in terms of the structure and dynamics of memory. Creat. Res. J. 2010, 22, 1–13. [Google Scholar] [CrossRef]
- Abbott, D.; Davies, P.C.W.; Pati, A.K. Quantum Aspects of Life; Particularly the Chapter by Bruza et al. on Quantum Models of Semantic Search; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Khrennikov, A. Ubiquitous Quantum Structure: From Psychology to Finance; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Aerts, D.; Broekaert, J.; Gabora, L.; Sozzo, S. Generalizing Prototype Theory: A Formal Quantum Framework. Front. Psychol. 2016, 7, 418. [Google Scholar] [CrossRef] [PubMed]
- Faro, S.; Pavone, A. Executable Notebook for “Simulating the Candle Problem with Quantum Walks”. Jupyter/Colab Notebook. Available online: https://colab.research.google.com/drive/1mBfkXOBIrES3DZ3Je8__vTsCGKuEWidV?usp=sharing (accessed on 25 July 2025).
- Duncker, K. On problem-solving. Psychol. Monogr. 1945, 58, i–113. [Google Scholar] [CrossRef]
- Smith, S.M. Fixation, Incubation, and Insight in Memory, Problem Solving, and Creativity. In The Creative Cognition Approach; Smith, S.M., Ward, T.B., Finke, R.A., Eds.; MIT Press: Cambridge, MA, USA, 1995; pp. 135–155. [Google Scholar]
- Ohlsson, S. Information-Processing Explanations of Insight and Related Phenomena. In Advances in the Psychology of Thinking; Keane, M.T., Gilhooly, K.J., Eds.; Harvester/Wheatsheaf: London, UK, 1992; Vol. 1, pp. 1–44. [Google Scholar]
- Knoblich, G.; Ohlsson, S.; Haider, H.; Rhenius, D. Constraint relaxation and chunk decomposition in insight problem solving. J. Exp. Psychol. Learn. Mem. Cogn. 1999, 25, 1534–1555. [Google Scholar] [CrossRef]
- Tenenbaum, J.B.; Kemp, C.; Griffiths, T.L.; Goodman, N.D. How to Grow a Mind: Statistics, Structure, and Abstraction. Science 2011, 331, 1279–1285. [Google Scholar] [CrossRef] [PubMed]
- Faro, S.; Pavone, A. Code and Data Repository for “Modeling the Emergence of Insight via Quantum Interference on Semantic Graphs”. Git Repository. Available online: https://www.ariannapavone.com/semantic_khop_pipeline/ (accessed on 25 July 2025).
- Gabora, L. Cognitive mechanisms underlying the creative process. In Proceedings of the C&C’02 4th Conference on Creativity & Cognition, Loughborough, UK, 13–16 October 2002; ACM: New York, NY, USA, 2002; pp. 126–133. [Google Scholar] [CrossRef]
- Gabora, L.; Aerts, D. Contextualizing concepts using a mathematical generalization of the quantum formalism. J. Exp. Theor. Artif. Intell. 2002, 14, 327–358. [Google Scholar] [CrossRef]
- Gabora, L.; Kitto, K. Toward a Quantum Theory of Humor. Front. Phys. 2017, 4, 53. [Google Scholar] [CrossRef]
- Bruza, P.; Kitto, K.; Nelson, D.; Mcevoy, C. Extracting Spooky-Activation-at-a-Distance from Considerations of Entanglement. In Proceedings of the QI ’09 3rd International Symposium on Quantum Interaction, Saarbrücken, Germany, 25–27 March 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 71–83. [Google Scholar] [CrossRef]
- Venegas-Andraca, S.E. Quantum walks: A comprehensive review. Quantum Inf. Process. 2012, 11, 1015–1106. [Google Scholar] [CrossRef]
- Portugal, R. Quantum Walks and Search Algorithms; Springer Publishing Company, Inc.: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Aerts, D.; Gabora, L.; Sozzo, S. Concepts and Their Dynamics: A Quantum-Theoretic Modeling of Human Thought. Top. Cogn. Sci. 2013, 5, 737–772. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).